经典四边形综合练习(附详细答案)

合集下载

中考数学真题解析_四边形综合题.(含答案)2

全国中考真题解析120考点汇编四边形综合题一、选择题1. （2011重庆江津区，10，4分）如图，四边形ABCD 中，AC ＝a ，BD ＝b ，且AC 丄BD ，顺次连接四边形ABCD 各边中点，得到四边形A 1B 1C 1D 1，再顺次连接四边形A 1B 1C 1D 1各边中点，得到四边形A 2B 2C 2D 2…，如此进行下去，得到四边形A n B n C n D n ．下列结论正确的有（）①四边形A 2B 2C 2D 2是矩形；②四边形A 4B 4C 4D 4是菱形；③四边形A 5B 5C 5D 5的周长是4a b +错误！未找到引用源。

④四边形A n B n C n D n 的面积是12n ab +错误！未找到引用源。

．A 、①②B 、②③C 、②③④D 、①②③④考点：三角形中位线定理；菱形的判定与性质；矩形的判定与性质。

专题：规律型。

分析：首先根据题意，找出变化后的四边形的边长与四边形ABCD 中各边长的长度关系规律，然后对以下选项作出分析与判断：①根据矩形的判定与性质作出判断；②根据菱形的判定与性质作出判断；③由四边形的周长公式：周长＝边长之和，来计算四边形A 5B 5C 5D 5 的周长；④根据四边形A n B n C n D n 的面积与四边形ABCD 的面积间的数量关系来求其面积．点评：本题主要考查了菱形的判定与性质、矩形的判定与性质及三角形的中位线定理（三角形的中位线平行于第三边且等于第三边的一半）．解答此题时，需理清菱形、矩形与平行四边形的关系．2. （2011重庆市，9，4分）如图，在平行四边形 ABCD 中(AB≠BC)，直线EF经过其对角线的交点O,且分别交AD 、BC 于点M 、N ，交BA 、DC 的延长线于点E 、F ，下列结论：①AO=BO ；②OE=OF ； ③△EAM ∽△EBN ；④△EAO ≌△CNO ，其中正确的是A. ①②B. ②③C. ②④D.③④考点：相似三角形的判定与性质；全等三角形的判定与性质；平行四边形的性质．分析：①根据平行四边形的对边相等的性质即可求得AO≠BO ，即可求得①错误； ②易证△AOE ≌△COF ，即可求得EO=FO ；③根据相似三角形的判定即可求得△EAM ∽△EBN ；④易证△EAO ≌△FCO ，而△FCO 和△CNO 不全等，根据全等三角形的传递性即可判定该选项错误．点评：本题考查了相似三角形的判定，考查了全等三角形对应边相等的性质，考查了平行四边形对边平行的性质，本题中求证△AOE ≌△COF 是解题的关键．3. （2010重庆，10，4分）如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( ) 9题图BA ．1B ．2C ．3D ．4 考点：翻折变换（折叠问题）；全等三角形的判定与性质；勾股定理分析：根据翻折变换的性质和正方形的性质可证△ABG ≌△AFG ；在直角△ECG 中，根据勾股定理可证BG =GC ；通过证明∠AGB =∠AGF =∠GFC =∠GCF ，由平行线的判定可得AG ∥CF ；由于S △FGC =S △GCE ﹣S △FEC ，求得面积比较即可．点评：本题综合性较强，考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，三角形的面积计算，有一定的难度．4. （2011山东省潍坊， 11，3分）己知直角梯形ABCD 中，AD ∥BC ．∠BCD=90°，BC=CD=2AD ，E 、F 分别是BC 、CD 边的中点．连接BF 、DF 交于点P ．连接CP 并延长交AB 于点Q ，连揍AF ，则下列结论不正确．．．的是( )． A ．CP 平分∠BCDB ．四边形ABED 为平行四边形C ，CQ 将直角梯形ABCD 分为面积相等的两部分D ．△ABF 为等腰三角形A B C DFEG10题图【考点】直角梯形；全等三角形的判定与性质；平行四边形的判定与性质．【专题】证明题；几何综合题．【分析】本题可用排除法证明，即证明A、B、D正确，C不正确；易证△BCF≌△DCE （SAS），得∠FBC=∠EDC，∴△BPE≌△DPF，∴BP=DP；∴△BPC≌△DPC，∴∠BCP=∠DCP，∴A正确；∵AD=BE且AB∥BE，所以，四边形ABED为平行四边形，B正确；∵BF=ED，AB=ED，∴AB=BF，即D正确；【点评】本题考查了等腰三角形、平行四边形和全等三角形的判定，熟记以上图形的性质，并能灵活运用其性质，是解答本题的关键，本题综合性较好．5.（2011•河池）如图，在平行四边形ABCD中，E为AB的中点，F为AD上一点，EF交AC于G，AF=2cm，DF=4cm，AG=3cm，则AC的长为（）A、9cmB、14cmC、15cmD、18cm考点：平行线分线段成比例；平行四边形的性质。

(完整版)四边形经典试题50题及答案

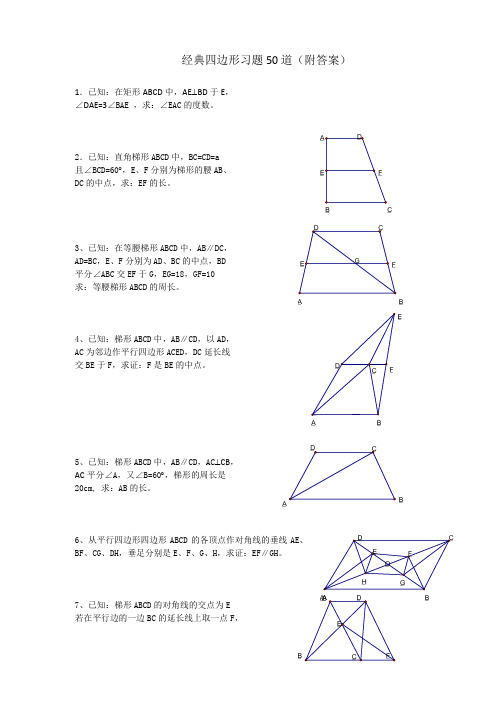
经典四边形习题50道（附答案）1．已知：在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE ，求：∠EAC的度数。

2．已知：直角梯形ABCD中，BC=CD=a且∠BCD=60︒，E、F分别为梯形的腰AB、DC的中点，求：EF的长。

3、已知：在等腰梯形ABCD中，AB∥DC，AD=BC，E、F分别为AD、BC的中点，BD平分∠ABC交EF于G，EG=18，GF=10求：等腰梯形ABCD的周长。

4、已知：梯形ABCD中，AB∥CD，以AD，AC为邻边作平行四边形ACED，DC延长线交BE于F，求证：F是BE的中点。

5、已知：梯形ABCD中，AB∥CD，AC⊥CB，AC平分∠A，又∠B=60︒，梯形的周长是20cm, 求：AB的长。

6、从平行四边形四边形ABCD的各顶点作对角线的垂线AE、BF、CG、DH，垂足分别是E、F、G、H，求证：EF∥GH。

7、已知：梯形ABCD的对角线的交点为E若在平行边的一边BC的延长线上取一点F，_B_C_A_B_A_B_E_A_B_B使S ABC ∆=S EBF ∆，求证：DF ∥AC 。

8、在正方形ABCD 中，直线EF 平行于对角线AC ，与边AB 、BC 的交点为E 、F ，在DA 的延长线上取一点G ，使AG=AD ，若EG 与DF 的交点为H ，求证：AH 与正方形的边长相等。

9、若以直角三角形ABC 的边AB 为边，在三角形ABC 的外部作正方形ABDE ，AF 是BC 边的高，延长FA 使AG=BC ，求证：BG=CD 。

10、正方形ABCD ，E 、F 分别是AB 、AD 延长线上的一点，且AE=AF=AC ，EF 交BC 于G ，交AC 于K ，交CD 于H ，求证：EG=GC=CH=HF 。

11、在正方形ABCD 的对角线BD 上，取BE=AB ，若过E 作BD 的垂线EF 交CD 于F ，求证：CF=ED 。

12、平行四边形ABCD 中，∠A 、∠D 的平分线相交于E ，AE 、DE与DC 、AB 延长线交于G 、F ，求证：AD=DG=GF=FA 。

经典三角形和四边形综合练习(附详细答案)

第六讲三角形和四边形（附详细答案）1.（2008龙岩）如图1，在Rt △ABC 中，∠CAB =90°，AD 是∠CAB 的平分线，tan B =21，则CD ∶DB = . 2.（2008宁德）如图2，将矩形纸ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，若EH ＝3厘米，EF ＝4厘米，则边AD 的长是_______厘米.3.（2008莆田）如图3，四边形ABCD 是一张矩形纸片，AD = 2AB ，若沿过点D 的折痕DE 将A 角翻折，使点A 落在BC 上的A 1处，则∠EA 1B=_________度.4．（2008厦门）如图4，为了测量电线杆的高度AB ，在离电线杆25米的D 处，用高1.20米的测角仪CD 测得电线杆顶端A 的仰角22α= ，求电线杆AB 的高．（精确到0.1米）参考数据：sin 220.3746=，cos 220.9272=，tan 220.4040= ，cot 22 2.4751= ．5.（2008三明）如图5，在△ABC 中，D 、E 分别是AB 、AC 的中点，BE=2DE ，延长DE 到点F ，使得EF=BE ，连接CF. （1）求证：四边形BCEF 是菱形；（2）若CE=4，∠BCF=130°，求菱形BCEF 的面积. 参考数据： tan 65°=2.15。

6.（2008南平）如图1，图2，图3，在ABC △中，分别以AB AC ，为边，向ABC △外作正三角形，正四边形，正五边形，BE CD ，相交于点O ．①如图1，求证：ABE ADC △≌△；②探究：如图1，BOC ∠= ；如图2，BOC∠= ；如图3，BOC ∠= ．（2）如图4，已知：AB AD ，是以AB 为边向ABC △外所作正n 边形的一组邻边；AC AE ，是以AC 为边向ABC △外所作正n 边形的一组邻边．BE CD ，的延长相交于点O ．①猜想：如图4，BOC ∠= （用含n 的式子表示）；②根据图4证明你的猜想．图1B E 图3图5ABE C Dα图47.（2008宁德）如图1，在正方形ABCD 中，E 是AB 上一点， F 是AD 延长线上一点，且DF ＝BE ． ⑴求证：CE ＝CF ；⑵在图1中，若G 在AD 上，且∠GCE ＝45°，则GE ＝BE ＋GD 成立吗？为什么？ ⑶运用⑴⑵解答中所积累的经验和知识，完成下题：如图2，在直角梯形ABCD 中，AD ∥BC （BC ＞AD ），∠B ＝90°，AB ＝BC ＝12， E 是AB 上一点，且∠DCE ＝45°，BE ＝4，求DE 的长．8.（2008泉州）在图6中，直线l 所对应的函数关系式为551+-=x y ，l 与y 轴交于点C ，O 为坐标原点。

2022年人教版中考数学一轮复习：四边形综合专项练习题2(Word版,含答案)

2022年人教版中考数学一轮复习：四边形综合专项练习题21．如图，已知四边形ABCD是平行四边形，从①AB＝AD，②AC＝BD，③∠ABC＝∠ADC中选择一个作为条件，补充后使四边形ABCD成为菱形，则其选择是（限填序号）．2．如图1，平行四边形纸片ABCD的面积为120，AD＝15．今沿两对角线将四边形ABCD剪成甲、乙．丙、丁四个三角形纸片．若将甲、丙合并（AD、CB重合）形成一个对称图形戊，如图2所示．则图形戊的两条对角线长度之和为．3．如图，菱形ABCD的两条对角线AC，BD交于点O，BE⊥AD于点E，若AC＝8，BD＝6，则BE的长为．4．如图，在▱ABCD中，∠A＝70°，DB＝DC，CE⊥BD于E，则∠BCE＝．5．如图，在菱形ABCD中，AB＝BD，点E、F分别在AB、AD上，且AE＝DF，连接BF与DE交于点H，若CG＝1，则S＝．四边形BCDG6．如图，正方形瓷砖图案是四个全等且顶角为45°的等腰三角形．已知该瓷砖的面积是1m2，则中间小正方形的面积为m2．7．如图所示，在Rt△ABC外作等边△ADE，点E在AB边上，AC＝5，∠ABC＝30°，AD＝3．将△ADE沿AB方向平移，得到△A′D′E′，连接BD′．给出下列结论：①AB＝10；②四边形ADD′A′为平行四边形；③AB平分∠D′BC；④当平移的距离为4时，BD′＝3．其中正确的是（填上所有正确结论的序号）．8．如图，菱形ABCD的对角线AC，BD相交于点O，P为AB边上一动点（不与点A，B重合），PE⊥OA于点E，PF⊥OB于点F，若AB＝4，∠BAD＝60°，则EF的最小值为．9．如图，在正方形ABCD中，点E为BC边上一点，且CE＝2BE，点F为对角线BD上一点，且BF＝2DF，连接AE交BD于点G，过点F作FH⊥AE于点H，若HG＝2cm，则正方形ABCD 的边长为cm．10．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．11．如图，在正方形ABCD内有一点P，若AP＝4，BP＝7，DP＝9，则∠APB的度数为．12．如图是两个边长分别为2a，a的正方形，则△ABC的面积是．13．如图，点P是正方形ABCD内一点，连接AP、BP、DP，若AP＝1，PD＝，∠APB＝135°，则正方形ABCD的面积为．14．如图，正三角形ABC与正方形CDEF的顶点B，C，D三点共线，动点P沿着CA由C向A 运动．连接EP，若AC＝10，CF＝8．则EP的最小值是．15．如图，正方形ABCD中，H为CD上一动点（不含C、D），连接AH交BD于G，过点G作GE⊥AH交BC于E，过E作EF⊥BD于F，连接AE，EH．下列结论：①AG＝EG；②∠EAH＝45°；③BD＝2GF；④GE平分∠FEC．正确的是（填序号）．16．如图，平面内三点A、B、C，AB＝4，AC＝3，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是．17．如图，在正方形ABCD中，点E在对角线AC上，EF⊥AB于点F，EG⊥BC于点G，连接FG，若AB＝8，则FG的最小值为．18．如图，正方形ABCD的边长为2，点E是BC的中点，连接AE与对角线BD交于点G，连接CG并延长，交AB于点F，连接DE交CF于点H，连接AH．以下结论：①CF⊥DE；②＝；③GH＝；④AD＝AH，其中正确结论的序号是．19．如图，矩形ABCD中，对角线AC、BD交于点O，AE⊥BD于E，若∠DAE＝3∠BAE．则的值为．20．将矩形ABCD按如图所示的方式折叠，BE、EG、FG为折痕，若顶点A、C、D都落在点O 处，且点B、O、G在同一条直线上，同时点E、O、F在另一条直线上．（1）的值为．（2）若AD＝4，则四边形BEGF的面积为．参考答案1．解：①∵四边形ABCD是平行四边形，AB＝AD，∴平行四边形ABCD是菱形；②∵四边形ABCD是平行四边形，AC＝BD，∴平行四边形ABCD是矩形；③∵四边形ABCD是平行四边形，∴∠ABC＝∠ADC，因此∠ABC＝∠ADC时，四边形ABCD还是平行四边形；故答案为：①．2．解：如图，连接AD、EF，则可得对角线EF⊥AD，且EF与平行四边形的高相等．∵平行四边形纸片ABCD的面积为120，AD＝1520，∴BC＝AD＝15，EF×AD＝×120，∴EF＝8，又BC＝15，∴则图形戊中的四边形两对角线之和为20+3＝23，故答案为23．3．解：∵四边形ABCD是菱形，∴AO＝CO＝4，BO＝DO＝3，AC⊥BD，∴AD＝＝＝5，＝AD×BE＝×AC×BD，∵S菱形ABCD∴BE＝，故答案为：．4．解：∵四边形ABCD是平行四边形，∴∠BCD＝∠A＝70°，∵DB＝DC，∴∠DBC＝∠BCD＝70°，∵CE⊥BD，∴∠CEB＝90°，∴∠BCE＝20°．故答案为：20°．5．解：过点C作CM⊥GB于M，CN⊥GD，交GD的延长线于N．∵四边形ABCD为菱形，∴AB＝AD＝CD＝BC，∵AB＝BD，∴AB＝BD＝AD＝CD＝BC，∴△ABD为等边三角形，△BCD是等边三角形，∴∠A＝∠BDF＝60°，∠ADC＝60°，在△ADE和△DBF中，，∴△ADE≌△DBF（SAS），∴∠ADE＝∠DBF，∵∠FBC ＝60°+∠DBF ，∠NDC ＝180°﹣（120°﹣∠ADE ）＝60°+∠ADE ，∴∠NDC ＝∠FBC ，在△CDN 和△CBM 中，，∴△CDN ≌△CBM （AAS ），∴CM ＝CN ，在Rt △CBM 与Rt △CDN 中，，∴Rt △CBM ≌Rt △CDN （HL ），∴S 四边形BCDG ＝S 四边形CMGN ．S 四边形CMGN ＝2S △CMG ，∵∠CGM ＝60°，∴GM ＝CG ＝，CM ＝CG ＝，∴S 四边形BCDG ＝S 四边形CMGN ＝2S △CMG ＝2×××＝，故答案为：．6．解：如图，作大正方形的对角线，作小正方形的对角线并延长交大正方形各边于中点，设小正方形的边长为xm ，则大正方形的边长为x +x x ＝（1）xm ， ∵瓷砖的面积是1m 2，∴大正方形的边长为1m ，即（1）x ＝1，解得x ＝﹣1， ∴中间小正方形的面积为（）2＝3﹣2，故答案为：3﹣2．7．解：∵∠ACB＝90°，AC＝5，∠ABC＝30°，∴AB＝2AC＝10，故①正确；由平移的性质得：A'D'＝AD，A'D'∥AD，∴四边形ADD′A′为平行四边形，故②正确；当平移的距离为4时，EE'＝4，∴BE'＝AB﹣AE﹣EE'＝10﹣3﹣4＝3，由平移的性质得：∠A'D'E'＝∠A'E'D'＝∠AED＝60°，A'D'＝D'E'＝DE＝AD＝3，∴BE'＝D'E'，∴∠E'BD'＝∠E'D'B＝∠A'E'D'＝30°，∴∠A'D'B＝60°+30°＝90°，∴BD'＝A'D'＝3，故④正确；由④得：当平移的距离为4时，∠E'BD'＝∠ABC＝30°，故③错误；故答案为：①②④．8．解：连接OP，∵四边形ABCD是菱形，∴AC⊥BD，∠CAB＝DAB＝30°，∵PE⊥OA于点E，PF⊥OB于点F，∴∠EOF＝∠OEP＝∠OFP＝90°，∴四边形OEPF是矩形，∴EF＝OP，∵当OP取最小值时，EF的值最小，∴当OP⊥AB时，OP最小，∵AB＝4，∴OB＝AB＝2，OA＝AB＝2，∴S＝OA•OB＝AB•OP，△ABO∴OP＝＝，∴EF的最小值为，故答案为：．9．解：如图，过F作FI⊥BC于I，连接FE，FA，∴FI∥CD，∵CE＝2BE，BF＝2DF，∴设BE＝EI＝IC＝a，CE＝FI＝2a，AB＝3a，∴则FE＝FC＝FA＝a，∴H为AE的中点，∴AH＝HE＝AE＝a，∴AG＝AH+GH＝a+2，∵四边形ABCD是正方形，∴BE∥AD，∴＝＝，∴GE＝AG＝（a+2），∵GE＝HE﹣GH＝a﹣2，∴（a+2）＝a﹣2，解得，a＝，∴AB＝3a＝．故答案为：．10．解：设图1中分成的直角三角形的长直角边为a，短直角边为b，，得，∴图1中菱形的面积为：×4＝48，故答案为48．11．解：∵四边形ABCD为正方形，∴∠ABC＝90°，BA＝BC，∴△BAP绕点A逆时针旋转90°可得△ADE，连接PE，由旋转的性质得，ED＝BP＝7，AE＝AP＝4，∠PBE＝90°，∠AED＝∠APB，∴△APE为等腰直角三角形，∴PE＝AP＝4，∠AEP＝45°，在△PED中，∵PD＝9，ED＝7，PE＝4，∴DE2+PE2＝DP2，∴△PED为直角三角形，∠PED＝90°，∴∠AED＝90°+45°＝135°，∴∠APB＝135°，故答案为：135°．12．解：∵两个正方形的边长分别为2a，a，∴△ABC的的高为：2a+a，底边为：BC＝a，∴△ABC的面积是：（2a+a）•a＝a2．故答案为：a2．13．解：如图，将△APB绕点A逆时针旋转90°得到△AHD，连接PH，过点A作AE⊥DH交DH的延长线于E，∴△APB≌△AHD，∠PAH＝90°，∴PB＝DH，AP＝AH＝1，∠APB＝∠AHD＝135°，∴PH＝AP＝，∠APH＝∠AHP＝45°，∴∠PHD＝90°，∴DH＝＝＝2，∵∠AHD＝135°，∴∠AHE＝45°，∵AE⊥DH，∴∠AHE＝∠HAE＝45°，∴AE＝EH，AH＝AE，∴AE＝EH＝，∴DE＝，∵AD2＝AE2+DE2＝13，∴正方形的面积为13，故答案为：13．14．解：如图，过点E作EP⊥AC，交FC于点G，当EP⊥AC时，EP取得最小值，∵正三角形ABC与正方形CDEF的顶点B，C，D三点共线，∴∠ACB＝60°，∠FCD＝90°，∴∠ACF＝30°，∴∠CGP＝∠EGF＝60°，∵∠F＝90°，∴∠FEG＝30°，设PG＝x，则CG＝2x，∴FG＝CF﹣CG＝8﹣2x，∴EG＝2FG＝2（8﹣2x），∵FG＝EF，∴8﹣2x＝8×，∴x＝4﹣，∴EP＝EG+PG＝2（8﹣2x）+x＝16﹣3x＝4+4．故答案为：4+4．15．解：连接GC，延长EG交AD于点L，∵四边形ABCD为正方形，∴AD∥CB，AD＝CD，∠ADG＝∠CDG＝45°，∵DG＝DG，∴△ADG≌△CDG（SAS），∴AG＝GC，∠HCG＝∠DAG，∵∠HCG+∠GCB＝90°，∴∠DAG+∠GCB＝90°，∵GE⊥AH，∴∠AGL＝90°，∴∠ALG+∠LAG＝90°，∵AD∥CB，∴∠ALG＝∠GEC，∴∠GEC+∠LAG＝90°，∴∠GEC＝∠GCE，∴GE＝GC，∴AG＝EG，故①正确；∵GE⊥AH，∴∠AGE＝90°，∵AG＝EG，∴∠EAH＝45°，故②正确；连接AC交BD于点O，则BD＝2OA，∵∠AGF+∠FGE＝∠GEF+∠EGF＝90°，∴∠AGF＝∠GEF，∵AG＝GE，∠AOG＝∠EFG＝90°，∴△AOG≌△GFE（AAS），∴OA＝GF，∵BD＝2OA，∴BD＝2GF，故③正确．过点G作MN⊥BC于点N，交AD于点M，交BC于点N，∵G是动点，∴GN的长度不确定，而FG＝OA是定值，∴GE不一定平分∠FEC，故④错误；故答案为：①②③．16．解：将△ABD绕点D顺时针旋转90°，得△MCD，如图：由旋转不变性可得：CM＝AB＝4，AD＝MD，且∠ADM＝90°，∴△ADM是等腰直角三角形，∴AD＝AM，AD最大，只需AM最大，而在△ACM中，AM＜AC+CM，∴当且仅当A、C、M在一条直线上，即不能构成△ACM时，AM最大，且最大值为AC+CM ＝AC+AB＝7，此时AD＝AM＝，故答案为：．17．解：连接BE，如图：∵四边形ABCD是正方形，∴∠ABC＝90°，又EF⊥AB于点F，EG⊥BC，∴四边形FBGE是矩形，∴FG＝BE，所以当BE最小时，FG就最小，根据垂线段最短，可知当BE⊥AC时，BE最小，当BE⊥AC时，在正方形ABCD中，△AEB是等腰直角三角形，在Rt△ABE中，根据勾股定理可得2BE2＝AB2＝64，解得BE＝4，∴FG最小为4；故答案为4．18．解：∵四边形ABCD是边长为2的正方形，点E是BC的中点，∴AB＝AD＝BC＝CD＝2，BE＝CE＝，∠DCE＝∠ABE＝90°，∠ABD＝∠CBD＝45°，∴△ABE≌△DCE（SAS），∴∠CDE＝∠BAE，DE＝AE，∵AB＝BC，∠ABG＝∠CBG，BG＝BG，∴△ABG≌△CBG（SAS），∴∠BAE＝∠BCF，∴∠BCF＝∠CDE，又∵∠CDE+∠CED＝90°，∴∠BCF+∠CED＝90°，∴∠CHE＝90°，∴CF⊥DE，故①正确；∵CD＝2，CE＝，由勾股定理得，DE＝＝＝5，＝CD×CE＝DE×CH，∵S△DCE∴CH＝2，∵∠CHE＝∠CBF，∠BCF＝∠ECH，∴△ECH∽△FCB，∴＝，∴＝，∴CF＝5，∴HF＝CF﹣CH＝3，∴＝，故②正确；如图，过点A作AM⊥DE于点M，∵DC＝2，CH＝2，由勾股定理得，DH＝＝＝4，∵∠CDH+∠ADM＝90°，∠DAM+∠ADM＝90°，∴∠CDH＝∠DAM，又∵AD＝CD，∠CHD＝∠AMD＝90°，∴△ADM≌△DCH（AAS），∴CH＝DM＝2，AM＝DH＝4，∴MH＝DM＝2，又∵AM⊥DH，∴AD＝AH，故④正确；∵DE＝5，DH＝4，∴HE＝1，∴ME＝HE+MH＝3，∵AM⊥DE，CF⊥DE，∴∠AME＝∠GHE，∵∠HEG＝∠MEA，∴△MEA∽△HEG，∴＝，∴＝，∴HG＝，故③错误．综上，正确的有：①②④．故答案为：①②④．19．解：∵四边形ABCD是矩形，∴∠BAD＝90°，OA＝AC，OB＝BD，AC＝BD，∴OA＝OB，∴∠OAB＝∠OBA，∵∠DAE＝3∠BAE，∴∠BAE＝×90°＝22.5°，∵AE⊥BD，∴∠OAB＝∠OBA＝90°﹣22.5°＝67.5°，∴∠OAE＝67.5°﹣22.5°＝45°，∴△AOE是等腰直角三角形，∴OA＝OE，设OE＝a，则OB＝OA＝a，∴BE＝OB﹣OE＝（﹣1）a，BD＝2OB＝2a，∴DE＝BD﹣BE＝2a﹣（﹣1）a＝（+1）a，∴＝＝，故答案为：．20．解：（1）由折叠可得，AE＝OE＝DE，CG＝OG＝DG，∴E，G分别为AD，CD的中点，设CD＝2a，AD＝2b，则AB＝OB＝2a，DG＝OG＝CG＝a，BG＝3a，BC＝AD＝2b，∵∠C＝90°，在Rt△BCG中，CG2+BC2＝BG2，∴a2+（2b）2＝（3a）2，∴b＝a，∴＝＝＝，由折叠可得：∠ABE＝∠EBG，∠AEB＝∠BEO，∠DEG＝∠GEO，∵∠AEB＝∠BEO+∠DEG＝∠GEO＝180°，∴∠BEG＝90°，∵∠A＝∠BEG＝90°，∠ABE＝∠EBG，∴△ABE∽△EBG，∴＝＝，故答案为：；（2）∵AD＝BC＝2b＝4，∴b＝2，a＝2，∴AB＝OB＝4，CG＝2，AE＝OE＝2，∴BG＝6，∵∠OBF ＝∠CBG ，由折叠可得∠BOF ＝∠BCG ＝90°， ∴△BOF ∽△BCG ， ∴＝，即＝，∴OF ＝，∴S 四边形EBFG ＝S △BEG +S △BFG ＝×6×2+×6×＝9．故答案为：9．。

2019年全国各地中考真题压轴题精选：四边形综合(带答案解析)

四边形综合题一．选择题（共1小题）1．（2019•连云港）如图，利用一个直角墙角修建一个梯形储料场ABCD ，其中∠C ＝120°．若新建墙BC 与CD 总长为12m ，则该梯形储料场ABCD 的最大面积是（）A ．18m 2B ．18√3m 2C ．24√3m 2D ．45√32m 2 二．填空题（共2小题）2．（2019•日照）规定：在平面直角坐标系xOy 中，如果点P 的坐标为（a ，b ），那么向量OP→可以表示为：OP →=（a ，b ），如果OA →与OB →互相垂直，OA →=（x 1，y 1），OB →=（x 2，y 2），那么x 1x 2+y 1y 2＝0．若OM →与ON →互相垂直，OM →=（sin α，1），ON →=（2，−√3），则锐角∠α＝．3．（2019•上海）如图，在正六边形ABCDEF 中，设BA →=a →，BC →=b →，那么向量BF →用向量a →、b →表示为．三．解答题（共38小题）4．（2019•抚顺）如图，点E ，F 分别在正方形ABCD 的边CD ，BC 上，且DE ＝CF ，点P在射线BC 上（点P 不与点F 重合）．将线段EP 绕点E 顺时针旋转90°得到线段EG ，过点E 作GD 的垂线QH ，垂足为点H ，交射线BC 于点Q ．（1）如图1，若点E 是CD 的中点，点P 在线段BF 上，线段BP ，QC ，EC 的数量关系为．（2）如图2，若点E 不是CD 的中点，点P 在线段BF 上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由．（3）正方形ABCD的边长为6，AB＝3DE，QC＝1，请直接写出线段BP的长．5．（2019•盘锦）如图，四边形ABCD是菱形，∠BAD＝120°，点E在射线AC上（不包括点A和点C），过点E的直线GH交直线AD于点G，交直线BC于点H，且GH∥DC，点F在BC的延长线上，CF＝AG，连接ED，EF，DF．（1）如图1，当点E在线段AC上时，①判断△AEG的形状，并说明理由．②求证：△DEF是等边三角形．（2）如图2，当点E在AC的延长线上时，△DEF是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由．6．（2019•朝阳）如图，四边形ABCD是正方形，连接AC，将△ABC绕点A逆时针旋转α得△AEF，连接CF，O为CF的中点，连接OE，OD．（1）如图1，当α＝45°时，请直接写出OE与OD的关系（不用证明）．（2）如图2，当45°＜α＜90°时，（1）中的结论是否成立？请说明理由．（3）当α＝360°时，若AB＝4√2，请直接写出点O经过的路径长．7．（2019•鄂尔多斯）（1）【探究发现】如图1，∠EOF的顶点O在正方形ABCD两条对角线的交点处，∠EOF＝90°，将∠EOF 绕点O旋转，旋转过程中，∠EOF的两边分别与正方形ABCD的边BC和CD交于点E 和点F（点F与点C，D不重合）．则CE，CF，BC之间满足的数量关系是．（2）【类比应用】如图2，若将（1）中的“正方形ABCD”改为“∠BCD＝120°的菱形ABCD”，其他条件不变，当∠EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由．（3）【拓展延伸】如图3，∠BOD＝120°，OD=34，OB＝4，OA平分∠BOD，AB=√13，且OB＞2OA，点C是OB上一点，∠CAD＝60°，求OC的长．8．（2019•湘潭）如图一，在射线DE的一侧以AD为一条边作矩形ABCD，AD＝5√3，CD ＝5，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求∠CAD的大小；（2）问题探究：动点M在运动的过程中，①是否能使△AMN为等腰三角形，如果能，求出线段MC的长度；如果不能，请说明理由．②∠MBN的大小是否改变？若不改变，请求出∠MBN的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M运动到AC的中点时，AM与BN的交点为F，MN的中点为H，求线段FH的长度．9．（2019•娄底）如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA（不包括端点）上运动，且满足AE＝CG，AH＝CF．（1）求证：△AEH≌△CGF；（2）试判断四边形EFGH的形状，并说明理由．（3）请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．10．（2019•陕西）问题提出：（1）如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；问题探究：（2）如图2，在矩形ABCD中，AB＝4，BC＝10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；问题解决：（3）如图3，有一座塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的景区BCDE．根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）11．（2019•贵阳）（1）数学理解：如图①，△ABC是等腰直角三角形，过斜边AB的中点D 作正方形DECF，分别交BC，AC于点E，F，求AB，BE，AF之间的数量关系；（2）问题解决：如图②，在任意直角△ABC内，找一点D，过点D作正方形DECF，分别交BC，AC于点E，F，若AB＝BE+AF，求∠ADB的度数；（3）联系拓广：如图③，在（2）的条件下，分别延长ED，FD，交AB于点M，N，求MN，AM，BN的数量关系．12．（2019•通辽）如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时旋转90°，得到线段CQ，连接BP，DQ．（1）如图1，求证：△BCP≌△DCQ；（2）如图，延长BP交直线DQ于点E．①如图2，求证：BE⊥DQ；②如图3，若△BCP为等边三角形，判断△DEP的形状，并说明理由．13．（2019•吉林）如图，在矩形ABCD中，AD＝4cm，AB＝3cm，E为边BC上一点，BE ＝AB，连接AE．动点P、Q从点A同时出发，点P以√2cm/s的速度沿AE向终点E运动；点Q以2cm/s的速度沿折线AD﹣DC向终点C运动．设点Q运动的时间为x（s），在运动过程中，点P，点Q经过的路线与线段PQ围成的图形面积为y（cm2）．（1）AE＝cm，∠EAD＝°；（2）求y关于x的函数解析式，并写出自变量x的取值范围；（3）当PQ=54cm时，直接写出x的值．14．（2019•长春）如图，在Rt△ABC中，∠C＝90°，AC＝20，BC＝15．点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿射线CB运动，它们的速度均为每秒5个单位长度，点P到达终点时，P、Q同时停止运动．当点P不与点A、C重合时，过点P作PN⊥AB于点N，连结PQ，以PN、PQ为邻边作▱PQMN．设▱PQMN与△ABC重叠部分图形的面积为S，点P的运动时间为t秒．（1）①AB的长为；②PN的长用含t的代数式表示为．（2）当▱PQMN为矩形时，求t的值；（3）当▱PQMN与△ABC重叠部分图形为四边形时，求S与t之间的函数关系式；（4）当过点P且平行于BC的直线经过▱PQMN一边中点时，直接写出t的值．15．（2019•吉林）性质探究如图①，在等腰三角形ABC中，∠ACB＝120°，则底边AB与腰AC的长度之比为．理解运用（1）若顶角为120°的等腰三角形的周长为8+4√3，则它的面积为；（2）如图②，在四边形EFGH中，EF＝EG＝EH．①求证：∠EFG+∠EHG＝∠FGH；②在边FG，GH上分别取中点M，N，连接MN．若∠FGH＝120°，EF＝10，直接写出线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为（用含α的式子表示）．16．（2019•常州）【阅读】数学中，常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．“算两次”也称做富比尼原理，是一种重要的数学思想．【理解】（1）如图1，两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形．用两种不同的方法计算梯形的面积，并写出你发现的结论；（2）如图2，n行n列的棋子排成一个正方形，用两种不同的方法计算棋子的个数，可得等式：n2＝；【运用】（3）n边形有n个顶点，在它的内部再画m个点，以（m+n）个点为顶点，把n边形剪成若干个三角形，设最多可以剪得y个这样的三角形．当n＝3，m＝3时，如图3，最多可以剪得7个这样的三角形，所以y＝7．①当n＝4，m＝2时，如图4，y＝；当n＝5，m＝时，y＝9；②对于一般的情形，在n边形内画m个点，通过归纳猜想，可得y＝（用含m、n的代数式表示）．请对同一个量用算两次的方法说明你的猜想成立．17．（2019•鸡西）如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，AB、BC的长分别是一元二次方程x2﹣7x+12＝0的两个根（BC＞AB），OA＝2OB，边CD交y轴于点E，动点P以每秒1个单位长度的速度，从点E出发沿折线段ED﹣DA向点A运动，运动的时间为t（0≤t＜6）秒，设△BOP与矩形AOED重叠部分的面积为S．（1）求点D的坐标；（2）求S关于t的函数关系式，并写出自变量的取值范围；（3）在点P的运动过程中，是否存在点P，使△BEP为等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由．18．（2019•舟山）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝a，AD＝h，求正方形PQMN的边长（用a，h表示）．（2）操作：如何画出这个正方形PQMN呢？如图2，小波画出了图1的△ABC，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在AB上任取一点P'，画正方形P'Q'M'N'，使点Q'，M'在BC边上，点N'在△ABC 内，然后连结BN'，并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：小波把图2中的线段BN称为“波利亚线”，在该线上截取NE＝NM，连结EQ，EM（如图3），当∠QEM＝90°时，求“波利亚线”BN的长（用a，h表示）．请帮助小波解决“温故”、“推理”、“拓展”中的问题．19．（2019•海南）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点（与点A 、D 不重合），射线PE 与BC 的延长线交于点Q ．（1）求证：△PDE ≌△QCE ；（2）过点E 作EF ∥BC 交PB 于点F ，连结AF ，当PB ＝PQ 时，①求证：四边形AFEP 是平行四边形；②请判断四边形AFEP 是否为菱形，并说明理由．20．（2019•益阳）如图，在平面直角坐标系xOy 中，矩形ABCD 的边AB ＝4，BC ＝6．若不改变矩形ABCD 的形状和大小，当矩形顶点A 在x 轴的正半轴上左右移动时，矩形的另一个顶点D 始终在y 轴的正半轴上随之上下移动．（1）当∠OAD ＝30°时，求点C 的坐标；（2）设AD 的中点为M ，连接OM 、MC ，当四边形OMCD 的面积为212时，求OA 的长；（3）当点A 移动到某一位置时，点C 到点O 的距离有最大值，请直接写出最大值，并求此时cos ∠OAD 的值．21．（2019•天水）如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD 中，AB ＝AD ，CB ＝CD ，问四边形ABCD 是垂美四边形吗？请说明理由；（2）性质探究：如图1，四边形ABCD 的对角线AC 、BD 交于点O ，AC ⊥BD ．试证明：AB 2+CD 2＝AD 2+BC 2；（3）解决问题：如图3，分别以Rt △ACB 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ，连结CE 、BG 、GE ．已知AC ＝4，AB ＝5，求GE 的长．22．（2019•无锡）如图1，在矩形ABCD中，BC＝3，动点P从B出发，以每秒1个单位的速度，沿射线BC方向移动，作△P AB关于直线P A的对称△P AB′，设点P的运动时间为t（s）．（1）若AB＝2√3．①如图2，当点B′落在AC上时，显然△P AB′是直角三角形，求此时t的值；②是否存在异于图2的时刻，使得△PCB′是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．（2）当P点不与C点重合时，若直线PB′与直线CD相交于点M，且当t＜3时存在某一时刻有结论∠P AM＝45°成立，试探究：对于t＞3的任意时刻，结论“∠P AM＝45°”是否总是成立？请说明理由．23．（2019•岳阳）操作体验：如图，在矩形ABCD中，点E、F分别在边AD、BC上，将矩形ABCD沿直线EF折叠，使点D恰好与点B重合，点C落在点C′处．点P为直线EF 上一动点（不与E、F重合），过点P分别作直线BE、BF的垂线，垂足分别为点M和N，以PM、PN为邻边构造平行四边形PMQN．（1）如图1，求证：BE＝BF；（2）特例感知：如图2，若DE＝5，CF＝2，当点P在线段EF上运动时，求平行四边形PMQN的周长；（3）类比探究：若DE＝a，CF＝b．①如图3，当点P在线段EF的延长线上运动时，试用含a、b的式子表示QM与QN之间的数量关系，并证明；②如图4，当点P在线段FE的延长线上运动时，请直接用含a、b的式子表示QM与QN之间的数量关系．（不要求写证明过程）24．（2019•盐城）如图①是一张矩形纸片，按以下步骤进行操作：（Ⅰ）将矩形纸片沿DF折叠，使点A落在CD边上点E处，如图②；（Ⅱ）在第一次折叠的基础上，过点C再次折叠，使得点B落在边CD上点B′处，如图③，两次折痕交于点O；（Ⅲ）展开纸片，分别连接OB、OE、OC、FD，如图④．【探究】（1）证明：△OBC≌△OED；（2）若AB＝8，设BC为x，OB2为y，求y关于x的关系式．25．（2019•苏州）已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2√5cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为cm/s，BC的长度为cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N 的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．26．（2019•资阳）在矩形ABCD中，连结AC，点E从点B出发，以每秒1个单位的速度沿着B→A→C的路径运动，运动时间为t（秒）．过点E作EF⊥BC于点F，在矩形ABCD 的内部作正方形EFGH．（1）如图，当AB＝BC＝8时，①若点H在△ABC的内部，连结AH、CH，求证：AH＝CH；②当0＜t≤8时，设正方形EFGH与△ABC的重叠部分面积为S，求S与t的函数关系式；（2）当AB＝6，BC＝8时，若直线AH将矩形ABCD的面积分成1：3两部分，求t的值．27．（2019•宁波）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD 上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF 交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．28．（2019•衡阳）如图，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E，连接PQ交AC边于D．以CQ、CE为边作平行四边形CQFE．（1）当t为何值时，△BPQ为直角三角形；（2）是否存在某一时刻t，使点F在∠ABC的平分线上？若存在，求出t的值，若不存在，请说明理由；（3）求DE的长；（4）取线段BC的中点M，连接PM，将△BPM沿直线PM翻折，得△B′PM，连接AB′，当t为何值时，AB'的值最小？并求出最小值．29．（2019•绵阳）如图，在以点O为中心的正方形ABCD中，AD＝4，连接AC，动点E从点O出发沿O→C以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，△ADE的外接圆交AB于点F，连接DF交AC于点G，连接EF，将△EFG沿EF翻折，得到△EFH．（1）求证：△DEF是等腰直角三角形；（2）当点H恰好落在线段BC上时，求EH的长；（3）设点E运动的时间为t秒，△EFG的面积为S，求S关于时间t的关系式．30．（2019•扬州）如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G不重合），在运动过程中始终保持线段PQ ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a 的取值范围．31．（2019•泰州）如图，线段AB＝8，射线BG⊥AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP＝∠BAP，直线CE与线段AB相交于点F（点F与点A、B不重合）．（1）求证：△AEP≌△CEP；（2）判断CF与AB的位置关系，并说明理由；（3）求△AEF的周长．32．（2019•嘉兴）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝6，AD＝4，求正方形PQMN的边长．（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC 边上，N'在△ABC内，连结BN'并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PPQMN．小波把线段BN称为“波利亚线”．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：在（2）的条件下，在射线BN上截取NE＝NM，连结EQ，EM（如图3）．当tan∠NBM=34时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．33．（2019•台州）我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．（1）已知凸五边形ABCDE的各条边都相等．①如图1，若AC＝AD＝BE＝BD＝CE，求证：五边形ABCDE是正五边形；②如图2，若AC＝BE＝CE，请判断五边形ABCDE是不是正五边形，并说明理由：（2）判断下列命题的真假．（在括号内填写“真”或“假”）如图3，已知凸六边形ABCDEF的各条边都相等．①若AC＝CE＝EA，则六边形ABCDEF是正六边形；（）②若AD＝BE＝CF，则六边形ABCDEF是正六边形．（）34．（2019•天津）在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD＝2．（Ⅰ）如图①，求点E的坐标；（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；②当√3≤S≤5√3时，求t的取值范围（直接写出结果即可）．35．（2019•青岛）已知：如图，在四边形ABCD中，AB∥CD，∠ACB＝90°，AB＝10cm，BC＝8cm，OD垂直平分A C．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动，另一个点也停止运动．过点P作PE⊥AB，交BC于点E，过点Q作QF∥AC，分别交AD，OD于点F，G．连接OP，EG．设运动时间为t（s）（0＜t＜5），解答下列问题：（1）当t为何值时，点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2），求S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使四边形PEGO的面积最大？若存在，求出t的值；若不存在，请说明理由；（4）连接OE，OQ，在运动过程中，是否存在某一时刻t，使OE⊥OQ？若存在，求出t的值；若不存在，请说明理由．36．（2019•白银）阅读下面的例题及点拨，并解决问题：例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°．点拨：如图②，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM ＝MN，可得∠3＝∠4；由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠5，又因为∠2+∠6＝120°，所以∠5+∠6＝120°，即：∠AMN＝60°．问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1＝M1N1．求证：∠A1M1N1＝90°．37．（2019•济宁）如图1，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．（1）求线段CE的长；（2）如图2，M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN＝∠DAM，设AM＝x，DN＝y．①写出y关于x的函数解析式，并求出y的最小值；②是否存在这样的点M，使△DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．38．（2019•连云港）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上．（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN 翻折，点P落在点P'处，若正方形ABCD的边长为4，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG=52，请直接写出FH的长．39．（2019•威海）如图，在正方形ABCD中，AB＝10cm，E为对角线BD上一动点，连接AE，CE，过E点作EF⊥AE，交直线BC于点F．E点从B点出发，沿着BD方向以每秒2cm的速度运动，当点E与点D重合时，运动停止．设△BEF的面积为ycm2，E点的运动时间为x秒．（1）求证：CE＝EF；（2）求y与x之间关系的函数表达式，并写出自变量x的取值范围；（3）求△BEF面积的最大值．40．（2019•达州）箭头四角形模型规律如图1，延长CO交AB于点D，则∠BOC＝∠1+∠B＝∠A+∠C+∠B．因为凹四边形ABOC形似箭头，其四角具有“∠BOC＝∠A+∠B+∠C”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用（1）直接应用：①如图2，∠A+∠B+∠C+∠D+∠E+∠F＝．②如图3，∠ABE、∠ACE的2等分线（即角平分线）BF、CF交于点F，已知∠BEC＝120°，∠BAC＝50°，则∠BFC＝．③如图4，BO i、CO i分别为∠ABO、∠ACO的2019等分线（i＝1，2，3， (2017)2018）．它们的交点从上到下依次为O1、O2、O3、…、O2018．已知∠BOC＝m°，∠BAC ＝n°，则∠BO1000C＝度．（2）拓展应用：如图5，在四边形ABCD中，BC＝CD，∠BCD＝2∠BAD．O是四边形ABCD内一点，且OA＝OB＝OD．求证：四边形OBCD是菱形．41．（2019•自贡）（1）如图1，E是正方形ABCD边AB上的一点，连接BD、DE，将∠BDE 绕点D逆时针旋转90°，旋转后角的两边分别与射线BC交于点F和点G．①线段DB和DG的数量关系是；②写出线段BE，BF和DB之间的数量关系．（2）当四边形ABCD为菱形，∠ADC＝60°，点E是菱形ABCD边AB所在直线上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转120°，旋转后角的两边分别与射线BC 交于点F和点G．①如图2，点E在线段AB上时，请探究线段BE、BF和BD之间的数量关系，写出结论并给出证明；②如图3，点E在线段AB的延长线上时，DE交射线BC于点M，若BE＝1，AB＝2，直接写出线段GM的长度．四边形综合题参考答案与试题解析一．选择题（共1小题）1．【解答】解：如图，过点C作CE⊥AB于E，则四边形ADCE为矩形，CD＝AE＝x，∠DCE＝∠CEB＝90°，则∠BCE＝∠BCD﹣∠DCE＝30°，BC＝12﹣x，在Rt△CBE中，∵∠CEB＝90°，∴BE=12BC＝6−12x，∴AD＝CE=√3BE＝6√3−√32x，AB＝AE+BE＝x+6−12x=12x+6，∴梯形ABCD面积S=12（CD+AB）•CE=12（x+12x+6）•（6√3−√32x）=−3√38x2+3√3x+18√3=−3√38（x﹣4）2+24√3，∴当x＝4时，S最大＝24√3．即CD长为4m时，使梯形储料场ABCD的面积最大为24√3m2；故选：C．二．填空题（共2小题）2．【解答】解：依题意，得2sinα+1×（−√3）＝0，解得sinα=√3 2．∵α是锐角，∴α＝60°．故答案是：60°．3．【解答】解：连接CF．∵多边形ABCDEF 是正六边形，AB ∥CF ，CF ＝2BA ，∴CF →=2a →，∵BF →=BC →+CF →，∴BF →=2a →+b →，故答案为2a →+b →．三．解答题（共38小题）4．【解答】解：（1）BP +QC ＝EC ；理由如下：∵四边形ABCD 是正方形，∴BC ＝CD ，∠BCD ＝90°，由旋转的性质得：∠PEG ＝90°，EG ＝EP ，∴∠PEQ +∠GEH ＝90°，∵QH ⊥GD ，∴∠H ＝90°，∠G +∠GEH ＝90°，∴∠PEQ ＝∠G ，又∵∠EPQ +∠PEC ＝90°，∠PEC +∠GED ＝90°，∴∠EPQ ＝∠GED ，在△PEQ 和△EGD 中，{∠EPQ =∠GEDEP =EG ∠PEQ =∠G，∴△PEQ ≌△EGD （ASA ），∴PQ ＝ED ，∴BP +QC ＝BC ﹣PQ ＝CD ﹣ED ＝EC ，即BP +QC ＝EC ；故答案为：BP +QC ＝EC ；（2）（1）中的结论仍然成立，理由如下：由题意得：∠PEG ＝90°，EG ＝EP ，∴∠PEQ +∠GEH ＝90°，∵QH ⊥GD ，∴∠H ＝90°，∠G +∠GEH ＝90°，∴∠PEQ ＝∠G ，∵四边形ABCD 是正方形，∴∠DCB ＝90°，BC ＝DC ，∴∠EPQ +∠PEC ＝90°，∵∠PEC +∠GED ＝90°，∴∠GED ＝∠EPQ ，在△PEQ 和△EGD 中，{∠EPQ =∠GEDEP =EG ∠PEQ =∠G，∴△PEQ ≌△EGD （ASA ），∴PQ ＝ED ，∴BP +QC ＝BC ﹣PQ ＝CD ﹣ED ＝EC ，即BP +QC ＝EC ；（3）分两种情况：①当点P 在线段BC 上时，点Q 在线段BC 上，由（2）可知：BP ＝EC ﹣QC ，∵AB ＝3DE ＝6，∴DE ＝2，EC ＝4，∴BP ＝4﹣1＝3；②当点P 在线段BC 上时，点Q 在线段BC 的延长线上，如图3所示：同（2）可得：△PEQ ≌△EGD （AAS ），∴PQ ＝DE ＝2，∵QC ＝1，∴PC ＝PQ ﹣QC ＝1，∴BP ＝BC ﹣PC ＝6﹣1＝5；综上所述，线段BP 的长为3或5．5．【解答】（1）①解：△AEG 是等边三角形；理由如下：∵四边形ABCD 是菱形，∠BAD ＝120°，∴AD ∥BC ，AB ＝BC ＝CD ＝AD ，AB ∥CD ，∠CAD =12∠BAD ＝60°，∴∠BAD +∠ADC ＝180°，∴∠ADC ＝60°，∵GH ∥DC ，∴∠AGE ＝∠ADC ＝60°，∴∠AGE ＝∠EAG ＝∠AEG ＝60°，∴△AEG 是等边三角形；②证明：∵△AEG 是等边三角形，∴AG ＝AE ，∵CF ＝AG ，∴AE ＝CF ，∵四边形ABCD 是菱形，∴∠BCD ＝∠BAD ＝120°，∴∠DCF ＝60°＝∠CAD ，在△AED 和△CFD 中，{AD =CD∠EAD =∠FCD AE =CF，∴△AED ≌△CFD （SAS ）∴DE ＝DF ，∠ADE ＝∠CDF ，∵∠ADC ＝∠ADE +∠CDE ＝60°，∴∠CDF +∠CDE ＝60°，即∠EDF ＝60°，∴△DEF 是等边三角形；（2）解：△DEF 是等边三角形；理由如下：同（1）①得：△AEG 是等边三角形，∴AG ＝AE ，∵CF ＝AG ，∴AE ＝CF ，∵四边形ABCD 是菱形，∴∠BCD ＝∠BAD ＝120°，∠CAD =12∠BAD ＝60°，∴∠FCD ＝60°＝∠CAD ，在△AED 和△CFD 中，{AD =CD∠EAD =∠FCD AE =CF，∴△AED ≌△CFD （SAS ），∴DE ＝DF ，∠ADE ＝∠CDF ，∵∠ADC ＝∠ADE ﹣∠CDE ＝60°，∴∠CDF ﹣∠CDE ＝60°，即∠EDF ＝60°，∴△DEF 是等边三角形．6．【解答】解：（1）OE ＝OD ，OE ⊥OD ；理由如下：由旋转的性质得：AF ＝AC ，∠AFE ＝∠ACB ，∵四边形ABCD 是正方形，∴∠ACB ＝∠ACD ＝∠F AC ＝45°，∴∠ACF ＝∠AFC =12（180°﹣45°）＝67.5°，∴∠DCF ═∠EFC ＝22.5°，∵∠FEC ＝90°，O 为CF 的中点，∴OE =12CF ＝OC ＝OF ，同理：OD =12CF ，∴OE ＝OD ＝OC ＝OF ，∴∠EOC ＝2∠EFO ＝45°，∠DOF ＝2∠DCO ＝45°，∴∠DOE ＝180°﹣45°﹣45°＝90°，∴OE ⊥OD ；（2）当45°＜α＜90°时，（1）中的结论成立，理由如下：延长EO 到点M ，使OM ＝EO ，连接DM 、CM 、DE ，如图2所示：∵O 为CF 的中点，∴OC ＝OF ，在△COM 和△FOE 中，{OM =EO∠COM =∠FOE OC =OF，∴△COM ≌△FOE （SAS ），∴∠MCF ＝∠EFC ，CM ＝EF ，∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ，∠BAC ＝∠BCA ＝45°，∵△ABC 绕点A 逆时针旋转α得△AEF ，∴AB ＝AE ＝EF ＝CD ，AC ＝AF ，∴CD ＝CM ，∠ACF ＝∠AFC ，∵∠ACF ＝∠ACD +∠FCD ，∠AFC ＝∠AFE +∠CFE ，∠ACD ＝∠AFE ＝45°， ∴∠FCD ＝∠CFE ＝∠MCF ，∵∠EAC +∠DAE ＝45°，∠F AD +∠DAE ＝45°，∴∠EAC ＝∠F AD ，在△ACF 中，∵∠ACF +∠AFC +∠CAF ＝180°，∴∠DAE +2∠F AD +∠DCM +90°＝180°，∵∠F AD +∠DAE ＝45°，∴∠F AD +∠DCM ＝45°，∴∠DAE ＝∠DCM ，在△ADE 和△CDM 中，{AE =CM∠DAE =∠DCM AD =CD，∴△ADE ≌△CDM （SAS ），∴DE ＝DM ，∵OE ＝OM ，∴OE ⊥OD ，在△COM 和△COD 中，{CM =CD∠MCF =∠FCD OC =OC，∴△COM≌△COD（SAS），∴OM＝OD，∴OE＝OD，∴OE＝OD，OE⊥OD；（3）连接AO，如图3所示：∵AC＝AF，CO＝OF，∴AO⊥CF，∴∠AOC＝90°，∴点O在以AC为直径的圆上运动，∵α＝360°，∴点O经过的路径长等于以AC为直径的圆的周长，∵AC=√2AB=√2×4√2=8，∴点O经过的路径长为：πd＝8π．7．【解答】解：（1）如图1中，结论：CE+CF＝BC．理由如下：∵四边形ABCD是正方形，∴AC⊥BD，OB＝OC，∠OBE＝∠OCF＝45°，∵∠EOF＝∠BOC＝90°，∴∠BOE＝∠OCF，∴△BOE≌△COF（ASA），∴BE＝CF，∴CE+CF＝CE+BE＝BC．故答案为CE+CF＝BC．（2）如图2中，结论不成立．CE+CF=12BC．理由：连接EF，在CO上截取CJ＝CF，连接FJ．∵四边形ABCD是菱形，∠BCD＝120°，∴∠BCO＝∠OCF＝60°，∵∠EOF+∠ECF＝180°，∴O，E，C，F四点共圆，∴∠OFE＝∠OCE＝60°，∵∠EOF＝60°，∴△EOF是等边三角形，∴OF＝FE，∠OFE＝60°，∵CF＝CJ，∠FCJ＝60°，∴△CFJ是等边三角形，∴FC＝FJ，∠EFC＝∠OFE＝60°，∴∠OFJ＝∠CFE，∴△OFJ≌△EFC（SAS），∴OJ＝CE，∴CF+CE＝CJ+OJ＝OC=12BC，（3）如图3中，由OB＞2OA可知△BAO是钝角三角形，∠BAO＞90°，作AH⊥OB于H，设OH＝x．在Rt△ABH中，BH=√13−3x2，∵OB＝4，∴√13−3x2+x＝4，解得x=32或12，∴OH=12或32，∴OA＝2OH＝1或3（舍弃），∵∠COD+∠ACD＝180°，∴A，C，O，D四点共圆，∵OA平分∠COD，∴∠AOC＝∠AOD＝60°，∴∠ADC＝∠AOC＝60°，∵∠CAD＝60°，∴△ACD是等边三角形，由（2）可知：OC+OD＝OA，∴OC＝1−34=14．8．【解答】解：（1）如图一（1）中，∵四边形ABCD是矩形，∴∠ADC＝90°，∵tan∠DAC=DCAD=553=√33，∴∠DAC＝30°．（2）①如图一（1）中，当AN＝NM时，∵∠BAN＝∠BMN＝90°，BN＝BN，AN＝NM，∴Rt△BNA≌Rt△BNM（HL），∴BA＝BM，在Rt△ABC中，∵∠ACB＝∠DAC＝30°，AB＝CD＝5，∴AC＝2AB＝10，∵∠BAM＝60°，BA＝BM，∴△ABM是等边三角形，∴AM＝AB＝5，∴CM＝AC﹣AM＝5．如图一（2）中，当AN＝AM时，易证∠AMN＝∠ANM＝15°，∵∠BMN＝90°，∴∠CMB＝75°，∵∠MCB＝30°，∴∠CBM＝180°﹣75°﹣30°＝75°，∴∠CMB＝∠CBM，∴CM＝CB＝5√3，综上所述，满足条件的CM的值为5或5√3．②结论：∠MBN＝30°大小不变．理由：如图一（1）中，∵∠BAN+∠BMN＝180°，∴A，B，M，N四点共圆，∴∠MBN＝∠MAN＝30°．如图一（2）中，∵∠BMN＝∠BAN＝90°，∴A，N，B，M四点共圆，∴∠MBN+∠MAN＝180°，∵∠DAC+∠MAN＝180°，∴∠MBN＝∠DAC＝30°，综上所述，∠MBN＝30°．（3）如图二中，∵AM＝MC，∴BM＝AM＝CM，∴AC＝2AB，∴AB＝BM＝AM，∴△ABM是等边三角形，∴∠BAM＝∠BMA＝60°，∵∠BAN＝∠BMN＝90°，∴∠NAM＝∠NMA＝30°，∴NA＝NM，∵BA＝BM，∴BN垂直平分线段AM，∴FM=5 2，∴NM=FMcos30°=5√33，∵∠NFM＝90°，NH＝HM，∴FH=12MN=5√36．9．【解答】证明：（1）∵四边形ABCD是矩形，∴∠A＝∠C．∴在△AEH与△CGF中，{AE=CG ∠A=∠C AH=CF，∴△AEH≌△CGF（SAS）；（2）∵由（1）知，△AEH≌△CGF，则EH＝GF，同理证得△EBF≌△GDH，则EF＝GH，∴四边形EFGH是平行四边形；（3）四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．理由如下：作G 关于BC的对称点G′，连接EG′，可得EG′的长度就是EF+FG的最小值．连接AC，∵CG′＝CG＝AE，AB∥CG′，∴四边形AEG′C为平行四边形，∴EG′＝AC．在△EFG′中，∵EF+FG′≥EG′＝AC，∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．10．【解答】解：（1）如图记为点D所在的位置．（2）如图，∵AB＝4，BC＝10，∴取BC的中点O，则OB＞AB．∴以点O为圆心，OB长为半径作⊙O，⊙O一定于AD相交于P1，P2两点，。

2020年中考数学压轴题专项训练：四边形的综合(含答案)

2020年数学中考压轴题专项训练：四边形的综合1．如图，四边形ABCD是直角梯形，AD∥BC，AB⊥AD，且AB＝AD+BC，E是DC的中点，连结BE并延长交AD的延长线于G．（1）求证：DG＝BC；（2）F是AB边上的动点，当F点在什么位置时，FD∥BG；说明理由．（3）在（2）的条件下，连结AE交FD于H，FH与HD长度关系如何？说明理由．（1）证明：∵AD∥BC，∴∠DGE＝∠CBE，∠GDE＝∠BCE，∵E是DC的中点，即DE＝CE，∴△DEG≌△CEB（AAS），∴DG＝BC．（2）解：当F运动到AF＝AD时，FD∥BG．理由：由（1）知DG＝BC，∵AB＝AD+BC，AF＝AD，∴BF＝BC＝DG，∴AB＝AG，∵∠BAG＝90°，∴∠AFD＝∠ABG＝45°，∴FD∥BG．（3）解：结论：FH＝HD．理由：由（1）知GE＝BG，又由（2）知△ABG为等腰直角三角形，所以AE⊥BG，∵FD∥BG，∴AE⊥FD，∵△AFD为等腰直角三角形，∴FH＝HD．2．如图，在矩形ABCD中，过BD的中点O作EF⊥BD，分别与AB、CD交于点E、F．连接DE、BF．（1）求证：四边形BEDF是菱形；（2）若M是AD中点，联结OM与DE交于点N，AD＝OM＝4，则ON的长是多少？（1）证明：∵四边形ABCD是矩形，∴AB∥CD，∴∠DFO＝∠BEO，∵∠DOF＝∠EOB，OD＝OB，∴△DOF≌△BOE（AAS），∴DF＝BE，∴四边形BEDF是平行四边形，∵EF⊥BD，∴四边形BEDF是菱形．（2）解：∵DM＝AM，DO＝OB，∴OM∥AB，AB＝2OM＝8，∴DN＝EN，ON＝BE，设DE＝EB＝x，在Rt△ADE中，则有x2＝42+（8﹣x）2，解得x＝5，∴ON＝．3．（1）如图1，四边形EFGH中，FE＝EH，∠EFG+∠EHG＝180°，点A，B分别在边FG，GH 上，且∠AEB＝∠FEH，求证：AB＝AF+BH．（2）如图2，四边形EFGH中，FE＝EH，点M在边EH上，连接FM，EN平分∠FEH交FM 于点N，∠ENM＝α，∠FGH＝180°﹣2α，连接GN，HN．①找出图中与NH相等的线段，并加以证明；②求∠NGH的度数（用含α的式子表示）．（1）证明：如图1中，延长BH到M，使得HM＝FA，连接EM．∵∠F+∠EHG＝180°，∠EHG+∠EHM＝180°，∴∠F＝∠EHM，∵AE＝HE，FA＝HM，∴△EFA≌△EHM（SAS），∴EA＝EM，∠FEA＝∠HEM，∵∠EAB＝∠FEH，∴∠FEA+∠BEH＝∠HEM+∠BEH＝∠BEM＝∠FEH，∴∠AEB＝∠BEM，∵BE＝BE，EA＝EM，∴△AEB≌△MEB（SAS），∴AB＝BM，∵BM＝BH+HM＝BH+AF，∴AB＝AF+BH．（2）解：①如图2中，结论：NH＝FN．理由：∵NE平分∠FEH，∴∠FEN＝∠HEN，∵EF＝EH，EN＝EN，∴△ENF≌△ENH（SAS），∴NH＝FN．②∵△ENF≌△ENH，∴∠ENF＝∠ENH，∵∠ENM＝α，∴∠ENF＝∠ENH＝180°﹣α，∴∠MNH＝180°﹣α﹣α＝180°﹣2α，∵∠FGH＝180°﹣2α，∴∠MNH＝∠FGH，∵∠MNH+∠FNH＝180°，∴∠FGH+∠FNH＝180°，∴F，G，H，N四点共圆，∵NH＝NF，∴＝，∴∠NGH＝∠NGF＝∠FGH＝90°﹣α．4．如图，已知△ABC中，∠ACB＝90°，AC＝4，BC＝3，点M、N分别是边AC、AB上的动点，连接MN，将△AMN沿MN所在直线翻折，翻折后点A的对应点为A′．（1）如图1，若点A′恰好落在边AB上，且AN＝AC，求AM的长；（2）如图2，若点A′恰好落在边BC上，且A′N∥AC．①试判断四边形AMA′N的形状并说明理由；②求AM、MN的长；（3）如图3，设线段NM、BC的延长线交于点P，当且时，求CP的长．解：（1）如图1中，在Rt△ABC中，∵∠C＝90°，AC＝4，BC＝3，∴AB＝＝＝5，∵∠A＝∠A，∠ANM＝∠C＝90°，∴△ANM∽△ACB，∴＝，∴＝，∴AM＝．（2）①如图2中，∵NA′∥AC，∴∠AMN＝∠NMA′，由翻折可知：MA＝MA′，∠AMN＝∠NMA′，∴∠MNA′＝∠A′MN，∴A′N＝A′M，∴AM＝A′N，∵AM∥A′N，∴四边形AMA′N是平行四边形，∵MA＝MA′，∴四边形AMA′N是菱形．②连接AA′交MN于O．设AM＝MA′＝x，∵MA′∥AB，∴＝，∴＝，解得x＝，∴AM＝，∴CM＝，∴CA′＝＝＝，∴AA′＝＝＝，∵四边形AMA′N是菱形，∴AA′⊥MN，OM＝ON，OA＝OA′＝，∴OM＝＝＝，∴MN＝2OM＝．（3）如图3中，作NH⊥BC于H．∵NH∥AC，∴＝＝∴＝＝∴NH＝，BH＝，∴CH＝BC﹣BH＝3﹣＝，∴AM＝AC＝，∴CM＝AC﹣AM＝4﹣＝，∵CM∥NH，∴＝，∴＝，∴PC＝1．5．如图，四边形ABCD为平行四边形，AD＝1，AB＝3，∠DAB＝60°，点E为边CD上一动点，过点C作AE的垂线交AE的延长线于点F．（1）求∠D的度数；（2）若点E为CD的中点，求EF的值；（3）当点E在线段CD上运动时，是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．解：（1）如图1中，∵四边形ABCD是平行四边形，∴AB∥CB，∠ADC+∠DAB＝180°，∵∠DAB＝60°，∴∠ADC＝120°．（2）如图1中，作AH⊥CD交CD的延长线于H．在Rt△ADH中，∵∠H＝90°，∠ADH＝60°，AD＝2，∴AH＝AD•sin60°＝，DH＝AD•cos60°＝，∵DE＝EC＝，∴EH＝DH+DE＝2，∴AE＝＝＝，∵CF⊥AF，∴∠F＝∠H＝90°，∵∠AEH＝∠CEF，∴△AEH∽△CEF，∴＝，∴＝，∴EF＝．（3）如图2中，作△AFC的外接圆⊙O，作AH⊥CD交CD的郯城县于H，作OK⊥CD于K，交⊙O于M，作FP∥CD交AD的延长线于P，作MN∥CD交AD的延长线于M，作NQ⊥CD于Q．∵DE∥PF，∴＝，∵AD是定值，∴PA定值最大时，定值最大，观察图象可知，当点F与点M重合时，PA定值最大，最大值＝AN的长，由（2）可知，AH＝，CH＝，∠H＝90°，∴AC＝＝＝，∴OM＝AC＝，∵OK∥AH，AO＝OC，∴KH＝KC，∴OK＝＝，∴MK＝NQ＝﹣，在Rt△NDQ中，DN＝＝＝﹣，∴AN＝AD+DN＝+，∴的最大值＝＝+．6．如图，在边长为2的正方形ABCD中，点P是射线BC上一动点（点P不与点B重合），连接AP、DP，点E是线段AP上一点，且∠ADE＝∠APD，连接BE．（1）求证：AD2＝AE•AP；（2）求证BE⊥AP；（3）直接写出的最小值．（1）证明：∵∠DAE＝∠PAD，∠ADE＝∠APD，∴△ADE∽△APD，∴＝，∴AD2＝AE•AP（2）证明：∵四边形ABCD是正方形，∴AD＝AB，∠ABC＝90°，∴AB2＝AE•AP，∴＝，∵∠BAE＝∠PAB，∴△ABE∽△APB，∴∠AEB＝∠ABP＝90°，∴BE⊥AP．（3）∵△ADE∽△APD，∴＝，∴＝，∵AD＝2，∴DE最小时，的值最小，如图，作△ABE的外接圆⊙O，连接OD，OE，易知OE＝1，OD＝，∴DE≥OD﹣OE＝﹣1，∴DE的最小值为﹣1，∴的最小值＝．7．在正方形ABCD中，点E是BC边上一点，连接AE．（1）如图1，点F为AE的中点，连接CF．已知tan∠FBE＝，BF＝5，求CF的长；（2）如图2，过点E作AE的垂线交CD于点G，交AB的延长线于点H，点O为对角线AC 的中点，连接GO并延长交AB于点M，求证：AM+BH＝BE．解：（1）Rt△ABE中，BF为中线，BF＝5，∴AE＝10，FE＝5，作FP⊥BC于点P，Rt△BFP中，，∴BP＝3，FP＝4，在等腰三角形△BFE中，BE＝2BP＝6，由勾股定理求得，∴CP＝8﹣3＝5，∴；（2）∵∠ACD＝∠BAC＝45°，AO＝CO，∠AOM＝∠COG，∴证明△AMO≌△CGO（ASA），∴AM＝GC，过G作GP垂直AB于点P，得矩形BCGP，∴CG＝PB，∵AB＝PG，∠AEB＝∠H，∠ABE＝∠GPH，∴△ABE≌△GPH（ASA），∴BE＝PH＝PB+BH＝CG+BH＝AM+BH．8．阅读理解：如图1，若一个四边形的两条对角线互相垂直，则称这个四边形为垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，试在垂美四边形ABCD中探究AB2，CD2，AD2，BC2之间的关系，并说明理由；（3）解决问题：如图3，分别以Rt△ABC的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE、BG、GE、CE交BG于点N，交AB于点M．已知AC＝，AB＝2，求GE的长．解：（1）如图2，四边形ABCD是垂美四边形；理由如下：连接AC、BD交于点E，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴直线AC是线段BD的垂直平分线，∴AC⊥BD，即四边形ABCD是垂美四边形；（2）猜想结论：AB2+CD2＝AD2+BC2，证明：如图1，在四边形ABCD中，∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得：AB2+CD2＝AO2+BO2+OD2+OC2AD2+BC2＝AO2+BO2+OD2+OC2∴AB2+CD2＝AD2+BC2，（3）如图3，连接CG，BE，∵∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，FMNG图 3EDCAB∴△GAB≌△CAE（SSS），∴∠ABG＝∠AEC，∵∠AEC+∠AME＝90°，∴∠ABG+∠BMN＝90°，∴∠BNC＝90°，即BG⊥CE，∴四边形CGEB是垂美四边形，由（2）得：EG2+BC2＝CG2+BE2∵，AB＝2，∴BC＝1，，，∴EG2＝CG2+BE2﹣BC2＝6+8﹣2＝13，∴．9．已知：如图，长方形ABCD中，∠A＝∠B＝∠B＝∠D＝90°，AB＝CD＝4米，AD＝BC＝8米，点M是BC边的中点，点P从点A出发，以1米/秒的速度沿AB方向运动再过点B沿BM方向运动，到点M停止运动，点O以同样的速度同时从点D出发沿着DA方向运动，到点A停止运动，设点P运动的时间为x秒．（1）当x＝2秒时，线段AQ的长是 6 米；（2）当点P在线段AB上运动时，图中阴影部分的面积发生改变吗？请你作出判断并说明理由．（3）在点P，Q的运动过程中，是否存在某一时刻，使得BP＝DQ？若存在，求出点P 的运动时间x的值；若不存在，请说明理由．解：（1）∵四边形ABCD是矩形，∴AD＝BC＝8，∵DQ＝2，∴AQ＝AD﹣DQ＝8﹣2＝6，故答案为6．（2）结论：阴影部分的面积不会发生改变．理由：连结AM，作MH⊥AD于H．则四边形ABMH是矩形，MH＝AB＝4．∵S阴＝S△APM+S△AQM＝×x×4+（8﹣x）×4＝16，∴阴影面积不变；（3）当点P在线段AB上时，BP＝4﹣x，DQ＝x．∵BP＝DQ，∴4﹣x＝x，∴x＝3．当点P在线段BM上时，BP＝x﹣4，DQ＝x．∵BP＝DQ，∴x﹣4＝x，∴x＝6．所以当x＝3或6时，BP＝DQ．10．A，B，C，D是长方形纸片的四个顶点，点E、F、H分别是边AB、BC、AD上的三点，连结EF、FH．（1）将长方形纸片ABCD按图①所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，点B'在FC'上，则∠EFH的度数为90°；（2）将长方形纸片ABCD按图②所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠B'FC'＝18°，求∠EFH的度数；（3）将长方形纸片ABCD按图③所示的方式折叠，FE、FH为折痕，点B、C、D折叠后的对应点分别为B'、C'、D'，若∠EFH＝m°，求∠B'FC'的度数为180°﹣2m°．解：（1）∵沿EF，FH折叠，∴∠BFE＝∠B'FE，∠CFH＝∠C'FH，∵点B′在FC′上，∴∠EFH＝（∠BFB'+∠CFC'）＝×180°＝90°，故答案为：90°；（2）∵沿EF，FH折叠，∴可设∠BFE＝∠B'FE＝x，∠C'FH＝∠CFH＝y，∵2x+18°+2y＝180°，∴x+y＝81°，∴∠EFH＝x+18°+y＝99°；（3）∵沿EF，FH折叠，∴可设∠BFE＝∠B'FE＝x，∠C'FH＝∠CFH＝y，∴∠EFH＝180°﹣∠BFE﹣∠CFH＝180°﹣（x+y），即x+y＝180°﹣m°，又∵∠EFH＝∠EFB'﹣∠B'FC'+∠C'FH＝x﹣∠B'FC'+y，∴∠B'FC'＝（x+y）﹣∠EFH＝180°﹣m°﹣m°＝180°﹣2m°，故答案为：180°﹣2m°．11．勾股定理是数学史上非常重要的一个定理．早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法．在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图，分别以Rt△ABC的三边为边长，向外作正方形ABDE、BCFG、ACHI．（1）连接BI、CE，求证：△ABI≌△AEC；（2）过点B作AC的垂线，交AC于点M，交IH于点N．①试说明四边形AMNI与正方形ABDE的面积相等；②请直接写出图中与正方形BCFG的面积相等的四边形．（3）由第（2）题可得：正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积，即在Rt△ABC中，AB2+BC2＝AC2．（1）证明：∵四边形ABDE、四边形ACHI是正方形，∴AB＝AE，AC＝AI，∠BAE＝∠CAI＝90°，∴∠EAC＝∠BAI，在△ABI和△AEC中，，∴△ABI≌△AEC（SAS）；（2）①证明：∵BM⊥AC，AI⊥AC，∴BM∥AI，∴四边形AMNI的面积＝2△ABI的面积，同理：正方形ABDE的面积＝2△AEC的面积，又∵△ABI≌△AEC，∴四边形AMNI与正方形ABDE的面积相等．②解：四边形CMNH与正方形BCFG的面积相等，理由如下：∵Rt△ABC中，AB2+BC2＝AC2，∴正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积，由①得：四边形AMNI与正方形ABDE的面积相等，∴四边形CMNH与正方形BCFG的面积相等；（3）解：由（2）得：正方形ABDE的面积+正方形BCFG的面积＝正方形ACHI的面积；即在Rt△ABC中，AB2+BC2＝AC2；故答案为：正方形ACHI，AC2．12．在长方形纸片ABCD中，点E是边CD上的一点，将△AED沿AE所在的直线折叠，使点D 落在点F处．（1）如图1，若点F落在对角线AC上，且∠BAC＝54°，则∠DAE的度数为18 °．（2）如图2，若点F落在边BC上，且AB＝6，AD＝10，求CE的长．（3）如图3，若点E是CD的中点，AF的沿长线交BC于点G，且AB＝6，AD＝10，求CG 的长．解：（1）∵四边形ABCD是矩形，∴∠BAD＝90°，∵∠BAC＝54°，∴∠DAC＝90°﹣54°＝36°，由折叠的性质得：∠DAE＝∠FAE，∴∠DAE＝∠DAC＝18°；故答案为：18；（2）∵四边形ABCD是矩形，∴∠B＝∠C＝90°，BC＝AD＝10，CD＝AB＝6，由折叠的性质得：AF＝AD＝10，EF＝ED，∴BF＝＝＝8，∴CF＝BC﹣BF＝10﹣8＝2，设CE＝x，则EF＝ED＝6﹣x，在Rt△CEF中，由勾股定理得：22+x2＝（6﹣x）2，解得：x＝，即CE的长为；（3）连接EG，如图3所示：∵点E是CD的中点，∴DE＝CE，由折叠的性质得：AF＝AD＝10，∠AFE＝∠D＝90°，FE＝DE，∴∠EFG＝90°＝∠C，在Rt△CEG和△FEG中，，∴Rt△CEG≌△FEG（HL），∴CG＝FG，设CG＝FG＝y，则AG＝AF+FG＝10+y，BG＝BC﹣CG＝10﹣y，在Rt△ABG中，由勾股定理得：62+（10﹣y）2＝（10+y）2，解得：y＝，即CG的长为．13．如图，矩形ABCD中，AB＝6cm，AD＝8cm，点P从点A出发，以每秒一个单位的速度沿A→B→C的方向运动；同时点Q从点B出发，以每秒2个单位的速度沿B→C→D的方向运动，当其中一点到达终点后两点都停止运动．设两点运动的时间为t秒．（1）当t＝7 时，两点停止运动；（2）设△BPQ的面积面积为S（平方单位）①求S与t之间的函数关系式；②求t为何值时，△BPQ面积最大，最大面积是多少？解：（1）∵四边形ABCD是矩形，∴AD＝BC＝8cm，AB＝CD＝6cm，∴BC+AD＝14cm，∴t＝14÷2＝7，故答案为7．（2）①当0＜t＜4时，S＝•（6﹣t）×2t＝﹣t2+6t．当4≤t＜6时，S＝•（6﹣t）×8＝﹣4t+24．当6＜t≤7时，S＝（t﹣6）•（2t﹣8）＝t2﹣10t+24．②当0＜t＜4时，S＝•（6﹣t）×2t＝﹣t2+6t＝﹣（t﹣3）2+9，∵﹣1＜0，∴t＝3时，△PBQ的面积最大，最小值为9．当4≤t＜6时，S＝•（6﹣t）×8＝﹣4t+24，∵﹣4＜0，∴t＝4时，△PBQ的面积最大，最大值为8，当6＜t≤7时，S＝（t﹣6）•（2t﹣8）＝t2﹣10t+24＝（t﹣5）2﹣1，t＝7时，△PBQ的面积最大，最大值为3，综上所述，t＝3时，△PBQ的面积最大，最大值为9．14．综合实践：问题情境数学活动课上，老师和同学们在正方形中利用旋转变换探究线段之间的关系探究过程如下所示：如图1，在正方形ABCD中，点E为边BC的中点．将△DCE以点D为旋转中心，顺时针方向旋转，当点E的对应点E'落在边AB上时，连接CE'．“兴趣小组”发现的结论是：①AE'＝C'E'；“卓越小组”发现的结论是：②DE＝CE'，DE⊥CE'．解决问题（1）请你证明“兴趣小组”和“卓越小组”发现的结论；拓展探究证明完“兴趣小组”和“卓越小组”发现的结论后，“智慧小组”提出如下问题：如图2，连接CC'，若正方形ABCD的边长为2，求出CC'的长度．（2）请你帮助智慧小组写出线段CC'的长度．（直接写出结论即可）（1）证明：①∵△DE'C'由△DEC旋转得到，∴DC'＝DC，∠C'＝∠DCE＝90°．又∵四边形ABCD是正方形，∴DA＝DC，∠A＝90°，∴DA＝DC'，∵DE'＝DE'，∴Rt△DAE≌Rt△DC'E′（HL），∴AE'＝C'E'．②∵点E为BC中点，C'E'＝AE'＝CE，∴点E'为AB的中点．∴BE′＝CE，又∵DC＝BC，∠DCE＝∠CBE'＝90°，∴△DCE≌△CBE'（SAS），∴DE＝CE'，∠CDE＝∠E'CB，∵∠CDE+∠DEC＝90°，∴∠E'CB+∠CED＝90°，∴DE⊥CE'．（2）解：如图2中，作C′M⊥CD于M，交AB于N．∵AB∥CD，C′M⊥CD，∴C′M⊥AB，∴∠DMC′＝∠C′NE′＝∠DC′E′＝90°，∴∠MDC′+∠DC′M＝90°，∠DC′M+∠E′CN＝90°，∴∠MDC′＝∠E′C′N，∴△DMC′∽△C′NE′，∴＝＝＝2，设NE′＝x，则AM＝AN＝1+x，C′M＝2x，C′N＝（1+x），∵MN＝AD＝2，∴2x+（1+x）＝2，解得x＝，∴CM＝2﹣（1+）＝，MC＝，∴CC′＝＝＝．15．在△ABC中，AD平分∠BAC交BC于D，∠MDN的两边分别与AB，AC相交于M，N两点，且DM＝DN．（1）如图甲，若∠C＝90°，∠BAC＝60°，AC＝9，∠MDN＝120°，ND∥AB．①写出∠MDA＝90 °，AB的长是18 ．②求四边形AMDN的周长．（2）如图乙，过D作DF⊥AC于F，先补全图乙再证明AM+AN＝2AF．解：（1）①∵AD平分∠BAC，∴∠BAD＝∠CAD＝∠BAC＝30°，∵ND∥AB，∴∠NDA＝∠BAD＝30°，∴∠MDA＝∠MDN﹣∠NDA＝120°﹣30°＝90°，∵∠C＝90°，∠BAC＝60°，∴∠ABC＝30°，∴AC＝AB，∴AB＝2AC＝18，故答案为：90，18；②∵∠ABC＝30°，ND∥AB，∴∠NDC＝30°，又∵∠MDN＝120°，∴∠MDB＝30°，∴∠MAD＝∠NAD＝∠ADN＝∠MBD＝30°，∴BM＝MD，DN＝AN，∵DM＝DN，∴BM＝MD＝DN＝AN，在Rt△ADM中，设MD＝x，则AM＝2x，BM＝MD＝DN＝AN＝x，∵AB＝18，∴3x＝18，∴x＝6，∴AM＝12，MD＝DN＝AN＝6，∴四边形AMDN的周长＝AM+MD+DN+AN＝12+6+6+6＝30；（2）补全图如图乙所示：证明：过点D作DE⊥AB于E，如图丙所示：∵DE⊥AB，DF⊥AC，AD平分∠BAC，∴∠DEM＝∠DFN＝90°，DE＝DF，在Rt△DEA和Rt△DFA中，，∴Rt△DEA≌Rt△DFA（HL），∴AE＝AF，在Rt△DEM和Rt△DFN中，，∴Rt△DEM≌Rt△DFN（HL），∴EM＝FN，∴AM+AN＝AE+EM+AF﹣NF＝2AF．。

初二数学经典四边形习题道(附标准答案)

初二数学经典四边形习题道(附答案)————————————————————————————————作者：————————————————————————————————日期：1．已知：在矩形ABCD 中，AE ⊥BD 于E ， ∠DAE=3∠BAE ，求：∠EAC 的度数。

2．已知：直角梯形ABCD 中，BC=CD=a 且∠BCD=60︒，E 、F 分别为梯形的腰AB 、 DC 的中点，求：EF 的长。

3、已知：在等腰梯形ABCD 中，AB ∥DC ， AD=BC ，E 、F 分别为AD 、BC 的中点，BD 平分∠ABC 交EF 于G ，EG=18，GF=10 求：等腰梯形ABCD 的周长。

4、已知：梯形ABCD 中，AB ∥CD ，以AD ， AC 为邻边作平行四边形ACED ，DC 延长线交BE 于F ，求证：F 是BE 的中点。

5、已知：梯形ABCD 中，AB ∥CD ，AC ⊥CB ， AC 平分∠A ，又∠B=60︒，梯形的周长是 20cm, 求：AB 的长。

6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ，垂足分别是E 、F 、G 、H ，求证：EF ∥GH 。

_O_A_ B_ D_C_ E_E_F_ A_B_D_ C_G _A _ B_D_ C_E _F _D _A _B _ C_E _F _A_B_D _C _O_D _C_F_E若在平行边的一边BC 的延长线上取一点F ，使S ABC ∆=S EBF ∆，求证：DF ∥AC 。

9、若以直角三角形ABC 的边AB 为边，在三角形ABC 的外部作正方形ABDE ，AF 是BC 边的高，延长FA 使AG=BC ，求证：BG=CD 。

2021年中考数学第三轮冲刺专题复习：四边形的综合 (含答案)

2021年中考数学第三轮冲刺专题复习：四边形的综合专项练习1、如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．2、如图，▱ABCD的对角线AC、BD相交于点O，EF经过O，分别交AB、CD于点E、F，EF的延长线交CB的延长线于M．（1）求证：OE＝OF；（2）若AD＝4，AB＝6，BM＝1，求BE的长．3、如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．4、如图，在平行四边形ABCD中，AE平分∠DAB，已知CE＝6，BE＝8，DE＝10．（1）求证：∠BEC＝90°；（2）求cos∠DAE．5、如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2．（1）求平行四边形ABCD的面积；（2）求证：BD⊥BC．6、如图所示，已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点，连接CE、DG．（1）求证：△DOG≌△COE；（2）若DG⊥BD，正方形ABCD的边长为2，线段AD与线段OG相交于点M，AM＝，求正方形OEFG 的边长．7、如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝，∠CBG＝45°，BC＝4，则▱ABCD的面积是24．8、如图，四边形ABCD是正方形，△EFC是等腰直角三角形，点E在AB上，且∠CEF＝90°，FG⊥AD，垂足为点C．（1）试判断AG与FG是否相等？并给出证明；（2）若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．9、定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．10、如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．（1）若DP＝2AP＝4，CP＝，CD＝5，求△ACD的面积．（2）若AE＝BN，AN＝CE，求证：AD＝CM+2CE．11、如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．12、如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G 不重合），在运动过程中始终保持线段PQ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a的取值范围．13、在矩形ABCD中，AE⊥BD于点E，点P是边AD上一点．（1）若BP平分∠ABD，交AE于点G，PF⊥BD于点F，如图①，证明四边形AGFP是菱形；（2）若PE⊥EC，如图②，求证：AE•AB＝DE•AP；（3）在（2）的条件下，若AB＝1，BC＝2，求AP的长．14、已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM 的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为cm/s，BC的长度为cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．15、如图1，正方形ABDE和BCFG的边AB，BC在同一条直线上，且AB＝2BC，取EF的中点M，连接MD，MG，MB．（1）试证明DM⊥MG，并求的值．（2）如图2，将图1中的正方形变为菱形，设∠EAB＝2α（0＜α＜90°），其它条件不变，问（1）中的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．16、综合与实践动手操作：第一步：如图1，正方形纸片ABCD沿对角线AC所在的直线折叠，展开铺平．在沿过点C的直线折叠，使点B，点D都落在对角线AC上．此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一条直线上，折痕分别为CE，CF．如图2．第二步：再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3．第三步：在图3的基础上继续折叠，使点C与点F重合，如图4，展开铺平，连接EF，FG，GM，ME．如图5，图中的虚线为折痕．问题解决：（1）在图5中，∠BEC的度数是，的值是．（2）在图5中，请判断四边形EMGF的形状，并说明理由；（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：．17、已知：在矩形ABCD中，E，F分别是边AB，AD上的点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O．（1）填空：点A（填“在”或“不在”）⊙O上；当＝时，tan∠AEF的值是；（2）如图1，在△EFH中，当FE＝FH时，求证：AD＝AE+DH；（3）如图2，当△EFH的顶点F是边AD的中点时，求证：EH＝AE+DH；（4）如图3，点M在线段FH的延长线上，若FM＝FE，连接EM交DC于点N，连接FN，当AE＝AD 时，FN＝4，HN＝3，求tan∠AEF的值．参考答案2021年中考数学第三轮冲刺专题复习：四边形的综合专项练习1、如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．【解答】解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH＝＝，∵CH＝0.5，CG＝，∴HG＝，∴HD＝HG．2、如图，▱ABCD的对角线AC、BD相交于点O，EF经过O，分别交AB、CD于点E、F，EF的延长线交CB的延长线于M．（1）求证：OE＝OF；（2）若AD＝4，AB＝6，BM＝1，求BE的长．【解答】（1）证明：∵四边形ABCD是平行四边形，∴OA＝OC，AB∥CD，BC＝AD，∴∠OAE＝∠OVF，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF；（2）解：过点O作ON∥BC交AB于N，则△AON∽△ACB，∵OA＝OC，∴ON＝BC＝2，BN＝AB＝3，∵ON∥BC，∴△ONE∽△MBE，∴＝，即＝，解得，BE＝1．3、如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．【解答】解：（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，∴△BGF≌△DEH（AAS），∴BG＝DE；（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，∵E为AD中点，∴AE＝ED，∵BG＝DE，∴AE＝BG，AE∥BG，∴四边形ABGE是平行四边形，∴AB＝EG，∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．4、如图，在平行四边形ABCD中，AE平分∠DAB，已知CE＝6，BE＝8，DE＝10．（1）求证：∠BEC＝90°；（2）求cos∠DAE．【解答】（1）证明：∵四边形ABCD是平行四边形，∴DC＝AB＝，AD＝BC，DC∥AB，∴∠DEA＝∠EAB，∵AE平分∠DAB，∴∠DAE＝∠EAB，∴∠DAE＝∠DEA∴AD＝DE＝10，∴BC＝10，AB＝CD＝DE+CE＝16，∵CE2+BE2＝62+82＝100＝BC2，∴△BCE是直角三角形，∠BEC＝90°；（2）解：∵AB∥CD，∴∠ABE＝∠BEC＝90°，∴AE＝＝＝8，∴cos∠DAE＝cos∠EAB＝＝＝．5、如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2．（1）求平行四边形ABCD的面积；（2）求证：BD⊥BC．【解答】解：（1）作CE⊥AB交AB的延长线于点E，如图：设BE＝x，CE＝h在Rt△CEB中：x2+h2＝9①在Rt△CEA中：（5+x）2+h2＝52②联立①②解得：x＝，h＝∴平行四边形ABCD的面积＝AB•h＝12；（2）作DF⊥AB，垂足为F∴∠DF A＝∠CEB＝90°∵平行四边形ABCD∴AD＝BC，AD∥BC∴∠DAF＝∠CBE又∵∠DF A＝∠CEB＝90°，AD＝BC∴△ADF≌△BCE（AAS）∴AF＝BE＝，BF＝5﹣＝，DF＝CE＝在Rt△DFB中：BD2＝DF2+BF2＝（）2+（）2＝16∴BD＝4∵BC＝3，DC＝5∴CD2＝DB2+BC2∴BD⊥BC．6、如图所示，已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点，连接CE、DG．（1）求证：△DOG≌△COE；（2）若DG⊥BD，正方形ABCD的边长为2，线段AD与线段OG相交于点M，AM＝，求正方形OEFG 的边长．【解答】解：（1）∵正方形ABCD与正方形OEFG，对角线AC、BD∴DO＝OC∵DB⊥AC，∴∠DOA＝∠DOC＝90°∵∠GOE＝90°∴∠GOD+∠DOE＝∠DOE+∠COE＝90°∴∠GOD＝∠COE∵GO＝OE∴在△DOG和△COE中∴△DOG≌△COE（SAS）（2）如图，过点M作MH⊥DO交DO于点H∵AM＝，DA＝2∴DM＝∵∠MDB＝45°∴MH＝DH＝sin45°•DM＝，DO＝cos45°•DA＝∴HO＝DO﹣DH＝﹣＝∴在Rt△MHO中，由勾股定理得MO＝＝＝∵DG⊥BD，MH⊥DO∴MH∥DG∴易证△OHM∽△ODG∴＝＝＝，得GO＝2则正方形OEFG的边长为27、如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝，∠CBG＝45°，BC＝4，则▱ABCD的面积是24．【解答】（1）证明：∵AE＝CF，∴AE﹣EF＝CF﹣EF，即AF＝CE，∵DF∥BE，∴∠DF A＝∠BEC，∵DF＝BE，∴△ADF≌△CBE（SAS），∴AD＝CB，∠DAF＝∠BCE，∴AD∥CB，∴四边形ABCD是平行四边形；（2）解：∵CG⊥AB，∴∠G＝90°，∵∠CBG＝45°，∴△BCG是等腰直角三角形，∵BC＝4，∴BG＝CG＝4，∵tan∠CAB＝，∴AG＝10，∴AB＝6，∴▱ABCD的面积＝6×4＝24，故答案为：24．8、如图，四边形ABCD是正方形，△EFC是等腰直角三角形，点E在AB上，且∠CEF＝90°，FG⊥AD，垂足为点C．（1）试判断AG与FG是否相等？并给出证明；（2）若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．【解答】解：（1）AG＝FG，理由如下：如图，过点F作FM⊥AB交BA的延长线于点M∵四边形ABCD是正方形∴AB＝BC，∠B＝90°＝∠BAD∵FM⊥AB，∠MAD＝90°，FG⊥AD∴四边形AGFM是矩形∴AG＝MF，AM＝FG，∵∠CEF＝90°，∴∠FEM+∠BEC＝90°，∠BEC+∠BCE＝90°∴∠FEM＝∠BCE，且∠M＝∠B＝90°，EF＝EC∴△EFM≌△CEB（AAS）∴BE＝MF，ME＝BC∴ME＝AB＝BC∴BE＝MA＝MF∴AG＝FG，（2）DH⊥HG理由如下：如图，延长GH交CD于点N，∵FG⊥AD，CD⊥AD∴FG∥CD∴，且CH＝FH，∴GH＝HN，NC＝FG∴AG＝FG＝NC又∵AD＝CD，∴GD＝DN，且GH＝HN∴DH⊥GH9、定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．【解答】解：（1）∵AB＝AC，AD是△ABC的角平分线，∴AD⊥BC，∴∠ADB＝90°，∴∠DAB+∠DBA＝90°，∴∠FBA与∠EBA互余，∴四边形ABEF是邻余四边形；（2）如图所示（答案不唯一），四边形AFEB为所求；（3）∵AB＝AC，AD是△ABC的角平分线，∴BD＝CD，∵DE＝2BE，∴BD＝CD＝3BE，∴CE＝CD+DE＝5BE，∵∠EDF＝90°，点M是EF的中点，∴DM＝ME，∴∠MDE＝∠MED，∵AB＝AC，∴∠B＝∠C，∴△DBQ∽△ECN，∴，∵QB＝3，∴NC＝5，∵AN＝CN，∴AC＝2CN＝10，∴AB＝AC＝10．10、如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．（1）若DP＝2AP＝4，CP＝，CD＝5，求△ACD的面积．（2）若AE＝BN，AN＝CE，求证：AD＝CM+2CE．【解答】（1）解：作CG⊥AD于G，如图1所示：设PG＝x，则DG＝4﹣x，在Rt△PGC中，GC2＝CP2﹣PG2＝17﹣x，在Rt△DGC中，GC2＝CD2﹣GD2＝52﹣（4﹣x）2＝9+8x﹣x2，∴17﹣x2＝9+8x﹣x2，解得：x＝1，即PG＝1，∴GC＝4，∵DP＝2AP＝4，∴AD＝6，∴S△ACD＝×AD×CG＝×6×4＝12；（2）证明：连接NE，如图2所示：∵AH⊥AE，AF⊥BC，AE⊥EM，∴∠AEB+∠NBF＝∠AEB+∠EAF＝∠AEB+∠MEC＝90°，∴∠NBF＝∠EAF＝∠MEC，在△NBF和△EAF中，，∴△NBF≌△EAF（AAS），∴BF＝AF，NF＝EF，∴∠ABC＝45°，∠ENF＝45°，FC＝AF＝BF，∴∠ANE＝∠BCD＝135°，AD＝BC＝2AF，在△ANE和△ECM中，，∴△ANE≌△ECM（ASA），∴CM＝NE，又∵NF＝NE＝MC，∴AF＝MC+EC，∴AD＝MC+2EC．11、如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．【解答】解：（1）∵四边形ABCD是正方形，∴AB＝CD，AB∥CD，∴∠DCA＝∠BAC，∵DF∥BE，∴∠CFD＝∠BEA，∵∠BAC＝∠BEA+∠ABE，∠DCA＝∠CFD+∠CDF，∴∠ABE＝∠CDF，在△ABE和△CDF中，∵，∴△ABE≌△CDF（AAS），∴BE＝DF，∵BH＝DG，∴BE+BH＝DF+DG，即EH＝GF，∵EH∥GF，∴四边形EHFG是平行四边形；（2）如图，连接BD，交EF于O，∵四边形ABCD是正方形，∴BD⊥AC，∴∠AOB＝90°，∵AB＝2，∴OA＝OB＝2，Rt△BOE中，EB＝4，∴∠OEB＝30°，∴EO＝2，∵OD＝OB，∠EOB＝∠DOF，∵DF∥EB，∴∠DFC＝∠BEA，∴△DOF≌△BOE（AAS），∴OF＝OE＝2，∴EF＝4，∴FM＝2，EM＝6，过F作FM⊥EH于M，交EH的延长线于M，∵EG∥FH，∴∠FHM＝∠GEH，∵tan∠GEH＝tan∠FHM＝＝2，∴，∴HM＝1，∴EH＝EM﹣HM＝6﹣1＝5，FH＝＝＝，∴四边形EHFG的周长＝2EH+2FH＝2×5+2＝10+2．12、如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G 不重合），在运动过程中始终保持线段PQ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为3；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a的取值范围．【解答】（1）解：①P在线段AD上，PQ＝AB＝20，AP＝x，AM＝12，四边形AMQP的面积＝（12+20）x＝48，解得：x＝3；故答案为：3；②当P，在AD上运动时，P到D点时四边形AMQP面积最大，为直角梯形，∴0＜x≤10时，四边形AMQP面积的最大值＝（12+20）10＝160，当P在DG上运动，10＜x≤20，四边形AMQP为不规则梯形，作PH⊥AB于M，交CD于N，作GE⊥CD于E，交AB于F，如图2所示：则PM＝x，PN＝x﹣10，EF＝BC＝10，∵△GDC是等腰直角三角形，∴DE＝CE，GE＝CD＝10，∴GF＝GE+EF＝20，∴GH＝20﹣x，由题意得：PQ∥CD，∴△GPQ∽△GDC，∴＝，即＝，解得：PQ＝40﹣2x，∴梯形AMQP的面积＝（12+40﹣2x）×x＝﹣x2+26x＝﹣（x﹣13）2+169，∴当x＝13时，四边形AMQP的面积最大＝169；（2）解：P在DG上，则10≤x≤20，AM＝a，PQ＝40﹣2x，梯形AMQP的面积S＝（a+40﹣2x）×x＝﹣x2+x，对称轴为：x＝10+，∵0≤x≤20，∴10≤10+≤15，对称轴在10和15之间，∵10≤x≤20，二次函数图象开口向下，∴当x＝20时，S最小，∴﹣202+×20≥50，∴a≥5；综上所述，a的取值范围为5≤a≤20．13、在矩形ABCD中，AE⊥BD于点E，点P是边AD上一点．（1）若BP平分∠ABD，交AE于点G，PF⊥BD于点F，如图①，证明四边形AGFP是菱形；（2）若PE⊥EC，如图②，求证：AE•AB＝DE•AP；（3）在（2）的条件下，若AB＝1，BC＝2，求AP的长．【解答】（1）证明：如图①中，∵四边形ABCD是矩形，∴∠BAD＝90°，∵AE⊥BD，∴∠AED＝90°，∴∠BAE+∠EAD＝90°，∠EAD+∠ADE＝90°，∴∠BAE＝∠ADE，∵∠AGP＝∠BAG+∠ABG，∠APD＝∠ADE+∠PBD，∠ABG＝∠PBD，∴∠AGP＝∠APG，∴AP＝AG，∵P A⊥AB，PF⊥BD，BP平分∠ABD，∴P A＝PF，∴PF＝AG，∵AE⊥BD，PF⊥BD，∴PF∥AG，∴四边形AGFP是平行四边形，∵P A＝PF，∴四边形AGFP是菱形．（2）证明：如图②中，∵AE⊥BD，PE⊥EC，∴∠AED＝∠PEC＝90°，∴∠AEP＝∠DEC，∵∠EAD+∠ADE＝90°，∠ADE+∠CDE＝90°，∴∠EAP＝∠EDC，∴△AEP∽△DEC，∴＝，∵AB＝CD，∴AE•AB＝DE•AP；（3）解：∵四边形ABCD是矩形，∴BC＝AD＝2，∠BAD＝90°，∴BD＝＝，∵AE⊥BD，∴S△ABD＝•BD•AE＝•AB•AD，∴AE＝，∴DE＝＝，∵AE•AB＝DE•AP；∴AP＝＝．14、已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM 的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为2cm/s，BC的长度为10cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．【解答】解：（1）∵t＝2.5s时，函数图象发生改变，∴t＝2.5s时，M运动到点B处，∴动点M的运动速度为：＝2cm/s，∵t＝7.5s时，S＝0，∴t＝7.5s时，M运动到点C处，∴BC＝（7.5﹣2.5）×2＝10（cm），故答案为：2，10；（2）①∵两动点M，N在线段BC上相遇（不包含点C），∴当在点C相遇时，v＝＝（cm/s），当在点B相遇时，v＝＝6（cm/s），∴动点N运动速度v（cm/s）的取值范围为cm/s＜v≤6cm/s；②过P作EF⊥AB于F，交CD于E，如图3所示：则EF∥BC，EF＝BC＝10，∴＝，∵AC＝＝5，∴＝，解得：AF＝2，∴DE＝AF＝2，CE＝BF＝3，PF＝＝4，∴EP＝EF﹣PF＝6，∴S1＝S△APM＝S△APF+S梯形PFBM﹣S△ABM＝×4×2+（4+2x﹣5）×3﹣×5×（2x﹣5）＝﹣2x+15，S2＝S△DPM＝S△DEP+S梯形EPMC﹣S△DCM＝×2×6+（6+15﹣2x）×3﹣×5×（15﹣2x）＝2x，∴S1•S2＝（﹣2x+15）×2x＝﹣4x2+30x＝﹣4（x﹣）2+，∵2.5＜＜7.5，在BC边上可取，∴当x＝时，S1•S2的最大值为．15、如图1，正方形ABDE和BCFG的边AB，BC在同一条直线上，且AB＝2BC，取EF的中点M，连接MD，MG，MB．（1）试证明DM⊥MG，并求的值．（2）如图2，将图1中的正方形变为菱形，设∠EAB＝2α（0＜α＜90°），其它条件不变，问（1）中的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．【解答】（1）证明：如图1中，延长DM交FG的延长线于H．∵四边形ABCD，四边形BCFG都是正方形，∴DE∥AC∥GF，∴∠EDM＝∠FHM，∵∠EMD＝∠FMH，EM＝FM，∴△EDM≌△FHM（AAS），∴DE＝FH，DM＝MH，∵DE＝2FG，BG＝DG，∴HG＝DG，∵∠DGH＝∠BGF＝90°，MH＝DM，∴GM⊥DM，DM＝MG，连接EB，BF，设BC＝a，则AB＝2a，BE＝2a，BF＝a，∵∠EBD＝∠DBF＝45°，∴∠EBF＝90°，∴EF＝＝a，∵EM＝MF，∴BM＝EF＝a，∵HM＝DM，GH＝FG，∴MG＝DF＝a，∴＝＝．（2）解：（1）中的值有变化．理由：如图2中，连接BE，AD交于点O，连接OG，CG，BF，CG交BF于O′．∵DO＝OA，DG＝GB，∴GO∥AB，OG＝AB，∵GF∥AC，∴O，G，F共线，∵FG＝AB，∴OF＝AB＝DF，∵DF∥AC，AC∥OF，∴DE∥OF，∴OD与EF互相平分，∵EM＝MF，∴点M在直线AD上，∵GD＝GB＝GO＝GF，∴四边形OBFD是矩形，∴∠OBF＝∠ODF＝∠BOD＝90°，∵OM＝MD，OG＝GF，∴MG＝DF，设BC＝m，则AB＝2m，易知BE＝2OB＝2•2m•sinα＝4m sinα，BF＝2BO°＝2m•cosα，DF＝OB＝2m•sinα，∵BM＝EF＝＝，GM＝DF＝m•sinα，∴＝＝．16、综合与实践动手操作：第一步：如图1，正方形纸片ABCD沿对角线AC所在的直线折叠，展开铺平．在沿过点C的直线折叠，使点B，点D都落在对角线AC上．此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一条直线上，折痕分别为CE，CF．如图2．第二步：再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3．第三步：在图3的基础上继续折叠，使点C与点F重合，如图4，展开铺平，连接EF，FG，GM，ME．如图5，图中的虚线为折痕．问题解决：（1）在图5中，∠BEC的度数是67.5°，的值是．（2）在图5中，请判断四边形EMGF的形状，并说明理由；（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：菱形EMCH或菱形FGCH．【解答】解：（1）由折叠的性质得：BE＝EN，AE＝AF，∠CEB＝∠CEN，∠BAC＝∠CAD，∵四边形ABCD是正方形，∴∠EAF＝90°，∴∠AEF＝∠AFE＝45°，∴∠BEN＝135°，∴∠BEC＝67.5°，∴∠BAC＝∠CAD＝45°，∵∠AEF＝45°，∴△AEN是等腰直角三角形，∴AE＝EN，∴＝＝；故答案为：67.5°，；（2）四边形EMGF是矩形；理由如下：∵四边形ABCD是正方形，∴∠B＝∠BCD＝∠D＝90°，由折叠的性质得：∠BCE＝∠ECA＝∠ACF＝∠FCD，CM＝CG，∠BEC＝∠NEC＝∠NFC＝∠DFC，∴∠BCE＝∠ECA＝∠ACF＝∠FCD＝＝22.5°，∠BEC＝∠NEC＝∠NFC＝∠DFC＝67.5°，由折叠可知：MH、GH分别垂直平分EC、FC，∴MC＝ME＝CG＝GF，∴∠MEC＝∠BCE＝22.5°，∠GFC＝∠FCD＝22.5°，∴∠MEF＝90°，∠GFE＝90°，∵∠MCG＝90°，CM＝CG，∴∠CMG＝45°，∵∠BME＝∠BCE+∠MEC＝22.5°+22.5°＝45°，∴∠EMG＝180°﹣∠CMG﹣∠BME＝90°，∴四边形EMGF是矩形；（3）连接EH、FH，如图所示：∵由折叠可知：MH、GH分别垂直平分EC、FC，同时EC、FC也分别垂直平分MH、GH，∴四边形EMCH与四边形FGCH是菱形，故答案为：菱形EMCH或菱形FGCH．17、已知：在矩形ABCD中，E，F分别是边AB，AD上的点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O．（1）填空：点A在（填“在”或“不在”）⊙O上；当＝时，tan∠AEF的值是；（2）如图1，在△EFH中，当FE＝FH时，求证：AD＝AE+DH；（3）如图2，当△EFH的顶点F是边AD的中点时，求证：EH＝AE+DH；（4）如图3，点M在线段FH的延长线上，若FM＝FE，连接EM交DC于点N，连接FN，当AE＝AD 时，FN＝4，HN＝3，求tan∠AEF的值．【解答】解：（1）连接AO，∵∠EAF＝90°，O为EF中点，∴AO＝EF，∴点A在⊙O上，当＝时，∠AEF＝45°，∴tan∠AEF＝tan45°＝1，故答案为：在，1；（2）∵EF⊥FH，∴∠EFH＝90°，在矩形ABCD中，∠A＝∠D＝90°，∴∠AEF+∠AFE＝90°，∠AFE+∠DFH＝90°，∴∠AEF＝∠DFH，又FE＝FH，∴△AEF≌△DFH（AAS），∴AF＝DH，AE＝DF，∴AD＝AF+DF＝AE+DH；（3）延长EF交HD的延长线于点G，∵F分别是边AD上的中点，∴AF＝DF，∵∠A＝∠FDG＝90°，∠AFE＝∠DFG，∴△AEF≌△DGF（ASA），∴AE＝DG，EF＝FG，∵EF⊥FG，∴EH＝GH，∴GH＝DH+DG＝DH+AE，∴EH＝AE+DH；（4）过点M作MQ⊥AD于点Q．设AF＝x，AE＝a，∵FM＝FEEF⊥FH，∴△EFM为等腰直角三角形，∴∠FEM＝∠FMN＝45°，∵FM＝FE，∠A＝∠MQF＝90°，∠AEF＝∠MFQ，∴△AEF≌△QFM（ASA），∴AE＝EQ＝a，AF＝QM，∵AE＝AD，∴AF＝DQ＝QM＝x，∵DC∥QM，∴，∵DC∥AB∥QM，∴，∴，∵FE＝FM，∴，∠FEM＝∠FMN＝45°，∴△FEN～△HMN，∴，∴．。

中考体系-74.四边形综合-3(最全,含答案)

四边形综合-3一、性质综合二、判定及综合三、中位线四、中点四边形五、剪拼五、剪拼1. 【易】（沈阳八年级）以不共线三点为三个顶点作平行四边形，一共可作平行四边形的个数是（） A ．2个 B ．3个 C ．4个 D ．5个【答案】B2. 【易】（沈阳八年级）用两个全等的三角形按不同的方法拼成四边形，在这些拼出的四边形中，平行四边形最多有（） A ．1个 B ．2个 C ．3个 D ．4个【答案】C3. 【易】（沈阳八年级）用两个能够完全重合的非等腰三角形拼成四边形则拼成平行四边形的最多个数有（） A ．1个 B ．2个 C ．3个 D ．4个【答案】C4. 【易】（初二下期末复习五）用两个能够完全重合的不等边三角形按不同的方式拼成的各种不同的四边形中，平行四边形有（） A ．1个 B ．2个 C ．3个 D ．4个【答案】C5. 【易】（沈阳初二）把两个全等的边长分别是6，7，8的三角形拼成平行四边形，则拼成的平行四边形的周长为___________．【答案】26，28或306. 【易】（2011年南平中考）有一等腰梯形纸片ABCD （如图），AD BC ∥，1AD =，3BC =，沿梯形的高DE 剪下，由DEC △与四边形ABED 不一定能拼成的图形是（）A ．直角三角形B ．矩形C ．平行四边形D ．正方形【答案】D7. 【易】（20届希望杯初二2试）将一张四边形纸片沿两组对边的中点连线剪开，得到四张小纸片，如图3所示．用这四张小纸片一定可拼成一个（）A ．梯形B ．矩形C ．菱形D ．平行四边形【答案】D8. 【中】（2012深圳初三月考）如果把左图的正方形纸板剪成四块恰好能拼成右图的矩形，则a 等于（）A ．51- B ．51+ C ．53+D ．21+【答案】B9. 【中】（河南省实验中学2011年内部中考数学第一轮复习资料4）如图，沿虚线将平行四边形剪开，则得到的四边形是（）A ．梯形B ．平行四边形C ．矩形D ．菱形【答案】A10. 【中】（石景山区2010年初三第一次统一练习暨毕业考试）⑴ 如图1，把边长是3的等边三角形的各边三等分，分别以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到图2，再把图2中图形各边三等分，分别ECBDA aa111EF ABCD ABFE D CF BAE以居中那条线段为一边向外作等边三角形，并去掉居中的那条线段，得到一个新图形，则这个新图形的周长是____________；⑵ 如图3，在的网格中有一个正方形，把正方形的各边三等分，分别以居中那条线段为斜边向外作等腰直角三角形，去掉居中的那条线段，得到图4，请把图4中的图形剪拼成正方形，并在图4中画出剪裁线，在图5中画出剪拼后的正方形．【答案】⑴16⑵11. 【中】（2011年天津市南开区初中毕业生学业水平质量调查（二））图1是一个八角星形纸板，图中有八个直角，八个相等的钝角，每条边都相等，如图2将纸板沿虚线进行切割，无缝隙无重叠的拼成图3所示的大正方形，其面积为8-则图3中线段AB 的长为________．112. 【中】（北大附中2012-2013学年度第二学期期中考试初二年级数学试卷）操作与探究邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又剩下一个四边形，称为第二操作；……依此类图2图155⨯图5图4图3推，若第n 次操作余下的四边形是菱形，则称原平行四边形为n 阶准菱形．如图1，ABCD 中，若1AB =，2BC =，则ABCD 为1阶准菱形．（1）判断与推理：①邻边长分别为2和3的平行四边形是_____阶准菱形（填空）； ②小明为了剪去一个菱形，进行了如下操作：如图2，把ABCD 沿BE 折叠（点E 在AD 上），使点A 落在BC 边上的点F ，得到四边形ABFE ．请证明四边形ABFE 是菱形．（2）操作、探究与计算：①已知ABCD 的邻边长分别为1，()1a a >，且是3阶准菱形，请画出ABCD 及裁剪线的示意图，并在图形下方写出a 的值；②已知ABCD 的邻边长分别为a ，()b a b >，满足6a b r =+，5b r =，则ABCD 是______阶准菱形（填空）【答案】（1）①2②略（2）①4②1013. 【中】（延庆县2012学年第一学期期末试卷）如图1，若将AOB △绕点O 逆时针旋转180︒得到COD △，则AOB COD △≌△．此时，我们称AOB △与COD △为“8字全等型”．借助“8字全等型”我们可以解决一些图形的分割与拼接问题．例如：图2中，ABC △是锐角三角形且AC AB >，点E 为AC 中点，F 为BC 上一点且BF FC ≠（F 不与B ．C 重合），沿EF 将其剪开，得到的两块图形恰能拼成一个梯形．请分别按下列要求用直线将图2中的ABC △重新进行分割，画出分割线及拼接后的图形．⑴ 在图3中将ABC △沿分割线剪开，使得到的两块图形恰能拼成一个平行四边形； ⑵ 在图4中将ABC △沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的两块为直角三角形；图1DCBA图2FEABCD图1 图2②②①E CFB AA B OC D⑶ 在图5中将ABC △沿分割线剪开，使得到的三块图形恰能拼成一个矩形，且其中的一块为锐角三角形．【答案】⑴⑵⑶14. 【中】（北京师大附中2012年第二学期期中考试·初二数学）动手做一做有一块形状如图的木板，经过适当的剪切后，拼成一块面积最大的正方形板材，请在图中画出剪切线，并把拼成的正方形在图中画出（保留剪切的痕迹，不写画法）【答案】图3 图4 图5AAB C B CB CA③③②①①CBA15. 【中】(2013年广东省佛山市高中阶段招生考试数学试题)我们知道，矩形是特殊的平行四边形，所以矩形除了具备平行四边形的一切性质还有其特殊的性质；同样，黄金矩形是特殊的矩形，因此黄金矩形有与一般矩形不一样的知识．已知平行四边形ABCD ，60A ∠=︒，2AB a =，AD a =．⑴ 把所给的平行四边形ABCD 用两种方式分割并作说明（见题答卡表格里的示例）；要求：用直线段分割，分割成的图形是学习过的特殊图形且不超出四个．⑵ 图中关于边、角和对角线会有若干关系或问题．现在请计算两条对角线的长度．要求：计算对角线BD 长的过程中要有必要的论证；直接写出对角线AC 的长．【答案】⑴①分割成两个等腰梯形．两个等腰梯形的腰长都为a ，上底长都为2a，下底长都为32a ，上底角都为120°，下底角都为60°. ②分割成一个等边三角形、一个等腰三角形、一个直角三角形．等边三角形的边长为a ，等腰三角形的腰长为a ，顶角为120°．直角三角形两锐角为30°、60°，三边为a、2a 。

四边形练习题（含答案）

四边形练习题（含答案）四边形练习题（含答案）1、阅读下⾯材料，再回答问题：有⼀些⼏何图形可以被某条直线分成⾯积相等的两部分，我们将“把⼀个⼏何图形分成⾯积相等的两部分的直线叫做该图形的⼆分线”，如：圆的直径所在的直线是圆的“⼆分线”，正⽅形的对⾓线所在的直线是正⽅形的“⼆分线”。

解决下列问题：（1）菱形的“⼆分线”可以是。

（2）三⾓形的“⼆分线”可以是。

（3）在下图中，试⽤两种不同的⽅法分别画出等腰梯形ABCD的“⼆分线”.2、⽤配⽅法解⽅程时，原⽅程可变形为（）A．B．C．D．3、⽤两块边长为a的等边三⾓形纸⽚拼成的四边形是【】A．等腰梯形B．菱形 C．矩形D．正⽅形4、在下⾯图形中，每个⼤正⽅形⽹格都是由边长为1的⼩正⽅形组成，则图中阴影部分⾯积最⼤的是（）5、下列命题中错误的是（）A．两组对边分别相等的四边形是平⾏四边形B．对⾓线相等的平⾏四边形是矩形C．⼀组邻边相等的平⾏四边形是菱形D．⼀组对边平⾏的四边形是梯形6、如图，每个⼩正⽅形的边长为1，把阴影部分剪下来，⽤剪下来的阴影部分拼成⼀个正⽅形，那么新正⽅形的边长是( )A． B．2C．D．7、将⼀正⽅形纸⽚按下列顺序折叠，然后将最后折叠的纸⽚沿虚线剪去上⽅的⼩三⾓形．将纸⽚展开，得到的图形是（）8、如下图1，在矩形ABCD中，动点P从点B出发，沿BC，CD，DA运动⾄点A停⽌．设点P运动的路程为x，△ABP 的⾯积为y，如果y关于x的函数图象如图2所⽰，则△ABC的⾯积是A．10 B．16 C．18D．209、如图，在梯形ABCD中，AD//BC，AD=2，AB=3，BC=6，沿AE翻折梯形ABCD，使点B落在AD的延长线上，记为B′，连接B′E交CD于F，则的值为( )A． B． C． D．10、⽤任意两个全等的直⾓三⾓形拼下列图形：①平⾏四边形②矩形③菱形④正⽅形⑤等腰三⾓形⑥等边三⾓形其中⼀定能够拼成的图形是_______（只填题号）．11、某陶瓷市场现出售的有边长相等的正三⾓形、正⽅形、正五边形的地板砖，某顾客想买其中的镶嵌着铺地板，则他可以选择的是．12、在⼀张三⾓形纸⽚中，剪去其中⼀个50°的⾓，得到如图所⽰的四边形，则图中∠1+∠2的度数为______________。

中考数学一轮复习《四边形》综合复习练习题(含答案)

中考数学一轮复习《四边形》综合复习练习题（含答案）一、单选题1．一个多边形的内角和为900°，则这个多边形是（）A ．七边形B ．八边形C ．九边形D ．十边形 2．如图，将三角形纸片剪掉一角得四边形，设△ABC 与四边形BCDE 的外角和的度数分别为α，β，则正确的是（）A ．0αβ-=B ．0αβ-<C ．0αβ->D ．无法比较α与β的大小3．如图，把一个长方形纸片沿EF 折叠后，点D 、C 分别落在D ′、C ′的位置，若∠EFB ＝65°，则∠AED ′等于（）A ．50°B ．55°C ．60°D ．65°4．若一个正多边形的一个外角是60°，则这个正多边形的边数是（）A ．10B ．9C ．8D ．65．如图，四边形ABCD 是平行四边形，下列结论中正确的是（）A ．当ABCD 是矩形时，90BAC ∠=︒B ．当ABCD 是菱形时，AB BC ⊥ C ．当ABCD 是正方形时，AC BD = D ．当ABCD 是菱形时，AB AC =6．如图，在正方形ABCD 中，AE 平分BAC ∠交BC 于点E ，点F 是边AB 上一点，连接DF ，若BE AF =，则CDF ∠的度数为（）A ．45︒B ．60︒C ．67.5︒D ．775︒.7．如图，要拧开一个边长为()=6mm a a 的正六边形，扳手张开的开口b 至少为（）A ．43mmB ．63mmC ． 42mmD ． 12mm8．如图，菱形ABCD 中，∠BAD = 60°，AB = 6，点E ，F 分别在边AB ，AD 上，将△AEF 沿EF 翻折得到△GEF ，若点G 恰好为CD 边的中点，则AE 的长为（）A ．34B ．214C 3154D ．39．以下说法不正确的是（）A ．平行四边形是抽对称图形B ．矩形对角线相等C ．正方形对角线互相垂直平分D ．菱形四条边相等10．陈师傅应客户要求加工4个长为4cm 、宽为3cm 的矩形零件．在交付客户之前，陈师傅需要对4个零件进行检测．根据零件的检测结果，图中有可能不合格的零件是（）A．B．C．D．11．如图，AB是半圆O的直径，以弦AC为折痕折叠AC后，恰好经过点O，则AOC∠等于（）A．120°B．125°C．130°D．145°12．如图，在平面直角坐标系中，矩形ABCD的对角线AC经过坐标原点O，矩形的边分别平行于坐标轴，点B在函数kyx=（k≠0，x＞0）的图像上，点D的坐标为（﹣3，1），则k的值为（）A．53B．3-C．3D．53-二、填空题13．如果一个多边形的每一个外角都是60︒，那么这个多边形的边数是_______．14．如图，在矩形ABCD中，E是AD边上一点，且2AE DE=，BD与CE相交于点F，若DEF 的面积是3，则BCF △的面积是______．15．如果正多边形的一个外角是45︒，则这个正多边形的内角和是________︒．16．巧板是我国古代劳动人民的一项发明，被誉为“东方魔板”，它由五块等腰直角三角形、一块正方形和一块平行四边形组成．如图是利用七巧板拼成的正方形，随机向该图形内抛一枚小针，则针尖落在阴影部分的概率为 _____．17．如图，四边形ABCD 是菱形，42BD =，26AD =，点E 是CD 边上的一动点，过点E 作EF ⊥OC 于点F ，EG ⊥OD 于点G ，连接FG ，则FG 的最小值为_________．18．如图，矩形ABCD 的对角线AC 、BD 相交于点O ，过点O 作OE AC ⊥交AD 于点E ，若4AB =，8BC =，则DE 的长为______．19．已知ABC 中，65A ∠=︒，将B C ∠∠、按照如图所示折叠，若35ADB '∠=︒，则123∠+∠+∠=_____︒．CE ，F 20．如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，5为DE的中点．若CEF△的周长为18，则OF的长为______．三、解答题21．如图，一组正多边形，观察每个正多边形中a的变化情况，解答下列问题．(1)将表格补充完整．正多边形的边数 3 4 5 6α的度数(2)观察上面表格中α的变化规律，角α与边数n的关系为．(3)根据规律，当α＝18°时，多边形边数n＝．22．如图，在ABCD中，AC=BC，M、N分别是AB和CD的中点．(1)求证：四边形AMCN是矩形；(2)若∠B=60°，BC=8，求ABCD的面积．23．如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD 的中点，延长AE至G，使EG＝AE，连接CG．(1)求证：△ABE≌△CDF；(2)当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．24．如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG．(1)求证：四边形CEFG是菱形；(2)若AB=6，AD=10，求四边形CEFG的面积．25．如图，点E为矩形ABCD外一点，AE = DE.求证：△ABE≌△DCE26．如图，已知四边形ABCD为正方形，AB＝2，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．(1)求证：矩形DEFG是正方形；(2)探究：①CE与CG有怎样的位置关系？请说明理由．②CE＋CG的值为．27．某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：【现察与猜想】(1)如图1，在正方形ABCD中，点E，F分别是AB，AD上的两点，连接DE，CF，DE⊥CF，则DECF的值为______．(2)如图2，在矩形ABCD中，AD=7，CD=4，点E是AD上的一点，连接CE，BD，且CE⊥BD，则CEBD的值______．【类比探究】(3)如图3，在四边形ABCD中，∠A=∠B=90°，点E为AB上一点，连接DE，过点C作DE 的垂线交ED的延长线于点G，交AD的延长线于点F，求证：DE•AB=CF•AD．28．在矩形ABCD中，AB＝6，AD＝4，点M为AB边上一个动点，连接DM，过点M作MN⊥DM，且MN＝32DM，连接DN．(1)如图1，连接BD与BN，BD交MN于点E．①求证：△ABD∽△MND；②求证：∠CBN＝∠DNM．(2)如图2，当AM＝4BM时，求证：A，C，N三点在同一条直线上．参考答案1．A2．A3．A4．D5．C6．C7．B8．B9．A10．C11．A12．B13．614．2715．108016．381718．319．265︒20．7221．（1）正多边形每个内角的度数为180(2)n n -． 1803,603n α===； 904,452n α===；正五边形的内角180(52)1085-=，1801085,362n α-===；正五边形的内角180(62)1206-=，1801206,302n α-===．（2）观察（1）中结论，1803,603n == 1804,454n == 1805,365n == 1806,306n == 总结规律，则有180n α=．（3）借助（2）中公式，有180n α=，即18018n= 解得10n =．22．（1）证明：∵四边形ABCD 是平行四边形， ∴AB ∥CD ，AB =CD ，∵M 、N 分别是AB 和CD 的中点， ∴AM =BM ，AM ∥CN ，AM =CN ， ∴四边形AMCN 是平行四边形，又∵AC =BC ，AM =BM ，∴CM ⊥AB ，∴∠CMA =90°，∴四边形AMCN 是矩形；（2）解：∵∠B =60°，BC =8，∠BMC =90°， ∴∠BCM =30°，∴Rt △BCM 中，BM =12BC =4，CM∵AC =BC ，CM ⊥AB ，∴AB =2BM =8，∴ABCD 的面积为AB ×CM23．（1）证明：∵四边形ABCD 是平行四边形， ∴AB =CD ，AB ∥CD ，OB =OD ，OA =OC ， ∴∠ABE =∠CDF ，∵点E ，F 分别为OB ，OD 的中点， ∴BE =12OB ，DF =12OD ，∴BE =DF ，在△ABE 和△CDF 中，AB CD ABE CDF BE DF ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABE ≌△CDF (SAS ) ．（2）当AB =12AC 时，四边形EGCF 是矩形；理由如下：当AB =12AC 时，∵AC =2OA ，AC =2AB ，∴AB =OA ，∵E 是OB 的中点，∴AG⊥OB，∴∠OEG=90°，同理：CF⊥OD，∴AG∥CF，∴EG∥CF，由（1）得：△ABE≌△CDF，∴AE=CF，∵EG=AE，∴EG=CF，∴四边形EGCF是平行四边形，∵∠OEG=90°，∴四边形EGCF是矩形．24．（1）证明：由题意可得，△BCE≌△BFE，∴∠BEC=∠BEF，FE=CE，∵FG∥CE，∴∠FGE=∠CEB，∴∠FGE=∠FEG，∴FG=FE，∴FG=EC，∴四边形CEFG是平行四边形，又∵CE=FE，∴四边形CEFG是菱形；（2）解：∵矩形ABCD 中，AB =6，AD =10，BC =BF ，∴∠BAF =90°，AD =BC =BF =10，∴AF =8，∴DF =2，设EF =x ，则CE =x ，DE =6-x ，∵∠FDE =90°，∴22+（6-x ）2=x 2，解得，x =103， ∴CE =103， ∴四边形CEFG 的面积是：CE •DF =103×2=203． 25．解：四边形ABCD 是矩形，AB DC ∴=，90BAD CDA ∠=∠=︒，AE DE =，EAD EDA ∴∠=∠，EAB BAD EAD CDA EDA EDC ∴∠=∠+∠=∠+=∠，在ABE ∆和DCE ∆中，AE DE EAB EDC AB DC =⎧⎪∠=∠⎨⎪=⎩()ABE DCE SAS ∴∆∆≌．26．（1）如图，作EM ⊥BC 于M ，EN ⊥CD 于N ，又∠BCD =90°，∴∠MEN ＝90°，∵点E 是正方形ABCD 对角线上的点，∴EM ＝EN ，∵∠DEF ＝90°，∴∠DEN ＝∠MEF ＝90°﹣∠FEN ，∵∠DNE ＝∠FME ＝90°，在△DEN 和△FEM 中，DNE FME EN EMDEN FEM ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△DEN ≌△FEM （ASA ），∴EF ＝DE ，∵四边形DEFG 是矩形，∴矩形DEFG 是正方形；（2）①CE ⊥CG ，理由如下：∵正方形DEFG 和正方形ABCD ，∴DE ＝DG ，AD ＝DC ，∵∠CDG +∠CDE ＝∠ADE +∠CDE ＝90°，∴∠CDG ＝∠ADE ，在△ADE 和△CDG 中，AD CD ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△CDG （SAS ），∴∠DAE ＝∠DCG ，∵∠ACD +∠CAD +∠ADC ＝180°，∠ADC ＝90°，∴∠ACG ＝∠ACD +∠DCG ＝∠ACD +∠CAD ＝90°， ∴CE ⊥CG ；②由①知，△ADE ≌△CDG ，∴AE ＝CG ，∴CE +CG ＝CE +AE ＝ACAB＝2，故答案为：2.27.（1）解：设DE与CF的交点为G，∵四边形ABCD是正方形，∴∠A=∠FDC=90°，AD=CD，∵DE⊥CF，∴∠DGF=90°，∴∠ADE+∠CFD=90°，∠ADE+∠AED=90°，∴∠CFD=∠AED，在△AED与△DFC中，A FDCCFD AEDAD CD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AED≌△DFC（AAS），∴DE=CF，∴DECF=1，故答案为：1；（2）解：如图，设DB与CE交于点G，∵四边形ABCD是矩形，∴∠A=∠EDC=90°，∵CE⊥BD，∴∠DGC=90°，∴∠CDG +∠ECD =90°，∠ADB +∠CDG =90°，∴∠ECD =∠ADB ，∵∠CDE =∠A ，∴△DEC ∽△ABD ， ∴47CE DC BD AD ==，故答案为：47；（3）证明：如图，过点C 作CH ⊥AF 交AF 的延长线于点H ，∵CG ⊥EG ，∴∠G =∠H =∠A =∠B =90°，∴四边形ABCH 为矩形，∴AB =CH ，∠FCH +∠CFH =∠DFG +∠FDG =90°，∴∠FCH =∠FDG =∠ADE ，∠A =∠H =90°，∴△AED ∽△HFC ，∴DE AD CF CH =， ∴DE AD CF AB=， ∴DE •AB =CF •AD ．28．（1）①证明：∵四边形ABCD 是矩形，DM ⊥MN ∴∠A ＝∠DMN ＝90°∵AB ＝6，AD ＝4，MN ＝32DM ∴23AD DM AB MN == ∴△ABD ∽△MND ．②证明：∵四边形ABCD 是矩形，DM ⊥MN ∴∠ABC ＝∠DMN ＝90°∴∠ABD ＋∠CBD ＝90°由①得△ABD ∽△MND∴∠ABD ＝∠DNM又∵∠MEB ＝∠DEN∴△MBE ∽△DNE ∴ME BE DE NE = ∴ME DE BE NE= 又∠MED ＝∠BEN∴△DME ∽△NBE∴∠NBE ＝∠DME ＝90°∴∠CBN ＋∠CBD ＝90°又∠ABD ＋∠CBD ＝90°，∠ABD ＝∠DNM ∴∠CBN ＝∠DNM ．（2）如图②，过点N 作NF ⊥AB 于点F ，连接AC ，AN ∴∠NF A ＝90°∵四边形ABCD 是矩形，AD ＝4，AB ＝6 ∴∠A ＝∠ABC ＝90°，BC ＝AD ＝4∴23BC AB =，∠ADM ＋∠AMD ＝90° ∵AM ＝4BM ，AB ＝6∴42455AM AB ＝＝又DM ⊥MN∴∠AMD ＋∠FMN ＝90° ∴∠ADM ＝∠FMN∴△ADM ∽△FMN ∴AD AM DM MF FN MN== 又MN ＝32DM ∴24425=3DM MF FN MN == ∴MF ＝6，FN ＝365∴AF ＝AM ＋MF ＝2454655+= ∴23NF AF = ∴NF BC AF AB = ∵∠ABC ＝∠AFN ＝90° ∴△ABC ∽△AFN∴∠BAC ＝∠F AN∴A ，C ，N 三点在同一条直线．。

人教备战中考数学平行四边形综合经典题及详细答案

一、平行四边形真题与模拟题分类汇编（难题易错题）1．如图，矩形ABCD 中，AB =6，BC =4，过对角线BD 中点O 的直线分别交AB ，CD 边于点E ，F ．（1）求证：四边形BEDF 是平行四边形；（2）当四边形BEDF 是菱形时，求EF 的长．【答案】（1）证明见解析；（2）133．【解析】分析：（1）根据平行四边形ABCD 的性质，判定△BOE ≌△DOF （ASA ），得出四边形BEDF 的对角线互相平分，进而得出结论；（2）在Rt △ADE 中，由勾股定理得出方程，解方程求出BE ，由勾股定理求出BD ，得出OB ，再由勾股定理求出EO ，即可得出EF 的长.详解：（1）证明：∵四边形ABCD 是矩形，O 是BD 的中点，∴∠A=90°，AD=BC=4，AB ∥DC ，OB=OD ，∴∠OBE=∠ODF ，在△BOE 和△DOF 中，OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF （ASA ），∴EO=FO ，∴四边形BEDF 是平行四边形；（2）当四边形BEDF 是菱形时，BD ⊥EF ，设BE=x ，则 DE=x ，AE=6-x ，在Rt △ADE 中，DE 2=AD 2+AE 2，∴x 2=42+（6-x ）2，解得：x=133， ∵22AD AB +13 ∴OB=1213 ∵BD ⊥EF ，∴EO=22BE OB -=2133， ∴EF=2EO=4133．点睛：本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键 2．已知矩形纸片OBCD 的边OB 在x 轴上，OD 在y 轴上，点C 在第一象限，且86OB OD ==，.现将纸片折叠，折痕为EF （点E ，F 是折痕与矩形的边的交点），点P 为点D 的对应点，再将纸片还原。

（I ）若点P 落在矩形OBCD 的边OB 上，①如图①，当点E 与点O 重合时，求点F 的坐标；②如图②，当点E 在OB 上，点F 在DC 上时，EF 与DP 交于点G ，若7OP =，求点F 的坐标：（Ⅱ）若点P 落在矩形OBCD 的内部，且点E ，F 分别在边OD ，边DC 上，当OP 取最小值时，求点P 的坐标（直接写出结果即可）。

2020年九年级中考数学复习专题训练：《四边形综合》(含答案)

中考数学复习专题训练：《四边形综合》1．问题发现：（1）如图①，在△ABC中，∠ACB＝90°，AC＝b，BC＝a，点E是AC的中点，点F在BC 边上，将△ECF沿着EF折叠后得到△EPF，连接BP并使得BP最小，请画出符合题意的点P；问题探究：（2）如图②，已知在△ABC和△EBD中，∠ACB＝∠BDE＝90°，AC＝BC＝4，BD＝DE ＝2，连接CE，点F是CE的中点，连接AF，求AF的最大值．问题解决：（3）西安大明宫遗址公园是世界文化遗产，全国重点文物保护单位，为了丰富同学们的课外学习生活，培养同学们的探究实践能力，周末光明中学的张老师在家委会的协助下，带领全班同学去大明宫开展研学活动．在公园开设的一处沙地考古模拟场地上，同学们参加了一次模拟考古游戏．张老师为同学们现场设计了一个四边形ABCD的活动区域，如图③所示，其中BD为一条工作人员通道，同学们的入口设在点A处，AD⊥BD，AD∥BC，∠DCB＝60°，AB＝2米．在上述条件下，小明想把宝物藏在距入口A尽可能远的C 处让小鹏去找，请问小明的想法是否可以实现？如果可以，请求出AC的最大值及此时△BCD区域的面积，如果不能，请说明理由．2．已知：如图，在菱形ABCD中，AC＝2，∠B＝60°．点E为边BC上的一个动点（与点B、C不重合），∠EAF＝60°，AF与边CD相交于点F，联结EF交对角线AC于点G．设CE ＝x，EG＝y．（1）求证：△AEF是等边三角形；（2）求y关于x的函数解析式，并写出x的取值范围；（3）点O是线段AC的中点，联结EO，当EG＝EO时，求x的值．3．已知在正方形ABCD和正方形CEFG中，直线BG，DE交于点H．（1）如图1，当B，C，E共线时，求证：BH⊥DE．（2）如图2，把正方形CEFG绕C点顺时针旋转α度（0＜α＜90），M，N分别为BG，DE的中点，探究HM，HN，CM之间的数量关系，并证明你的结论．（3）如图3，∠PDG＝45°，DH⊥PG于H，PH＝2，HG＝4．直接写出DH的长．4．[问题引入]（1）如图1，在正方形ABCD中，E、F分别是BC、CD两边上的点，且AE⊥BF，垂足为点P．求证：AE＝BF；[类比探究]（2）如图2，把（1）中正方形ABCD改为矩形ABCD，且AD＝2AB，其余条件不变，请你推断AE、BF满足怎样的数量关系，并说明你的理由；[实践应用]（3）如图3，Rt△ABC中，∠BAC＝30°，把△ABC沿斜边AC对折得到Rt△ADC，E、F分别为CD、AD边上的点，连接AE、BF，恰好使得AE⊥BF，垂足为点P．请求出的值．5．如图，已知正方形ABCD中，BC＝4，AC、BD相交于点O，过点A作射线AM⊥AC，点E是射线AM上一点，联结OE交AB边于点F．以OE为一边，作正方形OEGH，且点A在正方形OEGH的内部，联结DH．（1）求证：△HDO≌△EAO；（2）设BF＝x，正方形OEGH的边长为y，求y关于x的函数关系式，并写出定义域；（3）联结AG，当△AEG是等腰三角形时，求BF的长．6．阅读材料：等腰三角形具有性质“等边对等角”．事实上，不等边三角形也具有类似性质“大边对大角”，如图1，在△ABC中，如果AB＞AC，那么∠ACB＞∠ABC．证明如下：将AB沿△ABC的角平分线AD翻折（如图2），因为AB＞AC，所以点B落在AC的延长线上的点B′处．于是，由∠ACB＞∠B′，∠ABC＝∠B′，可得∠ACB＞∠ABC．（1）灵活运用：从上面的证法可以看出，折纸常常能为证明一个命题提供思路和方法．由此小明想到可用类似方法证明“大角对大边”，如图3，在△ABC中，如果∠ACB＞∠ABC，那么AB＞AC．小明的思路是：沿BC的垂直平分线翻折……请你帮助小明完成后面的证明过程．（2）拓展延伸：请运用上述方法或结论解决如下问题：如图4，已知M为正方形ABCD的边CD上一点（不含端点），连接AM并延长，交BC的延长线于点N．求证：AM+AN＞2BD．7．探究：如图1和图2，四边形ABCD中，已知AB＝AD，∠BAD＝90°，点E、F分别在BC、CD上，∠EAF＝45°．（1）①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，直接写出线段BE、DF和EF之间的数量关系；②如图2，若∠B、∠D都不是直角，但满足∠B+∠D＝180°，线段BE、DF和EF之间的结论是否仍然成立，若成立，请写出证明过程；若不成立，请说明理由．（2）拓展：如图3，在△ABC中，∠BAC＝90°，AB＝AC＝2．点D、E均在边BC边上，且∠DAE＝45°，若BD＝1，求DE的长．8．如图1，在矩形ABCD中，AB＝4，AD＝3，沿对角线AC剪开，再把△ADC沿AB方向平移，得到图2，其中A'D交AC于E，A'C'交BC于F．（1）在图2中，除△ABC与△C'DA'外，指出还有哪几对全等三角形（不能添加辅助线和字母），并选择一对加以证明；（2）设AA'＝x．①当x为何值时，四边形A'ECF是菱形？②设四边形A'ECF的面积为y，求y的最大值．9．在正方形ABCD中，BD为对角线，点E在BD上，过点E作EF⊥CE，交AB于点F，连接CF．（1）如图①，求证：∠ECF＝45°；（2）如图②，作FG⊥AB，交BD于点G，求证：DE＝GE；（3）在（2）的条件下，如图③，延长FG交CE于点K，延长CE交AD于点M，连接MG、BK，若MG＝2EK，GK＝2，求线段BK的长．10．如图，在正方形ABCD中，M、N分别是射线CB和射线DC上的动点，且始终∠MAN＝45°．（1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；（2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成立，给予证明，若不成立，写出正确的结论，并证明；（3）如图3，当点M、N分别在CB、DC的延长线上时，若CN＝CD＝6，设BD与AM的延长线交于点P，交AN于Q，直接写出AQ、AP的长．11．如图，菱形ABCD中，AB＝10，连接BD，点P是射线BC上一点（不与点B重合），AP 与对角线BD交于点E，连接EC．（1）求证：AE＝CE；（2）若sin∠ABD＝，当点P在线段BC上时，若BP＝4，求△PEC的面积；（3）若∠ABC＝45°，当点P在线段BC的延长线上时，请直接写出△PEC是等腰三角形时BP的长．12．如图，在正方形ABCD 中，P 是边BC 上的一动点（不与点B ，C 重合），点B 关于直线AP 的对称点为E ，连接AE ．连接DE 并延长交射线AP 于点F ，连接BF ．（1）若∠BAP ＝α，直接写出∠ADF 的大小（用含α的式子表示）；（2）求证：BF ⊥DF ；（3）连接CF ，用等式表示线段AF ，BF ，CF 之间的数量关系，并证明．13．已知正方形OABC 在平面直角坐标系中，点A ，C 分别在x 轴，y 轴的正半轴上，等腰直角三角形OEF 的直角顶点O 在原点，E ，F 分别在OA ，OC 上，且OA ＝4，OE ＝2．将△OEF 绕点O 逆时针旋转，得△OE 1F 1，点E ，F 旋转后的对应点为E 1，F 1．（Ⅰ）①如图①，求E 1F 1的长；②如图②，连接CF 1，AE 1，求证△OAE 1≌△OCF 1；（Ⅱ）将△OEF 绕点O 逆时针旋转一周，当OE 1∥CF 1时，求点E 1的坐标（直接写出结果即可）．14．菱形ABCD中，E，F为边AB，AD上的点，CF，DE相交于点G．（1）如图1，若∠A＝90°，DE＝CF，求证：DE⊥CF；（2）如图2，若∠EGC+∠B＝180°．求证：DE＝CF；（3）如图3，在（1）的条件下，平移线段DE到MN，使G为CF的中点，连接BD交MN 于点H，若∠FCD＝15°，BN＝，请直接写出FG的长度．15．我们定义：对角线互相垂直的四边形叫做垂美四边形．（1）如图1，垂美四边形ABCD的对角线AC，BD交于O．求证：AB2+CD2＝AD2+BC2；（2）如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结BE，CG，GE．①求证：四边形BCGE是垂美四边形；②若AC＝4，AB＝5，求GE的长．16．（1）观察猜想如图①，点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE＝90°，AD＝AE，则△ADB 和△EAC是否全等？（填是或否），线段AB、AC、BD、CE之间的数量关系为．（2）问题解决如图②，在Rt△ABC中，∠ABC＝90°，AC＝6，AB＝6，以AC为直角边向外作等腰Rt △DAC，连接BD，求BD的长．（3）拓展延伸如图③，在四边形ABCD中，∠ABC＝∠ADC＝90°，AB＝5，AD＝，DC＝DA，CG⊥BD于点G，求CG的长，17．已知，在▱ABCD中，AB⊥BD，AB＝BD，E为射线BC上一点，连接AE交BD于点F．（1）如图1，若点E与点C重合，且AF＝2，求AD的长；（2）如图2，当点E在BC边上时，过点D作DG⊥AE于G，延长DG交BC于H，连接FH．求证：AF＝DH+FH；（3）如图3，当点E在射线BC上运动时，过点D作DG⊥AE于G，M为AG的中点，点N 在BC边上且BN＝1，已知AB＝4，请直接写出MN的最小值．18．如图，在矩形ABCD中，E是AB边上的一个动点，把△BCE沿CE折叠，使点B落在点F 处，过点F作GH∥CE，分别交AB、CD于点G、H．（1）求证：△EFG是等腰三角形；（2）如图①，若F是GH中点，求∠FGE的度数；（3）如图②，若点G与点A重合，AB＝30，BC＝20，求FH的长．19．在平面直角坐标系中，已知A（﹣4，0），B（4，0），点C，D在x轴上方，且四边形ABCD的面积为32，（1）若四边形ABCD是菱形，求点D的坐标．（2）若四边形ABCD是平行四边形，如图1，点E，F分别为CD，BC的中点，且AE⊥EF，求AE+2EF的值．（3）若四边形ABCD是矩形，如图2，点M为对角线AC上的动点，N为边AB上的动点，求BM+MN的最小值．20．在平面直角坐标系中，点O为坐标原点，正方形OABC与长方形DEFG的位置如图所示，点A在x轴的正半轴上，点C在y轴的正半轴上，点B的横坐标为a，点D，E在x轴的负半轴上（点E在点D的右侧），点G的坐标为（b，﹣b），DE＝OA，实数a，b的值满足．（1）求点F的坐标；（2）长方形DEFG以每秒1个单位长度的速度向右平移t（t＞0）秒得到矩形D'E'F'G'，点D'，E'，F'，G'分别为点D，E，F，G平移后的对应点，设矩形D'E'F'G'与正方形OABC 重合部分的面积为S，用含t的式子表示S，并直接写出相应的t的范围；（3）在（2）的条件下，在长方形DEFG出发运动的同时，点P从点O出发，沿正方形的边以每秒2个单位长度的速度顺时针方向运动（即O→C→B→A→O→C），连接PD'，PG'，当三角形PD'G'的面积为15时，求S＞0时相应的t值，并直接写出此时刻S值及点P 的坐标．参考答案1．解：（1）如图①中，点P即为所求．当E，P，B共线时，BP的值最小．（2）如图②中，取BC的中点P，连接PA，PF．∵∠BDE＝90°，BD＝DE＝2，∴BE＝BD＝4，∴CF＝EF，CP＝PB＝2，∴PF＝BE＝2，∵∠ACP＝90°，AC＝4，CP＝2，∴PA＝＝＝2，∵AF≤PA+PF，∴AF≤2+2，∴AF的最大值为2+2．（3）如图③中，作△ABD的外接圆⊙O交CD于E，连接OE，EB，AC．∵∠DBC＝90°，∠DCB＝60°，∴∠CDB＝30°，∴∠EOB＝60°，∵EO＝EB，∴△EOB是等边三角形，BE＝OB＝，∵∠ECB＝60°，∴点C的运动轨迹是圆弧，不妨设圆心为P，连接PC，PE，PB，则∠EPB＝2∠ECB＝120°，作PT⊥BE于T，在Rt△PET中，∠PET＝30°，ET＝BT＝BE＝，∴PE＝PB＝PC＝＝，∵∠EBO＝60°，∠EBP＝30°，∴∠ABP＝90°，在Rt△ABP中，AP＝＝＝13，∵AC≤PA+PC，∴AC≤13+，∴AC的最大值为13+，此时A，P，C共线，如图③﹣1中，作CW⊥AB于W．∵PB∥CW，∴＝＝，∴＝＝，∴CW＝+1，BW＝2，∴BC＝＝＝，∴S＝•BC•BD＝•BC•BC＝×（26+2）＝13+．△BCD2．（1）证明：∵四边形ABCD为菱形，∴AB＝BC，∵∠B＝60°，∴△ABC为等边三角形，∴∠BAC＝60°，AC＝AB，∴∠BAE+∠EAC＝60°，∵AB∥CD，∴∠BAC＝∠ACF＝60°，∵∠EAF＝60°，即∠EAC+∠CAF＝60°，∴∠BAE＝∠CAF，在△AEB和△AFC中，，∴△AEB≌△AFC（ASA），∴AE＝AF，∴△AEF为等边三角形；（2）解：过点A作AH⊥BC于点H，∵△AEF为等边三角形，∴AE＝EF＝，∠AEF＝60°，∵∠ABH＝60°，∴，BH＝HC＝1，∴EH＝|x﹣HC|＝|x﹣1|，∴EF＝＝，∵∠AEF＝∠B＝60°，∴∠CEG+∠AEB＝∠AEB+∠BAE＝120°，∴∠CEG＝∠BAE，∵∠B＝∠ACE＝60°，∴△BAE∽△CEG，∴，∴，∴y＝EG＝（0＜x＜2），（3）解：∵AB＝2，△ABC是等边三角形，∴AC＝2，∴OA＝OC＝1，∵EG＝EO，∴∠EOG＝∠EGO，∵∠EGO＝∠ECG+∠CEG＝60°+∠CEG，∠CEA＝∠CEG+∠AEF＝60°+∠CEG，∴∠EGO＝∠CEA，∴∠EOG＝∠CEA，∵∠ECA＝∠OCE，∴△COE∽△CEA，∴，∴CE2＝CO•CA，∴x2＝1×2，∴x＝（x＝﹣舍去），即x＝．3．（1）证明：∵在正方形ABCD和正方形CEFG中，BC＝CD，CG＝CE，∠BCG＝∠DCE＝90°，∴△BCG≌△DCE（SAS），∴∠CBG＝∠CDE，∵∠CDE+∠DEC＝90°，∴∠HBE+∠BEH＝90°，∴∠BHE＝90°，∴BH⊥DE；（2）解：MH2+HN2＝2CM2，理由：∵在正方形ABCD和正方形CEFG中，BC＝CD，CG＝CE，∠BCD＝∠GCE＝90°，∴∠BCG＝∠DCE，∴△BCG≌△DCE（SAS），∴∠CBG＝∠CDE，BG＝DE，∵∠DPH＝∠CPM，∴∠DHP＝∠BCP＝90°，∴∠MHN＝90°，∵M，N分别为BG，DE的中点，∴BM＝BG，DN＝DE，∴BM＝DN，∵BC＝CD，∴△BCM≌△DCN（SAS），∴CM＝CN，∠BCM＝∠DCN，∴∠MCN＝∠BCP＝90°，∴MH2+HN2＝CM2+CN2＝2CM2；（3）解：∵DH⊥PG，∴∠DHP＝∠DHG＝90°，把△PDH沿着PD翻折得到△APD，把△GDH沿着DG翻折得到△DGC，∴AD＝DH＝CD，∠A＝∠C＝∠DHP＝90°，∠ADP＝∠HDP，∠GDH＝∠GDC，AP＝PH＝2，CG＝HG＝4，∵∠PDG＝45°，∴∠ADC＝90°，延长AP，CG交于B，则四边形ABCD是正方形，∴∠B＝90°，设DH＝AD＝AB＝BC＝x，∴PB＝x﹣2，BG＝x﹣4，∵PG2＝PB2+BG2，∴62＝（x﹣2）2+（x﹣4）2，解得：x＝3+（负值舍去），∴DH＝3+．4．证明：[问题引入]（1）∵正方形ABCD，∴∠ABC＝∠C，AB＝BC，∵AE⊥BF，∴∠APB＝∠BAP+∠ABP＝90°，∵∠ABP+∠CBF＝90°，∴∠BAP＝∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴AE＝BF；（2）BF＝2AE，理由如下：∵矩形ABCD，∴∠ABC＝∠C，AD＝BC＝2AB，∵AE⊥BF，∴∠APB＝∠BAP+∠ABP＝90°，∵∠ABP+∠CBF＝90°，∴∠BAP＝∠CBF，且∠ABE＝∠BCF＝90°，∴△ABE∽△BCF，∴＝2，∴BF＝2AE；（3）如图3，过点B作BH⊥AD于H，连接BD，∵把△ABC沿斜边AC对折得到Rt△ADC，∴AD＝AB，∠ABC＝∠ADC＝90°，∠DAC＝∠BAC＝30°，∴∠DAB＝60°，∴△ABD是等边三角形，且BH⊥AD，∴AD＝AB＝2AH，BH＝AH，∴，∵∠ADC+∠EPF+∠DEA+∠DFB＝360°，∴∠DEA+∠DFB＝180°，且∠DFB+∠BFA＝180°，∴∠DEA＝∠BFH，∵∠BHF＝∠ADE＝90°，∴△ADE∽△BHF，∴＝＝5．解：（1）∵在正方形ABCD中，AC⊥BD，∴∠AOD＝90°，AO＝OD，∵四边形OEGH是正方形，∴∠EOH＝90°，OE＝OH，∴∠AOE＝∠DOH，∴△HDO≌△EAO（SAS）；（2）如图1，过O作ON⊥AB于N，则AN＝BN＝ON＝AB＝2，∵BF＝x，∴AF＝4﹣x，∴FN＝2﹣x，∴OF＝＝＝，∴EF＝y﹣，∵AM⊥AC，∴AE∥OB，∴，∴＝，∴；（3）①当AE＝EG时，△AEG是等腰三角形，则AE＝OE，∵∠EAO＝90°，∴这种情况不存在；②当AE＝AG时，△AEG是等腰三角形，如图2，过A作AP⊥EG于P，则AP∥OE，∴∠PAE＝∠AEO，∴△APE∽△EAO，∴＝，∵AE＝AG，∴PE＝y＝，AE＝＝，∴＝，解得：x＝2，②当GE＝AG时，△AEG是等腰三角形，如图3，过G作GQ⊥AE于Q，∴∠GQE＝∠EAO＝90°，∴∠GEQ+∠EGQ＝∠GEQ+∠AEO＝90°，∴∠EGQ＝∠AEO，∵GE＝OE，∴△EGQ≌△OEA（AAS），∴EQ＝AO＝2，∴AE＝2EQ＝4＝，∴x＝，∴BF＝2或．6．解：（1）将∠B沿BC的中垂线DE翻折（如图3），使点B落在点C处．∵∠ACB＞∠ABC，∴CD在△ABC的内部，D落在AB上．连接DC，∵DE为BC的中垂线，∴DB＝DC，在△ADC中，AD+DC＞AC，∴AD+DB＞AC，即AB＞AC；（2）如图4，延长DC到点E，使得CE＝CN，连接AE交BC于点F，连接AC，∵四边形ABCD是正方形，∴∠ACD＝∠ACB＝45°，∴∠ACE＝∠ACN＝135°，∵AC＝AC，∴△ACE≌△ACN（SAS），∴AE＝AN，过点C作PQ⊥AC，分别交AN、AE于点P、Q，由∠ACP＝∠ACQ＝90°可知AP＞AC、AQ＞AC，∴AP+AQ＞2AC，∵∠ACD＞∠E，∠ACD＝45°，∠QCE＝45°，∴∠QCE＞∠E，∴QE＞CQ，同理可得PC＞PM，由全等或对称性可得PC＝CQ，∴QE＞PM．∴AM+AN＝AM+AE＝AM+AQ+QE＞AM+AQ+PM＝AP+AQ，又∵AP+AQ＞2AC，∴AM+AN＞2AC，∵正方形ABCD中，AC＝BD．∴AM+AN＞2BD．7．解：（1）①如图1，∵把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，∴AE＝AG，∠BAE＝∠DAG，BE＝DG，∠B＝∠ADG＝90°，∵∠ADC＝90°，∴∠ADC+∠ADG＝90°∴F、D、G共线，∵∠BAD＝90°，∠EAF＝45°，∴∠BAE+∠DAF＝45°，∴∠DAG+∠DAF＝45°，即∠EAF＝∠GAF＝45°，在△EAF和△GAF中，∵，∴△EAF≌△GAF（SAS），∴EF＝GF，∵BE＝DG，∴EF＝GF＝DF+DG＝BE+DF，故答案为：EF＝BE+DF；②成立，理由：如图2，把△ABE绕A点旋转到△ADG，使AB和AD重合，则AE＝AG，∠B＝∠ADG，∠BAE＝∠DAG，∵∠B+∠ADC＝180°，∴∠ADC+∠ADG＝180°，∴C、D、G在一条直线上，与①同理得，∠EAF＝∠GAF＝45°，在△EAF和△GAF中，∵，∴△EAF≌△GAF（SAS），∴EF＝GF，∵BE＝DG，∴EF＝GF＝BE+DF；（2）解：∵△ABC中，AB＝AC＝2，∠BAC＝90°，∴∠ABC＝∠C＝45°，由勾股定理得：BC＝＝4，如图3，把△AEC绕A点旋转到△AFB，使AB和AC重合，连接DF．则AF＝AE，∠FBA＝∠C＝45°，∠BAF＝∠CAE，∵∠DAE＝45°，∴∠FAD＝∠FAB+∠BAD＝∠CAE+∠BAD＝∠BAC﹣∠DAE＝90°﹣45°＝45°，∴∠FAD＝∠DAE＝45°，在△FAD和△EAD中，∴△FAD≌△EAD（SAS），∴DF＝DE，设DE＝x，则DF＝x，∵BC＝4，∴BF＝CE＝4﹣1﹣x＝3﹣x，∵∠FBA＝45°，∠ABC＝45°，∴∠FBD＝90°，由勾股定理得：DF2＝BF2+BD2，x2＝（3﹣x）2+12，解得：x＝，即DE＝．8．解：（1）△AA′E≌△C′CF，△A′BF≌△CDE，由题意得，四边形A′DCB是矩形，∴A′B＝DC，∴AA′＝CC′，∵AB∥CD，∴∠BA′F＝∠C′，由题意得，∠BA′F＝∠A，∴∠A＝∠C′，在△AA′E和△C′CF中，，∴△AA′E≌△C′CF（ASA）；（2）①设A′E＝a，A′F＝b，∵A′F∥AC，∴＝，即＝，解得，b＝，同理＝，解得，a＝x，当A′E＝A′F时，四边形A′ECF是菱形，∴＝x，解得，x＝，∴当x＝时，四边形A′ECF是菱形；②由①得，四边形A′ECF的面积为y＝3×（4﹣x）﹣×（3﹣x）×（4﹣x）×2＝﹣x2+3x＝﹣（x﹣2）2+3，∴当x＝2时，y的最大值为3．9．解：（1）如图①，连接AE，∵四边形ABCD是正方形，∴AB＝BC＝AD＝CD，∠ABD＝∠CBD＝45°，且BE＝BE，∴△ABE≌△CBE（SAS）∴AE＝CE，∠BAE＝∠BCE，∵∠ABC+∠FEC+∠BCE+∠EFB＝360°，∴∠BCE+∠BFE＝180°，∠BFE+∠AFE＝180°，∴∠AFE＝∠BCE，∴∠BAE＝∠AFE，∴EF＝AE＝EC，且∠FEC＝90°，∴△EFC是等腰直角三角形，∴∠ECF＝45°；（2）如图②，延长FG交CD于H，∵GF⊥AB，∠ABC＝∠BCD＝90°，∴四边形BCHF是矩形，∴FH＝BC＝CD，∠FHC＝90°，∵∠AFE＝∠BCE，∴∠EFH＝∠ECH，且EF＝EC，FH＝CD，∴△EFH≌△ECD（SAS）∴∠FHE＝∠CDE＝45°，且∠FHD＝90°，∴∠FHE＝∠CDE＝∠DGH＝∠DHE＝45°，∴EG＝EH，EH＝DE，∴EG＝DE；（3）如图③，延长FK交CD于H，连接FM，过点M作MP⊥FH于P，∵AD∥BC∥FH，∴∠MDE＝∠KGE，且DE＝EG，∠MED＝∠GEK，∴△MED≌△KEG（ASA）∴ME＝EK＝MK，MD＝GK＝2，∵MG＝2EK，∴MK＝MG，且MP⊥FH，∴GP＝PK＝1，∵∠ADH＝∠DHF＝∠MPH＝90°，∴四边形MDHP是矩形，∴MD＝PH＝2，∴GH＝3，∴FH＝BC＝AB＝AD＝3+FG，∴AM＝1+FG，∵FG⊥AB，∠ABD＝45°，∴△BFG是等腰直角三角形，∴BF＝FG，∴AF＝3，∵ME＝EK，EF⊥MK，∴FM＝FK＝FG+2，∵FM2＝AM2+AF2，∴（FG+2）2＝（FG+1）2+9，∴FG＝3，∴BK＝＝．10．解：（1）BM+DN＝MN，理由如下：如图1，在MB的延长线上，截取BE＝DN，连接AE，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝∠D＝90°，∴∠ABE＝90°＝∠D，在△ABE和△ADN中，，∴△ABE≌△ADN（SAS），∴AE＝AN，∠EAB＝∠NAD，∴∠EAN＝∠BAD＝90°，∵∠MAN＝45°，∴∠EAM＝45°＝∠NAM，在△AEM和△ANM中，，∴△AEM≌△ANM（SAS），∴ME＝MN，又∵ME＝BE+BM＝BM+DN，∴BM+DN＝MN；故答案为：BM+DN＝MN；（2）（1）中的结论不成立，DN﹣BM＝MN．理由如下：如图2，在DC上截取DF＝BM，连接AF，则∠ABM＝90°＝∠D，在△ABM和△ADF中，，∴△ABM≌△ADF（SAS），∴AM＝AF，∠BAM＝∠DAF，∴∠BAM+∠BAF＝∠BAF+∠DAF＝∠BAD＝90°，即∠MAF＝∠BAD＝90°，∵∠MAN＝45°，∴∠MAN＝∠FAN＝45°，在△MAN和△FAN中，，∴△MAN≌△FAN（SAS），∴MN＝NF，∴MN＝DN﹣DF＝DN﹣BM，∴DN﹣BM＝MN．（3）∵四边形ABCD是正方形，∴AB＝BC＝AD＝CD＝6，AD∥BC，AB∥CD，∠ABC＝∠ADC＝∠BCD＝90°，∴∠ABM＝∠MCN＝90°，∵CN＝CD＝6，∴DN＝12，∴AN＝＝＝6，∵AB∥CD，∴△ABQ∽△NDQ，∴＝＝＝＝，∴＝，∴AQ＝AN＝2；由（2）得：DN﹣BM＝MN．设BM＝x，则MN＝12﹣x，CM＝6+x，在Rt△CMN中，由勾股定理得：62+（6+x）2＝（12﹣x）2，解得：x＝2，∴BM＝2，∴AM＝＝＝2，∵BC∥AD，∴△PBM∽△PDA，∴＝＝＝，∴PM＝AM＝，∴AP＝AM+PM＝3．11．（1）证明：∵四边形ABCD是菱形，∴∠ABE＝∠CBE，AB＝BC，在△ABE和△CBE中，，∴△ABE≌△CBE（SAS），∴AE＝CE；（2）解：连接AC，交BD于O，如图1所示：∵四边形ABCD是菱形，∴AD∥BC，AD＝AB＝4，∠AOB＝90°，OB＝OD，OA＝OC，∴△BEP∽△DEA，∴＝＝，∴＝（）2＝，∵sin∠ABD＝＝＝，∴OA＝2，OB＝＝＝4，∴BD＝2OB＝8，∴＝，解得：DE＝，∴BE＝BD﹣DE＝8﹣＝，∴S△DEA＝OA•DE＝×2×＝，S△ABE ＝OA•BE＝×2×＝＝S△BEC，∴S△BEP ＝S△DEA＝×＝，∴S△PEC ＝S△BEC﹣S△BEP＝﹣＝；（3）解：①由（1）得：△ABE≌△CBE，∴∠BAE＝∠BCE，当∠BAE＝90°时，则∠BCE＝90°，∴∠ECP＝90°，∵∠ABC＝45°，∴∠EBC＝22.5°，∠CPE＝45°，∴△PEC是等腰直角三角形，∴CE＝CP，∠BEC＝90°﹣22.5°＝67.5°，过点E作∠FEC＝45°交BC于F，如图2所示：则CE＝CP＝CF，EF＝CF，∠BEF＝∠BEC﹣∠FEC＝67.5°﹣45°＝22.5°，∴∠BEF＝∠EBC，∴EF＝BF，∴CF+CF＝BC＝10，∴CF＝＝10（﹣1），∴BP＝BC+CP＝BC+CF＝10+10（﹣1）＝10；②由（1）得：△ABE≌△CBE，∴∠AEB＝∠CEB，当∠BAE＝105°时，∠AEB＝180°﹣105°﹣22.5°＝52.5°，∴∠AEC＝2∠AEB＝105°，∴∠CEP＝75°，∵∠APB＝180°﹣105°﹣45°＝30°，∴∠ECP＝180°﹣75°﹣30°＝75°，∴∠ECP＝∠CEP，∴△PEC是等腰三角形，过点A作AN⊥BP于N，如图3所示：则△ABN是等腰直角三角形，∴AN＝BN＝AB＝5，∵∠APB＝30°，∴tan30°＝，即＝，∴PN＝5，∴BP＝BN+PN＝5+5，综上所述，△PEC是等腰三角形时BP的长为10或5+5．12．（1）解：由轴对称的性质得：∠EAP＝∠BAP＝α，AE＝AB，∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∴∠DAE＝90°﹣2α，AD＝AE，∴∠ADF＝∠AED＝（180°﹣∠DAE）＝（90°+2α）＝45°+α；（2）证明：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∵点E与点B关于直线AP对称，∴∠AEF＝∠ABF，AE＝AB．∴AE＝AD．∴∠ADE＝∠AED．∵∠AED+∠AEF＝180°，∴在四边形ABFD中，∠ADE+∠ABF＝180°，∴∠BFD+∠BAD＝180°，∴∠BFD＝90°∴BF⊥DF；（3）解：线段AF，BF，CF之间的数量关系为AF＝BF+CF，理由如下：过点B作BM⊥BF交AF于点M，如图所示：∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°，∴∠ABM＝∠CBF，∵点E与点B关于直线AP对称，∠BFD＝90°，∴∠MFB＝∠MFE＝45°，∴△BMF是等腰直角三角形，∴BM＝BF，FM＝BF，在△AMB和△CFB中，，∴△AMB≌△CFB（SAS），∴AM＝CF，∵AF＝FM+AM，∴AF＝BF+CF．13．（Ⅰ）①解：∵等腰直角三角形OEF的直角顶点O在原点，OE＝2，∴∠EOF＝90°，OF＝OE＝2，∴EF＝＝＝2，∵将△OEF绕点O逆时针旋转，得△OE1F1，∴E1F1＝EF＝2；②证明：∵四边形OABC为正方形，∴OC＝OA．∵将△OEF绕点O逆时针旋转，得△OE1F1，∴∠AOE 1＝∠COF 1，∵△OEF 是等腰直角三角形，∴△OE 1F 1是等腰直角三角形，∴OE 1＝OF 1．在△OAE 1和△OCF 1中，∴△OAE 1≌△OCF 1（SAS ）；（Ⅱ）解：∵OE ⊥OF ，∴过点F 与OE 平行的直线有且只有一条，并与OF 垂直，当三角板OEF 绕O 点逆时针旋转一周时，则点F 在以O 为圆心，以OF 为半径的圆上．∴过点F 与OF 垂直的直线必是圆O 的切线，又点C 是圆O 外一点，过点C 与圆O 相切的直线有且只有2条，不妨设为CF 1和CF 2，此时，E 点分别在E 1点和E 2点，满足CF 1∥OE 1，CF 2∥OE 2．当切点F 1在第二象限时，点E 1在第一象限．在直角三角形CF 1O 中，OC ＝4，OF 1＝2，cos ∠COF 1＝＝＝，∴∠COF 1＝60°，∴∠AOE 1＝60°．∴点E 1的横坐标＝2cos60°＝1，点E 1的纵坐标＝2sin60°＝，∴点E 1的坐标为（1，）；当切点F 2在第一象限时，点E 2在第四象限．同理可求：点E 2的坐标为（1，﹣）．综上所述，当OE 1∥CF 1时，点E 1的坐标为（1，）或（1，﹣）．14．解：（1）证明：∵菱形ABCD中，∠A＝90°∴菱形ABCD是正方形∴AD＝DC，∠A＝∠CDF＝90°在Rt△ADE与Rt△DCF中∴Rt△ADE≌Rt△DCF（HL）∴∠ADE＝∠DCF∴∠DCF+∠CDE＝∠ADE+∠CDE＝∠ADC＝90°∴∠CGD＝90°∴DE⊥CF（2）证明：∵四边形ABCD是菱形∴AD＝CD，∠B＝∠ADC，AD∥BC∴∠A+∠B＝180°∵∠EGC+∠B＝180°，∠EGC+∠CGD＝180°∴∠A＝∠EGC＝∠DGF，∠CGD＝∠B＝∠ADC∵∠A＝∠DGF，∠ADE＝∠GDF∴△ADE∽△GDF∴∴∵∠CGD＝∠CDF，∠DCG＝∠FCD∴△DCG∽△FCD∴∴∵AD＝DC∴DE＝CF（3）如图，过点N作NP⊥CD于点P，连接FM ∴∠CPN＝∠MPN＝90°∵四边形ABCD是正方形∴∠ABC＝∠BCD＝∠ADC＝90°，BC＝CD∴四边形BCPN是矩形∴NP＝BC＝CD，PC＝BN＝在Rt△NPM与Rt△CDF中∴Rt△NPM≌Rt△CDF（HL）∴PM＝DF设PM＝DF＝x，则CM＝PC+PM＝+x∵由（1）得MN⊥CF，G为CF中点∴MN垂直平分CF∴MF＝MC∴∠MFC＝∠FCD＝15°∴∠DMF＝∠MFC+∠FCD＝30°∴Rt△DMF中，MF＝2DF＝2x，DM＝DF＝x ∴2x＝+x∴x＝∴DF＝，CM＝2，CD＝CM+DM＝2+∵∠GCM＝∠MCF，∠CGM＝∠CDF＝90°∴△CGM∽△CDF∴＝∴2CG2＝CD•CM＝（2+）＝8+4∴CG2＝4+2＝12+2+（）2＝（1+）2∴FG＝CG＝1+15．（1）证明：∵垂美四边形ABCD的对角线AC，BD交于O，∴AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得：AD2+BC2＝AO2+DO2+BO2+CO2，AB2+CD2＝AO2+BO2+CO2+DO2，∴AD2+BC2＝AB2+CD2；（2）①证明：连接BG、CE相交于点N，CE交AB于点M，如图2所示：∵正方形ACFG和正方形ABDE，∴AG＝AC，AB＝AE，∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，∵∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，∴∠ABG+∠BMN＝90°，即CE⊥BG，∴四边形BCGE是垂美四边形；②解：∵四边形BCGE是垂美四边形，∴由（1）得：CG2+BE2＝CB2+GE2，∵AC＝4，AB＝5，∴BC＝＝＝3，∵正方形ACFG和正方形ABDE，∴CG＝AC＝4，BE＝AB＝5，∴GE2＝CG2+BE2﹣CB2＝（4）2+（5）2﹣32＝73，∴GE＝．16．解：（1）观察猜想结论：AB+AC＝BD+CE，理由如下：如图①，∵DB⊥BC，EC⊥BC，∴∠B＝∠C＝90°，∠DAE＝90°，∴∠D+∠DAB＝∠DAB+∠EAC＝90°，∴∠D＝∠EAC，在△ADB和△EAC中，，∴△ADB≌△EAC（AAS），∴BD＝AC，EC＝AB，∴BC＝AB+AC＝BD+CE，故答案为：是，AB+AC＝BD+CE；（2）问题解决如图②，过D作DE⊥AB，交BA的延长线于E，由（1）得：△ABC≌△DEA（AAS），∴DE＝AB＝6，AE＝BC＝＝＝12，Rt△BDE中，BE＝AB+AE＝18，由勾股定理得：BD＝＝＝6；（3）拓展延伸如图③，过D作DE⊥BC于E，作DF⊥AB于F，则四边形DEBF是矩形，同（1）得：△CED≌△AFD（AAS），∴CE＝AF，DE＝DF，∴四边形DEBF是正方形，设AF＝x，则BF＝DE＝DF＝x+5，在Rt△ADF中，由勾股定理得：x2+（x+5）2＝（）2，解得：x＝，或x＝﹣（舍去），∴AF＝，DF＝，∴BD＝DF＝，四边形ABCD的面积＝正方形DEBF的面积＝（）2＝，△ABD的面积＝AB×DF＝×5×＝，∴△BCD的面积＝四边形ABCD的面积﹣△ABD的面积＝BD×CG＝﹣＝51，∴CG＝＝6．17．（1）解：如图1中，∵AB＝BD，∠BAD＝45°，∴∠BDA＝∠BAD＝45°，∴∠ABD＝90°，∵四边形ABCD是平行四边形，∴E、C重合时BF＝BD＝AB，在Rt△ABF中，∵AF2＝AB2+BF2，∴（2）2＝（2BF）2+BF2，∴BF＝2，AB＝4，在Rt△ABD中，AD＝＝4；（2）证明：如图2中，在AF上截取AK＝HD，连接BK，∵∠AFD＝∠ABF+∠2＝∠FGD+∠3，∠ABF＝∠FGD＝90°，∴∠2＝∠3，在ABK和△DBH中，，∴△ABK≌△DBH，∴BK＝BH，∠6＝∠1，AK＝DH，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠4＝∠1＝∠6＝45°，∴∠5＝∠ABD﹣∠6＝45°，∴∠5＝∠1，在△FBK和△FBH中，，∴△FBK≌△FBH，∴KF＝FH，∵AF＝AK+KF，∴AF＝DH+FH；（3）解：连接AN并延长到Q，使NQ＝AN，连接GQ，取AD的中点O，连接OG，∵∠AGD＝90°，∴点G的轨迹是以O为圆心，以OG为半径的弧，且OG＝4，当O，G，Q在同一条直线上时，QG的值最小，∴OQ＝10，OG＝4，∴GQ最小值为6，∵MN是△AGQ的中位线，∴MN的最小值为3．18．解：（1）∵把△BCE沿CE折叠，使点B落在点F处，∴∠BEC＝∠FEC，∵GH∥CE，∴∠FGE＝∠CEB，∠GFE＝∠FEC，∴∠EGF＝∠EFG，∴EG＝EF，∴△EFG是等腰三角形；（2）如图①，取CE的中点M，连接FM，∵把△BCE沿CE折叠，使点B落在点F处，∴∠EFC＝∠B＝90°，∴EM＝FM，∵AB∥CD，GH∥CE，∴四边形GECH是平行四边形，∴GH＝CE，∵F是GH中点，∴FG＝EM，∴四边形GEMF是平行四边形，∴GE＝FM，由（1）知，GE＝EF，∴EG＝GF＝EF，∴△EFG是等边三角形，∴∠FGE＝60°；（3）由（2）知，BE＝EF，AE＝EF，∴AE＝BE＝AB＝15，∴CH＝AE＝15，∴DH＝30﹣15＝15，∴AH＝＝＝25，如图②，过E作EN⊥AF于N，∴∠ANE＝∠B＝90°，∵CE∥AH，∴∠EAN＝∠BEC，∴△AEN∽△ECB，∴＝，∴＝，∴AN＝9，∴AF＝18，∴FH＝25﹣18＝7．19．解：（1）如图1，过D作DH⊥AB于H，∵A（﹣4，0），B（4，0），∴OA＝OB＝4，∴AB＝8，∵四边形ABCD的面积为32∴8DH＝32，∴DH＝4，∵四边形ABCD是菱形，∴AD＝AB＝8，∴AH＝＝＝4，∴OH＝AH﹣OA＝4﹣4，∴D（4﹣4，4）；（2）如图1，延长EF交x轴于G，∵四边形ABCD是平行四边形，∴CD∥AB，∴∠C＝∠FBG，∠CEF＝∠FGB，∵CF＝BF，∴△CEF≌△BGF（AAS），∴EF＝FG，CE＝BG，∴EG＝2EF，过E作EP⊥x轴于P，∴EP＝DH＝4，∵CD＝AB＝8，∴设D（a，4）则C（8+a，4），∵点E为CD的中点，∴E（4+a，4），∴AP＝8+a，PG＝4﹣a，∴PE2＝AP•PG，∴（8+a）•（4﹣a）＝16，∴a＝2﹣2（负值舍去），∴AP＝6+2，PG＝6﹣2，∴AE＝＝4，EG＝＝4，∴AE+2EF＝AE+EG＝4+8；（3）∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝4，∴AC＝＝4，作B关于AC的对称点M′，连接BM′交AC于E，则BM′＝2BE＝2×＝2×＝，过M′作M′N⊥AB于N交AC于M，则此时，BM+MN的值最小，且BM+MN的最小值＝M′N，∵∠M′EM＝∠CEB＝90°，BE＝，BC＝4，∴CE＝，∴CM＝2CE＝，∴AM＝，∴AM2﹣AN2＝BM2﹣BN2，∴（）2﹣AN2＝42﹣（8﹣AN）2，∴AN＝，∴MN＝＝，∴M′N＝，∴BM+MN的最小值为．20．解：（1）∵，∴a﹣4＝0，b+6＝0，∴a＝4，b＝﹣6，∵四边形OABC是正方形，点B的横坐标为a，∴OA＝4，∵四边形DEFG为长方形，点G的坐标为（b，﹣b），∴F的纵坐标为：﹣b＝6，OD＝6，∵DE＝OA，∴OE＝OD﹣DE＝OD﹣OA＝6﹣4＝2，∴F（﹣2，6）（2）∵OE＝2，AD＝2OA+OE＝2×4+2＝10，AE＝OA+OE＝4+2＝6，长方形DEFG以每秒1个单位长度的速度向右平移，∴当0＜t≤2，t≥10时，S＝0；当2＜t≤6时，点E'在OA上，如图1所示：S＝OC•OE′＝4（t﹣2）＝4t﹣8；当6＜t＜10时，点D'在OA上，如图2所示：S＝AB•AD'＝4（10﹣t）＝40﹣4t；∴S＝；（3）∵D′G′＝DG＝6，当三角形PD'G'的面积为15时，∴点P到D′G′的距离为5，∵长方形DEFG以每秒1个单位长度的速度向右平移，点P从点O出发，沿正方形的边以每秒2个单位长度的速度顺时针方向运动（即O→C→B→A→O→C），∵当点P再次运动到AO、OC时，△PD'G'的面积＜15，∴分两种情况：①当t＝3s时，点P在BC的中点处，如图3所示：即PC＝2，DG向右平移了3个单位长度，OD′＝OD﹣3＝6﹣3＝3，此时，PC+OD′＝2+3＝5，即点P到D′G′的距离为5，P的坐标为：（2，4），OE′＝D′E′﹣OD′＝4﹣3＝1，∴S＝OC•OE′＝4×1＝4；②当t＝5s时，点P在AB的中点处，如图4所示：即AP＝2，DG向右平移了5个单位长度，OD′＝OD﹣5＝6﹣5＝1，此时，OA+OD′＝4+1＝5，即点P到D′G′的距离为5，P的坐标为：（4，2），OE′＝D′E′﹣OD′＝4﹣1＝3，∴S＝OC•OE′＝4×3＝12．。

中考数学总复习《四边形的综合题》练习题附带答案

中考数学总复习《四边形的综合题》练习题附带答案一、单选题1．如图，两个平行四边形的面积分别为18、12，两阴影部分的面积分别为a、b （a＞b），则(a−b)等于（）A．3B．4C．5D．6 2．如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ABD＝60°，则∠BOC的大小为（）A．30°B．60°C．90°D．120°3．若一个多边形的内角和是外角和的2.5倍，则该多边形为（）A．五边形B．六边形C．七边形D．八边形4．如图，矩形ABCD对角线相交于点O，∠AOB=60°，AB=4，则矩形的对角线AC 为（）A．4 B．8 C．4√3D．10 5．一个长方形的周长为28厘米，长的2倍比宽的3倍多3厘米，则这个长方形的面积是（）A．45平方厘米B．35平方厘米C．25平方厘米D．20平方厘米6．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE垂直平分BO，AE=√3cm，则OD=（）A．1cm B．1.5cm C．2cm D．3cm 7．如图，矩形纸片ABCD中，AB=4，AD=8 ，将纸片沿EF折叠使点B与点D 重合，折痕EF与BD相交于点O，则DF的长为()A．3B．4C．5D．6 8．如图，⊙O的半径为4，点P是⊙O外的一点PO=10，点A是⊙O上的一个动点，连接PA，直线l垂直平分PA，当直线l与⊙O相切时PA的长度为（）A．10B．212C．11D．434 9．已知平行四边形一边长为8，一条对角线长为6，则另一条对角线α满足（）A．10＜α＜22B．4＜α＜20C．4＜α＜28D．2＜α＜1410．如图，两张等宽的纸条交又重叠在一起，重叠的部分为四边形ABCD，若测得A，C之间的距离为6cm，点B，D之间的距离为8cm，则线段AB的长为（）A．a2B．5cm C．2√7cm D．6cm 11．如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF，将∠BCE绕着正方形的中心O按逆时针方向旋转到∠CDF的位置，则旋转角是（）A ．45°B ．60°C ．90°D ．120°12．Rt∠ABC 两直角边的长分别为6cm 和8cm ，则连接这两条直角边中点的线段长为( ) A ．10cmB ．3cmC ．4cmD ．5cm二、填空题13．如图，点E 在边长为2的正方形ABCD 内，满足∠AEB ＝90°，若∠DAE ＝30°，则图中阴影部分的面积为．14．把一把直尺和一块三角板如图放置，若∠1=42°，则∠2的度数为 °.15．已知 ▱ABCD 中一条对角线分 ∠A 为35°和45°，则 ∠B = 度. 16．如图，在一块长AB =26m ，宽BC =18m 的长方形草地上，修建三条宽均为3m 的长方形小路，则这块草地的绿地面积（图中空白部分）为 m 217．如图，在∠ABC 中，∠ABC ＝90°，E 为AC 的中点，AD∠BE 交BC 于D ，若AD＝152，BE ＝5，则BD ＝ .18．如图，在四边形ABCD中，∠A＝90°，AB＝12，AD＝5．点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的最大值是．三、综合题19．如果抛物线C1：y=ax2+bx+c与抛物线C2：y=−ax2+dx+e的开口方向相反，顶点相同，我们称抛物线C2是C1的“对顶”抛物线.（1）求抛物线y=x2−4x+7的“对顶”抛物线的表达式；（2）将抛物线y=x2−4x+7的“对顶”抛物线沿其对称轴平移，使所得抛物线与原抛物线y=x2−4x+7形成两个交点M、N，记平移前后两抛物线的顶点分别为A、B，当四边形AMBN是正方形时求正方形AMBN的面积.（3）某同学在探究“对顶”抛物线时发现：如果抛物线C1与C2的顶点位于x轴上，那么系数b与d，c与e之间的关系是确定的，请写出它们之间的关系.20．解答题（1）如图1，在平行四边形ABCD 中，已知点E 在AB 上，点F 在CD 上，且AE=CF ．求证：DE=BF ；（2）如图2，AB 是∠O 的直径，点C 在AB 的延长线上，CD 与∠O 相切于点D ，若∠C=20°，求∠CDA 的度数．21．如图，▱ABCD 放置在平面直角坐标系申，已知点A （-2，0）、B （-6，0）、D（0，3）．点C 在反比例函数y=k x的图象上。

四边形综合题(含答案解析)

四边形综合题1.已知△ABC是等腰直角三角形，∠BAC=90∘，AB=AC，点D是边BC上的一个动点(不运动至点B，C)，点E在BC所在直线上，连结AD，AE，且∠DAE=45∘(1)若点E是线段BC上一点，如图1，作点D关于直线AE的对称点F，连结AF，CF，DF，EF①求证：△ABD≌△ACF；②若BD=1，DE=2，求CE的长；，AB=√2，求CE的长.(直接写出答案即可)(2)如图2，若BD=85【答案】解：(1)①∵点D与点F关于直线AE的对称，∴AE垂直平分DF，∴AD=AF，∴∠DAE=∠FAE=45∘，即∠DAF=90∘，∴∠DAC+∠FAC=90∘，∵∠BAC=90∘，∴∠DAC+∠BAD=90∘，∴∠BAD=∠FAC，在△ABD与△ACF中，{AB =AC ∠BAD =∠CAF AD =AF，∴△ABD ≌△ACF(SAS)；②由①可得：△ABD ≌△ACF ，∴∠B =∠ACF =45∘，BD =CF =1，∴∠ECF =∠ACB +∠ACF =90∘，∵AE 垂直平分DF ，∴DE =EF =2，∴CE =√EF 2−CF 2=√3；(2)CE =3或54．理由：如图所示，当点E 在BC 延长线上时，作点D 关于直线AE 的对称点F ，连结AF ，CF ，EF ，根据△ABD ≌△ACF ，可得BD =CF =85，在等腰直角三角形ABC 中，AB =√2，∴BC =2，∴CD =25，∴DE =CE +25=EF ，在Rt △CEF 中，CE 2+(85)2=(CE +25)2，解得CE =3；如图所示，当点E 在线段BC 上时，作点D 关于直线AE的对称点F ，连结AF ，BF ，EF ，根据△ABF ≌△ACD ，可得BF =CD =25，∴DE =CE −25=EF ，又∵BE =BC −CE =2−CE ，∴在Rt △BEF 中，(25)2+(2−CE)2=(CE −25)2，解得CE =54．【解析】(1)①根据轴对称的性质，得到AD =AF ，∠DAE =∠FAE =45∘，再根据同角的余角相等，得到∠BAD =∠FAC ，即可判定△ABD ≌△ACF(SAS)； ②由①可得：△ABD ≌△ACF ，据此得出∠B =∠ACF =45∘，BD =CF =1，进而得到∠ECF =∠ACB +∠ACF =90∘，再根据DE =EF =2，运用勾股定理求得CE 即可；(2)分两种情况进行讨论：当点E 在BC 延长线上时，作点D 关于直线AE 的对称点F ，连结AF ，CF ，EF ；当点E 在线段BC 上时，作点D 关于直线AE 的对称点F ，连结AF ，BF ，EF.分别根据全等三角形的性质以及勾股定理，求得CE 的长即可．本题属于三角形综合题，主要考查了全等三角形的性质以判定，等腰直角三角形的性质，勾股定理以及对称轴的性质的综合应用，解决问题的关键是掌握全等三角形的判定方法，解题时注意分类思想的运用．2. 如图①，在矩形ABCD 中，AB =√3，BC =3，在BC 边上取两点E 、F(点E 在点F 的左边)，以EF 为边所作等边△PEF ，顶点P 恰好在AD 上，直线PE 、PF 分别交直线AC 于点G 、H ．(1)求△PEF 的边长；(2)若△PEF 的边EF 在线段CB 上移动，试猜想：PH 与BE 有何数量关系？并证明你猜想的结论；(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示，CF>1，P不与A重合)，(2)中的结论还成立吗？若不成立，直接写出你发现的新结论．【答案】解：(1)过P作PQ⊥BC于Q(如图1)，∵四边形ABCD是矩形，∴∠B=90∘，即AB⊥BC，又∵AD//BC，∴PQ=AB=√3，∵△PEF是等边三角形，∴∠PFQ=60∘，在Rt△PQF中，∠FPQ=30∘，设PF=2x，QF=x，PQ=√3，根据勾股定理得：(2x)2=x2+(√3)2，解得：x=1，故PF=2，∴△PEF的边长为2；(2)PH−BE=1，理由如下：∵在Rt△ABC中，AB=√3，BC=3，∴由勾股定理得AC=2√3，∴CD=1AC，2∴∠CAD=30∘∵AD//BC，∠PFE=60∘，∴∠FPD=60∘，∴∠PHA=30∘=∠CAD，∴PA=PH，∴△APH是等腰三角形，作ER⊥AD于R(如图2)Rt△PER中，∠RPE=60∘，PE=1，∴PR=12∴PH−BE=PA−BE=PR=1．(3)结论不成立，当1<CF<2时，PH=1−BE，当2<CF<3时，PH=BE−1．【解析】(1)过P作PQ⊥BC，垂足为Q，由四边形ABCD为矩形，得到∠B为直角，且AD//BC，得到PQ=AB，又△PEF为等边三角形，根据“三线合一”得到∠FPQ为30∘，在Rt△PQF中，设出QF为x，则PF=2x，由PQ的长，根据勾股定理列出关于x的方程，求出x的值，即可得到PF的长，即为等边三角形的边长；(2)PH−BE=1，过E作ER垂直于AD，如图所示，首先证明△APH为等腰三角形，在根据矩形的对边平行得到一对内错角相等，可得∠APE=60∘，在Rt△PER中，∠REP= 30∘，根据直角三角形中，30∘角所对的直角边等于斜边的一半，由PE求出PR，由PA=PH，则PH−BE=PA−BE=PA−AR=PR，即可得到两线段的关系；(3)当若△PEF的边EF在射线CB上移动时(2)中的结论不成立，由(2)的解题思路可知当1<CF <2时，PH =1−BE ，当2<CF <3时，PH =BE −1．此题综合考查了矩形的性质，等腰三角形的判别与性质、等边三角形的性质及直角三角形的性质.学生作第三问时，应借助第二问的结论，结合图形，多次利用数学中等量代换的方法解决问题，这就要求学生在作几何题时注意合理运用各小题之间的联系．3. 已知，正方形ABCD 中，∠MAN =45∘，∠MAN 绕点A 顺时针旋转，它的两边长分别交CB 、DC(或它们的延长线)于点M 、N ，AH ⊥MN 于点H ．(1)如图①，当∠MAN 点A 旋转到BM =DN 时，请你直接写出AH 与AB 的数量关系：______ ；(2)如图②，当∠MAN 绕点A 旋转到BM ≠DN 时，(1)中发现的AH 与AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；(3)如图③，已知∠MAN =45∘，AH ⊥MN 于点H ，且MH =2，NH =3，求AH 的长．【答案】AH =AB【解析】解：(1)如图①AH =AB ，∵四边形ABCD 是正方形，∴AB =AD ，∠B =∠D =90∘，在△ABM 与△ADN 中，{AB =AD∠B =∠D BM =DN，∴△ABM ≌△ADN ，∴∠BAM =∠DAN ，AM =AN ，∵AH ⊥MN ，∴∠MAH =12MAN =22.5∘，∵∠BAM +∠DAN =45∘，∴∠BAM =22.5∘，在△ABM 与△AHM 中，{ ∠BAM =∠HAM∠B =∠AHM =90∘AM =AM， ∴△ABM ≌△AHM ，∴AB =AH ；故答案为：AH =AD ；(2)数量关系成立.如图②，延长CB 至E ，使BE =DN ．∵ABCD 是正方形，∴AB =AD ，∠D =∠ABE =90∘，在Rt △AEB 和Rt △AND 中，{AB =AD∠ABE =∠ADN BE =DN，∴Rt △AEB ≌Rt △AND ，∴AE =AN ，∠EAB =∠NAD ，∴∠EAM =∠NAM =45∘，在△AEM 和△ANM 中，{AE =AN∠EAM =∠NAM AM =AM，∴△AEM ≌△ANM ，∴S △AEM =S △ANM ，EM =MN ，∵AB 、AH 是△AEM 和△ANM 对应边上的高，∴AB=AH；(3)如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，∴BM=2，DN=3，∠B=∠D=∠BAD=90∘，分别延长BM和DN交于点C，得正方形ABCD，由(2)可知，AH=AB=BC=CD=AD，设AH=x，则MC=x−2，NC=x−3，在Rt△MCN中，由勾股定理，得MN2=MC2+NC2，∴52=(x−2)2+(x−3)2，解得x=6，x2=−1(不符合题意，舍去)1∴AH=6．(1)由三角形全等可以证明AH=AB，(2)延长CB至E，使BE=DN，证明△AEM≌△ANM，能得到AH=AB，(3)分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，然后分别延长BM 和DN交于点C，得正方形ABCE，设AH=x，则MC=x−2，NC=x−3，在Rt△MCN 中，由勾股定理，解得x．本题考查了正方形的性质，全等三角形的性质和判定，勾股定理，翻折的性质，此题比较典型，具有一定的代表性，且证明过程类似，同时通过做此题培养了学生的猜想能力和类比推理能力．4.已知在四边形ABCD中，点E、F分别是BC、CD边上的一点．(1)如图1：当四边形ABCD是正方形时，作出将△ADF绕点A顺时针旋转90度后的图形△ABM；并判断点M、B、C三点是否在同一条直线上______ (填是或否)；(2)如图1：当四边形ABCD是正方形时，且∠EAF=45∘，请直接写出线段EF、BE、DF三者之间的数量关系______ ；(3)如图2：当AB=AD，∠B=∠D=90∘，∠EAF是∠BAD的一半，问：(2)中的数量关系是否还存在，并说明理由；(4)在(3)的条件下，将点E平移到BC的延长线上，请在图3中补全图形，并写出EF、BE、DF的关系．【答案】是；EF=BE+DF【解析】(1)解：如图1：根据旋转的性质，∠ABM=90∘，∵四边形ABCD是正方形，∴∠ABC=90∘，∴M、B、C三点在一条直线上．故答案为：是；(2)由旋转的性质可得：AM=AF，∠BAM=∠DAF，BM=DF，∵四边形ABCD是正方形，∠EAF=45∘，∴∠DAF+∠BAE=45∘，∴∠EAM=∠BAM+∠BAE=45∘，_ ∴∠EAM =∠EAF ，在△EAM 和△EAF 中，{AM =AF∠EAM =∠EAF AE =AE，∴△EAM ≌△EAF(SAS)，∴EF =EM =BM +BE =BE +DF ；故答案为：EF =BE +DF ；(3)存在理由如下：延长CB 到P 使BP =DF ， ∵∠B =∠D =90∘，∴∠ABP =90∘，∴∠ABP =∠D ，在△ABP 和△ADF 中，{AB =AD∠ABP =∠D BP =DF，∴△ABP ≌△ADF(SAS)，∴AP =AF ，∠BAP =∠DAF ， ∵∠EAF =12∠BAD ，∴∠BAE +∠DAF =∠EAF ， ∴∠BAP +∠FAD =∠EAF ，即：∠EAP =∠EAF ，在△APE 和△AFE 中，{AP =AF∠EAP =∠FAE AE =AE ，∴△APE ≌△AFE(SAS)，∴PE =FE ，∴EF =BE +DF ；(4)如图3，补全图形．证明：在BC 上截取BP =DF ，∵∠B =∠ADC =90∘，∴∠ADF =90∘，∴∠B =∠ADF ，在△ABP 和△ADF 中，{AB =AD∠B =∠ADF BP =DF，∴△ABP ≌△ADF(SAS)，∴AP =AF ，∠BAP =∠DAF ，∵∠EAF =12∠BAD ， ∴∠DAE +∠DAF =12∠BAD ，∴∠BAP +∠EAD =12∠BAD ，∴∠EAP =12∠BAD =∠EAF ，在△APE 和△AFE 中，{AP =AF∠EAP =∠FAE AE =AE，∴△APE ≌△AFE(SAS)，∴PE =FE ，∴EF =BE −BP =BE −DF ．(1)首先由旋转的性质，画出旋转后的图形，然后由∠ABM =∠D =∠ABC =90∘，证得点M、B、C三点共线；(2)首先由旋转的性质可得：AM=AF，∠BAM=∠DAF，BM=DF，然后由∠EAF= 45∘，证得∠EAM=∠EAF，继而证得△EAM≌△EAF，继而证得结论；(3)首先延长CB到P使BP=DF，证得△ABP≌△ADF(SAS)，再证得△APE≌△AFE(SAS)，继而证得结论；(4)首先在BC上截取BP=DF，证得△ABP≌△ADF(SAS)，再证得△APE≌△AFE(SAS)，即可得EF=BE−BP=BE−DF．此题属于四边形的综合题.考查了旋转的性质以及全等三角形的判定与性质.注意掌握旋转前后图形的对应关系，注意准确作出辅助线是解此题的关键．5.正方形ABCD中，点E是射线AB上一动点，点F是线段BC延长线上一动点，且AE=CF，(1)如图1，连接DE、DF，若正方形的边长为4，AE=3，求EF的长？(2)如图2，连接AC交EF与G，求证：AC=√2AE+2CG；(3)如图3，当点E在AB延长线上时，AE=CF仍保持不变，试探索线段AC、AE、CG之间的数量关系，并说明理由．_【答案】(1)解：∵正方形的边长为4，AE=3，∴BE=4−3=1，∵AE=CF，∴CF=3，∴BF=BC+CF=7，∴EF=√BE2+BF2=5√2；(2)证明：如图2，作EH//BC交AC于H，∵四边形ABCD是正方形，∴∠BAC=45∘，∴AH=EH=√2AE，∵AE=CF，∴EH=CF，又EF//CF，∴HG=CG，即HC=2CG，∴AC=AH+HC=√2AE+2CG；(3)AC=√2AE−2CG．证明：如图3，作EP//BC交AC的延长线于P，∵四边形ABCD是正方形，∴∠BAC=45∘，∴AP=EP=√2AE，∵AE=CF，∴EP=CF，又EF//CF，∴PG=CG，即PC=2CG，∴AC=AP−PC=√2AE−2CG．【解析】(1)根据题意分别求出BE、BF的长，根据勾股定理计算即可；(2)作EH//BC交AC于H，根据正方形的性质得到∠BAC=45∘，根据勾股定理得到AH=√2AE，根据平行线分线段成比例定理得到HC=2CG，得到答案；(3)作EP//BC交AC的延长线于P，与(2)的方法类似，证明即可．本题考查的是正方形的性质、平行线分线段成比例定理以及全等三角形的判定和性质，掌握相关的性质定理、灵活运用类比思想是解题的关键．6.如图，正方形ABCD边长为6，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，连接CF．(1)求证：∠HEA=∠CGF；(2)当AH=DG=2时，求证：菱形EFGH为正方形；(3)设AH=2，DG=x，△FCG的面积为y，求y与x之间的函数解析式，并直接写出x的取值范围；(4)求y的最小值．【答案】(1)证明：如图1，连接GE，∵AB//CD，∴∠AEG=∠CGE，∵GF//HE，∴∠HEG=∠FGE，∴∠HEA=∠CGF；(2)证明：∵四边形ABCD是正方形，∴∠D=∠A=90∘，∵四边形EFGH是菱形，∴HG =HE ，在Rt △HAE 和Rt △GDH 中，{AH =DG HE =HG， ∴Rt △HAE ≌Rt △GDH ，∴∠AHE =∠DGH ，又∠DHG +∠DGH =90∘，∴∠DHG +∠AHE =90∘，∴∠GHE =90∘，∴菱形EFGH 为正方形；(3)解：作FM ⊥DC ，交DC 的延长线于M ，在Rt △AHE 和Rt △GFM 中，{ ∠A =∠M∠AEH =∠FGMHE =FG， ∴Rt △AHE ≌Rt △GFM ，∴MF =AH =2，∵DG =x ，∴CG =6−x ，∴y =12×CG ×FM =12×2×(6−x)=6−x(0≤x ≤2√6)； (4)∵k =−1<0，∴y 随x 的增大而减小，∴x =2√6时，y 的最小值是6−2√6．【解析】(1)连接GE ，根据正方形的性质和平行线的性质得到∠AEG =∠CGE ，根据菱形的性质和平行线的性质得到∠HEG =∠FGE ，解答即可；(2)证明Rt △HAE ≌Rt △GDH ，得到∠AHE =∠DGH ，证明∠GHE =90∘，根据正方形的判定定理证明；(3)作FM⊥DC，证明Rt△AHE≌Rt△GFM，得到MF=AH=2，根据三角形的面积公式得到解析式；(4)根据一次函数的性质：当k<0时，y随x的增大而减小解答即可．本题考查的是正方形的性质、菱形的性质、全等三角形的判定和性质、一次函数解析式的求法和一次函数的性质，正确作出辅助线、灵活运用相关的性质定理和判定定理是解题的关键．7.四边形ABCD为正方形，点E为射线AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．(1)如图1，当点E在线段AC上时．①求证：矩形DEFG是正方形；②求证：AC=CE+CG；(2)如图2，当点E在线段AC的延长线上时，请你在图2中画出相应图形，并直接写出AC、CE、CG之间的数量关系；(3)直接写出∠FCG的度数．【答案】(1)①证明：作EP⊥CD于P，EQ⊥BC于Q，∵∠DCA=∠BCA，∴EQ=EP，∵∠QEF +∠FEC =45∘，∠PED +∠FEC =45∘，∴∠QEF =∠PED ，在Rt △EQF 和Rt △EPD 中，{ ∠QEF =∠PEDEQ =EP ∠EQF =∠EPD， ∴Rt △EQF ≌Rt △EPD ，∴EF =ED ，∴矩形DEFG 是正方形；②∵∠ADE +∠EDC =90∘，∠CDG +∠EDC =90∘，∴∠ADE =∠CDG ，在△AED 和△CGD 中，{AD =CD∠ADE =∠CDG DE =DG，∴△AED ≌△CGD ，∴AE =CG ，∴AC =CE +AE =CE +CG ；(2)AC +CE =CG ，证明：由(1)得，矩形DEFG 是正方形，∴DE =DG ，∵∠ADC =∠EDG =90∘，∴∠ADE =∠CDG ，在△ADE 和△CDG 中，{AD =DC∠ADE =∠CDG DE =DG，∴△ADE ≌△CDG ，∴AE=CG，∴AC+CE=CG；(3)如图1，当点E为线段AC上时，∵△ADE≌△CDG，∴∠DCG=∠DAE=45∘，∴∠FCG=∠FCD+∠DCG=135∘；如图2，当点E为线段AC的延长线上时，∠FCG=∠FCD−∠DCG=45∘．【解析】(1)①作EP⊥CD于P，EQ⊥BC于Q，证明Rt△EQF≌Rt△EPD，得到EF=ED，根据正方形的判定定理证明即可；②根据三角形全等的判定定理证明△AED≌△CGD，得到AE=CG，证明结论；(2)根据题意画出图形，与(1)的方法类似，证明△ADE≌△CDG，得到AE=CG，即可得到答案；(3)根据全等三角形的性质和点E的不同位置求出∠FCG的度数．本题考查的是正方形的判定和性质、全等三角形的判定和性质，掌握相关的定理、正确作出辅助线是解题的关键，注意分情况讨论思想的运用．8.在△ABC中，AB=AC，点P△ABC为所在平面内一点，过点P分别作PE//AC交AB于点E，PF//AB交BC于点D，交AC于点F(1)当点P在BC边上(如图1)时，请你探索线段PD，PE，PF，AB与之间的数量关系，并给出证明；(2)当点P在△ABC内(如图2)时，(1)中的结论是否成立？若成立，请给出证明；若不成立，线段PD，PE，PF，AB与之间又有怎样的数量关系．(3)当点P在△ABC外(如图3)时，线段PD，PE，PF，AB与之间又有怎样的数量关系．【答案】(1)答：PD+PE+PF=AB．证明如下：∵点P在BC上，∴PD=0，∵PE//AC，PF//AB，∴四边形PFAE是平行四边形，∴PF=AE，∵PE//AC，∴∠BPE=∠C，∴∠B=∠BPE，∴PE=BE，∴PE+PF=BE+AE=AB，∵PD=0，∴PD+PE+PF=AB；(2)证明：∵AB=AC，∴∠B=∠C，∵PF//AB，∴∠B=∠CDF，∴∠C=∠CDF，∴CF=PD+PF，∵PE//AC，PF//AB，∴四边形PFAE是平行四边形，∴PE=AF，∴PD+PE+PF=AC，∴PD+PE+PF=AB；(3)证明：同(2)可证DF=CF，PE=AF，∵AF+CF=AC，∴PE+PF−PD=AC，∴PE+PF−PD=AB．【解析】(1)先求出四边形PFAE是平行四边形，根据平行四边形对边相等可得PF=AE，再根据两直线平行，同位角相等可得∠BPE=∠C，然后求出∠B=∠BPE，利用等角对等边求出PE=BE，然后求解即可；(2)根据等边对等角可得∠B=∠C，再根据两直线平行，同位角相等可得∠B=∠CDF，然后求出∠C=∠CDF，再根据等角对等边可得CF=PD+PF，然后求出四边形PFAE 是平行四边形，根据平行四边形对边相等可得PE=AF，然后求出PD+PE+PF=AC，等量代换即可得证；(3)证明思路同(2)．本题考查了平行四边形的判定与性质，等腰三角形的性质，熟记平行四边形的判定方法与性质，并准确识图理清图中边的关系是解题的关键，此类题目，关键在于后面小题与前面小题的求解思路相同．9.如图，在菱形ABCD中，E是BC上一点，F是CD上一点，连接AE、AF、EF，且∠AEB=∠AEF．(1)如图1，求证：AF平分∠EFD；(2)如图2，若∠C=90∘，求证：EF=BE+DF；(3)在(2)的条件下，若AB=3BE，AE=2√10，求AF的长．【答案】解：(1)证明：过点A作AG⊥BC于G，过A作AH⊥EF于H，过A作AM⊥CD 于M，连接AC，∵四边形ABCD是菱形，∴AC平分∠BCD，又∵AG⊥BC，AM⊥CD，∴AG=AM，∵∠AEB=∠AEF，∴AE平分∠BEF，又∵AG⊥BC，AH⊥EF，∴AG=AH，∴AH=AM，∴AF平分∠EFD；(2)∵四边形ABCD是菱形，又∵∠C=90∘，∴四边形ABCD是正方形，∴∠B=∠D=90∘，∴AB⊥BC，AD⊥CD，过A作AH⊥EF于H，∴∠AHE=∠AHF=90∘，∴AE平分∠BEF，又∵AB⊥BC，AH⊥EF，∴AB=AH，∵AE=AE，在Rt△ABE与Rt△AHE中，{AB=AHAE=AE∴Rt△ABE≌Rt△AHE(HL)∴BE=HE，同理Rt△ADF≌Rt△AHF(HL)，∴DF=HF，∵EF=EH+FH，∴EF=BE+DF；(3)设BE=a，则AB=3a，在Rt△ABE中，BE2+AB2=AE2，∴a2+(3a)2=(2√10)2，∴a=2，∴AB=3a=6，由(2)知四边形ABCD是正方形，∴BC=CD=AB=6，∴CE=BC−BE=4，设DF=m，则CF=CD−DF=6−m，由(2)知EF=BE+DF，∴EF=2+m，在Rt△ECF中，CE2+CF2=EF2，∴42+(6−m)2=(2+m)2，∴m=3，在Rt△ADF中，DF2+AD2=AF2，∴AF=√32+62=3√5．【解析】(1)根据菱形的性质得出AC平分∠BCD，再根据角平分线的性质证明即可．(2)根据正方形的性质和全等三角形的判定和性质证明即可；(3)根据勾股定理进行解答即可．此题主要考查了菱形的性质，关键是判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．。

2020年中考数学复习专题练：《四边形综合》(包含答案)

2020年中考数学复习专题练：《四边形综合》1．如图①所示，已知正方形ABCD 和正方形AEFG ，连接DG ，BE ．（1）发现：当正方形AEFG 绕点A 旋转，如图②所示．①线段DG 与BE 之间的数量关系是；②直线DG 与直线BE 之间的位置关系是；（2）探究：如图③所示，若四边形ABCD 与四边形AEFG 都为矩形，且AD ＝2AB ，AG ＝2AE 时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG 、DE ，若AE ＝1，AB ＝2，求BG 2+DE 2的值（直接写出结果）．2．如图1，在正方形ABCD 中，点E 是CD 上一点（不与C ，D 两点重合），连接BE ，过点C 作CH ⊥BE 于点F ，交对角线BD 于点G ，交AD 边于点H ，连接GE ，（1）求证：△DHC ≌△CEB ；（2）如图2，若点E 是CD 的中点，当BE ＝8时，求线段GH 的长；（3）设正方形ABCD 的面积为S 1，四边形DEGH 的面积为S 2，当的值为时，的值为．3．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（6，0），点B（0，8）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F，记旋转角为α（0°＜α＜90°）．（I）如图①，当α＝30°时，求点D的坐标；（Ⅱ）如图②，当点E落在AC的延长线上时，求点D的坐标；（Ⅲ）当点D落在线段OC上时，求点E的坐标（直接写出结果即可）．4．如图，BD是平行四边形ABCD的对角线，DE⊥AB于点E，过点E的直线交BC于点G，且BG＝CG．（1）求证：GD＝EG．（2）若BD⊥EG垂足为O，BO＝2，DO＝4，画出图形并求出四边形ABCD的面积．（3）在（2）的条件下，以O为旋转中心顺时针旋转△GDO，得到△G′D'O，点G′落在BC上时，请直接写出G′E的长．5．（1）【探索发现】如图1，在正方形ABCD中，点M，N分别是边BC，CD上的点，∠MAN＝45°，若将△DAN 绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为8，则正方形ABCD的边长为．（2）【类比延伸】如图2，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M，N分别在边BC，CD上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．（3）【拓展应用】如图3，在四边形ABCD中，AB＝AD＝2，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，AN，△ABM是等边三角形，AM⊥AD于点A，∠DAN＝15°，请直接写出△CMN 的周长．6．（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝，则的值是；（2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE 和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；（3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝，当CD＝6，AD＝3时，请直接写出线段BD的长度．7．如图1，长方形ABCD中，∠DAB＝∠B＝∠DCB＝∠D＝90°，AD＝BC＝6，AB＝CD＝10．点E为射线DC上的一个动点，把△ADE沿直线AE翻折得△AD′E．（1）当D′点落在AB边上时，∠DAE＝°；（2）如图2，当E点与C点重合时，D′C与AB交点F，①求证：AF＝FC；②求AF长．（3）连接D′B，当∠AD′B＝90°时，求DE的长．8．在平面直角坐标系中，点O是坐标原点，A（0，m），B（n，O），AC∥OB，且AC＝OB，连接BC交x轴于点F，其中m、n满足方程+n2+8n+16＝0．（1）求A、B两点坐标；（2）过A做AE⊥BC于E，延长AE交x轴于点D，动点P从点B出发以每秒2个单位的速度向x轴正半轴方向运动，设△PFD的面积为S，请用含t的式子表示S，并直接写出t的取值范围；（3）在（2）的条件下，连接PE，将△PED沿PE翻折到△PEG的位置（点D与点G对应），当四边形PDEG为菱形时，求点P和点G的坐标．9．已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．（1）如图1，连接BG、DE．求证：BG＝DE；（2）如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD．①求∠BDE的度数；②若正方形ABCD的边长是，请求出△BCG的面积．10．【综合与实践】如图①，在正方形ABCD中，点E、F分别在射线CD、BC上，且BF＝CE，将线段FA绕点F顺时针旋转90°得到线段FG，连接EG，试探究线段EG和BF的数量关系和位置关系．【观察与猜想】任务一：“智慧小组”首先考虑点E、F的特殊位置如图②，当点E与点D重合，点F与点C重合时，易知：EG与BF的数量关系是，EG与BF的位置关系是．【探究与证明】任务二：“博学小组”同学认为E、F不一定必须在特殊位置，他们分两种情况，一种是点E、F分别在CD、BC边上任意位置时（如图③）；一种是点E、F在CD、BC边的延长线上的任意位置时（如图④），线段EG与BF的数量关系与位置关系仍然成立．请你选择其中一种情况给出证明．【拓展与延伸】“创新小组”同学认为，若将“正方形ABCD”改为“矩形ABCD，且＝k（k≠1）”，点E、F分别在射线CD、BC上任意位置时，仍将线段FA绕点F顺时针旋转90°，并适当延长得到线段FG，连接EG（如图⑤），则当线段BF、CE、AF、FG满足一个条件时，线段EG与BF的数量关系与位置关系仍然成立．（请你在横线上直接写出这个条件，无需证明）11．在平面直角坐标系xOy中，四边形OADC为正方形，点D的坐标为（4，4），动点E沿边AO从A向O以每秒1cm的速度运动，同时动点F沿边OC从O向C以同样的速度运动，连接AF、DE交于点G．（1）试探索线段AF、DE的关系，写出你的结论并说明理由；（2）连接EF、DF，分别取AE、EF、FD、DA的中点H、I、J、K，则四边形HIJK是什么特殊平行四边形？请在图①中补全图形，并说明理由．（3）如图②当点E运动到AO中点时，点M是直线EC上任意一点，点N是平面内任意一点，是否存在点N使以O，C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．12．综合与实践动手操作：第一步：在矩形纸片ABCD的边BC，AD上分别取两点E，F，使CE＝AF；第二步：分别以DE，BF为对称轴将△CDE与△ABF翻折得到△C'DE与△A'BF，且边C'E 与A'B交于点G，边A'F与C'D交于一点H．问题解决：（1）求证：△BEG≌△DFH；（2）请判断四边形A'HC'G的形状，并证明你发现的结论；（3）已知tan∠EBG＝，A'G＝6，C'G＝1，求矩形纸片ABCD的面积．13．如图1，矩形ABCD中，∠ACB＝30°，将△ACD绕C点顺时针旋转α（0°＜α＜360°）至△A'CD'位置．（1）如图2，若AB＝2，α＝30°，求S△BCD′．（2）如图3，取AA′中点O，连OB、OD′、BD′．若△OBD′存在，试判定△OBD′的形状．（3）当α＝α1时，OB＝OD′，则α1＝°；当α＝α2时，△OBD′不存在，则α2＝°．14．已知矩形ABCD 中，AB ＝2，BC ＝m ，点E 是边BC 上一点，BE ＝1，连接AE ．（1）沿AE 翻折△ABE 使点B 落在点F 处，①连接CF ，若CF ∥AE ，求m 的值；②连接DF ，若≤DF ≤，求m 的取值范围．（2）△ABE 绕点A 顺时针旋转得△AB 1E 1，点E 1落在边AD 上时旋转停止．若点B 1落在矩形对角线AC 上，且点B 1到AD 的距离小于时，求m 的取值范围．15．如图1，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，连接BE 、DG ．（1）BE 和DG 的数量关系是，BE 和DG 的位置关系是；（2）把正方形ECGF 绕点C 旋转，如图2，（1）中的结论是否还成立？若成立，写出证明过程，若不成立，请说明理由；（3）设正方形ABCD 的边长为4，正方形ECGF 的边长为3，正方形ECGF 绕点C 旋转过程中，若A 、C 、E 三点共线，直接写出DG 的长．16．如图，正方形ABCD的边长为a，射线AM是∠BAD外角的平分线，点E在边AB上运动（不与点A、B重合），点F在射线AM上，且AF＝BE，CF与AD相交于点G，连结EC、EF、EG．（1）求证：CE＝EF；（2）求△AEG的周长（用含a的代数式表示）；（3）试探索：点E在边AB上运动至什么位置时，△EAF的面积最大．17．问题情境：矩形ABCD中，∠ACB＝30°，将一块直角三角板的直角顶点P放在两对角线的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB、BC所在的直线相交，交点为E、F．探究1：如图1，当PE⊥AB，PF⊥BC时，则＝．探究2：如图2，在（1）的基础上，将三角板绕点P逆时针旋转，旋转角为α，（0°＜α＜60°），试求的值．探究3：在（2）的基础上继续旋转，当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如图3，试求的值．18．在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D从点B出发，以每秒3个单位的速度沿B→A→C运动，到点C停止．在点D运动的过程中，过点D作DE⊥BC，垂足为E，以DE为一边在右侧作矩形DEFG，点F在BC边上，且EF：DE＝4：3，连结AG，CG，设运动时间为t（秒），矩形DEFG与△ABC重叠部分面积为S．（1）当AG＝CG时，求t的值．（2）当点D在边AB上运动时，求S与t的函数关系式．（3）当△ACG的面积为6时，直接写出t的值．19．如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝32，DC＝24，AD＝42，动点P从点D出发，沿射线DA的方向以每秒4个单位长的速度运动，动点Q从点C出发，在线段CB 上以每秒2个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．（1）设△BPQ的面积为S，求S与t之间的函数关系式；（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？（3）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．20．（1）【发现证明】如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则（1）中的结论还成立吗？请写出证明过程．②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是（不要求证明）（3）【联想拓展】如图1，若正方形ABCD的边长为6，AE＝3，求AF的长．参考答案1．解：（1）①如图②中，∵四边形ABCD和四边形AEFG是正方形，∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，∴∠BAE＝∠DAG，在△ABE和△DAG中，，∴△ABE≌△ADG（SAS），∴BE＝DG；②如图2，延长BE交AD于T，交DG于H．由①知，△ABE≌△DAG，∴∠ABE＝∠ADG，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG，故答案为：BE＝DG，BE⊥DG；（2）数量关系不成立，DG＝2BE，位置关系成立．如图③中，延长BE交AD于T，交DG于H．∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴＝＝，∴△ABE∽△ADG，∴∠ABE＝∠ADG，＝，∴DG＝2BE，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图④中，作ET⊥AD于T，GH⊥BA交BA的延长线于H．设ET＝x，AT＝y．∵△AHG∽△ATE，∴＝＝＝2，∴GH＝2x，AH＝2y，∴4x2+4y2＝4，∴x2+y2＝1，∴BG2+DE2＝（2x）2+（2y+2）2+x2+（4﹣y）2＝5x2+5y2+20＝25．2．证明（1）∵四边形ABCD是正方形，∴CD＝BC，∠HDC＝∠BCE＝90°，∴∠DHC+∠DCH＝90°，∵CH⊥BE，∴∠EFC＝90°，∴∠ECF+∠BEC＝90°，∴∠CHD＝∠BEC，∴△DHC≌△CEB（AAS）．（2）解：∵△DHC≌△CEB，∴CH＝BE，DH＝CE，∵CE＝DE＝CD，CD＝CB，∴DH＝BC，∵DH∥BC，∴．∴GC＝2GH，设GH＝x，则，则CG＝2x，∴3x＝8，∴x＝．即GH＝．（3）解：∵，∴，∵DH＝CE，DC＝BC，∴，∵DH∥BC，∴，∴，，设S△DGH ＝9a，则S△BCG＝49a，S△DCG＝21a，∴S△BCD＝49a+21a＝70a，∴S1＝2S△BCD＝140a，∵S△DEG ：S△CEG＝4：3，∴S△DEG＝12a，∴S2＝12a+9a＝21a．∴．故答案为：．3．解：（I）过点D作DG⊥x轴于G，如图①所示：∵点A（6，0），点B（0，8）．∴OA＝6，OB＝8，∵以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，∴AD＝AO＝6，α＝∠OAD＝30°，DE＝OB＝8，在Rt△ADG中，DG＝AD＝3，AG＝DG＝3，∴OG＝OA﹣AG＝6﹣3，∴点D的坐标为（6﹣3，3）；（Ⅱ）过点D作DG⊥x轴于G，DH⊥AE于H，如图②所示：则GA＝DH，HA＝DG，∵DE＝OB＝8，∠ADE＝∠AOB＝90°，∴AE＝＝＝10，∵AE×DH＝AD×DE，∴DH＝＝＝，∴OG＝OA﹣GA＝OA﹣DH＝6﹣＝，DG＝＝＝，∴点D的坐标为（，）；（Ⅲ）连接AE，作EG⊥x轴于G，如图③所示：由旋转的性质得：∠DAE＝∠AOC，AD＝AO，∴∠OAC＝∠ADO，∴∠DAE＝∠ADO，∴AE∥OC，∴∠GAE＝∠AOD，∴∠DAE＝∠GAE，在△AEG和△AED中，，∴△AEG≌△AED（AAS），∴AG＝AD＝6，EG＝ED＝8，∴OG＝OA+AG＝12，∴点E的坐标为（12，8）．4．证明：（1）如图1，延长EG交DC的延长线于点H，∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，AB＝CD，AB∥CD，∵AB∥CD，∴∠H＝GEB，且BG＝CG，∠BGE＝∠CGH，∴△CGH≌△BGE（AAS）∴GE＝GH，∵DE⊥AB，DC∥AB，∴DC⊥DE，且GE＝GH，∴DG＝EG＝GH；（2）如图1：∵DB⊥EG，∴∠DOE＝∠DEB＝90°，且∠EDB＝∠EDO，∴△DEO∽△DBO，∴∴DE×DE＝4×（2+4）＝24，∴DE＝2，∴EO＝＝＝2，∵AB∥CD，∴， ∴HO ＝2EO ＝4， ∴EH ＝6，且EG ＝GH ， ∴EG ＝3，GO ＝EG ﹣EO ＝， ∴GB ＝＝＝，∴BC ＝2＝AD ， ∴AD ＝DE ，∴点E 与点A 重合，如图2：∵S 四边形ABCD ＝2S △ABD ，∴S 四边形ABCD ＝2××BD ×AO ＝6×2＝12；（3）如图3，过点O 作OF ⊥BC ，∵旋转△GDO ，得到△G ′D 'O ，∴OG ＝OG '，且OF ⊥BC ，∴GF ＝G 'F ，∵OF ∥AB ，∴＝＝，∴GF＝BG＝，∴GG'＝2GF＝，∴BG'＝BG﹣GG'＝，∵AB2＝AO2+BO2＝12，∵EG'＝AG'＝＝，＝．5．解：（1）如图1中，∵△MAN≌△MAG，∴MN＝GM，∵DN＝BG，GM＝BG+BM，∴MN＝BM+DN，∵△CMN的周长为：MN+CM+CN＝8，∴BM+CM+CN+DN＝8，∴BC+CD＝8，∴BC＝CD＝4，故答案为4；（2）如图2中，结论：MN＝NM+DN．延长CB至E，使BE＝DN，连接AE，∵∠ABC+∠D＝180°，∠ABC+∠ABE＝180°，∴∠D＝∠ABE，在△ABE和△ADN中，，∴△ABE≌△ADN（SAS），∴AN＝AE，∠DAN＝∠BAE，∵∠BAD＝2∠MAN，∴∠DAN+∠BAM＝∠MAN，∴∠MAN＝∠EAM，在△MAN和△MAE中，，∴△MAN≌△MAE（SAS），∴MN＝EM＝BE+BM＝BM+DN，即MN＝BM+DN；（3）如图3，延长BA，CD交于G，∵∠BAM＝60°，∠MAD＝90°，∴∠BAD＝150°，∴∠GAD＝30°，∵AD＝2，∴DG＝1，AG＝，∵∠DAN＝15°，∴∠GAN＝45°，∴AG＝GN＝，∴BG＝2+，∴BC＝2BG＝4+2，CG＝BG＝2+3，∴CD＝CG﹣DG＝2+2，由（2）得，MN＝BM+DN，∴△CMN的周长＝CM+CN+MN＝CN+DN+CM+BM＝BC+CD＝4+2+2+2＝6+4．6．解：（1）∵DE∥BC，∴＝＝＝；故答案为：；（2）的值不变化，值为；理由如下：由（1）得：DE∥B，∴△ADE∽△ABC，∴＝，由旋转的性质得：∠BAD＝∠CAE，∴△ABD∽△ACE，∴＝＝；（3）在AB上截取AM＝AD＝3，过M作MN∥BC交AC于N，把△AMN绕A逆时针旋转得△ADE，连接CE，如图所示：则MN⊥AC，DE＝MN，∠DAE＝∠BAC，∴∠AED＝∠ANM＝90°，∵AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝＝，∴BC：AC：AB＝3：4：5，同（2）得：△ABD∽△ACE，∴＝＝，∵MN∥BC，∴△AMN∽△ABC，∴＝，∴MN＝×AM＝×3＝，∵∠BAC＝∠ADC＝θ，∴∠DAE＝∠ADC＝θ，∴AE∥CD，∴∠CDE+∠AED＝180°，∴∠CDE＝90°，∴CE＝＝＝，∴BD＝CE＝×＝．7．解：（1）由题意知△ADE≌△AD′E，∴∠DAE＝∠D′AE，∵D′点落在AB边上时，∠DAE+∠D′AE＝90°，∴∠DAE＝∠D′AE＝45°，故答案为：45；（2）①如图2，由题意知∠ACD＝∠ACD′，∵四边形ABCD是矩形，∴AB∥CD，∴∠ACD＝∠BAC，∴∠ACD′＝∠BAC，∴AF＝FC；②设AF＝FC＝x，则BF＝10﹣x，在Rt△BCF中，由BF2+BC2＝CF2得（10﹣x）2+62＝x2，解得x＝6.8，即AF＝6.8；（3）如图3，∵△AD′E≌△ADE，∴∠AD′E＝∠D＝90°，∵∠AD′B＝90°，∴B、D′、E三点共线，又∵△ABD′∽△BEC，AD′＝BC，∴△ABD′≌△BEC，∴BE＝AB＝10，∵BD′＝＝＝8，∴DE＝D′E＝10﹣8＝2；如图4，∵∠ABD″+∠CBE＝∠ABD″+∠BAD″＝90°，∴∠CBE＝∠BAD″，在△ABD″和△BEC中，∵，∴△ABD″≌△BEC，∴BE＝AB＝10，∴DE＝D″E＝8+10＝18．综上所知，DE＝2或18．8．解：（1）∵，，（n+4）2≥0，∴m﹣4＝0，n+4＝0，∴m＝4，n＝﹣4，∴A（0，4），B（﹣4，0）；（2）∵AC∥OB，∴∠C＝∠CBO，∠CAF＝∠BOF，∵AC＝OB，∴△ACF≌△OBF（ASA），∴AF＝OF＝2，∵OA＝OB，∠OAD＝∠OBF，∠BOF＝∠AOD，∴△BOF≌△AOD（ASA），∴OF＝OD＝2，∴BD＝6，①当0≤t＜3时，S＝PD•OF＝（6﹣2t）×2＝6﹣2t；②当t＞3时，S＝PD•OF＝（2t﹣6）×2＝2t﹣6；（3）①当0≤t＜3，如图2，∵AO＝4，OD＝2，∴AD＝，∵BD×OA＝AD×BE，∴BE＝，∴DE＝，∵四边形PDEG为菱形，∴DP＝DE＝EG＝，∵D（2，0），∴P（2﹣，0），作EH⊥BD于H，∵BE×DE＝BD×EH，∴EH＝，∴HD＝，∴OH＝，∴E（，），∵EG∥OB，∴G与E的纵坐标相同，∴G（﹣，）②当t＞3时，如图3，同理求得P（2+，0），G（+，）．9．（1）证明：∵四边形ABCD和四边形CEFG为正方形，∴BC＝DC，CG＝CE，∠BCD＝∠GCE＝90°．∴∠BCD+∠DCG＝∠GCE+∠DCG，∴∠BCG＝∠DCE．在△BCG和△DCE中，，∴△BCG≌△DCE（SAS）．∴BG＝DE；（2）解：①连接BE，如图2所示：由（1）可知：BG＝DE，∵CG∥BD，∴∠DCG＝∠BDC＝45°，∴∠BCG＝∠BCD+∠DCG＝90°+45°＝135°，∵∠GCE＝90°，∴∠BCE＝360°﹣∠BCG﹣∠GCE＝360°﹣135°﹣90°＝135°，∴∠BCG＝∠BCE，在△BCG和△BCE中，，∴△BCG≌△BCE（SAS），∴BG＝BE，∵BG＝BD＝DE，∴BD＝BE＝DE，∴△BDE为等边三角形，∴∠BDE＝60°；②延长EC交BD于点H，过点G作GN⊥BC于N，如图3所示：在△BCE和△DCE中，，∴△BCE≌△BCG（SSS），∴∠BEC＝∠DEC，∴EH⊥BD，BH＝BD，∵BC＝CD＝，∴BD＝BC＝2，∴BE＝2，BH＝1，∴CH＝1，在Rt△BHE中，由勾股定理得：EH＝＝＝，∴CE＝﹣1，∵∠BCG＝135°，∴∠GCN＝45°，∴△GCN是等腰直角三角形，∴GN＝CG＝（﹣1），＝BC•GN＝××（﹣1）＝．∴S△BCG10．【观察与猜想】解：∵四边形ABCD是正方形，∴∠B＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝AD，∠ACB＝∠ACD＝45°，由旋转的性质得：GC＝AC，∠ACG＝90°，∴∠ACB＝∠GCD＝45°，在△ABC和△GDC中，，∴△ABC≌△GDC（SAS），∴AB＝GD，∠GDC＝∠B＝90°，∴DG∥BC，△CDG是等腰直角三角形，∴DG＝CD＝BC，∵点E与点D重合，点F与点C重合，∴EG＝BF，EG∥BF；故答案为：EG＝BF，EG∥BF；【探究与证明】证明：点E、F分别在CD、BC边上任意位置时，如图③所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；点E、F在CD、BC边的延长线上的任意位置时，如图④所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；【拓展与延伸】解：＝＝k（k≠1）时，线段EG与BF的数量关系与位置关系仍然成立；理由如下：作GM⊥BC，交BC延长线于M，如图⑤所示：则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，∠B＝∠GMF，由旋转的性质得：∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，∴△ABF∽△FMG，∴＝＝，∵＝＝k，∴＝＝k，＝＝k，∴FM＝BC，GM＝CE，∴BF＝CM，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；故答案为：＝＝k（k≠1）．11．解：（1）AF＝DE．理由如下：∵四边形OADC是正方形，∴OA＝AD，∠DAE＝∠AOF＝90°，由题意得：AE＝OF，在△AOF和△DAE中，，∴△AOF≌△DAE（SAS），∴AF＝DE．（2）四边形HIJK是正方形．理由如下：如图①所示：∵H、I、J、K分别是AE、EF、FD、DA的中点，∴HI＝KJ＝AF，HK＝IJ＝ED，HI∥AF，HK∥ED，∵AF＝DE，∴HI＝KJ＝HK＝IJ，∴四边形HIJK是菱形，∵△AOF≌△DAE，∴∠ADE＝∠OAF，∵∠ADE+∠AED＝90°，∴∠OAF+∠AED＝90°，∴∠AGE＝90°，∴AF⊥ED，∵HI∥AF，HK∥ED，∴HI⊥HK，∴∠KHI＝90°，∴四边形HIJK是正方形．（3）存在，理由如下：∵四边形OADC为正方形，点D的坐标为（4，4），∴OA＝AD＝OC＝4，∴C（4，0），∵点E为AO的中点，∴OE＝2，E（0，2）；分情况讨论：如图②所示，①当OC是以O，C、M、N为顶点的菱形的对角线时，OC与MN互相垂直平分，则M为CE 的中点，∴点M的坐标为（2，1），∵点M和N关于OC对称，∴N（2，﹣1）；②当OC是以O，C、M、N为顶点的菱形的边时，若M在y轴的左侧时，∵四边形OCM'N'是菱形，∴OM'＝OC＝4，M'N'∥OC，∴△M'FE∽△COE，∴＝＝2，设EF＝x，则M'F＝2x，OF＝x+2，在Rt△OM'F中，由勾股定理得：（2x）2+（x+2）2＝42，解得：x＝，或x＝﹣2（舍去），∴M'F＝，FN＝4﹣M'F＝，OF＝2+＝，∴N'（，）；若M在y轴的右侧时，作N''P⊥OC于P，∵ON''∥CM''，∴∠PON''＝∠OCE，∴tan∠PON''＝＝tan∠OCE＝＝，设PN''＝y，则OP＝2y，在Rt△OPN''中，由勾股定理得：y2+（2y）2＝42，解得：y＝，∴PN''＝，OP＝，∴N''（，﹣）；综上所述，存在点N使以O，C、M、N为顶点的四边形是菱形，点N的坐标为（2，﹣1）或（，）或（，﹣）．12．（1）证明：∵四边形ABCD为矩形，∴BC＝AD，CD＝AB，∠C＝∠ABC＝∠A＝∠ADC＝90°，∵CE＝AF，∴BC﹣CE＝AD﹣AF，即BE＝DF，在△DCE和△BAF中，，∴△DCE≌△BAF（SAS），∴∠CDE＝∠ABF，∠CED＝∠AFB，由折叠的性质得：∠CDE＝∠C′DE，∠ABF＝∠A′BF，∠CED＝∠C′ED，∠AFB＝∠A′FB，∵∠CDE+∠C′DE+∠HDF＝90°，∠ABF+∠A′BF+∠GBE＝90°，∠CED+∠C′ED+∠GEB＝180°，∠AFB+∠A′FB+∠HFD＝180°，∴∠HDF＝∠GBE，∠GEB＝∠HFD，在△BEG和△DFH中，，∴△BEG≌△DFH（ASA）；（2）解：四边形A'HC'G的形状是矩形；理由如下：由折叠的性质得：∠C＝∠DC′E＝∠A＝∠BA′F＝90°，由（1）得：△BEG≌△DFH，∴∠BGE＝∠DHF，∵∠BGE＝∠A′GC′，∠DHF＝∠A′HC′，∴∠A′GC′＝∠A′HC′，∵∠DC′E+∠BA′F+∠A′GC′+∠A′HC′＝90°+90°+∠A′GC′+∠A′HC′＝360°，∴∠A′GC′+∠A′HC′＝180°，∴∠A′GC′＝∠A′HC′＝90°，∴∠DC′E＝∠BA′F＝∠A′GC′＝∠A′HC′＝90°，∴四边形A'HC'G是矩形；（3）解：由（2）知：∠BGE＝∠A′GC′＝90°，∵tan∠EBG＝，∴设EG＝3x，则BG＝4x，BE＝＝5x，由折叠的性质得：CE＝C′E＝EG+C′G＝3x+1，CD＝AB＝A′B＝BG+A′G＝4x+6，∴BC＝CE+BE＝3x+1+5x＝8x+1，S矩形ABCD＝CD•BC＝4×CD•CE+2×EG•BG﹣A'G•C'G，即（4x+6）（8x+1）＝4×（3x+1）（4x+6）+2×3x•4x﹣6×1，整理得：x2﹣2x＝0，解得：x1＝2，x2＝0（不合题意舍去），∴CD＝4×2+6＝14，CB＝8×2+1＝17，∴S矩形ABCD＝CD•BC＝14×17＝238．13．解：（1）作D'E⊥BC交BC的延长线于E，如图2所示：则∠E＝90°，∵四边形ABCD是矩形，∴∠ABC＝90°，AB∥CD，AD∥BC，CD＝AB＝2，∴∠ACD＝∠BAC，∠DAC＝∠ACB＝30°，∵∠ACB＝30°，∴BC＝AB＝2，∠ACD＝∠BAC＝60°，由旋转的性质得：CD'＝CD＝2，∠ACA'＝30°，∴∠D'CE＝180°﹣30°﹣30°﹣60°＝60°，∴∠CD'E＝30°，∴CE＝CD'＝1，D'E＝CE＝，∴S＝BC×D'E＝×2×＝3；△BCD′（2）△OBD′是直角三角形，理由如下：连接OC，如图3所示：由旋转的性质得：CA'＝CA，∠AD'C＝∠ADC＝90°，∠D'A'C＝∠DAC＝30°，∵O是AA′的中点，∴OC⊥AA'，∴∠AOC＝∠AOC＝90°＝∠ABC＝∠AD'C，∴∠ABC+∠AOC＝180°，∴A、B、C、O四点共圆，∴∠BOC＝∠BAC＝60°，同理；A、D'、C、O四点共圆，∴∠D'OC＝∠D'A'C＝30°，∴∠BOD'＝90°，∴△BOD'是直角三角形；（3）若B、C、D'三点不共线，如图3所示：由（2）得：∠OBC＝∠OAC，∠OD'C＝∠OA'C，∠OAC＝∠OA'C，∴∠OBC＝∠OD'C，∵OB＝OD，∴∠OBD'＝∠OD'B，∴∠CBD'＝∠CD'B，∴CB＝CD'，∵CD'＝CD，∴BC＝CD，这与已知相矛盾，∴B、C、D'三点共线；分两种情况：当点D'在BC的延长线上时，如图4所示：＝90°；α＝α1当点D'在边BC上时，如图5所示：＝360°﹣90°＝270°；α＝α1故答案为：90°或270；时，△OBD′不存在时，分两种情况：当α＝α2当O与D'重合时，如图6所示：∵CA'＝CA，∠CAD'＝∠CA'D'＝30°，∴∠ACA'＝120°，＝360°﹣120°＝240°；∴α＝α2当O与B重合时，如图7所示：则AA'＝2AB＝4，∵CA＝CA'＝2AB＝4＝AA'，∴△ACA'是等边三角形，∴∠A'CA＝60°，＝360°﹣60°＝300°；∴α＝α2故答案为：240°或300．14．解：（1）①如图1，∵CF∥AE ∴∠FCE＝∠AEB，∠CFE＝∠AEF∵△ABE翻折得到△AFE∴EF＝BE＝1，∠AEF＝∠AEB∴∠FCE＝∠CFE∴CE＝EF＝1∴m＝BC＝BE+CE＝2∴m的值是2．②如图2，过点F作GH⊥AD于点G，交BC于点H ∴GH⊥BC∴∠AGF＝∠FHE＝90°∵四边形ABCD是矩形∴∠BAD＝∠B＝90°∴四边形ABHG是矩形∴GH＝AB＝2，AG＝BH∵△ABE翻折得到△AFE∴EF＝BE＝1，AF＝AB＝2，∠AFE＝∠B＝90°∴∠AFG+∠EFH＝∠AFG+∠FAG＝90°∴∠EFH＝∠FAG∴△EFH∽△FAG∴设EH＝x，则AG＝BH＝x+1∴FG＝2EH＝2x∴FH＝GH﹣FG＝2﹣2x∴解得：x＝∴AG＝，FG＝∵AD＝BC＝m∴DG＝|AD﹣AG|＝|m﹣|∴DF 2＝DG 2+FG 2＝（m ﹣）2+2≥，即可把DF 2看作关于m 的二次函数，抛物线开口向上，最小值为∵∴∵（m ﹣）2+2＝解得：m 1＝，m 2＝1 ∴根据二次函数图象可知，1≤m（2）如图3，过点B 1作MN ⊥AD 于点M ，交BC 于点N ∴MN ∥AB ，MN ＝AB ＝2∵AC ＝ ∴sin ∠ACB ＝∵AD ∥BC ，点B 1在AC 上∴∠MAB 1＝∠ACB∴sin ∠MAB 1＝ ∴∵点B 1到AD 的距离小于∴MB 1＝解得：∵m＞0 ∴m＞如图4，当E1落在边AD上，且B1在AC上时，m最大，此时，∠ACB＝∠B1AE1＝∠BAE∴tan∠ACB＝tan∠BAE∴∴m＝BC＝2AB＝4∴m的取值范围是＜m≤415．解：（1）BE＝DG．BE⊥DG；理由如下：∵四边形ABCD和四边形CEFG为正方形，∴CD＝BC，CE＝CG，∠BCE＝∠DCG＝90°，在△BEC和△DGC中，，∴△BEC≌△DGC（SAS），∴BE＝DG；如图1，延长GD交BE于点H，∵△BEC≌△DGC，∴∠DGC＝∠BEC，∴∠DGC+∠EBC＝∠BEC+∠EBC＝90°，∴∠BHG＝90°，即BE⊥DG；故答案为：BE＝DG，BE⊥DG．（2）成立，理由如下：如图2所示：同（1）得：△DCG≌△BCE（SAS），∴BE＝DG，∠CDG＝∠CBE，∵∠DME＝∠BMC，∠CBE+∠BMC＝90°，∴∠CDG+∠DME＝90°，∴∠DOB＝90°，∴BE⊥DG；（3）由（2）得：DG＝EB，分两种情况：①如图3所示：∵正方形ABCD的边长为4，正方形ECGF的边长为3，∴AC⊥BD，BD＝AC＝AB＝4，OA＝OC＝OB＝AC＝2，CE＝3，∴AE＝AC﹣CE＝，∴OE＝OA﹣AE＝，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；②如图4所示：OE＝CE+OC＝2+3＝5，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；综上所述，若A、C、E三点共线，DG的长为或．16．（1）证明：过点F作FH⊥AB于H，如图1所示：则∠AHF＝90°，∵AM平分∠DAH，∴∠FAH＝45°，∴△AFH是等腰直角三角形，∴FH＝AH，AF＝AH＝FH，∵AF＝BE，∴FH＝AH＝BE，∴AH+AE＝BE+AE，∴HE＝AB＝BC，在△FEH和△ECB中，，∴△FEH≌△ECB（SAS），∴CE＝EF；（2）解：∵△FEH≌△ECB，∴∠FEH＝∠ECB，∵在Rt△BCE中，∠ECB+∠CEB＝90°，∴∠FEH+∠CEB＝90°，∴∠CEF＝90°，由（1）知，CE＝EF，∴△CEF是等腰直角三角形，∠ECF＝∠EFC＝45°，把Rt△CDG绕点C逆时针旋转90°至Rt△CBN位置，如图2所示：则∠GCN＝90°，CG＝CN，DG＝BN，∴∠NCE＝∠GCN﹣∠GCE＝45°，∴∠NCE＝∠GCE，在△CEG和△CEN中，，∴△CEG≌△CEN（SAS），∴GE＝NE＝EB+BN＝EB+DG，∴△AEG的周长＝AE+GE+AG＝AE+EB+DG+AG＝AB+AD＝2a；（3）解：设AE＝x，由（1）得：FH＝BE＝a﹣x，则△EAF的面积＝AE×FH＝x（a﹣x）＝﹣（x﹣）2+，∴当x＝，即点E在AB边中点时，△EAF的面积最大，最大值为．17．解：（1）∵矩形ABCD，∴AB⊥BC，PA＝PC；∵PE⊥AB，BC⊥AB，∴PE∥BC，∴∠APE＝∠PCF；∵PF⊥BC，AB⊥BC，∴PF∥AB，∴∠PAE＝∠CPF．∵在△APE与△PCF中，，∴△APE≌△PCF（ASA），∴PE＝CF．在Rt△PCF中，＝tan30°＝，∴＝，故答案为：．（2）如答图1，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN．0°～30°时∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝，由（1）知，＝，∴＝．同理30°～60°时，＝；（3）当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如答图2，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN，PM∥BC，PN∥AB．∵PM∥BC，PN∥AB，∴∠APM＝∠PCN，∠PAM＝∠CPN，∴△APM∽△PCN，∴＝＝，得CN＝2PM．在Rt△PCN中，＝＝tan30°＝，∴＝．∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝＝．18．解：（1）∵四边形DEFG是矩形，∴DG＝BF，GF＝BD，∠BDG＝∠BFG＝90°，∴∠ADG＝∠CFG＝90°，由题意得：BD＝3t，则AD＝6﹣3t，DG＝4t，CF＝8﹣4t，FG＝BD＝3t，当AG＝CG时，由勾股定理得：AG2＝AD2+DG2，CG2＝FG2+FC2，∴AD2+DG2＝FG2+FC2，即（6﹣3t）2+（4t）2＝（3t）2+（8﹣4t）2，解得：t＝1，即当AG＝CG时，t＝1秒；（2）分两种情况：①当0＜t≤1时，如图1所示：S＝矩形DEFG的面积＝3t×4t＝12t2；即S＝12t2（0＜t≤1）；②当1＜t≤2时，如图2所示：∵∠ADH＝∠B＝90°，∠A＝∠A，∴△ADH∽△ABC，∴＝，即＝，解得：DH＝8﹣4t，同理得：FM＝6﹣3t，∴S＝×6×8﹣×2×（6﹣3t）（8﹣4t）＝﹣12t2+48t﹣24；即S＝﹣12t2+48t﹣24（1＜t≤2）；（3）分三种情况：①如图1所示：由题意得：×6×8﹣12t2﹣×4t×（6﹣3t）﹣×3t×（8﹣4t）＝6，解得：t＝；②如图3所示：由题意得：×4t×（6﹣3t）+×3t×（8﹣4t）+3t×4t﹣×6×8＝6，解得：t＝；③如图4所示：由勾股定理得：AC＝＝＝10，∴CD＝6+10﹣3t＝16﹣3t，同（2）得：△CDE∽△CAB，∴＝＝，即＝＝，解得：DE＝（16﹣3t），CE＝（16﹣3t），由题意得EF＝（16﹣3t），∴C与F重合，∴×8×（16﹣3t）＝6，解得：t＝；综上所述，当△ACG的面积为6时，t的值为秒或秒或秒．19．解：（1）如图1，过点P作PM⊥BC，垂足为M，则四边形PDCM为矩形．∴PM＝DC＝24．∵QB＝32﹣t，∴S＝×24×（32﹣2t）＝384﹣24t（0≤t＜16）；（2）由图可知：CM＝PD＝4t，CQ＝2t．以B、P、Q三点为顶点的三角形是等腰三角形，可以分三种情况：①若PQ＝BQ．在Rt△PMQ中，PQ2＝4t2+242，由PQ2＝BQ2得4t2+242＝（32﹣2t）2，解得t＝；②若BP＝BQ．在Rt△PMB中，BP2＝（32﹣4t）2+242．由BP2＝BQ2得：（32﹣4t）2+242＝（32﹣2t）2即3t2﹣32t+144＝0．由于△＝﹣704＜0，∴3t2﹣32t+144＝0无解，∴PB≠BQ．③若PB＝PQ．由PB2＝PQ2，得4t2+242＝（32﹣4t）2+242整理，得3t 2﹣64t +256＝0．解得t 1＝，t 2＝16（舍去）综合上面的讨论可知：当t ＝秒或t ＝秒时，以B 、P 、Q 三点为顶点的三角形是等腰三角形．（3）设存在时刻t ，使得PQ ⊥BD ．如图2，过点Q 作QE ⊥AD 于E ，垂足为E ．∵AD ∥BC∴∠BQF ＝∠EPQ ，又∵在△BFQ 和△BCD 中∠BFQ ＝∠C ＝90°，∴∠BQF ＝∠BDC ，∴∠BDC ＝∠EPQ ，又∵∠C ＝∠PEQ ＝90°，∴Rt △BDC ∽Rt △QPE ， ∴＝，即＝，解得t ＝9．所以，当t ＝9秒时，PQ ⊥BD ．20．（1）【发现证明】证明：把△ABE 绕点A 顺时针旋转90°至△ADG ，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）【类比引申】①不成立，结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），。

2022年沪科版八年级数学下册第19章四边形综合测评练习题(含详解)

沪科版八年级数学下册第19章四边形综合测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图是用若干个全等的等腰梯形拼成的图形，下列说法错误的是（）A．梯形的下底是上底的两倍B．梯形最大角是120︒C．梯形的腰与上底相等D．梯形的底角是60︒2、如图所示，公路AC、BC互相垂直，点M为公路AB的中点，为测量湖泊两侧C、M两点间的距离，若测得AB的长为6km，则M、C两点间的距离为（）A．2.5km B．4.5km C．5km D．3km∠+∠+∠+∠=（）3、如图，在六边形ABCDEF中，若1290∠+∠=︒，则3456A．180°B．240°C．270°D．360°4、如图，矩形OABC的边OA长为2，边AB长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点，则这个点表示的实数是（）A．2.5 B．C D5、四边形四条边长分别是a，b，c，d，其中a，b为对边，且满足222222+，则这++=+a b c d ab cd个四边形是（）A．任意四边形B．平行四边形C．对角线相等的四边形D．对角线垂直的四边形6、如图，四边形ABCD中，∠A=60°，AD=2，AB=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（）A B C D7、绿丝带是颜色丝带的一种，被用来象征许多事物，例如环境保护、大麻和解放农业等，同时绿丝带也代表健康，使人对健康的人生与生命的活力充满无限希望．某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带（丝带的对边平行且宽度相同），如图所示，丝带重叠部分形成的图形是（）A．矩形B．菱形C．正方形D．等腰梯形8、在Rt△ABC中，∠C＝90°，若D为斜边AB上的中点，AB的长为10，则DC的长为（）A．5 B．4 C．3 D．29、下列测量方案中，能确定四边形门框为矩形的是（）A．测量对角线是否互相平分B．测量两组对边是否分别相等C．测量对角线是否相等D．测量对角线交点到四个顶点的距离是否都相等10、如图，已知正方形ABCD的边长为6，点E，F分别在边AB，BC上，BE＝CF＝2，CE与DF交于点H，点G为DE的中点，连接GH，则GH的长为（）A B C．4.5 D．4.3第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在△ABC中，D，E分别是边AB，AC的中点，∠B＝50°．现将△ADE沿DE折叠点A落在三角形所在平面内的点为A1，则∠BDA1的度数为 _____．2、在平行四边形ABCD 中，BF 平分∠ABC ，交AD 于点F ，CE 平分∠BCD ，交AD 于点E ，AB =6，EF =2，则BC 的长为_____．3、如图，在四边形ABCD 中，90ABC DCB ∠+∠=︒，,E F 分别是,AD BC 的中点，分别以,AB CD 为直径作半圆，这两个半圆面积的和为8π，则EF 的长为_______．4、七边形内角和的度数是__________．5、在边长为4dm 的正方形纸片（厚度不计）上，按如图的实线裁剪，将阴影部分按虚线折叠成一个有盖的正方体盒子，则这个盒子的容积为______3dm ．三、解答题（5小题，每小题10分，共计50分）1、已知矩形ABCD ，AB =6，BC =10，以BC 所在直线为x 轴，AB 所在直线为y 轴，建立如图所示的平面直角坐标系，在CD 边上取一点E ，将△ADE 沿AE 翻折，点D 恰好落在BC 边上的点F 处．（1）求线段EF 长；（2）在平面内找一点G ，①使得以A、B、F、G为顶点的四边形是平行四边形，请直接写出点G的坐标；②如图2，将图1翻折后的矩形沿y轴正半轴向上平移m(m＞0)个单位，若以A、O、F、G为顶点的四边形为菱形，请求出m的值并写出点G的坐标．2、如图，在△ABC中，点D是BC边的中点，点E是AD的中点，过A点作AF∥BC，且交CE的延长线于点F，联结BF．（1）求证：四边形AFBD是平行四边形；（2）当AB=AC时，求证：四边形AFBD是矩形．3、如图，四边形ABCD是正方形，BE⊥BF，BE＝BF，EF与BC交于点G．（1）求证：AE＝CF；（2）若∠ABE＝62°，求∠GFC+∠BCF的值．4、如图1，ABC 在平面直角坐标系中，且::2:3:4BO AO CO =；（1）试说明ABC 是等腰三角形；（2）已知2160cm ABC S =△．写出各点的坐标：A ( ， )，B ( ， )，C ( ， )．（3）在（2）的条件下，若一动点M 从点B 出发沿线段BA 向点A 运动，同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动，当其中一点到达终点时整个运动都停止．①若OMN 的一条边与BC 平行，求此时点M 的坐标；②若点E 是边AC 的中点，在点M 运动的过程中，MOE △能否成为等腰三角形？若能，求出此时点Ｍ的坐标；若不能，请说明理由．5、如图，矩形ABCD 中，8AB =，4BC =，过对角线BD 中点O 的直线分别交AB ，CD 边于点E ，F ．（1）求证：四边形BEDF 是平行四边形．（2）当四边形BEDF 是菱形时，求EF 的长．-参考答案-一、单选题1、D【分析】如图（见解析），先根据平角的定义可得123180∠+∠+∠=︒，再根据123∠=∠=∠可求出12360∠=∠=∠=︒，由此可判断选项,B D ；先根据等边三角形的判定与性质可得,60DE CD CDE =∠=︒，再根据平行四边形的判定可得四边形ABCE 是平行四边形，根据平行四边形的性质可得AE BC =，然后根据菱形的判定可得四边形DEFG 是菱形，根据菱形的性质可得DE EF AD ==，最后根据线段的和差、等量代换可得,2CD AD BC AD ==，由此可判断选项,A C ．【详解】解：如图，123180,123∠+∠+∠=︒∠=∠=∠，12360∴∠=∠=∠=︒，AD BC ，1801120ADC ∴∠=︒-∠=︒，梯形ABCD 是等腰梯形，160,120,ABC BAD ADC CD CE ∴∠=∠=︒∠=∠=︒=，则梯形最大角是120︒，选项B 正确；没有指明哪个角是底角，∴梯形的底角是60︒或120︒，选项D错误；如图，连接DE，=∠=︒，,260CD CE∴是等边三角形，CDE∴=∠=︒，DE CD CDE,60∴∠+∠=︒，180ADC CDEA D E共线，∴点,,∠=∠=︒，ABC360∴，AB CE=，AB CE∴四边形ABCE是平行四边形，∴=，AE BC∠=∠=︒，CGF CDE60∴，DE FGEF DG，EF FG=，∴四边形DEFG是菱形，∴==，DE EF AD==+=，选项A、C正确；BC AE AD DE AD∴=，2CD AD故选：D．【点睛】本题考查了等腰梯形、菱形的判定与性质、等边三角形的判定与性质等知识点，熟练掌握各判定与性质是解题关键．2、D【详解】AB，即可求出CM．根据直角三角形斜边上的中线性质得出CM＝12【解答】解：∵公路AC，BC互相垂直，∴∠ACB＝90°，∵M为AB的中点，AB，∴CM＝12∵AB＝6km，∴CM＝3km，即M，C两点间的距离为3km，故选：D．【点睛】本题考查了直角三角形的性质，解题关键是掌握直角三角形斜边上的中线的性质：直角三角形斜边上的中线等于斜边的一半．3、C【分析】根据多边形外角和360 求解即可．【详解】解：123456360∠+∠+∠+∠+∠+∠=︒ ，1290∠+∠=︒()345636012270∴∠+∠+∠+∠=︒-∠+∠=︒，故选：C【点睛】本题考查了多边形的外角和定理，掌握多边形外角和360︒是解题的关键．4、D【分析】利用矩形的性质，求证明90OAB ∠=︒，进而在Rt AOB ∆中利用勾股定理求出OB 的长度，弧长就是OB 的长度，利用数轴上的点表示，求出弧与数轴交点表示的实数即可．【详解】解：四边形OABC 是矩形，∴90OAB ∠=︒，在Rt AOB ∆中，由勾股定理可知：222OB OA AB =+，OB ∴==∴故选：D ．【点睛】本题主要是考查了矩形的性质、勾股定理解三角形以及数轴上的点的表示，熟练利用矩形性质，得到直角三角形，然后通过勾股定理求边长，是解决该类问题的关键．5、B【分析】根据完全平方公式分解因式得到a=b ，c=d ，利用边的位置关系得到该四边形的形状．【详解】解：222222+，++=+a b c d ab cd22220a ab bc cd d-++-+=，2222-=a b+-（，c d()0)--=a b=，0,0c d∴a=b，c=d，∵四边形四条边长分别是a，b，c，d，其中a，b为对边，∴c、d是对边，∴该四边形是平行四边形，故选：B．【点睛】此题考查了完全平方公式分解因式，平行四边形的判定方法，熟练掌握完全平方公式分解因式是解题的关键．6、A【分析】DN，从而可知DN最大时，EF最大，因为N与B重合时DN最大，根据三角形的中位线定理得出EF=12此时根据勾股定理求得DN，从而求得EF的最大值．连接DB，过点D作DH⊥AB交AB于点H，再利用直角三角形的性质和勾股定理求解即可；【详解】解：∵ED=EM，MF=FN，DN，∴EF=12∴DN最大时，EF最大，∴N与B重合时DN=DB最大，在R t△ADH中，∵∠A=60°ADH∴∠=︒30∴AH=2×1=1，DH=2∴BH=AB﹣AH=3﹣1=2，∴DBDB，∴EF max=12∴EF故选A【点睛】本题考查了三角形的中位线定理，勾股定理，含30度角的直角三角形的性质，利用中位线求得EF=1DN是解题的关键．27、B【分析】首先可判断重叠部分为平行四边形，且两条丝带宽度相同；再由平行四边形的面积可得邻边相等，则重叠部分为菱形．【详解】解：过点A作AE⊥BC于E，AF⊥CD于F，因为两条彩带宽度相同，所以AB∥CD，AD∥BC，AE=AF．∴四边形ABCD是平行四边形．∵S▱ABCD=BC•AE=CD•AF．又AE=AF．∴BC=CD，∴四边形ABCD是菱形．故选：B【点睛】此题考查了菱形的判定，平行四边形的面积公式以及平行四边形的判定与性质，利用了数形结合的数学思想，其中菱形的判定方法有：一组邻边相等的平行四边形为菱形；对角线互相垂直的平行四边形为菱形；四条边相等的四边形为菱形，根据题意作出两条高AE和AF，熟练掌握菱形的判定方法是解本题的关键8、A【分析】利用直角三角形斜边的中线的性质可得答案．【详解】解：∵∠C=90°，若D为斜边AB上的中点，AB，∴CD=12∵AB的长为10，∴DC=5，故选：A．【点睛】此题主要考查了直角三角形斜边的中线，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．9、D【分析】由平行四边形的判定与性质、矩形的判定分别对各个选项进行判断即可．【详解】解：A、∵对角线互相平分的四边形是平行四边形，∴对角线互相平分且相等的四边形才是矩形，∴选项A不符合题意；B、∵两组对边分别相等是平行四边形，∴选项B不符合题意；C、∵对角线互相平分且相等的四边形才是矩形，∴对角线相等的四边形不是矩形，∴选项C不符合题意；D、∵对角线交点到四个顶点的距离都相等，∴对角线互相平分且相等，∵对角线互相平分且相等的四边形是矩形，∴选项D符合题意；故选：D．【点睛】本题考查了矩形的判定、平行四边形的判定与性质、解题的关键是熟记矩形的判定定理．【分析】根据正方形的四条边都相等可得BC ＝DC ，每一个角都是直角可得∠B ＝∠DCF ＝90°，然后利用“边角边”证明△CBE ≌△DCF ，得∠BCE ＝∠CDF ，进一步得∠DHC ＝∠DHE ＝90°，从而知GH ＝12DE ，利用勾股定理求出DE 的长即可得出答案．【详解】解：∵四边形ABCD 为正方形，∴∠B ＝∠DCF ＝90°，BC ＝DC ，在△CBE 和△DCF 中，BC CC B DCF BE CF =⎧⎪∠=∠⎨⎪=⎩， ∴△CBE ≌△DCF （SAS ），∴∠BCE ＝∠CDF ，∵∠BCE +∠DCH ＝90°，∴∠CDF +∠DCH ＝90°，∴∠DHC ＝∠DHE ＝90°，∵点G 为DE 的中点，∴GH ＝12DE ，∵AD ＝AB ＝6，AE ＝AB ﹣BE ＝6﹣2＝4，∴DE == ∴GH【点睛】本题主要考查了正方形的性质，全等三角形的性质与判定，勾股定理，直角三角形斜边上的中线，解题的关键在于能够熟练掌握相关知识进行求解．二、填空题1、80°【分析】由翻折的性质得∠ADE＝∠A1DE，由中位线的性质得DE//BC，由平行线的性质得∠ADE＝∠B＝50°，即可解决问题．【详解】解：由题意得：∠ADE＝∠A1DE；∵D、E分别是边AB、AC的中点，∴DE//BC，∴∠ADE＝∠B＝∠A1DE＝50°，∴∠A1DA＝100°，∴∠BDA1＝180°−100°＝80°．故答案为：80°．【点睛】本题主要考查了翻折变换及其应用问题；同时还考查了三角形的中位线定理等几何知识点．熟练掌握各性质是解题的关键．2、10或14或10【分析】=，通过BF和CE 利用BF平分∠ABC， CE平分∠BCD，以及平行关系，分别求出AB AF=、DE DC是否相交，分两类情况讨论，最后通过边之间的关系，求出BC的长即可．解：四边形ABCD是平行四边形，∥，==，AD BCAB CDAD BC∴=，6∠=∠，AFE FBC∴∠=∠，DEC ECBBF平分∠ABC， CE平分∠BCD，∠=∠，ABF FBC∴∠=∠，DCE ECB∠=∠，AFE ABF∴∠=∠，DCE DEC∴由等角对等边可知：6==，DE DCAF AB==，6情况1：当BF与CE相交时，如下图所示：AD AF DE EF=+-，AD∴=，10∴=，BC10情况2：当BF与CE不相交时，如下图所示：=++AD AF DE EF∴=AD，14∴=，BC14故答案为：10或14．【点睛】本题主要是考查了平行四边形的性质，熟练运用平行关系+角平分线证边相等，是解决本题的关键，还要注意根据BF和CE是否相交，本题分两类情况，如果没考虑仔细，会漏掉一种情况．3、4【分析】根据题意连接BD，取BD的中点M，连接EM、FM，EM交BC于N，根据三角形的中位线定理推出EM=12 CD，EM∥AB，FM∥CD，推出∠ABC=∠ENC，∠MFN=∠C，求出∠EMF=90°，根据勾股定理求AB，FM=12出ME2+FM2=EF2，根据圆的面积公式求出阴影部分的面积即可．【详解】解：连接BD，取BD的中点M，连接EM、FM，延长EM交BC于N，∵∠ABC+∠DCB=90°，∵E、F、M分别是AD、BC、BD的中点，∴EM=12AB，FM=12CD，EM∥AB，FM∥CD，∴∠ABC=∠ENC，∠MFN=∠C，∴∠MNF+∠MFN=90°，∴∠NMF=180°-90°=90°，∴∠EMF=90°，由勾股定理得：ME2+FM2=EF2，∴阴影部分的面积是：12π（ME2+FM2）=12EF2π=8π，∴EF=4.故答案为：4．【点睛】本题主要考查对勾股定理，三角形的内角和定理，多边形的内角和定理，三角形的中位线定理，圆的面积，平行线的性质，面积与等积变形等知识点的理解和掌握，能正确作辅助线并求出ME2+FM2的值是解答此题的关键．4、900°900度【分析】根据多边形内角和公式计算即可．【详解】解：七边形内角和的度数是(72)180900-⨯︒=︒，故答案为：900°．【点睛】本题考查了多边形内角和公式，解题关键是熟记n 边形内角和公式：2180()n -⨯︒．5、【分析】根据题意可得，设正方体的棱长为a dm ，则减去的部分为2个边长为a dm 的正方形，将阴影部分按虚线折叠成一个有盖的正方体盒子，则四个角折叠后刚好凑成1个边长为a dm 的正方形，据此列一元二次方程求解，进而即可求得正方体的容积【详解】解：设正方体的棱长为a dm ()0a >，则222426a a -=解得a∴这个盒子的容积为3dm故答案为：【点睛】本题考查了一元二次方程的应用，立方体展开图，正方形的性质，根据题意列出一元二次方程是解题的关键．三、解答题1、（1）103；（2）①点G 的坐标为（﹣8，6）或（8，6）或（8，﹣6）；②4,8,6m G 或6,8,6.m G 或732,8,33m G ⎛⎫= ⎪⎝⎭．【分析】（1）由矩形的性质得AD ＝BC ＝OC ＝10，CD ＝AB ＝OA ＝6，∠AOC ＝∠ECF ＝90°，由折叠性质得EF ＝DE ，AF ＝AD ＝10，则CE ＝6﹣EF ，由勾股定理求出BF ＝OF ＝8，则FC ＝OC ﹣OF ＝2，在Rt △ECF 中，由勾股定理得出方程，解方程即可；（2）①分三种情况，当AB 为平行四边形的对角线时；当AF 为平行四边形的对角线时；当BF 为平行四边形的对角线时，分别求解点G 的坐标即可；②分三种情况讨论，当OF 为对角线时，由菱形的性质得OA ＝AF ＝10，则矩形ABCD 平移距离m ＝OA ﹣AB＝4，即OB＝4，设FG交x轴于H，证出四边形OBFH是矩形，得FH＝OB＝4，OH＝BF＝8，则HG＝6，如图，当AO为菱形的对角线时，当AF为菱形的对角线时，结合矩形与菱形的性质同理可得出答案．【详解】解：（1）∵四边形ABCD是矩形，∴AD＝BC＝OC＝10，CD＝AB＝OA＝6，∠AOC＝∠ECF＝90°，由折叠性质得：EF＝DE，AF＝AD＝10，∴CE＝CD﹣DE＝CD﹣EF＝6﹣EF，由勾股定理得：BF＝OF22221068AF OA，∴FC＝OC﹣OF＝10﹣8＝2，在Rt△ECF中，由勾股定理得：EF2＝CE2+FC2，即：EF2＝（6﹣EF）2+22，解得：EF＝103；（2）①如图所示：当AB为平行四边形的对角线时，AG＝BF＝8，AG BF∥，∴点G的坐标为：（﹣8，6）；当AF为平行四边形的对角线时，AG'＝BF＝8，'AG BF，∴点G'的坐标为：（8，6）；FG AB，当BF为平行四边形的对角线时，FG''＝AB＝6，''∴点G''的坐标为：（8，﹣6）；综上所述，点G的坐标为（﹣8，6）或（8，6）或（8，﹣6）；②如图，当OF为菱形的对角线时，∵四边形AOGF为菱形，∴OA＝AF＝10，∴矩形ABCD平移距离m＝OA﹣AB＝10﹣6＝4，即OB＝4，设FG交x轴于H，如图所示：∵OA FG∥轴，∥，BC x∴∠FBO＝∠BOH＝∠OHF＝90°，∴四边形OBFH是矩形，∴FH＝OB＝4，OH＝BF＝8，∴HG＝10﹣4＝6，∴点G的坐标为：（8，﹣6）．如图，当AO 为菱形的对角线时，则6,8,,AB OB GB BF AO GF6,8,6.m G 如图，当AF 为菱形的对角线时，同理可得：,6,OA OF OA m 且,,GF OA GF BC ∥0,6,8,,A m F m 22268,m m 解得：7,3m2570,,8,,33A F 所以7258,33G 即328,.3G 综上：平移距离m 与G 的坐标分别为：4,8,6m G 或()6,8,6m G =-或732,8,.33mG ．【点睛】本题是四边形综合题目，考查了矩形的判定与性质、菱形的判定与性质，坐标与图形性质、平行四边形的性质、勾股定理、折叠变换的性质、平移的性质等知识；熟练掌握矩形的性质和折叠的性质是解题的关键．2、（1）见解析（2）见解析【分析】（1）首先证明△AEF ≌△DEC （AAS ），得出AF =DC ，进而利用AF ∥B D 、AF =BD 得出答案；（2）利用等腰三角形的性质，结合矩形的判定方法得出答案．【小题1】解：证明：（1）∵AF ∥BC ，∴∠AFC =∠FC D ．在△AFE 和△DCE 中，AEF DEC AFE DCE AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△DEC （AAS ）．∴AF =DC ，∵BD =DC ，∴AF =BD ，∴四边形AFBD 是平行四边形；【小题2】∵AB =AC ，BD =DC ，∴AD ⊥B C ．∴∠ADB =90°．∵四边形AFBD 是平行四边形，∴四边形AFBD 是矩形．【点睛】此题主要考查了平行四边形的判定以及矩形的判定方法、全等三角形的判定与性质，正确掌握平行四边形的判定方法是解题关键．3、（1）证明见解析；（2）73°．【分析】（1）根据正方形的性质及各角之间的关系可得：ABE CBF ∠=∠，由全等三角形的判定定理可得AEB CFB ≌，再根据其性质即可得证；（2）根据垂直及等腰三角形的性质可得45BEF EFB ∠=∠=︒，再由三角形的外角的性质可得EGC GFC BCF EBG BEF ∠=∠+∠=∠+∠，由此计算即可．【详解】（1）证明：∵四边形ABCD 是正方形，∴90ABC ∠=︒，AB BC =，∵BE BF ⊥，∴90FBE ∠=︒，∵90ABE EBC ∠+∠=°，90CBF EBC ∠+∠=︒，∴ABE CBF ∠=∠，在AEB 和CFB 中，AB BC ABE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩， ∴AEB CFB ≌，∴AE CF =；（2）解：∵BE ⊥BF ，∴90FBE ∠=︒，又∵BE BF =，∴45BEF EFB ∠=∠=︒，∵四边形ABCD 是正方形，∴90ABC ∠=︒，∵62ABE ∠=︒，∴906228EBG ∠=︒-︒=︒，∴452873EGC GFC BCF EBG BEF ∠=∠+∠=∠+∠=︒+︒=︒．∴GFC BCF ∠+∠的值为73︒．【点睛】题目主要考查全等三角形的判定和性质，正方形的性质，三角形的外角性质，理解题意，熟练运用各个定理性质是解题关键．4、（1）见解析；（2）12，0；-8，0；0，16；（3）①当M 的坐标为（2，0）或（4，0）时，△OMN 的一条边与BC 平行；②当M 的坐标为（0，10）或（12，0）或（253，0）时，，△MOE 是等腰三角形．【分析】（1）设2BO m =，3AO m =，4CO m =，则5AB AO BO m =+=，由勾股定理求出AC ，即可得出结论；（2）由ABC 的面积求出m 的值，从而得到OB 、OA 、OC 的长，即可得到A 、B 、C 的坐标；（3）①分当//BC MN 时，AM AN =；当//ON BC 时，AO AN =；得出方程，解方程即可； ②由直角三角形的性质得出10cm OE =，根据题意得出MOE △为等腰三角形，有3种可能：如果OE OM =；如果EO EM =；如果MO ME =；分别得出方程，解方程即可．【详解】解：（1）证明：设2BO m =，3AO m =，4CO m =，则5AB AO BO m =+=，在Rt ACO 中，5AC m ==，AB AC ∴=，∴ABC 是等腰三角形；（2）∵115416022ABC S AB OC m m =⋅=⨯⋅=，0m >，∴4m =，∴8cm BO =，12cm AO =，16cm CO =，20cm AC =．∴A 点坐标为（12，0），B 点坐标为（-8，0），C 点坐标为（0，16），故答案为：12，0；-8，0；0，16；（3）①如图3-1所示，当MN ∥BC 时，∵AB =AC ，∴∠ABC =∠ACB ，∵MN ∥BC ，∴∠AMN =∠ABC ，∠ANM =∠ACB ，∴∠AMN=∠ANM，∴AM=AN，∴AM=BM，∴M为AB的中点，AB=，∵20cm∴10cmAM=，∴2cmOM=，∴点M的坐标为（2，0）；如图3-2所示，当ON∥BC时，同理可得12cm===，OA AN BM∴4cm=-=，OM BM OB∴M点的坐标为（4，0）；∴综上所述，当M的坐标为（2，0）或（4，0）时，△OMN的一条边与BC平行；②如图3-3所示，当OM=OE时，∵E是AC的中点，∠AOC=90°，20cmAC=，∴110cm2OM OE AE AC====，∴此时M的坐标为（0，10）；如图3-4所示，当=10cmOE ME=时，∴此时M点与A点重合，∴M点的坐标为（12，0）；如图3-5所示，当OM=ME时，过点E作EF⊥x轴于F，∵OE=AE，EF⊥OA，∴1=6cm2OF OA=，∴8cm EF，设cm OM ME n ==，则()6cm MF OM OF n =-=-，∵222ME EF FM =+，∴()22286n n =+-，解得253n =， ∴M 点的坐标为（253，0）；综上所述，当M 的坐标为（0，10）或（12，0）或（253，0）时，，△MOE 是等腰三角形．【点睛】本题主要考查了坐标与图形，勾股定理，等腰三角形的性质与判定，直角三角形斜边上的直线，三角形面积等等，解题的关键在于能够利用数形结合和分类讨论的思想求解．5、（1）证明见解析；（2）EF=【分析】（1）由题意知BE DF ∥，OD OB =，通过BOE DOF ≌得到BE DF =，证明四边形BEDF 平行四边形．（2）四边形BEDF 为菱形，DB EF ⊥，DB =BE BF x ==，8CF AE x ==-；在Rt BCF 中用勾股定理，解出BF 的长，在Rt BOF 中用勾股定理，得到OF 的长，由2EF OF =得到EF 的值．【详解】（1）证明：∵四边形ABCD 是矩形，O 是BD 的中点∴BE DF ∥，OD OB =OBE ODF ∴∠=∠在BOE △和DOF △中OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BOE DOF △△≌（ASA ） ∴BE DF =∴四边形BEDF 是平行四边形．（2）解：∵四边形BEDF 为菱形，∴BE BF =，DB EF ⊥又∵8AB =，4BC =∴BD ==BO =设BE BF x ==，则8CF AE x ==-在Rt BCF 中，()22248x x +-=∴5x =在Rt BOF中，OE =∴2EF OE ==【点睛】本题考察了平行四边形的判定，三角形全等，菱形的性质，勾股定理．解题的关键与难点在于对平行四边形的性质的灵活运用．。

2020年中考数学压轴题专题讲解：四边形综合题(含答案)

备战2020年中考数学压轴题专题讲解：四边形综合题1．如图，四边形ABCD是菱形，120BAD∠=︒，点E在射线AC上（不包括点A和点)C，过点E的直线GH交直线AD于点G，交直线BC于点H，且//GH DC，点F在BC的延长线上，CF AG=，连接ED，EF，DF．（1）如图1，当点E在线段AC上时，①判断AEG∆的形状，并说明理由．②求证：DEF∆是等边三角形．（2）如图2，当点E在AC的延长线上时，DEF∆是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由．2．（1）如图1，在四边形ABCD中，AB AD=，180B D∠+∠=︒，E，F分别是边BC，CD上的点，且12EAF BAD∠=∠，则BE，EF，DF之间的数量关系是EF BE DF=+．（2）如图2，若E，F分别是边BC，CD延长线上的点，其他条件不变，则BE，EF，DF 之间的数量关系是什么？请说明理由．（3）如图3，在某次军事演习中，舰艇甲在指挥中心(O处）北偏西30︒的A处，舰艇乙在指挥中心南偏东70︒的B处，并且两舰艇到指挥中心的距离相等，接到行动命令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50︒的方向以80海里/小时的速度前进，1.5小时后，指挥中心观察到舰艇甲、乙分别到达E，F处，且两舰艇与指挥中心O 连线的夹角70EOF∠=︒，试求此时两舰艇之间的距离．3．将一个等边三角形纸片AOB 放置在平面直角坐标系中，点(0,0)O ，点(6,0)B ．点C 、D 分别在OB 、AB 边上，//DC OA ，23CB =．()I 如图①，将DCB ∆沿射线CB 方向平移，得到△D C B '''．当点C 平移到OB 的中点时，求点D '的坐标；()II 如图②，若边D C ''与AB 的交点为M ，边D B ''与ABB ∠'的角平分线交于点N ，当BB '多大时，四边形MBND '为菱形？并说明理由．()III 若将DCB ∆绕点B 顺时针旋转，得到△D C B ''，连接AD '，边D C ''的中点为P ，连接AP ，当AP 最大时，求点P 的坐标及AD '的值．（直接写出结果即可）．4．如图（1），在ABC ∆中，AB AC =，90BAC ∠=︒，AD BC ⊥于点D ，20BC cm =，10AD cm =．点P 从点B 出发，在线段BC 上以每秒2cm 的速度向点C 匀速运动，与此同时，垂直于AD 的直线t 从点A 沿AD 出发，以每秒1cm 的速度沿AD 方向匀速平移，分别交AB 、AC 、AD 于M 、N 、E ．当点P 到达点C 时，点P 与直线l 同时停止运动，设运动时间为t 秒(0)t >．（1）在运动过程中（点P 不与B 、C 重合），连接PN ，求证：四边形MBPN 为平行四边形；（2）如图（2），以MN 为边向下作正方形MFGN ，FG 交AD 于点H ，连结PF 、PG ，当1003t <<时，求PFG ∆的面积最大值；（3）在整个运动过程中，观察图（2）、（3），是否存在某一时刻t ，使PFG ∆为等腰三角形？若存在，直接写出t 的值；若不存在，请说明理由．5．如图①，在矩形ABCD 中，动点P 从点A 出发，以1/cm s 的速度沿AD 向终点D 移动，设移动时间为()t s ，连接PC ，以PC 为一边作正方形PCEF ，连接DE 、DF ，设PCD ∆的面积为2()y cm ，y 与t 之间的函数关系如图②所示．（1）AB = cm ，AD = cm ；（2）当t 为何值时，DEF ∆的面积最小？请求出这个最小值；（3）当t 为何值时，DEF ∆为等腰三角形？请简要说明理由．6．如图，在平行四边形ABCD 中，AC BC ⊥，10AB =．6AC =．动点P 在线段BC 上从点B 出发沿BC 方向以每秒1个单位长的速度匀速运动；动点Q 在线段DC 上从点D 出发沿DC 的力向以每秒1个单位长的速度匀速运动，过点P 作PE BC ⊥．交线段AB 于点E ．若P 、Q 两点同时出发，当其中一点到达终点时整个运动随之停止，设运动时间为t 秒．（1）当t 为何值时，//QE BC ？（2）设PQE ∆的面积为S ，求出S 与t 的函数关系式：（3）是否存在某一时刻t ，使得PQE ∆的面积S 最大？若存在，求出此时t 的值；若不存在，请说明理由．（4）是否存在某一时刻t ，使得点Q 在线段EP 的垂直平分线上？若存在，求出此时t 的值；若不存在，请说明理由．7．如图一，在射线DE的一侧以AD为一条边作矩形ABCD，53AD=，5CD=，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求CAD∠的大小；（2）问题探究：动点M在运动的过程中，①是否能使AMN∆为等腰三角形，如果能，求出线段MC的长度；如果不能，请说明理由．②MBN∠的大小是否改变？若不改变，请求出MBN∠的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M运动到AC的中点时，AM与BN的交点为F，MN的中点为H，求线段FH的长度．8．如图，点E，F分别在正方形ABCD的边CD，BC上，且DE CF=，点P在射线BC上（点P不与点F重合）．将线段EP绕点E顺时针旋转90︒得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q．（1）如图1，若点E是CD的中点，点P在线段BF上，线段BP，QC，EC的数量关系为+=．BP QC EC（2）如图2，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由．（3）正方形ABCD的边长为6，3QC=，请直接写出线段BP的长．=，1AB DE9．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在ABC ∆中，AD BC ⊥于点D ，正方形PQMN 的边QM 在BC 上，顶点P ，N 分别在AB ，AC 上，若BC a =，AD h =，求正方形PQMN 的边长（用a ，h 表示）．（2）操作：如何画出这个正方形PQMN 呢？如图2，小波画出了图1的ABC ∆，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在AB 上任取一点P '，画正方形P Q M N ''''，使点Q '，M '在BC 边上，点N '在ABC ∆内，然后连结BN '，并延长交AC 于点N ，画NM BC ⊥于点M ，NP NM ⊥交AB 于点P ，PQ BC ⊥于点Q ，得到四边形PQMN ．（3）推理：证明图2中的四边形PQMN 是正方形．（4）拓展：小波把图2中的线段BN 称为“波利亚线”，在该线上截取NE NM =，连结EQ ，EM （如图3)，当90QEM ∠=︒时，求“波利亚线” BN 的长（用a ，h 表示）．请帮助小波解决“温故”、“推理”、“拓展”中的问题．10．性质探究如图①，在等腰三角形ABC 中，120ACB ∠=︒，则底边AB 与腰AC 的长度之比为 3 ．理解运用（1）若顶角为120︒的等腰三角形的周长为843+，则它的面积为；（2）如图②，在四边形EFGH中，EF EG EH==．①求证：EFG EHG FGH∠+∠=∠；②在边FG，GH上分别取中点M，N，连接MN．若120EF=，直接写出FGH∠=︒，10线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为（用含α的式子表示）．11．如图1，在矩形ABCD中，3BC=，动点P从B出发，以每秒1个单位的速度，沿射线t s．BC方向移动，作PAB∆关于直线PA的对称PAB∆'，设点P的运动时间为()（1）若23AB=．①如图2，当点B'落在AC上时，显然PAB∆'是直角三角形，求此时t的值；②是否存在异于图2的时刻，使得PCB∆'是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．（2）当P点不与C点重合时，若直线PB'与直线CD相交于点M，且当3t<时存在某一时刻有结论45PAMt>的任意时刻，结论“45∠=︒”是否总是PAM∠=︒成立，试探究：对于3成立？请说明理由．12．如图，在以点O为中心的正方形ABCD中，4AD=，连接AC，动点E从点O出发沿∆的外→以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，ADEO C接圆交AB于点F，连接DF交AC于点G，连接EF，将EFG∆．∆沿EF翻折，得到EFH （1）求证：DEF∆是等腰直角三角形；（2）当点H 恰好落在线段BC 上时，求EH 的长；（3）设点E 运动的时间为t 秒，EFG ∆的面积为S ，求S 关于时间t 的关系式．13．操作体验：如图，在矩形ABCD 中，点E 、F 分别在边AD 、BC 上，将矩形ABCD 沿直线EF 折叠，使点D 恰好与点B 重合，点C 落在点C '处．点P 为直线EF 上一动点（不与E 、F 重合），过点P 分别作直线BE 、BF 的垂线，垂足分别为点M 和N ，以PM 、PN为邻边构造平行四边形PMQN ．（1）如图1，求证：BE BF =；（2）特例感知：如图2，若5DE =，2CF =，当点P 在线段EF 上运动时，求平行四边形PMQN 的周长；（3）类比探究：若DE a =，CF b =．①如图3，当点P 在线段EF 的延长线上运动时，试用含a 、b 的式子表示QM 与QN 之间的数量关系，并证明；②如图4，当点P 在线段FE 的延长线上运动时，请直接用含a 、b 的式子表示QM 与QN 之间的数量关系．（不要求写证明过程）14．在矩形ABCD 中，连结AC ，点E 从点B 出发，以每秒1个单位的速度沿着B A C →→的路径运动，运动时间为t （秒）．过点E 作EF BC ⊥于点F ，在矩形ABCD 的内部作正方形EFGH ．（1）如图，当8AB BC ==时，①若点H 在ABC ∆的内部，连结AH 、CH ，求证：AH CH =；②当08t <时，设正方形EFGH 与ABC ∆的重叠部分面积为S ，求S 与t 的函数关系式；（2）当6AB=，8BC=时，若直线AH将矩形ABCD的面积分成1:3两部分，求t的值．15．如图，在平面直角坐标系xOy中，矩形ABCD的边4AB=，6BC=．若不改变矩形ABCD 的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动．（1）当30OAD∠=︒时，求点C的坐标；（2）设AD的中点为M，连接OM、MC，当四边形OMCD的面积为212时，求OA的长；（3）当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos OAD∠的值．参考答案1、【解答】（1）①解：AEG ∆是等边三角形；理由如下：四边形ABCD 是菱形，120BAD ∠=︒，//AD BC ∴，AB BC CD AD ===，//AB CD ，1602CAD BAD ∠=∠=︒， 180BAD ADC ∴∠+∠=︒， 60ADC ∴∠=︒， //GH DC ，60AGE ADC ∴∠=∠=︒， 60AGE EAG AEG ∴∠=∠=∠=︒， AEG ∴∆是等边三角形；②证明：AEG ∆是等边三角形， AG AE ∴=， CF AG =， AE CF ∴=，四边形ABCD 是菱形， 120BCD BAD ∴∠=∠=︒， 60DCF CAD ∴∠=︒=∠，在AED ∆和CFD ∆中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，()AED CFD SAS ∴∆≅∆DE DF ∴=，ADE CDF ∠=∠，60ADC ADE CDE ∠=∠+∠=︒， 60CDF CDE ∴∠+∠=︒，即60EDF ∠=︒， DEF ∴∆是等边三角形；（2）解：DEF ∆是等边三角形；理由如下：同（1）①得：AEG ∆是等边三角形， AG AE ∴=，CF AG =， AE CF ∴=，四边形ABCD 是菱形， 120BCD BAD ∴∠=∠=︒，1602CAD BAD ∠=∠=︒， 60FCD CAD ∴∠=︒=∠，在AED ∆和CFD ∆中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，()AED CFD SAS ∴∆≅∆， DE DF ∴=，ADE CDF ∠=∠，60ADC ADE CDE ∠=∠-∠=︒， 60CDF CDE ∴∠-∠=︒，即60EDF ∠=︒， DEF ∴∆是等边三角形．2、【解答】解：（1）延长FD 到点G ，使DG BE =，连结AG ，如图1所示：在ABE ∆和ADG ∆中，90BE DG B ADG AB AD =⎧⎪∠=∠=︒⎨⎪=⎩，()ABE ADG SAS ∴∆≅∆， AE AG ∴=，BAE DAG ∠=∠，12EAF BAD ∠=∠， GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠，在AEF ∆和GAF ∆中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()AEF AGF SAS ∴∆≅∆， EF FG ∴=，FG DG DF BE DF =+=+， EF BE DF ∴=+，故答案为：EF BE DF =+；（2）BE ，EF ，DF 之间的数量关系是：EF BE DF =-；理由如下：在CB 上截取BM DF =，连接AM ，如图2所示：180B D ∠+∠=︒，180ADC ADF ∠+∠=︒，B ADF ∴∠=∠，在ABM ∆和ADF ∆中，AB ADB ADF BM DF=⎧⎪∠=∠⎨⎪=⎩，()ABM ADF SAS ∴∆≅∆，AF AM ∴=，DAF BAM ∠=∠，BAD MAF ∴∠=∠，2BAD EAF ∠=∠，2MAF EAF ∴∠=∠，MAE EAF ∴∠=∠，在FAE ∆和MAE ∆中，AE AEFAE MAE AF AM=⎧⎪∠=∠⎨⎪=⎩，()FAE MAE SAS ∴∆≅∆，EF EM BE BM BE DF ∴==-=-，即EF BE DF =-；（3）连接EF ，延长AE 、BF 相交于点C ，如图3所示：3090(9070)140AOB ∠=︒+︒+︒-︒=︒，70EOF ∠=︒，12EOF AOB ∴∠=∠，OA OB =，(9030)(7050)180OAC OBC ∠+∠=︒-︒+︒+︒=︒，∴符合（1）中的条件，即结论EF AE BF =+成立，1.5(6080)210EF ∴=⨯+=（海里）．答：此时两舰艇之间的距离是210海里．3、【解答】解：（Ⅰ）如图①中，作DH BC ⊥于H ．AOB ∆是等边三角形，//DC OA ，60DCB AOB ∴∠=∠=︒，60CDB A ∠=∠=︒，CDB ∴∆是等边三角形， 23CB =DH CB ⊥，3CH HB ∴==3DH =，(63D ∴，3)，3C B '=，233CC ∴'=-，233DD CC ∴'='=-，(33D ∴'+3)．（Ⅱ）当3BB '=时，四边形MBND '是菱形．理由：如图②中，ABC ∆是等边三角形，60ABO ∴∠=︒，180120ABB ABO '∴∠=︒-∠=︒， BN 是ACC '∠的角平分线， 1602NBB ABB D C B ''∴∠'=∠=︒=∠''，//D C BN ''∴，//AB B D ''∴四边形MBND '是平行四边形，60ME C MCE '''∠=∠=︒，60NCC NC C ''∠=∠=︒，∴△MC B ''和NBB '∆是等边三角形，MC CE '∴=，NC CC '=，23B C ''=，四边形MBND '是菱形，BN BM ∴=，132BB B C '''∴==；（Ⅲ）如图连接BP ，在ABP ∆中，由三角形三边关系得，AP AB BP <+，∴当点A ，B ，P 三点共线时，AP 最大，如图③中，在△D BC ''中，由P 为D C ''的中点，得AP D C ''⊥，3PD '=，3CP ∴=，639AP ∴=+=，在Rt APD '∆中，由勾股定理得，AD '==此时15(2P ，．4、【解答】（1）证明：l AD ⊥，BC AD ⊥，//l BC ∴， ∴AM ANAB AC =，AB AC =，AM AN ∴=，90BAC ∠=︒，ME NE ∴=，22MN AE t ∴==，2BP t =，MN BP ∴=，∴四边形MBPN 为平行四边形；（2）解：四边形MFGN 是正方形，22FG MN MF AE t ∴====，2EH MF t ==，103DH AD AH t ∴=-=-，2115252(103)3()2233PFG S FG DH t t t ∆∴==⨯⨯-=--+，30a =-<，1003t <<，∴当53t =时，PFG S ∆最大253=；（3）解：存在，当t =5t =或10t =时，PFG ∆为等腰三角形；理由如下：利用勾股定理得：222(103)PF t =-，222(103)(10)PG t t =-+-，又22(2)FG t =，当PF FG =时，则222(103)(2)t t -=，解得：t =，当PF PG =时，2222(103)(103)(10)t t t -=-+-，解得：5t =，或0t =（舍去）；当FG PG =时，222(2)(103)(10)t t t =-+-，解得：10t =，或103t =（舍去）；综上所述，t =5t =或10t =时，PFG ∆为等腰三角形．5、【解答】解：（1）由图②知：5AD =，当0t =时，P 与A 重合，152y AD CD =⨯⨯=，1552CD ⨯⨯=，2CD cm =，四边形ABCD 是矩形，2AB CD cm ∴==，故答案为：2，5；（2）由题意得：AP t =，5PD t =-，112(5)522y CD PD t t ∴==-=-，四边形EFPC 是正方形，12DEF PDC EFPC S S S ∆∆∴+=正方形，222PC PD CD =+，22222(5)1029PC t t t ∴=+-=-+，222111913(1029)(5)4(4)22222DEF S t t t t t t ∆∴=-+--=-+=-+，当t 为4时，DEF ∆的面积最小，且最小值为32；（3）当DEF ∆为等腰三角形时，分四种情况：①当FD FE =时，如下图所示，过F 作FG AD ⊥于G ，四边形EFPC 是正方形，PF EF PC ∴==，90FPC ∠=︒，PF FD ∴=，FG PD ⊥， 12PG DG PD ∴==， 90FPG CPD CPD DCP ∠+∠=∠+∠=︒，FPG DCP ∴∠=∠，90FGP PDC ∠=∠=︒，()FPG PDC AAS ∴∆≅∆，2PG DC ∴==，4PD ∴=，541AP ∴=-=，即1t =；②当DE DF =时，如下图所示，E 在AD 的延长线上，此时正方形EFPC 是正方形，2PD CD ==，523AP t ∴==-=；③当DE EF =时，如下图所示，过E 作EG CD ⊥于G ，FE DE EC ==，112CG DG CD ∴===，同理得：()PDC CGE AAS ∆≅∆，1PD CG ∴==，514AP t ∴==-=，④当DF EF =时，如下所示，2PC EF PF ===，且PC BC ⊥，此时P 与D 重合，5t =，综上，当1t s =或3s 或4s 或5s 时，DEF ∆为等腰三角形．6、【解答】解：（1）如图1，记EQ 与AC 的交点为G ，AC BC ⊥，90ACB ∴∠=︒，在Rt ABC ∆中，10AB =，6AC =，根据勾股定理得，8BC =，3tan 4AC B BC ==，四边形ABCD 是平行四边形，10CD AB ∴==，8AD BC ==，由运动知，BP t =，DQ t =，8PC t ∴=-，10CQ t =-，PE BC ⊥，90BPE ∴∠=︒，在Rt BPE ∆中，3sin 5B =，4cos 5B =，3tan 4PE PE B BP t ===， 34PE t ∴=， //EQ BC ，90PEQ BPE ∴∠=∠=︒，∴四边形CPEG 是矩形，34CG PE t ∴==， //EQ BC ，CGQ CAD ∴∆∆∽， ∴CG CQ AC CD=， ∴3104610t t -=． 409t ∴=；（2）如图2，过点Q 作QH BC ⊥交BC 的延长线于H ，四边形ABCD 是平行四边形，//AB CD ∴，DCH B ∴∠=∠，在Rt CHQ ∆中，3sin 105QH QH QCH CQ t ∠===-， 3(10)5QH t ∴=-，4cos 105CH CH HCQ CQ t ∠===-， 4(10)5CH t ∴=-， 498(10)1655PH PC CH t t t ∴=+=-+-=-， ()()2133919327404010161610()25452554093QPH QHPE S S S t t t t t t ∆⎡⎤⎛⎫⎛⎫∴=-=-+⨯--⨯-⨯-=--+ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭梯形，点E 在线段AB 上，∴点P 在线段BC 上，08t ∴<，点Q 在CD 上，010t ∴<<，08t ∴<，即：2274040()(08)4093S t t =--+<；（3）由（2）知，2274040()(08)4093S t t =--+<；409t ∴=时，403S =最大；（4）如图3，过点Q 作QM PE ⊥于M ，交AC 于N ，点Q 在线段EP 的垂直平分线上，1328PM PE t ∴==，同（2）的方法得，3(10)5CN t =-，易知，四边形PCNM 是矩形，PM CN ∴=，∴33(10)85t t =-，8013t ∴=．7、【解答】解：（1）如图一（1）中，四边形ABCD 是矩形，90ADC ∴∠=︒，53tan 353DC DAC AD ∠===，30DAC ∴∠=︒．（2）①如图一（1）中，当AN NM =时，90BAN BMN ∠=∠=︒，BN BN =，AN NM =， Rt BNA Rt BNM(HL)∴∆≅∆，BA BM ∴=，在Rt ABC ∆中，30ACB DAC ∠=∠=︒，5AB CD ==， 210AC AB ∴==，60BAM ∠=︒，BA BM =，ABM ∴∆是等边三角形，5AM AB ∴==，5CM AC AM ∴=-=．如图一（2）中，当AN AM =时，易证15AMN ANM ∠=∠=︒，90BMN ∠=︒，75CMB ∴∠=︒，30MCB ∠=︒，180753075CBM ∴∠=︒-︒-︒=︒，CMB CBM ∴∠=∠，3CM CB ∴==，综上所述，满足条件的CM 的值为5或53②结论：30MBN ∠=︒大小不变．理由：如图一（1）中，180BAN BMN ∠+∠=︒，A ∴，B ，M ，N 四点共圆，30MBN MAN ∴∠=∠=︒．如图一（2）中，90BMN BAN ∠=∠=︒，A ∴，N ，B ，M 四点共圆，180MBN MAN ∴∠+∠=︒，180DAC MAN ∠+∠=︒，30MBN DAC ∴∠=∠=︒，综上所述，30MBN ∠=︒．（3）如图二中，AM MC =，BM AM CM ∴==，2AC AB ∴=，AB BM AM ∴==，ABM ∴∆是等边三角形，60BAM BMA ∴∠=∠=︒，90BAN BMN ∠=∠=︒，30NAM NMA ∴∠=∠=︒，NA NM ∴=，BA BM =，BN ∴垂直平分线段AM ，52FM ∴=，53cos303FM NM ∴==︒，90NFM ∠=︒，NH HM =，12FH MN ∴==8、【解答】解：（1）BP QC EC +=；理由如下：四边形ABCD 是正方形，BC CD ∴=，90BCD ∠=︒，由旋转的性质得：90PEG ∠=︒，EG EP =，90PEQ GEH ∴∠+∠=︒，QH GD ⊥，90H ∴∠=︒，90G GEH ∠+∠=︒，PEQ G ∴∠=∠，又90EPQ PEC ∠+∠=︒，90PEC GED ∠+∠=︒， EPQ GED ∴∠=∠，在PEQ ∆和EGD ∆中，EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩，()PEQ EGD ASA ∴∆≅∆，PQ ED ∴=，BP QC BC PQ CD ED EC ∴+=-=-=，即BP QC EC +=；故答案为：BP QC EC +=；（2）（1）中的结论仍然成立，理由如下：由题意得：90PEG ∠=︒，EG EP =，90PEQ GEH ∴∠+∠=︒，QH GD ⊥，90H ∴∠=︒，90G GEH ∠+∠=︒，PEQ G ∴∠=∠，四边形ABCD 是正方形，90DCB ∴∠=︒，BC DC =，90EPQ PEC ∴∠+∠=︒，90PEC GED ∠+∠=︒，GED EPQ ∴∠=∠，在PEQ ∆和EGD ∆中，EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩，()PEQ EGD ASA ∴∆≅∆，PQ ED ∴=，BP QC BC PQ CD ED EC ∴+=-=-=，即BP QC EC +=；（3）分两种情况：①当点P 在线段BC 上时，点Q 在线段BC 上，由（2）可知：BP EC QC =-，36AB DE ==，2DE ∴=，4EC =，413BP ∴=-=；②当点P 在线段BC 上时，点Q 在线段BC 的延长线上，如图3所示：同（2）可得：()PEQ EGD AAS ∆≅∆，2PQ DE ∴==，1QC =，1PC PQ QC ∴=-=，615BP BC PC ∴=-=-=；综上所述，线段BP 的长为3或5．9、【解答】（1）解：如图1中，//PN BC，APN ABC∴∆∆∽，∴PN AEBC AD=，即PN h PNa h-=，解得ah PNa h=+（2）能画出这样的正方形，如图2中，正方形PNMQ即为所求．（3）证明：如图2中，由画图可知：90QMN PQM NPQ BM N∠=∠=∠=∠''=︒，∴四边形PNMQ是矩形，//MN M N''，∴△BN M BNM''∆∽，∴M N BN MN BN'''=，同理可得：P N BN PN BN '''=∴M N P N MN PN''''=，M N P N''=''，MN PN∴=，∴四边形PQMN是正方形（4）如图，过点N作ND ME⊥于点D图3MN EN =，ND ME ⊥，NEM MNE ∴∠=∠，ED DM =90BMN QEM ∠=∠=︒90EQM EMQ ∴∠+∠=︒，90EMQ EMN ∠+∠=︒EMN EQM ∴∠=∠，且MN QN =，90QEM NDM ∠=∠=︒()QEM MDN AAS ∴∆≅∆12EQ DM EM ∴==，90BMN QEM ∠=∠=︒90BEQ NEM ∴∠+∠=︒，90BME NME ∠+∠=︒BEQ BME ∴∠=∠，且MBE MBE ∠=∠BEQ BME ∴∆∆∽ ∴12BQ BE EQ BE BM EM ===，2BM BE ∴=，2BE BQ =4BM BQ ∴=3QM BQ MN ∴==，5BN BQ = ∴3355MN BQ BN BQ ==55()33ahBN MN a h ∴==+10、【解答】性质探究解：作CD AB ⊥于D ，如图①所示：则90ADC BDC ∠=∠=︒，AC BC =，120ACB ∠=︒，AD BD ∴=，30A B ∠=∠=︒，2AC CD ∴=，AD =，2AB AD ∴==，∴AB AC =；理解运用（1）解：如图①所示：同上得：2AC CD =，AD =，8AC BC AB ++=+，48CD ∴+=+解得：2CD =，AB ∴=，ABC ∴∆的面积11222AB CD =⨯=⨯=故答案为：（2）①证明：EF EG EH ==，EFG EGF ∴∠=∠，EGH EHG ∠=∠，EFG EHG EGF EGH FGH ∴∠+∠=∠+∠=∠； ②解：连接FH ，作EP FH ⊥于P ，如图②所示：则PF PH =，由①得：120EFG EHG FGH ∠+∠=∠=︒，360120120120FEH ∴∠=︒-︒-︒=︒，EF EH =，30EFH ∴∠=︒，152PE EF ∴==，PF ∴==，2FH PF ∴==，点M 、N 分别是FG 、GH 的中点，MN ∴是FGH ∆的中位线， 1532MN FH ∴==；类比拓展解：如图③所示：作AD BC ⊥于D ，AB AC =，BD CD ∴=，12BAD BAC α∠=∠=，sin BDAB α=，sin BD AB α∴=⨯，22sin BC BD AB α∴==⨯，∴2sin 2sin BC AB AB AB αα==；故答案为：2sin α．11、【解答】解：（1）①如图1中，四边形ABCD 是矩形，90ABC ∴∠=︒，2221AC AB BC ∴=+=PCB ACB ∠'=∠，90PB C ABC ∠'=∠=︒， PCB ACB ∴∆'∆∽，∴CB PB CB AB ''=，∴2123323PB -'=，274PB ∴'=-．274t PB ∴==-． ②如图21-中，当PCB ∠’ 90=︒时，四边形ABCD 是矩形，90D ∴∠=︒，23AB CD ==，3AD BC ==，22(23)33DB ∴'=-=，3CB CD DB ∴'=-'=，在Rt PCB ∆'中，222B P PC B C '=+'，222(3)(3)t t ∴=+-，2t ∴=．如图22-中，当PCB ∠’ 90=︒时，在Rt ADB ∆'中，223DB AB AD '='-=， 33CB ∴'=在Rt PCB ∆’中则有：222(33)(3)t t +-=，解得6t =．如图23-中，当CPB ∠’ 90=︒时，易证四边形ABP ’为正方形，易知23t =．综上所述，满足条件的t 的值为2s 或6s 或23s ．（2）如图31-中，45PAM ∠=︒2345∴∠+∠=︒，1445∠+∠=︒又翻折，12∴∠=∠，34∠=∠，又ADM AB ∠=∠’ M ，AM AM =， ()AMD AMB AAS ∴∆≅∆'，AD AB ∴=’ AB =，即四边形ABCD 是正方形，如图，设APB x ∠=．90PAB x ∴∠=︒-，DAP x ∴∠=，易证MDA ∆≅△B ’ ()AM HL ， BAM DAM ∴∠=∠，翻折，PAB PAB ∴∠=∠’ 90x =︒-， DAB ∴∠’ PAB =∠’ 902DAP x -∠=︒-， 12DAM DAB ∴∠=∠’ 45x =︒-，45MAP DAM PAD ∴∠=∠+∠=︒．12、【解答】（1）证明：四边形ABCD 是正方形， 45DAC CAB ∴∠=∠=︒，FDE CAB ∴∠=∠，DFE DAC ∠=∠， 45FDE DFE ∴∠=∠=︒， 90DEF ∴∠=︒，DEF ∴∆是等腰直角三角形；（2）设OE t =，连接OD ， 90DOE DAF ∴∠=∠=︒， OED DFA ∠=∠，DOE DAF ∴∆∆∽，∴22OEODAF AD ==，∴2AF t =，又AEF ADG ∠=∠，EAF DAG ∠=∠，AEF ADG ∴∆∆∽， ∴AE AFAD AG =， ∴42AG AE AD AF t ==，又AE OA OE t =+=+，∴AG =，EG AE AG ∴=-=当点H 恰好落在线段BC 上454590DFH DFE HFE ∠=∠+∠=︒+︒=︒， ADF BFH ∴∆∆∽，∴FH FB FD AD ==， //AF CD ，∴FG AF DG CD ==∴FG DF =∴=，解得：1t =-，2t =（舍去），EG EH ∴====-；（3）过点F 作FK AC ⊥于点K ，由（2）得EG =，DE EF =，90DEF ∠=︒，DEO EFK ∴∠=∠，()DOE EKF AAS ∴∆≅∆，FK OE t ∴==， 31242EFG t S EG FK ∆+∴==13、【解答】（1）证明：如图1中，四边形ABCD 是矩形，//AD BC ∴，DEF EFB ∴∠=∠，由翻折可知：DEF BEF ∠=∠，BEF EFB ∴∠=∠，BE BF ∴=．（2）解：如图2中，连接BP ，作EH BC ⊥于H ，则四边形ABHE 是矩形，EH AB =．5DE EB BF ===，2CF =，7AD BC ∴==，2AE =，在Rt ABE ∆中，90A ∠=︒，5BE =，2AE =，225221AB ∴=-=，BEF PBE PBF S S S ∆∆∆=+，PM BE ⊥，PN BF ⊥， ∴111222BF EH BE PM BF PN =+， BE BF =，21PM PN EH ∴+==，四边形PMQN 是平行四边形，∴四边形PMQN 的周长2()221PM PN =+=（3）①证明：如图3中，连接BP ，作EH BC ⊥于H ．ED EB BF a ===，CF b =，AD BC a b ∴==+，AE AD DE b ∴=-=， 22EH AB a b ∴==-，EBP BFP EBF S S S ∆∆∆-=，∴111222BE PM BF PN BF EH -=， BE BF =，22PM PN EH a b ∴-==-，四边形PMQN 是平行四边形，22()QN QM PM PN a b ∴-=-=-．②如图4，当点P 在线段FE 的延长线上运动时，同法可证：22QM QN PN PM a b -=-=-．14、【解答】解：（1）①如图1中，四边形EFGH 是正方形，AB BC =，BE BG ∴=，AE CG =，90BEH BGH ∠=∠=︒，90AEH CGH ∴∠=∠=︒，EH HG =，()AEH CGH SAS ∴∆≅∆，AH CH ∴=．②如图1中，当04t <时，重叠部分是正方形EFGH ，2S t =．如图2中，当48t <时，重叠部分是五边形EFGMN ，2211882(8)163222ABC AEN CGM S S S S t t t ∆∆∆=--=⨯⨯-⨯-=-+-．综上所述，22(04)1632(48)t t S t t t ⎧<=⎨-+-<⎩．（2）如图31-中，设直线AH 交BC 于M ，当4BM CM ==时，直线AH 将矩形ABCD 的面积分成1:3两部分．//EH BM ，∴AE EH AB BM =， ∴664t t -=， 125t ∴=．如图32-中，设直线长AH 交CD 于M 交BC 的延长线于K ，当3CM DM ==时，直线AH 将矩形ABCD 的面积分成1:3两部分，易证8AD CK ==，//EH BK ，∴AE EH AB BK=，∴6616t t -=， 4811t ∴=．如图33-中，当点E 在线段AC 上时，设直线AH 交CD 于M ，交BC 的延长线于N ．当CM DM =时，直线AH 将矩形ABCD 的面积分成1:3两部分，易证8AD CN ==．在Rt ABC ∆中，226810AC =+=，//EF AB ，∴CE EFCA AB =，∴16106tEF-=，3(16)5EF t ∴=-，//EH CN ，∴EH AECN AC =，∴3(16)65810t t --=，解得727t =．当正方形EFGH 在AC 的左边时，由EH AE CN AC =，可得3(16)65410t t --=，解得12t =．综上所述，满足条件的t 的值为125或4811或727或12．15、【解答】解：（1）如图1，过点C 作CE y ⊥轴于点E ，矩形ABCD 中，CD AD ⊥，90CDE ADO ∴∠+∠=︒，又90OAD ADO ∠+∠=︒，30CDE OAD ∴∠=∠=︒，∴在Rt CED ∆中，122CE CD ==，2223DE CD CE =-=在Rt OAD ∆中，30OAD ∠=︒，132OD AD ∴==，∴点C 的坐标为(2,33)+（2）M 为AD 的中点，3DM ∴=，6DCM S ∆=，又212OMCD S =四边形，92ODM S ∆∴=，9OAD S ∆∴=，设OA x =、OD y =，则2236x y +=，192xy =，222x y xy ∴+=，即x y =，将x y =代入2236x y +=得218x =，解得32x =（负值舍去），32OA ∴=（3）OC 的最大值为8，如图2，M 为AD 的中点，3OM ∴=，225CM CD DM =+=，8OC OM CM ∴+=，当O 、M 、C 三点在同一直线时，OC 有最大值8，连接OC ，则此时OC 与AD 的交点为M ，过点O 作ON AD ⊥，垂足为N ， 90CDM ONM ∠=∠=︒，CMD OMN ∠=∠，CMD OMN ∴∆∆∽， ∴CDDMCMON MN OM ==，即4353ON MN ==，解得95MN =，125ON =，65AN AM MN ∴=-=，在Rt OAN ∆中，22655OA ON AN =+=，5cos 5ANOAD OA ∴∠==．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五讲四边形1.（08山东潍坊）如图1，梯形ABCD 中，AD BC ∥，AD AB =，BC BD =，100A = ∠，则C =∠（）A ．80B ．70C ．75D ．602.（08年江苏无锡）如图2，E F G H ，，，分别为正方形A B C D 的边AB，BC，CD，DA上的点，且13AE BF CG DH AB ====，则图中阴影部分的面积与正方形ABCD 的面积之比为（）A ．25B ．49C ．12D ．353.（08湖北荆州）如图3，直角梯形ABCD 中，∠BCD ＝90°，AD ∥BC ，BC ＝CD ，E 为梯形内一点，且∠BEC ＝90°，将△BEC 绕C 点旋转90°使BC 与DC 重合，得到△DCF ，连EF 交CD 于M ．已知BC ＝5，CF ＝3，则DM:MC 的值为（） A.5:3 B.3:5 C.4:3 D.3:44.（08天津市卷）如图4，在正方形ABCD 中，E 为AB 边的中点，G ，F 分别为AD ，BC 边上的点，若1=AG ，2=BF ，︒=∠90GEF ，则GF 的长为．5.（08山东枣庄）如图5，将边长分别为2、3、5的三个正方形按如图方式排列，则图中阴影部分的面积为．6.（08浙江义乌）如图6，直角梯形纸片ABCD ，AD ⊥AB ，AB =8，AD =CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．（1）当AE =5，P 落在线段CD 上时，PD = ；（2）当P 落在直角梯形ABCD 内部时，PD 的最小值等于．7.(08福建厦门)如图7，点G 是ABC △的重心，CG 的延长线交AB 于D ，5cm GA =，4cm GC =，3cm GB =，将AD G △绕点D 旋转180得到BDE △，则DE= cm ，ABC △的面积= cm 2．8.（08湖南怀化24题）如图8，四边形ABCD 、DEFG 都是正方形，连接AE 、CG,AE 与CG 相交于点M ，CG 与AD 相交于点N ．求证：（1）CG AE =；（2）.AN DN CN MN ⋅=⋅9.（08四川乐山）如图9，梯形ABCD 中，AD BC ∥，点E 是边AD 的中点，连结BE 交AC 于点F ，BE 的延长线交CD 的延长线于点G ．（1）求证：GE AEGB BC=；（2）若2GE =，3BF =，求线段EF 的长．10.（08山东潍坊21题）如图10，ABCD 为平行四边形，AD a =，BE AC ∥，DE 交AC 的延长线于F点，交BE 于E 点．（1）求证：DF FE =；（2）若2AC CF =，60ADC = ∠，AC DC ⊥，求BE 的长；（3）在（2）的条件下，求四边形ABED 的面积．D ABADC BFGE AD FEBC GCDE ABFEA BGCD E图1 图2 图3 图4图5 图6 图7 图8图9图10D A BE FC P G图1 D CGPA B EF图211.(08福建龙岩25题)如图11，等腰梯形ABCD 中，AB=4，CD=9，∠C=60°，动点P 从点C 出发沿CD 方向向点D 运动，动点Q 同时以相同速度从点D 出发沿DA 方向向终点A 运动，其中一个动点到达端点时，另一个动点也随之停止运动. （1）求AD 的长；（2）设CP=x ，问当x 为何值时△PD Q 的面积达到最大，并求出最大值；（3）探究：在BC 边上是否存在点M 使得四边形PDQM 是菱形？若存在，请找出点M ，并求出BM 的长；不存在，请说明理由.12.(08北京市卷25题)如图，在菱形ABCD 和菱形BEFG 中，点A B E ，，在同一条直线上，P是线段DF 的中点，连结PG PC ，．若60ABC BEF ∠=∠= ，探究PG 与PC 的位置关系及PG PC的值．小聪同学的思路是：延长GP 交DC 于点H ，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）写出上面问题中线段PG 与PC 的位置关系及PGPC 的值；（2）将图1中的菱形BEFG 绕点B 顺时针旋转，使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上，原问题中的其他条件不变（如图2）．你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．（3）若图1中2(090)ABC BEF αα∠=∠=<< ，将菱形BEFG 绕点B 顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出PGPC的值（用含α的式子表示）．13.（08湖北黄石26题）如图12，ABM ∠为直角，点C 为线段BA 的中点，点D 是射线BM 上的一个动点（不与点B 重合），连结AD ，作BE AD ⊥，垂足为E ，连结CE ，过点E 作EF CE ⊥，交BD 于F ．（1）求证：BF FD =；（2）A ∠在什么范围内变化时，四边形ACFE 是梯形，并说明理由；（3）A ∠在什么范围内变化时，线段DE 上存在点G ，满足条件14DG DA =，并说明理由．14．(2008年湖州市) 已知：在矩形AOBC 中，4OB =，3OA =．分别以OB OA ，所在直线为x 轴和y 轴，建立如图13所示的平面直角坐标系．F 是边BC 上的一个动点（不与B C ，重合），过F点的反比例函数(0)ky k x=>的图象与AC 边交于点E ．（1）求证：AOE △与BOF △的面积相等；（2）记OEF ECF SS S =-△△，求当k 为何值时，S 有最大值，最大值为多少？（3）请探索：是否存在这样的点F ，使得将CEF △沿EF 对折后，C 点恰好落在OB 上？若存在，求出点F 的坐标；若不存在，请说明理由．ABC D FEM图12图13第五讲四边形答案1~3 B A C 4. 3 5. 1546. 2，87. 2，18 8．证明：（1）四边形A BC 和四边形D EF 都是正方形,,9A D C D D E D G A D C E DG ∴==∠=∠=,A D E C D G A D E C D G ∴∠=∠∴△≌△， AE CG ∴=（2）由（1）得，又CND ANM DCG DAE CDG ADE ∠=∠∠=∠∴∆≅∆,,AN MNAN DN CN MNCN DN ∴=∙=∙，即∴∆AMN∽∆CDN9．（1）证明：A D B C ∥G E D G B C ∴△∽△， GE EDGB BC∴=，又AE ED= ，GE AEGB BC∴=．（2）解：AD BC AEF CBF∴ ∥，△∽△，AE EF BC BF ∴=，由（1）知GE AEGB BC=， EF GE BF GB ∴=，设EF x =，则5GB x =+，则有235x x=+，即2560x x +-=，解得：1x =或6x =-，经检验，1x =或6x =-都是原方程的根，但6x =-不合题意，舍去．故EF 的长为1．10.(1)证明：延长DC 交BE 于点M ，∵B E ∥AC ，AB ∥DC ,∴四边形ABMC 是平行四边形，∴CM=AB=DC,C 为DM 的中点，B E ∥AC ，DF=FE;（2）由（2）得CF 是△DME 的中位线，故ME=2CF,又∵AC=2CF ，四边形ABMC 是平行四边形，∴BE=2BM=2ME=2AC, 又∵A C ⊥DC, ∴在Rt △ADC 中利用勾股定理得AC=a 23, ∴=a 3. (3)可将四边形ABED 的面积分为两部分，梯形ABMD 和三角形DME,在Rt △ADC 中利用勾股定理得DC=2a ,由CF 是△DME 的中位线得CM=DC=2a ,四边形ABMC 是平行四边形得AM=MC=2a ,BM=AC=a 23,∴梯形ABMD 面积为：=⨯⨯⎪⎭⎫ ⎝⎛+21232a a a 2833a ;由A C ⊥DC 和B E ∥AC 可证得三角形DME 是直角三角形，其面积为：4323212a a a =⨯⨯,∴四边形ABED 的面积为2833a +8354322a a =11．（14分）（1）解法一：过A 作AE ⊥CD ，垂足为E . 依题意，DE =25249=-. 在Rt △ADE 中，AD =522560=⨯=︒cos DE .（2）解： ∵CP =x ，h 为PD 边上的高,依题意，△PD Q 的面积S 可表示为：S=21PD ·h =21(9－x )·x ·sin60°=43(9x －x 2)=－43(x －29)2＋16381.由题意，知0≤x ≤5 . 当x =29时（满足0≤x ≤5），S 最大值=16381.（3）假设存在满足条件的点M ，则PD 必须等于D Q 于是9－x =x ，x =29. 此时，点P 、Q 的位置如图25-3所示，连Q P .△PD Q 恰为等边三角形 . 过点Q 作Q M ∥DC ，交BC 于M ，点M 即为所求.连结MP ，以下证明四边形PD Q M易证△MCP ≌△Q DP ，∴∠D=∠3 . MP =PD ，∴MP ∥Q D , ∴四边形PD Q M 又MP =PD , ∴四边形PD Q M 是菱形 . 所以存在满足条件的点M ，且BM =BC －MC =512．解：（1）线段PG 与PC 的位置关系是PG PC ⊥；PGPC= （2）猜想：（1）中的结论没有发生变化．证明：如图，延长GP 交AD 于点H ，连结CH CG ，．P 是线段DF 的中点， FP DP ∴=．由题意可知AD FG ∥．GFP HDP ∴∠=∠．GPF HPD ∠=∠ ，GFP HDP ∴△≌△．GP HP ∴=，GF HD =．四边形ABCD 是菱形，CD CB ∴=，60HDC ABC ∠=∠= ．由60ABCBEF ∠=∠= ，且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上，可得60GBC∠= ． HDC GBC ∴∠=∠．四边形BEFG 是菱形，GF GB ∴=．HD GB ∴=．HDC GBC ∴△≌△．CH CG ∴=，DCH BCG ∠=∠．120DCH HCB BCG HCB ∴∠+∠=∠+∠= ．即120HCG ∠= ．CH CG = ，PH PG =， PG PC ∴⊥，60GCP HCP ∠=∠=．PG PC ∴=3）PGPC=tan(90)α- ．13．（1）在Rt AEB △中，AC BC = ，12CE AB ∴=，CB CE ∴=，CEB CBE ∴∠=∠．90CEF CBF ∠=∠= ，BEF EBF∴∠=∠，EF BF ∴=．90BEFFED ∠+∠= ，90EBD EDB ∠+∠= ， FED EDF ∴∠=∠．EF FD = ．BF FD ∴=．（2）由（1）BF FD =，而BC CA =，CF AD ∴∥，即AE CF ∥．若AC EF ∥，则AC EF =，BC BF ∴=．BA BD ∴=，45A ∠= ．∴当045A <∠< 或4590A <∠< 时，四边形ACFE 为梯形．（3）作GHBD ⊥，垂足为H，则GH AB ∥．14DGDA = ，14DH DB ∴=．又F 为BD 中点，H ∴为DF 的中点．GH ∴为DF 的中垂线．GDF GFD ∴∠=∠．点G 在ED h 上，EFD GFD ∴∠∠≥．180EFD FDE DEF ∠+∠+∠= ，180GFD FDE DEF ∴∠+∠+∠ ≤．3180EDF ∴∠ ≤．A BCD FEMG HD CG PA BEFH60EDF ∴∠ ≤．又90A EDF ∠+∠= ，3090A ∴∠< ≤．∴当3090A ∠< ≤时，DE 上存在点G ，满足条件14DG DA =． 14．（1）证明：设11()E x y ，，22()F x y ，，AOE △与FOB △的面积分别为1S ，2S ，由题意得11ky x =，22k y x =．1111122S x y k ∴==，2221122S x y k ==．12S S ∴=，即AOE △与FOB △的面积相等．（2）由题意知：E F ，两点坐标分别为33k E ⎛⎫⎪⎝⎭，，44k F ⎛⎫⎪⎝⎭，，1111432234ECF S EC CF k k ⎛⎫⎛⎫∴==-- ⎪⎪⎝⎭⎝⎭ △，11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S ∴=---=---=--△△△△△△矩形11112212243234OEF ECF ECF S S S k S k k k ⎛⎫⎛⎫∴=-=--=--⨯-- ⎪⎪⎝⎭⎝⎭△△△2112S k k ∴=-+．当161212k =-=⎛⎫⨯- ⎪⎝⎭时，S 有最大值．131412S -==⎛⎫⨯- ⎪⎝⎭最大值．（3）解：设存在这样的点F ，将CEF △沿EF 对折后，C 点恰好落在OB 边上的M 点，过点E 作EN OB ⊥，垂足为N．由题意得：3ENAO ==，143EM EC k ==-，134MF CF k ==-，90EMN FMB FMB MFB ∠+∠=∠+∠= ，EMN MFB ∴∠=∠．又90ENM MBF ∠=∠= ，ENM MBF ∴△∽△．EN EM MB MF ∴=，11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭∴==⎛⎫-- ⎪⎝⎭， 94MB ∴=．222MB BF MF += ，222913444k k ⎛⎫⎛⎫⎛⎫∴+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得218k =．21432k BF ∴==．∴存在符合条件的点F，它的坐标为21432⎛⎫ ⎪⎝⎭，．。