【精编文档】黑龙江省大庆十中2018-2019学年高二数学下学期第一次月考试卷理.doc
【精编文档】黑龙江省大庆十中2018-2019学年高二化学下学期第一次月考试卷.doc

黑龙江省大庆十中2018-2019学年高二化学下学期第一次月考试题可能用到的相对原子质量:H 1 C 12 Al 27 0 16 Na 23 Cl 35.5 Mg 24第I卷(选择题)(66分)一、选择题(本题总分66分,有22小题,每小题3分,每小题只有一个选项符合题意)1、下列第三周期元素的离子中,半径最小的是()A、Na+B、Al3+C、S2-D、Cl-2、已知X、Y是主族元素,I为电离能,单位是kJ・mol-1。
请根据下表所列数据判断,错误的是()A.元素X的常见化合价是+1B.元素Y是ⅢA族元素C.元素X与氯元素组成化合物时,化学式可能是XClD.若元素Y处于第3周期,它可与冷水剧烈反应3、下列有关电负性的说法中正确的是( )A.主族元素的电负性越大,元素原子的第一电离能一定越大B.在元素周期表中,元素电负性从左到右越来越大C.金属元素电负性一定小于非金属元素电负性D.在形成化合物时,电负性越小的元素越容易显示正价4、根据“相似相溶”规则和实际经验,下列叙述不正确的是()A .白磷(P 4)易溶于CS 2,也易溶于水B .NaCl 易溶于水,难溶于CCl 4C .碘易溶于苯,微溶于水D .卤化氢易溶于水,难溶于CCl 45、有机分子中碳原子连接四个不同的原子或原子团时,称为不对称碳原子(或手性碳原子),下图有机物中的手性碳原子个数是( )A 1个B 2个C 3个D 4个6、BF 3是典型的平面三角形分子,它溶于氢氟酸或NaF 溶液中都形成BF 4-离子,则BF 3和BF 4-中的B 原子的杂化轨道类型分别是( ) A 、sp2、sp2 B 、sp3、sp3 C 、sp2、sp3 D 、sp 、sp2 7.下列说法不正确的是( )A .某微粒空间构型为平面三角形,则中心原子一定是sp 2杂化B .某微粒空间构型为V 形,则中心原子一定有孤电子对C .某微粒空间构型为三角锥形,则该微粒一定是极性分子D .某微粒空间构型为正四面体,则键角一定是109°28’8.由配位键形成的离子[Pt(NH 3)6]2+和[PtCl 4]2—中,两个中心离子的化合价分别是( )A .+8 +6B .+6 +6C .+2 +4D .+2 +2 9. 下列物质中存在配位键的是 ( ) ①H 3O + ②[B (OH )4]- ③CH 3COO - ④NH 3 ⑤CH 4 A .①②B .①③C .④⑤D .②④10.下列气态氢化物中最不稳定的是( )A .3PHB .3NHC .O H 2D .S H 211.下列化合物中阳离子半径与阴离子半径比值最小的是( ) A .NaF B .2MgI C .2BaI D .KBr12、实验测得 BeCl 2为共价化合物,两个Be-Cl 键间的夹角为180°,由此可见BeCl2属于()A.由极性键构成的极性分子B.由极性键构成的非极性分子C.由非极性键构成的极性分子D.由非极性键构成的非极性分子13.下列说法正确的是()A.冰融化时,分子中H—O键发生断裂B.随着电子层数的增加,卤化物CX4分子间作用力逐渐增大,所以它们相应的熔沸点也逐渐升高C.由于H—O键比H—S键牢固,所以水的熔沸点比H2S高D.在由分子所构成的物质中,分子间作用力越大,该物质越稳定14.有关杂化轨道的说法不正确的是( )A.杂化前后的轨道数不变,但轨道的形状发生了改变B.sp3、sp2、sp杂化轨道的夹角分别为109°28′、120°、180°C.部分四面体形、三角锥形、V形分子的结构可以用sp3杂化轨道解释D.杂化轨道全部参与形成化学键15.根据下列微粒的最外层电子排布,能确定该元素在元素周期表中位置的是()A. 1s2B. 3s23p1C. 2s22p6D. ns2np316.通常把原子总数和价电子总数相同的分子或离子称为等电子体.等电子体具有相似的化学结构,则下列有关说法中正确的是()A、CH4和NH4+是等电子体,化学键类型完全相同B、NO3-和CO32-是等电子体,均为平面正三角形结构C、H3O+和PCl3是等电子体,均为三角锥形结构D、SO2和O3是等电子体,SO2和O3具有相同的化学性质17.已知N2+O2=2NO为吸热反应,ΔH=+180 kJ·mol-1,其中N≡N、O=O键的键能分别为946 kJ·mol-1、498 kJ·mol-1,则NO键的键能为( ) A.1264 kJ·mol-1B.632 kJ·mol-1 C.316 kJ·mol-1 D.1624 kJ·mol -118.下列有关σ键和π键的说法错误的是()A.在某些分子中,化学键可能只有σ键而没有π键B.分子中σ键的键能一定大于π键的键能C.σ键的特征是轴对称,π键的特征是镜面对称D.SO2形成π键与O3的π键是相似的19.下列说法正确的是()A.所有金属元素都分布在d区和ds区B.元素周期表ⅢB到ⅡB族10个纵行的元素都是金属元素C.最外层电子数为2的元素都分布在S区D.S区均为金属元素20.区分晶体和非晶体的最科学的方法是( )A.测固体的熔点B.看固体是否易被压缩C.对固体进行X射线衍射实验D.比较固体的导热性21.已知元素周期表中1~18号元素的离子W3+、X+、Y2-、Z-都具有相同的电子层结构,下列关系正确的是( )A.原子的第一电离能:X>W B.原子半径:X<WC.氢化物的稳定性:H2Y>HZ D.离子的还原性:Y2->Z-22.下列每组物质中化学键类型和分子的极性都相同的是()A.H2O和CH4B.NaCl和HCl C.CO2和CS2D.O2和HBr第II卷(非选择题)(34分)二、简答题23.(12分)向盛有硫酸铜水溶液的试管里加入氨水,首先形成难溶物,继续添加氨水,难溶物溶解得到深蓝色的透明溶液.(1)下列对此现象的说法正确的是 ( )A.反应后溶液中不存在任何沉淀,所以反应前后Cu2+的浓度不变B.沉淀溶解后,将生成深蓝色的配合离子[Cu(NH3)4]2+C.在[Cu(NH3)4]2+中,Cu2+给出孤对电子,NH3中的N原子提供空轨道D.向反应后的溶液中加入乙醇,溶液没有发生变化,因为[Cu(NH3)4]2+不会与乙醇发生反应(2)写出实验过程中的离子方程式 :______________; ______________(3)[Cu(NH3)4]2+的中心离子是______________,配体是______________(4)[Cu(NH3)4]2+具有对称的空间构型,[Cu(NH3)4]2+中的两个NH3被两个Cl-取代,能得到两种不同结构的产物,则[Cu(NH3)4]2+的空间构型为______________.24.(10分)某离子晶体晶胞结构如下图所示,x位于立方体的顶点,Y位于立方体中心。
黑龙江省大庆实验中学2018-2019学年高二下学期开学考试数学(文)试题

样抽一个容量为 45 的样本,高一年级被抽取 20 人,高二年级被抽取乙或丙得到物理书;
乙说:甲或丙得到英语书;
丙说:数学书被甲得到;
丁说:甲得到物理书。
最终结果显示:甲、乙、丙、丁四个人的预测均不正确,那么甲、乙、丙、丁四个人得到的
书分别为(
)
A.化学、英语、数学、物理
B.英语、化学、数学、物理
C. 化学、英语、物理、数学
D.数学、英语、化学、物理
12. 过抛物线 y2 2px( p 0) 的焦点 F 作斜率大于 0 的直线 l 交抛物线于 A, B 两点( A 在
x
4.命题“ x R,使得 x2 1 ”的否定是(
)
A. x R, 都有x2 1
B. x R,使得 x2 1
C. x R,使得 x2 1
D. x R, 都有 x2 1
5.一组数据从小.到.大.. 的顺序排列为 1,2, 2, x,5,10 ,其中 x 5 ,已知该组数据的中位数是众
3
数的 倍,则该组数据的平均数为(
)
2
A. 5
B .4
C.
3 D .2
6.设 m, n 是空间两条直线, , 是空间两个平面,则下列命题中不正确...的是(
)
A.若 m , m ,则
B .若 m ,n / / ,则 n / / m
C.若 n , n ,则 / /
D .若 m ,n ,则 m n
-1-
7. 数学名著《算学启蒙》中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,
C.命题 " 若 a b, 则ac2 bc2 " 的逆命题为真命题
D.命题 " a b 5,则 a 2或 b 3" 为真命题
【精编文档】黑龙江省大庆市第四中学2018-2019学年高二数学下学期第一次检测试卷文.doc

2018~2019学年度第二学期第一次检测高二年级数学(文科)试题考试时间:120分钟 分值:150分本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题 共60分)一、选择题:(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合A ={2,3,4},B ={x |1+x >3},则A ∩B =( ) A .{4}B .{2}C .{3,4}D .{2,3}2.在极坐标系中的点(2,)化为直角坐标是( )A .B .C .D .3.若z =1﹣2i ,则iz z 21-⋅( ) A .2B .﹣2iC .﹣2D .2i4.极坐标方程ρcos2θ=0表示的曲线为( ) A .极点 B .极轴C .一条直线D .两条相交直线5.已知z 是复数z 的共轭复数,(z +1)(﹣1)是纯虚数,则|z |=( ) A .1B .C .2D .6.命题“∀x ∈R ,x 3﹣x 2+1≤0”的否定是( )A .不存在x ∈R ,x 3﹣x 2+1≤0B .∃x 0∈R ,x 03﹣x 02+1≥0C .∃x 0∈R ,x 03﹣x 02+1>0D .∀x ∈R ,x 3﹣x 2+1>07.已知函数f (x )的定义域为[1,9],则函数y =f (x ﹣1)+f (x 2)的 定义域为( )A .[1,9]B .[1,3]C .[1,2]D .[2,3]8.若命题“022,0200<+++∈∃m mx x R x ”为假命题,则m 的取值范围 是( )A .(﹣∞,﹣1)∪(2,+∞)B .[﹣1,2]C .(﹣1,2)D .(﹣∞,﹣1]∪[2,+∞)9.元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着 游春走,遇店添一倍,逢友饮一斗,店友经四处,没了壶中酒,借问此壶中, 当原多少酒?”用程序框图表达如图所示,即最终输出的x =0,则一开始输入的x 的值为( ) A .B .C .D .10.已知函数()()⎩⎨⎧≥<-+-=1,1,1623x a x a x a x f x在(﹣∞,+∞)上单调递减,那么实数a 的取值范围( ) A .(0,1) B .C .D .11.设y =f (x )在[0,+∞)上有定义,对于给定的实数K ,定义函数()()()()⎩⎨⎧>≤=k x f k kx f x f x f k ,,,给出函数f (x )=2﹣x ﹣x 2,若对于任意x ∈[0,+∞),恒有()x f k =f (x ),则( ) A .k 的最大值为 B .k 的最小值为C .k 的最大值为2D .k 的最小值为212.已知函数f (x )=﹣x 2+ax ﹣6,g (x )=x +4,若对任意x 1∈(0,+∞),存在x 2∈(﹣∞,﹣1],使f (x 1)≤g (x 2),则实数a 的最大值为( ) A .6B .4C .3D .2第II 卷二、填空题:(本大题共4小题,每小题5分,满分20分.) 13.已知集合A ={0,1},则集合A 的真子集个数为____________14.已知3f (x )+2f (﹣x )=x +3,则f (x )的解析式为()=x f _____________ 15.设a ∈R 且a ≠0,则a >1是11<a的______________条件.(充分必要,充分不必要,必要不充分,既不充分也不必要)16.已知函数()()()[]1123lg 22+-++-=x m x m m x f 的定义域为R ,则实数m 的取值范围是______________三、解答题:(本大题共6小题,满分70分.解答须写出文字说明证明过程和演算步骤.)17.在极坐标系中,已知圆C 经过点P (2,),圆心C 为直线2)4sin(-=-πθρ与极轴的交点,求圆C 的极坐标方程.18.已知命题p :x 2﹣4x ﹣5≤0,命题q :x 2﹣2x +1﹣m 2≤0(m >0). (1)若p 是q 的充分条件,求实数m 的取值范围.(2)若m =5,p ∨q 为真命题,p ∧q 为假命题,求实数x 的取值范围.19.已知直线l 的参数方程为,曲线C 的参数方程为,设直线l 与曲线C 交于两点A ,B(1)将直线l 和曲线C 化为普通方程;(2)若P (1,),求|PA |+|PB |及|PA |•|PB |的值.20.大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表(1)所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表(2)所示.30表(1)表(2)(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?(Ⅱ)现从表(2)中成功完成时间在[20,30)和[30,40]这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.附参考公式及数据:22()()()()()n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.21.已知曲线1C 的参数方程为)(sin 2cos 3为参数ϕϕϕ⎪⎩⎪⎨⎧==y x ,在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线2C 的极坐标方程为θθρsin 2cos 10+=.(1)写出曲线1C 的普通方程和曲线2C 直角坐标方程;(2)在曲线1C 上求一点M ,使点M 到曲线2C 距离的最小,并求出最小距离.22.在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎨⎧=+=ααsin 3cos 32y x (α为参数).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,直线)(3:,)sin (cos :21R l s l ∈==+ρπθθθρ.(1)求曲线C 的极坐标方程;(2)设直线2l 与直线1l 交于点M ,与曲线C 交于Q P ,两点,若10||||||=⋅⋅OQ OP OM ,求实数s 的值.2018~2019学年度第二学期第一次检测高二年级文科数学试题答案一、选择题:(本大题共12小题,每小题5分,满分60分)13、3 14、 ()53+=x x f 15.充分不必要条件 16、m >或m ≤1三.解答题17(本小题满分10分)解:∵圆C 经过点P (2,),P 点的直角坐标为(1,),圆心C 为直线ρsin ()=﹣与极轴的交点,直线ρsin ()=﹣的直角坐标方程为x ﹣y ﹣2=0,∴圆心C 的直角坐标为(2,0), ∴圆半径r =|PC |==2,∴圆C 的直角坐标方程为(x ﹣2)2+y 2=4,即x 2+y 2﹣4x =0, ∴圆C 的极坐标方程为ρ=4cos θ.18.(本小题满分12分)已知命题p :x 2﹣4x ﹣5≤0,命题q :x 2﹣2x +1﹣m 2≤0(m >0).(1)若p 是q 的充分条件,求实数m 的取值范围.(2)若m =5,p ∨q 为真命题,p ∧q 为假命题,求实数x 的取值范围. 解:(1)不等式x 2﹣4x ﹣5≤0的解集为P={}51≤≤-x x不等式x 2﹣2x +1﹣m 2≤0(m >0)的解集为q={}11+≤≤+-m x m x因为p 是q 的充分条件,所以P 是q 的子集,所以⎩⎨⎧-≤+-≥+1151m m ,解得4m ≥(2)当m =5时,q={}64≤≤-x x ,因为p ∨q 为真命题,p ∧q 为假命题,所以()()Q P x Q P x ∉∈且,所以14-<≤-x 或65≤<x19(本小题满分12分)(1)由得x +2y =2,∴直线l 的普通方程为x +2y﹣2=0. 由得,∴=1.∴曲线C 的普通方程为=1.(2)直线l 的标准参数方程为,⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 5515521 代入=1得:即﹣=0.∴t =±.∴|PA |=|PB |=,∴|PA |+|PB |==,|PA |•|PB |=.20.(本小题满分12分)解:(Ⅰ)根据题意填写列联表如下;由表中数据计算K 2=≈5.223>5.024,所以能在犯错误的概率不超过0.025的前提下认为喜欢盲拧与性别有关; (II )从成功完成时间在[20,30)和[30,40]这两组内的6名男生中任意抽取2人,记完成时间在[20,30)内的4人分别为4321,,,a a a a ,完成时间在[30,40]的2人为21,b b 基本事件为,,,,,,,42322111413121a a a a b a b a a a a a a a ,,,,,2313432212b a b a a a b a b a 212414,,b b b a b a 共15种,这2人恰好在同一组内的基本事件为,,,,,4232413121a a a a a a a a a a 43a a 21,b b 共7种, 故所求的概率为P =.21(本小题满分12分)解:(1)曲线1C 的普通方程为14922=+x x 曲线2C 的直角坐标方程为0102=-+y x(2)设点M 的坐标为()ϕϕ,2sin 3cos ,由点到直线的距离公式,点M 到直线2C 的距离为510sin 4cos 3-+=ϕϕd =51054sin 53cos 5-⎪⎭⎫ ⎝⎛⋅+⋅ϕϕ=()10cos 5510--ϕϕ.其中0ϕ满足54sin ,53cos 00==ϕϕ由三角函数性质,当0-0=ϕϕ时,d 取最小值5,此时59cos 3cos 30==ϕϕ 58sin 2sin 20==ϕϕ 因此,当点M 位于⎪⎭⎫⎝⎛5859,时 M 到曲线2C 距离的最小值是 522.(本小题满分12分)解:(1)曲线C 的极坐标方程为ρ2﹣4ρcos θ﹣5=0. (2)将代入ρ(cos θ+sin θ)=s 中,得,则,∴,将代入ρ2﹣4ρcosθ﹣5=0中,得ρ2﹣2ρ﹣5=0,设点P的极径为ρ1,点Q的极径为ρ2,则ρ1•ρ2=﹣5,所以|OP|•|OQ|=5.又|OM|•|OP||OQ|=10,则,∴或.。
—19学年高二10月月考数学试题(附答案)
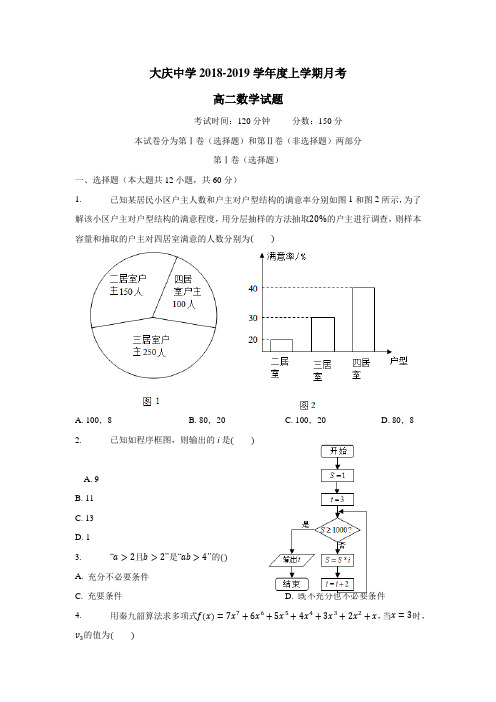
大庆中学2018-2019学年度上学期月考高二数学试题考试时间:120分钟分数:150分本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题)一、选择题(本大题共12小题,共60分)1.已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为()A. 100,8B. 80,20C. 100,20D. 80,82.已知如程序框图,则输出的i是()A.9B. 11C. 13D. 13.“a>2且b>2”是“ab>4”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x,当x=3时,v3的值为()A. 27B. 86C. 262D. 7895.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )A. 至少有一个白球;都是白球B. 至少有一个白球;至少有一个红球C. 至少有一个白球;红、黑球各一个D. 恰有一个白球;一个白球一个黑球 6. 已知等差数列{a n }中,S n 是{a n }的前n 项和,且S 3=30,S 6=100,则S 9的值为() A. 260 B. 130C. 170D. 2107. 某四棱锥的三视图如图所示,该四棱锥的侧面积为( ) 8.A. 8B. 16C. 10D. 6 9.2016年2月,为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.5,则4a +1b 的最小值为( ) A. 9 B. 92C. 8D. 410. 长方体的三个相邻面的面积分别为2,3,6,则该长方体外接球的表面积为( ) A.7π2B. 56πC. 14πD. 64π11. 甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领到的钱数不少于其他任何人)的概率是( ) A. 13 B. 310C. 25D. 3412.在区间[0,1]上随机取两个数x ,y ,记P 为事件“x +y ≤23”的概率,则P =( )A. 23B. 12C. 49D. 2913.圆C 1:(x −1)2+(y −3)2=9和C 2:x 2+(y −2)2=1,M ,N 分别是圆C 1,C 2上的点,P 是直线y =−1上的点,则|PM |+|PN |的最小值是( ) A. 5 2−4 B. 17−1C. 6−2 2D. 17第Ⅱ卷(非选择题)二、填空题(本大题共4小题,共20分) 14. 已知一组数据4.8,4.9,5.2,5.5,5.6,则该组数据的方差是______.15.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的办法分成50个部分.如果第一部分编号为0001,0002,…,0020,从中随机抽取一个号码为0015,则第40个号码为______. 16.某学校有8个社团,甲、乙两位同学各自参加其中一个社团,且他俩参加各个社团的可能性相同,则这两位同学参加同一个社团的概率为______ . 17.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,其中a =2,c =3,且满足(2a −c )⋅cos B =b ⋅cos C ,则AB ⋅BC =______ .三、解答题(本大题共6小题,共70分) 18.(10分)国家二孩政策放开后,某市政府主管部门理论预测2018年到2022年全市人口总数与年份的关系有如表所示:(1)请根据表中提供的数据,运用最小二乘法求出y 关于x 的线性回归方程; (2)据此,估计2023年该市人口总数.【附】参考公式:b = x i n i =1y i −nxyx ii =1−nx2,a =y −b x . 19.(12分)在△ABC 中,(角A ,B ,C 的对应边分别为a ,b ,c ),且b sin A = 3a cos B .(1)求角B 的大小;(2)若△ABC的面积是33,且a+c=5,求b.420.(12分)共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.(1)求图中x的值;(2)求这组数据的平均数和中位数;(3)已知满意度评分值在[50,60)内的男生数与女生数的比为3:2,若在满意度评分值为[50,60)的人中随机抽取2人进行座谈,求恰有1名女生的概率.21.(12分)已知数列a n是等比数列,a2=4,a3+2是a2和a4的等差中项.(1)求数列a n的通项公式;(2)设b n=2log2a n−1,求数列a n⋅b n的前n项和T n.22.(12分)如图,在四棱锥P −ABCD 中,底面为直角梯形,AD //BC ,∠BAD =90∘,PA ⊥底面ABCD ,M 、N 分别为PC 、PB 的中点.PA =AB .(1)求证:MN //平面PAD ; (2)求证:PB ⊥DM . 23.(12分)在平面直角坐标系xOy 中,已知圆x 2+y 2−12x +32=0的圆心为Q ,过点P (0,2)且斜率为k 的直线与圆Q 相交于不同的两点A ,B . (1)求k 的取值范围;(2)是否存在常数k ,使得向量OA +OB 与PQ 共线?如果存在,求k 值;如果不存在,请说明理由.大庆中学2018-2019学年度上学期月考(高二数学)答案和解析【答案】 1. A 2. C 3. A 4. C 5. C 6. D 7. B 8. B9. C10. C11. D12. A13. 0.1 14. 0795 15. 18 16. −317. 解:(1)由题设,得x =2,y =10, x i 5i =1y i =0×5+1×7+2×8+3×11+4×19=132, x i 25i =1=02+12+22+32+42=30,∴b =i ni =1i −nxyx 2n −nx2=132−5×2×1030−5×22=3.2,a =y −b x =3.6.∴所求y 关于x 的线性回归方程为y=3.2x +3.6. (2)由(1)及题意,当x =5时,y=3.2×5+3.6=19.6. 据此估计2023年该市人口总数约为196万. 18. 解:(1)∵b sin A = a cos B , ∴asin A =3cos B,又∵a sin A =bsin B , ∴ 3cos B =sin B ,∴tan B = 3,∵0<B <π,∴B =π3. (2)∵S △ABC =12ac sin B =3ac4=3 34,∴ac =3∴a 2+c 2=(a +c )2−2ac =19, ∴b 2=a 2+c 2−2ac ⋅cos B =16,∴b =4.19. 解:(1)由(0.005+0.02+0.035+0.030+x )×10=1, 解得x =0.01.(2)这组数据的平均数为55×0.05+65×0.2+75×0.35+85×0.3+95×0.1=77. 中位数设为m ,则0.05+0.2+(m −70)×0.035=0.5,解得m =5407.(3)满意度评分值在[ [50,60)内有100×0.005×10=5人, 其中男生3人,女生2人.记为21321,,,,B B A A A ,记“满意度评分值为[50,60)的人中随机抽取2人进行座谈,恰有1名女生”为事件A 通过列举知总基本事件个数为10个,A 包含的基本事件个数为6个,利用古典概型概率公式可知,53)(A P20. 解:(1)设数列 a n 的公比为q ,因为a2=4,所以a3=4q,a4=4q2.因为a3+2是a2和a4的等差中项,所以2a3+2= a2+a4.即24q+2=4+4q2,化简得q2−2q=0.因为公比q≠0,所以q=2.所以a n=a2q n−2=4×2n−2=2n(n∈N∗).(2)因为a n=2n,所以b n=2log2a n−1=2n−1.所以a n b n=2n−12n.则T n=1×2+3×22+5×23+⋅⋅⋅+2n−32n−1+2n−12n,①2T n=1×22+3×23+5×24+⋅⋅⋅+2n−32n+2n−12n+1.②①−②得,−T n=2+2×22+2×23+⋅⋅⋅+2×2n−2n−12n+1,−2n−12n+1=−6−2n−32n+1,=2+2×41−2n−11−2所以T n=6+2n−32n+1.21. 证明:(1)因为M、N分别为PC、PB的中点,BC.所以MN//BC,且MN=12又因为AD//BC,所以MN//AD.又AD⊂平面PAD,MN不属于平面PAD,所以MN//平面PAD.(2)因为AN为等腰三角形ABP底边PB上的中线,所以AN⊥PB.因为PA⊥平面ABCD,AD⊂平面ABCD,所以AD⊥PA.又因为AD⊥AB,且AB∩AP=A,所以AD⊥平面PAB.又PB⊂平面PAB,所以AD⊥PB.因为AN⊥PB,AD⊥PB,且AN∩AD=A,所以PB⊥平面ADMN.又DM⊂平面ADMN,所以PB⊥DM.22. 解:(1)圆的方程可写成(x−6)2+y2=4,所以圆心为Q(6,0),过P(0,2)且斜率为k的直线方程为y=kx+2.代入圆方程得x2+(kx+2)2−12x+32=0,整理得(1+k2)x2+4(k−3)x+36=0.①直线与圆交于两个不同的点A,B等价于△=[4(k−3)2]−4×36(1+k2)=42(−8k2−6k)>0,解得−34<k<0,即k的取值范围为(−34,0).(2)设A(x1,y1),B(x2,y2),则OA+OB=(x1+x2,y1+y2),由方程①,x1+x2=−4(k−3)1+k②又y1+y2=k(x1+x2)+4.③而P(0,2),Q(6,0),PQ=(6,−2).所以OA+OB与PQ共线等价于(x1+x2)=−3(y1+y2),将②③代入上式,解得k=−34.由(Ⅰ)知k∈(−34,0),故没有符合题意的常数k.【解析】1. 解:样本容量为:(150+250+100)×20%=100,∴抽取的户主对四居室满意的人数为:100×100150+250+100×40%=8.故选:A.利用统计图结合分层抽样性质能求出样本容量,利用条形图能求出抽取的户主对四居室满意的人数.本题考查样本容量和抽取的户主对四居室满意的人数的求法,是基础题,解题时要认真审题,注意统计图的性质的合理运用.2. 解:经过第一次循环得到S=1×3=3,i=5经过第二次循环得到S=3×5=15,i=7经过第三次循环得到S=15×7=105,i=9经过第四次循环得到S=105×9=945,i=11经过第五次循环得到S=945×11=10395,i=13此时,满足判断框中的条件输出i故选C写出前5次循环的结果,直到第五次满足判断框中的条件,执行输出.解决程序框图中的循环结构的问题,一般先按照框图的流程写出前几次循环的结果,找规律.3. 【分析】【解答】解:若a>2且b>2,则ab>4成立,故充分性易证若ab>4,如a=8,b=1,此时ab>4成立,但不能得出a>2且b>2,故必要性不成立由上证明知“a>2且b>2”是“ab>4”的充分不必要条件.故选A.4. 解:f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x=(((((7x+6)x+5)x+4)x+3)x+2)x+1)x故v3=((7x+6)x+5)x+4当x=3时,v3=((7×3+6)×3+5)×3+4=262故选C.根据秦九韶算法求多项式的规则变化其形式,得出结果即可本题考查排序问题与算法的多样性,正确理解秦九韶算法求多项式的原理是解题的关键5. 解:袋中装有红球3个、白球2个、黑球1个,从中任取2个,在B中,至少有一个白球和至少有一个红球两个事件能同时发生,不是互斥事件,故B不成立;在C中,至少有一个白球和红、黑球各一个两个事件不能同时发生但能同时不发生,是互斥而不对立的两个事件,故C成立;在D中,恰有一个白球和一个白球一个黑球两个事件能同时发生,不是互斥事件,故D不成立;在A中,至少有一个白球和都是白球两个事件能同时发生,不是互斥事件,故A不成立.故选:C.利用互斥事件、对立事件的定义直接求解.本题考查互斥而不对立事件的判断,是基础题,解题时要认真审题,注意互斥事件、对立事件的定义的合理运用.6. 解:由题意可得S3,S6−S3,S9−S6,成等差数列,故2(S6−S3)=S3+(S9−S6),代入数据可得2(100−30)=30+S9−100,解之可得S9=210故选D.由等差数列的性质可得S3,S6−S3,S9−S6,成等差数列,由已知数据代入计算可得.本题考查等差数列的前n项和的性质,得出S3,S6−S3,S9−S6,成等差数列是解决问题的关键,属基础题.7. 解:由三视图知:此四棱锥为正四棱锥,底面边长为4,高为2,则四棱锥的斜高为4+4=22,∴四棱锥的侧面积为S=4(12×4×22)=162.故选B.根据三视图可得四棱锥为正四棱锥,判断底面边长与高的数据,求出四棱锥的斜高,代入棱锥的侧面积公式计算.本题考查了由三视图求几何体的侧面积,根据三视图的数据求相关几何量的数据是解答此类问题的关键.8. 解:根据茎叶图中的数据,该组数据的平均数为x=14(a+11+13+20+b)=11.5,∴a+b=2;∴4a +1b=2(a+b)a+a+b2b=2+2ba+a2b+12≥22ba⋅a2b+52=92,当且仅当a=2b,即a=43,b=23时取“=”;∴4a+1b的最小值为92.故选:B.根据平均数的定义求出a+b=2,再利用基本不等式求出4a +1b的最小值即可.本题考查了平均数的定义与基本不等式的应用问题,是基础题目.10. 解:得到共计有10种领法,乙领2元获得“最佳手气”的情况有1种,乙领3元获得“最佳手气”的情况有2种,乙领4元获得“最佳手气”的情况有1种,乙获得“最佳手气”的情况总数m =4,∴乙获得“最佳手气”的概率p =410=25.故选:C .11. 解:由题意可得总的基本事件为{(x ,y )|0≤x ≤1,0≤y ≤1},事件P 包含的基本事件为{(x ,y )|0≤x ≤1,0≤y ≤1,x +y ≤23},它们所对应的区域分别为图中的正方形和阴影三角形,故所求概率P =12×23×231×1=29, 故选:D .由题意可得总的基本事件为{(x ,y )|0≤x ≤1,0≤y ≤1},事件P 包含的基本事件为{(x ,y )|0≤x ≤1,0≤y ≤1,x +y ≤23},数形结合可得.本题考查几何概型,数形结合是解决问题的关键,属中档题.12. 解:圆C 1关于y =−1的对称圆的圆心坐标A (1,−5),半径为3,圆C 2的圆心坐标(0,2),半径为1,由图象可知当P ,C 2,C 3,三点共线时,|PM |+|PN |取得最小值,|PM |+|PN |的最小值为圆C 3与圆C 2的圆心距减去两个圆的半径和,即:|AC 2|−3−1= 1+49−4=5 2−4.故选:A .求出圆C 1关于x 轴的对称圆的圆心坐标A ,以及半径,然后求解圆A 与圆C 2的圆心距减去两个圆的半径和,即可求出|PM |+|PN |的最小值.本题考查圆的对称圆的方程的求法,两个圆的位置关系,两点距离公式的应用,考查转化思想与计算能力.13. 解:数据4.8,4.9,5.2,5.5,5.6的平均数为:x=15×(4.8+4.9+5.2+5.5+5.6)=5.2,∴该组数据的方差为:S2=15×[(4.8−5.2)2+(4.9−5.2)2+(5.2−5.2)2+(5.5−5.2)2+(5.6−5.2)2]=0.1.故答案为:0.1.14. 解:∵系统抽样是先将总体按样本容量分成k=Nn段,再间隔k取一个.又∵现在总体的个体数为1000,样本容量为50,∴k=20∴若第一个号码为0015,则第40个号码为0015+20×39=0795故答案为0795本题考查了抽样方法中的系统抽样,掌握系统抽样的规律.15. 解:∵每位同学参加各个小组的可能性相同,∴这两位同学同时参加一个兴趣小组的概率为:P=8×18×18=18.故答案为:18.由于每位同学参加各个小组的可能性相同,故这两位同学同时参加一个兴趣小组的概率为8×18×18=18.本题主要考查相互独立事件的概率,等可能事件的概率,属于基础题.16. 解:∵(2a−c)cos B=b cos C根据正弦定理得:(2sin A−sin C)cos B=sin B cos C2sin A cos B=sin B cos C+sin C cos B2sin A cos B=sin(B+C)2sin A cos B=sin A∴cos B=12∴B=60∘∴AB⋅BC=−|AB|⋅|BC|cos B=−(2×3×12)=−3故答案为:−3通过正弦定理把a,c,b换成sin A,sin B,sin C代入(2a−c)⋅cos B=b⋅cos C,求得B,再根据向量积性质,求得结果.本题主要考查了正弦定理和向量积的问题.再使用向量积时,要留意向量的方向.17. (Ⅰ)请根据表中提供的数据,运用最小二乘法:b = x i n i =1y i −nxy x i i =1−nx 2,a =y −b x ,求出样本中心,然后求解y 关于x 的线性回归方程;(Ⅱ)把x =5代入回归直线方程,即可得到结果.本题考查线性回归方程的求法,考查最小二乘法,属于基础题.18. (1)将b sin A = 3a cos B 变形为a sin A = 3cos B ,结合正弦定理可得出tan B = 3,从而解出B ;(2)由S △ABC =12ac sin B =3 34可得ac =3,结合a +c =5,即可解出a ,c ,然后利用余弦定理求出b .本题考查了正余弦定理在解三角形中的应用,是必须掌握的题型.19. 本题考查了频率分布直方图,众数、中位数、平均数和古典概型的计算与应用.(1)利用频率分布直方图,得(0.005+0.02+0.035+0.030+x )×10=1,由此解得x 的值;(2)利用频率分布直方图,结合平均数,中位数的概念计算得结论;(3)满意度评分值在[ [50,60)内有100×0.005×10=5人,利用古典概型的计算得结论. 20. 本题考查等比数列的通项公式以及利用错位相减法求和.(Ⅰ)设出等比数列的公比,由等差中项的概念求出公比和首项,利用等比数列的通项公式求出通项;(Ⅱ)利用错位相减法求和.21. (1)欲证MN //平面PAD ,根据线面平行的判定定理知,只须证明MN //AD ,结合中点条件即可证明得;(2)欲证PB ⊥DM ,根据线面垂直的性质定理,只须证明PB ⊥平面ADMN ,也就是要证明AN ⊥PB 及AD ⊥PA ,而这此垂直关系的证明较为明显,从而即可证得结论.本小题主要考查直线与平面平行的判定、直线与平面垂直的性质等基础知识,考查运算求解能力,考查空间想象力.属于基础题.22. (Ⅰ)先把圆的方程整理成标准方程,进而求得圆心,设出直线方程代入圆方程整理后,根据判别式大于0求得k的范围,(Ⅱ)A(x1,y1),B(x2,y2),根据(1)中的方程和韦达定理可求得x1+x2的表达式,根据直线方程可求得y1+y2的表达式,进而根据以OA+OB与PQ共线可推知(x1+x2)=−3(y1+y2),进而求得k,根据(1)k的范围可知,k不符合题意.本题主要考查了直线与圆的方程的综合运用.常需要把直线方程与圆的方程联立,利用韦达定理和判别式求得问题的解.。
2018-2019学年黑龙江省大庆中学高二10月月考数学试卷含答案

2018-2019学年黑龙江省大庆中学高二10月月考数学试题数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单选题1.已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为A . 100,8B . 80,20C . 100,20D . 80,82.已知如程序框图,则输出的i 是A . 9B . 11C . 13D . 153.“且”是“”的 A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件 4.用秦九韶算法求多项式,当时,的值为 A . 27 B . 86 C . 262 D . 789 5.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是 A . 至少有一个白球;都是白球 B . 至少有一个白球;至少有一个红球 C . 至少有一个白球;红、黑球各一个 D . 恰有一个白球;一个白球一个黑球 6.已知等差数列中,是的前n 项和,且,,则的值为 A . 260 B . 130 C . 170 D . 210 7.某四棱锥的三视图如图所示,该四棱锥的侧面积为 A . 8 B .C . 10D .8.2016年2月,为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为,则的最小值为A . 9B .C . 8D . 4 9.长方体的三个相邻面的面积分别为2,3,6,则该长方体外接球的表面积为 A .B .C .D .10.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”即乙领到的钱数不少于其他任何人的概率是此卷只装订不密封班级姓名准考证号考场号座位号A.B.C.D.11.在区间上随机取两个数x,y,记P为事件“”的概率,则A.B.C.D.12.圆:和:,M,N 分别是圆,上的点,P 是直线上的点,则的最小值是A.B.C.D.二、填空题13.已知一组数据,,,,,则该组数据的方差是______.14.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,,1000,打算从中抽取一个容量为50的样本,按系统抽样的办法分成50个部分如果第一部分编号为0001,0002,,0020,从中随机抽取一个号码为0015,则第40个号码为______.15.某学校有8个社团,甲、乙两位同学各自参加其中一个社团,且他俩参加各个社团的可能性相同,则这两位同学参加同一个社团的概率为______ .16.在中,角A,B,C所对的边分别为a,b,c,其中,,且满足,则______ .三、解答题17.国家二孩政策放开后,某市政府主管部门理论预测2018年到2022年全市人口总数与年份的关系有如表所示:年人口数十万请根据表中提供的数据,运用最小二乘法求出y关于x的线性回归方程;据此,估计2023年该市人口总数.(附)参考公式:,.18.在中,角A ,B,C的对应边分别为a,b,,且.求角B的大小;若的面积是,且,求b .19.共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网”,符合“低碳出行”的理念,已越来越多地引起了人们的关注某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值百分制按照,,,分成5组,制成如图所示频率分直方图.求图中x的值;求这组数据的平均数和中位数;已知满意度评分值在内的男生数与女生数的比为,若在满意度评分值为的人中随机抽取2人进行座谈,求恰有1名女生的概率.20.已知数列是等比数列,,是和的等差中项.求数列的通项公式;设,求数列的前n项和.21.如图,在四棱锥中,底面为直角梯形,,,底面ABCD,M、N分别为PC、PB的中点.求证:平面PAD;求证:.22.在平面直角坐标系xOy中,已知圆的圆心为Q,过点且斜率为k的直线与圆Q相交于不同的两点A,B.求k的取值范围;是否存在常数k ,使得向量与共线?如果存在,求k值;如果不存在,请说明理由.2018-2019学年黑龙江省大庆中学高二10月月考数学试题数学答案参考答案1.A【解析】由题设中提供的直方图与扇形统计图可知样本容量是,其中对四居室满意的人数为,应选答案A。
黑龙江省大庆实验中学2018-2019学年高二10月月考数学(文)试题及答案

大庆实验中学2018-2019学年度下学期十月份月考高二 数学(文)试题第Ⅰ卷(选择题 共60分)一.选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题x x q x p >>2:,1:,p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 2.设命题:,2ln 2xp x Q x ∃∈-<,则p ⌝为( ) A .,2ln 2xx Q x ∃∈-≥ B .,2ln 2xx Q x ∀∈-< C .,2ln 2xx Q x ∀∈-≥ D .,2ln 2xx Q x ∀∈-= 3.袋中装有3个白球,4个黑球,从中任取3个球,则①恰有1个白球和全是白球 ; ②至少有1个白球和全是黑球; ③至少有1个白球和至少有2个白球; ④至少有1个白球和至少有1个黑球. 在上述事件中,是对立事件的为( ) A .① B .② C .③ D .④4.将参加英语口语测试的1 000名学生编号为000,001,002,…,999,从中抽取一个容量为50的样本,按系统抽样的方法分为50组,如果第一组编号为000,001,002,…,019,且第一组随机抽取的编号为015,则抽取的第35个编号为( )A .700B .669C .695D .6765.甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为甲x 、乙x ,标准差分别为,甲乙σσ,则( ) A .甲乙x x <,甲乙σσ< B .甲乙x x <,甲乙σσ> C .甲乙x x >,甲乙σσ< D .甲乙x x >,甲乙σσ> 6.下列有关命题的说法正确的是( ) A . 命题“若,则”的否命题为“若,则” B . 命题“,”的否定是“,”C . 命题“若,则”的逆否命题为假命题D . 若“或”为真命题,则至少有一个真命题7. 执行右面的程序框图,如果输入a =4,那么输出的n 的值为( ). A .2B .3C .4D .58.下列正确的个数是( )(1) 在频率分布直方图中,中位数左边和右边的直方图的面积相等。
【精编文档】黑龙江省大庆市第四中学2018-2019学年高二数学下学期第一次检测试卷理.doc
2018~2019学年度第二学期第一次检测高二年级数学(理科)试题考试时间:120分钟 分值:150分本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题 共60分)一.选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知复数ii z ++=134,i 是虚数单位,则=||z( )D225 A 10 B 52 C252.已知复数)2)(1(i i z -+=,i 是虚数单位,则复数z 的共轭复数z 对应的点位于 ( )A 第一象限B 第二象限C 第三象限D 第四象限 3.设函数)(x f 在定义域内可导,)(x f y =的图 象如图所示,则导函数)(x f y '=的图象可能是 ( )A B C D 4.已知函数)(x f 的导函数为)(x f ',若2)1()(23-'+=x f x x f ,则)1(f '的值为( )A 0B 2-C 3-D 4-5.1231(tan 1)x x x dx -++⎰的值为( )A 0B 23C 2D 36.已知函数ax x x f -+=)1ln()(,若曲线)(x f y =在点))0(,0(f 处的切线方程为x y 2=,则实数a 的值为( )A 2-B 1-C 1D 2 7.执行如图所示的程序框图后,输出的值为4,则P 的取值范围是 ( )A715816P <≤ B 1516P >C 715816P ≤<D 3748P <≤8.函数2)(3-+=ax x x f 在区间),1(+∞-上是增函数,则实数a 的取值范围是( ) A [)∞+,0 B ),0(+∞ C [)+∞-,3 D ),3(+∞-9.有这样一个有规律的步骤:对于数25,将组成它的数字2和5分别取立方再求和为133,即23+53=133;对于133也做同样操作:13+33+33=55,如此反复操作,则第2017次操作后得到的数是 ( )A 25B 55C 133D 250第7题图10.已知函数),,(2)(234R b a R x b x ax x x f ∈∈+++=,若函数)(x f 仅在0=x 处有极值,则实数a的取值范围为( )A )38,38(-B ⎥⎦⎤⎢⎣⎡-38,38C ),38()38,(+∞--∞D ⎥⎦⎤⎢⎣⎡+∞⎥⎦⎤⎢⎣⎡-∞-,3838,11.已知函数13)(23+-=x ax x f ,若)x f (存在唯一的零点0x ,且00>x ,则a 的取值范围是 ( )A ),(∞+2B ),(∞+1C )(2,-∞- D )1,(--∞ 12.若实数d c b a ,,,满足0)2()ln 3(222=+-+-+d c a a b ,则22)()(d b c a -+-的最小值为( )A 8B 22C 2D 2第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,满分20分.) 13.复数ii+-331的虚部是____________ 14.设R m ∈,复数i m m m m z )32()12(22++-+-+=,若z 为纯虚数,则______=m 15.函数)(x f 的定义域为,6)1(=f R ,对任意,2)(,>'∈x f R x 则4ln 2)(ln +>x x f 的解集为___________16.在等比数列{}n a 中,若,,r s t 是互不相等的正整数,则有等式1r s s t t r t r s a a a ---⋅⋅=成立。
2018-2019黑龙江省大庆高二寒假开学检测数学(理)试题 Word版

大庆一中2018-2019学年高二年级下学期第一次阶段考试数学试卷一、选择题:(每小题5分满分60分)1. 命题“若a>b,则a2>b2”的逆否命题是 ( )A. 若,则B. 若,则C. 若,则D. 若,则2. “m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 执行如右图所示的程序框图,若输出的S=2,则判断框内可以填入()A. B. C. D.4. 下列说法正确的是()A. “若,则”的否命题是“若,则”B. “若,则”是真命题C. ,成立D. 为等比数列,则“”是“”的既不充分也不必要条件5. 某校高二某班共有学生60人,现根据座号,用系统抽样的方法,抽取一个容量为5的样本,已知3号,15号,45号,53号同学在样本中,那么样本中还有一个同学座号不能是()A. 26B. 31C. 36D. 376. 在长方体中,,,则异面直线与所成角的余弦值为()A. B. C. D.7. 已知变量,之间的线性回归方程为,且变量,之间的一组相关数据如下表所示,则下列说法错误的是()6 8 10 126 3 2A. 变量x,y之间呈现负相关关系B. 可以预测,当时,C. D. 由表格数据知,该回归直线必过点8.设不等式组,表示的平面区域为Ω,在区域Ω内任取一点P(x,y),则P点的坐标满足不等式的概率为 ( )A. B. C. D.9. 正四棱锥S-ABCD的侧棱长为,底边长为,E是SA的中点,则异面直线BE和SC所成的角等于()A. B. C. D.10.P为双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,且,直线PF2交y轴于点A,则△AF1P的内切圆半径为()A. 2B. 3C.D.11. 己知抛物线y2=2px(p>0)的焦点为F,过点F作互相垂直的两直线AB,CD与抛物线分别相交于A,B以及C,D若,则四边形ACBD的面积的最小值为()A. 32B. 30C. 18D. 3612. 已知椭圆,与双曲线具有相同焦点、,且在第一象限交于点P,椭圆与双曲线的离心率分别为、,若,则的最小值是A. B. C. D.二.填空题:(每小题5分满分20分)13.将一颗质地均匀的骰子先后抛掷2次,则出现向上点数之和小于10的概率是_____________.14.已知样本7,5,,3,4的平均数是5,则此样本的方差为15.已知抛物线C:y2=2px(p>0)的焦点为F,过F且倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,与它的准线交于点P,则= ______ .16.已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点.下列结论中,正确结论的序号是____________.①过E,F,G三点作正方体的截面,所得截面为正六边形;②B1D1∥平面EFG;③BD1⊥平面ACB1;④异面直线EF与BD1所成角的正切值为;⑤四面体ACB1D1的体积等于三、解答题:(满分70分)17.(满分10分)命题p :函数有意义,命题q:实数x满足(1)当且为真,求实数x的取值范围;(2)若是的充分不必要条件,求实数a的取值范围.18.(满分12分)为了了解“中国好声音”在大众中的熟知度,随机对15~65岁的人群抽样了n人回答有关问题,统计结果如下图表.组号分组回答正确的人数回答正确的人数占本组的频率第1组[15,25)a0.5 第2组[25,35)18 x第3组[35,45)b0.9第4组[45,55)9 0.36第5组[55,65] 3 y(1)分别求出a,b,x,y的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.19.(满分12分)如图,在多面体ABCDEF中,ABCD是正方形,平面ABCD,平面ABCD,,点M为棱AE的中点.求证:平面平面EFC;若,求直线AE与平面BDM所成的角的正弦值.20.(满分12分)抛物线Q:,焦点为F.若是抛物线内一点,P是抛物线上任意一点,求的最小值;过F的两条直线,,分别与抛物线交于A、B和C、D四个点,记M、N 分别是线段AB、CD的中点,若,证明:直线MN过定点,并求出这个定点坐标.21.(满分12分)如图,四棱锥P-ABCD的底面ABCD是平行四边形,∠BAC=∠PAD=∠PCD=90°.(1)求证:平面PAB⊥平面ABCD;(2)若AB=AC=PA=3,E为BC的中点,F为棱PB上的点,PD∥平面AEF,求二面角A-DF-E的余弦值22.(满分12分)已知椭圆C:=1(a>b>0)的离心率为,以椭圆长、短轴四个端点为顶点的四边形的面积为4.(1)求椭圆C的方程;(2)如图所示,记椭圆的左、右顶点分别为A、B,当动点M在定直线x=4上运动时,直线AM、BM分别交椭圆于P、Q两点,求四边形APBQ面积的最大值.大庆一中高二年级下学期第一次阶段考试数学答案一、选择题:CACB DACA DBAD二、填空题:13. 14.2 15. 16. ①③④三、解答题:17.解:(1)由-x2+4ax-3a2>0得x2-4ax+3a2<0,即(x-a)(x-3a)<0,其中a>0,得a<x<3a,a>0,则p:a<x<3a,a>0.若a=1,则p:1<x<3,由解得2<x<3.即q:2<x<3.若p∧q为真,则p,q同时为真,即,解得2<x<3,∴实数x的取值范围(2,3).(2)若¬p是¬q的充分不必要条件,即q是p的充分不必要条件,∴即(2,3)是(a,3a)的真子集.所以,解得1≤a≤2.实数a的取值范围为[1,2].18.解:(Ⅰ)由频率表中第4组数据可知,第4组总人数为,再结合频率分布直方图可知n=,∴a=100×0.01×10×0.5=5,b=100×0.03×10×0.9=27,…(Ⅱ)因为第2,3,4组回答正确的人数共有54人,所以利用分层抽样在54人中抽取6人,每组分别抽取的人数为:第2组:人;第3组:人;第4组:人设第2组2人为:A1,A2;第3组3人为:B1,B2,B3;第4组1人为:C1.则从6人中随机抽取2人的所有可能的结果为:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1)共15个基本事件,其中恰好没有第3组人共3个基本事件,∴所抽取的人中恰好没有第3组人的概率是:.19.证明:连结AC,交BD于点N,为AC的中点,.平面EFC,平面EFC,平面EFC.,DE都垂直底面ABCD,.,为平行四边形,平面EFC,平面EFC,平面EFC.又,平面平面EFC.解:由已知,平面ABCD,是正方形.两两垂直,如图,建立空间直角坐标系.设,则,从而,,设平面的一个法向量为,由得.令,则,从而.,设与平面所成的角为,则,所以,直线与平面所成角的正弦值为.20.解:由抛物线定义知,等于P到准线的距离,的最小值即为点E到准线的距离,等于4.证明:由,得:,解得,代入,得,同理,,,:,变形得:,因为,所以进一步化简得,所以MN恒过定点.21.解:(1)证明:∵AB∥CD,PC⊥CD,∴AB⊥PC,∵AB⊥AC,AC∩PC=C,∴AB⊥平面PAC,∴AB⊥PA,又∵PA⊥AD,AB∩AD=A,∴PA⊥平面ABCD,PA⊂平面PAB,∴平面PAB⊥平面ABCD;(2)连接BD交AE于点O,连接OF,∵E为BC的中点,BC∥AD,∴==,∵PD∥平面AEF,PD⊂平面PBD,平面AEF∩平面PBD=OF,∴PD∥OF,∴==,以AB,AC,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系A-xyz,则A(0,0,0),B(3,0,0),C(0,3,0),D(-3,3,0),P(0,0,3),E(,,0),F(2,0,1),设平面ADF的法向量m=(x1,y1,z1),∵=(2,0,1),=(-3,3,0),由•m=0,•m=0得取m=(1,1,-2).设平面DEF的法向量n=(x2,y2,z2),∵=(,-,0),=(,-,1),由•n=0,•n=0得取n=(1,3,4).cos⟨m,n>==-,∵二面角A-DF-E为钝二面角,∴二面角A-DF-E的余弦值为-.22.解:(Ⅰ)根据题意,椭圆C:=1(a>b>0)的离心率为,则有a=2c,以椭圆长、短轴四个端点为顶点的四边形的面积为4,则有2ab=4,又a2=b2+c2,解得a=2,b=,c=1,故椭圆C的方程为+=1;(Ⅱ)由于对称性,可令点M(4,t),其中t>0.将直线AM的方程y=(x+2)代入椭圆方程+=1,得(27+t2)x2+4t2x+4t2-108=0,由x A•x P=,x A=-2得x P=-,则y P=.再将直线BM的方程y=(x-2)代入椭圆方程+=1得(3+t2)x2-4t2x+4t2-12=0,由x B•x Q=,x B=2得x Q=,则y Q=.故四边形APBQ的面积为S=|AB||y P-y Q|=2|y P-y Q|=2(+)===.由于λ=≥6,且λ+在[6,+∞)上单调递增,故λ+≥8,从而,有S=≤6.当且仅当λ=6,即t=3,也就是点M的坐标为(4,3)时,四边形APBQ 的面积取最大值6.。
黑龙江省大庆市第十中学2017_2018学年高二数学下学期第一次月考试题文201805041706

黑龙江省大庆市第十中学 2017-2018学年高二数学下学期第一次月考试题 文(时间:120分钟 满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第 I 卷(选择题)一、选择题(本大题共 12小题,每小题 5分,共 60分)'1.函数 f (x ) 1 sin x ,其导数是 f ' (x ),则)f ( 的值为()31B : A:21 23D : C :23 22.函数 f (x ) x 3 x 在 x 1处的切线方程是( )A: 4x y 2 0B : 4x y 2 0C : 4x y 2 0D : 4x y 2 03.在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结 论,并且有99%以上的把握认为这个结论是成立的,则下列说法中正确的是( ) A:100个吸烟者中至少有 99人患有肺癌 B :1个人吸烟,那么这人有99%的概率患有肺癌C :在 100个吸烟者中一定有患肺癌的人D :在 100个吸烟者中可能一个患肺癌的人也没 有f (x 3 x ) f (x )4.设函数 y f (x )可导,则 lim=()x 03 x1'A: f '(x )B :3 f '(x )C : f (x )D :以上答案都不对35. 某种产品的广告费支出 x 与销售额 y (单位:百万元)之间有如下对应数据:x 2 4 5 6 8 y3040t5070^根据上表提供的数据,求出y关于x的回归直线方程为y 6.5x 17.5,则t的值为()A: 40 B:50 C:60 D:70- 1 -6.在线性回归模型中,分别选择了4个不同的模型,它们的相关指数R2依次为0.36、0.95、0.74、0.81,其中回归效果最好的模型的相关指数R2为()A: 0.95B:0.81C:0.74D:0.367.“e是无限不循环小数,所以e为无理数.”该命题是演绎推理中的三段论推理,其中大前提是()A: 无理数是无限不循环小数B:有限小数或有限循环小数为有理数C:无限不循环小数是无理数D:无限小数为无理数8.函数fln x (x) ,则()xA: x e是函数f(x)的极大值点B:x e是函数f(x)的极小值点11C:x 是函数f(x)的极大值点D:x 是函数f(x)的极小值点e e19.已知f(x) x2 2xf'(2018),则f'(2018)=()2A:2017B: 2017C:2018D: 201810.函数y f(x)的导函数f'(x)的图象如图所示,则下列说法正确的是()A:函数y f(x)在( ,0)上单调递增B::函数y f(x)的单调递减区间为(3,5) C:函数y f(x)在x 0处取得极大值D:函数y f(x)在x 5处取得极小值(10题图)11. 若函数f(x) x3 3bx 1在区间R内是减函数,b R,则()A:b 0B:b 0C:b 0D:b 0 12.函数f(x)的定义域为R,f( 2) 2018,对 x R,都有f'(x) 2x成立,则不等式f(x) x2 2014的解集为()A: ( ,2)B:( 2, )C:( 2,2)D:(2, )- 2 -第II卷(非选择题)二、填空题(本大题共4小题,每小题5分,共20分)13. 甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,甲说:我去过的城市比乙多,但没去过B城市;乙说:我没去过C城市;丙说:我们三人去过同一城市;由此可判断乙去过的城市为_____________14. 已知边长分别为a,b,c的三角形ABC面积为S,内切圆O的半径为r,连OA,OB,OC111111 则三角形OAB,OBC,OAC的面积分别为cr ar,br得,,由S cr ar br2222222,类比得四面体的体积为V,四个面的面积分别为Sr S,则内切球的1,S,S,Sa b c234半径R ____________15.曲线y ln x上的点到直线x y 0的最短距离是____________16.函数f(x) x(x c)2在x 2处有极大值,则c的值为___________三、解答题(本大题共6小题,共70分)17.(10分)已知函数f(x) x2 ln x。
【高中教育】黑龙江省大庆十中2018-2019学年高二数学下学期第一次月考试卷文.doc

2018-2019学年度第二学期高二(文科)数学第一次月考试题(时间:120分钟 满分:150分)一、单选题(本大题共12小题,每小题5分,共60分) 1.复数ii-+11等于( ) A .i B .i - C .1- D .1 2.直线的参数方程为(为参数),则直线的一般方程为 ( ) A .B .C .D .3.由 ①菱形的对角线互相垂直;②正方形的对角线互相垂直;③正方形是菱形。
写一个“三段论”形式的推理,则作为大前提,小前提和结论的分别为( )A .②③①B .①③②C .①②③D .③②①4.点的直角坐标是,则点的极坐标是( )A .B .C .D .5..如图,这是一个正六边形的序列,则第n 个图形的边数为( ).A .5n-1B .6nC .5n+1D .4n+26.已知的取值如下表所示:若与线性相关,且 ,则( )A .B .C .D .7.通过随机询问110名性别不同的学生是否爱好某项运动,得到如下的列联表:由K 2= 算得, K 2≈7.8.参照附表,得到的正确结论是( )A .有99%以上的把握认为“爱好该项运动与性别有关”B .有99%以上的把握认为“爱好该项运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” 8.用反证法证明命题:“若整系数一元二次方程()200ax bx c a ++=≠有偶数根,那么,,a b c 中至少有一个是偶数”时,下列假设中正确的是( )A .假设,,a b c 不都是偶数B .假设,,a b c 至多有两个是偶数C .假设,,a b c 至多有一个是偶数D .假设,,a b c 都不是偶数 9.已知数列中,a 1=1,当n ≥2时,,依次计算a 2,a 3,a 4后,猜想的一个表达式是( )A .n 2-1B .(n -1)2+1C .2n -1D .2n -1+1 10.设实数a,b,c 满足a+b+c=1,则a,b,c 中至少有一个数不小于 ( )A .0B .13C .12D .111.在符合互化条件的直角坐标系和极坐标系中,直线l :与曲线C :相交,则k 的取值范围是A .B .C .D .但12.直线l 的极坐标方程为ρ(cos θ+sin θ)=6,圆C : { x cos y sin θθ== (θ为参数)上的点到直线l 的距离为d ,则d 的最大值为( )A.1 B..1 D.2 二、填空题(本大题共4小题,每小题5分,共20分)13.用线性回归模型求得甲、乙、丙3组不同的数据对应的2R 的值分别为0.81,0.98,0.63,其中__________(填甲、乙、丙中的一个)组数据的线性回归的效果最好. 14.复数z满足方程,则______.15.直线2212x ty ⎧=+⎪⎪⎨⎪=-+⎪⎩(t 为参数)被圆229x y +=截得的弦长为 .16.以极坐标系中的点 1 , 6π⎛⎫ ⎪⎝⎭为圆心,1为半径的圆的极坐标方程是 .三、解答题(本大题共6小题,共70分;其中17题10分,其他每道大题12分) 17.已知是虚数单位,复数满足.求;18.已知复数()()222332z m m m m i =--+++,( i 为虚数单位)根据以下条件分别求实数m 的值或范围.(1)z 是纯虚数; (2)z 对应的点在复平面的第二象限.19.在平面直角坐标系中,以坐标原点O 为极点, x 轴的正半轴为极轴建立极坐标系.已知直 线l的参数方程为1{ (x t y ==为参数),曲线C 的极坐标方程为4cos ρθ=;(Ⅰ)求直线l 的直角坐标方程和曲线C 的直角坐标方程; (Ⅱ)若直线l 与曲线C 交点分别为,A B , 点()1,0P ,求11PA PB+的值. 20.已知直线l的参数方程是2{x y ==+(t 是参数),以坐标原点为原点, x轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为4cos 4πρθ⎛⎫=+ ⎪⎝⎭.(1)判断直线l 与曲线C 的位置关系;(2)过直线l 上的点作曲线C 的切线,求切线长的最小值. 21.已知数列{}n a 满足()111,2n na a a n N a ++==∈-. (1)求234,,a a a ;(2)猜想数列{}n a 的通项公式,并用数学归纳法证明.22.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的50人进行问卷调查,得到了如下的列联表:(1)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人? (2)在上述抽取的6人中选2人,求恰好有1名女性的概率;(3)为了研究心肺疾病是否与性别有关,请计算出统计量2K ,你有多大把握认为心肺疾病与性别有关?(公式及临界值可参照第7题)参考答案1.A【解析】试题分析:1(1)(1)2==1(1)(1)2i i i iii i i+++=--+;考点:1.复数的运算;2.D【解析】由题意,联立两式消去t得,,即。
2018-2019黑龙江省大庆十中高二下学期月考数学(理)试题 解析版

黑龙江省大庆十中2018-2019学年高二下学期第二次月考数学理科试题(时间:120分钟 满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(本大题共12小题,每小题5分,共60分) 1.若218x C -=38x C +,则x 的值为( )A .1或2B .3或4C .1或3D .2或4 2.设是一个离散型随机变量,其分布列为:则等于( ) A .1 B . C .D .3.已知复数满足,则( )A .B .C .1D .54.己知,则( ).A .B .C .D . 5.由数字1,2,3,4,5组成没有重复数字的五位数,其中偶数共有 ( )个。
A.60 B.48 C.36 D.246.有6人被邀请参加一项活动,必然有人去,去几人自行决定,共有( )种不同去法 A .36种 B .35种 C .63种 D .64种7.将5件相同的小礼物全部送给3个不同的球迷,让每个球迷都要得到礼物,不同的分法种数是 ( ) A .2种 B .10种 C .5种 D .6种8.如图,在一花坛A ,B ,C ,D 四个区域种花,现有4种不同的花供选种,要求在每块里种1种花,且相邻的两块种不同的花,则不同的种法总数为 ( )A 、60B 、48C 、84D 、72 9.已知在为单调增函数,则实数m 的取值范围为( )A .B .C .D .10.函数的图象与直线相切,则实数A .B .1C .2D .411.已知函数恰有两个极值点,则的取值范围是( ) A .B .C .D .12.定义在上的偶函数的导函数为,若对任意的实数,都有恒成立,则使成立的实数的取值范围为( ) A .B .C .D .第II 卷(非选择题)二、填空题(本大题共4小题,每小题5分,共20分)13.有4种不同的蔬菜,从中选出3种,分别种植在不同土质的3块土地上进行实验,则不同的种植方法共______种.(用数字作答) 14.设()f x x =,则22()f x dx -=⎰15.已知,则二项式的展开式中的系数为____________.16.已知,则______________;三、解答题(本大题共6小题,共70分;其中17题10分,其他每道大题12分) 17.已知复数,(,i 是虚数单位)(1).若z 是纯虚数,求m 的值;(2).设是z的共轭复数,在复平面上对应的点在第四象限,求m的取值范围.18.有3本不同的语文书和3本不同的数学书,求满足下列条件的方法总数(用数字作答)(1)6本排成一排;(2)6本排成一排,其中3本数学书必须相邻;(3)6本排成一排,其中语文书互不相邻.19.从某小组的5名女生和4名男生中任选3人去参加一项公益活动。
2018-2019学年黑龙江省大庆中学高二10月月考数学试题 解析版

绝密★启用前黑龙江省大庆中学2018-2019学年高二10月月考数学试题一、单选题1.已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为A.100,8 B.80,20 C.100,20 D.80,8【答案】A【解析】由题设中提供的直方图与扇形统计图可知样本容量是,其中对四居室满意的人数为,应选答案A。
2.已知如程序框图,则输出的i是A.9 B.11 C.13 D.15【答案】C【解析】试题分析:经过第一次循环得到S=1×3=3,i=5经过第二次循环得到S=3×5=15,i=7经过第三次循环得到S=15×7=105,i=9经过第四次循环得到S=105×9=945,i=11经过第五次循环得到S=945×11=10395,i=13此时,满足判断框中的条件输出.考点:程序框图.3.“且”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】【分析】由题意分别考查充分性和必要性是否成立即可求得最终结果.【详解】若且,则成立,故充分性易证,若,如,,此时成立,但不能得出且,故必要性不成立,由上证明知“且”是“”的充分不必要条件.本题选择A选项.【点睛】本题主要考查充分必要条件的判定,不等式的性质等知识,意在考查学生的转化能力和计算求解能力.4.用秦九韶算法求多项式,当时,的值为A.27 B.86 C.262 D.789【答案】C【解析】【分析】首先将所给的算式写成秦九韶的形式,然后计算的值即可.【详解】故当时,本题选择C选项.【点睛】本题主要考查秦九韶算法及其应用等知识,意在考查学生的转化能力和计算求解能力. 5.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是A.至少有一个白球;都是白球B.至少有一个白球;至少有一个红球C.至少有一个白球;红、黑球各一个D.恰有一个白球;一个白球一个黑球【答案】C【解析】【分析】由题意逐一考查所给的事件是否互斥、对立即可求得最终结果.【详解】袋中装有红球3个、白球2个、黑球1个,从中任取2个,逐一分析所给的选项:在A中,至少有一个白球和都是白球两个事件能同时发生,不是互斥事件,故A不成立.在B中,至少有一个白球和至少有一个红球两个事件能同时发生,不是互斥事件,故B 不成立;在C中,至少有一个白球和红、黑球各一个两个事件不能同时发生但能同时不发生,是互斥而不对立的两个事件,故C成立;在D中,恰有一个白球和一个白球一个黑球两个事件能同时发生,不是互斥事件,故D 不成立;本题选择C选项.【点睛】“互斥事件”与“对立事件”的区别:对立事件是互斥事件,是互斥中的特殊情况,但互斥事件不一定是对立事件,“互斥”是“对立”的必要不充分条件.6.已知等差数列中,是的前n项和,且,,则的值为A.260 B.130 C.170 D.210【答案】D【解析】【分析】由题意结合等差数列的性质整理计算即可求得最终结果.【详解】由题意可得,,,成等差数列,故,代入数据可得,解之可得本题选择D选项.【点睛】本题主要考查等差数列前n项和的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.7.某四棱锥的三视图如图所示,该四棱锥的侧面积为A.8 B.C.10 D.【答案】B【解析】由三视图可知,侧面的高为主视图的腰长,故侧面的高为,故侧面积为.点睛:本题主要考查由三视图求几何体的侧面积. 思考三视图还原空间几何体首先应深刻理解三视图之间的关系,遵循“长对正,高平齐,宽相等”的基本原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.由三视图画出直观图的步骤和思考方法:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.8.2016年2月,为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为,则的最小值为A.9 B.C.8 D.4【答案】B【解析】试题分析:由题意,得,即,且,则(当且仅当,即取等号);故选B.考点:1.茎叶图;2.基本不等式.9.长方体的三个相邻面的面积分别为2,3,6,则该长方体外接球的表面积为A.B.C.D.【答案】C【解析】【分析】由题意首先求得长方体的棱长,然后求解其外接球的表面积即可.【详解】设长方体的棱长分别为,则,所以,于是,设球的半径为,则,所以这个球面的表面积为.本题选择C选项.【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.10.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”即乙领到的钱数不少于其他任何人的概率是A.B.C.D.【答案】C【解析】设乙,丙,丁分别领到x元,y元,z元,记为,则基本事件有:共10个,其中符合乙获得“最佳手气”的有4个,故概率为,应选C.11.在区间上随机取两个数x,y,记P为事件“”的概率,则A.B.C.D.【答案】D【解析】【分析】由题意结合几何概型计算公式求解满足题意的概率值即可.【详解】如图所示,表示的平面区域为,平面区域内满足的部分为阴影部分的区域,其中,,结合几何概型计算公式可得满足题意的概率值为.本题选择D选项.【点睛】数形结合为几何概型问题的解决提供了简捷直观的解法.用图解题的关键:用图形准确表示出试验的全部结果所构成的区域,由题意将已知条件转化为事件A满足的不等式,在图形中画出事件A发生的区域,据此求解几何概型即可.12.圆:和:,M,N分别是圆,上的点,P是直线上的点,则的最小值是A.B.C.D.【答案】A【解析】【分析】首先求得圆关于的对称的圆的性质,然后将问题转化为三点共线的问题求解最值即可.【详解】圆关于的对称圆的圆心坐标,半径为3,圆的圆心坐标,半径为1,由图象可知当P,,,三点共线时,取得最小值,的最小值为圆与圆的圆心距减去两个圆的半径和,即:.本题选择A选项.【点睛】本题主要考查圆与圆的位置关系,等价转化的数学思想等知识,意在考查学生的转化能力和计算求解能力.第II卷(非选择题)请点击修改第II卷的文字说明二、填空题13.已知一组数据,,,,,则该组数据的方差是______.【答案】【解析】数据4.8,4.9,5.2,5.5,5.6的平均数为×(4.8+4.9+5.2+5.5+5.6)=5.2,∴该组数据的方差为:s2=×[(4.8–5.2)2+(4.9–5.2)2+(5.2–5.2)2+(5.5–5.2)2+(5.6–5.2)2]=0.1.故答案为:0.1.14.将参加数学竞赛的1000名学生编号如下:0001,0002,0003,,1000,打算从中抽取一个容量为50的样本,按系统抽样的办法分成50个部分如果第一部分编号为0001,0002,,0020,从中随机抽取一个号码为0015,则第40个号码为______.【答案】0795【解析】【分析】首先求得分段间隔,然后结合所给号码的数值求解第40个号码即可.【详解】系统抽样是先将总体按样本容量分成段,再间隔k取一个.又现在总体的个体数为1000,样本容量为50,若第一个号码为0015,则第40个号码为故答案为0795【点睛】(1)系统抽样适用的条件是总体容量较大,样本容量也较大.(2)使用系统抽样时,若总体容量不能被样本容量整除,可以先从总体中随机地剔除几个个体,从而确定分段间隔.(3)起始编号的确定应用简单随机抽样的方法,一旦起始编号确定,其他编号便随之确定.15.某学校有8个社团,甲、乙两位同学各自参加其中一个社团,且他俩参加各个社团的可能性相同,则这两位同学参加同一个社团的概率为______ .【答案】【解析】试题分析:这是一古典概率模型,基本事件有种,具体事件中含有基本事件的个数为,则概率为:.考点:古典概率的运算16.在中,角A,B,C所对的边分别为a,b,c,其中,,且满足,则______ .【答案】【解析】【分析】由题意利用正弦定理边化角,求得∠B的值,然后结合数量积的定义求解的值即可.【详解】根据正弦定理得:,故答案为:【点睛】本题主要考查正弦定理、余弦定理的应用等知识,意在考查学生的转化能力和计算求解能力.三、解答题17.国家二孩政策放开后,某市政府主管部门理论预测2018年到2022年全市人口总数与年份的关系有如表所示:年十万请根据表中提供的数据,运用最小二乘法求出y关于x的线性回归方程;据此,估计2023年该市人口总数.(附)参考公式:,.【答案】(1);(2)估计2023年该市人口总数约为196万.【解析】分析:(Ⅰ)直接利用最小二乘法原理求关于的线性回归方程.( Ⅱ)令回归方程中的x=5得2023年该市人口总数.详解:(Ⅰ)由题设,得,,,,∴,所以∴所求关于的线性回归方程为.(Ⅱ)由(Ⅰ)及题意,当时,.据此估计2023年该市人口总数约为196万.点睛:本题主要考查回归分析,考查最小二乘法,意在考查学生对这些基础知识的掌握能力及基本的运算能力.18.在中,角A,B,C的对应边分别为a,b,,且.求角B的大小;若的面积是,且,求b.【答案】(1);(2).【解析】【分析】由题意利用正弦定理角化边,结合同角三角函数基本关系和特殊角的三角函数值可得.结合三角形面积公式和余弦定理计算可得.【详解】,,又,,,,.,,,,.【点睛】在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.19.共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网”,符合“低碳出行”的理念,已越来越多地引起了人们的关注某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值百分制按照,,,分成5组,制成如图所示频率分直方图.求图中x的值;求这组数据的平均数和中位数;已知满意度评分值在内的男生数与女生数的比为,若在满意度评分值为的人中随机抽取2人进行座谈,求恰有1名女生的概率.【答案】(1);(2)平均数为,中位数为;(3).【解析】【分析】利用频率分布直方图小长方形面积之和为1求解x的值即可;由平均数公式计算平均数即可,利用左右两侧面积均为0.5计算中位数即可.首先确定男女生的人数,然后利用古典概型计算公式求解满足题意的概率值即可.【详解】由,解得.这组数据的平均数为.中位数设为,则,解得.满意度评分值在内有人,其中男生3人,女生2人.记为,记“满意度评分值为的人中随机抽取2人进行座谈,恰有1名女生”为事件A通过列举知总基本事件个数为10个,A包含的基本事件个数为6个,利用古典概型概率公式可知.【点睛】解决频率分布直方图的问题,关键在于找出图中数据之间的联系.这些数据中,比较明显的有组距、,间接的有频率、小长方形的面积,合理使用这些数据,再结合两个等量关系:小长方形面积=组距×=频率,小长方形面积之和等于1,即频率之和等于1,就可以解决直方图的有关问题.20.已知数列是等比数列,,是和的等差中项.求数列的通项公式;设,求数列的前n项和.【答案】(1);(2).【解析】【分析】设数列的公比为q,结合是和的等差中项求得q的值,然后求解数列的通项公式即可;首先求得的通项公式,然后错位相减求解其前n项和即可.【详解】设数列的公比为q,因为,所以,.因为是和的等差中项,所以.即,化简得.因为公比,所以.所以因为,所以.所以.则,得,,,所以.【点睛】本题的核心是考查错位相减求和的方法,一般地,如果数列{a n}是等差数列,{b n}是等比数列,求数列{a n·b n}的前n项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列{b n}的公比,然后作差求解.21.如图,在四棱锥中,底面为直角梯形,,,底面ABCD,M、N分别为PC、PB的中点.求证:平面PAD;求证:.【答案】(1)证明见解析;(2)证明见解析.【解析】【分析】由题意结合几何关系和线面平行的判定定理证明平面P AD即可;利用几何体的空间特征可证得平面ADMN,然后利用线面垂直的定义即可证得题中的结论.【详解】因为M、N分别为PC、PB的中点,所以,且.又因为,所以.又平面P AD,MN不属于平面P AD,所以平面P AD.因为AN为等腰三角形ABP底边PB上的中线,所以.因为平面ABCD,平面ABCD,所以.又因为,且,所以平面P AB.又平面P AB,所以.因为,,且,所以平面ADMN.又平面ADMN,所以.【点睛】本题主要考查线面平行的判定定理,线面垂直的定义与判定定理等知识,意在考查学生的转化能力和计算求解能力.22.在平面直角坐标系xOy中,已知圆的圆心为Q,过点且斜率为k的直线与圆Q相交于不同的两点A,B.求k的取值范围;是否存在常数k,使得向量与共线?如果存在,求k值;如果不存在,请说明理由.【答案】(1)k的取值范围为;(2)没有符合题意的常数k.【解析】【分析】首先写出直线方程,联立直线方程与圆的方程,结合韦达定理得到关于k的不等式,求解不等式即可求得k的取值范围;假设存在满足题意的常数k,由题意求得实数k的值,结合(1)中求得的k的取值范围可得没有符合题意的常数k.【详解】圆的方程可写成,所以圆心为,过且斜率为k的直线方程为.代入圆方程得,整理得直线与圆交于两个不同的点A,B等价于,解得,所以k的取值范围为.设,,则,由方程,又而.所以与共线等价于,将代入上式,解得.由1知,故没有符合题意的常数k.【点睛】处理直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法.。
黑龙江省大庆十中2018-2019高二下学期期末考试数学(文)试卷

2018-2019学年度下学期高二文科数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知i 为虚数单位,则复数1ii=+( ) A .1122+i B .1i -C .1122-i D .1122--i 2.设命题p:nn N n 2,2>∈,则为( )A .nn N n 2,2>∈∀ B .nn N n 2,2≤∈∃ C .nn N n 2,2≤∈∀ D .nn N n 2,2=∈∃ 3.当3,5,7a b c ===时,执行如图所示的程序框图,输出的m 值为( )A .12B .12-C .2D . 4.已知{}37A x x =≤<,{}214400B x x x =-+<,则A B =A .[)3,10B .()4,7C .[)7,10D .[]3,45.已知3a e =,33log 5log 2b =-,c =a ,b ,c 的大小关系为() A .a c b >> B .b c a >> C .c a b >> D .c b a >>6.今年六一儿童节,阿曾和爸爸,妈妈,妹妹小丽来到游乐园玩.一家四口走到一个抽奖台前各抽一次奖,抽奖前,爸爸,妈妈,阿曾,小丽对抽奖台结果进行了预测,预测结果如下: 妈妈说:“小丽能中奖”; 爸爸说:“我或妈妈能中奖”; 阿曾说:“我或妈妈能中奖”; 小丽说:“爸爸不能中奖”.抽奖揭晓后,一家四口只有一位家庭成员猜中,且只有一位家庭成员的预测结果是正确的,则中奖的是( ) A .妈妈B .爸爸C .阿曾D .小丽7.在同一直角坐标系中,函数()()0af x x x =≥,()log a g x x =-的的图象可能是()A .B .C .D .8.已知0a >,1a ≠,0M >,0N >,那么下列各式中错误.......的是( ) A .log ()log log a a a M N M N +=+B .log log log aa a MM N N=- C .log log na a M n M =D .log log log a a a MN M N =+9.若函数()1f x ax =+在区间(1,1)-上存在零点,则实数a 的取值范围是( ) A .(1,)+∞ B .(,1)-∞ C .(,1)(1,)-∞-+∞ D .(1,1)-10.函数()212()log 23f x x x =--的单调递减区间是( )A .(,1)-∞-B .(,1)-∞C . (3,)+∞D .(1,)+∞11.若函数()log (2)xa f x a x =++在[]0,1上的最大值和最小值之和为a ,则a 的值为( )A .16B .13C .12D .312.若定义运算:()()a ab a b b a b ≥⎧⊗=⎨<⎩,例如233⊗=,则下列等式可能不成立的是( )A .a b b a ⊗=⊗B .()()a b c a b c ⊗⊗=⊗⊗C .222()a b a b ⊗=⊗D .()()()c a b c a c b ⋅⊗=⋅⊗⋅(0)c >二、填空题13.函数21()4f x x =-的定义域是_____. 14.2.已知函数3()log 5f x x x =+-的零点0(,1)x a a ∈+,则整数a 的值为______15.给定两个命题p ,q ,若p ⌝是q 的必要不充分条件,则p 是q ⌝的________条件. 16.给出以下结论:①命题“若2340x x --=,则4x =”的逆否命题为“若4x ≠,则2340x x --≠”; ②“4x =”是“2340x x --=”的充分条件;③命题“若0m >,则方程20x x m +-=有实根”的逆命题为真命题; ④命题“若220m n +=,则0m =且0n =”的否命题是真命题. 则其中错误的是__________.(填序号) 三、解答题17.已知a R ∈,复数1a iz i-=+. (1)若z 为纯虚数,求a 的值;(2)在复平面内,若z 对应的点位于第二象限,求a 的取值范围.18.设a 是实数,命题p :函数22()233f x x x a a =-++-的最小值小于0,命题q :函数32()32f x ax x x =+-+在R 上是减函数,命题r :11m a m -≤≤+.(1)若“p ⌝”和“p q ∧”都为假命题,求实数a 的取值范围; (2)若p 是r 的充分不必要条件,求实数m 的取值范围. 19.已知函数()228f x x kx =-+(1)若函数()()2g x f x x =+是偶函数,求k 的值;(2)若函数()y f x =在[]1,2-上,()2f x ≥恒成立,求k 的取值范围.20.“双十一”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额t (百元)的频率分布直方图如图所示:(1)求网民消费金额t 的平均值和中位数0t ;(2)把下表中空格里的数填上,能否有90%的把握认为网购消费与性别有关.附表:22()()()()()n ad bc K a b c d a c b d -=++++.21.已知一次函数()f x 的图象过点()0,1-和()2,1,()(1)m g x m x =-为幂函数. (Ⅰ)求函数()f x 与()g x 的解析式;(Ⅱ)当a R ∈时,解关于x 的不等式:a f(x)<g(x).22.已知极坐标系的极点为直角坐标系xOy 的原点,极轴为x 轴的正半轴,两种坐标系中的长度单位相同,已知曲线C 的极坐标方程为ρ=2(cosθ+sinθ). (1)求曲线C 的直角坐标方程;(2)经过点P (0,1)直线1212x t l y t:⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数)与曲线C 交于A ,B 两点,求11PA PB +的值.参考答案1.A 【解析】 【分析】直接由复数代数形式的乘除运算化简得答案. 【详解】(1)1111(1)(1)222i i i i i i i i -+===+++- 本题正确选项:A 【点睛】本题考查了复数代数形式的乘除运算,是基础题. 2.C 【解析】试题分析:根据否命题的定义,即既否定原命题的条件,又否定原命题的结论,存在的否定为任意,所以命题的否命题应该为,即本题的正确选项为C.考点:原命题与否命题. 3.B 【解析】 【分析】根据框图,逐步执行,即可得出结果. 【详解】执行程序框图如下: 输入3,5,7a b c ===,则22219254915z a b c =+-=+-=-,2223530z ab ==⨯⨯=,则12151302z m z ==-=-, 输出12m =-. 故选B【点睛】本题主要考查程序框图,分析框图的作用,逐步执行即可,属于常考题型. 4.B 【解析】 【分析】由一元二次不等式解出集合B ,根据集合交集的定义即可求得A B 。
【高中教育】黑龙江省大庆十中2018-2019学年高一数学下学期第一次月考试卷.doc

黑龙江省大庆十中2018-2019学年高一数学下学期第一次月考试题一、选择题(本大题共12小题,共60.0分)1.已知向量,若与共线,则实数A. B. 1 C. D. 32.已知向量和的夹角为,,,则A. B. C. D.3.在等差数列中,已知,公差,则A. 10B. 12C. 14D. 164.与的等差中项是A. 1B.C.D.5.在等差数列中,,是方程的两个根,则为A. 12B. 13C. 14D. 156.已知数列1,,,,,,则是这个数列的A. 第10项B. 第11项C. 第12项D. 第21项7.设D为所在平面内一点,,则A. B.C. D.8.数列,,,,的一个通项公式可能是A. B. C. D.9.已知数列满足递推关系:,则A. B. C. D.10.设的内角A,B,C所对边分别为a,b,c若,,,则A. B. C. 或 D.11.设平面上有四个互异的点A、B、C、D,已知,则的形状是A. 直角三角形B. 等腰三角形C. 等腰直角三角D. 等边三角形12.设函数,数列满足,,且数列是递增数列,则实数a的取值范围是A. B. C. D.二、填空题(本大题共4小题,共20.0分)13.已知,,,则 ______ .14.已知三角形的三条边成公差为2的等差数列,且它的最大角的正弦值为,则这个三角形的周长为______ .15.在中,,,,则______.16.如图所示,为测一建筑物CD的高度,在地面上选取A,B 两点,从A,B两点分别测得建筑物顶端的仰角为,,且A,B两点间的距离为20m,则该建筑物的高度为_________________m.三、解答题(本大题共6小题,共70.0分)17.设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,且求B的大小;若,求b.18.已知,,.若A,B,C三点共线,求实数m的值;证明:对任意实数m,恒有成立19.在等差数列中,已知,.求该数列中的值;求该数列的通项公式.20.已知数列满足,,.求,,的值;求数列的通项公式.21.在内,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,且.求的值;若,求b的值.22.在中,角A,B,C的对边为a,b,c,角A,B,C的大小成等差数列,向量,,,若,试判断三角形ABC的形状;若,,求边c及.2108-2019年大庆市第十中学高一(下)数学试卷答案和解析【答案】1. A2. D3. B4. C5. D6. B7. A8. D9. D10. A11. B12. B13.14. 1515.16.17. 解:由,根据正弦定理得,所以,由为锐角三角形得.因为,由余弦定理得,所以.18. 解:,,B,C三点共线,向量是共线向量,得,解之得:分由,得,即对任意实数m,恒有成立.19. 解:由等差数列的性质可知,,所以,则;依题意得解得或,所以公差或,或.20. 解:数列满足,,,同理可得:,.数列满足,,.两边取倒数可得:,即,数列是等差数列,首项为1,公差为,,解得,.21. 解:内,a,b,c分别为角A,B,C所对的边,a,b,c成等差数列,所以:,且,解得:.所以:.由得:,解得:,由于:,则:,得:.所以:.进一步解得:.22. 解:,B,C成等差数列,可得:,又,.向量,,,,可得:.,可得:,可得:,即.三角形ABC的形状为:正三角形.,,,由余弦定理,可得:,整理可得:,解得:,或舍去,.【解析】1. 解:,,解得.故答案为A.利用向量共线定理即可得出,解出即可.熟练掌握向量共线定理是解题的关键.2. 解:,故选:D.首先把原式展开,再利用数量积求值.此题考查了数量积计算问题,属容易题.3. 解:等差数列,,公差,.故选:B.利用等差数列通项公式求解.本题考查等差数列的第12项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.4. 解:设x为与的等差中项,则,即故选:C由等差中项的定义易得答案.本题考查等差中项,属基础题.5. 【分析】本题考查了根与系数的应用问题,也考查了等差数列的性质与应用问题,是基础题.根据等差数列的通项公式与一元二次方程根与系数的关系,即可求出结果.【解答】解:等差数列中,,是方程的两个根,,;.故选D.6. 【分析】本题考查了不完全归纳法求数列的通项公式,做题时要注意观察,找到规律.可先找到数列的通项公式,在假设设是该数列的第n项,得到关于n的方程,再解方程即可.【解答】解:通过观察,可发现数列1,,,,,,的通项公式为,则,解得,.是这个数列的第11项.故选B.7. 解:;;.故选:A.根据向量减法的几何意义便有,,而根据向量的数乘运算便可求出向量,从而找出正确选项.考查向量减法的几何意义,以及向量的数乘运算.8. 解:数列,,,,的一个通项公式可能是.故选:D.利用符号为与绝对值为即可得出.本题考查了数列的通项公式,参考老头老娘了与计算能力,属于基础题.9. 【分析】本题考查了数列递推关系、等差数列的通项公式,考查了推理能力与计算能力,属于中档题,,可得再利用等差数列的通项公式即可得出.【解答】解:,,,数列是等差数列,首项为2,公差为1,故选D.10. 【分析】本题主要考查正弦定理,特殊角的三角函数值在解三角形中的应用,属于基础题.由已知及正弦定理可求,利用小边对小角可知B为锐角,利用特殊角的三角函数值即可解得B的值.【解答】解:,,,由正弦定理可得,,B为锐角,.故选A.11. 解:,,,即的形状是等腰三角形,故选B.由已知可得,即整理可得本题主要考查了向量的加法、减法的三角形法则的应用,向量数量积的运算,属于对基础知识的考查,试题难度不大.12. 解:函数,数列满足,,且数列是递增数列,解得:,即:,故选:B根据函数的单调性,,得出,求解即可.本题考查了函数的单调性,数列的特殊性,,属于中档题,容易出错,自变量的范围.13. 解:,,又,,.故答案为:.由,得,再由展开得答案.本题考查平面向量的数量积运算,考查向量模的求法,是基础题.14. 解:由题意可设三边为,a,则为最大边,根据三角形的大边对大角可知其对的角为最大角最大角的正弦值为,则最大角为由余弦定理可得,整理可得,解可得,即三角形的三边为3,5,7则周长为15由题意可设三边为,a,,由最大角的正弦值为,可知最大角为,结合余弦定理可得,可求a,进而可求15. 解:中,,,,由余弦定理,可得故答案为:利用余弦定理计算,再利用向量的数量积公式,即可求得结论.本题考查余弦定理,考查向量的数量积公式,考查学生的计算能力,正确运用余弦定理是关键.16. 解:如图所示,设,中,,;中,,,解得;建筑物CD的高度为.故答案为:.根据题意,利用直角三角形的边角关系和特殊角的三角函数值,即可求出建筑物CD的值.本题考查了直角三角形的边角关系应用问题,也考查了特殊角的三角函数值计算问题,是基础题.17. 本题考查了正弦定理和余弦定理.利用正弦定理将边的关系化为角的关系,然后即可求出角B的正弦值,再由为锐角三角形可得结论;根据中所求角B的值,结合余弦定理计算得b的值.18. 由平面向量的坐标运算,得到向量、的坐标,根据向量共线的充要条件列式,解之即可得到实数m的值;由平面向量数量积的坐标运算公式,得,结合二次函数的性质,可证出对任意实数m恒成立.本题给出含有字母m的向量坐标形式,在已知三点共线的情况下求参数m的值,并且证明不等式恒成立着重考查了平面向量数量积的运算公式和向量共线等知识,属于基础题.19. 本题主要考查了等差数列的性质,以及通项公式,同时考查了运算求解的能力,属于基础试题.利用等差数列的性质求出的值;得到,的方程组,从而求出,的值,得到公差d,可得通项公式.20. 由数列满足,,分别令,2,3,即可得出.数列满足,,两边取倒数可得:,再利用等差数列的通项公式即可得出.本题考查了等差数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.21. 利用等差中项建立a、b、c之间的联系,进一步求出的值.利用的结论,进一步求出的值,最后利用三角形的面积公式求出结果.本题考查的知识要点:余弦定理的应用,等差中项的应用,三角形面积公式的应用及相关的运算问题.22. 利用已知及等差数列的性质,三角形内角和定理可求,利用数量积的运算及三角函数恒等变换的应用可求,结合A的范围可求,即可得解.利用已知及余弦定理可求c,进而利用三角形面积公式即可计算得解.本题主要考查了等差数列的性质,三角形内角和定理,数量积的运算及三角函数恒等变换的应用,余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想和计算能力,属于中档题.。
黑龙江省大庆市高二数学下学期第一次月考试卷 理(含解析)

黑龙江省大庆市2016-2017学年高二数学下学期第一次月考试卷理一、选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|x2>1},N={﹣2,﹣1,0,1,2},则M∩N=()A.{0} B.{2} C.{﹣2,﹣1,1,2} D.{﹣2,2}2.命题“∀x∈R,x2+1>0”的否定是()A.∀x∈R,x2+1≤0 B.∀x∈R,x2+1<0C.∃x0∈R,x02+1<0 D.∃x0∈R,x02+1≤03.函数f(x)=x﹣sinx(x∈R),则f(x)()A.是奇函数,且在(﹣∞,+∞)上是减函数B.是偶函数,且在(﹣∞,+∞)上是减函数C.是偶函数,且在(﹣∞,+∞)上是增函数D.是奇函数,且在(﹣∞,+∞)上是增函数4.运行如图所示的程序框图,则输出s的值为()A.﹣2 B.3 C.4 D.85.已知双曲线﹣=1的一条渐近线方程为y=x,则此双曲线的离心率为()A.B.C.D.6.已知函数f(x)=﹣x3+x2﹣ax+1是R上的单调递减函数,则实数a的取值范围为()A. C.[,+∞)D.(﹣∞,]7.对于使f(x)≥N成立的所有常数N中,我们把N的最大值叫作f(x)的下确界.若a,b∈(0,+∞),且a+b=2,则+的下确界为()A.B.C.D.8.区间上随机取一个数x,sin的值介于到1之间的概率为()A.B.C.D.9.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n个这样的几何体拼成一个棱长为4的正方体,则V,n的值是()A.V=32,n=2 B.C.D.V=16,n=410.已知向量=(,),=(cosx,sinx),=,且,则cos(x+)的值为()A.﹣ B.C.﹣ D.11.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于()A.B.C.2 D.12.已知定义域为R的奇函数y=f(x)的导函数y=f′(x).当x≠0时,f′(x)+>0.若a=f(),b=﹣2f(﹣2),c=(ln)f(ln),则a、b、c的大小关系是()A.a<b<C B.b<c<a C.c<a<b D.a<c<b二、填空题:本大题共4小题,每小题5分.13.抛物线y2=10x的焦点到准线的距离是.14.已知在等差数列{a n}中,a1,a2017为方程x2﹣10x+16=0的两根,则a2+a1009+a2016的值为.15.已知f(x)=ax+b﹣1,若a,b都是从区间上任取的一个数,则f(2)<0成立的概率为.16.已知f(x)=2x2+x﹣k,g(x)=x3﹣3x,若对任意的x1∈,总存在x0∈,使得f(x1)≤g (x0)成立,则实数k的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知函数f(x)=lnx﹣ax.(Ⅰ)若函数f(x)在x=1处的切线与x轴平行,求a的值;(Ⅱ)若a=2,求函数f(x)在x=1处的切线方程;(Ⅲ)若a=1,请列出表格求函数f(x)的极大值.18.已知等差数列{a n}满足:a3=7,a5+a7=26.{a n}的前n项和为S n.(Ⅰ)求a n及S n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和T n.19.某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100只白鼠,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100只白鼠的感染数,得到如下资料:(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为x,y用(x,y)的形式列出所有的基本事件,其中(x,y)和(y,x)视为同一事件,并求|x﹣y|≤3或|x﹣y|≥9的概率.20.如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(1)求证:平面AEC⊥平面PDB;(2)当PD=AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.21.已知椭圆E:过点(0,),且离心率为.(1)求椭圆E的方程;(2)若以k(k≠0)为斜率的直线l与椭圆E相交于两个不同的点A,B,且线段AB的垂直平分线与两坐标轴围成的三角形面积为,求k的取值范围.22.已知函数f(x)=ln(x+a)﹣x2﹣x在x=0处取得极值.(1)求a的值;(2)求函数f(x)的单调区间;(3)若关于x的方程f(x)=﹣x+b在区间(0,2)有两个不等实根,求实数b的取值范围;(4)对于n∈N*,证明:.2016-2017学年黑龙江省大庆一中高二(下)第一次月考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|x2>1},N={﹣2,﹣1,0,1,2},则M∩N=()A.{0} B.{2} C.{﹣2,﹣1,1,2} D.{﹣2,2}【考点】1E:交集及其运算.【分析】求出M中不等式的解集确定出M,找出M与N的交集即可.【解答】解:由M中不等式解得:x>1或x<﹣1,即M={x|x<﹣1或x>1},∵N={﹣2,﹣1,0,1,2},∴M∩N={﹣2,2},故选:D.2.命题“∀x∈R,x2+1>0”的否定是()A.∀x∈R,x2+1≤0 B.∀x∈R,x2+1<0C.∃x0∈R,x02+1<0 D.∃x0∈R,x02+1≤0【考点】2J:命题的否定.【分析】本题中的命题是一个全称命题,其否定是一个特称命题,由规则写出否定命题即可.【解答】解:∵命题“∀x∈R,x2+1>0”∴命题“∀x∈R,x2+1>0”的否定是“∃x0∈R,x02+1≤0”故选:D.3.函数f(x)=x﹣sinx(x∈R),则f(x)()A.是奇函数,且在(﹣∞,+∞)上是减函数B.是偶函数,且在(﹣∞,+∞)上是减函数C.是偶函数,且在(﹣∞,+∞)上是增函数D.是奇函数,且在(﹣∞,+∞)上是增函数【考点】3N:奇偶性与单调性的综合.【分析】利用奇函数的定义,验证f(﹣x)=﹣x+sinx=﹣f(x),利用导数非负,确定函数f (x)=x﹣sinx(x∈R)在(﹣∞,+∞)上是增函数.【解答】解:∵f(﹣x)=﹣x﹣sin(﹣x)=﹣x+sinx=﹣(x﹣sinx)=﹣f(x),∴函数f(x)是奇函数.求导函数可得f′(x)=1﹣cosx.∵﹣1≤cosx≤1,∴f′(x)=1﹣cosx≥0.∴函数f(x)=x﹣sinx(x∈R)在(﹣∞,+∞)上是增函数.故选:D.4.运行如图所示的程序框图,则输出s的值为()A.﹣2 B.3 C.4 D.8【考点】EF:程序框图.【分析】会根据s←s+(﹣1)n n计算s的值及判断出当n←5时跳出循环结构,即可得出答案.【解答】解:∵n←1,s←1+(﹣1)1×1;∴n←2,s←0+(﹣1)2×2;∴n←3,s←2+(﹣1)3×3;∴n←4,s←﹣1+(﹣1)4×4;∴n←5,s←3+(﹣1)5×5.当n=6时,应跳出循环程序,并输出s的值是﹣2.故选A.5.已知双曲线﹣=1的一条渐近线方程为y=x,则此双曲线的离心率为()A.B.C.D.【考点】KC:双曲线的简单性质.【分析】因为焦点在 x轴上的双曲线方程的渐近线方程为y=±,由双曲线的一条渐近线方程为y=,就可得到含a,b的齐次式,再把b用a,c表示,根据双曲线的离心率e=,就可求出离心率的值.【解答】解:∵双曲线的焦点在x轴上,∴渐近线方程为y=±,又∵渐近线方程为y=,∴∴∵b2=c2﹣a2,∴化简得,即e2=,e=故选A6.已知函数f(x)=﹣x3+x2﹣ax+1是R上的单调递减函数,则实数a的取值范围为()A. C.[,+∞)D.(﹣∞,]【考点】6B:利用导数研究函数的单调性.【分析】求出f′(x),由题意f′(x)≤0在R上恒成立,利用二次函数的性质求出a的取值范围即可得到满足题意的a范围.【解答】解:f(x)=﹣x3+x2﹣ax+1,∴f′(x)=﹣3x2+2x﹣a,由题意f′(x)≤0在R上恒成立,∴△≤0,即4﹣4×3a≤0,解得:a≥,∴实数a的取值范围为[,+∞),故答案选:C.7.对于使f(x)≥N成立的所有常数N中,我们把N的最大值叫作f(x)的下确界.若a,b∈(0,+∞),且a+b=2,则+的下确界为()A.B.C.D.【考点】3H:函数的最值及其几何意义.【分析】理解题目所给的新定义,利用基本不等式求出+的最小值,即可求出+的下确界.【解答】解:因为a,b∈(0,+∞,且a+b=2,所以+=(a+b)(+)=()≥×=,当且仅当,即b=3a时,等号成立,所以+的下确界为,故选:B.8.区间上随机取一个数x,sin的值介于到1之间的概率为()A.B.C.D.【考点】CF:几何概型.【分析】求出0≤sin x≤的解集,根据几何概型的概率公式,即可求出对应的概率.【解答】解:当0≤x≤2,则0≤x≤π,由0≤sin x≤,∴0≤x≤,或≤x≤π,即0≤x≤,或≤x≤2,则sin x的值介于0到之间的概率P=;故选A.9.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n个这样的几何体拼成一个棱长为4的正方体,则V,n的值是()A.V=32,n=2 B.C.D.V=16,n=4【考点】L!:由三视图求面积、体积.【分析】由三视图可知,几何体为底面是正方形的四棱锥,再根据公式求解即可.【解答】解:由三视图可知,几何体为底面是正方形的四棱锥,所以V=,边长为4的正方体V=64,所以n=3.故选B10.已知向量=(,),=(cosx,sinx),=,且,则cos (x+)的值为( )A .﹣B .C .﹣D .【考点】GP :两角和与差的余弦函数;9R :平面向量数量积的运算.【分析】由平面向量的数量积和三角函数公式可得sin (x+),再由角的范围和同角三角函数基本关系可得.【解答】解:∵向量=(,),=(cosx ,sinx ),=,∴=cosx+sinx=2sin (x+)=,∴sin (x+)=,又∵,∴<x+<,∴cos (x+)=﹣=﹣,故选:A .11.直线x ﹣y+3=0被圆(x+2)2+(y ﹣2)2=2截得的弦长等于( )A .B .C .2D .【考点】JE :直线和圆的方程的应用.【分析】先根据点到直线的距离公式求出圆心到弦的距离即弦心距OD ,然后根据垂径定理得到垂足为弦长的中点D ,根据勾股定理求出弦长的一半BD ,乘以2即可求出弦长AB . 【解答】解:连接OB ,过O 作OD ⊥AB ,根据垂径定理得:D 为AB 的中点,根据(x+2)2+(y ﹣2)2=2得到圆心坐标为(﹣2,2),半径为.圆心O 到直线AB 的距离OD==,而半径OB=,则在直角三角形OBD 中根据勾股定理得BD==,所以AB=2BD=故选D .12.已知定义域为R的奇函数y=f(x)的导函数y=f′(x).当x≠0时,f′(x)+>0.若a=f(),b=﹣2f(﹣2),c=(ln)f(ln),则a、b、c的大小关系是()A.a<b<C B.b<c<a C.c<a<b D.a<c<b【考点】6B:利用导数研究函数的单调性.【分析】根据式子得出F(x)=xf(x)为R上的偶函数,利用f′(x)+>0.当x>0时,x•f′(x)+f(x)>0,当x<0时,x•f′(x)+f(x)<0,判断单调性即可证明a,b,c 的大小.【解答】解:∵定义域为R的奇函数y=f(x),∴F(x)=xf(x)为R上的偶函数,F′(x)=f(x)+xf′(x)∵当x≠0时,f′(x)+>0.∴当x>0时,x•f′(x)+f(x)>0,当x<0时,x•f′(x)+f(x)<0,即F(x)在(0,+∞)单调递增,在(﹣∞,0)单调递减.F()=a=f()=F(ln),F(﹣2)=b=﹣2f(﹣2)=F(2),F(ln)=c=(ln)f(ln)=F(ln2),∵ln<ln2<2,∴F(ln)<F(ln2)<F(2).即a<c<b故选:D二、填空题:本大题共4小题,每小题5分.13.抛物线y2=10x的焦点到准线的距离是 5 .【考点】K8:抛物线的简单性质.【分析】根据题中的抛物线方程并且结合抛物线的有关定义可得:焦点坐标为(,0),准线方程为x=,进而得到答案.【解答】解:由题意可得:抛物线的方程为y2=10x,所以根据抛物线的定义可得:焦点坐标为(,0),准线方程为x=,所以抛物线y2=10x的焦点到准线的距离是 5,.故答案为:5.14.已知在等差数列{a n}中,a1,a2017为方程x2﹣10x+16=0的两根,则a2+a1009+a2016的值为15 .【考点】8F:等差数列的性质.【分析】利用一元二次方程的根与系数的关系可得a1+a2017=10再利用等差数列的性质即可得出.【解答】解:∵a1,a2017为方程x2﹣10x+16=0的两根,∴a1+a2017=10=2a1009,∵数列{a n}是等差数列,则a2+a1009+a2016=3a1009=15.故答案为:15.15.已知f(x)=ax+b﹣1,若a,b都是从区间上任取的一个数,则f(2)<0成立的概率为.【考点】CF:几何概型.【分析】本题利用几何概型求解即可.在a﹣o﹣b坐标系中,画出f(2)<0对应的区域,和a、b都是在区间内表示的区域,计算它们的比值即得.【解答】解:f(2)=2a+b﹣1<0,即2a+b<1,如图,A(,0),B(0,1),S△ABO==,∴P==116.故答案为:.16.已知f(x)=2x2+x﹣k,g(x)=x3﹣3x,若对任意的x1∈,总存在x0∈,使得f(x1)≤g (x0)成立,则实数k的取值范围是k≥3 .【考点】2H:全称命题.【分析】对任意x1∈,x0∈,都有f(x1)≤g(x0)成立,即f(x)在区间上的最大值小于或等于g(x)的最大值,利用导数求g(x)的最大值,再由二次函数的最值求f(x)的最大值即可.【解答】解:若对任意x1∈,x0∈,都有f(x1)≤g(x0)成立,即f(x)在区间上的最大值都小于或等于g(x)的最大值,∵g(x)=x3﹣3x,∴g′(x)=3x2﹣3,令3x2﹣3=0,解得x=±1,当x∈(﹣1,1)时,g′(x)<0,g(x)单调递减,当x∈(1,3]时,g′(x)>0,g(x)单调递增,故当x=1时,函数g(x)取到极小值,也是该区间的最小值g(1)=﹣2,又g(﹣1)=2,g(3)=18.∴g(x)在上的最大值为18.而f(x)=2x2+x﹣k为开口向上的抛物线,对称轴为x=﹣,故当x=3时取最大值f(3)=21﹣k,由21﹣k≤18,解得k≥3.∴实数k的取值范围是k≥3.故答案为:k≥3.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知函数f(x)=lnx﹣ax.(Ⅰ)若函数f(x)在x=1处的切线与x轴平行,求a的值;(Ⅱ)若a=2,求函数f(x)在x=1处的切线方程;(Ⅲ)若a=1,请列出表格求函数f(x)的极大值.【考点】6D:利用导数研究函数的极值;6H:利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求出.由函数f(x)在x=1处的切线与x轴平行,利用导数的几何意义能求出a的值.(Ⅱ)当a=2时,f(x)=lnx﹣2x,f'(1)=ln1﹣2=﹣2,利用导数的几何意义能求出函数f (x)在x=1处的切线方程.(Ⅲ)当a=1时,f(x)=lnx﹣x,.令f'(x)=0,解得x=1,当x变化时,f'(x),f(x)的变化情况列表表示,由此能求出f(x)的极大值.【解答】解:(Ⅰ)∵f(x)=lnx﹣ax,∴f(x)的定义域为(0,+∞),.∵函数f(x)在x=1处的切线与x轴平行,∴f'(1)=1﹣a=0,解得a=1.(Ⅱ)当a=2时,f(x)=lnx﹣2x,∴f'(1)=ln1﹣2=﹣2,∴函数f(x)在x=1处的切点为(1,﹣2).∵,∴k=f'(1)=1﹣2=﹣1,∴函数f(x)在x=1处的切线方程为y﹣(﹣2)=﹣(x﹣1),即x+y+1=0.(Ⅲ)当a=1时,f(x)=lnx﹣x,.令f'(x)=0,解得x=1,当x变化时,f'(x),f(x)的变化情况如下:所以f(x)在x=1处取得极大值f(1)=﹣1.18.已知等差数列{a n}满足:a3=7,a5+a7=26.{a n}的前n项和为S n.(Ⅰ)求a n及S n;(Ⅱ)令b n=(n∈N*),求数列{b n}的前n项和T n.【考点】8E:数列的求和;84:等差数列的通项公式;85:等差数列的前n项和.【分析】(Ⅰ)设等差数列{a n}的公差为d,由于a3=7,a5+a7=26,可得,解得a1,d,利用等差数列的通项公式及其前n项和公式即可得出.(Ⅱ)由(I)可得b n==,利用“裂项求和”即可得出.【解答】解:(Ⅰ)设等差数列{a n}的公差为d,∵a3=7,a5+a7=26,∴,解得a1=3,d=2,∴a n=3+2(n﹣1)=2n+1;S n==n2+2n.(Ⅱ)===,∴T n===.19.某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100只白鼠,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100只白鼠的感染数,得到如下资料:(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为x,y用(x,y)的形式列出所有的基本事件,其中(x,y)和(y,x)视为同一事件,并求|x﹣y|≤3或|x﹣y|≥9的概率.【考点】CC:列举法计算基本事件数及事件发生的概率.【分析】(1)由已知利用平均数公式能求出这5天的平均感染数.(2)利用列举法求出基本事件总数n=10,设满足|x﹣y|≥9的事件为A,设满足|x﹣y|≤3的事件为B,利用列举法能求出|x﹣y|≤3或|x﹣y|≥9的概率.【解答】解:(1)由题意这5天的平均感染数为:.(2)(x,y)的取值情况有:(23,32),(23,24),(23,29),(23,17),(32,24),(32,29),(32,17),(24,29),(24,17),(29,17),基本事件总数n=10,设满足|x﹣y|≥9的事件为A,则事件A包含的基本事件为:(23,32),(32,17),(29,17),共有m=3个,∴P(A)=,设满足|x﹣y|≤3的事件为B,由事件B包含的基本事件为(23,24),(32,29),共有m′=2个,∴P(B)=,∴|x﹣y|≤3或|x﹣y|≥9的概率P=P(A)+P(B)=.20.如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(1)求证:平面AEC⊥平面PDB;(2)当PD=AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.【考点】LW:直线与平面垂直的判定;MI:直线与平面所成的角.【分析】(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.【解答】(Ⅰ)证明:∵四边形ABCD是正方形,∴AC⊥BD,∵PD⊥底面ABCD,∴PD⊥AC,∴AC⊥平面PDB,∴平面AEC⊥平面PDB.(Ⅱ)解:设AC∩BD=O,连接OE,由(Ⅰ)知AC⊥平面PDB于O,∴∠AEO为AE与平面PDB所的角,∴O,E分别为DB、PB的中点,∴OE∥PD,,又∵PD⊥底面ABCD,∴OE⊥底面ABCD,OE⊥AO,在Rt△AOE中,,∴∠AEO=45°,即AE与平面PDB所成的角的大小为45°.21.已知椭圆E:过点(0,),且离心率为.(1)求椭圆E的方程;(2)若以k(k≠0)为斜率的直线l与椭圆E相交于两个不同的点A,B,且线段AB的垂直平分线与两坐标轴围成的三角形面积为,求k的取值范围.【考点】K4:椭圆的简单性质.【分析】(1)运用椭圆的离心率公式和a,b,c的关系,即可得到椭圆方程;(2)设直线l的方程为y=kx+m(k≠0),A(x1,y1),B(x2,y2),联立方程,整理得(3+4k2)x2+8kmx+4m2﹣12=0,运用判别式大于0和韦达定理,以及中点坐标公式和两直线垂直的条件:斜率之积为﹣1,求得垂直平分线方程,求得与坐标轴的交点,可得三角形的面积,解不等式即可得到所求范围.【解答】解:(1)由题意可得b=,e==,a2﹣b2=c2,解得a=2,b=,c=1,∴椭圆E的方程为+=1;(II)设直线l的方程为y=kx+m(k≠0),A(x1,y1),B(x2,y2),联立方程,整理得(3+4k2)x2+8kmx+4m2﹣12=0,此方程有两个不等实根,可得△=(8km)2﹣4(3+4k2)(4m2﹣12)>0,整理得3+4k2﹣m2>0 ①.由根与系数的关系,可得线段AB的中点坐标(x0,y0)满足x0==﹣,y0=kx0+m=,∴AB的垂直平分线方程为y﹣=﹣(x+).此直线与x轴、y轴的交点坐标分别为(﹣,0),(0,﹣),由已知得||•||=.整理得m2=,k≠0 ②将②代入①得4k2﹣+3>0,整理得(3+4k2)(4k2﹣8|k|+3)<0,k≠0,解得<|k|<,所以k的取值范围为(﹣,﹣)∪(,).22.已知函数f(x)=ln(x+a)﹣x2﹣x在x=0处取得极值.(1)求a的值;(2)求函数f(x)的单调区间;(3)若关于x的方程f(x)=﹣x+b在区间(0,2)有两个不等实根,求实数b的取值范围;(4)对于n∈N*,证明:.【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性.【分析】(1)由函数f(x在x=0处取得极值,则有f'(x)=0,从而求解;(2)由由f'(x)>0得增区间;由f'(x)<0得减区间;(3)将方程f(x)=﹣x+b转化为g(x)=f(x)﹣(﹣x+b),利用根的分布求解;(4)由(2)可知当x≥0时ln(x+1)≤x2+x(当且仅当x=0时等号成立),可得到ln<,求得前n项不等式,采用累加法及对数函数的性质,即可证明不等式成立.【解答】解:(1)由已知得f′(x)=﹣2x﹣1=,∵f'(x)=0,∴=0∴a=1,(2)由(1)得f′(x)=,(x>﹣1)由f'(x)>0得﹣1<x<0,由f'(x)<0得x>0,∴f(x)的单调递增区间为(﹣1,0),单调递减区间为(0,+∞);(3)令g(x)=f(x)﹣(﹣x+b)=ln(x+1)﹣x2+x﹣b,x∈(0,2)则g′(x)=﹣2x+=﹣,令g'(x)=0得x=1或x=﹣(舍),当0<x<1时g'(x)>0,当1<x<2时g'(x)<0,即g(x)在(0,1)上递增,在(1,2)上递减,方程f(x)=﹣x+b在区间(0,2)上有两个不等实根,等价于函数g(x)在(0,2)上有两个不同的零点,∴⇒⇒,∴ln3﹣1<b<ln2+,即实数b的取值范围为ln3﹣1<b<ln2+;(4)由(2)可得,证明:(3)由(1)可得,当x≥0时ln(x+1)≤x2+x(当且仅当x=0时等号成立),设x=,则ln(1+)<+,即ln<①,∴>ln,>ln,>ln,…,>ln,将上面n个式子相加得: +++…+>ln+ln+ln+…+ln =ln(n+1),故:.。
黑龙江省大庆十中2018-2019高二下学期第一次月考数学(理)试卷附答案

大庆十中2018-2019高二下学期第一次月考数学(理)试卷(时间:120分钟 满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(本大题共12小题,每小题5分,共60分) 1.若函数,则( )A .B .C .D . 2.复数i i+-321等于( ) A .1075i - B .1071i + C .871i - D .1071i -3.已知函数的导函数的图象如图所示,则的图象可能是( )A .B .C .D .4.设复数 (i 是虚数单位),则复数 的虚部是( )A .B .C .D .5.是虚数单位,复数在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限6. 设()[]]⎪⎩⎪⎨⎧∈∈=e x xx x x f ,1(,11,0, ,则dx x f e⎰)( 的值为A .3B .23 C .21D .2 7.过函数图象上点O (0,0)作切线,则切线方程为 ( ) A .B .C .D .8.函数()22ln f x x x =-的递增区间是( ).A .10,2⎛⎫ ⎪⎝⎭ B .11,0,,22⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭ C .1,2⎛⎫+∞ ⎪⎝⎭ D .11,,0,22⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭9.由抛物线与直线所围成的图形的面积是( ).A .4B .C .5D .10.函数在内有极小值,则实数的取值范围是( )A .B .C .D .11.已知ax x x f -=3)(在(-∞,-1)上单调递增,则a 的取值范围是( )A .a <3B .a ≤3C .a >3D .a ≥312.设函数有两个极值点,则实数的取值范围是( )A .B .C .D .第II 卷(非选择题)二、填空题(本大题共4小题,每小题5分,共20分) 13.定积分的值为__________.14.函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a = .15.已知点P ()2,2在曲线3y ax bx =+上,如果该曲线在点P 处切线的斜率为9,那么ab =____________.16.设,当时,恒成立,则实数的取值范围为 。
黑龙江省大庆市第十中学高二数学下学期第一次月考试题 理

黑龙江省大庆市第十中学2017-2018学年高二数学下学期第一次月考试题 理(时间:120分钟 满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(本大题共12小题,每小题5分,共60分)1.函数x x f sin 1)(+=,其导数是)('x f ,则)3('πf 的值为( )A:21-B :21C :23- D :232.函数x x x f +=3)(在1=x 处的切线方程是( )A: 024=+-y x B :024=--y x C :024=++y x D :024=-+y x 3.已知)2,0,1(λλ+=→a ,)2,12,6(-=→μb ,→→b a //,则λ和μ的值分别是( )A:21,51 B :2,5 C :21,51-- D :2,5-- 4.设函数)(x f y =可导,则xx f x x f x ∆-∆+→∆)()3(lim 0=( )A: )('x f B :3)('x f C :)(31'x f D :以上答案都不对5.直三棱柱111C B A ABC -中,若→→=a CA ,→→=b CB ,→→=c CC 1,则=→B A 1( ) A: →→→-+c b a B :→→→+-c b a C :→→→++-c b a D :→→→-+-c b a 6.已知x xf x x f ln 2018)2018(221)('2-+=,则)2018('f =( ) A:2017 B :2017- C :2018 D :2018- 7.函数xxx f ln )(=,则( ) A: e x =是函数)(x f 的极大值点 B :e x =是函数)(x f 的极小值点 C :e x 1=是函数)(x f 的极大值点 D :ex 1=是函数)(x f 的极小值点 8.正方体1111D C B A ABCD -中,F E ,分别是111,CC D C 的中点,则异面直线AE 与B F 所成角的余弦值是( ) A:1865-B :55-C :56D :5529.函数)(x f y =的导函数)('x f 的图象如下图所示,则下列说法正确的是( )A :函数)(x f y =在)0,(-∞上单调递增B ::函数)(x f y =的单调递减区间为)5,3( C:函数)(x f y =在0=x 处取得极大值 D :函数)(x f y =在5=x 处取得极小值(9题图) (11题图)10.若函数13)(3+-=bx x x f 在区间)2,1(内是减函数,R b ∈,则( ) A:4≤b B :4<b C :4≥b D :4>b 11. 如上图,以等腰直角三角形斜边BC 上的高AD 为折痕,把ABD ∆和ACD ∆折成互相垂直的两个平面后,某个学生得出下列四个结论,其中正确的是( )①0≠⋅→→AC BD ;②ο60=∠BAC ;③三棱锥ABC D -是正三棱锥;④平面ADC 的法向量与平面ABC 的法向量互相垂直;A: ①② B :③④ C :②③ D :①④ 12.函数)(x f 的定义域为R ,2018)2(=-f ,对R x ∈∀,都有x x f 2)('<成立,则不等式2014)(2+<x x f 的解集为( )A: )2,(-∞ B :),2(+∞- C :)2,2(- D :),2(+∞第II 卷(非选择题)二、填空题(本大题共4小题,每小题5分,共20分)13.已知向量)0,1,1(=→a ,)1,0,1(-=→b ,且→→+b a k 与→a 互相垂直,则=k ______________ 14. 在空间直角坐标系中,已知)1,3,1(),2,0,1(-B A ,若点M 在y 上,且MB MA =,则M 点坐标是_____________15.曲线x y ln 2=上的点到直线032=+-y x 的最短距离是____________ 16.函数2)()(c x x x f -=在2=x 处有极大值,则c 的值为___________ 三、解答题(本大题共6小题,共70分) 17.(10分)(1已知函数x x x f ln )(2-=。
2018-2019学年黑龙江省高中学业水平测试数学试题 Word版

2018年黑龙江省高中学业水平测试数学试题(试题总分:150分 答题时间:120分钟)命题人:于连祉 审核人:孙德军 校对人:张丽华 温馨提示:沉着应对,冷静作答,成功属于自信的你一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知直线l 的方程为1y +-=x ,则直线l 的倾斜角为( ) A .4πB.3πC.43π D.6π 2.已知直线02-x :m =-y a 和直线01)2(:=+-+y x a n 相互垂直,则实数a 的值为( )A 0B -1C 1D 23.过点)3,1(p 且在x 轴上的截距和在y 轴上的截距相等的直线方程为( ) A 04=-+y x B 03或04=+=-+y x y x C 0x 3=-y D 03或04=-=-+y x y x4.点A (2a ,a -1)在以点C (0,1)为圆心,半径为5的圆上,则a 的值为( ) A 1或-1 B 0或1 C -1或51 D -51或1 5.圆心在x 轴上,半径为1,且过点(2,1)的圆的方程是( ) A ()()13122=-+-y x B ()1222=+-y xC ()1222=-+y x D ()1222=++y x6.过点P (-2,4)作圆C:()()03:直线,的切线251222=-=-+-y ax m l y x 与直线m l l 与平行,则直线的距离为( ) A512 B 58C 4D 27. 已知椭圆的中心为坐标原点,一个焦点为()0,3-,长轴长是短轴长的2倍,则这个椭圆的标准方程为( ) A1422=+yx B 13x 22=+yC 14x 22=+y D 1322=+y x8.如果双曲线112422=-y x 上一点P 到它的右焦点的距离是8,那么点P 到它的左焦点的距离是( )A 4B 12C 6D 4或12 9.设∈≠a a ,0R ,则抛物线24ax y =的焦点坐标为( ) A (a,0) B (0,a) C (0,a161) D 随a 的符号而定 10.若双曲线()0,0,12222 b a b y a x =-的离心率为3,则其渐近线的斜率为( )A 2±B 2±C 22±D 21±11.若一个椭圆中心在原点,焦点)3,2(轴上,在F ,F 21P x 是椭圆上一点,且2211PF ,F F ,PF 成等差数列,则椭圆方程为( )A16822=+y x B14822=+y xC161622=+y x D141622=+y x12.设椭圆()012222>>=+n m ny m x 的右焦点与抛物线x y 82=的焦点相同,椭圆的离心率为21,则此椭圆方程为( )A1161222=+y x B1121622=+y xC1644822=+y x D1486422=+y x二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中横线上)13.已知()()m m B m ,2,1,1A 2+-+,若直线AB 与斜率为2的直线平行,则m 的值为14.若两圆01186和2222=--++=+y x y x m y x 有公共点,则实数m 的取值范围为15.若椭圆的焦距,短轴长,长轴长构成一个等比数列,则椭圆的离心率为16.已知双曲线1922=-ay x 的右焦点为()0,13,则该双曲线的渐近线方程为三、解答题(本大题共4小题,共40分,解答应写出文字说明、证明过程或演算步骤)17.(12分)求满足下列条件的直线的一般方程(1)经过点A (-1,-3),且斜率等于0183=-+y x 的斜率的2倍。
黑龙江大庆实验中学18-19学度高二下开学考试-数学(文)

黑龙江大庆实验中学18-19学度高二下开学考试-数学(文)一.选择题:本大题共12小题,每题5分,在每题给同的四个选项中,只有一项为哪一项符合题目要求的. 1、在等差数列{}n a 中,假设4566a a a ++=,那么该数列的前9项的和为〔 〕 A 、17B 、18C 、19D 、20 2、点()1,1-到直线10x y -+=的距离为〔 〕 A 、12B 、32CD3、角θ的终边过点P(-4k ,3k ) (0<k ), 那么θ+θcos sin 2的值是〔 〕A 、52 B 、 52或52- C 、52- D 、以上都不对4. 函数2cos y x x=+在π02⎡⎤⎢⎥⎣⎦,上取最大值时,x的值为〔 〕 A、0B、π6C、π3D、π25、4张卡片上分别写有数字1、2、3、4,从这4张卡片中随机抽取2张,那么取出的2张卡片上的数字之和为奇数的概率为 〔 〕 A.13B.12C.23D.34〔〕 A 、假设,//,a M a N M N ⊥⊥则 B 、假设//,,M a M b a ⊥⊥则bC 、假设//,//,//a M b M a b 则D 、假设,,,a M b M l a l b ⊂⊂⊥⊥且,那么l M ⊥ 7、βα,均为锐角,假设:sin sin(),:,2p q p qπααβαβ<++<则是的〔〕A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分也不必要条件12、在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[k],即[k]={5n+k|n∈Z},k=0,1,2,3,4、给出如下四个结论:①2017∈[1];②-3∈[3];③z=[0]∪[1]∪[2]∪[3]∪[4]; ④“整数a ,b 属于同一‘类”的充要条件是“a-b ∈[0]” 其中,正确结论的个数是〔〕 A 、1 B 、2 C 、3 D 、4 二、填空题:本大题共4小题,每题5分13.数据x 1,x 2,…,x 8的平均数为6,标准差为2,那么数据2x 1-6,2x 2-6,…,2x 8-6的方差为_________. 14、sin2α=34,32ππα<<,那么sin α+cos α的值为15、函数()y f x =的图象在点(1(1))M f ,处的切线方程是122y x =+,那么(1)(1)f f '+= 16、过抛物线x y 42=的焦点作直线,与抛物线交于B A ,两点,C 为准线上一点,假设直线AC 与直线BC 的斜率之和为2-,那么点C 的坐标为___________ 【三】解答题:解承诺写出文字说明,证明过程或演算步骤 17、(本小题总分值10分)设命题2:(43)1;p x -≤命题2:(21)(1)0,q x a x a a -+++≤假设p 是q 的充分不必要条件,求实数a 的取值范围. 18、〔本小题总分值12分〕在锐角三角形中,边a 、b 是方程x 2-2 3 x+2=0的两根,角A 、B 满足: 2sin(A+B)- 3 =0,求角C 的度数,边c 的长度及△ABC 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年度第二学期高二数学(理科)第一次月考试题(时间:120分钟 满分:150分)注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(本大题共12小题,每小题5分,共60分) 1.若函数,则( )A .B .C .D . 2.复数i i+-321等于( ) A .1075i - B .1071i + C .871i - D .1071i -3.已知函数的导函数的图象如图所示,则的图象可能是( )A .B .C .D .4.设复数 (i 是虚数单位),则复数 的虚部是( )A .B .C .D .5.是虚数单位,复数在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限6. 设()[]]⎪⎩⎪⎨⎧∈∈=e x xx x x f ,1(,11,0, ,则dx x f e⎰)(的值为A .3B .23 C .21D .2 7.过函数图象上点O (0,0)作切线,则切线方程为 ( ) A .B .C .D .8.函数()22ln f x x x =-的递增区间是( ).A .10,2⎛⎫ ⎪⎝⎭B .11,0,,22⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭C .1,2⎛⎫+∞ ⎪⎝⎭D .11,,0,22⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭9.由抛物线与直线所围成的图形的面积是( ).A .4B .C .5D . 10.函数在内有极小值,则实数的取值范围是( ) A .B .C .D .11.已知ax x x f -=3)(在(-∞,-1)上单调递增,则a 的取值范围是( )A .a <3B .a ≤3C .a >3D .a ≥3 12.设函数有两个极值点,则实数的取值范围是( )A .B .C .D .第II 卷(非选择题)二、填空题(本大题共4小题,每小题5分,共20分) 13.定积分的值为__________.14.函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a = . 15.已知点P ()2,2在曲线3y ax bx =+上,如果该曲线在点P 处切线的斜率为9,那么ab =____________.16.设,当时,恒成立,则实数的取值范围为 。
三、解答题(本大题共6小题,共70分;其中17题10分,其他每道大题12分)17.实数m 取什么数值时,复数分别是:(1)实数? (2)虚数? (3)纯虚数?18.已知函数()32f x x ax bx c =+++在1x =-与2x =处都取得极值. (1)求,a b 的值;(2)求函数()f x 的单调区间。
19.己知函数.( I)求函数f(x)的极值;(II)求函数f(x)在[0,2]上的最大值。
20.设函数()ln f x x a x =-(其中a R ∈).(Ⅰ)当1a =时,求函数()f x 在1x =时的切线方程; (Ⅱ)求函数()f x 的极值. 21.设 (1)求的最小值;(2)证明:.22.已知函数,其中.(1)当时,求曲线在点处的切线方程;(2)记的导函数为,若不等式在区间上恒成立,求的取值范围;参考答案1.B【解析】试题分析:因为,所以则.故选B.考点:导数的基本运算. 2.D 【解析】 试题分析:()()()()123121733310i i i ii i i ----==++-.考点:复数的运算. 3.D【解析】观察可知导函数图像由正变负,则原函数应先递增,后递减,故选择D. 方法点睛:辨识函数图像与导数图像主要是依据利用导数研究函数的单调性,当函数在区间上满足,则在区间上单调递增,当函数在区间上满足,则在区间上单调递减.4.A 【解析】由,得,故其虚部为,故选A.5.C【解析】分析:首先根据复数的运算法则,分子和分母同时乘以分母的共轭复数,将其化简,从而得到复数的实部和虚部,之后借助于其在复平面内对应的点的坐标的符号判断得出结果.详解:因为,所以该复数在复平面内对应的点的坐标为,所以该复数在复平面内对应的点在第三象限,故选C.点睛:该题考查的是有关复数的概念和计算,以及复数在复平面内对应的点的坐标的形式,从而求得结果,属于基础题. 6.B【解析】解:因为()[]]⎪⎩⎪⎨⎧∈∈=e x x x x x f ,1(,11,0,,则e 1e00113f (x)dx xdx dx x 2=+=⎰⎰⎰,选B7.A【解析】函数,导函数,时,,所求切线斜率为,所求切线方程为,故选A.【方法点晴】本题主要考查利用导数求曲线切线方程,属于难题.求曲线切线方程的一般步骤是:(1)求出在处的导数,即在点出的切线斜率(当曲线在处的切线与轴平行时,在 处导数不存在,切线方程为);(2)由点斜式求得切线方程.8.C【解析】解:因为()()()22121141'4x x x f x x x x x-+-=-==,因为x>0那么利用导数的正号和负号,就可以判定单调增区间即为使得导数大于零的解集1,2⎛⎫+∞ ⎪⎝⎭。
9.B【解析】分析:先把直线方程和抛物线方程联立求得交点坐标,进而用定积分的知识求得图中阴影部分的面积.详解:解得x=1,y=﹣1或x=4,y=2,即交点坐标为(1,﹣1),(4,2)∴图中阴影部分的面积是.故选:B .点睛:本题主要利用定积分计算曲边图象的面积,属于基础题.10.D【解析】试题分析:,当,所以函数单调递增,,所以函数单调递减,,所以函数单调递增,所以函数的极小值点为,解得考点:本题考查极值问题点评:解决本题的关键是求导判断单调性先增再减再增,求得极小值点11.B【解析】试题分析:先求函数f(x)的导数,然后根据f'(x)=3x2-a≥0在R上恒成立即可得到答案.解:∵f(x)=x3-ax∴f'(x)=3x2-a,∵f(x)在R上单调递增∴f'(x)=3x2-a≥0在R上恒成立即a≤3x2在(-∞,-1)上恒成立,a小于等于3x2的最小值即可∴a 3,故选B考点:利用导数研究函数的单调性点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.12.B【解析】【分析】先求得函数的定义域,对函数求导,利用其导函数有两个零点,结合判别式以及二次函数的零点分布情况,求得的取值范围.【详解】的定义域为.,令其分子为,在区间上有两个零点,故,解得,故选B.【点睛】本小题主要考查已知函数的极值点个数来求解析式中参数的取值范围,考查二次函数零点分布有关问题的求解策略.属于中档题.有关函数极值点问题,首先要求得函数的定义域,在定义域的范围内来研究.对函数求导并通分后,根据通分后所得二次函数中所含参数的位置,结合二次函数对称轴以及零点位置,来求得参数的取值范围.13.【解析】根据定积分的定义知,,故填.14.5 【解析】略 15.3-【解析】3y ax bx =+求导得: 2'3y ax b =+ 根据题意有: 129{ 822a b a b +=+=,解得1{ 3a b ==-.所以3ab =-.点睛:求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出切点()00,P x y 及斜率,其求法为:设()00,P x y 是曲线()y f x =上的一点,则以P 的切点的切线方程为: ()()000'y y f x x x -=-.若曲线()y f x =在点()()00,P x f x 的切线平行于y 轴(即导数不存在)时,由切线定义知,切线方程为0x x =. 16.【解析】试题分析:∵,∴2()32f x x x '=--,根据导数知识易求时,,又当时,恒成立,∴max ()7m f x >=考点:本题考查了导数的运用点评:解决此类问题通常有以下两种思路;max)]([)(x f m D x x f m ≥⇔∈≥上恒成立在min )]([)(x f m D x x f m ≤⇔∈≤上恒成立在 17.(1);(2);(3).【解析】本试题主要是考查了复数的概念的运用。
先求解实数和虚数以及纯虚数的前提下各个参数m 的取值问题。
注意虚数虚部不为零,虚部为零是实数,实部为零,虚部不为零是纯虚数,因此可知结论。
解:(1)当,即时,复数z 是实数;……4分 (2)当,即时,复数z 是虚数;……8分 (3)当,且时,即时,复数z 是纯虚数.…12分18.(1)3{26a b =-=-, ()f x 的减区间为()1,2-,增区间为(),1-∞-, ()2,+∞;试题解析:(1)()232f x x ax b =++',由题意得: ()()10{20f f ''-==即320{1240a b a b -+=++=,解得3{26a b =-=-∴()32362f x x x x c =--+, ()2336f x x x '=--. 令()0f x '<,解得12x -<<,令()0f x '>,解得1x <-或2x >∴()f x 的减区间为()1,2-,增区间为(),1-∞-, ()2,+∞. 19.(I )极大值,极小值;(II )最大值【解析】分析:( I) 求导数得到函数的单调性,然后可得极值.(II)结合函数的单调性求得在区间[0,2]上的极值和端点处的函数值可得结论. 详解:( I)∵, ∴,∴当时,单调递增, 当时,单调递减, 当时,单调递增.∴当时,有极大值,且极大值为; 当时,有极小值,且极小值为.(II )由( I)知,在上单调递减,在上单调递增,又∴在[0,2]最大值为.点睛:求函数的极值时首先要判断出函数的单调性,结合单调性可得到函数的极值;求最值时也要在函数单调性的基础上,通过求出函数的极值和区间的端点值,比较大小后可得所求.20.(1)1y =(2)当0a ≤时,函数()f x 无极值,当0a >时,函数()f x 在x a =处取得极小值ln a a a -,无极大值.【解析】试题分析: ()1将1a =代入,算出1x =时的切线方程()2求导,讨论当0a ≤时、当0a >时的极值情况 解析:(Ⅰ)定义域为()0,+∞,1a =时, ()ln f x x x =-,()11f x x'=-,()11101f =-=', ()11ln11f =-=,所以切线方程为1y =;(Ⅱ)()1a x a f x x x'-=-=,定义域为()0,+∞, ①当0a ≤时, ()0f x '>,函数()f x 在()0,+∞上为增函数,此时函数()f x 无极值; ②当0a >时,令()0f x '=,解得x a =,当()0,x a ∈时, ()0f x '<,当(),x a ∈+∞时, ()0f x '>,所以函数()f x 在x a =处取得极小值,且极小值为()ln f a a a a =-,无极大值, 综上,当0a ≤时,函数()f x 无极值,当0a >时,函数()f x 在x a =处取得极小值ln a a a -,无极大值.21.(1)见解析;(2)见解析【解析】【分析】(1)由题意,求得,利用导数得到函数的单调性,进而求解函数的最小值;(2)由,令, 利用导数求得函数的单调性,求得函数的最小值,即可得到证明.【详解】(1) 所以当x ∈(0,)时,<0,f(x)单调递减; 当x ∈(,+∞)时,>0,f(x)单调递增.所以x=时,f(x)取得最小值f()=1-.(2)x2-x++2lnx-f(x)=x(x-1)--2(x-1)lnx=(x-1)(x--2lnx),令g(x)=x--2lnx,则=1+-=≥0,所以g(x)在(0,+∞)上单调递增,又因为g(1)=0,所以当0<x<1时,g(x)<0;当x>1时,g(x)>0,所以(x-1)(x--2lnx)≥0,即f(x)≤x2-x++2lnx.【点睛】本题主要考查导数在函数中的应用,以及不等式的证明,着重考查了转化与化归思想、逻辑推理能力与计算能力,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,求解曲线在某点处的切线方程;(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数;(3)利用导数求函数的最值(极值),解决函数的恒成立与有解问题,同时注意数形结合思想的应用.22.(1);(2);(3)【解析】【分析】(1)当时,得到函数的解析式,求得,求得的值得出直线的斜率,利用到时几何意义,即可求解切线的方程;(2)依题意,不等式在区间上恒成立,即对任意实数恒成立,令,分类讨论得到函数的单调性和最值,即可求解;【详解】(1)当时, (其中),所以,,.所以,曲线在点处的切线方程为,即.(2)由,得().依题意,知对任意实数恒成立,即对任意实数恒成立.令(),所以.()①当时,,此时函数在上单调递增,所以,所以,时,符合题意.②当时,令,得 (舍去).所以,当时,,此时函数在单调递减,所以,此与题意相矛盾,所以,不符合题意.综上所述,所求实数的取值范围是.【点睛】本题主要考查导数在函数中的应用,以及不等式恒成立问题的求解,着重考查了转化与化归思想、逻辑推理能力与计算能力,对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,求解曲线在某点处的切线方程;(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数;(3)利用导数求函数的最值(极值),解决函数的恒成立与有解问题,同时注意数形结合思想的应用.。
