测试技术(第二版)_贾民平_习题答案
《测试技术》(第二版)课后习题答案贾民平

电桥输入与输出信号的频谱图如下图所示。
本量题也可用三角函数的积化和差公式来计算:
[注:
解:调幅波中所包含的各分量的频率及幅值大小:
调制信号与调幅波的频谱分别如下图所示。
解:
1)各环节输出信号的时域波形图如下:
2)各环节输出信号的频谱图
信号的调制:
输入/输出自功率谱密度函数与系统频率响应函数关系
单输入、单输出的理想线性系统
解:fn=800Hz, =0.14, f=400
解:
由
得
解:
由Su=U0/a , Sq=Q/a 得:Su/ Sq=U0/Q=
第五章 习 题(
解: (1)半桥单臂
(2)半桥双臂
半桥双臂是半桥单臂灵敏度的两倍。
解:均不能提高灵敏度,因为半桥双臂灵敏度 ,与供桥电压成正比,与桥臂上应变片数无关。
解:
得电桥输入和输出信号的傅里叶变换:
当x=0时,
(10)自(互)相关函数、相关系数
相关系数
自相关函数的性质:
自相关函数为实偶函数
周期函数的自相关函数仍为同频率的周期函数
互相关函数
随机信号的自功率谱密度函数(自谱)为:
其逆变换为
两随机信号的互功率谱密度函数(互谱)为:
其逆变换为
自功率谱密度函数和幅值谱 或能谱之间的关系
自功率谱密度 与幅值谱 及系统频率响应函数H(f)的关系
而在h高度处温度计所记录的温度t‘=A( )t=A( )(t0-h*0.15/30)
由于在3000m高度温度计所记录的温度为-1℃,所以有
-1=A( )(t0-3000*0.15/30)
求得t0=-0.75℃
《测试技术》(第二版)课后习题标准答案--

解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:T 0/2-T 0/21x (t ) t. . . . . .⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:故有)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ 0ωA (ω)ω0 3ω0 5ω0 0ωω0 3ω0 5ω0 ϕ (ω)24π294π2254π 21 2π C 0 =a 0C N =(a n -jb n )/2 C -N =(a n +jb n )/2 R e C N =a n /2 I m C N =-b n /2)(212122000n n n e n m n n n n n a barctg C R C I arctg A b a C a A C -===+===φ R e C N =a n /2⎪⎩⎪⎨⎧====,6,4,20,5,3,122sin 222222n n n n n πππI m C N =-b n /2 =0单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π 21 292π2252π5ω0 -ω0 -3ω0 292π2252π-5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωR e C nω03ω0 22π21 292π2252π 5ω0 -ω0 -3ω0 292π 2252π-5ω0 22π虚频谱双边相频谱实频谱双边幅频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
《测试技术》(第二版)课后习题答案

解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
测试技术 第二版 习题答案 完整版 贾民平 吐血拼整

绪论1 .举例说明什么是测试?答:(1) 测试例子:为了确定一端固定的悬臂梁的固有频率,我们可以采用锤击法对梁进行激振,再利用压电传感器、电荷放大器、波形记录器记录信号波形,由衰减的振荡波形便可以计算出悬臂梁的固有频率。
(2)结论:由本例可知:测试是指确定被测对象悬臂梁的属性—固有频率的全部操作,是通过一定的技术手段—激振、拾振、记录、数据处理等,获取悬臂梁固有频率的信息的过程。
2. 测试技术的任务是什么?答:测试技术的任务主要有:通过模型试验或现场实测,提高产品质量;通过测试,进行设备强度校验,提高产量和质量;监测环境振动和噪声,找振源,以便采取减振、防噪措施;通过测试,发现新的定律、公式等;通过测试和数据采集,实现对设备的状态监测、质量控制和故障诊断。
3. 以方框图的形式说明测试系统的组成,简述主要部分的作用。
(1)测试系统方框图如下:(2)各部分的作用如下:传感器是将被测信息转换成某种电信号的器件;信号的调理是把来自传感器的信号转换成适合传输和处理的形式;信号处理环节可对来自信号调理环节的信号,进行各种运算、滤波和分析;信号显示、记录环节将来自信号处理环节的信号显示或存贮。
模数(A/D)转换和数模(D/A)转换是进行模拟信号与数字信号相互转换,以便用计算机处理。
4.测试技术的发展动向是什么?传感器向新型、微型、智能型方向发展;测试仪器向高精度、多功能、小型化、在线监测、性能标准化和低价格发展;参数测量与数据处理向计算机为核心发展;第一章1 求周期方波的傅立叶级数(复指数函数形式),画出|c n|-w和j-w图。
解:(1)方波的时域描述为:(2) 从而:2 . 求正弦信号的绝对均值和均方根值。
解(1)(2)3.求符号函数和单位阶跃函数的频谱。
解:(1)因为不满足绝对可积条件,因此,可以把符合函数看作为双边指数衰减函数:其傅里叶变换为:(2)阶跃函数:4. 求被截断的余弦函数的傅里叶变换。
解:(1)被截断的余弦函数可以看成为:余弦函数与矩形窗的点积,即:(2)根据卷积定理,其傅里叶变换为:5.设有一时间函数f(t)与其频谱如图所示。
(整理)测试技术(第二版)贾民平习题答案

测试技术与信号处理习题解答授课教师:陈杰来第一章 习 题(P29)解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(100000000000002020000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(0000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
《测试技术》(第二版)课后习题答案-_.

解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:T 0/2-T 0/21x (t ) t. . . . . .⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:故有)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ 0ωA (ω)ω0 3ω0 5ω0 0ωω0 3ω0 5ω0 ϕ (ω)24π294π2254π21 2π C 0 =a 0C N =(a n -jb n )/2 C -N =(a n +jb n )/2 R e C N =a n /2 I m C N =-b n /2)(212122000n n n e n m n nn n n a barctg C R C I arctg A b a C a A C -===+===φ R e C N =a n /2⎪⎩⎪⎨⎧====,6,4,20,5,3,122sin 222222n n n n n πππI m C N =-b n /2 =0单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π 21 292π2252π5ω0 -ω0 -3ω0 292π 2252π-5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωR e C nω03ω0 22π21 292π2252π 5ω0 -ω0 -3ω0 292π 2252π-5ω0 22π虚频谱双边相频谱实频谱双边幅频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
测试技术)贾民平_习题答案

1 T0
0
∫
/2
T0
0
x (t ) dt
T0
1 T [ T0 ∫0
sin 2π f 0 dt + ∫
T0 / 2 0
T0 / 2
( − sin 2π f 0 ) dt ]
T0 T0 / 2
1 [ − cos 2π f 0 t T0 = 2 /π
+ cos 2π f 0 t
]
2 ψx = ( x rms ) 2 =
2 T0
2 t )]} T0
0 − T0 / 2
−1 2 {[ − 1 + j 2πf T0
∫
T0 / 2
0
e − j 2 π ft dt ] + [1 −
T0 / 2 0
∫
]
e − j 2π ft dt ]}
−2 −1 ⋅ [e − j 2 π ft j 2πfT0 j 2π f
− e − j 2 π ft
1 T0
∫
T0
0
x 2 (t ) dt
= = =
1 T0
∫
T0
0
sin 2 2πf 0t dt
T0
1 2T 0
∫
0
(1 − cos 4 πf 0 t ) dt
T0 0
1 1 ( T0 − sin 4 πf 0t 2T 0 4 πf 0
)
=1/ 2
11
第二章
=
习
题( P68)
解: Ψ 2 = R (0 ) = lim( 60 ) sin(50τ ) = lim 3000( sin 50τ ) = 3000 x x
=
ω0 a 2 + ω0 − ω 2 + j 2aω
贾民平主编 测试技术_第二版 第二章 2-2
测试技术与信号处理
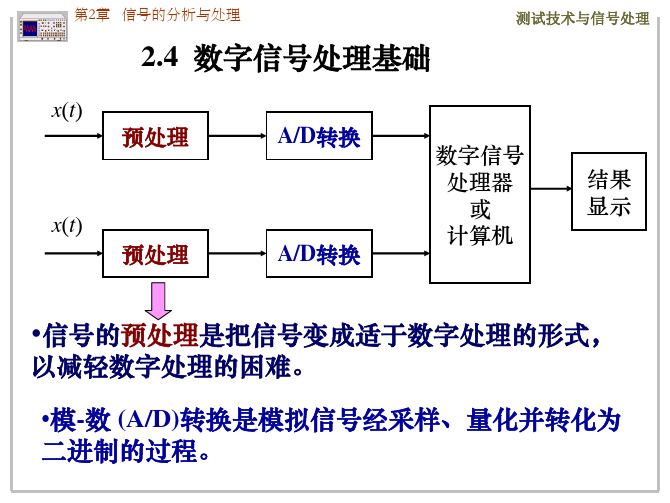
2.4 数字信号处理基础
x(t) 预处理 A/D转换 数字信号 处理器 或 计算机
x(t) 预处理 A/D转换
结果 显示
•信号的预处理是把信号变成适于数字处理的形式, 以减轻数字处理的困难。 •模-数 (A/D)转换是模拟信号经采样、量化并转化为 二进制的过程。
x(t) w(t) 0 s2(t) -T 0 T [x(t) w(t)]* s2(t) 0 T t -f0
0
f0
f
S2(f ) 0 [X(f )*W(f )] S2(f ) f
T
-f0
0
f0
f
频域采样
测试技术与信号处理
经频域采样后的频谱仅在各采样点上存在,而非采样 点的频谱则被“挡住”无法显示(视为0),这种现 象称为栅栏效应。显然,采样必然带来栅栏效应。 •在时域,只要满足采样定理,栅栏效应不会丢失信 号信息 •在频域,则有可能丢失重要的或具有特征的频率成 分(由于泄漏,丢失频率成分附近的频率有可能存 在),导致谱分析结果失去意义。
1 Ts f s 1 f N N T
测试技术与信号处理
由于谱线是离散的,因此频谱谱线对应的频率值都是 f 整数倍。对于简谐信号,为了得到特定频率 f0的谱 线,必须满足
f0 整数 f
T 整数 T0
T:信号分析时长;T0:频率为 f0 信号的周期。 上式表明:只有信号的截断长度T为待分析信号周 期的整数倍时,才可能使谱线落在 f0处,获得准确的 频谱。此即为整周期截断。 整周期采样的结果是使得频域抽样后所拓展的周 期时域信号完全等同于实际的周期信号。
… -fh 0 fh fs 不产生混叠的条件 fh
《测试技术》(第二版)课后习题答案-_

解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
《测试技术》(第二版)课后习题标准答案--

解:(1)瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2)准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3)周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解: x(t)=sin2f0 t 的有效值(均方根值):xrms1 T0x 21T 02 2 f 0 t dt(t) dt sinT 0T 01T 0cos 4 f 0 t ) dt1(T 01T 0) (1sin 4 f 0 t02T 002T 04 f 01(T 01sin 4 f 0 T 0 ) 1 / 22T 0 f 04解:周期三角波的时域数学描述如下:x(t )1. ..-T 0/2 0T 0/2A2 A t T 0t 0T 0 2 x ( t )A2 A 0T 0t tT 02x ( t nT 0 ). ..t(1)傅里叶级数的三角函数展开:a1 T 0/22 T 0 /2 2t )dt1 0T 0 x(t )dtT 0(12T 0/2T 0an 2T 0 / 2 0t dtT 0x(t) cosnT 0/24 T 0 /2 2t ) cos n 0 t dt0 (1T 0T 04 42 nn1, 3, 5,2 sinn 22n2 2n2, 4, 6,2b nT 0 / 20t dt,式中由于 x(t) 是偶函数, sin n 0t 是奇函数,T 0x(t )sin nT 0/2则 x(t) sin nt也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故b n0。
因此,其三角函数展开式如下:x(t )1 41cos n0 t1 41sin(n 0 t2)22 n 1 n 222 n 1 n 2(n=1, 3, 5,其频谱如下图所示:A( )( )142224492225003050003050单边幅频谱单边相频谱(2)复指数展开式复指数与三角函数展开式之间的关系如下:C0 =a0R e C N =a n/2C N =(a n-jb n)/2I m C N =-b n/2C-N =(a n +jb n)/2故有2sin2n 2e N n n2 2 RC =a /2n2220I C =-b/2=0m N nC0A0 a01 2C n 1a n2b n21A n =1a n 222n arctgImCn arctg (b n)0R e C n a nC 0A0a0C n1a n2b n21A n22narctgImCn arctg (bn )R e C n a nn1, 3, 5,n 2, 4, 6,实频谱229 225 2-50-30虚频谱-50-30双边幅频谱229 2252-50-30R e C n122222292-00030I m C n-00030C n122222292-00030n225 25 05 0225 25 0双边相频谱-50 -30-0003050解:该三角形窗函数是一非周期函数,其时域数学描述如下:x(t)12T 0 t 0 1t2x(t )T 02T 010 tt-T 0/2 0T 0/2tT 02用傅里叶变换求频谱。
《测试技术》[第二版]课后习题答案解析
![《测试技术》[第二版]课后习题答案解析](https://img.taocdn.com/s3/m/daccf7fd2cc58bd63186bddb.png)
完美WORD 格式编辑解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:T 0/2-T 0/21x (t ) t. . . . . .⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(00000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dtt n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:故有)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ 0ωA (ω)ω0 3ω0 5ω0 0ωω0 3ω0 5ω0 ϕ (ω)24π294π2254π21 2π C 0 =a 0C N =(a n -jb n )/2 C -N =(a n +jb n )/2 R e C N =a n /2 I m C N =-b n /2)(212122000n n n e n m n n n n n a barctg C R C I arctg A b a C a A C -===+===φ R e C N =a n /2⎪⎩⎪⎨⎧====,6,4,20,5,3,122sin 222222n n n n n πππI m C N =-b n /2 =0单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π21292π2252π5ω0 -ω0 -3ω0 292π 2252π -5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωR e C nω03ω0 22π21 292π2252π5ω0 -ω0 -3ω0 292π 2252π-5ω0 22π虚频谱双边相频谱实频谱双边幅频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
测试技术第二阶段

测试技术贾民平主编高等教育出版社第二阶段选择题1.理想线性系统的输出与输入之间呈单调、___________的关系。
A、双曲线B、线性比例C、抛物线所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:B2._________是指系统在稳定条件下,输出增量对输入增量的比。
A、灵敏度B、线性度C、分辨力所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:A3.__________是指测试系统的输入、输出关系保持常值线性比例关系的程度。
A、灵敏度B、非线性度C、分辨力所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:B4._______是指测试系统所能检测出来的输入量的最小变化量。
通常是以最小单位输出量所对应的输入量表示。
A、灵敏度B、非线性度C、分辨力所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:C5.一个测试系统的分辨力越高,表示它所能检测出的输入量的最小变化量值_______。
A、越大B、不确定C、越小所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:C6._________的存在是由于仪器仪表中磁性材料的磁滞、弹性材料的迟滞现象,以及机械结构中的摩擦和游隙等原因,反映在测试过程中输入量在递增过程中的定度曲线与输入量在递减过程中的定度曲线往往不重合。
A、回程误差B、系统误差C、粗大误差所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:A7.____________是指测试系统在输入不变的条件下,输出随时间而变化的趋势。
A、漂移B、系统误差C、粗大误差所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:A8.在规定的条件下,当输入不变时在规定时间输出的变化,称为______。
A、温漂B、点漂C、零漂所属知识点:测试系统的静态特性所属阶段:第二所属章节:3.2标准答案:B9.最常见的漂移是__________。
《测试技术》(第二版)课后习题参考答案

《测试技术》(第二版)课后习题参考答案解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(100000000000002020000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(0000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章习 题(P29)解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(10000000000000202000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:T 0/2-T 0/21x (t ) t. . . . . .⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(0000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:故有)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ 0ωA (ω)ω0 3ω0 5ω0 0ωω0 3ω0 5ω0 ϕ (ω)24π294π2254π21 2π C 0 =a 0C N =(a n -jb n )/2 C -N =(a n +jb n )/2 R e C N =a n /2 I m C N =-b n /2)(212122000n n n e n m n n n n n a barctg C R C I arctg A b a C a A C -===+===φ R e C N =a n /2⎪⎩⎪⎨⎧====,6,4,20,5,3,122sin 222222n n n n n πππI m C N =-b n /2 =0单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π21292π2252π5ω0 -ω0 -3ω0 292π 2252π -5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωR e C nω03ω0 22π21 292π2252π5ω0 -ω0 -3ω0 292π 2252π-5ω0 22π虚频谱双边相频谱实频谱双边幅频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
T 0/2 -T 0/21x (t )t⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤-+=20210221)(0T t t T t T t T t x ⎰⎰---∞∞-==2/2/2200)()()(T T ft j ftj dte t x dt et x f X ππsin 2sin 2sin 21]cos 1[1]11[21][2122]}21[]21{[21})]21()21[()]21()21{[(21])21()21([21)21()21(02002002022002202202/22/02002/202/0202/0202/202/022/02002/202/02002/202/02000000000000000fT c T fT T fT T f fT T f e e T f e e fj fT j dt e T dt eT f j t T d e e t T t T d ee t Tf j de t T de t T f j dte t T dt e t T fT j fT j T ftj T ftj T ft j T ftj T ft j T ftj T ftj T ftj T ft j T ftj T ft j T ftj ππππππππππππππππππππππππππ⋅=⋅=⋅=-=+---=--⋅-=-++--=+-++----=++--=++-=-------------------⎰⎰⎰⎰⎰⎰⎰⎰解:方法一,直接根据傅里叶变换定义来求。
X (f )T 0/22 T 02 T 0f6 T 06 T 0ϕ(f )π0 2 T 0 4 T 0 6 T 02 T 0 4 T 0 6 T 04 T 04 T 0f方法二,根据傅里叶变换的频移特性来求。
单边指数衰减函数:其傅里叶变换为⎩⎨⎧≥><=-0,000)(t a et t f at22)(10)()()(ωωωωωωωω+-=+=∞+-⋅=⋅==----∞-∞∞-⎰⎰a j a j a j a e e dte e dt e tf F t j at t j at t j ωωωωωωωωωωωωωωωωωωωωωωωωωωωa j a j a j a j j j a e j j a e j dt e e j dte e je dt e t e dt e t x X t j j a t j j a t j j a t j j a t j t j t j a t j at t j 2])(1)(1[2])()([2)[2)(2sin )()(22020000)(00)()()(0)(000000000+-+=-+-++=-++++-=-=-⋅=⋅==∞-+-∞++--+-++-∞-+-∞--∞-∞∞-⎰⎰⎰⎰aarctga F ωωφωω-=+=)(1)(22根据频移特性可求得该指数衰减振荡函数的频谱如下:ωω0ω-)(ωF 0)(ωX 1/aa21 a21 根据频移特性得下列频谱ωωωωωωωωωωωωωωa j a j a j a j F F jt t f FT X 2])(1)(1[21)]()([21]sin )([)(220200000+-+=++--+=+--==ω)]()([2100ωωωω++-F F解:利用频移特性来求,具体思路如下:当f 0<f m 时,频谱图会出现混叠,如下图所示。
f 0f 0fA/2A/2解:)]([t w FT ][cos 0t FT ω0ω0ω0ω-卷积2121)(ωW ωT2T210)(ωX 0ω0ω-ωTT1-Tww (t )-T1 cos ω0tt]cos )([0t t w FT ωtt w t x 0cos )()(ω=由于窗函数的频谱 )(sin 2)(T c T W ωω=,所以其频谱图如上图所示。
解:πππππμ/2]2cos 2cos [1])2sin (2sin [1)(100000002/02/0002/02/0000=+-=-+==⎰⎰⎰T T T T T T T tf t f T dt f dt f T dtt x T x2/1)4sin 41(21)4cos 1(212sin 1)(1)(0000000000202022=-=-====⎰⎰⎰T T T T rms xt f f T T dtt f T dtt f T dtt x T x ππππψ ])(sin )([sin )]()([21)(0000T c T c T W W X ωωωωωωωωω++-=++-=解:解:解:代入上式,则得=令=是余弦函数的周期,式中,θφωωπ+t /2T Tωτθωτθθπτπcos A 21]cos[cos 2A )(2202 =+=⎰d R x若x(t)为正弦信号时,)(τx R 结果相同。
3000)5050sin (3000lim )50sin()60(lim )0(02====ψ→→ττττττx x R -=ττττττa at a Ta at T Tt a at T TTT x e aA e e aA dte e A dtAe Ae dtt x t x R -∞----∞→+--∞→-∞→=-=⋅=⋅=+=⎰⎰⎰2)21(lim lim)()(lim )(20220220)(⎰⎰++++=T Tx dt t t T dtt x t x T R 02])(cos[)cos(A 1)()(1)(φτωφωττ=周期代替其整体,故有对于周期信号可用一个解:S =S 1S 2S 3=80nc/MP a ×0.005V/nc ×25mm/V=10 mm/ MP a △P=△x/S=30mm/10(mm/ MP a )=3 MP a解:S =S 1S 2=404×10-4Pc/Pa ×0.226mV/Pc=9.13×10-3mV/PaS 2=S/S 1=Pc/Pa10404m V /Pa 10104-6⨯⨯= 2.48×108mV/Pc解: τ=2s, T=150s, ω=2π/T300-9965.0×100=200.35℃ 300+9965.0×100=399.65℃ 故温度变化范围在200.35~399.65℃.9965.0)150/4(11)(11)(22=+=+=πωτωA解: τ=15s, T=30/5=6s, ω=2π/Th 高度处的实际温度t=t 0-h*0.15/30而在h 高度处温度计所记录的温度t ‘=A(ω)t =A(ω)(t 0-h*0.15/30) 由于在3000m 高度温度计所记录的温度为-1℃,所以有-1= A(ω)(t 0-3000*0.15/30) 求得 t 0=-0.75℃当实际温度为t =-1℃时,其真实高度可由下式求得:t=t 0-h*0.15/30,h=(t 0- t)/0.005=(-0.75+1)/0.005=50m解: (1)则 τ≤7.71×10-4 S (2)ϕ(ω)= -arctg ωτ = -arctg (41071.7250-⨯⨯⨯π)= -13.62°0635.0)6/215(11)(11)(22=⨯+=+=πωτωA %10)2100(111)(111)(1)(22≤⨯+-=+-=-=∆πτωτωωA A %81.2)1071.7250(111)(111)(1)(242≤⨯⨯⨯+-=+-=-=∆-πωτωωA A解:τ=0.04 S ,(1)当f=0.5Hz 时,(2)当f=1Hz 时,(3)当f=2Hz 时,解:τ=0.0025 S则 ω<131.5(弧度/s ) 或 f <ω/2π=20.9 Hz相位差:ϕ(ω)= -arctg ωτ = -arctg (0025.05.131⨯) = -18.20°解:f n =800Hz, ξ=0.14, f=400 5.0800/400/===n n f f ωω22)2(111)(111)(1)(τπωτωωf A A +-=+-=-=∆%78.0)04.05.02(111)(111)(1)(22=⨯⨯+-=+-=-=∆πωτωωA A %02.3)04.012(111)(111)(1)(22=⨯⨯+-=+-=-=∆πωτωωA A %65.10)04.022(111)(111)(1)(22=⨯⨯+-=+-=-=∆πωτωωA A %5)0025.0(111)(111)(1)(22≤+-=+-=-=∆ωωτωωA A ()57.105.015.014.0212)(22-=-⨯⨯-=--=arctg arctgn n ωωωωξωϕ()[]()[]()31.15.014.045.011411)()(22222222=⨯⨯+-=+-==n nH A ωωξωωωω解: 由 得)(47.2)1094.4(5100321格变化格数 ±=⨯±⨯⨯=∆-C S S解:由S u =U 0/a , S q =Q/a 得:S u / S q =U 0/Q= ca C C +1C a R a C c R i C i20000δεεδδAC C S ==∆∆=)(1094.4)(1094.43.0/)101(41085.8131526212200PF F A C ----⨯±=⨯±=⨯±⨯⨯⨯⨯⨯-=∆-=∆πδδεεca C C Q C Q U +==0Q4-94-10解: (1)半桥单臂2mv21020002412000v 2210224126060=时,=当=时,=当--⨯⨯⨯⨯=⨯⨯⨯⨯=u u μεεμμεε (2)半桥双臂 4mv21020002212000v 4210222126060=时,=当=时,=当--⨯⨯⨯⨯=⨯⨯⨯⨯=u u μεεμμεε)(121/)(5.041/000000V u R R u ,SV u R R u S i 双i 单==∆===∆=半桥双臂是半桥单臂灵敏度的两倍。
