第0709章习题课
VerilogHDL与FPGA设计基础_授课教案0709

西安邮电大学课程教案课程名称:VerilogHDL与FPGA设计基础授课教师:**授课教师所在学院:电子工程学院授课班级:电路1201~02授课学期:2014-2015-01学期一、基本信息二、课程大纲《VerilogHDL与FPGA设计基础》课程教学大纲The fundamental of FPGA Design with Verilog HDL课程编号:DZ140340适用专业:集成电路设计与系统集成先修课程:数字电路,电路分析学分数:4总学时数:64 实验(上机)学时:24考核方式:考试执笔者:李哲编写日期:2014年7月7日一、课程性质和任务本课程是集成电路设计与系统集成专业的一门院定选修专业基础课程。
学生通过本课程学习之后应当熟悉Verilog HDL语言的基本语法和语义、自顶向下的设计方法学、能用Verilog HDL语言在不同的抽象层次上描述数字电路、掌握用Verilog HDL实现数字电路仿真的方法;同时能够应用Verilog HDL语言进行基于FPGA的电路设计。
一方面可以使学生掌握一种适合产品样机和小批量生产的理想手段,另一方面也为进一步学习专用集成电路芯片设计打下了良好基础。
通过本课程的学习可以使学生掌握1)自顶向下的全正向设计思想;2)可编程逻辑器件的基本知识和相关软件的使用方法;3)FPGA电路设计的方法和技巧。
基本具备中小规模可编程逻辑器件的设计开发能力。
二、课程教学内容和要求本课程系统的介绍用VerilogHDL设计和验证数字硬件电路,重点讨论综合VerilogHDL子集在设计数字电路中的应用,讨论FPGA现场可编程阵列器件的结构、特点和相应的集成环境的使用以及目前工业界最常用的仿真工具Modelsim 的使用。
重点讲授基于FPGA的数字电路设计流程中的基本概念、所采用的步骤和应该遵循的原则,包括模块划分原则、可综合VerilogHDL编码风格、验证程序的编写方法和静态时序分析等。
操作系统概念第七版7-9章课后题答案(中文版)

7.1假设有如图7.1所示的交通死锁。
a.证明这个例子中实际上包括了死锁的四个必要条件。
b.给出一个简单的规则用来在这个系统中避免死锁。
a.死锁的四个必要条件: (1)互斥;(2)占有并等待;(3)非抢占;(4)循环等待。
互斥的条件是只有一辆车占据道路上的一个空间位置。
占有并等待表示一辆车占据道路上的位置并且等待前进。
一辆车不能从道路上当前的位置移动开(就是非抢占)。
最后就是循环等待,因为每个车正等待着随后的汽车向前发展。
循环等待的条件也很容易从图形中观察到。
b.一个简单的避免这种的交通死锁的规则是,汽车不得进入一个十字路口如果明确地规定,这样就不会产生相交。
7.2考虑如下的死锁可能发生在哲学家进餐中,哲学家在同个时间获得筷子。
讨论此种情况下死锁的四个必要条件的设置。
讨论如何在消除其中任一条件来避免死锁的发生。
死锁是可能的,因为哲学家进餐问题是以以下的方式满足四个必要条件:1)相斥所需的筷子, 2 )哲学家守住的筷子在手,而他们等待其他筷子, 3 )没有非抢占的筷子,一个筷子分配给一个哲学家不能被强行拿走,4 )有可能循环等待。
死锁可避免克服的条件方式如下: 1 )允许同时分享筷子, 2 )有哲学家放弃第一双筷子如果他们无法获得其他筷子,3 )允许筷子被强行拿走如果筷子已经被一位哲学家了占有了很长一段时间4 )实施编号筷子,总是获得较低编号的筷子,之后才能获得较高的编号的筷子。
7.3一种可能以防止死锁的解决办法是要有一个单一的,优先于任何其他资源的资源。
例如,如果多个线程试图访问同步对象A•…E,那么就可能发生死锁。
(这种同步对象可能包括互斥体,信号量,条件变量等),我们可以通过增加第六个对象来防止死锁。
每当一个线程希望获得同步锁定给对象A•••E,它必须首先获得对象F的锁.该解决方案被称为遏制:对象A•••E的锁内载对象F的锁。
对比此方案的循环等待和Section7.4.4的循环等待。
这很可能不是一个好的解决办法,因为它产生过大的范围。
电子技术基础 数字 康华光 课后答案

电子技术基础康华光课后习题答案(完整版)第一章数字逻辑1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于42(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H (4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕ AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 110 0 111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。
屈婉玲高教版离散数学部分答案2

第七章部分课后习题参考答案7.列出集合A={2,3,4}上的恒等关系I A ,全域关系E A ,小于或等于关系L A ,整除关系D A .解:I A ={<2,2>,<3,3>,<4,4>}E A ={<2,2>,<2,3>,<2,4>,<3,4>,<4,4>,<3,2>,<3,3>,<4,2>,<4,3>}L A ={<2,2>,<2,3>,<2,4>,<3,3>,<3,4>,<4,4>} D A ={<2,4>}13.设A={<1,2>,<2,4>,<3,3>} B={<1,3>,<2,4>,<4,2>}求A ⋃B,A ⋂B, domA, domB, dom(A ⋃B), ranA, ranB, ran(A ⋂B ), fld(A-B). 解:A ⋃B={<1,2>,<2,4>,<3,3>,<1,3>,<4,2>} A ⋂B={<2,4>}domA={1,2,3} domB={1,2,4} dom(A ∨B)={1,2,3,4}ranA={2,3,4} ranB={2,3,4} ran(A ⋂B)={4}A-B={<1,2>,<3,3>},fld(A-B)={1,2,3} 14.设R={<0,1><0,2>,<0,3>,<1,2>,<1,3>,<2,3>}求R R, R -1, R ↑{0,1,}, R[{1,2}] 解:R R={<0,2>,<0,3>,<1,3>}R -1,={<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>}R ↑{0,1}={<0,1>,<0,2>,<0,3>,<1,2>,<1,3>} R[{1,2}]=ran(R|{1,2})={2,3}16.设A={a,b,c,d},1R ,2R 为A 上的关系,其中1R ={},,,,,a a a b b d{2,,,,,,,R a d b c b d c b=求23122112,,,R R R R R R 。
商品编码第5讲讲义及习题(第7到第9章)

商品编码第5讲讲义及习题(第7到第9章)第七章食用蔬菜、可食用根及块茎(一)本章的编排结构:1、本章包括各种供食用的蔬菜和含高淀粉、高菊粉的植物块茎及块根(0714),如甘薯,木薯,荸荠,藕等,这些产品的加工方法为简单加工(冷藏、冷冻、干制、用二氧化硫或盐水或亚硫酸水防腐处理过、以及它们的什锦化),但0710的蔬菜是特例。
本章的产品若深加工(油炸,烹煮,烘炒等)归到20章。
2、本章14个品目可分成四大块:0701—09鲜或冷藏、0710冷冻(不论是否蒸煮)、0711暂时保藏、0712—13干制,0714则是某些含高淀粉,高菊粉的产品。
(二)本章的归类要点:(1)马铃薯(又名土豆):鲜冷0701,冷冻0710,二氧化硫、盐水、亚硫酸处理0711,干制0712,磨粉1105,提取淀粉1108,醋酸处理2001,蒸煮2005(蒸煮后再冷冻则归入0710),注意:0701中包括种用的马铃薯,一般蔬菜种子归1209.9100。
马铃薯粉归1105。
(2)对于甘蓝类要分清食用与非食用,作为蔬菜供食用的放在本章,如果是作为动物饲料的芜菁甘蓝等归到1214。
(3)0706是供食用的根茎类蔬菜,这类产品一般还带有叶子,叶子一般供动物食用,如胡萝卜叶子要归到2308。
(4)0709中的伞菌属蘑菇主要包括:白蘑菇,小白蘑菇等。
(5)注意0710.4000中提到的甜玉米(不论是否带芯),它与普通的玉米是不同的,甜玉米含有较高的糖分,很嫩,而普通玉米是作为谷物归到1005中,但是两者又有联系,甜玉米的细粉,粗粉和团粒,磨碎等要按玉米的细粉,出粉,团粒,磨碎等归到1102至1104中。
(6)0710的加工方法很特殊,冷冻蔬菜,不论是否蒸煮!一般是冻前蒸过或用水煮过的冷冻蔬菜归0710.(7)注意油橄榄属于蔬菜归入本章,不能当作油原料放在第12章或者当作水果放在第8章。
(8)品目07.12包括干制的归入品目0701至品目0711的各种蔬菜,而且包括这类蔬菜的粉,一般提到蔬菜粉,考虑归0712,但是辣椒干和辣椒粉要按调料来归,归入09.04。
运筹学 第二版 (吴祁宗 著) 课后习题答案 机械工业出版社

1 3 P3 2 0 1 0 P5 2 1 2 1 P4 3 0 3 0 P5 0 1 1
(2) M inf x1 5 x2 2 x3
3x1 2 x 2 4 x3 6 2 x 3 x x 5 1 2 3 s.t : x1 x 2 x3 9 x1 0, x 2 0
令 z f , 则Maxz x1 5 x 2 2 x3
2 3
X2
2 1 0
X2
1 2 A
3 4 B
D
x1
5 B 4 3 2 1 0 1 2 3
C A Z
*
T z * 13
4 5 6 x1
4
(3)Max z= x1+ 2x2 s.t: 2x1- x2≤6 (A) 3x1+ 2x2≤12 (B) x1 ≤3 (C) x1,x2≥0 从图中可知,最优解为 0
T
T
同时为基本可行解, z 2 3 同时为基本可行解, z 1
对应 B6的基本解为0 1 0 对应 B7的基本解为0 对应 B8的基本解为0 对应 B9的基本解为0 对应 B10的基本解为0 ∴最优解为 x 14 3
5
B9 P3
共 10 个基
2 0 P5 1 1
B10 P4
1 0 P5 0 1
x1 20 3 x1 x 2 6 对应B1的基本解为:令x 3 x 4 x5 0得 2 x1 4 x 2 4 x 2 3
15 x1
1 1 2 1 0 A P1 1 4 1 0 1 B1 P1 B3 P1 B5 P2 B7 P2 1 1 P2 1 4 1 1 P4 1 0 1 2 P3 4 1 1 0 P5 4 1
管理运筹学第二版 课后习题答案 (韩伯棠主编) 高教版
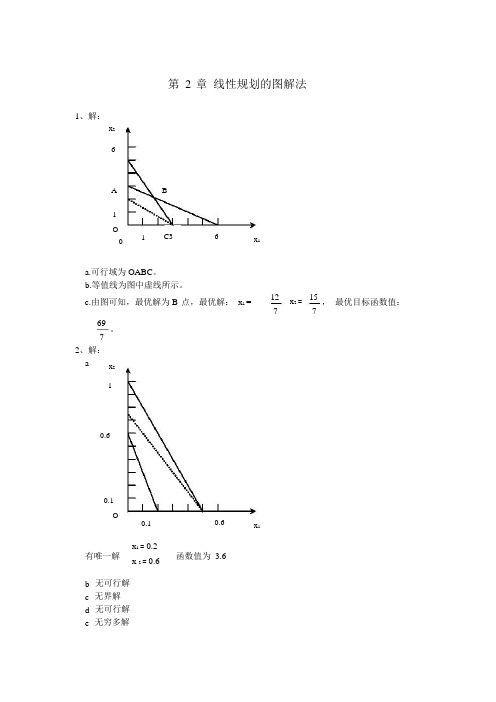
第2 章线性规划的图解法1、解:x26A1O01BC36x1a.可行域为 OABC。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解:x1 =1215x2 =,最优目标函数值:7769。
72、解:a x210.60.1O0.10.6x1有唯一解x1 = 0.2x 2 = 0.6函数值为3.6b c d e 无可行解无界解无可行解无穷多解20x1 =923f 有唯一解函数值为83x2 =33、解:a 标准形式:max f = 3x1 + 2 x 2 + 0s1 + 0 s 2 + 0s 39 x1 + 2 x 2 + s1 = 303x1 + 2 x 2 + s 2 = 132 x1 + 2 x 2 + s3 = 9x1 , x 2 , s1 , s 2 , s3 ≥ 0b 标准形式:max f = −4 x1 − 6 x3 − 0s1 − 0s23x1 − x 2 − s1 = 6x1 + 2 x 2 + s 2 = 107 x1 − 6 x 2 = 4x1 , x 2 , s1 , s 2 ≥ 0c 标准形式:max f = − x1' + 2 x2 − 2 x2 − 0s1 − 0s2'''− 3x1 + 5 x 2 − 5 x 2' + s1 = 70''2 x1' − 5 x 2 + 5 x 2' = 50''3x1' + 2 x 2 − 2 x 2' − s 2 = 30''x1' , x 2 , x 2' , s1 , s 2 ≥ 0''4 、解:标准形式:max z = 10 x1 + 5 x 2 + 0 s1 + 0 s 23x1 + 4 x 2 + s1 = 95 x1 + 2 x 2 + s 2 = 8x1 , x 2 , s1 , s 2 ≥ 0s1 = 2, s2 = 0标准形式:min f = 11x1 + 8 x 2 + 0s1 + 0s 2 + 0s310 x1 + 2 x 2 − s1 = 203x1 + 3x 2 − s 2 = 184 x1 + 9 x 2 − s3 = 36x1 , x 2 , s1 , s 2 , s3 ≥ 0 s1 = 0, s2 = 0, s3 = 136 、解:b 1 ≤ c1 ≤ 3c 2 ≤ c2 ≤ 6d x1 = 6x2 = 4x 2 = 16 − 2 x1e x1 ∈[4,8]f 变化。
7-9 习题课27页PPT

qB
qB
对载F 流 d f 导 Ild B 线
对载流 M 线 L m B 圈 L m NS I
对大块U 导 H体 Bbvn1qIdB(霍耳效应
例1.将相同的几根导线焊成立方体 ,并在其对顶角A、B接上电源,则 立方体框架中的电流在其中心处产 生的磁感应强度等于 0 。
B .O
A
例2.两个同心导体圆线圈(R,I),分别竖直和水平放置,
则圆心O处的BO=_______
(A) 0 I (B) 0 I (C) 2 0 I
R
2R
2R
B 0I
2R
(D) 0 I
4R
B
B
•O I
例3 氢原子(m、e)沿某一园轨道绕原子核运动,其
等效L p 园Lm 电 m 流m R 的2IvPp v mm R 与m 电R R m 2子v 轨R 2I e道R vS 运R 动2 2I e的m 动量I 矩eLn之比e2—vR—。
习题课----稳恒磁场(7、8、9章)
一、电流激发磁场的规律
1.毕萨定律:
dB0 4
运动电荷产生的场
Idl rˆ
r2
B
B dB L4 0 Irld2rˆ
0 q0vrˆ
2.高斯定理: Bds 0 4 r2
s
3.安培环路定理:
BevEe BvU vU
B
h Bh D
V
nesvU nevUD
I
Inesv
Bh B
例11 电流I在无限长铜片(宽a)流过,求与铜片共面
外b处的p点的B.
I
解: dB2(a 0dbIx)
dI I dx a
第七章 章末复习课

章末复习课一、互斥事件与对立事件1.互斥事件是不可能同时发生的两个事件;对立事件除要求这两个事件不同时发生外,还要求二者必须有一个发生.因此对立事件一定是互斥事件,但互斥事件不一定是对立事件,对立事件是互斥事件的特殊情况.2.掌握互斥事件和对立事件的概率公式及应用,提升逻辑推理和数学运算素养.例1根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;(2)求该地1位车主甲、乙两种保险都不购买的概率.解记A表示事件:该车主购买甲种保险;B表示事件:该车主购买乙种保险但不购买甲种保险;C表示事件:该车主至少购买甲、乙两种保险中的1种;D表示事件:该车主甲、乙两种保险都不购买.(1)由题意得P(A)=0.5,P(B)=0.3,又C=A∪B,所以P(C)=P(A∪B)=P(A)+P(B)=0.5+0.3=0.8.(2)因为D与C是对立事件,所以P(D)=1-P(C)=1-0.8=0.2.反思感悟求复杂事件的概率常用的两种方法(1)将所求事件转化成彼此互斥的事件的和.(2)先求其对立事件的概率,然后再应用公式P(A)=1-P(A)求解.跟踪训练1 (多选)从1,2,3,…,7这7个数中任取两个数,其中不是对立事件的是( ) A .恰有一个是偶数和恰有一个是奇数 B .至少有一个是奇数和两个都是奇数 C .至少有一个是奇数和两个都是偶数 D .至少有一个是奇数和至少有一个是偶数 答案 ABD解析 C 中“至少有一个是奇数”,即“两个奇数或一奇一偶”,而从1~7中任取两个数,根据取到数的奇偶性可认为共有三个事件:“两个都是奇数”、“一奇一偶”、“两个都是偶数”,故“至少有一个是奇数”与“两个都是偶数”是对立事件,易知其余都不是对立事件. 二、古典概型1.古典概型是一种最基本的概率模型,是学习其他概率模型的基础,解题时要紧紧抓住古典概型的两个基本特征,即有限性和等可能性.在应用公式P (A )=mn 时,关键在于正确理解试验的发生过程,求出试验的样本空间的样本点总数n 和事件A 的样本点个数m . 2.掌握古典概型的概率公式及其应用,提升数学抽象、数据分析的数学素养. 例2 甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女. (1)若从甲校和乙校报名的教师中各任选1名,求选出的2名教师性别相同的概率; (2)若从报名的6名教师中任选2名,求选出的2名教师来自同一学校的概率.解 (1)从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男),共9种;选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男2,乙男)、(甲女,乙女1)、(甲女,乙女2),共4种,所以选出的2名教师性别相同的概率为49.(2)从报名的6名教师中任选2名,所有可能的结果为(甲男1,乙男)、(甲男2,乙男)、(甲男1,乙女1)、(甲男1,乙女2)、(甲男2,乙女1)、(甲男2,乙女2)、(甲女,乙女1)、(甲女,乙女2)、(甲女,乙男)、(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共15种;选出的2名教师来自同一学校的所有可能的结果为(甲男1,甲男2)、(甲男1,甲女)、(甲男2,甲女)、(乙男,乙女1)、(乙男,乙女2)、(乙女1,乙女2),共6种,所以选出的2名教师来自同一学校的概率为615=25.反思感悟 古典概型概率计算问题的关注点 (1)判断:该试验类型是否为古典概型问题.(2)关键:写出样本空间所包含的样本点及所求事件所包含的样本点. (3)注意:①弄清“放回”抽取还是“不放回”抽取; ②灵活运用互斥事件、对立事件的概率公式.跟踪训练2 某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)(1)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;(2)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A 1,A 2,A 3,A 4,A 5,3名女同学B 1,B 2,B 3.现从这5名男同学和3名女同学中各随机选1人,求A 1被选中且B 1未被选中的概率.解 (1)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人, 故至少参加上述一个社团的共有45-30=15(人),所以从该班随机选1名同学,该同学至少参加上述一个社团的概率为P =1545=13.(2)从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的样本空间Ω={A 1B 1,A 1B 2,A 1B 3,A 2B 1,A 2B 2,A 2B 3,A 3B 1,A 3B 2,A 3B 3,A 4B 1,A 4B 2,A 4B 3,A 5B 1,A 5B 2,A 5B 3},共含15个样本点.根据题意这些样本点出现的可能性相等.事件“A 1被选中且B 1未被选中”所包含的样本点有A 1B 2,A 1B 3,共2个. 所以其概率为P =215.三、相互独立事件1.相互独立事件的概率通常和互斥事件的概率综合在一起考查,这类问题具有一个明显的特征,那就是在题目的条件中已经出现一些概率值,解题时先要判断事件的性质(是互斥还是相互独立),再选择相应的公式计算求解.2.掌握相互独立事件的概率公式的应用,提升数学抽象和逻辑推理的数学素养.例3某项选拔共有四轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为0.6,0.4,0.5,0.2.已知各轮问题能否正确回答互不影响.(1)求该选手被淘汰的概率;(2)求该选手在选拔中至少回答了2个问题后最终被淘汰的概率.解设“该选手能正确回答第i轮的问题”为事件A i(i=1,2,3,4),则P(A1)=0.6,P(A2)=0.4,P(A3)=0.5,P(A4)=0.2.(1)方法一该选手被淘汰的概率为P=P(A1∪A1A2∪A1A2A3∪A1A2A3A4)=P(A1)+P(A1)P(A2)+P(A1)P(A2)P(A3)+P(A1)P(A2)·P(A3)P(A4)=0.4+0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.976.方法二P=1-P(A1A2A3A4)=1-P(A1)P(A2)·P(A3)P(A4)=1-0.6×0.4×0.5×0.2=1-0.024 =0.976.(2)方法一所求概率P=P(A1A2∪A1A2A3∪A1A2A3A4)=P(A1)P(A2)+P(A1)P(A2)P(A3)+P(A1)P(A2)P(A3)·P(A4)=0.6×0.6+0.6×0.4×0.5+0.6×0.4×0.5×0.8=0.576.方法二所求概率P=1-P(A1)-P(A1A2A3A4)=1-(1-0.6)-0.6×0.4×0.5×0.2=0.576.反思感悟利用相互独立事件求复杂事件概率的解题思路(1)将待求复杂事件转化为几个彼此互斥的简单事件的和.(2)将彼此互斥的简单事件中的简单事件,转化为几个已知(易求)概率的相互独立事件的积事件.(3)代入概率的积、和公式求解.跟踪训练3设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立,则同一工作日至少3人需使用设备的概率为()A.0.25 B.0.30 C.0.31 D.0.35答案 C解析设甲、乙、丙、丁需使用设备分别为事件A,B,C,D,则P(A)=0.6,P(B)=0.5,P(C)=0.5,P(D)=0.4,所以同一工作日至少3人需使用设备的概率为P(ABC D+AB C D+A B CD+A BCD+ABCD)=0.6×0.5×0.5×0.6+0.6×0.5×0.5×0.4+0.6×0.5×0.5×0.4+0.4×0.5×0.5×0.4+0.6×0.5×0.5×0.4=0.31.四、频率与概率1.概率是随机事件发生可能性大小的度量,是随机事件A 的本质属性,随机事件A 发生的概率是大量重复试验中事件A 发生的频率的近似值.2.掌握频率与概率的关系,在具体的问题中会用频率估计概率,进一步提升数据分析与数学运算的核心素养.例4 某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(1)记A 为事件“一续保人本年度的保费不高于基本保费”.求P (A )的估计值;(2)记B 为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P (B )的估计值;(3)求续保人本年度平均保费的估计值.解 (1)事件A 发生当且仅当一年内出险次数小于2. 由所给数据知,一年内出险次数小于2的频率为 60+50200=0.55,故P (A )的估计值为0.55. (2)事件B 发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为30+30200=0.3,故P (B )的估计值为0.3.(3)由所给数据得调查的200名续保人的平均保费为0.85a ×0.30+a ×0.25+1.25a ×0.15+1.5a ×0.15+1.75a ×0.10+2a ×0.05=1.192 5a .因此,续保人本年度平均保费的估计值为1.192 5a . 反思感悟 频率与概率问题的关注点(1)依据概率的定义,可以用事件发生的频率去估计概率.(2)频率的计算公式为频率=mn,其中m 是事件出现的频数,n 为重复试验次数.跟踪训练4 为了为奥运会做准备,某射击运动员在相同条件下进行射击训练,结果如下表:射击次数n 10 20 50 100 200 500 击中靶心次数m 8 19 44 92 178 455 击中靶心的频率0.80.950.880.920.890.91(1)该射击运动员射击一次,击中靶心的概率大约是多少?(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗? 解 (1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9. (2)击中靶心的次数大约是300×0.9=270(次).(3)由概率的意义,可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍是0.9,所以不一定击中靶心.1.(2020·全国Ⅰ)设O 为正方形ABCD 的中心,在O ,A ,B ,C ,D 中任取3点,则取到的3点共线的概率为( ) A.15 B.25 C.12 D.45 答案 A解析 从O ,A ,B ,C ,D 这5个点中任取3点,取法有{O ,A ,B },{O ,A ,C },{O ,A ,D },{O ,B ,C },{O ,B ,D },{O ,C ,D },{A ,B ,C },{A ,B ,D },{A ,C ,D },{B ,C ,D },共10种,其中取到的3点共线的只有{O ,A ,C },{O ,B ,D }这2种取法,所以所求概率为210=15.2.(2018·全国Ⅱ)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为( )A .0.6B .0.5C .0.4D .0.3答案 D解析 设2名男同学为a ,b,3名女同学为A ,B ,C ,从中选出两人的情形有(a ,b ),(a ,A ),(a ,B ),(a ,C ),(b ,A ),(b ,B ),(b ,C ),(A ,B ),(A ,C ),(B ,C ),共10种,而都是女同学的情形有(A ,B ),(A ,C ),(B ,C ),共3种,故所求概率为310=0.3.3.(2017·全国Ⅱ)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( ) A.110 B.15 C.310 D.25答案 D解析 从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:基本事件总数为25,第一张卡片上的数大于第二张卡片上的数的事件数为10, ∴所求概率P =1025=25.4.(2016·北京)袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒,每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( ) A .乙盒中黑球不多于丙盒中黑球 B .乙盒中红球与丙盒中黑球一样多 C .乙盒中红球不多于丙盒中红球 D .乙盒中黑球与丙盒中红球一样多 答案 B解析 取两个球往盒子中放有4种情况: ①红+红,则乙盒中红球数加1; ②黑+黑,则丙盒中黑球数加1;③红+黑(红球放入甲盒中),则乙盒中黑球数加1;④黑+红(黑球放入甲盒中),则丙盒中红球数加1.因为红球和黑球个数一样,所以①和②的情况一样多.③和④的情况完全随机,③和④对B 选项中的乙盒中的红球数与丙盒中的黑球数没有任何影响.①和②出现的次数是一样的,所以对B选项中的乙盒中的红球数与丙盒中的黑球数的影响次数一样.综上选B. 5.(2020·江苏)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是________.答案1 9解析列表如下:点数的和共有36,其中和为5的共有4,由古典概型的概率公式可得点数和为5的概率P=436=19.6.(2019·全国Ⅱ)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为________.答案0.98解析经停该站高铁列车所有车次的平均正点率的估计值为10×0.97+20×0.98+10×0.9910+20+10=0.98.。
第9章 综合练习题(2).pdf[共17页]
![第9章 综合练习题(2).pdf[共17页]](https://img.taocdn.com/s3/m/8238c410aa00b52acec7caca.png)
199第9章综合练习题(2)说明读者可以把“C:\Sjzd\”下的文件夹“20070101”复制到E 盘中练习(所有文件可以从“http://www. /jsj/”下载)。
网络部分的练习需要使用OutlookExpress 和InternetExplorer 模拟环境,请在机房提供的软件中进入相应环境。
练 习 11.Windows 基本操作(共10分)(1)在Winkt 文件夹下面建立Exam_A 文件夹。
(2)在Exam_A 文件夹下新建文件“信息技术成绩单.xls ”。
(3)在“考生考号”文件夹范围内搜索“WinRARA.exe ”文件,并在Exam_A 文件夹下建立它的快捷方式,名称为“WinRARA ”。
(4)将Winkt 文件夹下所有扩展名为“.exe ”的文件复制到Test 文件夹下。
(5)在“考生考号”文件夹范围内搜索“信息技术.doc ”文件,将其设置为“只读”、“隐藏”属性。
2.字、表、图混排操作(共20分)(1)编辑、排版。
打开Wordkt 文件夹下的“Worda.doc ”文件,按如下要求进行编辑、排版。
A .基本编辑。
y 删除文中所有的空行。
y 将文中“三、组织/功能分析”与“四、功能重组与组织变革的分析”两部分的内容进行位置调换(包含小标题)。
y 将文中的符号“●”替换为“■”。
B .排版。
y 页边距的上、下、左、右均为2cm ,页眉、页脚距页边距均为1.5cm ,纸张大小为16开。
y 页眉为“管理信息系统”,页脚为“第X 页共Y 页”(X 表示当前页数,Y 表示总页数),页眉、页脚均为楷体_GB2312、五号、居中。
y 将文章标题“第2节组织结构与功能凋查分析”设置为首行无缩进、居中、黑体、三号200 字,段前0.5行、段后0.5行。
y小标题(一、组织结构调查,…,四、功能重组与组织变革的分析)段前0.3行、段后0.3行、黑体、蓝色(RGB=0,0,255)、小四号字。
课内第七章习题

第七章习题(一)1. 求2w z =在z=I 处的伸缩率和旋转角。
问此变换将经过点z=i 且平行于实宙正方向的曲线的切线方向变换成w 平面上哪一个方向?并用图。
2. 试利用保域定理7.1简捷地证明第二章习题(一)6(3)、(4)。
3. 在整线性变换w iz =下,下列图形分别变成什么图形?(1)以123,1,1z i z z ==-=为顶点的三角形;(2)闭圆|1|1z -≤.4. 下列各题中,给出了三对对应点112233,,z w z w z w ↔↔↔的具体数值,写出相应的分式线性变换,并指出此变换把通过z 1,z 2,z 3的圆周的内部,或直线左边(顺着z 1,z 2,z 3观察)变成什么区域。
(1)11,0,1i i ↔↔-↔-;(2)1,1,10i ↔∞↔--↔;(3)0,,0i i ∞↔↔↔∞;(4)0,01,1∞↔↔↔∞.5. z 平面上有三个互相外切的圆周,切点之一在原点,函数1w z=将此三个圆周所围成的区域变成w 平面上什么区域?6. 如az b w cz d +=+将单位圆周变成直线,其系数应满足什么条件?7. 分别求将上半z 平面Im 0z >共形映射成单位圆 ||1w <的分式线性变换()w L z =,使符合条件:(1)()0,()0L i L i '=>;(2)()0,arg ()2L i L i π'==.8. 分别求将单位圆 ||1z <共形映射成单位圆||1w <的分式线性变换()w L z =,使符合条件:(1)10,(1)12L L ⎛⎫==- ⎪⎝⎭; (2)110,arg 222L L π⎛⎫⎛⎫'==- ⎪ ⎪⎝⎭⎝⎭. 9. 求出将圆 |4|2z i -<变成半平面v u >的共形映射,使得圆心变到-4,而圆周上的点2i 变到0.w =10. 求出将上半z 平面Im 0z >共形映射成圆||w R <的分式线性变换()w L z =,使符合条件()0L i =;如果再要求()1L i '=,此变换是否存在?11. 求将圆||z ρ<共形映射成圆||w R <的分式线性变换,使(||)z a a ρ=<变成w=0。
第七章练习试卷.doc

七年级第七章练习试卷1、如图,当直线a、b被直线c所截,下列说法正确的是( )(A)当Z1=Z2 时,一定有 a〃b (B)当 a〃b 时,一定有Z1=Z2(C)当 a〃b 时,一定有Zl+Z2=180°(D)当 a〃b 时,一定有Zl+Z2=90°2、在下列各图的AABC中,正确画出AC边上的高的图形是( )3、一个多边形的每个内角都等于108。
,则此多边形是( )(A)五边形 (B) 六边形 (C) 七边形 (D) 八边形4、已知三角形的两边分别为4和9,则此三角形的第三边可能是()(A) 4 (B) 5 (C) 9 (D) 135、一个多边形的每个内角都等于144° ,则这个多边形的边数是()A. 8B. 9C. 10D. 116、对于平移后,对应点所连的线段,下列说法正确的是( )①对应点所连的线段一定平行,但不一定相等;②对应点所连的线段一定相等,但不一定平行,有可能相交;③对应点所连的线段平行且相等,也有可能在同一条直线上;④有可能所有对应点的连线都在同一条直线上。
A.①③B.②③C.③④D.①②7、若多边形的内角和等于外角和的3倍,则这个多边形的边数是8、在AABC 中,ZA-ZB=36° , ZC=2ZB,贝UZA=, ZB=, ZC9、在AABC中,如果ZA=35° , ZB=68°,那么与匕C相邻的一个外角等于°10、已知竖直方向的线段AB长6cm.如果AB沿水平方向平移8cm,那么AB扫过的区域图形的面积是 cm2.11、三角形的三个外角的比为2:3:4,则三个内角的比为.12、(1)作出右图中AABC的高应?,角平分线BE,中线 S(2)将XABC 平移,平移方向箭头所示,平移的距离为所示箭头的长度。
13、平面内的两条直线有相交和平行两种位置关系.(1)AB//CD.如图a,点F在A3、%外部时,由AB〃CD,有ZB= 4B0D,又因Z BOD 是APOD 的外角,故-BOD=踪BPD * 么D,得一BPD=£B—/D.如图b,以上结论是否成立?若不成立,贝\\ZBPD、曷、匕力之间有何数量关系?请证明你的结论; A -y5图a图》(2)在图力中,将直线0绕点月逆时针方向旋转一定角度交直线⑦于点0,如图c,则/BPD、/B、4 Z醐之间有何数量关系?(不需证明);(3)根据(2)的结论求图d中ZJ+ ZB+ Z C+ ZD+ ZE+ AF的度数.图d14、操作与探究探索在如图25 —1至图25-3中,AABC的面积为a.(1)如图25-1,延长AABC的边BC到点D,使CD=BC,连结DA.若AACD的面积为S”则S】= (用含a的代数式表示);(2)如图25-2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC, AE=CA,连结DE.若ADEC的面积为S2,则S2=(用含a的代数式表示),并写出理由;(3)在图25—2的基础上延长AB到点F,使BF=AB,连结FD, FE,得到ADEF (如图 25-3).若阴影部分的面积为S3,贝!JS3= (用含a的代数式表示).发现像上面那样,将AABC各边均顺次延长一倍,连结所得端点,得到ADEF (如图25-3),此时,我们称AABC向外扩展了一次.可以发现,扩展一次后得到的ADEF 的面积是原来AABC面积的倍.15、已知a, b, c是一个三角形的三条边长,化简:| a-b-c | +1b-a-c |-| c-a+b|16、如图所示,在AABC中,ZB=90° , AB=12cm, BC=16cm, P点从A开始沿AB边向B点以Icm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,几秒后APQB为等腰三角形?17、如图,已知直线1,//12,且L和匕、分别交于A、B两点,点P在直线AB上.(1)试找出/I、Z2. Z3之间的关系并说明理由;(2)当点P在A、B两点之间运动时,问Z1、匕2、Z3之间的关系是否发生变化?(3)如果点P在A、B两点外侧运动时,试探究匕1、匕2、Z3之间的关系(点P 和3A、B不重合,只要写出结论,不要证明)18、现有两块大小祖同的直角三角板△ ABC> AD EF, ZACB=ZDFE=90° , ZA=ZD=30° . %1将这两块三角板摆成如图a的形式,使B、F、E、A在同一条直线上,点C在边DF 上,DE与AC相交于点G,试求NAGD的度数.%1将图a中的AABC固定,把ADEF绕着点F逆时针旋转成如图b的形式,当旋转的角度等于多少度时,DF〃AC?并说明理由.。
习题课

一、主要内容
洛必达法则 Cauchy 中值定理
F ( x) x
0 ,1 , 型
0 0
型
f g 1 g 1 f 1 g 1 f
0 型 0 型
令y f 取对数
g
0 型
f g f 1g
Lagrange f (a ) f (b) Rolle 中值定理 定理
5 函数 y ln sin x 在 [ , ] 上满足罗尔定理 6 6 的条件.
由 y cot x 0,
5 在 ( , ) 内显然有解 x . 2 6 6 取 , 则 f ( ) 0. 2
这就验证了命题的正确性.
例2
x2 求极限 lim 5 . x 0 1 5 x (1 x )
导数的应用 单调性,极值与最值, 凹凸性,拐点,函数 图形果函数 f ( x ) 在闭区间 [a , b]上连续,在开区间(a , b ) 内可导,且在区间端 点的函数值相等,即 f (a ) f (b ) ,那末在(a , b ) 内至少有一点(a b ),使得函数 f ( x ) 在该 点的导数等于零, f ' ( ) 0 即
(1) (2)
注意到
f (0) 0, f (1) 1,
由(1), (2)有 (4)
a f ( ) a b f ( ) f ( )
b 1 f ( ) a b (3) 1 f ( ) f ( )
a b (3)+(4),得 1 f ( )(a b ) f ( )(a b ) a b a b. f ( ) f ( )
第一步
f ' ( x ) 0 和 f " ( x ) 0 在函数定义 求出方程 域内的全部实根,用这些根同函数的间断点或导数 不存在的点把函数的定义域划分成几个部分区间.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
样例输入输出
张山 咸宁西路28号 西安 710049 张山 address: 710049 西安 咸宁西路28号 李四 李四 address: 710049 西安 咸宁西路28号
2018/10/20 13
class Address{ char Name[30]; char StreetAddress[30]; char City[30]; char Postcode[30]; public: Address(char *a,char *b,char *c,char *d){ strcpy(Name,a); strcpy(StreetAddress,b); strcpy(City,c); strcpy(Postcode,d); } 2018/10/20
void Init() { cin>>name>>age>>sex>>weight; } void ShowDog() { cout<<"Dog's name:"<<name<<endl; cout<<"Dog's age:"<<age<<endl; cout<<"Dog's sex:"<<sex<<endl; cout<<"Dog's weight:"<<weight<<endl; }
2018/10/20
19
计算机程序设计(C++)
第8章 习题
杨 琦
西安交通大学 计算机教学实验中心
2018/10/20
2012.10
20
20
1. 设计一个点类Point和其派生类彩色点类ColorPoint。
样例输入输出
11345 [x,y]=1,1 r*256*256+g*256+b=197637
2018/10/20
{}
6
double Area() { return (double)fabs((x1-x2)*(y1-y2))/4*pi;
}
}; int main(){ int x1,y1,x2,y2; cin >> x1 >> y1 >> x2 >> y2; Ellipse e1(x1,y1,x2,y2); cout << "The area of e1:" << e1.Area() << endl; cout << "The perimeter of e1:" << e1.Perimeter() << endl; return 0; } 2018/10/20 7
2. 设计一个Person类和其派生类教师teacher,新增的 属性有专业、职称和主讲课程,并为这些属性定义 相应的方法。
样例输入输出
11050632 Jack male 32 math prof mathapp 身份证号:11050632 姓名:Jack 性别:male 年龄:32 专业:math 职称:prof 主讲课程:mathapp
{
25
virtual void display() { cout<<"身份证号:"<<ID<<endl; cout<<"姓名:"<<Name<<endl; cout<<"性别:"<<Sex<<endl; cout<<"年龄:"<<Age<<endl; } };
2018/10/20
26
class teacher:public Person{ string Major; //专业 string Title; //职称 string Course; //主讲课程 public: teacher(string id, string name, string sex, int age, string major, string title, string course):Person(id,name,sex,age) { Major=major; Title=title; Course=course; } 2018/10/20 27
22
public: ColorPoint(int a,int bb,int c,int d,int e):Point(a,bb){ r=c;g=d;b=e; } void Print() { cout<<"[x,y]="<<x<<","<<y<<endl; cout<<"r*256*256+g*256+b="<<r*256*256+g*256+b<<endl; } }; int main(){ int a,b,c,d,e; cin>>a>>b>>c>>d>>e; ColorPoint x(a,b,c,d,e); x.Print(); return 0; 2018/10/20 23 }
9
};
int type() { double a,b,c,d; a=f1; b=f2; c=f3; if(a>b) { d=a; a=b;b=d; } if(b>c) { d=b; b=c;c=d; } if(a*a+b*b==c*c) return 0;//直角 else if(a*a+b*b<c*c) return 1;//钝角 else return -1;//锐角 } 2018/10/20
2018/10/20 1
class Dog{ char name[20]; int age; char sex; float weight; public: Dog(char *Name="a", int Age=0, char Sex='m', float Weight=0) { strcpy(name,Name); age = Age; sex = Sex; weight = Weight; 2018/10/20 2 }
{
break; break; break;
11
}
} else
cout<<"不能构成三角形"<<endl; return 0; }
201实现地址类Address,包括姓名、所居住的
街道地址、城市和邮编等属性以及改变对象姓名的 Changename函数、显示地址信息的Display函数。
2018/10/20 24
class Person{ string ID; //身份证号 string Name; //姓名 string Sex; //性别 int Age; //年龄 public: Person(string id, string name, string sex, int age) ID= id; Name= name; Sex= sex; Age= age; } 2018/10/20
2018/10/20
21
#include <iostream> using namespace std; class Point{ public: int x, y; Point( int a= 0, int b= 0 ) { x=a;y=b; } }; class ColorPoint : public Point{ int r, g, b; 2018/10/20
样例输入输出
1123 The area of e1:1.5708 The perimeter of e1:5.14159
2018/10/20 5
const double pi=3.1415926; class Ellipse{ double x1,y1,x2,y2; public: Ellipse(int a,int b,int c,int d):x1(a),y1(b),x2(c),y2(d) double Perimeter() { double a=fabs(x1-x2)/2; double b=fabs(y1-y2)/2; if(a>=b) return 2*pi*b+4*(a-b); else return 2*pi*a+4*(b-a); }
计算机程序设计(C++)
第7章 习题
杨 琦
西安交通大学 计算机教学实验中心
2018/10/20
2012.10
0
0
1. 定义并实现Dog类,包含name、age、sex、weight 等属性以及初始化和显示属性的方法,要求用一般 成员函数和构造函数两种方法实现初始化操作。
样例输入输出
Ahuang 3 m 2.5 Dog's name:Ahuang Dog's age:3 Dog's sex:m Dog's weight:2.5
14
void Changename(char *a) { strcpy(Name,a); } void Display() { cout<<Name<<" address:"<<endl; cout<<Postcode<<" "<<City<<" "<<StreetAddress<<endl; } };
