广东省肇庆市实验中学高中数学必修二3.1.3直线的点斜式方程(3) “三四五”高效课堂教学设计
人教版高中数学必修第二册直线方程的点斜式

直线方程的点斜式课 型 新授课教学目标1.掌握由一点和斜率导出直线方程的方法2.掌握直线方程的点斜式,知道斜截式是点斜式的特例 3能根据条件熟练地求出直线的方程,并写出斜率和截距教学重点 根据条件写直线的点斜式方程教学难点点斜式方程的推导 一复习引入1.直线的倾斜角α的X 围是⎥⎦⎤⎢⎣⎡65,3ππ ,那么该直线斜率的取值X 围是 2.假设斜率为2的直线L 上有三个点A(2,3),B(1,y),C(x,-5)那么x= ,y=3.确定一条直线需要哪些条件?二.新课讲解1.直线方程的点斜式[问题]假设直线经过点P 0(x 0,y 0)且斜率为k ,求直线L 的方程这个方程是由直线上一点和直线的斜率确定的,叫做直线方程的点斜式注① 要注意到)(00x x k y y -=-与k x x y y =--00是不同的,前者表示整条直线,后者表示直线上缺少一个点P 0②如果直线过点P 0且平行于x 轴,直线方程是y=y 0③如果直线于y 轴,直线方程不能用点斜式表示,但上每一点的横坐标都等于x 0,它的方程是x= x 0 例1一条直线经过点〔-2,3〕,倾斜角为450,求这条直线的方程并画出图形 练习P39 T1,T22,直线方程的斜截式[问题]直线的斜率是k ,与y 轴的交点是P(0,b),求直线的方程注①b 为直线在轴上的截距,这个方程是由直线的斜率和它在轴的截距确定的,称为直线方程的斜截式②一次函数y=kx+b 中,常数K 是直线的斜率,常数b 就是直线在轴上的截距例2 一直线l 经过点P(-2,2),且倾斜角是直线x-3y-6=0倾斜角的一半,求直线l 的方程例3直线l过点〔2,1〕和点〔a,2〕,求它的方程三.小结四.作业。
高中数学 第三章 直线与方程 3.2.1 直线的点斜式方程课件 新人教A版必修2

【思维激活】 已知△ABC中,A(1,-4),B(2,6),C(-2,0),AD⊥BC于D,求 直线AD的方程.
解:由题意知,kBC= 6 0 = 3 ,因为 AD⊥BC,所以直线 AD 的斜率存在, 22 2
且 kAD=- 2 . 3
故直线 AD 的方程为 y+4=- 2 (x-1). 3
【备用例1】 已知直线l过点A(2,1),且斜率与直线y-1=4x-3的斜率互为 负倒数,求直线l的方程.
3.(直线的斜截式方程)直线y=2x-4在y轴上的截距为( C ) (A)-2 (B)2 (C)-4 (D)4
4.(直线的斜截式方程)在y轴上的截距为2,且与直线y=-3x-4平行的直线的
斜截式方程为
.
答案:y=-3x+2
5.(两直线平行或垂直关系) 若直线l1:y=(2a-1)x+3与直线l2:y=4x-3垂直,
(2)说明:如图所示,过定点P(x0,y0),倾斜角是90°的直线没有点斜式,其 方程为x-x0=0,或 x=x.0
2.直线的斜截式方程 (1)定义:如图所示,直线l的斜率为k,且与y轴的交点为(0,b),则方程 y=kx+b叫 做直线l的斜截式方程,简称斜截式.
(2)说明:一条直线与y轴的交点(0,b)的纵坐标b叫做直线在y轴上的 截距 . 倾斜角是 直角 的直线没有斜截式方程.
3 又直线 l 过点(3,4),所以 4= 3 ×3+b,所以 b=4- 3 ,
3 所以直线 l 的方程为 y= 3 x- 3 +4.
5
5
题型二 直线的斜截式方程
【教师备用】 1.直线的斜截式方程与一次函数有何关系? 提示:当k≠0时,斜截式方程y=kx+b是一次函数的形式;而一次函数 y=kx+b中,k是直线的斜率,常数b是直线在y轴上的截距,一次函数表示直 线,但是有些直线的方程不一定能写成一次函数的形式. 2.截距与距离有何区别? 提示:截距与距离是两个不同的概念,截距b可以大于等于或小于0,而距离 只能是非负的实数.
人教版高中数学必修二课件:3.2.1 直线的点斜式方程(讲授式) (共28张PPT)

新课引入
直线的方程
引入新课
在平面直角坐标系内,如果给定一条直
线 l 经过的一个点 P0(x0,y0)和斜率k,能否将直线l上所
有点的坐标(x,y)满足的关系表示出来?
本节课我们将要学习直线的方程来解决这个问题.
新课讲授
直线方程的概念
思考3: 已知直线 l 经过已知点P0(x0,y0),并且它
的斜率是k,P(x,y)是直线 l 上不同于点P0的任意一点,那
学中普遍存在相互联系、相互转化等观点,使学
生能用联系的观点看问题.
学习目标
三维目标及重难点分析
4 .重点与难点 重点 直线的点斜式方程和斜截式方程.
难点
直线的点斜式方程和斜截式方程的应用.
复习回顾
直线的倾斜角和斜率
思考1
在平面直角坐标系内如何确定一条直线呢?
答:(1)已知两点可以确定一条直线. (2)已知直线上的一点和这条直线的一个方向(斜率 或倾斜角)可以确定一条直线. 思考2 答: 直线的斜率公式是什么? 时直线斜率不存在.
几何意义. 答:方程y=kx+b左端y的系数恒为1; 右端x的系数为直线的斜率,常数项b为直线的纵截距. 直线方程的斜截式:由于方程y=kx+b是由直线的斜率k与它在y轴 上的截距b确定,所以我们称方程y=kx+b为直线方程的斜截式. 适用条件:直线的斜率k和在y轴上的截距b均存在, 因此不能用来表示斜率不存在的直线.
答:斜率不存在或倾斜角为90°时,
显然直线 l 上的任何一点的横坐标均相同, y 均为x0,而y0可以为任意实数,所以这时的 直线方程为x= x0 或x- x0=0. 特别的,y 轴所在的直线上的每一点的横坐
O
l ������0 ������0 ,
高中数学必修二《直线的点斜式方程》PPT

由一般到特殊的思想、数形结合思想、转化思想、方程思想
复习回顾:
一、直线的倾斜角与斜率
(1)直线的倾斜角;
(2)直线的斜率; k tan ( 90 ) 倾斜角为 90 时,斜率不存在
(3)两点间斜率公式.
k
y2 x2
y1 x1
( x1
x2 )
二、直线的关系
(1)直线的倾斜角;l1 // l2 k1 k2 或斜率都不存在
(2)直线的斜率;l1 l2 k1 k2 1
与直线l1:y=kx+b1平行的所有直线的方程为:y=kx+b
练习2.
1、写出下列直线的斜截式方程:
(1)斜率是
3 ,在 y 轴上的截距是 2; y
2
3 x2 2
(2)斜率是 2,在 y轴上的截距是 4 ; y 2x 4
2、判断下列各对直线是否平行或垂直:
(1)
l1
:
y
1 2
x
3
,
l2
:
y
1 2
y-b=k(x-0), 即y=kx+b。(2)
(0,b)
O
x
直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。 方程(2)是由直线的斜率k与它在y轴上的截距b确定, 所以方程(2)叫做直线的斜截式方程,简称斜截式。
注意:斜截式方程的形式特点并对比一次函数形式
例2.斜率是5,在y轴上的截距是4的直线方程。
3.指出直线y-4= 3 (x+3)的倾斜角和所经过的定点。
【解析】由点斜式方程的特点,直线过定点(-3,4),
斜率 k= 3 ,设倾斜角为 α, 则 tanα= 3 ,∴α=120°.
2019-2020年高中数学必修二教案:3-2《直线的点斜式方程》

2019-2020年高中数学必修二教案:3-2《直线的点斜式方程》教学目标1.使学生掌握点斜式和斜截式的推导过程,并能根据条件,熟练求出直线的点斜式方程和斜截式方程.2.会用直线的方程求出斜率、倾斜角、截距等问题,并能根据方程画出方程所表示的直线.3.培养学生化归数学问题的能力及利用知识解决问题的能力.4.理解直线方程点斜式和斜截式的形式特点和适用范围.教学重点与难点重点:直线方程的点斜式的公式推导以及有已知条件求直线的方程.难点:直线方程点斜式推导过程的理解.教学过程一、创设情景师:上一节我们分析了在直角坐标系内确定一条直线的几何要素。
那么,我们能否用给定的条件(点P 0的坐标和斜率k ,或P 1,P 2的坐标),将直线上的所有点的坐标(,x y )满足的关系表示出来呢?这节课,我们一起学习直线的点斜式方程.二、探求新知师:若直线l 经过点000(,)P x y ,且斜率为k ,求直线l 的方程.生:(给学生以适当的引导)设点P (,x y )是直线l 上不同于点0P 的任意一点,因为直线l 的斜率为k ,由斜率公式得:00y y k x x -=-,可化为: 00()y y k x x -=- ①〖探究〗:思考下面的问题:(不必严格地证明,只要求验证)(1)、过点000(,)P x y ,斜率为k 的直线l 上的点,其坐标都满足方程①吗?(2)、坐标满足方程①的点都在过点000(,)P x y ,斜率为k 的直线l 上吗?生:经过探究和验证,上述的两条都成立.所以方程①就是过点000(,)P x y ,斜率为k 的直线l 的方程.因此得到:(一)、直线的点斜式方程:其中(00,x y )为直线上一点坐标,k 为直线的斜率.方程①是由直线上一定点及其斜率确定,叫做直线的点斜式方程,简称点斜式.师:直线的点斜式方程能否表示坐标平面上的所有直线呢?(让学生思考,互相讨论) 生1:不能,因为不是所有的直线都有斜率.生2:对,因为直线的点斜式方程要用到直线的斜率,有斜率的直线才能写成点斜式方程,如果直线没有斜率,其方程就不能用点斜式表示.师:very good !那么,x 轴所在直线的方程是什么?y 轴所在直线的方程又是什么?生:因为x 轴所在直线的斜率为k =0,且过点(0,0),所以x 轴所在直线的方程是y =0.(即:x 轴所在直线上的每一点的纵坐标都等于0.)而y 轴所在直线的斜率不存在,它的方程不能用点斜式表示。
高中数学必修二人教A版课件:3.2.1 直线的点斜式方程

4.(直线的斜截式方程)在y轴上的截距为2,且与直线y=-3x-4平行的直线的 斜截式方程为 答案:y=-3x+2 .
5.(两直线平行或垂直关系)若直线l过点(0,7),且与直线y=-4x+2垂直,则直 线l的方程为 .
答案:y=
1 x+7 4
课堂探究·素养提升
题型一 直线的点斜式方程 【例1】 (2018· 烟台调研)求满足下列条件的直线方程: (1)过点P(-4,3),斜率k=-3; (2)过点P(3,-4),斜率k=3; 解 : (1) 因为直线过点 P(-4,3), 斜率 k=-3, 所以直线的点斜式方程为 y-3= -3(x+4),即y=-3x-9. (2)因为直线过点P(3,-4),斜率k=3,所以直线的点斜式方程为y+4=3(x-3), 即y=3x-13.
负时,它等于直线与y轴交点到原点距离的相反数.
自我检测
1.(直线的点斜式方程)直线方程可表示成点斜式方程的条件是( A (A)直线的斜率存在 (B)直线的斜率不存在 (C)直线不过原点 (D)以上均不正确
x-2y-4=0 的斜率的倒数,则直线 l 的方程为( A (A)y= 3 x+2 (C)y= 3 x+ (B)y= 3 x-2 (D)y=- 3 x+2
课堂探究
新知探求·素养养成
点击进入 情境导学
知识探究
1.直线的点斜式方程 (1)定义:如图所示,直线l过定点P(x0,y0),斜率为k,则把方程y-y0=k(x-x0) 叫做直线l的点斜式方程,简称点斜式.
(2)说明:如图所示,过定点P(x0,y0),倾斜角是90°的直线没有点斜式,其方 x=x0 程为x-x =0,或 .
标,均可用直线方程的点斜式表示,直线方程的点斜式,应在直线斜率存在的 条件下使用.当直线的斜率不存在时,直线方程为x=x0.
高中数学必修二教案-直线的点斜式方程

直线的点斜式方程【教学目标】1.掌握由一点和斜率导出直线方程的方法,掌握直线的点斜式方程,了解直线方程的斜截式是点斜式的特例;培养学生思维的严谨性和相互合作意识,注意学生语言表述能力的训练.2.引导学生根据直线这一结论探讨确定一条直线的条件,并会利用探讨出的条件求出直线的方程.培养学生形成严谨的科学态度和求简的数学精神.3.掌握直线方程的点斜式的特征及适用范围,培养和提高学生联系、对应、转化等辩证思维能力.【重点难点】教学重点:引导学生根据直线这一结论探讨确定一条直线的条件,并会利用探讨出的条件求出直线的方程.教学难点:在理解的基础上掌握直线方程的点斜式的特征及适用范围.【课时安排】1课时【教学过程】导入新课方程y=kx+b与直线l之间存在着什么样的关系?让学生边回答,教师边适当板书.它们之间存在着一一对应关系,即(1)直线l上任意一点P(x1,y1)的坐标是方程y=kx+b的解.(2)(x1,y1)是方程y=kx+b的解 点P(x1,y1)在直线l上.这样好像直线能用方程表示,这节课我们就来学习、研究这个问题——直线的方程(宣布课题).推进新课新知探究提出问题①如果把直线当做结论,那么确定一条直线需要几个条件?如何根据所给条件求出直线的方程?②已知直线l的斜率k且l经过点P1(x1,y1),如何求直线l的方程?③方程导出的条件是什么?④若直线的斜率k 不存在,则直线方程怎样表示?⑤k=11x x y y --与y-y 1=k(x-x 1)表示同一直线吗?⑥已知直线l 的斜率k 且l 经过点(0,b),如何求直线l 的方程? 讨论结果:①确定一条直线需要两个条件: a.确定一条直线只需知道k 、b 即可;b.确定一条直线只需知道直线l 上两个不同的已知点.②设P(x ,y)为l 上任意一点,由经过两点的直线的斜率公式,得k=11x x y y --,化简,得y -y 1=k(x -x 1).③方程导出的条件是直线l 的斜率k 存在. ④a.x=0;b.x=x 1.⑤启发学生回答:方程k=11x x y y --表示的直线l 缺少一个点P 1(x 1,y 1),而方程y -y 1=k(x -x 1)表示的直线l 才是整条直线. ⑥y=kx+b. 应用示例例1 已知直线l 1:y=4x 和点P(6,4),过点P 引一直线l 与l 1交于点Q ,与x 轴正半轴交于点R ,当△OQR 的面积最小时,求直线l 的方程.活动:因为直线l 过定点P(6,4),所以只要求出点Q 的坐标,就能由直线方程的两点式写出直线l 的方程.解:因为过点P(6,4)的直线方程为x=6和y -4=k(x -6),当l 的方程为x=6时,△OQR 的面积为S=72;当l 的方程为y -4=k(x -6)时,有R(k k 46-,0),Q (k k 46-,41624--k k ),此时△OQR 的面积为S=21×k k 46-×41624--k k =)4()23(82--k k k .变形为(S -72)k 2+(96-4S)k -32=0(S≠72). 因为上述方程根的判别式Δ≥0,所以得S≥40. 当且仅当k=-1时,S 有最小值40.因此,直线l 的方程为y -4=-(x -6),即x +y -10=0.点评:本例是一道有关函数最值的综合题.如何恰当选取自变量,建立面积函数是解答本题的关键.怎样求这个面积函数的最值,学生可能有困难,教师宜根据学生的实际情况进行启发和指导. 变式训练如图1,要在土地ABCDE 上划出一块长方形地面(不改变方向),问如何设计才能使占地面积最大?并求出最大面积(精确到1 m 2)(单位:m ).图1解:建立如图直角坐标系,在线段AB 上任取一点P 分别向CD 、DE 作垂线,划得一矩形土地.∵AB 方程为2030x x +=1,则设P(x,20-32x)(0≤x≤30), 则S 矩形=(100-x)[80-(20-32x)] =-32(x-5)2+6 000+350(0≤x≤30), 当x=5时,y=350,即P (5,350)时,(S 矩形)max =6 017(m 2).例2 设△ABC 的顶点A(1,3),边AB 、AC 上的中线所在直线的方程分别为x -2y+1=0,y=1,求△ABC 中AB 、AC 各边所在直线的方程.活动:为了搞清△ABC 中各有关元素的位置状况,我们首先根据已知条件,画出简图3,帮助思考问题.解:如图2,设AC 的中点为F ,AC 边上的中线BF :y=1.图2AB 边的中点为E ,AB 边上中线 CE :x -2y +1=0.设C 点坐标为(m ,n),则F(23,21++n m ). 又F 在AC 中线上,则23+n =1,∴n=-1.又C 点在中线CE 上,应当满足CE 的方程,则m -2n +1=0. ∴m=-3.∴C 点为(-3,-1).设B 点为(a,1),则AB 中点E(213,21++a ),即E(21a+,2). 又E 在AB 中线上,则21a+-4+1=0.∴a=5.∴B 点为(5,1).由两点式,得到AB ,AC 所在直线的方程AC :x -y +2=0,AB :x +2y -7=0. 点评:此题思路较为复杂,应使同学们做完后从中领悟到两点: (1)中点分式要灵活应用;(2)如果一个点在直线上,则这点的坐标满足这条直线的方程,这一观念必须牢牢地树立起来. 变式训练已知点M (1,0),N (-1,0),点P 为直线2x-y-1=0上的动点,则|PM|2+|PN|2的最小值为何?解:∵P 点在直线2x-y-1=0上,∴设P (x 0,2x 0-1).∴|PM|2+|PN|2=10(x 0-52)2+512≥512.∴最小值为512.拓展提升已知直线y=kx +k +2与以A(0,-3)、B(3,0)为端点的线段相交,求实数k 的取值范围.图3活动:此题要首先画出图形3,帮助我们找寻思路,仔细研究直线y=kx +k +2,我们发现它可以变为y -2=k(x +1),这就可以看出,这是过(-1,2)点的一组直线.设这个定点为P(-1,2).解:我们设PA 的倾斜角为α1,PC 的倾斜角为α,PB 的倾斜角为α2,且α1<α<α2.则k 1=tan α1<k <k 2=tan α2.又k 1=132-+=-5,k 2=312--=-21,则实数k 的取值范围是-5<k <-21.课堂小结通过本节学习,要求大家:1.掌握由一点和斜率导出直线方程的方法,掌握直线的点斜式方程,了解直线方程的斜截式是点斜式的特例.2.引导学生根据直线这一结论探讨确定一条直线的条件,并会利用探讨出的条件求出直线的方程. 作业习题3.2 A 组2、3、5.。
24【提高】直线的点斜式与两点式方程知识讲解-高中数学必修二

故直线 l 的方程为 x=1 或 y 3 (x 1) 。 3
2
【总结升华】(1)由于直线 l 过点(1,0),因此求直线 l 的方程的关键在于求出它的斜率,由此可知,
何时选择点斜式来求直线方程的依据是题目是否给出了(或者能够求出)直线上的一点的坐标和其斜率。 (2)利用点斜式求直线方程的步骤是:①判断斜率 k 是否存在,并求出存在时的斜率;②在直线上
(2)直线 MN 的斜率 k 2 2 0 ,所以该直线平行于 x 轴. 5 (1)
又直线 l 垂直于直线 MN,因此直线 l 的倾斜角为 90°,又直线 l 过点 P(2,-3),所以直线 l 的方程
为 x-2=0,即 x=2. 【总结升华】用点斜式求直线方程,首先要确定一个点的坐标,其次判断斜率是否存在,只有在斜率
【答案】(1)x+y-7=0(2)x=2
【解析】(1)直线 y=x+1 的斜率 k=1,所以倾斜角为 45°.由题意知,直线 l 的倾斜角为 135°,所 以直线 l 的斜率 k'=tan135°=-1.
又点 P(3,4)在直线 l 上,由点斜式方程知,直线 l 的方程为 y-4=-(x-3),即 x+y-7=0.
1
4.在应用两点式求直线方程时,往往把分式形式
y y1 y2 y1
x x1 x2 x1
( x1
x2 , y1
y2 ) 通过交叉相乘转
化为整式形式 ( y y1)(x2 x1) ( y2 y1)(x x1) ,从而得到的方程中,包含了 x1=x2 或 y1=y2 的情况,但
此转化过程不是一个等价的转化过程,不能因此忽略由 x1、x2 和 y1、y2 是否相等引起的讨论.要避免讨论, 可直接假设两点式的整式形式.
2019高中数学必修2教案3.2.1 直线的点斜式方程

教师课时教案备课人授课时间课题 3.2.1 直线的点斜式方程课标要求直线的点斜式、斜截式方程教学目标知识目标理解直线方程的点斜式、斜截式的形式特点和适用范围;技能目标能正确利用直线的点斜式、斜截式公式求直线方程。
情感态度价值观让学生体会直线的斜截式方程与一次函数的关系,培养学生数形结合的思想渗透数学中普遍存在相互联系、相互转化等观点重点直线的点斜式方程和斜截式方程。
难点直线的点斜式方程和斜截式方程的应用。
教问题与情境及教师活动学生活动学过程及方法一、创设情境问题:坐标系内确定一条直线,应知道哪些条件?已知直线上的一点和直线的倾斜角(斜率)可以确定一条直线,已知两点也可以确定一条直线.在直线坐标系中,给定一个点),(yxP和斜率k,或给定两个点),(),,(222211yxPxxP,就能唯一确定一条直线.也就是说,平面直线坐标系中的点在不在这条直线上是完全确定的.节课研究的是给定一个点),(yxP和斜率k,怎样确定一条直线?二、直线的点斜式方程直线l经过点),(yxP,且斜率为k.设点),(yxP是直线l上不同于点P的任意一点,因为直线l的斜率为k,根据斜率公式得,当xx≠时,xxyyk--=,即)(xxkyy-=-(1).yxOPP0注:1.过点),(yxP,斜率是k的直线l上的点,其坐标都满足方程(1).学生回顾,并回答学生验证1教师课时教案问题与情境及教师活动学生活动。
广东省肇庆市实验中学高中数学二:3.1.3直线的点斜式方程(2)“三四五”高效课堂教学设计

(2) 方法一: 设所求直线的斜率为 k1 ,因为直线 y 2x 1的斜
学必求其心得,业必贵于专精
率为
k
2
,根据两直线垂直的条件,可得
2
k1
1
,即
k1
1 2
,由点
斜式可得 y 3 1 (x 2) ,即 y 1 x 4 为所求.
2
2
方法二: 设所求的直线方程为 y 1 x b ,将点 A 的坐标代入 2
学必求其心得,业必贵于专精
“三四五”高效课堂教学设计:
(授课日期:
年月
日 星期
班
级
)
拟
课
授课题
时
第 31 课 直线的点斜式方程(2)
目
第
课
时
明 确 目 根据确定直线位置的几何要素,探索并掌握直线方程
标
的点斜式.
重 点 难 重点:
点
难点:
课型 □ 讲 授
□习题
□复习
□讨论
□其它
教学内容与教师活动设计
学生
得 , 3 1 2 b 解得 b 4 ,所以,所求直线方程为 y 1 x 4 。
2
2
【点评】一般地,求与直线 l1 : y kx b1 平行的直线方程可设为
y
kx
b2
(b1
b2
)
,求与直线
l1
垂直的直线的方程可设为
y
1 k
x
b(k
0)
☆自主探究 2
(1)已知直线 l1 的倾斜角为 300 ,则过点 P(2,3) 且与直线 l1 平行的
直线 3x y 2 0 的斜率和在 y 轴上的截距. 【解析】直线方程 3x y 2 0 可化为 y 3x 2 所以,直线 3x y 2 0 的斜率为 k 3 ,它在 y 轴上的截距为 b 2 。 【点评】已知直线的方程求斜率和截距的步骤是:第一步:
广东省肇庆市实验中学高中数学必修二:3.1.3直线的点斜式方程(3) “三四五”高效课堂教学设计

“三四五”高效课堂教学设计:(授课日期: 年月 日 星期 班级 )授课题目 第32课 直线的点斜式方程(3)拟 课时第 课时明确目标 根据确定直线位置的几何要素,探索并掌握数学思想方法. 重点难点重点: 难点:课型□讲授 □习题 □复习 □讨论 □其它 教 学 内 容 与 教 师 活 动 设 计学生活动设计一、先学后讲1. 直线l 过点000(,)P x y 且斜率为k 的直线的方程为2.直线的斜截式方程为 二、合作探究 1. 数形结合的思想 例1方程10y ax a--=表示的直线可能是图中的( )【思路分析】要注意题设中的隐含条件:斜率为a 、截距为1a中都含同一个字母a ,且a≠0.抓住这一点,通过等价转化将方程化为熟悉的一元一次函数,再运用分类讨论思想使问题获得解决.将方程变形为1y ax a=+,则a 为直线的斜率, 1a为直线在y 轴上的截距.因为a ≠0,所以a >0或a <0. 4. 直线1:20l y +=与直线2:30l x -=的位置关系是5. 斜率与直线3x-2y=0的斜率相等,且过点(4,3)P-的直线方程是_____.当a>0时,四个图形都不可能是方程的直线;当a<0时,图形B是方程的直线.【解析】B【点评】根据直线的方程判断直线的形状,通常把直线转化成斜截式的形式,利用斜率和截距的几何意义作出判断.☆自主探究1直线y=ax+b(a+b=0)的图象是( )2. 分类讨论思想例2已知直线l经过点(5,4)P--,且l与两坐标轴围成的三角形的面积为5,求直线l的方程.【思路分析】经过点(5,4)P--且l与两坐标轴能围成的三角形的直线有两种:一种是斜率大于零,另一种是斜率小于零,因此要对斜率进行分类讨论。
【解析】由已知得l与两坐标轴不垂直.∵直线l经过点(5,4)P--,∴可设直线l的方程为(4)[(5)]y k x--=--,即4(5)y k x+=+.则直线l在x轴上的截距为45k-,在y轴上的截距为54k-.根据题意得14|5||54|52kk--=g g,即2(54)10||k k-=.①当0k>时,原方程可化为2(54)10k k-=,解得1228,55k k==;②当0k<时,原方程可化为2(54)10k k-=-,此方程无实数解.综上所得直线l的方程为24(5)5y x+=+,或84(5)5y x+=+.即25100x y--=或85200x y-+=.【点评】已知直线过一点时,常设其点斜式方程,但需注意斜率不存在的直线不能用点斜式表示,从而使用点斜式或斜截式方程时,要考虑斜率不存在的情况,以免丢解. 而直线在坐标轴上的截距,可正、可负,也可以为零,不能与距离混为一谈,注意如何由直线方程求其在坐标轴上的截距. ☆自主探究2a 为何值时,直线210x ax +-=与直线(31)10a x ax ---=平行?三、总结提升1、本节课你主要学习了 四、问题过关1. 直线l 的方程为y kx b =+,图象如图所示,则,k b 满足( )A. 0,0k b >>B. 0,0k b ><C. 0,0k b <>D. 0,0k b << 2. 已知直线l 1:0ax y b --=,l 2:0bx y a -+= ,当a 、b 满足一定的条件时,它们的图形可能是图中的( )3. 若直线0ax by c ++=的图象过第一、二、三象限,则( )A.0,0ab bc >>B. 0,0ab bc ><C. 0,0ab bc <>D. 0,0ab bc <<4. 直线l 的方程为y kx b =+,图象如图所示,则_____,____k b ==.因材施教:教学后记:。
广东省肇庆市实验中学高中数学二:3.3.1两条直线的交点坐标“三四五”高效课堂教学设计

“三四五”高效课堂教学设计:
(授课日期: 年月日星期班
级)
所以直线l的方程为4x+3y-6=0.
【点评】两条直线的位置与两条直线的交点存在着等价关系,两条直线的交点又与其方程组成的方程组存在着等价关系,即两直线相交有一个交点方程组有唯一解,对于垂直直线的斜率,两者之积为-1,知其一可求另一个;平行直线的斜率相等。
☆自主探究1
求经过两直线l1:x-2y+4=0和l2:x+y-2=0的交点P,且与直线l3:3x-4y+5=0平行的直线l的方程。
三、总结提升
1、本节课你主要学习了
四、问题过关
1.求经过直线l1:x-3y+4=0和l2:2x+y+5=0的交点,并且经过原点的直线的方程.。
高中数学必修二导学案:第三章第二节直线的点斜式方程

第三章第二节直线的点斜式方程三维目标1.掌握直线方程的点斜式、斜截式的形式特点和适用范围; 2.能正确利用直线的点斜式、斜截式公式求直线方程; 3. 学生学会由一般到特殊的处理问题方法,体会数形结合思想.________________________________________________________________________________ 目标三导 学做思1*问题1.直线l 经过定点)2,1(0P ,且斜率为3.设点),(y x P 是直线l 上不同于0P 的任意一点,请表示出y x ,之间关系。
问题2.在问题1中,经过点)2,1(0P ,且斜率为3的直线l 上任意一点的坐标是否都满足方程(我们所求出y x ,的关系)呢?反过来,是否所有坐标满足该方程的点都在直线l 上呢?问题3. 直线l 经过定点),(000y x P ,且斜率为k 的直线方程是什么?该方程的名称是什么?它是否表示坐标平面上经过),(000y x P 的所有直线呢?问题4.经过点),(000y x P 且平行于x 轴(即垂直于y 轴)的直线方程是什么?经过点),(000y x P 且平行于y 轴(即垂直于x 轴)的直线方程是什么?x 轴所在直线的方程是什么?y 轴所在直线的方程是什么?问题5.若直线l 的斜率为k ,与y 轴的交点坐标为(0,b),请先求出直线l 的方程,然后思考:符合条件的直线l 的方程具有怎样的特点?它和一次函数有何关系?其中k,b 分别有何几何意义?【学做思2】1. 写出满足下列条件的直线方程(1)过点(-1,2); (2)过点(-1,-3),倾斜角为135°; (3)倾斜角是60°,在y 轴上的截距是5.2. 已知直线111:l y k x b =+;直线222:l y k x b =+,试讨论 (1) 21//l l 的条件是什么? (2) 21l l ⊥的条件是什么?3.写出分别满足下列条件的直线1l 的方程(1)直线1l 在y 轴上截距为-2,且与直线2l :y =-x +2垂直 (2) 直线1l 在x 轴上截距为-2,且与直线2l :y =2x +7平行达标检测1. 经过点(-1,1),倾斜角是直线y =33x -2的倾斜角的2倍的直线方程是( ) A .x =-1 B .y =1 C .y -1=233(x +1) D .y -1=3(x +1)2. 直线l :y -1=k (x +2)的倾斜角为135°,则直线l 在y 轴上的截距是( ) A .1B .-1 C.22D .-23. 与直线y =2x +1垂直,且在y 轴上的截距为4的直线的斜截式方程为( ) A .142y x =+ B . 24y x =+ C. 24y x =-+ D .142y x =-+ 4. 过点P(2,1),平行于y 轴的直线方程为_______ _;过点P(2,1),平行于x 的轴的直线方程为______ __.5. 不论k 取何值,直线kx -y +k +3=0恒过定点__________.第三章 第二节 直线的两点式方程三维目标1.掌握直线方程的两点式的形式特点及适用范围; 2.了解直线方程截距式的形式特点及适用范围;3.学会用联系的观点看问题,认识事物之间的普遍联系与相互转化.________________________________________________________________________________目标三导 学做思1问题1.请尝试用直线的点斜式方程解决:若直线l 经过两点A(2,1)、B(0,3),求直线l 的方程.问题2.一般地,若直线l 经过两点),(),,(222111y x P y x P 其中),(2121y y x x ≠≠,如何求直线l 的方程呢?请写出过程.问题3.试求经过两点)3,2(),2,1(21-P P 的直线l 的方程.问题4.在问题2中,如果两点),(),,(222111y x P y x P 的横坐标相等()21x x =,此时直线l 的方程是什么?如果两点),(),,(222111y x P y x P 的纵坐标相等()21y y =,此时直线l 的方程又是什么?问题5.若直线l 与x 轴的交点为A )0,(a ,与y 轴的交点为B ),0(b ,其中0,0≠≠b a ,你能用两点式求出直线l 的方程吗?【学做思2】1. 已知三角形的三个顶点分别为A(-5,0),B(3,-3),C(0,2),求(1)AB边所在直线的方程;(2)AC边所在直线的方程;(3)BC边上的中线所在的直线方程.2. 已知直线l经过点P(5,0),且在两坐标轴上的截距之差为2,求直线l的方程。
【精品教案】高中数学必修2第三章《直线的点斜式方程》教案
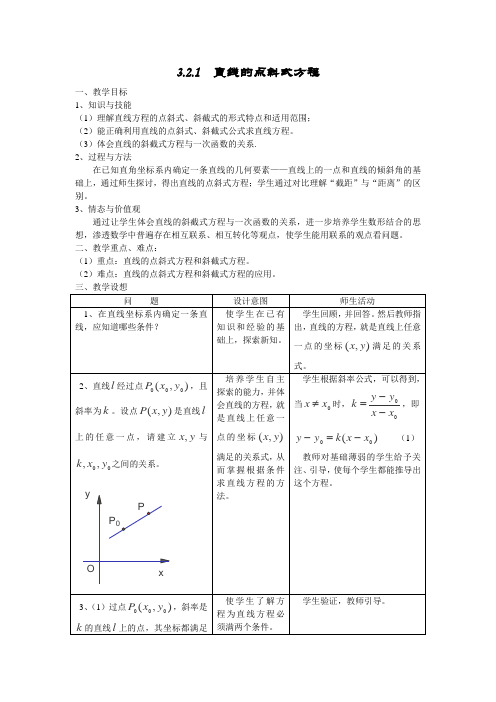
3.2.1 直线的点斜式方程
一、教学目标
1、知识与技能
(1)理解直线方程的点斜式、斜截式的形式特点和适用范围;
(2)能正确利用直线的点斜式、斜截式公式求直线方程。
(3)体会直线的斜截式方程与一次函数的关系.
2、过程与方法
在已知直角坐标系内确定一条直线的几何要素——直线上的一点和直线的倾斜角的基础上,通过师生探讨,得出直线的点斜式方程;学生通过对比理解“截距”与“距离”的区别。
3、情态与价值观
通过让学生体会直线的斜截式方程与一次函数的关系,进一步培养学生数形结合的思想,渗透数学中普遍存在相互联系、相互转化等观点,使学生能用联系的观点看问题。
二、教学重点、难点:
(1)重点:直线的点斜式方程和斜截式方程。
(2)难点:直线的点斜式方程和斜截式方程的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
) 课时 课时
学 内 容 与 教 师 活 动 设 计
)
【思路分析】要注意题设中的隐含条件:斜率为 a、截距为
1 中都含同一个字母 a,且 a
a≠0.抓住这一点,通过等价转化将方程化为熟悉的一元一次函数,再运用分类讨论思想 使问题获得解决.将方程变形为 y ax 截距.因为 a≠0,所以 a>0 或 a<0. 4. 直线 l1 : y 2 0 与直线 l2 : x 3 0 的位置关系是 5. 斜率与直线 3x-2y=0 的斜率相等,且过点 P (4,3) 的直线方程是_____.
2 5 8 5
丢解. 而直线在坐标轴上的截距,可正、可负,也可以为零,不能与距离混为一谈, 注意如何由直线方程求其在坐标轴上的截距. ☆自主探究 2
a 为何值时,直线 x 2ax 1 0 与直线 (3a 1) x ax 1 0 平行?
三、总结提升 1、本节课你主要学习了
四、问题b ,图象如图所示,则 k , b 满足( )
A. k 0, b 0
B. k 0, b 0
C. k 0, b 0
D. k 0, b 0
2. 已知直线 l1: ax y b 0 ,l2: bx y a 0 ,当 a、b 满足一定的条件时,它们的图形 可能是图中的( )
3. 若直线 ax by c 0 的图象过第一、二、三象限,则( A. ab 0, bc 0 B. ab 0, bc 0 C. ab 0, bc 0
“三四五”高效课堂教学设计: (授课日期: 授课题目 明确目标 重点难点 年 月 日 星期 班级 拟 第 32 课 直线的点斜式方程(3) 第 根据确定直线位置的几何要素,探索并掌握数学思想方法. 重点: 难点: 课型 □讲授 教 □习题 □复习 □讨论 □其它 学生活动 设计 一、先学后讲 1. 直线 l 过点 P0 ( x0 , y0 ) 且斜率为 k 的直线的方程为 2.直线的斜截式方程为 二、合作探究 1. 数形结合的思想 例 1 方程 y ax
) D. ab 0, bc 0
4. 直线 l 的方程为 y kx b ,图象如图所示,则 k _____, b ____ .
因材施教:
教学后记:
1 1 ,则 a 为直线的斜率, 为直线在 y 轴上的 a a
当 a>0 时,四个图形都不可能是方程的直线;当 a<0 时,图形 B 是方程的直线. 【解析】B 【点评】根据直线的方程判断直线的形状,通常把直线转化成斜截式的形式,利用斜 率和截距的几何意义作出判断. ☆自主探究 1 直线 y=ax+b(a+b=0)的图象是( )
2. 分类讨论思想 例 2 已知直线 l 经过点 P(5, 4) ,且 l 与两坐标轴围成的三角形的面积为 5,求直线 l 的 方程. 【思路分析】经过点 P(5, 4) 且 l 与两坐标轴能围成的三角形的直线有两种:一种是 斜率大于零,另一种是斜率小于零,因此要对斜率进行分类讨论。 【解析】由已知得 l 与两坐标轴不垂直. ∵ 直 线 l 经 过 点 P(5, 4) , ∴ 可 设 直 线 l 的 方 程 为 y (4) k[ x (5)] , 即
②当 k 0 时,原方程可化为 (5k 4)2 10k ,此方程无实数解. 综上所得直线 l 的方程为 y 4 ( x 5) ,或 y 4 ( x 5) . 即 2 x 5 y 10 0 或 8 x 5 y 20 0 . 【点评】已知直线过一点时,常设其点斜式方程,但需注意斜率不存在的直线不 能用点斜式表示,从而使用点斜式或斜截式方程时,要考虑斜率不存在的情况,以免
y 4 k ( x 5) .
则直线 l 在 x 轴上的截距为 5 ,在 y 轴上的截距为 5k 4 . 根据题意得
1 4 | 5 | | 5k 4 | 5 ,即 (5k 4)2 10 | k | . 2 k
4 k
2 8 ①当 k 0 时,原方程可化为 (5k 4)2 10k ,解得 k1 , k2 ; 5 5
