《小学数学报》第04届数学竞赛决赛试题及答案

合集下载

【新】苏教版6六年级数学下册《小学生数学报》学习能力检测卷及答案(全套)

新苏教版六年级数学下册全套试卷（小学生数学报）特别说明：本试卷为最新苏教版教材（新版）配套试卷。

全套试卷共8份。

试卷内容如下：1. 第一单元使用2. 第二单元使用3. 第三单元使用4. 第四单元使用5. 第五单元使用6. 第六单元使用7. 第七单元使用8. 期末测试卷《小学生数学报》数学学习能力检测卷(最新修订版)苏教版六年级(下) 第一单元使用(本卷总分120分，共4页，建议完成时间90分钟) 班级姓名学号得分参考答案第一单元答案《小学生数学报》数学学习能力检测卷(最新修订版)苏教版六年级(下) 第二单元使用(本卷总分120分，共4页，建议完成时间90分钟)班级姓名学号得分一、计算题。

(共16分)1.计算下面圆柱的表面积(单位：厘米)。

(5分)2.计算下面圆锥的体积(单位：分米)。

(5分)3．下面是一个高5厘米的圆柱的侧面展开图，求这个圆柱的体积(单位：厘米)。

(6分)二、填空题。

(共17分，每空1分)1.25立方厘米=( )毫升 300立方分米=( )立方米1.8升=( )立方厘米 270毫升=( )立方分米2．一个圆柱的底面半径是2厘米，高是3厘米，这个圆柱的侧面积是( )平方厘米，体积是( )立方厘米，和它等底等高的圆锥的体积是( )立方厘米。

3．有一个圆柱，已知它的高每减少1厘米，表面积就减少25.12平方厘米，如果它的高是3厘米，这个圆柱的体积是( )立方厘米。

4.把一个长6厘米、宽和高都是4厘米的长方体橡皮削成一个体积最大的圆锥，这个圆锥的体积是( )立方厘米。

5．如果圆柱的侧面展开是一个边长为6.28分米的正方形，那么这个圆柱的高是( )分米，底面积是( )平方分米。

6.一个圆柱的高是5分米，底面周长是25.12分米，体积是( )立方分米。

7．等底等高的圆柱与圆锥容器各一个，将圆柱容器内装满水后，再倒入圆锥容器内。

当圆柱容器内水倒光后，结果溢出水46毫升，这时圆锥容器里有水( )毫升。

01《小学数学报》数学竞赛决赛

第六届数学竞赛决赛（满分120分）一、计算题（能用简便方法计算的，要用简便算法。

每题4分，共12分。

）2. 77×13+255×999+510二、填空题（1～9题每空 4分，10～12题每空 3分，共 54分。

）1.a=8.8+8.98+8.998+8.9998+8.99998，a 的整数部分是____。

2.1995的约数共有____。

3.等式“学学×好好+数学=1994”，表示两个两位数的乘积，再加上一个两位数，所得的和是1994。

式中的“学、好、数”3个汉字各代表3个不同数字，其中“数”代表____。

4.如图1，“好、伙、伴、助、手、参、谋”这7个汉字代表1～7这7个数字。

已知3条直线上的3个数相加、2个圆圈上3个数相加所得的5个和都相等。

图中间的“好”代表____。

5.农民叔叔阿根想用20块长2米、宽1.2米的金属网建一个靠墙的长方形鸡窝（如图2）。

为了防止鸡飞出，所建鸡窝高度不得低于2米。

要使所建的鸡窝面积最大，BC 的长应是米。

7.小胡和小涂计算甲、乙两个两位数的乘积，小胡看错了甲数的个位数字，计算结果为1274；小涂看错了甲数的十位数字，计算结果为819。

甲数是____。

8.1994年“世界杯”足球赛中，甲、乙、丙、丁4支队分在同一小组。

在小组赛中，这4支队中的每支队都要与另3支队比赛一场。

根据规定：每场比赛获胜的队可得3分；失败的队得0分；如果双方踢平，两队各得1分。

已知：（1）这4支队三场比赛的总得分为4个连续奇数；（2）乙队总得分排在第一；（3）丁队恰有两场同对方踢平，其中有一场是与丙队踢平的。

根据以上条件可以推断：总得分排在第四的是____队。

9.一块空地上堆放了216块砖（如图3），这个砖堆有两面靠墙。

现在把这个砖堆的表面涂满石灰，被涂上石灰的砖共有____块。

10.南方某城市的一家企业有90％的员工是股民，80％的员工是“万元户”，60％的员工是打工仔。

小学数学竞赛几何题集锦

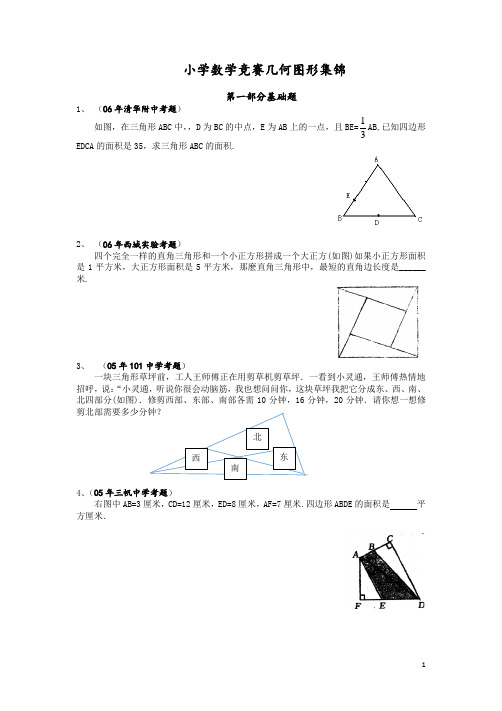
小学数学竞赛几何图形集锦第一部分基础题1、（06年清华附中考题）如图，在三角形ABC 中，，D 为BC 的中点，E 为AB 上的一点，且BE=13AB,已知四边形EDCA 的面积是35，求三角形ABC 的面积.2、（06年西城实验考题）四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.3、（05年101中学考题）一块三角形草坪前，工人王师傅正在用剪草机剪草坪．一看到小灵通，王师傅热情地招呼，说：“小灵通，听说你很会动脑筋，我也想问问你，这块草坪我把它分成东、西、南、北四部分(如图)．修剪西部、东部、南部各需10分钟，16分钟，20分钟．请你想一想修剪北部需要多少分钟？4、（05年三帆中学考题）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE 的面积是平方厘米．西南东北5、 (06年北大附中考题)三角形ABC 中，C 是直角，已知AC ＝2，CD ＝2,CB=3,AM=BM ，那么三角形AMN （阴影部分）的面积为多少？6、（★★）如右图所示，已知三角形ABC 面积为1，延长AB 至D ，使BD=AB ；延长BC 至E ，使CE=2BC ；延长CA 至F ，使AF=3AC ，求三角形DEF 的面积。

7、（★★）右图是一块长方形耕地，它由四个小长方形拼合而成，其中三个小长方形的面积分别为15、18、30公顷，问图中阴影部分的面积是多少？8、正方形ABFD 的面积为100平方厘米，直角三角形ABC 的面积，比直角三角形（CDE 的面积大30平方厘米，求DE 的长是多少？9、（★★★）如下图，已知D 是BC 的中点，E 是CD 的中点，F 是AC 的中点，且ADG ∆的面积比EFG ∆的面积大6平方厘米。

?的面积是多少平方厘米ABC ∆ABCDEF G10、（★★）长方形ABCD 的面积为36平方厘米，E 、F 、G 分别为边AB 、BC 、CD 的中点，H 为AD 边上的任一点。

小学数学《三角形的等积变形》练习题(含答案)

于是：三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=（12+4）×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以，三角形ABC的面积是三角形ABD面积的4/3倍；三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论：两个三角形等高时，面积的倍数=底的倍数
【例2】如右图，E在AD上，AD垂直BC，AD=12厘米，DE=3厘米。
而四边形CEFH是它们的公共部分，
所以三角形DHF的面积=三角形BCH的面积，
进而可得阴影面积=三角形BDF的面积=三角形BCD的面积= 10×10÷2=50（平方厘米）。
法2：连接CF，那么CF平行BD，
所以，阴影面积=三角形BDF的面积=三角形BCD的面积=50（平方厘米）。
附加题目
【附1】如右图，四边形ABCD面积为1，且AB=AE，BC=BF，DC=CG，AD=DH．求四边形EFGH的面积．
巩固理解结论：两个三角形等底时，面积的倍数=高的倍数
【例3】用两种不同的方法，把任意一个三角形分成四个面积相等的三角形．
分析：法1：如图（1），将BC边四等分，连接各等分点，则△ABD、△ADE、△AEF、△AFC面积相等。
法2：如图（2），D是BC的二等分点，E、F是AC、AB的中点，从而得到四个等积三角形△ADF、△BDF、△DCE、△ADE．
【例7】图中△AOB的面积为15cm2，线段OB的长度为OD的3倍，求梯形ABCD的面积.
分析：
【例8】（北京市第一届“迎春杯”刊赛）如右图.将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC边延长3倍到F.如果三角形ABC的面积等于l，那么三角形DEF的面积是？
分析：连结AE、BF、CD(如右下图).由于三角形AEB与三角ABC的高相等，而底边EB=2BC，所以三角形AEB的面积是2.同理，三角形CBF的面积是3，三角形ACD的面积是1.

小学生四年级《小学生数学报》读报用报知识竞赛试题及答案

四年级《小学生数学报》读报用报知识竞赛班级姓名得分一、填空。

（5分，共50分）1、加括号使等式成立 240 ÷18 + 6 × 2=82、等腰三角形的顶角是一个底角的3倍，这个三角形的底角（）°，顶角（）°3、小迷糊在计算一道末尾有0的乘法时，忘记在积的到末尾添上一个0，结果比正确的答案少了6372，那么正确的答案（）4、用一根360厘米的铁丝最多能做成（）个边长8厘米的等边三角形。

（所有三角形都排成一排）5、游击队接到一份情报：敌人将在a 月b 日（a ×b=66）这天的时针和分针的夹角成120°的整点时刻来扫荡，敌人可能是什么时候来，有（）种可能。

6、一列火车长240米，每秒行15米，全车通过一个山洞需要40秒，山洞长（）米。

7、A ÷B=C A ×B ×C=64 如果B=2 那么A=（）C=（）8、找规律填空9、AB 两人同时爬楼梯，A 爬到第4层时，B 恰好爬到第3层。

照这样计算，当A 爬到第16层时，B 爬到第（）层。

10、如右图一共有（）正方形二、综合应用。

（每题10分，共50分）1、在一个湖泊的周围筑成周长3060米的大堤，在大堤上每隔6米载一棵柳树，然后在相邻的柳树之间载2棵桃树，问;大堤上柳树、桃树各有多少棵？2、甲乙两箱苹果共重50千克。

如果从甲中取出6千克放到乙箱中，这时甲箱就比乙箱少2千克，问：甲箱原来有多少千克？3、用56米长的木条围成长或宽是20米的长方形，其中一条边利用围墙，怎样才能使围成的面积最大?4、某市的电话号码是6位数，首位不能是0，其余的各位可以是0~9中的任一个，并且不同数位上的数字可以重复。

这个市最多可以装多少部电话机？5、在图中合适的位置再画一个梯形，是它和原来的梯形形成轴对称图形（至少3种类型）参考答案填空1、240÷（18+6×2）=82、36 1083、70804、225、46、3607、8 48、999996000003 11111111222222229、共4种、10、55二．综合应用1、柳树510棵桃树1020棵2、甲303、20*18=360（平方米）4、9*10*10*10*10*10=900000（部）5、略。

《小学数学报》第03届数学竞赛初赛试题及答案

一、填空题（共 37 分）1.甲乙两数的和是 231，已知甲数的末端是 0，假如把甲数末位的 0 去掉，正好等于乙数。

乙数是（），甲数是（）。

2.已知 a、b、c 都不等于 0，并且 a＞ b＞c，当 a=____，b=____，3.将 1、2、3、4、5、6、7、8 这八个数字填入下边算式中的八个“□”内（每个数字只好用一次），使得数最小。

□□.□□-□□. □□4.从右侧表格中各数摆列的规律能够看出：①“☆”代表 ____，“△”代表 ____；②81 排在第 ____行第 ________列。

5.把 160 支铅笔、128 本练习簿、 96 册故事书最多能够分红 ____份同样的奖品，在每份奖品中，有铅笔____支，练习簿 ____本，故事书 ____ 册。

6.在左侧的算式中，“三”“好”“学”“生”四个汉字各代表一个阿拉伯数字。

此中“三” 代表 ____,“好”代表 ___，“学”代表 ___，“生”代表 ___。

7. 某市派出 60 名选手参加 1988 年“贝贝杯”少年田径邀请赛，其中女拖沓机 4 小时可耕这块田的 ____。

9.要在 20 米长的水泥露台上放 11 盆花。

不论怎么放，起码有 ____ 盆之间的距离不超出 2 米。

10.右图中每个格子（小正方形）的面积表示 1 平方厘米。

梯形面积为____平方厘米。

11.一个正方体的棱长扩大 a 倍，那么它的体积扩大 ____倍。

12.食堂原有煤 600 公斤，第一天烧掉 148 公斤，次日烧掉 150 公斤，第三天烧的比次日多 2 公斤。

三天后本来的煤少了 ____公斤。

13.有 249 朵花，按 5 朵红花， 9 朵黄花， 13 朵绿花的次序摆列，最后一朵花是 ___色的，这 249 朵花中，红花是（）朵，黄花是（）朵，绿花是（）朵。

4 分，不选二、选择题（将正确答案的序号填在横线上。

每题选对得得 1 分，选错得 0 分）（共 28 分）①311；②31；③29；④ 352.如右图，正方形被一条曲线分红了 A、B 两部分。

2005《小学生数学报》竞赛试题六年级

《小学生数学报》竞赛（六年级）2005《小学生数学报》优秀小读者评选初评活动六年级材料（时间：2005年3月19日9：00—10：30）一、填空题：1、甲、乙、丙、丁、戊五位同学参加一次节日活动，很幸运的是，他们都得到了一份精美的礼物。

事情是这样的：墙上挂着两串礼物（如图1）每次只能从其中一串的最下端取一件，直到礼物取完为止。

甲第一取得礼物，然后，乙、丙、丁、戊依次取得第2到第5件礼物，当然取法各种各样，那么共有（）种不同的取法。

事后他们打开这些礼物仔细比较，发现礼物D最精美，那么取得礼物D可能性最大的是（），可能性最小的是（）。

2、扑克牌中的J、Q、K分别表示11、12、13。

甲取13张红心，乙取13张草花，两人都各自任意出一张牌凑成一对，这样一共可凑成13对。

如果将每对求和，再将这13个和相乘。

从积的奇偶性看，积应是（）数。

3、分母不超过2005的所有真分数的和是（）。

4、小赵、小张、小王三位同学对小麦斯书包里的书数目作了一个估计。

小赵说：“书包里至少有10本，至多15本。

”小张说：“书包里不到10本书。

”小王说：“书包里至少1本，至多15本。

”小麦斯却说：“你们三人的估计只有一人说对了。

”这样，小麦斯书包里有（）本书。

5、如图2，用若干个体积相同的小正方体堆积成一个大正方体，要使大正方体的所有对角线（正方体八个顶点中距离最远的两个顶点的连线）穿过的小正方体都是黑色的，其余小正方体都是白色的，并且大正方体每条边上有偶数个小正方体，当堆积完成后，白色正方体的体积占总体积的96%，那么一共用了（）个黑色的小正方体。

6、在0~9中取八个不同数字，组成两个差是2005的四位数，那么这两个四位数的和最大是（），最小是（）。

7、某班全体学生进行一次篮球投篮练习，每人都要投球10个，每投进一球得1分。

得分的情况如右表：又知该班学生中，至少得3分的人的平均得分为6分，得分不到8分的人的平均得分为3分，那么该班学生有（）人。

2004小学数学奥林匹克试题和解答

2004年全国小学奥林匹克预赛试卷（A）1. 计算：＝________.2. 计算：＝________.3. 在下面的数之间适当填上＋、－、×、÷运算符号及括号，使算式的结果等于2004.2 2 2 2 2 2 2 2 2 2＝20044. 自然数N是一个两位数，它是一个质数，而且N的个位数字与十位数字都是质数，这样的自然数有________个.5. 在算式A×（B＋C）＝110＋C中，A、B、C是三个互不相等的质数，那么B＝________.6. 在12＝1、22＝4、32＝9、42＝16、……中，1、4、9、16、……叫做“完全平方数”.从1到500这500个整数中，去掉所有“完全平方数”，剩下的整数的和是多少________.7. 下面各数的和是________.8. 有一次考试中，甲、乙两人考试结果如下：甲答错了全部试题的1/3，乙答错了7题，甲、乙答错的试题占全部试题的1/5，那么甲、乙答对的试题至少有________题.9. 如图，设AD＝1/3AB、BE＝1/4BC、FC＝1/5AC.如果三角形DEF的面积是19平方厘米，那么三角形ABC的面积是________.10. 张先生以标价的95％买下一套房子，经过一段时间后，他又以超出原标价的40％的价格将房子卖出.这段时间物价的总涨幅为20％，张先生买进和卖出这套房子所得的利润为________％.11. 某人到商店买红蓝两种笔，红笔定价5元，蓝笔定价9元，由于购买量较多，商店给予优惠：红笔85折，蓝笔8折，结果此人付的钱比原来节省了18％，已知他买了蓝笔30支，那么红笔买了________支.12. 一位富豪有350万元遗产，在临终前，他对怀孕的妻子写下这样的一份遗嘱：如果生下来是个男孩，就把遗产的三分之二给儿子，母亲拿三分之一；如果生下来是个女孩，就把遗产的三分之一给女儿，三分之二给母亲.结果他的妻子生了双胞胎（一男一女），按遗嘱的要求，母亲可以得到________万元.1、 2、 3、[(2222－222)÷2＋2]×2＝2004或(2222÷2＋2)×2－222＝2004 4、4 5、2 6、121455 7、122500 8、6 9、10、22.8％ 11、36 12、1001．【解】原式＝()×65＝×65＝2．【解】原式＝()×＝3××＝3．【解】 [(2222－222)÷2＋2]×2＝2004或(2222÷2＋2)×2－222＝20044．【解】一位质数有：2，3，5，7，所以N为23，37，53，73共4个。

《小学生数学报》答案六年级上册第六单元

《小学生数学报》答案六年级上册第六单元一、选择题（每小题2分，共20分）1. 下列四个数中，最大的数是（）A. -3B. -2C. 2D. 3答案：D. 32. 下列四个数中，最小的数是（）A. -3B. -2C. 2D. 3答案：A. -33. 下列四个数中，正数有（）A. -3B. -2C. 2D. 3答案：C. 2 D. 34. 下列四个数中，负数有（）A. -3B. -2C. 2D. 3答案：A. -3 B. -25. 下列四个数中，零有（）A. -3B. -2C. 2D. 3答案：无6. 下列四个数中，正数和负数的和是（）A. -5B. -1C. 1D. 5答案：C. 17. 下列四个数中，正数和负数的差是（）A. -5B. -1C. 1D. 5答案：D. 58. 下列四个数中，正数和负数的积是（）A. -6B. -2C. 2D. 6答案：B. -29. 下列四个数中，正数和负数的商是（）A. -1B. -1/2C. 1/2D. 1答案：A. -110. 下列四个数中，正数和负数的平均数是（）A. -1B. -1/2C. 1/2D. 1答案：B. -1/2二、填空题（每小题2分，共20分）11. 两个正数的和是：________答案：正数12. 两个负数的和是：________答案：负数13. 一个正数和一个负数的和是：________答案：零14. 一个正数和一个负数的差是：________答案：两倍的正数或负数15. 一个正数和一个负数的积是：________答案：负数16. 一个正数和一个负数的商是：________答案：负数17. 一个正数和一个负数的平均数是：________答案：零。

《小学数学报》历届数学竞赛第一试试题及详解答案

小学数学报第一届数学竞赛第一试试题及答案一、填充。

1.1990年全国发电量将达到五千五百亿（）左右；钢材产量将达到四千四百万（）左右。

3.两个数的最小公倍数是180，最大公约数是 30。

已知其中一个数是90，另一个数是（）。

4.顺次写出除以4余2，除以5余3的三个数：（）。

5.找规律，填数：4，7，10，13，（），（），（）；6，12，24，48，（），（），（）。

6.一根铁丝长48厘米。

如果把它围成一个正方形，它的面积是（）；如果围成长方形，宽是2厘米、宽是5厘米、宽是10厘米，它们的面积分别是（），（），（）。

7.90°的角是（）角；小于90°的角叫做（）角；大于90°、小于180°的角叫做（）角。

（）左右（整数）。

9.右边算盘图上所表示的多位数（“·”表示个位）应该读作（）。

二、计算。

2.（口算）4＋6＋8＋10＋12＋14＋16＋18＋20＋22＋24＋26＋28＋30＋32＋34＋36三、解答应用题。

1.王新同学期末考试成绩如下：语文和数学平均成绩是94分；数学和外语平均成绩是88分；外语和语文平均成绩是86分。

王新同学语文、数学、外语各得多少分？2.苏小牛在菜场买菠菜5斤，萝卜3斤共付0.87元。

张老师在菜场买同样的菠菜3斤，萝卜5斤共付0.81元。

问菠菜、萝卜每斤各多少元？3.第一块麦田有a亩，平均亩产400斤。

第二块麦田有b亩，平均亩产500斤。

请列出式子表示：（1）两块田共有多少亩？（2）第一块田共产多少斤麦子？（3）第二块田共产多少斤麦子？（4）两块田共产多少斤麦子？（5）这两块田平均亩产多少斤麦子？式，不计算）5.求右图中阴影部分面积和平行四边形面积。

6.把7个同样大小的苹果平均分给12个小朋友。

要把几个苹果平均切成7.兰兰向妈妈要六分钱买一根冰棒。

妈妈叫兰兰从袋子里取硬币。

袋子里有1分、2分、5分硬币各六枚。

兰兰要拿六分钱，可以有几种拿法，用算式表示出来。

[精品]2005《小学生数学报》竞赛试题(四、五、六年级)

[精品]2005《小学生数学报》竞赛试题（四、五、六年级）2005《小学生数学报》竞赛试题(四、五、六年级) 《小学生数学报》竞赛(四年级)2005 ...................................... 1 第七届《小数报》初赛试题 .............................................. 3 第五届数学竞赛决赛试题及答案 ......................................... 5 第六届数学竞赛初赛试题及答案 . (21)《小学生数学报》竞赛(四年级)2005一、填空题:1、 2005年3月19日是星期六，那么今年的教师节是( )。

2、在1~9这9个数字中间，添上“+、-”两种运算符号，使等式成立。

1 2 3 4 5 6 7 8 9=1003、从公园同往湖心的小岛有一条长1020米的小路，在这条小路的两侧，从头到尾每隔15米栽一棵桃树，一共需要栽( )棵桃树。

4、在右图中，外圈最大正方形的边长为8厘米，那么最中间的小正方形的面积是( )平方厘米。

5、 50个学生解答A、B两题，其中没答对A题的有12人，答对A题的且没答对B题的有30人。

那么A、B两题都答对的有( )人。

6、 2、4、6、8、...98这49个偶数各位数的和是( )。

7、一本书有200页，数字1在所有页码中一共出现了( )次。

8、有一列由三个数组成的数组:(1，1，1)、(2，4，8)、(3，9，27)......第12个数组中三个数的和比第6个数组中的三个数的和大( )。

9、从9开始，把9的倍数依次写下去，一直写到999，成了一个很大的数:918273645546372819099 (990)999。

这数共有( )位。

10、有两批人要做到排成一排的120个座位上，第一批人坐下后，恰好使得第二批入座的人必定在与第一批入座的人相邻的座位上。

第一批入座的人至少有( )人。

第4届《小学生数学报》赛题

第四届《小学生数学报》数学竞赛初赛试题第一部分一、填空题（答题时只要将正确答案填在题中的横线上）（共38分）1.被减数、减数与差的和，除以被减数，商是____。

（2分）2.有一个两位数，它的十位数字比个位数字多5。

用算盘上的算珠来表示这个两位数的话，共需要用9个算珠。

这个两位数是____。

（3分）3.四个数的平均数是 18，如果每个数都增加x，这四个数的和是____。

（2分）4.“12345 6 7 8 9 1 0 1 1 1 2…… 4 8 4 9 5 0”是一个位数很多的多位数，从中划去80个数字，使剩下的数字（先后顺序不变）组成最大的多位数。

这个最大的多位数是____。

（4分）（3分）6.图 1中的“○”内分别有五个数 A、B、C、D、E；“□”内的数表示与它相连的所有“○”中的数的平均数。

C=____。

（4分）8.在线段AB上插入六个不同的点以后，图2中的线段一共增加了____条。

（2分）9.四个连续奇数的连乘积是326025，它们的和是____。

（4分）数，使它们的和等于1。

这7个不同的分数从大到小依次是____、__、__ 、____、____、____、____（4分）11.在左边的减法竖式中，“☆”“△”“○”各代表一个不同的数字。

可以推算出“○”代表____。

（3分）12.从南京到上海的某次快车中途要停靠六个大站。

铁路局要为这次快车准备____种不同的车票，这些车票中有____种不相同的票价。

（4分）二、选择题（每题后面都附有四个答案，其中只有一个是正确的。

将正确答案的序号填入题中的横线上。

选对一题得4分，不选或选错得0分。

）（共20分）1.设A=9876543×3456789， B=9876544 ×3456788。

那么____。

①A＞B ②A=B ③A＜B ④A≤B根绳子相比较是____。

①甲绳长②一样长③乙绳长④不能肯定哪个长3.如果“○”是一个质数，“□”是一个合数，下列第____项的值一定是一个质数。

2004年第四届康大杯复赛四年级数学答案

3
1
原式＝45×27＋73×45 或＝45×（27＋73）＝4500
（2）原式＝（219＋51）＋（648－548）－（138＋62）
（5）原式＝440×（96÷48）＝440×2 ＝880 （6）原式＝（6×15）×（8×125）＝90×1000 ＝90000 （7）原式＝（100＋99－98－97）＋（96＋95－94－93）＋…＋（8 ＋7－6－5）＋（4＋3－2－1）＝4×25 ＝100 三、解答题 1、9＋6＝15（厘米） 15×2＝30（厘米）答：长方形 ABCD 的周长为 30 厘米 2、4＋3＋2＋1＝10 3＋2＋1＝6 10×6＝60 答：右下图中共有 60 个长方形 3、（如图）分对一组得 1 分，两组、三组均得 2 分，四组得 3 分，六组得 4 分）四、应用题：（每题 6 分）（1）183＋4－7＝180 180÷（1＋2＋3）＝30 30×2－4＝56 30×3＋7＝97 答：甲数 97，乙数 56，丙数 30
答：甲原有 260 元，乙有 160 元，丙有 300 元。（5）12－（5－4）×2＝10（根） 10÷（6－5）＝10（组） 10×6＝60（根）或 2×4＋5×（10－2）+12＝60（根）答：共有跳绳 60 根。（6）（208＋64）÷2＝136（分） 136－64＝72（分）（20×10－72）÷（20＋12）＝4（发） 10－4＝6（发）（20×10－136）÷（20＋12）＝2（发） 10－2＝8（发）答：小张射中 8 发，小李射中 6 发
2
（2）92÷2＝46（米）（46＋12）÷2＝29（米） 29－12＝17（米） 29×17＝493（平方米）答：这块地的面积为 493 平方米。（3）30÷（4－1）＝10（岁） 10－3＝7（岁）答：儿子今年 7 岁。（4）原来第一次之后第二次之后第三次之后甲Байду номын сангаас乙丙 260 160 300 220 200 300 220 170 330 240 240 240

北京市石油学院附属小学四年级数学竞赛试卷及答案

北京市石油学院附属小学四年级数学竞赛试卷及答案一、拓展提优试题1．已知x，y是大于0的自然数，且x+y＝150，若x是3的倍数，y是5的倍数，则（x，y）的不同取值有对．2．甲，乙两人分别从A，B两地同时出发，相向而行，甲到达A，B中点C 时，乙距C点还有240米，乙到达C点时，甲已经超过C点360米，则两人在D点相遇时，CD的距离是米．3．（8分）小红去买水果，如果买5千克苹果则少4元，如果买6千克梨则少3元，已知苹果比梨每500克贵5角5分，那么小红买水果共带了元．4．有一个学生在做计算题时，最后一步应当除以20，但却错误地加上20，因而得到错误的结果是180．请问这道计算题的正确得数应是．5．只能被1和它本身整除的自然数叫做质数，如：2，3，5，7等．那么，比40大并且比50小的质数是，小于100的最大的质数是．6．如图，一小正方形的边为边向小正方形外作四个正方形，再依次连接几个定点，若图中阴影三角形的面积是S，则面积为2S的三角形有个，面积为8S 的正方形有个．7．（7分）后羿朝三个箭靶分别射了三支箭，如图：他在第一个箭靶上得了29分，第二个箭靶上得了43分．请问他在第三个箭靶上得了分．8．（7分）棱长都是1厘米的63个白色小正方体和1个黑色小正方体，可以拼成一个大正方体，问：一共可以拼成种不同的含有64个小正方体的大正方体．9．一列火车身长90米，火车以每分钟160米的速度通过山洞，用了3分钟，山洞长390米．10．一辆公共汽车有78个座位，空车出发，第一站上一位乘客，第二站上二位乘客，第三站上三位乘客，依次下去，多少站以后，车上坐满乘客？11．甲、乙两个油桶中共有100千克油，将乙桶中的15千克油注入甲桶，此时甲桶中的油是乙桶中的油的4倍．那么，原来甲桶中油比乙桶中的油多千克．12．如图，将一张圆形纸片对折，再对折，又对折，…，到第六次对折后，得到的扇形的面积是5，那么，圆形纸片的面积是．13．（8分）有10张卡片，上面分别写着1，2，3，…，9，10．那么至少取出6张卡片，才能保证取出的卡片中，有两张卡片上的数字之和为11．14．袋子中有黑白两种颜色的棋子，黑子的个数是白子的个数的2倍，每次从袋中同时取出3个黑子和2个白子，某次取完后，白子剩下1个，黑子剩下31个，则袋中原有黑子个．15．（8分）杨树、柳树、槐树、桦树和梧桐树各一棵树种成一排，相邻两颗树之间的距离都是1米．杨树与柳树、槐树之间的距离相等，桦树与杨树、槐树之间的距离相等．那么梧桐树与桦树之间的距离是米．【参考答案】一、拓展提优试题1．【分析】首先根据5的整除特性可知尾数是0或者5，那么150和5的倍数差依然是尾数是0或者5的数字枚举即可．解：根据5的整除特性可知尾数是0或者5．那么150减去这个数字尾数还是0或者5．可以找到尾数是0或者5的数字是3的倍数．30，60，90，120，15，45，75，105，135共9个数字满足条件．对应的数字就有9对．故答案为：9．【点评】本题是考察数的整除特性，关键在于找到尾数是0或5的数字是3的倍数，枚举即可解决问题．2．【分析】由题目中的已知条件，得出甲乙的速度比，进而又得出他们的路程比，这样求出甲到达中点后再与乙共行240米，甲行的路程即CD之间的距离．解：由题意知“甲走360米时乙正好走240米”，甲、乙的速度比是360：240＝3：2相同时间内，甲、乙的路程比等于他们的速度比即3：2甲乙共行240米，甲行的路程是240×3÷（2+3）＝144（米）故：CD的距离是144米．【点评】解此题的突破口就是能得出他们的速度比，之后就可轻松解答了．3．解：设梨每千克x元，则每千克苹果x+0.55×2＝（x+1.1）元6x﹣3＝5×（x+1.1）﹣46x﹣3＝5x+5.5﹣46x﹣5x＝1.5+3x＝4.56×4.5﹣3＝27﹣3＝24（元）答：小红买水果共带了24元．故答案为：24．4．解：设最后一步之前运算的结果是a，a+20＝180，那么：a＝180﹣20＝160；正确的计算结果是：a÷20＝160÷20＝8；故答案为：8．5．【分析】根据质数的概念：指在一个大于1的自然数中，除了1和此整数自身外，没其它约数的数；然后列举出比40大并且比50小的质数；求小于100的最大的质数，应从100以内的最大数找起：99、98是合数；进而得出结论．解：比40大比50小的质数有：41、43、47；小于100的最大质数是97；故答案为：41、43、47，97．【点评】解答此题的关键：根据质数的定义，并结合题意，进行例举即可．6．【分析】（1）观察题干可知，阴影部分的面积是S，则面积为2S的三角形是每个小正方形的面积的一半，即三角形的两条直角边都是小正方形的边长，由此即可计数；（2）阴影部分的面积是S，则它所在的正方形的面积是4S，则面积为8S的正方形只有中间1个，解：（1）观察图形可知，面积为2S的独三角形有4个；由两个面积为S的三角形组成的三角形有4×4＝16（个），所以一共有4+16＝20（个）；（2）面积为8S的正方形只有1个．故答案为：20；1．【点评】本题考查平面图形数量的确定，属于中档题目，注意仔细地观察图形，要做到不重不漏．7．【分析】这个箭靶共三个环，设最小的环为a分，中间环为b分，最外环为c分，得：第一个靶得分为：2b+c＝29①第二个靶得分为：2a+c＝43②第三个靶得分为：a+b+c③通过等量代换，解决问题．解：设最小的环为a分，中间环为b分，最外环为c分，得：第一个靶得分为：2b+c＝29①第二个靶得分为：2a+c＝43②第三个靶得分为：a+b+c③由①+②得：2a+2b+2c＝29+43＝72即a+b+c＝36即第三个靶的得分为36分．答：他在第三个箭靶上得了36分故答案为：36．8．【分析】一共64个，4×4×4，①把黑色正方体放在顶点处，1种；②把黑色正方体放在棱中间，任选一个，2种；③把正方体放在每个面的中间4个，任选一个，4种；④把黑色正方体放在里面，从外边看不到，8种；然后把几种情况的种数相加即可．解：①把黑色正方体放在顶点处，1种；②把黑色正方体放在棱中间，任选一个，2种；③把正方体放在每个面的中间4个，任选一个，4种；④把黑色正方体放在里面，从外边看不到，8种；共：1+2+4+8＝15（种）；答：一共可以拼成15种不同的含有64个小正方体的大正方体．故答案为：15．9．解：160×3﹣90，＝480﹣90，＝390（米），答：山洞长390米．故答案为：390．10．解：设第n站以后车上坐满了乘客，可得：[1+1+（n﹣1）×1]×n÷2＝78[2+n﹣1]×n÷2＝78，[1+n]×n÷2＝78，（1+n）×n＝156，由于12×13＝156，即n＝12．答：12站以后，车上坐满乘客．11．【分析】根据题意，把甲乙两个油桶的共存油看作5份，可以计算出每份是多少千克油，将乙桶中的15千克油注入甲桶后，甲桶占了其中的4份，乙桶占了其中的1份，1份即100÷5＝20千克，可以计算出注入后各个油桶的千克，再用乙桶的油减去15千克，甲桶的油加上15千克，即是甲乙两桶原存油的数量，再用甲桶原存油的数量减去一桶原存油的数量，列式解答即可解：100÷（1+4）＝20（千克）注入后的甲桶：4×20＝80（千克）倒出后的乙桶：1×20＝20（千克）原甲桶存油：80﹣15＝65（千克）原乙桶存油：20+15＝35（千克）甲桶中油比乙桶中的油多：65﹣35＝30（千克）答：原来甲桶中油比乙桶中的油多30千克．故答案为：30．【点评】解答此题的关键是分清注入后甲乙两桶油的关系，即甲桶存油等于乙桶存油的4倍，然后可计算出注入后甲乙两桶油的存量，再计算出注入前两桶油的重量，二者相减即可．12．【分析】把这张圆形纸片对折1次，折成的角是以这张圆形纸片的圆心为顶点，两条半径为边的平角，平角＝180°，再对折1次，就是把平角平均分成2分，每份是90°，再对折1次，就是把90°的角再平均分成2份，每份是45°，第六次对折后，平均分成了（2×2×2×2×2×2）＝64份，得到的扇形的面积是圆面积的；由此解答即可．解：5＝320答：圆形纸片的面积是320；故答案为：320．【点评】本题是考查简单图形的折叠问题，明确把圆对折6次后，得到的图形的面积是圆面积的．13．解：10÷2＝5（个）5+1＝6（个）故填614．【分析】因黑子个数是白子个数的2倍，可假设黑子每次取的个数也是白子的2倍，即黑子每次2×2＝4个、白子每次取2个，则白子余1个时，黑子余2个．现每次黑子取少4﹣3＝1个了，则黑子多出来的数量，除以应取和实取的差，就是取的次数．据此解答．解：假设黑子每次取的个数也是白子的2倍，即黑子每次2×3＝6个、白子每次取3个，则：（31﹣1×2）÷（2×2﹣3）＝29÷1＝29（次）3×29+31＝87+31＝118（个）答：袋中原有黑子 118个．故答案为：118．【点评】本题的关键是根据黑子是白子个数的2倍，假设每次取黑子的个数是白子的2倍，与实际取黑子的差，及实际取与假设取应剩下黑子的差，进行解答．15．解：杨树与柳树、槐树之间的距离相等，所有三种树的位置有可能是：柳□杨□槐，柳杨槐□□，□柳杨槐□，□□柳杨槐，其中□表示暂时不知道．而桦树与杨树、槐树之间的距离相等，所以只有可能是：柳□杨桦槐，剩余的一个位置是梧桐树，所以梧桐树和桦树间的距离是2米．故答案为：2．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《小学数学报》第04届数学竞赛决赛试题及答
案
一、选择题（将正确答案的序号填入题后的横线上，每题选对得4分，不选或选错都得0分）（共24分）
1.某工人原打算10小时完成的工作，8小时就全部完成了，他的工作效率比原打算提高了_____。

①20％；②120％；③25％；④80％
3.在三角形ABC中，∠A=∠B＋∠C，那么那个三角形是__。

①锐角三角形；②直角三角形；③钝角三角形；④无法确定
4.三个质数△、□、○，假如□＞△＞1。

△＋□=○，那么△=__。

①5；②7；③13；④2
5.图1是下面__的表面展开图。

①甲正方体；
②乙正方体；
③丙正方体；
④甲正方体或丙正方体
6.某工厂为了夸奖好人好事核实一件事，厂方找了A、B、C、D四人。

A说：“是B做的。

”B说：“是D做的。

”C说：“不是我做的。

”D 说：“B说的不对。

”这四人中只有一人说了实话。

问这件好事是__做的。

①A；②B；③C；④D
二、填空题（共42分）
1.从3、13、17、29、31这五个自然数中，每次取两个数分别作一个分数的分子和分母，一共可组成__个最简分数。

（3分）
填__。

（“□”表示同一个数）（3分）
3.三名工人师傅张强、李辉和王充分别加工200个零件。

他们同时开始工作，当李辉加工200个零件的任务全部完成时，张强才加工了160个，王充还有48个没有加工。

当张强加工200个零件的任务全部完成时，王充还有__个零件没有加工。

（4分）
4.图2是一个表面被涂上红色的棱长为10厘米的正方体木块，假如把它沿虚线切成8个正方体，这些小正方体中没有被涂上红色的所有表面的面积和是__平方厘米。

（3分）
5.把同一个三角形的三条边分别五等分、七等分（如图3、图4），然后适当连接这些等分点，便得到了若干个面积相等的小三角形。

已知图3中阴影部分面积是294平方分米，那么，图4中阴影部分的面积是__平方分米。

（4分）
6.有8只盒子，每只盒内放有同一种笔。

8只盒子所装笔的支数分别为17支、23支、33支、36支、38支、42支、49支、51支。

在这些笔中，圆珠笔的支数是钢笔的支数的2倍，钢笔支数是铅笔支
7.由1、3、4、5、7、8这六个数字所组成的六位数中，能被11整除的最大的数是__。

（4分）
8.王亮从1月5日开始读一部小说。

假如他每天读80页，到1月9日读完；假如他每天读90页，到1月8日读完。

为了不阻碍正常学习，王亮预备减少每天的阅读量，并决定分a天读完，如此，每天都读a页便刚好全部读完。

这部小说共有__页。

（4分）
9.右边的式子表示两个三位数相加，式中的每个字母代表0～9中的一个数字。

假如在算盘上先拨上三位数“abc”，再把三位数“def”加上，那么依次用四句口诀：六上六，七上二去五进一，八去二进一，一下五去四。

问a=__，b=__，c=__。

（3分）
10.如图5，七枚棋子围成一个圆圈，从①开始，每隔一个取一个，依次取走①、③、⑤、⑦、④、②，最后剩下⑥。

二十枚棋子围成一个圆圈（如图6），从__开始，每隔一个取一个，最后将只剩下一枚棋子是几？（4分）
11.在图7的每个方格中填入九个不同的自然数，使得每一行、每一列以及两条对角线（左上角到右下角，右上角到左下角）上的三个数的乘积都相等。

（5分）
三、运算题（能用简便方法运算的，尽可能用简便方法运算）（共8分）
四、作图题（4分）
请画出图8中阴影部分以图中的虚线为对称轴的轴对称图形，并用阴影来表示。

五、应用题（共42分）
3.一根长方体木料，体积是0.078立方米。

已知这根木料长1.3米，宽为3分米，高该是多少分米？孙健同学把高错算为3分米。

如此，这根木料的体积要比0.078立方米多多少？（4分）
4.有一大一小两个正方形，它们的周长相差20厘米，面积相差55
平方厘米。

小正方形的面积是多少平方厘米？（6分）
5.有9个小长方形，它们的长和宽分别相等，用这9个小长方形拼成的大长方形的面积是45平方厘米，求那个大长方形的周长。

（7分）
6.A、B、C三个油桶各盛油若干千克。

第一次把A桶的一部分油倒入
B、C两桶，使B、C两桶内的油分别增加到原先的2倍；第二次从B桶把油倒入
C、A两桶，使C、A两桶内的油分别增加到第二次倒之前桶内油的2倍；第三次从C桶把油倒入A、B两桶，使A、B两桶内的油分别增加到第三次倒之前桶内油的2倍，如此，各桶的油都为16千克。

问A、B、C 三个油桶原先各有油多少千克？（5分）
7.甲、乙、丙、丁四个旅行团分别有游客69人、85人、93人、97人。

现在要把这四个旅行团分别进行分组，使每组差不多上A名游客，以便乘车前往参观游玩。

已知甲、乙、丙三个旅行团分成每组A人的若干组后，所剩的人数都相同，问丁旅行团分成每组A人的若干组后还剩几人？（5分）
8.有一个蓄水池装有9根水管，其中一根为进水管，其余8根为相同的出水管。

进水管以平均的速度不停地向那个蓄水池注水。

后来有人想打开出水管，使池内的水全部排光（这时池内已注入了一些水）。

假如把8根出水管全部打开，需3小时把池内的水全部排光；假如仅打开5根出水管，需6小时把池内的水全部排光。

问要想在4.5小时内把池内的水全部排光，需同时打开几个出水管？（6分）
答案
一、选择题
1.③；
2.②；
3.②；
4.④；
5.①；
6.③
二、填空题
1.5×（5-1）=20（个）；
2.2；
3.10个；
4.600平方厘米；
5.200平方分米；
6.49支；
7.875413； 8.324页； 9.a=3，b=7，c=2；10.(19)；
11.
本题答案不唯独，那个地点仅介绍两种。

三、运算题
四、作图题（略）
五、应用题
2.解：设甲、乙两班学生数的和为单位“1”，依照题意有：
108-45=63（人）…………………………乙班原有人数
答：甲班原有人数45人，乙班原有人数63人。

3.解：①0.078÷（1.3×0.3）=0.2（米）
0.2米=2分米
②1.3×0.3×0.3-0.078
=0.117-0.078
=0.039（立方米）
或0.078÷2=0.039（立方米）
答：①高该是2分米；
②这根木料的体积要比0.078立方米多0.039立方米。

4.解：设小正方形边长为x厘米，那么大正方形边长为“x+20÷4”厘米，依照题意，列方程（x＋5）2-x2=55，化简得10x=30，x=3，x2=9（平方厘米）
答：小正方形的面积是9平方厘米。

÷9=5（平方厘米）
大长方形的周长是（2.5×4＋2＋2.5）×2=29（厘米）
答：那个大长方形的周长是29厘米。

6.解：用“倒推法”列出右表。

从表中看出：原先A桶有油26千克，B桶有油14千克，C桶有油8千克。

答：略。

7.解：依照题意，知69、85、93对A同余。

由85-69=16，93-85=8，93-69=24，可推出A=8或4或2，97÷8=12……1。

因此丁团分成每组A 人的若干组后还剩1人。