第六届华杯赛团体决赛口试试题及答案
第六届华杯赛初赛试题 (2)

第六届华杯赛初赛试题1.香港回归祖国之日是星期几?今天距回归之日还有多少天。
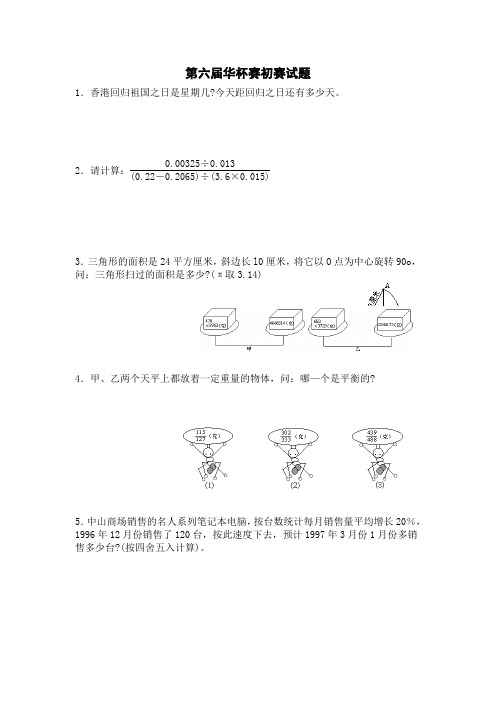
2.请计算:3.三角形的面积是24平方厘米,斜边长l0厘米,将它以O点为中心旋转90o,问:三角形扫过的面积是多少?(π取3.14)4.甲、乙两个天平上都放着一定重量的物体,问:哪—个是平衡的?5.中山商场销售的名人系列笔记本电脑,按台数统计每月销售量平均增长20%,1996年12月份销售了120台,按此速度下去,预计1997年3月份1月份多销售多少台?(按四舍五入计算)。
6.编号为l,2,3的三只蚂蚁分别举起一个重物。
问:金、银、铜奖牌分别发给几号蚂蚁?7.—辆汽车的速度是每小时50千米,现有一块每5小时慢2分的表,若用该表计时,测得这辆汽车的时速是多少?(得数保留一位小数) 8.哥德巴赫猜想是说:“每个大于2的偶数都可以袤示成两个质数之和”。
问:168是哪两个两位数的质数之和,并且其中的一个的个位数宇是1?9.右图中有九个空格,要求每个格中填入互不相同的数,使得每行、每列、每条对角线上的三个数之和都相等。
问:图中左上角的数是多少?10.某工厂原用长4米,宽l米的铁皮围成无底无顶的的正方体形状的产品存放处,恰好够放—周的产品。
现在产量增加了27%,问:能否还用原来的铁皮围成存放处,装下现在一周的产品?11.甲管注水速度是乙管的—倍半,同时开放甲、乙两个水管向游泳池注水,12小时可注满。
现在先开甲管向游泳池注水若干小时,剩下的由乙管注9小时将游泳池注满,问:甲管注水时间是多少?12.用棱长是1厘米的立方块拼成如右图所示的立体图形,求该图形的表面积。
13.威力集团生产的某种洗衣机的外形是长方体,装衣物部分是圆柱形的桶,直径40厘米,深36厘米,已知该洗衣机装衣物的空间占洗衣机体积的25%,长方体外形的长为52厘米,宽50厘米。
问:高是多少厘米?15.在周长为200米的圆形跑道—条直径的两端,甲、乙两人分别以6米/秒,5米/秒的骑车速度同时同向出发,沿跑道行驶。
第六届华杯赛全套试题
第六届华杯赛初赛试题1.香港回归祖国之日是星期几?今天距回归之日还有多少天。
2.请计算:0.00325÷0.013(0.22-0.2065)÷(3.6×0.015)3.三角形的面积是24平方厘米,斜边长l0厘米,将它以O点为中心旋转90o,问:三角形扫过的面积是多少?(π取3.14)4.甲、乙两个天平上都放着一定重量的物体,问:哪—个是平衡的?5.中山商场销售的名人系列笔记本电脑,按台数统计每月销售量平均增长20%,1996年12月份销售了120台,按此速度下去,预计1997年3月份1月份多销售多少台?(按四舍五入计算)。
6.编号为l,2,3的三只蚂蚁分别举起一个重物。
问:金、银、铜奖牌分别发给几号蚂蚁?7.—辆汽车的速度是每小时50千米,现有一块每5小时慢2分的表,若用该表计时,测得这辆汽车的时速是多少?(得数保留一位小数)8.哥德巴赫猜想是说:“每个大于2的偶数都可以袤示成两个质数之和”。
问:168是哪两个两位数的质数之和,并且其中的一个的个位数宇是1?9.右图中有九个空格,要求每个格中填入互不相同的数,使得每行、每列、每条对角线上的三个数之和都相等。
问:图中左上角的数是多少?10.某工厂原用长4米,宽l米的铁皮围成无底无顶的的正方体形状的产品存放处,恰好够放—周的产品。
现在产量增加了27%,问:能否还用原来的铁皮围成存放处,装下现在一周的产品?11.甲管注水速度是乙管的—倍半,同时开放甲、乙两个水管向游泳池注水,12小时可注满。
现在先开甲管向游泳池注水若干小时,剩下的由乙管注9小时将游泳池注满,问:甲管注水时间是多少?12.用棱长是1厘米的立方块拼成如下图所示的立体图形,求该图形的表面积。
13.威力集团生产的某种洗衣机的外形是长方体,装衣物部分是圆柱形的桶,直径40厘米,深36厘米,已知该洗衣机装衣物的空间占洗衣机体积的25%,长方体外形的长为52厘米,宽50厘米。
华杯赛英语试题及答案

华杯赛英语试题及答案1. 单项选择题:从下列各题的选项中,选择一个最佳答案。
A. What is your name?B. How old are you?C. Where are you from?D. What do you do?答案:A2. 完形填空题:阅读下面的短文,从每题所给的选项中选择一个最佳答案填空。
My name is Tom. I am a student. I study in a school. I have many friends. We often play together.A. andB. butC. or答案:A3. 阅读理解题:阅读下面的短文,然后回答后面的问题。
Today is a sunny day. I went to the park with my family. We played games and had a picnic. It was a great day.Question: What did the author do today?A. Went to the beachB. Went to the parkC. Stayed at home答案:B4. 翻译题:将下列句子从英语翻译成中文。
The cat is on the table.答案:猫在桌子上。
5. 写作题:写一篇不少于100字的短文,描述你最喜欢的季节和原因。
提示:可以描述季节的特点,以及在这个季节你喜欢做的活动。
答案示例:My favorite season is spring. The weather iswarm and the flowers are blooming. I like to go for a walk in the park and enjoy the beautiful scenery. Spring is also a great time for outdoor activities like hiking and cycling. I feel energetic and happy during this season.请注意,以上试题及答案仅供参考,实际考试内容和形式可能会有所不同。
华杯赛决赛试题及答案

华杯赛决赛试题及答案一、选择题(每题5分,共20分)1. 若一个数的平方根是a,则这个数是:A. a^2B. -a^2C. |a|D. a^32. 一个等差数列的前三项分别为2,5,8,则此数列的通项公式为:A. 3n - 1B. 3n - 2C. 3n + 2D. 3n - 33. 对于函数f(x) = ax^2 + bx + c,若a < 0,b > 0,则f(x)的图像可能是:A. 一个开口向上的抛物线B. 一个开口向下的抛物线C. 一个开口向上的双曲线D. 一个开口向下的双曲线4. 一个圆的半径为r,圆心到直线的距离为d,若圆与直线相交,则:A. d > rB. d < rC. d = rD. d ≤ r答案:1. A2. B3. B4. B二、填空题(每题5分,共10分)1. 一个圆的周长为2π,那么它的面积是______。
2. 如果一个三角形的两边长分别为3和4,夹角为60度,那么第三边的长度是______。
答案:1. π2. √13三、解答题(每题15分,共30分)1. 证明:若一个三角形的两边长分别为a和b,且满足a^2 + b^2 = c^2,则这个三角形是直角三角形。
2. 解方程组:\[\begin{cases}x + y = 5 \\2x + 3y = 11\end{cases}\]答案:1. 证明:根据勾股定理的逆定理,如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
设三角形ABC,其中AB=a,BC=b,AC=c。
根据题目条件,有a^2 + b^2 = c^2。
根据勾股定理的逆定理,可以得出∠C=90°,即三角形ABC是直角三角形。
2. 解:将第一个方程乘以2得到2x + 2y = 10。
然后用这个新方程减去第二个方程,得到y = 1。
将y = 1代入第一个方程,得到x + 1 = 5,解得x = 4。
因此,方程组的解为x = 4,y = 1。
华杯赛试题及答案小学

华杯赛试题及答案小学一、选择题(每题5分,共20分)1. 下列哪个选项是最小的质数?A. 0B. 1C. 2D. 32. 如果一个数的因数只有1和它本身,那么这个数是:A. 合数B. 质数C. 偶数D. 奇数3. 一个长方体的长、宽、高分别是2cm、3cm、4cm,那么它的体积是:A. 24立方厘米B. 26立方厘米C. 28立方厘米D. 30立方厘米4. 一个数的平方是36,那么这个数是:A. 6B. -6C. 6或-6D. 无法确定二、填空题(每题5分,共20分)1. 一个数的最小倍数是______。
2. 一个数的最大因数是______。
3. 一个数的因数的个数是______。
4. 一个数的倍数的个数是______。
三、解答题(每题10分,共30分)1. 一个长方体的长、宽、高分别是5cm、4cm、3cm,求它的体积。
2. 一个数的平方是64,求这个数。
3. 一个班级有45名学生,如果每排坐5名学生,那么需要排几排?四、应用题(每题15分,共30分)1. 小明买了3支铅笔和2本笔记本,每支铅笔的价格是1元,每本笔记本的价格是2元。
请问小明一共花了多少钱?2. 一个长方体的长是10cm,宽是8cm,高是6cm,求它的表面积。
答案:一、选择题1. C2. B3. A4. C二、填空题1. 它本身2. 它本身3. 有限个4. 无限个三、解答题1. 体积 = 长× 宽× 高= 5cm × 4cm × 3cm = 60立方厘米2. 这个数是8或-8(因为8^2 = 64且(-8)^2 = 64)3. 需要排的排数 = 学生总数÷ 每排人数= 45 ÷ 5 = 9排四、应用题1. 小明一共花了3 × 1元+ 2 × 2元 = 3元 + 4元 = 7元2. 表面积= 2 × (长× 宽 + 长× 高 + 宽× 高)= 2 × (10cm × 8cm + 10cm × 6cm + 8cm × 6cm) = 2 × (80平方厘米 + 60平方厘米 + 48平方厘米) = 2 × 188平方厘米 = 376平方厘米。
华杯赛小学决赛试题及答案

华杯赛小学决赛试题及答案题一:“自然界的奇妙景色”自然界是一个充满奇妙景色的地方。
从峡谷到瀑布,从雪山到沙漠,每一个角落都散发着独特的魅力。
接下来,我们将带你领略一些自然界最令人惊叹的景色。
1. 峡谷峡谷是由地壳运动和水的侵蚀所形成的。
它们通常有着陡峭的峭壁和蜿蜒的河流。
例如,美国的大峡谷就是世界上最壮观的峡谷之一。
漫步在峡谷的边缘,你可以欣赏到令人窒息的景色,仿佛置身于大自然的壮丽画卷之中。
2. 瀑布瀑布是水流从高处跌落到低处的景象。
它们以其惊人的能量和美丽的水流而闻名。
例如,尼亚加拉瀑布是世界上最著名的瀑布之一。
当你站在瀑布附近,听到水流的轰鸣声,你会被这股力量和壮观的景象所震撼。
3. 雪山雪山是天然的美丽画作。
它们被冰雪覆盖,傲立在高山之巅。
喜马拉雅山脉是世界上最高的山脉之一,被誉为地球的屋顶。
站在雪山的顶峰,你会被周围的巍峨山峰和绵延不绝的雪景所包围,仿佛置身于仙境。
4. 沙漠沙漠是世界上最广阔的生态系统之一,不仅有广阔的沙丘和沙漠风暴,还有令人难以置信的星空。
例如,撒哈拉沙漠是世界上最大的沙漠,拥有壮丽的沙丘和恢宏的沙漠风景。
夜晚时,你可以在撒哈拉沙漠的边缘观赏到无数明亮的星星,仿佛置身于一个星空仙境中。
总之,自然界中有无尽的奇妙景色等待我们去探索。
无论是峡谷、瀑布、雪山还是沙漠,它们都展现着大自然的鬼斧神工和无穷的魅力。
希望每一个人都能亲身体验这些令人惊叹的景色,与大自然真正融合。
题二:“小动物的朋友——蜜蜂”蜜蜂是我们身边最可爱的小动物之一。
它们不仅负责传播花粉,助力植物的繁衍,还生产出美味的蜂蜜。
现在,让我们来了解一下蜜蜂的生活和工作。
1. 居住环境蜜蜂生活在蜂巢中,蜂巢通常由蜂蜡制成。
蜜蜂会细心地为蜂巢打造出六角形的蜂房,用来储存花粉和蜜。
蜂巢是蜜蜂家族的家园,它们通过密切合作来照顾和保护蜂巢。
2. 分工合作蜜蜂社会非常有组织和分工合作。
每只蜜蜂在蜜蜂家族中都有自己特定的角色和任务。
华杯赛历年真题

华杯赛历年真题1. 简介华杯赛是中国知名的大学生科技创新大赛,旨在发掘和培养高校学生的创新能力和实践能力。
自1998年首次举办以来,华杯赛已经成为中国高校学生科技创新的重要舞台之一。
每年,来自全国各地的大学生团队在华杯赛上展示他们的创新项目,并与其他团队进行竞争。
在华杯赛的过程中,参赛团队需要解决一系列的科学和技术问题,所以往年的比赛真题是很好的学习资源。
本文将梳理华杯赛历年真题,并为读者提供学习华杯赛相关知识的指导。
2. 历年真题2.1 2020年华杯赛2.1.1 题目一:智能交通题目描述:设计一个智能交通系统,能够实时监测道路交通流量并进行智能调度。
要求考虑城市交通特点和实际情况,使交通系统更加高效和安全。
解题思路:首先,需要收集、分析和处理交通数据,可以利用传感器、摄像头等设备获取实时数据。
然后,需要设计一个算法来实时监测交通情况,并进行智能调度。
最后,需要将结果展示给用户,例如通过移动应用或网页。
2.1.2 题目二:智能农业题目描述:设计一个智能农业系统,能够自动监测和控制农作物的生长环境,提高农作物的产量和质量。
要求考虑土壤湿度、气温、光照等因素,并能够实时告警和调整环境参数。
解题思路:首先,需要收集土壤湿度、气温、光照等环境数据,可以利用传感器和气象站等设备获取实时数据。
然后,需要设计一个算法来分析环境数据,并根据需要调整环境参数。
最后,需要将结果展示给用户,例如通过移动应用或网页。
2.2 2019年华杯赛2.2.1 题目一:智能家居题目描述:设计一个智能家居系统,能够自动控制家庭设备,提高生活的便利性和舒适性。
要求考虑家庭成员的习惯和需求,使系统能够根据不同的场景做出相应的调整。
解题思路:首先,需要收集家庭成员的习惯和需求数据,可以通过家庭问卷调查等方式获取信息。
然后,需要设计一个算法来分析数据,并根据需要调整家庭设备的状态。
最后,需要将结果展示给用户,例如通过移动应用或智能音箱。
华杯赛历届试题

第一届华杯赛决赛一试试题1. 计算:2.975×935×972×(),要使这个连乘积的最后四个数字都是“0”,在括号内最小应填什么数?3.把+、-、×、÷分别填在适当的圆圈中,并在长方形中填上适当的整数,可以使下面的两个等式都成立,这时,长方形中的数是几?9○13○7=100 14○2○5=□4.一条1米长的纸条,在距离一端0.618米的地方有一个红点,把纸条对折起来,在对准红点的地方涂上一个黄点然后打开纸条从红点的地方把纸条剪断,再把有黄点的一段对折起来,在对准黄点的地方剪一刀,使纸条断成三段,问四段纸条中最短的一段长度是多少米?5.从一个正方形木板锯下宽为米的一个木条以后,剩下的面积是平方米,问锯下的木条面积是多少平方米?6.一个数是5个2,3个3,2个5,1个7的连乘积。
这个数当然有许多约数是两位数,这些两位的约数中,最大的是几?7.修改31743的某一个数字,可以得到823的倍数,问修改后的这个数是几?8.蓄水池有甲、丙两条进水管,和乙、丁两条排水管,要灌满一池水,单开甲管需3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时,现在池内有池水,如果按甲、乙、丙、丁的顺序,循环各开水管,每天每管开一小时,问多少时间后水清苦始溢出水池?9.一小和二小有同样多的同学参加金杯赛,学校用汽车把学生送往考场,一小用的汽车,每车坐15人,二小用的汽车,每车坐13人,结果二小比一小要多派一辆汽车,后来每校各增加一个人参加竞赛,这样两校需要的汽车就一样多了,最后又决定每校再各增加一个人参加竞赛,二小又要比一小多派一辆汽车,问最后两校共有多少人参加竞赛?10.如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少?11.若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了,小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下,小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子,问共有多少个盒子?12.如右图,把1.2,3.7, 6.5, 2.9, 4.6,分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一个填法,使△中的数尽可能小,那么△中填的数是多少?13.如下图,甲、乙、丙是三个站,乙站到甲、丙两站的距离相等。
“华罗庚金杯”少年数学邀请赛(口试)试题1-10届

华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形,正方形边长20厘米,问七巧板中平行四边形的一块(如右图中阴影部分)的面积是多少?2.从所有分母小于10的真分数中,找出一个最接近0.618的分数。
3.有49个小孩子,每人胸前有一个号码,号码从1到49各不相同,请你挑选出若干个小孩,排成一个圆圈,使任何相邻两个小孩的号码数的乘积小于100,你最多能挑选出多少个小孩子?4.有一路公共汽车,包括起点和终点站共有15个车站,如果有一辆车,除终点到站外,每一站上车的乘客中,恰好各有一位乘客从这一站到以后的每一站,为了使每位乘客都有座位,问这辆公共汽车最少要有多少个座位?5.正方形的树林每边长1000米,里面有白杨树和榆树,小明从树林的西南角走入树林,碰见一株白杨树就往正北走,碰见一株榆树就往正东走,最后他走了东北角上,问:小明一共走了多少米的距离?6.自然数按从小到大的顺序排成螺旋形,在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯……问拐第二十个弯的地方是哪一个数?第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形,黑色部分面积大还是阴影部分面积大?2、你能不能将自然数1到9分别填入右面的方格中,使得每个横格中的三个数之和都是偶数?3、司机开车按顺序到五个车站接学生到学校(如下图),每个站都有学生上车,第一站上了一批学生,以后每站上车的人数都是前一站上车人数的一半,车到学校时,车上最少有多少学生?4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。
问:白色部分面积与阴影部分面积之比是多少?5、用1、2、3、4、5这五个数两两相乘,可以得到10个不同的乘积,问乘积中是偶数多还是奇数多?6、7、将右边的硬纸片沿虚线折起来,便可作成一个正方体,问:这个正方体的2号面对面是几号面?(如下图)8、下面是一个11位数,它的每三个相邻数之和都是20,你知道打“?”的数字是几?9、有八张卡片,右图分别写着自然数1到8,从中取出三张,要使这三张卡片上的数字之和为9,问有多少种不同的取法?第03届华罗庚金杯少年数学邀请赛团体决赛口试1.一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如右图阴影所示部分,红条宽都是2厘米.问:这条手帕白色部分的面积是多少?2.伸出你的左手,从大拇指开始如图所示的那样数数字,1,2,3,……,问:数到1991时,你数在那个手指上?3.有3个工厂共订300份吉林日报,每个工厂订了至少99份,至多101份.问:一共有多少种不同的订法?4.图上有两条垂直相交的直线段AB、CD,交点为E(如下图).已知:DE=2CE,BE=3AE.在AB和CD上取3个点画一个三角形.问:怎样取这3个点,画出的三角形面积最大?5.如下图中有两个红色的圆,两个蓝色的圆,红色圆的直径分别是1992厘米和1949厘米,蓝色圆的直径分别是1990厘米和1951厘米.问:红色二圆面积大还是蓝色二圆面积大?6.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来(如下图),填在这个方格中,例如a=5+3=8.问:填入的81个数字中,奇数多还是偶数多?7.能不能在下式:1□2□3□4□5□6□7□8□9=10的每个方框中,分别填入加号或减号,使等式成立?8.把一个时钟改装成一个玩具钟(如右图),使得时针每转一圈,分针转16圈,秒针转36圈.开始时3针重合.问:在时针旋转一周的过程中,3针重合了几次?(不计起始和终止的位置).9.将1,2,3,4,5,6,7,8这8个数分成3组,分别计算各组数的和.已知这3个和互不相等,且最大的和是最小的和的2倍.问:最小的和是多少?10.这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如下图)?11.这是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%(如右图).问:大圆的面积是多少?12.有一根1米长的木条,第一次去掉它的,第二次去掉余下木条的;第三次又去掉第二次余下木条的,等等;这样一直下去,最后一次去掉上次余下木条的.问:这根木条最后还剩下多长?13.这是一个楼梯的截面图(如下图),高2.8米,每级台阶的宽和高都是20厘米.问:此楼梯截面的面积是多少?14.请找出6个不同的自然数,分别填入6个括号中,使这个等式成立.第04届华罗庚金杯少年数学邀请赛团体决赛口试1.2×3×5×7×11×13×17这个算式中有七个数连乘,请回答:最后得到的乘积中,所有数位上的数字和是多少?请讲一讲你是怎样算的?2.这是一个中国象棋盘(图中小方格都是相等的正方形,“界河”的宽等于小正方形边长),黑方有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12, 13,14中的两个位置.问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管(加工损耗忽略不计)问:剩余部分的管子最少是多少厘米?4.乙两人同时从A出发向B行进,甲速度始终不变,乙在走前面路程时,速度为甲的2倍,而走后面路程时,速度是甲的,问甲、乙二人谁选到B?请你说明理由。
第六届华杯赛复赛试题及答案

第六届华杯赛复赛试题1.计算:(1+)×(1+)×(1+)×…×(1+)×(1-)×(1-)×…(1+)=?2.—套绞盘和二组滑轮形成一个提升机构,如图所示:其中盘A直径为10厘米,B直径为40厘米,C直径为20厘米。
问:A顺时针方向转动—周时,重物上升多少厘米? (取π=3.14)3.计算:(1995.5-1993.5)÷1998×1999÷(得数保留三位小数)4.用一平面去截一个立方体,得到一个矩形的截口,而把立方体截成两个部分。
问:这两个部分各是几个面围成的?5.右图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有—直径为6厘米的卷轴。
已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?6.李师傅加工—批零件。
如果每天做50个,要比原计划晚8天完成;如果每天做60个,就可以提前5天完或。
这批零件共有多少个?7.某商店某一个月内销售A,B,C,D四种商品,情况如下表所示:已知:商品销售的毛利率=×100%。
今知A,B,C,D 四种商品的毛利率依次为9%,12%,20%,30%。
问:本月四种商品的毛利率是多少?8.问:与相比较,哪个更大,为什么?9.设有甲、乙、丙三人,他们步行的速度相同,骑车的速度也相同,骑车的速度是步行速度的3倍。
现甲自A地去B地,乙、丙从B地去A 地,双方同时出发。
出发时,甲、乙为步行,丙骑车。
途中,当甲、丙相遇时,丙将车给甲骑,自己改为步行,三人仍按各自原有方向继续前进;当甲、乙相遇时,甲将车给乙骑,自己重又步行,三人仍按各自原有方向继续前进。
问:三人之中谁最先到达自己的目的地?谁最后到达目的地?10.在某市举行的一次乒乓球邀请赛上,有三名专业选手与三名业余选手参加。
比赛采用单循环方式进行,就是说每两名选手都要比赛一场。
为公平起见,用以下方法记分。
开赛前每位迭手各有10分作为底分,每赛—场,胜者加分,负者扣分。
初中华杯赛总决赛6~8届数学题及答案

11 8 第六届 “ 华杯赛” 初一组第一试决赛试题1 .解方程x - x - 3.1415926 +y + - 2 y - 7.13 = 0 2.n 是自然数, N=[ n + l , n + 2 ,… , 3n ] 是 n + l , n + 2 ,… , 3n 的最小公倍数, 如果 N 可以表示成N = 210 ⨯ 奇数请回答 n 的可能值共有多少个?3 .一段跑道长 100 米,甲、乙分别从 A 、B 端点同时相向出发, 各以每秒 6 米和每秒 4.5 米的速度在跑道上来回往返练习跑步. 问:在 10分钟内( 包括第 10 分钟 ),① 甲和乙在途中迎面相遇多少次? ② 甲在途中追上乙多少次? ③ 甲和乙在 A ,B 两端点共相遇多少次:4 .一堆球 ,如果 是偶数个 ,就平均 分成两堆并拿走一堆 ,如果是 奇数个,就添加一个, 再平均分成两堆, 也拿走一堆, 这个过程称为一次“ 均分”.若只有 1 个球, 就不做“ 均分”. 当最初一堆球, 奇数个, 约七百多个,经 10 次均分和共添加了 8 个球后,仅余下 1 个球.请计算一下最初这堆球是多少个?5.一批大小略有不同的长方体盒子, 它们的高都等于 6 厘米,长和宽都 大于 5 厘米,且长宽比不小于 2 . 若在任一盒子中放一层边长为 5 厘米的小立方体, 无论怎样放, 放完后被小立方体所覆盖的底面积都不超过原底面积的 40 % , 现往盒子中注水, 问: ① 要使得最小的盒子不往外溢,最多能 注多少立方厘米水? ② 要使得最大的盒子开始往外溢, 最少要注进去多少立方厘米的水?6 . 若干台计算机联网, 要求: ① 任意两台之间最多用一条电缆连接; ② 任意三台之间最多用两条电缆连接; ③ 两台计算机之间如果没有连接电缆, 则必须有另一台计算机和它们都连接电缆. 若按此要求最多可以连 1600 条,问:① 参加联网的计算机有多少台? ②这些计算机按要求联网, 最少需要连多少条电缆?第 6 届小学组决赛 1 试答案1.N 等于 10 个 2 与某个奇数的积。
华杯赛决赛试题及答案

华杯赛决赛试题及答案一、选择题1. 下列哪个选项是正确的?A. 2 + 3 = 5B. 3 + 4 = 7C. 5 - 2 = 2D. 4 - 3 = 2答案:A2. 如果一个数的平方根是正数,那么这个数是:A. 负数B. 零C. 正数D. 任意实数答案:C二、填空题1. 圆的周长公式是 ________ 。
答案:2πr2. 一个直角三角形的两个直角边长分别为3和4,斜边长为________ 。
答案:5三、简答题1. 请解释什么是质数,并给出一个质数的例子。
答案:质数是指在大于1的自然数中,除了1和它本身以外,不能被其他自然数整除的数。
例如,2是一个质数,因为它只能被1和2整除。
2. 什么是勾股定理,并给出一个应用的例子。
答案:勾股定理是指在一个直角三角形中,直角边的平方和等于斜边的平方。
例如,如果一个直角三角形的两个直角边长分别为3和4,根据勾股定理,斜边的长度应该是√(3² + 4²) = 5。
四、计算题1. 计算下列表达式的值:(3 + 4) × (8 - 2) ÷ 2答案:352. 一个数的平方是36,求这个数的值。
答案:±6五、证明题1. 证明:对于任意正整数n,n² - 1总是能被8整除。
答案:对于任意正整数n,可以表示为n = 8k + r,其中k是整数,r是0到7之间的整数。
那么n² - 1 = (8k + r)² - 1 = 64k² +16kr + r² - 1 = 8(8k² + 2kr) + (r² - 1)。
由于r² - 1是8的倍数或者-1,所以n² - 1能被8整除。
2. 证明:在一个直角三角形中,如果斜边是直角边的两倍,那么这个三角形是等腰直角三角形。
答案:设直角三角形的直角边长分别为a和b,斜边为c。
根据题意,c = 2a。
第六届“华罗庚金杯”少年数学邀请赛团体决赛口试模拟押题
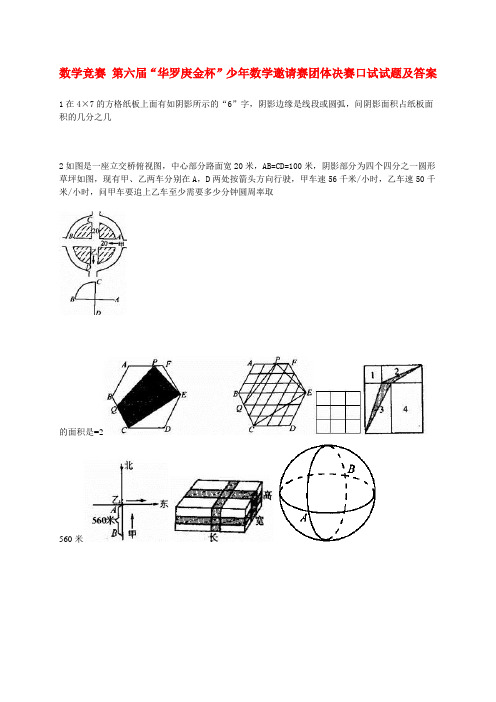
数学竞赛第六届“华罗庚金杯”少年数学邀请赛团体决赛口试试题及答案1在4×7的方格纸板上面有如阴影所示的“6”字,阴影边缘是线段或圆弧,问阴影面积占纸板面积的几分之几2如图是一座立交桥俯视图,中心部分路面宽20米,AB=CD=100米,阴影部分为四个四分之一圆形草坪如图,现有甲、乙两车分别在A,D两处按箭头方向行驶,甲车速56千米/小时,乙车速50千米/小时,问甲车要追上乙车至少需要多少分钟圆周率取的面积是=2560米11m9cm7cm3cm1cm28-6-36千米80米60米560米560米140米560米80米60米3m11cm9cm7cm次操作后能使表中各数都相等,此时表中诸数总和为:)。
它仍应是个被3除余1的数,但表中九个数变为相等,其总和应被3整除,这就得出矛盾!所以,无论经过多少次操作,表中的数都不会变为九个相同的数。
12.7分解:四个队单循环赛共6场比赛,每场均有胜负,6场最多共计18分。
若该队积7分,剩下的11分被3个队去分,那么,不可能再有两个队得7分,即至多再有一个队可得7分以上。
这样该队可以出线。
其次,如果该队积6分,则剩下12分,可能有另两队各得6分,如果这另两队小分都比该队高,该队就不能出线了。
所以,一个队至少要积7分才能保证必然出线。
13.答:镜面中的所见四面体的像如下图所示(其中A、B、C、D标出是为帮助大家想象)14解:将长条形纸带的一端作二次翻转,再将两端粘在一起,沿中线剪开,得到两个套在一起的经过一次翻转粘结两端而成的纸带,如下图所示。
15.403<V<445正确解:汽车模型由下部长方体与上面的台体组合而成如图所示,长方体体积,而台体看成底面积为21,高在7与9之间的台体。
即∴。
16.解:①4A格中有地雷,因为5A格相邻的格中有4A中可能有地雷,且肯定有一个。
②由于IC格中数字是2,而1B,1D中又无地雷,所以2B,2C,2D三格中必有两格有地雷,若2C有地雷,则无论2B或2D中有地雷都与其左边格中数字为1矛盾,所以2B,2D中各有一个地雷。
最新小学华杯赛试题及答案

最新小学华杯赛试题及答案以下是最新小学华杯赛的试题及答案。
请同学们认真阅读题目并选择最合适的答案。
答案将在试题结束后公布。
第一节:选择题1. 下面哪个是地球的大洲?A. 北极洲B. 夏威夷C. 亚马逊河D. 太阳系2. 以下哪个国家是世界上最大的国家?A. 美国B. 中国C. 加拿大D. 日本3. 铁是哪种物质?A. 液体B. 气体C. 固体D. 火星4. 西瓜属于以下哪个类别?A. 水果B. 蔬菜C. 肉类D. 饮料5. 恒星是由什么组成的?A. 水B. 空气C. 树木D. 氢和氦气体第二节:填空题1. 太阳是一个恒星,它处于太阳系的_________。
2. 中国的首都是_________。
3. 北京是哪个省的首府?4. 学生应该_______勤奋学习才能取得好成绩。
5. 跑步是一项很好的_______。
第三节:问答题1. 简述地球自转和公转的概念。
2. 什么是环保?为什么我们应该保护环境?第四节:阅读理解阅读下面的短文,然后回答问题。
学唱歌有很多好处。
首先,唱歌可以让人快乐。
当我们唱歌的时候,我们的身体会释放出一种叫做“快乐激素”的化学物质,这会使我们更加开心。
其次,唱歌还可以训练我们的声音和听觉。
唱歌可以让我们更敏感地听到声音的变化,并且提高我们的音准。
最后,在唱歌的过程中,我们还可以锻炼我们的肺活量和呼吸能力。
问题:1. 唱歌对人有哪些好处?2. 唱歌可以训练哪些技能?答案:第一节:选择题1. A2. C3. C4. A5. D第二节:填空题1. 中心2. 北京3. 北京市4. 努力5. 锻炼第三节:问答题1. 地球自转是指地球绕着自己的轴心旋转,并且在24小时内完成一次旋转。
公转是指地球绕太阳运动,一年绕行一周。
2. 环保是指保护环境并且减少对环境的污染。
我们应该保护环境,因为一个健康的环境对人类的生存和发展至关重要,而且保护环境也是我们应尽的责任。
第四节:阅读理解问题:1. 唱歌可以让人快乐,并且释放出快乐激素。
华杯赛试题 (4)

华杯赛试题一、赛事背景华杯赛是每年华国举办的一项重要体育赛事,旨在提倡体育精神、弘扬民族体育文化。
作为一场国际性的体育盛事,华杯赛引来了众多顶尖运动员和观众的瞩目。
今年的华杯赛将举办多个项目的比赛,其中包括田径、游泳、篮球、足球等多个体育项目。
二、试题内容1. 田径项目请设置一个「100米赛跑」的比赛,比赛规则如下:•每个参赛者需要在指定的起点和终点之间跑完100米的距离•多个参赛者将同时进行比赛•参赛者的名字和成绩需要记录下来,成绩按照跑完100米所用的时间计算2. 游泳项目请设计一个「200米自由泳」的比赛,要求如下:•每个参赛者需要在指定的起点和终点之间游完200米的距离•多个参赛者将同时进行比赛•参赛者的名字和成绩需要记录下来,成绩按照游完200米所用的时间计算3. 篮球项目请设置一个「三人篮球」的比赛,要求如下:•每个参赛队伍由三名球员组成,共进行两个半场比赛•每个半场的比赛时间为15分钟•比赛结束后,记录下每个参赛队伍的得分情况4. 足球项目请设计一个「11人制足球」的比赛,要求如下:•每个参赛队伍由11名球员组成•比赛时间为2个45分钟的半场,中场休息时间为15分钟•比赛结束后,记录下每个参赛队伍的得分情况三、比赛规则和评分标准1. 田径项目田径比赛按照跑完100米所用的时间来评分。
时间越短,成绩越好。
成绩以秒为单位记录,到小数点后两位。
2. 游泳项目游泳比赛按照游完200米所用的时间来评分。
时间越短,成绩越好。
成绩以秒为单位记录,到小数点后两位。
3. 篮球项目篮球比赛按照每个参赛队伍得分来评分。
每个队伍在每个半场结束后的得分总和为最终得分。
4. 足球项目足球比赛按照每个参赛队伍得分来评分。
每个队伍在比赛结束时的得分为最终得分。
四、总结华杯赛是一项重要的国际体育比赛,其中包括田径、游泳、篮球和足球等多个项目。
每个项目都有各自的比赛规则和评分标准。
田径项目根据跑完100米的时间来评分,游泳项目根据游完200米的时间来评分,篮球和足球项目则根据得分情况进行评分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六届华杯赛团体决赛口试试题1.在4×7的方格纸板上面有如阴影所示的“6”字,阴影边缘是线段或圆弧,问阴影面积占纸板面积的几分之几?2.如图是一座立交桥俯视图,中心部分路面宽20米,AB=CD=100米,阴影部分为四个四分之一圆形草坪(如右图),现有甲、乙两车分别在A,D两处按箭头方向行驶,甲车速56千米/小时,乙车速50千米/小时,问甲车要追上乙车至少需要多少分钟?(圆周率取3.1)3.如下图中正六边形ABCDEF的面积是54.AP=2PF,CQ=2BQ,求阴影四边形CEPQ 的面积.4.轮船从武汉到九江要行驶5小时,从九江到武汉要行驶7小时,问一长江飘流队员要从武汉乘木筏自然飘流到九江需要多少小时?5.你能在3×3的方格表中每个格子里都填一个自然数,使得每行、每列及两条对角线上的三数之和都等于1997吗?若能,请填出一例,若不能,请说明理由.6.用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个大长方形.问:图中阴影部分面积是多少?7.某城市东西路与南北路交汇于路口A.甲在路口A南边560米的B点,乙在路口A.甲向北,乙向东同时匀速行走,4分钟后二人距A的距离相等.再继续行走24分钟后,二人距A的距离恰又相等.问:甲、乙二人的速度各是多少?(如下图)8.某工人用薄木板钉成一个长方体的邮件包装箱,并且尼龙编织条如下图所示在三个方向上加固,尼龙编织条分别为365厘米,405厘米,485厘米,若每个尼龙条加固时接头重叠都是5厘米.问这个长方体包装箱的体积是多少立方米?9.小地球仪上赤道大圆与过南北极的某大圆相交于A、B两点(如下图).有黑、白二蚁从A点同时出发分别沿着这两个大圆爬行.黑蚁爬赤道大圆一周要10秒钟,白蚁爬过南北极的大圆一周要8秒钟.问:在10分钟内黑、白二蚁在B点相遇几次?为什么?10.有一长为11m,宽为9cm,高为7cm的长方体木块,能否切割成77块长、宽都是3cm,高是1cm的长方体形状的体积木块?说明理由.11.在3×3的方格表中已填入了九个质数,如果将表中同一行或同一列的三个数加上相同的自然数称为一次操作,问:你能通过若干次操作使得表中九个数都变为相同的数吗?为什么?12.①世界杯足球小组赛,每组四个队进行单循环比赛,每场比赛胜队得3分,败队记0分,平局时两队各记1分,小组各队全赛完以后,总积分最高的两个队出线进入下轮比赛,如果总积分相同,还要按小分排序.问:一个队至少要积几分才能保证本队必然出线?简述理由.13.一个正四面体放在桌面上,正对你的面(ABC)是红色,写有数字1;右侧面(ACD)是蓝色,写有数字2;左侧面(ABD)是黄色,写有数字3.如果在你的对面垂直于桌面放一面镜子,使这个四面体恰在你与镜子之间.请你画出镜面中你看到的这个四面体的形象(面上涂上颜色与数字的形象).14.将一长条形纸带两面都画上中轴线,然后将纸带的一端翻转,把两端粘在一起,如下图所示.再沿中轴线剪开,请你观察所得结果,并准备进如下操作:若将一长条形纸的一端作二次翻转后再将两端粘在一起,然后沿中轴线剪开,请在一分钟之内完成,展开出你的结果.15.(如下图)是一辆汽车模型纸工平面展开图,中轴线上面的一半标出了尺寸,将该图剪下折叠粘合(相同字母标记处粘合在一起)作成汽车模型的体积为V.请回答:1)403<V<445; 2)473<V<500哪一个正确,为什么?16.这是一个挖地雷的游戏,在64个方格中一共有10个地雷,每个方格中至多有一个地雷,对于写有数字的方格,其格中无地雷,但与其相邻的格中有可能有地雷,地雷的个数与该数字相等,请你指出哪些方格中有地雷.17.台球桌上有15个红球(每球1分),另有六个高分球;黄色球(2分),棕色球(3分),绿色球(4分),蓝色球(5分),粉色球(6分),黑色球(7分),台球比赛规则:①先打红球,打完所有红球后,再将高分球依次由低分到高分打入袋中,称为打完一局.②在打进两个红球之间可先后连续打进任意两个高分球,然后再取出这两个高分球放回原处,每打进一个球,选手得到该球的分值.问:小白兔打完一局最高能得多少分?18.在1,2,3,…,1996,1997这1997个自然数中,含数码1的数共有多少个?19.将100以内的质数从小到大排成一个数字串,依次完成以下五项工作叫做一次操作:①将左边第一个数码移到数字串的最右边;②从左到右两位一节组成若干个两位数;③划去这些两位数中的合数;④所剩的两位质数中有相同者,保留左边的一个,其余划去;⑤所余的两拉质数保持数码次序又组成一个新的数字串问:经过1997次操作,所得到数字串是什么?20.现有如下一系列图形(如下图)当n=1时,长方形ABCD分为2个直角三角形,总计数出5条边.当n=2时,长方形ABCD分为8个直角三角形,总计数出16条边.当n=3时,长方形ABCD分为18个直角三角形,总计数出33条边.……按如上规律请你回答:当n=100时,长方形ABCD应分为多少个直角三角形?总计数出多少条边?21.华罗庚数学小组的同学们在图书馆发现一块古代楔形文字泥板的图片,同学们猜测它是一种乘法表的记录,请你根据这个猜测,判定表示什么数?(如图)22.下面是主试委员会为第六届华杯赛写的一首诗:美少年华朋会友,幼长相亲同切磋;杯赛联宜欢声响,念一笑慰来者多;九天九霄志凌云,九七共庆手相握;聚起华夏中兴力,同唱移山壮丽歌请你将诗中56个字从第1行左边第一字起逐行逐字编为1~56号,再将号码中的质数由小到大找出来,将它们对应的字依次排成一行,组成一句话,请读出这句话.参考答案1.解:矩形纸板共28个小正方格,其中弧线都是圆周,非阴影部分共6个,也共六个,可拼成6个小正方格.因此阴影部分共28-6-3=19个小正方格.(如右图)所以,阴影面积占纸板面积的.2.2.62分钟解:依交通规则,甲车行进路线为A→B C→D(其中表示沿弧线行进),因而两车初始相距:(米)现甲车每小时比乙车多行6千米,所以每分钟甲车可追及乙车米所以(分)即甲车至少需检经过2.62分钟才能追及乙车.3.31解:如题图,将正六边形ABCDEF等分为54个小正三角形,根据平行四边形对角线平分平行四边形面积,采用数小三角形的办法来计算机积.四边形面积=11.上述三块面积之和为3+9+11=23.因此,阴影四边形CEPQ面积为54-23=314.35小时解:轮船顺水速=静水船速+水速;轮船逆水速=静水船速-水速;由于武汉到九江距离为定值,所以,(静水船速+水速)×5=(静水船速-水速)×7这表明12×水速=2×静水船速,即6×水速=静水船速,也就是,轮船以7×水速的速度5小时可从武汉到九江.所以,木筏以1个水速的速度要35小时可从武汉(自然飘流)到九江.5.不能解:若能填入九个自然数,,…,,满足题设条件,则相加得:而所以与是自然数矛盾.6.解:如右图,大长方形面积为1+2+3+4=10,延长RA交底边于Q,延长SB交底边于P,矩形ABPR面积是上部阴影三角形面积的2倍,矩形ABSQ是下部阴影三角形面积的2倍,所以矩形RQSP的面积是阴影部分面积的两倍.易知,∴因此矩形RQSP的面积是大矩形面积的,阴影部分面积是大矩形面积的.阴影部分面积=.7.80米;60米解:行走4分钟甲到C、乙到D.AC=AD,可见甲、乙二人4分钟共行AB=560米.如右图(甲速+乙速)×4=560米∴甲速+乙速=140米/分(1)再行走24分钟甲到E,乙到F已知AE=AF,所以甲28分钟行BE,乙28分钟行AF,因此甲28分钟比乙28分钟多行AB=560米.即(甲速-乙速)×28=560米甲速-乙速=20米/分(2)由(1),(2)知甲速=80米/分乙速=60米/分.8.1.001立方米解:长方体中:高+高=(1)高+长=(2)(3)(2)-(1):长-宽=20(4)+(3):长=130,从而宽=110,代入(1)得高=70所以长方体体积为:(立方厘米)=(立方米)9.0解:黑蚁爬半圆需要5秒钟,白蚁爬半圆需要4秒钟.黑、白二蚁同时从A点出发,要在B点相遇,必须满足两个条件:①黑、白二蚁爬行时间相同,②在此时间内二蚁爬行奇数个半圆,但黑蚁爬行奇数个半圆要用奇数秒(5×奇数),白蚁爬行奇数个半圆要用偶数秒(4×偶数),奇数与偶数不能相等,所以黑、白二蚁永远不能在B点相遇.10.不能解:木块体积为11×9×7=693立方厘米,77块3×3×1立方厘米的积木也恰为693立方厘米.如果能将11×9×7立方厘米的木块切割为77块3×3×1立方厘米的积木,那么11×7的侧面将被小积木的侧面盖满,而小积木侧面面积要么是3平方厘米,要么是9平方厘米.由11×7=3m=9n,可知:3×11×7,得出矛盾.所以长为11cm,宽为9cm,高为7cm的木块不能切割成77块3×3×1立方厘米的长方体积木.11.不能!解:表中九个质数之和恰为100,被3除余1,经过每一次操作,总和增加3的倍数.设m次操作后能使表中各数都相等,此时表中诸数总和为:).它仍应是个被3除余1的数,但表中九个数变为相等,其总和应被3整除,这就得出矛盾!所以,无论经过多少次操作,表中的数都不会变为九个相同的数.12.7分解:四个队单循环赛共6场比赛,每场均有胜负,6场最多共计18分.若该队积7分,剩下的11分被3个队去分,那么,不可能再有两个队得7分,即至多再有一个队可得7分以上.这样该队可以出线.其次,如果该队积6分,则剩下12分,可能有另两队各得6分,如果这另两队小分都比该队高,该队就不能出线了.所以,一个队至少要积7分才能保证必然出线.13.答:镜面中的所见四面体的像如下图所示(其中A、B、C、D标出是为帮助大家想象)14.解:将长条形纸带的一端作二次翻转,再将两端粘在一起,沿中线剪开,得到两个套在一起的经过一次翻转粘结两端而成的纸带,如下图所示.15.403<V<445正确解:汽车模型由下部长方体与上面的台体组合而成如图所示,长方体体积,而台体看成底面积为21,高在7与9之间的台体.即∴.16.解:①4A格中有地雷,因为5A格相邻的格中有4A中可能有地雷,且肯定有一个.②由于IC格中数字是2,而1B,1D中又无地雷,所以2B,2C,2D三格中必有两格有地雷,若2C有地雷,则无论2B或2D中有地雷都与其左边格中数字为1矛盾,所以2B,2D中各有一个地雷.③由1F到4F中数字0及1G到4G中的数字可以判断出1H到4H四个格中可能有地雷.首先如果1H中有地雷,则由1G格中数字为1,知2H一定无地雷.由于2G格数字为2,所以3H格有地雷.再由3G中的数字为2推断出4H中有地雷,则与4G相邻的格3H 与4H中都有地雷,与4G格数字1矛盾.因此,4H无地雷.同理可推断1H格中无地雷.最后由2G,3G中的数字2可得2H,3H中各有一个地雷.④由于6A格周围只有一个地雷且只有7B中可能有地雷,所以7B中有一个地雷,由于7A数字为2,则7B中有一个地雷,所以8A和8B格中只能一个地雷,再由8C格中的数字1可得8A中有一个地雷.⑤由7F中的数字3,可推出6E,8E,8F和8G四格中有三个格中有雷,加上前面已找出7个地雷,又恰有10个地雷,所以8H中无地雷.由7H中的1推出8G中有一个地雷,由7G的数字1,推出8F中无地雷,因而6E,8E中各有一个地雷.答:地雷分布如上图所示17.224解:小白兔一杆打完从未失误,每次按规则都打最高分的球,共得14×(1+6+7)+(1+2+3+4+5+6+7)=224分18.1269解:从100~1997共998个含数码1的数,在001~999这999个数中,1~99中含数码1的数共19个,在100~199共100个含数码1的数,所以在001~999这999个数中,共有19×9+100=271个含有数码1的数因此,在1,2,3,…,1996,1997中,含数码1的数共有:998+271=1269个19.1731解:第1次操作得数字串711131131737;第2次操作得数字串11133173;第3次操作得数字串111731;第4次操作得数字串1173;第5次操作得数字串1731;第6次操作得数字串7311;第7次操作得数字串3117;第8次操作得数字串1173;以下以4为周期循环,即4k次操作均为1173,1996=4×499,所以第1996次操作得数字串1173,因此第1997次操作得数字串1731.20.20000;30200解:n=1时,直角三角形个,边数=n=2时,直角三角形个,边数n=3时,直角三角形个,边数对一般的n,共分为个直角三角形,总计数出条边.所以n=100时,共分为个直角三角形,总计数出条边.21.3952解:图片中记录的是自然数乘以9的运算结果,左列是被乘数,右列是该数乘以9的积数,经过分析可知:其中▽代表1,代表10,代表60.因此,表示60×6+10×3+5×1=39522.少年朋友亲切联欢,一九九七相聚中山解:1 (2)(3) 4 (5) 6 (7)美少年华朋会友,8 9 10 (11)12 (13)14幼长相亲同切磋;15 16 (17)18 (19)20 21杯赛联谊欢声响,22 (23)24 25 26 27 28念一笑慰来者多;(29)30 31 32 33 34 35九天九霄志凌云,36 (37)38 39 40 (41)42九七共庆手相握;43 44 45 46 47 48 49聚起华夏中兴力,50 51 52 53 54 55 56同唱移山壮丽歌。
