中学数学试讲题(北师版)(2)
初中数学教师招聘面试--试讲逐字稿模板

初中数学教师招聘面试--试讲逐字稿模板
1. 介绍自己和教学背景(大约1分钟)
大家好,我是XXX。
我毕业于XXX大学数学专业并获得了硕士学位。
在过去的X年里,我一直从事初中数学教学工作,并积累了丰富的教学经验。
2. 课程目标和布置(大约1分钟)
今天的课程是关于解一元一次方程的,主要目标是让同学们掌握通过实际问题解方程的方法。
首先,我会提供一些简单的示例来引起学生的兴趣,然后逐步引导他们探索问题解决的方法。
3. 示范解题(大约3分钟)
让我们从一个简单的例子开始。
假设有一个问题:一辆汽车以每小时60公里的速度行驶,行程是240公里,我们需要计算行驶所需的时间。
我们可以设x为行驶的时间,然后根据速度与时间的
关系建立方程60x=240,通过解这个方程我们可以得到答案x=4小时。
通过这个例子,我们学到了如何通过方程来求解实际问题。
4. 学生练与评价(大约3分钟)
现在,我请同学们打开课本的第XX页,完成练题X。
你们可以自己或与同桌合作解答,我将会在课后给予评价和指导。
5. 结束语(大约1分钟)
今天的课程即将结束。
通过今天的研究,希望大家可以掌握解一元一次方程的方法,并能够应用到实际问题中去。
谢谢大家的参与和合作!
以上就是我今天试讲的内容,谢谢各位评委的聆听。
北师大版九年级上册数学第二章一元二次方程(解析版)

第二章一元二次方程一、单选题1.下列各方程中,一定是关于X的一元二次方程的是()A. 2x2+3=2x (5+x)B, ax2+c=0C.(a+1)炉+6升1=0D. (^2+l) x2- 3x+l=0【答案】D【解析】4.*+3=M5+、)整理得,10x-3=0,故不是一元二次方程;B.当a=0时,。
炉+。
=0不是一元二次方程:C.当a=-l时,(什1濡+6升1=0不是一元二次方程:D. aa2>0,二届+1 翔,匚d+lM -3x+l = 0 是一元二次方程:故选D.2.关于工的一元二次方程(。
-1)/+»/_] = 0的一个根是0,则。
值为()A. 1B. -1C. 1 或—1D. i【答案】B【解析】把0代入原方程,再根据原方程是一元二次方程,得到关于a的方程及不等式,解之即可.解:根据题意得:解得:a=-\.故选:B.3.下列说法不正确的是()A.方程工2=%有一根为0B.方程/一1=0的两根互为相反数C.方程(x-l)2-l = 0的两根互为相反数D.方程N—x + 2 = 0无实数根【答案】C【解析】解:A./=x,移项得:x2—x = 0,因式分解得:x(x-l)=0,解得x=0或x=l,所以有一根为0,此选项正确;B. ?-1 = 0,移项得:W=i,宜接开方得:x=l或x=-l,所以此方程的两根互为相反数,此选项正确:C. *-1)2-1 = 0,移项得:(X -1>=1,直接开方得:x-l=l或解得x=2或x=0,两根不互为相反数,此选项错误:D./ 7+2 = 0,找出a=l, b=-l, c=2,则二=l-8=-7V0,所以此方程无实数根,此选项正确.所以说法错误的选项是C.故选C.4.用配方法解一元二次方程2/—3x —1=0,配方正确的是().A. 3 工一一4)1716B.3丫X- -4J【答案】A【解析】按照配方法的步骤进行求解即可得答案.解:2X 2-3X -1 = 0移项得2/—3x = l ,,3 1二次项系数化1的厂--A = 一,3 配方得Y-二X + 2 1716故选:A本题考查了配方法解一元二次方程,配方法的一般步骤为(1)把常数项移到等号的右边:(2)把二次项的 系数化为1:(3)等式两边同时加上一次项系数一半的平方.5 .关于x 的一元二次方程(m-l )x?-2mx + m+l = 0,下列说法正确的是().【答案】C【解析】根据一元二次方程判别式的性质分析,即可得到答案.(m-l )x 2 - 2mx+ m + l = O 的判别式为: X —— 13 7=-+ 3 4;A.方程无实数根B.方程有两个相等的实数根C.方程有两个不相等的实数根D.方程的根无法确定△二(一2〃。
(常考题)北师大版初中数学九年级数学上册第四单元《图形相似》测试题(答案解析)(2)

一、选择题1.如图,在Rt ABC 中,90ACB D ∠=︒,是AB 边的中点,AF CD ⊥于点E ,交BC 边于点F ,连接DF ,则图中与ACE △相似的三角形共有( )A .2个B .3个C .4个D .5个2.如图,在ABC 中,D ,E 分别是AB,AC 上的点,且DE// BC ,若AE : EC=1: 4,那么:ADE BEC S S △△的值为( )A .1∶16B .1∶18C .1∶20D .1∶24 3.如图,ABC 中,AD BC ⊥于点D ,下列条件中不.能判定ABC 是直角三角形的是( )A .B DAC ∠=∠B .90B DAC ∠+∠=︒ C .2AB BD BC =⋅D .2AC CD BC =⋅ 4.如图,在▱ABCD 中,E 是BC 的中点,DE ,AC 相交于点F ,S △CEF =1,则S △ADC =( )A .3B .4C .5D .6 5.如图,在平面直角坐标系中,矩形ABCD 的对角线//BD x 轴,若(1,0),(0,2)A D ,则点C 的坐标为( )A .(4,3)B .(4,4)C .(3,4)D .(2.5,4) 6.如图,4AB =,射线BM 和AB 互相垂直,点D 是AB 上的一个动点,点E 在射线BM 上,12BE DB =,作EF DE ⊥并截取EF DE =,连结AF 并延长交射线BM 于点C .设BE x =,BC y =,则y 关于x 的函数解析式是( )A .124x y x =--B .21x y x =--C .31x y x =--D .84x y x =-- 7.点B 是线段AC 的黄金分割点,且AB <BC .若AC=4,则BC 的长为( ) A .252+ B .252- C .51- D .51- 8.如图,ABC 中,90ABC ∠=︒,点E 在CB 的延长线上,13BE AB =,过点E 作ED AC ⊥于D .若AD ED =,6AC =,则CD 的长为( )A .1.5B .2C .2.5D .4 9.若275x y z ==,则2x y z x z +-+的值是( ) A .67 B .13 C .49 D .410.如图,点D 、E 、F 分别是ABC 的边AB 、AC 、BC 上的点,若//DE BC ,//EF AB ,则下列比例式一定成立的是( )A .EF FC AD BF =B .AD DE DB BC = C .BF EF BC AD = D .EF DE AB BC = 11.若ad=bc ,则下列不成立的是( )A .a c b d =B .a c a b d b -=-C .a b c d b d ++=D . 1 111a c b d ++=++ 12.如图,直线123////l l l ,直线a 、b 与1l 、2l 、3l 分别交于点A 、B 、C 和点D 、E 、F ,若:1:2AB BC =,6DF =,则EF 的长为( )A .2B .3C .4D .5二、填空题13.如图,点P 是ABC 的重心,过P 作AB 的平行线DE ,分别交AC 于点D 、交BC 于点E ;作//DF BC ,交AB 于点F ,若ABC 的面积为36,则四边形BEDF 的面积为________.14.如图,在ABC 中,90ACB ∠=︒,30A ∠=︒,3BC =.点D 是AB 上一动点,以DC 为斜边向右侧作等腰直角三角形CDE ,使90CED ∠=︒,连接BE . (1)若点E 恰好落在AB 上,则AD 的值为______;(2)线段BE 的最小值为______.15.如图所示是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的半径为0.8m ,桌面距离地面1m ,若灯泡距离地面3m ,则地面上阴影部分的面积为_________m 2(结果保留)π.16.如图,已知在Rt ABC 中,C 90∠=︒,AC 3=,BC 4=,分别将Rt ABC 的三边向外平移2个单位并适当延长,得到111A B C △,则111A B C △的面积为______.17.如图,正方形ABCD 和正方形EFOG 是位似图形,其中点A 与点E 对应,点A 的坐标为()4,2-,点E 的坐标为()1,1-,则这两个正方形位似中心的坐标为______.18.在Rt △ABC 中,AB =6,AC =5,点D 在边AB 上,且AD =2,点E 在边AC 上,当△ADE ∽△ABC 时,AE =____.19.如图,有一个池塘,要测量池塘两端A 、B 的距离,可先在平地上取一点O ,从O 点不经过池塘可以直接到达点A 和点B ,连接AO 并延长到点C ,连接BO 并延长到点D ,使3AO BO CO DO==,测得36CD m =,则池塘两端AB 的距离为________m .20.如图,若ABC 与DEF 都是正方形网格中的格点三角形(顶点在格点上),则DEF 与ABC 的周长比为_________.三、解答题21.我国古代数学著作《九章算术》中有“井深几何”问题:“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深儿何?”它的大意是:如图,已知四边形BCDE 是矩形,5CD =尺,5AB =尺,0.4BF =尺,求井深BC 为多少尺?22.如图,在正方形ABCD 中,E 为边AD 上的点,点F 在边CD 上,∠BEF =90°且CF =3FD .(1)求证:△ABE ∽△DEF ;(2)若AB =4,延长EF 交BC 的延长线于点G ,求 CG 的长.23.如图,点C ,B ,E 在同一条直线上,AC ⊥BC ,BD ⊥DE ,BC =ED =6,BE =10,∠BAC =∠DBE .(1)求证:△ABC ≌△BED ;(2)求△ABD 的面积.24.如图,在△ABC 中,∠C =∠ADE ,AB =3,AD =2,CE =5,求证:(1)△ADE ∽△ACB ;(2)求AE 的长.25.如图1,在等边ABC 中,点D 是BC 边上的动点(不与点B 、C 重合),点E 、F 分别在AB 和AC 边上,且EDF=60.(1)求证:BDE CFD △∽△;(2)若点D 移至BC 的中点,如图2,求证:FD 平分EFC ∠.26.已知::2:3:4a b c =,且2316a b c -+=,求232a b c +-的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】利用直角三角形斜边上的高线模型,可判断有2个三角形与ACE △相似,利用直角三角形斜边上的中线等于斜边的一半,传递一组等角,得到第3个三角形.【详解】∵∠EAC=∠CAF ,∠AEC=∠ACF ,∴△ACE ∽△AFC ;∵∠EAC+∠AFC=90°,∠ECF+∠AFC=90°,∴∠EAC=∠ECF ,∵∠AEC=∠CEF ,∴△ACE ∽△CFE ;∵90ACB D ∠=︒,是AB 边的中点,∴DC=DB ,∴∠ECF=∠EAC=∠B ,∵∠AEC=∠BCA ,∴△ACE ∽△BAC ;共有3个,故选B.【点睛】本题考查了直角三角形的相似,熟练运用三角形相似的判定定理是解题的关键. 2.C解析:C【分析】 由已知条件可求得ABE EBC S S ∆∆,又由平行线分线段成比例可求得ADE BDES S ∆∆,结合S △BDE =S △ABE -S △ADE 可求得答案.【详解】解:∵AE 1EC 4=, ∴14ABE EBC S S ∆∆=, ∴14ABE EBC S S ∆∆=, ∵DE ∥BC ,∴14AD AE DB EC ==, ∴14ADE BDE S S ∆∆=, ∴S △BDE =4S △ADE ,又∵S △BDE =S △ABE -S △ADE ,∴4S △ADE =14S △EBC -S △ADE , ∴120ADE EBC S S ∆∆=, 故选:C .【点睛】本题主要考查了平行线分线段成比例的性质及三角形的面积,掌握同高三角形的面积比即为底的比是解题的关键.3.B解析:B【分析】根据已知对各个条件进行分析,从而得到答案.【详解】解:A.能,∵AD ⊥BC ,∴∠B+∠BAD=90°,∵∠B=∠DAC ,∴∠BAC=∠BAD+∠DAC=∠BAD+∠B=90°;∴△ABC 是直角三角形;B.不能,∵AD ⊥BC ,∴∠B+∠BAD=90°,∵∠B+∠DAC=90°,∴∠BAD=∠DAC ,∴△ABD ≌△ACD (ASA ),∴AB=AC ,∴△ABC 是等腰三角形,∴无法证明△ABC 是直角三角形;C.能,∵2AB BD BC =⋅ ∴AB BC BD AB= ∵∠B=∠B∴△CBA ∽△ABD ,∴∠ADB=∠BAC ,∵AD ⊥BC ,∴∠ADB=∠ADC=90°,∴∠BAC=90°∴△ABC 是直角三角形;D.能,∵2AC CD BC =⋅, ∴AC BC CD AC= ∵∠C=∠C ∴△CBA ∽△CAD ,∴∠ADC=∠BAC=90°∴△ABC 是直角三角形.故选:B【点睛】此题考查了相似三角形的判定与性质、直角三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用,注意相似三角形的判定与性质的应用.4.D解析:D【分析】根据已知可得△CEF ∽△ADF ,及EF 和DF 的关系,从而根据相似三角形的性质和三角形的面积得到答案.【详解】解:∵四边形ABCD 是平行四边形∴AD=BC ,△CEF ∽△ADF , ∴EC EF AD DF= ∵E 是BC 的中点,∴EC=1122BC AD = ∴12EC EF AD DF == ∴2211()()24CEF ADF S EF S DF ∆∆=== ∵S △CEF =1,∴S △ADF =4, ∵12EF DF = ∴DF=2EF∴S △D CF =2 S △CEF =2,∴S △ADC =S △ADF + S △D CF =4+2=6故选:D .【点睛】本题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的面积比等于相似比的平方是解答此题的关键.5.B解析:B【分析】过点B 作BF ⊥x 轴,垂足为F ,证明△ADO ∽△BAF ,确定点B 的坐标,利用中点坐标公式确定点E 的坐标,二次运用中点中点坐标公式即可确定点C 的坐标.【详解】如图,过点B 作BF ⊥x 轴,垂足为F ,∵四边形ABCD 是矩形,∴∠DAB=90°,∴∠DAO+∠BAF=90°,∵∠DAO+∠ADO=90°,∴∠ADO=∠BAF ,∴△ADO ∽△BAF ,∴OA :BF=OD :FA ,∵//BD x 轴,若(1,0),(0,2)A D ,∴OA=1,OD=2,BF=2,∴1:2=2:FA ,∴FA=4,∴点B (5,2),∵四边形ABCD 是矩形,∴点E 是BD 的,AC 的中点,∴点E (52,2), 设点C 的坐标为(m ,n ), ∴150,2,222m n ++== ∴m=4,n=4, ∴点C 的坐标为(4,4),故选C .【点睛】本题考查了矩形的性质,三角形相似的判定与性质,中点坐标公式,平行x 轴直线上点的坐标特点,构造辅助线证明三角形的相似,灵活运用中点坐标公式是解题的关键. 6.A解析:A【分析】作FG ⊥BC 于G ,依据已知条件求得△DBE ≌△EGF ,得出FG =BE =x ,EG =DB =2x ,然后根据平行线的性质即可求得.【详解】解:作FG ⊥BC 于G ,∵∠DEB +∠FEC =90°,∠DEB +∠BDE =90°;∴∠BDE =∠FEG ,在△DBE 与△EGF 中,B FGE BDE FEG DE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DBE ≌△EGF ,∴EG =DB ,FG =BE =x ,∴EG =DB =2BE =2x ,∴GC =y -3x ,∵FG ⊥BC ,AB ⊥BC ,∴FG ∥AB ,CG :BC =FG :AB , 即34x y x y-=, ∴124x y x =--, 故选:A .【点睛】本题考查了三角形全等的判定和性质,以及平行线分线段成比例,辅助线的做法是解题的关键.7.B解析:B【分析】根据黄金分割的定义可得出较长的线段BC=512AC,将AC=4代入即可得出BC的长度.【详解】解:∵点B是线段AC的黄金分割点,且AB<BC,∴BC=512AC,∵AC=4,∴BC=252.故选:B.【点睛】本题考查了黄金分割的定义:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中51-AB≈0.618AB,并且线段AB的黄金分割点有两个.8.B解析:B【分析】证明△ADF≌△EDC,得到DC=DF,设DC=x,再证明△EBF∽△ABC,求出x即可.【详解】解:∵∠ABC=90°,ED⊥AC,∴∠EBA=∠ADE=90°,又∠1=∠2,∴∠E=∠A,∵AD=ED,∴△ADF≌△EDC,∴DC=DF,设DC=x,∴DF=x,∴AD=ED=6-x ,∴EF=6-2x ,∵∠E=∠A ,∠FBE=∠ABC ,∴△EBF ∽△ABC , ∴BE EF AB AC =, ∵AC=6,BE=13AB , ∴163EF =, ∴EF=6-2x=2,∴x=2,∴CD=2,故选B .【点睛】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,解题的关键是掌握相应的判定方法,利用性质定理求出结果.9.C解析:C 【分析】 根据275x y z k ===,则x =2k ,y =7k ,z =5k ,代入2x y z x z+-+进行计算即可. 【详解】 解:275x y z k ===(k≠0), 则x =2k ,y =7k ,z =5k , ∴2x y z x z+-+=2754495k k k k k +-+=, 故选:C .【点睛】 本题考查了比例的性质,解题的关键是掌握比例的性质进行解题.10.A解析:A 【分析】根据平行可得EC FCAE BF=,EC BDAE DA=,再根据平行四边形的性质得EF=BD即可.【详解】解:∵//EF AB,∴EC FCAE BF=∵//DE BC,∴EC BDAE DA=,∴FC BDBF DA=∵//DE BC,//EF AB,∴四边形BFED是平行四边形,∴EF=BD,∴EF FCAD BF=,故选:A.【点睛】本题考查了平行线分线段成比例定理,解题关键是根据平行线列出恰当的比例式,再结合平行四边形性质进行推理.11.D解析:D【分析】根据比例和分式的基本性质,进行各种演变即可得到结论.【详解】A 由a cb d=可以得到ad=bc,故本选项正确,不符合题意;B、由a c ab d b-=-可得:(a-c)b=(b-d)a,即ad=bc,故本选项正确,不符合题意;C、由a b c db d++=可得(a+b)d=(c+d)b,即ad=bc,故本选项正确,不符合题意;D、由1?111a cb d++=++,可得(a+1)(d+1)=(b+1)(c+1),即ad+a+d=bc+c,不能得到ad=bc,故本选项错误,符合题意;故选:D.【点睛】本题考查了比例线段,根据比例的性质能够灵活对一个比例式进行变形.12.C解析:C【分析】连接AF 交2l 于点G ,根据平行线分线段成比例,得出12AB AG BC GF ==和21FG FE GA ED ==,则23EF DF =,即可求出结果. 【详解】 解:如图,连接AF 交2l 于点G ,∵23//l l , ∴12AB AG BC GF ==, ∵12l l //, ∴21FG FE GA ED ==, ∵6DF =,∴243EF DF ==. 故选:C .【点睛】 本题考查平行线分线段成比例,解题的关键是熟练掌握平行线分线段成比例的性质.二、填空题13.16【分析】延长CP 交AB 于G 由CP :PG=2:1推出CE :BC=2:3AD :AC=1:3由△CED ∽△CBA △AFD ∽△ABC 推出S △CED=×S △ABC=16S △AFD=×S △ABC=4由此即可解析:16【分析】延长CP 交AB 于G .由CP :PG =2:1,推出CE :BC =2:3,AD :AC =1:3,由△CED ∽△CBA ,△AFD ∽△ABC ,推出S △CED =49×S △ABC =16,S △AFD =19×S △ABC =4,由此即可解决问题.【详解】解:如图,延长CP 交AB 于G .∵点P 是△ABC 的重心,∴CP :PG =2:1,∵DE ∥AB ,∴CE :BE =2:1,AD :CD =1:2,∴CE :CB =2:3,AD :AC =1:3,∵ED ∥AB ,DF ∥BC ,∴△CED ∽△CBA ,△AFD ∽△ABC ,∴S △CED =49×S △ABC =16,S △AFD =19×S △ABC =4, ∴S 平行四边形BEDF =S △ABC -S △CED -S △AFD =36-16-4=16,故答案为:16. 【点睛】本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.14.【分析】(1)根据含30°的直角三角形的性质可得AB=6BE=CE=再根据等腰直角三角形的性质得出CE=DE=最后依据AD=AB-BE-ED 得出结果;(2)以BC 为直角边向左构造以∠CBH 为直角的等 933-324 【分析】(1)根据含30°的直角三角形的性质可得AB=6,BE=32,33,再根据等腰直角三角形的性质得出CE=DE=332,最后依据AD=AB-BE-ED 得出结果; (2)以BC 为直角边向左构造以∠CBH 为直角的等腰直角三角形BCH ,先证明△CDH ∽△CEB ,得出2DH BE=DH 取最小值时,BE 边为最小值,当DH ⊥AB 时,DH最小,即图中的D H ',根据含30°的直角三角形的性质可得出结论.【详解】(1)如图所示:∵∠ACB=90°,∠A=30°,BC=3,∴AB=6,BE=32,CE=332, ∵△CDE 为等腰直角三角形,∴CE=DE=332, ∴AD=6-32-332=933- (2)以BC 为直角边向左构造以∠CBH 为直角的等腰直角三角形BCH ,∵△CDE 为等腰直角三角形,∴∠DCE=∠HCB=45°,∠DCH=∠HCB , ∵2CD CH CE CB== ∴△CDH ∽△CEB , ∴2DH BE= ∴当DH 取最小值时,BE 边为最小值,当DH ⊥AB 时,DH 最小,即图中的D H ',∵∠A=30°,∠ACB=90°∴∠ABC=60°∵∠CBH=90°∴D BH '∠=30°∵BH=BC=3 ∴32D H '= ∴3242BE '=最小值,故答案为933-,324.【点睛】本题考查了相似三角形的判定和性质,含30°的直角三角形的性质,等腰三角形的性质,解题的关键是证明△CDH ∽△CEB .15.44π【分析】证明△OBQ ∽△OAP 根据相似三角形的性质求出AP 根据圆的面积公式计算得到答案【详解】解:如图由题意得OB=08mOQ=OP-PQ=3-1=2(m )BQ ∥AP ∴△OBQ ∽△OAP ∴即解解析:44π【分析】证明△OBQ ∽△OAP ,根据相似三角形的性质求出AP ,根据圆的面积公式计算,得到答案.【详解】解:如图,由题意得,OB=0.8m ,OQ=OP-PQ=3-1=2(m ),BQ ∥AP , ∴△OBQ ∽△OAP ,∴BQ OQ AP OP =,即0.823AP =, 解得,AP=1.2(m ), 则地面上阴影部分的面积=π×1.22=1.44π(m 2),故答案为:1.44π.【点睛】本题考查的是相似三角形的应用,掌握相似三角形的判定定理和性质定理是解题的关键. 16.54【分析】作于点D 作于点E 作于点F 分别证明△和△求出和再根据三角形面积公式求解即可【详解】解:作于点D 作于点E 作于点F ∵三边向外平移个单位∴∵∴∠且∠∴△∴又∵∠且∠∴△∴∴∴又∵△∴∴∴【点睛】 解析:54【分析】作11CD B C ⊥于点D ,作11BE B C ⊥于点E ,作11BF A B ⊥于点F ,分别证明△ACB BFG ∆∽和△1GHB ACB ∆∽,求出11A C 和11B C ,再根据三角形面积公式求解即可.【详解】解:作11CD B C ⊥于点D ,作11BE B C ⊥于点E ,作11BF A B ⊥于点F ,∵Rt ABC ∆三边向外平移个单位,∴1=22,2,C D CD BE GH BF ====,∵11//AB A B∴∠ABC AGC =∠且∠90ACB BFG =∠=︒∴△ACB BFG ∆∽ ∴103BG = 又∵∠11B A GC ABC =∠=∠,且∠190GHB ACB =∠=︒∴△1GHB ACB ∆∽ ∴1AC GH BC B H= ∴183B H = ∴1111C B CD DE EH HB =+++ 1082433=+++ 12=又∵△111ABC A B C ∆∽ ∴1111AC B C AC BC= ∴119A C = ∴111111112A B C S AC B C ∆=⨯⨯ 11292=⨯⨯ 54=【点睛】此题主要考查了相似三角形的性质与判定,能正确作出辅助线证明三角形是解答此题的关键.17.【分析】连接AE 并延长交x 轴于H 求AE 解析式即可【详解】解:∵点与点对应∴点B 与点F 对应BF 都在x 轴上连接AE 并延长交x 轴于H 则点H 为位似中心∵点A 的坐标为(﹣42)点E 的坐标为(﹣11)设AE 的解解析:()2,0【分析】连接AE 并延长交x 轴于H ,求AE 解析式即可.【详解】解:∵点A 与点E 对应,∴点B 与点F 对应,B 、F 都在x 轴上,连接AE 并延长交x 轴于H ,则点H 为位似中心,∵点A 的坐标为(﹣4,2)点E 的坐标为(﹣1,1),设AE 的解析式为y=kx+b ,把(﹣4,2),(﹣1,1)代入得,421k b k b -+=⎧⎨-+=⎩, 解得,1323k b ⎧=-⎪⎪⎨⎪=⎪⎩AE 的解析式为1233y x =-+, 当y=0时,x=2,H 点坐标为(2,0),故答案为:(2,0)【点睛】本题考查的是位似变换的概念和性质、待定系数法求一次函数解析式,掌握位似图形的对应点连线的交点是位似中心是解题的关键.18.【分析】根据相似三角形的对应边成比例求解即可求得答案【详解】解:∵△ADE ∽△ABC ∴即解得:AE =;故答案为:【点睛】此题考查了相似三角形的性质掌握相似三角形的性质是解题的关键 解析:53【分析】根据相似三角形的对应边成比例求解,即可求得答案.【详解】解: ∵△ADE ∽△ABC , ∴AD AE AB AC =, 即265AE =, 解得:AE =53; 故答案为:53. 【点睛】此题考查了相似三角形的性质.掌握相似三角形的性质是解题的关键.19.108【分析】先证明△AOB ∽△COD 然后根据相似三角形的性质求解即可【详解】解:∵∠AOB=∠COD ∴△AOB ∽△COD ∴∵∴AB=36×3=108m 故答案为:108【点睛】本题考查了相似三角形的解析:108【分析】先证明△AOB ∽△COD ,然后根据相似三角形的性质求解即可.【详解】解:∵3AO BO CO DO==,∠AOB=∠COD , ∴△AOB ∽△COD ,∴3AO BO AB CO DO CD===, ∵36CD m =,∴AB=36×3=108m .故答案为:108.【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解答本题的关键.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形. 20.【分析】设正方形网格的边长为1根据勾股定理求出△EFD △ABC 的边长运用三边对应成比例则两个三角形相似这一判定定理证明△EDF ∽△BAC 即可解决问题【详解】解:设正方形网格的边长为1由勾股定理得:D【分析】设正方形网格的边长为1,根据勾股定理求出△EFD 、△ABC 的边长,运用三边对应成比例,则两个三角形相似这一判定定理证明△EDF ∽△BAC ,即可解决问题.【详解】解:设正方形网格的边长为1,由勾股定理得:DE 2=22+22,EF 2=22+42,∴DE =EF =同理可求:AC ,BC∵DF =2,AB =2,∴1EF DE DF BC AB AC === ∴△EDF ∽△BAC ,∴DEF 与ABC,.【点睛】本题主要考查了勾股定理和相似三角形的判定及其性质,熟练掌握相似三角形的判定与性质是解题的关键.三、解答题21.井深BC 为57.5尺【分析】方法一:根据已知条件证明∽ABF ACD ,得到=AB BF AC CD,代入计算即可;方法二:根据已知条件证明ABF DEF ∽△△,得到AB BF DE EF =,代入计算即可 【详解】 解:方法一:四边形BCDE 是矩形,//BF CD ∴, ABF ACD ∴∽,AB BF AC CD∴=, 即5562.50.4AB CD AC BF ⋅⨯===. BC AC AB ∴=-62.55=-57.5=(尺).答:井深BC 为57.5尺.方法二:四边形BCDE 是矩形,//BF CD ∴,ABF DEF ∴∽,AB BF DE EF∴=, 即AB EF DE BF⋅= 5(50.4)57.50.4⨯-==. 57.5BC DE ∴==(尺). 答:井深BC 为57.5尺.【点睛】本题主要考查相似三角形的应用,准确计算是解题的关键.22.(1)见解析;(2)CG =6.【分析】(1)由正方形的性质得出∠A =∠D =90°,证出∠ABE =∠DEF ,即可得出△ABE ∽△DEF ; (2)求出DF =1,CF =3,由相似三角形的性质得出AE AB DF DE =,解得DE =2,证明△EDF ∽△GCF ,得出DE DF CG CF=,求出CG =6,即可得出答案. 【详解】(1)证明:∵四边形ABCD 为正方形,∴∠A =∠D =90°,∴∠ABE +∠AEB =90°,∵∠BEF =90°,∴∠DEF +∠AEB =90°,∴∠ABE =∠DEF ,∴△ABE ∽△DEF ;(2)解:∵AB =BC =CD =AD =4,CF =3FD ,∴DF =1,CF =3,∵△ABE ∽△DEF , ∴AE AB DF DE =,即441DE DE-=, 解得:DE =2,∵AD ∥BC ,∴△EDF ∽△GCF , ∴DE DF CG CF =,即213CG =, ∴CG =6.【点睛】 本题考查了相似三角形的判定与性质、正方形的性质、直角三角形的性质等知识;熟练掌握正方形的性质,证明三角形相似是解题的关键.23.(1)见解析,(2)ABD S40= 【分析】(1)由AC ⊥BC ,BD ⊥DE ,可得∠ACB=∠BDE=90°,可证△ACB ≌△BDE (AAS ); (2)由△ACB ≌△BDE ,可得AB=BE=10,,在Rt △BDE 中,由勾股定理8=,由∠CAB+∠ABC=90°可求∠ABD=180°-∠ABC-∠EBD=90°,可求S △ABD =1AB BD 2⋅即可. 【详解】解:(1)∵AC ⊥BC ,BD ⊥DE ,∴∠ACB=∠BDE=90°,在△ACB 和△BDE 中,ACB=BDE BAC=DBE BC=ED ∠∠⎧⎪∠∠⎨⎪⎩,∴△ACB ≌△BDE (AAS );(2)∵△ACB ≌△BDE ,∴AB=BE=10,在Rt △BDE 中,由勾股定理8==,又∵∠CAB+∠ABC=90°,∴∠ABC+∠EBD=90°,∴∠ABD=180°-∠ABC-∠EBD=90°,∴S △ABD =11AB BD=108=4022⋅⨯⨯. 【点睛】 本题考查三角形全等判定与性质,勾股定理,直角三角形面积,掌握三角形全等判定与性质,勾股定理应用方法,直角三角形面积的求法是解题关键.24.(1)见解析;(2)1【分析】(1)利用“两角法”进行证明;(2)利用(1)中相似三角形的对应边成比例来求AE 的长度.【详解】解:(1)证明:∵∠C =∠ADE ,∠A =∠A ,∴△ADE ∽△ACB(2)解:由(1)知,△ADE ∽△ACB , 则AD AE AC AB= ∵AB =3,AD =2,CE =5, ∴253AE AE =+, 得:121,6AE AE ==-(舍去)∴AE 的长是1【点睛】本题考查了相似三角形的判定与性质.本题关键是要懂得找相似三角形,利用相似三角形的性质求解.25.(1)见解析 (2)见解析【分析】(1)根据等腰三角形的性质得到∠B=∠C ,根据三角形的内角和定理和平角的定义得到∠BED=∠CDF ,于是得到△BDE ∽△CFD ;(2)根据相似三角形的性质得到对应边成比例,等量代换得到比例式,判定相似三角形,最后根据相似三角形的性质得出FD 平分∠EFC .【详解】解:(1)∵AB=AC=BC ,∴∠B=∠C=60°,∵∠BED=180°-∠B-∠BDE=120°-∠BDE ,∠CDF=180°-∠EDF-∠BDE=120°-∠BDE ,∴∠BED=∠CDF ,∴△BDE ∽△CFD ;(2)∵△BDE ∽△CFD , ∴BD DE CF DF=, ∵点D 是BC 的中点,∴BD=CD , ∴CD DE CF DF= ∵∠EDF=∠C=60°,∴△DEF ∽△CDF ,∴∠DFE=∠CFD ,∴FD 平分∠EFC .【点睛】本题考查了相似三角形的判定和性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.26.【分析】巧用未知数表示比值,转化为方程求解即可.【详解】::2:3:4a b c =,∴设2a k =,3b k =,4c k =,∵2316a b c -+=,261216k k k ∴-+=,解得2k =,4a ∴=, 6b =,8c =,2328181610a b c ∴+-=+-=.【点睛】本题考查了比例的性质,理解比例,合理引入未知数解题是解题的关键.。
2024-2025学年北师版中学数学八年级上册3.2平面直角坐标系(第2课时)教学课件

E F
BC
G
oA
x
① D(- 3,5),E(- 7,3), C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0), A(0,0),B(0,3)-1;
例题讲解
y
D
E
C
F
B
G
A
o
x
解答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段 EC 与 x 轴有什么位置关系?点 E 和点 C 的坐标
知识回顾
1、如图,请写出点A的坐标,在平面直角坐标系
中描出点B(–6, –3).
y
(–4, 5) A
5
–6 –4 O
x
B
–3
(–6, –3)
知识回顾
2.完成下表:
坐标轴上的 点
x轴、y轴上的点 不__属__于____
任何象限
对应关系
坐标平面内的点与有序实数对是 __一___一___对应的
合作探究
例题讲解
例2.在直角坐标系中描出下列各点,并将各组内 这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3), C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0), A(0,0),B(0,3);
观察所描出的图形,它像什么?
例题讲解
y
连接起来的图形像“房子”
1、写出图中的平行四边形ABCD各个顶点的坐标。
A(-3, 4) B(–6, –2)
(-3, 4)
Hale Waihona Puke (9, 4)C(6, –2) D(9, 4)
(–6, –2)
(6, –2)
北师大版八年级数学上册第2章-实数(培优试题)

第二章实数专题无理数近似值的确定1. 设面积为3的正方形的边长为x,那么关于x的说法正确的是()A.x是有理数 B.x取0和1之间的实数C.x不存在 D.x取1和2之间的实数2.(1)如图1,小明想剪一块面积为25cm2的正方形纸板,你能帮他求出正方形纸板的边长吗?(2)若小明想将两块边长都为3cm的正方形纸板沿对角线剪开,拼成如图2所示的一个大正方形,你能帮他求出这个大正方形的面积吗?它的边长是整数吗?若不是整数,那么请你估计这个边长的值在哪两个整数之间.3.你能估测一下我们教室的长、宽、高各是多少米吗?你能估测或实际测量一下数学课本的长、宽和厚度吗?请你再估算一下我们的教室能放下多少本数学书?这些数学书可供多少所像我们这样的学校的初一年级学生使用呢?请你对每一个问题给出估测的数据,再把估算的过程结果一一写出来.答案:1.D 【解析】 ∵面积为3的正方形的边长为x ,∴x 2=3,而12=1,22=4,∴1<x 2<4,∴1<x <2,故选D.2.解:(1)边长为5cm. (2)设大正方形的边长为x ,∵大正方形的面积=32+32=18,而42=16,52=25,∴16<x 2<25,∴4<x <5,故正方形的边长不是整数,它的值在4和5之间.3.解:估算的过程:教室的长、宽、高可以用我们的身高估计出来;数学课本的长、宽和厚度可以用我们的手指估计出来,也可以用直尺测量出来;我们用长宽高相乘估计出教室的容积与课本的体积相除算出能放下多少本数学书,就是能供多少名学生使用,再用本班人数乘一年级班数估计本校一年级人数,然后相处就可以估计出这些数学书可供多少所像我们这样的学校的初一年级学生使用了.估测的数据、估算的结果略.专题一 非负数问题1. 若2(a +与1+b 互为相反数,则a b -的值为( )A B1C1-D.1-2.设a,b,c都是实数,且满足(2-a)2,ax2+bx+c=0,求式子x2+2x的算术平方根.3.若实数x,y,z= 14(x+y+z+9),求xyz的值.专题二探究题4.研究下列算式,你会发现有什么规律?=2=5;…请你找出规律,并用公式表示出来.5.先观察下列等式,再回答下列问题:答案:(a+与|b+1|互为相反数,1.D 【解析】∵2(a++|b+1|=0,∴2a=0且b+1=0,∴+-=1 D.∴a=2,b=﹣1,a b2.解:由题意,得2-a=0,a2+b+c=0,c+8=0.∴a=2,c=-8,b=4.∴2x2+4x-8=0.∴x2+2x=4.∴式子x2+2x的算术平方根为2.3.解:将题中等式移项并将等号两边同乘以4得+9=0,∴+4)=0,∴-2)2-2)2-2)2=0,-2=0-2=0,=2,∴x=4,y-1=4 ,z-2=4,∴x=4,y=5,z=6.∴xyz=120.专题立方根探究性问题专题比较无理数大小2. 观察下列一组等式,然后解答后面的问题:(121++132++143++…+ 120132012+)•( 2013+1). (2)利用上面的规律,试比较1211-与1312-的大小.3. 先填写下表,通过观察后再回答问题.问: (1)被开方数a 的小数点位置移动和它的算术平方根a 的小数点位置移动有无规律? 若有规律,请写出它的移动规律;(2)已知:a =1800,- 3.24 =-1.8,你能求出a 的值吗?(3)试比较a 与a 的大小.答案:1.D 【解析】 ∵a 2=2000+21003997⨯,b 2=2000+21001999⨯,c 2=4004=2000+2×1002,1003×997=1 000 000-9=999 991,1001×999=1 000 000-1=999 999,10022=1 004 004. ∴c >b >a .故选D .2.解:(1)由上面的解题规律可直接写出111n n n n=+-++, 则(121++132++143++…+ 120132012+)•( 2013+1)=[(2-1)+ (3- 2)+(4-3)+…+(2013-2012)](2013+1)=( 2013-1) ( 2013+1)=2012.(2)∵11211-=1211+,11312-=1312+, 又1211+<1312+,∴11211-<11312-, ∴1211->1312-. 3.解:依次填:0.001,0.01,0.1,1,10,100,1000.(1)有规律,当被开方数的小数点每向左(或向右)移动2位,算术平方根的小数点向左(或向右)移动1位.(2)观察1.8和1800,小数点向右移动了3位,则a 的值小数点向右移动6位,即a=3240000;(3)当0<a <1时,a >a ;当a=1或0时,a =a ;当a >1时,a <a .专题 实数与数轴1.如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画弧,交数轴于点A ,则点A 表示的数是( )A .2B .22C .12D .122.如图所示,直线L 表示地图上的一条直线型公路,其中A 、B 两点分别表示公路上第140公里处及第157公里处.若将直尺放在此地图上,使得刻度15,18的位置分别对准A ,B 两点,则此时刻度0的位置对准地图上公路的第( )公里处3. 一个等腰直角三角形三角板沿着数轴正方向向前滚动,起始位置如图,顶点C 和A 在数轴上的位置表示的实数为-1和1.那么当顶点C 下一次落在数轴上时,所在的位置表示的实数是___________.4. 如图,已知A 、B 、C 三点分别对应数轴上的数a 、b 、c .(1)化简:|a-b|+|c-b|+|c-a|;(2)若a=4x y ,b=-z 2,c=-4mn .且满足x 与y 互为相反数,z 是绝对值最小的负整数,m 、n 互为倒数,试求98a+99b+100c 的值;(3)在(2)的条件下,在数轴上找一点D ,满足D 点表示的整数d 到点A ,C 的距离之和为10,并求出所有这些整数的和.答案:1.B 【解析】 由勾股定理得:正方形的对角线为2,设点A 表示的数为x ,则2-x=2,解得x=2-2.故选B .2.B 【解析】 根据题意,数轴上刻度15,18的位置分别对准A ,B 两点,而AB 两点间距离157-140=17(公里),即数轴上的3个刻度对应实际17公里的距离.又有数轴上刻度0与15之间有15个刻度,故刻度0的位置对准地图上公路的位置距A 点有15×173=85(公里), 140-85=55,故刻度0的位置对准地图上公路的55公里处.故选B .3.3+22 【解析】 在直角△ABC 中,AC=CB=2,根据勾股定理可以得到AB=22,则当顶点C下一次落在数轴上时,所在的位置表示的实数是4+22-1=3+22.故答案为:3+22.4.解:(1)由数轴可知:a-b>0,c-b<0,c-a<0,所以原式=(a-b)-(c-b)-(c-a)=a-b-c+b-c+a=2a-2c.(2)由题意可知:x+y=0,z=-1,mn=1,所以a=0,b=-(-1)2=-1,c=-4,∴98a+99b+100c=-99-400=-499.(3)满足条件的D点表示的整数为-7、3,它们的和为-4.专题一与二次根式有关的规律探究题1.将1、2、3、6按如图所示的方式排列.若规定(m,n)表示第m排从左到右第n个数,则(4,2)与(21,2)表示的两数之积是()A.1B.2C.232. 观察下列各式及其验证过程:322322=+=======. (1)按照上述两个等式及其验证过程,猜想1544+的变形结果并进行验证; (2)针对上述各式反映的规律,写出用a (a 为任意自然数,且2a ≥)表示的等式,并给出验证;(3)针对三次根式及n 次根式(n 为任意自然数,且2n ≥),有无上述类似的变形,如果有,写出用a (a 为任意自然数,且2a ≥)表示的等式,并给出验证.3. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+22=221)(+,善于思考的小明进行了以下探索:设a+b 2=22)(n m +(其中a 、b 、m 、n 均为正整数),则有a+b 2=m 2+2n 2+2mn 2, ∴a=m 2+2n 2,b=2mn.这样小明就找到了一种把部分a+b 2的式子化为平方式的方法. 请你仿照小明的方法探索并解决下列问题:(1)当a 、b 、m 、n 均为正整数时,若a +b 3=2)3(n m +,用含m 、n 的式子分别表示a 、b ,得:a = ,b = ;(2)利用所探索的结论,找一组正整数a 、b 、m 、n 填空: +=( +2;(3)若a +43=2)3(n m +,且a 、m 、n 均为正整数,求a 的值.专题二 利用二次根式的性质将代数式化简4. 化简二次根式22a a a 的结果是( ) A. 2a B. 2a C. 2a D. 2a5.如图,实数a .b 在数轴上的位置,化简:222)(b a b a -+-.答案:1.D 【解析】 从图示中知道,(4,2)所表示的数是6.∵前20排共有1+2+3+4+…+20=210个数,∴(21,2)表示的是第210+2=212个数.∵这些数字按照1、2、3、6的顺序循环出现,212÷4=53,∴(21,2)表示的数是6.∴(4,2)与(21,2)表示的两数之积是666⨯=.2.解:(14441515+=24644444415151515⨯+===. (22211a a a a a +=--(a 为任意自然数,且2a ≥). 3322221111a a a a a a a a a a a a -++===---- (3)333311-=-+a a a a a a (a 为任意自然数,且2a ≥).验证:a === =2a a =2a .故选 5.解:由图知,a <0,b >0,∴a ﹣b <0,222)(b a b -+-=|a |。
初中数学试讲题目教案

初中数学试讲题目教案一、教学目标:1. 让学生理解平方根的概念,掌握求一个数的平方根的方法。
2. 培养学生运用平方根解决实际问题的能力。
3. 培养学生的逻辑思维能力和团队合作精神。
二、教学内容:1. 平方根的定义2. 求一个数的平方根的方法3. 平方根的实际应用三、教学过程:1. 导入:利用生活中的实例,如:一个正方形的边长是a,求这个正方形的面积。
引导学生思考,如何求出一个数的平方根。
2. 讲解:(1)平方根的定义:如果一个数x的平方等于a,那么x是a的平方根,记作x = √a。
(2)求一个数的平方根的方法:① 如果一个数是正数,它有两个平方根,分别是正数和负数。
② 如果一个数是0,它的平方根是0。
③ 如果一个数是负数,它没有实数平方根。
(3)平方根的实际应用:利用平方根解决实际问题,如:一个长方形的面积是25平方厘米,长是5厘米,求宽。
3. 练习:让学生独立完成练习题,检验学生对平方根的理解和掌握程度。
4. 总结:对本节课的内容进行总结,强调平方根的概念和求法。
四、教学策略:1. 采用问题驱动的教学方法,引导学生思考和探索。
2. 用生活中的实例让学生直观地理解平方根的概念。
3. 利用练习题检验学生的学习效果。
4. 组织小组讨论,培养学生的团队合作精神。
五、教学评价:1. 学生能准确地回答平方根的定义和求法。
2. 学生能运用平方根解决实际问题。
3. 学生能在小组讨论中积极参与,展示自己的观点。
六、教学资源:1. PPT课件。
2. 练习题。
3. 小组讨论所需材料。
七、教学时间:1课时(40分钟)八、教学后记:通过本节课的教学,发现学生在理解平方根的概念上存在一定的困难,因此在教学中要注重引导学生思考,用生活中的实例帮助学生直观地理解平方根。
同时,要加强练习,让学生在实际问题中运用平方根。
在小组讨论环节,要注意调动每个学生的积极性,让他们在讨论中收获更多的知识和经验。
北师大版九年级数学2.3用公式法求解一元二次方程(2)课后练习

用公式法求解一元二次方程(第2课时)
1.用公式法解方程243x x =+时,24b ac ∆=-的值是( )
A.4
B.28
C.20 D .-4
2.若点P 的横、纵坐标恰好是方程22240x x --=的两根,则点P 在( )
A. 第二象限
B. 第四象限
C.第一象限 D 第二或第四象限
3.方程2269x x -=的根为
4.已知三角形的两边长为分别为3cm 和4cm ,第三边长是方程2650x x -+=的根,则该三角形的周长为 ,形状为 ,面积为
5.如图,某小区规划在一个长30 m 、宽20 m
的长方形土地上修建三条等宽的通道,使其
中两条与AB 平行,另外两条与AD 平行,
其余部分种花草,要使每一块花草的面积
都为 78 m2,那么通道宽应该设计为多少?
设通道宽为x m ,则由题意列的方程
为_____________________.
6. 某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长25 m),另外三边用木栏围成,木栏长40 m. 养鸡场的面积能达到180 m2 吗?如果能,请给出设计方案;如果不能,请说明理由.
7.要对一块长为60m ,宽为40m 的矩形荒地ABCD 进行绿化和硬化,设计方案如图所示,矩形P ,Q 为两块绿地,其余为硬化路面。
P ,Q 两块绿地周围的硬化路面宽度都相等,并且两块绿地的面积和矩形ABCD 面积的
14,求P ,Q 两块绿地周围硬化路面的宽。
Q P D C B A。
(常考题)北师大版高中数学必修四第一章《三角函数》测试题(包含答案解析)(2)
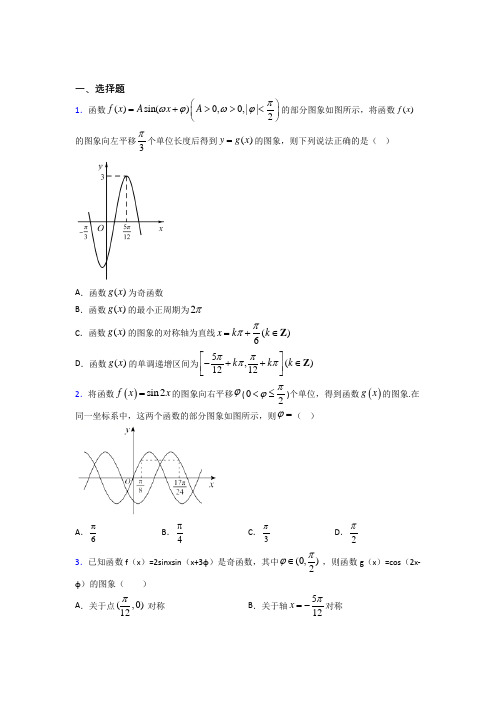
一、选择题1.函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象,则下列说法正确的是( )A .函数()g x 为奇函数B .函数()g x 的最小正周期为2πC .函数()g x 的图象的对称轴为直线()6x k k ππ=+∈ZD .函数()g x 的单调递增区间为5,()1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z2.将函数()sin 2f x x =的图象向右平移ϕ(02πϕ<≤)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则ϕ=( )A .6πB .4π C .3π D .2π 3.已知函数f (x )=2sinxsin (x+3φ)是奇函数,其中(0,)2πϕ∈ ,则函数g (x )=cos (2x-φ)的图象( ) A .关于点(,0)12π对称 B .关于轴512x π=-对称C .可由函数f (x )的图象向右平移6π个单位得到 D .可由函数f (x )的图象向左平移3π个单位得到 4.已知实数a ,b 满足0<2a <b <3-2a ,则下列不等关系一定成立的是( ) A .sin sin2b a < B .()2cos >cos 3a b -C .()2sin sin3a b +<D .23cos >sin 2b a ⎛⎫-⎪⎝⎭5.设函数()3cos22sin cos f x x x x =+,给出下列结论: ①()f x 的最小正周期为π ②()y f x =的图像关于直线12x π=对称③()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减 ④把函数2cos2y x =的图象上所有点向右平移12π个单位长度,可得到函数()y f x =的图象.其中所有正确结论的编号是( ). A .①④B .②④C .①②④D .①②③6.将函数()sin 3f x x π⎛⎫=- ⎪⎝⎭的图象横坐标缩短到原来的12(纵坐标不变),然后向左平移3π个单位,所得函数记为()g x .若1x ,20,2x π⎛⎫∈ ⎪⎝⎭,12x x ≠,且()()12g x g x =,则()12g x x +=( ) A .12-B .3-C .12D .327.函数()13cos313xxf x x -=+的图象大致是( ) A . B .C .D .8.函数1cos y x x=+的图象可能是( ) A . B .C .D .9.函数()()sin ln 0=->f x x x ωω只有一个零点,则实数ω的取值范围是( ) A .()0,πB .5,2⎫⎛⎪⎝⎭ππe C .50,2⎫⎛ ⎪⎝⎭πeD .5,2⎫⎛∞ ⎪⎝⎭π+e 10.已知函数()sin cos f x x x =+,则下列说法正确的是( ) A .()f x 的最小值为0 B .()f x 的最大值为2 C .()()2f x f x π-=D .1()2f x =在0,2π⎡⎤⎢⎥⎣⎦上有解 11.若函数)22()sin 23cos sin f x x x x =-的图像为E ,则下列结论正确的是( ) A .()f x 的最小正周期为2π B .对任意的x ∈R ,都有()()3f x f x π=-C .()f x 在7(,)1212ππ上是减函数D .由2sin 2y x =的图像向左平移3π个单位长度可以得到图像E 12.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象(如图所示),则下列有关函数()f x 的结论错误的是( )A .图象关于点,012π⎛⎫- ⎪⎝⎭对称 B .最小正周期是π C .在0,6π⎛⎫⎪⎝⎭上单调递减 D .在0,12π⎡⎤⎢⎥⎣⎦上最大值是3 二、填空题13.若函数()()()4sin 0f x x ωϕω=+>对任意的x 都有()3f x f x π⎛⎫+=- ⎪⎝⎭,则6f π⎛⎫⎪⎝⎭的值是___________. 14.已知函数()()πsin (00)2f x M x M ωϕωϕ=+>><,的部分图象如图所示,其中()23A ,(点A 为图象的一个最高点)502B ⎛⎫- ⎪⎝⎭,,则函数()f x =___________.15.已知函数()()2sin 0f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是-2,则ω的最小值等于__________.16.关于函数()()4sin 23f x x x R π⎛⎫=+∈ ⎪⎝⎭,有下列命题: ①函数()y f x =的表达式可以改写为4cos 26y x π⎛⎫=- ⎪⎝⎭; ②函数()y f x =是以2π为最小正周期的周期函数; ③函数()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称;④函数()y f x =的图象关于直线6x π=-对称.其中正确的序号是______.17.函数[]y x =的函数值表示不超过x 的最大整数,例如,[]3.54-=-,[]2.12=.则对于函数()[]f x x x =-,有下列说法:①()f x 的值域为[)0,1;②()f x 是1为周期的周期函数;③()f x 是偶函数;④()f x 在区间[)1,2上是单调递增函数.其中,正确的命题序号为___________.18.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min ,其中心O 离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?19.关于函数()sin |||sin |f x x x =+有下述四个结论: ①()f x 是偶函数;②()f x 在区间,2ππ⎛⎫⎪⎝⎭单调递增; ③()f x 在[],ππ-有4个零点;④()f x 的最大值为2; 其中所有正确结论的编号是_________. 20.已知函数sin cos |sin cos |3()22+--=+x x x x f x [0,]m 上恰有4个零点,则实数m 的取值范围为________.三、解答题21.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象如图所示.(1)求函数()f x 的解析式; (2)当113,33x ⎡⎤∈-⎢⎥⎣⎦时,试由实数m 的取值讨论函数()()2g x f x m =-的零点个数. 22.已知函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭的图象与直线2y =的相邻两个交点间的距离为2π,且________.在①函数6f x π⎛⎫+ ⎪⎝⎭为偶函数;②33f π⎛⎫=⎪⎝⎭;③x R ∀∈,()6f x f π⎛⎫≤⎪⎝⎭;这三个条件中任选一个,补充在上面问题中,并解答. (1)求函数()f x 的解析式;(2)求函数()f x 在[]0,π上的单调递增区间.23.广东省清远市美林湖摩天轮是国内最大的屋顶摩天轮,该摩天轮直径为84米,摩天轮的最高点距地面101米,摩天轮匀速转动,每转动一圈需要t 分钟,若小明从摩天轮的最低点处登上摩天轮,从小明登上摩天轮的时刻开始计时.(1)求小明与地面的距离y (米)与时间x (分钟)的函数关系式;(2)在摩天轮转动一圈过程中,小明的高度在距地面80米以上的时间不少于5分钟,求t 的最小值.24.已知函数21()3cos cos 2222x x x f x =++. (1)求函数()f x 的最小正周期;(2)将函数()y f x =的图象上的各点向左平移32π个单位,再保持纵坐标不变,横坐标缩短到原来的一半;得到函数()y g x =的图象,求函数()y g x =的最大值及取得最大值时x的取值集合.25.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;在落潮时返回海洋.下面是某港口在某季节每天的时间和水深关系表: 时刻 2:00 5:00 8:00 11:00 14:00 17:00 20:00 23:00 水深/米7.05.03.05.07.05.03.05.0()()sin ,0,2f t A t B A πωϕωϕ⎛⎫=++>< ⎪⎝⎭来描述.(1)根据以上数据,求出函数()()sin f t A t B ωϕ=++的表达式;(2)一条货船的吃水深度(船底与水面的距离)为4.0米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口然后离开港口?每次在港口能停留多久?26.已知向量a =(cosωx -sinωx ,sinωx),b =(-cosωx -sinωx,2cosωx).设函数f(x)=a b ⋅+λ(x ∈R)的图象关于直线x =π对称,其中ω,λ为常数,且ω∈1,12⎛⎫⎪⎝⎭.(1)求函数f(x)的最小正周期; (2)若y =f(x)的图象经过点,04π⎛⎫⎪⎝⎭,求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据图象得到函数()f x 解析式,将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象,可得()y g x =解析式,分别根据正弦函数的奇偶性、单调性、周期性与对称性,对选项中的结论判断,从而可得结论. 【详解】 由图象可知3A =,33253441234ππππω⎛⎫=⋅=--= ⎪⎝⎭T , ∴2ω=,则()3sin(2)f x x ϕ=+. 将点5,312π⎛⎫⎪⎝⎭的坐标代入()3sin(2)f x x ϕ=+中, 整理得5sin 2112πϕ⎛⎫⨯+= ⎪⎝⎭, ∴522,Z 122k k ππϕπ⨯+=+∈, 即2,Z 3k k πϕπ=-∈;||2ϕπ<, ∴3πϕ=-,∴()3sin 23f x x π⎛⎫=-⎪⎝⎭. ∵将函数()f x 的图象向左平移3π个单位长度后得到()y g x =的图象, ∴()3sin 23sin 2,333g x x x x R πππ⎡⎤⎛⎫⎛⎫=+-=+∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. ()()3sin 23sin 233g x x x g x ππ⎛⎫⎛⎫-=-+=--≠- ⎪ ⎪⎝⎭⎝⎭,∴()g x 既不是奇函数也不是偶函数, 故A 错误;∴()g x 的最小正周期22T ππ==, 故B 不正确. 令2,32πππ+=+∈x k k Z ,解得,122k x k Z ππ=+∈, 则函数()g x 图像的对称轴为直线,122k x k Z ππ=+∈. 故C 错误; 由222,232k x k k πππππ-++∈Z ,可得5,1212k x k k ππππ-+∈Z ,∴函数()g x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 故D 正确; 故选:D. 【点睛】关键点睛:本题主要考查三角函数的图象与性质,熟记正弦函数的奇偶性、单调区间、最小正周期与对称轴是解决本题的关键.2.C解析:C 【分析】由图可知,172482g f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭,根据函数图象的平移变化法则可知()()sin 2x g x ϕ=-,于是推出1717sin 224242g ππϕ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,即1722124k ππϕπ-=+或324k ππ+,k Z ∈,再结合02πϕ<≤,解之即可得ϕ的值.【详解】由图可知,17sin 22488g f πππ⎛⎫⎛⎫⎛⎫==⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 因为()f x 的图象向右平移ϕ个单位,得到函数()g x 的图象,所以()()sin 2x g x ϕ=-,所以171717sin 2sin 22424122g πππϕϕ⎛⎫⎛⎫⎛⎫=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以1722124k ππϕπ-=+或17322124k ππϕπ-=+,k Z ∈, 解得712k πϕπ=-或3k πϕπ=-,k Z ∈,因为02πϕ<≤,所以3πϕ=.故选:C 【点睛】本小题主要考查三角函数图象变换,属于中档题.3.B解析:B 【分析】利用三角函数的奇偶性求得φ,再利用三角函数的图象对称性、函数y=Asin (ωx+φ)的图象变换规律,判断各个选项是否正确,从而得出结论.【详解】函数f (x )=2sinxsin (x+3φ)是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭, ∴y=2sinxsin (x+3φ)是奇函数,∴3φ=2π,φ=6π,则函数g (x )=cos (2x ﹣φ)=cos (2x ﹣6π). 当12x π=时,206x π-=,112g π⎛⎫= ⎪⎝⎭,则函数不关于点,012π⎛⎫⎪⎝⎭对称,选项A 错误; 当512x π=-时,26x ππ-=-,则函数关于直线512x π=-对称,选项B 正确;函数()2sin sin 2sin cos sin 22f x x x x x x π⎛⎫=+== ⎪⎝⎭, 其图像向右平移6π个单位的解析式为sin 2sin 2sin 263y x x x ππ⎡⎤⎛⎫⎛⎫==-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项C 错误; 其图像向左平移3π个单位的解析式为2sin 2sin 2sin 233y x x x ππ⎡⎤⎛⎫⎛⎫==+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 选项D 错误; 故选B. 【点睛】本题主要考查三角函数的奇偶性、对称性,函数y=Asin (ωx+φ)的图象变换规律,属于中档题.函数()sin y A x ωϕ=+(A >0,ω>0)的性质:(1)奇偶性:=k ϕπ ,k Z ∈时,函数()sin y A x ωϕ=+为奇函数;=2k πϕπ+,k Z ∈时,函数()sin y A x ωϕ=+为偶函数.;(2)周期性:()sin y A x ωϕ=+存在周期性,其最小正周期为T =2πω;(3)单调性:根据y =sin t 和t =x ωϕ+的单调性来研究,由+22,22k x k k Z πππωϕπ-≤+≤+∈得单调增区间;由3+22,22k x k k Z πππωϕπ≤+≤+∈得单调减区间;(4)对称性:利用y =sin x 的对称中心为()(),0k k Z π∈求解,令()x k k ωϕπ+=∈Z ,求得x ;利用y =sin x 的对称轴为()2x k k Z ππ=+∈求解,令()+2x k k πωϕπ+=∈Z ,得其对称轴.4.D解析:D 【分析】对各个选项一一验证:对于A.由0<2a <b <3-2a ,可以判断出2ba <,借助于正弦函数的单调性判断; 对于B.由0<2a <b <3-2a ,可以判断出23a b <-,借助于余弦函数的单调性判断; 对于C.由0<2a <b <3-2a ,可以判断出23a b +<,借助于正弦函数的单调性判断; 对于D.先用诱导公式转化为同名三角函数,借助于余弦函数的单调性判断; 【详解】 因为0<2a <b <3-2a 对于A. 有0<2b a <, 若22b a π<<,有sin sin 2b a <;若22b a π<<,有sin sin 2ba >,故A 错; 对于B.有 23ab <-,若232a b π<<-,有()2cos >cos 3a b -,故B 错;对于C. 23a b +<,若232a b π<+<,有()2sin sin 3a b +>,故C 错;对于D. 222333sin cos cos 2222a a a ππ+⎛⎫⎛⎫⎛⎫-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又因为b <3-2a <3,所以2cos >cos(3)b a - ∵22332a a π+-<-∴()223cos 3cos 2a a π+⎛⎫->-⎪⎝⎭∴()22233cos cos 3cos sin 22a a b a π+⎛⎫⎛⎫>->-=- ⎪ ⎪⎝⎭⎝⎭,故D 对. 故选:D. 【点睛】利用函数单调性比较大小,需要在同一个单调区间内.5.C解析:C 【分析】根据题意,利用辅助角公式和两角和的正弦公式化简得()2sin(2)3f x x π=+,根据2T ωπ=求出最小正周期即可判断①;利用整体代入法求出()y f x =的对称轴,即可判断②;利用整体代入法求出()y f x =的单调减区间,从而可得在区间2,63ππ⎡⎤⎢⎥⎣⎦上先减后增,即可判断③;根据三角函数的平移伸缩的性质和诱导公式化简,即可求出平移后函数,从而可判断④. 【详解】解:函数()2sin cos sin 22sin(2)3f x x x x x x x π++=+,即:()2sin(2)3f x x π=+,所以()f x 的最小正周期为222T πππω===,故①正确; 令2,32πππ+=+∈x k k Z ,解得:,122k x k Z ππ=+∈, 当0k =时,则直线12x π=为()y f x =的对称轴,故②正确; 令3222,232k x k k Z πππππ+≤+≤+∈,解得:7,1212ππππ+≤≤+∈k x k k Z , 所以()f x 的单调递减区间为:7,,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦, 当0k =时,()f x 的一个单调递减区间为7,1212ππ⎡⎤⎢⎥⎣⎦, 则区间7,612ππ⎡⎤⎢⎥⎣⎦上单调递减,故在区间2121,3228,6ππππ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦上先减后增,故③错误; 把函数2cos2y x =的图象上所有点向右平移12π个单位长度,得到s 2)2cos 22co 22cos 2126332sin(2y x x x x πππππ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-=-=+-= ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎦⎣⎦+⎝⎭⎣即平移后得到函数()y f x =的图象,故④正确. 所以所有正确结论的编号是:①②④. 故选:C. 【点睛】关键点点睛:本题考查三角函数的图象和性质,熟练掌握正弦型函数的周期、对称轴、单调区间的求法,以及三角函数的平移伸缩是解题的关键,还考查辅助角公式、两角和的正弦公式以及诱导公式的应用,考查学生化简运算能力.6.D解析:D 【分析】先利用函数()sin y A ωx φ=+的图像变换规律求得()g x 的解析式,再利用正弦函数的图像的对称性,求得12x x +的值,可得()12g x x +的值. 【详解】将函数()sin 3f x x π⎛⎫=-⎪⎝⎭的图象横坐标缩短到原来的12(纵坐标不变),可得sin 23y x π⎛⎫=- ⎪⎝⎭的图象;再向左平移3π个单位,所得函数()sin 23g x x π⎛⎫=+ ⎪⎝⎭,若1x ,20,2x π⎛⎫∈ ⎪⎝⎭,12x x ≠,则142,333x πππ⎛⎫+∈ ⎪⎝⎭,242,333x πππ⎛⎫+∈ ⎪⎝⎭,()()12g x g x =,12223322x x πππ+++∴=,126x x π∴+=,则()122sin 2sin 6332g x x πππ⎛⎫+=⨯+==⎪⎝⎭. 故选:D. 【点睛】本题考查函数()sin y A ωx φ=+的图像变换规律,正弦函数的对称性,属于中档题.7.A解析:A 【分析】先判断奇偶性,可排除C ,D ,由特殊值()f π,可排除B ,即可得到答案.【详解】因为()()()1331cos 3cos31331x x xx f x x x f x -----=⋅-=⋅=-++,所以函数()f x 为奇函数,排除C ,D ;又()13cos3013f ππππ-=>+,排除B , 故选:A. 【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.8.C解析:C 【分析】利用函数的奇偶性和特殊的函数值的正负排除错误选项. 【详解】函数定义域是{|0}x x ≠,关于原点对称,记1()cos f x x x=+,则11()cos()cos f x x x x x-=-+=+-()f x =,是偶函数,排除BD ,11()cos 10f ππππ=+=-+<,排除A .故选:C . 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.9.C解析:C 【分析】函数()()sin ln 0=->f x x x ωω只有一个零点,等价于sin y x ω=与ln y x =图象只有一个交点,作出两个函数的图象,数形结合即可求解. 【详解】函数()()sin ln 0=->f x x x ωω只有一个零点, 可得sin ln 0x x ω-=只有一个实根,等价于sin y x ω=与ln y x =图象只有一个交点, 作出两个函数的图象如图所示,由sin y x ω=可得其周期2T πω=,当x e =时,ln 1y e ==sin y x ω=最高点5,12A πω⎛⎫⎪⎝⎭所以若恰有一个交点,只需要5ln 12πω>,即52e πω>, 解得:52e πω<,又因为0>ω,所以502eπω<<, 故选:C 【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.10.C解析:C 【分析】 可得()()2f x f x π+=,得出()f x 是以2π为周期的函数,故只需考虑0,2x π⎡⎤∈⎢⎥⎣⎦即可. 【详解】()()sin cos cos sin 222f x x x x x f x πππ⎛⎫⎛⎫+=+++=+= ⎪ ⎪⎝⎭⎝⎭,()f x ∴是以2π为周期的函数,当0,2x π⎡⎤∈⎢⎥⎣⎦时,()sin cos sin cos 4f x x x x x x π⎛⎫=+=+=+ ⎪⎝⎭,则3,444x πππ⎡⎤+∈⎢⎥⎣⎦,41x π⎛⎫+ ⎝∴≤⎪⎭≤根据函数的周期性可得()f x 的最小值为1,故AB 错误,∴1()2f x =在0,2π⎡⎤⎢⎥⎣⎦上无解,故D 错误, ()()sin cos cos sin222f x x x x x f x πππ⎛⎫⎛⎫-=-+-=+= ⎪ ⎪⎝⎭⎝⎭,故C 正确. 故选:C. 【点睛】本题考查三角函数的应用,解题的关键是得出()f x 是以2π为周期的函数,故只需考虑0,2x π⎡⎤∈⎢⎥⎣⎦即可. 11.C解析:C 【分析】利用二倍角和辅助角公式化简函数为()2sin(2+)3f x x π=;根据正弦型函数的性质验证选项得解 【详解】()sin 222sin(2+)3f x x x x π==()f x 最小正周期22T ππ==,A 错误; ()2sin[2()+]2sin(2)2sin 2333f x x x x ππππ-=-=-=,B 错误; 当7(,)1212x ππ∈时,32(,)322x πππ+∈ ()f x ∴在7(,)1212ππ上是减函数,C 正确; 将2sin 2y x =向左平移3π个单位长度得到22sin[2()]2sin(2)33y x x ππ=-=-,D 错误. 故选:C 【点睛】本题考查正弦型函数性质的相关命题的辨析,涉及到二倍角和辅助角公式化简三角函数、正弦型函数的周期性、对称性和单调区间的求解、三角函数平移变换的应用等知识;关键是能够熟练掌握整体对应的方法,通过代入检验,结合正弦函数图象可确定正弦型函数的性质.12.C解析:C 【分析】首先根据题中所给的函数图象,从最值、周期和特殊点着手将解析式确定,之后结合函数的性质对选项逐一分析,得到结果. 【详解】根据图象得到:2A =,311341264T πππ=-=,所以T π=, 所以2ππω=,解得2ω=,所以()()2sin 2f x x ϕ=+.将点,26π⎛⎫ ⎪⎝⎭代入,得到2sin 23πϕ⎛⎫+= ⎪⎝⎭,则()232k k Z ππϕπ+=+∈,得()26k k Z πϕπ=+∈,又2πϕ<,所以6π=ϕ,所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭. 对于A ,20126ππ⎛⎫⨯-+= ⎪⎝⎭,则函数()f x 关于,012π⎛⎫- ⎪⎝⎭对称,故A 正确; 对于B ,函数的周期22T ππ==,故B 正确; 对于C ,当0,6x π⎛⎫∈ ⎪⎝⎭时,2,662x πππ⎛⎫+∈ ⎪⎝⎭,此时函数()f x 为增函数,故C 错误; 对于D ,当0,12x π⎡⎤∈⎢⎥⎣⎦时,2,663x πππ⎡⎤+∈⎢⎥⎣⎦,则1sin 262x π⎡⎛⎫+∈⎢ ⎪⎝⎭⎣⎦,2sin 26x π⎛⎫⎡+∈ ⎪⎣⎝⎭,故()f x 在0,12π⎡⎤⎢⎥⎣⎦D 正确. 故选:C . 【点睛】该题考查的是有关三角函数的问题,涉及到的知识点有根据图象确定函数解析式,正弦型函数的相关性质,属于简单题目.二、填空题13.4或-4【分析】由题意可得故函数的周期为求得;在中令求得从而求得的值【详解】∵函数对任意的都有∴故函数的周期为∴所以∴在中令可得:即∴则故答案为:4或-4【点睛】求三角函数解析式的方法:(1)求A 通解析:4或-4. 【分析】由题意可得()23f x f x π⎛⎫+=⎪⎝⎭,故函数()f x 的周期为23π,求得=3ω;在()3f x f x π⎛⎫+=- ⎪⎝⎭中,令=0x ,求得sin 0ϕ=,从而求得6f π⎛⎫⎪⎝⎭的值. 【详解】∵函数()()()4sin 0f x x ωϕω=+>对任意的x 都有()3f x f x π⎛⎫+=- ⎪⎝⎭,∴()23f x f x π⎛⎫+= ⎪⎝⎭,故函数()f x 的周期为23π, ∴22=3ππω,所以=3ω. ∴()()4sin 3f x x ϕ=+.在()3f x f x π⎛⎫+=- ⎪⎝⎭中,令=0x ,可得:()03f f π⎛⎫= ⎪⎝⎭, 即()4sin =4sin πϕϕ+,∴sin =0ϕ.则=4sin()4cos 462f ππϕϕ⎛⎫+==± ⎪⎝⎭. 故答案为: 4或-4. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.14.【分析】由点的坐标可得的值由图象可求得函数的图象可得该函数的最小正周期可求得的值再将点的坐标代入函数的解析式结合的取值范围可求得的值可得出函数的解析式【详解】由于函数的图象的一个最高点为则由图象可知解析:ππ3sin 36x ⎛⎫- ⎪⎝⎭ 【分析】由点A 的坐标可得M 的值,由图象可求得函数()y f x =的图象可得该函数的最小正周期,可求得ω的值,再将点A 的坐标代入函数()y f x =的解析式,结合ϕ的取值范围可求得ϕ的值,可得出函数()y f x =的解析式. 【详解】由于函数()y f x =的图象的一个最高点为()2,3A ,则3M =,由图象可知,函数()y f x =的最小正周期为452632T ⎛⎫=+= ⎪⎝⎭,23T ππω∴==,()3sin 3x f x πϕ⎛⎫∴=+⎪⎝⎭, 将点A 的坐标代入函数()y f x =的解析式得()223sin 33f πϕ⎛⎫=+=⎪⎝⎭,可得2sin 13πϕ⎛⎫+= ⎪⎝⎭, 22ππϕ-<<,则27636πππϕ<+<,232ππϕ∴+=,解得6πϕ=-,()3sin 36x f x ππ⎛⎫∴=- ⎪⎝⎭故答案为:()3sin 36x f x ππ⎛⎫=- ⎪⎝⎭ 【点睛】本题考查利用三角函数图象求解函数解析式,考查计算能力,属于中等题.15.【分析】先根据函数在区间上的最小值是确定的取值范围进而可得到或求出的范围得到答案【详解】函数在区间上的最小值是则的取值范围是当时函数有最小值或或的最小值等于故答案为:【点睛】本题主要考查正弦函数的最解析:32【分析】先根据函数在区间[,]34ππ-上的最小值是2-确定x ω的取值范围,进而可得到32ωππ--或342ωππ,求出ω的范围得到答案. 【详解】函数()2sin (0)f x x ωω=>在区间[,]34ππ-上的最小值是2-, 则x ω的取值范围是[,]34ωπωπ-,当22x k πωπ=-+,k Z ∈时,函数有最小值2-,32ωππ∴--,或342ωππ,k Z ∈, ∴32ω≥,或6ω,k Z ∈, 0ω>,ω∴的最小值等于32.故答案为:32. 【点睛】本题主要考查正弦函数的最值的应用.考查基础知识的运用能力.三角函数式高考的重要考点,一定要强化复习.16.①③【分析】利用诱导公式化简函数判断①正误;求出函数周期判断②;求出函数的对称中心判断③;求出函数的对称轴判断④【详解】解:对于①所以①正确;对于②最小正周期所以②不正确;对于③因为所以为的对称中心解析:①③ 【分析】利用诱导公式化简函数()f x ,判断①正误;求出函数()f x 周期判断②;求出函数()f x 的对称中心判断③;求出函数()f x 的对称轴判断④. 【详解】解:对于①,()4sin 24cos 2323f x x x πππ⎛⎫⎛⎫=+=-- ⎪ ⎪⎝⎭⎝⎭ 4cos 24cos 2326x x πππ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭,所以①正确;对于②,最小正周期222T πππω===,所以②不正确; 对于③,因为4sin 4sin 00633f πππ⎛⎫⎛⎫-=-+== ⎪ ⎪⎝⎭⎝⎭所以,,06π⎛⎫- ⎪⎝⎭为()f x 的对称中心,故③正确;对于④,()()4sin 23f x x x R π⎛⎫=+∈ ⎪⎝⎭的对称直线满足2,32x k k Z πππ+=+∈,6x π=-不满足条件,所以④不正确.故答案为:①③. 【点睛】本题考查正弦函数的性质,考查基本概念、基本知识的理解掌握程度,属于基础题.17.①②④【分析】当时即可判断①④;计算即可判断②也可以作图;计算即可判断③【详解】当时所以故①④正确;当时则故②正确;所以③错误故答案为:①②④【点睛】本题考查利用所学知识研究新定义函数的性质涉及到周解析:①②④ 【分析】当[,1)x n n ∈+时,()f x x n =-,即可判断①④;计算(1)f x +,()f x 即可判断②,也可以作图;计算12()33f -=,11()33f =即可判断③. 【详解】当[,1)x n n ∈+时,[]x n =,()||f x x n x n =-=-,所以()[0,1)f x ∈,故①④正确; 当[,1)x n n ∈+时,则1[1,2)x n n +∈++,[1]1x n +=+,(1)|1[1]|f x x x +=+-+|1(1)|||()x n x n f x =+-+=-=,故②正确;1112()|[]|3333f -=---=,1111()|[]|3333f =-=,所以③错误.故答案为:①②④. 【点睛】本题考查利用所学知识研究新定义函数的性质,涉及到周期性、单调性、奇偶性以及值域,是一道中档题.18.【分析】根据题意得到化简得到或得到答案【详解】设时间为根据题意:故故或故或故故答案为:【点睛】本题考查了三角函数的应用意在考查学生的应用能力解析:【分析】 根据题意得到40sin 456562t ππ⎛⎫-+= ⎪⎝⎭,化简得到124t k =+或128t k =+,得到答案. 【详解】设时间为t ,0t >,根据题意:40sin 456562t ππ⎛⎫-+= ⎪⎝⎭,故1sin 622t ππ⎛⎫-= ⎪⎝⎭. 故2626t k ππππ-=+或52626t k ππππ-=+,故124t k =+或128t k =+,k Z ∈. 故1234564,8,16,20,28,32t t t t t t ======. 故答案为:32. 【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.19.①④【分析】结合题意得出函数的奇偶性根据奇偶性研究函数在时的性质对结论逐一判断即可【详解】解:∵定义域为∴∴函数是偶函数故①对;当时∴由正弦函数的单调性可知函数在区间上单调递减故②错;当时由得根据偶解析:①④ 【分析】结合题意,得出函数的奇偶性,根据奇偶性研究函数在0x >时的性质对结论逐一判断即可. 【详解】解:∵()sin |||sin |f x x x =+,定义域为R ,∴()()sin |||sin |f x x x -=-+-sin sin ()x x f x =+=, ∴函数()f x 是偶函数,故①对;当[]0,x π∈时,()sin |||sin |f x x x =+sin sin 2sin x x x =+=, ∴由正弦函数的单调性可知,函数()f x 在区间,2ππ⎛⎫⎪⎝⎭上单调递减,故②错; 当[]0,x π∈时,由()2sin 0f x x ==得0x =,x π=,根据偶函数的图象和性质可得,()f x 在[),0π-上有1个零点x π=- , ∴()f x 在[],ππ-有3个零点,故③错;当0x ≥时,()sin |||sin |f x x x =+sin sin x x =+2sin ,sin 00,sin 0x x x ≥⎧=⎨<⎩,根据奇偶性可得函数()f x 的图象如图,∴当sin 1x =时,函数()f x 有最大值()max 2f x =,故④对; 故答案为:①④. 【点睛】本题主要考查与三角函数有关的命题的真假判断,结合绝对值的应用以及利用三角函数的性质是解决本题的关键,属于中档题.20.【分析】周期为先考查一个周期函数判断零点个数及坐标再结合周期性即可求解【详解】是函数的一个周期当时当时只有四个零点在上恰有4个零点实数m 的取值范围为故答案为:【点睛】本题考查函数的零点个数求参数注意 解析:517[,)36ππ 【分析】()f x 周期为2π,先考查一个周期函数,判断零点个数及坐标,再结合周期性,即可求解【详解】2x π=是函数()f x 的一个周期,当[0,2]x π时,35cos [,]44()35sin [0,][,2]44x x f x x x πππππ⎧∈⎪⎪=⎨⎪+∈⋃⎪⎩当[0,2]x π时,()f x 只有四个零点5745,,,6633ππππ, 在[0,]m 上恰有4个零点,实数m 的取值范围为517[,)36ππ. 故答案为:517[,)36ππ. 【点睛】本题考查函数的零点个数求参数,注意函数图像和性质的应用,属于中档题.三、解答题21.(1)()2sin 412f x x ππ⎛⎫=- ⎪⎝⎭;(2)答案见解析. 【分析】(1)结合“五点法”求函数解析式:最大值确定A ,由周期确定ω,由最高点坐标确定ϕ.(2)确定113,33x ⎡⎤∈-⎢⎥⎣⎦时()f x 的图象与性质,由2y m =与()y f x =的交点个数确定m 的范围. 【详解】解:(1)由图可知2A =.函数()f x 最小正周期1374833T ⎛⎫=⨯-= ⎪⎝⎭,则28πω=.4πω∴=. 又772sin 2312f πϕ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,则72122k ππϕπ+=+,Z k ∈. 212k πϕπ∴=-+,Z k ∈.又2πϕ<,12πϕ∴=-.∴函数()f x 的解析式为()2sin 412f x x ππ⎛⎫=- ⎪⎝⎭.(2)由题意,()()2g x f x m =-在113,33⎡⎤-⎢⎥⎣⎦内的零点个数即函数()y f x =与2y m =的图象在113,33x ⎡⎤∈-⎢⎥⎣⎦时公共点的个数. 由(1),知()2sin 412f x x ππ⎛⎫=-⎪⎝⎭,113,33x ⎡⎤∈-⎢⎥⎣⎦. 113f ⎛⎫-=- ⎪⎝⎭,723f ⎛⎫= ⎪⎝⎭,1303f ⎛⎫= ⎪⎝⎭, 由图,知函数()f x 在区间17,33⎛⎫- ⎪⎝⎭上单调递增,在区间713,33⎛⎫ ⎪⎝⎭上单调递减. (i )当12m <-或1m 时, ()y f x =与2y m =的图象在113,33x ⎡⎤∈-⎢⎥⎣⎦时没有公共点,(ii )当102m -≤<或1m =时, ()y f x =与2y m =的图象在113,33x ⎡⎤∈-⎢⎥⎣⎦时恰有一个公共点;(iii )当01m ≤<时,()y f x =与2y m =的图象在113,33x ⎡⎤∈-⎢⎥⎣⎦时恰有两个公共点.综上可知,当12m <-或1m 时,函数()g x 的零点个数为0; 当102m -≤<或1m =时,函数()g x 的零点个数为1; 当01m ≤<时,函数()g x 的零点个数为2.【点睛】关键点点睛:本题考查求三角函数的解析式,考查真分数零点个数问题.解题关键是转化,函数零点个数转化为函数图象与直线的交点个数,基本方法是利用函数的性质,确定函数图象与直线交点个数得出参数范围.22.(1)()()2sin f x x ϕ=+;(2)答案见解析. 【分析】由已知得周期从而求得ω, 选①:(1)得出()6f x π+,根据偶函数与诱导公式求得ϕ;(2)求出()f x 的增区间,再与[0,]π求交集可得;选②:(1)解方程3f π⎛⎫= ⎪⎝⎭ϕ; (2)同选①选③:(1)由6f π⎛⎫ ⎪⎝⎭是最大值可得ϕ; (2)同选① 【详解】解:∵()f x 的图象与直线2y =的相邻两个交点间的距离为2π, ∴2T π=,即22ππω=,∴1ω=,∴()()2sin f x x ϕ=+. 方案一:选条件① (1)∵2sin 66f x x ππϕ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭为偶函数, ∴62k ππϕπ+=+,即3k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭.(2)令22232k x k πππππ-+≤+≤+,k Z ∈,得:52266k x k ππππ-+≤≤+,k Z ∈,令0k =,得566x ππ-≤≤, ∴函数()f x 在[]0,π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦(写成开区间也可得分) 方案二:选条件②(1)方法1:∵2sin 33f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭∴sin 32πϕ⎛⎫+= ⎪⎝⎭, ∴2k 33ππϕπ+=+或2233k ππϕπ+=+,k Z ∈, ∴2k ϕ=π或23k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭;方法2:∵2sin 33f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭∴sin 32πϕ⎛⎫+= ⎪⎝⎭, ∵02πϕ<<,∴5336πππϕ<+<, ∴233ππϕ+=即3πϕ=,∴()2sin 3f x x π⎛⎫=+ ⎪⎝⎭;(2)同方案一. 方案三:选条件③∵x R ∀∈,()6f x f π⎛⎫≤ ⎪⎝⎭,∴6f π⎛⎫⎪⎝⎭为()f x 的最大值,∴262k ππϕπ+=+,k Z ∈,即23k πϕπ=+,k Z ∈,∵02πϕ<<,∴3πϕ=,∴()2sin 3f x x π⎛⎫=+⎪⎝⎭; (2)同方案一. 【点睛】思路点睛:本题考查三角函数的图象与性质,掌握正弦函数的性质是解题关键.()sin()(0,0)f x A x A ωϕω=+>>,只要把x ωϕ+作为一个整体,用它替换sin y x =中的x 可确定函数的性质如单调性、对称中心、对称轴,最值,也可由()sin()(0,0)f x A x A ωϕω=+>>中x 的范围求出t x ωϕ=+的范围M ,然后考虑sin y x =在x M ∈时的性质得出结论.23.(1)242cos 59y x tπ⎛⎫=-+ ⎪⎝⎭(0x ,t 为参数);(2)15. 【分析】(1)以摩天轮最低点为原点,最低点的切线为x 轴建立直角坐标系,设sin()y A x b ωϕ=++,根据最高点和最低点的距离,求得,A b 的值,进而求得,ωϕ的值,即可求解.(2)由80y ≥,得到21cos 2x t π⎛⎫≤- ⎪⎝⎭,得到2533t t -≥,即可求解.【详解】(1)如图所示,以摩天轮最低点为原点,最低点的切线为x 轴建立直角坐标系, 由题意可设sin()(0,0,0)y A x b A b ωϕω=++>>因为摩天轮的最高点距地面101m ,最低点距地面1018417(m)-=, 所以101,17,A b A b +=⎧⎨-+=⎩解得42,59A b ==,又函数周期为t ,可得2t πω=,所以242sin 59(0)y x x t πϕ⎛⎫=++⎪⎝⎭. 又0x =时,17y =,所以21742sin 059t πϕ⎛⎫=⨯++ ⎪⎝⎭,即sin 1,ϕϕ=-可取2π-,所以2242sin 5942cos 592y x x t tπππ⎛⎫⎛⎫=-+=-+⎪⎪⎝⎭⎝⎭(0x ≥,t 为参数). (2)依题意,可知242cos 5980y x tπ⎛⎫=-+≥ ⎪⎝⎭,即21cos 2x tπ⎛⎫≤- ⎪⎝⎭,不妨取第一圈,可得2242,3333t tx x t πππ≤≤≤≤, 所以持续时间为2533t t-≥,即15t ≥,所以t 的最小值为15.【点睛】三角函数实际应用问题的处理策略: 1、已知函数模型求解数学问题;2、把实际问题抽象转化成数学问题,利用三角函数的有关知识解决问题;3、根据实际问题转化为已知条件转化为三角函数的解析式和图象,然后在根据数形结合思想研究三角函数的性质,进而加深理解函数的性质. 24.(1)2π;(2)2,5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 【分析】(1)先利用二倍角公式化简,再用辅助角公式化为()f x sin 16x π⎛⎫=++ ⎪⎝⎭,即可求出()f x 的最小正周期;(2)利用图像变换得到()y g x =的解析式,利用换元法就可以得到()y g x =的最大值及取得最大值时 x 的取值 【详解】(1)∵函数1cos 1()22x f x x +=++ sin 16x π⎛⎫=++ ⎪⎝⎭∴函数的周期为2π(2)依题意:函数()f x sin 16x π⎛⎫=++ ⎪⎝⎭的图象上的各点向左平移32π个单位,得到y 3sin +1= -cos 1626x x πππ⎛⎫⎛⎫=++++ ⎪ ⎪⎝⎭⎝⎭;再保持纵坐标不变,横坐标缩短到原来的一半,得到y = -cos 216x π⎛⎫++ ⎪⎝⎭; 所以()cos 216g x x π⎛⎫=-++ ⎪⎝⎭令226t x k πππ=+=+,即5()12x k k Z ππ=+∈ 使函数()g x 取得最大值2,即max ()2g x = 使函数()g x 取得最大值的集合为5,12x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭. 【注意】取得最大值的集合为7,12x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭也可以. 【点睛】:(1)关于三角函数图像平移伸缩变换:先平移的话,如果平移a 个单位长度那么相位就会改变ωa ;而先伸缩势必会改变ω大小,这时再平移要使相位改变值仍为ωa ,那么平移长度不等于a ;(2)求y =Asin (ωx +φ)+B 的值域通常用换元法;25.(1)()2sin 566f t t ππ⎛⎫=++ ⎪⎝⎭;(2)在0时进港4时出港或12时进港16时出港,每次在港内可停留4个小时. 【分析】由表格易知()()max min 7,3f t f t ==,由()()()()max minmax min,22f t f t f t f t A B -+==,求得A ,B ,再根据14212T =-=和2t =时,函数取得最大值,分别求得,ωϕ即可.(2)根据货船需要的安全水深度为6,由()2sin 5666f t t ππ⎛⎫=++≥ ⎪⎝⎭求解. 【详解】由表格可知()()max min 7,3f t f t ==,, 则()()()()max minmax min2,522f t f t f t f t A B -+====,又214212,6T T ππω=-===, 当2t =时,()22sin 2576f πϕ⎛⎫=⨯++= ⎪⎝⎭, 即sin 13πϕ⎛⎫+= ⎪⎝⎭, 所以232k ππϕπ+=+,又2πϕ<,所以6π=ϕ, 所以()2sin 566f t t ππ⎛⎫=++⎪⎝⎭. (2)因为货船需要的安全水深度为6, 所以()2sin 5666f t t ππ⎛⎫=++≥⎪⎝⎭,即1sin 662t ππ⎛⎫+≥ ⎪⎝⎭, 所以5226666k t k ππππππ+≤+≤+, 即12412k t k ≤≤+,又因为[]0,24t ∈,当0k =时,[]0,4t ∈,当1k =时,[]12,16t ∈,所以在0时进港4时出港或12时进港16时出港,每次在港内可停留4个小时. 【点睛】方法点睛:由函数y =A sin(ωx +φ)的图象或表格确定A ,ω,φ的题型,常常以“五点法”中的五个点作为突破口,要从图象的升降情况找准“零点”或“最大(小)值点”的位置.要善于抓住特殊量和特殊点.26.(1)65π;(2)1222⎡⎤---⎣⎦, . 【解析】 试题分析:(1)整理函数的解析式可得:56ω=,利用最小正周期公式可得函数的最小正周期为65π ; (2)化简三角函数的解析式()52sin 236f x x π⎛⎫=--⎪⎝⎭,结合函数的定义域可得函数的取值范围是12,22⎡⎤---⎣⎦ .试题(1)因为f(x)=sin 2ωx -cos 2ωx +2sinωx·cosωx +λ=-cos2ωx +sin2ωx +λ =2sin+λ.由直线x =π是y =f(x)图象的一条对称轴,可得sin =±1,所以2ωπ-=kπ+ (k ∈Z),即ω=+ (k ∈Z). 又ω∈,k ∈Z ,所以k =1,故ω=.所以f(x)的最小正周期是. (2)由y =f(x)的图象过点,得f =0, 即λ=-2sin=-2sin =-,即λ=-.故f(x)=2sin-,由0≤x≤,有-≤x-≤,所以-≤sin≤1,得-1-≤2sin x--≤2-.故函数f(x)在上的取值范围为[-1-,2-].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中学数学试讲题(北师版)
1、北师版七年级上册§1.4 《从不同方向看》
2、北师版七年级上册§2.4 《有理数的加法》
3、北师版七年级上册§5.5 《打折销售》
4、北师版七年级下册§1.7 《平方差公式》
5、北师版七年级下册§7.2 《简单的轴对称图形》(等腰三角形的判定)
6、北师版八年级上册§4.2 《平行四边形的判别》
7、北师版八年级上册§4.3 《菱形》
8、北师版八年级上册§4.5 《梯形》
9、北师版八年级上册§6.3 《一次函数的图象》
10、北师版八年级上册§4.2 《黄金分割》
11、北师版九年级上册§2.2 《配方法》
12、北师版九年级上册§5.1 《反比例函数》
13、北师版九年级上册§5.2 《反比例函数的图象与性质》
14、北师版九年级下册§3.2 《圆的对称性》(垂径定理)
15、北师版九年级下册§3.6 《圆与圆的位置关系》
中学物理试讲题(人教版)
第一章声现象第一节声音的产生与传播
第二章光现象第一节光的传播
第三章透镜及其应用第二节生活中的透镜
第四章物态变化第三节汽化和液化
第八章电功率第一节电能第二节电功率
第九章电与磁第七节磁生电
第十一章多彩的物质世界第二节质量第三节密度
第十二章运动和力第二节运动的快慢第五节你顿第一定律
第十三章力和机械第三节摩擦力
第十四章压强和浮力第一节压强
第十五章功和机械能第一节功第三节功率
中学科技科技试讲题
1.机器人的核心技术是什么
2. 飞机发动机的组成及工作原理
3. 数学模型中层次分析法的应用
4. 能量的转化和守恒
5. 凸透镜成像的规律
6. 热机
7. 电与磁
8.电影《2012》中飞船选址的科学依据
9. 近期发生的“天坑”现象
10. 人类模拟生物的发明创造
11. 低碳生活
12. 动物先天与后天行为
13. 颇有争议的“曹操墓”
14. SARS传播的数学模型
15.黄土高原土壤侵蚀
中学信息技术试讲题
1.宣传海报:保护环境——photoshop多滤镜综合特效
2.保护个人信息——网络安全
3.做个小管家——使用资源管理器
4.我的地盘我做主——建立自己的博客圈
5.声音也精彩——使用“录音机”
6.体验动画的魅力——幻灯片对象动画效果设置
7.Word综合实践——制作电子板报
8.Excel综合分析——排序与汇总
9.“大海捞针”的技巧——网上搜索
10.展示我的风采——frontpage丰富我的个人主页
11.进一步的美化——windows movie maker视频效果、视频过渡
12.沟通的纽带——在PPT中设置超级链接
13. 动态规划算法
14.万能转换工具——“格式工厂”的使用
15.神奇的文字——flash遮罩层的使用
说明:教材参考辽宁师范大学出版社出版,符泰民主编的初中信息技术教材。
中学语文试讲题(语文版)
七上:《小巷深处》、《空城计》
七下:《海燕》、《乡愁》、《苏州园林》
八上:《周庄水韵》、《最苦与最乐》、《茅屋为秋风所破歌》
八下:《背影》、《日出》
九上:《白杨礼赞》、《孔乙己》、《一厘米》
九下:《沁园春雪》、《故乡》
使用教材:语文出版社7-9年语文教材
试讲内容:以上课文的第二课时的教学内容(诗歌《乡愁》、《茅屋为秋风所破歌》、《沁园春雪》试讲分析部分)
中学英语试讲题(牛津版)
Lesson Type
7A Module 1 Unit 5 In the future p40+p41 Speaking
7A Module 2 Unit 2 Our animal friends p55 Speaking
7B Module 1 Unit 1 Information about fire(p3) Reading
7B Module 2 Unit 1 An accident (p31) Reading
7B Module 3 Unit 2 A surprise birthday party (p54) Speaking
8A Chapter 6 Pollution Fighters (p79) Reading
8A Chapter 4 Numbers: Everyone's language (p49) Reading
8A Chapter 3 Judy's diary (p44,p45) Writing
8B Chapter 3 A dangerous servant (p31) Reading
8B Chapter 4 Some days (p56) Speaking
9A Chapter 1 Protecting the innocent Writing
9A Chapter 2 Computers (p18) Reading
9A Chapter 5 Apologies and Excuses (p74) Speaking
9B Chapter 1 The green consumer (p2) Reading
9B Chapter 2 Educational visits (p22) Language
教材为牛津英语(上海教育出版社)
中学历史试讲题(人教版)
1、华夏之祖(七年级上册)
2、灿烂的青铜文明(七年级上册)
3、大一统的汉朝(七年级上册)
4、对外友好往来(七年级下册)
5、经济重心的南移(七年级下册)
6、君主集权的强化(七年级下册)
7、新文化运动(八年级上册)
8、中国近代民族工业的发展(八年级上册)
9、探索建设社会主义的道路(八年级下册)
10、独立自主的和平外交(八年级下册)
11、西方文明之源(九年级上册)
12、法国大革命和拿破仑帝国(九年级上册)
13、第一次世界大战(九年级上册)
14、经济大危机(九年级下册)
15、世界政治格局的多极化(九年级下册)
中学体育试讲题田径:(1)蹲踞式起跑
(2)接力跑
(3)耐力跑
(4)立定跳远
篮球:(5)单手肩上投篮
(6)篮球运球
(7)篮球转身运球
(8)篮球双手胸前传球
(9)行进间低手上篮
(10)原地起跳单人肩上投篮
(11)原地或行进间单手肩上投篮
(12)篮球二攻一配合
(13)排球传接配合
(14)篮球半场人盯人防守
排球:(15)正面双手垫球
中学美术试讲题
1、《在美术世界中遨游》
2、《格尔尼卡》
3、《生活中的色彩搭配》
4、《大家动手做条龙》
5、《宣传品的设计制作》
6、《布贴装饰画》
7、《雕塑自己的形象》
8、《商品包装的色彩搭配》
9、《民间美术》
10、《旅行团的旗帜和标志》
11、《班标设计》
12、《艺术源于生活,高于生活》
13、《美化生活的装饰布》
14、《居室的色彩搭配》
15、《卷筒造型》
中学心理试讲题
1、学困生的心理调节
2、如何培养学习兴趣
3、如何应对考试焦虑
4、如何克服恐惧心理
5、如何克服自卑心理
6、逆反心理的调适
7、耐挫能力的自我培养
8、认识中学生的“早恋”
9、青春期生理与心理的发展
10、如何处理同学关系
11、中学生如何处理与老师的关系
12、如何与异性同学正常交往
13、社交恐惧的调适
14、网络成瘾的调适
15、如何缓解青少年心理压力
中学校医请专业人士当面提出问题,考生解答。
