采用ABAQUS进行屈曲后屈曲和破坏分析
abaqus屈曲分析实例

整个计算过程包括2个分析步,第1步做屈曲分析,笫2步做极限强度分析。
第1步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle® Re Mbs M^nce C^wvoini live 2oc*$ *l^*«4 tjdp V :i.Jsa&# 录 +r A AJIu fffiC© fe3 Ha »<r epr a.c o 刖匚匹国o Ma&/3SiU*MMMC. Thit Hncticn «4I cruet a nrw p«ri a?d•»•••*> ;r•»•»<• < r*w 4 «»wmb>y fa-t n>rr •: OfEYcmv Se«今 gh 3,gqcvKeiry C*p*»9r « ♦O?lec?■ %«no«v C5廉 H5Wr> MM fa Tin* FortiSv Al€ *dep6»? ve^ tb<yrdc7 AtietiWf 二 Medel | ;狄2Eld 迫,“ j s&a夭 sufAuun*- \ M z t»e ^otop<e«l ou port )L>jUx9)lo t JeiWA Tc«D -^lQZlll«hQ we'Eejewwiw b>w* biE Glcte 」r»>w* 69D eJe*MKi r»jw* bee<i T?»* te:d*L d,说M? ■ ■ 20S27»l^:匕飞口 +r \nu fez: 匚圄国-a.SZ O A «MJ 划电口麻久&E ••却■一 .、・ 9 tf MwMtO) • aModHl6 b 5 131B& merdxR $>CWfcr*»9*^ s£ Zac®“ IraftetH U匕“rb ・2更 K«4dCu^u!R« 虫 Hntwr GUput b伽》ezi5 &■心 AcUxv« V H H«*»ctnr« 易 htecMtlar. hra,日 CcrtadCcrtra 0C«Wl >«wt K Ccctect sub lx權 CwMoarSt Hj fiUdi_n ,.. • •! •MCg WtW Swtfc lk2 pe**j<t»fo<C^ta 知 bynxHrt| <c»t*ve C4«c«lki«x f«v «ep oW Prc«・hr ・ t>". liwar p«nwbia«ko ▼ freque."拯 sufAuunThe 11«-51>^ )L>4ldH9jjn-2 “9 wioZ S *0 SxeU>* oil^ 51 “ed S iU* TO . <S0 . I 9ia ihe wtcc 0 . -SOOuscdftM-)i«jidfsnn -2 & 切 >0 . -ISO -MO mtb rew :t no 心 &逐Ply OCCOIIMV * 巧恪tc»:«L -5Moe>»* bw tZfft to ・D7cp 炉、?ZlHWr? Me"“乡“r»x HMldrann ・2 vd 乡 tygeJa* 400 0 0 with x*w :» «o tfi* oc<»Hifer«* 刃乡并在Model-Edit Keywords 的图中位置加入下面的文字,输出屈曲模态 *nodefile, global=yesU,® fit v<e»>si M E Of»r I«K “g deM ¥匚通国□ O Q€P# « • A mi 席邙0 fc3B ft •©« ©Eti.Z O "^■3剜电口丽:*> 5・<<b,w “ | >-dt»"W :aModd-l8 右 Dr Ol0 (八 »2 txta«e• IraHev 匕 ES a<A 2JJ a-> 禺: 虫n^sc^fiuir^ 虫 Hntorr Ottput to[*心》移 b ALT“A KM N H Htrxtijrw 易htefMtiar. Rr«|0 Ccctwct C«rtro Q U<Wt J^tWt K CerentSuUU § (cent 心b 僖 C«v^c«ar St87 fiekh ・H ・广 !Zfee '0 gpE 或5 o?lir« . 4S0 . I OS He Wtcc Q . -50Q 切,0 -ISO -HO with resc^:' rocct4LMV* 5^te«I~1 The “叭ei»x *« "33U* WM>X )ldqidf.9Jlh-2 W5 tX«i5Jd' -_u* *:<>*L 如心乂 r«s tc«> 处* to *i 两论 M dQidrann-: iw^Jdire^p 43i?2il wx»9 Wt«7 400 0 0 with r*MOKt to tt»*ccordiraex;«4jT W& D«UU MC . (X>1 ® Ht tgisi Mew $>ep gx< O#»£< 代《a •比 :匕飞口 +r \nu 吐二ti MW$CDr. Mpdri l F b 5 131 M 匕 Mad.O)0 CWfcr*»9*^ K 2 Mac® • Iraftet fr ti ^«rt>» t :<A 25 a* uii 更 K*l3CM^U!R4 虫 Hntw-f GUput b伽於心丹 &■心 V 辽 l*W*»ctisr« 易 htecMtlar. hra 日 CcrtadCcrtra 9 (如WJ2 \fi Ccctect SUU lx £|.Cc^^aaf C*ft 117 fiUdiLas _________________L_ McdW 1 5»?Pi[Z fcE feE J£臭 “zwi»x W *0 Sxe U>* oil^ (JsfxteO S Q" TO . <S0 . I 9ia ihe wtcc 0 . -S00 liscdftM-)i«jidfsnn -2 *■« txoasJdred 切 »o . -iso -HO with rew :' no 心 d^enbly OCCOILMV * 巧恪tc >:•!?. JM -s&we las t«<» ^oved to *D ''Te^p ^3i«eiii«u9 : •■Hwtaraiih-2 対5 列ord 5 $00 0 0 vjth to ocordNac ,▼別n^r •Me2MW2?Abaqus/CAE 6.11-1 Mode! Data base: G:\2014 年项目'gesid” 妙叙 TfSCoMHr 合同'逼壬左=20140724kbequ^iCreate job 名称为"Buckling n点击continue,完成第1步的汁算。
abaqus压杆屈曲分析

压杆屈曲分析1.问题描述在钢结构中,受压杆件一般在其达到极限承载力前就会丧失稳定性,所以失稳是钢结构最为突出的问题。
压杆整体失稳形式可以是弯曲、扭转和弯扭。
钢构件在轴心压力作用下,弯曲失稳是常见的失稳形式。
影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。
实际的轴心受压构件往往会存在上述的一种或多种缺陷,导致构件的稳定承载力降低。
本文利用abaqus对一定截面不同长细比下的H型钢构件进行屈曲分析,通过考虑材料非线性、几何非线性并引入初弯曲,得出构件发生弯曲失稳的极限荷载。
通过比较不同长细比下的弯曲失稳的临界荷载得出构件荷载位移曲线,并与《规范》中的构件曲线相比较。
钢构件的截面尺寸如图1-1所示。
构件的材料特性: , ,图1-12.长细比计算通过计算截面几何特性,截面绕y轴的回转半径为 ,长细比取值及杆件长度见表1:表13.模型分析ABAQUS非线性屈曲分析的方法有riks法,general statics法(加阻尼),或者动力法。
非线性屈曲分析采用riks算法实现,可以考虑材料非线性、几何非线性已及初始缺陷的影响。
其中,初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。
利用abaqus进行屈曲分析,一般有两步,首先是特征值屈曲分析,此分析为线性屈曲分析,是在小变形的情况进行的,也即上面提到过的模态,目的是得出临界荷载(一般取一阶模态的eigenvalue乘以所设定的load)。
其次,就是后屈曲分析,此步一般定义为非线性,原因在于是在大变形情况进行的,一般采用位移控制加修正的弧长法,可以定义材料非线性,以及几何非线性,加上初始缺陷,所以也称为非线性屈曲分析。
此步分析,为了得到极限值,需要得出荷载位移曲线的下降段。
缺陷较小的结构初始位移变形较小,在极值点突变,而初始缺陷较大的结构,载荷位移曲线较平滑。
4.建模计算过程建模计算过程以长细比为50的构件为例,其余构件建模计算过程与之类似。
基于abaqus的钢梁特征值屈曲与失稳分析

目录:1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4.结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要:钢结构的稳定性能是决定其承载力的一个特别重要的因素,稳定理论和设计方法需要完善。
近几十年以来,在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面,国内外都取得了长足的进步。
例如完善钢结构的弹塑性稳定理论,研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载,用数值法来解决这类问题等都取得了不少研究成果。
在作理论分析的同时进行稳定性能的试验验证,以及将理论研究结果利用图表表示或深化为计算公式,从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。
本文的主要内容是对现有失稳理论进行完善和发展及其总结,利用通用有限元abaqus软件,采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析,文中总共给了10个特征向量,进而得出相应的模态分析变形图,最后把lanczos 方法及子空间迭代法进行了比较,提出一些新的问题。
关键词:有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点,是制造结构物的一种极好的建筑材料。
钢材与在建筑结构中应用广泛的钢筋混凝土结构相比,对于受力功能相同的构件,具有截面轮廓尺寸小、构件细长和板件薄柔的特点。
但是对于因受压、受弯和受剪等存在受压区域的构件和板件,如果技术上处理不当,可能使钢结构出现整体失稳或局部失稳。
abaqus屈曲分析报告实例
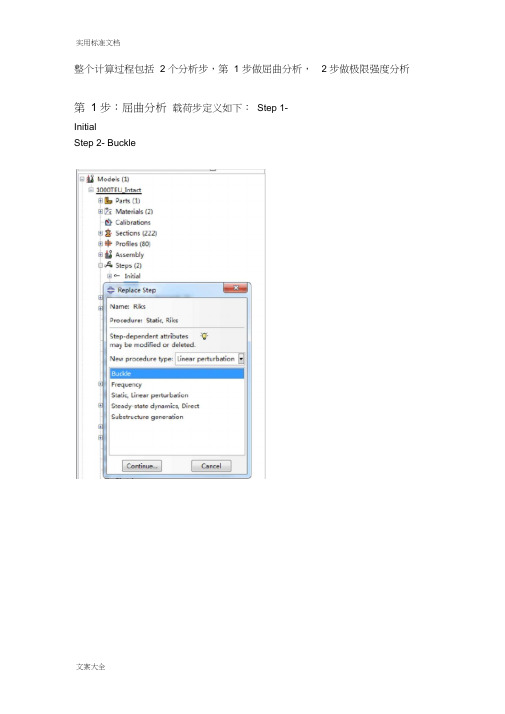
实用标准文档整个计算过程包括 2 个分析步,第 1 步做屈曲分析,第 1 步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle2 步做极限强度分析0奪莖UWICWHIK . 叽I J I*' *iirl |U*ii:* ri«-2- c.仲[U**t Wfl| «R =・|0T* |«|M4 11 屮W Ml 町扌垮・3 4M4; *E>|轴亠白*wr»44* «*M *A*S MMM-in 4414-* Ita1! I >H*d *■.■ Lrfi|i-t*b*i UWi^ *4」>jU***^ ::切2冲<a:K-.L口sMwSniLpc^l Efl «o 誓光n-3 wa HF HB・・n c:^ > q士* f *B£ -A <MI '■■*W■uTp*』«MLrii4 *M;■pofit ■直j.i t…叫町■ ' H.,机...i . r |fl»-L , | |-£I -t fr E叶*盅1并在Model-Edit Keywords 的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“ Buckling点击continue ,完成第 1 步的计算第 2 步:极限强度分析将“ buckle ”分析步替换为“ riks ”分析步在Basic 选项卡中,Nlgeom:选择打开在Instrumentation 选项卡中,定义如下参数,然后点击OK Array定义一个新计算工作,输入名称,点击continue在Parallelization 选项卡,选择 2 个CPU,如下所示,点击OK。
在此编辑Model-edit keywords ,删除“第 1 步”加入的文字“ *nodefile, global=yesU,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=1 1, 2.5点击OK,再保存文件最后提交计算。
基于abaqus的钢梁特征值屈曲与失稳分析

目录:1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4.结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要:钢结构的稳定性能是决定其承载力的一个特别重要的因素,稳定理论和设计方法需要完善。
近几十年以来,在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面,国内外都取得了长足的进步。
例如完善钢结构的弹塑性稳定理论,研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载,用数值法来解决这类问题等都取得了不少研究成果。
在作理论分析的同时进行稳定性能的试验验证,以及将理论研究结果利用图表表示或深化为计算公式,从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。
本文的主要内容是对现有失稳理论进行完善和发展及其总结,利用通用有限元abaqus软件,采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析,文中总共给了10个特征向量,进而得出相应的模态分析变形图,最后把lanczos 方法及子空间迭代法进行了比较,提出一些新的问题。
关键词:有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点,是制造结构物的一种极好的建筑材料。
钢材与在建筑结构中应用广泛的钢筋混凝土结构相比,对于受力功能相同的构件,具有截面轮廓尺寸小、构件细长和板件薄柔的特点。
但是对于因受压、受弯和受剪等存在受压区域的构件和板件,如果技术上处理不当,可能使钢结构出现整体失稳或局部失稳。
ABAQUS钢柱特征值屈曲分析

四、ABAQUS钢柱特征值屈曲分析问题描述:利用有限元软件分析咋爱不同特征值下的一个 4.2m高的钢柱的变形情况。
钢柱的截面尺寸如图所示。
钢柱的材料特性:弹性模量E=2.1e11N/m2,泊松比0.3,屈服强度f y=3.45e8 N/m2。
1.创建部件将Modeling Space设为3D,Shape设为shell,Type选择Extrusion,Approximate size项输入1,点击继续开始绘制草图。
以坐标的形式绘制线条,生成三维模型。
2.创建材料点击创建材料按钮,弹出对话框。
名称输入steel,在对话框中点击General(常规特性)-Density,在Mass Density中输入7850;点击Mechanical(力学特性)-Elasticity(弹性)-Elastic,将Young’s Modulus(弹性模量)设为2.0e11,Poisson’s Ratio为0.3。
3.创建截面属性点击创建截面按钮,将Category设为shell,Type设为Homogeneous,其余参数不变,点击继续弹出Edit section对话框,Value后面输入0.01,保持其余参数不变,完成对翼缘截面属性的定义。
同理输入0.006,完成对腹板截面属性的定义。
4.给部件赋予截面属性点击赋予截面属性按钮,分别赋予翼缘和腹板的截面属性。
5.定义装配件6.设置分析步点击创建分析步按钮,在名称后面输入load,procedure type项选择linear perturbation,下拉菜单中选择Buckle。
点击继续,弹出编辑分析步对话框,Eigensolver 项中选择Lanczos,在Number of eigenvalus requested(所需特征值数量)后输入10,即分析10个特征值下的变形情况,剩余参数不变。
7.定义荷载和边界条件●给钢柱施加边界荷载点击Create Load对话框,在名称后面输入load-1,step项中选择load,将出现的Type for Selected Step(所选分析步的荷载类型)设为Shell edge laod(壳体边缘荷载),保持其他不变,点击继续,提示区显示选择要添加荷载的壳体边缘,选择如图所示的边界,在弹出的对话框的Magnitude(幅值)后面输入1e4,剩余参数不变。
abaqus屈曲分析报告实例
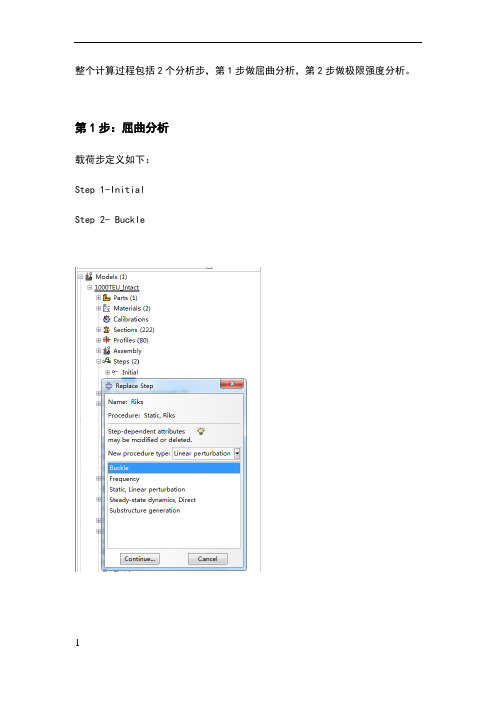
整个计算过程包括2个分析步,第1步做屈曲分析,第2步做极限强度分析。
第1步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue,完成第1步的计算。
第2步:极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中,Nlgeom:选择打开在Instrumentation选项卡中,定义如下参数,然后点击OK定义一个新计算工作,输入名称,点击continue在Parallelization选项卡,选择2个CPU,如下所示,点击OK。
在此编辑Model-edit keywords,删除“第1步”加入的文字“*nodefile, global=yesU,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=11,点击OK,再保存文件。
最后提交计算。
提取计算结果进入visualization Module 点击 Create XY data选择 ODB filed output,点击continuePosition选择 Unique Nodal, CF:point loads选择 CF2,再点击elements/nodes选项卡,选择跨中载荷加载点,最后点击save。
重复上一步操作,Position选择 Unique Nodal, U:spatial displacement 选择 U3,再点击elements/nodes选项卡,选择板格中心点,最后点击save。
点击Create XY data, 选择operate on XY data,点击continue选择Combine(X,X)命令,横坐标选择保存的displacement曲线,纵坐标选择保存的Point load曲线,点击最后一行Create XY Data与Save as。
ABAQUS中的屈曲分析riks

ABAQUS中的屈曲分析riks
RIKS 法将施加的荷载也作为一个未知量,通过同时约束荷载水平和位移向量来达到对非线性问题得求解,它属于一种广义得位移控制法,采用该迭代控制方法能较好地计算临近极值点结构地反映和下降段问题。
它的基本思想是引入一个在几何上相当于解曲线弧长的参数,通过控制弧长参数来实现每个增量步,从物理意义上看,这相当于对位移和荷载的综合控制。
当结构到达荷载极限点附近或结构进入下降段时,Newton -Raphson 法无法追踪结构的下降段,如图28所示情况需要采用弧长法进行求解。
弧长的定义为:
1)(+??=?T N
i N i i v l νλ 式中:l ?为增加的弧长
i λ?为荷载增加系数
N
i ν为位移增量与初次迭代得到的最大位移绝对值之比
图28 失稳状态下的荷载发展
图29 RIKS 法示意图
图29为RIKS 法计算过程中的迭代示意图。
具体计算流程如下所示:
初始情况下:
对于 i=迭代步 (i=1,2,3,etc): a. 形成内部节点应力矩阵I N
b. 检查平衡方程
如果R i N 足够小,则计算收敛,否则求解方程
得到v i N 和c i N
c. 将初始矢量(1,N i v )加上(N i N i c ρ,)(其中N
N N i i P P R /=ρ),这样解就由点A 1移动到点A 2,如图29所示。
求解等式
得到:
则最终的解为:
d. 更新到下一次迭代
返回到a,进行下一步迭代。
基于abaqus的钢梁特征值屈曲与失稳分析

目录:1. 绪论 (2)1.1背景 (2)1.2 钢梁稳定理论的发展状况 (2)2 . 稳定的概念 (3)3. 线性屈曲分析 (4)3.1 工程实例的简化 (4)3.2 有限元模型的建立 (4)3.2.1创建部件 (4)3.2.2创建材料和截面的属性 (6)3.2.3定义装配件 (7)3.2.4设置分析步 (7)3.2.5定义在载荷和边界条件 (8)3.2.6网格的划分 (9)3.2.7 提交分析作业 (9)3.2.8 模型数据的后处理 (10)3.2.9 数据分析总结 (12)4.结论 (12)基于abaqus的钢梁特征值屈曲与失稳分析摘要:钢结构的稳定性能是决定其承载力的一个特别重要的因素,稳定理论和设计方法需要完善。
近几十年以来,在研究发挥钢结构稳定性能的潜力和完善稳定计算的理论方面,国内外都取得了长足的进步。
例如完善钢结构的弹塑性稳定理论,研究有几何缺陷和残余应力的钢结构的实际受力性能和其极限荷载,用数值法来解决这类问题等都取得了不少研究成果。
在作理论分析的同时进行稳定性能的试验验证,以及将理论研究结果利用图表表示或深化为计算公式,从而将弹塑性稳定理论用于解决钢结构设计中的问题都取得了丰硕成果。
本文的主要内容是对现有失稳理论进行完善和发展及其总结,利用通用有限元abaqus软件,采用特征值的Lanczos方法及子空间迭代法对钢梁进行屈曲分析,文中总共给了10个特征向量,进而得出相应的模态分析变形图,最后把lanczos 方法及子空间迭代法进行了比较,提出一些新的问题。
关键词:有限元abaqus 失稳特征值屈曲分析1. 绪论1.1背景钢材具有强度高、质量轻、力学性能好的优点,是制造结构物的一种极好的建筑材料。
钢材与在建筑结构中应用广泛的钢筋混凝土结构相比,对于受力功能相同的构件,具有截面轮廓尺寸小、构件细长和板件薄柔的特点。
但是对于因受压、受弯和受剪等存在受压区域的构件和板件,如果技术上处理不当,可能使钢结构出现整体失稳或局部失稳。
abaqus屈曲分析报告实例
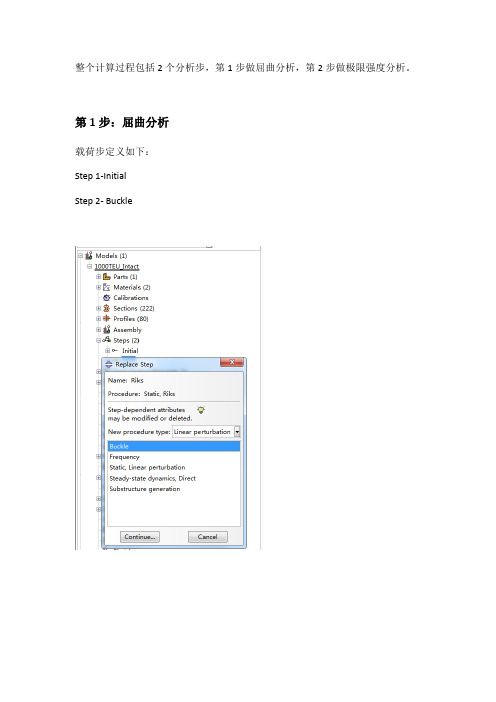
整个计算过程包括2个分析步,第1步做屈曲分析,第2步做极限强度分析。
第1步:屈曲分析载荷步定义如下:Step 1-InitialStep 2- Buckle并在Model-Edit Keywords的图中位置加入下面的文字,输出屈曲模态*nodefile, global=yesU,Create job 名称为“Buckling”点击continue,完成第1步的计算。
第2步:极限强度分析将“buckle”分析步替换为“riks”分析步在Basic选项卡中,Nlgeom:选择打开在Instrumentation选项卡中,定义如下参数,然后点击OK定义一个新计算工作,输入名称,点击continue在Parallelization选项卡,选择2个CPU,如下所示,点击OK。
在此编辑Model-edit keywords,删除“第1步”加入的文字“*nodefile, global=yes U,”,并在下图位置加入下段文字:*imperfection, file=buckling, step=11,点击OK,再保存文件。
最后提交计算。
提取计算结果进入visualization Module点击Create XY data选择ODB filed output,点击continuePosition选择Unique Nodal,CF:point loads选择CF2,再点击elements/nodes 选项卡,选择跨中载荷加载点,最后点击save。
重复上一步操作,Position选择Unique Nodal,U:spatial displacement选择U3,再点击elements/nodes选项卡,选择板格中心点,最后点击save。
点击Create XY data, 选择operate on XY data,点击continue选择Combine(X,X)命令,横坐标选择保存的displacement曲线,纵坐标选择保存的Point load曲线,点击最后一行Create XY Data与Save as。
abaqus后屈曲力位移曲线

abaqus后屈曲力位移曲线
在Abaqus中,后屈曲力位移曲线是指在结构发生屈曲后,随着位移的增加,结构所承受的力也随之变化的曲线。
这条曲线通常用于描述结构在屈曲后的非线性响应,包括结构的强度、刚度以及最终的破坏情况。
后屈曲分析是在特征值屈曲分析(即线性屈曲分析)的基础上进行的,它考虑了材料非线性、几何非线性以及初始缺陷的影响。
在后屈曲分析中,通常会使用Riks算法来模拟结构在屈曲后的行为。
以下是后屈曲力位移曲线的一些关键特点:
1. 初始阶段:在位移较小时,力位移曲线可能表现为线性增长,这时结构尚未发生屈曲。
2. 屈曲点:当位移达到一定值时,结构会发生屈曲,力位移曲线会出现转折点,这时的力称为屈曲力。
3. 非线性区域:屈曲后,结构进入非线性区域,力位移曲线会变得非线性,位移增加但力可能不再按比例增加,甚至可能减小。
4. 峰值力:在非线性区域中,可能会出现峰值力,这是结构在屈曲后能达到的最大力。
5. 下降段:峰值力之后,力位移曲线会进入下降段,这时结构的承载能力开始下降,最终可能导致结构的破坏。
6. 极限位移:在曲线的末端,力降至零,对应的位移称为极限位移,这时的结构已经失去了承载能力。
后屈曲力位移曲线对于评估结构的安全性和可靠性非常重要,它
可以帮助工程师了解结构在极端条件下的响应,从而在设计时采取相应的措施来防止屈曲和破坏。
abaqus中屈曲模式下的几何缺陷

在Abaqus中,屈曲模式下的几何缺陷可以通过以下方法引入:
1. 直接在模型中创建初始几何缺陷。
这可以通过在模型构建过程中调整节点位置或通过施加适当的边界条件来实现。
2. 使用Abaqus的“扰动”功能来引入几何缺陷。
这种方法涉及在计算过程中对模型施加小的随机扰动,以模拟实际结构中可能存在的不完美之处。
引入几何缺陷是为了更准确地模拟实际结构的屈曲行为,因为实际结构往往存在制造和安装误差,这些误差可能会对结构的稳定性产生影响。
需要注意的是,在引入几何缺陷时,应确保缺陷的幅度和分布合理,以反映实际结构的特点。
同时,还需要对模拟结果进行仔细的验证和确认,以确保结果的准确性和可靠性。
Abaqus屈曲分析(一)线性特征值屈曲

Abaqus屈曲分析(⼀)线性特征值屈曲∨本⽂由CAE数值优化轻量化授权转载结构稳定性问题是我们⽇常⽣活中经常遇到的问题,主要是发⽣在梁或壳结构中。
屈曲是⼀种失效模式,其特征是构件在⾼压应⼒作⽤下突然失效。
屈曲失效的实际压应⼒⼩于材料能够承受的最终压应⼒。
当构件或结构将膜应变能转换为弯曲应变能⽽外部施加的载荷不变时,会发⽣屈曲失效。
先来看⼀个简单的结构:⼀个长为L的细长杆,横截⾯积为A。
轴向刚度ka远⼤于弯曲刚度kb。
因此,微⼩的膜变形可以吸收⼤量的应变能。
然⽽,需要较⼤的横向挠度和横截⾯旋转来吸收弯曲中的能量。
如果让弯曲来吸收膜应变能,挠度将会远⼤于轴向变形。
⼏种典型稳定性问题:板件屈曲-分⽀问题:⼀般情况下,⼩的初始缺陷对平板的后屈曲响应没有显著影响,但可能影响屈曲⽅向。
突弹跳变(snap-through)-极限载荷问题预屈曲段的结构响应是⾮线性的。
因此,需要进⾏⼏何⾮线性分析来准确研究预屈曲⾏为。
结构不稳定发⽣在⼀个负载最⼤(极限载荷 点)位置。
⼀旦解在点A处变得奇异,结构就从A点翻转到B点。
在快速翻转过程中,响应变为动态的,结构释放弹性能转化为动能。
在B点存在⼀个稳定的静⼒平衡状态。
超过这⼀点,载荷P可以再次增加。
⽆加强筋的圆筒屈曲结构对⼩的初始缺陷表现出很强的敏感性。
对初始缺陷的考虑将分岔问题转化为极限载荷问题。
屈曲问题本质特征:A类问题:在分叉点前为线性响应B类问题:在缺陷敏感结构分叉点前为⾮线性响应缺陷敏感:实际结构的坍塌载荷受载荷⽅向、⽀承⽅式或⼏何形状的微⼩变化的强烈影响。
这些结构往往是求极限载荷问题。
ABAQUS⼀般有两种分析⼿段来处理这类分析问题:特征值屈曲分析和后屈曲分析。
A:线性特征值屈曲分析(针对A类问题):1. ⽤于估计刚性结构的临界(分岔)载荷。
2. 使⽤abaqus线性扰动求解。
通常⽤来估计刚性结构的临界屈曲载荷。
想要特征值屈曲分析可以得到可靠的屈曲载荷的估计,需要满⾜以下假设前提:⼩⼏何变化、线性弹性材料响应,且缺陷不敏感。
abaqus压杆屈曲分析报告

压杆屈曲非线性分析专业:结构工程******学号:**********压杆屈曲分析1.问题描述在钢结构中,受压杆件一般在其达到极限承载力前就会丧失稳定性,所以失稳是钢结构最为突出的问题。
压杆整体失稳形式可以是弯曲、扭转和弯扭。
钢构件在轴心压力作用下,弯曲失稳是常见的失稳形式。
影响轴心受压构件整体稳定性的主要因素为纵向残余应力、初始弯曲、荷载初偏心及端部约束条件等。
实际的轴心受压构件往往会存在上述的一种或多种缺陷,导致构件的稳定承载力降低。
本文利用abaqus 对一定截面不同长细比下的H 型钢构件进行屈曲分析,通过考虑材料非线性、几何非线性并引入初弯曲,得出构件发生弯曲失稳的极限荷载。
通过比较不同长细比下的弯曲失稳的临界荷载得出构件荷载位移曲线,并与《规范》中的构件曲线相比较。
钢构件的截面尺寸如图1-1所示。
构件的材料特性: E =2.0×1011 N m 2⁄ ,μ=0.3 , f y =3.45×108N m2⁄图1-1压杆截面尺寸(单位:m)2.长细比计算通过计算截面几何特性,截面绕y轴的回转半径为i y=0.0384m ,长细比取值及杆件长度见表1:表13.模型分析ABAQUS非线性屈曲分析的方法有riks法,general statics法(加阻尼),或者动力法。
非线性屈曲分析采用riks算法实现,可以考虑材料非线性、几何非线性已及初始缺陷的影响。
其中,初始缺陷可以通过屈曲模态、振型以及一般节点位移来描述。
利用abaqus进行屈曲分析,一般有两步,首先是特征值屈曲分析,此分析为线性屈曲分析,是在小变形的情况进行的,也即上面提到过的模态,目的是得出临界荷载(一般取一阶模态的eigenvalue乘以所设定的load)。
其次,就是后屈曲分析,此步一般定义为非线性,原因在于是在大变形情况进行的,一般采用位移控制加修正的弧长法,可以定义材料非线性,以及几何非线性,加上初始缺陷,所以也称为非线性屈曲分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Buckling, Postbuckling, and CollapseAnalysis with Abaqus| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Day 1•Lecture 1Basic Concepts and Overview •Workshop 1Buckling and Postbuckling Analyses of a Crane Structure •Lecture 2Finite Element Formulation•Lecture 3Finite Element Implementation in Abaqus •Lecture 4Eigenvalue Buckling Analysis •Workshop 2Eigenvalue Buckling of a Ring Subjected to External Pressure•Workshop 3Elastic Buckling of Ring-Supported Cylindrical Shell under Hydrostatic Pressure| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Buckling, Postbuckling, and Collapse Analysis with AbaqusDay 2•Lecture 5Regular and Damped Static Solution Procedures for Postbuckling Analyses•Workshop 4Nonlinear Buckling of Ring-Supported Cylindrical Shell under Hydrostatic Pressure•Workshop 5Static Buckling Analysis of a Circular Arch •Lecture 6Modified Riks Static Solution Procedure for Postbuckling Analyses•Workshop 5Static Buckling Analysis of a Circular Arch (continued)•Lecture 7Dynamic Analysis Solution Procedures for Postbuckling Analyses•Workshop 5Static Buckling Analysis of a Circular Arch (continued)•Workshop 6Tube Crush Dynamic Analysis •Lecture 8Putting It All Together…•Workshop 7Capstone Workshop: Lee’s Frame Buckling Problem •Workshop 8Buckling and Postbuckling Analyses of a Stiffened Panel| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Legal NoticesThe Abaqus Software described in this documentation is available only under license fromDassault Systèmes and its subsidiary and may be used or reproduced only in accordance with the terms of such license.This documentation and the software described in this documentation are subject to change without prior notice.Dassault Systèmes and its subsidiaries shall not be responsible for the consequences of any errors or omissions that may appear in this documentation.No part of this documentation may be reproduced or distributed in any form without prior written permission of Dassault Systèmes or its subsidiary.© Dassault Systèmes, 2011.Printed in the United States of AmericaAbaqus, the 3DS logo, SIMULIA and CATIA are trademarks or registered trademarks of Dassault Systèmes or its subsidiaries in the US and/or other countries.Other company, product, and service names may be trademarks or service marks of theirrespective owners. For additional information concerning trademarks, copyrights, and licenses, see the Legal Notices in the Abaqus 6.11 Release Notes and the notices at: /products/products_legal.html.| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Buckling, Postbuckling, and Collapse Analysis with AbaqusRevision StatusLecture 15/11Updated for 6.11Lecture 25/11Updated for 6.11Lecture 35/11Updated for 6.11Lecture 45/11Updated for 6.11Lecture 55/11Updated for 6.11Lecture 65/11Updated for 6.11Lecture 75/11Updated for 6.11Lecture 85/11Updated for 6.11Workshop 15/11Updated for 6.11Workshop 25/11Updated for 6.11Workshop 35/11Updated for 6.11Workshop 45/11Updated for 6.11Workshop 55/11Updated for 6.11Workshop 65/11Updated for 6.11Workshop 75/11Updated for 6.11Workshop 85/11Updated for 6.11| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 1Basic Concepts and Overview| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L1.2Overview•Introduction •Solution Techniques •Analysis Selection Guide•Example: Lee’s Frame Buckling Problem •Summary•Workshop| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 2Finite Element Formulation| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L2.2Introduction•Basic Equations in Finite Element Analysis •Linearization•Nonlinear Problems in Mechanics•Geometrically Nonlinear Analysis •Stress and Strain Measures•Equilibrium and Virtual Work •Summary| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 3FE Implementation in Abaqus| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L3.2Outline•Abaqus Definitions•General and Perturbation Procedures•Including Nonlinear Effects in an Abaqus Simulation •General Procedure Solution Techniques•Nonlinear Analysis Using Implicit Methods •Solution Control •Diagnostics •Riks Method•Automatic Time Incrementation•General Procedure Implicit Equation Solvers •Nonlinear Analysis Using Explicit Methods •Perturbation Procedure Solution Techniques•Introducing Imperfections for Postbuckling Simulations•Summary| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 4Eigenvalue Buckling Analysis| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L4.2Overview•Introduction•Eigenvalue Problem Formulation •Abaqus Usage•Example: Buckling of a Thin Cylindrical Shell •Closely Spaced Eigenvalues•Symmetry in Buckling Analyses •Concluding Remarks •Workshops| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 5Regular and Damped Static Solution Procedures forPostbuckling Analyses| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L5.2Overview•Motivation•Regular Static Procedure•Motivation for Damped Static Procedures•Automatic Stabilization •Dashpots•Postbuckling and Loss of Contact •Summary for Damped Static Procedures •Concluding Remarks •Workshops| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 6Modified Riks Static Solution Procedurefor Postbuckling Analyses| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L6.2Overview•Introduction•Abaqus Implementation •Abaqus Usage•Snap-Through Problems •Postbuckling Problems•Postbuckling Examples •Usage Tips •Limitations•Concluding Remarks •Workshop| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 7Dynamic Analysis Solution Procedures forPostbuckling Analyses| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L7.2Overview•What Makes a Problem Dynamic? •Equations for Dynamic Problems •Nonlinear Dynamics•Workshop•Analyzing Highly Nonlinear Quasi-Static Problems•Quasi-Static Simulations Using Explicit Dynamics •Example: Dynamic Tube Collapse •Concluding Remarks •Workshop| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |Lecture 8Putting It All Together…| w w w .3d s .c o m | © D a s s a u l t S y s t èm e s |L8.2Buckling, Postbuckling, and Collapse Analysis with Abaqus Overview•Buckling Analysis Selection Guide Revisited •Weatherseal Example•References for Further Study•Workshops。
