建模二作业二
第二次数学建模作业
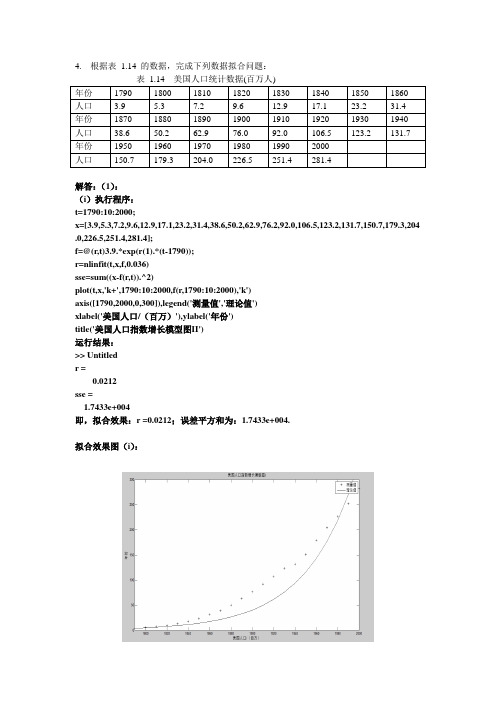
4. 根据表1.14 的数据,完成下列数据拟合问题:年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答:(1):(i)执行程序:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/(百万)'),ylabel('年份')title('美国人口指数增长模型图II')运行结果:>> Untitledr =0.0212sse =1.7433e+004即,拟合效果:r =0.0212;误差平方和为:1.7433e+004.拟合效果图(i):(ii)由表1.14我们知道,当t=1800时,有5)101(0≈+r x ,所以我们可以猜测,r=0.1,x =2.5.对待定参数0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下: >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道,拟合结果为:r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图(ii ):(iii)由表1.14我们知道,当t=1900时,有()76)-t 1900101(00≈+r x ,所以我们可以猜测,r=0.03,x =19, 0t =1800.对待定参数0t ,0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下:>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即,拟合效果:r =0,0x =7.9,0t =1742.5;误差平方和为:2.2657e+003我们由MATLAB9给出的警告信息,知道这个拟合存在病态条件,所以数据可能拟合的不太好。
海致大数据建模初级班第二次作业

海致大数据建模初级班第二次作业
【最新版】
目录
1.介绍海致大数据建模初级班的第二次作业
2.作业的目标和要求
3.作业的难点和挑战
4.完成作业的心得和体会
5.总结和展望
正文
海致大数据建模初级班第二次作业是基于大数据建模的一次实践。
作业的目标是通过对大数据的处理和分析,建立一个符合要求的模型,以解决实际问题。
这次作业的要求较高,需要我们具备一定的编程能力和数据处理能力,同时,也需要我们熟悉各种建模方法和技术。
在完成这次作业的过程中,我们遇到了不少难点和挑战。
首先,大数据的处理就需要我们掌握一定的编程技术,如 Python 和 R 语言等,这对于初学者来说无疑是一个巨大的挑战。
其次,数据处理的过程需要我们具备一定的数据分析能力,如何从大量的数据中提取出有用的信息,如何清洗和预处理数据等,都是我们需要解决的问题。
最后,建模过程也需要我们具备一定的建模知识和技术,如何选择合适的模型,如何调整模型的参数,如何评估模型的性能等,都是我们在完成作业过程中需要考虑的问题。
尽管这次作业的难度较大,但是通过完成这次作业,我们收获颇丰。
我们不仅提高了编程能力和数据处理能力,也提高了建模能力和解决问题的能力。
同时,我们也体验到了大数据建模的乐趣和成就感。
总的来说,海致大数据建模初级班第二次作业是一次非常有价值的实
践,它不仅检验了我们的学习成果,也提高了我们的实践能力和解决问题的能力。
我相信,通过这次作业,我们在大数据建模方面的能力得到了进一步的提升。
作业二___结构化需求建模(第5章)

作业二结构化需求建模(第5章)2-1、简答业务流程图与数据流程图的作用、含义和区别2-2、目前住院病人主要由护士护理,这样做不仅需要大量护士,而且由于不能随时观察危重病人的病情变化,还会延误抢救时机。
某医院打算开发一个以计算机为中心的患者监护系统,请分层次地画出描述本系统功能的数据流图。
医院对患者监护系统的基本要求是随时接收每个病人的生理信号(脉搏、体温、血压、心电图等),定时记录病人情况以形成患者日志,当某个病人的生理信号超出医生规定的安全范围时向值班护士发出警告信息,此外,护士在需要时还可以要求系统印出某个指定病人的病情报告。
2-3、银行计算机储蓄系统的工作过程大致如下:储户填写的存款单或取款单由业务员键入系统,如果是存款则系统记录存款人姓名、住址(或电话号码)、身份证号码、存款类型、存款日期、到期日期、利率及密码(可选)等信息,并印出存单给储户;如果是取款而且存款时留有密码,则系统首先核对储户密码,若密码正确或存款时未留密码,则系统计算利息并印出利息清单给储户。
请用数据流图描绘本系统的功能,并用实体-联系图描绘系统中的数据对象。
2-4、为了方便旅客,某航空公司拟开发一个机票预定系统。
旅行社把预定机票的旅客信息(姓名、性别、工作单位、身份证号码、旅行时间、旅行目的地等)输入该系统,系统为旅客安排航班,旅客在飞机起飞前一天凭取票通知和账单交款取票,系统核对无误即印出机票给顾客。
请画出描述本系统功能的数据流图。
2-5、复印机的工作过程大致如下:未接到复印命令时处于闲置状态,一旦接到复印命令则进入复印状态,完成一个复印命令规定的工作后又回到闲置状态,等待下一个复印命令;如果执行复印命令时发现没纸,则进入缺纸状态,发出警告,等待装纸,装满纸后进入闲置状态,准备接收复印命令;如果复印时发生卡纸故障,则进入卡纸状态,发出警告等待维修人员来排除故障,故障排除后回到闲置状态。
请用状态转换图描绘复印机的行为。
北京工业大学、薛毅、数学模型作业二、作业2、实验二

实验二解:(1)将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=1001若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=-2,q=det(A)=1,因为p<0,q>0,所以平衡点不稳定。
(2)将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=−1002若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=-1,q=det(A)=-2,因为p<0,q<0,所以平衡点不稳定。
(3)将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=01−20若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=0,q=det(A)=2,因为p=0,q>0,所以平衡点不稳定。
(4)将线性方程组写成矩阵形式dXdt =AX,A=a11a12a21a22=−100−2若det(A)≠0,则X0=(0,0)T,是唯一平衡点。
p=-(a11+a22)=3,q=det(A)=2,因为p>0,q>0,p2>4q,所以平衡点稳定。
解:f(N)=R-KN,令f(N)=0,则N=k/Rf`(N)=-K<0,则N=k/R是稳定的。
当N<k/R时f(N)>0,N`(t)>0,N(t)递增;N>k/R时f(N)<0,N`(t)<0,N(t)递减ð2N ðt2=∂f∂N∙ðNðt=-K(R-KN),表明N=k/R为拐点,当N<k/R时N``(t)<0,N>k/R时N``(t)>0从图中可以看出N=k/R是营养平衡值,无论大于或小于这个值,细胞都会向这个点调整,偏离越大调整速率越大,接近平衡值时速率变小。
解:列满足条件的微分方程∂N=r1N−r2N12求平衡点,令f N=r1N−r2N1=0,解得N1=0,N2=r22r12ð2N ðt =∂f∂N∙ðNðt=(r1−12r2N−12)(r1N−r2N12),解得N=r224r12从图中可以看出N1=0不稳定,N2=r22r12是稳定的解:令f x=r1−xNx−Ex=0得平衡点x1=N1−Er,x2=0f`(x1)=E-r,f`(x2)= r-E.若E<r,则有f`(x1)<0,f`(x2)>0.则x1是稳定的,x2是不稳定的。
数学建模(2)第二次作业word版
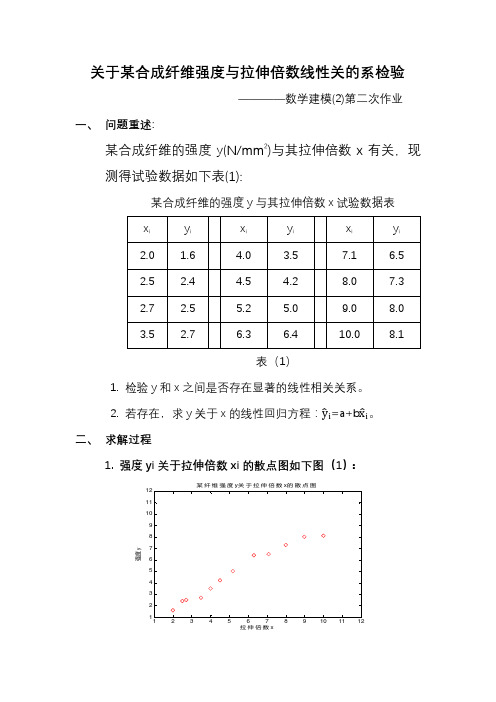
关于某合成纤维强度与拉伸倍数线性关的系检验————数学建模(2)第二次作业一、问题重述:某合成纤维的强度y(N/mm2)与其拉伸倍数x有关,现测得试验数据如下表(1):某合成纤维的强度y与其拉伸倍数x试验数据表表(1)1.检验y和x之间是否存在显著的线性相关关系。
2.若存在,求y关于x的线性回归方程:y i=a+b x i。
二、求解过程1.强度yi关于拉伸倍数xi的散点图如下图(1):图(1)2.样本相关系数计算 (1).计算公式r =nΣxy −ΣxΣynΣx 22nΣy 22(2)计算结果r =12∗382.17−3771.3612∗428.18−64.802∗ 12∗342.86−58.202=0.9859(3)结果分析r >0.8,说明该合成纤维强度y 与拉伸倍数x 成高度线性正相关关系。
2. 回归方程求解 (1).计算公式β1 =n ∑x i y i n i =1− ∑X i n i =1 ∑y i ni =1n x i2ni =1−∑x i n i =12某纤维强度y 关于拉伸倍数x 的散点图拉伸倍数x强度yβ 0=y −β1x (2).计算结果β 1= 12∗382.17−3771.3612∗428.18−64.802=0.8675β0=4.85−0.8675∗5.40=0.1655 (3).回归方程y i =0.1655+0.8675xi (4).回归前后图像对比图(2)回归系数β1=0.8675,表示拉伸倍数每增加一倍,该合成纤维强度增加0.08675。
三、 线性关系检验(1).提出假设123456789101112该纤维强度y 关于拉伸倍数x 的散点图及其线性回归方程拉伸倍数x强度yH0:β1=0线性关系不显著(2).计算检验统计量FF=SSR/1SSE/(n−2)= MSRMSE~F(1,n-2)F =58.89505/11.695902/(12−2)=347.2786(3).显著性水平α=0.05,根据分子自由度1和分母自由度12-2找出临界值Fα=4.965(4).F>Fα,拒绝H0,线性关系显著。
数学建模课后习题第二章参考答案

数学建模第二章课后习题第5题参考答案5.(1)at m me w w w w w t w --+=)()(000,要使,只需。
联系:在目前的情况下,当时,两个模型中猪的体重的变化都一样,当时,新的假设中猪的体重增长的比较快,当时,新的假设猪的体重增长的比较慢。
因为,所以函数为增函数,即当t 增大时,猪的体重会随着增加,这与原来的假设是一致的。
两个假设都满足'(0)w r =,在最佳出售时机附近误差微小。
区别:150200250300当a=1/60时两个假设模型的比较由图可知,新假设是阻滞增长模型,体重w 是t 的增函数,体重增加的速率先快后慢,时间充分长后,体重趋于w m 。
而原假设w(t)=0w +rt 只假设体重匀速增加。
从长时间来看,新假设比原假设更符合实际。
(2) 则t 天之后比现在出售多赚的纯利润为:0000((0))()()()()(0)(0)(0)()matm p gt w w Q t p t w t C t p w ct p w w w w e--=--=--+- 其中p(0)=12,g=0.08, 900=w ,270=m w ,,c=3.2,代入数据并用matlab 中的fminbnd 函数运算得到: 在t=14.4336时,纯利润到达最大值:Qm =12.1513。
代码如下:Q=@(t)((12-0.08*t)*90.*270)./(90+(270-90).*exp(-(1/60)*t))-3.2*t-12*90;nQ=@(t)-Q(t);[t,Q1]=fminbnd(nQ,0,100), Qm=-Q1 t = 14.4336 Q1 = -12.1513 Qm =12.1513 (3)所以,如果生猪体重wm 增加1%,灵敏度S(tm,dwm)= 3.7669,最佳出售时间tm 就推迟0.038%。
灵敏度比较小,所以wm 对tm 不灵敏。
程序如下:Q=@(t,wm)((12-0.08*t)*90.*wm)./(90+(wm-90).*exp(-(1/60)*t))-3.2*t-12*90;数值计算W m 对t m 的灵敏度(W m =270,t m =14.4336)m m w w +∆ ()/%m m w w ∆ m m t t +∆ ()/%m m t t ∆ (,)m m S w t272.70001.000014.9773 0.0377 3.7669 283.5000 5.0000 17.0565 0.1817 3.6345 297.0000 10.0000 19.46010.34833.4825数值计算W m 对Q m 的灵敏度(W m =270,Q m =12.1513) m m w w +∆ ()/%m m w w ∆ m m Q Q +∆ ()/%m m Q Q ∆ (,)m m S w Q272.7000 1.0000 13.1078 0.0787 7.8720 283.5000 5.0000 17.1208 0.4090 8.1794 297.0000 10.0000 22.47540.84968.4963d=[.01;.05;.1];dwm=d*270;Q1=@(t)-Q(t,270+dwm(1));[t1,Q1]=fminbnd(Q1,0,30);Q2=@(t)-Q(t,270+dwm(2));[t2,Q2]=fminbnd(Q2,0,30);Q3=@(t)-Q(t,270+dwm(3));[t3,Q3]=fminbnd(Q3,0,30);Qm1=-Q1;Qm2=-Q2;Qm3=-Q3;tm=14.4336;Qm=12.1513;Sw_t=@(t,w)((t-tm)/tm)./(w/270);Sw_Q=@(Q,w)((Q-Qm)/Qm)./(w/270);t=[t1;t2;t3],Q=[Qm1;Qm2;Qm3],a=[270+d.*270,d.*100,t,(t-tm)./tm,Sw_t(t,d.*270)],b=[270+d.*270,d.*100,Q,(Q-Qm)./Qm,Sw_Q(Q,d.*270)], t =14.977317.056519.4601Q =13.107817.120822.4754a =272.7000 1.0000 14.9773 0.0377 3.7669 283.5000 5.0000 17.0565 0.1817 3.6345 297.0000 10.0000 19.4601 0.3483 3.4825b =272.7000 1.0000 13.1078 0.0787 7.8720 283.5000 5.0000 17.1208 0.4090 8.1794297.0000 10.0000 22.4754 0.8496 8.4963 (4)由图可知,新假设模型是一个阻滞增长模型,比原来的模型更符合实际,可以在较长时间内使用。
数学建模作业2 统计模型

病人服药后病痛减轻时间与用药剂量、性别和血压组别关系模型摘要某医药公司为了掌握一种新止痛药的疗效,设计了一个药物实验,通过观测病人性别、血压和用药剂量与病痛时间的关系,预测服药后病痛明显减轻的时间。
我们运用数学统计工具minitab软件,对用药剂量,性别和血压组别与病痛减轻时间之间的数据进行深层次地处理并加以讨论概率值P(是否<0.05)和拟合度R-Sq的值是否更大(越大,说明模型越好)。
首先,假设用药剂量、性别和血压组别与病痛减轻时间之间具有线性关系,我们建立了模型Ⅰ。
对模型Ⅰ用minitab软件进行回归分析,结果偏差较大,说明不是单纯的线性关系,然后对不同性别分开讨论,增加血压和用药剂量的交叉项,我们在模型Ⅰ的基础上建立了模型Ⅱ,用minitab软件进行回归分析后,用药剂量对病痛减轻时间不显著,于是我们有引进了用药剂量的平方项,改进模型Ⅱ建立了模型Ⅲ,用minitab软件进行回归分析后,结果合理。
最终确定了女性病人服药后病痛减轻时间与用药剂量、性别和血压组别的关系模型:xY=31.8-3.491x+56.13x-9.321x3x+0.2621对模型Ⅱ和模型Ⅲ关于男性病人用minitab软件进行回归分析,结果偏差依然较大,于是改进模型Ⅲ建立了模型Ⅳ,用minitab软件进行回归分析后,结果合理。
最终确定了男性病人服药后病痛减轻时间与用药剂量、性别和血压组别的关系模型:xY=32.8-4.021x+0.9551x3x+0.0.042721一、问题重述一个医药公司的新药研究部门为了掌握一种新止痛剂的疗效,设计了一个药物实验,给患有同种病痛的病人使用这种新止痛剂的一下4个剂量中的某一个:2g,5g,7g和10g,并记录每个病人病痛明显减轻的时间(以分钟计)。
为了了解新药的疗效与病人性别和血压有什么关系,实验过程中研究人员把病人按性别及血压的低、中、高三档平均分配来进行测试。
通过比较给个病人血压的历史数据,从低到高分成三组,分别记作0.25,0.50和0.75.实验结束后,公司的记录结果附录1-1表(性别以0表示,1表示男)。
《计算机辅助设计作业设计方案》

《计算机辅助设计》作业设计方案一、课程背景《计算机辅助设计》是一门旨在通过计算机软件辅助学生进行设计、制图和模拟的课程。
本课程旨在培养学生的计算机辅助设计能力,提高他们的设计水平宁创新能力。
二、课程目标1.了解计算机辅助设计的基本观点和原理;2.掌握常用的计算机辅助设计软件的应用方法;3.能够运用计算机辅助设计软件进行设计、制图和模拟;4.培养学生的设计思维和创新能力。
三、作业设计方案1.作业一:软件基础操作练习要求:学生应用AutoCAD软件完成一份简单的平面图绘制,包括建筑结构、道路等基本因素。
要求学生掌握AutoCAD的基本操作方法,包括绘图、修改、图层管理等功能。
评判标准:图纸完备、比例准确、线条清晰、图层设置正确。
2.作业二:三维建模设计要求:学生应用SolidWorks软件进行三维建模设计,设计一个简单的物体或机械零件。
要求学生掌握SolidWorks的基本建模方法,包括绘制草图、拉伸、旋转、镜像等功能。
评判标准:模型完备、尺寸准确、细节处理到位、组件间干系正确。
3.作业三:仿真模拟实验要求:学生应用ANSYS软件进行仿真模拟实验,对一个简单的结构进行受力分析。
要求学生掌握ANSYS的基本操作方法,包括建模、加载、网格划分、求解等功能。
评判标准:仿真结果准确、分析逻辑清晰、结论合理、报告书写规范。
四、教学方法1.理论教学结合实践操作,通过案例分析和实例讲解,引导学生掌握计算机辅助设计的基本原理和方法。
2.教室互动,鼓励学生提出问题和分享经验,增进学生之间的合作和交流。
3.实验室实践,提供计算机辅助设计软件的操作环境,让学生通过实际操作提升技能。
五、评判方式1.作业成绩占总成绩的60%,包括操作实践和报告书写。
2.期末考试占总成绩的40%,主要考查学生对计算机辅助设计的理解和应用能力。
六、参考资料1.《AutoCAD操作手册》2.《SolidWorks建模指南》3.《ANSYS仿真实例》七、总结通过《计算机辅助设计》这门课程的进修,学生将能够掌握计算机辅助设计的基本原理和方法,提高设计水平宁创新能力,为将来的工程设计工作打下坚实的基础。
2024年春江苏开放大学建筑信息建模(BIM)技术应用第二次作业答案

2024年春江苏开放大学建筑信息建模(BIM)技术应用第二次作业答案原创作者李想一、2024年春江苏开放大学建筑信息建模(BIM)技术应用第二次作业单选题答案1、基于BlM技术的O是指建立统一的设计标准,包括图层、颜色、线型、打印样式等,在此基础上,所有设计专业及人员在一个统一的平台上进行设计,从而减少现行各专业之间(以及专业内部)由于沟通不畅或沟通不及时导致的错、漏、碰、缺。
A、参数化设计B、协同设计C、可视化设计D、三维设计学生答案:B2、BlM模型内某一构件的空间位置用。
来表示A、高程B、地理坐标C、坐标和高程D、坐标学生答案:C3、ReVit中创建第一个标高IF之后,免制IF标高到上方5000处,生成新标高名称为OA、以上都不对B、IGC、2GD、2F学生答案:B4、建筑工程信息模型的信息应包含几何信息和OA、属性信息B、非几何信息C、时间信息D、空间信息学生答案:B5、BIM技术和O的结合完美地解决了可视化资产监控、查询、定位管理A、3D扫描技术B、GlS技术C、VR技术D、物联网技术学生答案:D6、下列关于BiM技术与CAD技术在建筑信息表达的描述中,不正确的是OA、CAD技术只能将纸质图纸电子化B、BIM可提供工程量清单、施工管理等更加丰富的信息C、CAD包含了建筑的全部信息D、BIM可提供二维和三维图纸学生答案:C7、下列软件产品中,属于BlM建模软件的是OA、PKPMB、RobotC、EcotechD、GMT学生答案:D8、下列关于BiM建模过程说法正确的是OA、首先建立网格及楼层线,然后导入CAD文档,接着建立柱梁板墙等组件,而后进行明细表或CAD输出,最后进行彩现B、首先建立网格及楼层线,然后导人CAD文档,接着建立柱梁板墙等组件,而后进行彩现,最后进行明细表或CAD输出C、首先建立网格及楼层线,然后进行彩现,接着导人CAD文档,而后建立柱梁板墙等组件,最后进行明细表或CAD输出D、首先进行彩现,然后导入CAD文档,接着建立柱梁板墙等组件,而后建立网格及楼层线,最后进行明细表或CAD输出学生答案:B9、O实现建设项目施工阶段工程进度、人力、材料、设备、成本和场地布置的动态集成管理及施工过程的可视化模拟。
数学建模第二次作业(章绍辉版)
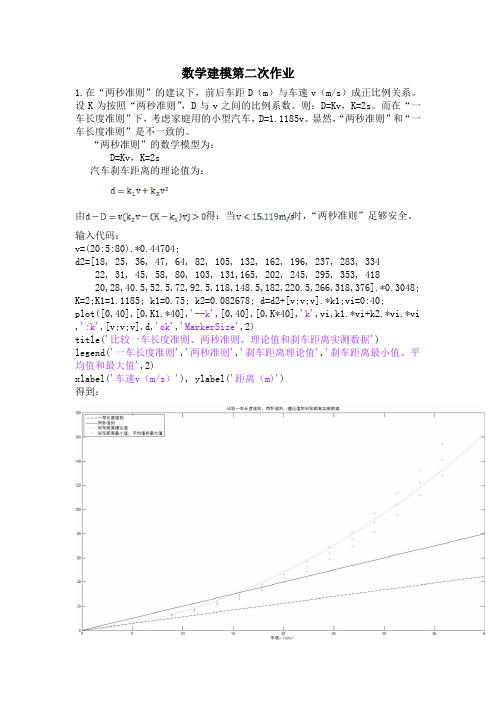
数学建模第二次作业1.在“两秒准则”的建议下,前后车距D(m)与车速v(m/s)成正比例关系。
设K为按照“两秒准则”,D与v之间的比例系数。
则:D=Kv,K=2s。
而在“一车长度准则”下,考虑家庭用的小型汽车,D=1.1185v。
显然,“两秒准则”和“一车长度准则”是不一致的。
“两秒准则”的数学模型为:D=Kv,K=2s汽车刹车距离的理论值为:由得:当时,“两秒准则”足够安全。
输入代码:v=(20:5:80).*0.44704;d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 33422, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376].*0.3048; K=2;K1=1.1185; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40;plot([0,40],[0,K1.*40],'--k',[0,40],[0,K*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2)title('比较一车长度准则、两秒准则、理论值和刹车距离实测数据')legend('一车长度准则','两秒准则','刹车距离理论值','刹车距离最小值、平均值和最大值',2)xlabel('车速v(m/s)'), ylabel('距离(m)')得到:由上图也可以看出当车速超过15米每秒时,“两秒准则”不安全。
2022年秋季-福师《数学建模》在线作业二-[复习资料]-答案3
![2022年秋季-福师《数学建模》在线作业二-[复习资料]-答案3](https://img.taocdn.com/s3/m/4eb6520c4a73f242336c1eb91a37f111f1850dbe.png)
2022年秋季-福师《数学建模》在线作业二-0003
试卷总分:100 得分:100
一、判断题 (共 40 道试题,共 80 分)
1.最小二乘法估计是常见的回归模型参数估计方法
<-A.->错误
<-B.->正确
【正确答案】:B
2.样本平均值和理论均值不属于参数检验方法
<-A.->错误
<-B.->正确
【正确答案】:A
3.量纲齐次原则指任一个有意义的方程必定是量纲一致的<-A.->错误
<-B.->正确
【正确答案】:B
4.对实际问题建模没有确定的模式
<-A.->错误
<-B.->正确
【正确答案】:B
5.数学建模以模仿为目标
<-A.->错误
<-B.->正确
【正确答案】:A
6.利用乘同余法可以产生随机数
<-A.->错误
<-B.->正确
【正确答案】:B
7.大学生走向工作岗位后就不需要数学建模了
<-A.->错误
<-B.->正确
【正确答案】:A。
《流程的设计作业设计方案-2023-2024学年高中通用技术粤科版》

《流程的设计》作业设计方案第一课时一、课程背景《流程的设计》是一门高等教育中重要的课程,旨在培养学生对于流程设计的理论和实践能力。
通过本门课程的学习,学生将能够掌握流程设计的基本原理、方法和工具,提高在工作中的流程设计能力,为未来的职业发展做好铺垫。
二、课程目标1. 理解流程设计的基本概念和原理。
2. 掌握流程分析与设计的方法和工具。
3. 能够运用流程设计工具进行实际的案例分析和解决问题。
4. 培养团队合作和创新精神。
三、课程内容1. 流程设计概述2. 流程建模方法3. 流程改进工具4. 流程评估与优化5. 实践案例分析四、作业设计方案1. 作业一:流程设计概述报告要求:学生根据课程内容和相关资料,撰写一份关于流程设计概述的报告。
报告应包括流程设计的定义、分类、重要性等内容,并结合实例进行说明。
报告需具备逻辑性和条理性。
2. 作业二:流程建模实践要求:学生选择一个实际的流程场景,通过流程建模工具(如Visio)对该流程进行建模。
学生需要包括流程的各个环节、参与者、时间节点等信息,同时对流程中可能存在的问题进行分析和优化建议。
3. 作业三:流程改进方案提出要求:学生根据作业二中建模的流程,提出针对其中存在问题的改进方案。
学生需要分析问题的原因,并提出具体的改进措施和实施计划。
同时,学生还需要对改进方案的效果进行评估和预测。
4. 作业四:流程设计案例分析要求:学生选择一个真实的流程设计案例,对该案例进行深入分析。
学生需要从流程的背景、问题、解决方案等方面进行详细的描述和评价,同时结合课程所学知识进行分析和总结。
五、评分标准1. 作业内容严谨、清晰,逻辑性强(30%)。
2. 基于理论知识的运用和深度分析(30%)。
3. 创新性和实践性(20%)。
4. 文字表达和排版规范(20%)。
六、作业提交方式学生需按时将作业提交至指定邮箱,并在规定时间内接受评分和反馈。
七、总结通过以上的作业设计方案,学生将能够全面掌握流程设计的理论和实践技能,提升自身在工作中的流程设计能力。
14秋福师《数学建模》在线作业二答案

福师《数学建模》在线作业二
判断题多选题
一、判断题(共40 道试题,共80 分。
)
1. 数学建模以模仿为目标
A. 错误
B. 正确
-----------------选择:A
2. 数学建模的误差是不可避免的
A. 错误
B. 正确
-----------------选择:B
3. 整个数学建模过程是又若干个有明显区别的阶段性工作组成
A. 错误
B. 正确
-----------------选择:B
4. 数学建模中常遇到微分方程的建立问题
A. 错误
B. 正确
-----------------选择:B
5. 数学建模是一种抽象的模拟,它用数学符号等刻画客观事物的本质属性
A. 错误
B. 正确
-----------------选择:B
6. 问题三要素结构是初态,目标态和过程
A. 错误
B. 正确
-----------------选择:B
7. 图示法是一种简单易行的方法
A. 错误
B. 正确
-----------------选择:B
8. 题名是人们检索文献资料的第一重要信息
A. 错误
B. 正确
-----------------选择:B
9. 利用无量纲方法可对模型进行简化
A. 错误
B. 正确
-----------------选择:B
10. 建模过程仅仅是建立数学表达式。
建模二作业二

衡阳师范学院数学与计算科学系学生实验报告实验课程名称:数学建模(2)系别:数计系年级: 2012 专业和班级:数学 2 班学生姓名学号开课时间: 2014 年下学期实验二:数据的预处理2014-09-25 星期四一、问题表述1、下面表格是某高校15个学院09级同一生源地新生的数学成绩抽样数据。
(1)将各个学院新生的数学成绩合并(按列拉直),并检验数据的正态性;若数据非正态,请进行适当的正态化变换;(2)数据集中是否存在异常值?若存在异常值,请作适当的处理。
二、实验过程与结果(含程序代码)(1)将各个学院新生的数学成绩合并(按列拉直),并检验数据的正态性;若数据非正态,请进行适当的正态化变换:首先,将各个学院新生的数学成绩求和得以下数据:置于work 文件夹下,在MATLAB 软件中使用xlsread 命令可以读取EXCEL 表格中的数据,这样就省去了输入大量数据的工作,然后用MATLAB 软件中的normplot 函数判断数据的正态性,程序代码如下: clear clcx=xlsread('shumo'); x=reshape(x,450,1); normplot(x)其中代码x=reshape(x,450,1)达到将各个学院新生的数学成绩合并(按列拉直)的目的。
以上程序代码得出下图:图一由上图可以看出,这些点并没有近似地在一条直线附近,其首尾部分有所偏离。
因此,数据不符合正态分布。
下面用幂变换将数据进行正态化变换,经典幂变换公式为: 改进的幂变换公式为:下面对幂变换进行分析。
幂变换后y 具有不同于x 的分布,其中幂指数λ按下列方法估计,即求λ,使得下面的)(λL 最大:其中求解过程的MATLAB 的程序为:function [lamda,y]=lamda(x) x=load('');x=reshape(x,450,1); [m,n]=size(x); if m~=1&&n~=1error('m or n must be 1 !'); return endif n==1 n=m; endf=@(s)(-*n*log(var((x.^s-1)/s))+(s-1)*n*mean(log(x))));%f 表示经验函数的相反数 ezplot(f);s0=input('请输入极值所在区间的左端点:');%输入0 s1=input('请输入极值所在区间的右断点:');%输入100lamda=fminbnd(f, s0, s1);%利用该函数找到固定区间内单变量函数最小值y=(x.^lamda-1)./lamda; figure(2); %参数lamda 的估计函数)(λL 图像 qqplot(y);title('yQ-Q 图');图二 估计函数)(λL 图像图三 正态变换后的Q-Q 图(2)数据集中是否存在异常值?若存在异常值,请作适当的处理:到目前为止,异常数据尚没有一个被普遍采纳的定义。
第二次作业饮酒驾车问题数学建模

dw = − kw dt w(0) = w0
其中 k 为吸收速率常数,解得: w( t) = w0 e− kT 时,由于经过时间间隔 T,又第二次饮酒,饮入量为 w0 ,所以 t=T 时
w(T ) = w0 + w0 e − kt
同理:当 t=2T 时,前两次酒精残余为: ( w0 + w0 e − kT )e − kT 并且当 t = 2T 时,又第三次饮酒,饮酒量仍为 w0 ,所以,
在前面就设好喝酒瓶数 n 比较方便)
问题一: (喝一瓶酒故参数 f/V 应代为 51.35) 下午六点检时测, t=6 时代入: w(6)= 19(mg/100ml) w(6)<20,即下午六点时没有检测出为饮酒驾车。 再次喝酒时,体内有酒精残余,有一个值为 19 的初始值, 凌晨两点再次检测时, t=8 代入: y(8)=27(mq/ml) 酒精含量 y(8)>20,因此大李被认定为饮酒驾车。
数学建模作业二:
饮酒驾车问题分析
一、 一次性饮酒的模型:
假设: 1 .酒精转移的速率与出发处酒精浓度成正比; 2 .过程为酒精从胃到体液到体外; 3. 酒精在血液与体液中含量相同; 4 在很短时间内饮酒,认为是一次性饮入,中间的时间差不计; 5.不考虑个体差异。
t为饮酒时间, y1 (t ) 为 t 时刻人体消化的酒精量, y2 (t ) 为 t 时刻人体的酒精
这样考虑 1.假设饮酒周期固定; 2.假设每次饮酒量也一定; 3.假设为一次性饮入; 4. 酒精浓度消除率为常数; 5.不考虑个体差异。 设 w(t ) 表式 t 时刻酒精在人体内的浓度, w(0) 表示 t=0 时饮入酒精量在体 内浓度, y (0) 表示饮入酒精量,T 表示周期,V 为体液体积,k 为酒精浓度消除 率。 饮酒后体内酒精的浓度逐渐降低, 酒精浓度消除率与饮酒量成线性比, 则有:
作业二 二维建模[1]
![作业二 二维建模[1]](https://img.taocdn.com/s3/m/f8d5210202020740be1e9bfe.png)
作业二二维建模
完成下面的作业。
第1题
设计主题
使用二维图形中的文本命令建立如下模型,效果如下图所示。
设计要求
1 创建文本“高新技术”及“Gaoxin jishu”,设置其字体大小为80,字间距为5,行间距为20,两行文字两端对齐。
2 设置“高新技术”及“Gaoxin jishu”可以渲染,渲染线框粗度为3。
3 将设计结果保存,文件名为“班级+姓名+02”,如土木0801王某某02。
第2题
设计主题
使用线、编辑样条线命令,创建并修改如下图形,并使用车削命令创建酒杯或纸杯模型(二选一)。
设计要求
1 尺寸不作具体要求,但酒杯、纸杯必须光滑
2 将设计结果保存,文件名为“班级+姓名+03”,如土木0801王某某03。
第3题
设计主题
使用二维图形创建、挤出等命令,建立人名印章或平顶房屋(门窗暂缺)模型(二选一)。
设计要求
1 尺寸不作具体要求。
3 将设计结果保存,文件名为“班级+姓名+04”,如土木0801王某某04。
海致大数据建模初级班第二次作业

海致大数据建模初级班第二次作业摘要:1.介绍海致大数据建模初级班的第二次作业2.作业的具体内容3.完成作业的步骤和方法4.总结正文:海致大数据建模初级班第二次作业旨在帮助学员巩固和提升大数据建模的基本知识和技能。
通过这次作业,学员们可以更好地理解大数据建模的流程,并熟练运用相关工具进行实践操作。
下面将详细介绍这次作业的具体内容、完成步骤和方法。
一、作业具体内容本次作业主要分为以下几个部分:1.数据预处理:对给定的数据进行清洗、转换和整理,以便后续建模分析。
2.特征工程:基于数据特点,选取合适的特征进行建模,并进行特征缩放、特征选择等操作。
3.模型选择与构建:根据问题类型和数据特点,选择合适的模型进行建模,并对模型参数进行调优。
4.模型评估与优化:通过评估模型的性能,选择最佳模型,并对模型进行优化。
5.结果可视化:将建模结果进行可视化展示,以便更好地理解模型的预测效果。
二、完成作业的步骤和方法1.数据预处理:首先,需要对给定的数据进行读取和清洗,处理缺失值、异常值等问题。
然后,对数据进行转换和整理,以便后续建模分析。
2.特征工程:在数据预处理的基础上,进行特征工程。
这一步主要包括特征缩放、特征选择等操作。
特征缩放是为了消除特征之间量纲的影响,特征选择则是为了选取对目标变量影响较大的特征。
3.模型选择与构建:根据问题类型(回归、分类、聚类等)和数据特点,选择合适的模型进行建模。
常见的模型有线性回归、逻辑回归、决策树、支持向量机、随机森林、K 近邻等。
在建模过程中,需要对模型参数进行调优,以提高模型的性能。
4.模型评估与优化:在模型构建完成后,需要对模型的性能进行评估,并选择最佳模型。
评估指标有均方误差(MSE)、均方根误差(RMSE)、准确率、精确率、召回率等。
针对评估结果,可以对模型进行优化,提高模型性能。
5.结果可视化:将建模结果进行可视化展示,可以使用matplotlib、seaborn 等库进行数据可视化,以便更好地理解模型的预测效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衡阳师范学院数学与计算科学系学生实验报告实验课程名称:数学建模(2)系别:数计系年级:2012 专业和班级:数学 2 班学生姓名学号开课时间:2014 年下学期每次试验得分平均分折合分30%评阅人阳志锋评阅时间2014年月日实验二:数据的预处理2014-09-25 星期四一、问题表述1、下面表格是某高校15个学院09级同一生源地新生的数学成绩抽样数据。
(1)将各个学院新生的数学成绩合并(按列拉直),并检验数据的正态性;若数据非正态,请进行适当的正态化变换;(2)数据集中是否存在异常值?若存在异常值,请作适当的处理。
学生学院1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 81 60 85 71 76 73 72 56 73 62 73 71 52 69 852 69 71 83 91 66 52 77 63 63 78 57 72 49 72 573 76 64 28 62 73 70 62 62 89 84 64 37 85 52 834 74 72 69 77 70 53 80 79 90 60 83 70 76 71 725 45 64 64 58 59 91 44 74 72 75 87 69 55 60 896 67 50 63 82 82 59 71 48 66 74 72 80 78 66 827 86 75 68 76 74 43 86 34 69 72 66 58 66 87 598 74 61 64 63 70 64 59 81 72 59 62 48 77 69 789 67 84 59 69 91 81 81 57 58 80 75 68 67 72 5510 84 63 88 60 63 72 72 79 86 69 88 74 55 65 6611 75 71 79 59 89 30 69 63 57 62 62 72 49 65 7612 75 68 54 93 65 64 83 63 53 83 64 84 41 79 7113 62 51 70 70 66 52 84 72 80 77 56 80 62 52 8714 73 52 63 76 90 73 79 67 68 73 83 95 45 70 9215 72 87 64 76 69 59 63 64 64 70 63 52 64 62 7716 61 56 76 79 72 78 66 65 73 68 70 53 46 58 5617 77 83 61 75 79 66 65 66 88 41 66 64 62 72 6718 75 80 70 88 51 62 47 78 74 68 55 46 53 67 6219 83 73 65 85 45 69 66 85 77 62 72 76 36 81 6820 75 58 78 67 67 72 53 90 68 59 61 57 65 49 7321 88 76 73 76 43 66 72 91 67 49 69 65 26 59 7022 83 66 63 71 79 63 75 59 83 75 77 52 50 62 7223 68 90 82 78 61 84 65 70 59 96 73 97 50 60 7724 57 70 88 91 86 56 81 85 56 58 76 69 90 66 6225 78 77 53 81 68 64 77 54 79 74 64 69 69 80 7026 88 85 68 75 74 47 65 71 76 59 78 93 48 71 7627 83 88 62 72 69 54 57 63 64 78 81 71 67 63 7828 79 60 73 79 67 39 52 54 49 70 71 63 68 88 6229 78 71 76 72 51 74 78 69 66 73 57 53 62 68 6830 66 64 85 58 68 48 69 73 68 85 60 59 87 58 45二、实验过程与结果(含程序代码)当的正态化变换:首先,将各个学院新生的数学成绩求和得以下数据:表一学生学院1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 81 60 85 71 76 73 72 56 73 62 73 71 52 69 852 69 71 83 91 66 52 77 63 63 78 57 72 49 72 573 76 64 2862 73 70 62 62 89 84 64 37 85 52 834 74 72 69 77 70 53 80 79 90 60 83 70 76 71 725 45 64 64 58 59 91 44 74 72 75 87 69 55 60 896 67 50 63 82 82 59 71 48 66 74 72 80 78 66 827 86 75 68 76 74 43 86 34 69 72 66 58 66 87 598 74 61 64 63 70 64 59 81 72 59 62 48 77 69 789 67 84 59 69 91 81 81 57 58 80 75 68 67 72 5510 84 63 88 60 63 72 72 79 86 69 88 74 55 65 6611 75 71 79 59 89 3069 63 57 62 62 72 49 65 7612 75 68 54 93 65 64 83 63 53 83 64 84 41 79 7113 62 51 70 70 66 52 84 72 80 77 56 80 62 52 8714 73 52 63 76 90 73 79 67 68 73 83 95 45 70 9215 72 87 64 76 69 59 63 64 64 70 63 52 64 62 7716 61 56 76 79 72 78 66 65 73 68 70 53 46 58 5617 77 83 61 75 79 66 65 66 88 41 66 64 62 72 6718 75 80 70 88 51 62 47 78 74 68 55 46 53 67 6219 83 73 65 85 45 69 66 85 77 62 72 76 36 81 6820 75 58 78 67 67 72 53 90 68 59 61 57 65 49 7321 88 76 73 76 43 66 72 91 67 49 69 65 2659 7022 83 66 63 71 79 63 75 59 83 75 77 52 50 62 7223 68 90 82 78 61 84 65 70 59 96 73 97 50 60 7724 57 70 88 91 86 56 81 85 56 58 76 69 90 66 6225 78 77 53 81 68 64 77 54 79 74 64 69 69 80 7026 88 85 68 75 74 47 65 71 76 59 78 93 48 71 7627 83 88 62 72 69 54 57 63 64 78 81 71 67 63 7828 79 60 73 79 67 39 52 54 49 70 71 63 68 88 6229 78 71 76 72 51 74 78 69 66 73 57 53 62 68 6830 66 64 85 58 68 48 69 73 68 85 60 59 87 58 45和2219 2090 2074 2230 2083 1878 2070 2035 2107 2093 2085 2017 1800 2013 2135由于本题涉及的数据较多,我们可以首先将上述表格用EXCEL软件保存并且命名为“shumo.xls”,再将其置于work文件夹下,在MATLAB软件中使用xlsread命令可以读取EXCEL表格中的数据,这样就省去了输入大量数据的工作,然后用MA TLAB软件中的normplot函数判断数据的正态性,程序代码如下:clearclcx=xlsread('shumo');x=reshape(x,450,1);其中代码x=reshape(x,450,1)达到将各个学院新生的数学成绩合并(按列拉直)的目的。
以上程序代码得出下图:图一由上图可以看出,这些点并没有近似地在一条直线附近,其首尾部分有所偏离。
因此,数据不符合正态分布。
下面用幂变换将数据进行正态化变换,经典幂变换公式为: 改进的幂变换公式为:下面对幂变换进行分析。
幂变换后y 具有不同于x 的分布,其中幂指数λ按下列方法估计,即求λ,使得下面的)(λL 最大:其中求解过程的MATLAB 的程序为:function [lamda,y]=lamda(x) x=load('shumo.txt'); x=reshape(x,450,1); [m,n]=size(x);if m~=1&&n~=1error('m or n must be 1 !'); return endif n==1 n=m; endf=@(s)(-(-0.5*n*log(var((x.^s-1)/s))+(s-1)*n*mean(log(x))));%f 表示经验函数的相反数 ezplot(f);s0=input('请输入极值所在区间的左端点:');%输入0 s1=input('请输入极值所在区间的右断点:');%输入100lamda=fminbnd(f, s0, s1);%利用该函数找到固定区间内单变量函数最小值y=(x.^lamda-1)./lamda; figure(2); %参数lamda 的估计函数)(λL 图像 qqplot(y); title('yQ-Q 图');图二 估计函数)(λL 图像图三 正态变换后的Q-Q 图(2)数据集中是否存在异常值?若存在异常值,请作适当的处理:到目前为止,异常数据尚没有一个被普遍采纳的定义。
这里引用Hawkins 对其的定义:异常数据是在数据集中与众不同的数据,使人怀疑这些数据并非随机偏差而产生,而是产生于完全不同的机制。
常用的异常值检验方法有σ3准则。
即设随机变量服从正态分布,其标准差为σ,σ3准则是建立在正态分布的等精度重复测量基础上而造成奇异数据的干扰或噪声难以满足正态分布。
