数模第二次作业题目
美国数学建模竞赛第二次模拟赛题

Problem A Rotating Grill Design for oscillating fanOne common type of oscillating directional electronic fan is a rotate grill fan. The key technology is the shape and speed of the rotating grill. The special-designed grill rotates to direct air for wide circulation. The clockwise and counter clockwise motion changes airflow direction.Please consider the factors of natural breeze, and build a breeze mode to design the grill to make the air from the fan to be comfortable.一种用于振动风机的旋转格栅设计问题一种常见的振动定向电子风机是一种旋转式格栅风机。
关键技术是旋转格栅的形状和速度。
特别设计的烧烤炉旋转,以直接空气流通。
顺时针和逆时针方向运动改变气流方向。
请考虑自然因素的微风,并建立风模式设计的格栅,使空气从风扇舒适。
Problem B Red Sun in the Morning: find an exit strategyRed sun at night, sailors' delight. Red sun in the morning, sailors take warning.Ten years ago hurricane Katrina had a devastating effect on the economies of several states, causing many deaths and much suffering. Comprehensive evacuation plans have been developed since then, but the authorities still want to improve their effectiveness. Your team has been hired by the Mississippi Emergency Management Administration (MSEMA) to review their current evacuation strategies.Things to keep in mind: All hurricanes are assigned a category: from 1 (the weakest) to 5 (the strongest, like Katrina). The category and the location of landfall are first predicted about 4 days in advance. Predictions are revised using updated information 48 hours later, and the final (most accurate) predictions become available 24 hours ahead of the expected landfall. The category of the hurricane and the actual location of the landfall determine which counties will be flooded. In addition, driving conditions in surrounding counties might be seriously affected by the size of the hurricane.Build a model to advise MSEMA on an optimal strategy: which counties should be ordered to evacuate, when, and where to. The first page of your manuscript should be a one page non-technical, executive summary for the governor of Mississippi. It should describe your main recommendations, the criteria you used to evaluate their effectiveness, and any caveats you believe are important to mention.%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Time permitting, your model should also account for the fact that evacuations initiated in Louisiana, Alabama, and Mississippi affect each other. For example, a large portion of the New Orleans population will likely evacuate through Jackson, MS using highways 59 and 55. If the population of Jackson needs to evacuate, much of it will be directed North within MS or West toward Monroe, LA. Parts of coastal counties in MS will evacuate through Mobile, AL.Despite these interdependencies, the decisions in each state are rarely made collaboratively. So, if you are a governor in one of these states and you order the evacuation later than the others, the population of your state might be at disadvantage since the roads will be already clogged by then. If thehurricane turns out to be stronger than expected, your constituents might end up stuck in traffic in affected areas. On the other hand, if you order the evacuation too early, this disruption carries a high economic cost –coastal areas generate much revenue for your state and early predictions about the expected hurricane strength/landfall time/location might be inaccurate.夜晚的红太阳,水手们的喜悦。
长春市高三下学期数学理第二次模拟试题带答案

适用精选文件资料分享2016 年长春市高三放学期数学理第二次模拟试题(带答案)长春市一般高中2016 届高三质量监测(二)数学理科(试卷种类 C)第Ⅰ卷(选择题,共60 分)一、选择题(本大题包含12 小题,每小题 5 分,共 60 分,每题给出的四个选项中,只有一项为哪一项吻合题目要求的,请将正确选项涂在答题卡上) 1.复数,在复平面内对应的点关于直线对称,且,则 A. B. C. D. 2.设会集,,则 A.B. C. D. 3.运转以以下图的程序框图,则输出的值为A. B. C.D. 4.若实数且,则以下不等式恒建立的是 A. B. C. D. 5.几何体三视图以以下图,则该几何体的体积为 A. B. C. D. 6.已知变量遵从正态分布,以下概率与相等的是 A. B. C. D. 7.已知为圆的直径,点为直线上任意一点,则的最小值为 A.B. C.D. 8.设等差数列的前项和为,且,当取最大值时,的值为 A. B. C. D. 9.小明试图将一箱中的24 瓶啤酒所有取出,每次小明在拿出啤酒时只好拿出三瓶或四瓶啤酒,那么小明拿出啤酒的方式共有种. A. B. C. D. 10.函数与的图象关于直线对称,则可能是 A. B. C. D. 11. 已知函数满足,当时,,当时,,若定义在上的函数有三个不一样的零点,则实数的取值范围是 A. B. C. D. 12. 过双曲线的右支上一点,分别向圆和圆作切线,切点分别为 , 则的最小值为 A. B. C. D. 第Ⅱ卷(非选择题,共 90 分)本卷包含必考题和选考题两部分,第 13 题― 21 题为必考题,每个试题考生都一定作答,第22 题― 24题为选考题,考生依据要求作答. 二、填空题 ( 本大题包含 4小题,每题 5 分,共 20 分,把正确答案填在答题卡中的横线上).13. 已知实数满足,则的最小值为 ___________. 14.已知向量,,则当时,的取值范围是 ___________. 15.已知,睁开式的常数项为 15,则 ___________. 16. 已知数列中,对任意的若满足(为常数),则称该数列为阶等和数列,此中为阶公和;若满足(为常数),则称该数列为阶等积数列,此中为阶公积 . 已知数列为首项为的阶等和数列,且满足;数列为公积为的阶等积数列,且,设为数列的前项和,则 ___________. 三、解答题(本大题包含 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤) . 17.(本小题满分 12 分)已知函数 . (1) 求函数的最小正周期和单调减区间;(2) 已知的三个内角的对边分别为,此中,若锐角满足,且,求的面积 . 18. (本小题满分 12 分)近来几年来我国电子商务行业迎来篷布发展的新时机, 2015 年双 11 时期,某购物平台的销售业绩高达918 亿人民币 . 与此同时,相关管理部门推出了针对电商的商品和服务的议论系统 . 现从议论系统中选出 200 次成功交易,并对其议论进行统计,对商品的好评率为 0.6 ,对服务的好评率为0.75 ,此中对商品和服务都做出好评的交易为 80 次. (1) 能否可以在犯错误概率不超出 0.1%的前提下,以为商品好评与服务好评相关?(2)若将频率视为概率,某人在该购物平台长进行的5 次购物中,设对商品和服务全好评的次数为随机变量:①求对商品和服务全好评的次数的分布列(概率用组合数算式表示);②求的数学希望和方差.(,此中)19.(本小题满分 12 分)在四棱锥中,底面是菱形,⊥平面,点为棱的中点,过作与平面平行的平面与棱,,订交于,,,.(1)证明:为的中点;(2)若,且二面角的大小为,、的交点为,连接 . 求三棱锥外接球的体积 . 20. (本小题满分 12 分)椭圆的左右焦点分别为,, 且离心率为, 点为椭圆上一动点,内切圆面积的最大值为 . (1) 求椭圆的方程 ; (2) 设椭圆的左极点为 ,过右焦点的直线与椭圆订交于,两点,连接,并延长交直线分别于,两点,以为直径的圆能否恒过定点?假如,央求出定点坐标;若不是 , 请说明原由 . 21. (本小题满分 12 分)已知函数在点处的切线与直线平行 . (1)务实数的值及的极值;(2)若对任意,,有,务实数的取值范围;请考生在22、23、24三题中任选一题作答,假如多做,则按所做的第一题记分. 22.(本小题满分10 分)选修 4―1:几何证明选讲 .如图,过圆外一点的作圆的切线,为切点,过的中点的直线交圆于、两点,连接并延长交圆于点,连接交圆于点,若.(1)求证:∽ ;(2)求证:四边形是平行四边形. 23.(本小题满分10分)选修4―4:坐标系与参数方程 .在直角坐标系中,曲线的参数方程为(是参数),以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为 . (1)求曲线的直角坐标方程,并指出其表示何种曲线;(2)若曲线与曲线交于 , 两点,求的最大值和最小值 . 24. (本小题满分10 分)选修 4―5:不等式选讲 . 设函数 . (1) 若不等式恒建立,务实数的取值范围; (2) 若不等式恒建立,务实数的取值范围. 长春市一般高中 2016 届高三质量监测(二)数学 ( 理科 ) 参照答案及评分参照 A 、B卷客观题答案一、选择题 ( 本大题包含 12 小题,每题 5分,共 60分9. A 10. C 11. B 12. D 简答与提示: 1. 【命题企图】本题主要观察会集的化简与走运算,属于基础题 . 【试题分析】C 由题意可知,则,所以 . 应选 C. 2. 【命题企图】本题观察复数的乘法运算,以及复平面上的点与复数的关系,属于基础题 . 【试题分析】D 复数在复平面内关于直线对称的点表示的复数,所以 . 应选 D. 3. 【命题企图】本题主要观察不等式的运算性质,是书中的原题改编,观察学生对函数图像的认识 . 【试题分析】 C 依据函数的图像与不等式的性质可知:当时,为正确选项,应选 C. 4. 【命题企图】本题观察程序流程图中循环结构的认识,是一道基础题 . 【试题分析】 A 由算法流程图可知,输出结果是首项为,公比也为的等比数列的前 9 项和,即为 . 应选 A. 5. 【命题企图】本题观察正态分布的看法,属于基础题,要修业生对正态分布的对称性有充分的认识 . 【试题解析】B 由变量遵从正态分布可知,为其密度曲线的对称轴,所以 .应选 B. 6. 【命题企图】本题经过几何体的三视图来观察体积的求法,对学生运算求解能力有必定要求. 【试题分析】 C 该几何体可视为长方体挖去一个四棱锥,所以其体积为. 应选C.7.【命题意图】本题主要等差数列的性质,借助前项的取值来确立项数,属于基础题 . 【试题分析】 B 由题意,没关系设,,则公差,此中,所以,,即当时,获得最大值 .应选 B. 8. 【命题企图】本题观察直线与圆的地点关系以及向量的运算. 【试题分析】 A由题可知,从圆外一点指向圆直径的两个端点的向量数目积为定值,即为,此中为圆外点到圆心的距离,为半径,所以当取最小值时,的取值最小,由方程的图像可知的最小值为,故的最小值为 1. 应选A. 9. 【命题企图】本题主要观察三角函数图像,学生对三角函数图像的对称,引诱公式的运用是解决本题的要点 . 【试题分析】A 由题意,设两个函数关于对称,则函数关于的对称函数为,利用引诱公式将其化为余弦表达式为,令,则 . 应选 A. 10. 【命题企图】本题是一道摆列组合问题,观察学生办理问题的方法,对学生的逻辑思想和抽象能力提出很高要求,属于中档题 . 【试题分析】C 由题可知,拿出酒瓶的方式有 3 类,第一类:取 6 次,每次拿出 4 瓶,只有1 种方式;第二类:取 8 次,每次拿出 3 瓶,只有 1 种方式;第三类:取 7次,3次4瓶和 4次 3瓶,取法为,为 35种;共计 37种取法.应选 C. 11. 【命题企图】本题主要观察双曲线的定义与圆切线的性质,是一道中档题 . 【试题分析】 B 由题可知,,所以 . 应选 B. 12. 【命题企图】本题是近来热门的函数图像辨析问题,是一道较为复杂的难题 .【试题分析】 D 由题可知函数在上的分析式为,又由可知的图像关于点对称,可将函数在上的大体图像体现如图:依据的几何意义,轴地点和图中直线地点为表示直线的临界地点,此中时,,联立,并令,可求得 . 所以直线的斜率的取值范围是 . 应选 D. C 、D卷客观题答案一、选择题 ( 本大题包含 12 小题,每题 5分,共 60分9. C 10. A 11. D 12. B 简答与提示: 1. 【命题企图】本题观察复数的乘法运算,以及复平面上的点与复数的关系,属于基础题 . 【试题分析】D 复数在复平面内关于直线对称的点表示的复数,所以 .应选 D. 2.【命题企图】本题主要观察会集的化简与走运算,属于基础题 . 【试题分析】 C 由题意可知,则,所以 . 应选 C. 3. 【命题企图】本题观察程序流程图中循环结构的认识,是一道基础题 . 【试题分析】 A 由算法流程图可知,输出结果是首项为,公比也为的等比数列的前 9 项和,即为 . 应选 A. 4. 【命题企图】本题主要观察不等式的运算性质,是书中的原题改编,观察学生对函数图像的认识 . 【试题分析】 C 依据函数的图像与不等式的性质可知:当时,为正确选项,应选 C. 5.【命题企图】本题经过几何体的三视图来观察体积的求法,对学生运算求解能力有必定要求.【试题分析】C该几何体可视为长方体挖去一个四棱锥,所以其体积为.应选C.6.【命题企图】本题观察正态分布的看法,属于基础题,要修业生对正态分布的对称性有充分的认识 . 【试题分析】B 由变量遵从正态分布可知,为其密度曲线的对称轴,所以 . 应选 B. 7. 【命题企图】本题观察直线与圆的地点关系以及向量的运算 . 【试题分析】A 由题可知,从圆外一点指向圆直径的两个端点的向量数目积为定值,即为,此中为圆外点到圆心的距离,为半径,所以当取最小值时,的取值最小,由方程的图像可知的最小值为,故的最小值为 1. 故选 A. 8.【命题企图】本题主要等差数列的性质,借助前项的取值来确立项数,属于基础题.【试题分析】B由题意,没关系设,,则公差,此中,所以,,即当时,获得最大值.应选 B. 9.【命题企图】本题是一道摆列组合问题,观察学生办理问题的方法,对学生的逻辑思想和抽象能力提出很高要求,属于中档题.【试题分析】C 由题可知,拿出酒瓶的方式有 3 类,第一类:取 6 次,每次拿出 4 瓶,只有 1 种方式;第二类:取 8 次,每次拿出 3 瓶,只有 1 种方式;第三类:取 7 次,3 次 4 瓶和 4 次 3 瓶,取法为,为 35 种;共计 37 种取法 . 应选 C. 10. 【命题企图】本题主要观察三角函数图像,学生对三角函数图像的对称,引诱公式的运用是解决本题的要点 . 【试题分析】 A由题意,设两个函数关于对称,则函数关于的对称函数为,利用引诱公式将其化为余弦表达式为,令,则 . 应选 A.11.【命题企图】本题是近来热门的函数图像辨析问题,是一道较为复杂的难题 . 【试题分析】 D 由题可知函数在上的分析式为,又由可知的图像关于点对称,可将函数在上的大体图像体现如图:依据的几何意义,轴地点和图中直线地点为表示直线的临界地点,此中时,,联立,并令,可求得 . 所以直线的斜率的取值范围是 . 应选 D. 12.【命题企图】本题主要观察双曲线的定义与圆切线的性质,是一道中档题 . 【试题分析】 B 由题可知,,所以 . 故选 B.E、 F 卷客观题答案一、选择题 ( 本大题包含 12 小题,每题 5 分,共60 分) 1.D【命题企图】本题观察复数的乘法运算,以及复平面上的点与复数的关系,属于基础题 . 【试题分析】 D 复数在复平面内关于直线对称的点表示的复数,所以 . 应选 D. 2.C 【命题企图】本题主要观察不等式的运算性质,是书中的原题改编,观察学生对函数图像的认识 . 【试题分析】C 依据函数的图像与不等式的性质可知:当时,为正确选项,应选 C. 3. C 【命题企图】本题主要观察会集的化简与走运算,属于基础题 . 【试题分析】 C 由题意可知,则,所以 . 应选 C.4. A 【命题企图】本题观察程序流程图中循环结构的认识,是一道基础题 . 【试题分析】 A 由算法流程图可知,输出结果是首项为,公比也为的等比数列的前 9 项和,即为 . 应选 A. 5. B【命题企图】本题主要等差数列的性质,借助前项的取值来确立项数,属于基础题 . 【试题分析】 B 由题意,没关系设,,则公差,此中,所以,,即当时,获得最大值 . 应选 B. 6. C 【命题意图】本题经过几何体的三视图来观察体积的求法,对学生运算求解能力有必定要求 . 【试题分析】 C 该几何体可视为长方体挖去一个四棱锥,所以其体积为 . 应选 C. 7. B 【命题企图】本题观察正态分布的看法,属于基础题,要修业生对正态分布的对称性有充分的认识 . 【试题分析】B 由变量遵从正态分布可知,为其密度曲线的对称轴,所以 . 应选 B. 8. A【命题企图】本题主要观察三角函数图像,学生对三角函数图像的对称,引诱公式的运用是解决本题的要点 . 【试题分析】 A 由题意,设两个函数关于对称,则函数关于的对称函数为,利用引诱公式将其化为余弦表达式为,令,则 . 故选 A. 9. A 【命题企图】本题观察直线与圆的地点关系以及向量的运算. 【试题分析】 A 由题可知,从圆外一点指向圆直径的两个端点的向量数目积为定值,即为,此中为圆外点到圆心的距离,为半径,所以当取最小值时,的取值最小,由方程的图像可知的最小值为,故的最小值为 1. 应选 A. 10. D【命题企图】本题是近来热门的函数图像辨析问题,是一道较为复杂的难题 . 【试题分析】 D 由题可知函数在上的分析式为,又由可知的图像关于点对称,可将函数在上的大体图像体现如图:依据的几何意义,轴地点和图中直线地点为表示直线的临界地点,此中时,,联立,并令,可求得 . 所以直线的斜率的取值范围是 . 应选 D. 11. C 【命题企图】本题是一道摆列组合问题,观察学生办理问题的方法,对学生的逻辑思想和抽象能力提出很高要求,属于中档题 . 【试题分析】 C 由题可知,拿出酒瓶的方式有 3 类,第一类:取 6 次,每次拿出 4 瓶,只有 1 种方式;第二:取 8 次,每次拿出 3 瓶,只有 1 种方式;第三:取 7 次, 3 次 4 瓶和 4 次 3 瓶,取法, 35 种;共 37 种取法 . 故 C. 12. B 【命意】本主要考双曲的定与切的性,是一道中档 . 【分析】 B 由可知,,所以 . 故 B.主答案二、填空(本大包含4小,每小5分,共20分)13.1 【命意】本主要考性划,是一道常. 从二元一次方程到可行域,再合目函数的几何意,全面地行考 . 【分析】依据方程得可行域以下,令,可化,所以,当直点,获得最小 1. 14. 【命意】平面向量的几何意是点,本合数形合思想,考平面向量的几何意,同也余弦定理的考,学生的算求解能力提出很高要求 . 【分析】由意,,依据向量的差的几何意,表示向量点到点的距离,当,距离获得最小 1,当,依据余弦定理,可算得距离获得最大,即的取范是 . 15.【命意】本考分的运算,是一道中档的常 . 【分析】由的常数,可得,所以原式 . 16. 【命意】本主要考特别数列乞降,学生的思能力提出很高要求,属于一道 . 【分析】由意可知,,,,,,,,,,,,,,⋯⋯,又是4等和数列,所以数列将会照此律循下去,同理,,,,,,,,,,,,,,⋯⋯,又是3等数列,所以数列将会照此律循下去,由此可知于数列,每 12 的和循一次,易求出,所以中有 168循构,故 . 三、解答 ( 本大必做 5 小,三一 1 小,共 70 分) 17.( 本小分 12 分) 【命意】本小主要考三角函数的化运算,以及三角函数的性,并借助正弦定理考角关系的运算,考生的化与化能力有高要求 . 【分析】解:(1) (3 分) 所以的最小正周期 . 的减区,即 . (6 分) (2) 由,又角, . 由正弦定理可得,,,由余弦定理可知,,可求得,故 . (12 分) 18 .( 本小分 12 分) 【命意】本小主要观察统计与概率的相关知识,包含独立性检验、失散型随机变量的分布列以及数学希望和方差的求法 . 本题主要观察学生对数据处理的能力 . 【试题分析】 (1) 由题意可得关于商品和服务议论的列联表:对服务好评对服务不满意共计对商品好评80 40 120 对商品不满意70 10 80 共计 150 50 200 ,可以在犯错误概率不超过 0.1%的前提下,以为商品好评与服务好评相关 . (6 分) (2) 每次购物时,对商品和服务都好评的概率为,且的取值可以是0,1,2,3,4,5.此中;;;;;.的分布列为:012345因为,则;.(12分)19. ( 本小题满分 12 分) 【命题企图】本小题主要观察立体几何的相关知识,详尽涉及到面面的平行关系、二面角的求法及空间向量在立体几何中的应用 . 本小题对考生的空间想象能力与运算求解能力有较高要求 . 【试题分析】解:(1) 连接 . ,即为△ 的中位线,即为中点 . (4 分) (2) 以为原点,方向为轴,方向为轴,方向为轴,建立空间直角坐标系,则,,,从而,,则,又,则 . 由题可知,,,,即三棱锥外接球为以、、为长、宽、高的长方体外接球,则该长方体的体对角线长为,即外接球半径为 .则三棱锥外接球的体积为. (12分)20.( 本小题满分 12 分) 【命题企图】本小题主要观察直线与圆锥曲线的综合应用能力,详尽涉及到椭圆方程的求法,直线与圆锥曲线的相关知识,以及恒过定点问题 . 本小题对考生的化归与转变思想、运算求解能力都有很高要求 . 【试题分析】解: (1) 已知椭圆的离心率为,没关系设,,即,此中,又△ 内切圆面积取最大值时,半径取最大值为,由,由为定值,所以也获得最大值,即点为短轴端点,所以,,解得,则椭圆的方程为 . (4 分) (2) 设直线的方程为,,联立可得,则,直线的方程为,直线的方程为,则,,假设为直径的圆能否恒过定点,则,,即即,即若为直径的圆能否恒过定点,即不论为什么值时,恒建立,所以,,或 . 即恒过定点和 .(12 分) 21.( 本小题满分 12 分) 【命题企图】本题主要观察函数与导数的综合应用能力,详尽涉及到用导数来描述原函数的单调性、极值等状况 . 本题对考生的逻辑推理与运算求解能力有较高要求 . 【试题分析】解 (1) 由题意得,又,解得 . 令,解得,即有极小值为 .(6 分)(2) 由,可得令,则,此中,,又,则,即,所以实数的取值范围是 . (12 分) 22.( 本小题满分 10 分) 【命题企图】本小题主要观察平面几何的证明,详尽涉及到切割线定理以及三角形相似等内容 . 本小题要点观察考生对平面几何推理能力 . 【试题分析】解 (1) 由题意可知,,则为的中点,则,即,所以△∽△,则,由可得,即,则∽. (5 分) (2) 由(1) ,又,则,可得,由,,则,可得,所以四边形是平行四边形 .(10 分) 23.( 本小题满分 10 分) 【命题企图】本小题主要观察极坐标系与参数方程的相关知识,详尽涉及到极坐标方程与平面直角坐标方程的互化、利用直线的参数方程的几何意义求解直线与曲线交点的距离等内容 . 本小题观察考生的方程思想与数形联合思想,对运算求解能力有必定要求 . 【试题分析】解(1) 关于曲线有,即,所以曲线的直角坐标方程为,其表示一个圆 . (5分) (2) 联立曲线与曲线的方程可得:,,所以的最小值为,最大值为 8. (10 分) 24.( 本小题满分 10 分) 【命题企图】本小题主要观察不等式的相关知识,详尽涉及到绝对值不等式及不等式证明等内容 . 本小题要点观察考生的化归与转变思想 . 【试题分析】 (1)当时,恒建立,当时,要保证恒建立,即的最小值,解得.(5分) (2) 依据函数图像的性质可知,当时,恒建立,即,所以的取值范围是时恒建立 . (10 分)。
第二次数学建模作业
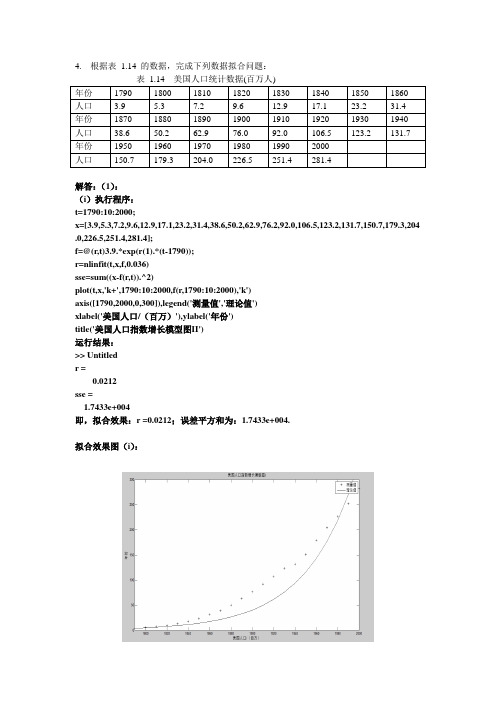
4. 根据表1.14 的数据,完成下列数据拟合问题:年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答:(1):(i)执行程序:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/(百万)'),ylabel('年份')title('美国人口指数增长模型图II')运行结果:>> Untitledr =0.0212sse =1.7433e+004即,拟合效果:r =0.0212;误差平方和为:1.7433e+004.拟合效果图(i):(ii)由表1.14我们知道,当t=1800时,有5)101(0≈+r x ,所以我们可以猜测,r=0.1,x =2.5.对待定参数0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下: >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道,拟合结果为:r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图(ii ):(iii)由表1.14我们知道,当t=1900时,有()76)-t 1900101(00≈+r x ,所以我们可以猜测,r=0.03,x =19, 0t =1800.对待定参数0t ,0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下:>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即,拟合效果:r =0,0x =7.9,0t =1742.5;误差平方和为:2.2657e+003我们由MATLAB9给出的警告信息,知道这个拟合存在病态条件,所以数据可能拟合的不太好。
《数学建模与数学实验》(第三版)6.5习题作业2

1.根据物理定律K K K R I V =,R I P 2=,建立如下模型:(1):目标函数为:∑==412k k k R IP 约束条件⎪⎪⎩⎪⎪⎨⎧===++=≤≤8,6,41023213214I I I I I I I I R I k k k 1)直接计算求解183214=++=I I I I()K K k K K K K R I I R I P ∑∑====41412min min=K k K V I∑=41min现在K V 一定,要想求P 的最小值,只需K I 最小即可。
又因为K I 已知,代入数据即可求解。
即218282624min 44332211⨯+⨯+⨯+⨯=+++=V I V I V I V I P2)有K I 已知及K V 的取值范围,可得K R 的取值范围。
min =I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4;I1=4;I2=6;I3=8;I4=18;R1>=1/2;R2>=1/3;R3>=1/4;R4>=1/9;R1<=5/2;R2<=5/3;R3<=5/4;R4<=5/9;EndGlobal optimal solution found.Objective value: 72.00000Total solver iterations: 0Variable Value Reduced Cost I1 4.000000 0.000000 R1 0.5000000 0.000000 I2 6.000000 0.000000 R2 0.3333333 0.000000 I3 8.000000 0.000000 R3 0.2500000 0.000000 I4 18.00000 0.000000 R4 0.1111111 0.000000Row Slack or Surplus Dual Price 1 72.00000 -1.000000 2 0.000000 -4.000122 3 0.000000 -4.000081 4 0.000000 -4.000061 5 0.000000 -4.000027 6 0.000000 -16.00000 7 0.000000 -36.00000 8 0.000000 -64.00000 9 0.000000 -324.0000 10 2.000000 0.000000 11 1.333333 0.000000 12 1.000000 0.000000 13 0.4444444 0.000000(2):目标函数:∑==412k k k R I P 约束条件为:⎪⎪⎩⎪⎪⎨⎧≤≤===≤≤++=628,6,4263213214k kk kI V V V V R V I I II1)183214=++=I I I I()K K k K KK K R I I R I P ∑∑====41412min min=K k K V I ∑=41min)min(44332211V I V I V I V I P +++=要使P 最小,取4V =0,则)min(332211V I V I V I P ++=现在K V 一定,要想求P 的最小值,只需K I 最小即可。
数模第二次作业题目

一.食谱问题
某公司饲养实验用的动物以供出售。
已知这些动物的生长对饲料中的三种营养成分:蛋白质、矿物质、维生素特别敏感,每个动物每天至少需要蛋白质70g 、矿物质3g 、维生素10g ,该公司能买到5种不同的饲料,每种饲料1kg 所含营养成分如表1,每种饲料1kg 的成本如表2。
求既能满足动物生长需要,又使总成本最低的饲料配方并进行相关的灵敏性讨论。
表2:5种饲料单位重量(1kg)的成本
二.工资问题
现有一个木工,一个电工和一个油漆工,三人相互同意彼此装修他们自己的房子。
在装修之前,他们达成了如下协议:
(1)
每人总共工作10天(包括给自己家干活在内); (2) 每人的日工资根据一般的市价在60----80元之间; (3) 每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案,如何计算出他们每人应得的工
现有一个木工,一个电工和一个油漆工,三人相互同意彼此装修他们自己的房子。
在装修之前,他们达成了如下协议:
(4)每人总共工作10天(包括给自己家干活在内);
(5)每人的日工资根据一般的市价在60----80元之间;
(6)每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案,如何计算出他们每人应得的工
三.投资效益问题
一个投资公司有22亿资金可用来投资,现有6个项目可供选择,各项目所需资金和预计收益如下表:
问:选择哪几个项目投资,可使投资收益最大?
要求:1. 建立数学模型。
2. 提出一般的求解方法。
(穷举法不得分)。
数学建模第二次作业

《数学建模》第二次作业一、填空题:一、一个连通图能够一笔画出的充分必要条件是( ).二、如图是一个邮路,邮递员从邮局A 动身走遍所有长方形街路后再返回邮局.若每一个小长方形街路的边长横向均为1km ,纵向均为2km ,则他至少要走( )km..3、设某种物资有两个产地21,A A ,其产量别离为10、20,两个销地21,B B 的销量相等均为15。
若是从任意产地到任意销地的单位运价都相等为,a 则最优运输方案与运价具有 两个特点。
4、设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若人口增加率是常数r ,那麽人口增加问题的马尔萨斯模型应为 .五、设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若允许的最大人口数为m x ,人口增加率由sx r x r -=)(表示,则人口增加问题的逻辑斯蒂克模型为 .二、分析判断题:一、从下面不太明确的叙述中肯定要研究的问题,需要哪些数据资料(至少列举3个),要做些甚麽建模的具体的前期工作(至少列举3个) ,成立何种数学模型:一座高层办公楼有四部电梯,早晨上班时刻超级拥堵,该如何解决。
二、一条公路交通不太拥堵,以至人们养成“冲过”马路的适应,不肯意走临近的“斑马线”。
交管部门不允许任意横穿马路,为方便行人,预备在一些特殊地址增设“斑马线”,以便让行人能够穿越马路。
那末“选择设置斑马线的地址”这一问题应该考虑哪些因素?试至少列出3种。
3、地方公安部门想明白,当紧急事故发生时,人群从一个建筑物中撤离所需要的时刻,假设有足够的安全通道.若指挥者想尽可能多且快地将人群撤离,应制定甚麽样的疏散计划.请就那个计划指出至少三个相关因素,并利用数学符号表示。
4、作为经济模型的一部份,若产量的转变率与生产量和需求量之差成正比,且需求量中一部份是常数,另一部份与产量成正比,那麽相应的微分方程模型是甚麽?五、某种疾病每一年新发生1000例,患者中有一半昔时可治愈.若2000年末时有1200个病人,到2005年将会出现甚麽结果?有人说,无论多少年过去,患者人数只是趋向2000人,但不会达到2000人,试判断那个说法的正确性。
数学建模(2)第二次作业word版
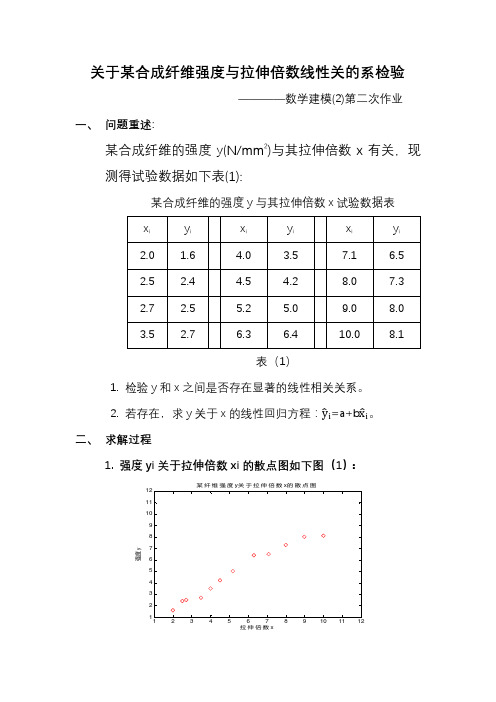
关于某合成纤维强度与拉伸倍数线性关的系检验————数学建模(2)第二次作业一、问题重述:某合成纤维的强度y(N/mm2)与其拉伸倍数x有关,现测得试验数据如下表(1):某合成纤维的强度y与其拉伸倍数x试验数据表表(1)1.检验y和x之间是否存在显著的线性相关关系。
2.若存在,求y关于x的线性回归方程:y i=a+b x i。
二、求解过程1.强度yi关于拉伸倍数xi的散点图如下图(1):图(1)2.样本相关系数计算 (1).计算公式r =nΣxy −ΣxΣynΣx 22nΣy 22(2)计算结果r =12∗382.17−3771.3612∗428.18−64.802∗ 12∗342.86−58.202=0.9859(3)结果分析r >0.8,说明该合成纤维强度y 与拉伸倍数x 成高度线性正相关关系。
2. 回归方程求解 (1).计算公式β1 =n ∑x i y i n i =1− ∑X i n i =1 ∑y i ni =1n x i2ni =1−∑x i n i =12某纤维强度y 关于拉伸倍数x 的散点图拉伸倍数x强度yβ 0=y −β1x (2).计算结果β 1= 12∗382.17−3771.3612∗428.18−64.802=0.8675β0=4.85−0.8675∗5.40=0.1655 (3).回归方程y i =0.1655+0.8675xi (4).回归前后图像对比图(2)回归系数β1=0.8675,表示拉伸倍数每增加一倍,该合成纤维强度增加0.08675。
三、 线性关系检验(1).提出假设123456789101112该纤维强度y 关于拉伸倍数x 的散点图及其线性回归方程拉伸倍数x强度yH0:β1=0线性关系不显著(2).计算检验统计量FF=SSR/1SSE/(n−2)= MSRMSE~F(1,n-2)F =58.89505/11.695902/(12−2)=347.2786(3).显著性水平α=0.05,根据分子自由度1和分母自由度12-2找出临界值Fα=4.965(4).F>Fα,拒绝H0,线性关系显著。
西南交大数学建模复赛a题论文自动倒车策略

西南交通大学峨眉校区2016年全国大学生数学建模竞赛第二次预选赛试题题目(A题自动倒车策略)姓名吴佩伦何青霞学号7182专业14级机电14级铁道运输联系电话自动倒车策略摘要本文针对自动泊车系统的研究,参考生活中人工入库的实际情况,对整个倒车过程车辆运动规律进行深入分析之后,运用了几何学相关知识求出了车辆在各段泊车的位置,列出了相关不等式并采用数形结合的方法,求解出了泊车起始点范围,并根据车辆在泊车点附近安全行驶的区域范围及泊车最终停靠位置的合理性,列出约束条件,通过构建多目标非线性规划模型,很好的解决了安全倒车入库的起始点位置问题和最佳泊车策略问题,最后运用了Matlab软件对模型进行求解。
问题一中,题目要求寻找能够安全倒车入库的起始点位置所在的区域范围,首先我们要明确的是影响汽车安全入库的因素就是车库周围物体的阻碍,然后我们将汽车倒车入库的过程划分为三个阶段,仔细分析汽车倒车入库的过程之后我们考虑这三段过程中可能会发生的接触车库警戒线,列出约束条件,建立数学模型,并采用数形结合的方法对模型进行求解,最终求出汽车能够安全入库的起始点位置范围为下列曲线6.747513.25; 2.47 5.27;<<-<<y x8.990.45( 2.47,3.97);y x x <++∈-22( 2.8)(9.22) 2.47,(3.97,5.27);x y x -+-<∈222( 3.97)(0.6) 6.44,(2.05,3.97)x y x -+-<∈所包络的不规则区域。
问题二中,题目要求设计出从任意倒车入库起始点开始的最佳泊车策略,并求出采用最佳策略时的前轮转角和后轮行驶距离。
我们应该在汽车能够安全倒车入库并停在最恰当位置的前提下寻求满足前轮转角之和最小和后轮行驶距离最短的最佳泊车策略,先针对设任意起始点00(,)x y 分析,对问题一中所构建的模型稍加改动,增加了对最终停车位置的约束条件,并针对前轮转角和后轮行驶距离构建双目标函数,由几何问题转化为多目标非线性规划问题,因为00(,)x y 非具体值,无法通过软件直接求解,通过任意选取多个具体00(,)x y 的值,运用Matlab 软件的fgoalattain 函数对该双目标非线性规划问题求解,得到多个起始点的最佳泊车策略,并进行了比较分析。
数模第二次作业

数模第二次作业姓名杜永志学号 ********学院理学院1.人员安排某公司的营业时间是上午8 点到22 点,以2 小时为一个时段,共7 个时段,各时段内所需的服务人员人数从早至晚分别为20,25,10,30,20,10,5,每个服务人员可在任一时段开始上班,但要连续工作8 小时,而工资相同,问应如何安排服务人员使公司所付工资总数最少,建立此问题的数学模型。
2、生产裸铜线和塑包线的工艺如下所示:1)拉丝机→裸铜线;2)拉丝机→塑包机→塑包线;3)联合机→塑包线某厂现有I型拉丝机和塑包机各一台,生产两种规格的裸铜线和相应达到两种规格的塑包线,没有联合机。
由于市场需求扩大和现有塑包机设备陈旧,计划新增II型拉丝机或联合机(每种设备最多1台),或改造塑包机,每种设备选用方案及相关数据如下:已知市场对两种规格裸铜线的需求量分别为3000km和2000km,对两种规格塑包线的需求分别为10000km和8000km。
按照规定,新购及改进设备按每年5%提取折旧费,老设备不提;每台机器每年最多只能工作8000小时。
为了满足需求,确定使费用最小的设备选用方案和生产计划。
(只建立规划模型,不必求解)1解:设xi(i=1、2、3、4、5、6、7)为第i个时间段开始工作的员工数优化目标min x1+x2+x3+x4+x5+x6+x7约束条件(1)x1≥20(2)x1+x2≥25(3)x1+x2+x3≥10(4)x1+x2+x3+x4≥30(5)x2+x3+x4+x5≥20(6)x3+x4+x5+x6≥10(7)x4+x5+x6+x7≥5(8)xi为正整数利用lingo软件求解输入:min x1+x2+x3+x4+x5+x6+x7stx1>20x1+x2>25x1+x2+x3>10x1+x2+x3+x4>30x2+x3+x4+x5>20x3+x4+x5+x6>10x4+x5+x6+x7>5endgin 7输出:Global optimal solution found.Objective value: 40.00000Objective bound: 40.00000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations:Variable Value Reduced CostX1 20.00000 1.000000X2 10.00000 1.000000X3 5.000000 1.000000X4 5.000000 1.000000X5 0.000000 1.000000X6 0.000000 1.000000X7 0.000000 1.000000 即公司安排20个员工第1个时间段开始工作,10个员工第2个时间段开始工作,5个员工第3个时间段开始工作,5个员工第4个时间段开始工作,这样员工数最少,为40人,工资也最少。
2021年高三下学期第二次模拟考试数学(理)试题 含解析

2021年高三下学期第二次模拟考试数学(理)试题含解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的.1.已知集合,,则A. B. C. D.【答案】A考点:集合的运算.2.若复数满足是虚数单位),则的共轭复数所对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】试题分析:,,对应的点在第四象限.考点:1.复数的概念与几何意义;2.复数的运算.3.已知为不共线的三点,则“”是“是钝角三角形”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】试题分析:由得到,即,即,可以得到为钝角,即是钝角三角形;但是钝角三角形时,角可能是钝角或锐角,不一定得到;所以“”是“是钝角三角形”的充分不必要条件. 考点:四种条件的判定.4.一个算法的程序框图如图所示,该程序输出的结果为 A. B. C. D.【答案】A 【解析】试题分析:由程序框图,可得3,4121)311[(21421311;2,31311=⎪⎭⎫ ⎝⎛-+-=⨯+⨯===⨯=i S i S ; 5536)111101211(21]1119110181)5131(4121311[21,=--+⨯=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=⋅⋅⋅S ,,结束循环,输出结果为.考点:1.程序框图;2.裂项抵消法. 5.不等式的解集是 A. B. C. D. 【答案】B 【解析】试题分析:由绝对值的几何意义,得表示数轴上的点到点的距离之和,易知,当或时,;所以的解集为.考点:1.绝对值的几何意义;2.绝对值不等式.6.设满足约束条件,若目标函数 的最大值为,则的图 象向右平移后的表达式为 A. B. C. D. 【答案】C 【解析】试题分析:作出可行域与目标函数基准线,由线性规划知识,可得当直线过点时,取得最大值,即,解得;则的图像向右平移个单位后得到的解析式为.考点:1.简单的线性规划;2.三角函数图像的变换. 7.为实数,表示不超过的最大整数,则函数在上为A.增函数B.周期函数C.奇函数D.偶函数 【答案】B 【解析】试题分析:对于任意整数,都有[][][])()()(x f x x k x k x k x k x k x f =-=+-+=+-+=+,所以是周期函数. 考点:函数的性质.8.已知棱长为的正方体的俯视图是一个面积为的正方形,则该正方体的正视图的面积不可能等于A. B. C. D. 【答案】A 【解析】试题分析:当正方体如图1放置时,其正视图是侧面,其面积为;当正方体如图2放置时,其正视图为对角面,其面积为,则无论如何放置,其正视图的面积在和,所以选A.图1 图2考点:几何体的三视图.9.已知点是双曲线的右焦点,点是该双曲线的左顶点,过且垂直于轴的直线与双曲线交于两点,若是钝角,则该双曲线的离心率的取值范围是A. B. C. D.【答案】C【解析】试题分析:由题意,得为双曲线的通径,其长度为,因为,所以;则,即,即,即,解得.考点:双曲线的几何性质.10.已知函数,若,则的取值范围是A. B. C. D.【答案】D【解析】试题分析:当时,不等式化为,即,而,即;当,不等式化为,即,令,则;令,则;当时,,即在为减函数,且,所以,即在为减函数,即无限接近0,则;所以的取值范围是.考点:1.分段函数;2.分类讨论思想.二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡中相应题的横线上.11.已知的取值如下表:从散点图分析,与线性相关,且回归方程为,则实数的值为 .【答案】【解析】试题分析:由所给数据,得,,将代入到回归方程,得,解得.考点:回归直线过样本点的中心.12.若在内任取一个实数,则使与圆无公共点的概率为 .【答案】考点:1.直线与圆的位置关系;2.几何概型.13.二项式的展开式中只有第六项的二项式系数最大,则展开式中常数项是 . 【答案】180【解析】试题分析:因为二项式的展开式中只有第六项的二项式系数最大,所以展开式中共有11项,即;则的展开式通项为,令,即,即展开式常数项为.考点:1.二项式系数的性质;2.二项式定理.14.设为单位向量,非零向量,若的夹角为,则的最大值等于.【答案】【解析】试题分析:由题意,得,则,即2121222222≤++⎪⎭⎫ ⎝⎛=++=x y x y xy y x x x,所以的最大值为. 考点:1.平面向量的模长;2.二次函数的最值.15.设抛物线的焦点为,直线过与交于两点,若,则的方程为 . 【答案】 【解析】试题分析:由题意,得抛物线的焦点,设,;则由得,即;联立,得,则,解得,又,即,,即直线的方程为.考点:1.抛物线的焦半径公式;2.直线与抛物线的位置关系.三、解答题:本大题共6小题,共75分. 把解答写在答题卡中.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分) 中所对的边分别为,且. (Ⅰ)求的大小;(Ⅱ)若求的面积并判断的形状. 【答案】(1);(2),等边三角形.考点:1.平面向量的数量积;2.二倍角公式;3.余弦定理;4.三角形的面积公式.17.(本小题满分12分)盒子里装有大小相同的个球,其中个号球,个号球,个号球.(Ⅰ)若第一次从盒子中任取一个球,放回后第二次再任取一个球,求第一次与第二次取到球的号码和是的概率;(Ⅱ)若从盒子中一次取出个球,记取到球的号码和为随机变量,求的分布列及期望.【答案】(1);(2)分布列略;.【解析】试题分析:(1)利用互斥事件有一个发生的概率公式和互相独立事件同时发生的概率公式进行求解;(2)写出随机变量的所有可能取值,利用超几何分布的概率公式求出概率,列表得到分布列,利用期望公式求其期望.试题解析:(Ⅰ)记“第一次与第二次取到的球上的号码的和是”为事件,……… 1分则……… 4分(Ⅱ)可能取的值是,……… 5分, ……… 6分, ……… 7分,… 8分 . ……… 9分∴的分布列为:10分399311051523456.2828281428284EX ∴=⨯+⨯+⨯+⨯+⨯== 故所求的数学期望为. ……… 12分考点:1.独立事件同时发生的概率;2.离散型随机变量的分布列和数学期望. 18.(本小题满分12分)已知数列是各项均为正数的等差数列,首项,其前项和为,数列是等比数列,首项,且. (Ⅰ)求数列和的通项公式; (Ⅱ)令,其中,求数列的前项和. 【答案】(1);(2). 【解析】试题分析:(1)设出的公差为,的公比为利用等差数列、等比数列的通项及求和公式得到关于的方程组,解得即可求解;(2)利用分组求和法和错位相减法进行求解. 试题解析:(Ⅰ)设的公差为,的公比为,则,依题意有, ………2分解得:或(舍去), ……… 4分 ,. ……… 6分(Ⅱ))()2()(212243121112n n n n nb a a b a a b a a c T ++++++++++=-+, ……… 7分令nn n n nb b b M 22322223221⨯++⨯+⨯+=+++= ①14322232222+⨯++⨯+⨯+=∴n n n M ②①-②得:22)1(22122222211112--=⨯---=⨯-+++=-++++n n n n nn n n n M……… 9分 , ……… 10分1212122)1(4322)1(41+++-++=+-++=∴n n n n n n n T . ……… 12分考点:1.等差数列;2.等比数列;3.分组求和法;4.错位相减法. 19.(本小题满分12分)如图,在正三棱柱中,,,是上的动点,且,是的中点. (Ⅰ)若,求证:平面平面;(Ⅱ)若直线与平面所成角的大小为,试求的值.【答案】(1)证明略;(2). 【解析】试题分析:(1):取中点,连结,得到平行四边形和线线平行,利用线面垂直的性质和等边三角形的三线合一证得线线垂直,进而得到线面垂直和面面垂直;(2)建立空间直角坐标系,利用直线的方向向量和平面的法向量进行求解.试题解析:(Ⅰ)证明:取中点,连结,则有与平行且相等. ∴四边形为平行四边形, ……1分∵面,∴,又为等边三角形,平面平面,…………3分 又平面,∴平面平面.……………4分(Ⅱ)以为轴,轴,在面内以过点且垂直于的射线为轴建系如图,)2,0,(),2,0,1()1,23,21(),0,0,1(1λλM B N B ,)1,23,21(),0,0,1()21,2321(==--=,,λλ ……6分ACBA 1C 1B 1MN设是平面的一个法向量,则∴,令∴…………8分 设与面所成角为 则431)21(43)21()12(2323,cos sin 221=+-++--+=><=λλλθn ………10分 ,化简得或由题意知, ∴ . …………………12分考点:1.空间中线面关系的转化;2.空间向量在立体几何中的应用. 20.(本小题满分13分)已知椭圆的中心在原点,焦点在轴上,它的一个顶点恰好经过抛物线的准线,且经过点. (Ⅰ)求椭圆的方程;(Ⅱ)若直线的方程为.是经过椭圆左焦点的任一弦,设直线与直线相交于点,记的斜率分别为.试探索之间有怎样的关系式?给出证明过程. 【答案】(1);(2). 【解析】试题分析:(1)由抛物线的方程得到其焦点坐标,即值,代入点即可求解;(2)联立直线与椭圆的方程,得到关于的一元二次方程,用坐标表示出,再进行求解. 试题解析:(Ⅰ)设方程为,因为抛物线的准线, …………1分 由点在椭圆上, ………3分 ∴椭圆C 的方程为. …………4分(Ⅱ)由题意知,直线斜率存在.设直线的方程为,代入,得 , ……5分 设由韦达定理得. ……6分由题意知121231233331222,,11142y y k k k k k x x --+====+++-+ ………8分 ,代人得1212121212231132()22112()1x x k k k k x x x x x x ++∴+=-+=-+++++ ……10分 2222222886343221412843243k k k k k k k k k -+++=-=+--+++ ………12分 ………13分考点:1.椭圆的标准方程;2.抛物线的几何性质;3.直线与椭圆的位置关系.21.(本小题满分14分)已知函数,.(Ⅰ)设,求的单调区间;(Ⅱ)若对,总有成立.(1)求的取值范围;(2)证明:对于任意的正整数,不等式恒成立.【答案】(1)当时,的增区间为,的减区间为;当时,的增区间为和,的减区间为;当时,的增区间为;当时,的增区间为和,的减区间为;(2);证明略.【解析】试题分析:(1)求导,确定出导函数的三个零点,讨论与0,1的大小关系确定其单调区间;(2)作差构造函数,利用导数证明函数的最大值非负即可;利用恒成立,将合理放缩:,再利用裂项抵消法进行证明.试题解析:(Ⅰ)x a x a x x g x f x h )1(ln 21)()()(2+-+=-=,定义域为, xa x x x a x a x a x x a x h ))(1()1()1()(2'--=++-=+-+=, …… 1分 (1)当时,令,,,令, ;(2)当时,令,则或,令, ; …… 3分(3)当时,恒成立;(4)当时,令,则或,令, ; …… 4分综上:当时,的增区间为,的减区间为;当时,的增区间为和,的减区间为;当时,的增区间为;当时,的增区间为和,的减区间为. ……5分(Ⅱ)(1)由题意,对任意,恒成立,即恒成立,只需. ……6分由第(Ⅰ)知:,显然当时, ,此时对任意,不能恒成立; (或者分逐个讨论) …… 8分当时,,;综上:的取值范围为. …… 9分(2)证明:由(1)知:当时,,……10分即,当且仅当时等号成立.当时,可以变换为, …… 12分在上面的不等式中,令,则有))(1(1)2)(1(1)1(1n m n m m m m m +-+++++++> )111()2111()111(nm n m m m m m +--++++-+++-= 不等式恒成立. …… 14分考点:1.函数的单调性;2.不等式恒成立问题;3.放缩法;4.裂项抵消法.30206 75FE 痾25656 6438 搸25209 6279 批F*c23955 5D93 嶓26549 67B5 枵TD22700 58AC 墬31907 7CA3 粣.26995 6973 楳。
数学建模第二次作业a

数学建模第二次作业a学生:陈耿1.产生一个1x10的随机矩阵,大小位于(-5 5),并且按照从大到小的顺序排列好!2.请产生一个100*5的矩阵,矩阵的每一行都是[1 2 3 4 5]3. 已知变量:A='ilovematlab';B=’matlab’, 请找出:(A)B在A中的位置。
(B)把B放在A后面,形成C=‘ilovematlabmatlab’4. 请修改下面的程序,让他们没有for循环语句!A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend5、下面程序实现什么功能?for n=100:200if rem(n,77)~=0continueendbreakendn6、请把变量A=[1 2 3; 4 5 6; 7 8 9]写到文件里(output.xls),写完后文件看起来是这样的:1 2 3 4 5 6 7 8 97、编写程序将30支股票数据.xls 文件中的数据读入MATLAB中,存为矩阵A,并将最后15组数据提取放入矩阵B中,将B写入b15.xls 保存。
8.a=[1 2 3 4 5],b=a(1)*a(5)+a(2)*a(4)+a(3)*a(3)+a(4)*a(2)+a(5)*a(1).试用MATLAB中最简单的方法计算b。
9、求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3x+8z- 5w=9-6x+5y-2z+10w=-8求系数矩阵的秩;求出方程组的解。
10、设 f(x)=x^5-4x^4+3x^2-2x+6(1)取x=[-2,8]之间函数的值(取100个点),画出曲线,看它有几个零点。
(提示:用polyval 函数) (2)用roots 函数求此多项式的根11、编写一个函数,使其能够产生如下的分段函数:⎪⎩⎪⎨⎧≤≤<-≤=x x x x x x f 65.0620.251.525.0)(,,,,并调用此函数,绘制[02]()(2)x f x f x 在,范围的曲线=+?。
2011大学生数学建模模拟试题二及解答

接力队选拔优化模型队员:董剑琦徐亚飞李江波完成日期:2011-8-23接力队选拔优化模型摘要:随着社会的发展,体育竞技已越来越被受人们的关注,他不仅能够强身健体,而且更为重要的是它是衡量一国国民综合素质的重要指标,在各种国际竞争中占据着重要地位。
本文主要利用分配的指派问题理论,用数学建模的方法建立了混合游泳中接力队选拔运动员的最优模型,从优选择,近而解决接力队选拔运动员的实际问题。
关键字:接力队选拔;分配指派;数学模型;从优。
一.问题重述我国素来以体育大国著称,在国际泳坛,为了迎接即将到来的4*100混合泳接力赛,国家体育总局必须在甲,乙,丙,丁,戊五人中选出四人参加比赛,现有四人选拔成绩及其后期努力后成绩波动变化,参考已有数据,从优选择,得出最佳选择方案。
在模型Ⅰ中,对问题一:即在不考虑队员成绩变化的情况下,按“分配指派”原则,得出了选拔队员方案。
在模型Ⅱ中,对问题二:即队员成绩发生变化的情况下做出方案调整,然后利用分配指派原则重新选择队员。
最后,讨论俩种队员选拔结果,从优选择。
二.模型假设根据建立模型的需要,作出如下假设:(1)参赛队员不受伤病及其他影响(2)参赛队员一旦确定成绩不会出现波动。
三.符号定义与说明i:代表参加选拔的队员j :代表参加选拔队员第j 种的成绩 cij :表示第i 个队员第j 种泳姿的成绩四.建立模型与求解:现在,利用0-1规划,对参赛队员成绩分析处理,作出选拔。
4.1建立模型 目标函数约束条件每人最多入选泳姿之一 ,每种泳姿有且只有1人4.2模型求解4.2.1不考虑队员成绩的变化min 66.811x +75.612x +8713x +58.614x +… … +67.451x +7152x +83.853x +62.454x11x +12x +13x +14x <=141x +42x +43x +44x <=111x +21x +31x +41x +51x =1… …x+24x+34x+44x+54x =114最优解:x14 = x21 = x32 = x43 = 1, 其它变量为0; 成绩为253.2(秒) 甲—自由泳、乙—蝶泳、丙—仰泳、丁—蛙泳.4.2.2 队员成绩发生变化当丁的蛙泳成绩退步1’15”2,戊的自由泳成绩进步到57”5 ,c43, c54 的新数据重新输入模型,用LINDO求解模型同上,求得最优解:x21 = x32 = x43 = x51 = 1, 其它变量为零;成绩为252.1(秒)乙—蝶泳、丙—仰泳、丁—蛙泳、戊—自由泳。
数学建模第二次作业(章绍辉版)
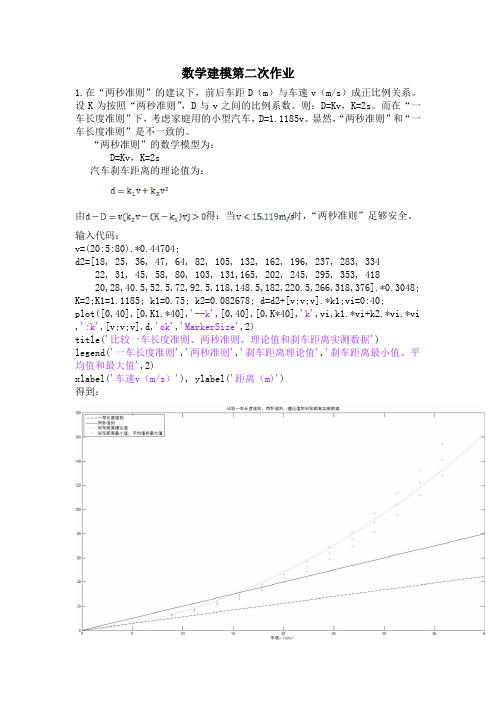
数学建模第二次作业1.在“两秒准则”的建议下,前后车距D(m)与车速v(m/s)成正比例关系。
设K为按照“两秒准则”,D与v之间的比例系数。
则:D=Kv,K=2s。
而在“一车长度准则”下,考虑家庭用的小型汽车,D=1.1185v。
显然,“两秒准则”和“一车长度准则”是不一致的。
“两秒准则”的数学模型为:D=Kv,K=2s汽车刹车距离的理论值为:由得:当时,“两秒准则”足够安全。
输入代码:v=(20:5:80).*0.44704;d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 33422, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376].*0.3048; K=2;K1=1.1185; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40;plot([0,40],[0,K1.*40],'--k',[0,40],[0,K*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2)title('比较一车长度准则、两秒准则、理论值和刹车距离实测数据')legend('一车长度准则','两秒准则','刹车距离理论值','刹车距离最小值、平均值和最大值',2)xlabel('车速v(m/s)'), ylabel('距离(m)')得到:由上图也可以看出当车速超过15米每秒时,“两秒准则”不安全。
数学建模2福州大学数学自考期末测试及答案

判断题(共40 道试题,共80 分。
)1. 数据的需求是与建立模型的目标密切相关的A. 错误B. 正确满分:2 分2. 有的建模问题可利用计算机求解A. 错误B. 正确满分:2 分3. 独立性检验是检验随机数中前后个数的统计相关性是否显著的方法A. 错误B. 正确满分:2 分4. 数学建模中常遇到微分方程的建立问题A. 错误B. 正确满分:2 分5. 交流中必须学会倾听A. 错误B. 正确满分:2 分6. 相对误差等于绝对误差加测量误差A. 错误B. 正确满分:2 分7. 数学建模以模仿为目标A. 错误B. 正确满分:2 分8. 图示法是一种简单易行的方法A. 错误B. 正确满分:2 分9. 国际上仅有一种单位体系A. 错误B. 正确满分:2 分10. 在建模中要不断进行记录A. 错误B. 正确满分:2 分11. 任何一个模型都会附加舍入误差A. 错误B. 正确12. 变量间关系通常分为确定性与不确定关系A. 错误B. 正确满分:2 分13. 求常微分方程的基本思想是将方程离散化转化为递推公式以求出函数值A. 错误B. 正确满分:2 分14. 回归分析是研究变量间相关关系的统计方法A. 错误B. 正确满分:2 分15. 量纲齐次原则指任一个有意义的方程必定是量纲一致的A. 错误B. 正确满分:2 分16. 人口预测模型用以预测人口的增长A. 错误B. 正确满分:2 分17. 引言是整篇论文的引论部分A. 错误B. 正确满分:2 分18. 系统模拟是研究系统的重要方法A. 错误B. 正确满分:2 分19. 任意齐次线性方程组的基本解组仅有一组A. 错误B. 正确满分:2 分20. 参考文献要反映出真实的科学依据A. 错误B. 正确满分:2 分21. 建模中的数据需求常常是一些汇总数据A. 错误B. 正确满分:2 分22. 样本平均值和理论均值不属于参数检验方法A. 错误B. 正确23. 题面见图片A. 错误B. 正确满分:2 分24. 研究新产品销售模型是为了使厂家和商家对新产品的推销速度做到心中有数A. 错误B. 正确满分:2 分25. 要获得真正理论意义上的最优回归方程是很困难的A. 错误B. 正确满分:2 分26. 题名是人们检索文献资料的第一重要信息A. 错误B. 正确满分:2 分27. 我们研究染色体模型是为了预防遗传病A. 错误B. 正确满分:2 分28. 明显歪曲实验结果的误差为过失误差A. 错误B. 正确满分:2 分29. 模型的成功与否取决于经受住实践检验A. 错误B. 正确满分:2 分30. 恰当的选择特征尺度可以减少参数的个数A. 错误B. 正确满分:2 分31. 通过实验收集和问卷调查等可以获取数据A. 错误B. 正确满分:2 分32. 摘要是对论文内容不加注释和评论的简短陈述A. 错误B. 正确满分:2 分33. 小组讨论要回避责任A. 错误B. 正确34. 建模假设应是有依据的A. 错误B. 正确满分:2 分35. 数学建模的误差是不可避免的A. 错误B. 正确满分:2 分36. 数学建模仅仅设计变量A. 错误B. 正确满分:2 分37. 常见的数据拟合方法有插值法最小二乘法等A. 错误B. 正确满分:2 分38. 建模主题任务是整个工作的核心部分A. 错误B. 正确满分:2 分39. 在构造一个系统的模拟模型时要抓住系统中的主要**素A. 错误B. 正确满分:2 分40. 模型不具有转移性A. 错误B. 正确满分:2 分福建师范2012秋福师《数学建模》在线作业二试卷总分:100 测试时间:--判断题多选题、多选题(共10 道试题,共20 分。
[理学]数学建模第2次模拟赛题
![[理学]数学建模第2次模拟赛题](https://img.taocdn.com/s3/m/db232cdea6c30c2258019e1b.png)
问题B:邮政运输网络中的邮路规划和邮车调度我国的邮政运输网络采用邮区中心局体制,即以邮区中心局作为基本封发单元和网路组织的基本节点,承担着进、出、转口邮件的处理、封发和运输任务,在此基础上组织分层次的邮政网。
邮路是邮政运输网络的基本组成单元,它是指利用各种运输工具按固定班期、规定路线运输邮件,并与沿线有交接频次的邮政局、所交换邮件总包所行驶的路线。
邮路的结构形式有三种:辐射形、环形和混合形。
如图1所示,邮路A为一条环形邮路,邮路B为一条辐射形邮路。
图1邮路示意图(1)辐射形邮路:是指从起点局出发,走直线或曲折线的邮路,其特点是不论用一种或几种运输工具联运,从起点到终点后,仍按照原路线返回出发地点。
因此须在同一条路线上往返两个行程。
这种邮路可以缩短运递时间,加快邮运速度。
但它的联系点较少,需用的运输工具较多,所耗费用较大。
(2)环形邮路:是指邮政运输工具走环形路线的邮路,即运输工具从起点出发单向行驶,绕行一周,经过中途各站,回到出发地点。
它的特点是不走重复路线,联系点较多,运输工具的利用率高,运费也较省。
但是邮件送到最后几个交接点的时间较长。
(3)混合形邮路:是指包含辐射形和环形两种结构形式的邮路。
某地区的邮政局、所分布如图2所示,分为地市中心局(简称地市局)、县级中心局(简称县局)和支局三级机构,该地区的邮政运输网络由区级邮政运输网和县级邮政运输网构成。
区级邮政运输网由从地市局出发并最终返回地市局的区级邮车所行驶的全部邮路构成,县级邮政运输网由从县局出发并最终返回县局的县级邮车所行驶的全部邮路构成。
为使邮政企业实现低成本运营和较高的服务质量,我们需要对该地区的邮政运输网络进行重构,确定合适的邮路规划方案并进行邮车的合理调度。
为了满足邮政的时限要求,必须尽可能地保证各县局、支局在营业时间内收寄的多数邮件能当天运送回地市局进行分拣封发等处理,以及每天到达地市局的多数邮件能当天运送到目的地县局、支局。
工程数学建模试验2

(1)将问题建立成一个线性规划模型,确定最优的生产方案。(2)对于操作1,假定超过它当前每天430分钟能力的任何附加时间必须依靠每小时50美元的加班获得。每小时成本包括劳动力和机器运行费两个方面。对于操作1,使用加班在经济上有利吗?如果有利,最多增加多少时间?
(3)假定操作2的操作员已同意每天加班工作2小时,其加班费是45美元一小时。还有,操作自身的成本是一小时10美元。这项活动对于每天收入的实际结果是什么?(4)操作3需要加班时间吗
运行结果为:
由运行结果可知,选x1、x2、x3、x5、x7、x9。即微积分,线性代数,最优化方法,应用统计,计算机编程,数学实验。
题目
某公司拿出15百万美元,最多建造7个发射台来覆盖15个相邻社区中尽可能多的人口。表2.7给出了各个社区的人口数目,表2.8给出了每个发射台可以覆盖的社区及建造这个发射台的费用,确定出哪几个发射台需要建造?
Y4+Y5>=X6;
Y3+Y5+Y6>=X7;
Y4>=X8;
Y3+Y4+Y5>=X9;
Y3+Y6>=X10;
Y5>=X11;
Y6+Y7>=X12;
Y7>=X13;
Y6+Y7>=X14;
Y7>=X15;
Xi,Yj为整数。
目标函数最大值即为最优解。
LINGO程序:
运行结果
由运行结果可知:
需要建造的发射台为2,4,5,6,7,只有1社区无法覆盖,覆盖最多人口为129千人。
解答:
设i为饲料类型,i=1为颗粒饲料,i=2为粉状饲料。J为营养成分,j=1为蛋白质,j=2为脂肪,j=3为纤维素。
数学建模第二次作业

数学建模作业作业次数:2组别:21小组成员:【问题2】一个运输公司每天有100吨的航空运输能力。
公司每吨收空运费250美元。
粗除了重量的限制外,由于飞机货场容积有限,公司每天只能运50000立方英尺的货物。
每天要运送的货物数量如下:货物重量(吨)体积(立方英尺/吨)1 30 5502 40 8003 50 400(1)求使得利润最大的每天航空运输的各种货物的吨数。
(2)计算每个约束的影子价格,解释它们的含义。
(3)公司有能力对它的一些旧的飞机进行改装来增大货运区域的空间。
每架飞机的改造要花费200000美元,可以增加2000立方英尺的容积。
重量限制仍保持不变。
假设飞机每年飞行250天,这些旧飞机剩余的使用寿命约为5年。
在这种情况下,是否值得改装?有多少架飞机时才值得改装?解:(a)(一)提出问题:变量:e=每天最大航空运力(吨)f=每天最大运送体积(立方英尺)g=每天空运的费用(美元/吨)p=每天运送货物1的总重量(吨/天)r=每天运送货物2的总重量(吨/天)t=每天运送货物3的总重量(吨/天)Q=货物1的总体积(立方英尺)M=货物2的总体积(立方英尺)N=货物3的总体积(立方英尺)S=最后利润(美元)假设:Q=30×pM=40×rN=50×tS=( Q+M+N) ×gp+r+t ≤eQ+M+N ≤fp ≤30r ≤40t ≤50目标:求S 的最大值(二)选择建模方法:此模型是典型的线性规划模型问题。
课利用LINDO 软件求解。
(三)推导模型公式:S=( p+r+t) ×g=250×(p+r+t )假设y=S 为需最大化目标量,1x =p, 2x =r, 3x =t 作为决策变量。
我们的问题现在化为在区域A={(1x ,2x ,3x ):1x +2x +3x ≤100, 550×1x +800×2x +400×3x ≤50000,1x ≤30,2x ≤40,3x ≤50}上求下面函数的最大值:y=f(1x ,2x ,3x )=250×(1x +2x +3x )(四)求解模型公式:利用LINDO 软件求解可得:LP OPTIMUM FOUND AT STEP 3OBJECTIVE FUNCTION VALUE1) 24218.75VARIABLE VALUE REDUCED COSTX1 30.000000 0.000000X2 16.875000 0.000000X3 50.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 3.125000 0.0000003) 0.000000 0.3125004) 0.000000 78.1250005) 23.125000 0.0000006) 0.000000 125.000000NO. ITERATIONS= 3RANGES IN WHICH THE BASIS IS UNCHANGED:OBJ COEFFICIENT RANGESVARIABLE CURRENT ALLOWABLE ALLOWABLECOEF INCREASE DECREASEX1 250.000000 INFINITY 78.125000X2 250.000000 113.636360 250.000000X3 250.000000 INFINITY 125.000000RIGHTHAND SIDE RANGESROW CURRENT ALLOWABLE ALLOWABLERHS INCREASE DECREASE2 100.000000 INFINITY 3.1250003 50000.000000 2500.000000 13500.0000004 30.000000 10.000000 30.0000005 40.000000 INFINITY 23.1250006 50.000000 6.250000 46.250000(五)回答问题:由我们的模型得到答案是当每天运送货物1为30吨,货物2为16.875吨,货物3为50吨,可达到最大利润为24218.75美元(b)由上表可知:每天运送货物的容积、货物1每天的运送重量和货物3每天的运送重量为紧约束,其他两个条件则为一般约束。
数学建模 第二次大作业

第二次大作业题目作业第一题: P130 习题一作业第二题: P131 习题二作业第三题: P131 习题三作业第四题: P131 习题四作业第五题: P132 习题六作业第六题: P130 习题七作业第七题:基站选址问题有一个移动电话运营商计划在一个目前尚未覆盖的区域开展业务,预算为1000万元。
调查表明,此区域有7个位置可以安设基站,每个基站只能覆盖一定数目的社区,具体数据见下表:表1:每个基站的建造费用(百万)和覆盖社区表2:社区居民数(千人)问:应在哪些地方建造基站使得基站覆盖的人口尽可能多?作业第八题:街道洒水车问题一辆洒水车从交汇点1出发,给每条街道洒水,最后回到出发点,要求单行道洒水一次,双向道来回各洒水一次,假定洒水车装的水足够多,请为洒水车制定行车路线,使得洒水车行走的总路程最短。
、第九题:发电机使用计划为了满足每日电力需求(单位:兆瓦),可以选用四种不同类型的发电机。
每日电力需求如下所示:一最小输出功率。
所有发电机都存在一个启动成本,以及工作于最小功率状态时的固定的每小时成本,并且如果功率高于最小功率,则超出部分的功率每兆瓦每小时还存在一个成本,即边际成本。
这些数据均列于下表中。
电机不需要付出任何代价。
我们的问题是:(1)在每个时段应分别使用哪些发电机才能够使每天的总成本最小?(2)如果型号2的发电机的可用数量变为6,问发电机的使用计划是否发生改变?(3)如果要求在任意时刻,正在工作的发电机组必须留出20%的发电能力余量,以防用电量突然上升,问发电机的使用计划如何?说明:同学们只需要完成第一问,其它两问作为加分项。
第十题:合理计税问题(2)充分分析该单位职工纳税的规律与特点,然后写一篇不超过800字的通俗短文,谈谈发放方案选择的要点以便于该单位的所有职工都能得到很好的指导。
(3)2011年3月1日的国务院常务会议上,原则通过了个人所得税法修正案草案,并确定了提高个人所得税起征点,以及调整级次级距的改革方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.食谱问题
某公司饲养实验用的动物以供出售。
已知这些动物的生长对饲料中的三种营养成分:蛋白质、矿物质、维生素特别敏感,每个动物每天至少需要蛋白质70g 、矿物质3g 、维生素10g ,该公司能买到5种不同的饲料,每种饲料1kg 所含营养成分如表1,每种饲料1kg 的成本如表2。
求既能满足动物生长需要,又使总成本最低的饲料配方并进行相关的灵敏性讨论。
表2:5种饲料单位重量(1kg)的成本
二.工资问题
现有一个木工,一个电工和一个油漆工,三人相互同意彼此装修他们自己的房子。
在装修之前,他们达成了如下协议:
(1)
每人总共工作10天(包括给自己家干活在内); (2) 每人的日工资根据一般的市价在60----80元之间; (3) 每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案,如何计算出他们每人应得的工
现有一个木工,一个电工和一个油漆工,三人相互同意彼此装修他们自己的房子。
在装修之前,他们达成了如下协议:
(4)每人总共工作10天(包括给自己家干活在内);
(5)每人的日工资根据一般的市价在60----80元之间;
(6)每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案,如何计算出他们每人应得的工
三.投资效益问题
一个投资公司有22亿资金可用来投资,现有6个项目可供选择,各项目所需资金和预计收益如下表:
问:选择哪几个项目投资,可使投资收益最大?
要求:1. 建立数学模型。
2. 提出一般的求解方法。
(穷举法不得分)。
