大学物理A1波动光学光栅的衍射-PPT精品文档

合集下载

《光栅的衍射》课件

《光栅的衍射》PPT课件
欢迎大家来到《光栅的衍射》PPT课件。本课件将带领你们探索光栅的神奇世界，了解衍射现象以及光栅在各个领域中的应用。
背景介绍
光栅是一种由许多等距且平行的刻槽组成的光学元件，可以用来分离和分析光的不同波长。在本节中，我们将深入研究光栅的定义、原理和结构。
光栅的衍射现象
衍射图案
实验步骤和操作
1. 准备实验装置
搭建光栅实验装置，确保光源、光栅和探测器正确设置。
2. 进行实验测量
用光栅照射光源，并使用探测器记录衍射图案和干涉条纹。
3. 测试不同波长
改变光源的波长，记录不同波长下的衍射和干涉现象。
实验结果和数据分析
衍射图案
光栅衍射图案清晰可见，条纹间距随波长变化。 1. 研究不同光源的衍射图案。 2. 计算出不同波长的衍射角度。
光栅通过衍射现象产生独特的图案，展示了光的波动性和干涉效应。
干涉条纹
不同波长的光在光栅上产生干涉，形成明暗相间的条纹，帮助我们研究光的特性。
光栅的应用
1
光谱学
光栅广泛应用于光谱学领域，用于分析光的成分和波长。
2
激光技术
光栅在激光技术中起到关键作用，用于光束展宽和光谱仪、光栅显微镜等，提供高分辨率的图像。
干涉条纹
干涉条纹清晰可见，条纹间距随波长变化。 1. 测量不同波长下的条纹间距。 2. 分析条纹的亮度和对比度。
结论和展望
通过本实验，我们深入了解了光栅的衍射现象和应用。光栅技术在科学研究和工程领域中的应用前景广阔。未来，我们可以进一步探索光栅的优化方法，研究更复杂的衍射现象，并将其应用于更多实际问题的解决。

大学物理光栅衍射完整ppt课件

2）主要公式
光栅方程： (ab)sink k01.2.3..
缺级公式：
ab d
k k'
k'
a.
a
k'1.2.103...
3）几点注意：
A）一定时，光栅常数越小，条纹越稀疏， B）d一定时，波长越大，衍射角越大。
C）当白色光入射光栅时，将产生彩色的衍射光谱。
-2级光谱 -1级光谱
非连续光谱
中央明纹
1级光谱
由明纹公式（光栅方程）：
(ab )sinkL(1 ) k01.2.3...
由单缝衍射的暗纹公式：
asink'L(2) k'1.2.3...
在同一衍射方向同时满足，
得：
ab k a k'
缺级公式：
k k'ab k 'd
a
a
. k'1.2.3...8
缺级公式：
k k' ab k' d aa
k'1.2.3...
0
f
两线谱重合 4 3
由①、 ② 1 =32/4 = 450nm
tg4=x/f ==0.1 4=5.7
sin4 tg4=0.1
代入①得：
d
= si4n14
==1.8103cm
.
15
例3．在垂直入射光栅的平行光中，有1和2两种波长。已知1的第四级光谱与2的第三级光谱恰好重合在离中央明纹5cm处。若 2=600nm，并发现2的第5级光谱线缺级，透镜的焦距f=0.5m。试问： (2) 最小缝宽? (3) 能观察到2的多少条光谱线？
2级光谱
-2级光谱
-1级光谱中央明. 纹
1级光谱

光栅衍射现象 ppt课件

(a b)sin k
将得到的K值取整，就得到

最大的K值:
kmax

(a

b)

取整
o
x
fP
一共可看到的谱线为2kmax 1 条（包括中央明纹）
在相邻暗条纹之间必定有明纹，称为次极大。相邻主极大之间有(N-2)个次极大。
当N 很大时，次极大的个数很多，在主极大明条纹之间实际上形成一片相当暗的背底。
在研究光栅问题时，主要研究主极大明纹。 PPT课件 7
3.光栅斜入射情况
两两相邻光线的光程差仍都相同。
k

(a b)sin (a b)sin
光栅衍射
PPT课件
1
一、光栅
大量等宽等间距的平行狭缝(或反射面)构成的光学元件。从工作原理分
衍射光栅 (透射光栅)
反射光栅(闪耀光栅)
光栅制作 •机制光栅：在玻璃片上刻划出一系列平行等距的划痕,刻过的地方不透光，未刻地方透光。 •全息光栅：通过全息照相，将激光产生的干涉条纹在干板上曝光，经显影定影制成全息光栅。
设1=450nm, 2=650nm, 则据光栅方程，1 和 2 的
第 2 级谱线有：
d sin 1 21 ; d sin 2 22
据上式得： 1 sin -1 2 1 d 26 .74
2 sin -1 2 2 d 40 .54
第2级光谱的宽度 x 2 - x1 f tg 2 - tg 1
通常在 1 cm 内刻有成P千PT课上件万条透光狭缝。
2
光栅常数
透光缝宽度 a
b a
不透光缝宽度 b
d
光栅常数:

光栅衍射讲稿课件

光栅衍射讲稿课件
• 光栅衍射的未来发展
光栅衍射的基本概念
光的波动性
01
光的波动性是指光在传播过程中表现出的振动和传播的特性。光波是一种横波，具有振幅、频率和波长等物理量。
02
光的波动性可以解释许多光学现象，如干涉、衍射和折射等。
光的衍射现象
光的衍射是指光在传播过程中遇到障碍物或孔隙时发生的绕射、反射和干涉等现象。
衍射现象是光的波动性的重要表现之一，它可以用来解释光的传播规律和光学元件的性能。
光栅的结构与分类
光栅是一种由许多平行、等间距的刻线组成的透射或反射元件。根据制作材料的不同，光栅可以分为玻璃光栅、金属光栅等。
光栅的刻线可以是规则的直线，也可以是曲线或其他形状。根据刻线的形状和排列方式，光栅可以分为闪耀光栅、全息光栅等不同类型。
光学通信器件
将光栅衍射技术应用于光学通信领域，开发新型的光纤通信器件和光调制器等。
光学传感仪器
利用光栅衍射技术，开发高灵敏度、高分辨率的光学传感仪器，用于环境监测和生物医学检测等领域。
光栅衍射在量子光学领域的应用
量子纠缠的产生
01
利用光栅衍射技术，设计和制备量子纠缠态，为量子信息处理
和量子计算提供基础。
光栅的衍射角计算
衍射角的定义
衍射角是指光束通过光栅后偏离原来直线方向的角度。
衍射角的计算公式
衍射角的大小与光波长、光栅常数和衍射级数等因素有关，可以通过菲涅尔衍射公式进行计算。
衍射角的影响因素
光波长越短、光栅常数越大或衍射级数越高，则衍射角越大。在实际应用中，需要根据具体需求选择合适的光波长、光栅常数和观察角度。
光学信息存储
随着信息技术的快速发展，光学信息存储技术在数据存储、档案保存等领域具有广泛的应用前景。

10-09 衍射光栅最新版物理学精品课件完美版

§10–9 衍射光栅
衍射光谱分类
连续光谱：炽热物体光谱线状光谱：钠盐、分立明线带状光谱：分子光谱光谱分析
第十章波动光学
由于不同元素（或化合物）各有自己特定的光谱，
所以由谱线的成分，可分析出发光物质所含的元素或
化合物；还可从谱线的强度定量分析出元素的含量。
上页下页返回帮助
(a b)sin k
上页下页返回帮助
§10–9 衍射光栅
讨论
光强分布
I
第十章波动光学
(a b)sin k
3
2

(a b) sin
条纹最高级数
k sin k ab
k kmax
上页
ab
下页返回帮助
§10–9 衍射光栅
一、光栅
第十章波动光学
由许多平行等距的相同的单缝构成的光学元件称为衍射光栅。
衍射角
L
E
P

o
f
上页下页返回帮助
§10–9 衍射光栅
衍射角
第十章波动光学
a
b

ab
光栅常数
(a b)sin
a ：透光部分的宽度
b
：不透光部分的宽度
光栅常数：104 ~ 106 m
§10–9 衍射光栅
三、衍射光谱
第十章波动光学
(a b)sin k
入射光为白光时，不同，k 不同，按波长分开形成光谱。
Ｋ=0(白色)
三级光谱
(k＝－3)
二级光谱 (k=－2)
一级光谱
一级光谱
（k=－1）（k=1）
二级光谱 (k=2)

《波动光学》ppt课件

物理意义
马吕斯定律是定量描述偏振光通过检偏器后透射光强与入射线偏振光和检偏器透振方向夹角之间关系的定律，是波动光学中的重要公式之一。
晶体中双折射现象解释
双折射现象
当一束光入射到各向异性的晶体时，会分成两束光沿不同方向折射的现象。
产生原因
晶体内部原子排列的规律性使得晶体具有各向异性，导致不同方向上折射率不同。
研究中的应用。
03
非线性波动光学应ห้องสมุดไป่ตู้领域
概述非线性波动光学在光通信、光计算、光信息处理等领域的应用前景。
量子波动光学发展动态
量子波动光学基本概念
阐述光的量子性质及其与波动光学的关系，包括光子、量子态、量子纠缠等。
量子波动光学研究方法
介绍量子光学实验技术、量子信息处理方法等在量子波动光学研究中的应用。
薄膜干涉实验操作
阐述薄膜干涉实验的基本原理和实验方法，包括等厚干涉和等倾干涉的实现方式及条纹特征。
衍射实验数据处理方法分享
衍射实验基本概念
解释衍射现象的产生条件和基本原理，介绍衍射光栅、单缝衍射等实验方法。
01
衍射光栅数据处理
分享衍射光栅实验的数据处理技巧，包括光栅常数、波长等参数的测量方法和误差分析。
03
复杂介质中波动光学应用领域
概述复杂介质中波动光学在生物医学成像、环境监测与治理、新能源等领域的应用前景。
06
实验方法与技巧指导
基本干涉实验操作规范介绍
干涉实验基本概念
阐述干涉现象的产生条件和基本原理，解释相干光波的概念及获得方法。
双缝干涉实验操作
详细介绍双缝干涉实验的实验装置、操作步骤和注意事项，以及双缝干涉条纹的特点和分析方法。

《光栅衍射讲》课件

前景
在光电子学、信息技术和生物医学等领域具有广阔的应用前景。
《光栅衍射讲》PPT课件
# 光栅衍射讲 PPT课件
光栅衍射是一种重要的光学现象，本课件将介绍光栅衍射的定义、应用和原理，以及光栅的构造、实验、性能指标和应用，最后总结其优缺点、未来发展和应用前景。
概述
1 光栅衍射的定义
光线通过光栅时产生的衍射现象。
2 光栅衍射的应用
用于光学、物理和化学等领域的实验和技术。
包括选择光源、调整光栅和观察衍射图
样等。
3
光栅衍射实验的注意事项
确保实验环境暗无光线干扰，准确记录实验结果。
光栅的性能指标
1 光栅的分辨率
能够区分最小特征的能力。
3 光栅的精度
与实际测量值的接近程度。
2 光栅的灵敏度
对入射光强的响应程度。
光栅衍射的应用
光栅衍射在光学中的应用
用于光谱分析、光学显微镜和激光技术等。
3 光栅衍射的原理
光波在光栅上的相位差导致光栅衍射。
光栅构造
光栅的结构
由一系列平行的凸起或凹陷的平行线组成。
光栅的类型
包括均匀光栅、非均匀光栅和衍射光栅等。
光栅参数的影响
包括光栅常数、光栅间距和光栅材料等。
光栅衍射的实验
1
光栅衍射实验的原理
通过光线通过光栅时产生的衍射现象来
光栅衍射实验步骤
2Leabharlann 验证光栅的特性。光栅衍射在物理中的应用
用于材料研究、波动力学和量子力学等。
光栅衍射在化学中的应用
用于表征化学物质的结构和分子间相互作用。
总结
1 光栅衍射的优缺点
提高光栅衍射的分辨率和灵敏度，但需要精确控制光栅参数。

光栅衍射现象课件

光栅衍射现象的应用领域不断拓展，未来需要进一步探索其在生物医学、环境监测、安全检测等领域的应用潜力。
提高测量精度和稳定性
光栅衍射现象的测量精度和稳定性是影响其应用的重要因素，未来需要加强这方面的研究和改进。
加强交叉学科合作
光栅衍射现象涉及到多个学科领域，如物理学、化学、材料科学等，未来需要加强交叉学科的合作与交流，推动光栅衍射现象的深入研究和应用拓展。
物分子。
光谱仪制造
光栅衍射现象是光谱仪的核心技术之一，用于制造高精度和高灵
敏度的光谱分析仪器。
05
光栅衍射现象的未来发展
新材料的应用
新型光栅材料
随着材料科学的不断发展，新型光栅材料如氮化硅、碳化硅等具有更高的热稳定性和化学稳定性，能够提高光栅的耐久性和可靠性。
光栅制造技术的改进
利用纳米制造技术，可以制造出更精细、更密集的光栅，提高衍射效率，改善光谱分辨率。
激光技术
其他领域
光栅可以用于激光谐振腔的设计和控制，以及激光的频率稳定和调谐等方面。
光栅衍射还应用于天文学、生物学、医学和环境监测等领域，为科学研究和技术创新提供了重要的工具和手段。
02
光栅衍射现象的基本原理
光的波动理论
01
02
03
光的波动性质
光波在空间中传播时，会形成波动，具有振幅、波长、频率等属性。
新技术的探索
光栅数字化技术
随着数字化技术的不断发展，光栅数字化技术成为新的研究热点。通过将光栅转化为数字信号，可以实现更快速、更准确的测量和数据处理。
光栅光学系统的优化
通过对光栅光学系统的优化设计，可以改善光线的入射角度、光强分布等因素，提高光栅的成像质量和稳定性。

大学高等物理课件光的衍射_光栅衍射(1)

第五讲光的衍射_光栅衍射_20140220 XCH
波动光学－大学物理
02 光栅衍射条纹
—— N条缝发出光在P点的叠加 N个子光源在 P点引起的振动便是 N个振幅相等，频率相同，相邻两个振动位相差

2
的简谐振动的合成。讨论： i. 明纹（主极大或主明纹）当 2k 时，d sin k —— N条缝发出光在P点的叠加是干涉相长__亮条纹
第五讲光的衍射_光栅衍射_20140220 XCH
05 / 33
波动光学－大学物理
02 光栅衍射条纹
讨论： ii. 暗纹（以光栅缝数N=6为例）
第五讲光的衍射_光栅衍射_20140220 XCH
波动光学－大学物理
02 光栅衍射条纹
讨论： ii. 暗纹（以光栅缝数N=6为例）当光矢量组成的多边形封闭时，合矢量为零，对应为暗纹

d sin
第五讲光的衍射_光栅衍射_20140220 XCH
波动光学－大学物理
多缝干涉明条纹也称为主极大明纹。 k=0，为零级主极大 k=1，为第一级主极大，其余依次类推。
主极大位置的方程 d sin k
—— 光栅方程
k 0, 1, 2,
第五讲光的衍射_光栅衍射_20140220 XCH
波动光学－大学物理
P点光的振幅
A A1 A2 A3 AN
如果各缝光的振幅相同
A1 A2 A3 AN A0 A NA0
亮条纹的强度 I N I 0 N 2 I 0 I 0
2
2 I 0 A0
多缝干涉是多个光矢量在空间的叠加。可以用N个相位差相同的振幅大小相同的振幅矢量的叠加来表示。

《衍射光栅衍射》课件

波动方程
描述光波传播的数学方程，通过求解波动方程可以预测光波的传播路径和强度分布。
波动理论的应用
解释了光的干涉、衍射等现象，为光栅衍射提供了理论基础。
光的干涉和衍射
光的干涉
干涉和衍射的区别与联系
当两束或多束相干光波相遇时，会形成稳定的加强或减弱区域的现象。
两者都是光波的波动性质的表现，但产生条件和表现形式有所不同。
衍射光栅的衍射原理是基于光的波动性和干涉现 02 象，通过多缝干涉实现光的衍射。
衍射光栅具有较高的色散率和较大的衍射角度， 03 广泛应用于光谱分析和光学仪器中。
学习重点和难点
01
学习重点
衍射光栅的原理、结构和工作方式，以及其在光谱分析和光学仪器中的应用。
02
学习难点
理解光的波动性和干涉现象，掌握衍射光栅的数学模型和计算方法。
光源
提供单色光，常用氦氖激光器。
屏幕
接收衍射光，呈现衍射图样。
光栅
由许多等宽、等间距的平行狭缝组成，是实验的核心部分。
光学仪器
包括透镜、反射镜等，用于调整光路和聚焦。
实验操作步骤
开启光源，预热
确保光源稳定输出。
调整光路
使用光学仪器，确保光束准直并照射到光栅上。
放置屏幕，调整距离
将屏幕置于光栅后方，适当调整屏幕与光栅的距离，以便清晰观察衍射图样。
数值计算
使用数学软件（如MATLAB、Python等）进行数值计算，如傅里叶变换、最小二乘法等，以提取更多有用的信息。
误差分析和不确定度评估
误差来源分析
分析实验过程中可能引入误差的来源，如光源的稳定性、测量设备的精度、环境因素等。
不确定度评估

光栅衍射讲稿PPT课件

方向上，求此光栅的光栅常数d。
解： d sin 1 k11 d sin 2 k22
sin 1 k11 2k1 sin 2 k22 3k2
两谱线重合，1
，所以
2
k1 k2
3 2
6 4
第二次重合k1=6,k2=4
d sin 600 61 d 3.05 103 mm
第三十三页，共39页。
例、波长为6000Å的单色光垂直入射在一光栅上，测得第二级主极大的衍射角为300，且第三级是缺级，求：
入射光线与衍射光
线在光栅平面法线的同侧取“+” 号，异侧时取“-” 号。
相邻两缝的入射光在入射到光栅平面上时已有光程差
(a+b)sin
(a+b)(sin +sin)=k k=0,±1, ±2, ±3 ···
第二十二页，共39页。
入射光线与衍射
(a+b)sin
光线在光栅平面法线的同侧取
“+”号，异侧时
是哪些级次？
解: (1) (a b) sin k
(a b) k 6m sin
(2)k (a b) k k 4, 取k 1 a
amin
a
4
b
1.5m
b d amin 4.5m
第三十五页，共39页。
例、波长为6000Å的单色光垂直入射在一光栅上，第二级主明纹和第三级主明纹分别出现在满足下式的方向上： sin2=0.2、 sin3=0.3 ，第4级为缺级。求：(1)光栅常数是多少？(2)狭缝的最小可能宽度是多少？ (3)按上述选定的a、b值，实际上能观察到的全部明纹数是多少？
第三十六页，共39页。
例、用波长为=590nm的单色光垂直照射在每毫米米刻有500条缝的光栅上，在光栅后放置一焦距f=0.2m的会聚透镜，求：（1）

《光栅的衍射》PPT课件

3
E1
E0
k"=3 k=1
d
e
3/4
3/2
E1
E4 E2 E3
2
E1 E3
E2 E4
E 0 E( ) 4E0( )
主极大矢量图：
A1 A2 A3 A4 A5 A6
0、2、4、
极小矢量图： ( N=6 )
A4
A5
A3
A6 A1 A2
3
632 5
1
4
2 3
4
2 4 6
1
1
3 5
a sin d sin
-5 -4 -2 -1 0 1 2
45
d sin
二、光栅衍射条纹的形成
1. 光栅衍射的图样
光栅衍射多缝干涉（多光束干涉）和单缝衍射的总效果。
因此，光栅衍射图样是多缝干涉光强分布受单缝衍射光强分布调制的结果。
例如：5条缝的光栅衍射(N=5， I d=3a)
单缝衍射光强分布
3 6
2
5
4 3
1
6
2
5
3
4
5 3
4. 缺级现象单缝衍射光强分布
-2
-1
5条光束干涉光强分布
I
5条缝的光栅衍射(N=5,d=3a)
0
1
I
a sin
2
I 光栅衍射光强分布
缺级
d sin
缺级
d sin
-5 -4
-2 -1 0 1 2
45
缺级的定量计算:
dsinθ kλ asinθ kλ
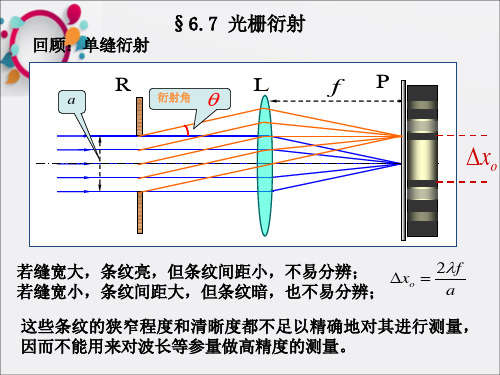
§6.7 光栅衍射
回顾：单缝衍射
R
L
a
衍射角

波动光学光的衍射PPT课件

于可见光波长的 10万分之一到 50 分之一。
42
劳厄的 X 射线衍射实劳验厄原理斑图
晶体
（硫化铜）
记
录
X 射
干板
线
衍射斑纹（劳厄斑）
晶体中有规则排列的原子，可看作一个立体的光栅。原子的线度和间距大约为10 - 10 m 数量级，根据前述可见光的光栅衍射基本原理推断，只要入射X 射线的波长与此数量级相当或更小些，就可能获得衍射现象。
波长 1,2 两谱线的间距为 l ，则
（1）l 随 f 的增大而增大
（2）l 随 f 的减小而减小；
（3）l 与 f 的大小无关；
（4） l 随参加衍射的总缝
数 N 的增大而增大
59
End
请在放映状态小下议点击链你认接为4是对的答案
若光栅常量 (ab) 一定，在光栅后观察衍射光谱的透镜焦距为 f ，在第二纹光谱中测得
66
谢谢您的观看与聆听
Thank you for watching and listening
67
X射线衍射 X ray diffraction
3
4
衍射现象
第一节
3-4-1 Huygens-Fresnel principle
5
惠菲原理
根据这一原理，原则上可计算任意形状孔径的衍射问题。本章的重点不是具体解算上述积分，而是运用该原理有关子波干涉的基本思想去分析和处理一些典型的衍射问题。 6
两类衍射
7
条件实现
8
第二节
3-4-2 single slit diffraction
9
单缝衍射
夫琅禾费单缝衍射基本光路
10
衍射图样
11

大学物理波动光学 (12)

由此可得斜入射时的光栅方程为
(a b)(sin sin ) k k 0, 1, 2
同样，k的可能最大值相应于 sin 1
在O点上方观察到的最大级次为 k1，取 90 得
k 1.70取 k 1 (ab)(sin90 sin 30 ) 2106 (10.5)
（3）对光栅公式两边取微分
(a b) coskdk kd
光栅光谱
波长为及 d 第k级的两条纹分开的
角距离为
d d k k (a b) cos k
光线正入射时，最大级次为第3级，相应的角
位置3 为
3

sin1
(
k
ab
)

sin ( ) 1 3589.3109 2106
钠光谱线（ 589.3 nm），问
（1）平行光线垂直入射时；（2）平行光线以入射角30入射时，最多能看见第几级条纹？总共有多少条条纹？
（3）由于钠光谱线实际上是 1 589.0nm及 589.6nm
两条谱线的平均波长，求在正入射时最高级条纹此双线分开的角距离及在屏上分开的线距离。设光栅后透镜的焦距为2m.
光栅光谱
（2）如平行光以角入射时，光程差的计算公式
应做适当的调整，如图所示。在衍射角的方向上，光程差为
P
A
O
B
斜入射时光栅光程差的计算
A

C
D B
光栅光谱
BD AC （a b）sin (a b) sin (a b)(sin sin )
a
I0单 I单
-2
-1
光栅衍射光强曲线
0
1

11-09衍射光栅PPT精品文档30页

( b b ')(s s iin i ) n k ( b b ')(s s iii n ) n k
k0,1,2,3,
A
i
Ci D
B
900 km上(bb)'(1sini)
i
A
Ci D
B
900km下(bb)'(-1sini)
§11-9 衍射光栅干涉和衍射的区别
没有本质的区别！
习惯上说，干涉是指那些有限多的分立的光束的相干叠加；
（ⅱ）若 N2k则 A0 （极小）
其中 k ' 1 ,2 ,3 , N 1 ,N 1 ,N 2
且 k'N,2N,3N
即在两个主极大间有N-1 个极小
（ⅲ）在 N-1极小之间，必有 N-2个次极大
§11-9 衍射光栅
I N=5
o
2 (N 1)
NN
N
主极大地半角宽度是多少？
(b+b')sin
b ：透光部分的宽度
b ' ：不透光部分的宽度
光栅常数：1 05~1 06m
讨论
§11-9 衍射光栅
( b b ') si n k ( k 0 ,1 ,2 , )
（1）光栅衍射条纹是以中央明纹（θ=0）为中心，两侧对称分布各级明条纹
（2）光栅衍射明纹亮度高、条纹窄，当 N 很大时，
明条之间为一暗区
当光垂直入射到光栅时，发现在24.46°角度处，红蓝谱线同时出现。（1）在什么角度下红蓝谱线再次同时出现；（2）在什么角度下只有红谱线出现。
解： bb'1m/m 300
（1）由在 24.46°角度处，红蓝谱线同时出现得
( b b ')si n 1 3 m s 02 m i0 .4 n 4 6 K RR K BB( 1 )