勾股定理1

合集下载

人教版八年级数学下册_第一节《勾股定理》勾股定理

下列说法中,正确的是
（
）
下列说法中,正确的是
（
）
2.你还有什么疑问，问问老师。通过前面的探究活动，你发现了直角三角形三边之间的关系规律了吗？
（1）若a=6，b=8，则c=
.
通过前面的探究活动，你发现了直角三角形三边之间的关系规律了吗？
在Rt△ABC中，∠C=90°.
思考：在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系？观察下边两幅图(每个小正方形的面积为单位1)：
1.本节课你有什么收获？你学到了什么？在Rt△ABC中，∠C=90°，a=6，c=10，则b=
.
通过前面的探究活动，你发现了直角三角形三边之间的关系规律了吗？
思考正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？
说给大家听听。如果直角三角形两直角边长分别为a，b，斜边长为c，那么a2+b2=c2．
（2）若c=13，b=12，则a=
.
在Rt△ABC中，两直角边长分别为3和，则斜边长为
.
第1课时勾股定理
思考：在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系？观察下边两幅图(每个小正方形的面积为单位1)：
9
13
右图 16
9
25
Hale Waihona Puke 思考正方形A、B、C 所围成的直角三角形三条边之间有怎样的特殊关系？
通过前面的探究活动，你发现了直角三角形
在Rt△ABC中，∠C=90°.
三边之间的关系规律了吗？在Rt△ABC中，两直角边长分别为3和，则斜边长为
.
已知a,b,c是三角形的三边，则a2+b2=c2

9-勾股定理1

勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一，其主要应用：
（1）已知直角三角形的两边求第三边（在中，，则，，）
（2）已知直角三角形的一边与另两边的关系，求直角三角形的另两边
（3）利用勾股定理可以证明线段平方关系的问题
【典型例题】
题型一：勾股定理的判定
例1:已知一个三角形的周长为12，其中两边长分别为3和4，则此三角形是（）三角形。
（2）.在 ABC中，若 =（ + ）（ - ），则 ABC是三角形，且 .
小试牛刀：
1、已知与互为相反数，试判断以、、为三边的三角形的形状。
2、.若 ABC的三边、、满足条件，试判断 ABC的形状。
3.已知则以、、为边的三角形是
例4：已知如图，在△ABC中，∠C=60°，AB= ，AC=4，AD是BC边上高，求BC的长。
4、如图，直线上有三个正方形，若的面积分别为5和11，则的面积为（）
（Ａ）4（Ｂ）6（Ｃ）16（Ｄ）55
5、一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.如图，火柴盒的一个侧面倒下到的位置，连结，设，请利用四边形的面积证明勾股定理： .
6、（2010年辽宁省丹东市）图①是一个边长为的正方形，小颖将
A、25海里B、30海里C、35海里D、40海里
3.勾股定理与勾股定理逆定理的区别与联系
区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理；
联系：勾股定理与其逆定理的题设和结论正好相反，都与直角三角形有关。
【典型例题】
题型一：直接考查勾股定理及逆定理
例1.在中中，
⑴已知，．求的长⑵已知，，求的长分析：

直角三角形-勾股定理1上海学

第讲勾股定理知识点睛1、勾股定理：如果直角三角形的两直角边上分别为a, b ，斜边长为c ，那么222a b c +=。

即直角三角形两直角边的平方和等于斜边的平方。

2、勾股定理的逆定理：如果三角形的三边长a 、b 、c 满足222a b c +=，那么这个三角形是直角三角形。

3、勾股定理的证明方法：法1（赵爽：内弦图）：甲的面积=（大正方形面积）-（4个直角三角形面积）．法2（赵爽：外弦图）：：四个直角三角形的面积和 +小正方形的面积 =大正方形的面积，222()ab a b c +-=，22222ab a ab b c +-+=，∴222a b c +=法3（美国第20任总统伽菲尔德的证法）：2111()()2222a b a b ab c ++=⨯+ 梯形面积=三个直角三角形的面积和22()2a b ab c +=+ 22222a ab b ab c ++=+∴222a b c +=法4（毕达哥拉斯的旋转证法）：若设AB=a ，BC=b ，DB=c ，则梯形A′B′BC 面积()()()21122S a b a b a b =++=+梯形ABBC ，又"""2111222BCD A B D DBB S S S S ab c ab ∆∆∆=++=++""梯形A B BC ，所以()2211112222a b ab c ab +=++，则22222a b ab c ab ++=+，即222a b c +=。

甲c ccbababa cb acb acb aab ca bcb-ab-acc cc甲丙乙ab cabc法5（新娘图法）：用方格来验证勾股定理法6（欧几里得证法）：如图2-16所示．在Rt△ABC的外侧，以各边为边长分别作正方形ABDE，BCHK，ACFG，它们的面积分别是c2，a2，b2．下面证明，大正方形的面积等于两个小正方形的面积之和．过C引CM∥BD，交AB于L，连接BG，CE．因为AB=AE，AC=AG，∠CAE=∠BAG，所以△ACE≌△AGB(SAS)．而所以 S AEML=b2，同理可证 S BLMD=a2．相加得S ABDE=S AEML+S BLMD=b2+a2，即 c2=a2+b2．法7：如图2-18．在直角三角形ABC的斜边AB上向外作正方形ABDE，延长CB，自E作EG⊥CB延长线于G，自D作DK⊥CB延长线于K，又作AF， DH分别垂直EG于F，H．由作图不难证明，下述各直角三角形均与Rt△ABC全等：△AFE≌△EHD≌△BKD≌△ACB．设五边形ACKDE的面积为S，一方面S=S ABDE+2S△ABC，另一方面S=S ACGF+S HGKD+2S△ABC，相加得所以 c2=a2+b2．练习：用下面各图验证勾股定理(虚线代表辅助线)：（1）赵君卿图(图2-27)； (2)项名达图(2-28)； (3)杨作枚图(图2-29)．CBA3、由勾股定理的基本关系式222a b c +=，还可得到一些变形关系式如：22c a b =+，222()()a c b c b c b =-=+-，22a c b =-，222()()b c a c a c a =-=+-，22b c a =-等。

《勾股定理》PPT优质课件(第1课时)

A． 3
B．3
C． 5
D．5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的
长为（ C）
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则
另一直角边长为（ A ）
A.8
B.40
C.50
D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则 a= _6_0___，b = __8_0___.
课堂检测
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面积之和为_____4_9_____cm2 ．
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：
当AB为斜边时，如图，BC 42 32 7;
形，拼成一个新的正方形.
探究新知剪、拼过程展示：
b
a ca
朱实
b 朱实黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实朱实
a
朱实
证明：∵S大正方形＝c2， S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
探究新知
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图示进行拼图，然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152，

第1讲勾股定理

第1讲勾股定理第一部分知识梳理1．勾股定理：直角三角形的两直角边的平方和等于斜边的平方。

若直角三角形的两条直角边为a 、 b ，斜边为c ，则a ²+b ²=c ²。

2．勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a ²+b ²=c ²，那么这个三角形是直角三角形。

3．满足a ²+b ²=c ²的三个正整数，称为勾股数。

若a ，b ，c 是一组勾股数，则ak ，bk ，ck （k 为正整数）也必然是一组勾股数。

常用的几组勾股数有3,4,5；5,12,13；6,8,10；7,24,25；8,15,17；9,40,41等。

4．勾股定理的应用:①圆柱形物体表面上的两点间的最短距离；②长方体或正方体表面上两点间的最短距离问题。

5．直角三角形的判别：①定义，判断一个三角形中有一个角是直角；②根据勾股定理的逆定理，三角形一边的平方等于另外两边的平方和，则该三角形是直角三角形。

6．勾股定理中的方程思想：勾股定理三角形有一个直角的“形”的特征，转化为三边“数”的关系，因此它是数形结合的一个典范．对于一些几何问题，往往借助于勾股定理，利用代数方法来解决．把一条边的长设为未知数，根据勾股定理列出方程，解方程求出未知数的值，即使有时出现了二次方程，大多可通过抵消而去掉二次项。

7．勾股定理中的转化思想：在利用勾股定理计算时，常先利用转化的数学思想构造出直角三角形，比如立体图形上两点之间的最短距离的求解，解答时先把立体图形转化为平面图形，在平面图形中构造直角三角形求解。

8．拓展：特殊角的直角三角形相关性质定理。

第二部分精讲点拨知识点1：勾股定理勾股定理内容：直角三角形两条直角边的平方和等于斜边的平方。

用数学语言描述：在RT △ABC 中，∠C=90°，AB=c ，AC=b ，BC=a ，则有222b a c +=. 勾股定理的变形公式：222222,a c b b c a -=-=直角三角形认识：直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦，“勾股定理”因此而得名.注意：1.勾股定理适用于任何一个直角三角形；2.勾股定理的内容描述的是直角三角形三边之间的数量关系，已知其中的任意两边可以求出第三边；题型1（利用勾股定理求第三边）【例1】在RT △ABC 中，∠C=90°，∠A 、∠B 、∠C 的对边分别是a 、b 、c . （1）已知8=a ，6=b ，求c ；（2）已知13=c ，12=b ，求a ；弦股勾（3）已知3:4:=b a ，5=c ，求b .变式训练：1.若直角三角形的两直角边长分别为3和4，则斜边上的高是（）A ．5B ．2.4C ．3.6D ．以上答案都不对 2.填空：（1）在RT △ABC 中，∠C=90°，5=a ，12=b ，则c = ；（2）在RT △ABC 中，∠B=90，3=a ,4=b ,则=2c ；（3）在RT △ABC 中，∠C=90°，∠A=45°，则222::c b a = ；3. 如图,已知直角三角形ABC 的两直角边AC,BC 的长分别为4cm,3cm,求斜边AB 上的高CD 的长.题型2（勾股定理的证明）【例2】如图：由四个全等直角三角形拼成如下大的正方形，求证：222a b c +=变式如图：由四个全等直角三角形拼成如下大的正方形，求证：222a b c +=小结：BAC D题型3（勾股定理的应用）勾股定理是直角三角形的一个重要性质.利用勾股定理，可以解决直角三角形的有关计算和证明问题，还可以解决生活生产中的一些实际问题.【例4】如图，铁路上A ，B 两点相距25km ，C ，D 为两村庄，DA ⊥AB 于A ，CB ⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个土特产品收购站E ，使得C ，D 两村到E 站的距离相等，则E 站应建在离A 站多少km 处？变式1 飞机在空中水平飞行，某一时刻刚好飞到一个男孩子头顶上方4000米处，过了20秒，飞机距离这个男孩子头顶5000米，飞机每小时飞行多少千米？变式2 一个25m 长的梯子AB ，斜靠在一竖直的墙AO 上，这时的AO 距离为24m ，如果梯子的顶端A 沿墙下滑4m ，那么梯子底端B 也外移4m 吗？变式3 如图，某学校（A 点）与公路（直线L ）的距离为300米，又与公路车站（D 点）的距离为500米，现要在公路上建一个小商店（C 点），使之与该校A 及车站D 的距离相等，求商店与车站之间的距离．变式4 如图，A 市气象站测得台风中心在A 市正东方向300千米的B 处，以107千米/时的速度向北偏西60°的BF 方向移动，距台风中心200•千米范围内是受台风影响的区域．（1）A 市是否会受到台风的影响？写出你的结论并给予说明；（2）如果A 市受这次台风影响，那么受台风影响的时间有多长？题型4（特殊角的直角三角形）【例3】已知：如图，在△ABC 中，90ACB ∠=，10AB cm =，8BC cm =，CD AB ⊥于D ，求CD 的长．C变式1 如图，已知：︒=∠=∠90C ABD ，12=AD ，BC AC =，︒=∠30DAB ，求BC 的长．变式2 如图，△ABC 中，AB ＞AC ，AD 是BC 边上的高．求证：AB 2-AC 2=BC(BD-DC)．知识点2. 直角三角形的判定1. 有一个角为90度的三角形是直角三角形2. 勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a ²+b ²=c ²，那么这个三角形是直角三角形（注意a,b,c 只是代表直角边，只要意义不变字母可以变动）题型1（判别直角三角形）【例5】三角形的三边为a 、b 、c ，由下列条件不能判断它是直角三角形的是（） A ．a :b :c=8∶16∶17 B ． a 2-b 2=c 2C ．a 2=(b+c)(b-c)D ． a :b :c =13∶5∶12 变式1 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A . 等边三角形B . 钝角三角形C . 直角三角形D . 锐角三角形.变式2 已知，△ABC 中，17AB cm =，16BC cm =，BC 边上的中线15AD cm =，试说明△ABC 是等腰三角形．A变式3 如图，在正方形ABCD 中，F 为DC 的中点，E 为BC 上一点，且EC=41BC ，求证：AF ⊥EF ．题型2（勾股定理及其逆定理应用）【例6】一个零件的形状如图，已知∠A=900，按规定这个零件中∠DBC 应为直角，工人师傅量得零件各边尺寸：AD = 4，AB = 3, BC = 12 , DC=13，问这个零件是否符合要求，并求四边形ABCD 的面积．变式1 如图示，有块绿地ABCD ，AD=12m ，CD=9m ，AB=39m ，BC=36m ， ∠ADC=90°，求这块绿地的面积。

勾股定理1

F D A E
75 45 M
B C
图1.1-1 图1.1-2 6. 如图如图1.1-2,在四边形在四边形ABCD中, ∠ BAD=90°, 在四边形中 ° 求正方形DCEF ∠ CBD=90°,AD=4,AB=3,BC=12,求正方形 ° 求正方形的面积. 的面积
飞机在空中水平飞行，例3 飞机在空中水平飞行，某一时刻刚好飞到一个男孩头顶正上方4000米处，过了秒，飞米处，一个男孩头顶正上方米处过了20秒机距离这个男孩5000米，飞机每小时飞行多少机距离这个男孩米千米？千米？
2= b
2 c
c
b
a
赵爽弦图的证法
S大正方形 = S小正方形 + 4S直角三角形 ab c = (b − a) + 4 ⋅ 2
2 2
朱实中黄实 c b a b- a) ( b- a) 2
化简得：化简得：
c2 =a2+
b2．
学以致用，做一做 y=0
1.求下列图中字母所代表的正方形的面积：求下列图中字母所代表的正方形的面积：
相传在2500年前，毕达哥拉斯有年前，毕达哥拉斯有相传在年前一次在朋友家做客时，一次在朋友家做客时，发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系，边的某种数量关系，我们一起来观察图中的地面，看看能发现什么。图中的地面，看看能发现什么。
毕达哥拉斯 (公元前公元前572----前492年), 公元前前年古希腊著名的哲学家、古希腊著名的哲学家、数学家、天文学家。数学家、天文学家。
因此，因此，
AC =
5 ≈ 2 .236 .
ＤＣ
因为AC大于木板的宽，大于木板的宽，所以木板能从门框内通过。所以木板能从门框内通过。

【数学课件】勾股定理(1)

同学们,再见
1、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力，而没有自我教育就不能想象会有完美的精神生活。我认为，教会学生自己教育自己，这是一种最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间ห้องสมุดไป่ตู้人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方，儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲，最大的乐趣就在于：在其有生之年，能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情，就是爱。教育没有了情爱，就成了无水的池，任你四方形也罢、圆形也罢，总逃不出一个空虚。班主任广博的爱心就是流淌在班级之池中的水，时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么，但它能启发儿童创造力以从事于创造工作。——陶行知

八上-第一章勾股定理

第一章勾股定理第1课时认识勾股定理1 我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称弦·直角三角形三边之间的关系称为勾股定理。

2 勾股定理是指直角三角形两直角边的平方和等于边的平方．如果用a，b和c分别表示直角三角形的两直角边和斜边，那么 a2＋b2＝c2 。

预学感知在Rt△ABC中，∠B＝90°，AC＝10，AB＝6，则则BC的长为。

知识点一勾股定理的认识【例1】在△ABC中，∠ACB＝90°，∠A，∠B，∠C的对边分别为a，b，C．当a＝9，c＝41时，则b= 。

【名师点拔】由于∠ACB＝90°，则有a2＝c2，因而只需把已知数据代入相应字母，即可求出第三条线段的长。

知识点二勾股定理的简单运用【例2】如图，△ABC中，∠ACB＝90°，AC=7，BC=24，CD⊥AB于点D。

求：（1）AB的长；（2）CD的长。

【名师点拔】由于△．ABC为直角三角形，就可先由匀股定理理求出AB，再根据面积求出CD的长。

1．已知直角三角形中两条边长，要弄清哪条是斜边，哪条是直角边，不能确定时，要分类讨论；2．在直角三角形中求斜边上的高，一般是借助面积这个中间量，21ab=21ch 。

1．在Rt △ABC 中，两直角边长分别为10和24，则斜边长等于（）A.25B.26C.27D.282．在Rt △ABC 中，斜边长BC ＝3，则AB 2＋AC 2＝。

3. 如图，分别以直角三角形的三边为边向外作正方形，则正方形A 的面积是，B 的面积是。

4. 要登上某建筑物，靠墙有一架梯子，底端离建筑物5m ，顶端离地面12m ，则梯子的长度为。

5. 如图，有两棵树，一棵高12m ，另一棵高6m ，两树相距8m ，一只鸟从一棵树的树梢飞到另一棵树梢，则小鸟至少飞行 m 。

6. 某天我国海监船驶向钓鱼岛海域执法时，海监船甲以15海里/时的速度离开港口向北航行，海监船乙同时以20海里/时的速度离开港口向东航行，则它们离开港口2h 后相距海里。

勾股定理(一)

国家之一。早在三千多年前，我国是最早了解勾股定理的
国家之一。早在三千多年前，国家之一。早在三千多年前，周国家之一。早在三千多年前，朝数学家商高就提出，将一根直国家之一。早在三千多年前，尺折成一个直角，如果勾等于三，国家之一。早在三千多年前，股等于四，那么弦就等于五，即国家之一。早在三千多年前， “勾三、股四、弦五”，它被记国家之一。早在三千多年前，载于我国古代著名的数学著作国家之一。早在三千多年前《周髀算经》中。
勾股世界
两千多年前，古希腊有个哥拉两千多年前，古希腊有个毕达哥拉斯斯学派，他们首先发现了勾股定理，因此学派，他们首先发现了勾股定理，因此在在国外人们通常称勾股定理为毕达哥拉斯国外人们通常称勾股定理为毕达哥拉斯定定理。为了纪念毕达哥拉斯学派， 1955 理。为了纪念毕达哥拉斯学派， 1955年年希腊曾经发行了一枚纪念票。希腊曾经发行了一枚纪念邮票。
2
a2 + b2 + 2ab = c2+2ab
b a
c
b
a
可得: a2 + b2 = c2
大正方形的面积该怎样表示?
汉代赵爽的证法
c b a
c2 = b2 + a2
b
c
c b
a
a
1 方法(一): (a b)(a b) 2
对比两种方法, 1 1 方法(二): 2 ab c c 你能得到什么?
SA+SB=SC c
Aa
C
A a
B b
图乙
c C
b B
图甲图甲图乙 4 9 A的面积 4 16 B的面积 C的面积 8 25 SA+SB=SC

人教版初中八年级下册数学课件《勾股定理》1(第1课时)

弦
即：勾2+股2=弦2
股
在我国又称商高定理，在外国则叫毕达哥拉斯定理，或百牛定理.
公式变形：
a c2 -b2 , b c2 -a2 c a2 b2
a、b、c为正数
典例精析
例1在Rt△ABC中，∠C=90° （1）已知a=b=5,求c; （2）已知a=1,c=2,求b;
解： (1)据勾股定理得
积. 某学习小组经过合作交流，给出了下面的解题思路， A
请你按照他们的解题思路完成解答过程.
作AD⊥BC于D, 设BD=x,用含x的代数式表示CD
根据勾股定理，利用AD作为“桥梁”建立方程模型求出x
B
DC
利用勾股定理求出AD的长，再计算三角形面积
解：如图，在△ABC中，AB=15,BC=14,AC=13, 设BD=x,则CD=14-x,
即 c2=4×12 ab+(b-a)2, c2=2ab+a2-2ab+b2
所以 a2+b2=c2.
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数学的骄傲.因为，这个图案被选为2002年在北京召开的国际数学大会的会徽.
朱实
赵爽
黄
弦c b 实
图
a
赵爽所用的这种方法是我国古代常用的“出入相补法”.在西方，人们称勾股定理为毕达哥拉斯定理.
问题1试问A、B、C面积之间有什么样的数量关系？
毕达哥拉斯
+ = 正方形A
的面积
正方形B 的面积
正方形C 的面积
AB C
问题2你能发现图中的等腰直角三角形有什么性质吗？
AB C
一直角边2 + 另一直角边2 = 斜边2

17.1.1勾股定理课件(45张)

大正方形的面积可以表示为 (a+b)2 ；
c a
b
c a
b
也可以表示为
c2
+4•
ab 2
∵ (a+b)2
c2
+4•
ab 2
= a2+2ab+b2 = c2 +2ab
c a
b
c a
b
∴a2+b2=c2
美国总统的证明
伽菲尔德经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法．1876年4月1日，伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。 1881年，伽菲尔德就任美国第二十任总统后，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就称这一证法称为“总统”证法。
章前图中左下角的图案有什么意义？为什么选它作为2002年在北京召开的国际数学家大会的会徽？
本章我们将探索并证明勾股定理及其逆定理，并运用这两个定理去解决有关问题，由此可以加深对直角三角形的认识。
读一读勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角三角形，如果勾等于三，股等于四，那么弦就等于五。即 “勾三、股四、弦五”。故称之为“勾股定理”或“商高定理” 。图1-1称为“弦图”，最早是由公元前3世纪我国汉代的数学家赵爽在为《周髀算经》注解时给出的. 赵爽利用它来证明勾股定理。在这本书中的另一处，还记载了勾股定理的一般形式。
C A C的面积怎么求呢？
S正方形c
=
72
-4×
1 2
×4×3
25 （面积单位）
B
C

勾股定理 1

a b c
2 2
2
赵爽弦图证明勾股定理.gsp
总统巧证勾股定理
学过几何的人都知道勾股定理．它是几何中一个比较重要的定理，应用十分广泛．迄今为止，关于勾股定理的证明方法已有500余种．其中，美国第二十任总统伽菲尔德的证法在数学史上被传为佳话．总统为什么会想到去证明勾股定理呢？难道他是数学家或数学爱好者？答案是否定的．事情的经过是这样的： 1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德．他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨．由于好奇心驱使伽菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么．只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形．于是伽菲尔德便问他们在干什么？只见那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”伽菲尔德答到：“是5呀．”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”伽菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方．”小男孩又说道：“先生，你能说出其中的道理吗？”伽菲尔德一时语塞，无法解释了，心理很不是滋味．于是伽菲尔德不再散步，立即回家，潜心探讨小男孩给他留下的难题．他经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法．
百牛定理
毕达哥拉斯（Pythagoras，前572～前497），西方理性数学创始人，古希腊数学家，他是公元前五世纪的人，比商高晚出生五百多年．
“勾股定理”在国外，尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”．毕达哥拉斯有一次应邀参加一位富有政要的餐会，这位主人豪华宫殿般的餐厅铺着是正方形美丽的大理石地砖，由于大餐迟迟不上桌，这些饥肠辘辘的贵宾颇有怨言．毕达哥拉斯却凝视脚下这些排列规则、美丽的方形磁砖，这位善于观察和理解的数学家不只是欣赏磁砖的美丽，而是想到它们和数之间的关系，于是拿了画笔并且蹲在地板上，选了一块磁砖以它的对角线为边画一个正方形，他发现这个正方形面积恰好等于两块磁砖的面积和．他很好奇，于是再以两块磁砖拼成的矩形之对角线作另一个正方形，他发现这个正方形之面积等于5块磁砖的面积，也就是以两股为边作正方形面积之和．至此毕达哥拉斯作了大胆的假设：任何直角三角形，其斜边的平方恰好等于另两边平方之和．那一顿饭，这位古希腊数学大师，视线都一直没有离开地面，就这样毕达哥拉斯也发现了勾股定理．

勾股定理1全面版

勾股定理
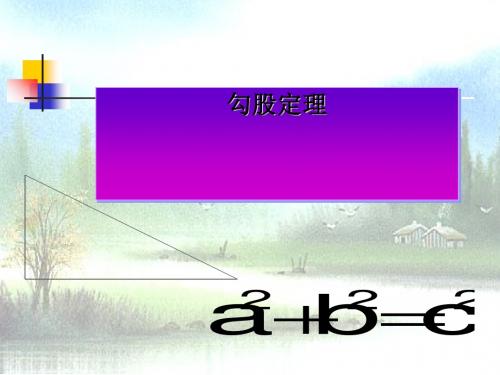
a2b2c2
定理和证明
勾股定理直角三角形两直角边的a、 b的平方和，等于斜边c的平方。
a2b2c2
证明方法
练
基础练习
习
1、在Rt△ABC中，∠C= Rt∠, (1)已知a=6,c=10,求b； b=8 (2)已知a=40,b=9,求c； c=41 (3)已知c=25,b=15,求a；a=20 (4)已知a:b=1:2,且c=5,求a、b； (5)已知∠A=1/2 ∠B, 且 a=2,求b、c.
练：如果一个三角形的三条边长分别是a＝m² －n²，b＝2mn，c＝m²＋n²（m>n），则这个三角形是直角三角形。
利用比例关系证明Rt △
例：如图，四边形ABCD是正方形，M为AB的
中点，E为AD上一点，且AE=1/4AD，求证
△EMC是直角三角形。A
M
B
E
D
C
面积分割
例：四边形ABCD中，∠B＝90°，AB＝3， BC＝4，CD＝12，AD＝13，求四边形ABCD 的面积。
角与角的关系：两个锐角互余。
思考：
直角三角形的三条角平分线的交点在
哪里？
形内
三条中线呢？形内Biblioteka 三条高呢？直角顶点
三条垂直平分线？斜边中点
练习
应用练习
4、作长为 2 、 3 、 5 的线段。
5、求如图所示（单
21
位：mm）的矩形
零件上两孔中心A
A
和B的距离（精确 41 到0.1mm）。
60
B 21
勾股定理的逆定理
a2b2c2
古埃及人画直角的方法：
把一根长绳打上等距离的13个结，然后用桩钉如图那样钉成一个三角形，其中一个角便是直角

勾股定理(1)教学课件

即直角三角形两直角边的平方和等于斜边的平方.
勾
a
弦c
股b
弦图
• 赵爽
• 东汉末至三国时代吴国人
• 为《周髀算经》作注，并著有《勾股圆方图说》。
伽菲尔德证法:
a
bc
c a
b
s梯形=
1 (a+b)(a+b)=
2
1 (a2+2ab+b2)
2
= 1 a2+ab+ 1 b2
2
2
s梯形=2×
1 ab+ 1 c2=ab+ 1 c2
连结AC,在Rt△ABC中,根据勾股定理,
AC 2 AB2 BC2 12 22 5 D C
5 因此,AC=
≈2.236
2m
因为AC_大__于___木板的宽,
AB
所以木板_能___ 从门框内通过.
学以致用
例1 飞机在空中水平飞行，某一时刻刚好飞
到一个男孩头顶上方4000米处，过了20秒，飞
5 .在直角△ ABC中,a=5,c=13,则△ ABC的面积 S=_____________.
6. 在直角△ ABC中, ∠C=90°,c=20,b=15,则 a=__________.
小结：
1.这节课你学到了什么知识？
勾股定理：如果直角三角形两直角边分别为a， b，斜边为c，那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方。
2
2
2
∵s梯形=s梯形 ∴ 1 a2+ab+ 1 b2=ab+ 1 c2
2
2
2
∴a2+b2=c2
学以致用 1、已知：a＝3，

勾股定理1

人教版八年级数学下册_第一节《勾股定理》勾股定理

9-勾股定理1

直角三角形-勾股定理1上海学

《勾股定理》PPT优质课件(第1课时)

第1讲 勾股定理

勾股定理1

【数学课件】勾股定理(1)

八上-第一章勾股定理

勾股定理(一)

人教版初中八年级下册数学课件 《勾股定理》1(第1课时)

17.1.1勾股定理课件(45张)

勾股定理 1

勾股定理1全面版

勾股定理(1)教学课件

第1讲勾股定理

人教版初中八年级下册数学课件《勾股定理》1(第1课时)