三角形面积公式——之水平宽铅垂高(叶茂恒)

合集下载

直角坐标系下三角形面积求法——水平宽铅垂高

直角坐标系下三角形面积求法——水平宽铅垂高前一阶段我们探讨了一次函数和三角形的面积问题，后台有一些同仁提出了一些宝贵的看法，在此笔者表示感谢。

我们知道对于不规则三角形的面积肯定是用割补法，由此引申出一种水平宽铅垂高的做法，也就是铅垂法。

今天我们来深入地探讨一下铅垂法的做法依据。

我们先从三个顶点都确定的三角形来看。

如图，在直角坐标系中，△ABC三个顶点的坐标为A（1，1）、B （3，4）、C（5，2），试求△ABC的面积。

显然这个三角形属于我们说的所谓不规则三角形（三条边均不和坐标轴平行，且不在坐标轴上），所以我们的基本思路是割补法。

由于此题相对来讲比较简单，我就简单用图形罗列一下各种不同的解法。

方法一：方法二：方法三：方法三是过点B作AC的平行线将不规则的△ABC转化为规则的△ADC从而来求解的过程，其实我们还可以过点A作BC的平行线或者过点C作AB的平行线来进行转化。

鉴于这不是本文研究的重点，另外两种方法在此略过。

方法四：方法五：方法六：方法七：方法八：方法九：方法四、方法五都是在点B处处理，方法四是在点B处作y轴的平行线，方法五是在点B处作x轴的平行线；方法六、方法七都是在点A处处理，方法六是在点A处作y轴的平行线，方法七是在点A处作x轴的平行线；方法八、方法九都是在点C处处理，方法八是在点C处作y轴的平行线，方法九是在点C处作x轴的平行线。

我们再来研究这六个图：如果我们对这六种方法都进行运算、思考，我们就会发现△ABC的面积为图中两个红色线段（一横一竖）乘积的一半。

这就是所谓的铅垂法求面积。

那么如何构造这些线呢？我的看法是选三角形的两个顶点（比如A和B），将AB之间的横坐标体现的横着的线段找出来（图５中的AM），最后一个顶点C作竖着的直线交AB边于点D，此时竖着的线段就是CD，然后利用AM和CD乘积的一半来求解。

或者将AB之间的纵坐标体现的竖着的线段找出来（图6中的AM），过第三个顶点C 作横着的直线交AB边于点D，此时横着的线段就是CD，然后利用AM和CD乘积的一半来求解。

三角形面积公式——之水平宽铅垂高(叶茂恒) (2)

三角形的面积公式计算较多，而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解，但有时采用水平宽铅垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 轴的垂线，其中过A ，C 两条垂线与x 轴交于点E ，F ，线段EF 的长度称为△ABC 的水平宽，而过B 点的垂线与边AC 交于点D ，线段BD BD ，此即为三角形水平宽铅垂高面积公式，其中水平宽通常取最外两条垂线的宽度，对应铅垂高取经过夹在中间的顶点（B ）之间的距离. 公式推导如右图，过点A ，C 作铅垂高BD 上的高AG ，CH1122AG BD CH BD +＝()12AG CH BD +＝12EF BD . 公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 的正方形E ABCD ,为AD 的中点，P 为CE 的中点，F 为中点，则△BFD 的面积是（）.A .281a B . 2161a C . 2321a D .说明：本题可以连结CF ，由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得. 解析：不妨以B 为原点，BC 为x 轴，BA 为y 建立平面直角坐标系，则点C 坐标为（a ，0）点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ），∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2（适合八年级）如图，直线1y x =+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a值.说明：本题常见解法有三，一是连结OP ，△的面积＝△AOB 面积+△BOP 面积－△AOP 积，然后用a 的代数式表示，与Rt △ABC 相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC 相等，则可得PC ’//AB ，因此，可以由点A ，C 求C ’坐标，再根据AB 的斜率与点C ’的解析式，将点P 纵坐标代入，即可求a 的值三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，从A ，B ，方向作垂线），仿公式求解.现解析如下.解析：过A ，B ，P 三点作y 轴的垂线，则OB 可以看成公式中的水平宽，而PE 可以看成公式中的铅垂高，（不习惯的同学可以将屏幕或头转个90度）由AB 的解析式可以得OAOB ＝1，而P 的纵坐标为12，所以E 为AB 的中点，所以PE ＝-a从而有11221222a ⎛⨯⨯=⨯⨯-+ ⎝⎭，解得42a =-. 公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有12EF CG . 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH -＝12EF CG . 说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）. 例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 翻折，点A 落到点C ，抛物线过点B ，C 和D （3，0（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 标轴上，以点N ，B ，D 为顶点的三角形与△MCD 似，求所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q若存在，请直接写出点Q 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后：从以上几例可以看到，形面积问题，尤其是在例3，可以将P 对值）问题求解，可以有效回避原本点P 在BD 作法，使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。

水平宽铅垂高的公式

《水平宽×铅垂高的公式》是一个早已被广泛使用的数学公式，通常用于计算几何图形的面积。

该公式是：面积=水平宽×铅垂高。

水平宽是指平面上的某一物体的宽度，而铅垂高是指从水平宽上端到该物体下端的垂直距离。

这两个参数一般可以根据实际测量结果确定，也可以从图表中确定。

该公式用于计算多边形、梯形、椭圆形等几何图形的面积，也可用于计算曲线下的面积。

例如，在计算椭圆形面积时，需要将椭圆形分割成多边形，然后再利用该公式计算面积。

《水平宽×铅垂高的公式》在计算几何图形面积时显得非常有用，它也是许多学科研究、建筑设计和其他实际应用中常用的一种数学计算方法。

角形面积公式——之水平宽铅垂高

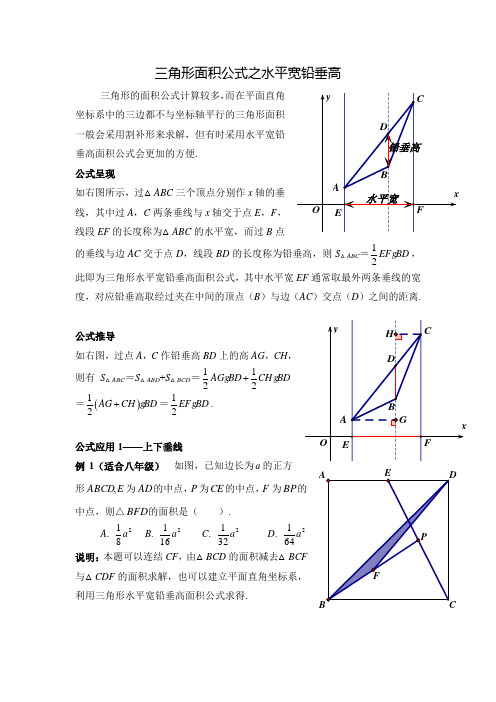
三角形的面积公式计算较多，垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 线，其中过A ，C 两条垂线与x 轴交于点E ，F 线段EF 的长度称为△ABC 的水平宽，而过B 的垂线与边AC 交于点D ，线段BD 度，对应铅垂高取经过夹在中间的顶点（B公式推导如右图，过点A ，C 作铅垂高BD 上的高AG ，则有S △ABC ＝S △ABD +S △BCD ＝1122AG BD CH +g g ＝()12AG CH BD +g ＝12EF BD g .公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 形E ABCD ,为AD 的中点，P 为CE 的中点，F 为中点，则△BFD 的面积是（）.A .281a B . 2161a C . 2321a D .说明：本题可以连结CF ，由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得.解析：不妨以B 为原点，BC 为x 轴，BA 为y 轴建立平面直角坐标系，则点C 坐标为（a ，0），点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==g g .公式应用2——左右垂线例2（适合八年级）如图，直线13y x =-+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a 的值.说明：本题常见解法有三，一是连结OP ，△ABP 的面积＝△AOB 面积+△BOP 面积－△AOP 面积，然后用a 的代数式表示，与Rt △ABC相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC P相等，则可得PC ’三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y 轴作垂解.解析：过线，则OB 而PE 度）由AB 的解析式可以得OA ，OB ＝1，而P的纵坐标为12，所以E 为AB 的中点，所以PE ＝-a 从而有11221222a ⎛⨯⨯=⨯⨯-+ ⎝⎭，解得42a =-.公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有12EF CG g . 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH -g g ＝12EF CG g . 说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）.例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 轴翻折，点A 落到点C ，抛物线过点B ，C 和D （3，0）．（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 在坐标轴上，以点N ，B ，D 为顶点的三角形与△MCD 相似，求所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q 使得CQ BQ 的值最大，若存在，请直接写出点Q 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，xyEDBA C OPxy EDBCOP即当P（－1，8）或P（4，3）时，S△PBD=6.解后：从以上几例可以看到，灵活运用水平宽与铅垂高公式，可以有效解决三角形面积问题，尤其是在例3，可以将P点的两种不同的位置分类统一为PE长（绝对值）问题求解，可以有效回避原本点P在BD上方时，几何法要构造高等繁杂作法，使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。

三角形面积铅垂法公式

三角形面积铅垂法公式
就是沿三角形的最高点做一条垂直于平面的直线,另外两点作这条线的垂线,如果在平面直角坐标系中,两条高就是两个点横坐标的差,再求出那条直线在三角形内的长就行了。

设三角形abc，铅垂线ad垂直bc焦点d，面积为ad*bc/2。

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。

常用的三角形按边棕斑普通三角形（三条边都不成正比），等腰三角（腰与底左右的等腰三角形、腰与底成正比的等腰三角形即为等边三角形）；按角分存有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形泛称横三角形。

从动点向另外两点所在的固定直线作铅垂，将变化的竖直线段作为三角形的底，则高就是两个定点的横坐标之差，然后结合三角形的面积公式表达。

铅垂高水平宽求三角形面积

铅垂高水平宽求三角形面积
S△ABC＝1\2ah。

过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的水平宽(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的铅垂高(h)，我们可得出一种计算三角形面积的新方法：S△ABC＝1\2ah，即三角形面积等于水平宽与铅垂高乘积的一半。

铅垂高法是解决与二次函数相关的三角形面积问题的一个特殊的方法。

铅垂高
任何物件如铅垂一样的与地成正垂直，就是铅垂方向，沿铅垂方向的高度就是铅垂高，即在铅垂方向的投影；
与铅垂方向垂直的方向就是水平方向，物体沿水平方向的宽度就是水平宽。

把三角形沿水平方向分割成上下两部分，上部分面积＝水平宽×h1×1/2，下部分面积＝水平宽×h2×1/2，h1+h2＝铅垂高，结论得证。

三角形面积公式——之水平宽铅垂高(叶茂恒) (2)

三角形面积公式之水三角形的面积公式计算较多，而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解，但有时采用水平宽铅垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 轴的垂线，其中过A ，C 两条垂线与x 轴交于点E ，F ，线段EF 的长度称为△ABC 的水平宽，而过B 点的垂线与边AC 交于点D ，线段BD 此即为三角形水平宽铅垂高面积公式，其中水平宽度，对应铅垂高取经过夹在中间的顶点（B 公式推导如右图，过点A ，C 作铅垂高BD上的高AG ，CH 1122AG BD CH BD +g g ＝()12AG CH BD +g ＝12EF BD g . 公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 的正方形E ABCD ,为AD 的中点，P 为CE 的中点，F 为中点，则△BFD 的面积是（）.A .281a B . 2161a C . 2321a D .说明：本题可以连结CF ，由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得. 解析：不妨以B 为原点，BC 为x 轴，BA 为y 建立平面直角坐标系，则点C 坐标为（a ，0）点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ），∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==g g .公式应用2——左右垂线例2（适合八年级）如图，直线1y x =+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a值.说明：本题常见解法有三，一是连结OP ，△的面积＝△AOB 面积+△BOP 面积－△AOP 积，然后用a 的代数式表示，与Rt △ABC 相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC 相等，则可得PC ’//AB ，因此，可以由点A ，C 求C ’坐标，再根据AB 的斜率与点C ’的解析式，将点P 纵坐标代入，即可求a 的值三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，从A ，B ，方向作垂线），仿公式求解.现解析如下.解析：过A，B，P三点作y轴的垂线，则OB可以看成公式中的水平宽，而PE 可以看成公式中的铅垂高，（不习惯的同学可以将屏幕或头转个90度）由AB的解析式可以得OA＝3，OB＝1，而P的纵坐标为12，所以E为AB的中点，所以PE＝-a+32，从而有11322122a⎛⎫⨯⨯=⨯⨯-+⎪⎪⎝⎭，解得34 a=-.公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x轴，也可以作向y轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有1 2EF CGg.简单推导：S△ABC＝S△ACG－S△BCG＝1122CG EH CG FH-g g＝12EF CGg.说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB）的延长线相交，此时顶点（C）到交点（G）的距离为铅垂高（CG）.例3（适合九年级）如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y 翻折，点A落到点C，抛物线过点B，C和D（3，0（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N标轴上，以点N，B，D为顶点的三角形与△MCD 似，求所有满足条件的点N的坐标．x y铅垂高水平宽GF HEDOACB（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q若存在，请直接写出点Q 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后：从以上几例可以看到，形面积问题，尤其是在例3，可以将P 对值）问题求解，可以有效回避原本点P 在BD 作法，使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。

三角形面积公式之水平宽铅垂高叶茂恒

三角形面积公式之水平宽铅垂高叶茂恒集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#三角形的面积公式计算较多，而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解，但有时采用水平宽铅垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 轴的垂线，其中过A ，C 两条垂线与x 轴交于点E ，F而过B 点的垂线与边AC 交于点D ，线段BD 12EF BD 的宽度，对应铅垂高取经过夹在中间的顶点（B 公式推导如右图，过点A ，C 作铅垂高BD 上的高AG ，CH ，则有S △ABC ＝S △ABD +S △BCD ＝1122AG BD CH BD +＝()12AG CH BD +＝12EF BD . 公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 的正方形E ABCD ,为AD 的中点，P 为CE 的中点，F 为BP 的中点，则△BFD 的面积是（）.A . 281aB . 2161aC . 2321a D . 2641a 说明：本题可以连结CF ，由△BCD 的面积减去△BCF 与△CDF 的面积求解，也可以建立平面直角坐标系，利用三角形水平宽铅垂高面积公式求得.解析：不妨以B 为原点，BC 为x 轴，BA 为y 轴建立平面直角坐标系，则点C 坐标为（a ，0），点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ）， ∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2（适合八年级）如图，直线13y x =-+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a 的值.说明：本题常见解法有三，一是连结OP ，△ABP 的面积＝△AOB 面积+△BOP 面积－△AOP 面积，然后用a 的代数式表示，与Rt △ABC 的面积相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC 面积与△ABC ’面积相等，若△ABP 的面积与Rt △ABC 的面积相等，则可得PC ’三是垂线（即左右方向作垂线），仿公式求解.现解析如下.解析：过A ，B ，P 三点作y 轴的垂线，则OB 可以看成公式中的水平宽，而PE 可以看成公式中的铅垂高，（不习惯的同学可以将屏幕或头转个90度）由AB 的解析式可以得OA OB ＝1，而P 的纵坐标为12，所以E 为AB 的中点，所以PE ＝-a +2，从而有1122122a ⎛⨯⨯=⨯⨯-+ ⎝⎭ ，解得4a =. 公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有时根据需要也可以取任意两条直线的宽度，则公式可以变化为：S 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH -＝12EF CG . D说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）. 例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 轴翻折，点A 落到点C ，抛物线过点B ，C 和D （3，0）．（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 在坐标轴上，以点N ，B ，D 为顶点的三角形与△MCD 相似，求所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q 使得CQ BQ 的值最大，若存在，请直接写出点Q 的坐标；若不存在，请说明理由解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后：从以上几例可以看到，灵活运用水平宽与铅垂高公式，可以有效解决三角形面积问题，尤其是在例3，可以将P 点的两种不同的位置分类统一为PE 长（绝对值）问题求解，可以有效回避原本点P 在BD 上方时，几何法要构造高等繁杂作法，使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。

铅垂高水平宽求三角形面积的原理

铅垂高水平宽求三角形面积的原理以铅垂高水平宽求三角形面积的原理为题，我们将从三角形的定义、铅垂线的概念以及如何利用这些概念来求解三角形面积等方面进行讨论。

让我们回顾一下三角形的定义。

三角形是由三条线段连接而成的图形，其中每条线段称为三角形的边，而三个顶点则是这些边的交点。

根据三角形的性质，我们可以将三角形分为不同的类型，例如等边三角形、等腰三角形、直角三角形等。

接下来，我们来介绍一下铅垂线的概念。

铅垂线是从一个点向一个平面垂直下落的线段。

在三角形中，我们可以通过顶点向对边引一条垂直线，这条垂直线即为铅垂线。

铅垂线与对边的交点称为垂足。

利用铅垂线，我们可以将三角形分割为两个直角三角形，从而简化问题的求解。

那么，如何利用铅垂高和水平宽来求解三角形的面积呢？我们可以利用三角形面积公式S = 1/2 * 底边长* 高来求解。

在这里，底边长即为水平宽，高即为铅垂高。

为了更好地理解这个公式，我们可以通过一个具体的例子来进行说明。

假设我们有一个三角形ABC，其中AB为底边，C为顶点，D为AB 的中点，AD为铅垂高，CD为水平宽。

我们最终的目标是求解三角形ABC的面积。

我们可以通过测量或已知条件得到底边AB的长度和铅垂高AD的长度。

接下来，我们可以利用铅垂线的性质，将三角形ABC分割为两个直角三角形ACD和BCD。

对于直角三角形ACD，我们可以利用三角形面积公式S = 1/2 * 底边长* 高来求解。

在这里，底边长即为水平宽CD的长度，高即为铅垂高AD的长度。

将这两个值代入公式中，即可计算出直角三角形ACD的面积。

同样地，对于直角三角形BCD，我们也可以利用三角形面积公式求解。

底边长为水平宽CD的长度，高为铅垂高AD的长度。

将这两个值代入公式中，即可计算出直角三角形BCD的面积。

我们将直角三角形ACD和BCD的面积相加，即可得到三角形ABC 的面积。

通过以上步骤，我们可以利用铅垂高和水平宽来求解三角形的面积。

这种方法可以简化计算过程，减少复杂度，提高求解效率。

铅锤高定理公式

铅锤高定理公式
解析
铅垂线定理公式是三角形面积=铅锤高×水平宽的一半三角形面积。

物体重心与地球重心的连线称为铅垂线（用圆锥形铅垂测得）。

多用于建筑测量。

用一条细绳一端系重物，在相对于地面静止时，这条绳所在直线就是铅垂线，又称重垂线。

铅垂线地球重力场中的重力方向线。

它与水准面正交，是野外观测的基准线。

悬挂重物而自由下垂时的方向，即为此线方向，包含它的平面则称铅垂面。

判断物体是否与地面垂直，可用铅垂线法，即一根线加上一个重物。

此重物称为铅锤，铅锤受重力作用，即受万有引力的一个分力作用，让线与地面垂直，成90度角度。

三角形面积公式——之水平宽铅垂高

三角形面积公式——之水平宽铅垂高三角形是几何学中最基本的形状之一，它由三个边和三个角组成。

理解三角形面积的公式对于解决各类几何问题至关重要。

有几种不同的方法可以计算三角形的面积，其中一种基本方法是使用三角形的底和高的长度。

在本文中，我将详细介绍水平宽和垂直高的概念，并展示如何使用这些概念来计算三角形的面积。

水平宽是指从一个顶点到另一个顶点的水平距离，也就是三角形的底边。

垂直高是指从三角形的一个顶点到底边上的垂直距离。

水平宽和垂直高之间的关系可以用来计算三角形的面积。

首先，我们需要明确水平宽和垂直高对于三角形面积的重要性。

在一个三角形中，两个相邻边形成一个角，而这个角的大小取决于它们之间的夹角。

为了计算这两个边之间的角度，我们需要引入正弦和余弦等三角函数。

在一个直角三角形中，正弦函数定义为垂直高与斜边之间的比例，即sin(θ) = h/c，其中θ是角度，h是垂直高，c是斜边的长度。

正弦函数在大多数三角函数表中都有详细的值，可以通过查表或计算器来获得。

现在，让我们考虑如何使用水平宽和垂直高来计算三角形的面积。

首先，我们需要将水平宽和垂直高表示为变量。

假设水平宽为b，垂直高为h。

根据三角形的面积公式，三角形的面积等于底边的长度乘以垂直高的长度的一半，即A=(1/2)*b*h。

这个公式的推导可以用几何方法或三角函数来解释。

从几何的角度来看，可以将三角形划分为两个直角三角形，每个直角三角形的面积等于底边长度乘以垂直高的长度再除以2、因此，整个三角形的面积等于这两个直角三角形的面积之和。

另一种推导方法是使用三角函数。

根据正弦函数的定义，sin(θ) =h / c，其中h是垂直高，c是斜边的长度。

我们可以通过将等式两边都乘以c来得到h = c * sin(θ)。

由于三角形的面积等于底边乘以高的一半，所以A = (1/2) * b * h = (1/2) * b * c * sin(θ)。

这个公式的意义在于，我们可以用底边长度、斜边长度和夹角的正弦值来计算三角形的面积。

(完整word版)三角形面积公式——之水平宽铅垂高叶茂恒

三角形面积公式之三角形的面积公式计算较多，而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解，但有时采用水平宽铅垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 轴的垂线，其中过A ，C 两条垂线与x 轴交于点E ，F ，线段EF 的长度称为△ABC 的水平宽，而过B 点的垂线与边AC 交于点D ，线段BD 形水平宽铅垂高面积公式，其中水平宽EF 过夹在中间的顶点（B ）与边（AC ）交点（D 公式推导如右图，过点A ，C 作铅垂高BD 上的高1122AG BD CH BD +g g ＝()12AG CH BD +g ＝12EF BD g . 公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 的正方形E ABCD ,为AD 的中点，P 为CE 的中点，F 为中点，则△BFD 的面积是（）.A .281a B . 2161a C . 2321a D .说明：本题可以连结CF ，由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得. 解析：不妨以B 为原点，BC 为x 轴，BA 为y 建立平面直角坐标系，则点C 坐标为（a ，0点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==g g .公式应用2——左右垂线例2（适合八年级）如图，直线1y x =+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a值.说明：本题常见解法有三，一是连结OP ，△的面积＝△AOB 面积+△BOP 面积－△AOP 积，然后用a 的代数式表示，与Rt △ABC 相等列方程求解；二是将点C 沿AB翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC 相等，则可得PC ’//AB ，因此，可以由点A ，C 求C ’坐标，再根据AB 的斜率与点C ’的解析式，将点P 纵坐标代入，即可求a 的值三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y解析：过A ，B ，P 三点作y 轴的垂线，则OB 可以看成公式中的水平宽，而PE 可以看成公式中的铅垂高，（不习惯的同学可以将屏幕或头转个90度）由AB 的解析式可以得OA ＝3，OB ＝1，而P 的纵坐标为12，所以E 为AB 的中点，所以PE ＝-a +3，从而有11322122a ⎛⎫⨯⨯=⨯⨯-+ ⎪ ⎪⎝⎭，解得342a =-. 公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有时根据需要也可以取任意两条直线的宽度，则公式可以变化为：S △ABC ＝2EF 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH-g g ＝12EF CG g . 说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）. 例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 轴翻折，点A 落到点C ，抛物线过点B ，C 和D ）．（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 轴上，以点N ，B ，D 为顶点的三角形与△MCD 所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．xy铅垂高水平宽GFHEDOA CB（4）点Q直接写出点Q 的坐标；若不存在，请说明理由. 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后题，尤其是在例3，可以将P 可以有效回避原本点P 在BD 快捷.老叶2015年1月26日记于温十七中。

三角形水平宽铅垂高面积公式

三角形水平宽铅垂高面积公式在我们学习数学的奇妙旅程中，三角形这个家伙可是个常客。

今天咱们就来聊聊三角形的水平宽铅垂高面积公式，这可是个相当有趣又实用的小知识！先来说说啥是三角形的水平宽和铅垂高。

想象一下，有一个三角形稳稳地躺在平面直角坐标系里。

水平宽呢，就是三角形底边在 x 轴上的投影长度；铅垂高呢，则是从三角形的顶点向 x 轴作垂线，垂线的长度就是铅垂高。

我记得有一次给学生们讲这个知识点的时候，有个小家伙瞪着大眼睛一脸懵地问我：“老师，这水平宽和铅垂高怎么就跟面积有关系啦？”我笑着告诉他：“别着急，咱们一起来探究探究。

”咱们来看个具体的例子。

假设有个三角形，三个顶点的坐标分别是A(1, 2)，B(3, 4)，C(5, 1)。

首先，咱们来找出底边，假设底边是线段BC，那它在 x 轴上的投影长度就是水平宽。

B 点和 C 点的横坐标分别是 3 和 5，所以水平宽就是 5 - 3 = 2。

接下来找铅垂高。

咱们从 A 点向 x 轴作垂线，与 x 轴交点设为 D，那 AD 的长度就是铅垂高。

A 点的纵坐标是 2，所以铅垂高就是 2。

这时候，根据三角形水平宽铅垂高面积公式，面积就等于水平宽乘以铅垂高的一半。

也就是 2×2÷2 = 2。

再比如，还有个三角形，顶点坐标是 E( -1, 3)，F(2, 5)，G(4, -1)。

同样的方法，先找底边 FG 在 x 轴上的投影，也就是水平宽，4 - 2 = 2。

再找顶点 E 到 x 轴的垂线长度，也就是铅垂高，是 3。

那这个三角形的面积就是 2×3÷2 = 3。

同学们在做这类题的时候，可一定要仔细看准坐标，别把数值弄混了。

有个同学就因为粗心，把横坐标看成纵坐标，算出的面积差了十万八千里，自己还纳闷怎么不对呢！其实啊，这个公式的妙处就在于，它能让我们在面对一些复杂的三角形时，不用费力地去分割或者转化，就能轻松算出面积。

在实际生活中，这个公式也有大用处。

铅垂高水平宽求三角形面积例题

铅垂高水平宽求三角形面积例题在阳光明媚的下午，咱们来聊聊三角形的面积吧。

说到三角形，大家肯定脑海里会浮现出那种简单的形状，有点像一块比萨饼对吧？三角形其实特别有趣，它的面积计算方法可不是随便来的哦。

咱们得提到一个重要的概念——铅垂高和水平宽。

听起来高大上，其实很简单。

想象一下，你在草地上用手指画出一个三角形，底边是宽宽的，顶尖儿高高的。

这个时候，铅垂高就像是从三角形的顶点垂下来的一条线，正好碰到底边的中间。

就好像是你在给三角形“量身高”，是不是很有意思？再说说那水平宽，它就是底边的长度，宽宽的，能让你坐下去的那种。

这两个东西的关系可重要了，正是它们让我们能算出这个三角形的面积。

哎，你知道吗？算三角形的面积其实也不难。

只要你把底边的长度和铅垂高的长度相乘，然后再除以二，简单吧？就像你在切蛋糕，先量好每块蛋糕的宽度，然后把它们的高度也量好，再除个二，嘿！这就搞定了。

公式看起来是这样的：面积=（底边×铅垂高）÷2。

就这么简单，人人都能学会！不过话说回来，面积这个概念其实在生活中到处都有。

你有没有想过，为什么房子要有面积？因为咱们得知道房子能住多少人，对吧？当你在厨房里忙活的时候，想想你做饭的那片地方，面积也在告诉你能放多少锅碗瓢盆，真是无处不在的数字。

回过头来，三角形的面积也能让我们理解更多事物，比如一些艺术作品的设计，或者是风景中的山丘，甚至是纸飞机的造型，都少不了这个简单的计算。

说到这里，不禁让我想起小时候学数学的那些日子。

记得那时候，数学老师会拿着黑板，兴致勃勃地给我们讲解这些概念，有时还会用一些生动的例子。

她说，三角形就像是站在高处的守护者，脚下稳稳的，顶上又高又尖。

而我们就是要学会利用这些知识，去探索更大的世界。

三角形的形状让人感到一种力量，那种尖锐的感觉让人觉得无所不能。

哎，别以为我光在说三角形，其实这也是个哲理的寓言。

人生不就是一个个三角形吗？有高有低，有宽有窄。

我们在这个世界上拼搏，就像在量三角形的高和宽，最终才能找到自己的位置，算出自己生活的“面积”。

三角形面积公式——之水平宽铅垂高(叶茂恒)

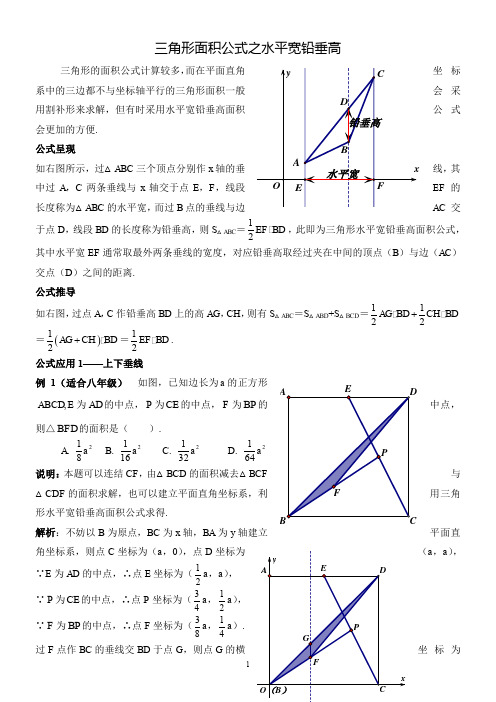
1三角形的面积公式计算较多，而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解，但有时采用水平宽铅垂高面积公式会更加的方便. 公式呈现如右图所示，过△ABC 三个顶点分别作x 轴的垂线，其中过A ，C 两条垂线与x轴交于点E ，F ，线段EF 的长度称为△ABC 的水平宽，而过B 点的垂线与边AC 交于点D ，线段BD 的长度称为铅垂高，则S △ABC ＝12BD ，此即为三角形水平宽铅垂高面积公式，其中水平宽EF 通常取最外两条垂线的宽度，对应铅垂高取经过夹在中间的顶点（AC ）交点（D ）之间的距离.公式推导如右图，过点A ，C 作铅垂高BD 上的高AG ，CH ，12CH BD+＝()12AG CH BD +＝12EF BD . 公式应用1——上下垂线例1（适合八年级）如图，已知边长为a 的正方形E ABCD ,为AD 的中点，P 为CE 的中点，F 为BP 的中点，则△BFD 的面积是（）.A .281a B . 2161a C . 2321a D .2641a 说明：本题可以连结CF ，由△BCD 的面积减去△BCF 与△CDF 的面积求解，也可以建立平面直角坐标系，利用三角形水平宽铅垂高面积公式求得.解析：不妨以B 为原点，BC 为x 轴，BA 为y 平面直角坐标系，则点C 坐标为（a ，0），点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为238a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ， ∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2（适合八年级）如图，直线1y x =+与x轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a 的值.说明：本题常见解法有三，一是连结OP ，△的面积＝△AOB 面积+△BOP 面积－△AOP 面积，后用a的代数式表示，与Rt △ABC 解；二是将点C 沿AB 翻折到C ’位置，则△ABC与△ABC ’面积相等，若△ABP 的面积与Rt △的面积相等，则可得PC ’//AB ，因此，可以由点A ，先求C ’坐标，再根据AB 的斜率与点C ’坐标求直线解析式，将点P 纵坐标代入，即可求a 的值.三是考虑水平宽铅垂高公式来计算，但如果从P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y 轴作垂线（即左右方向作垂线）解析：过OB OA OB ＝1，而P 的纵坐标为2，所以E 为AB 的中点，所以PE ＝-a从而有11221222a ⎛⎫⨯⨯=⨯⨯-+ ⎪ ⎪⎝⎭ ，解得42a =-. 公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有时根据需要也可以取任意两条直线的宽度，则公式可以变化为：S △ABC ＝12EF CG .简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH-＝12EF CG . 说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）.例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y 轴翻折，点A落到点C ，抛物线过点B ，C 和D （3，0）．（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 点N ，B ，D 为顶点的三角形与△MCD 相似，点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6在，求出点P 的坐标；若不存在，说明理由．（4）点Q 出点Q 的坐标；若不存在，请说明理由. 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；4当P 在BD 上方时，POD ＝3为水平宽，则铅垂高PE ＝2343x x x x -+-+-=-234x x -=±.两种情况合起来就是213362x x ⨯⨯-=，即当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6. 解后：从以上几例可以看到，灵活运用水平宽与铅垂高公式，可以有效解决三角形面积问题，尤其是在例3，可以将P 点的两种不同的位置分类统一为PE 长（绝对值）问题求解，可以有效回避原本点P 在BD 上方时，.26日记于温十七中。

三角形面积公式——之水平宽铅垂高(叶茂恒) (2)

坐标会采公式线，其中过A 的长交于点DBD ，此即为三角形水平宽铅垂高面积公式，其通常取最外两条垂线的宽度，对应铅垂高取经过夹在中间的顶点（AC ）交点（D 2AG BD CH BD +＝()12AG BD +＝2EF BD . ——上下垂线例1（适合八年级）如图，已知边长为ABCD ,中点，则△A 说明：与△CDF 三角形解析：不妨以B 为原点，BC 为x 轴，BA 为y 轴建立平面直角坐标系，则点C 坐标为（a ，0），点D 坐标为（a ，a ），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2x轴，y 在第在第Rt △ABC 说明：的面积＝△用a 的二是与△ABC 面积相等，求C ’坐标，析式，将点P 三是P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y 轴作垂线（即左右方向作垂线）解析：过A 或头转个OB ＝2AB 的中点，所以PE ＝-a+2，从而有1122122a ⎛⨯⨯=⨯⨯-+ ⎝⎭，解得4a =-.从例CG .S △ABC ＝12CG EH CG FH -＝12EF 说明条垂线到交点（G 例3与x 轴交于点点A 落到点C （1（2）若点N ，B 点N （3求出点（4）点Q 使得BQ -解析解析式FHEOy为243y x x=-+，BD解析式为3y x=-+，由于问题中并未交待P点在BD的上方或下方，故要分类讨论：当P在BD下方时，如右上图，水平宽为OD＝3，铅垂高为PE＝224333x x x x x-++-=-；当P在OD＝3为两种情23x x-当23x-不可当23x-即当P解后垂高公，可以将P上方时，。

三角形面积铅直高乘水平宽

您所指的公式是指三角形的面积，当三角形的高度是从基底到相反顶点的垂直线时，三角形的宽度是基点两个端点之间的水平距离。

公式是：
面积=（1/2）x底座x高度
其中底座是三角形的水平宽度，高度是从底座到相反顶点的垂直距离。

这被称为“按基数和高度划分的三角形面积”公式，它适用于任何三角形，无论其形状或大小。

该公式之所以有效，是因为三角形的面积等于其基数和高度乘积的一半。

需要注意的是，只有当高度是从基底到相反顶点的垂直线，并且宽度是基座两个端点之间的水平距离时，这个公式才有效。

如果高度不是垂直的或宽度不是水平的，公式将不起作用，应使用其他方法来找到区域。

铅垂法算三角形面积的公式

铅垂法算三角形面积的公式铅垂法是一种常用的三角形面积计算方法，它基于三角形的底边和高，通过求得三角形的底边长度和垂直高度，进而计算出三角形的面积。

在几何学中，三角形面积计算是一个基础而重要的问题，而铅垂法正是解决这一问题的有效方法。

我们需要明确铅垂法的基本原理。

对于任意一个三角形ABC，我们可以作出一条垂直于底边AB并经过顶点C的线段CD，将三角形分割为两个直角三角形ACD和BCD。

根据直角三角形的性质，我们可以通过底边AB和高CD的长度，计算出两个直角三角形的面积，然后再将它们相加，即可得到整个三角形ABC的面积。

接下来，我们来具体讨论如何计算三角形的底边和垂直高度。

首先，我们需要确定底边的长度。

底边的长度可以通过两个顶点的坐标计算得出。

假设顶点A的坐标为(x1, y1)，顶点B的坐标为(x2, y2)，那么底边AB的长度可以通过勾股定理计算得出：AB = √((x2 - x1)^2 + (y2 - y1)^2)接下来，我们需要确定垂直高度的长度。

垂直高度的长度可以通过顶点C的坐标计算得出。

假设顶点C的坐标为(x3, y3)，那么垂直高度CD的长度可以通过以下公式计算得出：CD = |Ax + By + C| / √(A^2 + B^2)其中，A、B、C分别为直线AB所对应的一般方程Ax + By + C = 0的系数。

有了底边AB和垂直高度CD的长度，我们就可以计算出两个直角三角形ACD和BCD的面积了。

根据直角三角形的面积公式S = 1/2 * 底边长度 * 高的长度，我们可以得到：SACD = 1/2 * AB * CDSBCD = 1/2 * AB * CD将两个直角三角形的面积相加，即可得到整个三角形ABC的面积：SABC = SACD + SBCD = AB * CD通过以上步骤，我们就可以利用铅垂法准确地计算出三角形的面积了。

需要注意的是，在实际应用中，我们可以根据具体问题的要求选择不同的坐标系和计算方法，以便更方便地计算三角形的面积。