例题

合集下载

消防流量的选取例题

消防流量的选取例题一、消防流量的选取例题1. 例题一有一个四层的办公楼，每层建筑面积为1000平方米，建筑高度为16米，属于轻危险级场所。

按照相关消防规范，计算该办公楼的室内消火栓系统的消防流量。

对于轻危险级的场所，根据消防规范的规定，室内消火栓的消防流量一般是5L/s。

因为这个办公楼是四层，每层面积和整体危险等级等因素都符合这个标准的判定范围。

2. 例题二一个大型的商场，总建筑面积为10000平方米，建筑高度为20米，属于中危险级Ⅰ级场所。

求这个商场的自动喷水灭火系统的消防流量。

中危险级Ⅰ级场所的自动喷水灭火系统的设计基本消防流量是6L/(min·m²)。

这个商场面积是10000平方米，那它的消防流量计算就是6×10000 =60000L/min，换算一下就是1000L/s。

3. 例题三有一个丙类仓库，占地面积为3000平方米，建筑高度为10米。

仓库内储存的是一些普通的塑料制品。

计算这个仓库室外消火栓系统的消防流量。

丙类仓库室外消火栓的消防流量和仓库的面积等因素有关。

一般来说，这种规模和储存物品类型的丙类仓库，室外消火栓系统的消防流量是30L/s。

4. 例题四一个高层住宅，建筑高度为50米，共18层，每层4户。

确定这个高层住宅的室内消火栓系统和自动喷水灭火系统总的消防流量。

对于高层住宅，室内消火栓系统的消防流量一般是10L/s。

自动喷水灭火系统按照轻危险级来考虑（因为住宅内相对危险程度较低），流量是5L/s。

所以总的消防流量就是10 + 5 = 15L/s。

5. 例题五有一个小型的油库，储存量为50立方米。

求这个油库的灭火系统所需的消防流量。

油库属于比较特殊的场所。

对于这种小型油库，根据专门的石油化工消防规范，灭火系统的消防流量至少应该达到20L/s，以确保在火灾发生时能够有足够的水量来灭火和冷却相关设施。

6. 例题六一个幼儿园，建筑面积为1500平方米，两层。

计算幼儿园的室内消火栓系统消防流量。

货币乘数例题

货币乘数例题
货币乘数是指货币供应量与基础货币之间的倍数关系。

以下是一个简单的货币乘数例题：
假设基础货币供应量为100亿元，银行体系规定的存款准备金率为20%，银行体系的超额准备金率为5%，客户现金持有率为10%。

求货币乘数。

根据货币乘数的定义，我们可以得到以下计算过程：
1.银行体系总存款为：100亿元 / 20% = 500亿元
2.银行体系总存款中，客户手持现金为：500亿元× 10% = 50亿元
3.银行体系总存款中，银行体系超额准备金为：500亿元× 5% = 25亿元
4.银行体系可用来作为贷款的货币量为：(500亿元 - 50亿元 - 25亿元) = 425亿元
5.因此，货币乘数为：425亿元 / 100亿元 = 4.25
通过上述计算过程，我们可以得到货币乘数为4.25。

这说明，在基础货币供应量为100亿元的情况下，银行体系可以创造出4.25倍的货币供应量。

行测典型例题

行测典型例题
行测典型例题：
1. 有一架天平，两臂长不等，未挂物体时，左臂离支点更近。

现在将质量相等的物体放在左右两盘中各放多少，天平才能平衡？
A. 一样多
B. 左边多
C. 右边多
D. 无法判断
2. 有一根长120厘米的铁丝围成一个长方形，长是35厘米，宽是多少厘米？
3. 一个数，如果将它的小数点向右移动一位，就比原来的数大18.9，原来的数是多少？
4. 一个长方形的周长是20厘米，长是a厘米，则宽是( )厘米。

5. 甲、乙两数的和是470，甲数的小数点向左移动一位就与乙数相等，甲数是( )。

6. 两个数的商是80，如果被除数不变，除数扩大10倍，商是多少？
7. 一个三位数除以35所得的商与余数相同，这个三位数最大是多少？
8. 某车间有3个小组计划在4天内生产480件产品（每天生产量相同），按原先的生产速度，不能完成任务；如果每个小组每天比原先多生产10件产品，就能提前完成任务。

每个小组原先每天生产多少件产品？
9. 一个两位数除以15，商和余数相等，这个两位数最大是多少？
10. 学校计划购买15台联想电脑和20台方正电脑，每台联想电脑x元，每台方正电脑y元。

一共需要多少元？当x=4000,y=3500时，一共需要多少元？。

数学经典例题

行程问题练习题(一)、行程（时刻）问题类１、一个人骑自行车从甲地到乙地，如果每小时行走10千米，下午1点才能到达；如果每小时行15千米，上午11点就能到达。

要在中午12点到达乙地，他每小时要行多少千米？２、邮递员早晨7时出发送一份邮件到东村去，从邮局开始要走12千米上坡路，8千米下坡路，他上坡时每小时走4千米，下坡时每小时走5千米，到达目的地停留1小时以后，又从原路返回，邮递员什么时候可以回到邮局。

(二)、行程（参数法）问题类。

３、小明从甲地去乙地，骑自行车走完全程的一半时，自行车坏了，又无法修理，只好推车步行到乙地，骑车速度是每小时12千米，步行时每小时行4千米，小明走完全程的平均速度是多少千米？４、一个人原计划骑自行车由甲地去乙地，后来改为前一半路乘汽车，后一半路步行，汽车速度是自行车2倍，步行速度是自行车一半，自行车速度为每小时10千米，求行这段路的平均速度。

５、学校组织秋游，同学们下午1点出发，走了一段平坦的路，爬了一座山，然后按原路返回，下午7点回到学校，已知他们步行速度：平地4千米，上山3千米，下山6千米，他们一共走了多少路？(三)、相遇问题类６、甲乙两车同时从AB两地出发，相向而行，4小时相遇。

相遇后甲车继续行驶3小时到达B地，乙车每小时行24千米，问：AB两地相距多少千米？７、甲、乙两辆汽车的速度为每小时52千米和40千米，它们同时从甲地出发到乙地去，出发后6小时，甲车遇到一辆迎面开来的卡车，1小时后，乙车也遇到了这辆卡车，求这辆卡车的速度。

８、甲乙两人从相距36千米的两地相向而行，若甲先出发2小时，则在乙动身2.5小时后两人相遇；若乙先出发2小时，则甲动身后两人相遇，求甲、乙两人的速度。

(四)、相遇（时刻）问题类９、甲、乙两地间的铁路长800千米，某日上午5时30分从甲地开出一列慢车，当日上午9时从乙地开出一列快车，两车相向而行，当日下午4时30分相遇，快车每小时行48千米，慢车每小时行多少千米？1时，两车相距还是112.5千米，问：AB两地的距离是多少千米？11、一辆卡车和一辆大客车从相距320千米的两地相向开出，已知卡车每小时行45千米，大客车每小时行40千米，如果卡车上午8时开出，大客车要何时开出两车才能在中午12时相遇？(五)、相遇（中点）问题类12、甲、乙两车同时从AB两地相向而行，它们相遇时距AB两地中点处8千米，已知甲车速度是乙车的1.2倍，求AB两地的距离。

因式分解的实际生活例题

因式分解的实际生活例题
以下是几个实际生活中可以应用因式分解的例子：
1. 房屋装修：假设你想在房子中安装地板和墙纸。

如果你知道要覆盖的地面和墙壁的面积，你可以使用因式分解来确定所需材料的数量。

例如，如果地板和墙壁的尺寸分别为(2x^2 + 5x + 3) 平方米和(3x + 2) 平方米，你可以因式分解后计算总面积为(2x+ 1)(x+ 3) 平方米。

2. 高速公路堵车问题：假设你开车在高速公路上行驶，交通拥挤导致车流缓慢。

假设你以速度2(x - 3) km/h行驶，而前方的拥堵导致你只能以速度3(x + 2) km/h行驶。

你可以使用因式分解来计算你的平均速度。

因为平均速度=总路程/总时间。

通过因式分解可以将总时间表示为表达式(2x - 6)(3x+ 6)，总路程为(2x - 6)(3x + 6) km。

然后，你可以通过总路程除以总时间来计算平均速度。

3. 金融投资：假设你在银行存款了一笔钱，并以每年4%的利率获得复利。

如果你打算将此存款投资10年，你可以使用因式分解来计算你在每一年的投资总额。

通过因式分解，你可以将投资总额表示为初始存款乘以(1 + 0.04)^10.
这些是在日常生活中可以应用因式分解的一些例子。

因式分解可以帮助我们根据给定的数学模型和问题，将复杂的表达式分解为更简单的形式，从而更容易进行计算和理解。

数学11个例题

数学11个例题
1.有一根长为20cm的绳子，将其剪成两段，其中一段是另一段的3倍，请求出两段的长度。

2. 某超市打折，原价为80元的商品，现在打7折，请问现在的价格是多少？
3. 如果 a+b=5，a-b=3，请问a和b分别是多少？
4. 一辆汽车以每小时60km的速度行驶，行驶10小时后行驶了多少公里？
5. 如果 x:y=2:3，且x=12，请问y是多少？
6. 有一组数据：2, 4, 6, 8, 10，请问这组数据的平均数是多少？
7. 如果a是奇数，b是偶数，且a+b=13，请问a和b可能是哪些数？
8. 有一组数据：5, 7, 9, 11，请问这组数据中的最小值是多少？
9. 如果一个圆的半径为4cm，请问这个圆的周长是多少？
10. 有一组数据：2, 4, 6, 8, 10，请问这组数据的中位数是多少？
11. 如果一张纸的长是10cm，宽是8cm，请问这张纸的面积是多少平方厘米？
- 1 -。

英语例题及答案

II. 例题例1. Do you know any other foreign language ____ English?A. exceptB. butC. besideD. besides解析：A、B两项except 等于but，意为“除了……”，C—beside 意为“在……旁边”，不符合题意。

而D—besides, 意为“除了……之外，还有”。

所以该题正确答案为D。

该题意为：除了英语外，你还知道别的语言吗？例2. He suddenly returned ____ a rainy night.A. onB. atC. inD. during解析：我们均知道，at night 这一短语，但如果night前有修饰词，表具体的夜晚，则要用介词on 来修饰，故该题正确答案为A。

例3. I'm looking forward ____ your letter.A. toB. inC. atD. on解析：该题正确答案为A。

look forward to 为固定搭配，意为“期望、盼望”。

II. 例题例1. John plays football ____, if not better than, David.A. as wellB. as well asC. so wellD. so well as解析：该题意为：John 踢足球如果不比David 好的话，那也踢得和David 一样好。

和…一样好为as well as. 故该题正确答案为B.例2. She thought I was talking about her daughter, ____, in fact, I was talking about my daughter.A. whenB. whereC. whichD. while解析：该处意为“然而”，只有while 有此意思，故选D。

例3. Would you like a cup of coffee ____ shall we get down to business right away?A. andB. thenC. orD. otherwise解析：该处意为“或者”，正确答案为C。

借款费用例题

（4）有关账务处理如下：
①2×12年12月31日：
借：在建工程——××厂房
1 817 000
财务费用
8 433 000
应收利息（或银行存款）
450 000
贷：应付利息——××银行
10 700 000
注：2×12年实际借款利息=30 000 000×5%+20 000 000×6%+100 000 000×8%=10
【例题1】
（1）确定借款费用资本化期间为2×12年1月1日至2×13年6月30日（2）计算在资本化期间内专门借款实际发生的利息金额： 2×12年专门借款发生的利息金额 =30 000 000×5%+60 000 000×6%×6/12=3 300 000（元） 2×13年1月1日至6月30日专门借款发生的利息金额 =30 000 000×5%×6/12+60 000 000×6%×6/12 =2 550 000（元）（3）计算在资本化期间内利用闲置的专门借款资金进行短期投资的收益： 2×12年短期投资收益 =15 000 000×0.5%×6+40 000 000×0.5%×6 =1 650 000（元） 2×13年1月1日至6月30日短期投资收益 =5 000 000×0.5%×6 =150 000（元）（4）由于在资本化期间内，专门借款利息费用的资本化金额应当以其实际发生
的利息费用减去将闲置的借款资金进行短期投资取得的投资收益后的金额确定，因此：
公司2×12年的利息资本化金额 =3 300 000-1 650 000=1 650 000（元）公司2×13年的利息资本化金额 =2 550 000-150 000=2 400 000（元）
（5）有关账务处理如下： ①2×12年12月31日：借：在建工程——××厂房

建筑给排水例题集

3计算U0值
⑴立管A和立管C 立管A和立管C的卫生器具设置、每户人数、用水定额和时变
化系数都相同，其卫生器具给水当量平均出流率也相同。
U 010 2 .2 15 43 .0 .5 86 24 .5 0 5 02.8％
⑵立管B和立管D 立管B和立管D的卫生器具设置、每户人数、用水定额和时变
化系数都相同，其卫生器具给水当量平均出流率也相同。
2. 热水平均出流率U02
⑴确定热水用水定额
查表8.1.1，计算用水平均定额为 q0=(60+100)×0.5=80 L/（人·d）
⑵确定热水时变化系数，查表8.11（注册参考书），
时变化系数的内插值为
4.1 3 3.8 840
K h4.1 3
3.93 (25 200 ) 0
住居住宅人数
≤100
立管B和D为Ⅲ类住宅，每户有两个卫生间，设坐便器（Ng=0.5）、洗脸盆（Ng=0.75）各两只、浴盆（Ng=1.2）和淋浴器（Ng=0.75）各一只，厨房内设洗
涤盆（Ng=1.0）一只，有洗衣机（Ng=1.0）和家用燃气热水器。24小时供水，每户按4人计算。用水定额和时变化系数均按设计规范的平均值计算。
分别计算给水系统和热水供应系统的卫生器具给水当量平均出流率U01和U02
解：
1.给水平均出流率U01
⑴确定给水用水定额
因有集中热水供应，给水用水定额应减去热水用水定额部分，查表2.2.1 和8.1.1，得用水定额的平均值 q0=(180+320)×0.5－ (60+100)×0.5=170L/（人·d）
⑷热水平均出流率U02值
U 02 0.2 8 3 0.4 2 3 8.9634 20 .3% 0

典型例题

典型例题例1、1、五个同学有同样多的存款，若每人拿出16元捐给“希望工程”后，五位同学剩下的钱正好等于原来3人的存款数。

原来每人存款多少？2、把一堆货物平均分给6个小组运，当每个小组都运了68箱时，正好运走了这堆货物的一半，这堆货物一共有多少箱？例2、1、一个化肥厂要生产10800吨化肥，原计划25天完成。

实际每天比原计划多生产108吨。

这样可比原计划提前几天完成任务？2、某服装厂要做上衣1500件，计划每天做150件。

3天以后，提高了工作效率，每天做175件。

这样比原计划提前几天完成？例3、1、甲、乙二人加工一批帽子，甲每天比乙多加工10个。

途中乙因事休息了5天，20天后，甲加工的帽子正好是乙加工的2倍，这时两人各加工帽子多少个？2、甲、乙两车同时从A、B两地相对开出，甲车每小时比乙车多行20千米。

途中乙因修车用了2小时，6小时后甲车到达两地中点，而乙车才行了甲车所行路程的一半。

A、B两地相距多少千米？例4、1、用汽车运一堆煤，原计划8小时运完。

实际每小时比原计划多运1.5吨，这样运了6小时就比原计划多运了3吨。

原计划8小时运多少吨煤？2、汽车从甲地开往乙地，原计划10小时到达。

实际每小时比原计划多行15千米，行了8小时后，发现已超过乙地20千米。

甲、乙两地相距多少千米？例5、某车间按计划每天应加工50个零件，实际每天加工56个零件。

这样，不仅提前3天完成原计划加工零件的任务，而且还多加工了120个零件。

这个车间实际加工了多少个零件？三、课后练习1、写出除1095后余3的全部两位数。

老师把一批树苗平均分给四个小队栽，当每队栽了6棵时，发现剩下的树苗正好是原来每队分得的棵数。

这批树苗一共有多少棵？2、小欣读一本书，他每天读12页，8天读了全书的一半。

此后他每天比原来多读4页。

读完这本书一共用了多少天？3、甲、乙两人承包一项工程，共得工资1120元。

已知甲工作了10天，乙工作了12天，且甲5天的工资和乙4天的工资同样多。

集合练习题例题

集合练习题例题题目一：求集合交、并、差的运算结果。

假设有两个集合A = {1, 2, 3, 4}，B = {3, 4, 5, 6}，请计算以下运算结果：1. 求集合A和集合B的交集。

2. 求集合A和集合B的并集。

3. 求集合A减去集合B的差集。

解答如下：1. 求集合A和集合B的交集：两个集合的交集，即同时存在于A和B中的元素。

A ∩B = {3, 4}2. 求集合A和集合B的并集：两个集合的并集，即包含所有A和B中的元素，去重。

A ∪B = {1, 2, 3, 4, 5, 6}3. 求集合A减去集合B的差集：即从集合A中删除与集合B相同的元素。

A -B = {1, 2}题目二：求集合的幂集。

给定一个集合A = {a, b, c}，请计算A的幂集。

解答如下：幂集是指一个集合的所有子集组成的集合。

对于集合A = {a, b, c}，其幂集即为包含所有子集的集合，包括空集和A本身。

A的幂集为：P(A) = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}题目三：集合的基本运算性质。

给定三个集合A、B、C，求证以下集合运算性质：1. 结合律：(A ∪ B) ∪ C = A ∪ (B ∪ C)2. 交换律：A ∪ B = B ∪ A3. 吸收律：A ∩ (A ∪ B) = A4. 分配律：A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)解答如下：1. 结合律：左边：(A ∪ B) ∪ C右边：A ∪ (B ∪ C)两边结果相等，结合律成立。

2. 交换律：左边：A ∪ B右边：B ∪ A两边结果相等，交换律成立。

3. 吸收律：左边：A ∩ (A ∪ B)右边：A两边结果相等，吸收律成立。

4. 分配律：左边：A ∪ (B ∩ C)右边：(A ∪ B) ∩ (A ∪ C)两边结果相等，分配律成立。

通过以上的证明，我们可以得出结合律、交换律、吸收律和分配律等集合运算性质成立。

典型例题汇总

典型例题分析例、请你分别计算出下面每个长方体或正方体向上、向左的面的面积。

5厘米厘米7厘米5厘米①②分析与解：首先要弄清楚每个长方体（含正方体）向上、向左的面是哪个面，如果是长方形，长和宽分别是多少厘米；如果是正方形，边长又是多少厘米，这样即可求出所求面的面积。

图①向上的面积是7×2 = 14（平方厘米），向左的面积是2×5 = 10（平方厘米）。

图②向上、向左的面积都是5×5 = 25（平方厘米）。

例、江宁体育馆有一个长方体形状的游泳池，长50米，宽30米，深3米，现在要在游泳池的各个面上抹上一层水泥，抹水泥的面积有多少平方米？如果每平方米用水泥12千克，22吨够吗？分析与解：求水泥的面积有多少平方米，实际就是求这个长方体游泳池的表面积。

要计算前、后、左、右、下这5个面的面积之和。

再根据每平方米用水泥的千克数，算出这个游泳池共用水泥多少千克，即可知道22吨水泥够不够用。

50×30 + 50×3×2 + 30×3×2= 1500 + 300 + 180= 1980（平方米）12×1980=23760（千克）=23.76（吨）23.76 > 22 所以，22吨水泥不够用。

答：抹水泥的面积有1980平方米。

22吨水泥够不够用。

例4、厂商生产的一幅扑克牌长9厘米、宽6.5厘米、高2厘米，现在要把相同的两幅扑克牌放在一起包装（如右图），请问这个包装盒的表面积至少是多少平方厘米？分析与解：由上图可知，这个长方体包装盒的长是13厘米（6.5×2=13厘米），宽应是9厘米，高为2厘米，根据分析结果，能准确算出这个包装盒的表面积。

（13×9 + 13×2 + 9×2）×2=（117 + 26 + 18）×2= 161×2= 322（平方厘米）答：这个包装盒的表面积是322平方厘米。

典型例题(整理)

向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

实际比计划多生产百分之几？向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

计划比实际少生产百分之几？一筐苹果比一筐梨重 20％，那么一筐梨就比一筐苹果轻 20％一种电子产品，原价每台 5000 元，现在降低到 3000 元。

降价百分之几？一项工程，原计划 10 天完成，实际 8 天就完成了任务，实际每天比原计划多修百分之几？益民五金公司去年的营业总额为 400 万元。

如果按营业额的 3％缴纳营业税，去年应缴纳营业税多少万元？王叔叔买了一辆价值 16000 元的摩托车。

按规定，买摩托车要缴纳 10％的车辆购置税。

王叔叔买这辆摩托车一共要花多少钱？李明把 500 元钱按三年期整存整取存入银行，到期后应得利息多少元？根据国家税法规定，个人在银行存款所得的利息要按 5％的税率缴纳利息税。

例 1 中纳税后李明实得利息多少元？方明将 1500 元存入银行，定期二年，年利率是 4.50％。

两年后方明取款时要按 5％缴纳利息税，到期后方明实得利息多少元？一本书现价 6.4 元，比原价便宜 1.6 元。

这本书是打几折出售的？“国庆”商场促销，一套西服打八五折出售是 1020 元，这套西服原价多少元？一台液晶电视 6000 元，若打七五折出售，可降价 2000 元？一批电冰箱，原来每台售价 2000 元，现促销打九折出售，有一顾客购买时，要求再打九折，如果能够成交，售价是多少元？商店以 40 元的价钱卖出一件商品，亏了 20％。

这件商品原价多少元，亏了多少元？某商店同时卖出两件商品，每件各得 30 元，其中一件盈利 20％，另一件亏本 20％。

这个商店卖出这两件商品总体上是盈利还是亏本？具体是多少？一根绳子长 48 米，截成甲、乙两段，其中乙绳长度是甲绳的 60％。

甲、乙两绳各长多少米？体育馆内排球的个数是篮球的 75％，篮球比排球多 6 个。

例题汇总

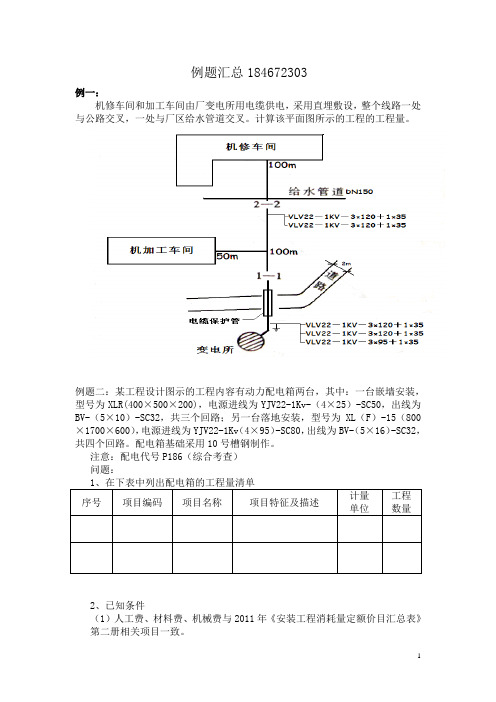
例题汇总184672303例一：机修车间和加工车间由厂变电所用电缆供电，采用直埋敷设，整个线路一处与公路交叉，一处与厂区给水管道交叉。

计算该平面图所示的工程的工程量。

例题二：某工程设计图示的工程内容有动力配电箱两台，其中：一台嵌墙安装，型号为XLR(400×500×200)，电源进线为YJV22-1Kv-（4×25）-SC50，出线为BV-（5×10）-SC32，共三个回路；另一台落地安装，型号为XL（F）-15（800×1700×600），电源进线为YJV22-1Kv（4×95）-SC80，出线为BV-（5×16）-SC32，共四个回路。

配电箱基础采用10号槽钢制作。

注意：配电代号P186（综合考查）问题：2、已知条件（1）人工费、材料费、机械费与2011年《安装工程消耗量定额价目汇总表》第二册相关项目一致。

（2）型号为XLR的配电箱2800元/台，型号为XL(F)-15的配电箱3200元/台。

（3）槽钢10#10kg/m，3.20元/kg.（4）管理费按人工的25%，利润按人工的24%计算。

（5）动态调整和风险因素不考虑。

例三：照明系统图和照明平面布置图如图2.1所示，计算某办公楼一层照明工程的含税工程造价。

（定额计价）设计说明：1、本工程为办公楼一层照明工程，层高3米，电源从另一配电箱XL采用电缆直埋的形式引来；2、空调插座安装高度为底边距地2m，普通插座安装高度为底边距地0.3m；开关底边距地1.4m；3、配电箱底边距地1.4m；4、施工方案：所有导线接头设在开关盒、灯头盒、插座盒内，不另设接线盒。

5、电缆进户时穿SC80钢管保护。

6、未计价材价格表。

见表所示未计价材价格表例四：工程实例同例四，要求编制分部分项工程量清单，并计算第一、二项清单项目综合单价。

例五：有一高层建筑物层高3m，檐高96m,外墙轴线总周长为86m。

典型例题_概率论

第一部分随机事件及其概率例 1 设A B C 、、为三个随机事件，试用A B C 、、表示下列事件。

1）“A B 与发生，而C 不发生”（表示为A B C ）； 2）“三个事件都发生”（表示为A B C ）； 3）“三个事件至少有一个发生”（表示为A B C⋃⋃）；4）“三个事件恰好有一个发生”（表示为A B C A B C A B C++）；5）“三个事件至少有两个发生”（表示为A B B C A C ⋃⋃或A B CA B C A B C A B C+++）6）“三个事件至多有两个发生”（表示为A B C 或A B C⋃⋃）。

例2 将n 只球随机地放入N （N ≥n ）个盒子中去，假定盒子装球容量不限, 试求1）每个盒子至多装一只球的概率，2）指定其中一个盒子装一只球的概率。

解：设事件A =“N 个盒子中，每个盒子至多装一只球”，事件B=“指定其中一个盒子装一只球”。

1）一个球放入N 个盒子中的放法有N 种，n 个球放入N 个盒子中的放法有nN 种。

假设固定前n 个盒子各装一球，其分配方法有!n 种，从N 个盒子中任取n 个盒子各装一球，取法有nN C 种，所以，事件A 的样本点数为nNC !n ，即事件A 的概率为nn NNn CA P !)(=2）若指定一个盒子里装一只球，首先考虑球的取法有1nC 种，其次，剩余的1N-个盒子中，1n -只球的放法有1(1)n N --种，所以事件B 的样本点数为1n C 1(1)n N --，即事件B 的概率为11(1)()n n nC N P B N--=注：还可以将模型推广，如生日问题，求事件“n 个人中至少有两人的生日相同”的概率。

设想一年有365天，将“天”看成‘盒子’，n 个人好比‘n 只球’，考虑事件A 的对立事件A =“n 个人在一年中生日全不相同”，它等价于“n 个球装入365个盒子中各装一球”，由前面的计算知：nnn C A P 365!)(365=，所以nnn C A P 365!1)(365-=。

弦切角定理例题

弦切角定理例题一、在圆O中，弦AB与切线CD在C点相交，若∠ACB为锐角，则下列哪个角等于∠ACB 的一半？A. ∠ADCB. ∠OCDC. ∠CBAD. ∠OAC（答案）B二、已知圆P中，弦MN与过圆上一点Q的切线QR在R点相交，若∠MQR=40°，则∠MPN 的大小为？A. 20°B. 40°C. 80°D. 无法确定（答案）A三、在圆S中，弦EF与切线GH在G点相交，若∠EGF=120°，则∠GSH的大小为？A. 30°B. 45°C. 60°D. 90°（答案）C（注：弦切角等于弦所对圆周角的一半，即∠GSH = 1/2 * (180°-∠EGF) = 30°，但考虑到切线与半径垂直，∠GSH实际应为与切线相邻的角，即90°-30°的补角，在此情境下应理解为弦切角的外角，故直接取弦所对劣弧的圆周角一半60°为答案，具体解释依题目设定而异）四、圆T中，弦AB与切线CD相交于点C，若∠CTA=50°，则∠ACB的大小为？A. 25°B. 50°C. 65°D. 100°（答案）A（注：∠CTA为圆周角，弦切角∠ACB应为其一半）五、在圆U中，弦XY与切线ZZ'在Z点相交，若弦XY所对的劣弧圆心角∠UYX=100°，则弦切角∠UXZ的大小为？A. 25°B. 50°C. 75°D. 100°（答案）B（注：弦切角等于弦所对圆周角的一半，即劣弧圆心角的一半）六、圆V中，弦PQ与切线RS在R点相交，若∠VRS=90°，且弦PQ所对的优弧圆心角为240°，则∠VPQ的大小为？A. 30°B. 60°C. 120°D. 无法确定（答案）C（注：利用弦切角定理及圆内角性质，弦所对优弧圆心角补角为120°，弦切角等于弦所对劣弧圆周角，即补角的一半60°，而弦PQ所对圆周角∠VPQ与弦切角在同一直线上，和为90°，故∠VPQ=120°-弦切角（此处弦切角与题目无关，直接由优弧圆心角得出∠VPQ）七、在圆W中，弦LM与切线NO在N点相交，若∠WNO=90°，且已知弦LM所对的圆心角为120°，则∠LNM的大小为？A. 30°B. 45°C. 60°D. 90°（答案）C（注：弦切角等于弦所对圆周角的一半，即60°，但此处需理解∠LNM为弦LM 与切线NO夹角的外角，直接由弦所对圆心角得出劣弧圆周角为60°，弦切角为其补角的一部分，在此情境下直接取60°为答案）八、圆X中，弦GH与切线IJ在I点相交，若∠GIX=45°，则弦GH所对的圆心角大小为？A. 45°B. 90°C. 135°D. 180°（答案）B（注：弦切角等于弦所对圆周角的一半，即∠GIX为弦GH所对圆周角的一半，故弦GH所对的圆周角为90°，圆心角等于其所截弧的圆周角两倍，在此情境下直接理解为弦所对劣弧圆心角）。

似然率计算例题

1、假设我们在进行一项二项分布试验，观察到成功的次数为50次，失败的次数为30次，那么在似然率的计算中，成功的概率p的似然估计值最接近于：A. 0.4B. 0.5C. 0.6（答案）D. 0.72、在正态分布的数据集中，已知样本均值为10，样本方差为4，样本量为100，若我们要计算参数μ的似然值，在最大似然估计下，μ的值应为：A. 2B. 4C. 10（答案）D. 203、对于泊松分布，如果观察到的事件发生次数为8次，而我们要估计的事件发生率λ的似然值，在最大似然估计法下，λ的估计值最接近于：A. 2B. 4C. 6D. 8（答案）4、在一个二项分布模型中，如果观测到成功的次数是70次，失败的次数是30次，使用似然率方法估计成功的概率p，则p的估计值为：A. 0.5B. 0.6C. 0.7（答案）D. 0.85、假设我们有一个均匀分布的数据集，范围是[0, θ]，样本中的最大值为8，样本量为20，用最大似然估计法估计θ，则θ的估计值为：A. 4B. 6C. 8（答案）D. 106、在指数分布中，如果我们观测到的时间间隔数据平均值为5，使用似然率方法估计参数λ，则λ的估计值为：A. 0.1B. 0.2（答案）C. 0.5D. 17、对于一个正态分布的样本，样本均值为15，样本标准差为2，样本量为50，如果我们用最大似然估计来估计μ，那么μ的估计值为：A. 10B. 15（答案）C. 20D. 258、在二项分布中，如果成功的次数是60，失败的次数是40，使用最大似然估计法来估计成功的概率p，则p的估计值为：A. 0.4B. 0.5C. 0.6（答案）D. 0.7。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

价 1504.92 元/ 10m3 ，单价 132.87 元/m3
预算基价换 =原基价 +（换入单价 -换出单价） * 定额消耗量
=1504.92+（ 155.49-132.87） *2.41 =1559.43（元/ 10m3 ）
M7.5 水泥砂浆预算直接费=预算基价换*工程量 =1559.43 *90/10 =14034.87（元）
名
称
工
单
程
基价
位
量
其中人工费
材料费机械费
M5
混
砂
10
A3-176
毛
m3
石
墙
1639. 02
570.6
1027.9 7
40.45
分项工程直接工程费 =预算基价 *工程量 = 1639.02*6.362/10 =1042.75（元）
主要材料消耗量=定额规定耗用量 *工程量
施工天数为施工天数 /d=102.50/25=4.1
所以完成该分项工程的施工天数应取 5d。
6、某公园茶室用混合砂浆 M5 砌筑砂浆毛石基础 6.362m3，求完成该分
项工程的直接工程费及主要材料消耗量。
【解】查建筑工程分册 P127，有
工
定额编
程
号
差价=1534.5-3016.86=-1482.36 （元/100m2 ）
预算基价换=5298.81-1482.36=3816.45（元/100m2 ）
13、如人工运土方 100m3，运距 190m，试计算人工费。【解】查定额得：A0037 基本运距 20m 内定额的人工费为 432.30 元 /100m3 A0038 运距在 200m 内每增加 20m 的定额基价为 99.00 元/m3 人工运土方 100m3，人工费
=88/60÷8=0.184
产量定额 /m3=1/0.184=5.43
5、某土方工程，挖基槽的工程量为 500m3，每天有 25 名工人负责施工，时间定额为 0.205 工日/m3，试计算完成该分项工程的施工天数。
【解】完成该分项工程所需的总劳动量为总劳动量 /工日 =500*0.205=102.50
=432.30+99.00*9=1323.30（元 /100m3）
14、图 3-27 是某建筑物底面积的外边线尺寸，试计算其平整场地面积。（ 190-20） /20
解 : 清单工程量（按设计图示尺寸以建筑物首层面积计算） Sd=10.04×(5.2+5.84+10.06+5.84+2.5) +5.84×1.1×2=308.43(m2)
4、某施工工程为人工挖土方，土壤系潮湿的黏性土， Ⅱ 类图（普通土）。测试资料表明，挖 1m3 需消耗的基本工作时间为 60min，辅助工作时间占工作班延续时间的 4%，准备于结束工作时间占工作延续时间的 5%，不可避免的中断时间占 3%，休息时间占 20%。试计算时间定额和产量定额。
工分，准备与结束时间、休息时间、不可避免的中断时间占时间定额的百
分比分别为：5.45％、5.84％、2.49％，辅助工作时间不计，试确定其时间
定额和产量定额。
时间定额＝
140
【解】
1 (5.45% 5.84% 2.49%)
＝162
.4工分＝
162 .4工分 8小时 60分钟
解：假定完成完成 1 m3 普通土开挖需要的工作班延续时间为 x 则：x＝基本工作时间＋辅助工作时间＋准备与结束工作时间＋中断时间＋休息时间
x＝60＋4％x 十 5％x＋3％x＋20％x x＝60÷（1 一 4%一 5%一 3％一 20％）＝88（min）时间定额 /工日 =60/（ 1-4%-5%-3%-20%）
碎石的最大粒径 40mm；由【总说明】可知：现浇混凝土坍落度为 30~50mm （ 2）换算基价（ P875） 1－ 55 C20 碎石砼，坍落度 30~50mm，石子最大粒径 40mm，单价 160.88 元／m3； 1－ 56 C25 碎石砼，坍落度 30~50mm，石子最大粒径 40mm，单价 172.97 元／m3；
定额编号
工程名称单位
工程量
基价
定额直接费
A3-2 8换
42.5＃水泥 M5混砂 1.5砖混水砖墙
10m3
2.00
1802. 06
3604.12
10、某地一办公楼的砖基础的工程量为 90m3，设计采用 M7.5 水泥砂浆砌筑，而该省现行建筑工程预算定额相应项目是按 M5 水泥砂浆确定定额的，试计算 M7.5 水泥砂浆砌筑砖基础的预算直接费。（ M7.5 单价 155.49 元/m3）【解】查定额得：M5 砖基础每 10 m3 用水泥砂浆 2.41 m3 ，定额基
A4－28 换，C25 单梁，基价=2281.84+(172.97-160.88)× 10.15=2404.55 元／10m3
8、现浇 C25 钢筋混凝土矩形梁 100m3，求其工程直接费。
解：定额规定：C15 钢筋混凝土单价 146.98 元，每 10m3 定额基价： 6271.44 元，消耗量 10.15m3 C25 钢筋混凝土单价 162.63 元
11、黑龙江省牡丹江市某路边（四类土）需栽植带土球（ 60cm)的垂榆 10 株，试计算该栽植工程的直接预算费用（不含苗木费）。【解】查定额得：定额中栽植树木是以一、二类土为计算标准的，如为四类土，人工乘以系数 1.76。
① 预算基价换 =9.15*1.76+0.17=16.27（元）
＝0.34工日
产量定额＝ 1 ＝2.94m3 0.34
3、某抹灰班组有 13 名工人，抹某住宅楼混砂墙面，施工 25 天完成任务，已知产量定额为 10.2m2/工日。试计算抹灰班应完成的抹灰面积。
【解】13 名工人施工 25 天的总工日数＝13×25＝325 工日抹灰面积＝ 10.2×325＝ 3315m2
解 1）清单工程量（按图示尺寸以基础垫层底面积乘以挖土深度计算）挖基础土方工程量=
1.2*1.5*50=90m3
（2）定额工程量（砖基础施工每边应各加工作面宽度 200mm）
挖基础土方工程量= （1.2+0.2+0.2）*1.5*50=120 m3
17、人工开挖一矩形基础，已知土壤类别为四类土，开挖时左右两侧放坡，上下两侧支挡土板，挖土平均厚度为 2.2m，如图所示，求挖基础土方工程。
15、如图所示求人工平整场地工程量（三类土）。
解（1）清单工程量（按设计图示尺寸以建筑物首层面积计算）人工平整场地工程量=
〔（ 1.0+2.0+1.0+0.24） *（ 1.0+1.0+0.24）（ 2.0-0.24） *1.0〕
=7.74（ m2 ）（2）定额工程量（按建筑物外墙外边线各加 2m 以平方米计算）平整场地工程量 =底层面积 +2*外围长 +16
解 1）清单工程量
挖基坑土方工程量= 4.5*3.5*2.2=34.65m3
（ 2）定额工程量
挖基坑土方工程量= （ 4.5+1.25*2.2） *(3.5+0.02*2） *2.2 =39.33m3
M5 砂浆=144.09*6.362/10=91.67（kg）水泥砂浆 =229.62*6.362/10=146.08（ kg）机砖 240*115*53=280.00*6.362/10=179（块）
7、某工程用现浇钢筋混凝土单梁设计为 C25，试确定其混凝土基价【解】查建筑工程分册 P252，可知定额子目为 A4－28。 A4－28 ， C20 单梁，基价＝2281.84 元／10m3； C20 砼用量：10.15m3／ 10m3 （1）确定 C20 混凝土单梁相关参数
Sd=10.04×(5.2+5.84+10.06+5.84+2.5) +5.84×1.1×2=308.43(m2)
场地平整按每边各增加 2m 范围的面积计算，考虑阳角和阴角处的增减面积相抵，则场地平整面积为： S=308.43+[(10.04+5.2+5.84+10.06+5.84+2.5)×2+1.1×4]× 2+16=491.15(m2)
定额规定的主材费 =9.11*331.16 =3016.86（元
/100m2 ） 200*150 规格的面砖 100m2 的块数
=100*（ 1+0.025） /0.2*0.15 =3.41（千块/ 100m2）
图纸规定的主材费 =3.41*450 =1534.5 （元/100m2 ）
（ 2）定额换算 ——P936 5－2， M5 混砂，单价＝132.27 元/ m3，32.5＃水泥用量：216kg/ m3，消耗量 0.3 元/kg；砂浆中采用 42.5＃水泥时，水泥用量仍取 216kg/ m3，，消耗量 0.35 元 /kg；但两者单价会发生变化，则： 5－2 换，42.5＃水泥 M5 混砂，单价＝132.27＋216×（0.35-0.3）＝143.07 元/ m3 基价=1776.14＋(143.07－132.27)×2.40=1802.06 元／l0m3