5方差分析-2
合集下载
第十讲 第五章 方差分析2
B与C比：23-18=5<5.07，不显著
D与C比：24-18=6>5.23，显著
结论：只有处理D和C的差异在a=0.05水平显著， 其余皆不显著。
2.q检验：
q检验与SSR检验相似，其区别仅在a，而是查qa。
查qa值后，即有:
LSR= s x ×qa
3.各方法的异同
课堂练习：完全随机试验设计试验结果的统计分析
.
[例4] 研究6种氮肥施用方法(K=6)对小麦的效应,每种施 肥方法种5盆小麦(n=5),完全随机设计,最后测定它们的含 氮量,其结果如下表.试作方差分析
表 6种施肥法小麦植株含氮量
处理
施 12
氮法 34 5
6 总和
2.9 4 2.6 0.5 4.6 4
第五章 方差分析2 三、多重比较
F检验是一个整体的概念。仅能测出不同处理效应的平均 数的显著差异性。但是，是否各个平均数间都有显著差异性？ 还是仅有部分平均数间有显著差异而另一部分平均数间没有 显著差异？它不曾提供任何信息。
要明确各个平均数间的差异显著性，还必须对各平均数 进行多重比较。
多重比较的方法主要有两大类： （一）LSD法：t检验法 （二）LSR法：分为SSR法、q检验法
表8 新复极差检验的LSR值
p
2
3
4
5
SSR0.05 SSR0.01 LSR0.05 LSR0.01
2.92 3.96 0.304 0.412
3.07 4.14 0.319 0.431
3.15 4.24 0.328 0.441
3.22 4.33 0.335 0.450
6 3.28 4.39 0.341 0.457
(二)平方和分解
方差分析
方差分析方差分析方差分析是比较多个总体的均值是否相等，但本质上它所研究的是变量之间的关系。
在研究一个（或多个）分类型自变量与一个数值型因变量之间的关系时，方差分析就是其中的只要方法之一。
一、方差分析引论假设需要检验4个总体的均值分别为4321,,,μμμμ，如果用一般假设检验方法，如t 检验，一次只能研究两个样本，要检验4个总体的均值是否相等，需要做6次检验，如果在0.05的置信水平下检验，每次检验犯第Ⅰ类错误的概率都是0.05，检验完成时，犯第Ⅰ类错误的概率会大于0.05，即连续作6次检验第Ⅰ类错误的概率为6)1(1α--=0.265,而置信水平则会降低到0.735（即695.0）。
随着增加个体显著性检验的次数，偶然因素导致差别的可能性也会增加（并非均值真的存在差别）。
而方差分析方法则是同时考虑所有的样本，因此排除了错误累计的概率，从而避免拒绝一个真实的原假设。
1、方差分析及其有关术语方差分析：就是通过检验各总体均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
例1：为了对几个行业的服务质量进行评价，消费者协会在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业作为样本。
其中零售业7家，旅游业抽取6家，航空公司抽取5家，家电制造业抽取5家。
最后统计出最近一年中消费者对总共23家企业投诉的次数。
如下表所示。
消费者对四个行业的投诉次数行业零售业 旅游业 航空业 家电制造业57 68 31 44 66 39 49 51 49 29 21 65 40 45 34 77 34 56 40 58 53 51 44要分析四个行业之间的服务质量是否有显著差异，实际上就是要判断“行业”对“投诉次数”是否有显著影响，做出这种判断最终被归结为检验这四个行业被投诉次数的均值是否相等。
在方差分析中，要检验的对象称为因素或因子。
因素不同的表现称为水平或处理。
每个因子水平下得到的样本数据称为观测值。
在例1中，“行业”是要检验的对象，称为“因素”或“因子”；零售业，旅游业，航空公司，家电制造业是行业这一因素的具体表现，称为“水平”或“处理”；在每个行业下得到的样本数据（被投诉次数）称为观测值。
第六章方差分析(二)
1.46
1.03
1.62
1.27
31.50
28.97
合计
2.08 2.97
2.08 2.49
2.06 2.91
2.30 3.08
2.24 2.58
SST SSA SSB
2.自由度的分解
总自由度：dfT ab 1
A的自由度：dfA a 1 B的自由度：dfB b 1
组内自由度：dfe (a 1)(b 1)
3. 方差计算：
s
2 A
SS A df A
sB2
SSB df B
se2
SSe dfe
方差分析表
变异来源 df A因素 a－1 B因素 b－1
SSR值与LSR值（dfe = 27）
M SSR0.05 SSR0.01 LSR0.05 LSR0.01
2 2.905 3.925 9.267 12.521
3 3.055 4.095 9.745 13.063
光照（A）
5h/d 10h/d 15h/d
平均数
Tij
90 -9 -17
差异显著性
α=0.05 α=0.01
…
Xabn
T•b
T
x•b
x
线性数学模型：
A、B的交互作用
随机误差，独立，正态分布
xijk i i ( )ij＋ ijk
A因素的效应
B因素的效应
1. 总变异
自由度 平方和
2. A因素引起的变异
自由度 平方和
3. B因素引起的变异
自由度 平方和
4. A、B因素的交互作用引起的变异
自由度 平方和
1. 平方和的分解
矫正数：C T 2 ab
第4讲5(1) 正交试验设计(方差分析)
处理号 1 2
第1列（A） 1 1
表 L9(34)正交表
第2列 1 2
第3列 1 2
第4列 1 2
因素A第1 试验结果y水i 平3次
重复测定 y1 值 y2
3
1
3
3
3
y3
单4 因素 2
1
2
3
y4
试5 验数 2
2
3
1
y5
因素A第2
SS据A6＝资13（料y1 y22
格式 78＝13（K12
3 K322
y3）2 （y43y5
K32）-
T2 9
1 2
y6）2 （ 1 y7 3 1
y 82y 9）2 2 3
（y1yy62 ...
9
y7 y8
y水9）平2（修 3次正重项） 复测定值
9
3
3
2
1
y9
分析第1列因素时，其它列暂不考虑，将其看做条件因因素素A。第3
因素 重复1 重复2 重复3
显著影响
（6）列方差分析表
（1）偏差平方和分解：
总偏差平方和＝各列因素偏差平方和+误差偏差平方和
SST SS因素 SS空列（误差）
（2）自由度分解：
dfT df因素 df空列（ 误列（
（3）方差：MS因素＝
SS因素 df因素
，MS误差＝
SS误差 df误差
（4）构造F统计量：
F因素＝
MS因素 MS误差
（5）列方差分析表，作F检验
若计算出的F值F0>Fa，则拒绝原假设，认为 该因素或交互作用对试验结果有显著影响；若 F0≼Fa，则认为该因素或交互作用对试验结果 无显著影响。
第4讲5(2) 正交试验设计(方差分析)
2
1 1 2 2 1 10.12 10.09 0.03
2
1 2 1 1 2 10.19 10.02 0.17
2.66
2.58 2.36 2.4 2.79 2.76
0.0055 0.0078 0.0091 0.0001 0.0036
返回15
链接
（2）显著性检验
变异来源 A 平方和 自由度 0.0210 1
0.575
1.845 0.11 12.745
1
1 2 7
0.575
1.845 0.055
10.455
33.545 *
根据F值的大小排出因子的主次： 主 次
A×B、A、B×C、B、（A×C、 C）
A×B的重要性排在A、B的前面，挑选A、B的最优水平时 要从A×B的最优搭配来考虑,同理C的最优水平也应以B×C为 主. A×B的最优搭配的选取是通过A、B搭配效果表决定的。 A、B搭配效果表
B与C的最优搭配：B1C2 从A×B和B×C的最优搭配中,B因素的最优水平矛盾, 但是A×B的重要性排在B×C的前面,所以,从A×B来考选B2, 当B因素选B2时,由B×C的搭配表C选C1,综合考虑其最优工 艺为：A2B2C1. 因为,本例三个因素的所有搭配就是正交表中的8次试 验,从表中试验数据也可以看到,A2B2C1是第7号试验,不匀率 为3.17是8次试验中最小的,即为最优组合（最优工艺）。
它用多水平正交表安排水平数较少的因素的一种方法
例：在高效液相色谱法测定食品中胡萝卜素 的研究中，欲通过正交试验选择柱层析法净 化条件，试验指标为胡萝卜素回收率，不考 虑交互作用，试验因素水平表见表4-35。
表4-35 因素水平表
1
活化温度 ℃ A 100
第三章 正交试验设计中的方差分析2-例题分析
由极差看B的影响最小，即络合剂是测定的次要因素。 由极差看 的影响最小，即络合剂是测定的次要因素。 的影响最小 第五步，进一步画出指标－因素趋势图观察。 第五步，进一步画出指标－因素趋势图观察。
24 23 22 21 Abs
Abs 21.5 21 20.5 20 19.5 19 18.5
Abs 24 23 22 21 20 19 18 17 16 15
三．实际应用举例 例8：用原子吸收光谱测定铝合金中痕量铁时， ：用原子吸收光谱测定铝合金中痕量铁时， 需要选择以下三个因素的最适宜条件： ） 需要选择以下三个因素的最适宜条件：1）酸度 (用1:1盐酸的体积代表 ；2）络合剂（5％的8用 盐酸的体积代表 盐酸的体积代表)； ）络合剂（ ％ 羟基喹啉）加入量；3）释放剂（20mg/ml的锶 羟基喹啉）加入量； ）释放剂（ 的锶 盐）加入量。每个因素考虑三个水平，分别是： 加入量。每个因素考虑三个水平，分别是： 4ml、7ml、10ml；3ml、6ml、9ml；1ml、 、 、 ； 、 、 ； 、 9ml、17ml。如何安排这个试验，并对结果进 、 。如何安排这个试验， 行分析。 行分析。
同样： 同样：QB=10.9；QC=76.2； ； ；
总的方差和Q 如下计算： 总的方差和 T如下计算：
那么试验误差的差方和就可如下计算： 那么试验误差的差方和就可如下计算： Qe＝QT－（ A＋QB＋QC） －（Q －（66.9＋10.9＋76.2） ＝168.2－（ －（ ＋ ＋ ） ＝14.2 其次，计算自由度： 其次，计算自由度： fT＝n－1＝9－1＝8； － ＝ － ＝ ； fA＝fB＝fC＝m－1＝3－1＝2 ； － ＝ － ＝ fe=fT－fA－fB－fC＝2 。
正交试验设计的方差分析小结
第5章_方差分析(第2节)
（三）多重比较结果的表示方法
1、三角形法 此法是将多重比较结果直接标记在平均数 多重比较表上，如表5-4、表5-5所示。由于 在多重比较表中各个平均数差数构成一个三角 形阵列，故称为三角形法。此法的优点是简便 直观，缺点是占的篇幅较大。
2、标记字母法
先将各处理平均数由大到小自上而下 排列；然后在最大平均数后标记字母a，并 将该平均数与以下各平均数依次相比 ，凡 差异不显著标记同一 字母a，直到某一与 其差异显著的平均数标记字母 b 为止；
在利用字母标记法表示多重比较结果时， 常在三角形法的基础上进行。此法的优点是占 篇幅小，在科技文献中常见。 对于【例5·1】，根据表5-4所表示的用
SSR法进行的多重比较结果，用字母标记如表
5-8所示。
表5-8 表5-4多重比较结果的字母标记 (SSR测验)
处 理 平均产量 (克/盆) 31.5 28.5
上一张 下一张 主 页
退 出
式中 μ为总平均数； αi，βj分别为Ai、Bj的效应: αi=μi-μ，βj=μj-μ μi、μj分别为Ai、Bj观测值总体平均数， 且Σαi=0,Σβj=0; εij为随机误差 ，相互独立 ， 且服从N (0，σ2)。
上一张 下一张 主 页 退 出
交叉分组两因素单个观测值的试验，A因
4
5
3.18
3.25
4.33
4.40
1.988
2.031
2.706
2.750
表5-19 5个玉米品种平均穗长多重比较表(SSR法)
品种 平均数
B1
B4
20.2
19.6
3.6**
3.0**
3.0**
2.4*
1.9
1.3
1、三角形法 此法是将多重比较结果直接标记在平均数 多重比较表上，如表5-4、表5-5所示。由于 在多重比较表中各个平均数差数构成一个三角 形阵列，故称为三角形法。此法的优点是简便 直观，缺点是占的篇幅较大。
2、标记字母法
先将各处理平均数由大到小自上而下 排列；然后在最大平均数后标记字母a，并 将该平均数与以下各平均数依次相比 ，凡 差异不显著标记同一 字母a，直到某一与 其差异显著的平均数标记字母 b 为止；
在利用字母标记法表示多重比较结果时， 常在三角形法的基础上进行。此法的优点是占 篇幅小，在科技文献中常见。 对于【例5·1】，根据表5-4所表示的用
SSR法进行的多重比较结果，用字母标记如表
5-8所示。
表5-8 表5-4多重比较结果的字母标记 (SSR测验)
处 理 平均产量 (克/盆) 31.5 28.5
上一张 下一张 主 页
退 出
式中 μ为总平均数； αi，βj分别为Ai、Bj的效应: αi=μi-μ，βj=μj-μ μi、μj分别为Ai、Bj观测值总体平均数， 且Σαi=0,Σβj=0; εij为随机误差 ，相互独立 ， 且服从N (0，σ2)。
上一张 下一张 主 页 退 出
交叉分组两因素单个观测值的试验，A因
4
5
3.18
3.25
4.33
4.40
1.988
2.031
2.706
2.750
表5-19 5个玉米品种平均穗长多重比较表(SSR法)
品种 平均数
B1
B4
20.2
19.6
3.6**
3.0**
3.0**
2.4*
1.9
1.3
方差分析(研) 2012-2
2013-8-9 38
补充例题
两因素：疾病种类（A）与护士年龄（B）
a=4（心脏病、肿瘤、脑血管意外、结核病）
b=3（20～、30～、40～），N=60 观察变量为访视时间（分钟） 问：
(1) 不同年龄组护士进行家庭访视所花时间是否不同？ (2) 疾病病种是否对护士的家庭访视时间有显著影响？ (3) 护士年龄与疾病病种间是否存在交互作用？
2013-8-9 2
第五节 交叉设计的方差分析
2013-8-9
3
• 交叉设计（cross-over design）
– 医学研究中多用于止痛、镇静、降压等药物疗 效的研究，可分为两阶段交叉设计和多阶段交 叉设计。
• 两阶段交叉设计方差分析的变异分解为：
SS总 SS处理 SS阶段 SS个体 SS误差
第 十 章
黄志刚 公卫学院 流行病与统计教研室
2013-8-9 1
• 方差分析的基本思想
– 将所有观察值之间的变异（称总变异）根据离 均差平方和划分的原理，按设计和需要分解成 两个或多个部分。每一部分变异都反映了研究
工作中某种特定的内容（如某种处理因素的作
用、随机误差的影响等），通过对平均变异
（MS）的比较，做出相应的统计判断。
31
23
78
80
25
18
18
42
完全随机的两因素2×2析因设计
乙药
甲药
用
64
不用
56
用
78
80
44
42
28
不用 31 23
16
25 18
实例2：白血病患儿的淋巴细胞转化率（％），问① 不同缓解程度、不同化疗期淋转率是否相同？②两者 间有无交互作用?
补充例题
两因素：疾病种类（A）与护士年龄（B）
a=4（心脏病、肿瘤、脑血管意外、结核病）
b=3（20～、30～、40～），N=60 观察变量为访视时间（分钟） 问：
(1) 不同年龄组护士进行家庭访视所花时间是否不同？ (2) 疾病病种是否对护士的家庭访视时间有显著影响？ (3) 护士年龄与疾病病种间是否存在交互作用？
2013-8-9 2
第五节 交叉设计的方差分析
2013-8-9
3
• 交叉设计（cross-over design）
– 医学研究中多用于止痛、镇静、降压等药物疗 效的研究，可分为两阶段交叉设计和多阶段交 叉设计。
• 两阶段交叉设计方差分析的变异分解为：
SS总 SS处理 SS阶段 SS个体 SS误差
第 十 章
黄志刚 公卫学院 流行病与统计教研室
2013-8-9 1
• 方差分析的基本思想
– 将所有观察值之间的变异（称总变异）根据离 均差平方和划分的原理，按设计和需要分解成 两个或多个部分。每一部分变异都反映了研究
工作中某种特定的内容（如某种处理因素的作
用、随机误差的影响等），通过对平均变异
（MS）的比较，做出相应的统计判断。
31
23
78
80
25
18
18
42
完全随机的两因素2×2析因设计
乙药
甲药
用
64
不用
56
用
78
80
44
42
28
不用 31 23
16
25 18
实例2：白血病患儿的淋巴细胞转化率（％），问① 不同缓解程度、不同化疗期淋转率是否相同？②两者 间有无交互作用?
方差分析(2次)
பைடு நூலகம்
它除了推断k个样本所代表的总体均数µ1 ，µ2 ， µ3 ，…是否相等外，还要推断b个区组所代表 的总体均数是否相等。由于从总变异中分离出 配伍组变异，考虑了个体变异对处理的影响， 使误差更能反映随机误差的大小，因而提高了 研究效率。
SS总 = SS处理 + SS配伍 + SS误差 df总 = df处理 + df配伍 + df误差
第一节
完全随机设计的方差分析
试验设计时，将受试对象随机分配到两组或 多组中进行实验观察，这里只涉及一个因素， 该因素的各个水平就是各个处理组。
单因素方差分析
或称单向方差分析（one way analysis of variance）或 成组设计（完全随机设计）方差分析，是指试验研究 的处理因素，或调查研究资料的分类方式只有一种。 这个处理因素（或分类方式）包含有多个离散的水平， 分析在不同水平上应变量的平均值是否来自相同总体
Xi = ∑ Xij ni
j =1
ni
X = ∑∑ Xij N = ∑ni Xi N
i =1 j =1 i =1
k
ni
k
SS总 = ∑∑ Xij − X
i=1 j =1
k
ni
(
)
2
ν总 = N −1
2、组间变异 、
SS组间 = ∑ni Xi − X
k
ν组间 = k −1
3、组内变异
i =1
(
)
2
MS组间 = SS组间 ν组间
一、基本思想
*
Xij表示第i个处理组的第j个观察值，i=1,2,…k, j=1,2,…ni
方差分析基本思想示意图
变异原因
它除了推断k个样本所代表的总体均数µ1 ，µ2 ， µ3 ，…是否相等外，还要推断b个区组所代表 的总体均数是否相等。由于从总变异中分离出 配伍组变异，考虑了个体变异对处理的影响， 使误差更能反映随机误差的大小，因而提高了 研究效率。
SS总 = SS处理 + SS配伍 + SS误差 df总 = df处理 + df配伍 + df误差
第一节
完全随机设计的方差分析
试验设计时，将受试对象随机分配到两组或 多组中进行实验观察，这里只涉及一个因素， 该因素的各个水平就是各个处理组。
单因素方差分析
或称单向方差分析（one way analysis of variance）或 成组设计（完全随机设计）方差分析，是指试验研究 的处理因素，或调查研究资料的分类方式只有一种。 这个处理因素（或分类方式）包含有多个离散的水平， 分析在不同水平上应变量的平均值是否来自相同总体
Xi = ∑ Xij ni
j =1
ni
X = ∑∑ Xij N = ∑ni Xi N
i =1 j =1 i =1
k
ni
k
SS总 = ∑∑ Xij − X
i=1 j =1
k
ni
(
)
2
ν总 = N −1
2、组间变异 、
SS组间 = ∑ni Xi − X
k
ν组间 = k −1
3、组内变异
i =1
(
)
2
MS组间 = SS组间 ν组间
一、基本思想
*
Xij表示第i个处理组的第j个观察值，i=1,2,…k, j=1,2,…ni
方差分析基本思想示意图
变异原因
方差分析二：双向方差分析
Yijk
ik
S j
Yij2k
ik
20 557
20 596
20 659
16613
18000
22843
华中科技大学同济医学院 宇传华制作，2004，9
60 1812
57456
21
两因素析因分析的方差分析步骤
1.整理数据：求出处理因素 A、B 及其交互项 AB 的观
察值之和，一个因素的观察值平方和、总和、总平方和等。
110447.5 6
变异分解
(1) 总变异： 所有观察值之间的变异
(2) 处理间变异：处理因素＋随机误差
(3) 区组间变异：区组因素＋随机误差
(4) 误差变异：
随机误差
S S 总 S S 处 理 S S 区 组 S S 误 差
总 处 理 区 组 误 差
华中科技大学同济医学院 宇传华制作，2004，9
双向方差分析前面内容回顾析因设计factorialdesignanova所关心的问题析因设计的4个实例析因设计的特点2个或以上处理因素factor分类变量本节只考虑两个因素每个因素有2个或以上水平level每一组合涉及全部因素每一因素只有一个水平参与几个因素的组合中至少有2个或以上的观察值观测值为定量数据需满足随机独立正态等方差的anova条件三交互作用三交互作用图第三节两因素析因设计方差分析中的多重比较第四节裂区设计splitplotdesign资料的方差分析裂区设计资料的特点一级单位大区间主区家庭学校二级单位小区内即裂区家庭成员学生两因素裂区设计资料的方差分析方法先按随机区组析因设计的方法分析因素a家庭拥挤程度区组家庭的主效应及其交互作用
变异来源 处理 区组 误差 总
离均差平方和 SS 283.83
5-2正交试验设计(方差分析)
• 确定试验中所考虑的因子与水平，并确 定可能存在并要考察的交互作用；
• 选用合适的正交表，进行表头设计，列 出试验计划。
例2 为提高某种农药的收率，需要进行试验。 试验目的：提高农药的收率 试验指标：收率
确定因子与水平以及所要考察的交互作用：
表 4 .8 因子 A： 反 应 温 度 （ ℃ ） B： 反 应 时 间 （ 小 时 ） C： 两 种 原 料 配 比 D ： 真 空 度 （ kP a ）
yi
T=1651 2 =310519
表4.6
来源 因子 A 因子 B 因子 C 误差 e T 平方和 S 1 4 2 1 .6 5 6 8 6 .9 4 2 7 .6 1 1 6 .2 7 6 5 2 .2
例4.1的方差分析表
自由度 f 2 2 2 2 8 均方和 V 7 1 0 .8 2 8 4 3 .4 2 1 3 .8 5 8 .1
（一）试验的设计
在安排试验时，一般应考虑如下几步：
（1）明确试验目的；
（2）明确试验指标；
（3）确定因子与水平； （4）选用合适的正交表，进行表头设计，列出试 验计划。
在本例中： 试验目的：提高磁鼓电机的输出力矩
试验指标：输出力矩
确定因子与水平：
表 4 .2
因子水平表
水平 因子 A ： 充 磁 量 （ 10
表4.9 L8（27）的交互作用表
555 594 502 185 198 1 6 7 .3 3 0 .7
T
R
（2）各因子对指标影响程度大小的分析 极差的大小反映了因子水平改变时对试验结 果的影响大小。这里因子的极差是指各水平平均 值的最大值与最小值之差，譬如对因子A来讲：
RA=198－167.3=30.7
医学统计学方差分析 (2)
试验指标：要考察的指标称为试验指标----例1为全肺
湿重，例2为抑菌圈的直径；
因素：影响试验指标的条件称为因素----例1为组别，
例2为药物（及剂量）、菌株来源；
水平：因素所处的状态称为该因素的水平----例1组别
这个因素有3个不同的水平；例2药物（及剂量） 因素有4个水平，菌株来源有7个水平。
在一项试验中，如果影响试验指标的因素只有 一个，则称该试验为单因素试验(例1)；如果影响试 验指标的因素有多个，则称该试验为多因素试验(例 2)。
…
μg
数
22
假定处理组各水平Aj均为正态总体N(μj,σ2),区组 各水平Bk均为正态总体N(βk,σ2),方差分析的任务是：
对假设：
进行检验。
H0：μ1= μ2= …=μg H0：β1= β2 =…= βn
与完全随机设计的情形类似，我们将总平方和
分解为：
S S 总 S S 处 理 组 S S 区 组 + S S 误 差
方差分析----
多个样本均数比较的假设检验
1. 基本概念 t检验解决了推断两个总体均数是否相等的问题，
但实际工作中还会遇到需要推断多个总体均数是否相 等的问题。如：
Ex1 为研究煤矿粉尘作业环境对尘肺的影响，将18只
大鼠随机分到甲、乙、丙三个组，每组6只，分别在
地面办公楼、煤碳仓库和矿井下染尘，12周后测量大
s nj
SS总 (xij x)26.5628 j1 i1
s
SS组 间 nj(x•j x)22.5278 j1
S S 组 内 S S 总 S S 组 间 6 . 5 6 2 8 2 . 5 2 7 8 4 . 0 3 5 0
16
M S组 间 SsS 组 1 间2.3 5 27 181.264 M S组 内 S nS 组 内 s4 1.8 03 5 3 00.269
湿重，例2为抑菌圈的直径；
因素：影响试验指标的条件称为因素----例1为组别，
例2为药物（及剂量）、菌株来源；
水平：因素所处的状态称为该因素的水平----例1组别
这个因素有3个不同的水平；例2药物（及剂量） 因素有4个水平，菌株来源有7个水平。
在一项试验中，如果影响试验指标的因素只有 一个，则称该试验为单因素试验(例1)；如果影响试 验指标的因素有多个，则称该试验为多因素试验(例 2)。
…
μg
数
22
假定处理组各水平Aj均为正态总体N(μj,σ2),区组 各水平Bk均为正态总体N(βk,σ2),方差分析的任务是：
对假设：
进行检验。
H0：μ1= μ2= …=μg H0：β1= β2 =…= βn
与完全随机设计的情形类似，我们将总平方和
分解为：
S S 总 S S 处 理 组 S S 区 组 + S S 误 差
方差分析----
多个样本均数比较的假设检验
1. 基本概念 t检验解决了推断两个总体均数是否相等的问题，
但实际工作中还会遇到需要推断多个总体均数是否相 等的问题。如：
Ex1 为研究煤矿粉尘作业环境对尘肺的影响，将18只
大鼠随机分到甲、乙、丙三个组，每组6只，分别在
地面办公楼、煤碳仓库和矿井下染尘，12周后测量大
s nj
SS总 (xij x)26.5628 j1 i1
s
SS组 间 nj(x•j x)22.5278 j1
S S 组 内 S S 总 S S 组 间 6 . 5 6 2 8 2 . 5 2 7 8 4 . 0 3 5 0
16
M S组 间 SsS 组 1 间2.3 5 27 181.264 M S组 内 S nS 组 内 s4 1.8 03 5 3 00.269
第5章方差分析2
【例5-1】以淀粉为原料生产葡萄糖过程中，残留 的许多糖蜜可用于酱色生产。生产酱色之前应尽可 能彻底除杂，以保证酱色质量。今选用5中除杂方 法，每种方法做4次试验，试验结果见表5-2，试 分析不同除杂方法的除杂效果有无差异？
除杂方法（Ai）
A1 A2 A3 A4 A5
表5-2 不同除杂方法的除杂量
除杂量（xij）
（1）总偏差平方和的分解 在表5-1中，反映全部观测值总变异的
总偏差平方和是各观测值xij与总平均数 x..
的离均差平方和，记为SST。即
kn
SST
( xij x.. )2
i1 j1
上一张 下一张 主 页 退 出
k n
kn
(xij x..)2
(xi. x..) (xij xi.) 2
(xij xi. ) 2
i1 j1
SST =SSt+SSe
（5-8）
所以
总偏差平方和=处理间偏差平方和+处理内偏差平方和
或 =因素偏差平方和+误差偏差平方和
上一张 下一张 主 页 退 出
各偏差平方和计算公式：
kn
SST
xi2j C
i1 j 1
SS t
1 n
k i 1
xi2.
C
(5-9)
来表示，则
xij x.. (xi. x.. ) (xij xi. ) x.. ti e（ij 5-6） 与（5-4）式比较可知， x.. 、(xi. x.. ) ti 、
(xij xi. ) eij 分 别是μ、（μi-μ）= 、i
（xij- i ） = ij 的估计值。
13518.7875 13390.3125 128.4750
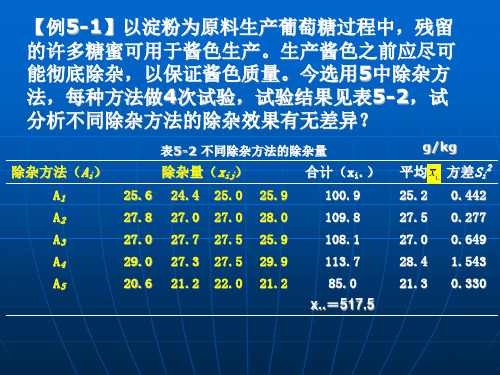
除杂方法（Ai）
A1 A2 A3 A4 A5
表5-2 不同除杂方法的除杂量
除杂量（xij）
（1）总偏差平方和的分解 在表5-1中，反映全部观测值总变异的
总偏差平方和是各观测值xij与总平均数 x..
的离均差平方和，记为SST。即
kn
SST
( xij x.. )2
i1 j1
上一张 下一张 主 页 退 出
k n
kn
(xij x..)2
(xi. x..) (xij xi.) 2
(xij xi. ) 2
i1 j1
SST =SSt+SSe
（5-8）
所以
总偏差平方和=处理间偏差平方和+处理内偏差平方和
或 =因素偏差平方和+误差偏差平方和
上一张 下一张 主 页 退 出
各偏差平方和计算公式：
kn
SST
xi2j C
i1 j 1
SS t
1 n
k i 1
xi2.
C
(5-9)
来表示，则
xij x.. (xi. x.. ) (xij xi. ) x.. ti e（ij 5-6） 与（5-4）式比较可知， x.. 、(xi. x.. ) ti 、
(xij xi. ) eij 分 别是μ、（μi-μ）= 、i
（xij- i ） = ij 的估计值。
13518.7875 13390.3125 128.4750
方差分析(二)
给定假设检验水准 α ＝ 0.05。
3.计算离均差平方和及自由度 关数据计算如下：
利用式（9-3）及表9-3有
SS总＝2733.6，v总＝60-1＝59 SSA＝1580.93，vA＝4-1＝3 SSB＝264.90，v总＝3-1＝2 SSAB＝356.97，vAB＝(4-1)(3-1)＝6 SS误差＝530.80，v误差＝4×3×（5-1）＝48 4.计算各种均方及F值并列出方差分析表 见表9-4。有三 种假设，故需计算三个F值。各F值均以MS误差为分母进行计 算。
ij
ij
(Y i Y )2
(Y j Y )2
(Yij Y i Y j Y )2
即：SS总＝SSi 处j理+SS区组+i SSj 误差
ij
(9 1)
式（9-1）中 和 分别表示对i从1到a求和与j从1到n求和。
i
j
式中各符号的意义及简化计算公式为：
22析因设计模型
a1
设：因素A有二个水平
a2
b1 因素B有二个水平
b2
因素B
因素A
a1
a2
b1
a1b1
a2b1
b2
a1b2
a2b2
一、两因素析因实验的方差分析模型
处理因素A及B分别有a及b个水平，总共有a×b种组合。在每一种组 合下即每一个格子中配有n个受试对象。全部实验受试对象总数N＝ n×a×b。用i（i＝l，2…，a）表示因素A的水平号，j（j＝l，2，…b） 表示因素B的水平号，k（k＝l，2，…，n）表示在ab每一水平组合的受 试对象号与表示应变量的观察值
j
Tj2
T2 N
3.计算离均差平方和及自由度 关数据计算如下：
利用式（9-3）及表9-3有
SS总＝2733.6，v总＝60-1＝59 SSA＝1580.93，vA＝4-1＝3 SSB＝264.90，v总＝3-1＝2 SSAB＝356.97，vAB＝(4-1)(3-1)＝6 SS误差＝530.80，v误差＝4×3×（5-1）＝48 4.计算各种均方及F值并列出方差分析表 见表9-4。有三 种假设，故需计算三个F值。各F值均以MS误差为分母进行计 算。
ij
ij
(Y i Y )2
(Y j Y )2
(Yij Y i Y j Y )2
即：SS总＝SSi 处j理+SS区组+i SSj 误差
ij
(9 1)
式（9-1）中 和 分别表示对i从1到a求和与j从1到n求和。
i
j
式中各符号的意义及简化计算公式为：
22析因设计模型
a1
设：因素A有二个水平
a2
b1 因素B有二个水平
b2
因素B
因素A
a1
a2
b1
a1b1
a2b1
b2
a1b2
a2b2
一、两因素析因实验的方差分析模型
处理因素A及B分别有a及b个水平，总共有a×b种组合。在每一种组 合下即每一个格子中配有n个受试对象。全部实验受试对象总数N＝ n×a×b。用i（i＝l，2…，a）表示因素A的水平号，j（j＝l，2，…b） 表示因素B的水平号，k（k＝l，2，…，n）表示在ab每一水平组合的受 试对象号与表示应变量的观察值
j
Tj2
T2 N
方差分析简介
方差分析简介1. 引言方差分析（analysis of variance，简称ANOV A）是一种假设检验方法，即基本思想可概述为：把全部数据的总方差分解成几部分，每一部分表示某一影响因素或各影响因素之间的交互作用所产生的效应，将各部分方差与随机误差的方差相比较,依据F分布作出统计推断，从而确定各因素或交互作用的效应是否显著。
因为分析是通过计算方差的估计值进行的，所以称为方差分析。
方差分析的主要目标是检验均值间的差别是否在统计意义上显著。
如果只比较两个均值，事实上方差分析的结果和t检验完全相同。
只所以很多情况下采用方差分析，是因为它具有如下两个优点：（1）方差分析可以在一次分析中同时考察多个因素的显著性，比t检验所需的观测值少；（2）方差分析可以考察多个因素的交互作用。
方差分析的缺点是条件有些苛刻，需要满足如下条件：（1）各样本是相互独立的；（2）各样本数据来自正态总体（正态性：normality）；（3）各处理组总体方差相等（方差齐性：homogeneity of variance）。
因此在作方差分析之前，要作正态性检验和方差齐性检验，如不满足上述要求，可考虑作变量变换。
常用的变量变换方法有平方根变换，平方根反正弦变换、对数变换及倒数变换等。
方差分析在医药、制造业、农业等领域有重要应用，多用于试验优化和效果分析中。
2. 单因素方差分析2.1 基本概念（1）试验指标：在一项试验中，用来衡量试验效果的特征量称为试验指标，有时简称指标，也称试验结果，通常用y表示。
它类似于数学中的因变量或目标函数。
试验指标用数量表示称为定量指标，如速度、温度、压力、重量、尺寸、寿命、硬度、强度、产量和成本等。
不能直接用数量表示的指标称为定性指标。
如颜色，人的性别等。
定性指标也可以转化为定量指标，方法是用不同的数表示不同的指标值。
（2）试验因素：试验中，凡对试验指标可能产生影响的原因都称为因素(factor)，也称因子或元，类似于数学中的自变量。
方差分析
方差分析一、单因素试验的方差分析：在科学试验、生产实践和社会生活中，影响一个事件的因素往往很多。
例如，在工业生产中，产品的质量往往受到原材料、设备、技术及员工素质等因素的影响；又如，在工作中，影响个人收入的因素也是多方面的，除了学历、专业、工作时间、性别等方面外，还受到个人能力、经历及机遇等偶然因素的影响. 虽然在这众多因素中，每一个因素的改变都可能影响最终的结果，但有些因素影响较大，有些因素影响较小. 故在实际问题中，就有必要找出对事件最终结果有显著影响的那些因素. 方差分析就是根据试验的结果进行分析，通过建立数学模型，鉴别各个因素影响效应的一种有效方法.在上一章，我们讨论了具有相同方差的两个正态总体的均值是否有显著差异的检验问题。
在这一章里，将讨论具有相同方差的k (k >2)个正态总体的均值是否有显著性差异的检验问题。
初看起来，这个问题似乎不难解决。
只要运用上一章介绍的T－检验法，将每一对正态总体都检验一次就可以了，然而这样做是不能达到预期目的的。
因为这样做不但非常繁琐，而且往往会导致错误的结论。
例如有5个方差相同的正态C=10对正态总体逐对进总体，要检验它们的均值是否有显著差异，就必须对25行检验，若要求的显著性水平为0.05，那么，每对“μi =μj成立（i≠j）”这个结论是正确的概率为0.95，但是“五个正态总体的均值都相等”这个结论正确的概率却是( 0.95 )10 = 0.5987因此，得到错误结论的概率是1－0.5987=0.4013，这就是说，犯第一类错误的概率将达到40.13.%，这是无法接受的。
如果总体的个数更多，那么犯第一类错误的概率也将更大。
即使只有3个总体，得到错误结论的概率也将达到14.3% 。
从以上的分析，迫使我们寻求另外的方法，将所有的总体一起加以考虑。
而方差分析正是检验同方差的若干正态总体均值是否相等的一种统计方法。
方差分析的方法广泛地运用在工农业生产、科学研究和经营管理中。
方差分析(二)
LSD②求 LSD- t 值
M 误 = 4 1 4, X24h =12.76, X0 = 8 04, n h = n =10 S 差 . 8 . 24 0
1 1 SXi −Xj = M 误 ( + ) = S 差 ni nj
LSDLSD- t =
1 1 41 ( + ) = 09 5 . 84 . 1 1 0 10
泸州医学院流行病与卫生统计教研室
一、SNK－q检验 SNK－
SNK（Student-Newman-Keuls）检验，亦称q检验
Xi − Xj SXi−X j
M误 1 1 S 差 ， ν= ν 误 差 ， SX −X = + i j 2 n nj i
q=
Xi ， ni 和 Xj ， nj 为两对比组的样本均数和样本例数。
泸州医学院流行病与卫生统计教研室
例 4 -3 续例 4 -1 试比较三个组两两之间的差别。 解：1 . 建立假设并确定检验水准 α ； 2. 计算 q 值 H0 ： µi = µj H ： µi ≠ µj ； α = 0.05 1 将三个样本均数从小到大排列，并赋予秩次 均数 8.04 9.25 12.76 组别 A 组 C 组 B 组 SXi −Xj = 4.184( 1 + 1 ) = 0.647 2 10 10 秩次 1 2 3 表 4-7 多个均数两两比较 q 值表 比较组秩次 （1 ） 1 , 2 1 , 3 2 , 3
①建立假设并确定检验水准 α ；
H0 ： µ24h = µ96h ； H ： µ24h ≠ µ96h ； α = 0.05 1
LSD②求 LSD- t 值
M 误 = 4.184, X24h =12.76, X96h = 9.25, n24h = n =10 S 差 96
M 误 = 4 1 4, X24h =12.76, X0 = 8 04, n h = n =10 S 差 . 8 . 24 0
1 1 SXi −Xj = M 误 ( + ) = S 差 ni nj
LSDLSD- t =
1 1 41 ( + ) = 09 5 . 84 . 1 1 0 10
泸州医学院流行病与卫生统计教研室
一、SNK－q检验 SNK－
SNK（Student-Newman-Keuls）检验，亦称q检验
Xi − Xj SXi−X j
M误 1 1 S 差 ， ν= ν 误 差 ， SX −X = + i j 2 n nj i
q=
Xi ， ni 和 Xj ， nj 为两对比组的样本均数和样本例数。
泸州医学院流行病与卫生统计教研室
例 4 -3 续例 4 -1 试比较三个组两两之间的差别。 解：1 . 建立假设并确定检验水准 α ； 2. 计算 q 值 H0 ： µi = µj H ： µi ≠ µj ； α = 0.05 1 将三个样本均数从小到大排列，并赋予秩次 均数 8.04 9.25 12.76 组别 A 组 C 组 B 组 SXi −Xj = 4.184( 1 + 1 ) = 0.647 2 10 10 秩次 1 2 3 表 4-7 多个均数两两比较 q 值表 比较组秩次 （1 ） 1 , 2 1 , 3 2 , 3
①建立假设并确定检验水准 α ；
H0 ： µ24h = µ96h ； H ： µ24h ≠ µ96h ； α = 0.05 1
LSD②求 LSD- t 值
M 误 = 4.184, X24h =12.76, X96h = 9.25, n24h = n =10 S 差 96
方差分析(Version2)
( yij yi yi y ) 2
i 1 j 1 r m
r
( yij yi ) 2 ( yi y ) 2
i 1 j 1 i 1 j 1
r
m
Se S A
其中 ( yij yi )( yi y ) 0
i 1 j 1 r m
总偏差平方和 ST:
ST ( yij y )2
i 1 j 1
r
m
因子A偏差平方和 r m r 2 2 S ( y y ) m ( y y ) (组间偏差平方和) SA : A i i
i 1 j 1 i 1
随机偏差平方和 r m (组内偏差平方和) Se : Se ( yij yi )2
SPSS ANALYZE Compare Means One-way ANOVA
两因子方差分析(无交互作用)
分析两个因子单独对指标的影响问题 一个因子水平下的好坏及其程度不受另一 个因子不同水平影响的情况，称为两因子 间无交互作用
品牌和销售地区对电脑销售量影响的分析
1、模型与假设的提出
考虑因子A取r个水平，因子B取s个水平， 分析这r×s个水平组合(A i ,B j)对指标 yij的影响 在每个(A i ,B j)下,只做 1 次试验， 一般情况，假定在(A i ,B j)水平组合下 的指标 y i j ～ N(μi j,σ2), i=1,2,…,r; j=1,2,…,s 其中要求y i j 的方差σ2是相同的
检验假设H0的拒绝域为
F SA f A F (r 1, r (m 1)) Se f e
其中 为显著性水平， F (r 1, r (m 1)) 是自由度为 r 1, r (m 1) 的F分布 上侧分位数。 越小，拒绝H0的把握越大，因子A的显著性越高。
统计学自由度计算公式
统计学自由度计算公式
统计学自由度是指在进行统计推断时，样本数据可以自由变化的数量。
在不同的统计分析方法中，自由度的计算公式也不同。
以下是一些常见的统计学自由度计算公式：
1. 单因素方差分析的自由度计算公式：
自由度=总体样本数-组数
2. 双因素方差分析的自由度计算公式：
自由度=总体样本数-组数1-组数2+1
3. 卡方检验的自由度计算公式：
自由度=(行数-1)×(列数-1)
4. t检验的自由度计算公式：
自由度=样本量-2
5. F检验的自由度计算公式：
分子自由度=分子样本数-1
分母自由度=分母样本数-1
以上是一些常见的统计学自由度计算公式，希望能对您有所帮助。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 12
L8 ( 2 )
7
5.7.2 正交设计应用举例 P167
proc anova data=L3.anovazhjiao5_17; class a b c d e; model y=a b c d e a*b a*c a*e ; means a b c d e a*b a*c a*e/duncan ; /*多重比较的duncan’s检验*/ run; proc anova data=L3.anovazhjiao5_17; class a b c d e; model y=a c d e a*c ; means a c d e a*c /duncan; run; quit;
换一种方式理解
5.4.1 一元应用实例
程序如下：
DATA L3.anova5_7; DO g=1 TO 4; DO week=1 TO 7; INPUT y @@; OUTPUT; END; END; CARDS;
21.5 20.72 20.85 20.24 21.91 21.41 21.99 22.31 23.34 23.47 23.84 24.23 24.23 24.37 22.37 22.49 21.55 20.99 21.54 20.63 22.39 22.12 21.03 19.8 21.38 21.51 22.79 22.9
5.6.1 CONTRAST语句说明 （见P141-143）
5.6.2 应用实例 例5.12 选择两个品种的玉米，分为a、b两种。 按两种密度播种，分别为2500株/亩和3500株/ 亩两种。施氮量两个水平，分别为4公斤/亩和8 公斤/亩两种。互相搭配得8个处理组合。共3个 区组，即3次重复，共有24个观测数据。分析各 因素对产量的影响及各因素交互作用对产量的 影响。试验数据在程序中表示。 变量说明：s：品种、d：密度（株/亩）、n：氮 肥（公斤/亩）、y：小区产量（公斤/亩）。 程序见： glmxiyin5_12.sas
• 课后自看分析过程
5.7 正交设计及其统计分析
5.7.1 正交设计简介 1.必要性:当涉及的因素在三个或三个以上,且因素间可能存在交 互作用时,此时使用拉丁设计就不适合. 而且若用析因涉及,则处 理的组合数也会太多,如三因素三水平,则有27组合;四因素四水 平则有4的4次方,即256个组合. 所以随着因素水平的增加,我们有必要引入正交设计. 2.概念: 利用一套规格化的表格----正交表,科学合理地安排实 验.它是由试验因素的全部水平组合中，挑选部分有代 表性的水平组合进行试验的，通过对这部分试验结果的分析了 解全面试验的情况，找出最优的水平组合。 3.特点: i)任一因素不同水平下的实验数目都一样; ii)任何两个因素之间都是交叉分组的全面试验. 正交实验可以只用较少的实验达到预期的目的.
P143
data L3.glm5_13; input a $ b $ y @@; cards; a1 b1 28.0 a1 b2 30.0 a1 b3 33 a1 b1 22.5 a1 b2 25.0 a1 b3 28.5 a1 b1 21.5 a1 b2 22.5 a1 b3 25.0 a1 b1 23.0 a1 b2 24.0 a1 b3 25.0 a2 b1 32.5 a2 b2 30.0 a2 b3 26.5 a2 b1 30.5 a2 b2 29.0 a2 b3 26.5 a2 b1 30.0 a2 b2 28.0 a2 b3 24.0 a2 b1 31.5 a2 b2 30.0 a2 b3 27.5 a3 b1 30.0 a3 b2 31.0 a3 b3 36.5 a3 b1 30.5 a3 b2 34.0 a3 b3 38.5 a3 b1 25.0 a3 b2 33.5 a3 b3 38.5 a3 b1 26.5 a3 b2 30.0 a3 b3 32.5 ;
5.6 析因设计及其统计分析
一、使用范围：当因素间有交互作用时，可用此设计 (当然不存在交互作用时也可用.)
二、析因设计：各因素各种水平的每个组合都要做相同的
重复次实验。 见P146例5.13中的数据. 三、优点：可以节约样本含量。 四、分析方法： 先考察各因素间是否存在交互作用，如果存在交互作 用，此时各因子的主效应检验结果无实际意义，应按各因素 各水平的组合来研究，以选找最佳实验组合。从而需要用 glm过程中的的contrast 语句来进行各因素各水平间的两两 比较。
run;
Contrast语句格式可参见p142
5.5 拉丁方设计及其统计分析
一、使用范围： 当实验中涉及三个因素，三个因素水平数 相同，且它们之间无交互作用或交互作用可以忽略不计时， 可以用拉丁方设计的方差分析。P135
二、拉丁方试验设计：
三、 拉丁方设计应用实例 P136
三个因素是： 饲料、时间、乳牛
contrast ‘（d24-1 vs d24-2）/kt3 ' d24 1 -1 0 kt*d24 0 0 0 0 0 0 1 -1 0;
run ; quit ; proc glm data=L3.glm5_8; class d24 kt; model y=d24 kt d24*kt ;
contrast ‘(kt2 vs kt3)/d24 -1' kt 0 1 -1 d24*kt 0 1 -1;
proc glm data=L3.glm5_13 ; class a b; model y=a b a*b / ss3; contrast '(b1 vs b2)/a1 ' b 1 -1 0 a*b 1 -1 0; contrast '(b1 vs b3)/a1 ' b 1 0 -1 a*b 1 0 -1; contrast '(b2 vs b3)/a1 ' b 0 1 -1 a*b 0 1 -1; contrast '(b1 vs b2)/a2 ' b 1 -1 0 a*b 0 0 0 1 -1 0; contrast '(b1 vs b3)/a2 ' b 1 0 -1 a*b 0 0 0 1 0 -1; contrast '(b2 vs b3)/a2 ' b 0 1 -1 a*b 0 0 0 0 1 -1; contrast '(b1 vs b2)/a3 ' b 1 -1 0 a*b 0 0 0 0 0 0 1 -1 0; contrast '(b1 vs b3)/a3 ' b 1 0 -1 a*b 0 0 0 0 0 0 1 0 -1; contrast '(b2 vs b3)/a3 ' b 0 1 -1 a*b 0 0 0 0 0 0 0 1 -1;情况: 其中： L------正交表(标识符) n------实验的次数(正交表的行数) P165: k------水平数 m------因素个数(正交表的列数) 更正为:
m
L 3 (3 ) L 9 (3 )
3
3
混合水平情况,如: 见下表：
L9 ( 4 2 )
; PROC ANOVA data=L3.anova5_7; CLASS g week ; MODEL y=g week ; MEANS g week/regwq snk; MEANS g / dunnett ('2' ) ; RUN; quit;
5.4.2 多因素多水平间的多重比较
程序如下：glm5_8me.sas
说明:(1)P146的更正：anova 改为glm (2)四种类型的估计函数“Type I SS”、 “Type II SS” 、“Type III SS”、“Type IV SS”
Type I SS: 是效应的I类估计函数的离差平方 和,它是按各因素之间有交互作用的情况 计算的,并按此做出各效应统计意义检验; Type III SS: 是效应的III类估计函数的离差平 方和,它只按主效应计算的离差平方和,并 按此做出各效应统计意义检验;
得:品种a,株距b,以及它们的交互作用a*b都是显著的; (2) 由means 语句的结果,可以判断a, b 到底哪些水平是 有显著性差异的, 以及a和b的哪种搭配是最好的. 例5.13-2 为获得关于几种组合更细致的分析结果，在前 例分析的基础上，运用contrast 语句作进一步的分析。 程序如下:
proc anova data=L3.glm5_8; class d24 kt; model y=d24 kt d24*kt ; means d24 kt d24*kt/duncan;; run; quit;
程序见glm5_9me.sas
proc glm data=L3.glm5_8; class kt d24 ; model y=kt d24 kt*d24 ;
结果分析:
(1)由 anlysis of variance中的输出结果:
Source a b a*b DF Type III SS Mean Square 2 256.8472222 128.4236111 2 38.7638889 19.3819444 4 191.3611111 47.8402778 F Value Pr > F 20.40 <.0001 3.08 0.0624 7.60 0.0003
5.8 协 方 差 分 析
5.8.1 协方差分析简介 1.概念： 协方差分析是将回归分析和方差分析结合起来的 一种统计分析方法。 它利用回归的关系消除对比各族自变量值不同所 产生的影响后，再进行方差分析。例如： 在营养实验中，初始重量对喂养过程中增重的影 响很大。方差分析忽略了始重不同的影响，因而不能 反映出食料的真实效应。 处理：用直线回归把初始重量与所增重的关系找 出来，然后求出当初始重量化为相等时，各饲料组动 物所增加体重的调整均数，用协方差分析检验调整均 数间的差异。
data L3.glm5_8; do n=1 to 3; do d24=0 to 0.10 by 0.05; do kt=0 to 0.10 by 0.05 ; input y @@; output; end; end; end; cards; 0.24 0.35 0.38 0.20 0.25 0.36 0.28 0.50 0.30 0.26 0.31 0.35 0.21 0.21 0.35 0.20 0.51 0.31 0.25 0.32 0.35 0.22 0.26 0.34 0.21 0.52 0.32 ;
L8 ( 2 )
7
5.7.2 正交设计应用举例 P167
proc anova data=L3.anovazhjiao5_17; class a b c d e; model y=a b c d e a*b a*c a*e ; means a b c d e a*b a*c a*e/duncan ; /*多重比较的duncan’s检验*/ run; proc anova data=L3.anovazhjiao5_17; class a b c d e; model y=a c d e a*c ; means a c d e a*c /duncan; run; quit;
换一种方式理解
5.4.1 一元应用实例
程序如下：
DATA L3.anova5_7; DO g=1 TO 4; DO week=1 TO 7; INPUT y @@; OUTPUT; END; END; CARDS;
21.5 20.72 20.85 20.24 21.91 21.41 21.99 22.31 23.34 23.47 23.84 24.23 24.23 24.37 22.37 22.49 21.55 20.99 21.54 20.63 22.39 22.12 21.03 19.8 21.38 21.51 22.79 22.9
5.6.1 CONTRAST语句说明 （见P141-143）
5.6.2 应用实例 例5.12 选择两个品种的玉米，分为a、b两种。 按两种密度播种，分别为2500株/亩和3500株/ 亩两种。施氮量两个水平，分别为4公斤/亩和8 公斤/亩两种。互相搭配得8个处理组合。共3个 区组，即3次重复，共有24个观测数据。分析各 因素对产量的影响及各因素交互作用对产量的 影响。试验数据在程序中表示。 变量说明：s：品种、d：密度（株/亩）、n：氮 肥（公斤/亩）、y：小区产量（公斤/亩）。 程序见： glmxiyin5_12.sas
• 课后自看分析过程
5.7 正交设计及其统计分析
5.7.1 正交设计简介 1.必要性:当涉及的因素在三个或三个以上,且因素间可能存在交 互作用时,此时使用拉丁设计就不适合. 而且若用析因涉及,则处 理的组合数也会太多,如三因素三水平,则有27组合;四因素四水 平则有4的4次方,即256个组合. 所以随着因素水平的增加,我们有必要引入正交设计. 2.概念: 利用一套规格化的表格----正交表,科学合理地安排实 验.它是由试验因素的全部水平组合中，挑选部分有代 表性的水平组合进行试验的，通过对这部分试验结果的分析了 解全面试验的情况，找出最优的水平组合。 3.特点: i)任一因素不同水平下的实验数目都一样; ii)任何两个因素之间都是交叉分组的全面试验. 正交实验可以只用较少的实验达到预期的目的.
P143
data L3.glm5_13; input a $ b $ y @@; cards; a1 b1 28.0 a1 b2 30.0 a1 b3 33 a1 b1 22.5 a1 b2 25.0 a1 b3 28.5 a1 b1 21.5 a1 b2 22.5 a1 b3 25.0 a1 b1 23.0 a1 b2 24.0 a1 b3 25.0 a2 b1 32.5 a2 b2 30.0 a2 b3 26.5 a2 b1 30.5 a2 b2 29.0 a2 b3 26.5 a2 b1 30.0 a2 b2 28.0 a2 b3 24.0 a2 b1 31.5 a2 b2 30.0 a2 b3 27.5 a3 b1 30.0 a3 b2 31.0 a3 b3 36.5 a3 b1 30.5 a3 b2 34.0 a3 b3 38.5 a3 b1 25.0 a3 b2 33.5 a3 b3 38.5 a3 b1 26.5 a3 b2 30.0 a3 b3 32.5 ;
5.6 析因设计及其统计分析
一、使用范围：当因素间有交互作用时，可用此设计 (当然不存在交互作用时也可用.)
二、析因设计：各因素各种水平的每个组合都要做相同的
重复次实验。 见P146例5.13中的数据. 三、优点：可以节约样本含量。 四、分析方法： 先考察各因素间是否存在交互作用，如果存在交互作 用，此时各因子的主效应检验结果无实际意义，应按各因素 各水平的组合来研究，以选找最佳实验组合。从而需要用 glm过程中的的contrast 语句来进行各因素各水平间的两两 比较。
run;
Contrast语句格式可参见p142
5.5 拉丁方设计及其统计分析
一、使用范围： 当实验中涉及三个因素，三个因素水平数 相同，且它们之间无交互作用或交互作用可以忽略不计时， 可以用拉丁方设计的方差分析。P135
二、拉丁方试验设计：
三、 拉丁方设计应用实例 P136
三个因素是： 饲料、时间、乳牛
contrast ‘（d24-1 vs d24-2）/kt3 ' d24 1 -1 0 kt*d24 0 0 0 0 0 0 1 -1 0;
run ; quit ; proc glm data=L3.glm5_8; class d24 kt; model y=d24 kt d24*kt ;
contrast ‘(kt2 vs kt3)/d24 -1' kt 0 1 -1 d24*kt 0 1 -1;
proc glm data=L3.glm5_13 ; class a b; model y=a b a*b / ss3; contrast '(b1 vs b2)/a1 ' b 1 -1 0 a*b 1 -1 0; contrast '(b1 vs b3)/a1 ' b 1 0 -1 a*b 1 0 -1; contrast '(b2 vs b3)/a1 ' b 0 1 -1 a*b 0 1 -1; contrast '(b1 vs b2)/a2 ' b 1 -1 0 a*b 0 0 0 1 -1 0; contrast '(b1 vs b3)/a2 ' b 1 0 -1 a*b 0 0 0 1 0 -1; contrast '(b2 vs b3)/a2 ' b 0 1 -1 a*b 0 0 0 0 1 -1; contrast '(b1 vs b2)/a3 ' b 1 -1 0 a*b 0 0 0 0 0 0 1 -1 0; contrast '(b1 vs b3)/a3 ' b 1 0 -1 a*b 0 0 0 0 0 0 1 0 -1; contrast '(b2 vs b3)/a3 ' b 0 1 -1 a*b 0 0 0 0 0 0 0 1 -1;情况: 其中： L------正交表(标识符) n------实验的次数(正交表的行数) P165: k------水平数 m------因素个数(正交表的列数) 更正为:
m
L 3 (3 ) L 9 (3 )
3
3
混合水平情况,如: 见下表：
L9 ( 4 2 )
; PROC ANOVA data=L3.anova5_7; CLASS g week ; MODEL y=g week ; MEANS g week/regwq snk; MEANS g / dunnett ('2' ) ; RUN; quit;
5.4.2 多因素多水平间的多重比较
程序如下：glm5_8me.sas
说明:(1)P146的更正：anova 改为glm (2)四种类型的估计函数“Type I SS”、 “Type II SS” 、“Type III SS”、“Type IV SS”
Type I SS: 是效应的I类估计函数的离差平方 和,它是按各因素之间有交互作用的情况 计算的,并按此做出各效应统计意义检验; Type III SS: 是效应的III类估计函数的离差平 方和,它只按主效应计算的离差平方和,并 按此做出各效应统计意义检验;
得:品种a,株距b,以及它们的交互作用a*b都是显著的; (2) 由means 语句的结果,可以判断a, b 到底哪些水平是 有显著性差异的, 以及a和b的哪种搭配是最好的. 例5.13-2 为获得关于几种组合更细致的分析结果，在前 例分析的基础上，运用contrast 语句作进一步的分析。 程序如下:
proc anova data=L3.glm5_8; class d24 kt; model y=d24 kt d24*kt ; means d24 kt d24*kt/duncan;; run; quit;
程序见glm5_9me.sas
proc glm data=L3.glm5_8; class kt d24 ; model y=kt d24 kt*d24 ;
结果分析:
(1)由 anlysis of variance中的输出结果:
Source a b a*b DF Type III SS Mean Square 2 256.8472222 128.4236111 2 38.7638889 19.3819444 4 191.3611111 47.8402778 F Value Pr > F 20.40 <.0001 3.08 0.0624 7.60 0.0003
5.8 协 方 差 分 析
5.8.1 协方差分析简介 1.概念： 协方差分析是将回归分析和方差分析结合起来的 一种统计分析方法。 它利用回归的关系消除对比各族自变量值不同所 产生的影响后，再进行方差分析。例如： 在营养实验中，初始重量对喂养过程中增重的影 响很大。方差分析忽略了始重不同的影响，因而不能 反映出食料的真实效应。 处理：用直线回归把初始重量与所增重的关系找 出来，然后求出当初始重量化为相等时，各饲料组动 物所增加体重的调整均数，用协方差分析检验调整均 数间的差异。
data L3.glm5_8; do n=1 to 3; do d24=0 to 0.10 by 0.05; do kt=0 to 0.10 by 0.05 ; input y @@; output; end; end; end; cards; 0.24 0.35 0.38 0.20 0.25 0.36 0.28 0.50 0.30 0.26 0.31 0.35 0.21 0.21 0.35 0.20 0.51 0.31 0.25 0.32 0.35 0.22 0.26 0.34 0.21 0.52 0.32 ;