2018全国卷3理数(含答案)-18年全国卷三
2018年高考全国卷新课标III卷(含答案)(Word精校版)

绝密★启用前2018年普通高等学校招生全国统一考试(新课标III卷)英语注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳答案。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.18.C.£9.15.1.What does John find difficult in learning German?A .Pronunciation.B.V ocabulary.C. Grammar.2.What is the probable relationship between the speakers?A. Colleagues.B. Brother and sister.C. Teacher and student.3.Where does the conversation probably take place?A. In a bank.B. At a ticket office.C. On a train.4. What are the speakers talking about?A.A restaurant.B.A street.C.A dish.5.What does the woman think of her interview?A. It was tough.B. It was interesting.C. It was successful.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
2018年高考理科数学全国卷3(含答案与解析)
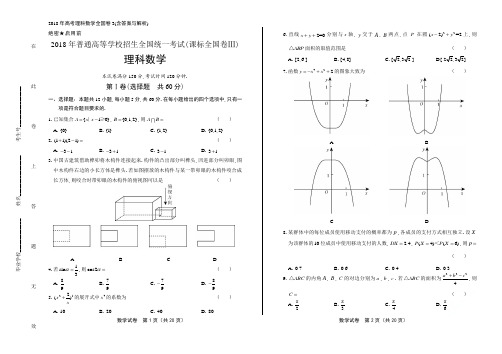
2018年高考理科数学全国卷3(含答案与解析) 数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学本试卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{10}A x x =-∣≥,{0,1,2}B =,则A B = ( )A .{0}B .{1}C .{1,2}D .{0,1,2} 2.()(1i 2i)+-=( )A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )ABC D 4.若1sin 3α=,则cos2α=( )A .89B .79C .79-D .89-5.252()x x+的展开式中4x 的系数为( )A .10B .20C .40D .806.直线2=0x y ++分别与x 轴,y 交于A ,B 两点,点P 在圆22(2)=2x y -+上,则ABP △面积的取值范围是( )A .[2,6 ]B .[4,8]C .[2,3 2 ]D [ 22,32] 7.函数422y x x =-++的图象大致为( )ABCD8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数, 2.4DX =,()6(4)P X P X ==<,则p =( )A .0.7B .0.6C .0.4D .0.39.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC △的面积为2224,则C = ( )A .π2B .π3C .π4D .π6毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)10.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为( )A .123B .183C .243D .54311.设1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1||6||PF OP =,则C 的离心率为 ( )A .5B .2C .3D .2 12.设0.2log 0.3a =,2log 0.3b =,则( )A .0a b ab +<<B .ab a b +<<0C .0a b ab +<<D .0ab a b +<<第Ⅱ卷(非选择题 共90分)二、填空题:本题共4小题,每小题5分,共20分.13.已知向量2)(1,=a ,)2(2,=-b ,),(1λ=c .若2()+∥c a b ,则=λ . 14.曲线)e (1xy ax =+在点(0,1)处的切线的斜率为2-,则a = .15函数π()cos(3)6f x x =+在[0,π]的零点个数为 .16.已知点1()1,M -和抛物线C :²4y x =,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若90AMB ∠=,则k = .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分. 17.(12分)等比数列{}n a 中,11a =,534a a =. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高,并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过超过m不超过m第一种生产方式 第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()(a b)(c d)(a c)(b d)n ad bc K -=++++,2()P K k ≥0.050 0.010 0.001k3.841 6.635 10.82819.(12分)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------2018年高考理科数学全国卷3(含答案与解析)数学试卷 第5页(共20页) 数学试卷 第6页(共20页)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.20.(12分)已知斜率为k 的直线l 与椭圆C :22143x y +=交于A ,B 两点,线段AB 的中点为(1,)()M m m >0.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB成等差数列,并求该数列的公差. 21.(12分)已知函数22()()ln(1)2f x a x x x x +=-++.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >时,()0f x >; (2)若=0x 是()f x 的极大值点,求a .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,O 的参数方程为cos ,sin x y θθ=⎧⎨=⎩(θ为参数),过点(0,2)且倾斜角为α的直线l 与O 交于A ,B 两点. (1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.[选修4—5:不等式选讲](10分) 设函数()211f x x x =++-. (1)画出() y f x =的图象;(2)当[ 0),x ∈+∞,()b x f ax +≤,求a b +的最小值.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共20页) 数学试卷 第8页(共20页)2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】∵={1}A x x |≥,{0,1,2}B =,∴={1,2}A B ,故选C .2.【答案】D【解析】21i 2i)(2i 2i i 3i )(+-=-+-=+,故选D . 3.【答案】A【解析】两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A .故选A . 4.【答案】B 【解析】由1sin 3α=,得22127cos212sin 12()=1=399αα=-=-⨯-.故选B .5.【答案】C【解析】252()x x+的展开式的通项251103155()(2)2r r r r r r r T C x x C x ---+==,令1034r -=,得2r =,所以4x 的系数为225240C ⨯=.故选C . 6.【答案】A【解析】由圆22(2)=2x y -+可得圆心坐标(2,0),半径r =ABP △的面积记为S ,点P 到直线AB 的距离记为d ,则有12S AB d =.易知AB =maxd ==min d =所以26S ≤≤,故选A .7.【答案】D【解析】∵42()2f x x x =-++,∴3()42f x x x '=-+,令()0f x '>,解得x <或x 0<此时,()f x 递增;令()0f x '<,解得x <0或x ,此时,()f x 递减.由此可得()f x 的大致图象.故选D . 8.【答案】B【解析】由题知~1()0,X B p ,则(101 2.4)DX p p =⨯⨯-=,解得0.4p =或0.6.又∵()6(4)P X P X ==<,即446664221010(1)(1)(1)0.5C P p C P p p p p --⇒-⇒<<>,∴0.6p =,故选B .9.【答案】C【解析】根据余弦定理得2222cos a b c ab C +-=,因为2224ABCa Sbc +-=△,所以c 42os ABC ab C S =△,又1sin 2ABC S ab C =△,所以tan 1C =,因为π()0,C ∈,所以4C π=.故选C .10.【答案】B【解析】设ABC △的边长为a ,则1sin60=932ABC S a a =△,解得6a =(负值舍去).ABC △的外接圆半径r 满足62sin60r=,得r =球心到平面ABC 的距离为2=.所以点D 到平面ABC 的最大距离为246+=,所以三棱锥DABC -体积的最大值为163⨯=故选B .11.【答案】C【解析】点2(,0)F c 到渐近线b y x a =的距离2(0)PF b b ==>,而2OF c =,所以在2Rt OPF △中,由勾股定理可得OP a ,所以1PF ==.在2Rt OPF △中,222cos PF b PF O OF c∠==,在12F F P△中,2222222121221246cos 22PF F F PF b c a PF O PF F F b c+-+-∠==⋅⋅2,所以222222463464b b c a b c a c bc +-=⇒=-,则有22223()46c a c a -=-值舍去),即e =.故选C .2018年高考理科数学全国卷3(含答案与解析)数学试卷 第9页(共20页) 数学试卷 第10页(共20页)12.【答案】B【解析】解法一:∵0.20.2log 0.3log 1=0a =>,22log 0.3log 1=0b =<,∴0ab <,排除C . ∵0.20.20log 0.3log 0.2=1<<,22log 0.3log 0.5=1-<,即01a <<,1b <-,∴0a b +<,排除D .∵220.2log 0.3lg0.2log 0.2log 0.3lg 2b a ===,∴2223log 0.3log 0.2log 12b b a -=-=<,∴1bb ab a b a+⇒+<<,排除A .故选B . 解法二:易知01a <<,1b -<,∴0ab <,0a b +<, ∵0.30.30.311log 0.2log 2log 0.41a b +=+=<, 即1a bab+<,∴a b ab +>, ∴0ab a b +<<.故选B .第Ⅱ卷二、填空题13.【答案】12【解析】由已知得2(4,2)+=a b .又,()1c λ=,2()+∥c a b ,所以42=0λ-,解得12λ=. 14.【答案】3-【解析】设(e ))1(x f x ax =+,则()()1e x f x ax a '=++,所以曲线在点(0,1)处的切线的斜率(0)12k f a '==+=-,解得3a =-. 15.【答案】3【解析】令()0f x =,得πcos(3)6x +,解得ππ+()39k x k =∈Z .当0k =时,π9x =;当1k =时,4π9x =;当2k =时,7π9x =,又[ 0,π]x ∈,所以满足要求的零点有3个.16.【答案】2【解析】解法一:由题意可知C 的焦点坐标为(1,0),所以过焦点(1,0),斜率为k 的直线方程为1y x k =+,设111,y A y k ⎛⎫+ ⎪⎝⎭,221,y B y k ⎛⎫+ ⎪⎝⎭,将直线方程与抛物线方程联立得21,4,y x k y x ⎧=+⎪⎨⎪=⎩整理得2440y y k --=,从而得124y y k +=,124y y =-.∵1()1,M -,90AMB ∠=,∴0MA MB =,即1212(2)(2)(1)(1)0y yy y k k+++--=,即2440k k -+=,解得2k =.解法二:设11A(,)x y ,22(),B x y ,则2112224,4,y x y x ⎧=⎨=⎩①②②-①得2221214()y y x x -=-,从而2121124y y x x k y y --+==.设AB 的中点为M ',连接MM '.∵直线AB 过抛物线24y x =的焦点,∴以线段AB 为直径的M '⊙与准线:1l x =-相切.∵1()1,M -,90AMB ∠=,∴点M 在准线:1l x =-上,同时在M '⊙上,∴准线l 是M '⊙的切线,切点M ,且MM l '⊥,即MM '与x 轴平行,∴点M '的纵坐标为1,即1212221y y y y =⇒++=,故124422y y k =+==. 故答案为:2. 三、解答题17.【答案】(1)解:设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=. (2)若1(2)n n a -=-,则1(2)3nn S --=.数学试卷 第11页(共20页) 数学试卷 第12页(共20页)由63m S =得(2)188m -=-.此方程没有正整数解.若12n n a -=,则21n n S =-.由63m S =得264m =,解得6m =. 综上,6m =.【解析】(1)解:设{}n a 的公比为q ,由题设得1n n a q-=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m -=-。
2018年全国卷高考物理试题及答案

2018年高考全国卷物理试题2018全国Ⅰ卷物理2018全国Ⅱ卷物理2018全国Ⅲ卷物理2018年高考全国卷Ⅰ物理试题14.高铁列车在启动阶段的运动可看作初速度为零的均加速直线运动,在启动阶段列车的动能A.与它所经历的时间成正比B.与它的位移成正比C.与它的速度成正比D.与它的动量成正比15.如图,轻弹簧的下端固定在水平桌面上,上端放有物块P,系统处于静止状态,现用一竖直向上的力F作用在P上,使其向上做匀加速直线运动,以x表示P离开静止位置的位移,在弹簧恢复原长前,下列表示F和x之间关系的图像可能正确的是A.B.C.D.16.如图,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm。
小球c所受库仑力的合力的方向平衡于a、b的连线。
设小球a、b所带电荷量的比值的绝对值为k,则A.a、b的电荷同号,169 k=B.a、b的电荷异号,169 k=C.a、b的电荷同号,6427 k=D.a、b的电荷异号,6427 k=17.如图,导体轨道OPQS固定,其中PQS是半圆弧,Q为半圆弧的中心,O为圆心。
轨道的电阻忽略不计。
OM是有一定电阻。
可绕O转动的金属杆。
M端位于PQS上,OM与轨道接触良好。
空间存在半圆所在平面垂直的匀强磁场,磁感应强度的大小为B,现使OQ位置以恒定的角速度逆时针转到OS位置并固定(过程Ⅰ);再使磁感应强度的大小以一定的变化率从B增加到B'(过程Ⅱ)。
在过程Ⅰ、Ⅱ中,流过OM的电荷量相等,则BB等于A.54B.32C.74D.218.如图,abc是竖直面内的光滑固定轨道,ab水平,长度为2R:bc是半径为R的四分之一的圆弧,与ab相切于b点。
一质量为m的小球。
始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动,重力加速度大小为g。
小球从a点开始运动到其他轨迹最高点,机械能的增量为A.2mgR B.4mgR C.5mgR D.6mgR19.如图,两个线圈绕在同一根铁芯上,其中一线圈通过开关与电源连接,另一线圈与远处沿南北方向水平放置在纸面内的直导线连接成回路。
(完整版)二项式定理高考题(带答案)

1.2018年全国卷Ⅲ理】的展开式中的系数为A. 10B. 20C. 40D. 80【答案】C【解析】分析:写出,然后可得结果详解:由题可得,令,则,所以故选C.2.【2018年浙江卷】二项式的展开式的常数项是___________.【答案】7【解析】分析:先根据二项式展开式的通项公式写出第r+1项,再根据项的次数为零解得r,代入即得结果.详解:二项式的展开式的通项公式为,令得,故所求的常数项为3.【2018年理数天津卷】在的展开式中,的系数为____________. 【答案】决问题的关键.4.【山西省两市2018届第二次联考】若二项式中所有项的系数之和为,所有项的系数的绝对值之和为,则的最小值为()A. 2B.C.D.【答案】B5.【安徽省宿州市2018届三模】的展开式中项的系数为__________.【答案】-132【解析】分析:由题意结合二项式展开式的通项公式首先写出展开式,然后结合展开式整理计算即可求得最终结果.详解:的展开式为:,当,时,,当,时,,据此可得:展开式中项的系数为.6.【2017课标1,理6】621(1)(1)x x++展开式中2x 的系数为 A .15B .20C .30D .35【答案】C【解析】试题分析:因为6662211(1)(1)1(1)(1)x x x x x ++=⋅++⋅+,则6(1)x +展开式中含2x 的项为2226115C x x ⋅=,621(1)x x ⋅+展开式中含2x 的项为44262115C x x x⋅=,故2x 前系数为151530+=,选C.情况,尤其是两个二项式展开式中的r 不同.7.【2017课标3,理4】()()52x y x y +-的展开式中x 3y 3的系数为 A .80-B .40-C .40D .80【答案】C 【解析】8.【2017浙江,13】已知多项式()1x +3()2x +2=5432112345x a x a x a x a x a +++++,则4a =________,5a =________.【答案计数.9.【2017山东,理11】已知()13nx +的展开式中含有2x 项的系数是54,则n = . 【答案】4【解析】试题分析:由二项式定理的通项公式()1C 3C 3rr r r r r n n x x +T ==⋅⋅,令2r =得:22C 354n ⋅=,解得4n =.【考点】二项式定理10.【2015高考陕西,理4】二项式(1)()n x n N ++∈的展开式中2x 的系数为15,则n =( )A .4B .5C .6D .7 【答案】C【解析】二项式()1nx +的展开式的通项是1C r r r n x +T =,令2r =得2x 的系数是2C n ,因为2x 的系数为15,所以2C 15n =,即2300n n --=,解得:6n =或5n =-,因为n +∈N ,所以6n =,故选C . 【考点定位】二项式定理.【名师点晴】本题主要考查的是二项式定理,属于容易题.解题时一定要抓住重要条件“n +∈N ”,否则很容易出现错误.解本题需要掌握的知识点是二项式定理,即二项式()na b +的展开式的通项是1C k n k k k n ab -+T =. 11.【2015高考新课标1,理10】25()x x y ++的展开式中,52x y 的系数为( )(A )10 (B )20 (C )30 (D )60 【答案】C12.【2015高考湖北,理3】已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )A.122 B .112 C .102D .92【答案】D【解析】因为(1)n x +的展开式中第4项与第8项的二项式系数相等,所以73nn C C =,解得10=n ,所以二项式10(1)x +中奇数项的二项式系数和为9102221=⨯.13.【2015高考重庆,理12】53x ⎛+ ⎝的展开式中8x 的系数是________(用数字作答).【答案】52【解析】二项展开式通项为7153521551()()2k k kkk k k T C x C x --+==,令71582k-=,解得2k =,因此8x 的系数为22515()22C =.14.【2015高考广东,理9】在4)1(-x 的展开式中,x 的系数为 . 【答案】6.【解析】由题可知()()44214411r rrrrr r T CC x--+=-=-,令412r-=解得2r =,所以展开式中x 的系数为()22416C -=,故应填入6.【名师点睛】涉及二项式定理的题,一般利用其通项公式求解.15.【2015高考天津,理12】在614x x ⎛⎫- ⎪⎝⎭ 的展开式中,2x 的系数为 .【答案】1516【解析】614x x ⎛⎫- ⎪⎝⎭展开式的通项为6621661144r rr r r r r T C x C x x --+⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,由622r -=得2r =,所以222236115416T C x x ⎛⎫=-= ⎪⎝⎭,所以该项系数为1516.16.【2015高考新课标2,理15】4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a =__________. 【答案】3【解析】由已知得4234(1)1464x x x x x +=++++,故4()(1)a x x ++的展开式中x 的奇数次幂项分别为4ax ,34ax ,x ,36x ,5x ,其系数之和为441+6+1=32a a ++,解得3a =.【考点定位】二项式定理.17.【2015高考湖南,理6】已知5-的展开式中含32x 的项的系数为30,则a =( )B. C.6 D-6 【答案】D.18.【2015高考上海,理11】在10201511x x ⎛⎫++ ⎪⎝⎭的展开式中,2x 项的系数为(结果用数值表示). 【答案】45【解析】因为10101019102015201520151111(1)(1)(1)x x x C x x x x ⎛⎫⎛⎫++=++=++++ ⎪ ⎪⎝⎭⎝⎭,所以2x 项只能在10(1)x +展开式中,即为8210C x ,系数为81045.C =19.(2016年北京高考)在6(12)x -的展开式中,2x 的系数为__________________.(用数字作答)【答案】60.20.(2016年山东高考)若(a x 25的展开式中x 5的系数是—80,则实数a =_______. 【答案】-221.(2016年上海高考)在nx x ⎪⎭⎫ ⎝⎛-23的二项式中,所有项的二项式系数之和为256,则常数项等于_________ 【答案】11222.(2016年四川高考)设i 为虚数单位,则6(i)x +的展开式中含x 4的项为(A )-15x 4 (B )15x 4 (C )-20i x 4 (D )20i x 4 【答案】A23.(2016年天津高考)281()x x-的展开式中x 2的系数为__________.(用数字作答) 【答案】56-24.(2016年全国I 高考)5(2x +的展开式中,x 3的系数是 .(用数字填写答案) 【答案】10。
2018 年全国 III 卷数学(理)答案及解析

a1 = 1 ,
an = 2n −1 或 an =
( −2 )
n −1
S = 63 , (2) mn −1 ∴ 当通项公式为 an = 2 时, 1 − 2
(1 − 2 ) = 63
m
,得 m =6
当通项公式为
an =
( −2 )
n −1
1 − ( −2 )m = 63 m −1) 2m = 188 ( + 1 2 时, ,得 ,
− x + x + 2 的图像大致为( 7.函数 y =
4 2
)
A.
B.
C.
D.
【答案】D 【考点】函数图像以及性质 【难易程度】基础题 【解析】当 x=1 时,函数值大于 0,排除 A、B;因为 F(x)=F(-x),函数为偶函数,图像关于 y 轴
−4 x 3 + 2 x =0 ,解得 x=0、 、 对称, 令F '( x) =
,函数在(-∞,
)单调递增, (
,0)
单调递减, (0, )单调递增, ( ,+∞)单调递减,故选 D。
8.某群体中的每位成员使用移动支付的概率都为 体的 10 位成员中使用移动支付的人数, A. 0.7 【答案】B 【考点】二项分布概率与方差 【难易程度】基础题 【解析】使用移动支付符合二项分布, B.0.6
是带卯眼的木构件的俯视图可以是(
)
A.
B.
C. 【答案】A 【考点】三视图 【难易程度】基础题
D.
【解析】卯眼的空间立体图如图,同时需要注意在三视图中,看不见的线用虚线表示, 故答案选 A
4、若
,则
(
)
A. 【答案】B
2018年全国卷3理科数学试题和参考答案

20 20 20 20
故有 99% 的把握认为两种生产方式的效率有差异
【考点】茎叶图、均值及其意义、中位数、独立性检验
19. (12 分)
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在的平面垂直, M 是 CD 上 异于 C, D 的点.
(1) 证明:平面 AMD 平面 BMC ; (2) 当三棱锥 M ABC 体积的最大时,求面 M AB 与面 MCD 所成二面角的正弦值 .
在本试卷上无效 .
3. 考试结束后,将本试卷和答题卡一并交回 .
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的 .
1.已知集合 A x | x 1 0 , B 0, 1, 2 ,则 A B ( )
A. 0
B. 1
C. 1, 2
【答案】 C
【解析】 A : x 1, A B 1, 2
ABC 等边 S ABC 9 3
AB 6 ,
D
O
A
FE
B
C
在等边 ABC 中, BF
2 BE
3 AB
2 3,
3
3
在 Rt OFB 中,易知 OF
2 , DF
6 ,故 VD ABC max
1 9 3 6 18 3
3
【考点】外接球、椎体体积最值
11. 设 F1,
F2 是双曲线
x2 C : a2
的一条渐近线的垂线,垂足为
M
y1 y2 4m
x my 1,联立
可求
,由
y2 4 x
y1 y2 4
MB MA y1 y2
y1 y2 1 x1x2
x1 x2
2018年高考数学全国卷三理科试题(附答案)

2018年高考数学全国卷三理科试题(附答案) 2018年高考数学全国卷三理科考试已经落下帷幕,本试卷为考生带来了挑战,让大家从中更加深入的了解数学知识,本试卷的答案让大家从中收获了成长。
2018年高考数学全国卷三理科试题2018年高考数学全国卷三理科试题出炉,考生们做好了准备,及时解决遇到的问题,取得优异的成绩。
本次全国卷三包括4个部分组成,分别是选择题、填空题、解答题和分析题。
如下:一、选择题1. 若集合A={x|-2≤x≤2},集合B={x|x2<4},则A∩B= (A) {-2,2} (B) {-2,0,2} (C) {-1,1} (D) {0,2}2. 若平面上的两个点的坐标分别A(2,3),B(4,-3),那么它们之间的距离是(A)2(B)5(C)7(D)63. 若复数z1=1-i,z2=1+i,则z1、z2的共轭复数分别为(A)1-i,1+i(B)1+i,1-i(C)-1+i,-1-i(D)-1-i,-1+i4. 若函数y=3x3-6x2+9x+3在x=2处取得极值,则极大值为(A)-12(B)-9(C)15(D)185. 若两个圆O1,O2的半径分别是6,9,则O1, O2相切的条件是(A)r1=r2(B)r1+r2=15(C)r1-r2=3(D)r1+r2=3二、填空题1. 下列各式中,(1+√5)5次方的展开式中,常数项为a_1r_1+a_3r_3+a_5r_5,其中a_1,a_3,a_5分别为______,_______,_______。
答案:a_1=5 ; a_3=-5 ; a_5=12.函数f (x)=2x2+8x+9,x≤1时的最大值为_________。
答案:13三、解答题1.求实数a,b满足等式|a-3|-|b+3|=4的解。
答:解得a=-1、b=-72.曲线y=x3+3x2+3x+c的图象经过点(1,1),求参数c的值。
答:设y=x3+3x2+3x+c设点P(1,1)在曲线上,即1=1+3+3+cc=0四、分析题1.已知实数x,y满足约束条件2x+y≤12,x,y≥0,求此约束条件下的最大值。
2018高考数学全国卷含答案解析

21.(12分)
解:(1) 的定义域为 , .
(i)若 ,则 ,当且仅当 , 时 ,所以 在 单调递减.
(ii)若 ,令 得, 或 .
当 时, ;
当 时, .所以 在 单调递减,在 单调递增.
(2)由(1)知, 存在两个极值点当且仅当 .
由于 的两个极值点 满足 ,所以 ,不妨设 ,则 .由于
A.p1=p2B.p1=p3
C.p2=p3D.p1=p2+p3
11.已知双曲线Biblioteka : ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若 为直角三角形,则|MN|=
A. B.3C. D.4
12.已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为
19.(12分)
解:(1)由已知得 ,l的方程为x=1.
由已知可得,点A的坐标为 或 .
所以AM的方程为 或 .
(2)当l与x轴重合时, .
当l与x轴垂直时,OM为AB的垂直平分线,所以 .
当l与x轴不重合也不垂直时,设l的方程为 , ,
则 ,直线MA,MB的斜率之和为 .
由 得
.
将 代入 得
.
所以, .
23.[选修4—5:不等式选讲](10分)
解:(1)当 时, ,即
故不等式 的解集为 .
(2)当 时 成立等价于当 时 成立.
若 ,则当 时 ;
若 , 的解集为 ,所以 ,故 .
综上, 的取值范围为 .
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
2018年全国卷高考理科综合(理综)试题及详细解析(答案)(全国卷1、全国卷2、全国卷3)

- 1 -全国卷1生物部分 12写在本试卷上无效。
3H 1 Li 7 C 12 N 14 O 16 Na 23 S 32 Cl 35.5 Ar 40 Fe56 I 12766合题目要求的。
1. 生物膜的结构与功能存在密切的联系。
下列有关叙述错误的是A. 叶绿体的类囊体膜上存在催化ATP合成的酶B. 溶酶体膜破裂后释放出的酶会造成细胞结构的破坏C.D. 线粒体DNA【答案】D【解析】【分析】本题考查各种生物膜的结构和功- 2 - 【点睛】解答本题关键能识记生物膜的概念以及各种生物膜的结构和功能。
2. 生物体内的DNA DNA—蛋白质复合物的形式存在。
下列相关叙述错误的是A. 真核细胞染色体和染色质中都存在DNA—蛋白质复合物B. 真核细胞的核中有DNA—C. 若复合物中的某蛋白参与DNA DNA聚合酶D. 若复合物中正在进行RNA RNA聚合酶【答案】B【解析】【分析】据题干“DNA常与蛋白质结合,以DNA-DNA DNA-此回答各个选项。
DNADNA-A存在DNA-DNA-DNA进行复制或者转录的过程中都存在DNA DNA-蛋白质复合B DNA复制需要DNA DNA聚合酶C RNA的合成,RNA物中的某蛋白可能是RNA D正确。
DNA BCD三个选项。
3.A. 在酸N2和NO-3B. 农田适时松土有利于农作物根细胞对矿质元素的吸收C. 土壤微生物降解植物秸秆产生的无机离子可被根系吸收- 3 -D.根系水分外流引起“烧苗”现象【答案】A【解析】【分析】本题围绕植物根吸收物质的运输方式来考查植物根吸收无机盐的形式以及吸水和失水的条件。
N2不能直接A农田适BCD正确。
&网B选项的原理。
4. 已知药物X对细胞增值有促D可抑制药物X的作用。
某同学将同一瓶小鼠皮述不合理的是A. 乙组加入了药物X后再进行培养B. 丙组先加入药物X DC. 乙组先加入药物D XD. 若药物X D可能改变了药物X的空间结构【答案】C【解析】【分析】本题以“探究药物X对细胞增殖有促进作用,药物D可抑制药物X的作用”过观察指标从而得出实验结论。
2018年全国卷Ⅲ理综高考试题(含答案)
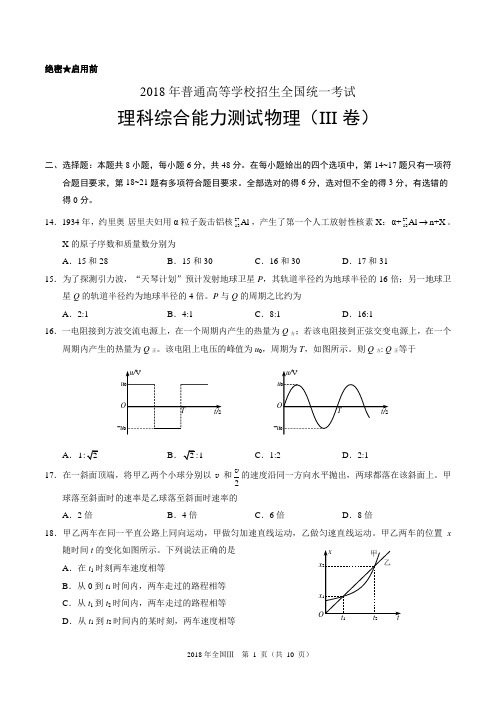
O T t/su 0 -u 0u/VO T t/s u 0 -u 0u/Vtxt 1t 2x 1 x 2甲乙O绝密★启用前2018年普通高等学校招生全国统一考试理科综合能力测试物理(III 卷)二、选择题:本题共8小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
14.1934年,约里奥-居里夫妇用α粒子轰击铝核2713Al ,产生了第一个人工放射性核素X :2713α+Al n+X 。
X 的原子序数和质量数分别为 A .15和28B .15和30C .16和30D .17和3115.为了探测引力波,“天琴计划”预计发射地球卫星P ,其轨道半径约为地球半径的16倍;另一地球卫星Q 的轨道半径约为地球半径的4倍。
P 与Q 的周期之比约为 A .2:1B .4:1C .8:1D .16:116.一电阻接到方波交流电源上,在一个周期内产生的热量为Q 方;若该电阻接到正弦交变电源上,在一个周期内产生的热量为Q 正。
该电阻上电压的峰值为u 0,周期为T ,如图所示。
则Q 方: Q 正等于A .1:2B .2:1C .1:2D .2:117.在一斜面顶端,将甲乙两个小球分别以v 和2v的速度沿同一方向水平抛出,两球都落在该斜面上。
甲球落至斜面时的速率是乙球落至斜面时速率的 A .2倍B .4倍C .6倍D .8倍18.甲乙两车在同一平直公路上同向运动,甲做匀加速直线运动,乙做匀速直线运动。
甲乙两车的位置x随时间t 的变化如图所示。
下列说法正确的是 A .在t 1时刻两车速度相等B .从0到t 1时间内,两车走过的路程相等C .从t 1到t 2时间内,两车走过的路程相等D .从t 1到t 2时间内的某时刻,两车速度相等tvt 02t 0Ov 0/2v 0①②OTt/siT /4T /23T /4RPQ 图(a )图(b )ab19.地下矿井中的矿石装在矿车中,用电机通过竖井运送至地面。
2018高考全国卷3地理试题(含答案及解析)高清Word版

2017年普通高等学校招生全国统一考试文科综合能力测试第Ⅲ套(丙卷)剪纸是中国传统民间艺术,2009年9月入选联合国教科文组织人类非物质文化遗产代表作名录。
剪纸表现的内容丰富多彩,反映人们的生活环境、习俗和风情等,寄托人们对美好生活的向往。
图1是一帧剪纸作品。
据此完成1~3题。
1.图1剪纸所反映的景观主要分布于我国图1A.四川盆地B.华北平原C.珠江三角洲D.长江三角洲2.形成这种景观特征的自然条件有A.沟壑纵横,降水集中B.地势低平,降水丰沛C.地形封闭,排水不畅D.山河相间,降水均匀3.该景观主要分布区具代表性的地方剧种是A.川剧B.豫剧C.粤剧D.越剧某条城市地铁线穿越大河,途经主要的客流集散地。
图2示意该地铁线各站点综合服务等级。
据此完成4~6题。
图24.地铁站点综合服务等级的高低主要取决于A.站点的用地面积B.周边的人流量C.站点的信息化水平D.周边的环境质量5.根据所处区位和地铁站点综合服务等级,推测甲、乙、丙站点沿线区域为A.中心商务区B.森林公园C.大型住宅区D.产业园区6.该城市空间形态的形成最有可能A.围绕一个核心向四周扩展B.沿河流呈条带状延展C.围绕多个核心向四周扩展D.沿交通线呈条带状延展一般情况下,海水中的浮游植物数量与营养盐、光照、水温呈正相关,但在不同的季节、海域,影响浮游植物生长繁殖的主导因素不同。
图3示意长江口附近海域某年8月浮游植物密度的水平分布。
据此完成7~9题。
图37.夏季图示海域浮游植物密度自西向东A.递减B.先减后增C.先增后减D.递增8.导致夏季图示海域浮游植物密度水平分布的主导因素是A.水体营养盐B.太阳辐射C.水体含沙量D.洋流流向9.与夏季相比,冬季图示海域浮游植物A.总数量减少,密度高值区向陆地方向移动B.总数量增多,密度高值区向外海方向移动C.总数量减少,密度高值区向外海方向移动D.总数量增多,密度高值区向陆地方向移动某日,小明在互联网上看到世界各地好友当天发来的信息:甲:温暖的海风夹着即将到来的夏天的味道扑面而来。
2018年普通高等学校招生全国统一考试理科综合全国卷3试题及答案

2018年普通高等学校招生全国统一考试理科综合能力测试注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 C12N14O16 Na 23 Mg 24 Al 27 S 32 Cr 52 Zn 65I 127一、选择题:本题共13个小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
学@科网1.下列研究工作中由我国科学家完成的是A.以豌豆为材料发现性状遗传规律的实验B.用小球藻发现光合作用暗反应途径的实验C.证明DNA是遗传物质的肺炎双球菌转化实验D.首例具有生物活性的结晶牛胰岛素的人工合成2.下列有关细胞的结构和生命活动的叙述,错误的是A.成熟个体中的细胞增殖过程不需要消耗能量B.细胞的核膜、内质网膜和细胞膜中都含有磷元素C.两个相邻细胞的细胞膜接触可实现细胞间的信息传递D.哺乳动物造血干细胞分化为成熟红细胞的过程不可逆3.神经细胞处于静息状态时,细胞内外K+和Na+的分布特征是A.细胞外K+和Na+浓度均高于细胞内B.细胞外K+和Na+浓度均低于细胞内C.细胞外K+浓度高于细胞内,Na+相反D.细胞外K+浓度低于细胞内,Na+相反4.关于某二倍体哺乳动物细胞有丝分裂和减数分裂的叙述,错误的是A.有丝分裂后期与减数第二次分裂后期都发生染色单体分离B.有丝分裂中期和减数第一次分裂中期都发生同源染色体联会C.一次有丝分裂与一次减数分裂过程中染色体的复制次数相同D.有丝分裂中期和减数第二次分裂中期染色体都排列在赤道板上5.下列关于生物体中细胞呼吸的叙述,错误的是A.植物在黑暗中可进行有氧呼吸也可进行无氧呼吸B.食物链上传递的能量有一部分通过细胞呼吸散失C.有氧呼吸和无氧呼吸的产物分别是葡萄糖和乳酸D.植物光合作用和呼吸作用过程中都可以合成ATP6.某同学运用黑光灯诱捕的方法对农田中具有趋光性的昆虫进行调查。
2018年全国统一高考数学真题试卷及答案解析【全国卷三】
2018年高考真题理科数学 (全国III卷)一、填空题:(本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知集合A={x∣x-1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2}2.(1+i)(2-i)=()A.-3-iB.-3+iC.3-iD.3+i3.中国古建筑借助棒卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()4.若,则( )A. B. C. D.5.的展开式中的系数为( )A.10B.20C.40D.806.直线x+y+2=0分别与x轴,y交于A,.两点,点P在圆(x-2)²+y ²=2上,则∆ABP面积的取值范围是( )A.[2,6]B.[4,8]C.D.7.函数y=-+x²+2的图像大致为A . B.C. D.8.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<p(x=6),则p=< span="">( )A .0.7 B.0.6 C.0.4 D.0.39.∆ABC的内角A,B,C的对边分别为a,b,c,若∆ABC的面积为,则C=( )A. B. C. D.10.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D-ABC体积的最大值为( )A.12B.18C.24D.5411.设F1、F2是双曲线的左、右焦点,O是坐标原点,过F2作C的一条渐近线的垂线,垂足为P,若,则C的离心率为( )A. B.2 C. D.二、填空题(本题共4小题,每小题5分,共20分。
2018年全国卷3(理科数学)含答案

绝密★启用前2018年普通高等学校招生全国统一考试理科数学(全国Ⅲ卷)注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则【C 】A .B .C .D . 2.【D 】 A .B .C .D .3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是【A 】{}|10A x x =-≥{}012B =,,A B ={}0{}1{}12,{}012,,()()1i 2i +-=3i --3i -+3i -3i+4.若,则【B 】 A .B .C .D . 5.的展开式中的系数为【C 】A .10B .20C .40D .806.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是【A 】 A .B .C .D .7.函数的图像大致为【D 】1sin 3α=cos2α=897979-89-522x x ⎛⎫+ ⎪⎝⎭4x 20x y ++=x y A B P ()2222x y -+=ABP △[]26,[]48,⎡⎣422y x x =-++8.某群体中的每位成员使用移动支付的概率都为,各成员的支付方式相互独立,设为该群体的10位成员中使用移动支付的人数,,,则【B 】 A .0.7B .0.6C .0.4D .0.39.的内角的对边分别为,,,若的面积为,则【C 】 A . B . C . D .10.设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为【B 】A .B .C .D .11.设是双曲线()的左,右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若,则的离心率为【C 】 AB.2CD12.设,,则【B 】A .B .C .D .二、填空题:本题共4小题,每小题5分,共20分。
2018年高考真题语文全国卷3(含答案)

2018年高考真题语文全国卷3(含答案)2018年普通高等学招生全国统一考试----全国卷3语文试卷注意事项:1、答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标或。
回答非选择题时,将答案写在大体看上。
写在本试卷上无效。
3、考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(36)(一)论述类文本阅读(本题共3小题,9分)对城市而言,文明弹性是一个城市体在生存、创新、适应、应变等方面的综合状态、综合能力,是公共性与私人性之间;多样性与共同性之间;稳定性与变迁性之间、柔性与刚性之间的动态和谐。
过于绵柔、松散,或者过于刚硬、密集,都是弹性不足或丧失的表现,是城市体出现危机的表征。
当代城市社会,尤其需要关注一下文明弹性问题。
其一,空间弹性。
城市具有良好空间弹性的一个重要表现,是空间的私人性与公共性关系能够得到较为合理的处理。
任何城市空间都是私人性与公共性的统一,空间弹性的核心问题,就是如何实现空间的公共性与私人性的有机统一、具体转换。
片面的强调空间公共性或片面的强调空间的私人性,都会使城市发展失去基础。
目前,人们更多地要求空间的人,注重把空间固化为永恒的私人所有物、占有物。
这种以私人化为核心的空间固化倾向,造成城市空间弹性不足,正在成为制约城市,发展的一个重要原因。
其二,制度弹性。
一种较为理想的、有弹性的城市制度,是能够在秩序与活力、生存与发展间取得相对平衡的制度。
城市有其发展周期、发展阶段,对一个正在兴起的城市而言,其主要任务是聚集更多的发展资源、激活发展活力。
而对一个已经发展起来的城市而言,人们会更为注重城市制度的稳定功能。
但问题在于,即使是正在崛起的城市,也需要面对秩序与稳定的问题;即使是一个已经发展起来的城市,也需要面对新活力的激活问题。
过于注重某种形式的城市制度,过于注重城市制度的某种目标,都是城市制度弹性不足、走向僵化的表现,都会妨害城市发展。
2018年高考文科数学全国卷3(含答案与解析)

2018年高考文科数学全国卷3(含答案与解析)2018年普通高等学校招生全国统一考试课标全国卷III数学(文科)本试卷满分150分,考试时间120分钟。
第Ⅰ卷(选择题共60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合$A=\{x|x-1\geq0\}$,$B=\{0,1,2\}$,则$AB=$A。
$\emptyset$ B。
$\{1\}$ C。
$\{1,2\}$ D。
$\{0,1,2\}$2.$(1+i)(2-i)=$A。
$-3-i$ B。
$-3+i$ C。
$3-i$ D。
$3+i$3.中国古建筑借助榫卯将木构件连接起来。
构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是ABCD4.若$\sin\alpha=\frac{1}{3}$,则$\cos2\alpha=$A。
$\frac{8}{9}$ B。
$\frac{7}{99}$ C。
$-\frac{7}{9}$ D。
$-\frac{8}{9}$5.若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A。
0.3 B。
0.4 C。
0.6 D。
0.76.函数$f(x)=\frac{\tan x}{1+\tan^2x}$的最小正周期为A。
$\frac{\pi}{4}$ B。
$\frac{\pi}{2}$ C。
$\pi$ D。
$2\pi$7.下列函数中,其图象与函数$y=\ln x$的图象关于直线$x=1$对称的是A。
$y=\ln(1-x)$ B。
$y=\ln(2-x)$ C。
$y=\ln(1+x)$ D。
$y=\ln(2+x)$成任务的时间,得到以下数据:第一组:12.15.13.14.16.18.17.14.16.15.13.12.14.15.13.16.17.14.15.13第二组:16.17.14.18.15.16.13.14.15.16.17.15.14.16.15.17.15.16.18.141)分别计算两组工人完成任务的平均时间和标准差;2)根据以上数据,判断两种生产方式哪一种更有效,并说明理由.19.(12分)已知函数f(x)在区间[0,1]上连续,且f(0)=f(1)=0.证明:对于任意正整数n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴氏教育新津总校——理数绝密★启用前2018 年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A x|x1≥0 ,B 0 ,1,2 ,则 A BA .0B. 1 C.1,2 D.0,1,22.1 i 2 iA . 3 i B.3i C.3i D. 3 i3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若sin 1,则 cos238 7 7 8A.B.C.D.99995.x 225x 的展开式中 x 4的系数为戴氏教育新津总校——理数戴氏教育新津总校——理数 A .10 B .20 C . 40 D .806.直线 x y 2 0分别与 x 轴, y 轴交于 A , B 两点,点 P 在圆 x 2 2 y 2 2上,则 △ABP 面积的取 值范围是 A . 2,6B . 4,8C . 2 ,3 2D . 2 2,3 27.函数 y x 4x 22 的图像大致为8.某群体中的每位成员使用移动支付的概率都为 p ,各成员的支付方式相互独立,设 X 为该群体的 10位成员中使用移动支付的人数, DX 2.4 , P X 4 P X 6 ,则 pA. 0.7 B .0.6 C . 0.4 D 0.3 9. △ ABC 的内角A ,B ,C 的对边分别为 a , b ,c ,若 △ABC 的面积为 2 a22 b c ,则 C 4 π π ππ A . B . C . D2 3 4610.设 A ,B ,C ,D 是同一个半径为 4 的球的球面上四点, △ ABC 为等边三角形且其面积为 93,则三棱 锥 D ABC 体积的最大值为A .12 3 B. 18 3 C. 24 3 D. 54 32211.设 F 1 ,F 2是双曲线 C :x 2 y2 1(a 0,b 0 )的左,右焦点, O 是坐标原点.过 F 2作C 的一条渐近 ab线的垂线,垂足为 P .若 PF 1 6 OP ,则 C 的离心率为A . 5B .2C . 3D . 212.设 a log 0.2 0.3 , b log 2 0.3 ,则 A . a b ab 0B . ab a b 0C . a b 0 abD . ab 0 a b 填空题:本题共 4 小题,每小题 5 分 ,共 20 分。
13.已知向量 a = 1,2 , b = 2, 2 , c = 1,λ.若 c ∥ 2a+ b ,则 _ 14.曲线 y ax 1 e x在点 0 ,1 处的切线的斜率为 2 ,则 a __16 .已知点 M 1,1 和抛物线 C :y 24x ,过 C 的焦点且斜率为 k 的直线与 C 交于 A , B 两点.若 ∠ AMB 90 ,则 k .三、解答题:共 70分。
解答应写出文字说明、证明过程或演算步骤。
第 17~21 题为必考题,每个试题考生 都必须作答。
第 22、 23 题为选考题,考生根据要求作答。
(一)必考题:共 60 分。
17.( 12 分)等比数列 a n 中, a 1 1,a 5 4a 3 .1)求 a n 的通项公式; 2)记 S n 为 a n 的前 n 项和.若 S m 63,求 m . 18.( 12 分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为 比较两种生产方式的效率,选取 40 名工人,将他们随机分成两组,每组 20 人。
第一组工人用第一种 生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位: min )绘制了如 下茎叶图:15.函数 f x cos3x 6π在 0, π的零点个数为(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求 40 名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:3)根据( 2)中的列联表,能否有 99%的把握认为两种生产方式的效率有差异?2n ad bc ,附: K2a b c d a c b d19.( 12 分)如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在平面垂直,M 是 CD 上异于 C ,D 的点.1)证明:平面AMD ⊥平面 BMC ;2)当三棱锥 M ABC 体积最大时,求面MAB 与面 MCD 所成二面角的正弦值.20.( 12 分)22已知斜率为 k的直线 l 与椭圆C:x y 1交于A,B两点,线段AB 的中点为M 1,m m0 .431( 1)证明: k ;2(2)设F 为C 的右焦点,P 为 C 上一点,且 FP FA FB 0.证明: FA , FP , FB 成等差戴氏教育新津总校——理数数列,并求该数列的公差.21.( 12 分)已知函数f x 2 x ax2 ln 1 x 2x .(1)若 a 0 ,证明:当 1 x 0时,f x 0;当 x 0 时,f x 0;(2)若 x 0 是f x 的极大值点,求 a .(二)选考题:共 10分。
请考生在第 22、23 题中任选一题作答。
如果多做,则按所做的第一题计分。
22.[选修 4—4:坐标系与参数方程](10 分)x cos ,在平面直角坐标系 xOy 中,⊙O 的参数方程为(为参数),过点 0, 2 且倾斜角为y sin的直线 l 与⊙O交于 A,B 两点.( 1)求的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.[选修 4—5:不等式选讲](10 分)设函数f x 2x 1 x 1 .( 1)画出y f x 的图像;(2)当x∈ 0,,f x ≤ax b ,求 a b的最小值.参考答案:113. 14. 3 15.3 16.2217.(12 分)解:( 1)设{ a n} 的公比为q ,由题设得a n q n 1.由已知得q4 4q2,解得q 0 (舍去),q 2或q 2.故a n ( 2)n 1或a n n1(2)若a n( 2)n 1,则S n 1 ( 2).由S m 63得( 2)m 188,此方程没有正整数解 .3若a n 2 ,则S n 2 1.由S m 63得2 64,解得m 6.综上,m 6.18.(12 分)解:( 1)第二种生产方式的效率更高 .理由如下:( i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80 分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多 79 分钟 .因此第二种生产方式的效率更高 .(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5 分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为 73.5 分钟.因此第二种生产方式的效率更高 .(iii )由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于 80 分钟;用第二种生产方式的工人完成生产任务平均所需时间低于 80 分钟,因此第二种生产方式的效率更高 .(iv )由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8 上的最多,关于茎 8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7 上的最多,关于茎7 大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高 .学科 * 网以上给出了 4 种理由,考生答出其中任意一种或其他合理理由均可得分 .戴氏教育新津总校——理数2)由茎叶图知m 79 81 80. 2列联表如下:超过m 不超过m 第一种生产方式15 5第二种生产方式 5 153)由于K 2 40(15 15 5 5)10 6.635,所以有 99%的把握认为两种生产方式的效率有差异20 20 20 2019.(12 分)解:(1)由题设知 ,平面 CMD ⊥平面 ABCD ,交线为 CD.因为 BC⊥CD,BC 平面 ABCD ,所以BC⊥平面 CMD, 故 BC⊥ DM.因为 M 为CD 上异于 C, D 的点 ,且 DC为直径,又 BC CM =C,所以 DM ⊥平面 BMC.而 DM 平面 AMD ,故平面 AMD ⊥平面 BMC.当三棱锥 M-ABC 体积最大时, M为CD的中点 .由题设得D(0,0,0), A(2,0,0), B(2,2,0), C(0,2,0), M (0,1,1) ,AM ( 2,1,1),AB (0,2,0), DA (2,0,0)设n (x,y,z) 是平面 MAB 的法向量 ,则n AM 0, 即2x y z 0,n AB 0. 2y 0.可取n (1,0, 2) .所以 DM ⊥CM.2)以 D 为坐标原点 ,DA 的方向为 x 轴正方向,建立如图所示的空间直角坐标系D- xyz.戴氏教育新津总校——理数DA 是平面 MCD 的法向量 ,因此n DA 5,5|n ||DA| sin n ,DA 2 5所以面 MAB 与面 MCD 所成二面角的正弦值是25 20. (12 分) 解:( 1)设A( x 1, y 1 ), B( x 2 , y 2),则22 x 1y 1 43221,x 42 y 32 1. 两式相减,并由y 1 y 2 k 得x1 x2x1x2y1 3y2k 0.由题设知 x 1 x 2 1,y 1 y2 m ,223.① 4m31由题设得 0 m ,故 k .2)由题意得 F (1,0) ,设 P(x 3,y 3),则(x 3 1, y 3) (x 1 1,y 1) (x 2 1,y 2) (0,0) .由( 1)及题设得x 3 3 (x 1 x 2) 1,y 3 (y 1 y 2) 2m 0.又点 3 3 3P 在 C 上,所以 m 3,从而 P(1, 3),|FP| 3.同理 x2|FB| 2 2 |FA| (x 1 1)2 y 12x1(x 1 1)2 3(1 41) 2 2所以 |FA| |FB | 4 1(x 1 x 2) 3.2故2| FP| |FA| |FB|,即 | FA |,| FP |,| FB |成等差数列 .cos戴氏教育新津总校——理数6a 1 如果 6a 1 0,则当 0 x6a 1,且 |x| min{ 1, 1} 时, h (x) 0,故 x 0不是 h(x) 的极 4a |a|当 1 x 0时, g (x) 0;当 x 0时, g (x) 0.故当 x 1时, g(x) g(0) 0,且仅当 x 0时, g(x) 0,从而 f (x) 0 ,且仅当 x 0时, f (x) 0.所以 f (x) 在 ( 1, ) 单调递增 .学.科网 又 f (0) 0,故当 1 x 0时, f (x) 0;当 x 0时, f (x) 0.2)( i)若 a 0,由( 1)知,当 x 0 时, f (x) (2 x)ln(1 x) 2x 0 f (0) ,这与 x 0是f (x) 的极大值点矛盾 . 2时, 2 x ax 20,故 h(x) 与 f (x) 符号相同 .又 h(0) f(0) 0,故 x 0是 f (x) 的极大值点当且仅当 x 0是 h(x) 的极大值点 .h(x)1 2(2 x ax 2) 2x(1 2ax) x 2(a 2x 2 4ax 6a 1) h(x)1 x (2 x ax 2 )2(x1)(ax 2 x 2)2设该数列的公差为 d ,则2|d| ||FB | |FA || 1| x 1 x 2 | 1(x 1 x 2)24x 1x 2 .②223将m 代入①得4 k1所以 l 的方程为 yx 47,代入 C 的方程,并整理得 7x 2 14x 1 0. 4故x 1 x 2 2, x 1x 21,代入②解得 |d| 3 2128 28所以该数列的公差为3 21 或3 21 28 2821. (12 分 )解:( 1)当 a 0时, f (x) (2 x)ln(1 x) 2x ,xf (x) ln(1 x) x1x设函数 g(x) f (x) ln(1 x) x,则 g (x) 1xx2.(1 x)2ii)若 a 0 ,设函数 h(x)2f x (x)ax 2ln(1 x)2x2 x ax 2由于当|x| min{1, |a|(2 x ax 2 )2大值点 .如果6a 1 0,则a 2x 2 4ax 6a 1 0存在根 x 1 0 ,故当 x (x 1,0) ,且 |x| min{ 1, 1}时,|a|h (x) 0,所以 x 0不是 h(x) 的极大值点 .h (x) 0.所以 x 0是 h( x)的极大值点,从而 x 0是1 综上, a 1.622. [选修 4—4:坐标系与参数方程 ](10 分)(4,2)或 (2, 4 ).( , ) .44x tcos ,2) l 的参数方程为(t 为参数,y 2 tsin如果 6a 1 0,则 h(x)x (x 24)(x 1)(x 26x 12)2 .则当x ( 1, 0)时, h(x) 0;当 x (0,1)时,f (x) 的极大值点 解析】(1) O 的直角坐标方程为 x 2 y 21.当2 时, l 与 O 交于两点.当时,2记 tan k ,则 l 的方程为 y kx 2 .2l 与 O 交于两点当且仅当 | 1 2k 2 | 1,解得 k 1 或 k 1 ,即 综上, 的取值范围是设 A ,B , P 对应的参数分别为 t A ,t B ,t P ,则t P t A2t B ,且 t A ,t B 满足 t 22 2tsin 1 0.于是t A t B 2 2sin , t P2sin .又点 P 的坐标 (x,y) 满足x t P cos ,2 t P sin .所以点 P 的轨迹的参数方程是2 x sin2 , 2 2 ( 为参数,2 2 4 y2 4).23. [选修 4—5:不等式选讲 ](10 分)13x,x ,21 解析】(1) f (x) x 2, x 1, y f (x) 的图像如图所示.23x,x 1.2)由( 1)知,y f ( x)的图像与y 轴交点的纵坐标为2 ,且各部分所在直线斜率的最大值为3,戴氏教育新津总校——理数故当且仅当a 3且b 2时,f (x) ax b 在[0, )成立,因此a b 的最小值为5.。
