非线性规划课程设计【共轭梯度法】
共轭梯度法公式

共轭梯度法公式
共轭梯度法是一种用于求解线性方程组的迭代算法。
其主要思想是通过利用前一次迭代的信息来加速当前迭代的速度,从而减少迭代次数和计算量。
共轭梯度法公式包括以下几个步骤:
1. 初始化:设初始解为x0,残量b0为Ax0-b,共轭方向d0=b0。
2. 迭代求解:对于第k次迭代,计算步长αk,使得xk+1=xk+αkd,其中d是共轭方向,满足dTkAd=0,即d是A的共轭向量。
3. 更新残量:计算新的残量bk+1=Axk+1-b,如果bk+1小于预设精度,则停止迭代。
4. 更新共轭方向:计算新的共轭方向dk+1=bk+1+βkdk,其中βk=(bk+1)Tbk+1/(bk)Tbk,保证dk+1与之前的共轭方向都是A的共轭向量。
5. 重复迭代,直到满足收敛条件,返回最终解xk+1。
共轭梯度法是一种高效的求解大型线性方程组的方法,尤其适用于稀疏矩阵和对称正定矩阵。
公式简单易懂,容易实现,且具有较快的收敛速度。
- 1 -。
非线性共轭梯度法

非线性共轭梯度法
(Nonlinear Conjugate Gradient Method)
非线性共轭梯度法是一种基于梯度的迭代优化方法,用于求解无约束最优化问题,即求解目标函数f(x)的最小值。
它可以用来求解深度神经网络中参数的最优化。
非线性共轭梯度法的基本思想是利用梯度下降法的思路,但是在每次迭代时都会调整步长,使得每次迭代可以尽可能地朝着最优解方向前进。
该方法有两个重要特征:1)步长调整。
2)共轭梯度(CG)。
步长调整:在每次迭代中,搜索方向不仅可以与梯度方向一样,而且也可以与之前的搜索方向有一定的关系。
通过调整步长,可以把搜索方向调整到最优方向,从而更快地收敛到最优解。
共轭梯度:对于多维的优化问题,搜索空间是一个高维空间,如果每次都沿着梯度方向搜索,就容易陷入局部最优解。
为了避免这种情况,非线性共轭梯度法引入了共轭搜索方向,即在每次迭代中,新的搜索方向都与上一次的搜索方向有一定的关系。
这样做的好处是,在不断地迭代中,法线方向也可以被搜索到,从而可以跳出局部最优解,有效地收敛到全局最优解。
共轭梯度法程序

一、共轭梯度法共轭梯度法(Conjugate Gradient)是共轭方向法的一种,因为在该方向法中每一个共轭向量都是依靠赖于迭代点处的负梯度而构造出来的,所以称为共轭梯度法。
由于此法最先由Fletcher和Reeves (1964)提出了解非线性最优化问题的,因而又称为FR 共轭梯度法。
由于共轭梯度法不需要矩阵存储,且有较快的收敛速度和二次终止性等优点,现在共轭梯度法已经广泛地应用于实际问题中。
共轭梯度法是一个典型的共轭方向法,它的每一个搜索方向是互相共轭的,而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合,因此,存储量少,计算方便,效果好。
二、共轭梯度法的原理设有目标函数f(X)=1/2X T HX+b T X+c 式1 式中,H作为f(X)的二阶导数矩阵,b为常数矢量,b=[b1,b2,b3,...b n]T 在第k次迭代计算中,从点X(k)出发,沿负梯度方向作一维搜索,得S(K)=-∆f(X(k))式2 X(k+1)=X(k)+ɑ(k)S(k) 式3在式中,ɑ(k)为最优步长。
设与S(k)共轭的下一个方向S(k+1)由点S(k)和点X(k+1)负梯度的线性组合构,即S (k+1)=-∆f (X (k+1))+β(k)S (k) 式4 根据共轭的条件有[S (k)]T ∆2f (X (k))S (k+1)=0 式5 把式2和式4带入式5,得-[∆f(X (k))]T ∆2f (X (k))[-∆f (X (k+1))+β(k)S (k) ]=0 式6 对于式1,则在点X (k)和点X (k+1)的梯度可写为∆f(X (k))=HX (k)+b 式7 ∆f (X (k+1))=HX (k+1)+b 式8 把上面两式相减并将式3代入得ɑ(k)H S (k)=∆f (X (k+1))-∆f(X (k)) 式9 将式4和式9两边分别相乘,并代入式5得-[∆f (X (k+1))+β(k)∆f(X (k))]T [∆f (X (k+1))-∆f(X (k)]=0 式10 将式10展开,并注意到相邻两点梯度间的正交关系,整理后得 β(k )=22||))((||||))1((||k X f k X f ∆+∆ 式11把式11代入式4和式3,得 S (k+1)=-∆f (X (k))+β(k )S (k )X (k+1)=X (k )+ɑ(k )S (k )由上可见,只要利用相邻两点的梯度就可以构造一个共轭方向。
共轭梯度法(精品文档)

1
g2T (g2 d1T (g2
g1) g1)
g2T g2 g1T g1
4) 一般地,在第 k 次迭代中,令
k 1
dk gk idi i0
适当选取 i ,使 dkTGdi 0 ( i 0,
, k 1),可得到
i
gkT Gdi diT Gdi
gkT (gi1 gi ) diT (gi1 gi )
§4.2 共轭梯度法
提纲
1、共轭梯度法---F-R共轭梯度法 2、共轭梯度法性质定理及例题 3、再开始FR共轭梯度法 4、Beale三项共轭梯度法 5、预条件共轭梯度法(了解)
共轭梯度法
在上一节中讨论了共轭方向法,其中n个共轭方向是预先设定好的。但是如何 让获取这些共轭方向并为提及。本节讨论一种重要的共轭方向法——共轭梯 度法。这种方法是将共轭性和最速下降方向相结合,利用已知迭代点处的梯 度方向构造一组共轭方向,并沿此方向进行搜索,求出函数的极小点。因在 迭代过程中通过对负梯度方向进行适当校正获得共轭方向,故而称之为共轭 梯度法。
算法步骤—FR共轭梯度法
1、选取初始数据,选取初始点 x0 ,给定允许误差 0 ;
2、检查是否满足终止准则,计算 f (x0 ) ,若 || f (x0 ) || ,迭代终
止,x0为近似最优解,否则转向3;
3、 构造初始搜索方向,计算 d0 f (x0 ), k 0;
而
k 1
gkT (gk gk1)
dT k 1
(
gk
gk 1 )
gkT gk gkT1 gk 1
共轭梯度法的迭代公式为:
共轭梯度法

题目:共轭梯度法及其数值实现院系:数理科学与工程学院应用数学系专业:数学与应用数学姓名学号:************************************************指导教师:张世涛日期:2015 年7 月 5 日最优化是一门应用性很强的学科,近年来,随着计算机的发展以及实际问题的需要,大规模优化问题越来越受到重视。
共轭梯度法是最优化中最常见的方法之一,他具有算法简单、存储需求少、有较快的收敛速度和二次终止性且易于实现等优点,十分适合于大规模优化问题。
非线性共轭梯度法已有五十多年的历史,最早由计算数学家Hestenes和几何学家Stiefel为求解线性方程组Ax=b,n Rx∈而独立提出的。
较著名的有FR方法、PRP方法、HS方法和LS方法等。
非线性最优化的共轭梯度算法的收敛性分析,也就是讨论各种共轭梯度算法在不同搜索下的收敛性质。
本文主要研究求解无约束优化问题的非线性共轭梯度法,并用Matlab软件对其数值实现。
关键词:无约束规划;非线性共轭梯度法;迭代;最优解;数值实现AbstractOptimization is strong discipline applied. In recent years, with the development of computer and practical issues,large-scale optimization problems are given more and more attention.Conjugate gradient method is one of the most commonly used methods in optimization. It is simply, storage needs less, easy to practice with faster convergence speed and quadratic termination. It is suitable for large-scale optimization problem.The conjugate gradient method have been more than 50 years of history. The pioneers were mathematician Hestenes and geometrician Stiefel. They independently proposed this method for solving system of linear equations Ax=b,n Rx∈. Well-known conjugate gradient method is FR method, PRP method, HS method, LS method and so on. The convergence analysis of the conjugate gradient algorithm for nonlinear optimization is also the convergence of various conjugate gradient algorithms under different search conditions. Global convergence and numerical result of nonlinear conjugate gradient method of unconstrained optimization is investigated in this paper. Besides, we use Matlab to get its numerical solution.Keywords:Unconstrained programming; Nonlinear conjugate gradient method;Iteration; Optimal solution; Numerical implementation第一章引言 (2)1.1无约束优化问题概述 (2)1.2 共轭方向 (2)1.3 共轭方向法 (3)第二章共轭梯度法 (4)2.1 基本原理 (4)2.2 算法步骤 (4)2.3 程序流程图 (5)第三章算例 (6)总结 (9)参考文献 (11)附录 (12)第一章引言1.1 无约束优化问题概述无约束最优化问题,即为在不对所求问题定义域或值域做任何限制情况下,对目标函数求最小值的一类问题。
运筹学实验共轭梯度法
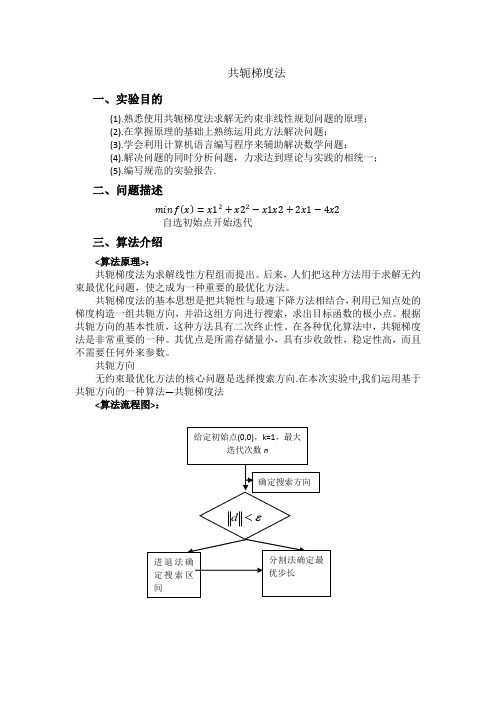
共轭梯度法一、实验目的(1).熟悉使用共轭梯度法求解无约束非线性规划问题的原理;(2).在掌握原理的基础上熟练运用此方法解决问题;(3).学会利用计算机语言编写程序来辅助解决数学问题;(4).解决问题的同时分析问题,力求达到理论与实践的相统一;(5).编写规范的实验报告.二、问题描述自选初始点开始迭代三、算法介绍<算法原理>:共轭梯度法为求解线性方程组而提出。
后来,人们把这种方法用于求解无约束最优化问题,使之成为一种重要的最优化方法。
共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点。
根据共轭方向的基本性质,这种方法具有二次终止性。
在各种优化算法中,共轭梯度法是非常重要的一种。
其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
共轭方向无约束最优化方法的核心问题是选择搜索方向.在本次实验中,我们运用基于共轭方向的一种算法—共轭梯度法<算法流程图>:四、程序%¾«È·ÏßËÑË÷,ÌݶÈÖÕÖ¹×¼Ôòfunction [ m,k,d,a,X,g1,fv] = GETD( G,b,c,X,e,method)if nargin<6error('ÊäÈë²ÎÊý±ØÐëΪ6');endn=length(G);if n==2format long e%ratsyms x1x2f=1/2*[x1,x2]*G*[x1;x2]+b'*[x1;x2]+c;g=[diff(f,x1);diff(f,x2)];g1=subs(subs(g,x1,X(1,1)),x2,X(2,1));d=-g1;a=-(d'*g1)/(d'*G*d);% a=-((X(:,1)'*G*d+b'*d)/(d'*G*d)); a=g1(:,1)'*g1(:,1)/(d(:,1)'*G*d(:,1));X(:,2)=X(:,1)+a*d;g1=[g1 subs(subs(g,x1,X(1,2)),x2,X(2,2))];m1=norm(g1(:,1));m=norm(g1(:,2));i=2;k=zeros(1);switch methodcase'FR'while m>=ek(i-1)=(m/m1)^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));%a1(i)=-((X(:,i)'*G*d(:,i)+b'*d(:,i))/(d(:,i)'*G*d(:,i)));a (i)=g1(:,i)'*g1(:,i)/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endcase'PRP'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(norm(g1(:,i-1)))^2;d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'HS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(g1(:,i)-g1(:,i-1))); d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'DY'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(g1(:,i)-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'LS'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-g1(:,i-1))/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m=norm(g1(:,i+1));i=i+1;endcase'CD'while m>=ek(i-1)=g1(:,i)'*g1(:,i)/(d(:,i-1)'*(-g1(:,i-1)));d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];i=i+1;endcase'WYL'while m>=ek(i-1)=g1(:,i)'*(g1(:,i)-(m/m1)*g1(:,i-1))/(m1^2);d(:,i)=-g1(:,i)+k(i-1)*d(:,i-1);a(i)=-(d(:,i)'*g1(:,i))/(d(:,i)'*G*d(:,i)); %a(i)=-((X(:,i)'*G*d(:,i) +b'*d(:,i))/(d(:,i)'*G*d(:,i)));X(:,i+1)=X(:,i)+a(i)*d(:,i);g1=[g1 subs(subs(g,x1,X(1,i+1)),x2,X(2,i+1))];m1=m;m=norm(g1(:,i+1));i=i+1;endendfv=subs(subs(f,x1,X(1,i)),x2,X(2,i));endl1=X(1,i);l2=X(2,i);w1=X(1,1);w2=X(2,1);v1=min(l1,w1)-abs(l1-w1)/10:abs(l1-w1)/10:max(l1,w1)+abs(l1-w1)/10;v2=min(l2,w2)-abs(l2-w2)/10:abs(l2-w2)/10:max(l2,w2)+abs(l2-w2)/10; [x,y]=meshgrid(v1,v2);s=size(x);z=zeros(size(x));for i=1:s(1)for j=1:s(2)z(i,j)=1/2*[x(i,j),y(i,j)]*G*[x(i,j);y(i,j)]+b'*[x(i,j);y(i,j)]+c;endend[px,py] = gradient(z,.2,.2);contour(v1,v2,z), hold on, quiver(v1,v2,px,py)[C,h] = contour(x,y,z);set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)x1=X(1,:);y1=X(2,:);plot(x1,y1,'r*:');五、计算结果如图所示,输入>> G=[2,-1;-1,2];>> b=[2;-4];>> c=0;X=[1;1];e=1e-3;method='FR';表示正定矩阵为G,b为一次元系数矩阵,c为常数0,X是初始迭代点,e 为精度,method为共轭梯度的公式方法。
共轭梯度法详细解读

共轭梯度法详细解读
嘿,朋友们!今天咱就来好好唠唠共轭梯度法。
你想想啊,咱平常解决问题就像走迷宫似的,有时候会在里面转来转去找不到出路,而共轭梯度法呀,就像是在迷宫里给咱指了一条明路!比如说你想找一条最快从山这头到那头的路,共轭梯度法就能帮上大忙啦!
它可不是随随便便就出现的哦,那可是数学家们绞尽脑汁研究出来的宝贝呢!就好比一个超级英雄,专门来打救我们这些在复杂问题里苦苦挣扎的人。
在实际应用里,它可厉害着呢!比如说在工程计算中,要设计一个最完美的结构,共轭梯度法就能迅速算出最优解。
哇塞,这不就相当于有个超厉害的军师在帮咱出谋划策嘛!
你再想想,我们日常生活中很多事情都可以类比成用共轭梯度法来解决问题呀。
比如说你要规划一次旅行,怎么安排路线最合理,不就是在找那个最优的旅行路径嘛,这时候共轭梯度法的思路就能派上用场啦!它就像一个隐藏在幕后的高手,默默地为我们排忧解难。
而且哦,一旦你掌握了它,那种感觉就像是你突然掌握了一种绝世武功,能在各种难题面前游刃有余。
这可太酷了吧!
哎呀呀,共轭梯度法真的是太神奇、太有用啦!大家可一定要好好去了
解它、运用它呀,你绝对会被它的魅力折服的!相信我,没错的!。
共轭梯度法总结

共轭梯度法总结
共轭梯度法总结
一、什么是共轭梯度法
共轭梯度法(Conjugate Gradient Method),是一种用于求解线性方程组的迭代优化算法,它是一种搜索梯度的迭代算法。
共轭梯度法的基本思想是沿梯度的反方向搜索,并在每一步令搜索的方向接近更新的局部梯度。
它是一种非常有效的求解有约束的非线性优化问题的方法,是求解线性方程组的有效算法。
共轭梯度法可以看作是一种极小化函数的迭代方法,它最主要的思想是不断更新梯度的方向,从而寻找函数值最小的点。
二、共轭梯度法的原理
共轭梯度法是一种迭代优化算法,它以凸二次型函数为例,可以用来求解最小值问题。
它的基本思想是:
(1)首先求得函数的梯度,即每一步优化的搜索方向,使梯度变为最小;
(2)以梯度的反方向搜索,令搜索的方向接近更新的局部梯度,而不是与旧的梯度成正比的步长;
(3)逐步更新搜索的方向为新的梯度;
(4)重复这个过程,直到所有的自变量满足限制条件。
三、共轭梯度法的优缺点
共轭梯度法最大的优点是它具有收敛速度快,可以在有限的迭代步数内收敛到最优解;另外,它还具有计算量小,不需要计算精确的
Hessian矩阵的优点。
共轭梯度法的缺点是它不能用来求解非凸优化问题,因为它只能求解凸优化问题;另外,它也不能用于强不可约的优化问题。
共轭梯度方法

共轭梯度方法(Conjugate Gradient Method)是求解线性方程组的一种迭代算法。
该方法适用于求解大型稀疏的对称正定线性方程组,可以显著减少计算量和存储空间。
该方法的主要思想是利用共轭方向(Conjugate Directions)的性质,在有限次迭代中求解方程组的解。
共轭梯度方法的基本步骤如下:
选取一个初值$x_0$,并令$r_0=b-Ax_0$,其中$b$ 为方程组的右端向量,$A$ 为系数矩阵。
计算一个共轭方向$p_0=r_0$,即$p_0$ 与$r_0$ 正交,并满足$Ap_0 \neq 0$。
对于$k=0,1,2,\ldots$,执行以下操作:
a. 计算$\alpha_k=\frac{r_k^Tr_k}{p_k^TAp_k}$。
b. 更新解向量$x_{k+1}=x_k+\alpha_kp_k$。
c. 计算残差向量$r_{k+1}=r_k-\alpha_kAp_k$。
d. 计算$\beta_k=\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}$。
e. 更新共轭方向$p_{k+1}=r_{k+1}+\beta_kp_k$,即$p_{k+1}$ 与$p_k$ 具有共轭性。
如果残差向量$r_k$ 较小,则停止迭代,输出解向量$x_k$。
共轭梯度方法具有收敛速度快、存储空间小等优点,但对于非对称和非正定的线性方程组,该方法可能不收敛。
同时,该方法也有一些变体,如预处理共轭梯度法、共轭残差法等,可以更好地解决不同类型的线性方程组求解问题。
共轭梯度法

p(1) = −g(1)
( 3 )T
p(2) = −g(2) + β1 p(1)
( 3 )T ( 3 )T
p(3) = − g(3) + β2 p(2)
Qp
(1)
证明: 是否Q共轭 证明: p(3)与p(1)是否 共轭
p Qp(1) = − g Qp(1) + β 2 p Qp(1)
( 3 )T
=
1
第三章 非线性规划
第四节 无约束优化问题的解法 最速下降法 Newton法 法 拟Newton法 法 共轭梯度法
四.共轭梯度法
( NP ) min f ( X ) X ∈R
n
共轭方向及其性质 二次函数共轭梯度法的迭代原理 二次函数共轭梯度法的迭代步骤 一般函数的共轭梯度法 PRP算法的迭代步骤 算法的迭代步骤 共轭梯度法的注释
λ ≥0 ( k + 1)
g
( k )T
p( k )
+λ
=
+ λk
X
= X ( k ) + λk p( k )
1 min f ( X ) = X T QX + bT X + c 的最优 经n次一维搜索收敛于 X∈Rn 次一维搜索收敛于 2 ∗
解 X。 推论: 推论:
g =0 则 ( 3)T ( 2) g g =0 g
线性规划3-4
2.二次函数共轭梯度法的迭代原理 2.二次函数共轭梯度法的迭代原理
Qp(1) = ?
1 T f ( X ) = X QX + bT X + c g( X ) = ∇f ( X ) = QX + b 2
g ( k ) = QX ( k ) + b
求解无约束优化问题及非线性方程组的共轭梯度法

求解无约束优化问题及非线性方程组的共轭梯度法求解无约束优化问题及非线性方程组的共轭梯度法一、引言无约束优化问题和非线性方程组是数学和工程领域中常见的问题。
它们的解决对于优化模型的求解以及工程实际问题的解决具有重要意义。
本文将介绍一种常用的求解无约束优化问题和非线性方程组的方法——共轭梯度法,包括算法原理、步骤和性能分析等。
二、共轭梯度法的算法原理共轭梯度法是一种迭代法,它通过计算一系列共轭方向,逐步接近于最优解。
具体而言,共轭梯度法的算法原理如下:(1)初始化。
选择一个起始值x0,设置迭代精度ε,取初始共轭方向d0=g0=-∇f(x0),其中g0为梯度的初始值。
(2)迭代过程。
从k=1开始,根据共轭方向的性质,可以得到更新公式xk=xk-1+αkdk,其中αk为步长,dk为共轭方向。
通过下面的迭代公式可以计算共轭方向dk:di=(-gi)+βidi-1βi=(gi,gi)/(gi-1,gi-1)其中gi为第i次迭代的梯度。
(3)收敛判断。
如果满足||gk||<ε,则停止迭代计算,得到近似解。
否则,继续迭代。
三、共轭梯度法的步骤根据共轭梯度法的算法原理,可以得到具体的步骤如下:(1)初始化。
选择起始点x0,设置迭代精度ε,取初始共轭方向d0=g0=-∇f(x0),其中g0为梯度的初始值。
(2)循环迭代。
从k=1开始,计算步长αk,更新公式xk=xk-1+αkdk,计算新的梯度gk,计算共轭方向dk。
(3)收敛判断。
如果满足||gk||<ε,则停止迭代。
(4)输出结果。
输出近似解xk。
四、共轭梯度法的性能分析共轭梯度法在求解无约束优化问题和非线性方程组时具有一些优良的性能特点:(1)收敛性。
共轭梯度法在理想情况下可以在n步内达到最优解,其中n为问题的维度。
(2)存储要求小。
共轭梯度法只需要存储上一次迭代的结果,存储量较小。
(3)不需要二阶导数信息。
与牛顿法等方法相比,共轭梯度法不需要二阶导数信息,计算速度更快。
共轭梯度法

一.介绍共轭梯度法(Conjugate Gradient )是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse 矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
在各种优化算法中,共轭梯度法是非常重要的一种。
其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
共轭梯度法中最关键的两点是,搜索方向)(k d 和最佳步长k α。
其基本步骤是在点)(k X 处选取搜索方向)(k d , 使其与前一次的搜索方向)1(-k d 关于A 共轭,即(1)()(1),0k k k d d Ad --<>=然后从点)(k X 出发,沿方向)(k d 求得)(X f 的极小值点)1(+k X , 即)(min )()()(0)1(k dX f X f k k αλ+=>+如此下去, 得到序列{)(k X }。
不难求得0,)1()(>=<-k k Ad d 的解为)()()1(k k k k d X X α+=+其中,><><-=)()()()(,,k k k k kAd d Ad r α注意到)(k d 的选取不唯一,我们可取)1(1)()()(--+-∇=k k k k d X f d β由共轭的定义0,)1()(>=<-k k Ad d 可得:><><-=----)1()1()1()(1,,k k k k k Ad d Ad r β 共轭梯度法的计算公式如下:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧+=><><-=+=><><-=-=-==+------(k)(k)1)(k )()()()()1(1(k))()1()1()1()(1(k)(k)(0)(0)d X X,,r ,,X r Xr d k k k k k k k k k k k k k k Ad d Ad r d d Ad d Ad r A b A b ααββ 二.程序框图定义矩阵A 和向量bAx=b定义x 的初值将x 代入计算公式误差到达精度要求Yes输出xNo 迭代出新的x 结束开始三.源码n=100;%矩阵阶数,可以按照题目需要更改syms x1 r1 d1A=zeros(n,n);b=zeros(n,1);b(1,1)=-1;b(n,1)=-1;for i=1:nA(i,i)=-2;endfor i=1:n-1A(i,i+1)=1;A(i+1,i)=1;endx1=zeros(n,1);for i=1:n*1000r1=b-A*x1;d1=r1;a=(r1'*d1)/(d1'*A*d1);x1=x1+a*d1;r2=b-A*x1;if(norm(x1)<=eps)breakendbb=-(r2'*A*d1)/(d1'*A*d1);d1=r2+bb*d1;enddisp([x1])四.结果矩阵A100阶的结果200阶的结果400阶的结果。
共轭梯度法

共轭梯度法简介共轭梯度法是一种迭代的最优化算法,用于求解线性方程组或求解非线性优化问题。
它在解决大规模线性方程组时表现出色,尤其适用于对称正定矩阵的问题。
共轭梯度法结合了最速下降法和共轭方向法的优点,能够在有限次数的迭代中快速收敛到最优解。
背景在数值计算和优化问题中,线性方程组的求解是一个常见且重要的问题。
例如,在图像处理、数据分析和机器学习等领域,我们经常需要求解一个大规模的线性方程组。
然而,传统的直接方法,如高斯消元法或LU分解,对于大规模问题往往计算量巨大,耗时较长。
因此,我们需要寻找一种高效的迭代方法来解决这些问题。
共轭梯度法的核心思想是通过一系列共轭的搜索方向来逼近最优解。
具体来说,对于一个对称正定的线性方程组Ax=b,共轭梯度法的步骤如下:1.初始化解向量x0和残差x0=x−xx0。
2.计算初始搜索方向x0=x0。
3.进行共轭梯度迭代:重复以下步骤n次或直到收敛为止。
a.计算步长$\\alpha_k=\\frac{r_k^Tr_k}{d_k^TAd_k}$。
b.更新解向量$x_{k+1}=x_k+\\alpha_kd_k$。
c.更新残差$r_{k+1}=r_k-\\alpha_kAd_k$。
d.计算新的搜索方向$d_{k+1}=r_{k+1}+\\frac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}d_k$。
共轭梯度法与其他迭代方法相比有以下特点:1.高效性:共轭梯度法能够在有限次数的迭代中收敛到最优解,尤其适用于对称正定矩阵。
相比于直接方法,其计算量较小,具有更高的计算效率。
2.无需存储完整矩阵:共轭梯度法只需知道矩阵A的乘法运算结果,不需要存储完整的矩阵。
这对于大规模问题是一个很大的优势。
3.不需要计算矩阵的特征值:相比于其他迭代方法,共轭梯度法不需要计算矩阵的特征值,因此在实际问题中更加实用。
算法应用共轭梯度法广泛应用于各个领域的优化问题和线性方程组求解问题,包括:1.图像处理:共轭梯度法用于图像恢复、图像去噪和图像分割等问题。
非线性规划课程设计【共轭梯度法】

题目:共轭梯度法及其数值实现院系:数理学院应用数学系专业:数学与应用数学姓名学号:谁知道089084000指导教师:张是淘日期:2012 年 6 月18 日摘要共轭梯度法原是为求解目标函数为二次函数的问题而设计的一类算法,这类算法的特点是:方法中搜索方向是与二次函数系数矩阵有关的所谓共轭方向。
用这类方法求解n元二次正定函数的极小问题,最多进行n次一维搜索便可求的极小点。
而可微的非二次函数在极小点附近的性态近似于二次函数,因此这类方法也能用于求可微的非二次函数的无约束极小问题。
关键词:最优化;共轭梯度法;二次函数;极小问题;AbstractConjugate Gradient Method solve the objective function for the original quadratic function problems and design for a class of algorithm, This algorithm is characteristic: Methods the search direction is associated with the quadratic function coefficient matrix related to so-called conjugate direction. With this kind of method for solving N yuan two positive definite functions minimax problems. Up to N times of one-dimensional search can find minimizers. And differentiable non two function in minimum near the behavior is similar to the two function, This method can also be used for differentiable non two function of unconstrained minimization problem.Keywords:Optimization; Conjugate Gradient Method; Quadratic function; minimum problem非线性规划课程设计目录第一章引言 (2)1.1无约束优化问题概述 (2)1.2 共轭方向……………………………………………………………………1.2 共轭方向法…………………………………………………………………第二章共轭梯度法………………………………………………………………2.1 基本原理……………………………………………………………………2.2 算法步骤……………………………………………………………………2.3 程序流程图…………………………………………………………………第三章算例………………………………………………………………………总结…………………………………………………………………………………参考文献……………………………………………………………………………附录…………………………………………………………………………………。
共轭梯度法原理

共轭梯度法原理共轭梯度法是一种用于解决大规模线性方程组或非线性优化问题的迭代算法。
它的原理基于寻找一个向量的共轭方向,以便在每一步迭代中最大限度地减少误差。
在本文中,我们将详细介绍共轭梯度法的原理及其应用。
首先,让我们来了解一下共轭梯度法的基本原理。
在解决线性方程组Ax=b时,共轭梯度法的核心思想是通过寻找一组共轭的搜索方向来逐步逼近最优解。
这些共轭方向是相互正交的,这意味着它们不会在同一个方向上重复搜索,从而有效地加速了收敛速度。
在每一步迭代中,共轭梯度法都会沿着一个共轭方向进行搜索,以找到一个最优的步长,使得误差函数能够得到最大程度的减少。
通过不断地迭代,我们可以逐渐逼近最优解。
这种方法在解决大规模线性方程组时非常高效,尤其是在稀疏矩阵和对称正定矩阵的情况下效果更佳。
除了解决线性方程组外,共轭梯度法还被广泛应用于非线性优化问题。
在这种情况下,我们需要通过最小化一个目标函数来寻找最优解。
共轭梯度法同样可以通过寻找共轭方向来逐步逼近最优解,从而在非线性优化问题中取得良好的效果。
总的来说,共轭梯度法是一种非常高效的优化算法,它通过寻找共轭方向来逐步逼近最优解,特别适用于解决大规模线性方程组和非线性优化问题。
它的原理简单而又高效,因此在实际应用中得到了广泛的应用。
在实际应用中,共轭梯度法还有许多改进的版本,例如预处理共轭梯度法、共轭梯度法的共轭梯度法等,这些改进版本都在一定程度上提高了算法的收敛速度和稳定性,使其更加适用于不同类型的问题。
综上所述,共轭梯度法是一种非常重要的优化算法,它通过寻找共轭方向来逐步逼近最优解,特别适用于解决大规模线性方程组和非线性优化问题。
在实际应用中,它的高效性和稳定性使其成为了解决实际问题的重要工具。
希望本文对共轭梯度法的原理有所帮助,谢谢阅读!。
共轭梯度法结论

共轭梯度法结论
共轭梯度法是一种常用的非线性优化算法,特别适合求解带正定对称矩阵的线性方程组。
该方法的基本思路是通过构建共轭方向序列,在每个方向上进行一维搜索,从而最小化一个二次型的目标函数。
共轭梯度法具有高精度、高效率、不需要存储大规模矩阵等优点,在科学计算、数学建模、图像处理等领域得到广泛应用。
共轭梯度法的基本结论可以概括为以下几点:
1. 共轭梯度法解决的是线性方程组求解问题。
其中,矩阵必须是正定对称的,否则求解过程可能不收敛,甚至得到错误解。
2. 共轭方向序列是该方法的核心。
共轭方向序列包括预处理共轭梯度法、FR共轭梯度法、PR共轭梯度法、PRP共轭梯度法等多种变体。
这些方法在不同条件下表现不同,选择合适的共轭方向序列能够提高算法收敛速度和精度。
3. 共轭梯度法并不需要储存大规模矩阵,而是利用矩阵向量乘法进行计算。
这一特点使得算法可以用于解决大规模矩阵问题,节省了存储和计算资源。
4. 共轭梯度法求解线性方程组问题的计算量和存储量都比其他经典方法如高斯消元、LU分解等小得多。
同时,算法的迭代次数与矩阵的条件数近似成反比例关系,可以提高求解精度。
5. 共轭梯度法也有一些局限性。
例如,在非正定矩阵情况下可能会出现振荡,需要使用修正的共轭梯度法,如拟共轭梯度法或CGS等。
总之,共轭梯度法是一种重要的数值优化算法,可以用于求解线性方程组等一系列问题。
要充分发挥其优点,需要根据实际问题选择合适的共轭方向序列,并注意算法的局限性。
共轭梯度算法的设计与实现毕业设计

共轭梯度算法的设计与实现毕业设计
首先,共轭梯度算法的设计需要明确以下几个步骤:初始化、迭代计算、收敛判断。
在初始化阶段,需要设置初始解向量和初始残差向量,并
计算初始共轭方向向量。
在迭代计算阶段,根据共轭方向向量和残差向量,通过求解步长和更新解向量来不断逼近准确解。
在收敛判断阶段,通过计
算残差的范数或迭代次数等指标来判断算法是否结束。
其次,共轭梯度算法的实现需要考虑以下几个方面:矩阵和向量的存储、步长的求解、解向量的更新、收敛判断的条件。
在存储方面,矩阵和
向量可以使用数组来表示,并利用索引进行读写操作。
在步长的求解方面,可以采用线或二次等方法来求解最优步长,以提高算法的收敛速度。
在解
向量的更新方面,可以使用矩阵向量乘法和向量加法等运算来更新解向量。
在收敛判断方面,可以设置收敛阈值或最大迭代次数等条件来判断算法是
否结束。
最后,为了进一步提高共轭梯度算法的性能,可以考虑以下几个改进
方法:预处理、并行计算、加速技术。
预处理可以通过矩阵分解等方法来
提前对矩阵进行优化,从而加快求解速度。
并行计算可以利用多核或集群
计算资源,将大规模计算任务分解为多个并行的小任务进行计算,以提高
计算效率。
加速技术可以利用加速硬件如GPU或FPGA等进行计算,以加
快算法的执行速度。
综上所述,共轭梯度算法的设计与实现是一个涉及多个方面的综合性
任务,需要考虑问题的数学模型、算法的理论基础以及计算机实现的技术
细节。
通过合理的设计和实现,可以提高共轭梯度算法的计算效率和性能,从而更好地应用于实际问题的求解中。
非线性规划课程设计【共轭梯度法】

题目:共轭梯度法及其数值实现院系:数理学院应用数学系专业:数学与应用数学姓名学号:谁知道089084000指导教师:张是淘日期:2012 年 6 月18 日共轭梯度法原是为求解目标函数为二次函数的问题而设计的一类算法,这类算法的特点是:方法中搜索方向是与二次函数系数矩阵有关的所谓共轭方向。
用这类方法求解n元二次正定函数的极小问题,最多进行n次一维搜索便可求的极小点。
而可微的非二次函数在极小点附近的性态近似于二次函数,因此这类方法也能用于求可微的非二次函数的无约束极小问题。
关键词:最优化;共轭梯度法;二次函数;极小问题;AbstractConjugate Gradient Method solve the objective function for the original quadratic function problems and design for a class of algorithm, This algorithm is characteristic: Methods the search direction is associated with the quadratic function coefficient matrix related to so-called conjugate direction. With this kind of method for solving N yuan two positive definite functions minimax problems. Up to N times of one-dimensional search can find minimizers. And differentiable non two function in minimum near the behavior is similar to the two function, This method can also be used for differentiable non two function of unconstrained minimization problem.Keywords:Optimization; Conjugate Gradient Method; Quadratic function; minimum problem第一章引言 (2)1.1无约束优化问题概述 (2)1.2 共轭方向……………………………………………………………………1.2 共轭方向法…………………………………………………………………第二章共轭梯度法………………………………………………………………2.1 基本原理……………………………………………………………………2.2 算法步骤……………………………………………………………………2.3 程序流程图…………………………………………………………………第三章算例………………………………………………………………………总结…………………………………………………………………………………参考文献……………………………………………………………………………附录…………………………………………………………………………………第一章引言1.1 无约束优化问题概述一个非线性规划问题的自变量x没有任何约束,或说可行域即是整个n维向量空间:,则称这样的非线性规划问题为无约束问题:或 (3.1.7)1.2共轭方向设一组非零向量,A为n阶对称正定阵,若下式成立:.称向量组关于A共轭。
共轭梯度法课程设计

最优化方法课程设计报告题目:共轭梯度软件设计院(系):专业:学生姓名:指导教师:题目类型:实验研究工程设计软件开发2010 年1月15 日摘要共轭梯度法最早是由Hestenes 和Stiefle (1952)提出来的,用于解正定系数矩阵的线性方程组,在这个基础上,Fletcher 和Reeves (1964)首先提出了解非线性最优化问题的共轭梯度法。
共轭梯度法是解决无约束非线性最优化问题的重要的方法之一(Conjugate gradient method to solve unconstrained nonlinear optimization problem, one of the important ways.),因为共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse 矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法一。
共轭梯度对于无约束优化问题Mlnf(x),x ∈R n 给出一初始值x1,算法选代产生x2,x3,x4,x 5,….希望某一k X是目标函数解或点收敛于解,在我们这次的运筹学课程设计当中我们正是用这种方法要求解最小问题的最优解的。
关键字:共轭梯度法;无约束优化AbstractConjugate gradient method was first used by Hestenes and Stiefle (1952) put forward for the solution of positive definite coefficient matrix of linear equations, on this basis, Fletcher and Reeves (1964) first put forward about the problem of nonlinear optimization conjugate gradient method.The conjugate gradient method to solve unconstrained nonlinear optimization problems, one of the important ways, as the conjugate gradient method is between steepest descent method and Newton's method between a method, it requires the use of a first-order derivative information, But the steepest descent method to overcome the shortcomings of slow convergence, but also avoid the need to store and calculate Newton's method and the inverse Hesse matrix of the shortcomings of the conjugate gradient method is not only a large-scale linear equations to solve one of the ways the most useful, but also large-scale solution nonlinear optimization algorithm is the most effective one.Conjugate gradient for the unconstrained optimization problem Mlnf (x), x ∈ given an initial value of x1, the election algorithm is generated on behalf of the x2, x3, x4, x 5, .... Hope that is the objective function of a solution or point of convergence in the solution, in our curriculum design, operations research this is exactly what we were using this method requires the smallest solution of the problem the optimal solution.Keywords: conjugate gradient method;unconstrained nonlinear optimization目录一、共轭梯度法的概念....................................................... 错误!未定义书签。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目:共轭梯度法及其数值实现
院系:数理学院应用数学系
专业:数学与应用数学
姓名学号:谁知道089084000
指导教师:张是淘
日期:2012 年 6 月18 日
共轭梯度法原是为求解目标函数为二次函数的问题而设计的一类算法,这类算法的特点是:方法中搜索方向是与二次函数系数矩阵有关的所谓共轭方向。
用这类方法求解n元二次正定函数的极小问题,最多进行n次一维搜索便可求的极小点。
而可微的非二次函数在极小点附近的性态近似于二次函数,因此这类方法也能用于求可微的非二次函数的无约束极小问题。
关键词:最优化;共轭梯度法;二次函数;极小问题;
Abstract
Conjugate Gradient Method solve the objective function for the original quadratic function problems and design for a class of algorithm, This algorithm is characteristic: Methods the search direction is associated with the quadratic function coefficient matrix related to so-called conjugate direction. With this kind of method for solving N yuan two positive definite functions minimax problems. Up to N times of one-dimensional search can find minimizers. And differentiable non two function in minimum near the behavior is similar to the two function, This method can also be used for differentiable non two function of unconstrained minimization problem.
Keywords:Optimization; Conjugate Gradient Method; Quadratic function; minimum problem
第一章引言 (2)
1.1无约束优化问题概述 (2)
1.2 共轭方向……………………………………………………………………
1.2 共轭方向法…………………………………………………………………第二章共轭梯度法………………………………………………………………
2.1 基本原理……………………………………………………………………
2.2 算法步骤……………………………………………………………………
2.3 程序流程图…………………………………………………………………第三章算例………………………………………………………………………总结…………………………………………………………………………………参考文献……………………………………………………………………………附录…………………………………………………………………………………
第一章引言
1.1 无约束优化问题概述
一个非线性规划问题的自变量x没有任何约束,或说可行域即是整个n维向量空间:,则称这样的非线性规划问题为无约束问题:
或 (3.1.7)
1.2共轭方向
设一组非零向量,A为n阶对称正定阵,若下式成立:
.称向量组关于A共
轭。
也称它们为一组A共轭方向(或称为A的n个共轭方向)。
设有二维二次函数:
(4.4.1) 其中A是二阶对称正定阵,是一个定点。
函数的等直线:
是以为中心的椭圆。
有(4.4.1)式可求得
,
及. (4.4.2)
由(4.4.2)式及A正定,可知是f(x)的极小点。
设是某等值线上一点,该等值线在点处的法向量
, (4.4.3)
若记
. (4.4.4)
又设是该等值线在点处的一个切向量,则有切向量
与法向量
正
交,即
(4.4.5)
考虑到(4.4.3)式及(4.4.4)式,(4.4.5
)式就可转化为
(4.4.6)
说明等值线上一点处的切向量与由该点指向极小点的向量关于A 共轭。
1.3 共轭方向法
考虑问题:
A 为正定矩阵,f(x)是凸函数.根据 1.2的共轭方向,相
继以
为搜索方向。
根据算法
()()()()
(1)()()
min ()()
k k k k k k k k k f x p f x p x x p λλλ+⎧''+=+⎪⎨=+⎪⎩
可以相继得到迭代点:(1)(2)()
,,,n x x x ,当
,则
就是平稳点。
第二章 共轭梯度法
2.1
基本原理
其中A 为n 阶对称正定阵,,,是常数.n n x b C ∉∉
由上f(x)是正定二次函数 ()f x Ax b ∇=+,
故有(1)()()()()k k k k f x f x Ap λ+∇=∇+ k=0,1,2,…,n-1.
又设以
迭代点沿搜索方向
进行一维搜索时采用最佳一维搜索求步长因子
k λ,即
(1)()()
()()()()
0,()min (),k k k k k k k k k x x p f x p f x p λλλλ+≥⎧=+⎪
⎨+=+⎪⎩
进行多次迭代,检验若 ()()0k f x ∇=,则()k x 就是最优解。
否则就继续进行迭代。
2.2算法步骤
由共轭梯度法公式:
(1)()()
()()
()()
(0)(0)(1)(1)()(1)()()()()()()()()()k k k k k T k k k T k k k k k k T k k k T k x x p f x p p Ap p f x p f x p f x p
p Ap λλββ++++⎧=+⎪∇⎪
=-⎪⎪⎪
=-∇⎨⎪=-∇+⎪
⎪∇⎪=-⎪⎩ 以
方向进行迭代,当
k βε≤ 结束迭代,最优解为()k x 。
2.3 程序流程图
第三章 算例
举例 试用共轭梯度法下述二次函数的极小点;
22
121212131(,)222
f x x x x x x x =
+-- 取4(0)
210,.4x ε-⎡⎤-==⎢⎥⎣⎦
Matlab 程序:
xk=input('input x0:')
ptol=1.0e-5; k=2;
while k==2 k=0; btk=0; dk=0; for k=0:2
gk=[3*xk(1,1)-xk(2,1)-2;xk(2,1)-xk(1,1)];
dk=-gk+btk*dk;
f1=gk;
G=[3,-1;-1,1];
a=-(dk'*f1)/(dk'*G*dk);
xk=xk+a*dk;
gk1=[3*xk(1,1)-xk(2,1)-2;xk(2,1)-xk(1,1)];
if norm(gk1)<ptol
break
end
btk=(norm(gk1)/norm(gk))^2;
end
if norm(gk1)<ptol
break
end
end
f=1.5*xk(1,1)^2+0.5*xk(2,1)^2-xk(1,1)*xk(2,1)-2*xk(1,1);
fprintf('\n 运用共轭梯度法迭代%d后得到极小点xk及极小值f为:\n',k);
disp(xk);
disp(f);
input x0:[1;2]
xk =
1
2
运用共轭梯度法迭代1次后得到极小点xk及极小值f为:
1.0000
1.0000
-1
总结
共轭梯度法是一种很有效求解无约束优化的方法,共轭梯度法是根据共轭方向去搜索,可以由较快的收敛速度找到最优解求得极小点。
参考文献
[1] 何坚勇. 最优化方法[M]. 北京: 清华大学出版社, 2007.
附录
共轭梯度法程序的matlab源代码:
xk=input('input x0:')
ptol=1.0e-5;
k=2;
while k==2
k=0;
btk=0;
dk=0;
for k=0:2
gk=[3*xk(1,1)-xk(2,1)-2;xk(2,1)-xk(1,1)];
dk=-gk+btk*dk;
f1=gk;
G=[3,-1;-1,1];
a=-(dk'*f1)/(dk'*G*dk);
xk=xk+a*dk;
gk1=[3*xk(1,1)-xk(2,1)-2;xk(2,1)-xk(1,1)];
if norm(gk1)<ptol
break
end
btk=(norm(gk1)/norm(gk))^2;
end
if norm(gk1)<ptol
break
end
end
f=1.5*xk(1,1)^2+0.5*xk(2,1)^2-xk(1,1)*xk(2,1)-2*xk(1,1);
fprintf('\n 运用共轭梯度法迭代%d后得到极小点xk及极小值f为:\n',k); disp(xk);
disp(f);。
