山东省临沂市2017年中考数学真题试题[精品]
2017年中考真题精品解析 数学(山东临沂卷)(含答案)

2017年中考真题精品解析 数学(山东临沂卷)第Ⅰ卷(共42分)一、选择题:本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.12007-的相反数是( ) A .12007 B .12007- C .2017 D .2017-2.如图,将直尺与含30︒角的三角尺摆放在一起,若120∠=︒,则2∠的度数是( )A .50︒B .60︒C .70︒D .80︒ 3.下列计算正确的是( )A .()a b a b --=--B .224a a a +=C .224a a a ⋅= D .()2224aba b =4.不等式组21,512x x ->⎧⎪⎨+≥⎪⎩①②中,不等式①和②的解集在数轴上表示正确的是( )A .B .C .D .5.如图所示的几何体是由五个小正方体组成的,它的左视图是( )A .B .C .D .6.小明和小华玩“石头、剪子、布”的游戏.若随机出手一次,则小华获胜的概率是( ) A .23 B .12 C .13 D .297.一个多边形的内角和是外角和的2倍,这个多边形是( ) A .四边形 B .五边形 C .六边形 D .八边形8.甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x 个,那么所列方程是( ) A .90606x x =+ B .90606x x =+ C .90606x x =- D .90606x x =- 9.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数 每人所创年利润(单位:万元)A 1 10B 3 8 C7 5 D43这15名员工每人所创年利润的众数、中位数分别是( ) A .10,5 B .7,8 C .5,6.5 D .5,510.如图,AB 是O e 的直径,BT 是O e 的切线,若45ATB ∠=︒,2AB =,则阴影部分的面积是( )A .2B .3124π-C .1D .1124π+11.将一些相同的“d ”按如图所示摆放,观察每个图形中的“d ”的个数,若第n 个图形中“d ”的个数是78,则n 的值是( )A .11B .12C .13D .1412.在ABC V 中,点D 是边BC 上的点(与B 、C 两点不重合),过点D 作DE AC ∥,DF AB ∥,分别交AB ,AC 于E 、F 两点,下列说法正确的是( )A .若AD BC ⊥,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形 C .若BD CD =,则四边形AEDF 是菱形 D .若AD 平分BAC ∠,则四边形AEDF 是菱形13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h (单位:m )与足球被踢出后经过的时间t (单位:s )之间的关系如下表:t 0 1 2 3 4 5 6 7 … h8141820201814…下列结论:①足球距离地面的最大高度为20m ;②足球飞行路线的对称轴是直线92t =;③足球被踢出9s 时落地;④足球被踢出1.5s 时,距离地面的高度是11m . 其中正确结论的个数是( )A .1B .2C .3D .414.如图,在平面直角坐标系中,发比例函数ky x=(0x >)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,OMN V 的面积为10.若动点P 在x 轴上,则PM PN +的最小值是( )A .62B .10C .226D .229第Ⅱ卷(共78分)二、填空题(每题3分,满分15分,将答案填在答题纸上)15.分解因式:29m m -= . 16.已知AB CD ∥,AD 与BC 相交于点O .若23BO OC =,10AD =,则AO = .17.计算:22x y xy y x x x ⎛⎫--+-= ⎪⎝⎭.18.在A B C D Y 中,对角线AC ,BD 相交于点O .若4AB =,10BD =,3sin 5BDC ∠=,则A B C D Y 的面积是 .19.在平面直角坐标系中,如果点P 坐标为(),m n ,向量OP uu u r 可以用点P 的坐标表示为(),OP m n =uu u r. 已知:()11,OA x y =uu r ,()22,OB x y =uu u r,如果12120x x y y ⋅+⋅=,那么OA uu r 与OB uu u r 互相垂直.下列四组向量:①()2,1OC =uu u r ,()1,2OD =-uuu r;②()cos30,tan 45OE =︒︒uu u r,()1,sin 60OF =︒uu u r ;③()32,2OG =--uuu r ,132,2OH ⎛⎫=+ ⎪⎝⎭uuu r ;④()0,2OM π=uuu r ,()2,1ON =-uuu r .其中互相垂直的是 (填上所有正确答案的序号).三、解答题 (本大题共7小题,共63分.解答应写出文字说明、证明过程或演算步骤.)20.计算:11122cos 4582-⎛⎫-+︒-+ ⎪⎝⎭.21.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:根据以上提供的信息,解答下列问题: (1)x =______,a =______,b =______; (2)补全上面的条形统计图;(3)若该校共有学生1000名.根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.如图,两座建筑物的水平距离30m BC =,从A 点测得D 点的俯角α为30︒,测得C 点的俯角β为60︒,求这两座建筑物的高度.23.如图,BAC ∠的平分线交ABC V 的外接圆于点D ,ABC ∠的平分线交AD 于点E . (1)求证:DE DB =;(2)若90BAC ∠=︒,4BD =,求ABC V 外接圆的半径.24.某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y (元)与每月用水量x (3m )之间的关系如图所示. (1)求y 关于x 的函数解析式;(2)若某用户二、三月份共用水340m (二月份用水量不超过325m ),缴纳水费79.8元,则该用户二、三月份的用水量各是多少3m ?25.数学课上,张老师出示了问题:如图1,AC 、BD 是四边形ABCD 的对角线,若ACB ACD ∠=∠=60ABD ADB ∠=∠=︒,则线段BC ,CD ,AC 三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB 到E ,使BE CD =,连接AE ,证得ABE ADC ≌V V ,从而容易证明ACE V 是等边三角形,故AC CE =,所以AC BC CD =+.小亮展示了另一种正确的思路:如图3,将ABC V 绕着点A 逆时针旋转60︒,使AB 与AD 重合,从而容易证明ACF V 是等比三角形,故AC CF =,所以AC BC CD =+. 在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“ACB ACD ∠=∠=60ABD ADB ∠=∠=︒”改为“ACB ACD ∠=∠=45ABD ADB ∠=∠=︒”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“ACB ACD ∠=∠=60ABD ADB ∠=∠=︒”改为“ACB ACD ∠=∠=ABD ADB α∠=∠=”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.如图,抛物线23y ax bx =+-经过点()2,3A -,与x 轴负半轴交于点B ,与y 轴交于点C ,且3OC OB =.(1)求抛物线的解析式;(2)点D 在y 轴上,且BDO BAC ∠=∠,求点D 的坐标;(3)点M 在抛物线上,点N 在抛物线的对称轴上,是否存在以点A ,B ,M ,N 为顶点的四边形是平行四边形?若存在。
2017年山东省临沂市中考数学试卷(答案与解析)
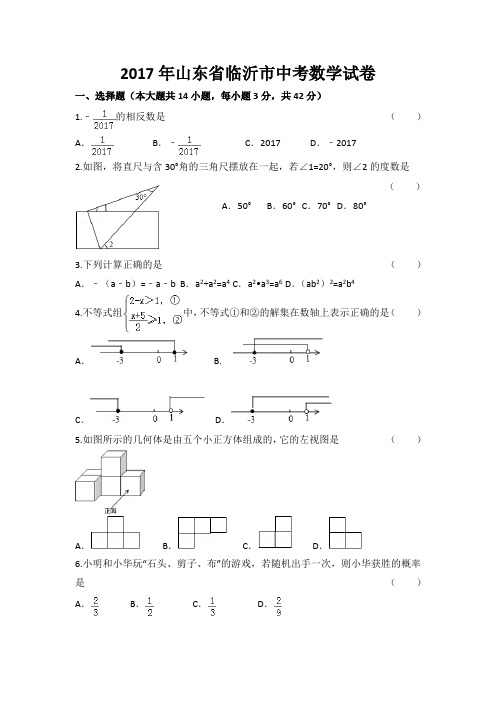
2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,每小题3分,共42分)1.﹣的相反数是()A.B.﹣C.2017 D.﹣20172.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°3.下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4 C.a2•a3=a6 D.(ab2)2=a2b44.不等式组中,不等式①和②的解集在数轴上表示正确的是()A. B.C.D.5.如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C.D.6.小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.7.一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形8.甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.=B.=C.=D.=9.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A110B38C75D43这15名员工每人所创年利润的众数、中位数分别是()A.10,5 B.7,8 C.5,6.5 D.5,510.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A.2 B.﹣πC.1 D.+π11.将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是()A.11 B.12 C.13 D.1412.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.414.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6 B.10 C.2D.2二、填空题(本大题共5小题,每小题3分,共15分)15.分解因式:m3﹣9m=.16.已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=.17.计算:÷(x﹣)=.18.在中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=,则ABCD的面积是.19.在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组向量:①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是(填上所有正确答案的符号).三、解答题(本大题共7小题,共63分)20.(7分)计算:|1﹣|+2cos45°﹣+()﹣121.(7分)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑510%朗读者15b%中国诗词大会a40%出彩中国人1020%根据以上提供的信息,解答下列问题:(1)x=,a=,b=;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.(7分)如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.23.(9分)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.24.(9分)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?25.(11分)数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.(13分)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.参考答案一、选择题1.A.2.A.3.D.4.B.5.D.6.C.7.C.8.B.9.D.10.C.解:∵BT是⊙O的切线;设AT交⊙O于D,连结BD,∵AB是⊙O的直径,∴∠ADB=90°,而∠ATB=45°,∴△ADB、△BDT都是等腰直角三角形,∴AD=BD=TD=AB=,∴弓形AD的面积等于弓形BD的面积,=××=1.∴阴影部分的面积=S△BTD11.B.解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n个图形有1+2+3+…+n=个小圆;∵第n个图形中“○”的个数是78,∴78=,解得:n1=12,n2=﹣13(不合题意舍去),12.D.解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;13.B.解:由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,∴足球距离地面的最大高度为20.25m,故①错误,∴抛物线的对称轴t=4.5,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=1.5时,y=11.25,故④错误.∴正确的有②③,14.C.解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M(6,),N(,6),∴BN=6﹣,BM=6﹣,∵△OMN的面积为10,∴6×6﹣×6×﹣6×﹣×(6﹣)2=10,∴k=24,∴M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′===2,二、填空题(本大题共5小题,每小题3分,共15分)15.m(m+3)(m﹣3).16.4.17..18.24.解:作OE⊥CD于E,如图所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD=BD=5,CD=AB=4,∵sin∠BDC==,∴OE=3,∴DE==4,∵CD=4,∴点E与点C重合,∴AC⊥CD,OC=3,∴AC=2OC=6,∴▱ABCD的面积=CD•AC=4×6=24;19.①③④.解:①因为2×(﹣1)+1×2=0,所以与互相垂直;②因为cos30°×1+tan45°•sin60°=×1+1×=≠0,所以与不互相垂直;③因为(﹣)(+)+(﹣2)×=3﹣2﹣1=0,所以与互相垂直;④因为π0×2+2×(﹣1)=2﹣2=0,所以与互相垂直.综上所述,①③④互相垂直.三、解答题(本大题共7小题,共63分)20.解:|1﹣|+2cos45°﹣+()﹣1=﹣1+2×﹣2+2=﹣1+﹣2+2=1.21.解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;故答案为:50;20;30;(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:(3)根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名.22.解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30m,则CD=EC﹣ED=AB﹣ED=30﹣10=20m.23.(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.24.解:(1)当0≤x≤15时,设y与x的函数关系式为y=kx,15k=27,得k=1.8,即当0≤x≤15时,y与x的函数关系式为y=1.8x,当x>15时,设y与x的函数关系式为y=ax+b,,得,即当x>15时,y与x的函数关系式为y=2.4x﹣9,由上可得,y与x的函数关系式为y=;(2)设二月份的用水量是xm3,当15<x≤25时,2.4x﹣9+2.4(40﹣x)﹣9=79.8,解得,x无解,当0<x≤15时,1.8x+2.4(40﹣x)﹣9=79.8,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m3、28m3.25.解:(1)BC+CD=AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=45°,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=45°,AC=AE,∴△ACE是等腰直角三角形,∴CE=AC,∵CE=CE+DE=CD+BC,∴BC+CD=AC;(2)BC+C D=2AC•cosα.理由:如图2,延长CD至E,使DE=BC,∵∠ABD=∠ADB=α,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB+∠ACD=2α,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=α,AC=AE,∴∠AEC=α,过点A作AF⊥CE于F,∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,∴CE=2CF=2AC•cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC•cosα.26.解:(1)由y=ax2+bx﹣3得C(0.﹣3),∴OC=3,∵OC=3OB,∴OB=1,∴B(﹣1,0),把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得,∴,∴抛物线的解析式为y=x2﹣2x﹣3;(2)设连接AC,作BF⊥AC交AC的延长线于F,∵A(2,﹣3),C(0,﹣3),∴AF∥x轴,∴F(﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D(0,m),则OD=|m|,∵∠BDO=∠BAC,∴∠BDO=45°,∴OD=OB=1,∴|m|=1,∴m=±1,∴D1(0,1),D2(0,﹣1);(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF ⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).。
2017年山东省临沂市中考数学试卷

2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,每小题3分,共42分) 1.(3分)﹣12017的相反数是( )A .12017B .﹣12017C .2017D .﹣20172.(3分)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )A .50°B .60°C .70°D .80° 3.(3分)下列计算正确的是( )A .﹣(a ﹣b )=﹣a ﹣bB .a 2+a 2=a 4C .a 2•a 3=a 6D .(ab 2)2=a 2b 44.(3分)不等式组{2−x >1,①x+52≥1,②中,不等式①和②的解集在数轴上表示正确的是( )A .B .C .D .5.(3分)如图所示的几何体是由五个小正方体组成的,它的左视图是( )A .B .C .D .6.(3分)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )A .23B .12C .13D .297.(3分)一个多边形的内角和是外角和的2倍,则这个多边形是( ) A .四边形 B .五边形 C .六边形 D .八边形8.(3分)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x 个,那么所列方程是( )A .90x =60x+6B .90x+6=60xC .90x−6=60xD .90x =60x−69.(3分)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示: 部门人数每人创年利润(万元)A 1 10B 3 8C 7 5 D43这15名员工每人所创年利润的众数、中位数分别是( ) A .10,5 B .7,8C .5,6.5D .5,510.(3分)如图,AB 是⊙O 的直径,BT 是⊙O 的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )A .2B .32﹣14π C .1D .12+14π11.(3分)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n 个图形中“○”的个数是78,则n 的值是( )A.11 B.12 C.13 D.1412.(3分)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D 作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形13.(3分)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=92;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.414.(3分)如图,在平面直角坐标系中,反比例函数y=kx(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A .6√2B .10C .2√26D .2√29二、填空题(本大题共5小题,每小题3分,共15分) 15.(3分)分解因式:m 3﹣9m= .16.(3分)已知AB ∥CD ,AD 与BC 相交于点O .若BO OC =23,AD=10,则AO= .17.(3分)计算:x−y x ÷(x ﹣2xy−y 2x)= .18.(3分)在▱ABCD 中,对角线AC ,BD 相交于点O ,若AB=4,BD=10,sin ∠BDC=35,则▱ABCD 的面积是 .19.(3分)在平面直角坐标系中,如果点P 坐标为(m ,n ),向量OP →可以用点P 的坐标表示为OP →=(m ,n ).已知:OA →=(x 1,y 1),OB →=(x 2,y 2),如果x 1•x 2+y 1•y 2=0,那么OA →与OB →互相垂直,下列四组向量:①OC →=(2,1),OD →=(﹣1,2);②OE →=(cos30°,tan45°),OF →=(1,sin60°);③OG →=(√3﹣√2,﹣2),OH →=(√3+√2,12);④OM →=(π0,2),ON →=(2,﹣1).其中互相垂直的是 (填上所有正确答案的符号).三、解答题(本大题共7小题,共63分)20.(7分)计算:|1﹣√2|+2cos45°﹣√8+(12)﹣1.21.(7分)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑 5 10% 朗读者 15 b% 中国诗词大会 a 40% 出彩中国人1020% 根据以上提供的信息,解答下列问题: (1)x= ,a= ,b= ; (2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.(7分)如图,两座建筑物的水平距离BC=30m ,从A 点测得D 点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.23.(9分)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.24.(9分)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?25.(11分)数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.(13分)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.2017年山东省临沂市中考数学试卷参考答案与试题解析一、选择题(本大题共14小题,每小题3分,共42分)1.(3分)(2017•临沂)﹣12017的相反数是()A.12017B.﹣12017C.2017 D.﹣2017【分析】直接利用相反数的定义分析得出答案.【解答】解:﹣12017的相反数是:12017.故选:A.【点评】此题主要考查了相反数的定义,正确把握相反数的定义是解题关键.2.(3分)(2017•临沂)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,∴∠BEF=∠1+∠F=50°,∵AB∥CD,∴∠2=∠BEF=50°,故选A.【点评】本题主要考查了平行线的性质,解题的关键是掌握三角形外角的性质,此题难度不大.3.(3分)(2017•临沂)下列计算正确的是( )A .﹣(a ﹣b )=﹣a ﹣bB .a 2+a 2=a 4C .a 2•a 3=a 6D .(ab 2)2=a 2b 4【分析】根据去括号、同底数幂的乘法底数不变指数相加,积的乘方,可得答案. 【解答】解:A 、括号前是负号,去括号全变号,故A 不符合题意; B 、不是同底数幂的乘法指数不能相加,故B 不符合题意; C 、同底数幂的乘法底数不变指数相加,故C 不符合题意; D 、积的乘方等于乘方的积,故D 符合题意; 故选:D .【点评】本题考查了积的乘方,熟记法则并根据法则计算是解题关键.4.(3分)(2017•临沂)不等式组{2−x >1,①x+52≥1,②中,不等式①和②的解集在数轴上表示正确的是( )A .B .C .D .【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集. 【解答】解:解不等式①,得:x <1, 解不等式②,得:x ≥﹣3, 则不等式组的解集为﹣3≤x <1,故选:B .【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键5.(3分)(2017•临沂)如图所示的几何体是由五个小正方体组成的,它的左视图是( )A .B .C .D .【分析】根据三视图定义分别作出三视图即可判断. 【解答】解:该几何体的三视图如下:主视图:;俯视图:;左视图:,故选:D .【点评】本题主要考查三视图,掌握三视图的定义和作法是解题的关键.6.(3分)(2017•临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )A .23B .12C .13D .29【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案. 【解答】解:画树状图得:∵共有9种等可能的结果,小华获胜的情况数是3种,∴小华获胜的概率是:39=13.故选C .【点评】此题主要考查了列表法和树状图法求概率知识,用到的知识点为:概率=所求情况数与总情况数之比.7.(3分)(2017•临沂)一个多边形的内角和是外角和的2倍,则这个多边形是( )A .四边形B .五边形C .六边形D .八边形【分析】此题可以利用多边形的外角和和内角和定理求解. 【解答】解:设所求正n 边形边数为n ,由题意得 (n ﹣2)•180°=360°×2 解得n=6.则这个多边形是六边形. 故选:C .【点评】本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征:任何多边形的外角和都等于360°,多边形的内角和为(n ﹣2)•180°.8.(3分)(2017•临沂)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x 个,那么所列方程是( )A .90x =60x+6B .90x+6=60xC .90x−6=60xD .90x =60x−6【分析】根据甲乙的工作时间,可列方程.【解答】解:设乙每小时做x 个,甲每小时做(x +6)个,根据甲做90个所用时间与乙做60个所用时间相等,得90x+6=60x, 故选:B .【点评】本题考查了分式方程的应用,找到关键描述语,找到合适的等量关系是解决问题的关键.9.(3分)(2017•临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示: 部门人数每人创年利润(万元)A 1 10B 3 8C 7 5 D43这15名员工每人所创年利润的众数、中位数分别是( ) A .10,5 B .7,8C .5,6.5D .5,5【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数. 【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,∴这组数据的众数是5,中位数是5, 故选D .【点评】本题考查众数和中位数,解答本题的关键是明确众数和中位数的定义,会找一组数据的众数和中位数.10.(3分)(2017•临沂)如图,AB 是⊙O 的直径,BT 是⊙O 的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )A .2B .32﹣14π C .1D .12+14π【分析】设AT 交⊙O 于D ,连结BD ,先根据圆周角定理得到∠ADB=90°,则可判断△ADB 、△BDC 都是等腰直角三角形,所以AD=BD=CD=√22AB=√2,然后利用弓形AD 的面积等于弓形BD 的面积得到阴影部分的面积=S △BTD .【解答】解:∵BT 是⊙O 的切线; 设AT 交⊙O 于D ,连结BD , ∵AB 是⊙O 的直径, ∴∠ADB=90°, 而∠ATB=45°,∴△ADB 、△BDT 都是等腰直角三角形,∴AD=BD=TD=√22AB=√2,∴弓形AD 的面积等于弓形BD 的面积, ∴阴影部分的面积=S △BTD =12×√2×√2=1.故选C .【点评】本题考查了切线的性质,等腰直角三角形的性质,解决本题的关键是利用等腰直角三角形的性质把阴影部分的面积转化为三角形的面积.11.(3分)(2017•临沂)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n 个图形中“○”的个数是78,则n 的值是( )A .11B .12C .13D .14【分析】根据小圆个数变化规律进而表示出第n 个图形中小圆的个数,进而得出答案.【解答】解:第1个图形有1个小圆; 第2个图形有1+2=3个小圆; 第3个图形有1+2+3=6个小圆; 第4个图形有1+2+3+4=10个小圆;第n 个图形有1+2+3+…+n=n(n+1)2个小圆;∵第n 个图形中“○”的个数是78, ∴78=n(n+1)2,解得:n 1=12,n 2=﹣13(不合题意舍去), 故选:B .【点评】此题主要考查了图形变化类,正确得出小圆个数变化规律是解题关键.12.(3分)(2017•临沂)在△ABC 中,点D 是边BC 上的点(与B ,C 两点不重合),过点D 作DE ∥AC ,DF ∥AB ,分别交AB ,AC 于E ,F 两点,下列说法正确的是( )A .若AD ⊥BC ,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形 C .若BD=CD ,则四边形AEDF 是菱形 D .若AD 平分∠BAC ,则四边形AEDF 是菱形【分析】由矩形的判定和菱形的判定即可得出结论.【解答】解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A 错误;若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.【点评】本题考查了矩形的判定、菱形的判定;熟记菱形和矩形的判定方法是解决问题的关键.13.(3分)(2017•临沂)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=92;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.4【分析】由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,可得y=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.【解答】解:由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,∴足球距离地面的最大高度为20.25m,故①错误,∴抛物线的对称轴t=4.5,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=1.5时,y=11.25,故④错误.∴正确的有②③,故选B .【点评】本题考查二次函数的应用、求出抛物线的解析式是解题的关键,属于中考常考题型.14.(3分)(2017•临沂)如图,在平面直角坐标系中,反比例函数y=kx(x >0)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,△OMN 的面积为10.若动点P 在x 轴上,则PM +PN 的最小值是( )A .6√2B .10C .2√26D .2√29【分析】由正方形OABC 的边长是6,得到点M 的横坐标和点N 的纵坐标为6,求得M (6,k 6),N (k 6,6),根据三角形的面积列方程得到M (6,4),N (4,6),作M 关于x 轴的对称点M′,连接NM′交x 轴于P ,则NM′的长=PM +PN 的最小值,根据勾股定理即可得到结论. 【解答】解:∵正方形OABC 的边长是6, ∴点M 的横坐标和点N 的纵坐标为6,∴M (6,k 6),N (k6,6),∴BN=6﹣k 6,BM=6﹣k6,∵△OMN 的面积为10,∴6×6﹣12×6×k 6﹣12×6×k 6﹣12×(6﹣k6)2=10,∴k=24,∴M (6,4),N (4,6),作M 关于x 轴的对称点M′,连接NM′交x 轴于P ,则NM′的长=PM +PN 的最小值, ∵AM=AM′=4,∴BM′=10,BN=2,∴NM′=√BM′2+BN2=√102+22=2√26,故选C.【点评】本题考查了反比例函数的系数k的几何意义,轴对称﹣最小距离问题,勾股定理,正方形的性质,正确的作出图形是解题的关键.二、填空题(本大题共5小题,每小题3分,共15分)15.(3分)(2017•临沂)分解因式:m3﹣9m=m(m+3)(m﹣3).【分析】先提取公因式,再根据平方差公式进行二次分解.平方差公式:a2﹣b2=(a+b)(a﹣b).【解答】解:m3﹣9m,=m(m2﹣9),=m(m+3)(m﹣3).故答案为:m(m+3)(m﹣3).【点评】本题考查了用提公因式法和公式法进行因式分解的能力,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.16.(3分)(2017•临沂)已知AB∥CD,AD与BC相交于点O.若BOOC=23,AD=10,则AO=4.【分析】根据平行线分线段成比例定理列出比例式,计算即可. 【解答】解:∵AB ∥CD ,∴AO OD =BO OC =23,即AO 10−AO =23, 解得,AO=4, 故答案为:4.【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.17.(3分)(2017•临沂)计算:x−y x÷(x ﹣2xy−y 2x)=1x−y.【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.【解答】解:原式=x−y x÷x 2−2xy+y 2x=x−y x •x (x−y)2=1x−y,故答案为:1x−y.【点评】本题考查了分式的混合运算,能正确运用分式的运算法则进行化简是解此题的关键,注意运算顺序.18.(3分)(2017•临沂)在▱ABCD 中,对角线AC ,BD 相交于点O ,若AB=4,BD=10,sin ∠BDC=35,则▱ABCD 的面积是 24 .【分析】作OE ⊥CD 于E ,由平行四边形的性质得出OA=OC ,OB=OD=12BD=5,CD=AB=4,由sin ∠BDC=35,证出AC ⊥CD ,OC=3,AC=2OC=6,得出▱ABCD 的面积=CD•AC=24.【解答】解:作OE ⊥CD 于E ,如图所示: ∵四边形ABCD 是平行四边形,∴OA=OC ,OB=OD=12BD=5,CD=AB=4,∵sin ∠BDC=OE OD =35,∴OE=3,∴DE=√OD 2−OE 2=4, ∵CD=4,∴点E 与点C 重合, ∴AC ⊥CD ,OC=3, ∴AC=2OC=6,∴▱ABCD 的面积=CD•AC=4×6=24; 故答案为:24.【点评】本题考查了平行四边形的性质、三角函数、勾股定理等知识;熟练掌握平行四边形的性质,得出AC ⊥CD 是关键19.(3分)(2017•临沂)在平面直角坐标系中,如果点P 坐标为(m ,n ),向量OP →可以用点P 的坐标表示为OP →=(m ,n ).已知:OA →=(x 1,y 1),OB →=(x 2,y 2),如果x 1•x 2+y 1•y 2=0,那么OA →与OB →互相垂直,下列四组向量:①OC →=(2,1),OD →=(﹣1,2);②OE →=(cos30°,tan45°),OF →=(1,sin60°);③OG →=(√3﹣√2,﹣2),OH →=(√3+√2,12); ④OM →=(π0,2),ON →=(2,﹣1).其中互相垂直的是 ①③④ (填上所有正确答案的符号).【分析】根据向量垂直的定义进行解答.【解答】解:①因为2×(﹣1)+1×2=0,所以OC →与OD →互相垂直;②因为cos30°×1+tan45°•sin60°=√32×1+1×√32=√3≠0,所以OE →与OF →不互相垂直; ③因为(√3﹣√2)(√3+√2)+(﹣2)×12=3﹣2﹣1=0,所以OG →与OH →互相垂直; ④因为π0×2+2×(﹣1)=2﹣2=0,所以OM →与ON →互相垂直. 综上所述,①③④互相垂直.故答案是:①③④.【点评】本题考查了平面向量,零指数幂以及解直角三角形.解题的关键是掌握向量垂直的定义.三、解答题(本大题共7小题,共63分)20.(7分)(2017•临沂)计算:|1﹣√2|+2cos45°﹣√8+(12)﹣1. 【分析】根据绝对值的意义、特殊角的三角函数值、二次根式的化简和负指数幂的运算,分别求得每项的值,再进行计算即可.【解答】解:|1﹣√2|+2cos45°﹣√8+(12)﹣1 =√2﹣1+2×√22﹣2√2+2 =√2﹣1+√2﹣2√2+2=1.【点评】本题主要考查实数的运算及特殊角的三角函数值,注意绝对值和负指数幂的运算法则是解题的关键.21.(7分)(2017•临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目 人数(名)百分比最强大脑5 10% 朗读者15 b% 中国诗词大会a 40% 出彩中国人 10 20% 根据以上提供的信息,解答下列问题:(1)x= 50 ,a= 20 ,b= 30 ;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.【分析】(1)根据最强大脑的人数除以占的百分比确定出x 的值,进而求出a 与b 的值即可;(2)根据a 的值,补全条形统计图即可;(3)由中国诗词大会的百分比乘以1000即可得到结果.【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=1550×100=30; 故答案为:50;20;30;(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:(3)根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名.【点评】此题考查了条形统计图,用样本估计总体,以及统计表,弄清题中的数据是解本题的关键.22.(7分)(2017•临沂)如图,两座建筑物的水平距离BC=30m,从A点测得D 点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.【分析】延长CD,交AE于点E,可得DE⊥AE,在直角三角形ABC中,由题意确定出AB的长,进而确定出EC的长,在直角三角形AED中,由题意求出ED的长,由EC﹣ED求出DC的长即可.【解答】解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10√3m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30√3m,则CD=EC﹣ED=AB﹣ED=30√3﹣10√3=20√3m.【点评】此题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.23.(9分)(2017•临沂)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC 的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.̂=CD̂,由【分析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出BD圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;̂=CD̂,得出CD=BD=4,由圆周角定理得出BC是直径,∠(2)由(1)得:BDBDC=90°,由勾股定理求出BC=√BD2+CD2=4√2,即可得出△ABC外接圆的半径.【解答】(1)证明:∵AD平分∠BAC,BE平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,̂=CD̂,∴BD∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:BD̂=CD̂,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC=√BD2+CD2=4√2,∴△ABC外接圆的半径=12×4√2=2√2.【点评】本题考查了三角形的外接圆的性质、圆周角定理、三角形的外角性质、勾股定理等知识;熟练掌握圆周角定理是解决问题的关键.24.(9分)(2017•临沂)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?【分析】(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;(2)根据题意对x 进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m 3.【解答】解:(1)当0≤x ≤15时,设y 与x 的函数关系式为y=kx ,15k=27,得k=1.8,即当0≤x ≤15时,y 与x 的函数关系式为y=1.8x ,当x >15时,设y 与x 的函数关系式为y=ax +b ,{15a +b =2720a +b =39,得{a =2.4b =−9, 即当x >15时,y 与x 的函数关系式为y=2.4x ﹣9,由上可得,y 与x 的函数关系式为y={ 1.8x (0≤x ≤15)2.4x −9(x >15);(2)设二月份的用水量是xm 3,当15<x ≤25时,2.4x ﹣9+2.4(40﹣x )﹣9=79.8,解得,x 无解,当0<x ≤15时,1.8x +2.4(40﹣x )﹣9=79.8,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m 3、28m 3.【点评】本题考查一次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想和分类讨论的数学思想解答.25.(11分)(2017•临沂)数学课上,张老师出示了问题:如图1,AC ,BD 是四边形ABCD 的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC ,CD ,AC 三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB 到E ,使BE=CD ,连接AE ,证得△ABE ≌△ADC ,从而容易证明△ACE 是等边三角形,故AC=CE ,所以AC=BC +CD .小亮展示了另一种正确的思路:如图3,将△ABC 绕着点A 逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.【分析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.【解答】解:(1)BC+CD=√2AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=90°,∴∠BAD+∠BCD=180°,∴∠ABC +∠ADC=180°,∵∠ADC +∠ADE=180°,∴∠ABC=∠ADE ,在△ABC 和△ADE 中,{AB =AD ∠ABC =∠ADE BC =DE,∴△ABC ≌△ADE (SAS ),∴∠ACB=∠AED=45°,AC=AE ,∴△ACE 是等腰直角三角形,∴CE=√2AC ,∵CE=CD +DE=CD +BC ,∴BC +CD=√2AC ;(2)BC +CD=2AC•cosα.理由:如图2,延长CD 至E ,使DE=BC ,∵∠ABD=∠ADB=α,∴AB=AD ,∠BAD=180°﹣∠ABD ﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB +∠ACD=2α,∴∠BAD +∠BCD=180°,∴∠ABC +∠ADC=180°,∵∠ADC +∠ADE=180°,∴∠ABC=∠ADE ,在△ABC 和△ADE 中,{AB =AD ∠ABC =∠ADE BC =DE,∴△ABC ≌△ADE (SAS ),∴∠ACB=∠AED=α,AC=AE ,∴∠AEC=α,过点A 作AF ⊥CE 于F ,∴CE=2CF ,在Rt △ACF 中,∠ACD=α,CF=AC•cos ∠ACD=AC•cosα,∴CE=2CF=2AC•cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC•cosα.【点评】此题是几何变换综合题,主要考查了全等三角形的判定,四边形的内角和,等腰三角形的判定和性质,解本题的关键是构造全等三角形,是一道综合性较强的题目.26.(13分)(2017•临沂)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x 轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【分析】(1)待定系数法即可得到结论;(2)连接AC ,作BF ⊥AC 交AC 的延长线于F ,根据已知条件得到AF ∥x 轴,得到F (﹣1,﹣3),设D (0,m ),则OD=|m |即可得到结论;(3)设M (a ,a 2﹣2a ﹣3),N (1,n ),①以AB 为边,则AB ∥MN ,AB=MN ,如图2,过M 作ME ⊥对称轴y 于E ,AF ⊥x 轴于F ,于是得到△ABF ≌△NME ,证得NE=AF=3,ME=BF=3,得到M (4,5)或(﹣2,11);②以AB 为对角线,BN=AM ,BN ∥AM ,如图3,则N 在x 轴上,M 与C 重合,于是得到结论.【解答】解:(1)由y=ax 2+bx ﹣3得C (0.﹣3),∴OC=3,∵OC=3OB ,∴OB=1,∴B (﹣1,0),把A (2,﹣3),B (﹣1,0)代入y=ax 2+bx ﹣3得{4a +2b −3=−3a −b −3=0, ∴{a =1b =−2, ∴抛物线的解析式为y=x 2﹣2x ﹣3;(2)设连接AC ,作BF ⊥AC 交AC 的延长线于F ,∵A (2,﹣3),C (0,﹣3),∴AF ∥x 轴,∴F (﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D (0,m ),则OD=|m |,∵∠BDO=∠BAC ,∴∠BDO=45°,∴OD=OB=1,∴|m |=1,∴m=±1,∴D 1(0,1),D 2(0,﹣1);(3)设M (a ,a 2﹣2a ﹣3),N (1,n ),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF ⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,5);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,5)或(0,﹣3).【点评】本题考查了待定系数法求二次函数的解析式,全等三角形的判定和性质,平行四边形的判定和性质,正确的作出图形是解题的关键.。
2017年山东省临沂市中考数学试卷

2017年山东省临沂市中考数学试卷一.选择题1.(2017•临沂)﹣的相反数是()A. B. ﹣ C. 2017 D. ﹣2017【答案】A【考点】相反数【解析】【解答】解:﹣的相反数是:.故选:A.【分析】直接利用相反数的定义分析得出答案.2.(2017•临沂)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A. 50°B. 60°C. 70°D. 80°【答案】A【考点】余角和补角,平行线的性质【解析】【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,∴∠BEF=∠1+∠F=50°,∵AB∥CD,∴∠2=∠BEF=50°,故选A.【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.3.(2017•临沂)下列计算正确的是()A. ﹣(a﹣b)=﹣a﹣bB. a2+a2=a4C. a2•a3=a6D. (ab2)2=a2b4【答案】D【考点】整式的加减,同底数幂的乘法,幂的乘方与积的乘方【解析】【解答】解:A、括号前是负号,去括号全变号,故A不符合题意;B、不是同底数幂的乘法指数不能相加,故B不符合题意;C、同底数幂的乘法底数不变指数相加,故C不符合题意;D、积的乘方等于乘方的积,故D符合题意;故选:D.【分析】根据去括号、同底数幂的乘法底数不变指数相加,积的乘方,可得答案.4.(2017•临沂)不等式组中,不等式①和②的解集在数轴上表示正确的是()A. B.C. D.【答案】B【考点】在数轴上表示不等式的解集,解一元一次不等式组【解析】【解答】解:解不等式①,得:x<1,解不等式②,得:x≥﹣3,则不等式组的解集为﹣3≤x<1,故选:B.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.5.(2017•临沂)如图所示的几何体是由五个小正方体组成的,它的左视图是()A. B. C. D.【答案】D【考点】简单组合体的三视图【解析】【解答】解:该几何体的三视图如下:主视图:;俯视图:;左视图:,故选:D.【分析】根据三视图定义分别作出三视图即可判断.6.(2017•临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A. B. C. D.【答案】C【考点】列表法与树状图法【解析】【解答】解:画树状图得:∵共有9种等可能的结果,小华获胜的情况数是3种,∴小华获胜的概率是:= .故选C.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案.7.(2017•临沂)一个多边形的内角和是外角和的2倍,则这个多边形是()A. 四边形B. 五边形C. 六边形D. 八边形【答案】C【考点】多边形内角与外角【解析】【解答】解:设所求正n边形边数为n,由题意得(n﹣2)•180°=360°×2解得n=6.则这个多边形是六边形.故选:C.【分析】此题可以利用多边形的外角和和内角和定理求解.8.(2017•临沂)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A. = B. = C. = D. =【答案】B【考点】由实际问题抽象出分式方程【解析】【解答】解:设乙每小时做x个,甲每小时做(x+6)个,根据甲做90个所用时间与乙做60个所用时间相等,得= ,故选:B.【分析】根据甲乙的工作时间,可列方程.9.(2017•临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A 1 10B 3 8C 7 5D 4 3这15名员工每人所创年利润的众数、中位数分别是()A. 10,5B. 7,8C. 5,6.5D. 5,5【答案】D【考点】中位数、众数【解析】【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,∴这组数据的众数是5,中位数是5,故选D.【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.10.(2017•临沂)如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A. 2B. ﹣πC. 1D. + π【答案】C【考点】切线的性质,扇形面积的计算【解析】【解答】解:∵BT是⊙O的切线;设AT交⊙O于D,连结BD,∵AB是⊙O的直径,∴∠ADB=90°,而∠ATB=45°,∴△ADB、△BDT都是等腰直角三角形,∴AD=BD=TD= AB= ,∴弓形AD的面积等于弓形BD的面积,∴阴影部分的面积=S△BTD= × × =1.故选C.【分析】设AT交⊙O于D,连结BD,先根据圆周角定理得到∠ADB=90°,则可判断△ADB、△BDC都是等腰直角三角形,所以AD=BD=CD= AB= ,然后利用弓形AD的面积等于弓形BD的面积得到阴影部分的面积=S△BTD.11.(2017•临沂)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是()A. 11B. 12C. 13D. 14【答案】B【考点】探索图形规律【解析】【解答】解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n个图形有1+2+3+…+n= 个小圆;∵第n个图形中“○”的个数是78,∴78= ,解得:n1=12,n2=﹣13(不合题意舍去),故选:B.【分析】根据小圆个数变化规律进而表示出第n个图形中小圆的个数,进而得出答案.12.(2017•临沂)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A. 若AD⊥BC,则四边形AEDF是矩形B. 若AD垂直平分BC,则四边形AEDF是矩形C. 若BD=CD,则四边形AEDF是菱形D. 若AD平分∠BAC,则四边形AEDF是菱形【答案】D【考点】菱形的判定,矩形的判定【解析】【解答】解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;若AD 垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.【分析】由矩形的判定和菱形的判定即可得出结论.13.(2017•临沂)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t 0 1 2 3 4 5 6 7 …h 0 8 14 18 20 20 18 14 …下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A. 1B. 2C. 3D. 4【答案】B【考点】二次函数的应用【解析】【解答】解:由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,∴足球距离地面的最大高度为20.25m,故①错误,∴抛物线的对称轴t=4.5,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=1.5时,y=11.25,故④错误.∴正确的有②③,故选B.【分析】由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,可得y=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.14.(2017•临沂)如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC 的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A. 6B. 10C. 2D. 2【答案】C【考点】反比例函数的性质【解析】【解答】解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M(6,),N(,6),∴BN=6﹣,BM=6﹣,∵△OMN的面积为10,∴6×6﹣×6× ﹣6× ﹣×(6﹣)2=10,∴k=24,∴M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′= = =2 ,故选C.【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,),N(,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x 轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.二.填空题15.(2017•临沂)分解因式:m3﹣9m=________.【答案】m(m+3)(m﹣3)【考点】提公因式法与公式法的综合运用【解析】【解答】解:m3﹣9m,=m(m2﹣9),=m(m+3)(m﹣3).故答案为:m(m+3)(m﹣3).【分析】先提取公因式,再根据平方差公式进行二次分解.平方差公式:a2﹣b2=(a+b)(a﹣b).16.(2017•临沂)已知AB∥CD,AD与BC相交于点O.若= ,AD=10,则AO=________.【答案】4【考点】平行线分线段成比例【解析】【解答】解:∵AB∥CD,∴= = ,即= ,解得,AO=4,故答案为:4.【分析】根据平行线分线段成比例定理列出比例式,计算即可.17.(2017•临沂)计算:÷(x﹣)=________.【答案】【考点】分式的混合运算【解析】【解答】解:原式= ÷ = •= ,故答案为:.【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.18.(2017•临沂)在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ,则▱ABCD的面积是________.【答案】24【考点】平行四边形的性质,解直角三角形【解析】【解答】解:作OE⊥CD于E,如图所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD= BD=5,CD=AB=4,∵sin∠BDC= = ,∴OE=3,∴DE= =4,∵CD=4,∴点E与点C重合,∴AC⊥CD,OC=3,∴AC=2OC=6,∴▱ABCD的面积=CD•AC=4×6=24;故答案为:24.【分析】作OE⊥CD于E,由平行四边形的性质得出OA=OC,OB=OD= BD=5,CD=AB=4,由sin∠BDC= ,证出AC⊥CD,OC=3,AC=2OC=6,得出▱ABCD的面积=CD•AC=24.19.(2017•临沂)在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组向量:① =(2,1),=(﹣1,2);② =(cos30°,tan45°),=(1,sin60°);③ =(﹣,﹣2),=(+ ,);④ =(π0,2),=(2,﹣1).其中互相垂直的是________(填上所有正确答案的符号).【答案】①③④【考点】零指数幂,平面向量,解直角三角形【解析】【解答】解:①因为2×(﹣1)+1×2=0,所以与互相垂直;②因为cos30°×1+tan45°•sin60°= ×1+1× = ≠0,所以与不互相垂直;③因为(﹣)(+ )+(﹣2)× =3﹣2﹣1=0,所以与互相垂直;④因为π0×2+2×(﹣1)=2﹣2=0,所以与互相垂直.综上所述,①③④互相垂直.故答案是:①③④.【分析】根据向量垂直的定义进行解答.三.解答题20.(2017•临沂)计算:|1﹣|+2cos45°﹣+()﹣1.【答案】解:|1﹣|+2cos45°﹣+()﹣1= ﹣1+2× ﹣2 +2= ﹣1+ ﹣2 +2=1.【考点】实数的运算,负整数指数幂,特殊角的三角函数值【解析】【分析】根据绝对值的意义、特殊角的三角函数值、二次根式的化简和负指数幂的运算,分别求得每项的值,再进行计算即可.21.(2017•临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑 5 10%朗读者 15 b%中国诗词大会 a 40%出彩中国人 10 20%根据以上提供的信息,解答下列问题:(1)x=________,a=________,b=________;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.【答案】(1)50;20;30(2)(3)解:根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名【考点】用样本估计总体,统计表,条形统计图【解析】【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b= ×100=30;故答案为:50;20;30;【分析】(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;(2)根据a的值,补全条形统计图即可;(3)由中国诗词大会的百分比乘以1000即可得到结果.22.(2017•临沂)如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.【答案】解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10 m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30 m,则CD=EC﹣ED=AB﹣ED=30 ﹣10 =20 m.【考点】解直角三角形的应用-仰角俯角问题【解析】【分析】延长CD,交AE于点E,可得DE⊥AE,在直角三角形ABC中,由题意确定出AB的长,进而确定出EC的长,在直角三角形AED中,由题意求出ED的长,由EC﹣ED求出DC的长即可.23.(2017•临沂)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.【答案】(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC= =4 ,∴△ABC外接圆的半径= ×4 =2 .【考点】三角形的外接圆与外心【解析】【分析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得:,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC= =4 ,即可得出△ABC外接圆的半径.24.(2017•临沂)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?【答案】(1)解:当0≤x≤15时,设y与x的函数关系式为y=kx,15k=27,得k=1.8,即当0≤x≤15时,y与x的函数关系式为y=1.8x,当x>15时,设y与x的函数关系式为y=ax+b,,得,即当x>15时,y与x的函数关系式为y=2.4x﹣9,由上可得,y与x的函数关系式为y=(2)解:设二月份的用水量是xm3,当15<x≤25时,2.4x﹣9+2.4(40﹣x)﹣9=79.8,解得,x无解,当0<x≤15时,1.8x+2.4(40﹣x)﹣9=79.8,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m3、28m3【考点】一次函数的应用【解析】【分析】(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;(2)根据题意对x进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m3.25.(2017•临沂)数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.【答案】(1)解:BC+CD= AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=45°,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=45°,AC=AE,∴△ACE是等腰直角三角形,∴CE= AC,∵CE=CE+DE=CD+BC,∴BC+CD= AC(2)解:BC+CD=2AC•cosα.理由:如图2,延长CD至E,使DE=BC,∵∠ABD=∠ADB=α,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB+∠ACD=2α,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=α,AC=AE,∴∠AEC=α,过点A作AF⊥CE于F,∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,∴CE=2CF=2AC•cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC•cosα【考点】等腰三角形的判定与性质【解析】【分析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.26.(2017•临沂)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【答案】(1)解:由y=ax2+bx﹣3得C(0.﹣3),∴OC=3,∵OC=3OB,∴OB=1,∴B(﹣1,0),把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得,∴,∴抛物线的解析式为y=x2﹣2x﹣3(2)解:设连接AC,作BF⊥AC交AC的延长线于F,∵A(2,﹣3),C(0,﹣3),∴AF∥x轴,∴F(﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D(0,m),则OD=|m|,∵∠BDO=∠BAC,∴∠BDO=45°,∴OD=OB=1,∴|m|=1,∴m=±1,∴D1(0,1),D2(0,﹣1)(3)解:设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).【考点】二次函数的图象,二次函数的性质,二次函数的应用【解析】【分析】(1)待定系数法即可得到结论;(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(﹣1,﹣3),设D(0,m),则OD=|m|即可得到结论;(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.。
(完整)2017年山东省临沂市中考数学试卷(含答案解析版)(2),推荐文档

2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,每小题3分,共42分)1.﹣的相反数是()A.B.﹣C.2017 D.﹣20172.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°3.下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4 C.a2•a3=a6 D.(ab2)2=a2b44.不等式组中,不等式①和②的解集在数轴上表示正确的是()A.B.C.D.5.如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C. D.6.小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.7.一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形8.甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.=B.=C.=D.=9.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A110B38C75D43这15名员工每人所创年利润的众数、中位数分别是()A.10,5 B.7,8 C.5,6.5 D.5,510.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A.2 B.﹣πC.1 D. +π11.将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n 个图形中“○”的个数是78,则n的值是()A.11 B.12 C.13 D.1412.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.414.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6 B.10 C.2D.2二、填空题(本大题共5小题,每小题3分,共15分)15.分解因式:m3﹣9m=.16.已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=.17.计算:÷(x﹣)=.18.在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=,则▱ABCD的面积是.19.在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组向量:①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是(填上所有正确答案的符号).三、解答题(本大题共7小题,共63分)20.计算:|1﹣|+2cos45°﹣+()﹣1.21.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表百分比节目人数(名)最强大脑510%朗读者15b%中国诗词大会a40%出彩中国人1020%根据以上提供的信息,解答下列问题:(1)x=,a=,b=;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.23.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.24.某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?25.数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.2017年山东省临沂市中考数学试卷参考答案与试题解析一、选择题(本大题共14小题,每小题3分,共42分)1.﹣的相反数是()A.B.﹣C.2017 D.﹣2017【考点】14:相反数.【分析】直接利用相反数的定义分析得出答案.【解答】解:﹣的相反数是:.故选:A.2.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°【考点】JA:平行线的性质;IL:余角和补角.【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,∴∠BEF=∠1+∠F=50°,∵AB∥CD,∴∠2=∠BEF=50°,故选A.3.下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4 C.a2•a3=a6 D.(ab2)2=a2b4【考点】47:幂的乘方与积的乘方;44:整式的加减;46:同底数幂的乘法.【分析】根据去括号、同底数幂的乘法底数不变指数相加,积的乘方,可得答案.【解答】解:A、括号前是负号,去括号全变号,故A不符合题意;B、不是同底数幂的乘法指数不能相加,故B不符合题意;C、同底数幂的乘法底数不变指数相加,故C不符合题意;D、积的乘方等于乘方的积,故D符合题意;故选:D.4.不等式组中,不等式①和②的解集在数轴上表示正确的是()A.B.C.D.【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式①,得:x<1,解不等式②,得:x≥﹣3,则不等式组的解集为﹣3≤x<1,故选:B.5.如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C. D.【考点】U2:简单组合体的三视图.【分析】根据三视图定义分别作出三视图即可判断.【解答】解:该几何体的三视图如下:主视图:;俯视图:;左视图:,故选:D.6.小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.【考点】X6:列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有9种等可能的结果,小华获胜的情况数是3种,∴小华获胜的概率是:=.故选C.7.一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形【考点】L3:多边形内角与外角.【分析】此题可以利用多边形的外角和和内角和定理求解.【解答】解:设所求正n边形边数为n,由题意得(n﹣2)•180°=360°×2解得n=6.则这个多边形是六边形.故选:C.8.甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.=B.=C.=D.=【考点】B6:由实际问题抽象出分式方程.【分析】根据甲乙的效率,可设未知数,根据甲乙的工作时间,可列方程.【解答】解:设乙每小时做x个,甲每小时做(x+6)个,根据甲做90个所用时间与乙做60个所用时间相等,得=,故选:B.9.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A110B38C75D43这15名员工每人所创年利润的众数、中位数分别是()A.10,5 B.7,8 C.5,6.5 D.5,5【考点】W5:众数;W4:中位数.【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,∴这组数据的众数是5,中位数是5,故选D.10.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A.2 B.﹣πC.1 D. +π【考点】MC:切线的性质;MO:扇形面积的计算.【分析】设AC交⊙O于D,连结BD,先根据圆周角定理得到∠ADB=90°,则可判断△ADB、△BDC都是等腰直角三角形,所以AD=BD=CD=AB=,然后利.用弓形AD的面积等于弓形BD的面积得到阴影部分的面积=S△BTD【解答】解:∵BT是⊙O的切线;设AT交⊙O于D,连结BD,∵AB是⊙O的直径,∴∠ADB=90°,而∠ATB=45°,∴△ADB、△BDT都是等腰直角三角形,∴AD=BD=TD=AB=,∴弓形AD的面积等于弓形BD的面积,=××=1.∴阴影部分的面积=S△BTD故选C.11.将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n 个图形中“○”的个数是78,则n的值是()A.11 B.12 C.13 D.14【考点】38:规律型:图形的变化类.【分析】根据小圆个数变化规律进而表示出第n个图形中小圆的个数,进而得出答案.【解答】解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n个图形有1+2+3+…+n=个小圆;∵第n个图形中“○”的个数是78,∴78=,解得:n1=12,n2=﹣13(不合题意舍去),故选:B.12.在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形【考点】LC:矩形的判定;L9:菱形的判定.【分析】由矩形的判定和菱形的判定即可得出结论.【解答】解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A 错误;若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.4【考点】HE:二次函数的应用.【分析】由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,可得y=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.【解答】解:由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,∴足球距离地面的最大高度为20.25m,故①错误,∴抛物线的对称轴t=4.5,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=1.5时,y=11.25,故④错误.∴正确的有②③,故选B.14.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6 B.10 C.2D.2【考点】G5:反比例函数系数k的几何意义;PA:轴对称﹣最短路线问题.【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,),N(,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.【解答】解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M(6,),N(,6),∴BN=6﹣,BM=6﹣,∵△OMN的面积为10,∴6×6﹣×6×﹣6×﹣×(6﹣)2=10,∴k=24,∴M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′===2,故选C.二、填空题(本大题共5小题,每小题3分,共15分)15.分解因式:m3﹣9m=m(m+3)(m﹣3).【考点】55:提公因式法与公式法的综合运用.【分析】先提取公因式,再根据平方差公式进行二次分解.平方差公式:a2﹣b2=(a+b)(a﹣b).【解答】解:m3﹣9m,=m(m2﹣9),=m(m+3)(m﹣3).故答案为:m(m+3)(m﹣3).16.已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=4.【考点】S4:平行线分线段成比例.【分析】根据平行线分线段成比例定理列出比例式,计算即可.【解答】解:∵AB∥CD,∴==,即=,解得,AO=4,故答案为:4.17.计算:÷(x﹣)=.【考点】6C:分式的混合运算.【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.【解答】解:原式=÷=•=,故答案为:.18.在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=,则▱ABCD的面积是24.【考点】L5:平行四边形的性质;T7:解直角三角形.【分析】作OE⊥CD于E,由平行四边形的性质得出OA=OC,OB=OD=BD=5,CD=AB=4,由sin∠BDC=,证出AC⊥CD,OC=3,AC=2OC=6,得出▱ABCD的面积=CD•AC=24.【解答】解:作OE⊥CD于E,如图所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD=BD=5,CD=AB=4,∵sin∠BDC==,∴OE=3,∴DE==4,∵CD=4,∴点E与点C重合,∴AC⊥CD,OC=3,∴AC=2OC=6,∴▱ABCD的面积=CD•AC=4×6=24;故答案为:24.19.在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组向量:①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是①③④(填上所有正确答案的符号).【考点】LM:*平面向量;6E:零指数幂;T7:解直角三角形.【分析】根据向量垂直的定义进行解答.【解答】解:①因为2×(﹣1)+1×2=0,所以与互相垂直;②因为cos30°×1+tan45°•sin60°=×1+1×=≠0,所以与不互相垂直;③因为(﹣)(+)+(﹣2)×=3﹣2﹣1=0,所以与互相垂直;④因为π0×2+2×(﹣1)=2﹣2=0,所以与互相垂直.综上所述,①③④互相垂直.故答案是:①③④.三、解答题(本大题共7小题,共63分)20.计算:|1﹣|+2cos45°﹣+()﹣1.【考点】2C:实数的运算;6F:负整数指数幂;T5:特殊角的三角函数值.【分析】根据绝对值的意义、特殊角的三角函数值、二次根式的化简和负指数幂的运算,分别求得每项的值,再进行计算即可.【解答】解:|1﹣|+2cos45°﹣+()﹣1=﹣1+2×﹣2+2=﹣1+﹣2+2=1.21.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表百分比节目人数(名)最强大脑510%朗读者15b%中国诗词大会a40%出彩中国人1020%根据以上提供的信息,解答下列问题:(1)x=50,a=20,b=30;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.【考点】VC:条形统计图;V5:用样本估计总体;VA:统计表.【分析】(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;(2)根据a的值,补全条形统计图即可;(3)由中国诗词大会的百分比乘以1000即可得到结果.【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;故答案为:50;20;30;(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:(3)根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名.22.如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.【考点】TA:解直角三角形的应用﹣仰角俯角问题.【分析】延长CD,交AE于点E,可得DE⊥AE,在直角三角形ABC中,由题意确定出AB的长,进而确定出EC的长,在直角三角形AED中,由题意求出ED的长,由EC﹣ED求出DC的长即可.【解答】解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30m,则CD=EC﹣ED=AB﹣ED=30﹣10=20m.23.如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.【考点】MA:三角形的外接圆与外心.【分析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得:,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC==4,即可得出△ABC外接圆的半径.【解答】(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.24.某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?【考点】FH:一次函数的应用.【分析】(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;(2)根据题意对x进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m3.【解答】解:(1)当0≤x≤15时,设y与x的函数关系式为y=kx,15k=27,得k=1.8,即当0≤x≤15时,y与x的函数关系式为y=1.8x,当x>15时,设y与x的函数关系式为y=ax+b,,得,即当x>15时,y与x的函数关系式为y=2.4x﹣9,由上可得,y与x的函数关系式为y=;(2)设二月份的用水量是xm3,当15<x≤25时,2.4x﹣9+2.4(40﹣x)﹣9=79.8,解得,x无解,当0<x≤15时,1.8x+2.4(40﹣x)﹣9=79.8,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m3、28m3.25.数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.【考点】RB:几何变换综合题.【分析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.【解答】解:(1)BC+CD=AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=45°,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=45°,AC=AE,∴△ACE是等腰直角三角形,∴CE=AC,∵CE=CE+DE=CD+BC,∴BC+CD=AC;(2)BC+CD=2AC•cosα.理由:如图2,延长CD至E,使DE=BC,∵∠ABD=∠ADB=α,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB+∠ACD=2α,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=α,AC=AE,∴∠AEC=α,过点A作AF⊥CE于F,∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,∴CE=2CF=2AC•cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC•cosα.26.如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【考点】HF:二次函数综合题.【分析】(1)待定系数法即可得到结论;(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(﹣1,﹣3),设D(0,m),则OD=|m即可得到结论;(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.【解答】解:(1)由y=ax2+bx﹣3得C(0.﹣3),∴OC=3,∵OC=3OB,∴OB=1,∴B(﹣1,0),把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得,∴,∴抛物线的解析式为y=x2﹣2x﹣3;(2)设连接AC,作BF⊥AC交AC的延长线于F,∵A(2,﹣3),C(0,﹣3),∴AF∥x轴,∴F(﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D(0,m),则OD=|m|,∵∠BDO=∠BAC,∴∠BDO=45°,∴OD=OB=1,∴|m|=1,∴m=±1,∴D1(0,1),D2(0,﹣1);(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF ⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).。
2017年中考真题精品解析 数学(山东临沂卷)精编word版(解析版)

2021年中|考真题精品解析 数学 (山东临沂卷 )第|一卷 (共42分 )一、选择题:本大题共14个小题,每题3分,共42分.在每题给出的四个选项中 ,只有一项为哪一项符合题目要求的.1.12007-的相反数是 ( ) A .12007 B .12007- C .2021 D .2017-【答案】A 【解析】试题分析:根据只有符号不同的两数互为相反数 ,可知12007-的相反数为12007.应选:A 考点:相反数2.如图 ,将直尺与含30︒角的三角尺摆放在一起 ,假设120∠=︒ ,那么2∠的度数是 ( )A .50︒B .60︒C .70︒D .80︒ 【答案】A 【解析】试题分析:根据三角形的外角等于不相邻的两内角的和 ,可知∠3 =30° +∠1 =50° ,然后根据两直线平行 ,同位角相等 ,可得∠2 =∠3 =50°. 应选:A考点:1、三角形的外角 ,2、平行线的性质 3.以下计算正确的选项是 ( )A .()a b a b --=--B .224a a a +=C .236a a a ⋅= D .()2224ab a b =【答案】 D考点:1、整式的加减 ,2、同底数幂相乘 ,2、积的乘方4.不等式组21,512x x ->⎧⎪⎨+≥⎪⎩①②中 ,不等式①和②的解集在数轴上表示正确的选项是 ( )A .B .C .D . 【答案】B 【解析】试题分析:解不等式①可得x <1 ,解不等式②得x ≥ -3 ,根据不等式解集确实定法 "都大取大 ,都小取小 ,大小小大取中间 ,大大小小无解了〞 ,得到不等式组的解集为: -3≤x <1 ,由此可知用数轴表示为:考点:解不等式组5.如下列图的几何体是由五个小正方体组成的 ,它的左视图是 ( )A. B. C. D.【答案】D【解析】试题分析:根据三视图的意义 ,该几何体的三视图如下:主视图:;俯视图:;左视图:.应选:D考点:三视图6.小明和小华玩 "石头、剪子、布〞的游戏.假设随机出手一次 ,那么小华获胜的概率是 ( )A.23B.12C.13D.29【答案】C考点:概率7.一个多边形的内角和是外角和的2倍 ,这个多边形是 ( ) A.四边形 B.五边形 C.六边形 D.八边形【解析】试题分析:根据多边形的外角和为360° ,可知其内角和为720° ,因此可根据多边形的内角和公式 (n -2 )·180° =720° ,解得n =6 ,故是六边形.应选:C考点:多边形的内外角和x个 ,那么所列方程是 ( )A.90606x x=+B.90606x x=+C.90606x x=-D.90606x x=-【答案】B考点:分式方程的应用9.某公司有15名员工 ,他们所在部门及相应每人所创年利润如下表所示:部门人数每人所创年利润 (单位:万元 )A 1 10B 3 8C7 5D 4 3这15名员工每人所创年利润的众数、中位数分别是 ( )A.10 ,5 B.7 ,8 C.5 ,6.5 D.5 ,5【答案】D【解析】试题分析:根据表格可知出现最||多的是5万元 ,共有7次 ,因此众数是5 ,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3 ,中位数是中间的一个 ,是5万元 ,应选:D考点:众数与中位数10.如图 ,AB 是O 的直径 ,BT 是O 的切线 ,假设45ATB ∠=︒ ,2AB = ,那么阴影局部的面积是( )A .2B .3124π-C .1D .1124π+ 【答案】C考点:1、圆的切线 ,2、圆周角定理 ,3、等腰直角三角形 11.将一些相同的 "〞按如下列图摆放 ,观察每个图形中的 "〞的个数 ,假设第n 个图形中 "〞的个数是78 ,那么n 的值是 ( )A .11B .12C .13D .14 【答案】B 【解析】试题分析:第|一个图形有1个○ , 第二个图形有1 +2 =3个○ ,第三个图形有1 +2 +3 =6个○ , 第四个图形有1 +2 +3 +4 =10个○ , ……第n 个图形有1 +2 +3 +…… +n =(1)2n n +个○ , 故(1)2n n + =78 ,解得n =12或n = -13 (舍去 ). 应选:B 考点:规律探索12.在ABC 中 ,点D 是边BC 上的点 (与B 、C 两点不重合 ) ,过点D 作DE AC ∥ ,DF AB ∥ ,分别交AB ,AC 于E 、F 两点 ,以下说法正确的选项是 ( )A .假设AD BC ⊥ ,那么四边形AEDF 是矩形B .假设AD 垂直平分BC ,那么四边形AEDF 是矩形 C .假设BD CD = ,那么四边形AEDF 是菱形 D .假设AD 平分BAC ∠ ,那么四边形AEDF 是菱形 【答案】D考点:特殊平行四边形的判定13.足球运发动将足球沿与地面成一定角度的方向踢出 ,足球飞行的路线是一条抛物线 ,不考虑空气阻力 ,足球距离地面的高度h (单位:m )与足球被踢出后经过的时间t (单位:s )之间的关系如下表:t 0 1 2 3 4 5 6 7 … h8141820201814…以下结论:①足球距离地面的最||大高度为20m ;②足球飞行路线的对称轴是直线92t =;③足球被踢出9s 时落地;④足球被踢出1.5s 时 ,距离地面的高度是11m . 其中正确结论的个数是 ( )A .1B .2C .3D .4 【答案】B考点:二次函数的对称性14.如图 ,在平面直角坐标系中 ,反比例函数ky x=(0x > )的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点 ,OMN P 在x 轴上 ,那么PM PN +的最||小值是 ( )A .62B .10C .226D .229【答案】C 【解析】试题分析:由正方形OABC 的边长为6可得M 的坐标为 (6 ,6k ) ,N 的坐标为 (6k,6 ) ,因此可得BN =6 -6k ,BM =6 -6k ,然后根据△OMN 的面积为10 ,可得21116666(6)10262626k k k ⨯-⨯⨯-⨯⨯-⨯-= ,解得k =24 ,得到M (6 ,4 )和N (4 ,6 ) ,作M 关于x 轴的对称点M ′ ,连接NM ′交x 轴于P ,那么M ′N 的长 =PM +PN 的值最||小 ,最||后由AM =AM ′ =4 ,得到BM ′ =10 ,BN =2 ,根据勾股定理求得NM ′ 22=226BM BN +应选:C考点:1、反比例函数与正方形 ,2、三点之间的最||小值第二卷 (共78分 )二、填空题 (每题3分 ,总分值15分 ,将答案填在答题纸上 )15.分解因式:29m m -= . 【答案】()()33m m m +-考点:因式分解16.AB CD ∥ ,AD 与BC 相交于点O .假设23BO OC = ,10AD = ,那么AO = .【答案】4 【解析】试题分析:根据平行线分线段成比例定理 ,由AB ∥CD 可得BO OAOC OD= ,然后根据AD =10 ,可知OD =10 -OA ,代入可得2103BO OA OC OA ==- ,解得OA =4.故答案为:4考点:平行线分线段成比例定理17.计算:22x y xy y x x x ⎛⎫--+-= ⎪⎝⎭.【答案】1x y- 【解析】试题分析:先算括号内的减法 ,把除法变成乘法 ,再根据分式的乘法法那么进行计算:原式 =x y x-÷222x xy y x -+=x yx -•2()x x y - =1x y- , 故答案为:1x y-. 考点:分式的混合运算 18.在ABCD 中 ,对角线AC ,BD 相交于点O .假设4AB = ,10BD = ,3sin 5BDC ∠=,那么ABCD 的面积是 .【答案】24 【解析】试题分析:作OE ⊥CD 于E ,由平行四边形的性质得出OA =OC ,OB =OD =12BD =5 ,CD =AB =4 ,由sin ∠BDC =35,证出AC ⊥CD ,OC =3 ,AC =2OC =6 ,得出▱ABCD 的面积 =CD•AC =24. 故答案为:24.考点:1、平行四边形的性质 ,2、三角函数 ,3、勾股定理19.在平面直角坐标系中 ,如果点P 坐标为(),m n ,向量OP 可以用点P 的坐标表示为(),OP m n =. :()11,OA x y = ,()22,OB x y = ,如果12120x x y y ⋅+⋅= ,那么OA 与OB 互相垂直. 以下四组向量:①()2,1OC = ,()1,2OD =-;②()cos30,tan 45OE =︒︒ ,()1,sin 60OF =︒; ③()32,2OG =-- ,132,2OH ⎛⎫=+ ⎪⎝⎭;④()0,2OM π=,()2,1ON =-.其中互相垂直的是 (填上所有正确答案的序号 ). 【答案】①③④ 【解析】考点:1、平面向量 ,2、零指数幂 ,3、解直角三角形三、解答题 (本大题共7小题 ,共63分.解容许写出文字说明、证明过程或演算步骤. )20.计算:11122cos4582-⎛⎫-+︒-+ ⎪⎝⎭.【答案】1【解析】试题分析:根据绝||对值的意义、特殊角的三角函数值、二次根式的化简和负指数幂的运算,分别求得每项的值,再进行计算即可.试题解析:11 132cos4582-⎛⎫-+-+ ⎪⎝⎭22122222=-+⨯-+212222=-+-+=1.考点:1、实数的运算;2、负整数指数幂;3、特殊角的三角函数值21.为了解某校学生对<最||强大脑>、<朗读者>、<中|国诗词大会>、<出彩中|国人>四个电视节目的喜爱情况 ,随机抽取了x名学生进行调查统计 (要求每名学生选出并且只能选出一个自己最||喜爱的节目 ) ,并将调查结果绘制成如下统计图表:根据以上提供的信息 ,解答以下问题:(1 )x=______ ,a=______ ,b=______;(2 )补全上面的条形统计图;(3 )假设该校共有学生1000名.根据抽样调查结果 ,估计该校最||喜爱<中|国诗词大会>节目的学生有多少名.【答案】 (1 )50,20,30; (2 )图形见解析 (3 )400【解析】试题分析: (1 )根据最||强大脑的人数除以占的百分比确定出x 的值 ,进而求出a 与b 的值即可; (2 )根据a 的值 ,补全条形统计图即可;(3 )由中|国诗词大会的百分比乘以1000即可得到结果.试题解析: (1 )50,20,30.(2 )如图:(3 )100040%400⨯= (名 )答:该校有400名学生最||喜爱<中|国诗词大会>.考点:1、条形统计图;2、用样本估计总体;3、统计表22.如图 ,两座建筑物的水平距离30m BC = ,从A 点测得D 点的俯角α为30︒ ,测得C 点的俯角β为60︒ ,求这两座建筑物的高度.【答案】 (1 )两建筑物的高度分别是3m 和3m【解析】试题分析:延长CD ,交AE 于点E ,可得DE ⊥AE ,在直角三角形ABC 中 ,由题意确定出AB 的长 ,进而确定出EC 的长 ,在直角三角形AED 中 ,由题意求出ED 的长 ,由EC ﹣ED 求出DC 的长即可.试题解析:如图 ,过点A 作AE CD ⊥ ,垂足为E ,在ADE∆中 ,90AED ∠=,30AE = ,∴3tan 3030103DE AE =⋅== ,在ACE ∆中 ,90,30AEC AE ∠==,∴tan 60303CE AE =⋅=,∴303AB CE == ,303103203CD CE DE =-=-=.因此 ,两建筑物的高度分别是303m 和203m .考点:解直角三角形的应用﹣仰角俯角问题23.如图 ,BAC ∠的平分线交ABC 的外接圆于点D ,ABC ∠的平分线交AD 于点E .(1 )求证:DE DB =;(2 )假设90BAC ∠=︒ ,4BD = ,求ABC 外接圆的半径.【答案】【解析】试题分析: (1 )由角平分线得出∠ABE =∠CBE ,∠BAE =∠CAD ,得出BD CD = ,由圆周角定理得出∠DBC =∠CAD ,证出∠DBC =∠BAE ,再由三角形的外角性质得出∠DBE =∠DEB ,即可得出DE =DB ;(2 )由 (1 )得:BD CD = ,得出CD =BD =4 ,由圆周角定理得出BC 是直径 ,∠BDC =90° ,由勾股定理求出BC 22BD CD + 2 ,即可得出△ABC 外接圆的半径.试题解析: (1 )AD 平分BAC ∠ ,BE 平分ABC ∠ ,,BAD CAD ABE CBE ∴∠=∠∠=∠ ,又BED ABE BAD ∠=∠+∠ ,DBE DBC CBE ∠=∠+∠ ,DBC DAC ∠=∠,BED DBE ∴∠=∠.DE DB ∴=.(2 )解:连接CD ,90BAC ∠= ,BC ∴是圆的直径.90BDC ∴∠= ,90BDC ∴∠=.BAD CAD ∠=∠ ,BD CD ∴= ,BD CD ∴= ,BCD ∴∆是等腰直角三角形.4BD = ,42BC ∴=.ABC ∴∆的外接圆的半径为22.考点:1、三角形的外接圆的性质 ,2、圆周角定理 ,3、三角形的外角性质 ,4、勾股定理24.某市为节约水资源 ,制定了新的居民用水收费标准.按照新标准 ,用户每月缴纳的水费y (元 )与每月用水量x (3m )之间的关系如下列图.(1 )求y 关于x 的函数解析式;(2 )假设某用户二、三月份共用水340m (二月份用水量不超过325m ) ,缴纳水费79.8元 ,那么该用户二、三月份的用水量各是多少3m ?【答案】 (1 ) 1.8,0152.49,15x x y x x <<⎧=⎨-≥⎩ (2 )二、三月份用水量分别是312m 和328m 【解析】试题分析: (1 )根据函数图象可以分别设出各段的函数解析式 ,然后根据函数图象中的数据求出相应的函数解析式;(2 )根据题意对x 进行取值进行讨论 ,从而可以求得该用户二、三月份的用水量各是多少m 3. 试题解析: (1 )当015x <<时 ,设y mx = ,那么1527m = ,所以 1.8m = , 1.8y x =当15x ≥时 ,设y kx b =+ ,那么15272039k b k b +=⎧⎨+=⎩ ,解得 2.49k b =⎧⎨=-⎩ ,所以y 与x 的关系式是 1.8,0152.49,15x x y x x <<⎧=⎨-≥⎩.考点:一次函数的应用25.数学课上 ,张老师出示了问题:如图1 ,AC 、BD 是四边形ABCD 的对角线 ,假设ACB ACD ∠=∠=60ABD ADB ∠=∠=︒ ,那么线段BC ,CD ,AC 三者之间有何等量关系 ? 经过思考 ,小明展示了一种正确的思路:如图2 ,延长CB 到E ,使BE CD = ,连接AE ,证得ABE ADC ≌ ,从而容易证明ACE 是等边三角形 ,故AC CE = ,所以AC BC CD =+.小亮展示了另一种正确的思路:如图3 ,将ABC 绕着点A 逆时针旋转60︒ ,使AB 与AD 重合 ,从而容易证明ACF 是等比三角形 ,故AC CF = ,所以AC BC CD =+.在此根底上 ,同学们作了进一步的研究:(1 )小颖提出:如图4 ,如果把 "ACB ACD ∠=∠=60ABD ADB ∠=∠=︒〞改为"ACB ACD ∠=∠=45ABD ADB ∠=∠=︒〞 ,其它条件不变 ,那么线段BC ,CD ,AC 三者之间有何等量关系 ?针对小颖提出的问题 ,请你写出结论 ,并给出证明.(2 )小华提出:如图5 ,如果把 "ACB ACD ∠=∠=60ABD ADB ∠=∠=︒〞改为"ACB ACD ∠=∠=ABD ADB α∠=∠=〞 ,其它条件不变 ,那么线段BC ,CD ,AC 三者之间有何等量关系 ?针对小华提出的问题 ,请你写出结论 ,不用证明.【答案】2AC (2 )BC +CD =2AC•cosα【解析】试题分析: (1 )先判断出∠ADE =∠ABC ,即可得出△ACE 是等腰三角形 ,再得出∠AEC =45° ,即可得出等腰直角三角形 ,即可; (判断∠ADE =∠ABC 也可以先判断出点A ,B ,C ,D 四点共圆 )(2 )先判断出∠ADE =∠ABC ,即可得出△ACE 是等腰三角形 ,再用三角函数即可得出结论. 试题解析:2AC ;理由:如图1 ,延长CD 至||E ,使DE =BC ,∵∠ABD =∠ADB =45° ,∴AB =AD ,∠BAD =180°﹣∠ABD ﹣∠ADB =90° ,∵∠ACB =∠ACD =45° ,∴∠ACB +∠ACD =45° ,∴∠BAD +∠BCD =180° ,∴∠ABC +∠ADC =180° ,∵∠ADC +∠ADE =180° ,∴∠ABC =∠ADE ,在△ABC 和△ADE 中 ,AB AD ABC ADE BC DE =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△ADE (SAS ) ,∴∠ACB =∠AED =45° ,AC =AE ,∴△ACE是等腰直角三角形 ,∴CE =2AC ,∵CE =CE +DE =CD +BC ,∴BC +CD =2AC;(2 )BC +CD =2AC•cosα.理由:如图2 ,延长CD至||E ,使DE =BC ,∵∠ABD =∠ADB =α ,∴AB =AD ,∠BAD =180°﹣∠ABD﹣∠ADB =180°﹣2α ,∵∠ACB =∠ACD =α ,∴∠ACB +∠ACD =2α ,∴∠BAD +∠BCD =180° ,∴∠ABC +∠ADC =180° ,∵∠ADC +∠ADE =180° ,∴∠ABC =∠ADE ,在△ABC和△ADE中 ,AB ADABC ADE BC DE=⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△ADE (SAS ) ,∴∠ACB =∠AED =α ,AC =AE ,∴∠AEC =α ,过点A作AF⊥CE于F ,∴CE =2CF ,在Rt △ACF 中 ,∠ACD =α ,CF =AC•cos∠ACD =AC•cosα ,∴CE =2CF =2AC•cosα ,∵CE =CD +DE =CD +BC ,∴BC +CD =2AC•cosα.考点:1、几何变换综合题 ,2、全等三角形的判定 ,3、四边形的内角和 ,4、等腰三角形的判定和性质26.如图 ,抛物线23y ax bx =+-经过点()2,3A - ,与x 轴负半轴交于点B ,与y 轴交于点C ,且3OC OB =.(1 )求抛物线的解析式;(2 )点D 在y 轴上 ,且BDO BAC ∠=∠ ,求点D 的坐标;(3 )点M 在抛物线上 ,点N 在抛物线的对称轴上 ,是否存在以点A ,B ,M ,N 为顶点的四边形是平行四边形 ?假设存在 .求出所有符合条件的点M 的坐标;假设不存在 ,请说明理由.【答案】 (1 )y =x 2﹣2x ﹣3; (2 )D 1 (0 ,1 ) ,D 2 (0 ,﹣1 ); (3 )存在 ,M (4 ,5 )或 (﹣2 ,5 )或 (0 ,﹣3 )【解析】试题分析: (1 )待定系数法即可得到结论;(2 )连接AC ,作BF ⊥AC 交AC 的延长线于F ,根据条件得到AF ∥x 轴 ,得到F (﹣1 ,﹣3 ) ,设D (0 ,m ) ,那么OD =|m|即可得到结论;(3 )设M (a ,a 2﹣2a ﹣3 ) ,N (1 ,n ) ,①以AB 为边 ,那么AB ∥MN ,AB =MN ,如图2 ,过M 作ME ⊥对称轴y于E ,AF⊥x轴于F ,于是得到△ABF≌△NME ,证得NE =AF =3 ,ME =BF =3 ,得到M (4 ,5 )或 (﹣2 ,5 );②以AB为对角线 ,BN =AM ,BN∥AM ,如图3 ,那么N在x轴上 ,M与C重合 ,于是得到结论.(2 )设连接AC ,作BF⊥AC交AC的延长线于F ,∵A (2 ,﹣3 ) ,C (0 ,﹣3 ) ,∴AF∥x轴 ,∴F (﹣1 ,﹣3 ) ,∴BF =3 ,AF =3 ,∴∠BAC =45° ,设D (0 ,m ) ,那么OD =|m| ,∵∠BDO =∠BAC ,∴∠BDO =45° ,∴OD =OB =1 ,∴|m| =1 ,∴m =±1 ,∴D1 (0 ,1 ) ,D2 (0 ,﹣1 );(3 )设M (a ,a2﹣2a﹣3 ) ,N (1 ,n ) ,①以AB为边 ,那么AB∥MN ,AB =MN ,如图2 ,过M作ME⊥对称轴y于E ,AF⊥x轴于F ,那么△ABF≌△NME ,∴NE =AF =3 ,ME =BF =3 ,∴|a﹣1| =3 ,∴a =4或a =﹣2 ,∴M (4 ,5 )或 (﹣2 ,5 );②以AB为对角线 ,BN =AM ,BN∥AM ,如图3 ,那么N在x轴上 ,M与C重合 ,∴M (0 ,﹣3 ) ,综上所述 ,存在以点A ,B ,M ,N为顶点的四边形是平行四边形 ,M (4 ,5 )或 (﹣2 ,5 )或 (0 ,﹣3 ).公众号:惟微小筑考点:1、二次函数的综合 ,2、待定系数法求二次函数的解析式 ,3、全等三角形的判定和性质 ,4、平行四边形的判定和性质。
山东省临沂市2017年中考数学真题试题(含解析)

uu u r
uu u r
uቤተ መጻሕፍቲ ባይዱr
uu u r
uur
uu u r
uuu r uu u r
uuu r
uuu r
uuu r
uuu r 1 3 2, 2 , OH 3 2, ; 2
④ OM
uuur
, 2 , ON 2, 1 .
0
uuu r
其中互相垂直的是 【答案】①③④ 【解析】
山东省临沂市 2017 年中考数学真题试题
第Ⅰ卷(共 42 分) 一、选择题:本大题共 14 个小题,每小题 3 分,共 42 分.在每小题给出的四个选项中,只有一项是符合题 目要求的.
1 的相反数是( ) 2007 1 1 A. B. 2007 2007
1. 【答案】A 【解析】
C.2017
90 60 x x6
B.
90 60 x6 x
C.
90 60 x6 x
D.
90 60 x x6
【答案】B
考点:分式方程的应用 9.某公司有 15 名员工,他们所在部门及相应每人所创年利润如下表所示: 部门 人数 1 3 7 4 每人所创年利润(单位:万元) 10 8 5 3 ) D.5,5
B.12
C.13
D.14
试题分析:第一个图形有 1 个○, 第二个图形有 1+2=3 个○, 第三个图形有 1+2+3=6 个○, 第四个图形有 1+2+3+4=10 个○, ……
第 n 个图形有 1+2+3+……+n= 故
n(n 1) 个○, 2
n(n 1) =78,解得 n=12 或 n=-13(舍去). 2
2017年山东省临沂市中考数学试卷(解析版)

C.D .如图所示的几何体是由五个小正方体组成的,它的左视图是(A . B. C. D.2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,每小题3分,共42分) 1Jp —的相反数是( )A .B .-二C 2017D --20172•如图,将直尺与含30°角的三角尺摆放在一起,若/ 仁20°,则/2的度数是3•下列计算正确的是( )A . — ( a - b ) =- a - b B. a 2+a 2=a 4 C . a 2?a 3=a 6 D . (ab 2)r2-K>i, CD4 .不等式组 計5②中,不等式①和②的解集在数轴上表示正确的是 ( )( )D . 805.6.小明和小华玩石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概 率是( )A .7.—个多边形的内角和是外角和的 2倍,则这个多边形是( A .四边形 B .五边形 C.六边形 D .八边形8.甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小元) 10这15名员工每人所创年利润的众数、中位数分别是( A . 10,5 B . 7,8C. 5,6.5 D . 5,510.如图,AB 是。
O 的直径,BT 是。
O 的切线,若/ ATB=45, AB=2,贝U 阴影部11.将一些相同的 O”按如图所示摆放,观察每个图形中的 个图形中O”的个数是78,则n 的值是()D .时做x 个,那么所列方程是( A .90 60K +SB.90x+66Q C.) x-6D .9.某公司有 部门15名员工,他们所在部门及相应每人所创年利润如下表所示: 人数每人创年利润(万O”的个数,若第n90分的面积是( 卫I B112•在△ ABC 中,点D 是边BC 上的点(与B , C 两点不重合),过点D 作DE// AC, DF// AB,分别交AB, AC 于E , F 两点,下列说法正确的是()D CA. 若AD 丄BC,则四边形AEDF 是矩形B. 若AD 垂直平分BC,则四边形AEDF 是矩形 C •若BD=CD 则四边形AEDF 是菱形 D .若AD 平分/ BAC,则四边形AEDF 是菱形 13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的咼度 h (单位:m ) 与足球被踢出后经过的时间t (单位:S )之间的关系如下表:t1234567…h 08 14 18 20 20 1814 … F 列结论:①足球距离地面的最大高度为20m ;②足球飞行路线的对称轴是直线 t==;③足球被踢出9s 时落地;④足球被踢出1.5s 时,距离地面的高度是11m , 其中正确结论的个数是( )A . 1 B. 2 C. 3 D . 414.如图,在平面直角坐标系中,反比例函数 y=p (x >0)的图象与边长是6 的正方形OABC 的两边AB, BC 分别相交于M , N 两点,△ OMN 的面积为10.若 动点P 在x 轴上,则PM+PN 的最小值是( )厂\v-0P貝A. 6回B. 10C. 2西D. 2画、填空题(本大题共5小题,每小题3分,共15分)15 .分解因式:m3- 9m= _______ .16.已知AB// CD, AD与BC相交于点0.若器=f , AD=10,贝U AO= _________18. 在?ABCD中,对角线AC, BD相交于点O,若AB=4, BD=10, sin/19. 在平面直角坐标系中,如果点P坐标为(m, n),向量园可以用点P的坐标表示为| .= (m, n).已知:=(X1, y1),區=(x2, y2),如果X1?X2+y1?y2=0, 那么匚与—互相垂直,下列四组向量:①二=(2, 1), □= (- 1, 2);②吶二(cos30° tan45°,匚=(1, sin60);BDCd,③屈=(丽-丽,-2),园=(唾咆,舟;④風=(n, 2);H = (2,- 1).其中互相垂直的是_______ (填上所有正确答案的符号)•三、解答题(本大题共7小题,共63分)20 •计算:| 1 - ^]||+2cos45 22+ (目)1.21. 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑510%朗读者15b%中国诗词大会a40%出彩中国人1020%根据以上提供的信息,解答下列问题:(1)________ x= ________ ,a= ______ ,b= ;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.尹主星営罠汩芒巨人擞崔倾计图22. 如图,两座建筑物的水平距离BC=30m从A点测得D点的俯角a为30°105 OS惧营中汙大逮=且*■誓国■出申人测得C点的俯角B为60°,求这两座建筑物的高度.23. 如图,/ BAC的平分线交△ ABC的外接圆于点D,/ ABC的平分线交AD于点E,(1)求证:DE=DB(2)若/ BAC=90, BD=4,求厶ABC外接圆的半径.24. 某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y (元)与每月用水量x (m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?25. 数学课上,张老师出示了问题:如图1, AC, BD是四边形ABCD的对角线,若/ ACB=/ ACD=Z ABD=/ ADB=60 ,则线段BC, CD, AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD连接AE,证得△ ABE^A ADC,从而容易证明△ ACE是等边三角形,故AC=CE所以AC=B(+CD.小亮展示了另一种正确的思路:如图3,将厶ABC绕着点A逆时针旋转60°使AB与AD重合,从而容易证明厶ACF是等边三角形,故AC=CF所以AC=BGCD. 在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把2 ACB=/ ACD=Z ABD=Z ADB=60改为7 ACB= / ACD2 ABD=/ ADB=45 :其它条件不变,那么线段BC, CD, AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把2 ACB=/ ACD=Z ABD=/ ADB=60改为/ ACB= / ACD2 ABD=2 ADB a:,其它条件不变,那么线段BC, CD, AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26. 如图,抛物线y=a«+bx-3经过点A (2, - 3),与x轴负半轴交于点B,与y轴交于点C,且0C=30B(1)求抛物线的解析式;(2)点D在y轴上,且2 BDO=2 BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A, B, M , N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.2017年山东省临沂市中考数学试卷参考答案与试题解析一、选择题(本大题共14小题,每小题3分,共42分) 1.-,[.的相反数是( )A•上 B .-——C . 2017 D .- 2017 【考点】14:相反数.【分析】直接利用相反数的定义分析得出答案. 【解答】解:-丁一的相反数是:匕]|故选:A .2. 如图,将直尺与含30°角的三角尺摆放在一起,若/ 仁20°,则/2的度数是【考点】JA 平行线的性质;IL :余角和补角.【分析】首先根据三角形外角的性质求出/ BEF 的度数,再根据平行线的性质得 到/ 2的度数.【解答】解:I/ BEF >^AEF 的外角,/仁20°, / F=30°, •••/ BEF / 1+/ F=50°, ••• AB// CD,•••/ 2=/ BEF=50, 故选A .( )D . 803•下列计算正确的是( )A. — ( a - b ) =- a - bB. a 2+a 2=a 4 C . a 2?a 3=a 6 D . (ab 2)【考点】47:幕的乘方与积的乘方;44:整式的加减;46:同底数幕的乘法. 【分析】根据去括号、同底数幕的乘法底数不变指数相加,积的乘方,可得答案. 【解答】解:A 、括号前是负号,去括号全变号,故 A 不符合题意; B 、 不是同底数幕的乘法指数不能相加,故 B 不符合题意; C 同底数幕的乘法底数不变指数相加,故 C 不符合题意; D 、积的乘方等于乘方的积,故 D 符合题意; 故选:D .C2-z>l, ®4 .不等式组\計5” ②中,不等式①和②的解集在数轴上表示正确的是【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小 小大中间找、大大小小无解了确定不等式组的解集【解答】解:解不等式①,得:x v 1, 解不等式②,得:x >- 3, 则不等式组的解集为-3<x v 1, 故选:B.( )C.5•如图所示的几何体是由五个小正方体组成的,它的左视图是(6.小明和小华玩石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概 率是()A . F B.二 C 2 D .目【考点】X6:列表法与树状图法.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华•••共有9种等可能的结果,小华获胜的情况数是 3种, •••小华获胜的概率是: 故选C.【分析】 U2:简单组合体的三视图. 根据三视图定义分别作出三视图即可判断. 解:该几何体的三视图如下:【考点】【解答】故选:D .;俯视图:;左视图:获胜的情况数,再利用概率公式即可求得答案.7•—个多边形的内角和是外角和的 2倍,则这个多边形是( A .四边形 B .五边形 C.六边形 D .八边形 【考点】L3:多边形内角与外角.【分析】此题可以利用多边形的外角和和内角和定理求解. 【解答】解:设所求正n 边形边数为n ,由题意得 (n - 2) ?180° =36& 2 解得n=6. 则这个多边形是六边形. 故选:C.8.甲、乙二人做某种机械零件,已知甲每小时比乙多做 6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小 时做x 个,那么所列方程是()【考点】B6:由实际问题抽象出分式方程.【分析】根据甲乙的效率,可设未知数,根据甲乙的工作时间,可列方程. 【解答】解:设乙每小时做x 个,甲每小时做(x+6)个, 根据甲做90个所用时间与乙做60个所用时间相等,得I ,故选:B.9.某公司有 15名员工, 他们所在部门及相应每人所创年利润如下表所示: 部门人数 每人创年利润(万元)A 1 10B 3 8C 7 5 D43第12页(共31页)这15名员工每人所创年利润的众数、中位数分别是( )A . 10, 5B . 7, 8C. 5, 6.5 D . 5, 5A .【考点】W5:众数;W4:中位数.【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,•••这组数据的众数是5,中位数是5,故选D.10.如图,AB是。
山东省临沂市2017年中考数学试卷(含解析)

2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,毎小题3分,共42分)在每小题所给的四个选项中.只有一项是符合题目要求的。
1、(2017•临沂)下列各数中,比﹣1小的数是()A、0B、1C、﹣2D、2考点:有理数大小比较。
专题:探究型。
分析:根据有理数比较大小的法则进行比较即可.解答:解:∵﹣1是负数,∴﹣1<0,故A错误;∵2>1>0,∴2>1>0>﹣1,故B、D错误;∵|﹣2|>|﹣1|,∴﹣2<﹣1,故C正确.故选C.点评:本题考查的是有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.2、(2017•临沂)下列运算中正确的是()A、(﹣ab)2=2a2b2B、(a+b)2=a2+1C、a6÷a2=a3D、2a3+a3=3a3考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方。
分析:积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘;完全平方公式:两数和的平方等于它们的平方和加上它们积的2倍;同底数幂的除法,底数不变指数相减;合并同类项,系数相加字母和字母的指数不变;根据法则一个个筛选.解答:解:A、(﹣ab)2=(﹣1)2a2b2=a2b2,故此选项错误;B、(a+b)2=a2+2ab+b2,故此选项错误;C、a6÷a2=a6﹣2=a4,故此选项错误;D、2a3+a3=(2+1)a3=3a3,故此选项正确.故选D.点评:此题主要考查了积的乘方,完全平方公式,同底数幂的除法,合并同类项的计算,一定要记准法则才能做题.3、(2017•临沂)如图.己知AB∥CD,∠1=70°,则∠2的度数是()A、60°B、70°C、80°D、110考点:平行线的性质。
分析:由AB∥CD,根据两直线平行,同位角相等,即可求得∠2的度数,又由邻补角的性质,即可求得∠2的度数.解答:解:∵AB∥CD,∴∠1=∠3=70°,∵∠2+∠3=180°,∴∠2=110°.故选D.点评:此题考查了平行线的性质.注意数形结合思想的应用.4、(2017•临沂)计算﹣6+的结果是()A、3﹣2B、5﹣C、5﹣D、2考点:二次根式的加减法。
山东省临沂市中考数学试卷及答案与解析

山东省临沂市中考数学试卷及答案与解析精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-2017年山东省临沂市中考数学试卷参考答案与试题解析一、选择题(本大题共14小题,每小题3分,共42分)1.(3分)(2017?临沂)﹣的相反数是()A.B.﹣C.2017 D.﹣2017【解答】解:﹣的相反数是:.故选:A.2.(3分)(2017?临沂)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,∴∠BEF=∠1+∠F=50°,∵AB∥CD,∴∠2=∠BEF=50°,故选A.3.(3分)(2017?临沂)下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4C.a2a3=a6D.(ab2)2=a2b4【解答】解:A、括号前是负号,去括号全变号,故A不符合题意;B、不是同底数幂的乘法指数不能相加,故B不符合题意;C、同底数幂的乘法底数不变指数相加,故C不符合题意;D、积的乘方等于乘方的积,故D符合题意;故选:D.4.(3分)(2017?临沂)不等式组中,不等式①和②的解集在数轴上表示正确的是()A.B.C.D.【解答】解:解不等式①,得:x<1,解不等式②,得:x≥﹣3,则不等式组的解集为﹣3≤x<1,故选:B.5.(3分)(2017?临沂)如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C.D.【解答】解:该几何体的三视图如下:主视图:;俯视图:;左视图:,故选:D.6.(3分)(2017?临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.【解答】解:画树状图得:∵共有9种等可能的结果,小华获胜的情况数是3种,∴小华获胜的概率是:=.故选C.7.(3分)(2017?临沂)一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形【解答】解:设所求正n边形边数为n,由题意得(n﹣2)180°=360°×2解得n=6.则这个多边形是六边形.故选:C.8.(3分)(2017?临沂)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.=B.=C.=D.=【解答】解:设乙每小时做x个,甲每小时做(x+6)个,根据甲做90个所用时间与乙做60个所用时间相等,得=,故选:B.9.(3分)(2017?临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A 1 10B 3 8C 7 5D 4 3这15名员工每人所创年利润的众数、中位数分别是()A.10,5 B.7,8 C.5,D.5,5【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,∴这组数据的众数是5,中位数是5,故选D.10.(3分)(2017?临沂)如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A.2 B.﹣πC.1 D.+π【解答】解:∵BT是⊙O的切线;设AT交⊙O于D,连结BD,∵AB是⊙O的直径,∴∠ADB=90°,而∠ATB=45°,∴△ADB、△BDT都是等腰直角三角形,∴AD=BD=TD=AB=,∴弓形AD的面积等于弓形BD的面积,∴阴影部分的面积=S△BTD=××=1.故选C.11.(3分)(2017?临沂)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是()A.11 B.12 C.13 D.14【解答】解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n个图形有1+2+3+…+n=个小圆;∵第n个图形中“○”的个数是78,∴78=,解得:n1=12,n2=﹣13(不合题意舍去),故选:B.12.(3分)(2017?临沂)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形【解答】解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.13.(3分)(2017?临沂)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h (单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t 0 1 2 3 4 5 6 7 …h 0 8 14 18 20 20 18 14 …下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.4【解答】解:由题意,抛物线的解析式为y=ax(x﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣)2+,∴足球距离地面的最大高度为,故①错误,∴抛物线的对称轴t=,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=时,y=,故④错误.∴正确的有②③,故选B.14.(3分)(2017?临沂)如图,在平面直角坐标系中,反比例函数y=(x >0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6B.10 C.2D.2【解答】解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M(6,),N(,6),∴BN=6﹣,BM=6﹣,∵△OMN的面积为10,∴6×6﹣×6×﹣6×﹣×(6﹣)2=10,∴k=24,∴M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′===2,故选C.二、填空题(本大题共5小题,每小题3分,共15分)15.(3分)(2017?临沂)分解因式:m3﹣9m=m(m+3)(m﹣3).【解答】解:m3﹣9m,=m(m2﹣9),=m(m+3)(m﹣3).故答案为:m(m+3)(m﹣3).16.(3分)(2017?临沂)已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=4.【解答】解:∵AB∥CD,∴==,即=,解得,AO=4,故答案为:4.17.(3分)(2017?临沂)计算:÷(x﹣)=.【解答】解:原式=÷==,故答案为:.18.(3分)(2017临沂)在ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=,则?ABCD的面积是24.【解答】解:作OE⊥CD于E,如图所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD=BD=5,CD=AB=4,∵sin∠BDC==,∴OE=3,∴DE==4,∵CD=4,∴点E与点C重合,∴AC⊥CD,OC=3,∴AC=2OC=6,∴ABCD的面积=CDAC=4×6=24;故答案为:24.19.(3分)(2017?临沂)在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1x2+y1y2=0,那么与互相垂直,下列四组向量:①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是①③④(填上所有正确答案的符号).【解答】解:①因为2×(﹣1)+1×2=0,所以与互相垂直;②因为cos30°×1+tan45°?sin60°=×1+1×=≠0,所以与不互相垂直;③因为(﹣)(+)+(﹣2)×=3﹣2﹣1=0,所以与互相垂直;④因为π0×2+2×(﹣1)=2﹣2=0,所以与互相垂直.综上所述,①③④互相垂直.故答案是:①③④.三、解答题(本大题共7小题,共63分)20.(7分)(2017?临沂)计算:|1﹣|+2cos45°﹣+()﹣1.【解答】解:|1﹣|+2cos45°﹣+()﹣1=﹣1+2×﹣2+2=﹣1+﹣2+2=1.21.(7分)(2017?临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行调查统计9要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑 5 10%朗读者 15 b%中国诗词大会 a 40%出彩中国人 10 20%根据以上提供的信息,解答下列问题:(1)x=50,a=20,b=30;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;故答案为:50;20;30;(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:(3)根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名.22.(7分)(2017?临沂)如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.【解答】解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30m,则CD=EC﹣ED=AB﹣ED=30﹣10=20m.23.(9分)(2017?临沂)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.【解答】(1)证明:∵BE平分∠BAC,AD平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.24.(9分)(2017?临沂)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费元,则该用户二、三月份的用水量各是多少m3【解答】解:(1)当0≤x≤15时,设y与x的函数关系式为y=kx,15k=27,得k=,即当0≤x≤15时,y与x的函数关系式为y=,当x>15时,设y与x的函数关系式为y=ax+b,,得,即当x>15时,y与x的函数关系式为y=﹣9,由上可得,y与x的函数关系式为y=;(2)设二月份的用水量是xm3,当15<x≤25时,﹣9+(40﹣x)﹣9=,解得,x无解,当0<x≤15时,+(40﹣x)﹣9=,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m3、28m3.25.(11分)(2017?临沂)数学课上,张老师出示了问题:如图1,AC,BD 是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.【解答】解:(1)BC+CD=AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=45°,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=45°,AC=AE,∴△ACE是等腰直角三角形,∴CE=AC,∵CE=CE+DE=CD+BC,∴BC+CD=AC;(2)BC+CD=2AC?cosα.理由:如图2,延长CD至E,使DE=BC,∵∠ABD=∠ADB=α,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB+∠ACD=2α,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=α,AC=AE,∴∠AEC=α,过点A作AF⊥CE于F,∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC?cos∠ACD=AC?cosα,∴CE=2CF=2AC?cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC?cosα.26.(13分)(2017?临沂)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)由y=ax2+bx﹣3得C(0.﹣3),∴OC=3,∵OC=3OB,∴OB=1,∴B(﹣1,0),把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得,∴,∴抛物线的解析式为y=x2﹣2x﹣3;(2)设连接AC,作BF⊥AC交AC的延长线于F,∵A(2,﹣3),C(0,﹣3),∴AF∥x轴,∴F(﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D(0,m),则OD=|m|,∵∠BDO=∠BAC,∴∠BDO=45°,∴OD=OB=1,∴|m|=1,∴m=±1,∴D1(0,1),D2(0,﹣1);(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,11)或(0,﹣3).。
【真题】2017年山东省临沂市中考数学试卷含答案(word版)

2017年临沂市初中学业水平考试试题数学第Ⅰ卷(共42分)一、选择题:本大题共14个小题,每小题3分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.12007-的相反数是( )A .12007 B .12007- C .2017 D .2017-2.如图,将直尺与含30︒角的三角尺摆放在一起,若120∠=︒,则2∠的度数是()A .50︒B .60︒C .70︒D .80︒3.下列计算正确的是( )A .()a b a b --=--B .224a a a +=C .224a a a ⋅=D .()2224ab a b =4.不等式组21,512x x ->⎧⎪⎨+≥⎪⎩①②中,不等式①和②的解集在数轴上表示正确的是( )A .B .C .D .5.如图所示的几何体是由五个小正方体组成的,它的左视图是( )A .B .C .D .6.小明和小华玩“石头、剪子、布”的游戏.若随机出手一次,则小华获胜的概率是( )A .23B .12C .13D .297.一个多边形的内角和是外角和的2倍,这个多边形是( )A .四边形B .五边形C .六边形D .八边形8.甲、乙二人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x 个,那么所列方程是( )A .90606x x =+B .90606x x =+C .90606x x =-D .90606x x =- 9.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:这15名员工每人所创年利润的众数、中位数分别是( )A .10,5B .7,8C .5,6.5D .5,510.如图,AB 是O e 的直径,BT 是O e 的切线,若45ATB ∠=︒,2AB =,则阴影部分的面积是( )A .2B .3124π-C .1D .1124π+ 11.将一些相同的“d ”按如图所示摆放,观察每个图形中的“d ”的个数,若第n 个图形中“d ”的个数是78,则n 的值是( )A .11B .12C .13D .1412.在ABC V 中,点D 是边BC 上的点(与B 、C 两点不重合),过点D 作DE AC ∥,DF AB ∥,分别交AB ,AC 于E 、F 两点,下列说法正确的是( )A .若AD BC ⊥,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形C .若BD CD =,则四边形AEDF 是菱形D .若AD 平分BAC ∠,则四边形AEDF 是菱形13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h (单位:m )与足球被踢出后经过的时间t (单位:s )之间的关系如下表:下列结论:①足球距离地面的最大高度为20m ;②足球飞行路线的对称轴是直线2t =;③足球被踢出9s 时落地;④足球被踢出1.5s 时,距离地面的高度是11m .其中正确结论的个数是( )A .1B .2C .3D .414.如图,在平面直角坐标系中,发比例函数k y x=(0x >)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,OMN V 的面积为10.若动点P 在x 轴上,则PM PN +的最小值是( )A ..10 C . D .第Ⅱ卷(共78分)二、填空题(每题3分,满分15分,将答案填在答题纸上)15.分解因式:29m m -= .16.已知AB CD ∥,AD 与BC 相交于点O .若23BO OC =,10AD =,则AO = .17.计算:22x y xy y x x x ⎛⎫--+-= ⎪⎝⎭ . 18.在A B C D Y 中,对角线AC ,BD 相交于点O .若4AB =,10BD =,3sin 5BDC ∠=,则A B C D Y 的面积是 .19.在平面直角坐标系中,如果点P 坐标为(),m n ,向量OP uu u r 可以用点P 的坐标表示为(),OP m n =uu u r .已知:()11,OA x y =uu r ,()22,OB x y =uu u r ,如果12120x x y y ⋅+⋅=,那么OA uu r 与OB uu u r 互相垂直.下列四组向量:①()2,1OC =uuu r ,()1,2OD =-uuu r ;②()cos30,tan 45OE =︒︒uu u r ,()1,sin 60OF =︒uu u r ;③)2OG =-uuu r,12OH ⎫=⎪⎭uuu r ; ④()0,2OM π=uuu r ,()2,1ON =-uuu r . 其中互相垂直的是 (填上所有正确答案的序号).三、解答题 (本大题共7小题,共63分.解答应写出文字说明、证明过程或演算步骤.)20.计算:1112cos 452-⎛⎫+︒ ⎪⎝⎭. 21.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:根据以上提供的信息,解答下列问题:(1)x =______,a =______,b =______;(2)补全上面的条形统计图;(3)若该校共有学生1000名.根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.如图,两座建筑物的水平距离30m BC =,从A 点测得D 点的俯角α为30︒,测得C 点的俯角β为60︒,求这两座建筑物的高度.23.如图,BAC ∠的平分线交ABC V 的外接圆于点D ,ABC ∠的平分线交AD 于点E .(1)求证:DE DB =;(2)若90BAC ∠=︒,4BD =,求ABC V 外接圆的半径.24.某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y (元)与每月用水量x (3m )之间的关系如图所示.(1)求y 关于x 的函数解析式;(2)若某用户二、三月份共用水340m (二月份用水量不超过325m ),缴纳水费79.8元,则该用户二、三月份的用水量各是多少3m ?25.数学课上,张老师出示了问题:如图1,AC 、BD 是四边形ABCD 的对角线,若ACB ACD ∠=∠=60ABD ADB ∠=∠=︒,则线段BC ,CD ,AC 三者之间有何等量关系? 经过思考,小明展示了一种正确的思路:如图2,延长CB 到E ,使BE CD =,连接AE ,证得ABE ADC ≌V V ,从而容易证明ACE V 是等边三角形,故AC CE =,所以AC BC CD =+.小亮展示了另一种正确的思路:如图3,将ABC V 绕着点A 逆时针旋转60︒,使AB 与AD 重合,从而容易证明ACF V 是等比三角形,故AC CF =,所以AC BC CD =+.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“ACB ACD ∠=∠=60ABD ADB ∠=∠=︒”改为“ACB ACD ∠=∠=45ABD ADB ∠=∠=︒”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“ACB ACD ∠=∠=60ABD ADB ∠=∠=︒”改为“ACB ACD ∠=∠=ABD ADB α∠=∠=”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.如图,抛物线23y ax bx =+-经过点()2,3A -,与x 轴负半轴交于点B ,与y 轴交于点C ,且3OC OB =.(1)求抛物线的解析式;∠=∠,求点D的坐标;(2)点D在y轴上,且BDO BAC(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在。
2017年山东省临沂市中考数学试卷[1]
![2017年山东省临沂市中考数学试卷[1]](https://img.taocdn.com/s3/m/070a0b9790c69ec3d4bb754f.png)
2017年山东省临沂市中考数学试卷一、选择题(本大题共14小题,每小题3分,共42分)在每小题给出的四个选项中,只有一项是符合题目要求1.(3分)﹣的相反数是()A.B.﹣C.2017D.﹣2017 2.(3分)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60°C.70°D.80°3.(3分)下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4C.a2•a3=a6D.(ab2)2=a2b4 4.(3分)不等式组中,不等式①和②的解集在数轴上表示正确的是()A.B.C.D.5.(3分)如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C.D.6.(3分)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.7.(3分)一个多边形的内角和是外角和的2倍,这个多边形是()A.四边形B.五边形C.六边形D.八边形8.(3分)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.=B.=C.=D.=9.(3分)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人所创年利润(单位:万元)A110B38C75D43这15名员工每人所创年利润的众数、中位数分别是()A.10,5B.7,8C.5,6.5D.5,510.(3分)如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB =2,则阴影部分的面积是()A.2B.﹣πC.1D.+π11.(3分)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是()A.11B.12C.13D.1412.(3分)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D 作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形13.(3分)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t01234567…h08141820201814…下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是()A.1B.2C.3D.414.(3分)如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N两点.△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6B.10C.2D.2二、填空题(本大题共5小题,每小题3分,共15分)15.(3分)分解因式:m3﹣9m=.16.(3分)如图,已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO=.17.(3分)计算:÷(x﹣)=.18.(3分)在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin ∠BDC=,则▱ABCD的面积是.19.(3分)在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P 的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组向量:①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是(填上所有正确答案的符号).三、解答题(本大题共7小题,共63分)20.(7分)计算:|1﹣|+2cos45°﹣+()﹣1.21.(7分)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑510%朗读者15b%中国诗词大会a40%出彩中国人1020%根据以上提供的信息,解答下列问题:(1)x=,a=,b=;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.22.(7分)如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.23.(9分)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.24.(9分)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?25.(11分)数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC 三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC =CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.26.(13分)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.2017年山东省临沂市中考数学试卷参考答案一、选择题(本大题共14小题,每小题3分,共42分)1.(3分)(2017•临沂)﹣的相反数是()A.B.﹣C.2017 D.﹣2017【分析】直接利用相反数的定义分析得出答案.【解答】解:﹣的相反数是:.故选:A.【点评】此题主要考查了相反数的定义,正确把握相反数的定义是解题关键.2.(3分)(2017•临沂)如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是()A.50°B.60° C.70° D.80°【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.【解答】解:∵∠BEF是△AEF的外角,∠1=20°,∠F=30°,∴∠BEF=∠1+∠F=50°,∵AB∥CD,∴∠2=∠BEF=50°,故选A.【点评】本题主要考查了平行线的性质,解题的关键是掌握三角形外角的性质,此题难度不大.3.(3分)(2017•临沂)下列计算正确的是()A.﹣(a﹣b)=﹣a﹣b B.a2+a2=a4C.a2•a3=a6D.(ab2)2=a2b4【分析】根据去括号、同底数幂的乘法底数不变指数相加,积的乘方,可得答案.【解答】解:A、括号前是负号,去括号全变号,故A不符合题意;B、不是同底数幂的乘法指数不能相加,故B不符合题意;C、同底数幂的乘法底数不变指数相加,故C不符合题意;D、积的乘方等于乘方的积,故D符合题意;故选:D.【点评】本题考查了积的乘方,熟记法则并根据法则计算是解题关键.4.(3分)(2017•临沂)不等式组中,不等式①和②的解集在数轴上表示正确的是()A.B.C.D.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式①,得:x<1,解不等式②,得x≥﹣3,则不等式组的解集为﹣3≤x<1,故选:B.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键5.(3分)(2017•临沂)如图所示的几何体是由五个小正方体组成的,它的左视图是()A.B.C. D.【分析】根据三视图定义分别作出三视图即可判断.【解答】解:该几何体的三视图如下:主视图:;俯视图:;左视图:,故选:D.【点评】本题主要考查三视图,掌握三视图的定义和作法是解题的关键.6.(3分)(2017•临沂)小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是()A.B.C.D.【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小华获胜的情况数,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有9种等可能的结果,小华获胜的情况数是3种,∴小华获胜的概率是:=.故选C.【点评】此题主要考查了列表法和树状图法求概率知识,用到知识点为:概率=所求情况数与总情况数之比.7.(3分)(2017•临沂)一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形B.五边形C.六边形D.八边形【分析】此题可以利用多边形的外角和和内角和定理求解.【解答】解:设所求正n边形边数为n,由题意得(n﹣2)•180°=360°×2解得n=6.则这个多边形是六边形.故选:C.【点评】本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征:任何多边形的外角和都等于360°,多边形的内角和为(n﹣2)•180°.8.(3分)(2017•临沂)甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是()A.= B.= C.= D.=【分析】根据甲乙的工作时间,可列方程.【解答】解:设乙每小时做x个,甲每小时做(x+6)个,根据甲做90个所用时间与乙做60个所用时间相等,得=,故选:B.【点评】本题考查了分式方程的应用,找到关键描述语,找到合适的等量关系是解决问题的关键.9.(3分)(2017•临沂)某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:部门人数每人创年利润(万元)A 1 10B 3 8C 7 5D 4 3这15名员工每人所创年利润的众数、中位数分别是()A.10,5 B.7,8 C.5,6.5 D.5,5【分析】根据表格中的数据可以将这组数据按照从小到大的顺序排列起来,从而可以找到这组数据的中位数和众数.【解答】解:由题意可得,这15名员工的每人创年利润为:10、8、8、8、5、5、5、5、5、5、5、3、3、3、3,∴这组数据的众数是5,中位数是5,故选D.【点评】本题考查众数和中位数,解答本题的关键是明确众数和中位数的定义,会找一组数据的众数和中位数.10.(3分)(2017•临沂)如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是()A.2 B.﹣πC.1 D.+π【分析】设AT交⊙O于D,连结BD,先根据圆周角定理得到∠ADB=90°,则可判断△ADB、△BDC都是等腰直角三角形,所以AD=BD=CD=AB=,然后利用弓形AD的面积等于弓形BD的面积得到阴影部分的面积=S△BTD.【解答】解:∵BT是⊙O的切线;设AT交⊙O于D,连结BD,∵AB是⊙O的直径,∴∠ADB=90°,而∠ATB=45°,∴△ADB、△BDT都是等腰直角三角形,∴AD=BD=TD=AB=,∴弓形AD的面积等于弓形BD的面积,∴阴影部分的面积=S△BTD=××=1.故选C.【点评】本题考查了切线的性质,等腰直角三角形的性质,解决本题的关键是利用等腰直角三角形的性质把阴影部分的面积转化为三角形的面积.11.(3分)(2017•临沂)将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是()A.11 B.12 C.13 D.14【分析】根据小圆个数变化规律进而表示出第n个图形中小圆的个数,进而得出答案.【解答】解:第1个图形有1个小圆;第2个图形有1+2=3个小圆;第3个图形有1+2+3=6个小圆;第4个图形有1+2+3+4=10个小圆;第n个图形有1+2+3+…+n=个小圆;∵第n个图形中“○”的个数是78,∴78=,解得:n1=12,n2=﹣13(不合题意舍去),故选:B.【点评】此题主要考查了图形变化类,正确得出小圆个数变化规律是解题关键.12.(3分)(2017•临沂)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形【分析】由矩形的判定和菱形的判定即可得出结论.【解答】解:若AD⊥BC,则四边形AEDF是平行四边形,不一定是矩形;选项A错误;若AD垂直平分BC,则四边形AEDF是菱形,不一定是矩形;选项B错误;若BD=CD,则四边形AEDF是平行四边形,不一定是菱形;选项C错误;若AD平分∠BAC,则四边形AEDF是菱形;正确;故选:D.【点评】本题考查了矩形的判定、菱形的判定;熟记菱形和矩形的判定方法是解决问题的关键.13.(3分)(2017•临沂)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:t 0 1 2 3 4 5 6 7 …h 0 8 14 18 20 20 18 14 …下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是()A.1 B.2 C.3 D.4【分析】由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,可得y=﹣t2+9t=﹣(t﹣4.5)2+20.25,由此即可一一判断.【解答】解:由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,∴足球距离地面的最大高度为20.25m,故①错误,∴抛物线的对称轴t=4.5,故②正确,∵t=9时,y=0,∴足球被踢出9s时落地,故③正确,∵t=1.5时,y=11.25,故④错误.∴正确的有②③,故选B.【点评】本题考查二次函数的应用、求出抛物线的解析式是解题的关键,属于中考常考题型.14.(3分)(2017•临沂)如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是()A.6B.10 C.2D.2【分析】由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,),N(,6),根据三角形的面积列方程得到M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.【解答】解:∵正方形OABC的边长是6,∴点M的横坐标和点N的纵坐标为6,∴M(6,),N(,6),∴BN=6﹣,BM=6﹣,∵△OMN的面积为10,∴6×6﹣×6×﹣6×﹣×(6﹣)2=10,∴k=24,∴M(6,4),N(4,6),作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,∵AM=AM′=4,∴BM′=10,BN=2,∴NM′===2,故选C.【点评】本题考查了反比例函数的系数k的几何意义,轴对称﹣最小距离问题,勾股定理,正方形的性质,正确的作出图形是解题的关键.二、填空题(本大题共5小题,每小题3分,共15分)15.(3分)(2017•临沂)分解因式:m3﹣9m= m(m+3)(m﹣3).【分析】先提取公因式,再根据平方差公式进行二次分解.平方差公式:a2﹣b2=(a+b)(a ﹣b).【解答】解:m3﹣9m,=m(m2﹣9),=m(m+3)(m﹣3).故答案为:m(m+3)(m﹣3).【点评】本题考查了用提公因式法和公式法进行因式分解的能力,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.16.(3分)(2017•临沂)已知AB∥CD,AD与BC相交于点O.若=,AD=10,则AO= 4 .【分析】根据平行线分线段成比例定理列出比例式,计算即可.【解答】解:∵AB∥CD,∴==,即=,解得,AO=4,故答案为:4.【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关17.(3分)(2017•临沂)计算:÷(x﹣)= .【分析】先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.【解答】解:原式=÷=•=,故答案为:.【点评】本题考查分式的混合运算,能正确运用分式的运算法则进行化简是解此题的关键,注意运算顺序.18.(3分)(2017•临沂)在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin ∠BDC=,则▱ABCD的面积是24 .【分析】作OE⊥CD于E,由平行四边形的性质得出OA=OC,OB=OD=BD=5,CD=AB=4,由sin ∠BDC=,证出AC⊥CD,OC=3,AC=2OC=6,得出▱ABCD的面积=CD•AC=24.【解答】解:作OE⊥CD于E,如图所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD=BD=5,CD=AB=4,∵sin∠BDC==,∴OE=3,∴DE==4,∵CD=4,∴点E与点C重合,∴AC⊥CD,OC=3,∴AC=2OC=6,∴▱ABCD的面积=CD•AC=4×6=24;故答案为:24.【点评】本题考查了平行四边形的性质、三角函数、勾股定理等知识;熟练掌握平行四边形的性质,得出AC⊥CD是关键19.(3分)(2017•临沂)在平面直角坐标系中,如果点P坐标为(m,n),向量可以用点P的坐标表示为=(m,n).已知:=(x1,y1),=(x2,y2),如果x1•x2+y1•y2=0,那么与互相垂直,下列四组①=(2,1),=(﹣1,2);②=(cos30°,tan45°),=(1,sin60°);③=(﹣,﹣2),=(+,);④=(π0,2),=(2,﹣1).其中互相垂直的是①③④(填上所有正确答案的符号).【分析】根据向量垂直的定义进行解答.【解答】解:①因为2×(﹣1)+1×2=0,所以与互相垂直;②因为cos30°×1+tan45°•sin60°=×1+1×=≠0,所以与不互相垂直;③因为(﹣)(+)+(﹣2)×=3﹣2﹣1=0,所以与互相垂直;④因为π0×2+2×(﹣1)=2﹣2=0,所以与互相垂直.综上所述,①③④互相垂直.故答案是:①③④.【点评】本题考查了平面向量,零指数幂以及解直角三角形.解题的关键是掌握向量垂直的定义.三、解答题(本大题共7小题,共63分)20.(7分)(2017•临沂)计算:|1﹣|+2cos45°﹣+()﹣1.【分析】根据绝对值的意义、特殊角的三角函数值、二次根式的化简和负指数幂的运算,分别求得每项的值,再进行计算即可.【解答】解:|1﹣|+2cos45°﹣+()﹣1=﹣1+2×﹣2+2=﹣1+﹣2+2=1.【点评】本题主要考查实数的运算及特殊角的三角函数值,注意绝对值和负指数幂的运算法则是解题的关键.21.(7分)(2017•临沂)为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:学生最喜爱的节目人数统计表节目人数(名)百分比最强大脑 5 10%朗读者 15 b% 中国诗词大会 a 40%出彩中国人 10 20% 根据以上提供的信息,解答下列问题:(1)x= 50,a= 20 ,b= 30 ;(2)补全上面的条形统计图;(3)若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.【分析】(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;(2)根据a的值,补全条形统计图即可;(3)由中国诗词大会的百分比乘以1000即可得到结果.【解答】解:(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=×100=30;故答案为:50;20;30;(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:(3)根据题意得:1000×40%=400(名),则估计该校最喜爱《中国诗词大会》节目的学生有400名.【点评】此题考查了条形统计图,用样本估计总体,以及统计表,弄清题中的数据是解本题的关键.22.(7分)(2017•临沂)如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.【分析】延长CD,交AE于点E,可得DE⊥AE,在直角三角形ABC中,由题意确定出AB的长,进而确定出EC的长,在直角三角形AED中,由题意求出ED的长,由EC﹣ED求出DC 的长即可.【解答】解:延长CD,交AE于点E,可得DE⊥AE,在Rt△AED中,AE=BC=30m,∠EAD=30°,∴ED=AEtan30°=10m,在Rt△ABC中,∠BAC=30°,BC=30m,∴AB=30m,则CD=EC﹣ED=AB﹣ED=30﹣10=20m.【点评】此题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.23.(9分)(2017•临沂)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.【分析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得:,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC==4,即可得出△ABC外接圆的半径.【解答】(1)证明:∵AD平分∠BAC,BE平分∠ABC,∴∠ABE=∠CBE,∠BAE=∠CAD,∴,∴∠DBC=∠CAD,∴∠DBC=∠BAE,∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,∴∠DBE=∠DEB,∴DE=DB;(2)解:连接CD,如图所示:由(1)得:,∴CD=BD=4,∵∠BAC=90°,∴BC是直径,∴∠BDC=90°,∴BC==4,∴△ABC外接圆的半径=×4=2.【点评】本题考查了三角形的外接圆的性质、圆周角定理、三角形的外角性质、勾股定理等知识;熟练掌握圆周角定理是解决问题的关键.24.(9分)(2017•临沂)某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.(1)求y关于x的函数解析式;(2)若某用户二、三月份共用水40m3(二月份用水量不超过25m3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?【分析】(1)根据函数图象可以分别设出各段的函数解析式,然后根据函数图象中的数据求出相应的函数解析式;(2)根据题意对x进行取值进行讨论,从而可以求得该用户二、三月份的用水量各是多少m3.【解答】解:(1)当0≤x≤15时,设y与x的函数关系式为y=kx,15k=27,得k=1.8,即当0≤x≤15时,y与x的函数关系式为y=1.8x,当x>15时,设y与x的函数关系式为y=ax+b,,得,即当x>15时,y与x的函数关系式为y=2.4x﹣9,由上可得,y与x的函数关系式为y=;(2)设二月份的用水量是xm3,当15<x≤25时,2.4x﹣9+2.4(40﹣x)﹣9=79.8,解得,x无解,当0<x≤15时,1.8x+2.4(40﹣x)﹣9=79.8,解得,x=12,∴40﹣x=28,答:该用户二、三月份的用水量各是12m3、28m3.【点评】本题考查一次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想和分类讨论的数学思想解答.25.(11分)(2017•临沂)数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD 的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.【分析】(1)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再得出∠AEC=45°,即可得出等腰直角三角形,即可;(判断∠ADE=∠ABC也可以先判断出点A,B,C,D四点共圆)(2)先判断出∠ADE=∠ABC,即可得出△ACE是等腰三角形,再用三角函数即可得出结论.【解答】解:(1)BC+CD=AC;理由:如图1,延长CD至E,使DE=BC,∵∠ABD=∠ADB=45°,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=90°,∵∠ACB=∠ACD=45°,∴∠ACB+∠ACD=90°,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=45°,AC=AE,∴△ACE是等腰直角三角形,∴CE=AC,∵CE=CD+DE=CD+BC,∴BC+CD=AC;(2)BC+CD=2AC•cosα.理由:如图2,延长CD至E,使DE=BC,∵∠ABD=∠ADB=α,∴AB=AD,∠BAD=180°﹣∠ABD﹣∠ADB=180°﹣2α,∵∠ACB=∠ACD=α,∴∠ACB+∠ACD=2α,∴∠BAD+∠BCD=180°,∴∠ABC+∠ADC=180°,∵∠ADC+∠ADE=180°,∴∠ABC=∠ADE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠ACB=∠AED=α,AC=AE,∴∠AEC=α,过点A作AF⊥CE于F,∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC •cosα,∴CE=2CF=2AC•cosα,∵CE=CD+DE=CD+BC,∴BC+CD=2AC•cosα.【点评】此题是几何变换综合题,主要考查了全等三角形的判定,四边形的内角和,等腰三角形的判定和性质,解本题的关键是构造全等三角形,是一道综合性较强的题目.26.(13分)(2017•临沂)如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.(1)求抛物线的解析式;(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【分析】(1)待定系数法即可得到结论;(2)连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(﹣1,﹣3),设D(0,m),则OD=|m|即可得到结论;(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(﹣2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M 与C重合,于是得到结论.【解答】解:(1)由y=ax2+bx﹣3得C(0.﹣3),∴OC=3,∵OC=3OB,∴OB=1,∴B(﹣1,0),把A(2,﹣3),B(﹣1,0)代入y=ax2+bx﹣3得,∴,∴抛物线的解析式为y=x2﹣2x﹣3;(2)设连接AC,作BF⊥AC交AC的延长线于F,∵A(2,﹣3),C(0,﹣3),∴AF∥x轴,∴F(﹣1,﹣3),∴BF=3,AF=3,∴∠BAC=45°,设D(0,m),则OD=|m|,∵∠BDO=∠BAC,∴∠BDO=45°,∴OD=OB=1,∴|m|=1,∴m=±1,∴D1(0,1),D2(0,﹣1);(3)设M(a,a2﹣2a﹣3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图2,过M作ME⊥对称轴y于E,AF⊥x轴于F,则△ABF≌△NME,∴NE=AF=3,ME=BF=3,∴|a﹣1|=3,∴a=3或a=﹣2,∴M(4,5)或(﹣2,5);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,∴M(0,﹣3),综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(﹣2,5)或(0,﹣3).【点评】本题考查了待定系数法求二次函数的解析式,全等三角形的判定和性质,平行四边形的判定和性质,正确的作出图形是解题的关键.。
山东省临沂市中考数学试题

2017 年山东省临沂市中考数学试题2017 年临沂市初中学业水平考试一试题数学第Ⅰ卷(共 42 分)一、选择题:本大题共14 个小题 , 每题 3 分, 共 42 分.在每题给出的四个选项中,只有一项为哪一项吻合题目要求的.1.1)的相反数是(2007A.1.1. 2017B C .2017D200720072.如图,将直尺与含30角的三角尺摆放在一起,若 1 20 ,则 2 的度数是()A.50B.60C.70D.803.以下计算正确的选项是()A. a b a b B.a2a2a4C.a2a2a4D. ab 2 2a2b42x①1,4.不等式组x5②中,不等式①和②的解集在数轴上表示正确的选项是()12A.B.C.D.5.以下列图的几何体是由五个小正方体组成的,它的左视图是()A .B.C.D.6.小明和小华玩“石头、剪子、布”的游戏. 若随机出手一次,则小华获胜的概率是()A.2B.1C.1D.2 32397.一个多边形的内角和是外角和的 2 倍,这个多边形是()A.四边形B.五边形C.六边形D.八边形8.甲、乙二人做某种机械零件 . 已知甲每小时比乙多做 6 个,甲做 90 个所用时间与乙做60 个所用时间相等,求甲、乙每小时各做零件多少个. 若是设乙每小时做x 个,那么所列方程是()A.9060 x x6B.9060C.9060x 6x x 6xD.9060x x 69.某公司有15 名员工,他们所在部门及相应每人所创年利润以下表所示:部门人数每人所创年利润(单位:万元)A110B38C75D43这 15 名员工每人所创年利润的众数、中位数分别是()A. 10, 5B.7,8C.5,D. 5, 510.如图,AB是e O的直径,BT是e O的切线,若ATB 45 ,AB 2 ,则阴影部分的面积是()A. 2B.31C.1D.1 1242411.将一些相同的“ d ”按以下列图摆放,观察每个图形中的“d ”的个数,若第n个图形中“ d ”的个数是 78,则n的值是()A. 11B.12C.13D.1412.在V ABC中,点D是边BC上的点(与 B 、 C 两点不重合),过点 D 作 DE ∥ AC , DF ∥ AB ,分别交 AB , AC 于 E 、 F 两点,以下说法正确的选项是()A.若AD BC ,则四边形 AEDF 是矩形B.若AD垂直均分BC,则四边形AEDF是矩形C.若BD CD ,则四边形 AEDF 是菱形D.若AD均分BAC ,则四边形AEDF 是菱形13.足球运动员将足球沿与地面成必然角度的方向踢出,足球翱翔的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h (单位:m)与足球被踢出后经过的时间t (单位: s)之间的关系以下表:t01234567, h08141820201814,以下结论:①足球距离地面的最大高度为20m ;②足球翱翔路线的对称轴是直线t 99s ;③足球被踢出2时落地;④足球被踢出 1.5s 时,距离地面的高度是11m .其中正确结论的个数是()A. 1B.2C.3D.414.如图,在平面直角坐标系中,发比率函数y k0 )的图象与边长是6的正方形 OABC 的两边( xxAB , BC 分别订交于 M , N 两点, VOMN 的面积为10. 若动点P在x轴上,则PM PN 的最小值是()A.62B.10C.226D.229第Ⅱ卷(共 78 分)二、填空题(每题 3 分,满分 15 分,将答案填在答题纸上)15.分解因式:m29m.16.已知AB∥CD,AD与BC订交于点O . 若BO2, AD10 ,则 AO.OC317.计算:xy x 2 xy y2.x x18.在Y ABCD中,对角线 AC , BD 订交于点 O .若 AB 4 , BD10 ,sin BDC 3,则 Y ABCD 5的面积是.uuur uuur 19.在平面直角坐标系中,若是点P 坐标为m, n,向量OP可以用点 P的坐标表示为 OP m, n .uur uurx2 , y2,若是 x x y y uur uuur已知: OA x1 , y1, OB220 ,那么 OA 与 OB 互相垂直.11以下四组向量:uuur uuur1,2① OC2,1 , OD;uuur uuur1,sin 60② OE cos30 , tan 45 , OF;uuur uuur32, 1③ OG32, 2, OH;2uuur uuur2,1 .④ OM0 , 2 , ON其中互相垂直的是(填上所有正确答案的序号).三、解答题(本大题共7小题,共63分.解答应写出文字说明、证明过程或演算步骤.)20.计算:11 2 2cos 45821.21.为认识某校学生对《最富强脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x 名学生进行检查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将检查结果绘制成以下统计图表:依照以上供应的信息,解答以下问题:()x ,a ______, b;1____________(2)补全上面的条形统计图;(3)若该校共有学生 1000 名 . 依照抽样检查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名 .22.如图,两座建筑物的水平距离BC 30m ,从 A 点测得 D 点的俯角为30,测得C点的俯角为60 ,求这两座建筑物的高度.23.如图,BAC 的均分线交 V ABC 的外接圆于点 D ,ABC 的均分线交 AD 于点 E .( 1)求证:DE DB ;( 2)若BAC90 , BD 4 ,求 V ABC 外接圆的半径.24.某市为节约水资源,拟定了新的居民用水收费标准. 依照新标准,用户每个月缴纳的水费y (元)与每月用水量x (m3)之间的关系以下列图.( 1)求y 关于x 的函数剖析式;( 2)若某用户二、三月份共用水40m 3(二月份用水量不高出25m 3),缴纳水费79.8 元,则该用户二、三月份的用水量各是多少m3?25.数学课上,张老师出示了问题:如图1,AC、BD是四边形ABCD 的对角线,若ACB ACD ABD ADB60,则线段BC, CD,AC三者之间有何等量关系?经过思虑,小明显现了一种正确的思路:如图2,延长CB 到E ,使BE CD,连接AE,证得V ABE≌V ADC,从而简单证明V ACE是等边三角形,故AC CE,所以AC BC CD.小亮显现了另一种正确的思路:如图3,将V ABC绕着点 A 逆时针旋转60,使AB与AD 重合,从而容易证明V ACF是等比三角形,故AC CF,所以AC BC CD.在此基础上,同学们作了进一步的研究:( 1)小颖提出:如图“ACB ACD 4,若是把“ABDACBADB45ACD ABD ADB”,其他条件不变,那么线段60 ”改为BC , CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.( 2)小华提出:如图ACB ACD 5,若是把“ABDACBADBACD ABD ADB60BC”改为, CD , AC等量关系?针对小华提出的问题,请你写出结论,不用证明.26.如图,抛物线y ax2bx 3经过点 A 2, 3 ,与 x 轴负半轴交于点 B ,与 y 轴交于点 C ,且OC 3OB .( 1)求抛物线的剖析式;( 2)点 D 在y 轴上,且BDO BAC,求点 D 的坐标;( 3)点M在抛物线上,点N在抛物线的对称轴上,可否存在以点 A , B , M, N为极点的四边形是平行四边形?若存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
uuur
uuur
1
③ OG 3 2, 2 , OH 3 2, ;
2
uuur
uuur
④ OM 0, 2 , ON 2, 1 .
其中互相垂直的是
(填上所有正确答案的序号).
三、解答题 (本大题共 7 小题,共 63 分.解答应写出文字说明、证明过程或演算步骤.)
1
1 20.计算: 1 2 2 cos 45 8 .
B
3
8
C
7
5
D
4
3
这 15 名员工每人所创年利润的众数、中位数分别是( )
A.10,5
B.7,8
C.5,6.5
D.5,5
10.如图,AB 是 e O 的直径,BT 是 e O 的切线,若 ATB 45 ,AB 2 ,则阴影部分的面积是( )
3
31
11
A.2
B.
C.1
D.
24
24
11.将一些相同的“ d ”按如图所示摆放,观察每个图形中的“ d ”的个数,若第 n 个图形中“ d ”的个
等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图 5,如果把“ ACB ACD ABD ADB 60 ”改为 “ ACB ACD ABD ADB ”,其它条件不变,那么线段 BC ,CD , AC 三者之间有何等
量关系?针对小华提出的问题,请你写出结论,不用证明.
等,求甲、乙每小时各做零件多少个.如果设乙每小时做 x 个,那么所列方程是( )
90 60 A.
x x6
90 60 B.
x6 x
90 60 C.
x6 x
90 60 D.
x x6
9.某公司有 15 名员工,他们所在部门及相应每人所创年利润如下表所示:
部门
人数
每人所创年利润(单位:万元)
A
1
10
25.数学课上,张老师出示了问题:如图 1, AC 、 BD 是四边形 ABCD 的对角线,若 ACB ACD ABD ADB 60 ,则线段 BC , CD , AC 三者之间有何等量关系?
3
经过思考,小明展示了一种正确的思路:如图 2,延长 CB 到 E ,使 BE CD ,连接 AE ,证得 V ABE≌V ADC ,从而容易证明V ACE 是等边三角形,故 AC CE ,所以 AC BC CD .
3
3
3
3
3
3
.
OC 3
x y 2xy y2
17.计算:
x
.
x
x
3 18.在 Y ABCD 中,对角线 AC ,BD 相交于点 O .若 AB 4 ,BD 10 ,sin BDC ,则 Y ABCD
5
的面积是
.
uuur
uuur
19.在平面直角坐标系中,如果点 P 坐标为 m, n ,向量 OP 可以用点 P 的坐标表示为 OP m, n .
x
BC 分别相交于 M , N 两点,VOMN 的面积为 10.若动点 P 在 x 轴上,则 PM PN 的最小值是( )
A. 6 2
B.10
C. 2 26
D. 2 29
第Ⅱ卷(共 78 分)
二、填空题(每题 3 分,满分 15 分,将答案填在答题纸上)
15.分解因式: m2 9m
.
BO 2
16.已知 AB ∥CD , AD 与 BC 相交于点 O .若 , AD 10 ,则 AO
数是 78,则 n 的值是( )
A.11
B.12
C.13
D.14
12.在V ABC 中,点 D 是边 BC 上的点(与 B 、C 两点不重合),过点 D 作 DE ∥ AC , DF ∥ AB ,分
别交 AB , AC 于 E 、 F 两点,下列说法正确的是( )
A.若 AD BC ,则四边形 AEDF 是矩形
B.若 AD 垂直平分 BC ,则四边形 AEDF 是矩形
C.若 BD CD ,则四边形 AEDF 是菱形
D.若 AD 平分 BAC ,则四边形 AEDF 是菱形
13.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,
足球距离地面的高度 h (单位: m )与足球被踢出后经过的时间 t (单位: s )之间的关系如下表:
2017 年临沂市初中学业水平考试试题
数学
第Ⅰ卷(共 42 分)
一、选择题:本大题共 14 个小题,每小题 3 分,共 42 分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1
1.
的相反数是( )
2007
1
A.
2007
1 B.
2007
C.2017
D. 2017
2.如图,将直尺与含 30 角的三角尺摆放在一起,若 1 20 ,则 2 的度数是( )
3
uur
uuur
uur uuur
已知: OA x1, y1 , OB x2, y2 ,如果 x1 x2 y1 y2 0 ,那么 OA 与 OB 互相垂直.
下列四组向量:
uuur
uuur
① OC 2,1 , OD 1, 2 ;
uuur
uuur
② OE cos 30, tan 45 , OF 1,sin 60 ;
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
9 下列结论:①足球距离地面的最大高度为 20m ;②足球飞行路线的对称轴是直线 t ;③足球被踢出 9s 时
2
3
落地;④足球被踢出1.5s 时,距离地面的高度是11m .
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
k 14.如图,在平面直角坐标系中,发比例函数 y ( x 0 )的图象与边长是 6 的正方形 OABC 的两边 AB ,
5.如图所示的几何体是由五个小正方体组成的,它的左视图是( )
A.
B.
C.
D.
6.小明和小华玩“石头、剪子、布”的游戏.若随机出手一次,则小华获胜的概率是( )
2
A.
3
1
B.
2
1
C.
3
2
D.
9
7.一个多边形的内角和是外角和的 2 倍,这个多边形是( )
A.四边形
B.五边形
C.六边形
D.八边形
8.甲、乙二人做某种机械零件.已知甲每小时比乙多做 6 个,甲做 90 个所用时间与乙做 60 个所用时间相
A. 50
B. 60
C. 70
D. 80
3.下列计算正确的是( ). a2 a2 a4
D. ab2 2 a2b4
2 x 1, ①
4.不等式组 x 5
中,不等式①和②的解集在数轴上表示正确的是( )
2 1②
A.
B.
3
C.
D.
小亮展示了另一种正确的思路:如图 3,将V ABC 绕着点 A 逆时针旋转 60 ,使 AB 与 AD 重合,从而容 易证明V ACF 是等比三角形,故 AC CF ,所以 AC BC CD .
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图 4,如果把“ ACB ACD ABD ADB 60 ”改为 “ ACB ACD ABD ADB 45 ”,其它条件不变,那么线段 BC ,CD , AC 三者之间有何
24.某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费 y (元)与每月 用水量 x ( m3 )之间的关系如图所示. (1)求 y 关于 x 的函数解析式; (2)若某用户二、三月份共用水 40m3 (二月份用水量不超过 25m3 ),缴纳水费 79.8 元,则该用户二、 三月份的用水量各是多少 m3 ?
2
21.为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情
况,随机抽取了 x 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调
查结果绘制成如下统计图表:
根据以上提供的信息,解答下列问题:
(1) x ______, a ______, b ______;
26.如图,抛物线 y ax2 bx 3 经过点 A2, 3 ,与 x 轴负半轴交于点 B ,与 y 轴交于点 C ,且
OC 3OB .
(1)求抛物线的解析式;
(2)点 D 在 y 轴上,且 BDO BAC ,求点 D 的坐标;
3
(3)点 M 在抛物线上,点 N 在抛物线的对称轴上,是否存在以点 A , B , M , N 为顶点的四边形是平 行四边形?若存在。求出所有符合条件的点 M 的坐标;若不存在,请说明理由.
(2)补全上面的条形统计图; (3)若该校共有学生 1000 名.根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
22.如图,两座建筑物的水平距离 BC 30m ,从 A 点测得 D 点的俯角 为 30 ,测得 C 点的俯角 为 60 ,
3
求这两座建筑物的高度.
23.如图, BAC 的平分线交V ABC 的外接圆于点 D , ABC 的平分线交 AD 于点 E . (1)求证: DE DB ; (2)若 BAC 90 , BD 4 ,求V ABC 外接圆的半径.
