10上图论2
图论

7/12/2013 10:38 PM
20
Graphs/图论
说明: 哥尼斯堡七桥问题,由于四个顶点都是齐次 的,不可能有欧拉道路。
应用与推广: (1) 一笔画问题; (2) 如果齐次顶点个数为2K个,此问题是K 笔画问题。
7/12/2013 10:38 PM
21
Graphs/图论
例 8个顶点均为 3次,至少要 4笔。
7/12/2013 10:38 PM 10
Graphs/图论
b e1 a e5 e2 e3 c e4 d
(e5,e1 ,e2 ,e3,e4)是简单道路, 不是初级道路,因为(c,a,b,c,d, b)中b,c均出现了两次。但(c,d,b, c)是初级道路。
7/12/2013 10:38 PM 11
7/12/2013 10:38 PM 15
Graphs/图论
若图G存在奇次顶点,任取一个作为起点,若 不存在,则任取一个顶点作为起点。 若此图有n条边,总次为2n。每进入或离开 一个顶点,让此顶点的次减1,由于除了两个(或 没有)奇次顶点外,其余顶点次为偶数,只要进得 去,一定出得来,直至进入另一个奇次顶点(或起 点)作为终点。这样构造的是简单道路,如果经过 所有的边,即得到一条欧拉道路。 不然,记走过的简单道路为p1,p1上顶点集 V1,边集E1,G1=(V1,E1)是G的子图。
[定义]欧拉道路(回路): G=(V,E),称包含E中所有边的简 单道路为欧拉道路/Euler Path/E道路。 包含E中所有边的简单回路为欧拉回路 /Euler Circuit/E回路
。
7/12/2013 10:38 PM 13
Graphs/图论
[定理1](欧拉定理): 没有次为0的孤立顶点的无向图存 在欧拉道路的充要条件是: (1)图是连通的; (2)图中奇次顶点个数是0个或2个。
第10章知识图谱

5
2 语义网络
优点
①结构性:以节点和弧形式把事物属性 以及事物间的语义联想显式地表示出来。 ②联想性:作为人类联想记忆模型提出。 ③自然性:直观地把事物的属性及其语 义联系表示出来,便于理解,自然语言 与语义网络的转换比较容易实现。
84 语义Web源自奠基人Tim Berners-Lee 2016年图灵奖得 主万维网、语义网 之父,提出语义 Web
Web1.0
Web1.0,是以编辑为 特征,网站提供给用 户的内容是网站编辑 进行编辑处理后提供 的,用户阅读网站提 供的内容。这个过程 是网站到用户的单向 行 为 , web1.0 时 代 的 代表站点为新浪,搜 狐,网易三大门户, 强调的是文档互连。
作用
为真实世界的各个场 景直观地建模,运用 “图”这种基础性、通用 性的“语言”,“高保真” 地表达这个多姿多彩 世界的各种关系,并 且非常直观、自然、 直接和高效,不需要 中间过程的转换和处 理。
术语
①实体: 具有可区别 性且独立存在的某种 事物。 ②类别:主要指集合、 类别、对象类型、事 物的种类。 ③属性、属性值:实 体具有的性质及其取 值。 ④关系:不同实体之 间的某种联系,
11
10.2 知识图谱基本原理
10.2.1 10.2.2 10.2.3 10.2.4 10.2.5
认知智能是人工智能的高级目标 知识图谱概念 知识图谱模型 知识图谱特点 知识图谱分类
1 认知智能是人工智能的高级目标
13
2 知识图谱概念
定义
知识图谱用节点和关系 所组成的图谱。
图论及其应用课程教学的思考与探索

图论及其应用课程教学的思考与探索1. 引言1.1 绪论图论在教学中可以帮助学生培养抽象思维能力、逻辑推理能力和问题解决能力。
通过图论的学习,学生能够更好地理解图的性质和结构,掌握图的基本算法和应用技巧,提升数学建模和解决实际问题的能力。
图论的教学还能引导学生学会合作、团队协作,培养学生的创新精神和实践能力。
本文将从图论教学的重要性、图论教学的内容安排、图论应用案例探讨、图论课程的评价与改进以及图论教学的挑战与应对等方面展开讨论,旨在探索如何更好地开展图论及其应用课程的教学工作,促进学生对图论的深入理解和应用。
2. 正文2.1 图论教学的重要性图论教学可以拓展学生的数学知识面,让他们了解数学领域的另一种重要分支。
图论的理论相对简单,但在实际应用中却具有广泛的适用性,可以帮助学生更全面地了解数学在实际中的应用。
图论在计算机科学、网络科学、运筹学等领域中有着广泛的应用。
学习图论可以为学生打开更多的就业机会,使他们在未来的职业发展中具备更多的竞争力。
图论教学的重要性在于能够培养学生的抽象思维能力、拓展数学知识面、增加就业机会,并为他们的未来职业发展奠定良好的基础。
图论教学不仅有助于学生的学术发展,也具有实际的社会意义和价值。
2.2 图论教学的内容安排图论教学的内容安排是十分关键的,它直接影响着学生对图论知识的掌握和应用能力的培养。
在进行内容安排时,应该注重以下几个方面:1. 理论基础知识:首先要对图论的基本概念、性质和定理进行系统的讲解,如图的定义、连通性、路径、环、树等基本概念,以及图的表示方法、图的遍历算法、最短路径算法等基本性质和定理的讲解。
2. 经典算法介绍:在教学过程中,应该介绍一些经典的图论算法,如最小生成树算法(Prim算法、Kruskal算法)、最短路径算法(Dijkstra算法、Floyd算法)、最大流算法(Ford-Fulkerson算法、Edmonds-Karp算法)等,让学生了解到图论在实际问题中的应用。
第10章——第2节 最短路径与选址问题

从城镇v1到v7之间的最短路径为(v1,v2,v3,v5,v6,v7), 最短路径长度为13。
二、选址问题
选址问题,是现代地理学的分支学科——区位论 研究的 主要方向之一。选址问题涉及人类生产、生活、文化、 娱乐等各个方面。 选址问题的数学模型取决于两个方面的条件 :①可供选 址的范围、条件;②怎样判定选址的质量。 址的范围、 本节的讨论仅限于选址的范围 是一个地理网络,而且选 址位置 位于网络图的某一个或几个顶点上。 对这样的选址问题,根据其选址的质量判据,可以将其 归纳为求网络图的中心点与中位点 两类问题。
S (vi 0 ) = min S (vi ) = min ∑ a (v j )d ij
i i j =1
n
例 3:某县下属七个乡镇,各乡镇所拥有的人口数a(vi)(i=1,2, …,7),以及各乡镇之间的距离wij(i,j=1,2,…,7)如图所 示。现在需要设立一个中心邮局,为全县所辖的七个乡镇共同服 务。问该中心邮局应该设在哪一个乡镇(顶点)?
▇ 标号法具体计算步骤 开始,先给v1标上P标号P(v1)= 0,其余各点标上T标号 T(vj)=+∞(j≠1)。 ① 如果刚刚得到P标号的点是vi,那么,对于所有这样的点
{v (v , v )∈ E, 而且v 的标号是T标号}
j i j j
将其T标号修改为:min[T(vj),P(vi)+wij]。 ② 若G中没有T标号,则停止。否则,把点 v j 的T标号修改为 P标号,然后再转入①。 v 其中, j 满足:
§10.2 最短路径与选址问题
对于许多地理问题,当它们被抽象为图论意义下的网络 图时,问题的核心就变成了网络图上的优化计算问题。其中, 最为常见的是关于路径和顶点的优选计算问题。 在路径的优选计算问题中,最常见的是最短路径问题; 而在顶点的优选计算问题中,最为常见的是中心点和中位点 选址问题。
2的自然数

2的自然数一、2的基数和序数意义2是一个自然数,同时也是一个偶数、正整数、质数以及唯一的偶数质数。
在数学中,2的基数意义表示有两个元素属于一个二元组,同时也表示一个循环群的生成元个数。
序数意义则表示第二小的自然数,即排在1后面的第一个自然数。
二、2的算术性质2是唯一的偶数质数,具有很多独特的算术性质。
例如,2是唯一的偶数质数,因此,除了2之外的所有偶数都可以表示为两个质数的乘积。
此外,2也是唯一的以3个不同的数位之和等于10的数(2=1+0+1)。
三、2的数位及其关系在十进制中,2位于1和3之间,是一个重要的数字。
此外,2也是二进制中唯一的偶数。
在二进制中,2的表示方式为10,即只有两个数位,其中第1个数位为1,第2个数位为0。
在十进制中,2可以表示为10,而在其他进制中,2的表示方式会有所不同。
四、2的进制表示在二进制中,2被表示为10。
而在八进制中,2被表示为2,而在十六进制中,2被表示为2。
不同的进制对数字的表示方式不同,这有助于数字在不同领域的应用。
例如,在计算机科学中,二进制的使用非常普遍,因为二进制只有0和1两种状态,与计算机内部的逻辑电路相契合。
五、2的数学逻辑应用由于2具有独特的性质和关系,因此它在数学逻辑中有广泛的应用。
例如,根据排中律的推论(非P或非Q),任何自然数都可以分解成质因数并展开成欧几里得除法表达式$N=(an^2+bn+c)/(d×e),$同时它也在模运算中被广泛应用。
在证明费马小定理时,我们用到了二项式定理以及模运算的性质。
此外,2也被用于逻辑电路的设计中。
六、2在计算机科学中的应用二进制是计算机内部信息存储和处理的基本单位,这主要是因为二进制只有0和1两种状态,与计算机内部的逻辑电路相契合。
此外,在计算机科学中,许多算法和数据结构也涉及到数字2的使用。
例如,二叉树是一种重要的数据结构,其每个节点最多有两个子节点。
同时,二分查找算法也需要利用到数字2的特性。
第二篇 图论习题

习题课 2
1. 说明图中所示图(1)(2)是否是非平面图? 2.证明:彼得森图不是平面图。 (1) 收缩法;(2) 欧拉公式法;(3)收缩到K3,3。 3.设G是无向图,p<8,则G与Gc中至少有一个是平面图。 4.设平面图G的顶点数p=7,边数q=15,证明G是连通的。
习 题 课 3
1.判断下面命题是否正确,并说明理由。 任意平面图G的对偶图G*的对偶图G**与G同构。 2. 设G*是平面图G的对偶图,证明:p*=f,q*=q, f*=p-k+1。其中k(k≥1)为G的连通分支数。 3. 证明:若G是自对偶的平面图,则q=2p-2。其中p 和q是G的边与顶点数。 4.把平面分成p个区域,每两个区域都相邻,问p最 大为多少? 5.证明:不存在具有5个面,每两个面都共享一条公 共边的平面图G。
例15 设G为p个顶点的简单无向图。 (1) 若G的边数q= (p-1)· (p-2)/2+2,证明G为 哈密顿图。 (2) 若G的边数q= (p-1)· (p-2)/2+1,则G是否 一定为哈密顿图? 例16 如图所示的图G是哈密顿图。试证明:若图中 的哈密顿回路中含边e1,则它一定同时也含e2。 例17 已知9个人v1,v2,…,v9,其中v1和两个人握过手, v2,v3,v4,v5各和3个人握过手,v6和4个人握过手, v7,v8各和5个人握过手,v9和6个人握过手。证明:这 9个人中一定可以找出3个人互相握过手。
例8 有17位学者,每2位讨论3篇论文中的一篇且仅一 篇,证明:至少有3位学者,他们相互讨论的是同一篇 论文。
习题3
例1 设p,q为正整数,则 (1)p为何值时,无向完全图Kp是欧拉图?p为何值 时Kp为半欧拉图? (2)p,q为何值时Kp,q为欧拉图? (3)p,q为何值时Kp,q为哈密顿图? (4)p为何值时,轮图Wp为欧拉图? 例2 判断如图所示的图是否为哈密顿图,若是写出哈 密顿圈,否则证明其不是哈密顿图。
图论(张先迪-李正良)课后习题答案(第一章)

习题一作者---寒江独钓1.证明:在n 阶连通图中(1) 至少有n-1条边;(2) 如果边数大于n-1,则至少有一条闭迹;(3) 如果恰有n-1条边,则至少有一个奇度点。
证明: (1) 若G 中没有1度顶点,由握手定理:()2()21v V G m d v n m n m n ∈=≥⇒≥⇒>-∑若G 中有1度顶点u ,对G 的顶点数作数学归纳。
当n=2时,结论显然;设结论对n=k 时成立。
当n=k+1时,考虑G-u,它仍然为连通图,所以,边数≥k-1.于是G 的边数≥k.(2) 考虑G 中途径:121:n n W v v v v -→→→→L若W 是路,则长为n-1;但由于G 的边数大于n-1,因此,存在v i 与v j ,它们相异,但邻接。
于是:1i i j i v v v v +→→→→L 为G 中一闭途径,于是也就存在闭迹。
(3) 若不然,G 中顶点度数至少为2,于是由握手定理:()2()21v V G m d v n m n m n ∈=≥⇒≥⇒>-∑这与G 中恰有n-1条边矛盾! 2.(1)2n −12n 2−12n −1 (2)2n−2−1(3) 2n−2。
证明:u 1的两个邻接点与v 1的两个邻接点状况不同。
所以,两图不同构。
4.证明下面两图同构。
u 1 v 1证明:作映射f : v i ↔ u i (i=1,2….10)容易证明,对∀v i v j ∈E ((a)),有f (v i v j,),=,u i,u j,∈,E,((b))(1≤ i ≤ 10, 1≤j ≤ 10 )由图的同构定义知,图(a)与(b)是同构的。
5.指出4个顶点的非同构的所有简单图。
分析:四个顶点的简单图最少边数为0,最多边数为6,所以可按边数进行枚举。
(a)v 2 v 3u 4u(b)6.证明:1)充分性:当G 是完全图时,每个顶点的度数都是n −1,共有n 个顶点,总的度数为n(n −1),因此总的边数是n(n−1)2=(n 2). 2)必要性:因为G 是简单图,所以当G 是完全图的时候每个顶点的度数才达到最大:n −1.若G 不是完全图,则至少有一个顶点的度数小于n −1,这样的话,总的度数就要小于n (n −1),因此总的边数小于(n 2),矛盾。
第十章图论及LTI电路的矩阵法介绍

连通图与非连通图: 如果一个图,在它的任意两
个节点之间,至少存在一条通路,那样这样的图为
连通图。例如上图(a)是连通图,而图(b)是非连通图。
回路:构成闭合路径的支路集,就是回路。回路是
一个连通图。长度为m而始端节点与终端节点相重合的
通路称为长度为 m的回路,长度为1的回路称为自回路。
对于有向图给定的回路,常指定一顺时针方向,
bB};而所有的节点构成节点集合,用γ表示,
γ△{n1,n2,…,nN}。这里B是支路数,N是节
点数,因此一个图G可以用 G ( , )表示。
• 无向图与有向图:如果图 G中每条支路都不指
明支路方向,则称之为无向图,用 Gn 表示,如
图 8-1(b) 所示;如果图 G 中每条支路都规定一定
的方向,则称之为有向图,用 Gd 表示,如下图
所示。
•子图:如果图 Gs ( s , s ) 的节
点集γs是图G的节点集γ的子集,
支路集βs是支路集β的子集,则
称图Gs是图G的子图。
例如图中,由γs ={n1,n2,n3}和βs ={b1,b3,b5}构 成的图就是该图的子集,若子集仅由一个孤立的节
如图8-4(a)所示的图Gn,它的两个树分别如图8-4(b)、 (c),但是8-4(d)和(e)则不是它的一个树,因为(d)中包含
一个回路,而(e)是不连通的。同一连通图G具有许多不
同的树
树支、树余和连支:构成树的各条支路称为树支, 图Gn中除去树以外的所有支路形成Gn的另一个子图, 称为树余(反树),属于反树的各条支路称为连支。例 如图8-5中图Gn的树支如图8-5(b)实线所示,而(b)中虚 线为连支。
压和电流的参考方向以及网络中元件的特性。而
图论5-8章-习题课

证明:设 G 的对偶为 G*,则 G* 是连通的。必要性: G 为二部图,则 G 中无奇数长度回路,故 G* 中无奇数度顶点,因此 G* 是一个欧拉 图。充分性:G* 是一个欧拉图,则 G* 中无奇数度顶点,故 G 中 无奇数长度回路,因此 G 为一个二部图。
第二十八页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
14. 匈牙利算法求二部图的可增广道:如图,设初始匹配 {(x2, y2), (x3, y3), (x5, y5)},求其最大匹配。
x1
x2
x3
x4
x5
y1
y2
y3
y4
y5
28
第二十九页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
12
第十三页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图 G 中至少有 k(k1)/2 条边。
13
第十四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
7. 证明:k 色图G中至少有 k(k1)/2 条边。 证明:按 G 的一个 k 正常着色方案划分 G 的顶点为 k 个集合 V1,
第四页,编辑于星期六:八点 分。
《图论》4-8 章 习题课
2. 证明:Perterson 图不是平面图。
证二:反证。设其为平面图。由图示,每个面至少有5条边,即 l=5,代 入:
m (n 2)l l2
得: 3m 5(n2) 将 n =10, m =15 代入得 45 40,矛盾。
4
第五页,编辑于星期六:八点 分。
v1
v2
离散数学——图论

2021/10/10
11
哥尼斯堡七桥问题
❖ 把四块陆地用点来表示,桥用点与点连线表 示。
2021/10/10
12
❖ 欧拉将问题转化为:任何一点出发,是否存在通过 每条边一次且仅一次又回到出发点的路?欧拉的结 论是不存在这样的路。显然,问题的结果并不重要, 最为重要的是欧拉解决这个问题的中间步骤,即抽 象为图的形式来分析这个问题 。
2021/10/10
2
图论的发展
❖ 图论的产生和发展经历了二百多年的历史, 从1736年到19世纪中叶是图论发展的第一阶 段。
❖ 第二阶段大体是从19世纪中叶到1936年,主 要研究一些游戏问题:迷宫问题、博弈问题、 棋盘上马的行走线路问题。
2021/10/10
3
❖ 一些图论中的著名问题如四色问题(1852年)和哈密 尔顿环游世界问题(1856年)也大量出现。同时出现 了以图为工具去解决其它领域中一些问题的成果。
❖ P(G)表示连通分支的个数。连通图的连通 分支只有一个。
2021/10/10
40
练习题---图的连通性问题
❖ 1.若图G是不连通的,则补图是连通的。 ❖ 提示:直接证法。
根据图的不连通,假设至少有两个连通分 支;任取G中两点,证明这两点是可达的。
2021/10/10
41
❖ 2.设G是有n个结点的简单图,且 |E|>(n-1)(n-2)/2,则G是连通图。
❖ 例子
2021/10/10
29
多重图与带权图
❖ 定义多重图:包含多重边的图。 ❖ 定义简单图:不包含多重边的图。 ❖ 定义有权图:具有有权边的图。 ❖ 定义无权图:无有权边的图。
2021/10/10
30
图论第二版答案

图论第二版答案【篇一:图论与代数结构第一二三章习题解答】厂为一结点;若两个工厂之间有业务联系,则此两点之间用边相联;这样就得到一个无向图。
若每点的度数为3,则总度数为27,与图的总度数总是偶数的性质矛盾。
若仅有四个点的度数为偶数,则其余五个点度数均为奇数,从而总度数为奇数,仍与图的总度数总是偶数的性质矛盾。
(或者利用度数为奇数的点的个数必须为偶数个) 2. 若存在孤立点,则m不超过kn-1的边数, 故m = (n-1)(n-2)/2, 与题设矛盾。
?-3. 记ai为结点vi的正度数,ai为结点vi的负度数,则nnnn? 2? 22-ai?[(n?1)?ai]?n(n?1)?2(n?1)ai+ai-2, i?1i?1i?1i?1 nnn-2? 2 因为ai?cn?n(n?1)/2,所以ai?ai- 2。
i?1i?1i?14. 用向量(a1,a2,a3)表示三个量杯中水的量, 其中ai为第i杯中水的量, i = 1,2,3.以满足a1+a2+a3 = 8 (a1,a2,a3为非负整数)的所有向量作为各结点, 如果(a1,a2,a3)中某杯的水倒满另一杯得到( a’1, a’2, a’3 ) , 则由结点到结点画一条有向边。
这样可得一个有向图。
本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路,以下即是这样的一条: ( 8, 0, 0 ) ( 5, 0, 3 ) ( 5, 3, 0 ) ( 2, 3, 3 ) ( 2, 5,1 )(7, 0, 1 ) ( 7, 1, 0 ) ( 4, 1, 3 ) ( 4, 4, 0 )5. 可以。
???????6 若9个人中没有4个人相互认识,构造图g,每个点代表一个点,两个人相互认识则对应的两个点之间有边。
1)若可以找到点v,d(v)5,则与v相连的6个点中,要么有3个相互认识,要么有3个相互不认识(作k6并给边涂色:红=认识,蓝=不认识,只要证图中必有同色三角形。
运筹学及其应用10.2 最短路问题

3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 ∞,1
11,4
∞,1
v8
18
v2 5,3 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 6,2 2
∞,1
v9
6
3
3 4
10 4
v6 2 v7 9,5
10,5
12,5
v8
19
v2 5,3 1
9
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
10
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
10
v4
1,1
v5 ∞,1 2
6
3
4 10
4
v6
2
v7
∞,1
∞,1
∞,1
v9
3
∞,1
v8
11
v2 6,1 1
6 2
v1
3
3,1
v3
0,0
6
1
2
图论建模方法

上一页
返回
10.2图的矩阵表示
在同一顶点子集的任二顶点都相邻的简单二部图.称为完全二部图.两 个顶点子集大小分别为0、和,?,的完全二部图记为Knxm. • 设G.月是两个图.若V(H)∈ V(G),E(H) ∈E(G).则称H是G的子图;若 V(H)=V(G) ,E(H)c E(G).则称月是G的生成子图或支撑子图.
上一页 下一页 返回
• 有n个顶点m条边的图称为(n,m)图.(n,0)图叫零图.特别地.(0,0)图叫空 图.(1 ,0)图叫平凡图.没有环与平行边的图称为简单图.任意两顶点都相 邻的简单图称为完全图.有n个顶点的完全图记为Kn.若V(G)能分解为 V1与V2,使得
• V1∪V2= V(G).V1∩V2=Φ • 且V自身的顶点互不相邻(i=1,2).则称G是二部图.记为G=(V1,V2,E).不
• d (v) = d’ (v)十d (v) .v∈V(G)
上一页 下一页 返回
10.1图的基本概念和简单图论模型
• 各顶点的度都相同的图称为正则图 • 容易证明下面的定理. • 定理10. 1对图G=(V.E).有
• 没有重复边的通道称为迹.起点与终点重合的迹称为闭迹;不重合的称 为开迹.
• 没有重复顶点的开通道称为路径或路;起点与终点重合的路径称为 圈.
• 定义10. 2称G=(V.E)是一个有向图.如果 • (1)V是非空有限集合; • (2)E是V中兀索有序对所组成的集合.并把V的兀索称为顶点.E的兀
图论习题及答案

图论习题及答案(总24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业解答练习题2 利用matlab编程FFD算法完成下题:设有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。
解答一:function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD(降序首次适应)算法求解:先将物体按长度从大到小排序, %然后按FF算法对物体装箱%输入参数w为物品体积,capacity为箱子容量%输出参数num为所用箱子个数,s为元胞数组,表示装箱方案,s{i}为第i个箱子所装%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:nfor j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endendends = s(1:num);解答二:clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) endoutput:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三:function box_count=FFD(x)%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:nj=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;endendif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入:>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, i122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w= {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32,i22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。
离散数学 图论

第10章 图论(Graph Theory )
G1、G2是多重图 G3是线图
G4是简单图
第10章 图论(Graph Theory )
10.1 图的基本概念
(3)按G的边有序、无序分为有向图、无向图和混合图;
有向图:每条边都是有向边的图称为有向图
(图 10 .1.4 (b));
无向图:每条边都是无向边的图称为无向图;
度, 记为 d (v) 。结点v的入度与出度之和称为结 点v的度数,记为 d(v)或deg(v)。
第10章 图论(Graph Theory )
定义:
在无向图中,图中结点v所关联的边数
(有环时计算两次)称为结点v 的度数,记为d(v)
或deg(v) 。
最大度 (G) max{ (v) | v V } d 最小度 (G) min{d (v) | v V }
证明: 设V1和V2分别是G中奇数度数和偶数度数的结
点集。 由定理10.1.1知
vV1
deg(v) deg(v) 2是偶数之和, 必为偶数,
而2|E|也为偶数, 故 |V1|必为偶数。
V1
是偶数。 由此 deg( )
第10章 图论(Graph Theory )
第10章 图论(Graph Theory )
10.1 图的基本概念
证明: 设G=〈V ,E〉, |V|=6, v是G中一结点。 因为v 与G的其余5个结点或者在 G 中邻接, 或者在G 中邻接。 故不失一般性可假定, 有3个结点v1, v2, v3在G中与v邻接。 如果这3个结点中有两个结点(如v1 , v2 )邻接, 则它们与v 就是G中一个三角形的3个顶点。 如果这3 个结点中任意两个在G中均不邻接, 则v1, v2, v3就
图论 (2)

电子科技大学离散数学课程组——国家精品课程
例9.2.12
求右图中所有结点的度数、出度 和入度,指出悬挂结点和为悬挂 边。 解 deg(v1) = 1,deg+(v
1)
v1 v4 v2
1)
v5
=
0,deg-(v
= 1
v3
deg(v2) = 4,deg+(v2) = 3,deg-(v2) = 1
2013-7-10
143-22
电子科技大学离散数学课程组——国家精品课程
例9.3.1
判 断 下 图 G1 中 的 回 路 v3e5v4e7v1e4v3e3v2e1v1e4v3 、 v3e3v2e2v2e1v1e4v3 、v3e3v2e1v1e4v3 是否是简单回路、 基本回路?图G2 中的通路v1e1v2e6v5e7v3e2v2e6 v5e8v4 、 v1e5v5e7v3e2v2e6v5e8v4 、 v1e1v2e6v5e7v3e3v4 是否是简单通路、基本通路?并求其长度。
对于同构,形象地说,若图的结点可以任意挪 动位置,而边是完全弹性的,只要在不拉断的条件 下,一个图可以变形为另一个图,那么这两个图是 同构的。
2013-7-10 143-15
电子科技大学离散数学课程组——国家精品课程
两个图同构的必要条件
(1)结点数目相同;
(2)边数相同;
(3)度数相同的结点数相同。
9.3.1 通路与回路
通路与回路是图论中两个重要的基本概念。本 小节所述定义一般来说既适合有向图,也适合无向 图,否则,将加以说明或分开定义。
2013-7-10
143-20
电子科技大学离散数学课程组——国家精品课程
图论及其应用ch1-2详解

几个有趣的图论问题
Kö nigsberg七桥背后的故事
Graph Theory
/图论
Kö nigsberg七桥位于前苏联的加里宁格勒,历史上 曾是德国东普鲁士省的省会,霹雷格尔横 穿城堡,河中有两个小岛B与C,并有七座桥连接岛与 河岸及岛与岛(见图)。是否存在一种走发,从四块 陆地中的任意一块开始,通过每一座桥恰好一次再回 到起点。这就是著名的Kö nigsberg七桥问题,即一笔 画问题;也是图论的起源。
Graph Theory
/图论
在一个图G (V (G ), E (G ), G )中, 如果 G (e ) uv , 则说边e 连接 顶点u, v , 称u, v为e的端点 ,称u和v是 相邻的,而称u(或v )与e 关联。 与同一个顶点关联的若 干条边称为相邻的 。 两个端点重合为一个顶 点的边称为环; 关联于同一对顶点的两 条或以上的边称为 多重边 。
有
实际上,有向图即将无向图中的无序对看成有序对. 其中有向图对应的无向图称为有向图的基础图。 其中V(G)称为顶点集,E(G)称为边集(A(D)又称为 弧集).令p(G)=|V(G)|,q(G)=|E(G)|, 分别称为图的 阶和边数。举例说明。
11/19/2018 10:03 PM Li-Li Zhang 14
11/19/2018 10:03 PM Li-Li Zhang 12
1.2 图的定义
Graph Theory
/图论
生活中,人们常常需要考虑一些对象之间的某种特定 的关系 . 如某区域内,两城市之间有无交通线;一群 人中,两个人之间相识或不相识等等 . 这种关系是对 称的,即如果甲对于乙有某种关系,则乙对于甲也有 这种关系 . 可以用一个图形来描述给定对象之间的某 个关系:我们用平面上的点分别表示这些对象,若 对象甲和乙有关系,就用一条线连接表示甲和乙的 两个点 . 这种由一些点与连接其中某些点对的线所构 成的图形就是图论中所研究的图. 图/Graph:可直观地表示离散对象之间的相互关系, 研究它们的共性和特性,以便解决具体问题。
《图论》chap1-3练习提示

《图论》1-3章练习提示1. 证明:在10个人中,或有3个人互相认识,或有4个人互不认识。
解:设x为10人中之任意某人,则在余下9人中:(1) x至少认识其中4人,或(2) x至多认识其中3人(即至少不认识其中6人),两者必居其一。
(1) 若此x认识的4人互不相识,命题得证;否则,互相认识的2人加上x构成互相认识的3人,命题得证。
(2)若此x不认识的6人中有3人互相认识,命题得证;否则,由Ramsey(3,3)=6知,此6人中至少有3人互不认识,此3人加上x为互不认识的4人,命题得证。
(思考:以10个人为顶点,认识为红边,不认识为蓝边建立图的模型,上述过程如何叙述)2. 证明:Ramsey(3,4)=9。
(提示:1的推广)解:在9个人中,不可能每个人都恰好认识其他的3个人(即图的9个顶点不可能每个顶点的度都为3,否则违反图的奇数度的顶点必为偶数个的性质)。
设x不会恰好认识其他的3个人(即deg(x)≠3),则在余下8人中::(1) x至少认识其中4人,或(2) x至多认识其中2人(即至少不认识其中6人),两者必居其一。
由题1的过程,命题得证。
3. 证明:在至少有2人的团体中,总存在2个人,他们在这个团体中恰有相同数目的朋友。
解:在n个人的团体中,各人可能有的朋友数目为0, 1, 2, 3, …, n-1,共n个数,但其中0和n-1 不能共存,故n个人事实上可能的朋友数目只有n-1个。
由鸽巢原理,命题得证。
4. 设V={a,b,c,d},A={<a,b>,<a,c>,<b,c>,<b,d>,<c,d>}V={a,b,c,d,e},E={(a,b),(a,c),(b,c),(d,e)}分别画出上述图的图解。
解:略。
5. 试找出K3的全部子图,并指出哪些是生成子图。
解:给各个顶点标号后的K3共有17个子图。
其他略。
6.某次宴会上许多人互相握手。
图论经典问题
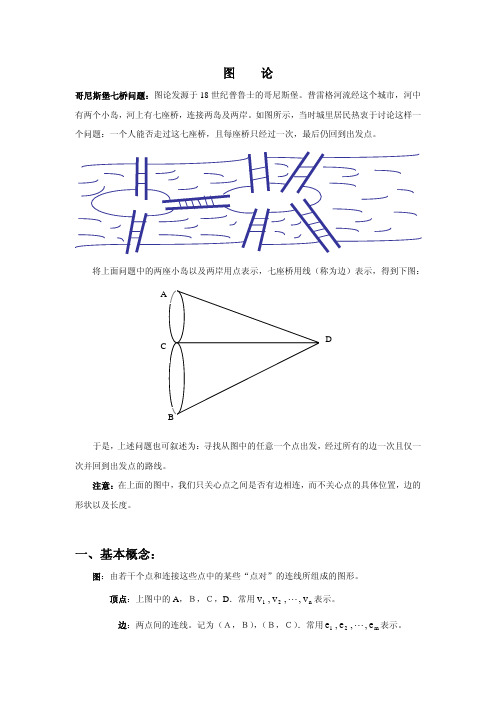
图 论哥尼斯堡七桥问题:图论发源于18世纪普鲁士的哥尼斯堡。
普雷格河流经这个城市,河中有两个小岛,河上有七座桥,连接两岛及两岸。
如图所示,当时城里居民热衷于讨论这样一个问题:一个人能否走过这七座桥,且每座桥只经过一次,最后仍回到出发点。
将上面问题中的两座小岛以及两岸用点表示,七座桥用线(称为边)表示,得到下图:于是,上述问题也可叙述为:寻找从图中的任意一个点出发,经过所有的边一次且仅一次并回到出发点的路线。
注意:在上面的图中,我们只关心点之间是否有边相连,而不关心点的具体位置,边的形状以及长度。
一、基本概念:图:由若干个点和连接这些点中的某些“点对”的连线所组成的图形。
顶点:上图中的A ,B,C,D .常用表示。
n 21 v , , v , v 边:两点间的连线。
记为(A,B),(B,C).常用表示。
m 21e , , e , e次:一个点所连的边数。
定点v的次记为d(v).图的常用记号:G=(V,E),其中,}{v V i =,}{e E i =子图:图G的部分点和部分边构成的图,成为其子图。
路:图G中的点边交错序列,若每条边都是其前后两点的关联边,则称该点边序列为图G的一条链。
圈(回路):一条路中所含边点均不相同,且起点和终点是同一点,则称该路为圈(回路)。
有向图:,其中(,)G N A =12{,,,}k N n n n = 称为的顶点集合,A a 称为G 的弧集合。
G {(,)ij i j }n n ==若,则称为的前驱, 为n 的后继。
(,)ij i j a n n =i n j n j n i 赋权图(网络):设是一个图,若对G 的每一条边(弧)都赋予一个实数,称为边的权,。
记为。
G (,,)G N E W =两个结论:1、图中所有顶点度数之和等于边数的二倍; 2、图中奇点个数必为偶数。
二、图的计算机存储:1. 关联矩阵简单图:,对应(,)G N E =N E ×阶矩阵()ik B b =10ik i k b ⎧=⎨⎩点与边关联否则简单有向图:,对应(,)G N A =N A ×阶矩阵()ik B b =110ik ik ik a i b a i ⎧⎪=−⎨⎪⎩弧以点为尾弧以点为头否则2. 邻接矩阵简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =10ij i j a ⎧=⎨⎩点与点邻接否则简单有向图:,对应(,)G N A =N N ×阶矩阵()ij A a =10ij i ja ⎧=⎨⎩有弧从连向否则5v 34v01010110100101011110101000110111101065432166654321⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=×v v v v v v A v v v v v v3. 权矩阵:简单图:,对应(,)G N E =N N ×阶矩阵()ij A a =ij ij i j a ω⎧=⎨∞⎩点与点邻接否则123456781234567802130654.5061002907250473080 v v v v v v v v v v v v v v v v 48∞∞∞∞⎡⎤⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞∞⎢⎥∞∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞⎢⎥⎢⎥∞∞∞∞⎢⎥∞∞∞∞∞∞⎢⎥⎣⎦三、图的应用:例:如图,用点代表7个村庄,边上的权代表村庄之间的路长,现在要在这7个村庄中布电话线,如何布线,使材料最省?分析:需要将图中的边进行删减,使得最终留下的图仍然连通,并且使总的权值最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A S1 C1
C
S B C
96上海应用竞赛题
设A,B,C三个工厂,它们的距离分别是 AB=13km,BC=14km,CA=15km. 要 求 寻 找一个供应站点H,使该点到三个工厂 的距离之和HA+HB+HC为最短,并求出 最短距离。
正方形中的费马点问题
有四个点位于正方形的四个顶点
上,需用线将它们连成一个网络, 问此网络应按什么方式连接这四 点方可使所用线的总长最小?
2 A 3 I 5 2 2 2 H 5 1 G B 1 4 S 1 C 3 2 1 D 4 3 2 E 2 F
斯坦纳最小树
在 欧 氏 平 面 上 任 给 有 限 点 集 R={u1, u2,…,un}, 试 求 一 点 集 S={s1,s2,…, sk},用线把点集R∪S连接起来,如何连 接才能使连线的总长度最短?
B a100 l100 A j 200 i150 I h90 k500 0400 n300 p300 G f90 F E e100 b100 C c200 D m400 d100
H g90
贪婪算法、破圈法
1 7 3 9 4
1
6 2 5
3 5
2
如图,某出口加工区总公司与下属各子公司 进行信息联网,已测得各子公司A、B、C、 D、E、F、G、H、I之间与总公司S联网费 用如图2所示(单位:千元)。现拟设计一 个联网优化方案,既要求各子公司之间以及 总公司都能连通,又要使联网费用最省最短的图, 称为斯坦纳最小树,记SRT。
1 若R={u1,u2,…,un},则SRT中斯坦纳 点的个数不大于n-2。 2 SRT上的斯坦纳点必在点集R的凸包之中。 3 SRT上每个点至多关联三条边,而每个斯 坦纳点恰好关联三条边。 4 SRT上,关联于同一点的任何两边的夹角 不小于120 0 ;关联于同一斯坦纳点的任何两 边夹角恰好为1200。
最小生成树和斯坦纳最小树
最小生成树
应用领域:——网络连接 铁路网,输电网,通信网,自来水管 道,煤气管道、分子结构等。 树:连通且无圈的图。 性质: 若树有n个顶点,则它有(n-1)条边。
有一个石油公司计划为它拥有的许多存储站设计一个管 道连接系统,它共有九个存储站,如果两个存储站之间 可以修管道,我们就用一条边连接起来,用一个数表示 修这两站之间的管道所需的费用(单位:千元),这样 这个公司所有的存储站和可能修管道的情况完全可以通 过下面这个图表示。公司设计计划要求:管道网可以把 任何两个存储站都连接起来,且装修费用最少。
D
局部调整.保持AM+BM不变时, 则M在以A,B为焦点的椭圆;保 持CN+DN不变时,N也在以C,D为 焦点的椭圆上。 调整M,N,当AM=BM,CN=DN时, M,N最近,即只有M,N在AB(或AD) 的中垂线上,总线长才会最短。
用费马点,知M,N为三角形 AOB与COD的费马点
B A
C
D
M
N
B
A O N
C
D
M
B
C
4)当网络中增加3个点时,
多 余
存在某个点是多余的。 同样,当网络增加3个以上点时,也只有其 中的两点时必须的。 综上所述,增加两个点时的情形所 用线的总长度最短。
问题
爱国华侨H先生准备在X市捐 建一座圆形公园,公园里要 建六个颇具特色的凉亭:在 圆形公园的六个角(即正六 F 边形的六个顶点)上和公园 中心各建一个美丽的凉亭。 要求:在六个凉亭和公园中 心间修道路,从每个亭子出 来都能走到另外任何一个亭 子,如何设计道路总长最短?
显然,符合要求的网络 一定是由直线段连成的。 按照网络中增加的点数进行分类。
1)当网络没增加点时, 相当于正方形的三边, 即最小生成树;
2)当网络中增加一个点时,
相当于正方形的两条对角线
3)当网络中增加两个点M,N时, 如何确定M,N的位置,使 (AM+BM)+MN+(CN+DN)最小?
A N M
费马点问题:
在欧氏平面上,任给一个三角形ABC,试 求一点S,使它到A、B、C三点的距离之 和为最小。
△ABC中,∠A最大,S是△ABC内的点。 1 ) 当 ∠ A<1200 时 , 若 S 满 足 ASB=∠BSC=∠CSA=1200,则它到A、B、 C三点的距离之和最小。 A
B1 S1
2)当∠A≥120时,所求的点为 S A;即SA+SB+SC≥AB+AC.
A
B
O
C
E
D
斯坦纳最小树
在 欧 氏 平 面 上 任 给 有 限 点 集 R={u1, u2,…,un},试求一点集S={s1,s2,…, sk},用线把点集R∪S连接起来,如何连 接才能使连线的总长度最短? 允许在已有图上的点以外添设其他点, 那么图上的最短线满足:最短线/原计算 线不超过0.866
