极坐标习题
极坐标方程大题练习题

极坐标方程大题练习题一、基本概念与性质1. 将直角坐标系下的点 (3, 4) 转换为极坐标系下的坐标。
2. 已知极坐标方程ρ = 4sinθ,求对应的直角坐标方程。
3. 判断下列极坐标方程是否表示圆:(1) ρ = 6cosθ(2) ρ = 3 + 2sinθ4. 已知极坐标方程ρ = 2cosθ,求极点与极轴之间的夹角。
二、极坐标方程的求解5. 求极坐标方程ρ = 4cosθ 与ρ = 2sinθ 的交点坐标。
6. 已知极坐标方程ρ = 3sinθ,求当θ =π/3 时的点坐标。
7. 解极坐标方程ρ = 5 3cosθ,求出所有可能的ρ 值。
8. 已知极坐标方程ρ = 4 2sinθ,求该曲线与极轴的交点坐标。
三、极坐标方程的应用9. 在极坐标系中,求直线ρcosθ = 3 与圆ρ = 4sinθ 的交点坐标。
10. 已知点 A 在极坐标方程ρ = 6sinθ 上,点 B 在极坐标方程ρ = 4cosθ 上,求线段 AB 的长度。
11. 在极坐标系中,求曲线ρ = 2 + 3sinθ 与极轴围成的面积。
12. 已知极坐标方程ρ = 5cosθ,求该曲线所围成的图形的面积。
四、综合题13. 在极坐标系中,求曲线ρ = 4sinθ 与直线θ = π/4 所围成的图形的面积。
14. 已知极坐标方程ρ = 2cosθ,求该曲线关于极轴的对称曲线方程。
15. 在极坐标系中,求曲线ρ = 3 + 2sinθ 与极轴之间的夹角。
16. 已知极坐标方程ρ = 4cosθ,求该曲线关于原点的对称曲线方程。
17. 在极坐标系中,求曲线ρ = 6sinθ 与直线ρcosθ = 3的交点坐标,并判断这些交点是否在第一象限。
18. 已知极坐标方程ρ = 5 4sinθ,求该曲线与极轴的交点坐标,并计算这些交点与极点之间的距离。
五、极坐标方程的变换与简化19. 将极坐标方程ρ = 8cosθ 转换为直角坐标系下的方程,并简化。
极坐标方程练习题

极坐标方程练习题极坐标方程练习题极坐标方程是一种用极径和极角来表示平面上点的坐标的方法。
它在数学中具有广泛的应用,尤其在物理学和工程学中常常被使用。
为了更好地理解和掌握极坐标方程,下面将介绍一些极坐标方程的练习题,并逐步解答。
1. 练习题一:给定一个极坐标方程r = 2cosθ,求解该方程的图形。
首先,我们可以通过观察方程,发现当极角θ为0时,极径r为2;当极角θ为π/2时,极径r为0;当极角θ为π时,极径r为-2。
根据这些点的坐标,我们可以绘制出一个图形。
此时,我们可以发现该图形是一个以原点为中心的圆形,半径为2。
2. 练习题二:给定一个极坐标方程r = 3sin2θ,求解该方程的图形。
同样地,我们可以观察方程,当极角θ为0时,极径r为0;当极角θ为π/4时,极径r为3;当极角θ为π/2时,极径r为0;当极角θ为3π/4时,极径r 为-3。
根据这些点的坐标,我们可以绘制出一个图形。
此时,我们可以发现该图形是一个以原点为中心的叶状曲线。
3. 练习题三:给定一个极坐标方程r = 4cos3θ,求解该方程的图形。
观察方程,当极角θ为0时,极径r为4;当极角θ为π/6时,极径r为2;当极角θ为π/3时,极径r为0;当极角θ为π/2时,极径r为-4。
根据这些点的坐标,我们可以绘制出一个图形。
此时,我们可以发现该图形是一个以原点为中心的心形曲线。
通过以上三个练习题,我们可以看到极坐标方程的图形多样且有趣。
通过观察方程中的极径和极角的变化,我们可以更好地理解和描述这些图形。
在实际应用中,极坐标方程也有很多用途。
例如,在天文学中,我们可以利用极坐标方程来描述行星的轨道;在物理学中,我们可以利用极坐标方程来描述电场的分布。
因此,掌握极坐标方程的技巧对于理解和解决实际问题具有重要意义。
除了上述的练习题外,还有许多其他类型的极坐标方程可以进行练习和探索。
通过不断地练习和思考,我们可以进一步加深对极坐标方程的理解和应用能力。
极坐标系的应用练习题

极坐标系的应用练习题极坐标系是一种描述平面上点位置的坐标系统,它由点到极点的距离和点与极轴的夹角两个参数确定。
在实际应用中,极坐标系有着广泛的应用。
本文将通过一些练习题来演示极坐标系的应用。
1. 题目一:求点的极坐标表示已知平面上一点P的直角坐标表示为(3, 4),求该点的极坐标表示。
解答:根据直角坐标到极坐标的转换公式,可以得到点到原点的距离r和点与x轴的夹角θ。
首先,通过勾股定理可以计算出点到原点的距离r:r = √(x^2 + y^2)代入已知坐标得:r = √(3^2 + 4^2) = 5接下来,使用反正切函数可以计算出点与x轴的夹角θ:θ = arctan(y / x)代入已知坐标得:θ = arctan(4 / 3)因此,该点的极坐标表示为(5, arctan(4 / 3))。
2. 题目二:求直线的极坐标方程已知平面上一直线L的直角坐标表示为2x + 3y = 6,求该直线的极坐标方程。
解答:直线的极坐标方程可以通过将直线方程转换为极坐标的形式得到。
首先,将直线方程转换为极坐标形式时,需要将直线方程写成标准形式,即y = f(x)的形式。
将2x + 3y = 6转换得:y = (6 - 2x) / 3接下来,可以通过直角坐标到极坐标的转换公式,将直线方程转换为极坐标的形式。
以点P(x, y)为例,将(x, y)代入上式得:r sin(θ) = (6 - 2r cos(θ)) / 3化简得:r = (6 sin(θ) - 2r cos(θ)) / 3sin(θ)移项得:r + 2r cos(θ) = 6 sin(θ) / 3sin(θ)化简得:r(1 + 2 cos(θ)) = 2因此,直线的极坐标方程为r = 2 / (1 + 2 cos(θ))。
3. 题目三:求曲线的极坐标方程已知平面上一曲线C的直角坐标表示为y = x^2,求该曲线的极坐标方程。
解答:曲线的极坐标方程可以通过将曲线方程转换为极坐标的形式得到。
极坐标系与参数方程专题

练习题学校:___________姓名:___________班级:___________考号:___________ 评卷人 得分一、选择题1.在极坐标系中,点)65,2(π到直线4)3sin(=-πθρ的距离为( ) A .1 B .2 C .3 D .4 2.在极坐标系中,设圆C :4cos ρθ=与直线:(R)4l πθρ=∈交于A ,B 两点,求以AB 为直径的圆的极坐标方程为( ) A .22sin()4πρθ=+B .22sin()4πρθ=-C .22cos()4πρθ=+D .22cos()4πρθ=-3.化极坐标方程2cos 0ρθρ-=为直角坐标方程为( ) A .221x y +=或1y = B .1x =C .221x y +=或1x = D .1y =4.已知圆的直角坐标方程为2220x y y +-=.在以原点为极点,x 轴正半轴为极轴的极坐标系中,该圆的方程为()A .2cos ρθ=B .2sin ρθ=C .2cos ρθ=-D .2sin ρθ=-5.在极坐标中,与圆4sin ρθ=相切的一条直线方程为( )A .sin 2ρθ=B .cos 2ρθ=C .cos 4ρθ=D .cos 4ρθ=-6.参数方程2cos (3sin x y θθθ=⎧⎨=⎩,,为参数)和极坐标方程4sin ρθ=所表示的图形分别是( )(A )圆和直线 (B )直线和直线 (C )椭圆和直线 (D )椭圆和圆 评卷人 得分二、填空题7.在极坐标系中,经过点)3,4(π且与极轴垂直的直线的极坐标方程为 .8.(坐标系与参数方程选做题)极坐标系下,直线2)4cos(=-πθρ与圆2=ρ的公共点个数是________;9.极坐标系中,圆θρsin 4=的圆心到直线)(3R ∈=θπθ 的距离是 .10.已知圆C 的参数方程为cos ,(1sin .x y ααα=⎧⎨=+⎩为参数),直线l 的极坐标方程为sin 1ρθ=,则直线l 与圆C 的交点的直角坐标为 .三、解答题(题型注释)11.在平面直角坐标系中,已知直线l 过点(),12P - ,倾斜角6πα=,再以原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为3ρ=. (Ⅰ)写出直线l 的参数方程和曲线C 的直角坐标方程;(Ⅱ)若直线l 与曲线C 分别交于、M N 两点,求PM PN ⋅的值.12.在极坐标系中,已知曲线)4sin(22:πθρ-=C ,P 为曲线C 上的动点,定点)4,1(πQ .(1)将曲线C 的方程化成直角坐标方程,并说明它是什么曲线; (2)求P 、Q 两点的最短距离.13.在平面直角坐标系xOy 中,直线l 经过点(10)A -,,其倾斜角是α,以原点O 为极点,以x 轴的非负半轴为极轴,与直角坐标系xOy 取相同的长度单位,建立极坐标系.设曲线C 的极坐标方程是26cos 5ρρθ=-.(Ⅰ)若直线l 和曲线C 有公共点,求倾斜角α的取值范围; (Ⅱ)设()B x y ,为曲线C 任意一点,求3x y +的取值范围.14.在直角坐标系xoy 中,直线l 的参数方程为212242x ty t ⎧=-⎪⎪⎨⎪=-⎪⎩(t 为参数).再以原点为极点,以x 正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy 有相同的长度单位.在该极坐标系中圆C 的方程为4sin ρθ=. (1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点A 、B ,若点M 的坐标为()2,1-,求MA MB +的值.15.在极坐标系中,已知点A 的极坐标为(22,)4π-,圆E 的极坐标方程为4cos 4sin ρθθ=+,试判断点A 和圆E 的位置关系16.已知曲线1C 的参数方程为45cos ,55sin x t y t=+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (1)把1C 的参数方程化为极坐标方程;(2)求1C 与2C 交点的极坐标(0,02ρθπ≥≤<).17.在平面直角坐标系xoy 中,已知曲线1cos :sin x C y θθ=⎧⎨=⎩(θ为参数),将1C 上的所有点的横坐标、纵坐标分别伸长为原来的2和2倍后得到曲线2C ,以平面直角坐标系xoy 的原点O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线():2cos sin 4l ρθθ+=.(1)试写出曲线1C 的极坐标方程与曲线2C 的参数方程;(2)在曲线2C 上求一点P ,使点P 到直线l 的距离最小,并求此最小值.18.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知曲线12cos :3sin x C y αα=-+⎧⎨=+⎩(α为参数),28cos :23sin x Cy θθ=⎧⎪⎨=⎪⎩(θ为参数). (1)将12,C C 的方程化为普通方程,并说明它们分别表示什么曲线; (2)若1C 上的点P 对应的参数为2πα=,Q 为2C 上的动点,求PQ 中点M 到直线l :cos 33πρθ⎛⎫-= ⎪⎝⎭的距离的最大值.19.在直角坐标系中,以O 为极点,x 轴正半轴为极轴建立极坐标系.曲线C 的极坐标方程为,M ,N 分别为C 与x 轴,y 轴的交点.(1)写出C 的直角坐标方程,并求M 、N 的极坐标; (2)设MN 的中点为P ,求直线OP 的极坐标方程.20.在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立坐标系.已知点A 的极坐标为2,4π⎛⎫⎪⎝⎭,直线的极坐标方程为cos 4a πρθ⎛⎫-= ⎪⎝⎭,且点A 在直线上.(1)求a 的值及直线的直角坐标方程;(2)圆C 的参数方程为1cos sin x y αα=+⎧⎨=⎩,(α为参数),试判断直线与圆的位置关系.21.在平面直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为()2sincos 0a a ρθθ=>,过点()2,4P --的直线l 的参数方程为222242x ty t ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t 为参数),直线l 与曲线C 相交于,A B 两点.(Ⅰ)写出曲线C 的直角坐标方程和直线l 的普通方程; (Ⅱ)若2PA PB AB ⋅=,求a 的值.22.在直角坐标系xoy 中,直线l 的参数方程为122322x t y t ⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数),若以直角极坐标方程为2cos()4πρθ=-.(1)求直线l 的倾斜角;(2)若直线l 与曲线C 交于,A B 两点,求AB 的距离.23.已知在直角坐标系xOy 中,曲线t t y t x C (,233,211:1⎪⎪⎩⎪⎪⎨⎧+-=+-=为参数,)2≠t ,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线θρsin 32:2=C ,曲线θρcos 2:3=C . (Ⅰ)求C 2与C 3交点的直角坐标;(Ⅱ)若C 2与C 1相交于点A ,C 3与C 1相交于点B ,求||AB 的值.24.在直角坐标系xOy 中,圆C 的参数方程1cos (sin x y ϕϕϕ=+⎧⎨=⎩为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系. (Ⅰ)求圆C 的极坐标方程; (Ⅱ)射线4:πθ=OM 与圆C 的交点为O 、P 两点,求P 点的极坐标.25.已知曲线C 的参数方程是()cos sin x y m ααα=⎧⎨=+⎩为参数,直线l 的参数方程为()5152545x t t y t ⎧=+⎪⎪⎨⎪=+⎪⎩为参数, (1)求曲线C 与直线l 的普通方程;(2)若直线l 与曲线C 相交于,P Q 两点,且455PQ =,求实数m 的值。
极坐标练习题

《极坐标》练习题1.已知⎪⎭⎫ ⎝⎛-3,5πM ,下列所给出的不能表示点M 的坐标的是( ) 2.点()3,1-P ,则它的极坐标是( )3.极坐标方程⎪⎭⎫⎝⎛-=θπρ4cos 表示的曲线是( ) 4.圆)sin (cos 2θθρ+=的圆心坐标是( )5.在极坐标系中,与圆θρsin 4=相切的一条直线方程为( )6、 已知点()0,0,43,2,2,2O B A ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--ππ则ABO ∆为( ) 7、)0(4≤=ρπθ表示的图形是( )8、直线αθ=与1)cos(=-αθρ的位置关系是( )9.两圆θρcos 2=,θρsin 2=的公共部分面积是( )10.极坐标方程cos 2sin 2ρθθ=表示的曲线为( )11、曲线的θθρcos 3sin -=直角坐标方程为_12.极坐标方程52sin42=θρ化为直角坐标方程是 13.圆心为⎪⎭⎫ ⎝⎛6,3πC ,半径为3的圆的极坐标方程为 14.已知直线的极坐标方程为22)4sin(=+πθρ,则极点到直线的距离是 15、在极坐标系中,点P ⎪⎭⎫ ⎝⎛611,2π到直线1)6sin(=-πθρ的距离等于____________。
16、与曲线01cos =+θρ关于4πθ=对称的曲线的极坐标方程是__________________。
17、 在极坐标中,若过点(3,0)且与极轴垂直的直线交曲线θρcos 4=于A 、B 两点, 则|AB|= 。
18、(1)把点M 的极坐标)32,8(π,),611,4(π),2(π-化成直角坐标 (2)把点P 的直角坐标)2,6(-,)15,0()2,2(--和化成极坐标19、极坐标与直角坐标互化(1)4=x(2)0132=--y x(3)(2cos 5sin )40ρθθ+-=(4)()6sin 3cos =+θθρ(5)(4cos 5sin )20ρθθ-+= (6)sin 24πρθ⎛⎫+= ⎪⎝⎭20、说明下列极坐标方程表示什么曲线,并画图。
极坐标方程基础习题附答案

极坐标方程基础习题附答案Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】1.已知点P 的极坐标为,则点P 的直角坐标为( ) A .(1,) B . (1,﹣) C . (,1) D . (,﹣1) 2.极坐标系中,B A ,分别是直线05sin 4cos 3=+-θρθρ和圆θρcos 2=上的动点,则B A ,两点之间距离的最小值是 .3.已知曲线C 的极坐标方程为2ρ=(0,02ρθπ>≤< ),曲线C 在点(2,4π)处的切线为l ,以极点为坐标原点,以极轴为x 轴的正半轴建立直角坐标系,则l 的直角坐标方程为 ▲ .4.在极坐标系中,已知直线把曲线所围成的区域分成面积相等的两部分,则常数a 的值是 .5.在极坐标系中,圆2cos ρθ=的圆心到直线cos 2ρθ=的距离是____________.6.在极坐标系中,圆4sin ρθ=的圆心到直线()6R πθρ=∈的距离是______________.7.在极坐标系(),ρθ(0,02πρθ>≤<)中,曲线2sin ρθ=与2cos ρθ=的交点的极坐标为_____8.(坐标系与参数方程选做题)曲线2cos 4πρθθ==关于直线对称的曲线的极坐标方程为 。
试卷答案考点:点的极坐标和直角坐标的互化.专题:计算题. 分析: 利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,可求出点的直角坐标.解答: 解:x=ρcosθ=2×cos =1, y=ρsinθ=2×sin = ∴将极坐标(2,)化为直角坐标是(1,). 故选A .点评: 本题主要考查了点的极坐标和直角坐标的互化,同时考查了三角函数求值,属于基础题. 2.略3. 4.1a =-略5.曲线θρcos 2=即()2211x y -+=,表示圆心在(1,0),半径等于1的圆,直线cos 2ρθ=即直线2=x ,故圆心到直线的距离为1。
极坐标练习题

一、选择题1.将曲线y =sin 2x 按照伸缩变换⎩⎨⎧x ′=2x ,y ′=3y 后得到的曲线方程为( )A.y =3sin xB.y =3sin 2xC.y =3sin 12xD.y =13sin 2x2.极坐标方程sin θ=12(ρ∈R ,ρ≥0)表示的曲线是( ) A.两条相交直线 B.两条射线 C.一条直线 D.一条射线 3.极坐标方程ρ=cos θ化为直角坐标方程为( )A.⎝ ⎛⎭⎪⎫x +122+y 2=14B.x 2+⎝ ⎛⎭⎪⎫y +122=14C.x 2+⎝ ⎛⎭⎪⎫y -122=14D.⎝ ⎛⎭⎪⎫x -122+y 2=144.与点A (-1,0)和点B (1,0)连线的斜率之和为-1的动点P 的轨迹方程是( ) A.x 2+y 2=3 B.x 2+2xy =1(x ≠±1) C.y =1-x 2D.x 2+y 2=9(x ≠0)5.如图1,已知点P 的极坐标是(1,π),则过点P 且垂直极轴的直线的极坐标方程是( ) A.ρ=1 B.ρ=cos θC.ρ=-1cos θD.ρ=1cos θ6.圆ρ=4cos θ的圆心到直线tan θ=1的距离为( ) A.22 B.2 C.2D.2 27.点M ⎝ ⎛⎭⎪⎫1,7π6关于直线θ=π4(ρ∈R )的对称点的极坐标为( )A.⎝ ⎛⎭⎪⎫1,4π3B.⎝ ⎛⎭⎪⎫1,2π3C.⎝ ⎛⎭⎪⎫1,π3D.⎝ ⎛⎭⎪⎫1,-7π6 8.极坐标方程ρcos θ=2sin 2θ表示的曲线为( )A.一条射线和一个圆B.两条直线C.一条直线和一个圆D.一个圆 9.圆ρ=r 与圆ρ=-2r sin ⎝ ⎛⎭⎪⎫θ+π4(r >0)的公共弦所在直线的方程为( )A.2ρ(sin θ+cos θ)=rB.2ρ(sin θ+cos θ)=-rC.2ρ(sin θ+cos θ)=rD.2ρ(sin θ+cos θ)=-r 10.圆ρ=2a sin θ关于极轴对称的圆的方程为( )A.ρ=2a cos θB.ρ=-2a cos θC.ρ=-2a sin θD.ρ=2a sin θ 11.直线θ=α和直线ρsin (θ-α)=1的位置关系是( ) A.垂直 B.平行 C.相交但不垂直 D.重合 二、填空题12.在极坐标系中,点⎝ ⎛⎭⎪⎫2,π6到直线ρsin ⎝ ⎛⎭⎪⎫θ-π6=1的距离是________.13.已知极坐标系中,极点为O ,将点A ⎝ ⎛⎭⎪⎫4,π6绕极点逆时针旋转π4得到点B ,且|OA |=|OB |,则点B 的直角坐标为________.三、解答题14.在同一平面直角坐标系中,经过伸缩变换⎩⎨⎧x ′=2x ,y ′=2y 后,曲线C 变为曲线(x ′-5)2+(y ′+6)2=1,求曲线C 的方程,并判断其形状.15.已知⊙C :ρ=cos θ+sin θ, 直线l :ρ=22cos ⎝ ⎛⎭⎪⎫θ+π4.求⊙C 上点到直线l 距离的最小值.16.(1)在极坐标系中,求以点(1,1)为圆心,半径为1的圆C 的方程; (2)将上述圆C 绕极点逆时针旋转π2得到圆D ,求圆D 的方程.17.在极坐标系中,极点为O ,已知曲线C 1:ρ=2与曲线C 2:ρsin ⎝ ⎛⎭⎪⎫θ-π4=2交于不同的两点A ,B .(1)求|AB |的值;(2)求过点C (1,0)且与直线AB 平行的直线l 的极坐标方程. 一、选择题1.将曲线y =sin 2x 按照伸缩变换⎩⎨⎧x ′=2x ,y ′=3y 后得到的曲线方程为( )A.y =3sin xB.y =3sin 2xC.y =3sin 12xD.y =13sin 2x【解析】 由伸缩变换,得x =x ′2,y =y ′3. 代入y =sin 2x ,有y ′3=sin x ′,即y ′=3sin x ′. ∴变换后的曲线方程为y =3sin x . 【答案】 A2.极坐标方程sin θ=12(ρ∈R ,ρ≥0)表示的曲线是( ) A.两条相交直线 B.两条射线 C.一条直线 D.一条射线【解析】 ∵sin θ=12,所以θ=π6(ρ≥0)和θ=56π(ρ≥0),故其表示两条射线. 【答案】 B3.极坐标方程ρ=cos θ化为直角坐标方程为( )A.⎝ ⎛⎭⎪⎫x +122+y 2=14B.x 2+⎝ ⎛⎭⎪⎫y +122=14C.x 2+⎝ ⎛⎭⎪⎫y -122=14D.⎝ ⎛⎭⎪⎫x -122+y 2=14 【解析】 由ρ=cos θ,得ρ2=ρcos θ,所以x 2+y 2=x ,即⎝ ⎛⎭⎪⎫x -122+y 2=14.故选D.【答案】 D4.与点A (-1,0)和点B (1,0)连线的斜率之和为-1的动点P 的轨迹方程是( ) A.x 2+y 2=3 B.x 2+2xy =1(x ≠±1) C.y =1-x 2D.x 2+y 2=9(x ≠0)【解析】 设P (x ,y ),则k P A =y x +1(x ≠-1),k PB =yx -1(x ≠1). 又k P A +k PB =-1,即y x +1+y x -1=-1,得 x 2+2xy =1(x ≠±1),故选B. 【答案】 B5.如图1,已知点P 的极坐标是(1,π),则过点P 且垂直极轴的直线的极坐标方程是( )A.ρ=1B.ρ=cos θC.ρ=-1cos θD.ρ=1cos θ【解析】 由题图可知ρcos(π-θ)=1, 即ρ=-1cos θ,故选C. 【答案】 C6.圆ρ=4cos θ的圆心到直线tan θ=1的距离为( ) A.22 B.2 C.2D.2 2【解析】 圆ρ=4cos θ的圆心C (2,0),如图,|OC |=2, 在Rt △COD 中, ∠ODC =π2,∠COD =π4, ∴|CD |= 2.即圆ρ=4cos θ的圆心到直线tan θ=1的距离为 2. 【答案】 B7.点M ⎝ ⎛⎭⎪⎫1,7π6关于直线θ=π4(ρ∈R )的对称点的极坐标为( )A.⎝ ⎛⎭⎪⎫1,4π3B.⎝ ⎛⎭⎪⎫1,2π3C.⎝ ⎛⎭⎪⎫1,π3D.⎝ ⎛⎭⎪⎫1,-7π6 【解析】 点M ⎝ ⎛⎭⎪⎫1,7π6的直角坐标为⎝ ⎛⎭⎪⎫cos 7π6,sin 7π6=⎝ ⎛⎭⎪⎫-32,-12,直线θ=π4(ρ∈R ),即直线y =x ,点⎝ ⎛⎭⎪⎫-32,-12关于直线y =x 的对称点为⎝ ⎛⎭⎪⎫-12,-32,再化为极坐标,即⎝ ⎛⎭⎪⎫1,4π3.【答案】 A8.极坐标方程ρcos θ=2sin 2θ表示的曲线为( ) A.一条射线和一个圆 B.两条直线 C.一条直线和一个圆 D.一个圆【解析】 方程ρcos θ=2sin 2θ可化为ρcos θ=4sin θcos θ,即cos θ=0或ρ=4sin θ,方程cos θ=0即θ=k π+π2,表示y 轴,方程ρ=4sin θ即x 2+y 2=4y ,表示圆,故选C.【答案】 C9.圆ρ=r 与圆ρ=-2r sin ⎝ ⎛⎭⎪⎫θ+π4(r >0)的公共弦所在直线的方程为( )A.2ρ(sin θ+cos θ)=rB.2ρ(sin θ+cos θ)=-rC.2ρ(sin θ+cos θ)=rD.2ρ(sin θ+cos θ)=-r 【解析】 圆ρ=r 的直角坐标方程为 x 2+y 2=r 2,① 圆ρ=-2r sin ⎝ ⎛⎭⎪⎫θ+π4=-2r ⎝ ⎛⎭⎪⎫sin θcos π4+cos θsin π4=-2r (sin θ+cos θ).两边同乘以ρ得ρ2=-2r (ρsin θ+ρcos θ). ∵x =ρcos θ,y =ρsin θ,ρ2=x 2+y 2, ∴x 2+y 2+2rx +2ry =0.②①-②整理得2(x +y )=-r ,即为两圆公共弦所在直线的普通方程.再将直线2(x +y )=-r 化为极坐标方程为2ρ(cos θ+sin θ)=-r .【答案】 D10.圆ρ=2a sin θ关于极轴对称的圆的方程为( )A.ρ=2a cos θB.ρ=-2a cos θC.ρ=-2a sin θD.ρ=2a sin θ 【解析】 法一:根据对称规律,把⎩⎪⎨⎪⎧θ′=-θ,ρ′=ρ代入原方程,可得原方程表示的曲线关于极轴对称的曲线方程.∴ρ=2a sin θ关于极轴对称的曲线方程为ρ′=2a sin (-θ),即ρ=-2a sin θ. 法二:因为圆ρ=2a sin θ的圆心是⎝ ⎛⎭⎪⎫a ,π2,半径为a ,该圆关于极轴对称的圆的圆心应为⎝ ⎛⎭⎪⎫a ,3π2,半径仍为a , 其方程应为:ρ=2a cos ⎝ ⎛⎭⎪⎫θ-3π2,即ρ=-2a sin θ. 【答案】 C11.直线θ=α和直线ρsin (θ-α)=1的位置关系是( ) A.垂直 B.平行 C.相交但不垂直 D.重合【解析】 直线θ=α化为直角坐标方程为y =x tan α,ρsin (θ-α)=1化为ρsin θcos α-ρcos θsin α=1,即y =x tan α+1cos α.所以两直线平行. 【答案】 B 二、填空题12.在极坐标系中,点⎝ ⎛⎭⎪⎫2,π6到直线ρsin ⎝ ⎛⎭⎪⎫θ-π6=1的距离是________.【解析】 点⎝ ⎛⎭⎪⎫2,π6化为直角坐标为(3,1),直线ρsin ⎝ ⎛⎭⎪⎫θ-π6=1化为ρ⎝ ⎛⎭⎪⎫32sin θ-12cos θ=1,32y -12x =1,12x -32y +1=0,点(3,1)到直线12x -32y +1=0的距离为⎪⎪⎪⎪⎪⎪12×3-32×1+1⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫-322=1.【答案】 113.已知极坐标系中,极点为O ,将点A ⎝ ⎛⎭⎪⎫4,π6绕极点逆时针旋转π4得到点B ,且|OA |=|OB |,则点B 的直角坐标为________.【解析】 依题意,点B 的极坐标为⎝ ⎛⎭⎪⎫4,5π12,∵cos 5π12=cos ⎝ ⎛⎭⎪⎫π4+π6=cos π4cos π6-sin π4sin π6=22·32-22·12=6-24, sin 5π12=sin ⎝ ⎛⎭⎪⎫π4+π6=sin π4cos π6+cos π4sin π6=22·32+22·12=6+24,∴x =ρcos θ=4×6-24=6-2,∴y =ρsin θ=4×6+24=6+2, ∴点B 的直角坐标为(6-2,6+2). 【答案】 (6-2,6+2) 三、解答题14.在同一平面直角坐标系中,经过伸缩变换⎩⎨⎧x ′=2x ,y ′=2y 后,曲线C 变为曲线(x ′-5)2+(y ′+6)2=1,求曲线C 的方程,并判断其形状. 【解】 将⎩⎪⎨⎪⎧x ′=2x ,y ′=2y 代入(x ′-5)2+(y ′+6)2=1,得(2x -5)2+(2y +6)2=1, 即⎝ ⎛⎭⎪⎫x -522+(y +3)2=14, 故曲线C 是以⎝ ⎛⎭⎪⎫52,-3为圆心,半径为12的圆.15.已知⊙C :ρ=cos θ+sin θ, 直线l :ρ=22cos ⎝ ⎛⎭⎪⎫θ+π4.求⊙C 上点到直线l 距离的最小值.【解】 ⊙C 的直角坐标方程是x 2+y 2-x -y =0, 即⎝ ⎛⎭⎪⎫x -122+⎝ ⎛⎭⎪⎫y -122=12.又直线l 的极坐标方程为ρ(cos θ-sin θ)=4, 所以直线l 的直角坐标方程为x -y -4=0.设M ⎝ ⎛⎭⎪⎫12+22cos θ,12+22sin θ为⊙C 上任意一点,M 点到直线l 的距离d =⎪⎪⎪⎪⎪⎪12+22cos θ-⎝ ⎛⎭⎪⎫12+22sin θ-42=4-cos ⎝ ⎛⎭⎪⎫θ+π42,当θ=7π4时,d min =32=322.16.(1)在极坐标系中,求以点(1,1)为圆心,半径为1的圆C 的方程; (2)将上述圆C 绕极点逆时针旋转π2得到圆D ,求圆D 的方程. 【解】 (1)设M (ρ,θ)为圆上任意一点,如图,圆C 过极点O ,∠COM =θ-1,作CK ⊥OM 于K , 则|OM |=2|OK |=2cos(θ-1), 故圆C 的极坐标为ρ=2cos(θ-1).(2)将圆C :ρ=2cos(θ-1)按逆时针旋转π2得到圆D :ρ=2cos ⎝ ⎛⎭⎪⎫θ-1-π2,即ρ=-2sin(1-θ),故ρ=2sin(θ-1)为所求.17.在极坐标系中,极点为O ,已知曲线C 1:ρ=2与曲线C 2:ρsin ⎝ ⎛⎭⎪⎫θ-π4=2交于不同的两点A ,B .(1)求|AB |的值;(2)求过点C (1,0)且与直线AB 平行的直线l 的极坐标方程. 【解】 (1)法一:∵ρ=2,∴x 2+y 2=4. 又∵ρsin ⎝ ⎛⎭⎪⎫θ-π4=2,∴y =x +2. ∴|AB |=2r 2-d 2=24-⎝ ⎛⎭⎪⎫222=2 2. 法二:设A (ρ,θ1),B (ρ,θ2),θ1,θ2∈[0,2π), 则sin ⎝ ⎛⎭⎪⎫θ1-π4=22,sin ⎝ ⎛⎭⎪⎫θ2-π4=22.∵θ1,θ2∈[0,2π),∴|θ1-θ2|=π2,即∠AOB =π2, 又|OA |=|OB |=2, ∴|AB |=2 2.(2)法一:∵曲线C 2的斜率为1,∴过点(1,0)且与曲线C 2平行的直线l 的直角坐标方程为y =x -1,∴直线l 的极坐标为ρsin θ=ρcos θ-1, 即ρcos ⎝ ⎛⎭⎪⎫θ+π4=22.法二:设点P (ρ,θ)为直线l 上任一点,因为直线AB 与极轴成π4的角, 则∠PCO =3π4或∠PCO =π4, 当∠PCO =3π4时,在△POC 中,|OP |=ρ,|OC |=1,∠POC =θ,∠PCO =3π4,∠OPC =π4-θ, 由正弦定理可知:1sin ⎝ ⎛⎭⎪⎫π4-θ=ρsin 34π, 即ρsin ⎝ ⎛⎭⎪⎫π4-θ=22, 即直线l 的极坐标方程为:ρsin ⎝ ⎛⎭⎪⎫π4-θ=22.同理,当∠PCO =π4时,极坐标方程也为 ρsin ⎝ ⎛⎭⎪⎫π4-θ=22.当P 为点C 时显然满足ρsin ⎝ ⎛⎭⎪⎫π4-θ=22.综上,所求直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫π4-θ=22.。
极坐标练习题

极坐标练习题极坐标是一种描述平面上点位置的坐标系统,它使用极径和极角来表示点的位置。
在极坐标系统中,每个点由一个非负的极径和一个以极轴正向为起点的极角唯一确定。
极坐标与直角坐标之间的转换关系可以用以下公式表示:x = r * cosθy = r * sinθ其中,(x, y)为点的直角坐标,r为点到极轴的距离(极径),θ为点与极轴的夹角(极角)。
为了加深对极坐标的理解,下面给出一些极坐标的练习题,供读者练习和思考。
练习题一:给定极坐标(r, θ) = (3, π/6),请将其转换为直角坐标。
解析:根据转换公式可得,x = 3 * cos(π/6)y = 3 * sin(π/6)计算得出,x ≈ 2.598y ≈ 1.5所以,极坐标(3, π/6) 对应的直角坐标为 (2.598, 1.5)。
练习题二:给定直角坐标 (x, y) = (4, -2),请将其转换为极坐标。
解析:根据转换公式可得,r = √(x^2 + y^2)θ = arctan(y/x)计算得出,r ≈ √(4^2 + (-2)^2) ≈ √20 ≈ 4.472θ = arctan((-2)/4) ≈ -0.464所以,直角坐标 (4, -2) 对应的极坐标为 (4.472, -0.464)。
练习题三:给定一点在极坐标系下的表示为(5, 3π/4),请将该点表示在极坐标系中。
解析:该点的极径为 5,极角为3π/4。
在极坐标系中,从极轴正向开始逆时针旋转3π/4 的角度,然后向外延伸 5 的距离,即可标示出该点。
练习题四:给定一点在直角坐标系下的表示为 (-1, -1),请将该点表示在极坐标系中。
解析:该点的直角坐标为 (-1, -1)。
首先,计算出该点到原点的距离:r = √((-1)^2 + (-1)^2) ≈ √2 ≈ 1.414然后,计算出该点与极轴的夹角:θ = arctan((-1)/(-1)) = arctan(1) ≈ 0.785所以,直角坐标 (-1, -1) 对应的极坐标为 (1.414, 0.785)。
极坐标练习题

日测极坐标1.曲线cos 10ρθ+=的直角坐标方程为( )A .1x = B. 1x =- C. 1y = D. 1y =- 2.若M 点的极坐标为(2,)6π--,则M 点的直角坐标是( )A .(B .(1)-C .1)-D . 3.曲线的极坐标方程θρsin 4=化成直角坐标方程为( ) A.4)2(22=++y xB.4)2(22=-+y xC.4)2(22=+-yx D.4)2(22=++yx4.在极坐标系中,圆心为(1,)2π,且过极点的圆的方程是 ( )(A )2sin =ρθ (B )2sin =-ρθ (C )2cos =ρθ ( D )2cos =-ρθ5.极坐标方程cos ρθ=和参数方程123x ty t =--⎧⎨=+⎩(t 为参数)所表示的图形分别是A 、圆、直线B 、直线、圆C 、圆、圆D 、直线、直线 6.在极坐标方程中,曲线C 的方程是ρ=4sinθ,过点(4,6π)作曲线C 的切线,则切线长为( ) A . C . D .7.在极坐标系中,圆θρcos 2=的垂直于极轴的两条切线方程分别为( )(A )2cos R 0=∈=θρρθ)和((B )2cos R 2=∈=θρρπθ)和( (C )1cos R 2=∈=θρρπθ)和( (D )1cos R 0=∈=θρρθ)和(8.极坐标方程0))(1(=--πθρ)0(≥ρ表示的图形是( )A.两个圆B.两条直线C.一个圆和一条射线D.一条直线和一条射线 9.(极坐标)以直角坐标系的原点为极点,x 轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位,点M 的极坐标是)32,4(π,则点M 直角坐标是 A .)3,2( B .)3,2(- C .)2,3( D .)2,3(- 10.极坐标方程cos 2sin 2ρθθ=表示的曲线为A .一条射线和一个圆B .两条直线C .一条直线和一个圆D .一个圆 11.下列结论中不正确的是( ) A .(2,)6π与(2,)6π-是关于极轴对称 B .(2,)6π与7(2,)6π是关于极点对称C .(2,)6π与5(2,)6π-是关于极轴对称 D .(2,)6π与5(2,)6π--是关于极点对称 12.极坐标系中,以(9,3π)为圆心,9为半径的圆的极坐标方程为( ) A. )(θπρ-3cos 18= B. )(θπρ-3cos 18-= C. )(θπρ-3sin 18= D. )(θπρ-3cos 9=13.圆5cos ρθθ=-的圆心坐标是( ) A.4(5,)3π--B.(5,)3π-C.(5,)3πD.5(5,)3π- 14.在极坐标系中,与圆相切的一条直线方程为( ) A . B . C . D . 15.极坐标方程cos 2ρθ=0 表示的曲线为( )A 、极点B 、极轴C 、一条直线D 、两条相交直线 16.在极坐标系中,曲线cos sin 2ρθρθ+=(0θ≤﹤2π)与4πθ=的交点的极坐标为( )(A)(1,1) (B)(1,)4π(C))4π (D)()4π17.直线45395x t y t⎧=⎪⎪⎨⎪=-+⎪⎩(t 为参数)与圆2cos 2sin x y θθ=⎧⎨=⎩(θ为参数)的位置关系是A .相离B .相切 C.过圆心 D .相交不过圆心 18.已知圆22:4C x y +=,直线:2l x y +=,以O 为极点,x 轴的正半轴为极轴,取相同的单位长度建立极坐标系.(1)将圆C 和直线l 方程化为极坐标方程;(2)P 是l 上的点,射线OP 交圆C 于点R ,又点Q 在OP 上且满足2|OQ ||OP ||OR |⋅=,当点P 在l 上移动时,求点Q 轨迹的极坐标方程.19.在平面直角坐标系xoy 中,曲线1C 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (0>>b a ,ϕ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线2C 是圆心在极轴上,且经过极点的圆,已知曲线1C 上的点)23,1(M 对应的参数3πϕ=,射线3πθ=与曲线2C 交于点)3,1(πD(1)求曲线1C ,2C 的方程; (2)若点),(1θρA ,)2,(2πθρ+B 在曲线1C 上,求222111ρρ+的值20.已知曲线C 的极坐标方程为θθρ2sin cos 4=,直线l 的参数方程为⎩⎨⎧+==ααsin 1cos t y t x ( t为参数,0≤α<π).(Ⅰ)把曲线C 的极坐标方程化为直角坐标方程,并说明曲线C 的形状; (Ⅱ)若直线l 经过点(1,0),求直线l 被曲线C 截得的线段AB 的长.参考答案1.B【解析】考点:极坐标方程【解析】A 。
高考极坐标与参数方程习题大全

一、选择题(每小题5分,共25分)1、已知点M 的极坐标为⎪⎭⎫⎝⎛35π,,下列所给出的四个坐标中能表示点M 的坐标是( )。
A. 53,-⎛⎝ ⎫πB. 543,π⎛⎝ ⎫⎭⎪C. 523,-⎛⎝ ⎫⎭⎪πD. ⎪⎭⎫ ⎝⎛-355π, 2、直线:3x-4y-9=0与圆:⎩⎨⎧==θθsin 2cos 2y x ,(θ为参数)的位置关系是( )A.相切B.相离C.直线过圆心D.相交但直线不过圆心3、在参数方程⎩⎨⎧+=+=θθsin cos t b y t a x (t 为参数)所表示的曲线上有B 、C 两点,它们对应的参数值分别为t 1、t 2,则线段BC 的中点M 对应的参数值是( )4、曲线的参数方程为⎩⎨⎧-=+=12322t y t x (t 是参数),则曲线是( ) A 、线段 B 、双曲线的一支 C 、圆 D 、射线 5、实数x 、y 满足3x 2+2y 2=6x ,则x 2+y 2的最大值为( )A 、27 B 、4 C 、29D 、5二、填空题(每小题5分,共30分)1、点()22-,的极坐标为 。
2、若A 33,π⎛⎝ ⎫⎭⎪,B ⎪⎭⎫ ⎝⎛-64π,,则|AB|=___________,S AOB ∆=___________。
(其中O 是极点)3、极点到直线()cos sin ρθθ+=________ _____。
4、极坐标方程2sin 2cos 0ρθθ-⋅=表示的曲线是_______ _____。
5、圆锥曲线()为参数θθθ⎩⎨⎧==sec 3tan 2y x 的准线方程是 。
6、直线l 过点()5,10M ,倾斜角是3π,且与直线032=--y x 交于M ,则0MM 的长为 。
三、解答题(第1题14分,第2题16分,第3题15分;共45分)1、求圆心为C 36,π⎛⎝ ⎫⎭⎪,半径为3的圆的极坐标方程。
2、已知直线l 经过点P(1,1),倾斜角6πα=,(1)写出直线l 的参数方程。
极坐标方程大题练习题

极坐标方程大题练习题极坐标方程大题练习题极坐标方程是一种描述平面上点的坐标系统,它使用极径(表示点到原点的距离)和极角(表示点与正半轴的夹角)来确定点的位置。
在数学学习中,我们经常会遇到一些关于极坐标方程的大题练习题,这些题目旨在帮助我们熟悉和掌握极坐标方程的性质和应用。
假设我们有以下练习题:1. 给定极坐标方程r = 2cos(θ),求解当极角θ 为π/4 时,对应的点的坐标。
2. 给定极坐标方程r = 3sin(θ),求解当极角θ 为3π/2 时,对应的点的坐标。
3. 给定极坐标方程r = 4 + 2cos(θ),求解当极径 r 为 6 时,对应的极角θ 的范围。
这些练习题涉及到了极坐标方程的基本概念和性质。
对于第一个问题,我们可以通过将极角θ 替换为π/4,然后计算出 r 的值,进而确定对应点的坐标。
类似地,对于第二个问题,我们可以将极角θ 替换为3π/2,计算出 r 的值,并确定对应点的坐标。
第三个问题涉及到了极坐标方程中的极径,我们需要解方程4 + 2cos(θ) = 6,求解出对应的极角θ 的范围。
通过解答这些练习题,我们可以加深对极坐标方程的理解和应用。
极坐标方程在物理学、工程学和计算机图形学等领域中都有广泛的应用。
它可以用来描述圆形、螺旋线、花朵等曲线形状,也可以用来表示天体运动、电磁场分布等物理现象。
除了解答练习题,我们还可以通过绘制极坐标图形来进一步理解和应用极坐标方程。
通过将极径和极角转换为直角坐标系中的坐标,我们可以绘制出各种曲线形状,从而更直观地观察和分析极坐标方程的性质。
总之,通过大题练习题和图形绘制,我们可以更好地掌握极坐标方程的概念、性质和应用。
这些练习题和图形绘制不仅有助于我们提高数学解题能力,还有助于培养我们的空间想象力和创造力。
希望大家能够积极参与这些练习,提升自己在极坐标方程中的应用能力。
极坐标参数方程经典练习题带详细解答

1.极坐标系与直角坐标系xoy 有相同的长度单位,以原点O 为极点,以x 轴正半轴为极轴.已知直线l 的参数程为1222x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),曲线C 的极坐标程为2sin 8cos ρθθ=.(Ⅰ)求C 的直角坐标程;(Ⅱ)设直线l 与曲线C 交于,A B 两点,求弦长||AB .2.已知直线l 经过点1(,1)2P ,倾斜角α=6π,圆C的极坐标程为)4πρθ=-. (1)写出直线l 的参数程,并把圆C 的程化为直角坐标程;(2)设l 与圆C 相交于两点A 、B ,求点P 到A 、B 两点的距离之积.3.(本小题满分10分)选修4-4:坐标系与参数程已知直线l 的参数程是)(242222是参数t t y t x ⎪⎪⎩⎪⎪⎨⎧+==,圆C 的极坐标程为)4cos(2πθρ+=. (I )求圆心C 的直角坐标;(Ⅱ)由直线l 上的点向圆C 引切线,求切线长的最小值.4.已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x 轴的正半轴重合,且两坐标系有相同的长度单位,圆C 的参数程为12cos 12sin x y αα=+⎧⎨=-+⎩(α为参数),点Q的极坐标为7)4π。
(1)化圆C 的参数程为极坐标程;(2)直线l 过点Q 且与圆C 交于M ,N 两点,求当弦MN 的长度为最小时,直线l 的直角坐标程。
5.在极坐标系中,点M 坐标是)2,3(π,曲线C 的程为)4sin(22πθρ+=;以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,斜率是1-的直线l 经过点M .(1)写出直线l 的参数程和曲线C 的直角坐标程;(2)求证直线l 和曲线C 相交于两点A 、B ,并求||||MB MA ⋅的值.6.(本小题满分10分) 选修4-4坐标系与参数程在直角坐标系中,曲线1C 的参数程为⎩⎨⎧+==ααsin 22cos 2y x ,(α为参数) M 是曲线1C 上的动点,点P 满足OM 2=,(1)求点P 的轨迹程2C ;(2)在以D 为极点,X 轴的正半轴为极轴的极坐标系中,射线3πθ=与曲线1C ,2C 交于不同于原点的点A,B 求AB7.在平面直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐V 标程为πcos =13ρθ⎛⎫- ⎪⎝⎭,M ,N 分别为曲线C 与x 轴、y 轴的交点. (1)写出曲线C 的直角坐标程,并求M ,N 的极坐标;(2)求直线OM 的极坐标程.8.在直角坐标系中,曲线C 1的参数程为:2cos x y αα=⎧⎪⎨=⎪⎩(α为参数),以原点为极点,x 轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C 2是极坐标程为:cos ρθ=,(1)求曲线C 2的直角坐标程;(2)若P ,Q 分别是曲线C 1和C 2上的任意一点,求PQ 的最小值.9.已知圆C 的极坐标程为2cos ρθ=,直线l的参数程为1221122x t x t ⎧=+⎪⎪⎨⎪=+⎪⎩(t 为参数),点A的极坐标为4π⎫⎪⎪⎝⎭,设直线l 与圆C 交于点P 、Q .(1)写出圆C 的直角坐标程;(2)求AP AQ ⋅的值.10.已知动点P ,Q 都在曲线C :2cos 2sin x t y t =⎧⎨=⎩(β为参数)上,对应参数分别为t α= 与2t α=(0<α<2π),M 为PQ 的中点。
高中数学选修4-4同步练习题库:极坐标(填空题:较易)

极坐标(填空题:较易)1、(坐标系与参数方程选做题)在极坐标系中,直线被圆截得的弦长为 .2、在极坐标系中,设曲线和直线交于、两点,则__________.3、在平面直角坐标系中,点在角的终边上,且,则点的坐标为__________.4、将点的极坐标化为直角坐标为___________.5、极坐标系中,两点与间的距离为________.6、一直曲线C的参数方程为(t为参数)C在点(1,1)处的切线为l,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,则l的极坐标方程为_________。
7、在极坐标系中,点在圆上,点的坐标为,则的最大值为__________.8、在极坐标系中,直线与圆的公共点的个数为___________.9、在极坐标系中,点关于直线ρcos θ=1的对称点的极坐标为________.10、点的直角坐标为,则点的极坐标为__________________.11、在极坐标系中,以为圆心,为半径的圆的极坐标方程为 .12、直角坐标的极坐标为.13、在极坐标系中,曲线的点到点的最小距离等于.14、在极坐标系中,圆心在()且过极点的圆的方程为.15、在极坐标系中,圆心在()且过极点的圆的方程为.16、点的极坐标化成直角坐标的结果是 .17、在极坐标系中,点,动点满足,则动点轨迹的极坐标方程为.18、已知圆的直角坐标方程为,则圆的极坐标方程为____________.19、在极坐标系中,经过点且与极轴垂直的直线的极坐标方程为.20、(坐标系与参数方程选做题)极坐标系下,直线与圆的公共点个数是________;21、在极坐标系中,点关于直线的对称点的一个极坐标为_____.22、已知圆C的参数方程为为参数),直线的极坐标方程为,则直线与圆C的交点的直角坐标为.23、极坐标系中,两点的距离AB= .24、(5分)(2015•广东)已知直线l的极坐标方程为2ρsin(θ﹣)=,点A的极坐标为A(2,),则点A到直线l的距离为.25、已知直线l的极坐标方程为,则直线l的斜率是___________.26、(选修4-4:坐标系与参数方程)已知直线与曲线(为参数),有且仅有一个公共点,则正实数的值为.27、(坐标系与参数方程选做题)在极坐标系中,圆的圆心到直线的距离是 .28、在极坐标系中,点,在以极点为坐标原点,极轴所在直线为轴的平面直角坐标系中,点的坐标为__________.29、在极坐标系中,点到直线的距离是.30、在极坐标系中,直线的方程为,则点到直线的距离为 .31、在极坐标系中,直线的方程为,则点到直线的距离为 .32、在极坐标系中,圆C的方程为ρ=1,直线l的方程为ρsin(θ+)=,则圆心C到直线l的距离为_________.33、极坐标系中,圆:的圆心到直线的距离是_______________.34、在极坐标系中,点到直线的距离是35、点P的极坐标为()与其对应的直角坐标是_________.36、在极坐标系中,点关于直线的对称点的极坐标为 .37、已知在平面直角坐标系中圆的参数方程为:,(为参数),以为极轴建立极坐标系,直线极坐标方程为:,则圆截直线所得弦长为 .38、(坐标系与参数方程选做题)在极坐标系中,圆的圆心到直线的距离是 .39、把极坐标系中的方程化为直角坐标形式下的方程为40、①在极坐标系中,点A(2,)到直线:的距离为②(不等式选讲选做题) 设函数f(x)=|x-2|+x,g(x)=|x+1|,则g(x)<f(x)成立时x的取值范围41、在直角坐标系中,圆的参数方程为(为参数);在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点为极点,以轴的正半轴为极轴)中,圆的方程为,则与的位置关系是______(在“相交、相离、内切、外切、内含”中选择一个你认为正确的填上).42、.已知两直线的极坐标方程和,则两直线交点的极坐标为________.43、(坐标系与参数方程选做题)设点的极坐标为,直线过点且与极轴所成的角为,则直线的极坐标方程为.44、在平面直角坐标系xoy中,已知点P是函数的图象上的动点,该图象在P处的切线交y轴于点M,过点P作的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________45、一动点M到x轴的距离比到点F(0,2)的距离小2,则此动点M的轨迹方程是46、把极坐标方程ρcos=1化为直角坐标方程是________47、在极坐标系中,点(1,0)到直线ρ(cos θ+sin θ)=2的距离为________48、(坐标系与参数方程选做题)在极坐标系中,若过点且与极轴垂直的直线交曲线于A、B两点,则______ _.49、把圆的普通方程x2+(y-2)2=4化为极坐标方程为____________.50、在极坐标系中,已知圆,则圆C的半径为。
典型极坐标参数方程练习题带答案

极坐标参数方程练习题1.在直角坐标系xOy 中,直线C 1:x =-2,圆C 2:(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (1)求C 1,C 2的极坐标方程; (2)若直线C 3的极坐标方程为θ=π4(ρ∈R ),设C 2与C 3的交点为M ,N ,求△C 2MN 的面积. 解:(1)因为x =ρcos θ,y =ρsin θ,所以C 1的极坐标方程为ρcos θ=-2,C 2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.(2)将θ=π4代入ρ2-2ρcos θ-4ρsin θ+4=0,得ρ2-32ρ+4=0,解得ρ1=22,ρ2= 2.故ρ1-ρ2=2,即|MN |= 2.由于C 2的半径为1,所以△C 2MN 的面积为12.4.(2014·辽宁,23,10分,中)将圆x 2+y 2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C .(1)写出C 的参数方程;(2)设直线l :2x +y -2=0与C 的交点为P 1,P 2,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程.解:(1)设(x 1,y 1)为圆上的点,经变换为C 上点(x ,y ),依题意,得⎩⎨⎧x =x 1,y =2y 1,由x 21+y 21=1得x 2+⎝ ⎛⎭⎪⎫y 22=1.即曲线C 的方程为x 2+y 24=1.故C 的参数方程为⎩⎨⎧x =cos t ,y =2sin t (t 为参数).(2)由⎩⎨⎧x 2+y 24=1,2x +y -2=0解得⎩⎨⎧x =1,y =0或⎩⎨⎧x =0,y =2.不妨设P 1(1,0),P 2(0,2),则线段P 1P 2的中点坐标为⎝⎛⎭⎪⎫12,1,所求直线斜率为k =12,于是所求直线方程为y -1=12⎝⎛⎭⎪⎫x -12.化为极坐标方程,并整理得2ρcos θ-4ρsin θ=-3, 即ρ=34sin θ-2cos θ.(2)(2015·吉林长春二模,23,10分)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρcos ⎝ ⎛⎭⎪⎫θ-π3=1,M ,N 分别为曲线C 与x轴,y 轴的交点.①写出曲线C 的直角坐标方程,并求M ,N 的极坐标; ②设M ,N 的中点为P ,求直线OP 的极坐标方程.【解析】 (1)将2ρcos 2θ=sin θ两边同乘以ρ,得2(ρcos θ)2=ρsin θ,化为直角坐标方程为2x 2=y ,①C 2:ρcos θ=1化为直角坐标方程为x =1,② 联立①②可解得⎩⎨⎧x =1,y =2,所以曲线C 1与C 2交点的直角坐标为(1,2). (2)①∵ρcos ⎝ ⎛⎭⎪⎫θ-π3=1,∴ρcos θ·cosπ3+ρsin θ·sin π3=1. 又⎩⎨⎧x =ρcos θ,y =ρsin θ,∴12x +32y =1,即曲线C 的直角坐标方程为x +3y -2=0. 令y =0,则x =2;令x =0,则y =233. ∴M (2,0),N ⎝ ⎛⎭⎪⎫0,233.∴M 的极坐标为(2,0),N 的极坐标为⎝ ⎛⎭⎪⎫233,π2.②M ,N 连线的中点P 的直角坐标为⎝ ⎛⎭⎪⎫1,33,P 的极角为θ=π6.∴直线OP 的极坐标方程为θ=π6(ρ∈R ). 注:极坐标下点的坐标表示不唯一.【点拨】 解答题(1)的关键是掌握直角坐标化为极坐标的方法;题(2)先转化为直角坐标问题求解,再转化为极坐标.(2013·课标Ⅰ,23,10分)已知曲线C 1的参数方程为⎩⎨⎧x =4+5cos t ,y =5+5sin t (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ.(1)把C 1的参数方程化为极坐标方程;(2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).【解析】 (1)将⎩⎨⎧x =4+5cos t ,y =5+5sin t 消去参数t ,化为普通方程为(x -4)2+(y -5)2=25,即C 1:x 2+y 2-8x -10y +16=0.将⎩⎨⎧x =ρcos θ,y =ρsin θ代入x 2+y 2-8x -10y +16=0,得 ρ2-8ρcos θ-10ρsin θ+16=0.所以C 1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0. (2)C 2的普通方程为x 2+y 2-2y =0.联立C 1,C 2的方程⎩⎨⎧x 2+y 2-8x -10y +16=0,x 2+y 2-2y =0, 解得⎩⎨⎧x =1,y =1或⎩⎨⎧x =0,y =2.所以C 1与C 2交点的极坐标分别为⎝⎛⎭⎪⎫2,π4,⎝ ⎛⎭⎪⎫2,π2. 【点拨】 本题主要考查圆的参数方程、极坐标方程和标准方程以及圆与圆的位置关系,解题的关键是将参数方程和极坐标方程化为直角坐标方程求解.(2012·辽宁,23,10分)在直角坐标系xOy 中,圆C 1:x 2+y 2=4,圆C 2:(x -2)2+y 2=4.(1)在以O 为极点,x 轴正半轴为极轴的极坐标系中,分别写出圆C 1,C 2的极坐标方程,并求出圆C 1,C 2的交点坐标(用极坐标表示);(2)求圆C 1与C 2的公共弦的参数方程.解:(1)由⎩⎨⎧x =ρcos θ,y =ρsin θ,x 2+y 2=ρ2知圆C 1的极坐标方程为ρ=2,圆C 2的极坐标方程为ρ=4cosθ.解⎩⎨⎧ρ=2,ρ=4cos θ得ρ=2,θ=±π3,故圆C 1与圆C 2的交点坐标为⎝ ⎛⎭⎪⎫2,π3,⎝ ⎛⎭⎪⎫2,-π3.注:极坐标系下点的表示不唯一.(2)方法一:由⎩⎨⎧x =ρcos θ,y =ρsin θ得圆C 1与C 2交点的直角坐标分别为(1,3),(1,-3).故圆C 1与C 2的公共弦的参数方程为⎩⎨⎧x =1,y =t (-3≤t ≤3).⎝ ⎛⎭⎪⎫或参数方程写成⎩⎨⎧x =1,y =y ,-3≤y ≤ 3 方法二:将x =1代入⎩⎨⎧x =ρcos θ,y =ρsin θ,得ρcos θ=1,从而ρ=1cos θ.于是圆C 1与C 2的公共弦的参数方程为⎩⎨⎧x =1,y =tan θ⎝ ⎛⎭⎪⎫-π3≤θ≤π3.5.(2015·河北邯郸二模,23,10分)已知圆C 的极坐标方程为ρ=2cos θ,直线l 的参数方程为⎩⎪⎨⎪⎧x =12+32t ,y =12+12t (t 为参数),点A 的极坐标为⎝ ⎛⎭⎪⎫22,π4,设直线l 与圆C 交于点P ,Q .(1)写出圆C 的直角坐标方程; (2)求|AP |·|AQ |的值.解:(1)因为圆C 的极坐标方程为ρ=2cos θ, 所以ρ2=2ρcos θ,将其转化成直角坐标方程为x 2+y 2=2x , 即(x -1)2+y 2=1.(2)由点A 的极坐标⎝ ⎛⎭⎪⎫22,π4得直角坐标为A ⎝ ⎛⎭⎪⎫12,12.将直线l 的参数方程⎩⎪⎨⎪⎧x =12+32t ,y =12+12t (t 为参数)代入圆C 的直角坐标方程(x -1)2+y2=1,得t 2-3-12t -12=0.设t 1,t 2为方程t 2-3-12t -12=0的两个根,则t 1t 2=-12, 所以|AP |·|AQ |=|t 1t 2|=12.2.(2015·课标Ⅱ,23,10分,中)在直角坐标系xOy 中,曲线C 1:⎩⎨⎧x =t cos α,y =t sin α,(t为参数,t ≠0),其中0≤α<π.在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=2sin θ,C 3:ρ=23cos θ.(1)求C 2与C 3交点的直角坐标;(2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB |的最大值. 解:(1)曲线C 2的直角坐标方程为x 2+y 2-2y =0, 曲线C 3的直角坐标方程为x 2+y 2-23x =0. 联立⎩⎨⎧x 2+y 2-2y =0,x 2+y 2-23x =0, 解得⎩⎨⎧x =0,y =0或⎩⎪⎨⎪⎧x =32,y =32.所以C 2与C 3交点的直角坐标为(0,0)和⎝ ⎛⎭⎪⎫32,32.(2)曲线C 1的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中0≤α<π. 因此A 的极坐标为(2sin α,α),B 的极坐标为(23cos α,α). 所以|AB |=|2sin α-23cos α| =4⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α-π3.当α=5π6时,|AB |取得最大值,最大值为4. 3.(2015·陕西,23,10分,易)在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =3+12t ,y =32t (t 为参数),以原点为极点,x 轴正半轴为极轴建立极坐标系,⊙C 的极坐标方程为ρ=23sin θ.(1)写出⊙C 的直角坐标方程;(2)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求P 的直角坐标. 解:(1)由ρ=23sin θ,得 ρ2=23ρsin θ, 从而有x 2+y 2=23y ,所以x 2+(y -3)2=3.(2)设P ⎝ ⎛⎭⎪⎫3+12t ,32t ,又C (0,3),则|PC |=⎝ ⎛⎭⎪⎫3+12t 2+⎝ ⎛⎭⎪⎫32t -32=t 2+12, 故当t =0时,|PC |取得最小值, 此时,P 点的直角坐标为(3,0).5.(2014·课标Ⅱ,23,10分,中)在直线坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,半圆C 的极坐标方程为ρ=2cos θ,θ∈⎣⎢⎡⎦⎥⎤0,π2.(1)求C 的参数方程;(2)设点D 在C 上,C 在D 处的切线与直线l :y =3x +2垂直,根据(1)中你得到的参数方程,确定D 的坐标.解:(1)C 的普通方程为(x -1)2+y 2=1(0≤y ≤1).可得C 的参数方程为⎩⎨⎧x =1+cos t ,y =sin t(t 为参数,0≤t ≤π).(2)设D (1+cos t ,sin t ).由(1)知C 是以G (1,0)为圆心,1为半径的上半圆.因为C 在点D 处的切线与l 垂直,所以直线GD 与l 的斜率相同,tan t =3,t =π3.故D 的直角坐标为⎝ ⎛⎭⎪⎫1+cos π3,sin π3,即⎝ ⎛⎭⎪⎫32,32.7.(2013·课标Ⅱ,23,10分,中)已知动点P ,Q 都在曲线C :⎩⎨⎧x =2cos t ,y =2sin t (t 为参数)上,对应参数分别为t =α与t =2α(0<α<2π),M 为PQ 的中点.(1)求M 的轨迹的参数方程;(2)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点. 解:(1)依题意有P (2cos α,2sin α),Q (2cos 2α,2sin 2α), 因此M (cos α+cos 2α,sin α+sin 2α).M 的轨迹的参数方程为⎩⎨⎧x =cos α+cos 2α,y =sin α+sin 2α(α为参数,0<α<2π). (2)M 点到坐标原点的距离d =x 2+y 2=2+2cos α(0<α<2π). 当α=π时,d =0,故M 的轨迹过坐标原点.(2014·课标Ⅰ,23,10分)已知曲线C :x 24+y 29=1.直线l :⎩⎨⎧x =2+t ,y =2-2t(t 为参数).(1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.【思路导引】 (1)由基本关系式可消参求出普通方程;(2)把|PA |用参数θ来表示,从而求其最值.【解析】 (1)曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数).直线l 的普通方程为2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|. 则|PA |=d sin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43. 当sin(θ+α)=-1时,|PA |取得最大值,最大值为2255. 当sin(θ+α)=1时,|PA |取得最小值,最小值为255. (2013·辽宁,23,10分)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系.圆C 1,直线C 2的极坐标方程分别为ρ=4sin θ,ρcos ⎝⎛⎭⎪⎫θ-π4=2 2.(1)求C 1与C 2交点的极坐标;(2)设P 为C 1的圆心,Q 为C 1与C 2交点连线的中点,已知直线PQ 的参数方程为⎩⎨⎧x =t 3+a ,y =b 2t 3+1(t ∈R 为参数),求a ,b 的值.【解析】 (1)圆C 1的直角坐标方程为x 2+(y -2)2=4, 直线C 2的直角坐标方程为x +y -4=0. 解⎩⎨⎧x 2+(y -2)2=4,x +y -4=0得⎩⎨⎧x 1=0,y 1=4,⎩⎨⎧x 2=2,y 2=2.所以C 1与C 2交点的极坐标为⎝ ⎛⎭⎪⎫4,π2,⎝ ⎛⎭⎪⎫22,π4.注:极坐标系下点的表示不唯一.(2)由(1)可得,P 点与Q 点的直角坐标分别为(0,2),(1,3).故直线PQ 的直角坐标方程为x -y +2=0.由参数方程可得y =b 2(x -a )+1=b 2x -ab2+1,所以⎩⎪⎨⎪⎧b2=1,-ab 2+1=2,解得a =-1,b =2.【点拨】 解答本题的关键是明确转化思想的运用,即把极坐标化为直角坐标,把参数方程化为普通方程求解问题.2011·课标全国,23,10分)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧x =2cos α,y =2+2sin α(α为参数),M 是C 1上的动点,P 点满足OP →=2OM →,P 点的轨迹为曲线C 2.(1)求C 2的方程;(2)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线θ=π3与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B ,求|AB |.解:(1)设P (x ,y ), 则由条件知M ⎝ ⎛⎭⎪⎫x 2,y 2.由于M 点在C 1上,所以⎩⎪⎨⎪⎧x 2=2cos α,y 2=2+2sin α,即⎩⎨⎧x =4cos α,y =4+4sin α. 从而C 2的参数方程为⎩⎨⎧x =4cos α,y =4+4sin α(α为参数).(2)C 1化为普通方程为x 2+(y -2)2=4,故曲线C 1的极坐标方程为ρ=4sin θ,同理可得曲线C 2的极坐标方程为ρ=8sin θ.射线θ=π3与C 1的交点A 的极径为 ρ1=4sinπ3=23, 射线θ=π3与C 2的交点B 的极径为 ρ2=8sinπ3=4 3. 所以|AB |=|ρ2-ρ1|=2 3.5.(2014·辽宁锦州一模,23,10分)已知圆的极坐标方程为ρ2-42ρcos(θ-π4)+6=0.(1)将极坐标方程化为普通方程;(2)若点P (x ,y )在该圆上,求x +y 的最大值和最小值. 解:(1)原方程变形为ρ2-4ρcos θ-4ρsin θ+6=0,化直角坐标方程为x 2+y 2-4x -4y +6=0,即(x -2)2+(y -2)2=2. (2)设圆的参数方程为⎩⎪⎨⎪⎧x =2+2cos α,y =2+2sin α(α为参数),点P (x ,y )在圆上,则x +y =4+2sin ⎝⎛⎭⎪⎫α+π4.所以x +y 的最大值为6,最小值为2.6.(2015·山西太原联考,23,10分)已知平面直角坐标系xOy ,以O 为极点,x 轴的非负半轴为极轴建立极坐标系,点P 的极坐标为⎝⎛⎭⎪⎫23,π6,曲线C 的极坐标方程为ρ2+23ρsin θ=1.(1)写出点P 的直角坐标及曲线C 的直角坐标方程;(2)若Q 为曲线C 上的动点,求PQ 中点M 到直线l :⎩⎨⎧x =3+2t ,y =-2+t(t 为参数)距离的最小值.解:(1)点P 的直角坐标为(3,3).由ρ2+23ρsin θ=1,得x 2+y 2+23y =1,即x 2+(y +3)2=4,∴曲线C 的直角坐标方程为x 2+(y +3)2=4.(2)曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =-3+2sin θ(θ为参数),直线l 的普通方程为x -2y -7=0. 设Q (2cos θ,-3+2sin θ),则M ⎝ ⎛⎭⎪⎫32+cos θ,sin θ,那么点M 到直线l 的距离为 d =⎪⎪⎪⎪⎪⎪32+cos θ-2sin θ-712+22=⎪⎪⎪⎪⎪⎪cos θ-2sin θ-1125=5sin (θ-φ)+1125≥ -5+1125=11510-1,115 10-1.∴点M到直线l的最小距离为。
直角坐标转极坐标练习题

直角坐标转极坐标练习题一、基础转换题1. 将点(3, 4)转换为极坐标。
2. 将点(5, 5)转换为极坐标。
3. 将点(0, 8)转换为极坐标。
4. 将点(6, 0)转换为极坐标。
5. 将点(3, 3)转换为极坐标。
二、混合转换题6. 将点(8, 8)转换为极坐标,并求出极径和极角。
7. 将点(10, 0)转换为极坐标,并求出极径和极角。
8. 将点(0, 12)转换为极坐标,并求出极径和极角。
9. 将点(15, 15)转换为极坐标,并求出极径和极角。
10. 将点(6, 6)转换为极坐标,并求出极径和极角。
三、应用题11. 在直角坐标系中,点A(4, 3)和点B(8, 6),将这两个点转换为极坐标。
12. 在直角坐标系中,点C(9, 0)和点D(0, 12),将这两个点转换为极坐标。
13. 在直角坐标系中,点E(7, 7)和点F(7, 7),将这两个点转换为极坐标。
14. 在直角坐标系中,点G(10, 0)和点H(0, 10),将这两个点转换为极坐标。
15. 在直角坐标系中,点I(5, 5)和点J(5, 5),将这两个点转换为极坐标。
四、综合题16. 已知点K(12, 16),求其极坐标,并判断该点位于哪个象限。
17. 已知点L(18, 0),求其极坐标,并判断该点位于哪个象限。
18. 已知点M(0, 24),求其极坐标,并判断该点位于哪个象限。
19. 已知点N(15, 15),求其极坐标,并判断该点位于哪个象限。
20. 已知点P(9, 9),求其极坐标,并判断该点位于哪个象限。
四、综合题(续)21. 已知点Q(6, 8),求其极坐标,并计算极径与极角的比值。
22. 已知点R(8, 6),求其极坐标,并计算极径与极角的乘积。
23. 已知点S(0, 10),求其极坐标,并判断极角是锐角、直角还是钝角。
24. 已知点T(10, 0),求其极坐标,并判断极角是第一象限角、第二象限角还是第三象限角。
25. 已知点U(5, 5),求其极坐标,并比较极径与极角的正切值。
极坐标、全参数方程题型大全

参 数 方 程 集 中 训 练 题 型 大 全答题时间:300分钟 满分:300分 命题人:杨晓帆参27.在极坐标系中,点(ρ,θ)与(-ρ, π-θ)的位置关系为( )。
A .关于极轴所在直线对称B .关于极点对称C .关于直线θ=2π (ρ∈R) 对称 D .重合28.极坐标方程 4ρsin 22θ=5 表示的曲线是( )。
A .圆 B .椭圆C .双曲线的一支D .抛物线29.点 P 1(ρ1,θ1) 与 P 2(ρ2,θ2) 满足ρ1 +ρ2=0,θ1 +θ2 = 2π,则 P 1、P 2 两点的位置关系是( )。
A .关于极轴所在直线对称B .关于极点对称C .关于θ=2π所在直线对称 D .重合30.椭圆⎩⎨⎧Φ+-=Φ+=sin 51cos 33y x 的两个焦点坐标是( )。
A .(-3, 5),(-3, -3) B .(3, 3),(3, -5)C .(1, 1),(-7, 1)D .(7, -1),(-1, -1) 六、1.若直线的参数方程为12()23x t t y t=+⎧⎨=-⎩为参数,则直线的斜率为( )A .23 B .23- C .32 D .32- 2.下列在曲线sin 2()cos sin x y θθθθ=⎧⎨=+⎩为参数上的点是( )A .1(,2B .31(,)42- C . D . 3.将参数方程222sin ()sin x y θθθ⎧=+⎪⎨=⎪⎩为参数化为普通方程为( )A .2y x =-B .2y x =+C .2(23)y x x =-≤≤D .2(01)y x y =+≤≤4.化极坐标方程2cos 0ρθρ-=为直角坐标方程为( ) A .201y y +==2x 或 B .1x = C .201y +==2x 或x D .1y =5.点M的直角坐标是(-,则点M 的极坐标为( ) A .(2,)3π B .(2,)3π- C .2(2,)3π D .(2,2),()3k k Z ππ+∈ 6.极坐标方程cos 2sin 2ρθθ=表示的曲线为( ) A .一条射线和一个圆 B .两条直线 C .一条直线和一个圆 D .一个圆七、1.直线l 的参数方程为()x a t t y b t=+⎧⎨=+⎩为参数,l 上的点1P 对应的参数是1t ,则点1P 与(,)P a b 之间的距离是( ) A .1t B .12t C1 D12.参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是( )A .一条直线B .两条直线C .一条射线D .两条射线3.直线112()x t t y ⎧=+⎪⎪⎨⎪=-⎪⎩为参数和圆2216x y +=交于,A B 两点,则AB 的中点坐标为( )A .(3,3)- B.( C.3)- D.(3, 4.圆5cos ρθθ=-的圆心坐标是( )A .4(5,)3π--B .(5,)3π-C .(5,)3πD .5(5,)3π- 5.与参数方程为)x t y ⎧=⎪⎨=⎪⎩为参数等价的普通方程为( ) A .214y +=2x B .21(01)4y x +=≤≤2xC .21(02)4y y +=≤≤2x D .21(01,02)4y x y +=≤≤≤≤2x 6.直线2()1x t t y t=-+⎧⎨=-⎩为参数被圆22(3)(1)25x y -++=所截得的弦长为( ) A.1404C八、1.把方程1xy =化为以t 参数的参数方程是( )A .1212x t y t -⎧=⎪⎨⎪=⎩B .sin 1sin x t y t =⎧⎪⎨=⎪⎩C .cos 1cos x t y t =⎧⎪⎨=⎪⎩D .tan 1tan x t y t =⎧⎪⎨=⎪⎩2.曲线25()12x t t y t=-+⎧⎨=-⎩为参数与坐标轴的交点是( )A .21(0,)(,0)52、 B .11(0,)(,0)52、 C .(0,4)(8,0)-、 D .5(0,)(8,0)9、 3.直线12()2x t t y t=+⎧⎨=+⎩为参数被圆229x y +=截得的弦长为( ) A .125 BC4.若点(3,)P m 在以点F 为焦点的抛物线24()4x t t y t⎧=⎨=⎩为参数上, 则PF 等于( )A .2B .3C .4D .55.极坐标方程cos 20ρθ=表示的曲线为( )A .极点B .极轴C .一条直线D .两条相交直线6.在极坐标系中与圆4sin ρθ=相切的一条直线的方程为( ) A .cos 2ρθ= B .sin 2ρθ=C .4sin()3πρθ=+D .4sin()3πρθ=-参、5.把参数方程⎩⎨⎧+==1cos sin ααy x (α为参数)化为普通方程,结果是。
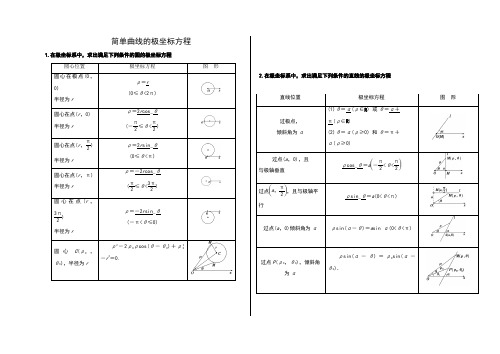
简单曲线的极坐标方程练习题有答案
简单曲线的极坐标方程1.在极坐标系中,求出满足下列条件的圆的极坐标方程圆心位置 极坐标方程图 形圆心在极点(0,0)半径为r ρ=r(0≤θ<2π)圆心在点(r ,0) 半径为r ρ=2r cos_θ(-π2≤θ<π2)圆心在点(r ,π2)半径为r ρ=2r sin_θ(0≤θ<π)圆心在点(r ,π) 半径为r ρ=-2r cos_θ(π2≤θ<3π2)圆心在点(r ,3π2) 半径为rρ=-2r sin_θ(-π<θ≤0)圆心C (ρ0,θ0),半径为rρ2-2ρ0ρcos(θ-θ0)+ρ2-r 2=0.2.在极坐标系中,求出满足下列条件的直线的极坐标方程直线位置极坐标方程图 形过极点, 倾斜角为α(1)θ=α(ρ∈R ) 或θ=α+π(ρ∈R )(2)θ=α(ρ≥0) 和θ=π+α(ρ≥0)过点(a ,0),且 与极轴垂直ρcos_θ=a ⎝⎛⎭⎪⎫-π2<θ<π2过点⎝⎛⎭⎪⎫a ,π2,且与极轴平行ρsin_θ=a (0<θ<π)过点(a ,0)倾斜角为α ρsin(α-θ)=a sin α(0<θ<π)过点P (ρ0,θ0),倾斜角为αρsin(α-θ)=ρ0sin(α-θ0).3.将下列曲线的直角坐标方程化为极坐标方程 ①x +y =0;②x 2+y 2+2ax =0(a ≠0).(2)将下列曲线的极坐标方程化为直角坐标方程;并判定曲线形状: ①ρcos θ=2;②ρ=2cos θ;③ρ2cos 2θ=2;④ρ=11-cos θ.[思路点拨] (1)先把公式x =ρcos θ,y =ρsin θ代入曲线(含直线)的直角坐标方程,再化简.(2)先利用公式ρcos θ=x ,ρsin θ=y ,ρ2=x 2+y 2代入曲线的极坐标方程,再化简.[解] (1)①将x =ρcos θ,y =ρsin θ代入x +y =0得ρcos θ+ρsin θ=0,即ρ(sin θ+cos θ)=0,∴tan θ=-1,θ=3π4(ρ≥0)和θ=7π4(ρ≥0),∴直线x +y =0的极坐标方程为θ=3π4(ρ≥0)和θ=7π4(ρ≥0).②将x =ρcos θ,y =ρsin θ代入x 2+y 2+2ax =0得ρ2+2aρcos θ=0,∴ρ=0或ρ=-2a cos θ.又ρ=0表示极点,而极点在圆ρ=-2a cos θ上 ∴所求极坐标方程为ρ=-2a cos θ(2)①∵ρcos θ=2,∴x =2,即直线ρcos θ=2的直角坐标方程为x =2,它表示过点(2,0)且垂直于x 轴的直线,②∵ρ=2cos θ,∴ρ2=2ρcos θ,即x 2+y 2=2x . ∴(x -1)2+y 2=1,即ρ=2cos θ的直角坐标方程. 它表示圆心为(1,0),半径为1的圆. ③∵ρ2cos 2θ=2, ∴ρ2(cos 2θ-sin 2θ)=2, 即ρ2cos 2θ-ρ2sin 2θ=2, ∴x 2-y 2=2,故曲线是中心在原点,焦点在x 轴上的等轴双曲线. ④∵ρ=11-cos θ,∴ρ=1+ρcos θ,∴x 2+y 2=1+x ,两边平方并整理得y 2=2⎝ ⎛⎭⎪⎫x +12,故曲线是顶点为⎝ ⎛⎭⎪⎫-12,0,焦点为F (0,0),准线方程为x =-1的抛物线. 4.曲线x 2+y 2=2x 2+y 2的极坐标方程是____________.解析:∵x 2+y 2=ρ2,ρ≥0,∴ρ=x 2+y 2, ∴x 2+y 2=2x 2+y 2可化为ρ2=2ρ,即ρ(ρ-2)=0. 答案:ρ(ρ-2)=05.曲线ρsin ⎝⎛⎭⎪⎫θ-π4=0的直角坐标方程是______________. 解析:∵ρsin ⎝ ⎛⎭⎪⎫θ-π4=0,∴22ρsin θ-22ρcos θ=0,∴ρsin θ-ρcos θ=0,即x -y =0. 答案:x -y =06.圆ρ=5cos θ-53sin θ的圆心坐标是( )解析:选D.∵ρ=5cos θ-5 3 sin θ, ∴ρ2=5ρcos θ-53ρsin θ, ∴x 2+y 2=5x -53y ,∴⎝ ⎛⎭⎪⎫x -52+⎝ ⎛⎭⎪⎫y +532=25, ∴圆心C ⎝ ⎛⎭⎪⎫52,-532,ρ=254+754=5, tan θ=y x =-3,θ=5π3∴圆心C 的极坐标为C ⎝⎛⎭⎪⎫5,5π3.7.极坐标方程ρ=cos(π4-θ)表示的曲线是( )A .双曲线B .椭圆C .抛物线D .圆解析:选D.∵ρ=cos ⎝ ⎛⎭⎪⎫π4-θ,即ρ=22(cos θ+sin θ),∴ρ2=22(ρcos θ+ρsin θ), ∴x 2+y 2=22x +22y ,即⎝⎛⎭⎪⎫x -24+⎝ ⎛⎭⎪⎫y -24=14. 8.曲线的极坐标方程为ρ=tan θ·1cos θ,则曲线的直角坐标方程为__________.解析:∵ρ=tan θ·1cos θ,∴ρcos 2θ=sin θ,∴ρ2cos 2θ=ρsin θ, ∴x 2=y . 答案:x 2=y9.直线2ρcos θ=1与圆ρ=2cos θ相交的弦长为________.[解析] (1)由公式x =ρcos θ,y =ρsin θ,得直线2ρcos θ=1的直角坐标方程为2x =1,圆ρ=2cos θ⇒ρ2=2ρcos θ的直角坐标方程为x 2+y 2-2x =0⇒(x -1)2+y 2=1,由于圆心(1,0)到直线的距离为1-12=12,所以弦长为21-⎝ ⎛⎭⎪⎫12= 3.10.已知圆的极坐标方程为ρ=4cos θ,圆心为C ,点P 的极坐标为⎝⎛⎭⎪⎫4,π3,则|CP |=________.(2)由圆的极坐标方程ρ=4cos θ得ρ2=4ρcos θ, 化为直角坐标方程为x 2+y 2-4x =0, 所以(x -2)2+y 2=4,所以圆心C (2,0),半径r =|OC |=2,如图,在△OCP 中, ∠POC =π3,|OP |=4.由余弦定理,得|PC |2=|OP |2+|OC |2-2|OP ||OC |·cos ∠POC =42+22-2×4×2cos π3=12,所以|PC |=2 3. [答案] (1) 3 (2)2311.(2015·高考全国卷Ⅰ)在直角坐标系xOy 中,直线C 1:x =-2,圆C 2:(x -1)2+(y -2)2=1,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系.(1)求C 1,C 2的极坐标方程;(2)若直线C 3的极坐标方程为θ=π4(ρ∈R),设C 2与C 3的交点为M ,N ,求△C 2MN 的面积.[解] (1)因为x =ρcos θ,y =ρsin θ,所以C 1的极坐标方程为ρcos θ=-2,C 2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.(2)将θ=π4代入ρ2-2ρcos θ-4ρsin θ+4=0,得ρ2-32ρ+4=0,解得ρ1=22,ρ2= 2.故ρ1-ρ2=2,即|MN |= 2.由于C 2的半径为1,所以△C 2MN 的面积为12.。
极坐标练习题(含详细答案)

D.+=1)=1+1)1-1)1-1)1),-3π,2π,,,,B .θ=π2(ρ∈R )和ρcos θ=2 C .θ=π2(ρ∈R )和ρcos θ=1 D .θ=0(ρ∈R )和ρcos θ=1 答案 B 解析 由题意可知,圆ρ=2cos θ可化为普通方程为(x -1)2+y 2=1. 所以圆的垂直于x 轴的两条切线方程分别为x =0和x =2,再将两条切线方程化为极坐标方程分别为θ=π2(ρ∈R )和ρcos θ=2,故选B. 7.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是( ) A .ρ=cos θ B .ρ=sin θ C .ρcos θ=1 D .ρsin θ=1 答案 C 解析 过点(1,0)且与极轴垂直的直线,在直角坐标系中的方程为x =1,所以其极坐标方程为ρcos θ=1,故选C. 8.(2013·天津)已知圆的极坐标方程为ρ=4cos θ,圆心为C ,点P 的极坐标为(4,π3),则|CP |=________. 答案 23 解析 由圆的极坐标方程为ρ=4cos θ,得圆心C 的直角坐标为(2,0),点P 的直角坐标为(2,23),所以|CP |=2 3. 9.(2014·唐山一中)在极坐标系中,点P (2,-π6)到直线l :ρsin(θ-π6)=1的距离是________.答案3+1 解析 依题意知,点P (3,-1),直线l 为x -3y +2=0,则点P 到直线l 的距离为3+1. 10.若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________.答案 x 2+y 2-4x -2y =0 解析 由îíìx =ρcos θ,y =ρsin θ⇒cos θ=x ρ,sin θ=y ρ,ρ2=x 2+y 2,代入ρ=2sin θ+4cos θ,得ρ=2y ρ+4xρ⇒ρ2=2y +4x ⇒x 2+y 2-4x -2y =0. 11.在极坐标系中,直线ρsin(θ+π4)=2被圆ρ=4截得的弦长为________. 答案 43 解析 直线ρsin(θ+π4)=2可化为x +y -22=0,圆ρ=4可化为x 2+y 2=16,由圆中的弦长公式,得2r 2-d 2=242-(222)2=4 3. 12.在极坐标系中,圆ρ=2cos θ的圆心的极坐标是________,它与方程θ=π4(ρ>0)所表示的图形的交点的极坐标是________. 答案 (1,0) (2,π4) 解析 ρ=2cos θ表示以点(1,0)为圆心,1为半径的圆,故圆心的极坐标为(1,0). 当θ=π4时,ρ=2,故交点的极坐标为(2,π4).13.在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ=2sin θ与ρcos θ=-1的交点的极坐标为________.答案 (2,3π4) 解析 ρ=2sin θ的直角坐标方程为x 2+y 2-2y =0, ρcos θ=-1的直角坐标方程为x =-1. 联立方程,得îíì x 2+y 2-2y =0,x =-1,解得îíìx =-1,y =1,即两曲线的交点为(-1,1).又0≤θ<2π,因此这两条曲线的交点的极坐标为(2,3π4).14.在极坐标系中,直线ρ(cos θ-sin θ)+2=0被曲线C :ρ=2所截得弦的中点的极坐标为________.÷ö2,4=2,∠=3π. ÷ö2,3π,11π)33,-)6cos=6cos =×3=3,6sin 1111ππ6=-π6)=-×12=-(33,-33,-,3π2)到直线=|3×0-4×(-2)-3|32+42=解析 (1)设动点P 的坐标为(ρ,θ), M 的坐标为(ρ0,θ),则ρρ0=12. ∵ρ0cos θ=4,∴ρ=3cos θ即为所求的轨迹方程.(2)由(1)知P 的轨迹是以(32,0)为圆心,半径为32的圆,易得|RP |的最小值为1. 18.在极坐标系下,已知圆O :ρ=cos θ+sin θ和直线l :ρsin(θ-π4)=22. (1)求圆O 和直线l 的直角坐标方程;的直角坐标方程; (2)当θ∈(0,π)时,求直线l 与圆O 公共点的极坐标.公共点的极坐标. 答案 (1)x 2+y 2-x -y =0,x -y +1=0 (2)(1,π2) 解析 (1)圆O :ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ,圆O 的直角坐标方程为x 2+y 2=x +y ,即x 2+y 2-x -y =0. 直线l :ρsin(θ-π4)=22,即ρsin θ-ρcos θ=1,则直线l 的直角坐标方程为y-x =1,即x -y +1=0. (2)由îíìx 2+y 2-x -y =0,x -y +1=0,得îíìx =0,y =1.故直线l 与圆O 公共点的极坐标为(1,π2).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极坐标习题二
1、已知⎪⎭⎫ ⎝
⎛-3,5πM ,下列所给出的不能表示点的坐标的是( ) A .⎪⎭⎫ ⎝⎛-3,5π B .⎪⎭⎫ ⎝⎛34,5π C .⎪⎭⎫ ⎝⎛-32,5π D .⎪⎭⎫ ⎝
⎛--35,5π
2、点M 的直角坐标是(1-,则点M 的极坐标为( )
A .(2,)3
π B .(2,)3π- C .2(2,)3π D .(2,2),()3k k Z ππ+∈ 3、)0(4≤=ρπ
θ表示的图形是( )
A .一条射线
B .一条直线
C .一条线段
D .圆
4、圆5cos ρθθ=-的圆心坐标是( )
A .4(5,)3π--
B .(5,)3π-
C .(5,)3π
D .5(5,)3
π- 5、极坐标方程cos 20ρθ=表示的曲线为( )
A .极点
B .极轴
C .一条直线
D .两条相交直线
6、在极坐标系中与圆4sin ρθ=相切的一条直线的方程为( )
A .cos 2ρθ=
B .sin 2ρθ=
C .4sin()3πρθ=+
D .4sin()3
πρθ=- 7、化极坐标方程2cos 0ρθρ-=为直角坐标方程为( )
A .201y y +==2x 或
B .1x =
C .201y +==2x 或x
D .1y =
8、直线cos sin 0x y αα+=的极坐标方程为____________________。
9、若A 33,π⎛⎝ ⎫⎭⎪,B ⎪⎭⎫ ⎝
⎛-64π,,则|AB|=_________,S AOB ∆=_________。
(其中O 是极点)
10、在极坐标中,若过点(3,0)且与极轴垂直的直线交曲线θρcos 4=于A 、B 两点.则|AB|=.
11、已知三点A(5,2π),B(-8,π611),C(3,π6
7),则ΔABC 形状为.
12、在极坐标系中,点P ⎪⎭
⎫ ⎝⎛611,2π到直线1)6sin(=-πθρ的距离等于____________。
13、与曲线01cos =+θρ关于4π
θ=对称的曲线的极坐标方程是______________。
14、已知⎪⎭
⎫ ⎝⎛π32,5P ,O 为极点,求使'POP ∆是正三角形的'P 点坐标。
(8分)
15、ABC ∆的底边,21,10B A BC ∠=∠=以B 点为极点,BC 为极轴,求顶点A 的轨迹方程。
(10分)。
