并行计算实验一:多线程计算π
并行计算的实验
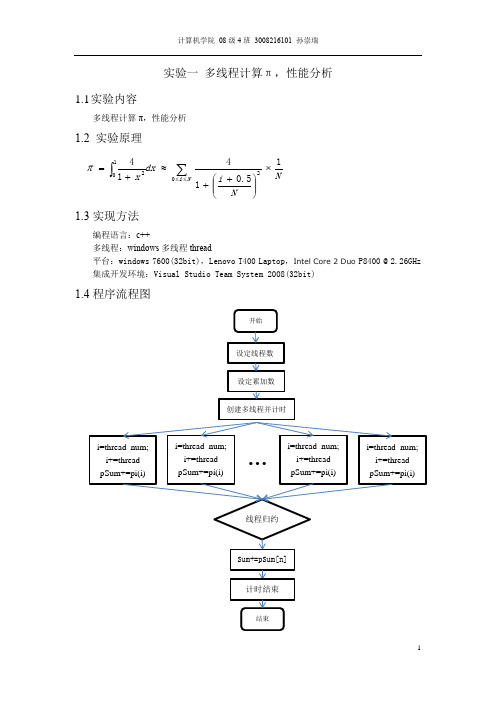
实验一多线程计算π,性能分析1.1 实验内容多线程计算π,性能分析1.2 实验原理1.3实现方法编程语言:c++多线程:windows 多线程thread平台:windows 7600(32bit),Lenovo T400 Laptop ,IntelCore 2 Duo P8400 @ 2.26GHz集成开发环境:Visual Studio Team System 2008(32bit)1.4程序流程图NN i dx x Ni 15.0141402102⨯⎪⎪⎭⎫⎝⎛++≈+=∑⎰≤≤π1.5实验结果线程数NUM_THREAD=4N π Time-cost100 3.14160098692312 3ms1000 3.14159273692313 4ms10000 3.14159265442313 5ms100000 3.14159265359813 25ms1000000 3.14159265358990 82ms1.6性能分析精度随叠加次数N的增大而趋近于π的真实值,计算时间也随之增高;相同的叠加次数下,因为是双核处理器,线程数为2时计算性能最高。
理论性能提升有极限值,所以不会因为线程的增多而性能无限增强。
当线程数很大时,计算时间增加很快。
1.7总结展望第一次编写并行化的程序,对多线程编程有了初步的认识。
由于是在Visual Studio平台下编程,很多知识是从Lunix平台移植过来的,虽然表现形式有少许差别,但核心思想一致。
通过学习,对windows多线程编程有了一定的掌握。
实验二3PCF计算多线程实现2.1实验内容▪定义:–点集D、R。
–定义D中的点为a i∈D,R中的点为b i∈R。
–距离:r1、r2、r3、err▪求:–满足以下条件的三元组(空间中三角形)的数目•<a i, b m, b n>,|a i-b m|=r1±err且|a i-b n|=r2±err且|b m-b n|=r3±err2.2实验原理对于D中每一点a i,在R中找到与之距离为r1的点集R’,找到与之距离为r2的点集R’’。
操作系统多线程求pi - 西南交大

西南交通大学多线程求PI值年级:学号:姓名:专业:一、实现过程描述自学C#程序设计语言,采用VisualC#控制台应用程序编写该实验。
通过函数piMain()计算圆周率pi的值。
在主函数中,先接收用户输入的精度来控制pi值小数点后的位数。
在主函数中创建线程myThread,并将委派ThreadStart所封装的方法定义为函数piMain()。
再通过对线程的暂停、继续、终止来控制pi值得输出位数,并了解线程的工作过程。
三、算法using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Threading;using System.Diagnostics;namespace pi2{public class Pi{Thread myThread;static int a = 10000, b, c = 3500, d, e, g,count=0,di;static int[] f;string pistr="";bool flag = true;void piMain(){ f = new int[3501];while (0 != b - c) f[b++] = a / 5;d = 0;g = c << 1;while (0 != g&&count<=di){b = c;d += f[b] * a;f[b--] = d % --g;d = d / g--;while (0 != b){ d = d * b + f[b] * a;f[b--] = d % --g;d = d / g--; }for (int i = 0; i < 4&&count<=di; i++){if (count == 1) pistr=pistr+".";pistr=pistr+(e + d / a).ToString().ElementAt(i);Thread.Sleep(500);count++;}c -= 14;e = d % a;d = 0;g = c * 2;}if (count > di){Console.Write("输出完毕:pi=" + pistr+"\n");flag = false;}}public static void Main(){Console.WriteLine("输入精度");di = Convert.ToInt32(Console.ReadLine());try {String strKeyValue = "";Pi myUsingSleep = new Pi();ThreadStart myThreadStart = new ThreadStart(myUsingSleep.piMain);myUsingSleep.myThread = new Thread(myThreadStart);myUsingSleep.myThread.Start();while (myUsingSleep.flag){Console.WriteLine("按P 暂停,按R 继续,按E 结束");strKeyValue = Console.ReadLine();Console.WriteLine();if (strKeyValue == "P"){Console.WriteLine("阻断目前myThread 线程的执行!!\n");myUsingSleep.myThread.Suspend();Console.WriteLine("目前pi =" + myUsingSleep.pistr + "\n");}else if (strKeyValue == "R"){Console.WriteLine("恢复目前myThread 线程的执行!!\n");myUsingSleep.myThread.Resume();}else if (strKeyValue == "E"){Console.WriteLine("终止目前myThread 线程的执行!!\n");myUsingSleep.myThread.Interrupt();Console.WriteLine("目前pi =" + myUsingSleep.pistr + "\n");myUsingSleep.flag = false;}else{return;}Console.WriteLine("----------------------------------------------------");}}catch (Exception e) { return; }}}}四、程序演示1、输入精度100,开始运行程序,并计算pi,按“P”第一次暂停,pi=3.1415926,恢复线程后,按“p”第二次暂停,pi=3.1415926535897932,按“E”则结束线程,此时pi的值如下图所示。
实验一多线程计算π及性能分析

实验一多线程计算π及性能分析作者:赵立夫完成时间:月5日1、实验内容1.掌握类用法2.掌握多线程同步方法3.使用多线程计算π;4.对结果进行性能评价。
2、实验原理计算π值,并使用3、程序流程图图主线程流程图4、实现方法1.方法简述:本程序使用多线程方法:首先启动主进程,输入基数和线程数;第二步,通过主进程创建子进程并为每个子进程分配计算任务;第三步,子进程执行计算认为并将结果返回到数组[]中;最后,主进程将[]元素进行累加得到最终结果并输出。
2.程序的主要方法类,实现计算指定区间内的累加和()启动子线程,子线程将自动执()方法()确保主进程在所有子进程计算完毕后执行后续任务。
5、实验结果1.实验结果数据表2.部分结果截图图单线程计算结果图图多线程计算结果图3.理论性能及实际结果分析本程序使用多线程方法来提升程序的执行速度,所以当线程数不断增多时,程序运行时间应逐渐减少;再考虑到创建进程和信息传递的开销,当线程数大于计算机的内核数量时,程序运行时间应该随着线程数目的增加而增加。
由于运行计算机为四核系统,所以当子线程数(除去主线程)由单线程增加到子线程运行时,程序运行时间降低,而当子线程增加到个(即线程数目大于内核数量时),程序运行时间又上升,这与预期结果相符合。
通过实验数据的分析验证了并行计算在程序运行性能上的理论。
6、总结展望这次实验较为简单,并行化的方法非常直观,程序的逻辑也十分清晰。
在并行化方面的开销较少。
通过本次实验主要是对并行化原理的一个验证,证明了由多处理器分别运行线程带来的性能上的提高。
也通过实验证明了当线程数超过实际处理器数量时,性能的下降。
实验二计算的多线程实现作者:赵立夫完成时间:月日一、实验内容已知:点集、。
定义中的点为∈,中的点为∈。
距离:、、、求:满足以下条件的三元组(空间中三角形)的数目<, , >,±且±且±二、实验原理对于中所有点,判断两两之间是否满足距离,若满足,保存点对。
本实验要求学生搭建并行环境并运行计算π的程序。

本实验要求学生搭建并行环境并运行计算π的程序实验目的本实验的目的是为了让学生了解并行计算的概念和基本原理,掌握搭建并行环境的方法,以及能够编写并行程序并在并行环境中运行。
实验要求硬件要求本实验要求使用至少两台计算机,并能够通过网络进行连接。
建议使用至少4台计算机,以便更好地体现并行计算的效果。
软件要求本实验需要使用MPI(Message Passing Interface)并行编程库和编译器。
建议使用C语言进行编程。
实验步骤1.搭建并行环境首先,需要将所有计算机连接到同一个网络中,并且保证能够互相通信。
接着,需要安装MPI软件,并按照MPI的要求进行配置。
2.编写并行程序本实验要求使用MPI编写程序来计算π的值。
在编写程序之前,需要了解如何将一个计算任务分割成多个子任务,并且如何让不同的计算机并行地执行这些子任务。
程序的具体实现方式可以参考MPI的官方文档。
3.编译程序将编写好的程序进行编译,并生成可执行文件。
4.运行程序在并行环境中运行程序,观察实验结果。
实验结果通过本实验,学生可以了解并行计算的概念和基本原理,熟悉MPI库的使用方法,并且能够搭建并行环境并运行并行程序。
此外,学生还可以通过实验结果来比较串行计算和并行计算在计算π方面的效率区别,从而更好地理解并行计算的优势和应用场景。
实验总结通过本实验,学生可以逐步了解并行计算的概念和基本原理,掌握搭建并行环境,编写并行程序的方法,能够使用MPI库进行程序开发。
本实验的设计旨在让学生在实践中深入理解并行计算的概念和原理,并为今后进行高效的计算科学研究打下坚实的基础。
如何在Python中实现并行计算

如何在Python中实现并行计算在Python中实现并行计算可以通过多种方法,包括使用多线程、多进程和分布式计算等。
并行计算可以大大提高程序的运行效率和性能,特别是在需要处理大数据集或复杂计算任务时。
下面将介绍三种常见的并行计算方法和对应的Python库。
1.多线程并行计算:多线程是指在同一个程序中同时执行多个线程,每个线程执行不同的任务,可以共享内存空间。
Python中的`threading`库提供了创建和管理线程的功能。
以下是一个使用多线程进行并行计算的示例代码:```pythonimport threading#定义一个任务函数def task(x):result = x * xprint(result)#创建多个线程执行任务threads = []for i in range(10):t = threading.Thread(target=task, args=(i,))threads.append(t)t.start()#等待所有线程完成for t in threads:t.join()```上述代码中,创建了10个线程分别执行`task`函数,每个线程计算传入的参数的平方并打印结果。
使用多线程时需要注意线程安全问题,例如共享资源的同步访问。
2.多进程并行计算:多进程指的是同时执行多个独立的进程,每个进程有自己独立的内存空间。
Python中的`multiprocessing`库提供了多进程并行计算的功能。
以下是一个使用多进程进行并行计算的示例代码:```pythonimport multiprocessing#定义一个任务函数def task(x):result = x * xprint(result)#创建多个进程执行任务processes = []for i in range(10):p = multiprocessing.Process(target=task, args=(i,))processes.append(p)p.start()#等待所有进程完成for p in processes:p.join()```上述代码中,创建了10个进程分别执行`task`函数,每个进程计算传入的参数的平方并打印结果。
多线程求pi实验报告

多线程求pi实验报告篇一:多核求PI实验报告Monte Carlo方法计算Pi一、实验要求以OpenMP实现Monte Carlo计算Pi的并行程序注意:? 制导循环编译? 共享变量的处理? 编译运行比较? 修改测试点数,提高计算精度。
? 利用OpenMP实现积分法,比较。
二、实验原理通过蒙特卡罗算法计算圆周率的主导思想是:统计学(概率)? 1.一个正方形有一个内切圆,向这个正方形内随机的画点,则点落在圆内的概论为P=圆面积/正方形面积。
? 2. 在一个平面直角坐标系下,在点(1,1)处画一个半径为R=1的圆,以这个圆画一个外接正方形,其边长为R=1(R=1时,圆面积即Pi)。
? 3. 随机取一点(X,Y)使得0<=X<=2R并且0<=Y<=2R,即随机点在正方形内。
? 4. 判断点是否在圆内,通过公式(X-R)(X-R)+(Y-R)(Y-R)<R*R计算。
? 5. 设所有点的个数为N,落在圆内的点的个数为M,则? P=M/N=4*R*R/Pi*R*R=4/Pi ? Pi=4*N/M? 当实验次数越多(N越大),所计算出的Pi也越准确。
? 但计算机上的随机数毕竟是伪随机数,当取值超过一定值,也会出现不随机现象,因为伪随机数是周期函数。
如果想提高精度,最好能用真正的随机数生成器(需要更深的知识)。
三、实验步骤1. 利用蒙特卡洛方法实现求PI值(利用OpenMP)思路:根据所给的串行程序,只需根据OpenMp的用法将其转换。
源码:#include "stdafx.h#include<stdio.h>#include<time.h> #include <omp.h> #include <iostream> using namespace std;int _tmain(int argc, _TCHAR* argv[]) {long max=1000000; long i,count=0;double x,y,bulk,starttime,endtime; time_t t;cout<<"请输入测试点的个数:"<<endl; cin>>max;starttime=clock();// 产生以当前时间开始的随机种子srand((unsigned) time(t)); #pragma omp parallel for num_threads(8) default(shared) private(x,y) reduction(+:count) for(i=0;i<max;i++) {x=rand();x=x/32767;y=rand(); y=y/32767;if((x*x+y*y)<=1) count++; }bulk=4*(double(count)/max); endtime= clock();printf("所得PI的值如下:%f \n", bulk); printf("计算PI的过程共用时间: %f 秒\n",(endtime-starttime)/ CLOCKS_PER_SEC); return 0; }2. 利用积分法实现求PI(利用OpenMP)思路:与上同样道理。
并行计算实验报告

分析 :这样的加速比 , 是符合预测 , 很好的 . 附 :(实验 源码 ) 1 pi.cpp #include <cstdio> #include <cstdlib> #include <cstring> #include <cctype> #include <cmath> #include <ctime> #include <cassert>
#include <climits> #include <iostream> #include <iomanip> #include <string> #include <vector> #include <set> #include <map> #include <queue> #include <deque> #include <bitset> #include <algorithm> #include <omp.h> #define MST(a, b) memset(a, b, sizeof(a)) #define REP(i, a) for (int i = 0; i < int(a); i++) #define REPP(i, a, b) for (int i = int(a); i <= int(b); i++) #define NUM_THREADS 4 using namespace std; const int N = 1e6; double sum[N]; int main() { ios :: sync_with_stdio(0); clock_t st, ed; double pi = 0, x; //串行 st = clock(); double step = 1.0 / N; REP(i, N) { x = (i + 0.5) * step; pi += 4.0 / (1.0 + x * x); } pi /= N; ed = clock(); cout << fixed << setprecision(10) << "Pi: " << pi << endl; cout << fixed << setprecision(10) << "串行用时: " << 1.0 * (ed - st) / CLOCKS_PER_SEC << endl; //并行域并行化 pi = 0; omp_set_num_threads(NUM_THREADS); st = clock(); int i; #pragma omp parallel private(i) { double x; int id; id = omp_get_thread_num();
多线程并行快速求解Pi的方法

多线程并行快速求解Pi的方法作者:于朋来源:《电子技术与软件工程》2016年第15期摘要本文首先分别应用不同的求Pi方法分析讲解了WinAPI、OpenMP、MPI三大并行算法中常遇到的一些问题,根据问题提出了相应的解决方案。
另外实现了对BBP算法的初步并行化,大大缩减了该算法的运行时间。
文章最后利用三种方法求解了蒙特卡洛算法求Pi,并对比分析了三种算法的优缺点。
【关键词】WinAPI OpenMP MPI1 问题背景与提出随着技术的发展,单片机越来越难满足人们对于大量数据处理的需求,因此,人们越来越依赖于利用并行计算技术来解决程序规模庞大,运算时间长及数据量大的课题。
本文即对当下比较常用的几种并行技术WinAPI、OpenMP、MPI三种并行模式进行讨论课研究,并以计算π值为例,将并行模式与串行模式进行对比,研究并行计算的机理、优缺点及一些常见问题。
2 模型建立2.1 蒙特卡罗思想,蒲风投针实验(1)取白纸一张,在上面画许多间距为d的等距平行线;(2)取一根长为l(l(3)直线与针相交概率p的近似值可用m/n得到,进而可得到圆周率的近似值为2nl/md。
2.2 级数方法2.3 并行BBP算法当今世界在进行计算机性能测试时往往选择在一定时间内计算Pi值得位数,而最常用的算法之一就是BBP算法。
该算法不需要多精度浮点算术运算的支持,在支持IEEE浮点运算的通用计算机上即可进行计算而且该算法只需要非常少的内存。
BBP算法也是目前算法中非常适用于并行计算的算法。
公式为:3 算法描述与实现3.1 API实现Windows实现多线程并行计算时会产生数据竞争,数据竞争(Data racing)导致计算结果不准确。
产生错误的原因在于两个线程在同时访问同一内存区域时,且一个线程在进行写操作。
为此采用同步技术,利用临界区解决此问题。
由于本次试验中,数据计算量较小,所以基本不会产生数据竞争的错误,但是一旦运行计算量较大或者在共享量上运算时间较长的程序时,就会产生数据竞争,在本例中,我们以cout输出程序为引子,观察使用临界区和不使用临界区的区别:代码如下:}pi= count*4.0 / numSteps;//EnterCriticalSection(&cs);coutpiSum+= pi;// LeaveCriticalSection(&cs);我们将输出程序置于piSum值之前,由于cout运行时,在屏幕上显示需要消耗较大时间,所以就会有机会产生数据重叠或者两者读到了一样的piSum值。
多线程并行快速求解Pi的方法

for(inti=1;j<N;i+=2) {
Y=1/double(2 i—1):
pi= pi+4 y;
表 1所 示 ) 。
3.3 BBP算法的 实现
M PI是 专 门 为 集 群 和 多 节 点 并 行 计 算 语 言,运行效率高 ,实现方式 多样 ,可 以进行主 从式、并列式 以及流水 线式等方式的实现 。在 利用 计算 机 多核 CPU,模 拟多 个节 点的 实现 方 式 。 改 造 成 主 从 式 程 序 ,利 用 0号 节 点 作 为 主 节 点 收 发 数 据 ,也 参 与计 算 , 而 其 他 节 点 只 进行计算 ,为负载均衡选择 详尽的计算量运行 到不同的节点上 。
序 号
1
2
3
1
2
3
表 2
运行时间 (S)
0.036
0.045
0.284 0.01
0.018
O.08l
表 3
小数 点位数
4
100
1000
4
l0O
1000
并行加速 比
1.0
1.0
1.0
3.6
2.5
3.51
计 算 方 式 串行 计 算
W inAPI OpenM P
3.14l59 3.14925
3.14159
3.14159
平 均 结 果 3.14159
3.14159
平 均 时 间 (s) 1.287
0.373
并 行 加 速 比
实验一多线程计算PI值

实验一、多线程计算PI值
1.实验要求
●将串行的积分法计算PI值程序改进成多线程层序
●解决同步问题
2.实验环境
Visual C++ 6.0
3.计算方法
矩形法则的数值积分方法估算PI的值
4.串行的积分法计算PI值
通过for循环,一个个的把sum值相加。
实现代码如下:
5.并行方法计算PI值
主要通过for循环的计算过程分到几个线程中去,每次计算都要更新sum的值,就有可能发生一个线程已经更新了sum的值,而另一个线程读到的还是旧的sum值,所以在这里要使用临界区,把sum放到临界区中,这样一次只能有一个线程访问和修改sum的值。
实现代码如下:
6.运行结果
并行程序运行结果:
串行程序运行结果:
7.实验结果的分析
运行结果显示,串行的计算时间比并行的计算时间短。
可能是因为分割的小矩形的数量不够大所导致的。
就像人们出安全通道一样,如果人数较多的话,那么大家抢着走,显然出去的速度是很慢的,如果大家排队,井然有序的出,那么效率显然会提高很多的。
8.附代码并行代码
串行代码:。
并行计算实验报告

并行计算实验报告并行计算实验报告引言:并行计算是一种有效提高计算机性能的技术,它通过同时执行多个计算任务来加速计算过程。
在本次实验中,我们将探索并行计算的原理和应用,并通过实验验证其效果。
一、并行计算的原理并行计算是指将一个计算任务分成多个子任务,并通过多个处理器同时执行这些子任务,以提高计算速度。
其原理基于两个关键概念:任务划分和任务调度。
1. 任务划分任务划分是将一个大的计算任务划分成多个小的子任务的过程。
划分的目标是使得每个子任务的计算量尽可能均衡,并且可以并行执行。
常见的任务划分方法有数据划分和功能划分两种。
- 数据划分:将数据分成多个部分,每个处理器负责处理其中一部分数据。
这种划分适用于数据密集型的计算任务,如图像处理和大规模数据分析。
- 功能划分:将计算任务按照功能划分成多个子任务,每个处理器负责执行其中一个子任务。
这种划分适用于计算密集型的任务,如矩阵运算和模拟仿真。
2. 任务调度任务调度是将划分后的子任务分配给不同的处理器,并协调它们的执行顺序和通信。
任务调度的目标是最大程度地减少处理器之间的等待时间和通信开销,以提高整体计算效率。
二、并行计算的应用并行计算广泛应用于科学计算、大数据处理、人工智能等领域。
它可以加速计算过程,提高计算机系统的性能,并解决一些传统计算方法难以处理的问题。
1. 科学计算并行计算在科学计算中起到至关重要的作用。
例如,在天气预报模型中,通过将地球划分成多个网格,每个处理器负责计算其中一个网格的气象数据,可以加快模型的计算速度,提高预报准确性。
2. 大数据处理随着大数据时代的到来,传统的串行计算方法已经无法满足大规模数据的处理需求。
并行计算可以将大数据分成多个部分,通过多个处理器同时处理,提高数据的处理速度。
例如,谷歌的分布式文件系统和MapReduce框架就是基于并行计算的思想。
3. 人工智能人工智能算法通常需要大量的计算资源来进行模型训练和推理。
并行计算可以在多个处理器上同时执行算法的计算任务,加快模型的训练和推理速度。
多线程圆周率

多线程圆周率计算圆周率π(pi)的算法中,多线程并发计算可以加速计算过程。
其中,著名的算法之一是蒙特卡洛方法。
蒙特卡洛方法通过在一个正方形内随机投放点,并统计落在圆内的点的比例来估算圆周率。
以下是一个使用Python的多线程实现的简单示例:pythonCopy codeimport threadingimport randomtotal_points = 1000000points_inside_circle = 0lock = threading.Lock()def monte_carlo(thread_points):global points_inside_circlelocal_inside_circle = 0for _ in range(thread_points):x = random.uniform(-1, 1)y = random.uniform(-1, 1)distance = x**2 + y**2if distance <= 1:local_inside_circle += 1with lock:points_inside_circle += local_inside_circledef calculate_pi(num_threads):global total_pointsthread_points = total_points // num_threadsthreads = []for _ in range(num_threads):thread = threading.Thread(target=monte_carlo, args=(thread_points,))threads.append(thread)thread.start()for thread in threads:thread.join()pi_estimate = (points_inside_circle / total_points) * 4return pi_estimateif __name__ == "__main__":num_threads = 4estimated_pi = calculate_pi(num_threads)print(f"Estimated value of pi: {estimated_pi}")此代码创建了多个线程,每个线程在随机位置投放点,并统计落在圆内的点的数量。
集算器并行计算之多线程
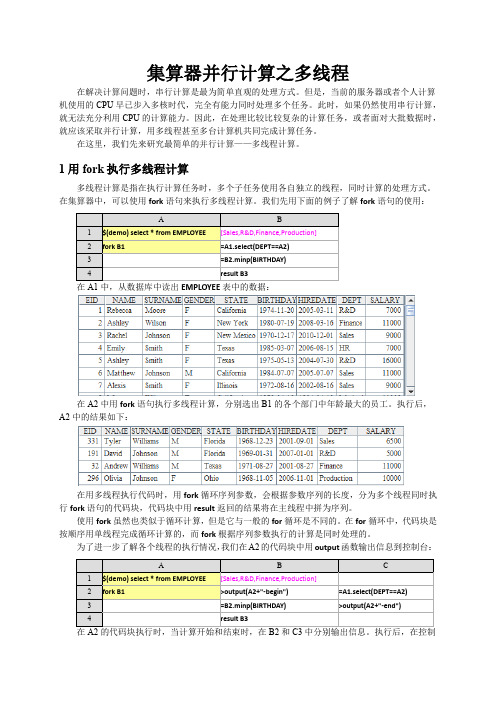
集算器并行计算之多线程在解决计算问题时,串行计算是最为简单直观的处理方式。
但是,当前的服务器或者个人计算机使用的CPU早已步入多核时代,完全有能力同时处理多个任务。
此时,如果仍然使用串行计算,就无法充分利用CPU的计算能力。
因此,在处理比较比较复杂的计算任务,或者面对大批数据时,就应该采取并行计算,用多线程甚至多台计算机共同完成计算任务。
在这里,我们先来研究最简单的并行计算——多线程计算。
1用fork执行多线程计算多线程计算是指在执行计算任务时,多个子任务使用各自独立的线程,同时计算的处理方式。
在集算器中,可以使用fork语句来执行多线程计算。
我们先用下面的例子了解fork语句的使用:A B1 $(demo) select * from EMPLOYEE [Sales,R&D,Finance,Production]2 fork B1 =A1.select(DEPT==A2)3 =B2.minp(BIRTHDAY)4 result B3在A1中,从数据库中读出EMPLOYEE表中的数据:在A2中用fork语句执行多线程计算,分别选出B1的各个部门中年龄最大的员工。
执行后,A2中的结果如下:在用多线程执行代码时,用fork循环序列参数,会根据参数序列的长度,分为多个线程同时执行fork语句的代码块,代码块中用result返回的结果将在主线程中拼为序列。
使用fork虽然也类似于循环计算,但是它与一般的for循环是不同的。
在for循环中,代码块是按顺序用单线程完成循环计算的,而fork根据序列参数执行的计算是同时处理的。
为了进一步了解各个线程的执行情况,我们在A2的代码块中用output函数输出信息到控制台:A B C1 $(demo) select * from EMPLOYEE [Sales,R&D,Finance,Production]2 fork B1 >output(A2+"-begin") =A1.select(DEPT==A2)3 =B2.minp(BIRTHDAY) >output(A2+"-end")4 result B3在A2的代码块执行时,当计算开始和结束时,在B2和C3中分别输出信息。
多线程计算π实验报告

一、实验目的1. 理解多线程编程的基本原理和概念。
2. 掌握多线程在计算密集型任务中的应用。
3. 通过实际操作,提高编程能力和问题解决能力。
4. 探讨多线程在计算π过程中的性能提升。
二、实验环境1. 操作系统:Windows 102. 编程语言:C++3. 编译器:Visual Studio 20194. 线程库:C++11标准线程库(<thread>)三、实验内容本实验旨在通过多线程编程技术,提高计算π的效率。
实验分为以下步骤:1. 设计一个计算π的函数,该函数采用蒙特卡洛方法进行估算。
2. 将整个计算任务划分为多个子任务,每个子任务由一个线程执行。
3. 利用C++11标准线程库中的thread类创建线程,并分配子任务。
4. 合并各线程计算的结果,得到最终的π值。
四、实验步骤1. 定义一个计算π的函数,采用蒙特卡洛方法进行估算。
```cpp#include <iostream>#include <random>#include <thread>#include <vector>double calculate_pi(int iterations) {std::random_device rd;std::mt19937 gen(rd());std::uniform_real_distribution<> dis(0.0, 1.0);int inside_circle = 0;for (int i = 0; i < iterations; ++i) {double x = dis(gen);double y = dis(gen);if (x x + y y <= 1.0) {++inside_circle;}}return 4.0 inside_circle / iterations;}```2. 将整个计算任务划分为多个子任务,每个子任务由一个线程执行。
集算器并行计算之多线程

集算器并行计算之多线程在计算机科学领域中,集算器并行计算是一种利用多个处理器(或多个内核)同时计算的技术,以提高计算机的计算能力和效率。
多线程是实现并行计算的主要方式之一,它可以使计算机同时执行多个线程,并发地进行计算。
多线程的工作原理是将程序的执行过程划分成多个较小的任务,然后将这些任务分配给不同的线程执行。
每个线程都有自己的计算能力和执行速度,因此它们可以并行地完成各自的任务。
使用多线程可以充分利用计算机的多核处理器,以提高计算速度和效率。
在集算器并行计算中,多线程可以应用于各种计算任务。
以下是一些常见的应用场景和实例:1.大规模数据处理:在处理大规模数据集时,多线程可以将数据划分成多个子集,每个线程处理一个子集,从而加快数据处理速度。
例如,可以将一个大型数据集分成若干部分,每个线程处理一个部分,并行计算数据的平均值、最大值或其他统计量。
2.图像处理:在图像处理中,多线程可以同时处理不同的图像区域或像素,以加快图像处理的速度。
例如,可以将图像划分成多个区域,每个线程负责处理一个区域,从而并行计算图像的滤波、边缘检测或其他图像处理操作。
3.并行算法:在算法中,多线程可以同时多个解空间的子空间,以加快速度。
例如,在解决棋类游戏中的最佳下法问题时,可以将空间划分成多个子空间,每个线程一个子空间,从而并行地最佳下法。
4.数值模拟和科学计算:在数值模拟和科学计算中,多线程可以同时计算多个模拟或计算任务,以加快模拟和计算的速度。
例如,在计算机流体力学中,可以将流域划分成多个子域,每个线程模拟一个子域的流动,从而实现并行计算。
多线程的并行计算有以下几个优点:1.提高计算速度:通过同时执行多个线程,可以充分利用计算机的多核处理器,加快计算速度和响应时间。
2.提高计算效率:多线程可以将计算任务划分成多个较小的子任务,并发地进行计算,从而提高计算效率。
3.提高系统资源利用率:通过充分利用计算机的多核处理器,多线程可以更好地利用系统资源,提高系统资源利用率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2 并行思想 在上述计算过程中唯一可以并行化的地方是随机数模拟了, 假设投入的总点 数为 kSamplePoints ,开启 num_threads 个线程,这样每个线程平均的去投 kSamplePoints/num_threads 个点,最后将所有线程的结果求和并计算概率 P, 这样比串行的效率高很多。
三、程序流程图
(1)串行流程图: 串行流程图只需要调用 hits 函数即可(hits 函数如下图) ,在此不再赘述。 (2)并行流程图
四、实验结果及分析
4.1 实验结果数据统计 (1)随机点个数为 107
串、并行运行结果: 线程数 PI 的值 0 3.1 411 3 153 947 1 1 2 3 4 5 6 7 8 9 10 3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14 3.14 113 113 113 113 113 113 113 113 113 113
4.2 加速比曲线 柱形图:
8 7 6 5 加速比 4 3 2 1 0 0 1 2 3 4 5 线程数 6 7 8 9 10 随机点个数为10^7 随机点个数为10^8
折线图:
8 7 6 5 加速比 4 3 2 1 0 0 1 2 3 4 5 线程数 6 7 8 9 10 随机点个数为10^7 随机点个数为10^8
ห้องสมุดไป่ตู้
3.89 5026
2.74 0197
(2)随机点个数为 10 线程数 PI 的值 运行时 间/微秒 加速比
8
串、并行运行结果: 0 1 2 3 4 5 6 7 8 9 10 3.1 3.14 3.14 3.14 3.14 3.14 3.1 3.14 3.14 3.14 3.1 417 17 17 17 17 17 417 17 17 17 417 153 1547 7974 5469 4191 3825 3352 2891 2304 2448 2865 49 93 15 72 35 31 52 11 34 736 753 1 1 0.99 1.92 2.81 3.66 4.01 4.5 5.31 6.67 6.27 5.3 3286 7849 0568 8113 8488 859 7178 1068 9787 653 2 7
1547 70 1075 52 1048 04 9090 5 6193 7 7704 6 4830 2 4142 5 3952 4 5618 1
运行时 间/微秒 加速比
0.99 4682
1.43 1373
1.46 8904
1.69 3493
2.48 5542
1.99 8118
3.18 7177
3.71 6282
一、实验内容
(1)利用蒙特卡罗方法求圆周率 PI (2)编写串行和多线程的代码分别计算并记录时间 (3)统计数据并画出加速比曲线 (4)对实验结果分析及感想
二、实验原理
2.1 计算原理 在数值积分法中, 我们利用求单位圆的 1/4 的面积来求得 Pi/4 从而得到 Pi。 单位圆的 1/4 面积是一个扇形, 它是边长为 1 单位正方形的一部分,只要能求出 扇行面积 S1 在正方形面积 S 中占的比例 K=S1/S 就立即能得到 S1,从而得到 Pi 的值。 怎样求出扇形面积在正方形面积中占的比例 K 呢?一个办法是在正方形中 随机投入很多点, 使所投的点落在正方形中每一个位置的机会相等看其中有多少 个点落在扇形内。 将落在扇形内的点数 m 与所投点的总数 n 的比 m/n 作为 k 的近 似值。 怎样实现这样的随机投点呢?任何一款计算机语言都有这种功能,能够产 生在区间[0,1]内均匀分布的随机数,产生两个这样的随机数 x,y,则以(x,y)为 坐标的点就是单位正方形内的一点 P,它落在正方形内每个位置的机会均等,P 落在扇形内的充要条件是 x^2+y^2<=1。 设投入的总点数为 S1 ,根据判定条件可计算出落入园内的为 S2 ,则有 ������ S2 =P= 4 S1 由上式即可算出������的值。
4.3 结果分析 分析结果得: (1)串行比单线程运行时间短(即加速比小于 1),此结果很好解释:单线程 相比于串行还要花费时间创建一个线程,自然运行时间比串行慢。 (2)理论上,随着线程数线性增大,运行速度应该相应的线性增大,但实际 上我们通过加速比曲线可以看出, 随着线程数的增大加速比大于 1 且总体趋势在 递增,但其增幅远远小于线性,分析此结果我认为是由于一下两个方面: 1)随着线程数的增大, 运行时需要开辟更多的内存空间,需要额外消耗一 部分时间。 2)本实验中的数据规模小于 108,故即使是采用 int 型的最大值 CPU 都可 以在很短的时间内计算完毕, 而开启线程所用的时间相对于此问题的计算时间来 说不能近似忽略,故采用多线程对速度的提升并不理想。 (3)对比 107 个随机点和 108 个随机点的加速比曲线,我们发现当数据点 越多时 PI 的计算越准确,而且由于计算时间的增大,创建线程所需的时间对总 时间的影响越小,从而多线程的优势越发明显。
并行计算实验一:多线程计算π
学院计算机科学与技术 专业计算机科学与技术 年级 2013 级 学号 姓名
2016 年 5 月 27 日
目录
一、实验内容................................................................................................................................... 3 二、实验原理................................................................................................................................... 3 2.1 计算原理........................................................................................................................... 3 2.2 并行思想........................................................................................................................... 4 三、程序流程图............................................................................................................................... 4 四、实验结果及分析....................................................................................................................... 6 4.1 实验结果数据统计 ........................................................................................................... 6 4.2 加速比曲线....................................................................................................................... 7 4.3 结果分析........................................................................................................................... 8 五、实验总结................................................................................................................................... 8
五、实验总结
通过这次实验我学会了很多内容,以前虽然学习过关于线程、进程的概念,但是 并没有真正的使用线程编写代码,利用随机数生成 PI 的多线程思想很简单,但 是从零开始的我花了好久才调通多线程的程序,当运行产生正确的输出结果时, 心里十分高兴。随后让我绝望的是,随着线程数的增加,运行时间成倍的上升, 这与实际矛盾,最后终于知道是由于在线程中生成随机数的原因,修改代码,并 行程序快的多了。 通过编写这个小的多线程程序,对计算机的线程、进程等资源的调度有了更 加深刻的认识。通过对实验的串行、并行结果的分析,更加清晰的认识到并行化 的重要性。
