关于库仑定律精确性的调研
静电学库仑定律的实践应用

静电学库仑定律的实践应用静电学是物理学中的一个重要分支,研究电荷、电场和电势之间的相互关系。
而库仑定律则是静电学的基石,描述了电荷之间的相互作用力。
本文将介绍静电学库仑定律的实践应用,并探讨其在日常生活和科技领域中的重要性。
一、静电学库仑定律简介静电学库仑定律是由法国物理学家库仑在18世纪提出的,它描述了两个电荷之间的作用力与它们之间的距离平方成正比,与电荷的大小成正比的关系。
数学表示为:F = k * (q1 * q2) / r^2,其中F是电荷之间的作用力,q1和q2分别是两个电荷的大小,r是它们之间的距离,k是一个比例常数。
二、静电粘贴静电粘贴是静电学库仑定律的一种实践应用。
我们在日常生活中会经常遇到,比如梳头后,头发会吸附在梳子上,或者使用胶带将灰尘粘在其上。
这些现象都可以用静电学库仑定律来解释。
当我们梳头时,梳子携带了一定的静电荷,头发带有相反的静电荷。
根据库仑定律,同种电荷之间的作用力是排斥的,不同电荷之间的作用力是吸引的。
因此,梳子和头发之间的静电力会使头发被吸附在梳子上。
同样地,当我们使用胶带粘取灰尘时,胶带也会带有静电荷,而灰尘则带有相反的静电荷。
根据库仑定律,胶带和灰尘之间的静电力会使灰尘被吸附在胶带上。
这种静电粘贴的应用在清洁工作中起到了很大的帮助。
三、静电防护静电防护是另一个实践应用,它在许多工业领域中具有重要作用。
在一些工作环境中,静电的产生可能会对电子设备和人员安全构成威胁,因此需要采取措施来防止静电的产生和积累。
根据库仑定律,电荷与电场之间存在一种相互作用力。
通过在工作环境中引入一定的导电材料并接地,可以将静电荷分散掉,减少电场的积累,从而避免了静电产生引起的问题。
例如,在石油工业中,由于流体的流动会导致静电的生成,而静电的积累可能导致火灾和爆炸。
因此,工作人员在操作过程中需要使用导电服装,并将其连接到地面,以确保静电荷的释放和安全。
四、静电喷涂静电喷涂是一种常见的工业技术应用,它利用了静电作用力来将涂层均匀地喷涂在物体表面上。
库仑定律教学探讨

库仑定律教学探讨◆卢翔远(曲阜师范大学附属中学)【摘要】对于物理学科而言,库仑定律应当属于核心性以及关键性的物理课内容。
然而实质上,库仑定律本身包含了多样化的定律内容,同时也呈现抽象性的表征。
针对上述定律如果要着手优化当前现有的物理课流程,那么需要从源头入手来优化并且改进当前现有的课堂模式。
因此可见,针对库仑定律涉及到的现阶段教学模式来讲,师生应当共同探求其相应的改进举措,运用多样化的手段与措施来实现教学优化。
【关键词】库仑定律课堂教学改进措施在电磁学的范围内,库仑定律被视作基础性的物理定律,因而在当前现有的物理学科体系中占据了主导性的位置。
从传统模式来看,教师通常为同学们讲授库仑定律密切相关的根本定理以及其中涉及到的习题,然后借助课堂演示让同学们对此深化理解。
但是近些年以来,新课改正在致力于全面推进,因此库仑定律涉及到的传统课堂模式也在实现相应转化。
为了优化课堂流程,针对库仑定律的相关课节就要融入更多物理实验,运用实验措施来激发学生针对上述知识点的浓厚兴趣,培育其更高层次的物理学科实践素养。
一、设置整体性的教学目标对于电磁学来讲,库仑定律应当属于其中不可或缺的核心性定律。
因此如果要深入探究电磁学,那么通常都会涉及到上述定律。
因此从基本特性的视角看,库仑定律密切连接了电磁学与力学,对于带电体能够发生的彼此作用予以详细阐释。
在学好库仑定律的前提下,学生就能顺利过渡至后期与之有关的电学学习。
库仑定律本身应当包含实验导入以及定性分析,上述二者共同构成了核心性的课堂流程。
针对电荷作用力应当予以深入探析,确保能够顺利予以课堂导入。
因此在设置课堂目标时,关键需要落实于电荷量、电荷距离以及电荷作用力,对于上述要素都要着手予以深入探究。
教师在开展实验演示的前提下,应当能够为同学们透彻阐释上述各项要素的相互关系。
实质上,点电荷与带电体应当可以实现彼此的转化,进而创建了联想状态的点电荷模型。
除此以外,教师还需要运用库仑扭秤实验的方式来深入阐释与之有关的公式,借助课堂实验来调动学生对此的参与热情以及探究兴趣。
关于库仑定律(成立条件、精确度、使用范围)

关于库仑定律(成立条件、精确度、使用范围)1785年(我国清代乾隆五十年),法国科学家库仑(Charles Augustin Coulomb ,1736~1806年,军事工程师,退休后从事电学研究)用扭秤实验得出:两个静止的点电荷之间的相互作用力与它们之间的距离平方成反比.这一规律的发现比牛顿发现万有引力迟100年.另外,值得指出的是,第一,在库仑做他的著名“扭秤”实验时,对电荷的量还没有明确的定义和度量方法,故在他的研究报告(《法兰西皇家科学院研究报告集》第569页)中,只强调了反平方定律,并没有明确提到电力与电荷的电量成正比.关于电量的严格定义是高斯等人在以后作出的,所以,现在我们所看到的库仑定律是后人在库仑扭秤实验结论基础上发展起来的.第二,如果真要用实验来确定两个点电荷之间的相互作用力,则应在真空中进行.如果在介质中进行,会影响测量的精确性.事实上,当初(1785年)库仑的所有测定都是在真空中做的.库仑定律不仅是静电学的基础,也是整个电磁理论的基础之一.由库仑定律可以推出静电场方程乃至整个麦克斯韦方程组,而且库仑定律还标志着:人们对电磁现象的研究由定性的观察过渡到用仪器作定量的测量,并总结出定量的规律,从而开创了用近代的科学方法研究电磁现象的道路.库仑定律在近代物理理论中也具有重要的意义,它隐含着光子的静电质量为零的结论.正因为库仑定律有如此的重要性,所以,我们有必要对库仑定律的成立条件、适用范围及平方反比的精度等问题作深入的研究和探讨.1、库仑定律的成立条件关于库仑定律的成立条件,尽管各书籍的说法不一,但归纳起来不外有三条,即,(1)电荷是点电荷;(2)在真空中;(3)电荷处于静止状态.下面,我们将逐条分析.条件(1)应该说是容易理解的,亦是正确的.因为用库仑定律计算两点电荷之间的作用力要用到距离,而只有点电荷,两带电导体之间的距离才有完全确定的意义(点电荷是个相对概念,详见扩展资料中“点电荷与检验电荷”).然而,从微积分的观点看,任何连续分布的电荷都可看成无限多个电荷元(即点电荷)的集合,再利用叠加原理,就可求出非点电荷情况下的电场分布.所以,从上述分析可知,条件(1)确是库仑定律的成立条件,但不是限制库仑定律的使用条件.条件(2)是完全多余的(但不能说错),因为只要是两个点电荷,不管它们在什么地方(是在真空、导体还是介质中),相互作用力都遵从库仑定律.但要注意的是,在有其他物质存在时,这些物质会受到原来两电荷的电场作用,从而产生极化电荷或感应电荷.因此,原来两个电荷中的每一个,都要受到这些极化电荷或感应电荷的影响,这时它们所受的作用力一般就比较复杂了,好在有一个例子能加以说明.在均匀无限大介质(0εεεr =)中,两个点电荷之间的作用力是真空中的r ε/1倍,即2021022144r rq q r rq q F r επεπε==(1)从形式上看,(1)式似乎就是库仑定律在介质中不成立的佐证.殊不知在均匀无限大介质中,两个点电荷还要使介质产生相应的宏观极化电荷,如图所示.很明显,点电荷1q 要受到三种电荷的作用力,极化电荷1q '-均匀地包围着,由对称性可知,其对1q 的作用力为零,极化电荷2q '-由于距1q 较远,可看作点电荷,位置与2q 相同,故根据库仑定律,1q 所受到的力为:20210202144r rq q r rq q F πεπε'==(2)由电磁学理论可以证明,2q '和2q 的关系满足下式: 2021q q ⎪⎭⎫ ⎝⎛-='εε (3) 将(3)式代入(2)式可得: 2201202201414q rq q q r q F εεπεεεπε=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--'=22141rq q πε= (4)(4)式写成矢量形式为:20214r rq q F r επε=(5)可见,(5)式与(1)式完全相同.由此可见,只要我们把介质中的宏观极化电荷与自由电荷同等看待,那么,它们彼此间的作用力都遵从库仑定律,因而没有必要强调一定要在真空中库仑定律才成立.至于条件(3),即电荷处于静止状态,也可以适当放宽,不必要两个点电荷都相对于观察者静止,只要源电荷(施力电荷)保持静止就可以,受力电荷可以是静止的,也可以做任意运动.道理很简单,静止电荷在空间激发的电场是不随时间变化的,仅是空间的函数,运动电荷所受到的由静止电荷所激发的电场力只与两电荷的相对位置和它们本身的电量有关,即遵从库仑定律.反之,静止电荷所受到的由运动电荷激发的电场力,由狭义相对论电动力学可知,这个力不但与两个电荷的相对位置和电量有关,而且还与运动电荷的速度有关,即它们之间的作用不再遵从库仑定律.在这种情况下,连牛顿第三定律也不再遵守.如图所示,设点电荷1q 以速度v 匀速向右运动,点电荷2q 静止不动,则由上述观点,2q作用在1q 上的力为:2021124r rq q F πε=(6)即遵从库仑定律.但反过来,1q 作用在2q 上的力却不遵从库仑定律.根据电动力学理论,1q 在2q 处激发的电场强度为:2/3222022201114⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⋅=cr r v c v r c v rq E πε (7)式中c 是真空中的光速.因此,按qE F =计算,1q 作用在2q 上的力便为:2/3222022202121114⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⋅=cr r v c v r c v rq q F πε (8)从(8)式可知,1q 作用在2q 上的力已不再遵从库仑定律;只有当0=v 时,(8)式才退化为真空中的库仑定律.比较(6)式和(8)式还可以看出,当两个点电荷有相对运动时,它们之间的相互作用力也不再遵从牛顿第三定律.但可以证明两点电荷与它们所产生的电磁场所构成的系统满足包括电磁动量和机械动量在内的动量守恒定律.2、平方反比律的精确度 库仑定律是一个实验定律,由于实验装备的精确度是有限的,所以实验结果与库仑定律并不完全一致.验证平方反比律的一种方法是假定力按δ±2/1r变化,然后用实验测出δ的值.显然,δ值越小,实验精确度越高,从而表明库仑定律越准确.事实上,对电荷之间作用力所遵循的规律,早在库仑以前就有人进行过研究.1769年,罗比逊第一个从实验确定δ值约为0.06;1773年,卡文迪许实验测出的δ不大于0.02;1785年,库仑自己测出的δ为百分之几.关于库仑定律平方反比律精确度的研究,一直为历代物理学家高度重视,迄今未停止过.由于实验装置精确度的不断提高,至今精度最高的是1971年威廉姆斯等人所作的实验,他们测出的16102-⨯≤δ.为便于查阅,现将自罗比逊以后各次主要实验所得到的偏差值列表如下验证平方反比律的实验结果近代许多科学家之所以重新对库仑定律中的平方反比关系发生那么大的兴趣,主要是与对光子的静质量的关心有关,而光子的静质量是否为零,又与相对论的基本假设之一的光速不变原理有关.可以证明,若0≠δ,则光子的静质量将不为零.目前这方面的探讨还与磁单极的探索相联系.如果真的发现了磁单极,则光子的静质量必为零,库仑定律的平方反比关系也就严格成立了.3、库仑定律的适用范围库仑定律除了有一个平方反比律的精度问题外,还有一个适用范围的问题,因为所有验证库仑定律的实验都是囿于0210~10-米的范围内进行的.试问,超出0210~10-米这个空间范围,库仑定律是否还成立呢?库仑定律的适用范围到底有多大呢?兰姆和卢瑟福对氢原子的能级作了精确测量,与用库仑定律计算出的结果相吻合;另外,卢瑟福的X 粒子散射实验的精确测量与库仑定律也相吻合,这表明库仑定律在原子范围内(1010-米)是成立的.近代核物理实验证明在原子核的大小范围(1510-米)内,库仑定律不再成立,但在1310-米范围内,库仑定律精确成立.地球物理实验证明库仑定律在710~10米范围内是精确成立的.在更大的距离(如天文距离——26710~10米)范围内,物理学家虽然没有对库仑定律进行过实验验证,但是,在那样巨大的空间中,电磁波仍然以光速在传播,电磁场的规律仍然起作用.因此,可以推断,在那样大的范围内,库仑定律仍然有效.库仑定律的实验验证虽然都是在0210~10-米范围内进行,但其适用范围可扩展到261310~10-米.。
库仑定律的实验验证

库仑定律的实验验证
库仑定律是1784--1785年间库仑通过扭秤实验总结出来的。
扭秤的结构如下图。
在细金属丝下悬挂一根秤杆,它的一端有一小球A,另一端有平衡体P,在A旁还置有另一与它一样大小的固定小球B。
为了研究带电体之间的作用力,先使A、B各带一定的电荷,这时秤杆会因A端受力而偏转。
转动悬丝上端的悬钮,使小球回到原来位置。
这时悬丝的扭力矩等于施于小球A 上电力的力矩。
如果悬丝的扭力矩与扭转角度之间的关系已事先校准、标定,则由旋钮上指针转过的角度读数和已知的秤杆长度,可以得知在此距离下A、B之间的作用力,并且通过悬丝扭转的角度可以比较力的大小。
关于库仑定律(成立条件、精确度、使用范围)

E
q1
2
4 0r
2
v
0
1 2r
c
v2
1
2
c
2 3/ 2
vr
cr
( 7)
式中 c 是真空中的光速.因此,按 F qE 计算, q1 作用在 q2 上的力便为:
F 21
q1 q2
2
4 0r
2
v
0
1 2r
c
2
v
1
2
c
3/ 2 2
vr
cr
( 8)
从( 8)式可知, q 1 作用在 q 2 上的力已不再遵从库仑定律;只有当 v 0 时,( 8)式才
100
年.另外,值得指出的是,第一,在库仑做他的著名“扭秤”实验时,对电荷的量还没有明
确的定义和度量方法,故在他的研究报告( 《法兰西皇家科学院研究报告集》 第 569 页)中, 只强调了反平方定律, 并没有明确提到电力与电荷的电量成正比. 关于电量的严格定义是高
斯等人在以后作出的, 所以, 现在我们所看到的库仑定律是后人在库仑扭秤实验结论基础上
如图所示, 设点电荷 q1 以速度 v 匀速向右运动, 点电荷 q 2 静止不动, 则由上述观点, q 2
作用在 q1 上的力为:
q1q 2
0
F12
2r
4 0r
(6)
即遵从库仑定律.但反过来, q1 作用在 q 2 上的力却不遵从库仑定律.根据电动力学理
论, q1 在 q 2 处激发的电场强度为:
实验者 罗比逊
验证平方反比律的实验结果 时间 1769
结果( ) 0 .06
卡文迪许 库仑
麦克思韦 普利姆顿等
考仑等 巴兰特等 威廉姆斯等
(完整版)库仑定律的创建与精确验证

量或模型,找出新的内容,正确表述); 考察成立条件、适用范围、精度、理论地
位及现代含义等 。
1、库仑定律创建的基础
吉尔 伯特 区别 电和 磁两 类不 同的 现象
1746年马赛布洛克发明莱顿瓶
1769年Robison首先用直接测量 方法确定电力定律,得到两个 同号电荷的斥力
f ∝ r-2.06
▪ 两个异号电荷的引力比平方反比 的方次要小些。(研究结果直到 1801年发表才为世人所知)
库仑的扭称实验
1785 年 电 斥 力 扭 称 实验装置精巧、技 术高超。
数据只有几个,且 不准确(因为漏 电 ) ——Coulomb 定律不是大量精确 实验的总结。
设计实验——
Robison的实验
1769年设计的一个杠 杆装置,利用活动杆所 受重力和电力的平衡, 从支架的平衡角度求电 力与距离的关系。不过, 他的装置只适于对同性 电荷进行实验。电力与 两球距离的关系如果用 公式f∝1/r2+ 表示, 他得到 δ=0.06。这个 δ就叫指数偏差。
Robison的杠杆实验
介绍库仑定律创建和精确验证 的历史过程
讨论从库仑定律创建的历史 过 程中我们可以获得哪些有益 的启示
一、库仑定律创建
以库仑定律为例说明:
一个物理定律的建立本身就是物理学 取得很大进展的标志
物理定律具有丰富、深刻的内涵和外 延
对于基本定律,我们究竟从那些方面 考察?
物理定律建立的一般过程
1744年Franklin观
看Spencer博士的电 学演示实验,对电产 生了兴趣。
1745年彼得发给他一 个“电子管”作为奖 品,自此开始了对电 的严谨而又有趣的研 究
自制仪器对库仑定律的探究

自制仪器对库仑定律的探究高中物理选修3-1中第一章静电场的库仑定律一节中,有一个演示实验,要求定性地演示静电力大随两个电荷间的距离的增大而减少、随两个电荷的电量乘积的增大而增大(教科书上图1.2-1)。
该实验是个定性实验,看似简单,但很难演示成功。
因为要使悬挂电荷的丝线偏离竖直方向有明显的偏角,小球必须带有足够大的电量,这点很难实现。
完成这个定律的验证通常是用库仑扭称装置(教科书上图1.2-2)来实现的,由于实验条件的限制,一般学校没有配置。
我考虑到静电力常数K要比万有引力常数G大得多,这就不用扭称而用天平也可以把静电力显示出来。
根据这一思路,我利用物理仪器室的物理演示天平加以改装,制成了一架长臂静电天平。
利用两个半径相同,相对都很小的带电球近似点电荷,移动游码可以测量出库仑力的大小,我们也可以改变电荷之间的距离。
关于该实验仪器的介绍将放在第一部分。
在实验中,我们得到了一系列数据。
对数据经过处理之后,利用Matlab进行了数据拟合。
通过本装置我们发现,库仑定律的反平方性质还是比较精确的。
这部分内容将在第二部分展现。
对与实验的分析,结果的讨论,以及本实验装置的不足不恰当之处将在第三部分给出。
一、材料与方法1.实验材料①自制的静电天平(图一)找一架200g的带有游码的物理演示天平,拆去托盘架和秤盘。
拆去天平横梁左端的平衡螺丝。
在右端平衡螺丝上再加一个25g的平衡块。
用厚4mm的有机玻璃裁成一条宽3cm长36cm的长条款,刻上以cm为单位的刻度,然后用胶水把它竖直地胶到天平的立柱上。
图一:两横杆中,上杆只可以上下移动,下杆只可以转动。
两杆之间距离可以直接从直杆中读取,最左端为两个镀化过的金属球。
表1 保持电量不变复位两杆距离,并且保持不动。
让小球2重新带电,接触小球1,然后,水平静止后读取数据。
利用第三个小球,先接触小球1,由于半径相同,使得小球1电量减半。
重新读数,把第三个小球接地放电,再接触小球2,使得小球2电量减半,以此类推,得到表2。
基于科学探究的“库仑定律”教材内容研究

第48卷第9期2019年9月力*F 我■学参考教材研究基于科学探老的“库仑定律”教材内家研屯张晓华(重庆市荣昌中学校重庆 402460)文章编号:1002-218X (2019)09-0064-01《普通高中物理课程标准(2017年版)》指出:提 出问题、猜想与假设、实验探究、交流、评估和反思是 科学探究的构成要素。
一个具体的教学过程只要具 有一两个这样的要素,就是科学探究。
一、 使用现行人教版教材中的困惑库仑定律不仅是整个电磁学的基石,而且还是力 学向电磁学过渡的桥梁。
但在教学实践中,一些学生 重在机械识记库仑定律,无法理解库仑定律是力学向 电磁学过渡的桥梁。
1. “探究影响电荷间相互作用力的因素”演示 实验猜想与假设是实验探究的前提。
教材有必要阐 释“探究影响电荷间相互作用力的因素”中“猜想与假 设”的相关内容。
同时,教材演示实验的结论猜想:电 荷之间作用力会不会与万有引力具有相似的形式呢? 师生对此深感突兀。
2. 库仑扭称实验教材花了较多篇幅介绍库仑扭称实验,旨在说明 库仑扭称实验对建立库仑定律的重要性。
事实上,在 知识层面上,涉及扭力的概念和力矩平衡的知识,超 出当前学生认知水平;在技能层面上,库仑扭称结构 复杂,难以驾驭。
而且教学实践还表明,此实验误差 较大,很难获得想要的结果。
二、 教材改编牛顿在研究出万有引力定律后,试图证明磁力和 电力有着与万有引力类似的规律,受当时条件所限, 未能如愿。
那么,电荷之间作用力的大小决定于哪些 因素呢?1.猜想与假设1750年,米切尔实验研究发现磁极间作用力服 从平方反比定律。
此后,牛顿关于电力规律猜想的证 实再次让科学家们充满期待。
1755年,富兰克林发现:带电罐头盒中的带电球 不受电作用。
富兰克林的好友普里斯特利进一步研 究发现:正如牛顿推证在地球里面的物体不受地球引力 一样,电荷间相互作用服从于与万有引力类似的规律。
不过,因为当时一直没有找到恰当的方式来对静电 作用力进行进一步的精确测量,仍停留在猜测的阶段。
高中物理_库仑定律教学设计学情分析教材分析课后反思

库仑定律教学设计库仑定律的学情分析1.学生在初中已经学习了电学的基本知识,知道了关于静电现象的一些实例,比如:摩擦起电;2.通过上节电荷及电荷守恒定律的学习,学生进一步了解了起电的方式,以及两种电荷间的排斥和吸引作用,从而为过渡到本节的学习起着铺垫作用。
3.学生已具备了一定的探究能力、逻辑思维能力及推理演算能力。
比如:学生已经具备对带电体进行受力分析的能力,并且能在老师指导下通过观察、思考,发现一些问题和解决问题,所以,学生可以独立思考,设计实验并进行解决问题。
4.提前让学生结合学案中的自学提纲预习教材,了解本节的主要内容,先独自解决部分问题。
库仑定律的效果分析1.通过引入练习,学生对前期的知识掌握还可,能通过观察得出电荷间哪种作用的结果。
2.通过实际研究对象和理论研究对象的类比得出点电荷,强化研究物理问题的思路,是从简单到复杂,结合质点,确定了点电荷这个理想化模型。
学生对点电荷的接受和理解及其意义还可,基本把握以质点去衡量是否看成点电荷的前提。
3.通过猜想,确立实验方法,到方案设计到方案是实施操作,学生基本都能达标,会通过观察,定性或定量的分析所研究问题的关键。
4.通过定性实验,学生能得出库仑力跟电荷量及电荷间距的定性关系。
5.通过观看视频和动画,学生理解库仑定律实验的过程方法,并了解库仑如何利用电荷平分思想解决问题的方法。
6.学生对库仑定律的内容理解及应用,接受也可以,知道了表达式的物理意义与数学形式的区别,并会用表达式解决了相应问题。
7.展示学生的收获过程中,学生能进一步呈现课堂思路和内容。
总之,本节课达到预期的效果,把在演示实验基础上,加入学生的定性探究实验,模拟规律探究的过程,使学生思维积极活跃,有认知冲突,有精彩观念;而且通过展示学生的计算结果和学生的互评环节,使学生参与度提高,从而达到教学目标的同时,也使不同层次的学生均有收获;而且各环节中,师生交流对话充分,教学相长,形成民主和谐、相互尊重、合作探究的教学氛围,反映出浓厚的课堂。
库仑定律的实验验证与应用

库仑定律的实验验证与应用库仑定律,又称为库伦定律,是电磁学中最基本的定律之一。
它是由法国物理学家库仑于18世纪末提出的,用以描述两个电荷之间的电力相互作用。
库仑定律的数学表达式为:两个电荷之间的电力的大小与两个电荷的电量的乘积成正比,与两个电荷之间的距离的平方成反比。
即库伦定律可以用公式表示为:F=K*q1*q2/r^2,其中F为两个电荷之间的电力的大小,q1和q2分别为两个电荷的电量,r为两个电荷之间的距离,K为比例常数。
为了验证库仑定律的准确性和应用,科学家们进行了大量的实验研究。
其中最著名的实验之一是质子电荷实验。
科学家发现在质子间的相互作用中,电力的大小与两个质子的电量的乘积正比,与两个质子之间的距离的平方成反比。
这一实验结果验证了库仑定律在微观领域中的准确性。
库仑定律的应用十分广泛。
在物理学和工程学的研究中,库仑定律被广泛应用于电磁场的计算和电磁力的描述。
例如,当我们计算电子在电场中受到的力时,可以利用库仑定律来计算。
通过测量电荷和距离,我们可以根据库仑定律准确计算出电场强度和电势差。
库仑定律还被应用于静电学中。
静电学是研究静电现象和静电场的学科,而库仑定律是静电学的基础。
静电学在现实生活中有着广泛的应用。
例如,在油漆喷涂工业中,我们常常会使用静电力使涂层均匀地附着在物体表面上。
这就是因为库仑定律使得带电颗粒受到静电力的作用,从而实现涂层均匀而高效的附着。
此外,静电学还应用于空气净化、印刷业、高压电源和电子设备等的设计和制造中。
库仑定律的实验验证和应用,不仅深化了我们对电荷之间相互作用的理解,也为电磁学和静电学等学科提供了重要的理论基础。
通过探究库仑定律实验结果的准确性和应用价值,科学家们不断推进着人类对电磁和电荷运动的认识,为科学研究和技术创新提供了坚实的基础。
库仑定律的实验验证和应用在电学领域中有着广泛的应用。
例如,在电动力学研究中,库仑定律被用于计算电荷之间的相互作用力,从而解释电场的行为。
库仑定律实验探究原理

库仑定律实验探究原理嘿,朋友们!今天咱来聊聊库仑定律实验探究原理。
你说这库仑定律啊,就像是物理学里的一把神奇钥匙,能打开好多知识的大门呢!想象一下,电荷之间的相互作用,就好像两个人在玩拔河比赛。
电荷就像是那拔河的双方,它们之间的力就是那根绳子。
做库仑定律实验的时候,就好像我们在观察这场拔河比赛。
我们得准备好各种道具,就像运动员要准备好跑鞋一样。
通过这个实验,我们能看到电荷之间的力是怎么变化的。
比如说,我们改变电荷的大小,那不就像是给拔河的一方增加或减少力量嘛!然后看看绳子会怎么变化,也就是力会怎么改变。
这多有趣啊!再比如,我们改变电荷之间的距离,这就好像是把拔河的两个人拉远或拉近。
那力肯定也会不一样啦,对吧?这个实验探究就像是一个大冒险!我们不断地尝试,不断地观察,就为了找到电荷之间相互作用的规律。
这难道不比玩游戏还有趣吗?你想想看,要是没有这个实验,我们怎么能知道电荷之间的那些小秘密呢?那我们对电的理解不就少了一大块嘛!而且哦,这个实验可不是随随便便就能做好的。
得细心,得耐心,就像绣花一样。
一点点的差错可能就会让结果变得不准确。
做这个实验就像是走在一条小路上,每一步都要走得稳稳的。
如果不小心摔了一跤,那可就前功尽弃啦!所以得打起十二分的精神来。
库仑定律实验探究原理真的很重要啊!它让我们对自然界的规律有了更深入的了解。
它就像一盏明灯,照亮了我们探索物理世界的道路。
通过这个实验,我们能更好地理解电荷的行为,这对我们学习电学、电磁学等等都有着至关重要的作用。
它就像是一个基础,没有它,那些高楼大厦可就建不起来啦!所以啊,大家可千万别小看了这个库仑定律实验探究原理。
它虽然看起来很普通,但却蕴含着无穷的奥秘和乐趣。
让我们一起沉浸在这个神奇的物理世界里,去探索,去发现吧!。
物理学中的库仑定律应用

物理学中的库仑定律应用库仑定律是物理学中的一项重要定律,它描述了电荷之间相互作用的力。
这个定律在物理学的各个领域都有广泛的应用,从原子结构到电磁场,甚至到生物学和化学等领域。
本文将探讨库仑定律在几个具体应用中的重要性和影响。
首先,库仑定律在原子结构研究中起着至关重要的作用。
原子由带正电荷的原子核和带负电荷的电子组成。
根据库仑定律,原子核和电子之间的相互作用力与它们之间的距离成反比。
这意味着原子核和电子之间的吸引力越强,它们之间的距离就越近。
这种相互作用力决定了原子的稳定性和化学性质。
例如,当原子中的电子数目与原子核的质子数目相等时,原子是稳定的。
如果电子数目较多或较少,原子就会变得不稳定,容易发生化学反应。
其次,库仑定律在电磁场的研究中也起着重要的作用。
电磁场是由带电粒子产生的,而库仑定律描述了电荷粒子之间的相互作用力。
根据这个定律,同种电荷之间的相互作用是排斥的,而异种电荷之间的相互作用是吸引的。
这种相互作用力决定了电荷粒子在电磁场中的运动轨迹和行为。
例如,当一个正电荷粒子和一个负电荷粒子之间存在相互作用力时,它们会互相吸引并形成一个稳定的电荷对。
这种电荷对的形成是电化学反应和电路中电流传导的基础。
除了原子结构和电磁场,库仑定律还在生物学和化学等领域有重要应用。
在生物学中,离子通道和神经传导等过程都涉及到电荷粒子之间的相互作用力。
库仑定律帮助我们理解这些过程的机制和行为。
例如,神经细胞之间的突触传递过程是通过电荷粒子的相互作用来实现的。
在化学反应中,电荷粒子之间的相互作用力决定了反应速率和反应产物的形成。
库仑定律帮助我们预测和解释化学反应的结果。
总的来说,库仑定律在物理学中的应用非常广泛。
它不仅帮助我们理解原子结构和电磁场的行为,还在生物学和化学等领域中起着重要作用。
通过库仑定律,我们能够解释和预测物质世界中的许多现象和现象。
因此,深入理解和应用库仑定律对于推动科学的发展和技术的进步至关重要。
关于库伦的论文

关于库伦的论文物理定律是在观察和实验基础上发现的实验规律。
各种物理定律从各自不同的角度和侧面揭示了事物的本质、规律和内在联系。
物理定律是物理理论赖以建立的基础,也是检验各种物理理论是非真理的标准。
因此,物理定律的建立是有关研究领域获得重要进展的标志。
在物理教学中,物理定律的阐述理说当然得占有重要的地位。
当然,在教学中,不可能也没有必要凡遇到物理定律都作系统全面的考察,但结合各定律的特点,有选择地作一些引申和发挥,注意把具体内容的讲授与科学思维能力的培养结合起来,是有益的,这也应该成为物理教学改革的一个重要方面。
下面以熟知的库仑定律为例进行讨论。
1785年库仑设计制作了一台精巧的扭秤,它能测量10-8牛顿的弱力。
通过扭秤实验,库仑得出:“两个带同种电荷的小球之间的相互排斥力和它们之间距离的平方成反比。
”库仑测出电引力单摆的振动周期与摆锤(点电荷)到电引力中心(另一异号点电荷)的距离成反比,从而证明两异号点电荷之间的电引力也与距离的平方成反比,又一次显示了类比的'威力。
库仑定律包括三个内容,即F∝r-2,F∝Q1Q2,F的方向沿两点电荷的连线。
除F∝r-2已被上述实验证实外,另两者来自何处呢?由于库仑力是电场力,与物体带电状况有关,在其表达式中需要引入定量描述物体带电状况的物理量——电量。
应该指出,F∝Q1Q2正是电量的定义,而并非实验结果,因为在尚未定义电量之前,是无法用实验来证明电场力与电量乘积成正比的。
同样,在万有引力定律的表达式中也包含了引力质量的定义,诸如此类,俯拾皆是。
借此,比较电量之类的异同,指出电场力与引力都与距离的平方成反比,电量和质量都遵循各自的守恒律,但电量有正负(这使得电场力有吸引、排斥之区别,且可以屏蔽),电量无相对论效应,电量具有量子性等等,以开阔视野,使学生对电量这个物理量具有较为广泛的了解,是适宜的。
至于电场力的方向沿两点电荷的连线,虽则包括库仑定律在内的一些现象表明大抵如此,但并非严格证明。
库仑定律定量实验的探究与设计
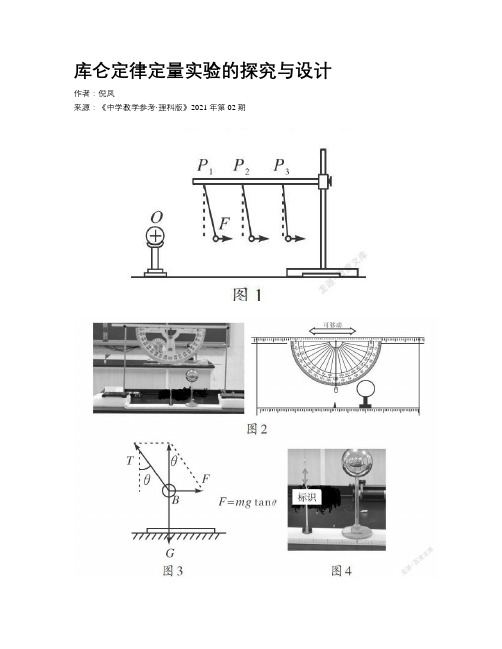
库仑定律定量实验的探究与设计作者:***来源:《中学教学参考·理科版》2021年第02期[摘要]库仑定律是人教版教材选修3-1第一章第二节的内容,是电学发展史上第一个定量规律,是高中物理核心规律之一。
在教材定性实验的基础上,改进完善了该定律的“定量实验”,让学生经历问题与猜想、收集证据、交流等探究环节,使学生成为规律的“发现者”。
同时,引发学生关于实验数据偏差的思考,帮助学生树立实事求是、追寻真理的科学信念。
[关键词]库仑定律;定量实验;科学探究[中图分类号] G633.7 [文献标识码] A [文章编号] 1674-6058(2021)05-0057-02一、教材实验分析库仑定律反映了真空中点电荷之间的相互作用力和电荷量、距离之间的定量关系,教材中关于实验的内容特征为以下两点。
1.教材回避了定量实验方案,演示实验为定性实验:“探究影响电荷间相互作用力的因素”,如图1所示。
通过本实验能够直观看出电荷量越大,相互作用力越大;距离越远,相互作用力越小。
课本之所以回避了定量实验,是因为实验难度很大,天气潮湿程度、实验材料、器材大小等诸多因素都会对实验数据有非常大的影响。
但是没有定量实验就少了规律探究步骤中最为核心的环节,所以教学设计时,首先要解决的就是“定量实验”方案,使得规律不仅仅是课本中的黑体字,而是在科学探究中“自然生成”的。
2.课本着重介绍了库仑实验装置以及在实验过程中的困难处理,进而给出定量表达式,其中用“半分法”定量测量物理量之间的关系是非常重要的科学实验方法。
在定量实验过程中也着重介绍和应用了该方法,并且让学生进一步认识“实验数据偏差”。
二、定量探究设计1.问题由前面的学习,我们知道自然界中有两种电荷:正电荷和负电荷,且电荷之间存在相互作用力。
电荷之间的作用力大小受哪些因素影响?遵循什么规律?根据生活现象和熟悉的实验合理推测:电荷所带电荷量q越大,相互作用力F就越大;电荷之间的距离r越大,力F就越小;对于定量关系的推测一定是从最简单的关系开始,可以先假设F和q成正比,F和r成反比,即F和r的乘积为定值。
库仑定律的验证与修正

库仑定律的验证与修正作者:马占峰来源:《赤峰学院学报·自然科学版》 2011年第5期马占峰(赤峰学院物理与信息工程系,内蒙古赤峰 024000)摘要:回顾了库仑定律精度验证的的历程;从量子理论出发,在细微尺度上阐述了量子场的基态,真空涨落,真空极化及其对库仑定律的影响.关键词:库仑定律;精度;量子场基态;真空涨落;真空极化;极化电荷云中图分类号:O441.1 文献标识码:A 文章编号:1673-260X(2011)05-0011-02库仑定律是电磁学的基础,也是经典物理学的基本定律之一;库仑定律又是最精确的实验定律之一.二百多年来,为了提高电力平方反比定律精度的努力经久不衰.究其原因是库仑电力平方反比定律关乎光子静止质量是否为零?若mz≠0,就会动摇物理学大厦的根基,例如可能出现光速可变,电荷不守恒,真空色散等问题.因此,准确把握库仑定律的精度,全面深入的认识它是必要的.1 库仑平方反比定律的验证库仑定律成立于真空中,适用于静止的点电荷,表达的内容一是两个点电荷之间的静电力,与它们所带电量的乘积成正比,与它们之间距离的平方成反比;二是隐含着电量的定义.其数学式为1785年库仑用扭秤证实这一定律时,由于测量方法的局限性,实验误差相当可观.为了从根本上提高测量精度,可采取间接实验.第一个定量实验是卡文迪许在1772年完成的.图1(a)是根据他的原始实验装置图改画的示意图.A是一个有绝缘支柱的金属球,B1和B2是两个金属半球,其内径比A半径稍大,B1和B2固定于绝缘架C1和C2上,C1和C2间装有铰链以便开合,将球壳合上并把A同心地包在里面[图1(b)].用丝线1挂一短导线2穿过球壳的小孔使内球与球壳接触,然后令球壳带电.根据前面的讨论,如果库仑平方反比律不成立,导线内部就有电场,电荷就会沿导线流到内球A.撤出导线,打开球壳,内球A应该带电[注:此时库仑力大小取一般表示式F则A不带电等价于δ=0,即等价于平方反比律.卡文迪许用木髓球静电计对A球进行仔细测量,没有发现带电迹象.这表明平方反比律是正确的.考虑到验电器灵敏度和球壳数据,他估计δ与0之差不会超过0.02,即库仑定律中r的指数只可能介于1.98~2.02之间.(可惜他的实验成果比库仑扭秤实验早13年却没有发表).1870年,麦克斯韦以改进的方式重做了卡文迪许的实验,方法上的主要不同在于:在撤去内外球连接导线后,他不把外球壳移走而是将它接地,再用一个“象限静电计”测量内球的电势V内.他在理论上推出一个关于V内与?課的关系式,该式表明δ=0与v内=0等价,结果他测得内球电势为零.根据所用测量装置的数据及静电计灵敏度,他估计δ与0之差不会超过1/21600(近似为5×10-5).1936年,里普姆顿与洛顿重做类似实验,把δ与0的差确定在2×10-9以内.1971年利用近代技术改进了实验方法,把δ与0的差值确定在(2.7±3.1)×10-16以内.2 在细微尺度上库仑定律的修正在经典物理学的概念中,真空是一无所有的空间.它也体现了绝对时空观的基本涵义,一切客体及自然现象在这样的时空中存在、演化.然而,随着科技的发展和人类认识水平的提高和深入,这种传统的真空概念也遭到了颠覆.量子理论的研究表明,真空具有非常丰富的物理内容,甚至可以说:“真空是物理学的全部”.以往经典物理学之所以未能揭示出真空的奥秘,缘于考察得不够细致.若要揭示真空的内涵,须在更细微的尺度(≤10-13cm),或更高的能量(≥1Gev)上研究.真空是量子场的基态.量子场是物质存在的最基本形式;自然界中的各种粒子,包括有质量和无质量的粒子都是相应量子场的激发态;当然它们的能量最低态,可视为未被激发的状态,亦可称之为量子场的基态.这种状态,可认为是粒子物理现象的某种背景,一切自然现象就是在这种背景下发生的.粒子未被激发的状态也表示没有任何实粒子(包括光子、电子等)存在的状态.这种特殊的状态可视为自然界中的真实.真空的极化.真空中尽管不存在实粒子,但仍然可能存在各种虚粒子.设想将一正电荷置于真空中,按经典物理学的认识来看,此时不会发生任何事情.而从量子理论的角度观察,电荷周围的电场与真空之间会发生相互作用.一方面使电荷周围的真空极化;另一方面,真空极化电荷会对原电荷产生屏蔽作用.真空极化源自真空涨落.根据海森伯不确定性原理及正反粒子可以从真空中出现的事实,由相对论质能关系可知,当能量超过电子静能(电子静能为0.51Mev)两倍时,就可能引起电子——正电子对产生.然而这种电子对仅存在于细微的时空区域,是“虚电子对”.若依此类推,在更为细微的时空尺度上,可能产生质量更大的正反粒子对,如虚质子对,虚π介子对、虚μ子对,甚至虚夸克对等.如果外界不能提供能量,这些虚粒子对便会湮灭.可见,真空中不断地有各种虚粒子产生、湮灭和相互转化,真空在存在虚无之间随机地涨落着.由于真空涨落,真空中各点处充满了虚正负电子对.正电荷所建立的电场要排斥虚正电子,吸引虚负电子,因而原先的电荷会被正负电子对所形成的虚电偶极子包围,如图2所示.这与经典物理学中将电荷放入介质后引起的介质极化效应相似.所以称之为“真空极化”.荷电粒子如质子和电子其周围的真空中存在明显极化效应区域的线度约为电子康普顿波长(λe=h/mc=3.86×10-11cm)的数量级.真空极化效应使原来的电荷周围包围了一层极化电荷云,在足够远的距离(指大于康普顿波长处)通过实验所探测到的将是被极化电荷云包围的一个整体,无法分辨出基本粒子的电荷与它周围的极化电荷云.这种带有真空极化云的粒子称为“物理粒子”,不带真空极化云的粒子叫“裸粒子”.而物理粒子所携带的电荷即物理电荷应该是一个有限值,实验测得的(物理)电子电荷为e=1.6×10-19c,的确是一个有限值.物理学的真空内涵丰富,有真空的涨落,真空的极化效应.这势必对真空中的库仑定律产生一定的影响.我们知道库仑定律的正确性如前所述已在很高的精确度上被实验所证实.如果考察库仑定律在更微小尺度上的精确度,一般采用电子——电子(或正电子)散射实验,实验表明,若两电子的能量不很高,它们相距的比真空极化效应显著区域的线度(λe≈10-11cm)大许多,则此时两电子的相互作用便取决于它们的物理电荷,此时库仑定律依然精确成立.但是在更高能量的电子——电子(或正电子)散射实验中,两电子可能相距很近,以致深入到彼此的真空极化电荷云之中.因为真空极化效应是一种屏蔽效应,所以这时彼此将会感受到比物理电荷略大些的电荷作用.因而在10-11cm附近及更小的线度上,库仑定律不再严格成立,将呈现出微小的修正.一般在细微尺度上,库仑定律的修正不能用简单的解析式表示,只有在如下两个区域内才能有简单表达式:其中,x=r/λe,为精细结构常数,c=0.577……为欧拉常数.可见,由于真空极化效应,点电荷库仑定律在康普顿波长线度附近需要修正;在该区域外,这种修正随r增加按指数规律迅速减小.参考文献:〔1〕关洪.量子力学的基本概念.高等教育出版社,1990.〔2〕倪光炯,李洪芳.近代物理.上海科学技术出版社,1979.〔3〕徐在新.物理学概观.上海科技出版社,2001.〔4〕梁灿彬.电磁学.高等教育出版社,2009.〔5〕赵近芳.大学物理学.北京邮电大学出版社,2008.。
库仑定律的发现和验证

库仑定律的发现和验证库仑定律是电磁学的基本定律之一。
它的建立既是实验经验的总结,也是理论研究的成果。
特别是力学中引力理论的发展,为静电学和静磁学提供了理论武器,使电磁学少走了许多弯路,直接形成了严密的定量规律。
从库仑定律的发现和验证可以获得许多启示,对阐明物理学发展中理论和实验的关系,了解物理学的研究方法均会有所裨益。
一. 库仑定律的发现1.1 从万有引力得到的启示18世纪中叶,牛顿力学已经取得辉煌胜利,人们借助于万有引力的规律,对电力和磁力作了种猜测。
德国柏林科学院院士爱皮努斯(F.U.T. Aepinus, 1724-1802)1759年对电力作了研究。
他在书中假设电荷之间的斥力和吸力随带电物体的距离的减少而增大,于是对静电感应现象作出了更完善的解释。
不过,他并没有实际测量电荷间的作用力,因而只是一种猜测。
1760年,D.伯努利首先猜测电力会不会也跟万有引力一样,服从平方反比定律。
他的想法显然有一定的代表性,因为平方反比定律在牛顿的形而上学自然观中是很自然的观念,如果不是平方反比,牛顿力学的空间概念就要重新修改。
富兰克林的空罐实验(也叫冰桶实验)对电力规律有重要启示。
1755年,他在给兰宁(John Lining)的信中,提到过这样的实验:“我把一只品脱银罐放在电支架(按:即绝缘支架)上,使它带电,用丝线吊着一个直径约为1英寸的木椭球,放进银罐中,直到触及罐的底部,但是,当取出时,却没有发现接触使它带电,象从外部接触的那样。
”富兰克林的这封信不久跟其他有关天电和尖端放电等问题的信件,被人们整理公开发表流传甚广,很多人都知道这个空罐实验,不过也和富兰克林一样,不知如何解释这一实验现象。
图1 富兰克林像图2 普利斯特列像富兰克林有一位英国友人,名叫普利斯特利(Joseph Priestley, 1733—1804),是化学家,对电学也很有研究。
富兰克林写信告诉他这个实验并向他求教。
普利斯特利专门重复了这个实验,在1767年的《电学历史和现状及其原始实验》一书中他写道1:“难道我们就不可以从这个实验得出结论:电的吸引与万有引力服从同一定律,即距离的平方,因为很容易证明,假如地球是一个球壳,在壳内的物体受到一边的吸引作用,决不会大于另一边的吸引。
关于库仑定律精确性的调研

调研题目:假设静电场库伦定律的平方反比关系不严格成立,即δ其中δ。
请推导静电场的各种性质。
例如新条件下高斯定理、环路定理的变化,电势的定义是否受到影响。
调查部分:①库仑定律严格成立的等价命题:光子净质量等于零。
平方反比不严格成立带来的问题:②库伦根据扭秤实验提出静电力平方反比定律的时候,实验精度并不高,指数的偏差δ达到0.04,他多半是受到万有引力的启示而猜测指数是2的。
而库仑定律的精确性问题却是关系物理学基础的根本性问题,假如平方反比律不严格成立,将会有很多不可思议的事情发生:比如光子的静质量不等于零将直接导致电磁场的规范不变性不成立;电荷守恒定律被破坏;电磁波在真空中也发生色散;光速不能保持不变;光子的独立偏振态不再是2而是3;麦克斯韦方程组就必须做重大的修改;真空中不同频率的电磁波, 就应以不同的速度传播;狭义相对论的“光速不变原理”就要被动摇,甚至由其建立起来的物理理论基础也会因此而受到怀疑。
如果真的发现了磁单极,则光子的静质量必为零,库仑定律的平方反比关系也就严格成立了。
③关于库仑定律平方反比律精确度的研究,一直为历代物理学家高度重视,迄今未停止过。
以下是历史上物理学家们所做的关于精确性验证的实验结果,迄今为止,δ的数量级已由减小到。
数量级越小,受实验仪器精度限制,实验条件越困难。
验证平方反比律的实验结果研究部分:一、高斯定理数学上的高斯定理:=dV *其中为一三维向量场。
首先应当说明,*式在数学上是严格成立的,无论的形式如何,只要它是个向量场。
因为我们将*式应用在物理上,才有了静电场高斯定理(其实物理上还有磁场高斯定理,名气略小而已)。
所以,如果库伦定律(即平方反比律)不严格成立,只要还是个场(甚至立方反比律F)就一定会有相对应的高斯定理。
现在,我们暂且承认两个点电荷、相距为r时的静,方向沿两者的连线,那么一个电力大小为δ,其中δ。
点电荷+q在真空激发的场为=δ来计算以点电荷+q为圆心的半径为r的球面的电通量Φ==δ=如果δ>0,那么r越大,Φ越小,意味着电场往无限远传播的过程中Φ不断耗散;如果δ<0,那么r越大,Φ越大,意味着电场往无限远传播的过程中Φ不断累积。
库仑定律发现过程研究论文

库仑定律发现过程研究论文库仑定律发现过程研究论文在物理学的早期,科学家们一直在想方设法研究电学现象,而其中最引人注目且最发明的一个研究是库仑定律的发现。
这个定律是一个基础概念,恰当地描述了电荷之间的相互作用。
这篇论文将简要介绍这个定律背后的历史进程,以及它是如何被发现的。
库仑定律是描述两个电荷之间相互作用的量。
它表明,两个单电荷之间的相互作用力正比于它们之间的距离,反比于它们之间的电荷大小的平方。
它可以用一个等式表示为F=k(q1q2)/r²,其中F是力,k是常数,q1和q2是两个电荷,r是它们之间的距离。
库仑定律最初是由英国科学家查尔斯·卡文迪什斯(Charles Cotesworth Coulomb)在18世纪末和19世纪初发现的。
当时,电荷的概念还未被确定下来。
在18世纪以前,许多人都有电的概念,但是他们无法区分正电和负电,电的数量也没有正确的单位。
当时,为了解释这种电性质,科学家们假设电荷是以太的一种形式。
以太是一种假想的物质,被认为是构成所有宇宙物质的基本组成部分。
人们在市场、实验室、遗骸甚至阴间寻找以太,但一切努力最终无功而返。
卡文迪什斯在努力研究他所谓的“以太”时,对研究电荷之间相互作用的概念产生了浓厚的兴趣。
通过电的实验,卡文迪什斯开始提出一些猜测,例如电荷之间的相互作用可能与力量的大小和距离的平方成正比,并提出了一个数学公式来描述这个过程。
为了验证他的理论,卡文迪什斯设计了一些简单的实验。
他首先选择了质量相近的小金球,将它们放在一起,然后用一根法国香槟酒瓶的串联系统把它们拉开。
当他观察到两个球互相靠近或排斥时,他意识到球上面有电荷,并且电荷直接影响了他的实验。
他惊奇地发现,如果同性球互相靠近,则它们会排斥,而如果异性球接近,则它们会吸引。
卡文迪什斯测量了存在于两个小球之间的电磁力量,并发现两个电荷平方的比值是恒定的,这个比值成为卡文迪什斯恒量。
换句话说,他确定了一个数值k,使上述等式成立,从而发现了库仑定律。
库仑定律的精确度和光子静质量问题

库仑定律的精确度和光子静质量问题
孔令光
【期刊名称】《海南大学学报:自然科学版》
【年(卷),期】1996(014)001
【摘要】引入场强张量和四维势矢量,在洛仑兹变换下,半麦克斯韦方程组的非齐次方程改变成协变形式,假定光子有非零静质量,在非昌次麦克斯韦方程协变形式中增添了一个“质量”项,修正写成普罗卡方程,在此基础上,以普利姆顿实验为例,通过理论推证,在准静态场中,如何从实验可测量算出光子静质量的上限。
【总页数】5页(P86-90)
【作者】孔令光
【作者单位】海南教育学院物理系
【正文语种】中文
【中图分类】O441.1
【相关文献】
1.光子静止质量在库仑定律中的地位 [J], 王芳
2.洛伦兹力可看作静止电荷所受电场力的相对论效应——兼论洛伦兹力公式具有与库仑定律相同的精确度 [J], 张祥雪;程艳霞;范秀华;刘家冈
3.库仑定律在近代物理学中的精确度 [J], 何炜煌;
4.从牛顿引力定律、库仑定律到电子和中微子的静质量及暗物质与暗能量 [J], 易照雄
5.光子静质量与库仑定律关系的再论证 [J], 何池航;李智华
因版权原因,仅展示原文概要,查看原文内容请购买。
对《库仑定律教学的高端备课》的点评.docx

对《库仑定律教学的高端备课》的点评湖北省恩施高中 陈恩谱本文作者对人教版课本存在的问题的确有深刻的见解,尤其是对物理学史的掌握可谓到家,很多中学老师估计都是不知道库伦扭秤实验实际上只探究出了同种电荷之间的作用力的平方反比律,对于异种电荷之间的相互作用规律,正如本文所述,是电引力扭摆实验得到的,至于静电力与两个带电体电荷量乘积成正比,一般物理学史都认为并非库伦实验得出的,而是库伦通过理论分析和猜想出来的。
然而,作者提出的对人教版教材问题的解决思路——类比电子绕原子核做圆周运动,从动力学角度类比万有引力,直接得到221r q q k F =的结论。
这里面存在两个明显的科学性错误: 其一,电子绕原子核做匀速圆周运动,这既不是事实——事实是电子在原子核外的分布要按波函数的模方概率出现的,并非所谓匀速圆周运动,也不是学生的预备知识——化学课本介绍的也是基于量子力学的壳层结构模型,而不是圆周轨道模型。
用一个错误的模型,岂能得到正确的结果?即便是电子绕原子核按经典规律运动,也需要特别说明是单电子原子——氢原子,显然,多电子原子中,核外电子之间的相互作用是会影响其运动轨迹的。
其二,即便是电子绕原子核做匀速圆周运动,也根本就不能得出221r q q k F =。
匀速圆周运动,只需要是由距离决定的中心引力即可,平方反比律的得出,显然需要其他的依据。
牛顿得出平方反比律,是依据开普勒三大定律;那么,本文作者依据什么呢?仅仅是类比!平方反比律的严谨得出,其实也是库伦实验无法担当的,毕竟其实验带电体不是点电荷!库伦实验也只是大致得出平方反比律,更精确的依据是电场的高斯定理,比如均匀带电球壳内部的电场强度处处为零。
显然本文作者指出的人教版教材的问题,实际上是高中阶段无法克服的,课本思路勉强还行,本文作者思路则硬是不行!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
调研题目:假设静电场库伦定律的平方反比关系不严格成立,即F=14πε0q1q2 r2+δ其中δ≪1。
请推导静电场的各种性质。
例如新条件下高斯定理、环路定理的变化,电势的定义是否受到影响。
调查部分:①库仑定律严格成立的等价命题:光子净质量等于零。
平方反比不严格成立带来的问题:②库伦根据扭秤实验提出静电力平方反比定律的时候,实验精度并不高,指数的偏差δ达到0.04,他多半是受到万有引力的启示而猜测指数是2的。
而库仑定律的精确性问题却是关系物理学基础的根本性问题,假如平方反比律不严格成立,将会有很多不可思议的事情发生:比如光子的静质量不等于零将直接导致电磁场的规范不变性不成立;电荷守恒定律被破坏;电磁波在真空中也发生色散;光速不能保持不变;光子的独立偏振态不再是2而是3;麦克斯韦方程组就必须做重大的修改;真空中不同频率的电磁波, 就应以不同的速度传播;狭义相对论的“光速不变原理”就要被动摇,甚至由其建立起来的物理理论基础也会因此而受到怀疑。
如果真的发现了磁单极,则光子的静质量必为零,库仑定律的平方反比关系也就严格成立了。
③关于库仑定律平方反比律精确度的研究,一直为历代物理学家高度重视,迄今未停止过。
以下是历史上物理学家们所做的关于精确性验证的实验结果,迄今为止,δ的数量级已由10−2减小到10−16。
数量级越小,受实验仪器精度限制,实验条件越困难。
验证平方反比律的实验结果研究部分:一、高斯定理数学上的高斯定理:A∙dS S =(∇∙VA)dV *其中A为一三维向量场。
首先应当说明,*式在数学上是严格成立的,无论A的形式如何,只要它是个向量场。
因为我们将*式应用在物理上,才有了静电场高斯定理(其实物理上还有磁场高斯定理,名气略小而已)。
所以,如果库伦定律(即平方反比律)不严格成立,只要还是个场(甚至立方反比律F∝1r)就一定会有相对应的高斯定理。
现在,我们暂且承认两个点电荷q1、q2相距为r时的静电力大小为F=14πε0q1q2r2+δ,方向沿两者的连线,那么一个点电荷+q在真空激发的场为E=14πε0qr3+δr,其中δ≪1。
来计算以点电荷+q为圆心的半径为r的球面的电通量Φ=E∙dSS =14πε0qr3+δr∙(dS∙rrS)=qε0∙1rδ如果δ>0,那么r越大,Φ越小,意味着电场往无限远传播的过程中Φ不断耗散;如果δ<0,那么r越大,Φ越大,意味着电场往无限远传播的过程中Φ不断累积。
这一点也可以通过计算空间任一点散度得出:∇∙E=∇∙(14πε0qr3+δr)=q4πε0∇∙(rr3+δ)=−q4πε0∙δr3+δ如果δ>0,那么∇∙E<0,Φ随r增大而减小,就像是电场线从真空一点突然钻到另外一个世界一样;如果δ<0,那么∇∙E>0,Φ随r变大而增加,仿佛电场线从另外一个世界通过空间上任一点窜出来。
(补充:电通量的大小表示电场线的条数多少。
)除非说在我们的世界之外还有另外一个世界,我们能与之交换电场线,且我们的世界中空间任何一点都是通向那个世界的门,这样的事情才可能发生!如果真是这样,是不是可以这么说:我们的世界并不是3维的,它还隐藏着δ的维度。
可维数不应该是整数吗?我们已经知道δ≪1,那么2<3+δ<4,有n=3,δ=0。
极有可能δ=0,因为非整数的维度不好理解。
平方反比律很可能隐藏着关于空间结构的奥秘,其意义不仅限于物理学,甚至数学的可靠性也与之有关。
二、环路定理环路定理对应数学上的Stokes公式:A∙dl L =(∇×A)∙dS s在静电场中表现为电场的第一类曲线积分与路径无关,即静电场是有势场或无旋场。
也以点电荷+q在真空中激发的电场为例:E=14πε0qr3+δr,则旋度∇×E=i j k∂∂x∂∂y∂∂zq4πε0∙xr3+δq4πε0∙yr3+δq4πε0∙zr3+δ=0。
但是数学上无旋场等价于保守场有个条件,就是必须保证在单连通区域,换句话说不能有奇点。
点电荷激发的场除了在r=0处是奇点外,其他点都可构成单连通区域,那么也就可以定义势函数。
平方反比时,我们知道电势ψ(r )=q 4πε0∙1r;现在我们来求新定律下的势函数Ψ(r ):∇Ψ(r )=-E,写开来就是以下三个式子∂Ψ∂x=−q 4πε0∙x r 3+δ∂Ψ∂y=−q4πε0∙y r 3+δ∂Ψ∂z =−q 4πε∙z r 3+δ解得Ψ(r )=11+δ∙q 4πε0∙1r 1+δ。
总结:新定律下的高斯定理: E ∙dS S = (∇ ∙V E )dV ,不同在于∇ ∙E ≠ρ; 环路定理: E ∙dl L=0; 新电势公式(点电荷):Ψ(r )=11+δ∙q 4πε0∙1r利用上述结果,我们可以看到一些奇怪事情的发生,比如一个均匀带电球壳,电荷面密度为ζ,球半径为r ,平方反比律下可证得球壳内场强处处为零,整个球壳及其内部是一个等势体。
而在新定律下,球壳与内部是有电势差的,我们来计算两个特殊点的电势:①中心点电势Ψ(0)。
由叠加原理, Ψ(0)= 11+δ∙∆q i 4πε0∙1r 1+δi=11+δ∙ζ∙4πr 24πε0∙1r 1+δ=1 1+δ∙ζε0∙r1−δ②球壳上一点P的电势Ψ(P)。
如图所示,对红色圆环电荷对P的电势作积分Ψ(P)=11+δ∙ζ∙(2πrsinθ∙rdθ)4πε0∙1x1+δπ0=11+δ∙ζr22ε0∙sinθdθ(2rsinθ2)1+δπ0=1 1+δ∙ζε0∙r1−δ22+δ2sinθ2cosθ2dθ(sinθ)1+δπ=1 1+δ∙ζε0∙r1−δ2δdttδ1(令sinθ2=t)=1 1+δ∙ζε0∙r1−δ2δ∙11−δ=1 1+δ∙ζε0∙r1−δ∙[12δ∙ 1−δ]=Ψ(0)2δ∙ 1−δ当δ=0时,Ψ(P)=Ψ(0),符合平方反比律的结果;取f(δ)=ln[2δ∙1−δ]= δ∙ln2-ln(1-δ);求导f′(δ)= ln2-11−δ;那么 f′(0)=ln2-1<0;而当f’(δ)=0时,δ=δ0=1-1ln2≈-0.44;又因为f″(δ)=-1(1−δ)2<0,故f(δ)为极大值。
于是可得:如果δ>0,那么f(δ) <f(0), Ψ(P)>Ψ(0),球壳电势高于中心电势;δ<δ<0,f(δ) >f(0), Ψ(P)<Ψ(0),球壳电势低于中心电势。
以上结果表明,如果新定律成立,一个均匀带电球壳内部并不处处等势(非特殊点的积分比较困难,但相信不同的r处电势Ψ(r)是不一样的),因而是有电场的。
这样的话,目前的静电屏蔽理论将失效,而且,假如是个金属导体球,我们往上面充电荷,电荷将在整个球上有一分布ρ(r),而非仅仅分布在球表面!当然以上只是理论推导的结果,事实上,根据目前已确定的δ的大小,设δ~10−16,Ψ(0)~1V,那么ΔΨ~2δ∙1−δ-1~(1+δln2)(1-δ)-1~(1-ln2) δ~10−17V;引起电势如此微小的变化只需一个电子偏移Δr, Δr~4πε0ΔΨr2/e~10−9∙10−17∙1019~10−7≪1(ΔΨ=Δ(e4πε0∙1r)=−e4πε0∙Δrr,另取r~1m)我们会认为电荷分布几乎无任何变化,并且微小差别观测起来亦非常困难。
有人认为,库伦定律之所以为定律,充其量也就是一个经验公式而已,肯定有其适用范围。
就像在-50℃~100℃的范围内我们认为铜丝电阻随温度变化是一个线性关系,事实上任何的曲线,当我们视野仅局限于其上一点附近的领域内,它的线性性是非常好的。
比如当x<10−3时用1+x 近似e x,误差控制在5×10−7内。
那么有没有可能库伦定律也只是我们管中窥豹只见一斑的结果呢?当代物理学研究已经证明库仑定律在10−13米~1026米范围内能非常精确地描述物理现象,但是更微观、更宏观的事情我们就不得而知了。
假如真有一天我们发现库仑定律在尺寸大于比如10100米时有另外一种表达式,并且该表达式在目前所认知的范围内有个很好的近似,就是库仑定律,那么我们就必须对库仑定律进行修正,而且也能给出一个δ的范围了。
最后,我想说,平方反比律是一种理想。
我追求完美,自然希望它能够严格成立,对于它的精确性验证,物理学家们依旧孜孜不倦地进行着。
我相信每个物理学家必是抱>0,使得δ≤着δ=0的信念的。
是不是会有一个阈值δδ时物理学的危机就会解除?或许这是个愚蠢的想法,总0之我总是希望δ越小越好的呀!。
