MATLAB作业3
matlb课程设计作业

matlb课程设计作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及应用方法,培养学生解决实际问题的能力。
具体目标如下:1.知识目标:(1)理解MATLAB的基本概念,如变量、数据类型、运算符等。
(2)掌握MATLAB编程的基本语法,如矩阵操作、函数定义与调用、循环结构、条件语句等。
(3)熟悉MATLAB与其他软件(如Mathematica、Python等)的接口转换。
(4)了解MATLAB在工程领域中的应用,如信号处理、控制系统、图像处理等。
2.技能目标:(1)能够运用MATLAB进行简单的数学计算、数据分析及图形绘制。
(2)具备编写MATLAB脚本文件和函数文件的能力。
(3)学会使用MATLAB解决实际问题,如编写程序实现线性方程组求解、最优化问题求解等。
(4)掌握MATLAB在实验数据处理、仿真实验等方面的应用。
3.情感态度价值观目标:(1)培养学生对科学探究的兴趣,提高其创新意识。
(2)培养学生团队协作、沟通交流的能力。
(3)培养学生具备良好的编程习惯和职业道德。
二、教学内容本课程的教学内容主要包括以下几个部分:1.MATLAB基本概念:变量、数据类型、运算符等。
2.MATLAB编程语法:矩阵操作、函数定义与调用、循环结构、条件语句等。
3.MATLAB高级应用:数组运算、图像处理、控制系统、信号处理等。
4.MATLAB与其他软件的接口转换。
5.实践项目:利用MATLAB解决实际问题,如线性方程组求解、最优化问题求解等。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合,以提高学生的学习兴趣和主动性。
1.讲授法:用于讲解MATLAB基本概念、语法和应用。
2.案例分析法:通过分析实际案例,使学生掌握MATLAB在各个领域的应用。
3.实验法:让学生亲自动手实践,培养其运用MATLAB解决实际问题的能力。
四、教学资源1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
电气工程软件训练(三)——Matlab 作业

D1(江苏大学《电气工程软件训练三》课程设计报告设计题目:MATLAB专业班级:J电气1401学生姓名:唐鹏学生学号:4141127007指导老师:完成日期:江苏大学京江学院一MATLAB课程设计的目的和要求1.MATLAB软件功能简介MATLAB的名称源自Matrix Laboratory,1984年由美国Mathworks公司推向市场。
它是一种科学计算软件,专门以矩阵的形式处理数据。
MATLAB将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制系统和信息处理等领域的分析、仿真和设计工作。
MATLAB 软件包括五大通用功能,数值计算功能(Nemeric)、符号运算功能(Symbolic)、数据可视化功能(Graphic)、数字图形文字统一处理功能(Notebook)和建模仿真可视化功能(Simulink)。
其中,符号运算功能的实现是通过请求MAPLE内核计算并将结果返回到MATLAB命令窗口。
该软件有三大特点,一是功能强大;二是界面友善、语言自然;三是开放性强。
目前,Mathworks公司已推出30多个应用工具箱。
MATLAB在线性代数、矩阵分析、数值及优化、数值统计和随机信号分析、电路与系统、系统动力学、次那好和图像处理、控制理论分析和系统设计、过程控制、建模和仿真、通信系统以及财政金融等众多领域的理论研究和工程设计中得到了广泛应用。
2.MATLAB课程设计的目的本次课程设计主要是为了使学生了解MATLAB软件的基本知识,熟悉MATLAB的上机环境,掌握MATLAB数值运算、程序设计、二维/三维绘图、符号运算、Simulink仿真等相关知识,并初步具备将一般数学问题转化为对应的计算机进行处理的能力,以便为今后进一步的学习打下坚定基础。
二MATLAB课程内容1 MATLAB语言基础实验目的:基本掌握MATLAB 向量、矩阵、数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
数学建模作业题+答案

数学建模MATLAB 语言及应用上机作业11. 在matlab 中建立一个矩阵135792468101234501234A ⎡⎤⎢⎥⎢⎥=⎢⎥-----⎢⎥⎣⎦答案:A = [1,3,5,7,9;2,4,6,8,10;-1,-2,-3,-4,-5;0,1,2,3,4]2. 试着利用matlab 求解出下列方程的解(线性代数22页例14)123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩ 答案:A=[2 ,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6]; B=[8;9;-5;0]; X=A\B 或A=[2,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6] b=[8,9,-5,0]' X=inv(A)*b3. 生成一个5阶服从标准正态分布的随机方阵,并计算出其行列式的值,逆矩阵以及转置矩阵。
答案:A=randn(5) det(A) inv(A) A'4. 利用matlab 求解出110430002A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的特征值和特征向量。
答案:A=[-1,1,0;-4,3,0;0,0,2] [V,D]=eig(A)5.画出衰减振荡曲线3sin3t y et -=在[0,4]π上的图像。
要求,画线颜色调整为黑色,画布底面为白色。
(在实际中,很多打印机时黑白的,因此大多数作图要考虑黑白打印机的效果。
) 给出恰当的x ,y 坐标轴标题,图像x 轴的最大值为4π。
6. 生成一个0-1分布的具有10个元素的随机向量,试着编写程序挑选出向量中大于0.5的元素。
数学建模和Matlab 上机作业2(2016-9-20)跟老师做(不用整合进作业中):上机演示讲解:函数,递归的两个例子的写法。
附:1. Fibonacci Sequence (斐波那契数列)在数学上,费波那西数列是以递归的方法来定义: F1= 1;F2= 1;F (n )=F (n-1)+F (n-2) 2. 阶乘举例:数学描述:n!=1×2×……×n ;计算机描述:n!=n*(n-1)!自己做(需要整合进作业中,提交到系统中):1. 写一个m 文件完成分值百分制到5分制的转换(即输入一个百分制,转换后输出一个5级对应的得分,联系条件控制语句)。
matlab课程设计大作业

matlab课程设计大作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及MATLAB 在工程计算和数据分析中的应用。
通过本课程的学习,学生将能够熟练使用MATLAB进行简单数学计算、线性方程组求解、函数图像绘制等。
1.掌握MATLAB基本语法和编程结构。
2.了解MATLAB在工程计算和数据分析中的应用。
3.熟悉MATLAB的函数库和工具箱。
4.能够使用MATLAB进行简单数学计算。
5.能够使用MATLAB求解线性方程组。
6.能够使用MATLAB绘制函数图像。
7.能够利用MATLAB进行数据分析和处理。
情感态度价值观目标:1.培养学生对计算机辅助设计的兴趣和认识。
2.培养学生团队合作和自主学习的能力。
二、教学内容本课程的教学内容主要包括MATLAB基本语法、编程技巧以及MATLAB在工程计算和数据分析中的应用。
1.MATLAB基本语法:介绍MATLAB的工作环境、基本数据类型、运算符、编程结构等。
2.MATLAB编程技巧:讲解MATLAB的函数调用、脚本编写、函数文件编写等编程技巧。
3.MATLAB在工程计算中的应用:介绍MATLAB在数值计算、线性方程组求解、图像处理等方面的应用。
4.MATLAB在数据分析中的应用:讲解MATLAB在数据采集、数据分析、数据可视化等方面的应用。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合的方式进行教学。
1.讲授法:通过讲解MATLAB的基本语法、编程技巧以及应用案例,使学生掌握MATLAB的基本知识和技能。
2.案例分析法:通过分析实际工程案例,使学生了解MATLAB在工程计算和数据分析中的应用。
3.实验法:安排上机实验,使学生在实际操作中巩固所学知识,提高实际编程能力。
四、教学资源本课程的教学资源包括教材、实验设备、多媒体资料等。
1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
2.实验设备:为学生提供计算机实验室,配备有MATLAB软件的计算机。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =ans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans =15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
MATLAB Char03-数据可视化与绘图作业20120412

【作业1】绘制函数 y xe 和 y2=exsin(x) 在0 x 1 时的曲线。两条曲线分别用红色实 线和绿色虚线表示,并用legend函数进行标识。
x
【作业2】使用axis equal语句画出球面正弦波:
a 10.0, b 1.0, c 0.3, 0 t 2
绘出下述级数的图形。除非特别指明,所有级数仅求 2n n 1,3,5,...
1 1 2 2
4
【作业6】请绘制如下分段函数的图形,其中x的取值范围为 [-10,10],并为图形的横坐标加上标签“x”,为图形的纵坐 标加上标签“f(x)”。
x 1 3 x 2, f x x, 1 x 1 2 x 3, x 1
【作业7】标准条件下钢管中流动的空气压降可由下式给出:
x cos(t ) b2 c 2 cos 2 (at ) y sin(t ) b2 c 2 cos 2 (at ) z c cos(at )
【作业3】用surf函数画出正螺旋面:
(c 1/ 2 , 0.5 u 0.5, 2 v 2 )
x u cos(v ) y u sin(v) z cv
【作业4】给定如下8点的x和y坐标向量,请由此7 点拟合成一条4次曲线方程,并在一图形窗口绘出 点和拟合曲线的图形。 x=[2 2.5 3 4 5 6 7 10] y=[4 3 5 6 8 5.6 9.8 12]
【作业5】从球面坐标到迪卡尔坐标的转换公式为: x=b sin a cos c y=b sin a sin c z=b cos a a 在[0 90]之间的范围内分10等份,c在[0 360]的范围内分24等 份。令b=2 ,计算x,y,z,并利用mesh(x,y,z)绘出这个半球形。
基于simulink的Matlab仿真作业(电气工程专业)3

基于MATLAB/SIMULINK 单相桥式半控整流电路带电阻负载建模与仿真张三(陕西西安西安科技大学710054)摘要:电力电子技术课程设计是在教学及实验基础上,对课程所学理论知识的深化和提高。
本次课程设计要完成单相桥式半控整流电路的设计,对电阻负载供电,并使输出电压在0到180伏之间连续可调,由于是半控电路,因此会用到晶闸管与电力二极管。
此外,还要用MATLAB对设计的电路进行建模并仿真,得到电压与电流波形,对结果进行分析。
关键词:整流器电压波形电流波形0 引言单相相控整流电路可分为单相半波、单相全波和单相桥式相控流电路,它们所连接的负载性质不同就会有不同的特点。
1电路的设计与工作原理单相相控整流电路可分为单相半波、单相全波和单相桥式相控流电路,它们所连接的负载性质不同就会有不同的特点。
而负载性质又分为带电阻性负载、电阻-电感性负载和反电动势负载时的工作情况。
单相桥式半控整流电路带电阻负载的电路图如图2-1所示。
图单相桥式半控整流电路带电阻负载在单向桥式半控整流电路中,VT1和VD4组成一对桥臂,VD2和VT3组成另一对桥臂。
在u正半周(即a点电位高于b点电位),若4个管子均不导通,负载电流id 为零,ud也为零,VT1、VD4串联承受电压u,设VT1和VD4的漏电阻相等,则各承受u的一半。
若在触发角α处给VT1加触发脉冲,VT1和VD4即导通,电流从电源a端经VT1、R、VD4流回电源b端。
当u过零时,流经晶闸管的电流也降到零,VT1和VD4关断。
在u负半周,仍在触发延迟角α处触发VD2和VT3,VD2和VT3导通,电流从电源b端流出,经VT3、R、VD2流回电源a端。
到u过零时,电流又降为零,VD2和VT3关断。
此后又是VT1和VD4导通,如此循环地工作下去。
晶闸管承受的最大正向电压和反向电压分别为22U和2U。
由于在交流电源的正负半周都有整流输出电流流过负载,故该电路为全波整流。
在u一个周期内,整流电压波形脉动2次,脉动次数多于半波整流电路,该电路属于双脉波整流电路。
Matlab上机作业部分参考答案

3. 设A为 数组,B为一个行数大于3的数组,请给出 (1)删除A的第4、8、12三列的命令; (2)删除B的倒数第3行的命令; (3)求符号极限 (4)求 的3阶导数
lim tan( mx ) 的命令集; x 0 nx x3 y arctan ln(1 e 2 x ) 的命令集; x2
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8
0
2
4
6
8
10
12
14
某校60名学生的一次考试成绩如下: 93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55 1)计算均值、标准差、极差、偏度、峰度,画出直方图; 2)检验分布的正态性; 3)若检验符合正态分布,估计正态分布的参数并检验参数。 解答: x=[93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55]; mean(x) std(x) range(x) skewness(x) kurtosis(x) hist(x) h=normplot(x) [muhat,sigmahat,muci,sigmaci]=normfit(x) [H,sig,ci]=ttest(x,80.1)
Matlab作业3(数值分析)答案

Matlab作业3(数值分析)机电工程学院(院、系)专业班组学号姓名实验日期教师评定1.计算多项式乘法(x2+2x+2)(x2+5x+4)。
答:2. (1)将(x-6)(x-3)(x-8)展开为系数多项式的形式。
(2)求解在x=8时多项式(x-1)(x-2) (x-3)(x-4)的值。
答:(1)(2)3. y=sin(x),x从0到2π,∆x=0.02π,求y的最大值、最小值、均值和标准差。
4.设x=[0.00.30.8 1.1 1.6 2.3]',y=[0.500.82 1.14 1.25 1.351.40]',试求二次多项式拟合系数,并据此计算x1=[0.9 1.2]时对应的y1。
解:x=[0.0 0.3 0.8 1.1 1.62.3]'; %输入变量数据xy=[0.50 0.82 1.14 1.25 1.35 1.40]'; %输入变量数据yp=polyfit(x,y,2) %对x,y用二次多项式拟合,得到系数px1=[0.9 1.2]; %输入点x1y1=polyval(p,x1) %估计x1处对应的y1p =-0.2387 0.9191 0.5318y1 =a) 1.29095.实验数据处理:已知某压力传感器的测试数据如下表p为压力值,u为电压值,试用多项式dcpbpappu+++=23)(来拟合其特性函数,求出a,b,c,d,并把拟合曲线和各个测试数据点画在同一幅图上。
解:>> p=[0.0,1.1,2.1,2.8,4.2,5.0,6.1,6.9,8.1,9.0,9.9];u=[10,11,13,14,17,18,22,24,29,34,39];x=polyfit(p,u,3) %得多项式系数t=linspace(0,10,100);y=polyval(x,t); %求多项式得值plot(p,u,'*',t,y,'r') %画拟和曲线x =0.0195 -0.0412 1.4469 9.8267。
MATELAB与数学实验第三次作业

《数学实验》报告实验名称 matlab作业 3 学院专业班级姓名学号2011年 10月一、【实验目的】学习编辑程序来绘制几何立体图等.二、【实验任务】(一)P79 习题5绘制圆锥螺线的图像并加各种标注,圆锥螺线的参数方程为x=tcos(π/6)ty=tsin(π/6)t, (0<=t<=20π)z=2t绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图,并通过改变观测点获得该图形在各个坐标平面上的投影。
画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.(二)P79 习题7用mesh与surf命令绘制三维曲面z=x^2+3y^2的图像,并使用不同的着色效果及光照效果。
(三)P79习题8绘制由函数x^2/9+y^2/16+z^2/4=1形成的立体图,并通过改变观测点获得该图形在各个坐标平面上的投影。
(四)P79习题9画三维曲面z=5-x^2-y^2(-2<=x,y<=2)与平面z=3的交线.【实验程序】(一)t=0:pi/50:20*pi;x=t.*cos((pi/6)*t);y=t.*sin((pi/6)*t);z=2*t;plot3(x,y,z)title('ÇúÏß4x^2+4y^2=z^2')xlabel('txÖá'),ylabel('tyÖá'),zlabel('tzÖá')(二)t=-5:0.1:5;[x,y]=meshgrid(t);z=x.^2+3*y^2;%meshÃüÁîsubplot(121);mesh(x,y,z);title('meshÃüÁî');shading flat;light('position',[0,0,10])%surfÃüÁîsubplot(1,2,2);surf(x,y,z);title('surfÃüÁî');shading faceted;light('position',[0,2,10])(三)a=3;b=4;c=2;[X,Y,Z]=ellipsoid(0,0,0,a,b,c,400);subplot(221),mesh(X,Y,Z)view(3)subplot(222),mesh(X,Y,Z)view(30,30)subplot(223),mesh(X,Y,Z)view(30,0)subplot(224),mesh(X,Y,Z)view(-120,30)axis equalaxis image(四)t=-2:0.1:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2;subplot(131)mesh(x,y,z1),title('z=5-x^2-y^2')z2=3*ones(size(x));subplot(132)mesh(x,y,z2),title('z=3')r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(133),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'x')三、【实验结果】(一)(二)(三)(四)【实验总结】学会使用关键字来绘制函数图象,包括加各种标注,画圆锥螺线,使用着色效果、光照效果,画椭球,并改变观测点获得不同坐标平面的投影,画曲面与平面的交线等。
内蒙古国开电大一网一《Matlab语言及其应用》形考作业三

试卷总分:100 得分:100
判断题(共17小题,1至15小题每小题6分,16至17小题每小题5分,共100分)1.matlab中有两种描述系统的方法:传递函数模型和零极点增益模型。
答案:正确
2.matlab中两种表示模型的方法之间可以相互转换。
答案:正确
3.matlab中支持的系统互联方式有三种:串联、并联和反馈。
答案:正确
4.方波信号的产生函数是square()。
答案:正确
5.冲激信号是特异信号。
答案:正确
6.系统反馈的函数为feedback。
答案:正确
7.step函数用于计算系统的冲激响应。
答案:错误
8.impulse函数用于计算系统的阶跃响应。
答案:错误
9.lism函数可用于求解系统对任意输入的响应。
答案:正确
10.一个线性系统对正弦信号的响应中,其频率、幅值和相角均有可能发生改变。
答案:错误
11.Matlab 中freqs函数用于绘制系统的幅频特性。
答案:正确
12.bode图可用于判断系统是否稳定。
答案:正确
13.M-函数是利用Matlab语言编写的特定功能函数。
答案:正确
14.simulink的S函数,可以是用C语言编写的。
答案:正确。
信号与系统Matlab实验作业

实验一典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号)1)画出教材P28习题1-1(3) ()[(63)(63)]t=----的波形图。
f t e u t u t2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)';f2='exp(0.4*t)*sin(8*t)';figure(1)ezplot(f1,t);grid on;figure(2)ezplot(f2,t);grid on;3)画出教材P16图1-18,即抽样信号Sa(t)的波形(-20<t<20)。
t=-10:0.01:10;f='sin(t)/t';ezplot(f,t);grid on;4)用符号函数sign画出单位阶跃信号u(t-3)的波形(0<t<10)。
t=0:0.01:10;f='(sign(t-3)+1)/2';ezplot(f,t);grid on;5)单位冲击信号可看作是宽度为∆,幅度为1/∆的矩形脉冲,即t=t 1处的冲击信号为11111 ()()0 t t t x t t t otherδ∆⎧<<+∆⎪=-=∆⎨⎪⎩画出0.2∆=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))';ezplot(f,t);grid on;axis([0 2 -1 6]);2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列)编写函数产生下列序列:1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。
4.建模作业_MATLAB(3)

《数学建模》课程作业题第七章MATLAB(3)1.MATLAB图形处理的高级技术都有哪些?颜色映像。
1)colormap函数进行调用颜色映像;2)Pcolor、rgbplot、colorbar等函数用户可以条用所定义的颜色映像为图形服务;3)pcolor一般与函数shading相结合,用于以不同方式为图形着色;4)Rgbplot是一种直接显示颜色的函数;5)第三个用来显示颜色映像最常用的函数是colorbar。
视角与光照。
1)视角控制函数view,viewmtx及rotate3D;2)光照控制函数lighting‘光源模式’;3)图像处理。
2.MATLAB图形处理的基本技术都有哪些?1)图像控制坐标控制:axis([xmin,xmax,ymin,ymax])平面坐标网格函数:grid on/grid off2)图形的标注①.坐标轴标注:xlabel(‘标注’,’属性’),ylabel,zlabel②.文本标注:text(x,y,’标注文本及控制字符串’)③.交互式文本标注:gtext④.图例标注:legend (‘标注1’,‘标注2’) 3)图形的保持与子图:hold on,hold off,subplot(m,n,p) 3.3. 编写如下问题的M 文件7.4.1绘制下列曲线.(1) 21100x y +=, 运行程序:clear; clc; x=0:0.1:1; y=100./(1+x.^2); plot(x,y);(2) 2221xe y -=π, 运行程序 clear;clc; x=0:0.01:1;y=(1/(2*pi))*exp(((-x.^2)/2)); plot(x,y);(3) 122=+y x ,ezplot('x^2+y^2=1')(4) ⎩⎨⎧==325ty t x . t=0:1:50; x=t.^2; y=t.^3; plot(x,y)title('参数方程 ');7.4.2绘制下列极坐标图.(1) 4cos 5+=θρ,clear; clc;x=0:0.01*pi:2*pi; y=5*cos(x)+4; polar(x,y)(2) θρ12=,clear; clc;x=0:0.01*pi:2*pi; y=12./sqrt(x); polar(x,y);(3) 7cos 5-=θρ, clear; clc;x=0:0.01*pi:2*pi; y=5./cos(x)-7; polar(x,y)(4) 23θπρ=.clear;clc;x=0:0.01*pi:2*pi; y=pi/3*x.^2; polar(x,y)7.4.3绘制下列三维图形.(1) ⎪⎩⎪⎨⎧===t z t y t x sin cos ,clear; clc;t=0:0.01*pi:2*pi; x=cos(t); y=sin(t); z=t;plot3(x,y,z)(2) ⎪⎩⎪⎨⎧=+=+=u z v u y v u x sin sin )cos 1(cos )cos 1(,u=0:pi/20:10*pi; v=0:pi/20:10*pi; x2=(1+cos(u)).*cos(v); y2=(1+cos(u)).*sin(v); z2=sin(u); plot3(x,y,z)(3) 5=z ,[x3,y3]=meshgrid(-100:100);%形成一个100×100的网格z3=5*ones(size(x3));%将Z与上面网格对应起来mesh(x3,y3,z3)(4) 半径为10的球面.x0=2;y0=3;z0=0;%球心r=10;%半径[x,y,z]=sphere;mesh(r*x+x0,r*y+y0,r*z+z0);axis equal7.4.4在同一图形窗口采用子图形式分别绘制正方形、圆、三角形和六边形.ord=[3 4 6 2^20] for i=1:4 subplot(2,2,i)theta=linspace(pi/ord(i),2*pi+pi/ord(i),ord(i)+1);%%圆等分点 plot(cos(theta),sin(theta));xlim(1.5*[-1,1]);ylim(1.5*[-1,1]);axis equal ; end7.4.5分别用plot 和fplot 函数绘制下列分段函数的曲线:⎪⎩⎪⎨⎧<--+=>+++=0 ,510 ,00 ,51)(342x x x x x x x x ffunction y=work414(x) y=[];%定义空矩阵 for i = x if i > 0y = [y, i^2+(1+i)^0.25+5]; %将算出值与矩阵y 结合形成新矩阵y elseif i == 0 y = [y, 0]; elsey = [y, i^3+sqrt(1-i)-5]; end end endclearclcx=-10:0.5:10;y=work414(x);subplot(2, 1, 1);plot(x,y)grid on; title('plot');subplot(2, 1, 2);fplot(@(x)work414(x),[-5,5])grid on; title('fplot');7.4.6某工厂2005年度各季度产值(单位:万元)分别为:450.6、395.9、410.2、450.9,试绘制折线图和柄状图,并说明图形的实际意义.subplot(1, 1, 1); clear; clc;x = 1 : 4;y = [450.6, 395.9, 410.2, 450.9];subplot(1, 2, 1);plot(x, y);title('折线图-四个季度产值变化'); xlabel('第i个季度'); ylabel('产值/万元'); grid on; axis([0, 5, 360, 480]);subplot(1, 2, 2);pie(y);title('饼图-每个季度占总产值的百分比');意义:第一季度与第四季度产值高,二三季度产值偏低7.4.7绘制一个长方形,将长方形3等份,每等份分别着不同的颜色.vert = [0, 0; 1, 0; 2, 0; 3, 0; 3, 1; 2, 1; 1, 1; 0, 1]; %画最大长方形fac = [1, 8, 7, 2; 2, 7, 6, 3; 3, 6, 5, 4];%区域涂色分割mc = jet(3);patch('Vertices', vert, 'Faces', fac, 'FaceVertexCData', mc, 'FaceColor', 'flat'); %着色函数7.4.8生成一个长方体,每小面着不同颜色,并进行光照和材质处理.clear;clc;vert = [0, 0, 0; 1, 0, 0; 1, 1, 0; 0, 1, 0; 0, 0, 1; 1, 0, 1; 1, 1, 1; 0, 1, 1];fac = [1, 5, 6, 2; 2, 6, 7, 3; 3, 7, 8, 4; 4, 8, 5, 1; 1, 4, 3, 2;5, 8, 7, 6];mc = jet(6);patch('Vertices', vert, 'Faces', fac, 'FaceVertexCData', mc,'FaceColor', 'Flat'); % 顶点集,小面上定点axis([-0.5, 2.5, -0.5, 2.5, -0.5, 2.5]); grid on; axis square;xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');title('方块');light('Color', 'b', 'Style', 'local', 'Position', [1, 1, 1]);lighting flat; % 均匀入射光material shiny; % 镜面反射光hold on;plot3(2, 2, 2, 'p'); text(2, 2, 2, 'light');hold off7.4.9气象变换情况的可视化:下表是气象学家测量得到的气象数据,它们分别表示在南半球地区按不同纬度、不同月份的平均气旋数字,根据这些数据,绘制出气旋分布曲面图,并计算2月份在纬度11度处的气旋值.南半球气旋数据表clear;clc;x=1:12;y=5:10:85;z=[2.4 1.6 2.4 3.2 1.0 0.5 0.4 0.2 0.5 0.8 2.4 3.6 ;18.7 21.4 16.2 9.2 2.8 1.7 1.4 2.4 5.8 9.2 10.3 16;20.8 18.5 18.2 16.6 12.9 10.1 8.3 11.2 12.5 21.1 23.9 25.5;22.1 20.1 20.5 25.1 29.2 32.6 33.0 31.0 28.6 32.0 28.1 25.6;37.3 28.8 27.8 37.2 40.3 41.7 46.2 39.9 35.9 40.3 38.2 43.4;48.2 36.6 35.5 40 37.6 35.4 35 34.7 35.7 39.5 40 41.9;25.6 24.2 25.5 24.6 21.1 22.2 20.2 21.2 22.6 28.5 25.3 24.3;5.3 5.3 5.4 4.9 4.9 7.1 5.3 7.3 7 8.66.3 6.6;0.3 0 0 0.3 0 0 0.1 0.2 0.3 0 0.1 0.3];[xi,yi]=meshgrid(1:12,5:1:85);zi=interp2(x,y,z,xi,yi,'cubic');z=interp2(x,y,z,2,11,'cubic')mesh(xi,yi,zi)hold on;plot3(2,11,z,'*r')xlabel('月份'),ylabel('纬度'),zlabel('气旋'),axis([0 12 0 90 0 50])title('南半球气旋可视化图形')红点表示2月份在纬度11度处的气旋值z =16.2040。
MATLAB第三章和第四章作业

习题三1.选择题(1)已知a=4,b='4',下面说法错误的为C 。
A. 变量a比b占用的存储空间大B. 变量a和b可以进行加、减、乘、除运算C. 变量a和b的数据类型相同D. 变量b可以用eval命令执行(2)已知s='显示"hello"',则s的元素个数是B 。
A. 12B. 9C. 7D. 18(3)运行命令>>a=sym('pi','d')则对于变量a的描述D是正确的。
A. a是符号变量B. a显示为10位的数值C. a显示为32位的数值D. a不存在(4)对于符号表达式g=sym('sin(a*z)+cos(w*v)'),如果运行命令diff(g),则求导自变量是D。
A. aB. zC. wD. v(5)运行命令>>a=double(sym('sin(pi/2)')),则变量a是 C。
A. 符号变量B. 字符串'1'C. double型的数值1D. 出错(6)运行命令>>y=dsolve('x*D2y-3*Dy=x^2','t')求解微分方程,则D。
A. Dy是指dy/dxB. 得出的y是通解有一个常数符C1C. D2y是指d2y/dxD. 得出的y是通解有两个常数符C1和C2(7)有一个2行2列的元胞数组c,则c(2)是指C 。
A. 第1行第2列的元素内容B. 第2行第1列的元素内容C. 第1行第2列的元素D. 第2行第1列的元素(8)对于一个2行2列的元胞数组c,如果要删除第二列的元素,应该使用的命令是B 。
A.c{:,2}=[]B.c(:,2)=[]C.A、B两种方式均可D.A、B两种方式均不可(9)有一个3行10列的构架数组student,每个构架有name(姓名)、scores两个字段,其中scores是以1×5数组表示的五门课的成绩,那么要查看第4个学生的第2门课成绩,采用的命令中达不到要求的是。
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
matlab作业

1、猜数游戏。
首先由计算机产生[1,100]之间的随机整数,然后由用户猜测所产生的随机数。
根据用户猜测的情况给出不同提示,如猜测的数大于产生的数,则显示“High”,小于则显示“Low”,等于则显示“You won”,同时退出游戏。
用户最多可以猜7次。
程序文件:nu m=fix(rand(1)*100);n=1;while n<=7a=input('请输入一个1到100的随机整数');n=n+1;if a>nu mdisp('High');elseif a<nu mdisp('low');elsedisp('won');break;endend2、从键盘输入5个数,求其中最大数和最小数。
并在屏幕上提示输入“请输入您要显示数字的序号”,输入后,回显“您要显示数字为……(此处为实际需要显示序号对应的数字)”。
程序文件:disp('请输入5个数字')for n=1:5;x=input('');A(1,n)=x;endAB=sort(A);Bdisp('最大值是');B(1,5)disp('最小值是');B(1,1)disp('请输入您要显示数字的序号');nu m=input('');disp('您要显示数字为');A(1,nu m)3、求Fibonacci数列(1)大于4000的最小项。
(2)5000之内的项数。
程序文件:(1)大于4000的最小项f=[1,1];j=1;while f(1,j+1)<4000f(1,j+2)=f(1,j)+f(1,j+1);j=j+1;endfdisp('大于4000的最小项是');f(1,j+1)运行结果f =Colu m ns 1 through 101 123 5 8 13 21 34 55Colu m ns 11 through 1989 144 233 377 610 987 1597 2584 4181大于4000的最小项是ans =4181(2)5000之内的项数f=[1,1];j=1;while f(1,j+1)<5000f(1,j+2)=f(1,j)+f(1,j+1);j=j+1;endfdisp('5000之内的项数');j运行结果f =Colu m ns 1 through 101 123 5 8 13 21 34 55Colu m ns 11 through 2089 144 233 377 610 987 1597 2584 4181 67655000之内的项数j =19。
机械原理matlab分析大作业3-28
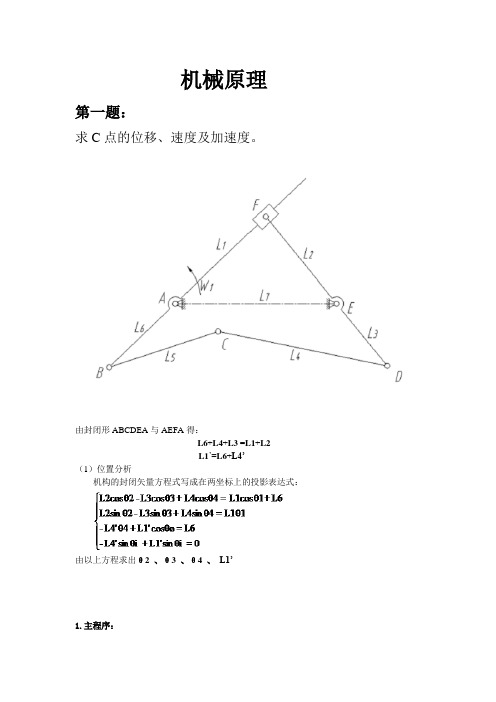
机械原理第一题:求C点的位移、速度及加速度。
由封闭形ABCDEA与AEFA得:L6+L4+L3 =L1+L2L1’=L6+L4’(1)位置分析机构的封闭矢量方程式写成在两坐标上的投影表达式:由以上方程求出θ2 、θ3 、θ4 、L1’1.主程序:%输入已知数据l2=60;l3=35;l4=75;l5=50;l6=40;l7=70;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%调用子函数计算角位移,角速度及角加速度for n1=1:66 %曲柄转角范围theta1(n1)=(n1-1)*hd;ll=[l2,l3,l4,l5,l6,l7];[theta,omega,alpha]=six_bar(theta1(n1),omega1,ll);l1(n1)=theta(1);theta2(n1)=theta(2);theta4(n1)=theta(3);theta3(n1)=theta(4);v1(n1)=omega(1);omega2(n1)=omega(2);omega3(n1)=omega(3);omega4(n1)=omega(4);a1(n1)=alpha(1);alpha2(n1)=alpha(2);alpha3(n1)=alpha(3);alpha4(n1)=alpha(4);e nd%图像输出figure(1);n1=1:66;t=(n1-1)*2*pi/360;subplot(2,2,1);%滑块F线位移L1图像输出plot(theta1*du,l1,'k');title('L1线位移图');xlabel('角位移\theta_1/\circ')ylabel('线位移/mm')grid on;hold on;gtext('L1')pause(1);subplot(2,2,2);%theta2、theta3、theta4角位移图像输出plot(theta1*du,theta2*du,'g',theta1*du,theta3*du,'r',theta1*du,th eta4*du);title('\theta_2、\theta_3、\theta_4角位移图');xlabel('角位移\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;legend('\theta_2','\theta_3','\theta_4');pause(1);subplot(2,2,3);%滑块F的速度图像输出plot(theta1*du,v1,'k');title('滑块F的速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;gtext('v1')pause(1);subplot(2,2,4);%滑块F的加速度图像输出plot(theta1*du,a1,'k');title('滑块F的加速度图');axis auto;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;gtext('a1');pause(5);figure(2);subplot(1,2,1);%omega2、omega3和omega4角位移图像输出plot(theta1*du,omega2,'g',theta1*du,omega3,'r',theta1*du,omega4,' b');title('\omega_2、\omega_3、\omega_4角速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')box on;legend('\omega_2','\omega_3','\omega_4');pause(1);subplot(1,2,2);%alpha2、alpha3和alpha4角加速度图像输出plot(theta1*du,alpha2,'g',theta1*du,alpha3,'r',theta1*du,alpha4,' b');title('\alpha_2、\alpha_3、\alpha_4角加速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')box on;legend('\alpha_2','\alpha_3','\alpha_4');pause(5);figure(3);xC=-l6*cos(theta1+pi)+l5*cos(theta3);yC=l6*sin(theta1+pi)+l5*sin(theta3);% rC=sqrt(xC.*xC+yC.yC)vCX=-omega1*l6*sin(theta1+pi)-omega3*l5.*sin(theta3);vCY=omega1*l6*cos(theta1+pi)+omega3*l5.*cos(theta3);% v3=sqrt(vCX.*vCX+vCY.*vCY);subplot(2,2,1);hold on;grid on;%C点x、y方向位移图像输出plot(theta1*du,xC,'r',theta1*du,yC);axis auto;hold on;grid on;title('C点位移图');xlabel('角位移\theta_1/\circ')ylabel('位移/mm')grid on;hold on;legend('xC','yC');pause(1);subplot(2,2,2);grid on;hold on;%C点x、y方向速度图像输出plot(theta1*du,vCX,'k',theta1*du,vCY);title('C点速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')legend('vCX','vCY');pause(1);aCX=omega1*omega1*l6*cos(theta1)-omega3.*omega3.*l5.*cos(theta3)-alpha3.*l5.*sin(theta3);aCY=omega1*omega1*l6*sin(theta1)-omega3.*omega3.*l5.*sin(theta3)+ alpha3.*l5.*cos(theta3);%a3=sqrt(aCX.*aCX+aCY.*aCY);subplot(2,2,3);%C点x、y方向加速度图像输出plot(theta1*du,aCX,'r',theta1*du,aCY,'b');title('C点加速度图');grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')box on;legend('aCX','aCY');%主程序结束2.子程序:%子函数function[theta,omega,alpha]=six_bar(theta1,omega1,ll)l2=ll(1);l3=ll(2);l4=ll(3);l5=ll(4);l6=ll(5);l7=ll(6);%1.计算角位移和线位移l1=l7*cos(theta1)+sqrt((l7*cos(theta1))*(l7*cos(theta1))-l7*l7+l2 *l2);theta2=asin((l1*sin(theta1))/l2);A=2*l4*(l6*sin(theta1)-l3*sin(theta2).*sin(theta2));B=2*l4*(l6*cos(theta1)+l7-l3*cos(theta2));C=l4*l4-l5*l5+l6*l6+l7*l7+l3*l3-2*l3*l6*(cos(theta1)*cos(theta2)+ sin(theta1)*sin(theta1))-2*l7*l3*cos(theta2)+2*l6*l7*cos(theta1); theta4=2*atan((A+sqrt(A.*A+B.*B-C.*C))/(B-C));theta3=asin((l6*sin(theta1)+l4*sin(theta4)-l3*sin(theta2))/l5); theta(1)=l1;theta(2)=theta2;theta(3)=theta4;theta(4)=theta3;%2利用矩阵计算角速度和线速度D=[-l5*sin(theta3),l4*sin(theta4),-l3*sin(theta2+pi),0l5*cos(theta3),-l4*cos(theta4),-l3*cos(theta2+pi),00,0,l2*sin(theta2),cos(theta1)0,0,-l2*cos(theta2),sin(theta1)];E=[l6*sin(theta1+pi);-l6*cos(theta1+pi);l1*sin(theta1);-l1*cos(theta1)];omega=D\(omega1*E);v1=omega(4);omega2=omega(3);omega3=omega(1);omega4=omega(2);%3利用矩阵计算角加速度和加速度Dt=[-l5*omega3*cos(theta3),l4*omega4*cos(theta4),-l3*omega2*cos(t heta2),0-l5*omega3*sin(theta3),l4*omega4*sin(theta4),-l3*omega2*sin(theta 2),00,0,l2*omega2*cos(theta2),-omega1*sin(theta1)0,0,l2*omega2*sin(theta2),omega1*cos(theta1)];Et=[l6*omega1*cos(theta1);l6*omega1*sin(theta1);l1*omega1*cos(theta1)+v1*sin(theta1);l1*omega1*sin(theta1)-v1*cos(theta1)];alpha=D\(-Dt*omega+omega1*Et);a1=alpha(4);alpha2=alpha(3);alpha3=alpha(1);alpha4=alpha(2);%3子程序结束3.图像输出:%1.滑块F线位移L1图像输出%2.theta2、theta3、theta4角位移图像输出%3.滑块F的速度图像输出%4.滑块F的加速度图像输出%5.omega2、omega3和omega4角位移图像输出%6.alpha2、alpha3和alpha4角加速度图像输出%7.C点x、y方向位移图像输出%8.C点x、y方向速度图像输出%9.C点x、y方向加速度图像输出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB 作业三
1、 请将下面给出的矩阵A 和B 输入到MA TLAB 环境中,并将它们转换成符号矩阵。
若某
一矩阵为数值矩阵,另以矩阵为符号矩阵,两矩阵相乘是符号矩阵还是数值矩阵。
57651653
5501232310014325462564206441211
346,3
9636623515
212107600774101
20172440773473
781248672171107681
5A B ⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢
⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢
⎥---⎢⎥⎢⎥⎢⎥⎢⎥--⎣
⎦⎣
⎦
解:
2、 利用MA TLAB 语言提供的现成函数对习题1中给出的两个矩阵进行分析,判定它们是
否为奇异矩阵,得出矩阵的秩、行列式、迹和逆矩阵,检验得出的逆矩阵是否正确。
解:
3、试求出习题1中给出的A和B矩阵的特征多项式、特征值与特征向量,并对它们进行LU 分解。
解:
4、试求下面齐次方程的基础解系。
1234512341234512345
12345647302786045680
3436921490
26122727170
x x x x x x x x x x x x x x x x x x x x x x x x ++--=⎧⎪---+=⎪⎪
-++-+=⎨⎪-++-+=⎪---++=⎪⎩ 解:
有两组解,分别是:
x1 = 237/80,x2 = 173/40,x3 = -151/40,x4 = 1,x5 = 0和 x1 = -61/80,x2 = -109/40,x3 = 103/40,x4 = 0,x5 = 1
5、试求下面线性代数方程的解析解与数值解,并检验解的正确性。
293
211401011050384824630335
6684953X -----⎡⎤⎡⎤
⎢⎥⎢⎥----⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥
------⎣⎦⎣⎦
解:
系数矩阵与增广矩阵的秩相等,则方程组有无穷多解。
(1) 解析解:
(2) 数值解:
正确性验证:
由此得到解析解是精确解,数值解是近似解。
6、试判定下面的线性代数方程是否有解。
162313151110839761244141517X ⎡⎤⎡⎤⎢⎥⎢⎥
⎢
⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦
解:
由于系数矩阵与增广矩阵的秩不相等,所以方程组无解。
7、求解能转换成多项式方程的联立方程,并检验得出的高精度数值解(准解析解)的精度。
222222323221222
222412410
1)2)234(2)(0.5)10
73x y zxy x yz xz x x xy yz x z xzy x x y x xy xz x zy ⎧--=⎧--=⎪
-=+⎨⎨-+--=⎩⎪-+=⎩
解: 1)
2)
8、用Jacobi 、Gauss-Seidel 迭代法求解方程组 12312312
31027210283542
x x x x x x x x x --=⎧⎪
-+-=⎨⎪--+=⎩,给定初值为
(0)(0,0,0)T x =。
解:
Jacobi 迭代17次后得到解x1=11.0000,x2=12.0000,x3=13.0000
Gauss-Seidel 迭代10次后得到解x1=11.0000,x2=12.0000,x3=13.0000 9、12
(0)
12323211.4,(1,1,1),202 1.8
T x x x
x x x x x ω-=⎧⎪
==-+-=⎨⎪-+=⎩
取用超松弛法解方程组
解:
SOR 迭代17次后得到解x1=0.6806,x2=0.3612,x3=0.0418。
