MATLAB作业
matlb课程设计作业

matlb课程设计作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及应用方法,培养学生解决实际问题的能力。
具体目标如下:1.知识目标:(1)理解MATLAB的基本概念,如变量、数据类型、运算符等。
(2)掌握MATLAB编程的基本语法,如矩阵操作、函数定义与调用、循环结构、条件语句等。
(3)熟悉MATLAB与其他软件(如Mathematica、Python等)的接口转换。
(4)了解MATLAB在工程领域中的应用,如信号处理、控制系统、图像处理等。
2.技能目标:(1)能够运用MATLAB进行简单的数学计算、数据分析及图形绘制。
(2)具备编写MATLAB脚本文件和函数文件的能力。
(3)学会使用MATLAB解决实际问题,如编写程序实现线性方程组求解、最优化问题求解等。
(4)掌握MATLAB在实验数据处理、仿真实验等方面的应用。
3.情感态度价值观目标:(1)培养学生对科学探究的兴趣,提高其创新意识。
(2)培养学生团队协作、沟通交流的能力。
(3)培养学生具备良好的编程习惯和职业道德。
二、教学内容本课程的教学内容主要包括以下几个部分:1.MATLAB基本概念:变量、数据类型、运算符等。
2.MATLAB编程语法:矩阵操作、函数定义与调用、循环结构、条件语句等。
3.MATLAB高级应用:数组运算、图像处理、控制系统、信号处理等。
4.MATLAB与其他软件的接口转换。
5.实践项目:利用MATLAB解决实际问题,如线性方程组求解、最优化问题求解等。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合,以提高学生的学习兴趣和主动性。
1.讲授法:用于讲解MATLAB基本概念、语法和应用。
2.案例分析法:通过分析实际案例,使学生掌握MATLAB在各个领域的应用。
3.实验法:让学生亲自动手实践,培养其运用MATLAB解决实际问题的能力。
四、教学资源1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
matlab整理

作业一:P55:1.在一个MATLAB命令中,6+7i和6+7*i有何区别?i和I有何区别?解:在MATLAB中6+7i是一个复数常量,6+7*i则是一个表达式。
i是虚数单位,而I是单位向量。
4.要产生均值为3,方差为1的500个正态分布的随机序列,写出相应的表达式。
解:y=3+sqrt(1)*randn(500)5.求下列矩阵的对角线元素、上三角矩阵、逆矩阵、行列式的值、秩、迹。
(1) A =1 -12 35 1 -4 23 0 5 211 15 0 9(2) B =0.43 43 2-8.9 4 21解:(1)A=[1,-1,2,3;5,1,-4,2;3,0,5,2;11,15,0,9]主对角元素:D=diag(A)上三角矩阵:B=triu(A)下三角矩阵:C=tril(A)逆矩阵:X=inv(A)行列式的值:E=det(A)秩:F=rank(A)逆:G=trace(A)运行结果:A =1 -12 35 1 -4 23 0 5 211 15 0 9主对角元素:D =1159上三角矩阵:B =1 -12 30 1 -4 20 0 5 20 0 0 9下三角矩阵:C =1 0 0 05 1 0 03 0 5 011 15 0 9逆矩阵:X =-0.1758 0.1641 0.2016 -0.0227 -0.1055 -0.1016 -0.0391 0.0664 -0.0508 -0.0859 0.1516 0.0023 0.3906 -0.0313 -0.1813 0.0281 行列式的值:E =1280秩:F =4逆:G =16(2)B = [0.43,43,2;-8.9,4,21]主对角元素:D=diag(B)上三角矩阵:Y=triu(B)下三角矩阵:C=tril(B)逆矩阵:X=pinv(B)行列式的值:E=det(B)秩:F=rank(B)迹:G= trace(B)运行结果:B =0.4300 43.0000 2.0000-8.9000 4.0000 21.0000主对角元素:D =0.43004.0000上三角矩阵:Y =0.4300 43.0000 2.00000 4.0000 21.0000下三角矩阵:C =0.4300 0 0-8.9000 4.0000 0逆矩阵:X =0.0022 -0.01750.0234 -0.0017-0.0035 0.0405行列式的值:E = 1.2526e+003秩:F=3迹:G =5.43006. 当A=[34,NaN,Inf,-Inf,-pi,eps,0]时,求函数all(A)、any(A)、isnan(A)、isinf(A)、isfinite(A)的值。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
MATLB实验作业

实验一MATLAB运算基础1、用逻辑表达式求下列分段函数的值。
t=0:0.5:2.5y=t.^2.*((t>=0)&(t<1))+(t.^2-1).*(( t>=1)&(t<2))+(t.^2-2*t+1).*((t>=2 )&(t<3))2、求[100,999]之间能被21整除的数的个数。
p=rem([100:999],21)==0;sum(p)3、建立一个字符串向量,删除其中的大写字母。
ch='KdDdfKaWdsfCI',k=find(ch>=' A'&ch<='Z'),ch(k)=[]4、输入矩阵,并找出A中大于或等于5的元素。
A=[1 2 3;4 5 6;7 8 9],[m,n]=find(A>=5),for j=1:length(m)x(j)=A(m(j),n(j))xend5、求矩阵的行列式值、逆和特征根。
a11=input('a11='),a12=input('a12 ='),a21=input('a21='),a22=input('a22 ='),A=[a11,a12;a21,a22],DA=det(A),IA=inv(A),EA=eig(A) 6、不采用循环的形式求出和式的数值解。
sum(2.^[0:63])实验二1、1行100列的Fibonacc数组a,a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),用for循环指令来寻求该数组中第一个大于10000的元素,并指出其位置i。
n=100;a=ones(1,n);for i=3:na(i)=a(i-1)+a(i-2);if a(i)>10000a(i),break;end;end,i2、编写M脚本文件,定义下列分段函数,并分别求出当()、()和()时的函数值。
Matlab基础及应用第一章上机作业

1、新建一个文件夹(自己的名字命名)
答:
2、启动MATLAB,将该文件夹添加到MATLAB路径管理器中。
保存,关闭对话框。
使用path命令查看MATLAB搜索路径。
3、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye。
4、使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
5、编写一段简短的脚本文件,保存并显示运行结果。
6、创建两个double型变量a=32、b=5,并计算a+b、a-b、a*b、a/b、a\b;
创建两个int8型变量a、b,取同样数值,并计算a+b、a-b、a*b、a/b、a\b,对于计算结果与前次计算结果不同的情形请给出解释。
7、查看int16数据类型的取值范围(intmin,intmax);查看单精度数据类型的取值范围和精度(realmin,realmax,eps)。
8、求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量:
(1)sin(60o) (2) e3 (3) cos(3/4π)
9、用两种定义复数的方法计算(直接定义,complex(a,b))
(1)(3-5i)(4+2i) (2) sin(2-8i)。
MATLAB平时作业(图文版)

MATLAB 平时作业第一章 习题16. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
”答:此种说法错误。
MATLAB 提供了控制数据显示格式的控制指format ,该指令并不改变MATLAB 内存中变量的精度,只是改变其显示精度。
(2)“MATLAB 指令窗中显示的数值有效位数不超过7位。
”答:此种说法错误。
当变量小于1000时,使用format 或format short 后,或者默认情况下,变量的显示精度最多不超过7位,但显示精度不等于变量的精度。
7. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:操作如图:第1、2条指令可以实现,第3条指令不可实现。
第三章 习题31.在MATLAB 中,先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7], C=reshape(1:6,3,2)生成阵列33⨯A ,23⨯B ,23⨯C ,然后根据运行结果回答以下问题:运行结果如图:(1)计算A*B, B*A ,这两个乘积相同吗? 计算结果如图:答:不同。
(2)计算A\B, B/A ,左除、右除结果相同吗?计算结果如图:答:不同。
(3)计算B( : ,[1,2]).*C和C.*B( : , [1,2]),这两个乘积相同吗?计算结果如图答:相同。
(4)计算A\A和A.\A,这两个计算结果相同吗?计算结果如图:答:相同。
(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?计算结果如图:答:不同。
(提示:根据对计算结果的目测回答问题)2.在MATLAB中,先运行A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5], 然后根据计算结果回答以下问题:创建数据步骤略(1)计算A^b和A.^b, 这两个计算结果相同吗?答:不同。
matlab作业3参考答案

matlab作业3参考答案Matlab作业3参考答案Matlab作业3是一个综合性的编程任务,要求学生运用Matlab的各种功能和工具来解决实际问题。
本文将提供Matlab作业3的参考答案,并对其中的关键步骤和思路进行详细解释。
一、问题描述在本次作业中,学生需要解决一个关于图像处理的问题。
具体来说,给定一张彩色图像,学生需要编写Matlab代码来实现以下功能:1. 将彩色图像转换为灰度图像;2. 对灰度图像进行高斯滤波;3. 对滤波后的图像进行边缘检测;4. 对边缘图像进行二值化处理。
二、解决方案1. 将彩色图像转换为灰度图像首先,我们需要读取彩色图像。
可以使用Matlab的imread函数来实现。
然后,使用rgb2gray函数将彩色图像转换为灰度图像。
代码如下:```matlabrgbImage = imread('image.jpg');grayImage = rgb2gray(rgbImage);```2. 对灰度图像进行高斯滤波接下来,我们需要对灰度图像进行高斯滤波。
高斯滤波是一种常用的图像平滑方法,可以有效地去除图像中的噪声。
Matlab提供了fspecial函数来生成高斯滤波器。
代码如下:```matlabh = fspecial('gaussian', [3 3], 1);filteredImage = imfilter(grayImage, h);```3. 对滤波后的图像进行边缘检测在这一步中,我们需要对滤波后的图像进行边缘检测。
边缘检测可以帮助我们找到图像中的边缘和轮廓。
Matlab提供了多种边缘检测算法,如Sobel算子和Canny算子。
代码如下:```matlabedgeImage = edge(filteredImage, 'canny');```4. 对边缘图像进行二值化处理最后,我们需要对边缘图像进行二值化处理,将图像中的边缘转换为黑白两种颜色。
Matlab习题及答案
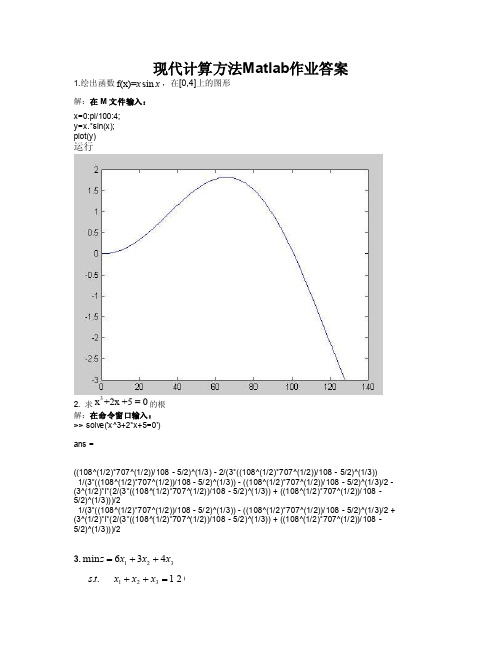
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =ans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u) ans =15.4189>> sqrt(u-3*v)/(u*v) ans =0 + 0.4410i 4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
MATLAB期末大作业

1.龟兔赛跑本题旨在可视化龟兔赛跑的过程。
比赛的跑道由周长为P面积为A的矩形构成。
每单位时间,乌龟沿跑道缓慢前进一步,而兔子信心满满,每次以一个固定的概率决定走或不走。
如果选择走,就从2-10步中等概率选择一个步长。
每个单位时间用一个循环表示。
赛跑从矩形跑道左上点(0,0)开始,并沿顺时针方向进行。
不管是乌龟或兔子,谁先到达终点,比赛就告结束。
要求:编写MATLAB程序可视化上述过程。
程序以P,A以及兔子每次休息或前进的概率为输入参量。
程序必须可视化每个时刻龟兔赛跑的进程,并以红色“*”表示乌龟,蓝色的“—”表示兔子。
测试时可取P=460,A=9000。
通过上述例子,可否从理论和实验角度估计兔子休息或前进的概率,是的兔子和乌龟在概率意义下打平手。
2.黄金分割Fibonacci数列F n通过如下递推格式定义F n=F n-1+F n-2,其中F0=F1=1要求:1.计算前51项Fibonacci数,并存入一个向量2.利用上述向量计算比值F n/F n-13.验证该比值收敛到黄金比例(1+5)/23.图像处理此题旨在熟悉图像处理的基本操作,请各位自己选择一张彩色图像pMATLAB以三维数组读取一张彩图。
该彩图上每个像素位置分别存放一个取值0-255的三维向量,其三个分量分别表示该点的红(R)绿(G)蓝(B)强度信息。
要求:编写MATLAB程序,读入原始彩色图像,并且在一个图形窗口界面下显示六张图像。
这六张图分别是原始RGB彩图,及其5各变形:RBG,BRG,BGR,GBR和GRB。
每张子图要求以其对应变形命名。
最后将图像以a.jpg形式保存并黏贴至报告中。
提示:imread, imshow, cat。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
MATLAB大作业题目

一、 程序分析题1、命令窗口中输入如下命令,在%号后写出每行命令的功能。
(不用写出运算结果) A=1; f0=4; phi=pi/3; w0=2*pi*f0;t=0:0.01:1; %__________________________________________ y=A*cos(w0*t+phi) ;axis off %__________________________________________ PT=plot(t,y); %__________________________________________ set(PT,’LineWidth ’,[5]); %__________________________________________ AX=gca; %__________________________________________ set(AX,’FontSize ’,14); %__________________________________________ axis square %__________________________________________ xlabel(‘时间[s]’); %__________________________________________ T=title(‘余弦波’) %__________________________________________ set(T,’FontSize ’,’16’); %__________________________________________ legend(‘cos ’); %__________________________________________ grid on %__________________________________________二、 程序设计题2、已知两个矩阵:3765213100132610A ---⎡⎤⎢⎥---⎢⎥=⎢⎥-⎢⎥-⎣⎦,1468237021570010B ⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥-⎣⎦将矩阵A 中所有等于-1的元素改为3,将矩阵B 中等于0的元素值改为新的矩阵A 中相应位置元素的值,最后将新的矩阵A 的第三、四列的元素全改为-1,编写相应的程序。
Matlab 作业1

喻晓磊 200731510103 电子科学与技术习题一:编写M文件,计算以下问题:口口口口×口=口口口口以上9个口代表1~9这9个数字,不得遗漏或重复要求:给出解算思路和M文件代码注意算法的效率解题理念:1,设以上方框中的数字分别是1~9之间的数字a、b、c、d、e、f、g、h、i。
2,我们可以推出,个位数e肯定不是1或者5 ,否则两个四位数的个位必然相等,即d=i;再者,其不可能等于9,由不重复的1~9组成的四位数,最大为9876,最小为1234,故e的最大可能取值为9876/1234=8.003……,即最大取8 。
3,我们看到,e的最小取值为2,那么a肯定不能大于或等于5 ,否则乘法运算后的结果为5位数,所以a 只能取1~4。
4,在此基础上,我们采取“穷举法”,逐个试验,从 a 开始,每一位与前面出现位的数字不相等,然后检测其是否满足算式。
程序代码如下:global aglobal bglobal cglobal dglobal eglobal fglobal gglobal hglobal ifor a=1:4for b=1:9if b~=a;for c=1:9if (c~=b)&&(c~=a);for d=1:9if (d~=b)&&(d~=a)&&(d~=c);for e=2:8 e~=5;if (e~=a)&&(e~=b)&&(e~=c)&&(e~=d);for f=1:9if (f~=a)&&(f~=b)&&(f~=c)&&(f~=d)&&(f~=e);for g=1:9if(g~=a)&&(g~=b)&&(g~=c)&&(g~=d)&&(g~=e)&&(g~=f);for h=1:9if(h~=a)&&(h~=b)&&(h~=c)&&(h~=d)&&(h~=e)&&(h~=f)&&(h~=g);for i=1:9if(i~=a)&&(i~=b)&&(i~=c)&&(i~=d)&&(i~=e)&&(i~=f)&&(i~=g)&&(i~=h);x=1000*a+100*b+10*c+d;y=e*x;z=1000*f+100*g+10*h+i;if y==z;r=xs=et=yend;end;******end;end;得到的结果如下:我们看到,结果有两组:1738 * 4= 69521963 * 4= 7852这两组结果都显示到了MATLAB软件的命令窗(COMMAND WINDOW)中,我们是使用了一个小技巧:将x、e、y的值赋给r、s、t时并没有在句末加分号,所以计算的过程也显示出来了,但是看工作区(work space)中,r、s、t 的值却只对应后面一组,这是因为,当循环进行到算出第二组结果时,便替换掉了第一组的值。
MATLAB基础训练作业(含答案)

实验一 MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条 (Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-522-70)3(2)>>area=pi*^2(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= (4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1( 2 , 3 )>>m1( 11 )>>m1( : , 3 )>>m1( 2 : 3 , 1 : 3 )>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1)(5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i )(6)执行命令>>x=0::6*pi;>>y=5*sin(x);>>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
四、思考题1、以下变量名是否合法为什么(1)x2(2)3col(3)_row(4)for2、求以下变量的值,并在MATLAB 中验证。
MATLAB第一次作业

(1)运行如下clear和clc命令,说明两个命令的区别a=1,b=2,c=2clcclear aClear 答:clear是清变量,clc是清屏。
(2)已知a=6.33,b=2.8,c=1.2求()ln() lg()a b ceb a ca b+-⨯+、(3)已知x=-11.7,求如下函数的值fix(x),round(x),floor(x),ceil(x),sign(x)(4)已知x=-3.7°,y=11.2°,z=39.2°求sin(||||||)tan(||)x y z x y z ++++答:(5)计算 1.2*4*acos(10)e-答:(6)已知:51237.9 2.5, 1.1 2.2, 2.1iz i z i z e π=-=+=,计算312z z z z =答:(7)115y =+(8)(365-52⨯2-70)÷3答(7) (8)(9)执行命令>>help abs ,查看函数abs 的用法及用途,计算abs( 3 + 4i )答:(10)已知x=1+2i ,37.9y =(cos(x+y )-sin(78))z=x+y答:(11)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= 答:(12)在MATLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a答:(13)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 分别执行以下命令,计算结果:m1( 2 , 3 ),m1( 11 ),m1( : , 3 ),m1( 2 : 3 , 1 : 3 ),m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1)答:(14)已知数组c = 1.1000 -3.2000 3.4000 0.6000 0.6000 1.1000 -0.6000 3.1000 1.3000 0.6000 5.5000 0⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦分别执行以下命令,查看结果:c(2,:); c(:,end); c(1:2, 2:end); c(6); c(4:end); c(1:2,2:4); c([1 4],2); c([2 2],[3 3])(15)计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
离散卷积MATLAB编程作业

一、离散卷积MATLAB编程作业(1)请编程实现一维卷积功能,即自己编写MATLAB中的CONV函数,自己写出一个CONV_NEW函数。
要求,请自己学习MATLAB向量运算操作,基于学习到的内容,用尽量少的代码实现CONV_NEW。
(a)请用例子检查你写的CONV_NEW是否与CONV的输出是否一致。
(b)请用两个10000维数组检测对比你写的CONV_NEW和CONV的时间复杂度。
请查资料大致回答,为什么MATLAB自带的CONV更快一些?(2)请查询自学二维卷积的知识(a)请写一个函数CONV2_NEW实现MATLAB中的二维卷积函数CONV2功能,请用例子检查你写的CONV2_NEW与CONV2的输出是否一致(b)请用此函数,做以下两个卷积核与附件图片lenna.jpg的卷积,将卷积结果打印出来。
并想一下为什么是这样。
(请查阅imread和imwrite函数)两点提示:由于imread和imwrite函数读入和写出的数值范围都是0到255,因此需要将结果归一化。
请参考一下函数程序读入写出例程。
A = imread(‘lenna.jpg’);B = double(A);Imwrite(uint8(B),’test.bmp’);(3)请编写MATLAB程序H = DECONV(X, Y)要求输入序列X和Y,输出序列H,使Y=X*H,若没有H满足要求,则输出错误信息”No sequence satisfies this condition.”二、傅里叶变换编程题对于卷积公式:x(t)*h(t) = y(t),则根据傅里叶变换和卷积性质,在已知x(t)和y(t)的情况下,h(t)可以写成:ℎ(t)=12π∫Y(jω)X(jω)e jωt dω+∞−∞(1)若x(t)和y(t)分别是如下函数,求h(t)。
(2)请用MATLAB画出h(t)在t=[-50,50]的函数图像。
(提示:用分成小段求矩形面积的形式近似求积分,注意规避分母等于0时候的情况)。
matlab作业练习及答案(有程序和截图)

1. 给出如下方程组:16323313915111081697612534141543s u p w s u p w s u p w s u p w +++=+++=+++=+++=求s ,u ,p ,w 的值,并求出系数行列式。
[答案:s =-0.1258,u =-8.7133,p =11.2875,w =-0.0500。
行列式=7680。
]>> A=[16 32 33 13;5 11 10 8;9 7 6 12;34 14 15 1];>> B=[91 16 5 43]';>> C=A\B2. 求矩阵H1()H X X X X -''=其中1731565419289121110X ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦〔答案:H =〔0.7294,0.9041,0.4477,0.9188〕'〕>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X/(X'*X)*X'>> X=[17 31 5;6 5 4;19 28 9;12 11 10]; >> H=X*inv((X'*X))*X'3.用MA TLAB语言实现下面的分段函数,()/,||,h x Dy f x h Dx x Dh x D>⎧⎪==≤⎨⎪-<-⎩。
y=h*(x>D)+h/D*x.x>=-D&x<=D)-h*(x<-D)4.636263 0S=2124822 ii==++++++∑①试不采用循环的形式,用数值方法求出上式的解。
②由于数值方法采用double形式进行计算,难以保证有效数字,试采用符号运算的方法求该式的精确解。
并给出保留16位有效数字的结果。
>> sum(2.^[1:63])>> sum(sym(2).^[1:63])5.编写一个矩阵相加函数mat_add(),使其具体的调用格式为,要求该函数能接受任意多个矩阵进行加法运算。
4个Matlab实验的作业

现给出bpsk、qpsk及“书上习题”的调制解调程序,理解各程序,完成以下习题。
将程序运行结果及各题目的解答写入word中:1.用matlab运行书上习题中的“bpskqpsk125.m”(a)说明bpsk、qpsk解调判决方法(b)误比特率为1e-2、1e-3及1e-4时的Eb/N0分别是多少?(c)从物理意义上说明为什么bpsk、qpsk误比特率曲线是重叠的(d)当samples减少为100000,10000,1000时观察误比特率曲线的变化,你得出什么结论。
2.用matlab运行“bpsk.m”、“qpsk.m”(a)在各程序中标注“注释”处加上注释(英文或中文)(b)说明加性高斯白噪声的产生方法,请再给出一种加性高斯白噪声的产生方法,并验证其正确性。
(c)参考“bpskqpsk125.m”的画图功能,给出Eb/N0---误比特率曲线和高斯信道下的理论误比特率曲线。
(d)观察nd及nloop参数变化时,曲线的现象,并说明原因。
(e)画出不同信噪比条件下的的星座图,解释其对误码率的影响。
(f)通过程序画出QPSK和BPSK的Eb/N0---误比特率曲线,观察曲线的现象,能得出什么结论。
3.若信源是你的学号,结合程序说明其在qpsk (调制mod)和(解调demod)子程序中的具体实现过程。
4.针对题目2中的BPSK、QPSK,(a)若信道使信号幅度呈瑞利衰落,画出Eb/N0---误比特率曲线和瑞利衰落下的理论误比特率曲线,说明与题目2观察结果的异同,并说明原因。
(b)若信道使信号幅度呈莱斯衰落,更改K值的大小,画出Eb/N0---误比特率曲线、瑞利衰落下的理论误比特率曲线和高斯信道下的理论误比特率曲线,观察曲线的现象,能得出什么结论。
现给出循环码及卷积码的编解码程序,理解各程序,完成以下习题。
将程序运行结果及各题目的解答写入word中:1.用matlab运行书上习题中的“clockcode.m”(a)说明(7,4)码的纠错检错方法(b)在程序中标注“注释”处加上注释(英文或中文)(c)对于编码和未编码的情况,误比特率为1e-2、1e-3及1e-4时的Eb/N0分别是多少?(d)从物理意义上说明编码增益问题(e)当采用(15,11)码时,观察与(7,4)码相比编码增益的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语言、MATLAB数学函数库、图形功能和应用程序接口五个部分组成。
2. 如何启动M文件编辑/调试器?答:在操作界面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动。
在命令窗口中键入“edit”命令也可以启动M文件编辑/调试器。
3. 存储在工作空间中的数组能编辑吗?如何操作?答:存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可。
4. 在MATLAB中有几种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗口键入“help” 命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数(4)模糊查询:输入命令的前几个字母,然后按Tab键,就可以列出所有以这几个字母开始的命令和函数。
5. 有几种建立矩阵的方法?各有什么优点?答:(1)以直接列出元素的形式输入;(2)通过语句和函数产生;(3).在m文件中创建矩阵;(4)从外部的数据文件中装入。
6. 命令文件与函数文件的主要区别是什么?答:命令文件: M文件中最简单的一种,不需输出输入参数,用M 文件可以控制工作空间的所有数据。
运行过程中产生的变量都是全局变量。
运行一个命令文件等价于从命令窗口中顺序运行文件里的命令,程序不需要预先定义,只要依次将命令编辑在命令文件中即可。
函数文件:如果M文件的第一个可执行行以function开始,便是函数文件,每一个函数文件定义一个函数。
函数文件区别于命令文件之处在于命令文件的变量在文件执行完成后保留在工作空间中,而函数文件内定义的变量只在函数文件内起作用,文件执行完后即被清除。
7. 创建符号变量有几种方法?答:创建符号变量和表达式的两个基本函数:sym, syms*x=sym(‘x’) 创建一个符号变量x,可以是字符、字符串、表达式或字符表达式。
*syms用于方便地一次创建多个符号变量,调用格式为: syms a b c d. 书写简洁意义清楚,建议使用。
8. 下面三种表示方法有什么不同的含义?(1)f=3*x^2+5*x+2(2)f='3*x^2+5*x+2'(3)x=sym('x')f=3*x^2+5*x+2答:(1)f=3*x^2+5*x+2为一函数表达式。
(2)f='3*x^2+5*x+2'为一符号函数。
(3)用sym函数定义的符号表达式。
9.什么是图形句柄?图形句柄有什么用途?答:图形对象的句柄是MATLAB显示图形数据和建立图形用户接口的基础,每个对象从产生时起就被赋予了一个唯一的标识,这种标识就是该对象的句柄。
利用句柄就可以操纵一个已经存在的图形对象的特性(属性)。
10. 什么是Simulink ?答:MATLAB Simulink是一个动态仿真系统,用于对动态系统进行仿真和分析,预先模拟实际系统的特性和响应,根据设计和使用要求,对系统进行修改和优化。
Simulink提供了图形化用户界面,只须点击鼠标就可以轻易的完成模型的创建、调试和仿真工作,用户不须专门掌握一种程序设计语言。
Simulink可将系统分为从高级到低级的几个层次,每层又可以细分为几个部分,每层系统构建完成后,将各层连接起来构成一个完整系统。
Simulink可以仿真线性和非线性系统,并能创建连续时间、离散时间或二者混合的系统。
支持多采样频率系统。
11.计算与的数组乘积。
x=[6 9 3,2 7 5];y=[2 4 1,4 6 8];z=x.*yz =12 36 3 8 42 4012.对于,如果,,求解X。
a=[4 9 2; 7 6 4; 3 4 7]b=[37 26 28]x=a/ba =4 9 27 6 43 4 7b =37 26 28x =0.15480.18630.145313. 求解多项式x3-7x2+2x+40的根。
a=[1 -7 2 40]r=roots(a)a =1 -72 40r =5.00004.0000-2.000014. 求解在x=8时多项式(x-1)(x-2) (x-3)(x-4)的值。
a=[1 2 3 4];pa=poly(a);ppa=polyval(pa,8)ppa = 84015. 计算多项式除法(3x3+13x2+6x+8)/(x+4)。
c=[3 13 6 8];[q2,r2]=deconv(c,[1,4])cc=conv(q2,[1,4])test=((c-r2)==cc)q2 =3 1 2r2 =0 0 0 0cc =3 13 6 8test =1 1 1 116.计算多项式的微分和积分。
微分:syms x;f=4*x^4-12*x^3-14*x^2+5*x+5;diff(f)ans =16*x^3-36*x^2-28*x+5积分:syms x;f=4*x^4-12*x^3-14*x^2+5*x+5;int(f)ans =4/5*x^5-3*x^4-14/3*x^3+5/2*x^2+5*x 17.解方程组。
a=[2 9 0,3 4 11,2 2 6]b=[13 6 6]x=a\ba =2 9 034 11 2 2 6b =13 6 6x =0 0 00 0 00 0 00 0 00 0 01.1818 0.5455 0.54550 0 00 0 00 0 018. y=sin(x),x从0到2,x=0.02,求y的最大值、最小值、均值和标准差。
x=0:0.02*pi:2*piy=sin(x)Amax=max(y)Amin=min(y)Amean=mean(y)Astd=std(y)Amax =1Amin =-1Amean =2.2995e-017Astd =0.707119.符号函数绘图法绘制函数x=sin(3t)cos(t),y=sin(3t)sin(t)的图形,t 的变化范围为[0,2]。
syms tfigure (1)ezplot(sin(3*t)*cos(t))figure (2)ezplot(sin(3*t)*sin(t))20.用sphere函数产生球表面坐标,绘制不通明网线图、透明网线图、表面图和带剪孔的表面图。
并将其中的带剪孔的球形表面图的坐标改变为正方形,以使球面看起来是圆的而不是椭圆的,然后关闭坐标轴的显示。
无透明处理:Z=sphere(64);mesh(Z)colormap([0,1,0])透明处理后:Z=sphere(64);mesh(Z)colormap([0,0.2,0.5])hidden off表面图:z=sphere(36);surf(z)带剪孔的表面图:p=sphere(64);p(20:23,9:15)=NaN*ones(4,7); %剪孔位置(将以部分网格设置为非数)meshz(p)21. 有一正弦衰减数据y=sin(x).*exp(-x/10),其中x=0:pi/5:4*pi,用三次样条法进行插值。
x0=0:4*pi;y0=sin(x0).*exp(-x0/10);x=0:pi/5:4*pi;y=spline(x0,y0,x);plot(x0,y0,'or',x,y,'k')22. 建立一个简单模型,用信号发生器产生一个幅度为2V、频率为0.5Hz的正弦波,并叠加一个0.1V的噪声信号,将叠加后的信号显示在示波器上并传送到工作空间。
23.矩阵,计算a的行列式和逆矩阵。
a=[4 2 -6;7 5 4;3 4 9];d1=det(a);x1=inv(a);>> a=[4 2 -6;7 5 4;3 4 9];d1=det(a)x1=inv(a)d1 =-64x1 =-0.4531 0.6562 -0.59370.7969 -0.8437 0.9062-0.2031 0.1562 -0.093724.,,计算x的协方差、y的协方差、x与y的互协方差。
x=[1 2 3 4 5];y=[2 4 6 8 10];cx=cov(x)cy=cov(y)cxy=cov(x,y)cx =2.5000cy =10cxy =2.5000 5.00005.0000 10.000025.用符号函数法求解方程a t2+b*t+c=0。
syms a b c xf=a*x^2+b*x+c;x=solve(f)S=solve(f);[S.x]x =[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))][ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]28.求代数方程组关于x,y的解。
syms a b c x yf=a*x^2-b*y+c;g=x+y;[x,y]=solve(f,g)S=solve(f,g);[S.x,S.y]x =[ -1/2/a*(b+(b^2-4*a*c)^(1/2))][ -1/2/a*(b-(b^2-4*a*c)^(1/2))]y =[ 1/2/a*(b+(b^2-4*a*c)^(1/2))][ 1/2/a*(b-(b^2-4*a*c)^(1/2))]ans =[ -1/2/a*(b+(b^2-4*a*c)^(1/2)), 1/2/a*(b+(b^2-4*a*c)^(1/2))] [ -1/2/a*(b-(b^2-4*a*c)^(1/2)), 1/2/a*(b-(b^2-4*a*c)^(1/2))] 2.求矩阵的行列式值、逆和特征根。
syms a11 a12 a21 a22;A=[a11 a12;a21 a22];t=det(A)m=inv(A)[b,c]=eig(A)t =a11*a22-a12*a21m =[ -a22/(-a11*a22+a12*a21), a12/(-a11*a22+a12*a21)][ a21/(-a11*a22+a12*a21), -a11/(-a11*a22+a12*a21)]b =[ -(1/2*a22-1/2*a11-1/2*(a22^2-2*a11*a22+a11^2+4*a12*a21)^(1/2))/a21, -(1/2*a22-1/2*a11+1/2*(a22^2-2*a11*a22+a11^2+4*a12*a21)^(1/2))/a21][ 1,1]c =[ 1/2*a22+1/2*a11+1/2*(a22^2-2*a11*a22+a11^2+4*a12*a21)^(1/2), 0][ 0, 1/2*a22+1/2*a11-1/2*(a22^2-2*a11*a22+a11^2+4*a12*a21)^(1/2)]3.,用符号微分求df/dx。
