自动控制原理简明版根轨迹法共36页
合集下载
自动控制原理第5章根轨迹分析法

04
CATALOGUE
根轨迹分析法的限制与挑战
参数变化对根轨迹的影响
参数变化可能导致根轨迹的形状和位置发生变化 ,从而影响系统的稳定性和性能。
对于具有多个参数的系统,根轨迹分析可能变得 复杂且难以预测。
需要对参数变化进行细致的监测和控制,以确保 系统的稳定性和性能。
复杂系统的根轨迹分析
对于复杂系统,根轨 迹分析可能变得复杂 且难以实现。
02
CATALOGUE
根轨迹的基本概念
极点与零点
极点
系统传递函数的极点是系统动态 特性的决定因素,决定了系统的 稳定性、响应速度和超调量等。
零点
系统传函数的零点对系统的动 态特性也有影响,主要影响系统 的幅值和相位特性。
根轨迹方程
根轨迹方程是描述系统极点随参数变 化的关系式,通过求解根轨迹方程可 以得到系统在不同参数下的极点分布 。
05
CATALOGUE
根轨迹分析法的改进与拓展
引入现代控制理论的方法
状态空间法
将根轨迹分析法与状态空间法相结合,利用状态空间法描述系统的动态行为,从而更全 面地分析系统的稳定性。
最优控制理论
将根轨迹分析法与最优控制理论相结合,通过优化系统的性能指标,提高系统的稳定性 和动态响应。
结合其他分析方法
根轨迹方程的求解方法包括解析法和 图解法,其中图解法是最常用的方法 。
根轨迹的绘制方法
手工绘制
通过选取不同的参数值,计算对应的极点,然后绘制极点分布图。这种方法比较繁琐,但可以直观地了解根轨迹 的形状和变化规律。
软件绘制
利用自动控制系统仿真软件,如MATLAB/Simulink等,可以方便地绘制根轨迹图,并分析系统的动态特性。
自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例:开环传递函数
Gs
k1
ss
a
开环系统两个极点为:P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程: s2 as k1 0
闭环特征根:s1,2
a 2
a 2
2
k1
(闭环极点)
3
自动控制原理
在p5附近取一实验点sd, 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明:根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例:sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点,复极点提供的相角和为 3600。
2
s1=-1.172,s2=-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为:
Z 1800
其中 z p(不包括本点)
34
自动控制原理
j p5
p5
p3 p3
p2
自动控制原理简明版第4章根轨迹法课件35页PPT

令 dK 1 0
ds
s2 2s2 K1 s2 s24s20
求得 s10.58(舍6去)
s23.414
7
(2)
m
1
n
1
i1 szi j1 spi
因为
P (s ) Q (s ) P (s ) Q (s ) 0
即
P(s) Q(s) P(s) Q(s)
d
d
[lnP(s)] [ln Q(s)]Βιβλιοθήκη dsIm a倾角。
s1
pa
在根轨迹曲线上取试验点s1,与
复极点-pa的距离为 。 当 0时,可近似地 认为s1在切线上,切线
3 p3
1 z1
1
0 p1
Re
的倾角就等于复极点的
p2
出射角。
2
1 (a 1 9 0 3 ) 1 ( 8 2 k 0 1 )
所以 a 的出射角:
a18 (2 0 k1)1(190 3)
d[G1(s)H1(s)]0 或
ds
d[G(s)H(s)]0 ds
以上分析没有考虑 K1 0 (且为实数)的约束条件,所以只有满 足 K1 0的这些解,才是真正的分离点(或会合点)。
2
例: 设系统
R(s)
K1(s 2) s2 2s 2
C(s)
试求该系统根轨迹在实轴上的会合点。
解:系统的开环传递函数:
9
Im
复杂情况用试探法。
在-2-3之间存在一个分离点。
3
2 1
0 Re
1 1 1 1 s1 s s2 s3
s2.4
1 ? 1 1 1
2 .412 .4 2 .42 2 .43
0.715 1.247
根轨迹法(自动控制原理)

自动控制原理4141根轨迹的基本概念根轨迹的基本概念4242绘制典型根轨迹绘制典型根轨迹4343特殊根轨迹图特殊根轨迹图4444用用matlabmatlab绘制根轨迹图绘制根轨迹图4545控制系统的根轨迹分析控制系统的根轨迹分析根轨迹法是一种图解法它是根据系统的开环零极点分布用作图的方法简便地确定闭环系统的特征根与系统参数的关系进而对系统的特性进行定性分析和定量计算
❖ 线性时不变系统的动态性能主要取决于闭环系统 特征方程的根(闭环极点),所以控制系统的动 态设计,关键就是合理地配置闭环极点。调整开 环增益是改变闭环极点的常用办法。
❖ 1948年伊凡思(W.R.Evans)提出了根轨迹法,它 不直接求解特征方程,而用图解法来确定系统的闭 环特征根。
所谓根轨迹,就是系统的某个参数连续变化时, 闭环特征根在复平面上画出的轨迹。如果这个参 数是开环增益,在根轨迹上就可以根据已知的开 环增益找到相应的闭环特征根;也可以根据期望 的闭环特征根确定开环增益。
闭环特征方程为:
1G (s)H (s)0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
G(s)H(s)1
这就是根轨迹的基本条件。
❖ 满足根轨迹上点的基本条件,又可分别表示为,
幅值条件:
G(s)H(s) 1
相角条件: G ( s ) H ( s ) ( 2 k 1 ) 18 k 0 , 0 1 ,2 ,
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
规则6:根轨迹的分离点
❖ 当从K零变到无穷大时,根轨迹可能出现先会合后分离, 这样的点称分离点。分离点对应重闭环极点。
❖ 线性时不变系统的动态性能主要取决于闭环系统 特征方程的根(闭环极点),所以控制系统的动 态设计,关键就是合理地配置闭环极点。调整开 环增益是改变闭环极点的常用办法。
❖ 1948年伊凡思(W.R.Evans)提出了根轨迹法,它 不直接求解特征方程,而用图解法来确定系统的闭 环特征根。
所谓根轨迹,就是系统的某个参数连续变化时, 闭环特征根在复平面上画出的轨迹。如果这个参 数是开环增益,在根轨迹上就可以根据已知的开 环增益找到相应的闭环特征根;也可以根据期望 的闭环特征根确定开环增益。
闭环特征方程为:
1G (s)H (s)0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
G(s)H(s)1
这就是根轨迹的基本条件。
❖ 满足根轨迹上点的基本条件,又可分别表示为,
幅值条件:
G(s)H(s) 1
相角条件: G ( s ) H ( s ) ( 2 k 1 ) 18 k 0 , 0 1 ,2 ,
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
规则6:根轨迹的分离点
❖ 当从K零变到无穷大时,根轨迹可能出现先会合后分离, 这样的点称分离点。分离点对应重闭环极点。
自动控制原理第四章根轨迹法(管理PPT)

根轨迹法的优化建议
结合其他方法
将根轨迹法与其他分析方 法(如频率响应法)相结 合,以获得更全面的系统 性能分析。
ቤተ መጻሕፍቲ ባይዱ开发软件工具
开发专门用于根轨迹分析 的软件工具,以提高分析 的效率和准确性。
加强实践应用
在实际工程中加强根轨迹 法的应用,通过实践不断 优化和完善该方法。
05
CATALOGUE
根轨迹法与其他控制方法的比较
根轨迹分析的实例
假设一个开环传递函数为 G(s)H(s) = (s+1)(s+2)/(s^2+2s+5),对其进行 根轨迹分析。
分析根轨迹图,确定系统的稳定性、 动态性能和系统参数的影响。
根据开环传递函数,绘制出根轨迹图 ,并标注出系统的极点和零点。
根据根轨迹图进行系统设计和优化, 例如调整开环传递函数的增益参数, 以改善系统的性能。
对于非线性系统,根轨迹法可能无法给出准确的描述和分析。
04
CATALOGUE
根轨迹法的改进与优化
根轨迹法的局限性与挑战
参数敏感性
根轨迹法对系统参数的微小变化非常敏感,可能导致根轨迹的剧 烈变化,影响系统的稳定性。
无法处理非线性系统
根轨迹法主要适用于线性系统,对于非线性系统的分析存在局限性 。
计算复杂度较高
和设计。
对于具有特定性能指标要求的系统,如 快速响应、低超调量等,可以根据系统 特性和性能要求选择适合的控制方法,
如状态反馈控制器等。
06
CATALOGUE
根轨迹法的实际应用案例
根轨迹法在工业控制系统中的应用
根轨迹法在工业控制系统中广泛应用于系统的分析和设计。通过绘制根轨迹图,可以直观地 了解系统性能的变化,如稳定性、响应速度和超调量等。
(完整版)第四章根轨迹法

j
8K * (1 K * )2 j
2
2
(1 K * ) K * 2 1
2
2 8K * (1 K * )2 8(2 1) 4 2 2 4 2
4
4
2 4 4 2 2
( 2)2 2
第四章 根轨迹法
自动控制原理课程的任务与体系结构
时域:微分方程 复域:传递函数 频域:频率特性
描述
控制系统
校正
时域法 复域法 频域法
评价系统的性能指标 稳定性 快速性(动态性能) 准确性(稳态性能)
分析
自动控制原理
§4 根轨迹法
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本法则 §4.3 广义根轨迹 §4.4 利用根轨迹分析系统性能
• s平面上满足相角条件的点(必定满足模值条件) 一定在根轨迹上。 满足相角条件是s点位于根轨迹上的充分必要条件。
• 根轨迹上某点对应的 K* 值,应由模值条件来确定。
§4.2
m
绘制根轨迹的基本法则(1) G(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
K*
(s zi )
i 1 n
1
(s pj)
— 模值条件
j 1
m
n
G(s)H (s) (s zi ) (s p j ) (2k 1)
i 1
j1
— 相(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
§4 根 轨 迹 法
根轨迹法: 三大分析校正方法之一
特点: (1)图解方法,直观、形象。 (2)适合于研究当系统中某一参数变化时,系统性能的变化
自动控制原理第四章 根 轨 迹 法
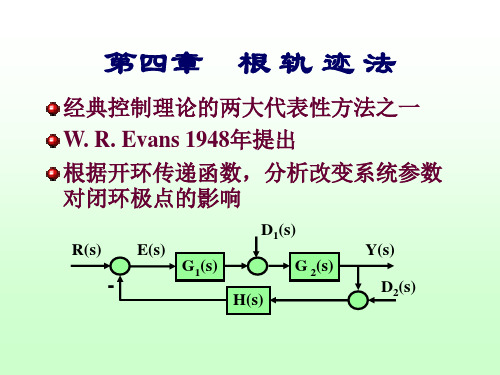
K=2.5
-2
>0.5时,特征根为共轭复根,欠阻尼系 统,响应为衰减振荡;可根据性能要求
K
设置闭环极点。
当特征方程>2阶时无法求解,如何绘制根轨迹图?
4-2. 绘制根轨迹的基本依据和条件
特征方程为: 1+G(s)H(s)=0
即: G(s)H(s)= -1
R(s)
Y(s)
G(s)
-
H(s)
G( s )H( s ) 1
4-1. 根轨迹基本概念
根轨迹的定义:
开环传递函数的某一参数从0变到∞时,闭环系 统特征方程式的根在s平面上的变化轨迹。
R(s)
-
E(s) G1(s)
D1(s) G 2(s)
H(s)
Y(s) D2(s)
如
G1( s )G2 ( s )H ( s )
Kg s( s 1 )( s 2 )
常规根轨迹
求解:设 Gk ( s ) KgG1( s ),则对于1 KgG1( s ) 0,有
dK g ds
d [G11( s )] ds
0 (Kg在根轨迹的分离点上取极值)
或 dG1( s ) 0 (特征式满足 d( s ) 0)
ds
ds
注:只须用其中之一,且只是必要条件
续前例:求分离点上的坐标。
幅值条件
G( s )H( s ) 180( 2k 1 ), k 0,1,2,
相角条件
零极点表达形式下的幅值条件和相角条件:
m
n
K g (s zi )
(s pi )
G(s)H(s)
i1 n
1 ,或
Kg
i1 m
,
(s pi )
(s zi )
自动控制课件第四章根轨迹法.ppt

第四章
根轨迹法
1
主要内容
4-1 根轨迹与根轨迹方程 4-2 绘制根轨迹的基本法则 4-3 开环零、极点变化时的根轨迹 4-4 系统闭环零、极点分布与阶跃
响应的关系 4-5 系统阶跃响应的根轨迹分析
返回主目录
2
基本要求
1.正确理解开环零、极点和闭环零、极点以及主导极 点、偶极子等概念。
2.正确理解和熟记根轨迹方程(模方程及相角方程)。 熟练运用模方程计算根轨迹上任一点的根轨迹增益 和开环增益。
f
(s zi )
K
* G
i 1 q
(s pi )
i 1
(4-5)
12
K
G
为前向通道增益,K
* G
为前向通道根轨迹增益
KG*
KG
1
2…
2
T1 T22…
(4-6)
l
(s z j)
H
(s)
K
* H
j 1 h
(s p j)
j 1
(4-7)
式中:K
* H
为反馈通道的根轨迹增益。
13
f
l
(s zi) (s z j)
G
(s)H
(s)
K
* G
K
* H
i1 q
j1 l
(s pi ) (s p j)
i1
i1
f
l
(s zi ) (s z j)
K*
i1 q
j1 h
(s pi ) (s p j)
i1
j1
(4-8)
14
闭环传递函数
f h
(s zk )
(s)
K
* G
k 1 n
根轨迹法
1
主要内容
4-1 根轨迹与根轨迹方程 4-2 绘制根轨迹的基本法则 4-3 开环零、极点变化时的根轨迹 4-4 系统闭环零、极点分布与阶跃
响应的关系 4-5 系统阶跃响应的根轨迹分析
返回主目录
2
基本要求
1.正确理解开环零、极点和闭环零、极点以及主导极 点、偶极子等概念。
2.正确理解和熟记根轨迹方程(模方程及相角方程)。 熟练运用模方程计算根轨迹上任一点的根轨迹增益 和开环增益。
f
(s zi )
K
* G
i 1 q
(s pi )
i 1
(4-5)
12
K
G
为前向通道增益,K
* G
为前向通道根轨迹增益
KG*
KG
1
2…
2
T1 T22…
(4-6)
l
(s z j)
H
(s)
K
* H
j 1 h
(s p j)
j 1
(4-7)
式中:K
* H
为反馈通道的根轨迹增益。
13
f
l
(s zi) (s z j)
G
(s)H
(s)
K
* G
K
* H
i1 q
j1 l
(s pi ) (s p j)
i1
i1
f
l
(s zi ) (s z j)
K*
i1 q
j1 h
(s pi ) (s p j)
i1
j1
(4-8)
14
闭环传递函数
f h
(s zk )
(s)
K
* G
k 1 n
大学自动控制原理第四章根轨迹法资料

4.1.3 绘制根轨迹步骤
1)找出s平面上满足相角条件的点并连成曲线; 2)用幅值条件确定相应点对应的K值。 例3 求例1所示系统的根轨迹 解:开环传函 G(s)H (s) K
s(s 1)
1)用相角条件绘制根轨迹
arg s arg s 1 2k 1 , k 0,1, 2,
2)用幅值条件确定增益K
假设系统开环传递函数用零、极点形式表示:
G
s
H
s
K s s
z1 p1 s
s z2 p2
s zm ,n m s pn
m
令s zi ie ji , s pl le jl ,
i 1,2, , m;
GsH s K
l 1,2, , n。
m
n
i j( i l )
➢开环传递函数的零点s=-zi (i=1,…,m)是m条根轨 迹分支的终点
K0 zi
K
i 1 n
pl
l 1
绘制根轨迹的基本规则 规则1:根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征 根或为实数,或为共轭复数,根轨迹必然对称于s 平面的实轴。 规则2:根轨迹的分支数及其起点和终
n
m
闭环特征方程: s pl K0 s zi 0
l 1
i 1
➢当K0由0→∞变化时,方程中任一根由始点连续 地向终点变化的轨迹称为根轨迹的一条分支;
第一节 根轨迹的基本概念
1948年,伊凡思(W.R.Evans)根据控制系统的开环 传递函数与其闭环特征方程式之间的内在联系,提 出了根轨迹法。
4.1.1 根轨迹的定义
例1 对右图所示系统,求 当参变量K从0向变化时, 系统闭环特征根在复平面 上的变化轨迹。
自动控制原理第四章根轨迹法

当S→∞时(试验点设在无穷远处): (n-m)∠S = (2K+1)π
∠S =φa= (2K+1)π/(n-m) 无穷远处闭环极点的方向角,就是渐近线的方向角.
绘制根轨迹的基本法则
开环传递函数的标准形式举例
例:将下面的开环传递函数化成标准形式
10(5S+1)
10*5[S+(1/5)]
25/3(S+1/5)
G(S)H(S)= —————— = ————————— = ———-———
(2S+1)(3S+1) 2*3(S+1/2)(S+1/3) (S+1/2)(S+1/3)
K = 10 ————开环增益
根轨迹举例
由上述根轨迹图可知: 1.当开环增益由0到∞变化时,根轨迹均在S平面的左半部,
因此系统对所有K值都是稳定的。 2.当0<K<0.5时,闭环特征根为实根,系统呈过阻尼状
态,阶跃响应为非周期过程。
根轨迹举例
3.当K=0.5时,闭环特征根为重根,系统呈临界阻尼状态, 阶跃响应为非周期过程。
4.当K>0.5时,闭环特征根为共轭复根,系统呈欠阻尼状态, 阶跃响应为衰减振荡。
可以认为开环零点和极点到达Sn的矢量的长度是相等的。对 无穷远处的试验点Sn而言,所有的零极点都汇集到实轴上的 一点σa。
σa= Zi= Pi ΣPi-ΣZi = (n-m)σa σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
又: K*(S-Z1)(S-Z2)…(S-Zm) ——————————— = -1 (S-P1)(S-P2)…(S-Pn)
绘制根轨迹的基本法则
一对共轭的开环复数极点(或零点)对S1(在实轴上的试验 点)的相角等值反号,相互抵消;而开环复数极点(或零点)又 一定成对出现,所以实轴上的根轨迹与复数零(极)点无关。
∠S =φa= (2K+1)π/(n-m) 无穷远处闭环极点的方向角,就是渐近线的方向角.
绘制根轨迹的基本法则
开环传递函数的标准形式举例
例:将下面的开环传递函数化成标准形式
10(5S+1)
10*5[S+(1/5)]
25/3(S+1/5)
G(S)H(S)= —————— = ————————— = ———-———
(2S+1)(3S+1) 2*3(S+1/2)(S+1/3) (S+1/2)(S+1/3)
K = 10 ————开环增益
根轨迹举例
由上述根轨迹图可知: 1.当开环增益由0到∞变化时,根轨迹均在S平面的左半部,
因此系统对所有K值都是稳定的。 2.当0<K<0.5时,闭环特征根为实根,系统呈过阻尼状
态,阶跃响应为非周期过程。
根轨迹举例
3.当K=0.5时,闭环特征根为重根,系统呈临界阻尼状态, 阶跃响应为非周期过程。
4.当K>0.5时,闭环特征根为共轭复根,系统呈欠阻尼状态, 阶跃响应为衰减振荡。
可以认为开环零点和极点到达Sn的矢量的长度是相等的。对 无穷远处的试验点Sn而言,所有的零极点都汇集到实轴上的 一点σa。
σa= Zi= Pi ΣPi-ΣZi = (n-m)σa σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
又: K*(S-Z1)(S-Z2)…(S-Zm) ——————————— = -1 (S-P1)(S-P2)…(S-Pn)
绘制根轨迹的基本法则
一对共轭的开环复数极点(或零点)对S1(在实轴上的试验 点)的相角等值反号,相互抵消;而开环复数极点(或零点)又 一定成对出现,所以实轴上的根轨迹与复数零(极)点无关。
自动控制原理根轨迹

自动控制原理根轨迹自动控制系统的根轨迹是描述系统稳定性和性能的重要工具之一。
根轨迹是以闭环传递函数的极点和零点的运动轨迹形状为基础绘制而成的。
在绘制根轨迹时,假设系统的闭环传递函数为G(s),其极点和零点分别为p1, p2, ..., pn和z1, z2, ..., zm。
根轨迹将从零点或者无穷远点开始,经过一系列的线段和曲线,最终到达极点或无穷远点。
根轨迹的演变与系统的开环传递函数有关,而开环传递函数可以表示为G(s) = K(s + z1)(s + z2)...(s + zm)/(s + p1)(s + p2)...(s + pn),其中K是系统的增益。
根轨迹的绘制规则如下:1. 根轨迹总是从系统的零点(实部为负的零点或倾角为奇数倍的复的零点)或者无穷远点开始。
2. 根轨迹图的总数等于系统的开环极点数和零点数之差。
3. 根轨迹的虚轴交点总数等于零点数和极点数之差的绝对值。
4. 根轨迹总是对称于实轴。
5. 根轨迹总是在实轴的左半平面。
通过绘制根轨迹,可以分析系统的稳定性和性能。
当根轨迹与虚轴相交时,系统就有可能发生震荡或振荡。
当根轨迹与实轴相交时,可以得到系统的过渡过程、稳态误差以及系统的稳定性等信息。
绘制根轨迹可以通过手绘或者使用计算机辅助工具进行。
一般来说,使用计算机辅助工具可以更加方便和准确地绘制根轨迹,并且可以对参数和增益进行调整来观察系统的性能变化。
常用的计算机辅助工具有MATLAB、Simulink等。
总之,根轨迹是描述自动控制系统稳定性和性能的重要工具,可以通过绘制闭环传递函数的极点和零点的运动轨迹来得到。
绘制根轨迹可以用于分析系统的震荡性质、过渡过程、稳定性和稳态误差等,并可以通过调整参数和增益来改善系统的性能。
自动控制原理第4章-根轨迹

zl
1800
m
( zl
j 1 jl
zj)
n
( zl
j 1
p
j
)
第四章 根轨迹法
4.2.3 绘图示例
G(s)H (s)
K
s(s 1)(s 2)
闭环特征方程 : s3 3s2 2s K 0
按7个基本规则绘制根轨迹图:
首先,系统有三个无穷远
零点,有三个开环极点:
p1=0,p2=-1,p3=-2,将它们 标在复平面上。
第四章 根轨迹法
7、 根轨迹的出射角和入射角
根轨迹从某个开环极点出发时的切线与正实轴的夹角称
为出射角,根轨迹从开环极点pi出发的出射角为:
pi
1800
m
( pi
j 1
zj)
n
( pi
j 1
p
j
)
ji
根轨迹进入某个开环零点的切线与正实轴的夹角称为 入射角,根轨迹进入开环零点Zl的入射角为:
根据规则1)和2),根轨
迹将有3支,分别开始于这
三个开环极点,趋向无穷
远。
第四章 根轨迹法
根据规则3),根轨迹有3根渐近线,它们与实轴的夹角是:
k
(2k
1)1800 3
,
k 0,1,2
0 600 ,1 1800 ,2 3000
所有渐近线交于实轴上 的一点,其坐标为:
0 1 2 1
3
1 K (s z1 )(s z2 )....(s zm ) 0 (s p1 )(s p2 )....(s pn )
m
上式变形: K (s zl )
l 1 n
1 0 ——典型根轨迹方程
(s pi )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
55、 为 中 华 之 崛起而 读书。 ——周 恩来
自动控制原理简明版根轨迹法
1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——波 洛克Fra bibliotek谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
自动控制原理简明版根轨迹法
1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——波 洛克Fra bibliotek谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
