第9周电子表格强化练习
艾宾浩斯表格周计划52周364天

周数
学习日期 序号
第1周 第2周
月 日
1
月 日
2
月 日
3
月 日
4
月 日
5
月 日
6
月 日
7
月 日
8
月 日
9
月 日
10
月 日11Fra bibliotek月 日
12
月 日
13
月 日
14
月 日
15
复习计划表
学习内容
第 1 页,共 25 页
长期记忆复习周期(复习后打 钩)
1天 2天 4天 7天 15天 1个月 3个月 6个月
-------1------21-----32-----431----542----653----7641---8752---9863---10 9 7 4 - - - 11 10 8 5 - - - 12 11 9 6 - - - 13 12 10 7 - - - 14 13 11 8 - - - -
目标:
周数
学习日期 序号
第20周 第21周 第22周
月 日
136
月 日
137
月 日
138
月 日
139
月 日
140
月 日
141
月 日
142
月 日
143
月 日
144
月 日
145
月 日
146
月 日
147
月 日
148
月 日
149
月 日
150
复习计划表
学习内容
第 10 页,共 25 页
长期记忆复习周期(复习后打 钩)
目标:
周数
周例会表格

会议主题
序号完成情况
1234
5678
910序号1234
5678910
会议主题
序号完成情况
1234
5678
周例会会议
上周例会
上周讨论结果
本周例会
讨论主题第一周
周例会会议
上周例会
上周讨论结果
910序号1234
5678910
会议主题
序号完成情况
1234
5678
910序号1234
56789
本周例会
讨论主题
本周例会
讨论主题
第三周周例会会议
上周例会
上周讨论结果
第二周
10
会议主题
序号完成情况
1234
5678
910序号1234
5678910
本周例会
讨论主题第四周
周例会会议
上周例会
上周讨论结果
完成时间
完成时间
未完成理由
会会议纪要
讨论结果主要负责人会会议纪要
处理意见
未完成理由
处理意见
协助负责人要求完成日
会议时间
会议时间
完成时间
讨论结果主要负责人讨论结果会会议纪要
主要负责人未完成理由
处理意见
协助负责人要求完成日
会议时间
协助负责人要求完成日
完成时间
讨论结果主要负责人会会议纪要
协助负责人要求完成日
未完成理由
会议时间
处理意见
负责人完成日期
负责人
完成日期
负责人完成日期
负责人完成日期。
2021-2022年小学数学三年级下册提优强化专项训练第九章《数据的收集和整理二》(苏教版含解析)

苏教版数学三年级下册提优强化专项训练第九章《数据的收集和整理(二)》一、单选题1.下面是我们学校三年级植树情况统计表,4个班平均植树()棵。
A. 7B. 8C. 9D. 4【答案】A【解析】【解答】(9+4+7+8)÷4=7(棵)2.红红调查同学们最喜欢吃的水果,结果如下。
喜欢吃香蕉的有()人。
A. 12B. 8C. 7D. 15【答案】A【解析】【解答】喜欢吃香蕉的有12人。
3.红红调查同学们最喜欢吃的水果,结果如下:从统计图汇总可以看出,红红调查了()名同学。
A. 40B. 41C. 42【答案】C【解析】【解答】将喜欢各种水果的人数加起来就是调查的总人数8+12+5+7+10=42,故选C4.学校有8个班参加了回收废报纸活动。
第一天回收废报纸43千克;第二天回收废报纸38千克;第三天回收废报纸39千克。
平均每天回收废报纸()千克。
A. 39B. 40C. 41D. 42【答案】B【解析】【解答】(43+38+39)÷3=40(千克)5.下面是某年级(二)班同学对水果的爱好情况统计表。
爱好()的人最多,爱好()的人最少。
A. 苹果、香蕉B. 梨、香蕉C. 苹果、梨【答案】C【解析】【解答】可以看出苹果有18人,喜欢梨的有9人,喜欢香蕉的有10人,喜欢桃的有15人,所以正确选择C6.小明的期末成绩如下:语文数学英语自然科学95 87 82 89那么小明得分最高的学科是哪一科比得分最低的学科多几分()A. 语文、13B. 语文、8C. 自然科学、12【答案】A【解析】【解答】语文得分最高为95,英语最低为82,95-82=13 【分析】考查数据的整理和计算7.老师要给演讲比赛中得奖的同学发奖励,买了两个笔记本,一本字典,五支铅笔,其中得奖的有10名同学,老师应该再买()个奖品才能保证每位同学都得到奖励A. 1B. 2C. 3【答案】B【解析】【解答】老师一共买了2+1+5=8个奖品,还缺少10-8=2个。
excel练习题

●注意:全文内容、位置不得随意变动;
红框之内的文字不得做任何修改。
1.按“班级”从小到大和按“姓名”字母顺序递增排序
2.按作业的周次从小到大将作业得分情况排序
3.将所有学生四次作业成绩合计起来,填入相应单元格中
4.将成绩低于60分的所有单元格底纹颜色改为“红色”
5.筛选出四次绘画作业得分都不低于90分的学生,并将学生姓名填入下面绿色单元格内:
学生姓名:
6.将以下列表格中的“丁晓雪”同学周1至周4四次作业得分作为数据源,制作一个嵌入式折线来表示该同学从周1至周4作业得分的变化情况
绘图作业得分情况
班级姓名周3周1周4周2作业得分合计
1孙莹98758474
2吕鹏92686072
3刘成雪88688486
1祖华93765984
2范恩良82985474
3刘晓91919094
1刘春臻92947576
2刘双会87587591
3赵洪霞90778787
1刘凯99457881
2李萌86658579
3夏家丽85527586
1刘洋88737084
2王明英87706782
3安慧79568487
1朱祥娇89378086
2公维鑫73646682
3刘越87505673
1刘召华77486285
2张慧90597384
3张德柱78764574
1孙晶晶82487886
2马强强81814680
3于通76937372
1王菲96397782
2张鹏76534978
3王浩69506281
1刘艳79397773
2张悦74797473
3王慧兰76505488
1丁晓雪72786471
式折线图,。
电子表格Excel操作题4.Excel操作题练习四Excel题4

打开“4.Excel操作题练习四”下的文件"Excel素材4.xls"(如下给出效果图),并完成以下操作,最后以原文件名保存。
①将sheet1工作表标签命名为score1
②设置“班级学习成绩表”为A1:E1区域居中(只考虑水平居中),并将字体加粗、字号为20磅;将“高一”和“高二”分别在B2:C2和D2:E2区域调整为居中显示并设置字体为加粗、字号为16磅以及设置品红色底纹(图案),各班级标题居中、加粗,其余各单元格采用常规格式,最后将A2:A3单元格合并。
③在A2:E6区域,设置边框线,要求是:外粗线内细线。
④通过条件格式设置,在成绩区当分数为不及格(<60)时则采用红色和单下划线显示。
⑤在原有的3个工作表sheet1、sheet2、sheet3的基础上,在后面依次插入工作表sheet4、sheet5、sheet6。
然后依次删除工作表sheet2、sheet4、sheet6。
并保留下来的工作表score1、sheet3、sheet5的标签颜色依次地设置为红色、黄色和蓝色。
【工作表】。
Excel电子表格(教案)

Excel电子表格一、教学目标1. 让学生了解Excel电子表格的基本概念和功能。
2. 培养学生掌握Excel的基本操作技巧。
3. 让学生能够运用Excel解决实际问题。
二、教学内容1. Excel的基本概念和界面布局2. 数据输入与编辑3. 单元格格式设置4. 公式与函数的使用5. 数据排序与筛选三、教学重点与难点1. Excel的基本概念和界面布局2. 数据输入与编辑3. 公式与函数的使用4. 数据排序与筛选四、教学方法1. 讲授法:讲解Excel的基本概念、界面布局、数据输入与编辑、公式与函数的使用、数据排序与筛选等知识点。
2. 示范法:通过示范操作,展示Excel的各种操作步骤和技巧。
3. 练习法:让学生通过实际操作,巩固所学知识。
4. 讨论法:组织学生进行小组讨论,分享学习心得和解决问题的方法。
1. 安装有Excel的计算机2. 投影仪或白板3. 教学PPT4. 练习数据和案例5. 教学笔记板书工具教案内容请参考下篇。
六、教学过程1. 导入:通过展示实际案例,引发学生对Excel电子表格的兴趣,激发学习动机。
2. 新课内容:讲解Excel的基本概念、界面布局、数据输入与编辑、公式与函数的使用、数据排序与筛选等知识点。
3. 示范操作:演示Excel的各种操作步骤和技巧,让学生清晰地了解操作方法。
4. 练习:学生通过实际操作,巩固所学知识。
教师巡回指导,解答学生的问题。
5. 小组讨论:组织学生进行小组讨论,分享学习心得和解决问题的方法。
6. 总结与拓展:总结本节课所学内容,布置课后作业,鼓励学生进行拓展学习。
七、教学评价1. 课堂参与度:观察学生在课堂上的积极参与程度,了解他们的学习兴趣。
2. 操作练习:检查学生的操作练习结果,评估他们掌握Excel技能的程度。
3. 小组讨论:评价学生在小组讨论中的表现,了解他们的合作能力和解决问题的能力。
4. 课后作业:通过课后作业的完成情况,评估学生对课堂所学知识的巩固程度。
1_语文7~9年级古诗词打卡记录表格(2021

长期记忆复习周期
1天 完成 2天 完成 3-4天 完成 5-7天 完成 15天 完成 30天 完成 60天 完成
85
84
82
79
71
56
27
86
85
83
80
72
57
28
87
86
84
81
73
58
29
88
87
85
82
74
59
30
89
88
86
83
75
60
31
90
89
87
84
76
61
32
91
90
88
85
77
第8周 53
54 55 56
学习内容
登幽州台歌 望岳
登飞来峰 游山西村 已亥杂诗 河中石兽 泊秦淮
贾生 过松源晨炊漆公店
约客 三峡 答谢中书书 记承天寺夜游 与朱元思书 野望 黄鹤楼 使至塞上 渡荆门送别 钱塘湖春行 庭中有奇树 龟虽寿 赠从弟 梁甫行 得道多助,失道寡助 富贵不能淫 生于忧患死于安乐 愚公移山 昼夜夫军细柳
1天 完成 2天 完成 3-4天 完成 5-7天 完成 15天 完成 30天 完成 60天 完成
99
84
55
100
85
56
86
57
87
58
88
59
89
60
90
61
91
62
92
63
93
64
94
65
95
66
96
67
97
68
98
69
2021秋九上册阶段强化专训新版沪科版

阶段强化专训一:二次函数的图象与系数的关系名师点金:二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象有着密切的关系:a 的取值决定了开口方向和开口大小,a,b的取值影响对称轴的位置,c的取值决定了抛物线与y轴的交点位置,所以a,b,c这三个系数共同决定着抛物线的位置和大小,反之也可以根据二次函数图象情况确定a,b,c的系数符号或大小.a与图象的关系1.如图所示,四个函数的图象,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2,则a,b,c,d的大小关系为( )A.a>b>c>d B.a>b>d>cC.b>a>c>d D.b>a>d>c(第1题)2.在抛物线y=mx2与抛物线y=nx2中,若-m>n>0,则开口向上的抛物线是________,开口较大的抛物线是________.b与图象的关系(第3题)3.若二次函数y=3x2+(b-3)x-4的图象如图所示,则b的值是( )A.-5 B.0 C.3 D.44.当抛物线y=x2-nx+2的对称轴是y轴时,n______0;当对称轴在y轴左侧时,n______0;当对称轴在y轴右侧时,n______0.(填“>”“<”或“=”)c 与图象的关系5.下列抛物线可能是y =ax 2+bx 的图象的是( )6.若将抛物线y =ax 2+bx +c -3向上平移4个单位长度后得到的图象如图所示,则c =________.(第6题)(第7题)a ,b 与图象的关系7.二次函数y =ax 2+bx +c 的图象如图所示,则下列说法中不正确的是( )A .a >0B .b <0C .3a +b >0D .b >-2a8.如果抛物线y =m 2x 2+(n +2)x -5的对称轴是x =-32,则(3m -2n)2-2n +43m 的值为________.a ,c 与图象的关系9.二次函数y =(3-m)x 2-x +n +5的图象如图所示,试求(m -3)2+n 2-|m +n|的值.(第9题)a ,b ,c 与图象的关系10.在二次函数y =ax 2+bx +c 中,a <0,b >0,c <0,则符合条件的图象是( )(第11题)11.已知二次函数y =ax 2+bx +c(a≠0)的图象如图所示,对称轴为直线x =-12,下列结论中正确的是( )A .abc >0B .a +c =0C .b =2aD .4a +c =2b阶段强化专训二:求二次函数表达式的常见类型名师点金:求二次函数的表达式是解决二次函数问题的重要保证,在求解二次函数的表达式时一般选用待定系数法,但在具体题目中要根据不同条件,设出恰当的表达式,往往可以给解题过程带来简便.由函数的基本形式求表达式方法1 利用一般式求二次函数表达式1.已知一个二次函数的图象经过点A(1,0),点B(0,6)和点C(4,6),则这个抛物线的表达式为________.2.一个二次函数,当自变量x=-1时,函数值y=2;当x=0时,y=-1;当x=1时,y=-2.那么这个二次函数的表达式为______________.3.如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的表达式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.(第3题)方法2利用顶点式求二次函数表达式4.已知二次函数y=ax2+bx+c,当x=1时,有最大值8,其图象的形状、开口方向与抛物线y=-2x2相同,则这个二次函数的表达式是( )A.y=-2x2-x+3 B.y=-2x2+4C.y=-2x2+4x+8 D.y=-2x2+4x+65.已知某个二次函数的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6).求二次函数表达式.方法3利用交点式求二次函数表达式6.已知抛物线与x轴交于A(1,0),B(-4,0)两点,与y轴交于点C,且AB=BC,求此抛物线对应的函数表达式.方法4利用平移式求二次函数表达式7.(2015·绥化)把二次函数y=2x2的图象向左平移1个单位,再向下平移2个单位长度,平移后抛物线的表达式是______________.8.已知y=x2+bx+c图象向右平移2个单位,再向下平移3个单位,得到图象的表达式为y=x2-2x-3.(1)b=________,c=________;(2)求原函数图象的顶点坐标;(3)求两个图象顶点之间的距离.方法5利用对称轴法求二次函数表达式(第9题)9.如图,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数表达式是________.10.如图所示,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),抛物线的对称轴是直线x=-1 2 .(1)求抛物线的表达式;(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求点M的坐标.(第10题)方法6 灵活运用方法求二次函数的表达式11.已知抛物线的顶点坐标为(-2,4),且与x 轴的一个交点坐标为(1,0),求抛物线对应的函数表达式.由函数图象中的信息求表达式(第12题)12.如图,是某个二次函数的图象,根据图象可知,该二次函数的表达式是( )A .y =x 2-x -2B .y =-12x 2-12x +2 C .y =-12x 2-12x +1 D .y =-x 2+x +213.(2015·南京)某企业生产并销售某种产品,假设销售量与产量相等.下图中的折线ABD ,线段CD 分别表示该产品每千克生产成本y 1(单位:元),销售价y 2(单位:元)与产量x(单位:kg )之间的函数关系.(1)请解释图中点D 的横坐标、纵坐标的实际意义; (2)求线段AB 所表示的y 1与x 之间的函数表达式;(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?(第13题)由表格信息求表达式14.若y=ax2+bx+c,则由表格中信息可知y与x之间的函数关系式是( )x -1 0 1ax2 1ax2+bx+c 8 3A.y=x2-4x+3 B.y=x2-3x+4C.y=x2-3x+3 D.y=x2-4x+815.已知二次函数y=ax2+bx+c(a≠0)自变量x和函数值y的部分对应值如下表:x …-32-1 -1212132…y …-54-2 -94-2 -5474…则该二次函数的表达式为______________.几何应用中求二次函数的表达式16.如图,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线的表达式.(第16题)实际问题中求二次函数表达式17.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m,花园的面积为S.(1)求S与x之间的函数表达式;(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.(第17题)阶段强化专训三:二次函数图象信息题的四种常见类型名师点金:利用图象信息解决二次函数的问题主要是运用数形结合思想将图象信息转换为数学语言,掌握二次函数的图象和性质,把握二次函数的特点是解决此类问题的关键.根据抛物线的特征确定a,b,c及与其有关的代数式的符号1.(2015·孝感)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①a bc<0;②b2-4ac4a>0;③ac-b+1=0;④OA·OB=-ca.其中正确结论的个数是( )A.4 B.3 C.2 D.1(第1题)(第2题)利用二次函数的图象比较大小2.二次函数y=-x2+bx+c的图象如图,若点A(x1,y1),B(x2,y2)在此函数图象上,且x1<x2<1,则y1与y2的大小关系是( )A.y1≤y2B.y1<y2C.y1≥y2D.y1>y2利用二次函数的图象求方程或不等式的解3.(2014·黄石)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则当函数值y>0时,x的取值范围是( )A.x<-1 B.x>3C.-1<x<3 D.x<-1或x>3(第3题)(第4题)4.如图所示,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( ) A.-1≤x≤9 B.-1≤x<9C.-1<x≤9 D.x≤-1或x≥95.(2014·阜新)如图,二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是____________.(第5题)根据抛物线的特征确定其他函数的图象6.(中考·聊城)二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是( )(第6题)7.如图,A(-1,0),B(2,-3)两点在一次函数y1=-x+m与二次函数y2=ax2+bx -3的图象上.(1)求m的值和二次函数的解析式.(2)设二次函数的图象交y轴于点C,求△ABC的面积.(第7题)阶段强化专训四:用二次函数解决问题的三种类型名师点金:利用二次函数解决实际问题时,要注意数形结合,巧妙地运用二次函数解析式实行建模,从而达到应用二次函数的某些性质来解决问题的目的.建立平面直角坐标系解决实际问题题型1 拱桥(隧道)问题1.有一拱桥呈抛物线形状,这个桥洞的最大高度是16 m ,跨度为40 m ,现把它的示意图(如图所示)放在坐标系中,则抛物线的解析式为( )A .y =125x 2+58xB .y =-58x 2-125x C .y =-125x 2+85x D .y =-125x 2+85x +16(第1题)(第2题)2.如图,拱桥呈抛物线形,其函数的解析式为y =-14x 2,当水位线在AB 位置时,水面的宽度为12米,这时拱顶距水面的高度h 是________米.3.如图是某地区一条公路上隧道入口在平面直角坐标系中的示意图,点A 和A 1、点B 和B 1分别关于y 轴对称.隧道拱部分BCB 1为一段抛物线,最高点C 离路面AA 1的距离为8 m ,点B 离路面AA 1的距离为6 m ,隧道宽AA 1为16 m .(1)求隧道拱部分BCB 1对应的函数解析式.(2)现有一大型货车,装载某大型设备后,宽为4 m ,装载设备的顶部离路面均为7 m ,问:它能否安全通过这个隧道?并说明理由.(第3题)题型2 建筑物问题4.如图所示,某大学的楼门是一抛物线形水泥建筑物,大门的地面宽度为8 m ,两侧距离地面4 m 高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6 m ,则校门的高约为(精确到0.1 m ,水泥建筑物的厚度忽略不计)( )A .9.2 mB .9.1 mC .9.0 mD .8.9 m(第4题)(第5题)5.某公园草坪的防护栏由100段形状相同的抛物线组成,为了牢固,每段防护栏需要间距0.4 m 加设一根不锈钢的支柱,防护栏的最高点到底部距离为0.5 m (如图),则这条防护栏需要不锈钢支柱的总长度为( )A .50 mB .100 mC .160 mD .200 m题型3 物体运动类问题(第6题)6.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为y =-18x 2+12x +32,那么铅球运动过程中最高点离地面的距离为________米.7.如图,在水平地面点A 处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB 上点C(靠点B 一侧)处竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB =4米,AC =3米,网球飞行最大高度OM =5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).(1)如果竖直摆放5个圆柱形桶,网球能不能落入桶内? (2)当竖直摆放多少个圆柱形桶时,网球可以落入桶内?(第7题)建立二次函数模型解决几何最值问题题型1利用二次函数解决图形高度的最值问题8.某人从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球的运动时间t(单位:秒)之间的关系式是h=9.8t-4.9t2,那么小球运动中的最大高度为________.(第9题)9.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的高度为________米.题型2利用二次函数解决图形面积的最值问题(第10题)10用长8 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是( )A.6425m2B.43m2C.83m2D.4 m211.如图所示,正方形ABCD的边长为3a,两动点E,F分别从顶点B,C同时开始以相同速度沿边BC,CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B,E,C,G在一条直线上.(1)若BE=a,求DH的长.(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.(第11题)建立二次函数模型解决动点探究问题12.如图所示,直线y =12x -2与x 轴、y 轴分别交于点A ,C ,抛物线过点A ,C 和点B(1,0).(1)求抛物线的解析式;(2)在x 轴上方的抛物线上有一动点D ,当D 与直线AC 的距离DE 最大时,求出点D 的坐标,并求出最大距离.(第12题)阶段强化专训五:求反比例函数表达式的六种方法名师点金:确定反比例函数的表达式,关键是确定比例系数k 的值.求比例系数k 的值,可以根据反比例函数的定义及其性质列方程、不等式求解,可以根据图象中点的坐标求解,可以直接根据数量关系列表达式,也可以利用待定系数法求解,还可以利用比例系数k 的几何意义求解.其中待定系数法是常用方法.利用反比例函数的定义求表达式1.若y =(m +3)xm 2-10是反比例函数,试求其函数表达式.利用反比例函数的性质求表达式2.已知函数y =(n +3)xn 2+2n -9是反比例函数,且在每一个象限内,y 随x 的增大而减小,求其函数表达式.利用反比例函数的图象求表达式3.(2015·广安)如图,一次函数的图象与x 轴、y 轴分别相交于A 、B 两点,且与反比例函数y =kx (k≠0)的图象在第一象限交于点C ,如果点B 的坐标为(0,2),OA =OB ,B 是线段AC 的中点.求:(1)点A 的坐标及一次函数表达式; (2)点C 的坐标及反比例函数表达式.(第3题)利用待定系数法求表达式4.已知y 1与x 成正比例,y 2与x 成反比例,若函数y =y 1+y 2的图象经过点(1,2),⎝ ⎛⎭⎪⎫2,12,求y 与x 的函数表达式.利用图形的面积求表达式5.如图,点A 在双曲线y =1x 上,点B 在双曲线y =kx 上,且AB∥x 轴,C ,D 两点在x轴上,若矩形ABCD 的面积为6,求B 点所在双曲线的函数表达式.(第5题)利用实际问题中的数量关系求表达式6.某运输队要运300 t 物资到江边防洪.(1)运输时间t(单位:h )与运输速度v(单位:t /h )之间有怎样的函数关系?(2)运了一半时,接到防洪指挥部命令,剩下的物资要在2 h 之内运到江边,则运输速度至少为多少?阶段强化专训六:用反比例函数系数k 的几何意义解与面积相关问题名师点金:反比例函数的比例系数k 具有一定的几何意义,|k|等于反比例函数图象上任意一点向两坐标轴所作垂线段与坐标轴所围成的矩形的面积.在反比例函数的图象中,涉及三角形或矩形的面积时,常用比例系数k 的几何意义求解.)反比例函数的比例系数k 与面积的关系1.如图,点P 在反比例函数y =3x (x >0)的图象上,横坐标为3,过点P 分别向x 轴,y轴作垂线,垂足分别为M ,N ,则矩形OMPN 的面积为( )A .1B .2C .3D .4(第1题)(第2题)2.如图,P 是反比例函数y =kx 的图象上一点,过P 点分别向x 轴,y 轴作垂线,所得到的图中阴影部分的面积为6,则这个反比例函数的表达式为( )A .y =-6xB .y =6xC .y =-3xD .y =3x3.如图,A ,C 是函数y =1x 的图象上任意两点,过点A 作y 轴的垂线,垂足为B ,过点C 作y 轴的垂线,垂足为D ,记Rt △AOB 的面积为S 1,Rt △COD 的面积为S 2,则( )A .S 1>S 2B .S 1<S 2C .S 1=S 2D .S 1和S 2的大小关系不能确定(第3题)(第4题)4.如图,正比例函数y =x 与反比例函数y =1x 的图象相交于A ,B 两点,BC⊥x 轴于点C ,则△ABC 的面积为( )A .1B .2C .3D .45.如图,函数y =-x 与函数y =-4x 的图象相交于A ,B 两点,过A ,B 两点分别作y轴的垂线,垂足分别为点C ,D ,则四边形ACBD 的面积为( )A .2B .4C .6D .8(第5题)(第6题)6.如图,Rt △AO B 的一条直角边OB 在x 轴上,双曲线y =kx 经过斜边OA 的中点C ,与另一直角边交于点D.若S △OCD =9,则S △OBD =________.已知面积求反比例函数表达式题型1 已知三角形面积求表达式7.已知:如图,在平面直角坐标系xOy 中,直线AB 与x 轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连接BO ,若S △AOB =4.(1)求该反比例函数的表达式和直线AB 的函数表达式; (2)若直线AB 与y 轴的交点为C ,求△OCB 的面积.(第7题)题型2 已知四边形面积求表达式8.如图,矩形ABOD 的顶点A 是函数y =kx 与函数y =-x -(k +1)在第二象限的图象的交点,AB⊥x 轴于B ,AD⊥y 轴于D ,且矩形ABOD 的面积为3.(1)求两函数的表达式;(2)求两函数图象的交点A ,C 的坐标;(3)若点P 是y 轴上一动点,且S △APC =5,求点P 的坐标.(第8题)已知反比例函数表达式求图形的面积题型1 利用表达式求面积9.(2015·安徽)如图,已知反比例函数y =k 1x 与一次函数y =k 2x +b 的图象交于A(1,8),B(-4,m).(1)求k 1、k 2、b 的值; (2)求△AOB 的面积;(3)若M(x 1,y 1)、N(x 2,y 2)是反比例函数y =k 1x 的图象上的两点,且x 1<x 2,y 1<y 2,指出点M ,N 各位于哪个象限,并简要说明理由.(第9题)题型2 利用对称性求面积10.如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线函数表达式分别为y =-6x ,y =6x ,现用四根钢条固定这四条曲线.这种钢条加工成矩形产品按面积计算,每单位面积25元,请你帮助工人师傅计算一下,所需钢条一共花多少钱?(第10题)题型3 利用点的坐标及面积公式求面积11.如图,直线y =k 1x +b 与反比例函数y =k 2x (x <0)的图象相交于点A ,点B ,与x 轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4.(1)试确定反比例函数的表达式; (2)求△AOC 的面积.(第11题)阶段强化专训七:巧用一元二次方程的判别式解反比例函数图象的公共点问题名师点金:解反比例函数与一次函数的图象的公共点问题,可转化为一元二次方程根的情况 ,用判别式来辅助计算.有两个公共点,则判别式大于0;有一个公共点,则判别式等于0;没有公共点,则判别式小于0.无公共点(Δ<0)(第1题)1.关于x 的反比例函数y =a +4x的图象如图,A ,P 为该图象上的点,且关于原点成中心对称.在△PAB 中,PB∥y 轴,AB∥x 轴,PB 与AB 相交于点B.若△PAB 的面积大于12,则关于x 的方程(a -1)x 2-x +14=0的根的情况是________________.2.若反比例函数y =k x 的图象经过点P(a ,b),且a ,b 为一元二次方程x 2+kx +4=0的两根,那么点P 的坐标是________,到原点的距离为________.3.若反比例函数y =kx 与一次函数y =x +2的图象没有公共点,则k 的取值范围是________.有唯一公共点(Δ=0)4.如图,将直线y =x 沿x 轴负方向平移4个单位后,恰好与双曲线y =mx (x <0)有唯一公共点A ,并交双曲线y =nx(x >0)于B 点,若y 轴平分△AOB 的面积,求n 的值.(第4题)有两个公共点(Δ>0)5.如图,已知一次函数y =-x +8和反比例函数y =kx (k≠0)的图象在第一象限内有两个不同的公共点A ,B.(1)求实数k 的取值范围;(2)若△AOB 的面积为24,求k 的值.(第5题)有公共点(Δ≥0)(第6题)6.(2015·绍兴)在平面直角坐标系的第一象限内,边长为1的正方形ABCD 的边均平行于坐标轴,A 点的坐标为(a ,a).如图,若双曲线y =3x (x >0)与此正方形的边有交点,则a的取值范围是________.7.如图,过点C(1,2)分别作x 轴,y 轴的平行线,交直线y =-x +6于点A ,B ,若反比例函数y =kx(x >0)的图象与△ABC 有公共点,求k 的取值范围.(第7题)答案阶段强化专训一1.A 点拨:本题运用数形结合思想,在二次函数y =ax 2的图象中,|a|越大,图象的开口越小,所以①,②中,a >b >0,③,④中,d <c <0,所以a >b >c >d ,故选A .2.y =nx 2;y =mx 23.x <b a4.C 点拨:∵二次函数y =3x 2+(b -3)x -4的图象关于y 轴对称,∴b -3=0,b =3.5.=;<;>6.D 点拨:抛物线y =ax 2+bx 的图象一定经过原点. 7.1 8.D9.15 点拨:由题意得-n +2m =-32,∴3m -2n =4,3m =2n +4,∴(3m -2n)2-2n +43m =42-1=15.10.解:由图象知⎩⎪⎨⎪⎧3-m >0,n +5<0,解得⎩⎪⎨⎪⎧m <3,n <-5.∴m-3<0,m +n <-2.∴(m -3)2+n2-|m +n|=3-m -n +m +n =3.11.D12.D 点拨:由二次函数知a >0,c <0,由对称轴为直线x =-12,得-b 2a =-12,∴b=a >0,∴abc <0,∴A 选项不正确;∵抛物线经过(1,0),∴a +b +c =0,∴a +c =-b <0,故B 选项不正确;由b =a 知C 选项不正确;由对称轴为直线x =-12,且二次函数图象与x 轴一个交点为(1,0),知另一交点为(-2,0),∴4a -2b +c =0,∴4a +c =2b ,故D 选项不正确.阶段强化专训二1.y =2x 2-8x +6 2.y =x 2-2x -13.解:(1)把A(-2,-4),O(0,0),B(2,0)三点的坐标代入y =ax 2+bx +c 中,得⎩⎪⎨⎪⎧4a -2b +c =-4,4a +2b +c =0,c =0,解这个方程组,得⎩⎪⎨⎪⎧a =-12,b =1,c =0.所以解析式为y =-12x 2+x.(2)由y =-12x 2+x =-12(x -1)2+12,可得抛物线的对称轴为直线x =1,并且对称轴垂直平分线段OB , ∴OM =BM. ∴OM +AM =BM +AM.连接AB 交直线x =1于M 点,则此时OM +AM 最小.过点A 作AN⊥x 轴于点N ,在Rt △ABN 中,AB =AN 2+BN 2=42+42=42,因此OM +AM 的最小值为4 2.4.D5. 解:设二次函数图象的顶点坐标为(x ,2),则2=x +1,所以x =1,所以图象的顶点为(1,2).设二次函数的解析式为y =a(x -1)2+2,将(3,-6)代入上式,可得a =-2.所以该函数的解析式为y =-2(x -1)2+2,即y =-2x 2+4x.6.解:由A(1,0),B(-4,0)可知AB =5,OB =4. 又∵BC=AB ,∴BC =5.在Rt △BCO 中,OC =BC 2-OB 2=52-42=3, ∴C 点的坐标为(0,3)或(0,-3).设抛物线对应的函数解析式为y =a(x -1)(x +4),将点(0,3)的坐标代入得3=a(0-1)(0+4),解得a =-34;将点(0,-3)的坐标代入得-3=a(0-1)(0+4),解得a =34.∴该抛物线对应的函数解析式为y =-34(x -1)(x +4)或y =34(x -1)(x +4),即y =-34x 2-94x +3或y =34x 2+94x -3.点拨:若给出抛物线与x 轴的交点坐标或对称轴及抛物线与x 轴的两交点间的距离,通常可设交点式求解.7.y =2x 2+4x 8.解:(1)2;0(2)原函数的解析式为y =x 2+2x =(x +1)2-1. ∴其图象的顶点坐标为(-1,-1).(3)原图象的顶点为(-1,-1),新图象的顶点为(1,-4).由勾股定理易得两个顶点之间的距离为13.9.y =-x 2+2x +310.解:(1)设抛物线的解析式为y =a ⎝ ⎛⎭⎪⎫x +122+k. 把点(2,0),(0,3)的坐标代入得⎩⎪⎨⎪⎧254a +k =0,14a +k =3,解得⎩⎪⎨⎪⎧a =-12,k =258,∴y =-12⎝ ⎛⎭⎪⎫x +122+258,即y =-12x 2-12x +3.(2)由y =0,得-12⎝ ⎛⎭⎪⎫x +122+258=0,∴x 1=2,x 2=-3,∴B(-3,0).①当CM =BM 时,∵BO =CO =3,即△BOC 是等腰直角三角形,∴当M 点在原点O 处时,△MBC 是等腰三角形,∴M 点坐标为(0,0).②当BC =BM 时,在Rt △BOC 中,BO =CO =3,由勾股定理得BC =OC 2+OB 2=32,∴BM =32,∴M 点坐标为(32-3,0).综上所述,点M 坐标为(0,0)或(32-3,0). 点拨:本题求点M 坐标时运用了分类讨论思想.11.解:方法一:设抛物线对应的函数解析式为y =ax 2+bx +c ,由题意得⎩⎪⎨⎪⎧-b2a=-2,4ac -b24a =4,a +b +c =0,解得⎩⎪⎨⎪⎧a =-49,b =-169,c =209.∴抛物线对应的函数解析式为y =-49x 2-169x +209.方法二:设抛物线对应的函数解析式为y =a(x +2)2+4,将点(1,0)的坐标代入得0=a(1+2)2+4,解得a =-49.∴抛物线对应的函数解析式为y =-49(x +2)2+4,即y =-49x 2-169x +209.方法三:∵抛物线的顶点坐标为(-2,4),与x 轴的一个交点坐标为(1,0), ∴抛物线的对称轴为直线x =-2,与x 轴的另一个交点坐标为(-5,0).设抛物线对应的函数解析式为y =a(x -1)(x +5),将点(-2,4)的坐标代入得4=a(-2-1)(-2+5),解得a =-49.∴抛物线对应的函数解析式为y =-49(x -1)(x +5),即y =-49x 2-169x +209.点拨:本题分别运用了一般式、顶点式、交点式求二次函数解析式,求二次函数的解析式时要根据题目条件选择灵活的方法,如本题中:第一种方法列式较复杂,且计算量大,第二、三种方法较简便,计算量小.12.D13.解:(1)点D 的横坐标、纵坐标的实际意义:当产量为130 kg 时,该产品每千克生产成本与销售价相等,都为42元.(2)设线段AB 所表示的y 1与x 之间的函数解析式为y 1=k 1x +b 1. 因为y 1=k 1x +b 1的图象过点(0,60)与(90,42),所以⎩⎪⎨⎪⎧b 1=60,90k 1+b 1=42.解方程组得⎩⎪⎨⎪⎧k 1=-0.2,b 1=60.这个一次函数的解析式为y 1=-0.2x +60(0≤x≤90). (3)设y 2与x 之间的函数解析式为y 2=k 2x +b 2.因为y 2=k 2x +b 2的图象过点(0,120)与(130,42),所以⎩⎪⎨⎪⎧b 2=120,130k 2+b 2=42.解方程得⎩⎪⎨⎪⎧k 2=-0.6b 2=120. 这个一次函数的解析式为y 2=-0.6x +120(0≤x≤130). 设产量为x kg 时,获得的利润为W 元.当0≤x≤90时,W =x[(-0.6x +120)-(-0.2x +60)]=-0.4(x -75)2+2 250. 所以,当x =75时,W 的值最大,最大值为2 250.当90≤x≤130时,W =x[(-0.6x +120)-42]=-0.6(x -65)2+2 535. 当x =90时,W =-0.6×(90-65)2+2 535=2 160.由-0.6<0知,当x >65时,W 随x 的增大而减小,所以90≤x ≤130时,W ≤2 160.因此,当该产品产量为75 kg 时,获得的利润最大,最大利润是2 250元. 14.A 15. y =x 2+x -216.解:∵直线y =x +2与x 轴交于点A ,与y 轴交于点B ,∴A(-2,0),B(0,2),∴△ABO 为等腰直角三角形.又∵AB⊥BC,∴△BCO 也为等腰直角三角形.∴OC =OB =OA.∴C(2,0),设抛物线解析式为y =a(x -2)2,将B(0,2)的坐标代入得2=a(0-2)2,解得a =12,∴此抛物线的解析式为y =12(x -2)2,即y =12x 2-2x +2.17.解:(1)∵AB=x m ,∴BC =(28-x) m . 于是易得S =AB·BC=x(28-x)=-x 2+28x. 即S =-x 2+28x(0<x <28).(2)由题意可知,⎩⎪⎨⎪⎧x≥6,28-x≥15,解得6≤x≤13.由(1)知,S =-x 2+28x =-(x -14)2+196.易知当6≤x≤13时,S 随x 的增大而增大,∴当x =13时,S 最大值=195,即花园面积的最大值为195 m 2.阶段强化专训三1.B 点拨:因为抛物线开口向下,与y 轴交于正半轴,对称轴x =-b2a >0,且与x轴有两个交点,所以a <0,b >0,c >0,b 2-4ac >0,所以abc <0,b 2-4ac4a<0,故①正确,②错误.因为OA =OC ,所以点A 的坐标可表示为(-c ,0),代入解析式得ac 2-bc +c =0,所以ac -b +1=0,故③正确.设点A ,B 的坐标分别为(x 1,0),(x 2,0),所以x 1,x 2是方程ax 2+bx +c =0的两根,所以x 1x 2=c a ,又OA =-x 1,OB =x 2,所以OA·OB=-ca,故④正确.所以①③④正确.2.B 3.D 4.A 5.x 1=0,x 2=2 6.C7.解:(1)将点A(-1,0)的坐标代入y 1=-x +m ,得m =-1;将点A(-1,0),B(2,-3)的坐标分别代入y 2=ax 2+bx -3,得⎩⎪⎨⎪⎧a -b -3=0,4a +2b -3=-3,解得⎩⎪⎨⎪⎧a =1,b =-2, ∴y 2=x 2-2x -3.(2)易知C 点的坐标为(0,-3),一次函数的图象与y 轴的交点坐标为(0,-1).∴S △ABC =12×[-1-(-3)]×1+12×[-1-(-3)]×2=12×2×1+12×2×2=3.阶段强化专训四 1.C 2.9(第3题)3.解:(1)由已知得OA =OA 1=8 m ,OC =8 m .故C(0,8),B(-8,6).设抛物线BCB 1对应的函数解析式为y =ax 2+8,将B 点坐标代入,得a ·(-8)2+8=6,解得a =-132,所以y =-132x 2+8(-8≤x ≤8).(2)能.若货车从隧道正中行驶,则其最右边到y 轴的距离为2 m .如图,设抛物线上横坐标为2的点为点D ,过点D 作DE⊥AA 1于点E.当x =2时,y =-132×22+8=778,即D ⎝⎛⎭⎪⎫2,778,所以DE =778 m .因为778>7,所以该货车能安全通过这个隧道.4.B 5.C 6.2(第7题)7.解:(1)以点O 为原点,AB 所在直线为x 轴,AB 的垂直平分线为y 轴建立如图的直角坐标系,则有M(0,5),B(2,0),C(1,0),D ⎝ ⎛⎭⎪⎫32,0.设抛物线的解析式为y =ax 2+c ,由抛物线过点M 和点B ,可得a =-54,c =5.故抛物线的解析式为y =-54x 2+5.当x =1时,y =154;当x =32时,y =3516.故P ⎝ ⎛⎭⎪⎫1,154,Q ⎝ ⎛⎭⎪⎫32,3516两点在抛物线上.当竖直摆放5个圆柱形桶时,桶高为0.3×5=1.5=32(米).∵32<154且32<3516,∴网球不能落入桶内.(2)设竖直摆放m 个圆柱形桶时,网球可以落入桶内.由题意,得3516≤0.3m≤154,解得7724≤m≤1212.∵m 为整数,∴m 的值为8,9,10,11,12.∴当竖直摆放8,9,10,11或12个圆柱形桶时,网球可以落入桶内.8.4.9米 9.0.5 10.C11.解:(1)连接FH ,∵△EGH ≌△BCF ,∴HG =FC ,∠G =∠BCF ,∴HG ∥FC ,∴四边形FCGH 是平行四边形,∴FH 綊CG ,∴∠DFH =∠DCG=90°.由题意可知,CF =BE =a.在Rt △DFH 中,DF =3a -a =2a ,FH =a ,∴DH =DF 2+FH 2=5a. (2)设BE =x ,△DHE 的面积为y.依题意,得y =S △CDE +S 梯形CDHG -S △EGH =12×3a×(3a-x)+12(3a +x)x -12×3a×x,∴y =12x 2-32ax +92a 2,即y =12⎝ ⎛⎭⎪⎫x -32a 2+278a 2.∴当x =32a ,即E 是BC 的中点时,y 取得最小值,即△DHE 的面积取得最小值,最小值是278a 2.12.解:(1)在y =12x -2中,令x =0,得y =-2;令y =0,得x =4,∴A(4,0),C(0,-2).设抛物线的解析式为y =ax 2+bx +c(a≠0),∵点A(4,0),B(1,0),C(0,-2)在抛物线上,∴⎩⎪⎨⎪⎧16a +4b +c =0,a +b +c =0,c =-2,解得⎩⎪⎨⎪⎧a =-12,b =52,c =-2.∴抛物线的解析式为y =-12x 2+52x -2.(第12题)(2)设点D 的坐标为(x ,y),则y =-12x 2+52x -2(1<x <4).在Rt △AOC 中,OA =4,OC=2,由勾股定理得AC =2 5.如图所示,连接CD ,AD.过点D 作DF⊥y 轴于点F ,过点A 作AG⊥FD 交FD 的延长线于点G ,则FD =x ,DG =4-x ,OF =AG =y ,FC =y +2.S △ACD =S梯形AGFC-S △CDF -S △ADG =12(AG +FC)·FG-12FC·FD -12DG·AG=12(y +y +2)×4-12(y +2)·x-12(4-x)·y=2y -x +4.将y =-12x 2+52x -2代入,得S △ACD =2y -x +4=-x 2+4x =-(x -2)2+4,当x =2时,y =1,此时S △ACD 最大,∴D(2,1).∵S △ACD =12AC·DE,AC =25,∴当△ACD的面积最大时,高DE 最大,则DE 的最大值为412AC =412×25=455.∴当D 与直线AC 的距离DE 最大时,点D 的坐标为(2,1),最大距离为455.阶段强化专训五1.解:由反比例函数的定义可知⎩⎪⎨⎪⎧m 2-10=-1,m +3≠0,∴m =3. ∴此反比例函数的表达式为y =6x.易错点拨:该题容易忽略m +3≠0这一条件,出现m =±3的错误结论.2.解:由题意,得⎩⎪⎨⎪⎧n 2+2n -9=-1,n +3>0.解得n =2(n =4舍去).∴函数表达式是y =5x .3.解:(1)∵OA=OB ,B(0,2),A 在x 轴负半轴上. ∴A(-2,0).设一次函数表达式为:y =ax +b ,将A(-2,0),B(0,2)代入表达式得:⎩⎪⎨⎪⎧-2a +b =0b =2,∴⎩⎪⎨⎪⎧a =1b =2. ∴该一次函数表达式为:y =x +2.(第3题)(2)如图,过点C 作x 轴垂线交x 轴于点D , ∵B 为AC 中点,且BO∥CD, ∴BO CD =12.∴CD=4. 又∵C 点在第一象限,∴设C(x ,4),代入y =x +2中得:x =2.∴C(2,4).将C(2,4)代入y =kx (k≠0)中得k =8.∴反比例函数表达式为:y =8x.4.解:∵y 1与x 成正比例,∴设y 1=k 1x.又∵y 2与x 成反比例, ∴设y 2=k 2x .由y =y 1+y 2,得y =k 1x +k 2x.又∵y=y 1+y 2的图象经过(1,2)和⎝ ⎛⎭⎪⎫2,12两点,∴⎩⎪⎨⎪⎧2=k 1+k 2,12=2k 1+k 22.解此方程组得⎩⎪⎨⎪⎧k 1=-13,k 2=73.∴y 与x 的函数表达式是y =-13x +73x.点拨:遇到这种组合型函数的问题时可以分而解之.要特别注意在设待定系数时,不能设成同一个字母k ,而要分别设为k 1,k 2.一般来说它们是不相等的.5.解:延长BA 交y 轴于点E ,由题意可知,S 矩形ADOE =1,S 矩形OCBE =k. ∵S 矩形ABCD =6,∴k -1=6.∴k=7. ∴点B 所在双曲线的函数表达式是y =7x .6.解:(1)由已知,得vt =300.∴t 与v 之间的函数关系式为t =300v(v >0).(2)运了一半物资后还剩300×⎝ ⎛⎭⎪⎫1-12=150(t ),故t 与v 之间的函数关系式变为t =150v (v >0).将t =2代入t =150v ,得2=150v.解得v =75.因此剩下的物资要在2 h 之内运到江边,运输速度至少为75 t /h .点拨:运用实际问题中的数量关系求反比例函数的关系式,必须是a×b=c 型的数量关系.如:路程一定时,速度与时间的关系;总利润一定时,每件商品的利润与商品数量的关系等.阶段强化专训六 1.C 2.A 3.C 4.A 5.D 点拨:由题意,易求出。
艾宾浩斯记忆表格(一周一页标记版)
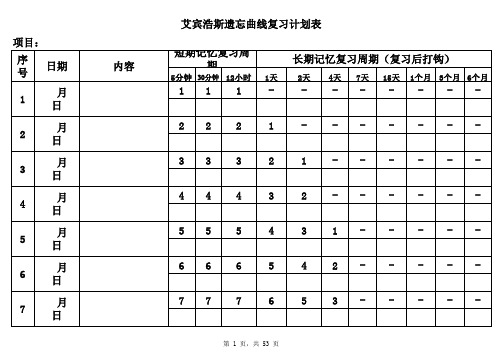
短期记忆复习周 期
长期记忆复习周期(复习后打钩)
5分钟 30分钟 12小时 1天 2天 4天 7天 15天 1个月 3个月 6个月
29 29 29 28 27 25 22 14 - - -
30 30 30 29 28 26 23 15 - - -
31 31 31 30 29 27 24 16 1 - -
项目:
序 号
日期
1
月 日
2
月 日
3
月 日
4
月 日
5
月 日
6
月 日
7
月 日
内容
艾宾浩斯遗忘曲线复习计划表
短期记忆复习周 期
长期记忆复习周期(复习后打钩)
5分钟 30分钟 12小时 1天 2天 4天 7天 15天 1个月 3个月 6个月
11 1 - - -- - - - -
22 2 1 - -- - - - -
5分钟 30分钟 12小时 1天 2天 4天 7天 15天 1个月 3个月 6个月
57 57 57 56 55 53 50 42 27 - -
58 58 58 57 56 54 51 43 28 - -
59 59 59 58 57 55 52 44 29 - -
60 60 60 59 58 56 53 45 30 - -
84 84 84 83 82 80 77 69 54 - -
第 12 页,共 53 页
项目:
序 号
日期
85
月 日
86
月 日
87
月 日
88
月 日
89
月 日
90
月 日
91
月 日
内容
艾宾浩斯遗忘曲线复习计划表
Excel表格练习题

电子表格练习题1、创建学生成绩单学生成绩单(1)启动Excel及汉字输入方法;(2)按试题容输入:(3)总评成绩必须是公式计算,总评成绩的算法是:平时成绩占10%、期中成绩占20%、期末成绩占70%:(4)按下列要求进行排版:标题为黑体、20号字、合并及居中、不加边框;列标题为居中对齐:正文加边框:“”一列分散对齐:备注中的容合并及居中,自动换行;(5)在C盘下创建文件夹,文件夹名为自己所抽取的技能现场号;把工作簿保存到自己创建的文件夹中,文件名为自己所抽取的技能现场号。
2、创建员工奖金表好汉公司员工一季度奖金表三、操作程序规定及说明1、操作程序说明(1)启动Excel及汉字输入方法:(2)按试题容输入:(3)手动输入公式计算平均每月(4)按下列要求进行排版:标题为隶书、20号字、合并及居中、无边框;列标题为粗体、14号字、居中对齐;正文居中对齐、字体、字号为默认;(5)在C盘下创建文件夹,文件夹名为自己所抽取的技能现场号:把工作簿保存到自己创建的文件夹中,文件名为自己所抽取的技能现场号。
3、设置条件格式三国学生成绩单三、操作程序规定及说明1、操作程序说明(1)启动Excel及汉字输入法:(2)按试题容输入工作表;平均成绩要求用公式计算:(3)按要求设巻格式:标题为合并及居中、华文宋体、20号字、无边框;列标题采用华文行楷、16号字,居中对齐:行标志采用华文新、14号字、分散对齐,正文采用居中对齐方式,英它正文采用默认格式;按要求设垃条件格式:90分以上(含90分)的成绩显示成粗体、深蓝色;60・90之间的(含60分,不含90分)显示绿色;低于60分的显示粗体、红色;(4)在C盘下创建文件夹,文件夹名为自己所抽取的技能现场号:把工作簿保存到自己创建的文件夹中,文件名为自己所抽取的技能现场号。
4、自动换行、缩小字体填充三、操作程序规定及说明1、操作程序说明<1)启动Excel及汉字输入法:(2)按试题容输入工作表;(3)按下列要求进行设置:将“毕业院校”一例隐藏起来:将“序号5”一行隐藏起来;标题为合并及居中、华文行楷、20号字、无边框;正文采用居中对齐方式,字体、字号采用默认格式;将“参加工作时间”设巻成自动换行「'家庭住址”一列设置成缩小字体填充:“”一列设程成分散对齐; 列标题设置成华文细黑、14号字;(4)在C盘下创建文件夹,文件夹名为自己所抽取的技能现场号:把工作簿保存到自己创建的文件夹中,文件需为自己所抽取的技能现场号。
二级MS_Office高级应用Excel电子表格软件的使用专项强化真题试卷73含答案解析

Excel 电子表格软件的使用---为题目类型王明是某在线销售数码产品公司的管理人员,于 2017 年初随机抽取了 100 名网站注册会员,准备使用 Excel 分析他们上一年度的消费情况。
根据下列要求,帮助他运用已有的数据完成这项工作。
1.在考生文件夹下,将“.Excel 一素材.xlsx”文件另存为名为“。
Excel.xlsm” (“xlsm”为扩展名)的 Excel 启用宏的工作簿,后续操作均基于此文件,否则不得分。
2.在“客户资料”工作表中,完成下列任务:①将数据区域 Al:F101 转换为表,将表的名称修改为“客户资料”,并取消隔行底纹的效果。
②将B 列中所有的“M”替换为“男”,所有的“F”替换为“女”。
③修改c 列中日期的格式,要求格式如“80年5 月9 日”(年份只显示后两位)。
④在D 列中,计算每位顾客到 2017 年1 月1 日止的年龄,规则为每到下一个生日,计 1 岁。
⑤在 E 列中,计算每位顾客到 2017 年1 月1 日止所处的年龄段,年龄段的划分标准位于“按年龄和性别”工作表的 A 列中。
(注意:不要改变顾客编号的默认排序,可使用中间表格进行计算) ⑥在F 列中计算每位顾客 2016 年全年消费金额,各季度的消费情况位于“2016年消费”工作表中,将 F 列的计算结果修改为货币格式,保留 0 位小数。
(注意:为便于计算,可修改“2016年消费”工作表的结构) ⑦为 B 列中的数据区域添加数据有效性,以便仅可在其中输入数据“男”或“女”,如果输入其他内容,则弹出样式为“停止”的出错警告,错误信息为“仅可输入中文!”。
⑧录制名为“最小年龄”宏,以便可以对选定单元格区域中数值最小的 10 项应用“浅红填充色深红色文本”的“项目选取规则”条件格式,将宏指定到快捷键“Ctrl+Shift+u”,并对 D 列中的数值应用此宏。
⑨为表格中的数据添加条件格式,将年消费金额最低的 15 位顾客所在的整行记录的文本颜色设置为绿色(注意:如果该顾客属于年龄最小的 10 位顾客,则年龄数值应保持为深红色文本)。
EXCEL专题强化训练五

EXCEL专题练习五班级:_____________ 姓名:________________1.用Excel软件对部分国家或地区进出口贸易情况的数据进行处理,如图a所示。
第1题图a请回答下列问题:(1)在图a所示工作表中,区域F4:F21中的数据是通过公式计算得到的。
则F4单元格输入的公式是________。
(提示:2月进出口贸易增幅=(2月进出口贸易总额-1月进出口贸易总额)/1月进出口贸易总额*100)(2)在图a所示工作表中,D9单元格中的数据________(单选,填字母:A.至少是10,000,000/B.至多是9,999,999/C.可能是:9,999,999)。
(3)为了更加直观地比较“1至2月进出口贸易总额”的情况,小张制作了如图b所示的图表。
该图表的数据区域是________,E3:E21。
第1题图b(4)为了筛选出“2月进出口贸易总额”最大的5个国家或地区,在设置筛选条件时应选择“数字筛选”中的________项。
2.小李用Excel软件处理某次编程能力竞赛成绩,如图a所示。
请回答下列问题;第2题图a(1)区域C18:H18的数据是通过下列操作得到的:选中C10单元格,执行复制操作,再选中C18单元格执行粘贴操作,最后用自动填充功能完成区域D18:H18的计算。
则C18单元格的公式是____________。
(2)如图a所示,高三年级已按“列H”和“列A”两个关键字排序,若高二年级也进行相同的排序,则排序后A5单元格的内容是____________。
(3)为直观地比较两个年级各题均分的差异,小李制作了如图b所示的图表。
该图表的数据区域是________。
第2题图b(4)由图b可知____________。
(多选、填字母:A.该图表垂直坐标轴的最小刻度是40B.本次竞赛难度最大的是第2题C.本次竞赛两个年级均分差距最大的是第3题)3.使用Excel软件处理全省2016年各地市网络零售和居民网络消费数据,如图a所示。
高三OFFICE强化练习

高三OFFICE强化练习一、是非选择题:1. 在Word环境下,用户使用系统提供的各种预定义模板可以简化用户的排版操作。
()2. 在Word环境下,如果想在表格的第二行与第三行之间插入一个空行,可以将光标移动到第二行最后一列表格外,回车后即可。
()3.除了菜单栏的下拉式菜单外,Word还提供单击鼠标右键获得快捷菜单的方法。
()4. 对于插入的图片,只能是图在上、文在下,或文在上、图在下,不能产生环绕效果。
5. 单击"文件"菜单,底部就可以列出最近打开过的几个文件的名字。
()6.在“工具栏”对话框中,如果看到“常用”和“格式”前面的方框中没有√,这说明这两组工具栏显示在屏幕上。
()7.当完成工作后,要退出Excel 2000,可按Ctrl+F4键。
()8.创建工作簿时,Excel将自动以Book1、Book2、Book3、……的顺序给新的工作簿命名。
()9.Excel提供了自动保存功能,设置以指定的时间间隔自动保存活动的工作簿或者所有打开的工作簿。
()10比较运算符用以对两个数值进行比较,产生的结果为逻辑值TRUE或FALSE。
比较运算符为:=、>、<、>=、<=、<>。
()11.工作薄窗口、菜单栏、工具栏、公式栏、状态栏五部分合称EXCEL工作区。
()12.EXCEL中每一个单元格有一个唯一的坐标。
()13.要想打开PowerPoint,只能从开始菜单选择程序,然后点击Microsoft PowerPoint。
14.PowerPoint中,在大纲视图模式下可以实现在其他视图中可实现的一切编辑功能。
15.PowerPoint中除了用内容提示向导来创建新的幻灯片,就没有其它的方法了。
()PowerPoint中,当本次复制文本的操作成功之后,上一次复制的内容自动丢失。
16.PowerPoint中,应用设计模板设计的演示文稿无法进行修改。
()17在普通视图中,选择要插入声音的幻灯片,选择“插入”菜单中的“影片和声音”命令,选择“文件中的声音”,可以选择所需的声音。
EXCEL操作练习题

练习1 EXCEL基本操作一、练习目的1.掌握EXCEL的启动2.掌握EXCEL中单元格的复制和粘贴二、练习内容1. 练习启动和退出EXCEL2. 利用快捷键CTRL+C和CTRL+V练习将一个单元格内容的复制到另一个单元格中。
3. 利用快捷键CTRL+C和CTRL+V练习将一个单元格内容的复制到几个不同的单元格中练习2 EXCEL基本操作一、练习目的掌握EXCEL单元格的自动填充二、练习内容1. 完成横向表格的月份自动填充。
2. 成纵向表格的年份自动填充。
三、操作提示1. 在一个单元格里输入“1月”,然后将这个单元的填充柄用鼠标左键按下,向右拖至12月,松开按键,即可完成。
2. 在一个单元格里输入“1991年”,然后将这个单元的填充柄用鼠标左键按下,向下右拖至1999年,松开按键,即可完成。
练习3 EXCEL基本操作一、练习目的1.掌握单元格的合并2.掌握单元格的对齐方式3.掌握单元格的插入145EXCEL 2000操作练习题146 二、练习内容1.输入下列表格中的内容。
2.将“学生英语成绩登记表”合并成一个单元格3.将单元格中的全部内容的对齐方式为水平居中、垂直居中4.在"江杰"前插入一个新行"张强80 75 87 57 "三、操作提示1.(略)2. 输入“学生英语成绩登记表”时只能在起始单元格中,在合并时,将这个单元格和它右边四个单元格选中,然后选择“格式”菜单中的“单元格”菜单项,弹出“单元格格式”的对话框,选择“对齐”的选择卡,在“文本控制”中选择“合并单元格”的复选框。
点击“确定”按钮即可,如图5-1所示图5-13. 将表中有输入内容的单元格选中,然后选择“格式”菜单中的“单元格”菜单项,弹出“单元格格式”的对话框,选择“对齐”的选择卡,在“文本对齐”中的“水平对齐”选取“居中”、在“垂直对齐”选取“居中”然后点击“确定”按钮即可,如图5-1所示。
EXCEL同步练习题

EXCEL同步练习题一、新建EXCEL工作薄,在sheet1工作表中输入内容(内容见样张),结果保存在F盘中自己的文件夹,文件名为:表0101.XLS。
1.表格的左上角从“序号”开始,“序号”输入到A1单元格。
2.参考样张将数据填充到表格中:二、新建EXCEL工作薄,在sheet1工作表中输入内容(内容见样张),标题文字输入在D1单元格,结果保存在F盘中自己的文件夹,文件名为:表0201.XLS。
三、打开素材文件:数据填充.XLS,按其中的题目要求完成全部操作。
四、新建工作薄1.在“sheet1”工作表中建立如下表格,请设置有效性使年龄列的数据应大于25岁,输入提示停息和错误提示信息如下:2.建立如下电子表格,操作步骤如下:a)创建自定义序列,并将序列填充到B2:H2。
b)在A7: C7中输入“张敏”、“王东风”、“李娜”。
c)设置B3: H5的数据有效性,选择“序列”,来源于A7: C7d)最后参照样张完成表格五、打开素材文件:习题4.XLS完成下列题目1.将工作表“sheet1”重命名为“销售记录”。
2.将该工作表复制到“sheet3”工作表之后。
3.在sheet2和sheet3之间插入一个新工作表,名子为sheet4。
4.新建一个工作薄,将本工作薄中的“销售记录”工作表移动到新工作薄中。
5.删除多余的空白工作薄,只保留有内容的工作表。
并将本工作薄以“销售记录”为名子保存。
六、新建EXCEL工作薄,完成操作后保存为EXCEL_1.XLS1.在工作表“sheet1”中建立如样张所示表格。
要求:从A1单元格开始建立2.在该表“王军”下方插入一行,并输入以下信息,最后重新调整“序号”。
003 刘俊1981年8月WINDOWS 1113.将工作表中“李平”出生年月改为“1978年10月”。
4.在sheet2表中按做题步骤完成档案信息表的建立,注意序列及数据有效性的使用。
1)创建自定义序列(序号、姓名、出生年月、模块、交费)并填充到A2:E22)在A9到E9中依次输入WORD、EXCEL、WINDOWS、POWERPOINT、INTERNET3)在D3到D7中采用数据有效性,选择“序列”,来源于A9:E94)在E3到E7中采用数据有效性,只允许输入整数75,输入信息和出错警告不用设置,出错警告样式选项选择“停止”5.保存文件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8周《算机基础》电子表格格式化强化练习
工作表编辑
1、在sheet3工作表之前插入一张工作表sheet4 。
2、将sheet1工作表改名为“成绩表”。
3、对“sheet2”拖移至最后:
4、将表格标题设置正确样式、设置成黑体加粗、靛(dian)色。
24磅大小,跨列居中对齐方式,水平垂直居中。
5、添加制表日期(当天时间:年月日)到表格的下放水平右对齐垂直居中,并设置成隶书、加粗倾斜、12磅。
6、将表格各栏列宽设置为7;列标题行行高设置为25、其余行高为最合适的行高;列标题粗体、水平和垂直居中;再将表格中的其他内容居中,数据保留小数1位;设置表格框线。
7、对“成绩表”工作表进行如下页面设置,并进行打印预览
8、纸张大小为A4,表格打印时水平、垂直剧中,上下页边距为3 厘米。
9、设置页眉“分类汇总表”居中、粗斜体,设置页脚为当前日期,靠右显示。
10、将结果以《教育技术班部分学生成绩表——“你的姓名”.xls保存,上传。
本次作业
1、全对的同学:+3分为A++,后面新的内容等着我们去探究。
2、认真完成并大部分联系能正确解决的同学:+2分。
3、整个联系过程中保持安静冷静思考(不要着急,学会让自己保持冷静),过程中不会的题我们用红色标记,最后我们来一起解决。
