七北数(下)第二章测试卷
北师大版七年级数学下册第二章相交线与平行线同步测试试题(含答案及详细解析)

北师大版七年级数学下册第二章相交线与平行线同步测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,直线b、c被直线a所截,则1∠与2∠是()A.对顶角B.同位角C.内错角D.同旁内角2、如图,射线AB的方向是北偏东70°,射线AC的方向是南偏西30°,则∠BAC的度数是()A.100°B.140°C.160°D.105°3、以下3个说法中:①连接两点间的线段叫做这两点的距离;②经过两点有一条直线,并且只有一条直线;③同一个锐角的补角一定大于它的余角.正确的是()A .①B .③C .①②D .②③4、下列关于画图的语句正确的是( ).A .画直线8cm AB =B .画射线8cm OA =C .已知A 、B 、C 三点,过这三点画一条直线D .过直线AB 外一点画一直线与AB 平行5、若α∠的补角是125°24',则α∠的余角是( )A .90°B .54°36'C .36°24'D .35°24'6、下列说法中,正确的是( )A .从直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离B .互相垂直的两条直线不一定相交C .直线AB 外一点P 与直线上各点连接而成的所有线段中最短线段的长是7cm ,则点P 到直线AB 的距离是7cmD .过一点有且只有一条直线垂直于已知直线7、若α∠的补角是150°,则α∠的余角是( )A .30°B .60°C .120°D .150°8、已知∠A =37°,则∠A 的补角等于( )A .53°B .37°C .63°D .143°9、在如图中,∠1和∠2不是同位角的是( )A .B .C .D .10、如图,若AB ∥CD ,CD ∥EF ,那么∠BCE =( )A .180°-∠2+∠1B .180°-∠1-∠2C .∠2=2∠1D .∠1+∠2第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B =40°,则∠DAC 的度数为____.2、(1)已知α∠与β∠互余,且3518α'∠=︒,则β∠=________.(2)82325'''︒+________=180°.(3)若27m n a b -+与443a b -是同类项,则m +n =________.3、如图,点O 在直线AB 上,OD ⊥OE ,垂足为O .OC 是∠DOB 的平分线,若∠AOD =70°,则∠COE =__________度.4、已知∠1=71°,则∠1的补角等于__________度.5、已知一个角的补角是这个角的余角的3倍,则这个角是______度.三、解答题(5小题,每小题10分,共计50分)1、如图,直线AB,CD相交于点O,90∠.∠=︒,OF平分AOEFOD(1)写出图中所有与AOD∠互补的角;(2)若120∠的度数.AOE∠=︒,求BOD2、如图,直线AB,CD,EF相交于点O,(1)指出∠AOC,∠EOB的对顶角及∠AOC的邻补角.(2)图中一共有几对对顶角?指出它们.3、如图,已知AB CD∠,求证1290∠,CE平分BCD∥,BE平分ABC∠+∠=︒.证明:∵BE平分ABC∠(已知),∴2∠=(),同理1∠=,∴1122∠+∠=,又∵AB CD∥(已知)∴ABC BCD∠+∠=(),∴1290∠+∠=︒.4、(感知)已知:如图①,点E在AB上,且CE平分ACD∠,12∠=∠.求证:AB CD∥.将下列证明过程补充完整:证明:∵CE平分ACD∠(已知),∴2∠=∠__________(角平分线的定义),∵12∠=∠(已知),∴1∠=∠___________(等量代换),∴AB CD ∥(______________).(探究)已知:如图②,点E 在AB 上,且CE 平分ACD ∠,AB CD ∥.求证:12∠=∠.(应用)如图③,BE 平分DBC ∠,点A 是BD 上一点,过点A 作AE BC ∥交BE 于点E ,:4:5ABC BAE ∠∠=,直接写出E ∠的度数.5、如图,直线AB 、CD 相交于点O ,∠EOC =90°,OF 是∠AOE 的角平分线,∠COF =34°,求∠BOD 的度数.-参考答案-一、单选题1、B【分析】根据对顶角、同位角、内错角、同旁内角的特征去判断即可.【详解】∠1与∠2是同位角故选:B【点睛】本题考查了同位角的含义,理解同位角的含义并正确判断同位角是关键.2、B【分析】BAD CAE DAE再利用角的和差关系可得答案. 根据方位角的含义先求解,,,【详解】解:如图,标注字母,射线AB的方向是北偏东70°,射线AC的方向是南偏西30°,907020,30,BAD CAE而90,DAE ∠=︒309020140,BAC CAE DAE BAD故选B【点睛】本题考查的是角的和差关系,垂直的定义,方位角的含义,掌握“角的和差与方位角的含义”是解本题的关键.3、D【分析】由题意根据线段的性质,余、补角的概念,两点间的距离以及直线的性质逐一进行分析即可.【详解】解:连接两点间的线段的长度,叫做这两点的距离,故①不符合题意;经过两点有一条直线,并且只有一条直线,故②符合题意;同一个锐角的补角一定大于它的余角,故③符合题意.故选:D.【点睛】本题考查线段的性质,余、补角的概念和两点间的距离以及直线的性质,主要考查学生的理解能力和判断能力.4、D【分析】直接利用直线、射线的定义分析得出答案.【详解】解:A 、画直线AB =8cm ,直线没有长度,故此选项错误;B 、画射线OA =8cm ,射线没有长度,故此选项错误;C 、已知A 、B 、C 三点,过这三点画一条直线或2条、三条直线,故此选项错误;D 、过直线AB 外一点画一直线与AB 平行,正确.故选:D .【点睛】此题主要考查了直线、射线的定义及画平行线,正确把握相关定义是解题关键.5、D【分析】根据题意,得α∠=180°-125°24',α∠的余角是90°-(180°-125°24')=125°24'-90°,选择即可.【详解】∵α∠的补角是125°24',∴α∠=180°-125°24',∴α∠的余角是90°-(180°-125°24')=125°24'-90°=35°24',故选D .【点睛】本题考查了补角,余角的计算,正确列出算式是解题的关键.6、C【分析】根据点到直线距离的定义分析,可判断选项A 和C ;根据相交线的定义分析,可判断选项B ,根据垂线的定义分析,可判断选项D ,从而完成求解.【详解】从直线外一点到这条直线的垂线段的长度,叫做这个点到这条直线的距离,即选项A 错误;在同一平面内,互相垂直的两条直线一定相交,即选项B错误;直线AB外一点P与直线上各点连接而成的所有线段中最短线段的长是7cm,则点P到直线AB的距离是7cm,即选项C正确;在同一平面内,过一点有且只有一条直线垂直于已知直线,即选项D错误;故选:C.【点睛】本题考查了点和直线的知识;解题的关键是熟练掌握点到直线距离、相交线、垂线的性质,从而完成求解.7、B【分析】根据补角、余角的定义即可求解.【详解】∠的补角是150°∵α∠=180°-150°=30°∴α∠的余角是90°-30°=60°∴α故选B.【点睛】此题主要考查余角、补角的求解,解题的关键是熟知如果两个角的和为90度,这两个角就互为余角;补角是指如果两个角的和是一个平角,那么这两个角叫互为补角,其中一个角叫做另一个角的补角8、D【分析】根据补角的定义:如果两个角的度数和为180度,那么这两个角互为补角,进行求解即可.【详解】解:∵∠A=37°,∴∠A的补角的度数为180°-∠A=143°,故选D.【点睛】本题主要考查了求一个角的补角,熟知补角的定义是解题的关键.9、D【分析】同位角的定义:两条直线a,b被第三条直线c所截,在截线c的同侧,被截两直线a,b的同一方向的两个角,我们把这样的两个角称为同位角,依此即可求解.【详解】解:A、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;B、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;D、∠1与∠2的一边不在同一条直线上,不是同位角,符合题意.故选:D.【点睛】本题题考查三线八角中的同位角识别,解题关键在于掌握判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.10、A【分析】根据两直线平行,内错角相等,同旁内角互补,这两条性质解答.【详解】∵AB∥CD,CD∥EF,∴∠1=∠BCD ,∠ECD +∠2=180°,∴∠BCE =∠BCD +∠ECD =180°-∠2+∠1,故选A .【点睛】本题考查了平行线的性质,正确选择合适的平行线性质是解题的关键.二、填空题1、40°【分析】根据平行线的性质可得∠EAD =∠B ,根据角平分线的定义可得∠DAC =∠EAD ,即可得答案.【详解】∵AD ∥BC ,∠B =40°,∴∠EAD =∠B =40°,∵AD 是∠EAC 的平分线,∴∠DAC =∠EAD =40°,故答案为:40°【点睛】本题考查平行线的性质及角平分线的定义,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;熟练掌握平行线的性质是解题关键.2、5442'︒ 972755'''︒ 3【分析】(1)根据余角的定义和角度的四则运算法则进行求解即可;(2)根据角度的四则运算法则求解即可;(3)根据同类项的定义,先求出m 、n 的值,然后代值计算即可.【详解】解:(1)α∠与β∠互余,且3518α'∠=︒,∴90=903518=5442βα'∠=︒-︒-︒'︒∠;故答案为:5442'︒;(2)18082325=972755''''''︒-︒︒;故答案为:972755'''︒;(3)∵27m n a b -+与443a b -是同类项,∴2474m n -=⎧⎨+=⎩, ∴63m n =⎧⎨=-⎩, ∴()633m n +=+-=.故答案为:3.【点睛】本题主要考查了求一个角的余角,角度的四则运算,同类项的定义,代数式求值,解一元一次方程,熟知相关知识是解题的关键.3、35【分析】根据补角的性质,可得∠BOD =110°,再由OC 是∠DOB 的平分线,可得1552COD BOC BOD ∠=∠=∠=︒ ,又由OD ⊥OE ,可得到∠BOE =20°,即可求解. 【详解】解:∵∠AOD=70°,∠AOD+∠BOD=180°,∴∠BOD=110°,∵OC是∠DOB的平分线,∴1552COD BOC BOD∠=∠=∠=︒,∵OD⊥OE,∴∠DOE=90°,∴∠BOE=∠BOD-∠DOE=20°,∴∠COE=∠BOC-∠BOE=35°.故答案为:35【点睛】本题主要考查了补角的性质,角平分线的定义,角的和与差,熟练掌握补角的性质,角平分线的定义,角的和与差运算是解题的关键.4、109【分析】两角互为补角,和为180°,那么计算180°-∠1可求补角.【详解】解:设所求角为∠α,∵∠α+∠1=180°,∠1=71,∴∠α=180°-71=109°.故答案为:109【点睛】此题考查的是角的性质,两角互余和为90°,互补和为180°.5、45︒【分析】设这个角为,x ︒ 则这个角的补角为:()180,x -︒ 这个角的余角为:()90,x -︒ 根据等量关系一个角的补角是这个角的余角的3倍,列方程()180390x x -=-,解方程可得.【详解】解:设这个角为,x ︒ 则这个角的补角为:()180,x -︒ 这个角的余角为:()90,x -︒()180390x x ∴-=-,1802703x x ∴-=- ,290x ∴=,45x ∴=,答:这个角为45︒.故答案为:45︒.【点睛】本题考查的是余角与补角的含义,一元一次方程的应用,掌握以上知识是解题的关键.三、解答题1、(1)AOC ∠,BOD ∠,DOE ∠;(2)30°【分析】(1)根据邻补角的定义确定出∠AOC 和∠BOD ,再根据角平分线的定义可得∠AOF =∠EOF ,根据垂直的定义可得∠COF =∠DOF =90°,然后根据等角的余角相等求出∠DOE =∠AOC ,从而最后得解;(2)根据角平分线的定义求出∠AOF ,再根据余角的定义求出∠AOC ,然后根据对顶角相等解答.【详解】解:(1)因为直线AB ,CD 相交于点O ,所以AOC ∠和BOD ∠与AOD ∠互补.因为OF 平分AOE ∠,所以AOF EOF ∠=∠.因为90FOD ∠=︒,所以18090COF FOD ∠=︒-∠=︒.因为90AOC COF AOF EOF ∠=∠-∠=︒-∠,90DOE FOD EOF EOF ∠=∠-∠=︒-∠,所以AOC DOE ∠=∠,所以与AOD ∠互补的角有AOC ∠,BOD ∠,DOE ∠.(2)因为OF 平分AOE ∠,所以111206022AOF AOE ∠=∠=⨯︒=︒,由(1)知,90COF ∠=︒,所以906030AOC COF AOF ∠=∠-∠=︒-︒=︒,由(1)知,AOC ∠和BOD ∠与AOD ∠互补,所以30BOD AOC ∠=∠=︒(同角的补角相等).【点睛】本题考查了余角和补角,对顶角相等的性质,角平分线的定义,难点在于(1)根据等角的余角相等确定出与∠AOD 互补的第三个角.2、(1)∠AOC 的对顶角是∠BOD ,∠EOB 的对顶角是∠AOF ,.∠AOC 的邻补角是∠AOD ,∠BOC ;(2)共有6对对顶角,它们分别是∠AOC 与∠BOD ,∠AOE 与∠BOF ,∠AOF 与∠BOE ,∠AOD 与∠BOC ,∠EOD 与∠COF ,∠EOC 与∠FOD【分析】根据对顶角的定义:两个角有一个公共点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角叫做对顶角;邻补角的定义:两个角有一条公共边,它们的另一边互为反向延长线,具有这种位置关系的两个角叫做邻补角,进行求解即可.【详解】解:(1)由题意得:∠AOC 的对顶角是∠BOD ,∠EOB的对顶角是∠AOF.∠AOC的邻补角是∠AOD,∠BOC.(2)图中共有6对对顶角,它们分别是∠AOC与∠BOD,∠AOE与∠BOF,∠AOF与∠BOE,∠AOD与∠BOC,∠EOD与∠COF,∠EOC与∠FOD.【点睛】本题主要考查了对顶角和邻补角的定义,熟知定义是解题的关键.3、12∠ABC;角平分线的定义;12∠BCD;(∠ABC+∠BCD);180°;两直线平行,同旁内角互补【分析】由平行线的性质可得到∠BAC+∠ACD=180°,再结合角平分线的定义可求得∠1+∠2=90°,可得出结论,据此填空即可.【详解】证明:∵BE平分∠ABC(已知),∴∠2=12∠ABC(角平分线的定义),同理∠1=12∠BCD,∴∠1+∠2=12(∠ABC+∠BCD),又∵AB∥CD(已知)∴∠ABC+∠BCD=180°(两直线平行,同旁内角互补),∴∠1+∠2=90°.故答案为:12∠ABC;角平分线的定义;12∠BCD;(∠ABC+∠BCD);180°;两直线平行,同旁内角互补.【点睛】本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.4、【感知】ECD;ECD;内错角相等,两直线平行;【探究】见解析;【应用】40°【分析】感知:读懂每一步证明过程及证明的依据,即可完成解答;探究:利用角平分线的性质得∠2=∠DCE,由平行线性质可得∠DCE=∠1,等量代换即可解决;应用:利用角平分线的性质得∠ABE=∠CBE,由平行线性质可得∠CBE=∠E,等量代换得∠E=∠ABE,由∠∠=即可求得∠ABC的度数,从而可求得∠E的度数.ABC BAE:4:5【详解】感知∵CE平分ACD∠(已知),∴2=ECD(角平分线的定义),∵12∠=∠(已知),∴1∠=∠ECD(等量代换),∴AB CD∥(内错角相等,两直线平行).故答案为:ECD;ECD;内错角相等,两直线平行探究∵CE平分ACD∠,∴2ECD∠=∠,∵AB CD∥,∴l ECD∠=∠,∵12∠=∠.应用∵BE 平分∠DBC , ∴12ABE CBE ABC ∠=∠=∠,∵AE ∥BC ,∴∠CBE =∠E ,∠BAE +∠ABC =180゜,∴∠E =∠ABE ,∵:4:5ABC BAE ∠∠=,∴∠ABC =80゜∴40ABE ∠=︒∴40E ∠=︒【点睛】本题考查平行线的判定与性质,角平分线的性质,掌握平行线的性质与判定是关键. 5、22︒【分析】根据90EOC ∠=︒、34COF ∠=︒可得56EOF ∠=︒,OF 是∠AOE 的角平分线,可得56AOF EOF ∠=∠=︒,所以22AOC AOF COF ∠=∠-∠=︒,再根据对顶角相等,即可求解.【详解】解:∵90EOC ∠=︒、34COF ∠=︒,∴56EOF ∠=︒,∵OF 是∠AOE 的角平分线,∴56AOF EOF ∠=∠=︒,∴22AOC AOF COF ∠=∠-∠=︒,∴22BOD AOC ∠=∠=︒,【点睛】此题考查了角平分线的有关计算,解题的关键是掌握角平分线的定义以及角之间的和差关系.。
(完整版)北师大版七年级下学期数学第二单元测试题及答案
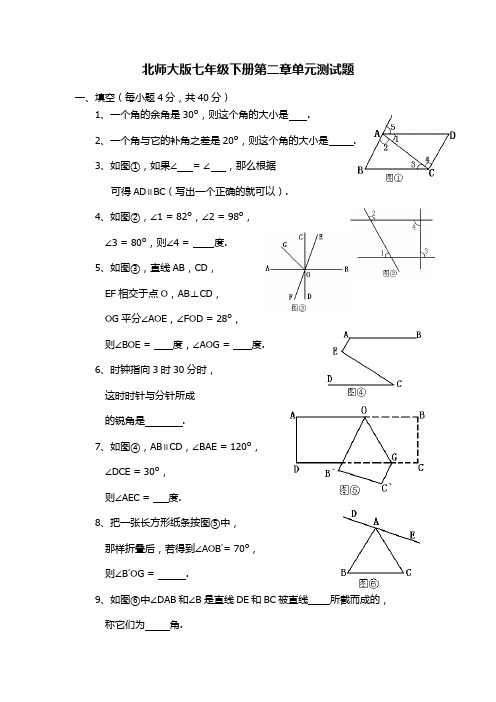
北师大版七年级下册第二章单元测试题一、填空(每小题4分,共40分)1、一个角的余角是30º,则这个角的大小是 .2、一个角与它的补角之差是20º,则这个角的大小是 .3、如图①,如果∠ = ∠ ,那么根据可得AD ∥BC (写出一个正确的就可以).4、如图②,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度.5、如图③,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD = 28º,则∠BOE = 度,∠AOG = 度.6、时钟指向3时30分时,这时时针与分针所成的锐角是 .7、如图④,AB ∥CD ,∠BAE = 120º,∠DCE = 30º,则∠AEC = 度.8、把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB ′= 70º,则∠B ′OG = .9、如图⑥中∠DAB 和∠B 是直线DE 和BC 被直线 所截而成的,称它们为 角.10、如图⑦,正方形ABCD 边长为8,M 在DC 上,且DM = 2,N 是AC上一动点,则DN + MN 的最小值为 .二、选择题(每小题3分,共18分)11、下列正确说法的个数是( )①同位角相等 ②对顶角相等③等角的补角相等 ④两直线平行,同旁内角相等A . 1, B. 2, C. 3, D. 412、如图⑧,在△ABC 中,AB = AC ,∠A = 36º,BD平分∠ABC ,DE ∥BC ,那么在图中与△ABC 相似的三角形的个数是( )A. 0,B. 1,C. 2,D. 313、下列图中∠1和∠2是同位角的是( )A. ⑴、⑵、⑶,B. ⑵、⑶、⑷,C. ⑶、⑷、⑸,D.⑴、⑵、⑸14、下列说法正确的是( )A.两点之间,直线最短;B.过一点有一条直线平行于已知直线;C.和已知直线垂直的直线有且只有一条;D.在平面内过一点有且只有一条直线垂直于已知直线.15、一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为()A. 45º,B. 60º,C. 75º,D. 80º16、如图⑨,DH ∥EG ∥EF ,且DC ∥EF ,那么图中和∠1相等的角的个数是( )A. 2,B. 4,C. 5,D. 6三、解答题:17、按要求作图(不写作法,但要保留作图痕迹)(3分)已知点P 、Q 分别在∠AOB 的边OA ,OB 上(如图 ).)①作直线PQ ,②过点P 作OB 的垂线,③过点Q 作OA 的平行线.18、已知线段AB,延长AB到C,使BC∶AB=1∶3,D为AC中点,若DC = 2cm,求AB的长. (7分)分)19、如图,,已知AB∥CD,∠1 = ∠2.求证.:∠E=∠F (620、如图所示,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个判断:⑴ AD = CB⑵ AE = FC⑶∠B = ∠D⑷ AD∥BC请用其中三个作为已知条件,余下一个作为结论,编一道数学问题,并写出解答过程. (8分)21、如图,ABCD是一块釉面砖,居室装修时需要一块梯形APCD的釉面砖,且使∠APC=120º.请在长方形AB边上找一点P,使∠APC=120º.然后把多余部分割下来,试着叙述怎样选取P点及其选取P点的理由.(8分)22、如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E =分)140º,求∠BFD的度数. (10第二单元答案一、填空题:1.60°;2.100°;3.∠5= ∠B,同位角相等,两直线平行;4.80°;5.62°,59°;6.75°;7.90°;8.55°;9.AB,内错;10.10.二、选择题:11.B; 12.C; 13.D; 14.D; 15.A; 16.C.三、解答题:17. 略;18. AB=3cm;19.略;20. 比如:已知:⑴⑵⑷.求证:⑶;求证过程略;21. 以C为顶点,CD为一边,在∠DCB内画∠DCP=60°,交AB于P,则P点为所选取的点.证明略;22.∠BFD=70°;。
北师大版七年级数学下册第二章《相交线与平行线》考试卷附解析版)
(3)利用上述结论解决问题:如图已知 , 和 的平分线相交于 , ,求 的度数.
22.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线 射到平面镜 上,被 反射到平面镜 上,又被 反射,若被 反射出的光线 与光线 平行,且 ,则 _________, ________.
4.如图, , ,则图中与 相等 角(不含 )有______个;若 ,则 ________.
5.在 、 两座工厂之间要修建一条笔直的公路,从 地测得 地的走向是南偏东 ,现 、 两地要同时开工,若干天后,公路准确对接,则 地所修公路的走向应该是( )
A.北偏西 B.南偏东 C.西偏北 D.北偏西
6.如图,直线l//m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为()
【答案】95°
【解析】
【详解】如图,作EF∥AB,则EF∥CD,
∴∠ABE+∠BEF=180°,∵∠ABE=120°,∴∠BEF=60°,
∵∠DCE=∠FEC=35°,∴∠BEC=∠BEF+∠FEC=95°.
故答案为95°.
点睛:本题关键在于构造平行线,再利用平行线的性质解题.
13.某人在练车场上练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则这两次拐弯的角度可能是________.①第一次向左拐 ,第二次向右拐 ;②第一次向右拐 ,第二次向左拐 ;③第一次向右拐 ,第二次向左拐 ;④第一次向左拐 ,第二次向左拐 .
A. 20°B. 25°C. 30°D. 35°
【答案】A
【解析】
【详解】如图,过点B作BD//l,
北师大版七年级数学下册第二章《相交线与平行线》单元同步练习题(含答案)
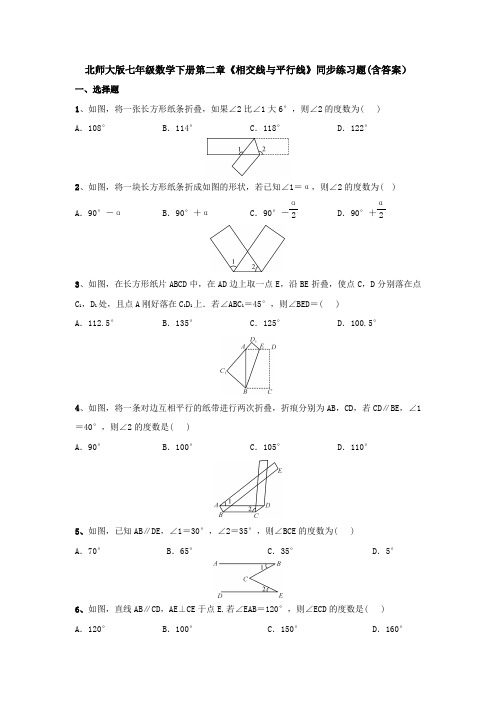
北师大版七年级数学下册第二章《相交线与平行线》同步练习题(含答案)一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为( ) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为( ) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =( ) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是( ) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为( ) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是( ) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于______.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=______.度,再沿BF折叠成图c.则图中的∠CFE=______度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=______度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=______.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=______.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=______.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为______度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.15、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.参考答案一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为(D) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为(C) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =(A) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是(B) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为(B) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是(C) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于105°.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=150度,再沿BF折叠成图c.则图中的∠CFE=135度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=30度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=90°.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?解:分两种情况:当两三角形在点O的同侧时,如图1,设CD与OB相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠OOE=180°-60°-40°-80°.∴∠DOE=∠COD-∠COE=10°.∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°.∵每秒旋转10°,∴旋转的时间为100÷10=10(秒).当两三角形在点O的异侧时,如图2,延长BO与CD相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠COE=180°-60°-40°=80°.∴旋转角为360°-∠COE=360°-80°=280°.∵每秒旋转10°,∴旋转的时间为280÷10=28(秒).综上所述,当旋转了10秒或28秒时,边CD恰好与边AB平行.14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为110度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.图1 图2解:∠APC=α+β.理由:过点P作PE∥AB交AC于点E,∵AB∥CD,∴AB∥PE∥CD.∴α=∠APE,β=∠CPE.∴∠APC=∠APE+∠CPE=α+β.(3)如图3,当P在BD延长线上时,∠CPA=α-β;如图4,当P在DB延长线上时,∠CPA=β-α.图3 图415、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.解:(1)∠A+∠C=90°(2)过点B作BG∥DM,∵BD⊥AM,∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°.又∵AB⊥BC,∴∠CBG+∠ABG=90°.∴∠ABD=∠CBG.∵AM∥CN,BG∥AM,∴CN∥BG.∴∠C=∠CBG.∴∠ABD=∠C.∴∠C+∠BAD=90°.(3)过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG.∴∠ABF=∠GBF.设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC =5∠DBE=5α,∴∠AFC=5α+β.∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=5α+β.在△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+5α+(5α+β)=180°.①由AB⊥BC,可得β+β+2α=90°.②由①②联立方程组,解得α=9°.∴∠ABE=9°.∴∠EBC=∠ABE+∠ABC=9°+90°=99°.。
七年级数学下册第二章测试卷-北师大版(含答案)

七年级数学下册第二章测试卷-北师大版(含答案)[时间:100分钟满分:120分]一、选择题(本大题共6小题,每小题3分,共18分)1.下列关于-3.782的说法正确的是()A.是负数,不是分数B.不是分数,是有理数C.是分数,不是有理数D.是分数,也是负数2.下列运算正确的有()(1)(-4)+(-4)=2×(-4);(2)(-2)3=-23;(3)(2×3)2=2×32;(4)(-2)2n=22n.A.1个B.2个C.3个D.4个3.下列说法错误的是()A.负数的绝对值为正数B.0没有倒数C.一个数的平方一定是正数D.数轴上的两个点表示的数,右边的点对应的数总比左边的大4.有理数a,b在数轴上对应的点的位置如图所示,则下列结论不正确的是()A.b>aB.a+b<0C.ba<0D.a-b>05.大于-2020而小于2021的所有整数的和是()A.-2021B.-2020C.2021D.20206.有下列说法:①若a+b=0,则a与b互为相反数;②若|a|=|b|,则a=b;③若a2=b2,则a=b;④若0>a>b>-1,则1a <1b.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(本大题共6小题,每小题3分,共18分)7.-2020的相反数是.8.用科学记数法表示1203000为.9.如果a与-2互为倒数,那么a2=.11.下面是一列按规律排列的数:-12,24,-38,416,-532,…,请观察此数列的规律,按此规律,则第n 个数应是 . 12.若|a|=2,|b|=3,且ab>0,则a-b 的值是 . 三、解答题(本大题共5小题,每小题6分,共30分) 13.计算:(1)(+4.3)-(-4)+(-2.3)-(+4);(2)(-12)÷6+|-5|×(-2).14.计算:(1)(-14+23-12)×48;(2)(-2)4×(-0.5)4.15.在数轴上表示出下列各数,并用“<”将它们连接起来:-312,0,-2,-(-4.5),|-12|.16.计算:-14-[-5+(0.2×13-1)÷(-125) ].17.若|a|=2,b=-3,c 是最大的负整数,求a+b-c 的值.四、解答题(本大题共3小题,每小题8分,共24分)18.若a 与b 互为相反数,m 与n 互为倒数,c 2=36,求2nm+3a-c+3b 的值.19.已知|x+1|+(2x-y+4)2=0.(1)求x,y的值;(2)求x2-y的值.20.某食品厂从生产的袋装食品中随机抽取20袋样品,检测每袋的质量是否符合标准质量,超过或不足的部分分别用正、负数来表示,记录如下表:与标准质量的差值(单位:g) -5 -2 0 1 3 6袋数 1 4 3 4 5 3(1)这20袋食品平均每袋的质量比标准质量多还是少?多了或少了多少克?(2)若标准质量是450 g,则这20袋食品的总质量是多少?五、解答题(本大题共2小题,每小题9分,共18分)21.已知a,b均为有理数,现我们定义一种新的运算,规定:a#b=a2+ab+3,例如:5#2=52+5×2+3=38.求:(1)(-3)#6的值;#(-9)]-[(-2)#3]的值.(2)[1322.股民小杨上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况:(上涨记为正,下跌记为负)星期一二三四五每股涨跌+2.20 +1.42 -0.80 -2.52 +1.30(2)本周内该股票的最高价是每股多少元?最低价是每股多少元?(3)已知小杨买进股票时付了1.5‰的手续费,卖出时还需要付成交额的1.5‰的手续费和1‰的交易税,如果小杨在星期五收盘前将全部股票卖出,那么他的收益情况如何?六、解答题(本大题共12分)23.如图所示,数轴上的三个点A,B,C表示的数分别为-3,-2,2,试回答下列问题:(1)A,C两点间的距离是多少?(2)若数轴上的点E与点B之间的距离是5,求点E与点C间的距离;(3)若将数轴折叠,使点A与点C重合,则点B与表示哪个数的点重合?为什么?参考答案1.D2.C3.C4.D5.D6.B7.20208.1.203×1069.1410.-1 11.(-1)n n2n 12.1或-113.解:(1)(+4.3)-(-4)+(-2.3)-(+4) =4.3+4-2.3-4 =4.3-2.3 =2.(2)(-12)÷6+|-5|×(-2) =-2+5×(-2) =-2+(-10) =-12.14.解:(1)(-14+23-12)×48=-48×14+48×23-48×12 =-12+32-24 =-4.(2)(-2)4×(-0.5)4 =[(-2)×(-0.5)]4 =14=1. 15.解:如图所示:用“<”连接:-312<-2<0<|-12|<-(-4.5). 16.解:-14-[-5+(0.2×13-1 )÷(-125)]=-1-[-5+(115-1)÷(-75) ]=-1-[-5+(-1415)×(-57 ) ] =-1-(-5+23) =-1-(-413) =-1+413=313.17.解:因为|a|=2,所以a=2或a=-2. 因为c 是最大的负整数,所以c=-1. 当a=2,b=-3,c=-1时, a+b-c =2+(-3)-(-1) =2-3+1 =0.当a=-2,b=-3,c=-1时, a+b-c =-2+(-3)-(-1) =-2-3+1 =-4.综上所述,a+b-c 的值为0或-4.18.解:因为a 与b 互为相反数,所以a+b=0. 因为m 与n 互为倒数,所以mn=1. 因为c 2=36,所以c=6或c=-6. 2nm+3a-c+3b=2nm+3(a+b )-c=2-c.①当c=6时,2-c=2-6=-4; ②当c=-6时,2-c=2+6=8.综上,2nm+3a-c+3b 的值为-4或8.所以x=-1,y=2.(2)当x=-1,y=2时,x 2-y=(-1)2-2=1-2=-1.20.解:(1)由题意,得(-5)×1+(-2)×4+0×3+1×4+3×5+6×3 =-5+(-8)+4+15+18 =24(g), 24÷20=1.2(g).答:这20袋食品平均每袋的质量比标准质量多,多了1.2 g . (2)20×450+24=9024(g).答:这20袋食品的总质量是9024 g . 21.解:(1)(-3)#6=(-3)2+(-3)×6+3=9-18+3=-6. (2)因为13#(-9)=(13)2+13×(-9)+3=19, (-2)#3=(-2)2+(-2)×3+3=1, 所以[13#(-9)]-[(-2)#3]=19-1=-89. 22.解:(1)+2.20+1.42-0.80=2.82(元). 答:星期三收盘时,该股票涨了2.82元. (2)由题意可知周一股价为27+2.20=29.20(元); 周二股价为29.20+1.42=30.62(元); 周三股价为30.62-0.80=29.82(元); 周四股价为29.82-2.52=27.3(元); 周五股价为27.3+1.30=28.6(元).所以本周内该股票的最高价为每股30.62元,最低价为每股27.3元. (3)买进时共支出了27×1000×(1+1.5‰)=27040.5(元),卖出时扣去手续费和交易税后得到的总金额为28.6×1000×(1-1.5‰-1‰)=28528.5(元), 纯收入为28528.5-27040.5=1488(元).答:如果小杨在星期五收盘前将全部股票卖出,他赚了1488元. 23.解:(1)2-(-3)=5,即A ,C 两点间的距离是5.(2)因为点E 与点B 之间的距离是5,所以点E 表示的数是3或-7. 当点E 表示的数是3时,点E 与点C 间的距离为1; 当点E 表示的数是-7时,点E 与点C 间的距离为9.理由:把数轴折叠后,记折点为F.因为A ,C 两点间的距离是5,点F 与A ,C 两点的距离相等, 所以点F 与A ,C 两点的距离都是52, 所以点F 在点A 的右侧52个单位长度处,所以点F 表示的数是-12,所以BF=-12-(-2)=112, 所以-12+112=1,即点B 与表示数1的点重合.。
北师大版七年级数学下册第二章《尺规作图》专项练习试题含答案

七年级数学下册第二章《尺规作图》专项练习班级:_________________ 姓名:_________________ 座号:________________ 评分:一. 选择题 (共10小题,答案写在表格内,否则答案无效)A .刻度尺和圆规B .不带刻度的直尺和圆规C .刻度尺D .圆规2.如图,用尺规作出∠OBF=∠AOB,作图痕迹MN 是( ).A .以点B 为圆心,OD 为半径的圆 B .以点B 为圆心,DC 为半径的圆 C .以点E 为圆心,OD 为半径的圆D .以点E 为圆心,DC 为半径的圆3.我们利用尺规作图可以作一个角()''A O B ∠等于已知角()AOB ∠,如下所示:(1)作射线OA ;(2)以O 为圆心,任意长为半径作弧,交OA 于C ,交OB 于D ; (3)以O '为圆心,OC 为半径作弧,交OA '于'C ; (4)以C '为圆心,OC 为半径作弧,交前面的弧于D ; (5)连接'O D '作射线,O B ''则A O B '''∠就是所求作的角. 以上作法中,错误的一步是( ) A .()2B .()3C .()4D .()54.下面出示的的尺规作图题,题中符号代表的内容正确的是( ) 如图,已知∠AOB ,求作:∠DEF ,使∠DEF =∠AOB作法:(1)以①为圆心,任意长为半径画弧,分别交OA 、OB 于点P 、Q ; (2)作射线EG ,并以点E 为圆心②长为半径画弧交EG 于点D ; (3)以点D 为圆心③长为半径画弧交(2)步中所画弧于点F ; (4)作④,∠DEF 即为所求作的角.A .①表示点EB .②表示PQC .③表示OQD .④表示射线EF5.用直尺和圆规作∠HDG=∠AOB 的过程中,弧②是( )A .以D 为圆心,以DN 为半径画弧B .以M 为圆心,以DN 长为半径画弧C .以M 为圆心,以EF 为半径画弧D .以D 为圆心,以EF 长为半径画弧6.如图,是用直尺和圆规作一个角等于己知角的方法,即作'''A O B AOB ∠=∠.这种作法依据的是( )A .SSSB .SASC .AASD .ASA7.用直尺和圆规作∠HDG =∠AOB 的过程,弧①是( )A .以D 为圆心,以DN 为半径画弧B .以D 为圆心,以EF 为半径画弧C .以M 为圆心,以DN 为半径画弧D .以M 为圆心,以EF 为半径画弧8.下面是黑板上出示的尺规作图题,需要回答横线上符号代表的内容:如图,已知AOB ∠,求作:DEF ∠,使DEF AOB ∠=∠.作法:(1)以为圆心,任意长为半径画弧,分别交OA 、OB 于点P 、Q ;(2)作射线EG ,并以点E 为圆心,长为半径画弧交EG 于点D ;(3)以点D 为圆心,长为半径画弧交(2)步中所画弧于点F ;(4)作,DEF ∠即为所求作的角.A .表示点EB .表示PQC .表示OQD .表示射线EF9.如图,点C 在AOB ∠的OB 边上,用尺规作出了BCD AOB ∠=∠.以下是排乱的作图过程:①以C 为圆心,OE 长为半径画MN ,交OB 于点M . ②作射线CD ,则BCD AOB ∠=∠.③以M 为圆心,EF 长为半径画弧,交MN 于点D .④以O 为圆心,任意长为半径画EF ,分别交OA ,OB 于点E ,F .则正确的作图顺序是( )A .①—②—③—④B .③—②—④—①C .④—①—③—②D .④—③—①—② 10.在△ABC 中,AB=AC ,∠A=80°,进行如下操作:①以点B 为圆心,以小于AB 长为半径作弧,分别交BA 、BC 于点E 、F ; ②分别以E 、F 为圆心,以大于12EF 长为半径作弧,两弧交于点M ;③作射线BM 交AC 于点D , 则∠BDC 的度数为( ).A .100°B .65°C .75°D .105°二.填空题(共7小题)11.在几何里,把只用_________和_________画图的方法称为尺规作图. 12.已知1∠和2∠,画一个角使它等于12∠+∠,画法如下: (1)画AOB ∠=______________.(2)以点O 为顶点,OB 为始边,在AOB ∠的__________作2BOC ∠=∠;则12AOC ∠=∠+∠.13.如图,∠CAD 为△ABC 的外角,按以下步骤作图:①以点B 为圆心,以适当长为半径画弧,交BA 于点M ,交BC 于点N ; ②以点A 为圆心,以BM 长为半径画弧,交AD 于点P ; ③以点P 为圆心,以MN 长为半径画弧,交前一条弧于点Q ; ④经过点Q 画射线AE ,若∠C=50°,则∠EAC 的大小是_____度.14.下列作图中:①用量角器画出90AOB ∠=︒;②作AOB ∠,使2AOB α∠=∠;③连接AB ;④用直尺和三角板作AB 的平行线CD ,属于尺规作图的是__________.(填序号)15.已知∠α和线段m ,n ,求作△ABC ,使BC =m ,AB =n ,∠ABC =∠α,作法的合理顺序为________.(填序号即可)①在射线BD 上截取线段BA =n ;②作一条线段BC =m ;③以B 为顶点,以BC 为一边,作∠DBC =∠α;④连接AC ,△ABC 就是所求作的三角形.16.如图,CAD ∠为ABC ∆的外角,按以下步骤作图:①以点B 为圆心,以适当长为半径画弧,交BA 于点M ,交BC 于点N ;②以点A 为圆心,以BM 长为半径画弧,交AD 于点P ;③以点P 为圆心,以MN 长为半径画弧,交前一条弧于点Q ;④经过点Q 画射线AE .若50C ∠=︒,则EAC ∠的大小是__________度.17.如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:①以点A 为圆心,小于AC 的长为半径.画弧,分别交AB 、AC 于点E 、F ; ②分别以点E 、F 为圆心,大于12EF 的长为半径画弧,两弧相交于点G ; ③作射线AG ,交BC 边于点D ,则∠ADC 的度数为_____.三.解答题18.如图,在△ABC 中,BD 是边AC 上的高.请用尺规作图法,在BD 上求作一点E ,使得∠CED +∠ABD =90°.(保留作图痕迹,不写作法)19.已知:线段c 和αβ∠∠,求作:ABC ,使得AB c A B αβ=∠=∠∠=∠,,(不写作法,但保留作图痕迹)20.已知线段a 及锐角α,用直尺和圆规作ABC ,使B α∠=∠,AB BC a ==.21.尺规作图:已知α∠,β∠,求一个角∠AOB ,使∠AOB =α∠+β∠.(保留作图痕迹)22.如图,已知三角形ABC 和射线EM ,用直尺和圆规按下列步骤作图(保留作图痕迹,不写作法):(1)在射线EM 的上方,作NEM B ∠=∠;(2)在射线EN 上作线段DE ,在射线EM 上作线段EF ,使得DE AB =,EF BC =;(3)连接DF ,观察并猜想:DF 与AC 的数量关系是DF ______AC ,填(“>”、“<”或“=”) 23.按要求作图(1)如图,已知线段,a b ,用尺规做一条线段,使它等于+a b (不要求写作法,只保留作图痕迹)(2)已知:∠α,求作∠AOB=∠α(要求:直尺和圆规作图,不写作法,保留作图痕迹)24.如图,已知ABC 中,AB AC =,点P 在BC 上.(1)试用直尺和圆规在AC 上找一点D ,使CPD BAP ∠=∠(不写作法,但需保留作图痕迹);(2)在(1)的条件下,若2APC ABC ∠=∠;求证://PD AB .25.(1)如图,在直线MN 的异侧有A 、B 两点,按要求画图,并注明画图的依据. 请在图1中直线MN 上画一点D ,使线段AD +BD 最短.依据是 . (2)如图2,已知∠AOB,用圆规和没有刻度的直尺求作∠A'O'B',使∠A'O'B'=∠AOB26.如图,已知锐角△ABC ,点D 是AB 边上的一定点,请用尺规在AC 边上求作一点E ,使∠ADE =∠ABC ,(保留作图痕迹,不写做法)27.如图,已知α∠,β∠.求作:AOB ∠,使AOB αβ∠=∠-∠.(尺规作图,保留作图痕迹,不写作法)28.尺规作图(1)如图所示,已知线段AB ,∠α,∠β,用尺规作一个△ABC,使它的两个角分别为∠CAB=∠α,∠CBA=∠β.(不写作法,保留作图痕迹,图作在空白处)(2)已知:点P 为∠CAB 边上的一点,求作:直线PQ ,使得PQ∥AB29.如图,已知AOB ∠和射线O A ''.(1) 请用尺规作图法,在射线O A ''上作A O B '''∠,使得A O B AOB '''∠=∠; (不要求写作法,保留作图痕迹).(2) 若40AOB ︒∠=,求AOB ∠的余角和补角.30.如图,已知点P 为∠AOB 一边OB 上的一点.(1)请利用尺规在∠AOB 内部作∠BPQ ,使∠BPQ =∠AOB ;(不写作法,保留作图痕迹)(2)根据上面的作图,判断PQ 与OA 是否平行?若平行,请说明理由.31.如图,在△ABC 中,∠C >∠B.(1)请用尺规过点C 作一条射线,与边AB 交于点D ,使△ACD ∽△ABC (保留作图痕迹,不写作法);(2)已知AB =6,AC =4,求AD 的长. 32.作图与计算(1)已知:AOB α∠∠,.求作:在图2中,以OA 为一边,在∠AOB 的内部作.∠AOC =α∠(要求:直尺和圆规作图,不写作法,保留图痕迹.)(2)过点O 分别引射线OA 、OB 、OC ,且∠AOB =65°,∠BOC =30°,求∠AOC 的度数.33.如图,一块大的三角板ABC ,D 是AB 上一点,现要求过点D 割出一块小的三角板ADE ,使∠ADE=∠ABC,(1)尺规作出∠ADE.(不写作法,保留作图痕迹,要写结论) (2)判断BC 与DE 是否平行,如果是,请证明.34.如图,点D 在ABC △的AB 边上,且ACD A ∠=∠. (1)作BDC ∠的平分线DE ,交BC 于点E (用量角器画).(2)在(1)的条件下,BDC ACD A ∠=∠+∠,判断直线DE 与直线AC 的位置关系.35.如图,已知△ABC,(1)作图:试过点C 作直线CD∥AB,(用尺规作图法,保留作图痕迹,不要求写作法); (2)请你写出(1)的作图依据: .参考答案一. 选择题(每小题3分,共10小题)二.填空题(每小题4分,共7小题)11. 没有刻度的直尺圆规12. ∠1, 外部13. 50 14. ②③15. ②③①④ 16. 50 17. 65°三.解答题(共8小题)18.解:如图,点E为所求.19. 解:△ABC为所求作.20. 解:如图所示:△ABC即为所作.21. 解:如图,AOB ∠即为所作.22. 解:(1)如图所示:作法:①以点B 为圆心任意长为半径画圆弧,交AB ,BC 于点G ,H ②再以点E 为圆心以①中的半径画圆弧,交EM 于点P③再以点P 为圆心GH 长为半径画圆弧,与②所画的圆弧交于点N ,连接EN 即可 (2)如图所示:作法:①用圆规取BC 的长度,以点E 为圆心BC 长为半径画弧,交EM 于点F ,则EF=BC ②用圆规取AB 的长度,以点E 为圆心AB 长为半径画弧,交EN 的延长线于点D ,则DE=AB(3)根据EF=BC ,DE=AB ,B NEM ∠=∠可证ABC EDF △≌△,则DF=AC23. 解:(1)作射线CF ,在射线上顺次截取CD=a ,DE=b ,如下图所示,线段CE 即为所求:(2)首先作射线OA ,如下图所示,∠AOB 即为所求:24. 解:解:(1)如图所示.(2)∵2APC APD DPC ABC BAP ABC ∠=∠+∠=∠+∠=∠∴BAP ABC ∠=∠∵BAP CPD ∠=∠∴CPD ABC ∠=∠∴//PD AB .25. 解:(1)D 点为线段AB 与直线MN 的交点,如图.依据为两点之间线段最短.(2)①作任意一射线O A '',如图2;②以O 点为圆心,任意长度为半径作弧交OA 、OB 于点M 、N ,如图1;③以O '点为圆心,同样的长度为半径作弧交O A ''于点M ',如图2;④以点M '为圆心,MN 为半径作弧交③的弧于点N ',如图2;⑤连接O N ''并延长至B ',如图2,则A O B '''∠即为所求的角.26. 解:解:如图所示:通过这个方法作图,可以证明()BGF DAH SSS ≅,就可以得到ADE ABC =∠∠.27. 解:作∠AOC=α∠,然后在∠AOC 内部作∠BOC=β∠,即可得到AOB αβ∠=∠-∠,如下图所示,∠AOB 即为所求.28. 解:(1)如图所示:;(2)如图所示:.29. 解:(1)所作图形如答图2所示,A O B '''∠即为所求.(2) 当40AOB ∠=︒时,AOB ∠的余角=904050︒-︒=︒.AOB ∠的补角18040140=-=︒︒︒.30. 解:(1)如图所示: ;(2)BPQ AOB ∠=∠,//PQ OA ∴(同位角相等,两直线平行).31. 解:(1)如图,CM 即为所求作的射线;(2)在△ABC和△ACD中,∵∠ACD=∠B,∠A=∠A,∴△ABC∽△ACD,∴AB AC AC AD=,∴224863ACADAB===.32. 解:(1)如图所示:∠AOC就是所求的角.(2)分两种情况讨论:①当OC在∠AOB内部时,如图1,∠AOC=∠AOB-∠BOC=65°-30°=35°;②当OC在∠AOB外部时,如图2,∠AOC=∠AOB+∠BOC=65°+30°=95°.33. 解:(1)如图,∠ADE为所作;(2)BC∥DE.理由如下:∵∠ADE=∠ABC,∴BC∥DE.34. 解:(1)如图:(2)DE∥AC,理由:∵∠BDC=∠A+∠DCA,∠A=∠DCA,∴∠BDC=2∠DCA,∵DE平分∠BDC,∴∠BDC=2∠EDC,∴∠EDC=∠DCA,∴DE∥AC.35. 解:(1)(2)同位角相等,两直线平行.。
北师大版七年级数学(下册)第二章测试卷(附参考答案)

数学七下北师测试卷第二章1.图1中共有对顶角( )图1A.5对B.6对C.7对D.8对2.下列说法中:①两条直线被第三条直线所截,同位角相等;②两点之间,线段最短;③相等的角是对顶角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确的个数是( )A.2B.3C.4D.53.下列作图语句正确的是( )A.以点O为圆心作弧B.延长射线AB到点CC.作∠AOB,使∠AOB=∠1D.作直线AB,使AB=a4.如果一个角的补角是150°,那么这个角的余角的度数是( )A.30°B.60°C.90°D.120°5.下列说法错误的是( )A.在同一平面内,两条不平行的直线是相交线B.与同一条直线平行的两条直线必平行C.与同一条直线相交的两条直线必相交D.过直线外一点有且只有一条直线与已知直线平行6.如图2,已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为( )图2A.40°B.60°C.80°D.100°7.如图3,BC⊥AE于点C,CD∥AB,∠B=40°,则∠ECD的度数是( )图3A.70°B.60°C.50°D.40°8.如图4,已知直线AB∥CD,且直线EF分别交AB,CD于M,N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )图4A.28°B.30°C.34°D.56°9.如图5所示,AB∥CD,∠A=88°,∠C=28°,则∠E为( )图5A.64°B.60°C.59°D.56°10.如图6,AB∥CD,则α,β,γ之间的关系是( )图6A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°11.如图7,直线a和直线b相交于点O,∠1=50°,则∠2=.图712.如图8所示,已知∠1=∠2,∠B=40°,则∠3=.图813.如图9,直线l1∥l2,AB⊥CD,∠1=34°,那么∠2=.图914.如图10,AB∥CD,AD⊥AC,∠ADC=32°,则∠CAB的度数是.图1015.如图11所示,添加条件: ,可使AC∥DF;添加条件: ,可使AB∥DE.(每空只填一个条件即可)图1116.将两块三角板的直角顶点重合为如图12所示的位置,若∠BOC=80°,则∠AOD=.图1217.如图13,AB∥CD,BC∥DE,那么∠B+∠D=.图1318.如图14,A,B之间是一座山,一条铁路要通过A,B两点,为此需要在A,B之间挖一条笔直的隧道,在A地测得铁路走向是北偏东63°,那么B地按南偏西度的方向施工,才能使铁路在山腰准确接通.图1419.如图15,∠1=100°,∠2=100°,∠3=120°,求∠4.填空:图15因为∠1=∠2=100°(已知),根据“”,所以m∥n.根据“”∴∠=∠.又∵∠3=120°(已知),∴∠4=.20.如图16,AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的度数.图1621.已知:∠α,线段m,如图17所示,按下列步骤作图.(1)作∠AOB=∠α;(2)在射线OA上,顺次截取OC=CD=DE=m;(3)在射线OB上任取一点P,连接EP;(4)分别过C,D两点作EP的平行线,交OB于M,N;(5)比较OM,MN,NP的大小(借助圆规而不用刻度尺测量).图1722.如图18,已知AB∥CD.(1)判断∠FAB与∠C的大小关系,并说明理由;(2)若∠C=35°,AB是∠FAD的平分线.图1823.如图19,AF平分∠BAC,DE平分∠BDF,且∠1=∠2,试说明DE∥AF,DF∥AC.图1924.如图20,∠ADE=∠B,∠1=∠2,GF⊥AB,试说明:CD⊥AB.解:因为∠ADE=∠B(已知),图20参考答案1.B2.A3.C4.B5.C6.D7.C8.A9.B10.C11.50°12.40°13.56°14.122°15.∠ACB=∠DFE∠B=∠E16.100°17.180°18.6319.内错角相等,两直线平行两直线平行,同位角相等 3 4 120°20.解:因为∠AOC=120°,根据“对顶角相等”,所以∠BOD=120°.因为∠AOC+∠AOD=180°,所以∠AOD=180°-120°=60°.因为OE平分∠AOD,所以∠AOE=∠AOD=30°.21.由作图可知:OM=MN=NP.22.①求∠FAD的度数;②若∠ADB=110°,求∠BDE的度数.解:(1)∠FAB与∠C的大小关系是相等,理由是:因为AB∥CD,所以∠FAB=∠C.(2)①因为∠FAB=∠C=35°,AB是∠FAD的平分线,所以∠FAD=2∠FAB=2×35°=70°.②因为∠ADB=110°,∠FAD=70°,所以∠ADB+∠FAD=110°+70°=180°,所以CF∥BD,所以∠BDE=∠C=35°.23.解:因为AF平分∠BAC,DE平分∠BDF,∠1=∠2,所以∠BDF=∠BAC,所以DF∥AC(同位角相等,两直线平行).又因为∠2=∠BAF(角平分线定义),所以∠1=∠BAF(等量代换),所以DE∥AF(同位角相等,两直线平行).24.所以DE∥BC(同位角相等,两直线平行),所以∠1=∠3(两直线平行,内错角相等).又因为∠1=∠2,所以∠2=∠3(等量代换),所以GF∥DC(同位角相等,两直线平行).又因为GF⊥AB,所以CD⊥AB.。
(完整版)北师大版七年级数学下册第二章测试题及答案,推荐文档

9.(1)∠NOD=90° (2)∠AOC=60°
∠MOD=15°10.∠AEC=90°
出题意图 本着对第二章内容全方位的考察为目的,特为学生设计此套测试 题,考察内容广泛,技巧灵活多样,让学生充分利用所学知识来解 决问题,有助于知识的升华。建议考试时间 100—120 分钟。
“
”
“
”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
北师大版七年级数学下册第二章相交线与平行线专项测试题 附答案解析(一)

第二章相交线与平行线专项测试题(一)一、单项选择题(本大题共有15小题,每小题3分,共45分)1).2、在下列命题中,一定正确的是( ).A. 对顶角相等B. 同旁内角互补C. 内错角相等D. 同位角相等3()4、过一点画已知直线的平行线()A. 不存在或有且只有一条B. 有两条C. 不存在D. 有且只有一条5、平面内三条直线的交点个数可能有()6)7、画一条线段的垂线,垂足在()A. 以上都有可能B. 线段的延长线上C. 线段的端点D. 线段上8)9、在同一平面内,两条直线的位置关系是()A. 平行,垂直或相交B. 垂直或相交C. 平行或相交D. 平行或垂直10)A. 垂直B. 相交或平行C. 平行D. 相交11)12、下列说法中:①棱柱的上、下底面的形状相同;③相等的两个角一定是对顶角;④不相交的两条直线叫做平行线;⑤直线外一点与直线上各点连接的所有线段中,垂线段最短.正确的有()13、下列语句:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;④如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有()14、用一把带有刻度的直角尺,(1)可以画出两条平行线;(2)可以画出一个角的平分线;(3)可以确定一个圆的圆心、以上三个判断中正确的个数是()15、尺规作图的画图工具是()A. 没有刻度的直尺和圆规B. 直尺、量角器C. 三角板、量角器D. 刻度尺、量角器二、填空题(本大题共有5小题,每小题5分,共25分)16、已知两条直线相交,有一组邻补角相等,则这两条直线的位置关系为 .17.18、三条直线相交,最多有个交点.19米,则小明从起跳点到落脚点的距离于”)20、作图题的书写步骤是_______、________、_______,而且要画出_______和_______,保留________.三、解答题(本大题共有3小题,每小题10分,共30分)21、如图,在铁路旁有一城镇,现在要建一火车站,为使城镇的人乘车方便(即距离最近),①请你在铁路边选一点建火车站,②说明理由.2223、如图,用数字标出的八个角中,同位角、内错角、同旁内角分别有哪些?请把它们一一写出来.第二章相交线与平行线专项测试题(一) 答案部分一、单项选择题(本大题共有15小题,每小题3分,共45分)1).【答案】D所以这两个角互为同位角.2、在下列命题中,一定正确的是( ).A. 对顶角相等B. 同旁内角互补C. 内错角相等D. 同位角相等【答案】A【解析】解:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;所以只说同位角相等,内错角相等,同旁内角互补都是错误的,对顶角相等是正确的.故答案应选:对顶角相等.3()【答案】A4、过一点画已知直线的平行线()A. 不存在或有且只有一条B. 有两条C. 不存在D. 有且只有一条【答案】A【解析】解:若点在直线上,过这点不能画已知直线的平行线;若点在直线外,根据平行公理,有且只有一条直线与已知直线平行.5、平面内三条直线的交点个数可能有()【答案】A【解析】解:如图所示,6)【答案】A7、画一条线段的垂线,垂足在()A. 以上都有可能B. 线段的延长线上C. 线段的端点D. 线段上【答案】A【解析】解:由垂线的定义可知,画一条线段的垂线,垂足可以在线段上,可以是线段的端点,也可以在线段的延长线上.8)【答案】B9、在同一平面内,两条直线的位置关系是()A. 平行,垂直或相交B. 垂直或相交C. 平行或相交D. 平行或垂直【答案】C【解析】在同一个平面内,两条直线只有两种位置关系,即平行或相交。
北师大版七年级数学(下)第二章测试卷

七年级数学(下)第二章测试卷学校 班别 姓名 学号 总分一、填空题。
(每空2分,共36分)1、判断两直线平行的三个条件是:① ② ③ 2、两直线平行的三个特征是:① ② ③3、一个角是52度,那么这个角的补角是 度,余角是 度。
4、如图1所示,直线a 、b 、c 两两相交,共构成 对对顶角。
5、如图2所示,已知CD AB //,AD 与BC 相交于点O ,∠A=∠AOB , ∠COD=66°,则∠A= ,∠C= 。
1= 时,AD//BC ;当∠1= 时,DC//AB 。
则∠B= 度,∠C= 度。
二、选择题。
(每题3分,共15分)1、如图6所示,∠1与∠2是一对( )A 、同位角B 、对顶角C 、内错角D 2、下列语句中正确的是( ) A 、 相等的角是对顶角B 、 有公共顶点且相等的角是对顶角C 、 有公共顶点的两个角是对顶角D 、 角的两边互为反向延长线的两个角是对顶角 3、下列说法正确的是( ) A 、 两直线平行,同旁内角相等 B 、 两直线平行,同位角相等C 、 两直线被第三条直线所截,内错角相等D 、 若一个角的两边分别与另一个角的两边平行,则这两个角相等 4、如图7,能与∠1构成同位角的角有( ) A 、2个 B 、3个 C 、4个 D 、5个 5、如图7,能与∠1构成同旁内角的角有( ) A 、2个 B 、3个 C 、4个 D 、5个三、利用尺规作图(共6分)①b AB 、CD 使AB=a+b ;CD=2a-b②(在原图作图)以点B 为顶点,射线BC 为一边,作一角∠EBC ,使得∠EBC=∠A四、求值题。
(共13分)1、如图,AB//CD ,∠1=50°,∠D=∠C ,依次求出∠D 、∠C 、∠B 的度数(7分)2、 如图,已知AB//CD ,∠1=120°,∠3=50°,求∠2和∠4的度数。
(6分)五、在空格内填上推理的理由(每个空格1分,共261、如图,已知AB//DE ,∠B=∠E ,求证:BC//EF证明: AB//DE ( )∴ ∠B= ( )又 ∠B=∠E ( )∴ = (等量代换)∴ // ( )2、已知,如图,∠1=120°,∠2=120°,求证:AB//CD 。
2021-2022学年北师大版七年级数学下册《第2章相交线与平行线》单元综合测试题(附答案)

2021-2022学年北师大版七年级数学下册《第2章相交线与平行线》单元综合测试题(附答案)一.选择题(共8小题,满分40分)1.如图,∠1和∠2是同位角的是()A.B.C.D.2.下列作图语言叙述规范的是()A.过点P作线段AB的中垂线B.在线段AB的延长线上取一点C,使AB=ACC.过点P作线段AB的垂线D.过直线a,b外一点P作直线MN,使MN∥a∥b3.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥OE,且∠AOC:∠COF=2:3,则∠DOF的度数为()A.105°B.112.5°C.120°D.135°4.如图,BD⊥AC于点D,AE⊥BC于点E,CF⊥AB于点F,AE、BD、CF交于点O,则图中能表示点A到直线OC距离的是线段()的长.A.AO B.AE C.AC D.AF5.如图,AB∥CD,∠2=70°,PE平分∠BEF,则∠CPE的度数为()A.70°B.110°C.145°D.160°6.如图,下列条件中,不能判定AD∥BC的是()A.∠1=∠2B.∠BAD+∠ADC=180°C.∠3=∠4D.∠ADC+∠DCB=180°7.如图,AB∥CD,BF,DF分别平分∠ABE和∠CDE,BF∥DE,∠F与∠ABE互补,则∠F的度数为()A.30°B.35°C.36°D.45°8.已知:如图AB∥EF,BC⊥CD,则∠α,∠β,∠γ之间的关系是()A.∠β=∠α+∠γB.∠α+∠β+∠γ=180°C.∠α+∠β﹣∠γ=90°D.∠β+∠γ﹣∠α=90°二.填空题(共8小题,满分40分)9.如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠7;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:.10.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,∠1=30°,则∠2的大小为度.11.如图AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,则∠DEG=°.12.如图,已知AE∥BD,∠1=3∠2,∠2=26°,求∠C=.13.如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为.14.如图,将一副三角板的直角顶点重合,摆放在桌面上,当∠AOC=时,AB所在直线与CD所在直线互相垂直.15.已知∠A的两边与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A=.16.如图,已知∠ABD=∠PCE,AB∥CD,∠AEC的角平分线交直线CD于点H,∠AFD =86°,∠H=22°,∠PCE=°.三.解答题(共6小题,满分40分)17.如图,直线CD,AB相交于点O,∠BOD和∠AON互余,∠AON=∠COM.(1)求∠MOB的度数;(2)若∠COM=∠BOC,求∠BOD的度数.18.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.19.“村村通”是国家的一个系统工程,其中包涵公路、电力、生活和饮用水、电话网、有线电视网、互联网等等,现计划在A,B,C周边修公路,公路从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村,那么要想从C村修路CE,沿什么方向修,可以保证CE与AB平行?20.如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.21.如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:①BD∥CE②DF∥AC.22.已知:AB∥CD,点E在直线AB上,点F在直线CD上.(1)如图(1),∠1=∠2,∠3=∠4.①若∠4=36°,求∠2的度数;②试判断EM与FN的位置关系,并说明理由;(2)如图(2),EG平分∠MEF,EH平分∠AEM,试探究∠GEH与∠EFD的数量关系,并说明理由.参考答案一.选择题(共8小题,满分40分)1.解:根据同位角的定义,观察上图可知,A、∠1和∠2是同位角,故此选项符合题意;B、∠1和∠2不是同位角,故此选项不符合题意;C、∠1和∠2不是同位角,故此选项不符合题意;D、∠1和∠2不是同位角,故此选项不合题意;故选:A.2.解:A、过点P作线段AB的中垂线,叙述错误,故此选项错误;B、在线段AB的延长线上取一点C,使AB=AC,叙述错误,应为BC=AB,故此选项错误;C、过点P作线段AB的垂线,叙述正确;D、过直线a外一点P作直线MN,使MN∥a,不能同时作平行于两条直线的直线;故选:C.3.解:设∠AOC=2α,∠COF=3α,∵∠AOC=∠BOD=2α,∵OE平分∠BOD,∴∠DOE=α,∵OF⊥OE,∴∠EOF=90°,∴∠DOE+∠EOF+∠COF=180°,∴α+90°+3α=180°,∴α=22.5°,∴∠DOF=∠EOF+∠DOE=90°+22.5°=112.5,故选:B.4.解:点A到直线OC的距离的线段长是AF,故选:D.5.解:∵AB∥CD,∠2=70°,∴∠BEF=∠2=70°,∵PE平分∠BEF,∴∠BEP=∠BEF=35°,∵AB∥CD,∴∠CPE=180°﹣∠BEP=145°;故选:C.6.解:A、∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行),故选项不符合题意;B、∵∠BAD+∠ADC=180°,∴AB∥DC(同旁内角互补,两直线平行),故选项符合题意;C、∵∠3=∠4,∴AD∥BC(内错角相等,两直线平行),故选项不符合题意;D、∵∠ADC+∠DCB=180°,∴AD∥BC,(同旁内角互补,两直线平行),故选项不符合题意.故选:B.7.解:∵BF,DF分别平分∠ABE和∠CDE,∴∠1=∠2,∠FBA=∠FBE,∵AB∥CD,∴∠FBA=∠3,∵BF∥DE,∠F与∠ABE互补,∴∠3=∠EDC=2∠2,∠F=∠1,∠F+∠ABE=180°,设∠2=x,则∠3=2x,∠ABE=4x,∴x+4x=180°,解得,x=36°,即∠F的度数为36°,故选:C.8.解:如图,分别过C、D作AB的平行线CM和DN,∵AB∥EF,∴AB∥CM∥DN∥EF,∴∠α=∠BCM,∠MCD=∠NDC,∠NDE=∠γ,∴∠α+∠β=∠BCM+∠CDN+∠NDE=∠BCM+∠MCD+∠γ,又BC⊥CD,∴∠BCD=90°,∴∠α+∠β=90°+∠γ,即∠α+∠β﹣∠γ=90°,故选:C.二.填空题(共8小题,满分40分)9.解:①∠1=∠7,对顶角相等不能判定a∥b,故①不符合题意;②∠3=∠6,可根据内错角相等,两直线平行得到a∥b,故②符合题意;③∠1=∠8,则∠1=∠2,可根据同位角相等,两直线平行得到a∥b,故③符合题意;④∠5+∠8=180°,可得∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b,故④符合题意;故答案为:②③④.10.解:如图,延长F A,由折叠的性质,可得∠3=∠1=30°,∴∠4=180°﹣30°﹣30°=120°,∵CD∥BE,BE∥AF,∴∠ACD=∠4=120°,又∵AC∥BD,∴∠2=180°﹣∠ACD=180°﹣120°=60°.故答案为:60.11.解:∵AB∥CD,∠B=72°,∴∠BEC=108°,∵EF平分∠BEC,∴∠BEF=∠CEF=54°,∵∠GEF=90°,∴∠GED=90°﹣∠FEC=36°.故答案为:36.12.解:∵∠1=3∠2,∠2=26°,∴∠1=78°,∵AE∥BD,∴∠3=∠1=78°,∴∠C=78°﹣26°=52°.故答案为:52°.13.解:∵∠1=70°,∠1与∠3是对顶角,∴∠3=∠1=70°.∵a∥b,点C在直线b上,∠DCB=90°,∴∠2+∠DCB+∠3=180°,∴∠2=180°﹣∠3﹣∠DCB=180°﹣70°﹣90°=20°.故答案为:20°.14.解:当AB⊥直线CD时,AB,BO分别交DC的延长线于M,N点,如图,∴∠BMN=90°,∵∠B=45°,∴∠CNO=∠BNM=45°,∵∠DCO=60°,∠DCO=∠CNO+∠BOC,∴∠BOC=60°﹣45°=15°,∵∠AOB=90°,∴∠AOC=∠AOB+∠BOC=90°+15°=105°;当AB⊥CD时,AB,AO分别交CD于点E,F,∴∠AEC=90°,∵∠A=45°,∴∠CFO=∠AFE=90°﹣45°=45°,∵∠CFO=∠AOD+∠D,∠D=30°,∴∠AOD=45°﹣30°=15°,∵∠COD=90°,∴∠AOC=∠COD﹣∠AOD=90°﹣15°=75°.综上,∠AOC的度数为105°或75°.15.解:设∠B是x,根据题意,得①两个角相等时,如图1:∠B=∠A=x,x=3x﹣40,解得,x=20°,故∠A=20°,②两个角互补时,如图2:x+3x﹣40=180,所以x=55°,3×55°﹣40°=125°综上所述:∠A的度数为:20°或125°.故答案为:125°或20°16.解:∵AB∥CD,∴∠ABD=∠PDB,∵∠ABD=∠PCE,∴∠PDB=∠PCE,∴BD∥CE,∴∠CEG=∠DGH,∵EH平分∠AEC,∴∠CEH=∠AEH,∵∠DGH=∠EGF,∴∠EGF=∠GEF,∵∠AFD=∠AEG+∠EGF=2∠EGF=86°,∴∠EGF=43°,∴∠DGH=43°,∴∠PCE=∠PDG=∠H+∠DGH=65°,故答案为:65.三.解答题(共6小题,满分40分)17.解:(1)∵∠BOD和∠AON互余,∴∠BOD+∠AON=90°,∵∠AON=∠COM,∴∠BOD+∠COM=90°,∴∠MOB=180°﹣(∠BOD+∠COM)=90°;(2)设∠COM=x,则∠BOC=5x,∴∠BOM=4x,∵∠BOM=90°,∴4x=90°,解得x=22.5°,∴∠BOD=90°﹣22.5°=67.5°.18.证明:∵∠A=∠EDF(已知),∴AC∥DF(同位角相等,两直线平行),∴∠C=∠CGF(两直线平行,内错角相等).又∵∠C=∠F(已知),∴∠CGF=∠F(等量代换),∴BC∥EF(内错角相等,两直线平行).19.解:使CE沿北偏东65°方向(或使CE与CB垂直),即可保证CE与AB平行.理由如下:如图,由题意得,AD∥BF,∴∠ABF=180°﹣65°=115°,∴∠ABC=115°﹣25°=90°,要使CE∥AB,则∠ECB=∠CBD=90°,∴CE⊥CB,则CE应沿北偏东65°方向修.20.证明:∵FG⊥AC,HE⊥AC,∴∠FGC=∠HEC=90°(垂线的定义),∴FG∥HE(同位角相等,两直线平行),∴∠3=∠4(两直线平行,内错角相等),又∵∠1=∠2,∴∠1+∠3=∠2+∠4,即∠DEF=∠EFC,∴DE∥BC(内错角相等,两直线平行).21.证明:∵∠1=∠4,∠1=∠2,∴∠2=∠4,∴BD∥CE,∴∠C=∠DBA,∵∠C=∠D,∴∠D=∠DBA,∴AC∥DF.22.解:(1)①∵AB∥CD,∴∠1=∠3,∵∠1=∠2,∠3=∠4,∴∠2=∠4=36°;②位置关系是:EM∥FN.理由:由①知,∠1=∠3=∠2=∠4,∴∠MEF=∠EFN=180°﹣2∠1,∴∠MEF=∠EFN∴EM∥FN(内错角相等,两直线平行)(2)关系是:∠EFD=2∠GEH.理由:∵EG平分∠MEF,∴∠MEG=∠GEH+∠HEF①∵EH平分∠AEM,∴∠MEG+∠GEH=∠AEF+∠HEF②由①②可得:∴∠AEF=2∠GEH,∵AB∥CD,∴∠AEF=∠EFD,∴∠EFD=2∠GEH.。
北师大版七年级下册数学第二章测试卷及答案共3套

第二章 相交线与平行线单元测试一、选择题l 、如果一个角的补角是 150,那么这个角的余角的度数是( )A.30B.60C.90D.1202、如图,下列条件中,能判定DE//AC 的是( )A.EDC=EFC ∠∠B.AFE ACD ∠=∠C.34∠=∠D.12∠=∠3、如图,//,AB CD 下列结论中错误的是( )A.12∠=∠B.25180∠+∠=C.23180∠+∠=D.34180∠+∠=4、如图,//D,1128,AB C ∠=FG 平分,EFD ∠则2∠的度数是( )A.46B.23C.26D.24 5、如图,,//,AD BC DE AB ⊥则B ∠和1∠的关系是( )A.相等B.互补C.互余D.不能确定6、将直尺与三角尺按如图所示的方式叠放在一起,在图中标记的角中,与∠1互余的角有( )个.A.2B.3C. 4D.57、如图,把矩形ABCD 沿EF 对折,若150,∠=则FED ∠等于( )A.50B.80C.65D.1158、已知两个角的两边互相平行,这两个角的差是o 40,则这两个角分别是( )A.140100和B.11070和C.7030和D.150110和9、一辆汽午在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )A.第一次右拐60,第二次左拐120 B.第一次左拐60,第二次右拐60 C.第一次左拐60,第二次左拐120 D.第一次右拐60,第二次右拐6010、把一张对面互相平行的纸条折成如图那样,EF 是折痕,若32EFB ∠=则下列结论正确有( )(1)32 (2)116'C EF AEC ∠=∠=(3)D 116 (4)=64BF BGE ∠=∠A 、1个B 、2个C 、3个D 、4个 二、填空题11、如图,已知直线a b 、被直线c 所截,//,1130,a b ∠=则2∠= .12、如图,//,AB CD 如果2,DHG AGE ∠=∠则DHG ∠= .13、一个角的余角是这个角的补角的1,3则这个角是 度.14、如图,40,60,ABC ACB ∠=∠=BO CO 、平分ABC ∠和ACB ∠,DE 过O 点,且//DE BC ,则BOC ∠= .15、如图,已知//,70AB DE B ∠=,CM 平分,BCE CN CM ∠⊥,那么DCN ∠= .16、如图,//,120,30AB CD BAE DCE ∠=∠=,则AEC ∠= .17、如图,直线AB 、CD 、EF 相交于点O ,140,70,AOD DOE ∠=∠=则AOF ∠= . 18、如图,DB 平分,//,80,ADE DE AB CDE ∠∠=则ABD ∠= ,A ∠= . 19、如图, 已知////,60,10,AB CD EF B D ∠=∠=EG 平分BED ∠,则GEF ∠= .20、如图,已知//,AB CD ABE ∠和CDE ∠的平分线相交于F ,140,E ∠=则BFD ∠的度数为 . 三、作图题(要求必须用尺规作图,不写作法,留下作图痕迹,要有结论)21、如图,一块大的三角板ABC ,D 是AB 上一点,现要求过点D 割出一块小的三角板ADE ,使//,DE BC 请作出DE.四、证明题22、已知,如图,//,,701150,EF BC A D AOB C ∠=∠∠=∠+∠=,求B ∠的度数.23、已知:如图,//D,D AC B A ∠=∠,求证:.E F ∠=∠24、如图,已知//,AB CD 猜想图1、图2、图3中,,B BED D ∠∠∠之间有什么关系?请用等式表示出它们的关系。
北师大版七年级数学下册第二章《相交线与平行线》单元测试卷附答案

第二章《相交线与平行线》单元测试卷(新题型卷共23小题,满分120分,考试用时90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.已知∠A=25°,则∠A的补角等于()A.65°B.75°C.155°D.165°2.如图,直线a与直线c相交于点O,则∠1的度数是()A.60°B.50°C.40°D.30°第2题图第3题图第4题图3.如图,∠1=15°,AO⊥CO,直线BD经过点O,则∠2的度数为()A.75°B.105°C.100°D.165°4.如图,直线c与直线a,b都相交.若a∥b,∠1=55°,则∠2=()A.60°B.55°C.50°D.45°5.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2=()A.55°B.65°C.75°D.85°第5题图第6题图第7题图第8题图6.如图,下列说法中正确的是()A.若∠2=∠4,则AB∥CDB.若∠BAD +∠ADC=180°,则AB∥CDC.若∠1=∠3,则AD∥BCD.若∠BAD +∠ABC=180°,则AB∥CD7.(传统文化)一条古称在称物时的状态如图所示,已知∠1=80°,则∠2=()A.20°B.80°C.100°D.120°8.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2=()A.90°B.65°C.60°D.50°9.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4等于()。
(完整版)七年级数学下册第二章单元测试题及答案

北师大版七年级数学下册第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=500,则∠2等于【】A.600B.500C.400D.3002、如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关系是()A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.①B.②③C.④D.②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为()A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC∥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,∠1与∠2的关系是( )更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( ) A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④评卷人得分二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
【重磅】北师大七数下第二章测试卷

第二章测试卷一、单项选择题1、已知∠α=35°19′,则∠α的余角等于()A 144°41′B144°81′C54°41′D54°81′2、下午2点30分时,时钟的分针与时针所成角的度数为()A90°B105°C120°D135°3、一副三角板不能拼出的角的度数是(拼接要求:既不重叠又不留空隙)()A75°B105°C120°D125°4、已知:如图,L1∥L2,∠1=50°,则∠2的度数是()A135°B130°C50°D40°5、如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55º,则∠2的度数为()A35ºB45ºC55ºD125º6、如图,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是()7、已知:如图,直线AB、CD被直线EF所截,则∠EMB的同位角是()8、如图,直线a∥b,直线c是截线,如果∠1=50°,那么∠2等于()9、如图,AB∥CD,则图中∠1、∠2、∠3关系一定成立的是()10、若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有()A2对B3对 C 4对 D 6对二、填空题11、将一个平角n等分,每份是15°,那么n等于________。
12、如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=_______。
13、已知∠α与∠β互余,且∠α=40°,则∠β的补角为________度.14、如图,已知直线,∠1=40°,那么∠2=____度.15、如图,AB∥CD,∠B=680,∠E=200,则∠D的度数为______.16、如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=60°,则∠2=___度。
北师大版七年级下册数学第二章相交线与平行线测试题

24.△ABC中,AC=BC,∠ACB=α,点D是平面内不与点A和点B重合 一点,连接DB,将线段DB绕点D顺时针旋转α得到线段DE,连接AE、BE、CD.
(1)如图①,点D与点A在直线BC 两侧,α=60°时, 的值是;直线AE与直线CD相交所成的锐角的度数是度;
(1)求点A,B的坐标;
(2)当CD∥x轴时,求抛物线 函数表达式;
(3)连接BD,当BD最短时,请直接写出抛物线的函数表达式.
(2)如图②,点D与点A在直线BC两侧,α=90°时,求 的值及直线AE与直线CD相交所成的锐角∠AMC的度数;
(3)当α=90°,点D在直线AB的上方,S△ABD= S△ABC,请直接写出当点C、D、E在同一直线上时, 的值.
25.如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2﹣5ax+4a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧.
又∠1和∠D互余,即∠1+∠D=90°,
∴∠1=∠C,
∴AB∥CD.
15.证明:∵∠ACB=90°,
∴∠B+∠A=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠B=∠ACD,
∵∠AEF=∠B,
∴∠AEF=∠ACD,
∴EF∥CD.
九年级(上)期末数学试卷
一.选择题(共10小题)
12.解:∠1和∠3是对顶角;∠1和∠2是邻补角,∠2与∠3是邻补角;
∠1和∠4是同位角,∠2与∠4是同旁内角,∠3与∠4是内错角.
北师大版数学七年级下第二章第2---4节能力检测题含答案

2.2 探索直线平行的条件一、单选题1.对于图中标记的各角,下列条件能够推理得到a∥b的是( )A. ∠1=∠2B. ∠2=∠4C. ∠3=∠4D. ∠1+∠4=180°2.如图,下列能判定AB∥CD条件有()个、( 1 )∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A. 4B. 3C. 2D. 13.学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A. ①②B. ②③C. ③④D. ①④4.下列说法错误的结论有()( 1 )相等的角是对顶角;(2)平面内两条直线的位置是相交,垂直,平行;(3)若∠A与B∠互补,则12∠A与12∠B互余,(4)同位角相等.A. 1个B. 2个C. 3个D. 4个5.下列图形中,∠1和∠2是同位角的是()A. B. C. D.6.如图,已知直线c与a,b分别交于点A,B,且∠1=120º,当∠2=()时,直线a ∥b.A. 60ºB. 120ºC. 30ºD. 150º7.某城市有四条直线型主干道分别为l1,l2,l3,l4,l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角()对.A. 4B. 8C. 12D. 168.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC中,相互平行的线段有()A. 4组B. 3组C. 2组D. 1组9.下列图中∠1和∠2不是同位角的是()A. B. C. D.10.三角形的三个内角两两一定互为()A. 同位角B. 内错角C. 同旁内角D. 邻补角二、填空题11.如图,直线a与直线b、c分别相交于点A、B,将直线b绕点A转动,当∠1=∠________时,c∥b12.若想检验一块儿破损的木板的两条直的边缘AB,CD是否平行,你的办法是________.(工具不限,可结合图形进行说明,只要能说清思路即可)13.阅读下面材料:在数学课上,老师提出如下问题:小凡利用两块形状相同的三角尺进行如下操作:老师说:“小凡的作法正确.”请回答:小凡的作图依据是________14.(2017•吉林)我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是________.15.已知:如图,∠1=∠2,求证:AB∥CD∵∠1=∠2,(已知)又∠3=∠2,(________)∴∠1=________.(________)∴ AB∥CD.(________,________)16.如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件________或________,使EF∥AB.三、解答题17.如图所示,在一个三角形支架上要加一根横杆DE,使DE∥BC,请你用尺规作出DE的位置.(不写作法,保留作图痕迹)18.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.19.如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,∠BDE=120°,写出图中平行的直线,并说明理由.20.如图,已知CD平分∠ACB,∠1=∠2,试判断AC与DE的位置关系,并说明理由.21.如图:(1)如果∠1=________,那么DE∥AC,理由:________.(2)如果∠1=________,那么EF∥BC,理由:________.(3)如果∠FED+∠EFC=180°,那么________,理由:________.(4)如果∠2+∠AED=180°,那么________,理由:________.22.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB;(2)求∠DFC的度数.参考答案一、单选题1. D2. B3.C4.C5.D6.B7.D8.B9.C 10.C二、填空题11.312.画一条直线截线段AB与CD,测量一对同位角,如果相等,则AB∥ CD,反之,则不平行;13.内错角相等,两直线平行14.同位角相等,两直线平行15.对顶角相等;∠;等量代换;同位角相等;两直线平行16.∠AEF=∠FAE;∠CFE=∠BAC;三、解答题17.解:如图所示18.证明:∵∠1=∠2,∠3=∠E,∴∠1+∠3=∠2+∠E.∵∠2+∠E=∠5,∴∠1+∠3=∠5,∴∠ADC=∠5,∴AD∥BE.19.解:EF∥BC,DE∥AB,理由是:∵∠1:∠2:∠3=2:3:4,∠1+∠2+∠3=180°,∴∠1=40°,∠2=60°,∠3═80°,∵∠AFE=60°,∠BDE=120°,∴∠AFE=∠2,∠BDE+∠2=180°,∴EF∥BC,DE∥AB20.解:AC∥DE,理由:∵CD平分∠ACB,∴∠1=∠ACD,∵∠1=∠2,∴∠ACD=∠2,∴AC∥DE.21.(1)∠C;同位角相等,两直线平行(2)∠FED;内错角相等,两直线平行(3)DE∥AC;同旁内角互补,两直线平行(4)DE∥AC;同旁内角互补,两直线平行22.(1)解:∵CF平分∠DCE ,∠DCE=90°∴又∵∠3=45°∴∠1=∠3∴CF∥AB;(2)解:∵∠D=30°∠1=45°∴∠DFC=180°-∠D-∠1=105°2.3 平行线的性质类型一. 平行线的性质1. 如图,AB∥CD, ∠D=42º, ∠CBA=64º, 则∠CBD的度数是( )A. 42ºB. 64ºC. 74ºD. 106º(1题)2. 下列选项中,过点P画AB的垂线CD, 三角板放法正确的是( )3. 如图,直线a, b被直线c所截,a∥b, ∠1=80º, 则∠2=()A. 130ºB. 120ºC. 110ºD.100º4. 如图,快艇从P处向正北航行到A处时,向左转50º航行到B处,再向右转80º继续航行,此时的航行方向为( )A. 北偏东30ºB. 北偏东80ºC. 北偏西30ºD. 北偏西50º5. 如图,直线AB∥CD, EF⊥CD, 垂足为F, 交AB于点E, 射线FG交AB于点H, 若∠1=30º,则∠2的度数为( )A. 30ºB. 40ºC. 50ºD.60º6. 将一块直角三角板和一把直尺按如图所示的方式放置,如果∠=43º,则∠的度数是( )A. 43ºB. 47ºC. 30ºD. 60º7. 如图,把一张长方形纸片ABCD沿着EF折叠后,点D, C分别落在, 的位置,若∠EFB=65º, 则∠AE的度数为______º8. 如图,∠ACB=60º, ∠ABC=50º, BO, CO分别是∠ABC, ∠ACB的平分线,EF经过O点且平行于BC, 则∠BOC=______º9. 如图,CD⊥AB,垂足为D, 过点D做DE∥BC交AC于E, 做EF∥AB交CD于F, 交BC于G, 若∠B=35º,求∠EDC和∠DEF的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七北数(下)第二章测试卷
一.选择题(共6小题)
1.下列作图语句正确的是()
A.以点O为顶点作∠AOB B.延长线段AB到C,使AC=BC C.作∠AOB,使∠AOB=∠αD.以A为圆心作弧
2.如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是()
A.线段CA的长B.线段CD的长
C.线段AD的长D.线段AB的长
3.如图,两条直线AB,CD交于点0,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM等于()
A.40°B.120°C.140°D.100°
4.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在()
A.A点B.B点C.C点D.D点
5.如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为()
A.70°B.100°C.110°D.120°
6.如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转()
A.70°B.50°C.30°D.20°
二.填空题(共4小题)
7.图中是对顶角量角器,用它测量角的原理是.
8.如图,已知直线AB与CD交于点O,ON平分∠DOB,若
∠BOC=110°,则∠AON的度数为度.
9.如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则∠1=度.
10.如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据.
三.解答题(共3小题)
11.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
12.如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,且∠DEC=90°,试判断AD与BC的位置关系,并说明理由.
13.如图,已知BC∥GE,AF∥DE,∠1=50°.
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.。
