计算机逻辑运算和逻辑部件-精品文档
计算机中常用的逻辑部件

2.1 三种基本逻辑操作及Boole代数
基本概念
逻辑图是用规定的图形符号来表示逻辑函数运算关系的 网络图形。
H=XY+XY
H=X○+ Y
2.1 三种基本逻辑操作及Boole代数
基本概念
卡诺图是一种几何图形,用来简化逻辑函数表达式,并 将表达式化为最简形式的有用工具。
以3-8译码器为例
module decode(in, out); input [2:0] in; output [7:0] out;
assign out[0] = (!in[2]) && (!in [1]) && (!in[0]); assign out[1] = (!in[2]) && (!in [1]) && ( in[0]); assign out[2] = (!in[2]) && ( in [1]) && (!in[0]); assign out[3] = (!in[2]) && ( in [1]) && ( in[0]); assign out[4] = ( in[2]) && (!in [1]) && (!in[0]); assign out[5] = ( in[2]) && (!in [1]) && ( in[0]); assign out[6] = ( in[2]) && ( in [1]) && (!in[0]); assign out[7] = ( in[2]) && ( in [1]) && ( in[0]);
第二章微型计算机基础知识

教学目标:
1.了解基本的逻辑电路和逻辑代数。 2. 掌握微机中基本部件的符号及性能。 3.掌握总线的基本概念、作用及使用。 4.掌握控制字的概念及用法。 5. 掌握依照控制字读写存储器的过程。 6.掌握微机系统的组成与分类 7.掌握微机的外部结构和基本工作原理
教学重点: 1. 掌握微机中基本部件的符号及性能。 2.掌握总线的基本概念、作用及使用。 3.掌握控制字的概念及用法。 4. 掌握依照控制字读写存储器的过程。 5.掌握微机的外部结构和基本工作原理 教学难点: 1.总线的基本概念、作用及使用 2.掌握控制字的概念及用法。 3.掌握依照控制字读写存储器的过程。
1.功能强 2.可靠性强 3.价格低 4.适应性强
5.周期短、见效快
6.体积小、重量轻、耗电省
7.维护方便
四、微型计算机的性能指标 衡量一台微机性能的优劣,主要由它的 系统结构、硬件组成、系统总线、外部设 备以及软件配置等因素来决定。具体体现 在以下几个主要技术指标上。 1.字长 微机的字长是指微处理器内部一次可以 并行处理二进制代码的位数。它与微处理 器内部寄存器以及CPU内部数据总线宽度 一致,字长越长,所表示的数据精度就越 高。
(2)第二个控制字是: CpEpLmEr =0001 即Er=1,令ROM放出数据。 也就是说,当Er为高电平,R0中的8位 数据就被送到W总线上去。这样的动作 不需等待 时钟脉冲的同步讯号。 (3)第三个控制字是: CpEpLmEr=1000 即Cp=1,这是命令PC加1,所以PC=0001 这是在取数周期完了时,要求PC进一步 ,以便为下一条指令准备条件。
六、存储器的符号
1.只读存储器(ROM) 只存储固定程序的存储器,一旦写入 后,一般不能改变。即不能再写入新的 字节,而只能从中“读”出其所存储的内 容。 (1)通用的写法是m×nROM
2:计算机的逻辑部件

四位一组的组进位传递函数PN为“1”的条件为: (1)X3,Y3中有一个为“1”。 (2)同时X2,Y2中有一个为“1”。 (3)同时X1,Y1中有一个为“1”。 (4)同时X0,Y0中有一个为“1”。 依此,可得PN的表达式为 PN=P3P2P1P0
把第0片ALU向第Ⅰ片、第Ⅰ片向第Ⅱ片、第Ⅱ片向第Ⅲ片传送 的进位分别命名为Cn+X、Cn+Y、Cn+Z。 把第0片ALU向第Ⅰ片、第Ⅰ片向第Ⅱ片、第Ⅱ片向第Ⅲ片的进 位传递表示为PN0、 PN1、 PN2。 GN0、 GN1、 GN2也是同理。
下图给出了二输入四输出译码器的逻辑图。译码器 中常设置“使能”控制端,当该端为“1”时,译码 器功能被禁止,此时所有输出均为“1”。使能端的 一个主要功能是用来扩充输入变量数。
二输入四输出译码器
用两片三输入八输出译码器扩展成一个四输入十六 输出译码器的实例。
(5) 数据选择器 数据选择器又称多路开关,它从多个输入通道中选 择某一个通道的数据作为输出,起到选择信号的作 用。
由功能表可知,当全加器的输入均取反码时,它的输 出也均取反码。据此,可把它们以“与非”、“或 非”、“与或非”的形式进行改写,形式如下: C1= P1+ G1C 0 C2= P2+ G2 P + G2G1C0 1
C3= P3+ G3 P + G3G2 P1+ G3 G2 G C0 2 1
C4= P + G4 P + G G3 P2+ G4 G3 G P1+ G G G G C 4 3 4 2 4 3 2 1 0 注意与非运算和或非运算!
正 逻
S3 H S2 L S1 L S0 L M=H 逻辑运算 A+B A B
计算机组成原理02计算机的逻辑部件

算决定的。
(2)逻辑函数的表示方法
逻辑表达式——由逻辑变量和与、或、非三种运算符 所构成的表达式
真值表——将输入逻辑变量的各种可能取值和相应的 函数值排列在一起而组成的表格。
逻辑图——用规定的图形符号来表示逻辑函数运算关 系的网络图形。
运算法则: 0·0=0,0·1=0,1·0=0,1·1=1
2、逻辑代数中的三种基本运算——或运算
决定某一事件发生的所有条件中,只要有一个或一个以上的条 件具备,这一事件就会发生,这种因果关系称为或逻辑。
A +U
B
F
或逻辑真值表
A
B
F
0
0
0
0
1
1
A ≥1 F
B A
F B
F AB 或F A B
卡诺图——是一种几何图形,主要用来化简逻辑函数 表达式。
波形图——用电平的高、低变化动态表示逻辑变量值 变化的图形。
硬件描述语言——采用硬件描述语言来描述逻辑函数 并进行逻辑设计的方法。目前应用最为广泛的有 ABLE-HDL、VHDL等。
逻辑表达式
逻辑表达式的书写及省略规则:
(1)进行非运算可不加括号。例如,A、A B等 (2)与运算符一般可省略。例如,A • B可写成AB (3)在一个表达式中,如果既有与运算,又有或运算,则按先与后或 的规则省去括号。例如,(A • B)(C • D)可写成AB CD (4)由于与运算和或运算都满足结合律,因此,(A B) C或A (B C)
直观明了。输入变量取值一旦确定之后,即可在 真值表中查出相应的函数值。
把一个实际逻辑问题抽象成为数学问题时,使用 真值表是最方便的。
精品文档-计算机组成与系统结构(裘雪红)-第3章

(4) 运算结果为补码表示。
第3章 运算方法与运算器
10
2. 溢出判断 1) 溢出的概念 例3.4 有两个定点整数63和85,利用补码加法求63+85=? 解 根据题意,用8位二进制补码表示63和85:
第3章 运算方法与运算器
11
例3.5 设正整数X=+1000001,Y= +1000011,若用8位补 码表示,则[X]补=01000001,[Y]补=01000011,求[X+Y]补。
第3章 运算方法与运算器
15
(2) 进位判决法。若Cn-1为最高数值位向最高位(符号位)的 进位,Cn表示符号位的进位(即进位标志CF),则判别溢 出的逻辑表达式为
(3-4)
OF=Cn-1⊕Cn
溢出判定如表3.1所示。在例3.6的运算过程中,Cn-1为0而 Cn为1 ,故Cn-1⊕Cn=1,表示运算结果有溢出。
第3章 运算方法与运算器
28
图 3.3 四位先行进位链电路
第3章 运算方法与运算器
29
5. BCD数加法器 1) 8421 BCD码
第2章中已详细地介绍了BCD码。在所描述的几种BCD码中, 计算机中应用最广泛的是8421 BCD码。8421 BCD码只利用了四 位二进制编码的0000~1001这十种来表示十进制数的0~9,剩余的
(3-6)
第3章 运算方法与运算器
19
3. 一位全加器的实现
设一位全加器的输入分别为Xi和Yi,低一位对该位的进位 为Ci, 全加器的结果和向高一位的进位分别用Zi和Ci+1表示, 则 一位全加器所实现的逻辑表达式如下:
(3-7)
(3-8)
第3章 运算方法与运算器
20
实现上述逻辑功能的一位全加器的逻辑电路及其框图分别
计算机逻辑部件

计算机逻辑部件
计算机逻辑部件是计算机中用于处理和执行逻辑运算的基本组件。
这些部件是构成计算机中央处理器(CPU)的重要组成部分,负责执行各种算术和逻辑操作。
常见的计算机逻辑部件包括:
逻辑门(Logic Gates):逻辑门是计算机中最基本的逻辑部件,用于执行逻辑运算,如与门、或门、非门等。
所有计算机的逻辑运算都是通过组合不同类型的逻辑门来实现的。
加法器(Adder):加法器用于执行二进制的加法运算,是计算机中常见的算术逻辑单元(ALU)的一部分。
算术逻辑单元(ALU):ALU是计算机中用于执行算术和逻辑运算的核心部件。
它可以执行加法、减法、逻辑与、逻辑或等操作。
寄存器(Register):寄存器是用于暂时存储数据的高速存储单元。
计算机的数据处理通常涉及将数据暂时存储在寄存器中,然后进行操作和传输。
随机存取存储器(RAM):RAM是用于临时存储数据和程序的主要内存。
它允许CPU快速读取和写入数据。
可编程逻辑器件(例如FPGA):这些器件允许用户根据需要配置和重新配置逻辑功能,从而实现特定的计算任务。
这些逻辑部件的组合和协调,使计算机能够进行复杂的计算和数据处理,从而实现各种应用和功能。
在现代计算机中,这些部件已经高度集成,并且存在于微处理器芯片中,使得计算机能够执行高效和多样化的任务。
计算机原理实验一 运算器实验 操作步骤[精品文档]
![计算机原理实验一 运算器实验 操作步骤[精品文档]](https://img.taocdn.com/s3/m/1acc4948af45b307e9719708.png)
1.1 基本运算器实验1.1.1 实验目的(1) 了解运算器的组成结构。
(2) 掌握运算器的工作原理。
1.1.2 实验设备PC机一台,TD-CMA实验系统一套。
1.1.3 实验原理本实验的原理如图1-1-1所示。
运算器内部含有三个独立运算部件,分别为算术、逻辑和移位运算部件,要处理的数据存于暂存器A和暂存器B,三个部件同时接受来自A和B的数据(有些处理器体系结构把移位运算器放于算术和逻辑运算部件之前,如ARM),各部件对操作数进行何种运算由控制信号S3…S0和CN来决定,任何时候,多路选择开关只选择三部件中一个部件的结果作为ALU的输出。
如果是影响进位的运算,还将置进位标志FC,在运算结果输出前,置ALU 零标志。
ALU中所有模块集成在一片CPLD中。
逻辑运算部件由逻辑门构成,较为简单,而后面又有专门的算术运算部件设计实验,在此对这两个部件不再赘述。
移位运算采用的是桶形移位器,一般采用交叉开关矩阵来实现,交叉开关的原理如图1-1-2所示。
图中显示的是一个4X4的矩阵(系统中是一个8X8的矩阵)。
每一个输入都通过开关与一个输出相连,把沿对角线的开关导通,就可实现移位功能,即:(1) 对于逻辑左移或逻辑右移功能,将一条对角线的开关导通,这将所有的输入位与所使用的输出分别相连,而没有同任何输入相连的则输出连接0。
(2) 对于循环右移功能,右移对角线同互补的左移对角线一起激活。
例如,在4位矩阵中使用‘右1’和‘左3’对角线来实现右循环1位。
(3) 对于未连接的输出位,移位时使用符号扩展或是0填充,具体由相应的指令控制。
使用另外的逻辑进行移位总量译码和符号判别。
运算器部件由一片CPLD实现。
ALU的输入和输出通过三态门74LS245连到CPU内总线上,另外还有指示灯标明进位标志FC和零标志FZ。
请注意:实验箱上凡丝印标注有马蹄形标记‘’,表示这两根排针之间是连通的。
图中除T4和CLR,其余信号均来自于ALU单元的排线座,实验箱中所有单元的T1、T2、T3、T4都连接至控制总线单元的T1、T2、T3、T4,CLR都连接至CON单元的CLR按钮。
计算机组成原理--实验二算术逻辑运算实验
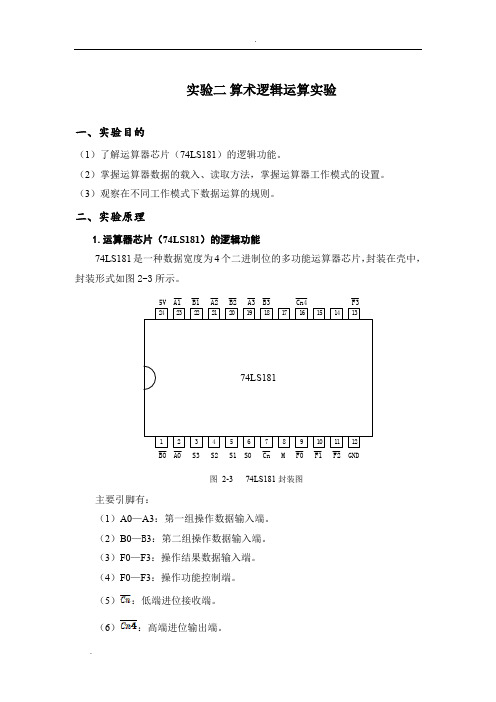
实验二算术逻辑运算实验一、实验目的(1)了解运算器芯片(74LS181)的逻辑功能。
(2)掌握运算器数据的载入、读取方法,掌握运算器工作模式的设置。
(3)观察在不同工作模式下数据运算的规则。
二、实验原理1.运算器芯片(74LS181)的逻辑功能74LS181是一种数据宽度为4个二进制位的多功能运算器芯片,封装在壳中,封装形式如图2-3所示。
5V A1 B1 A2 B2 A3 B3 Cn4 F3BO A0 S3 S2 S1 S0 Cn M F0 F1 F2 GND图2-374LS181封装图主要引脚有:(1)A0—A3:第一组操作数据输入端。
(2)B0—B3:第二组操作数据输入端。
(3)F0—F3:操作结果数据输入端。
(4)F0—F3:操作功能控制端。
(5):低端进位接收端。
(6):高端进位输出端。
(7)M:算数/逻辑功能控制端。
芯片的逻辑功能见表2-1.从表中可以看到当控制端S0—S3为1001、M为0、为1时,操作结果数据输出端F0—F3上的数据等于第一组操作数据输入端A0—A3上的数据加第二组操作数据输入端B0—B3上的数据。
当S0—S3、M 、上控制信号电平不同时,74LS181芯片完成不同功能的逻辑运算操作或算数运算操作。
在加法运算操作时,、进位信号低电平有效;减法运算操作时,、借位信号高电平有效;而逻辑运算操作时,、进位信号无意义。
2.运算器实验逻辑电路试验台运算器实验逻辑电路中,两片74LS181芯片构成一个长度为8位的运算器,两片74LS181分别作为第一操作数据寄存器和第二操作数据寄存器,一片74LS254作为操作结果数据输出缓冲器,逻辑结构如图2-4所示。
途中算术运算操作时的进位Cy判别进位指示电路;判零Zi和零标志电路指示电路,将在实验三中使用。
第一操作数据由B-DA1(BUS TO DATA1)负脉冲控制信号送入名为DA1的第一操作数据寄存器,第二操作数据由B-DA2(BUS TO DATA2)负脉冲控制信号送入名为DA2的第二操作数据寄存器。
计算机组成原理数据的机器运算

3
1、全加器(FA)
全加器真值表
全加器(FA)是最基本 的运算单元,由它构成 加法器。
全加器有三个输入量: 操作数Ai、Bi、以及低 位传来的进位信号Ci-1 。
全加器有两个输出量: 本位和Si、以及向高位 的进位信号Ci。
Ai 0 0 0 0 1 1 1 1
Bi 0 0 1 1 0 0 1 1
27
2、补码加减溢出的判别
例3、X=1011,Y=111 求X+Y。 解:[X]补=0,1011,[Y]补=0,0111 0,1011 (+11) 0,0111 (+7) 1,0010 例4、X=-1011,Y=-111 求X+Y。 解:[X]补=1,0101,[Y]补=1,1001 1,0101 (-11) 1,1001 (-7 ) 0,1110
参加运算的操作数用补码表 示。 补码的符号位与数值位同时 参加运算。 若做加法,则两数补码直接 相加; 若做减法,用被减数与减数 的机器负数相加。 运算结果为和、差的补码。 注:机器负数等于补码连同 符号位按位求反,末位加1。
26
补码加减示例
例1、A=0.1011, B=-0.1110,求A+B. 解: [A]补 = 0.1011, [B]补 = 1.0010 0.1011 + 1.0010 1.1101 ∴ [A+B]补 = 1.1101 A+B = -0.0011 例2、A=0.1011, B=-0.0010,求A-B. 解: [A]补 = 0.1011, [B]补 = 1.1110, [-B]补 = 0.0010 0.1011 + 0.0010 0.1101 ∴ [A-B]补 = 0.1101 A-B = 0.1101
第 2 章 数字逻辑电路基础和计算机中的逻辑部件

5. 逻辑功能的表示和等效电路
逻辑功能可以选用布尔代数式表示, 卡诺图表示, 逻辑功能可以选用布尔代数式表示, 卡诺图表示, 真值表 布尔代数式表示 表示,或者用线路逻辑图表示。 表示,或者用线路逻辑图表示。 真值表 与门、 或门、 的图形符号: 与门、 或门、 非门 的图形符号: A B X X=AB X= AB 0 0 0 A A A X X X 0 1 0 B B 1 0 0 非门 与门 与非门 1 1 1 A B 0 0 0 1 1 0 1 1 X 1 1 1 0
A B
与非门
X
用于写出功能需求
7. 基本定理和常用公式,逻辑化简 基本定理和常用公式,
A+0=A A+1=1 A+B=B+A (A+B)+C=A+(B+C) A(B+C)=AB+AC A+AB=A A+AB=A+B A B = A+B A0=0 A1=A A+A=1 A+A=A AB=BA AA=0 AA=A A=A
(AB) C=A(BC) A+ BC=(A+B) (A+C) A(A+B)= A A(A+B)=AB A+B=A B =A+B = AB
例如: 例如:AB+AB+AB = A(B+B) +AB=A+AB
8. 三态门电路
三态门电路是一种最重要的总线接口电路, 三态门电路是一种最重要的总线接口电路,它保留 了图腾输出结构电路信号传输速度快、 了图腾输出结构电路信号传输速度快、驱动能力强的特 又有集电极开路电路的输出可以“线与”的优点, 性,又有集电极开路电路的输出可以“线与”的优点, 是构建计算机总线的理想电路。 是构建计算机总线的理想电路。 三态” “三态”是指电路可以输出正常的 “0” 或 “1”逻 逻 辑电平,也可以处于高阻态,取决于输入和控制信号。 辑电平,也可以处于高阻态,取决于输入和控制信号。 为高阻态时, 的输出极都截止, 为高阻态时, “0” 和 “1”的输出极都截止,相当于与 的输出极都截止 所连接的线路断开, 所连接的线路断开,便于实现从多个数据输入中选择其 一。
组成原理第5章

第5章计算机组成原理课程设计在上一章中,我们详细地介绍了计算组成原理课程设计平台系统,知道了在模式开关的控制下有两种不同的工作平台。
《计算机组成原理》的所有课程设计都将在这两种工作模式下完满的得到实施。
一个完整的课程设计可以用多种形式来描述。
例如,一个简单的设计可能用硬件描述语言来描述就够了。
但一个复杂的设计可能要分成若干个功能模块来描述,而其中的每一个功能模块可能用硬件描述语言来描述,也可能用原理图来描述,这样的描述方式就是混合输入的设计方法。
结合《计算机组成原理》课程设计的特点和学生的实际情况,原理图输入方式最适合课程设计的实施。
以此为基点,《计算机组成原理》课程设计的步骤如图5-1所示。
课程设计共分三个阶段:1、设计初始阶段在该阶段中,学生根据所学内容,按照《计算机组成原理》课程设计的要求,在课程设计报告书中完成方案设计并画出逻辑线路图。
2、编程设计阶段在该阶段中,学生将以PC机为平台,在WINDOWS环境下,利用编程软件系统在PC机上生成所画出的逻辑线路,这就是所谓的原理图输入方式。
在逻辑线路的生成过程中,可调用元件库提供的元件(例算术逻辑部件、多路开关、寄存器、译码器、逻辑门等),也可以自定义元件。
这与常规《计算机组成原理》课程设计相比较,充分地体现了设计的灵活性,满足了学生的灵活设计思路,是对设计能力的最好体现。
当原理图输入完毕后,编程软件系统可对原理图文件进行编译、优化、适配,将错误消灭在设计阶段。
最后生成对isp LSI的编程文件。
3、isp LSI编程和测试阶段当一个设计完成且产生编程文件后,就可以对isp LSI进行编程。
对isp LSI的编程是由编程软件系统中的下载软件驱动的。
对ispLSI编程与测试阶段图5-1 课程设计步骤下载结束后,逻辑线路就固化在isp LSI1032E中,在模式开关的控制下选用不同的平台,利用提供的开关、指示灯、存储器等硬件资源对逻辑线路进行功能测试,若有错误,则通过审查、修改原理图文件、重新下载、重新测试直至成功为止。
3 计算机中常用的逻辑部件
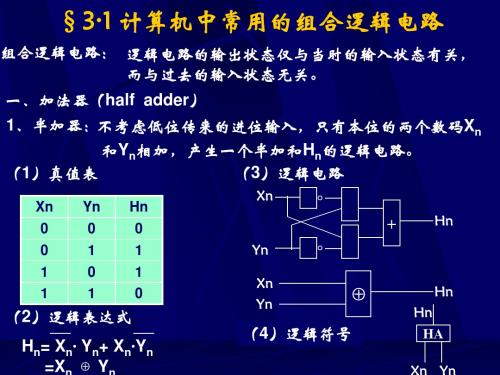
*练习 1、写出四位并行加法以Pi、Gi和C-1为输入信号的Ci 逻辑表 写出四位并行加法以Pi Gi和 为输入信号的Ci Pi、 达式, 并画出逻辑电路图。 达式, 并画出逻辑电路图。 写出四位并行加法以Pi Gi和 为输入信号的Ci Pi、 *作业 1、写出四位并行加法以Pi、Gi和C-1为输入信号的Ci 逻辑表 达式,并画出逻辑电路图。 达式,并画出逻辑电路图。 写出全加器的功能表、逻辑表达式,并画出由基本与、 2、写出全加器的功能表、逻辑表达式,并画出由基本与、 非门组成的逻辑电路和逻辑符号。 或、非门组成的逻辑电路和逻辑符号。
2、并行加法器 、 并行加法器由多个全加器组成, 并行加法器由多个全加器组成,其位数的多少取决于机器的长 各位同时运算。并行加法可同时对数据的各位相加, ,数据的 各位同时运算。并行加法可同时对数据的各位相加,由于 进位链: 进位链:进位信号的产生与传递逻辑 多个全加器的进位输出是另一个全加器的进位输入, 多个全加器的进位输出是另一个全加器的进位输入,因而并行加法 器中进位信号的传递问题是影响全加器本身速度的主要因素。 进位信号的传递问题是影响全加器本身速度的主要因素 器中进位信号的传递问题是影响全加器本身速度的主要因素。 (1)N位串行进位加法器 ) 位串行进位加法器 可知, 位的进位C 由Cn = Xn·Yn +(Xn+Yn)·Cn-1可知,第n位的进位Cn与第 ( 位有关, 位与i 位有关, ..最后一位 有关, n-1位有关,第i – 1位与i – 2位有关,……..最后一位C1与C0有关, ..最后一位C (高一级进位是低一级进位的函数)逐次连接起来,这个链叫串 高一级进位是低一级进位的函数)逐次连接起来, 行进位链。采用串行进位链的加法器为串行进位加法器。 行进位链。采用串行进位链的加法器为串行进位加法器。
计算机中的逻辑运算与逻辑部

当且仅当两个操作数中一个为 真,另一个为假时,结果才为
真。
真值与假值概念
真值
在逻辑运算中,通常将非零数值、非空字符串、非空对象等视为真值。例如,在 C语言中,任何非零整数都被视为真。
假值
与真值相反,假值通常表示零值、空字符串、空对象等。在逻辑运算中,假值表 示条件不成立或结果为否定。例如,在Python中,空列表、空字典和None都被 视为假值。
逻辑电路设计与实现
逻辑门电路
使用逻辑运算实现基本门电路 (如与门、或门、非门)的功能, 进而构建复杂的数字电路系统。
组合逻辑电路
通过逻辑运算组合多个输入信号, 产生特定的输出信号,实现数据 的处理和控制。
时序逻辑电路
在逻辑运算的基础上,引入时钟 信号,实现具有记忆功能的电路, 如触发器、寄存器等。
逻辑或运算的示例
|| 或 |。
如果 A 为真,B 为假,则 A || B 或 A | B 的结果为真。
非运算(NOT)
逻辑非运算的规则
对操作数的逻辑值取反。
逻辑非运算的符号
!。
逻辑非运算的示例
如果 A 为真,则 !A 的结果为假;如果 A 为假, 则 !A 的结果为真。
03
复合逻辑运算
与非运算(NAND)
多路分支等。
数据加密与解密中的应用
加密算法
01
在数据加密过程中,使用逻辑运算对数据进行变换和混淆,使
得加密后的数据难以被破解,如异或加密、置换加密等。
解密算法
02
通过对加密数据的逻辑运算进行逆操作,恢复出原始数据,实
现数据的解密过程。
密钥管理
03
在加密和解密过程中,使用逻辑运算对密钥进行生成、存储和
计算机组成原理3

存储体
IR 1 4 2 7 3 9
CU
ALU
控制 单元
PC
I/O
MAR
MDR
X
运算器
控制器
8
主存储器
第一章 第三节 计算机性能评价指标
基本性能指标
一些与硬件相关的性能指标。 主频
衡量计算机工作速度的主要指标之一 CPU的工作节拍是由时钟来控制的,时钟不断产生固定频率 的时钟脉冲,这个时钟的频率就是CPU的主频 通常用一秒钟内发出的电子脉冲数来表示,常用单位是兆赫 兹(MHz) CPU主频对系统性能的影响 :t= n × 1/f
运算器
A 硬件系统
C
内存储器
主机 外设
输入设备的功能是将程序和数据 从人们熟悉的形式转换成计算机 能接受的信息形式,输入到计算 机内部,如键盘和鼠标等。
输出设备用于输出计算机的处 理结果,它把内部的信息转换 成人们所需要或其它设备能接 受的信息形式,并传送到计算 机外部,如显示器和打印机。
输出设备
E
设计出了适合于各种类型应用的基准测试程序套件,且先后推出了多个版本。 如:SPEC89、SPEC92、SPEC95、SPEC2000和SPEC CPU2006等。 SPEC CPU2006有29个程序,其中整数程序12个(CINT2006),浮点程序17个 (CFP2006)。
计算机的性能指标
常见的输出设备:显示器,打印机等。
模型机硬件组织示意图(一台假想的简化了的计算机)
主机完成一条指令的过程 以取数指令为例
CPU
…
ACC MQ 5 6
存储体
IR 1 4
CU
ALU
2 7
3
8
算术逻辑运算部件

并行化
为了提高计算效率,算术逻 辑部件正在向并行化方向发 展,通过多核、多线程等技 术实现并行计算。
智能化
算术逻辑部件与人工智能技 术的结合,可以实现更智能 化的计算,例如自适应计算、 神经网络计算等。
算术逻辑运算部件的未来展望
更高效能
随着技术的不断进步,算术逻辑部件的计算能力将得到进 一步提升,能够处理更复杂、更高精度的计算任务。
集成电路时代
随着集成电路技术的发展,算术逻辑运算部件被集成在一块芯片上, 进一步提高了运算速度和可靠性。
现代计算机中的算术逻辑运算部件
现代计算机中的算术逻辑运算部件通常采用超大规模集成电路(VLSI) 技术实现,具有更高的集成度和运算性能。
02 算术逻辑运算部件的组成
加法器
总结词
加法器是算术逻辑运算部件中的基本组成之一,用于执行加法运算。
逻辑运算器
总结词
逻辑运算器是算术逻辑运算部件中的基 本组成之一,用于执行逻辑运算。
VS
详细描述
逻辑运算器用于实现逻辑运算,如与、或 、非等操作。它通常由多个门电路组成, 如AND门、OR门和NOT门等。逻辑运算 器在计算机中广泛应用于各种逻辑运算和 位操作任务,如位与、位或、位异或等操 作。
03 算术逻辑运算部件的工作原理
功能
算术逻辑运算部件接收来自寄存器或 内存的数据,执行相应的运算,并将 结果输出到寄存器或内存中。
算术逻辑运算部件的重要性
1 2
实现计算机的基本功能
算术逻辑运算部件是计算机中实现计算和数据处 理的核心部件,没有它,计算机将无法完成基本 的算术和逻辑运算任务。
提高计算机性能
高效的算术逻辑运算部件能够提高计算机的运算 速度和性能,从而提升计算机的整体表现。
逻辑结构_精品文档

逻辑结构逻辑结构是计算机科学中一个非常重要的概念。
在计算机程序设计和系统分析中,逻辑结构用于描述数据元素之间的关系和组织方式。
它是指数据元素之间的逻辑关系,而不是它们在内存中的物理存储方式。
逻辑结构可以分为四种基本类型:线性结构、树形结构、图形结构和集合结构。
首先,让我们来了解线性结构。
线性结构是一种简单的结构,其中数据元素之间是一对一的关系。
其特点是每个数据元素仅有一个直接前驱和一个直接后继。
常见的线性结构有数组、链表和队列等。
其中,数组是最简单的线性结构,它是一种连续存储的数据结构,可以直接通过下标访问元素。
链表则是一种通过指针相互连接的数据结构,它可以动态增删元素,但访问元素的效率较低。
队列是一种先进先出(FIFO)的数据结构,它可以在一端插入元素,在另一端删除元素。
接下来,我们将讨论树形结构。
树形结构是一种层次结构,其中每个数据元素可有多个直接前驱和多个直接后继。
树形结构由节点和边组成,每个节点代表一个数据元素,而边则表示元素之间的关系。
树形结构常用于表达分层次的数据关系,如文件系统、组织机构图等。
有些特殊的树形结构,如二叉树、AVL树和红黑树等,具有特定的性质和应用场景。
例如,二叉树是一种每个节点最多只有两个子节点的树形结构,它被广泛用于搜索和排序算法中。
然后,让我们来了解图形结构。
图形结构是一种数据元素之间多对多的关系。
它是由顶点和边组成的集合,其中顶点代表数据元素,边则表示元素之间的关系。
图形结构常用于描述网络、社交关系等复杂的数据关系。
有向图和无向图是两种常见的图形结构,它们分别表示顶点之间具有方向性和非方向性。
最后,我们将讨论集合结构。
集合结构是一种没有顺序关系的数据集合,其中每个元素都是唯一的。
集合结构的特点是元素之间不存在顺序关系和层次关系。
集合结构常用于数学和逻辑推理中,以及一些不重复元素的处理场景。
逻辑结构在计算机科学中发挥着重要的作用。
它不仅为我们理解数据的组织和关系提供了框架,还为我们设计高效的算法和数据结构提供了基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NO X1 X2 F M0 0 0 F0 M1 0 1 F1 M2 1 0 F2 M3 1 1 F3
X2 X1
0
1
0 M0 M1
1 M2 M3
三维卡诺图
输入为X1、X2、X3,输出为 F。 左下图为真值表,右下图为卡诺图。 卡诺图的左边上边书写自变量的可能取值, 规则是最小跳跃。中间则表明最小项。
1、真值表:
——由逻辑变量的所有可能取值的组合 及其对应的逻辑函数
值所构成的表格。
NO A B C F
例:设计三人表 M0 0 0 0 0
决逻辑电路。得
M1 0 M2 0
0 1
1 0
0 0
到真值表如右: M3 0 1 1 1
ABC为选票, F为选举结果。
M4 1 0 0 0 M5 1 0 1 1 M6 1 1 0 1
根据化简后的逻辑表达式 F=AB+BC+AC, 可以画出相应的三人表决逻辑电路如下:
A
AB
B
BC
F
AC C
由逻辑表达式进行化简需要较强的技巧, 不熟练者很难判断,而卡诺图则直观方便。
3、卡诺图:
——逻辑关系的一种图形表示形式。同 时也是化简逻辑表达式的一种非常有效 的方法。
卡诺图是一种直观的平面方块图。
每个逻辑表达式均可用一个逻辑电路实 现。如果能够用最简单的逻辑表达式描述一 个逻辑关系,就可以用最简单的电路实现之。 因此,化简逻辑表达式具有十分重要的意义。
下面以三人表决逻辑为例说明化简方法:
F ABCABCABCABC ABCABCABCABCABCABC (ABCABC)(ABCABC)(ABCABC) BC(AA)AC(BB)AB(CC) BCACAB
逻辑表达式: 电路符号:
.
L=A•B
AB L
00 1
01 1 10 1
A B
L
11 0
2)或非门 逻辑表达式:L=A—+—B
真值表: A B L
0 0 1 电路符号:
0 10
11L01 A 00 B
A B
L
3)异或门 逻辑表达式:L=A⊕B=A—B+—AB
真值表: A B L 电路符号:
000
NO X1 X2 X3 F
M0 0 0 0 F0 M1 0 0 1 F1 M2 0 1 0 F2 M3 0 1 1 F3 M4 1 0 0 F4 M5 1 0 1 F5 M6 1 1 0 F6 M7 1 1 1 F7
证明: (A+B) ·(A+C) =A·A+A·C+B·A+B·C =A(1+C+B)+B·C =A+B·C
3)交换律:
A+B=B+A
A·B=B·A
4)结合率:
(A+B)+ C = A+(B+C)
(A·B)·C = A·(B·C)
5)反演律:
A·B·C=A+B+C
A+B+C=A ·B ·C
2.2 逻辑函数三种表示法及关系
基本公式: 吸收律,分配律,交换律,结合律,反演律
1)吸收律:
A+A•B=A
证明:A+A•B=A(1+B)=A•1=A
A•(A+B)=A
证明:A•A+A•B=A+A•B=A
A+A•B=A+B
证明:A+A•B=A+A•B+A•B =A+(A+A)•B=A+1•B=A+B
2)分配律:
A·(B+C)=A·B+A·C (A+B) ·(A+C)=A+B·C
M7 1 1 1 1
2、逻辑表达式: ——由逻辑变量、逻辑常量和运算符组成的 表达式。它是逻辑变量的函数, 也是设计逻辑电路的根据。
根据真值表可以列出逻辑表达式。 方法是:把真值表中所有使函数值为1的自 变量组合项“或”起来。 如此,前述三人表决真值表的逻辑表达式为:
F(A,B,C)=ABC+ABC+ABC+ABC
它根据输入变量的数量n将平面划分为2n
个方格,用来表示全部输入变量组合项 或者表示全部输出项。
下面举例对此进行说明。
二维卡诺图
输入为X1、X2,输出为 F。 左下图为真值表,右下图为卡诺图。 卡诺图的左边上边书写自变量的可能取值, 中间则表明 Mi最小项。最小项即一行真 值表中各自变量或其“非”的逻辑乘积项。
1) 逻辑“与”运算和“与门” 电路
逻辑“与”又称为逻辑乘运算。
运算符号:“·”,“∧” ,“AND”等。
逻辑表达式:
L=A·B
=
A∧B=
1 0
(A、B均为1) (A、B中任一为0)
与门电路符号: A
L B
真值表:用表格说明输入输出变量之间的关系。
A B L= A·B
00 0 01 0 10 0 11 1
第二章 计算机中逻辑运算与逻辑器件
★ 计算机是由数字逻辑电路组成的。 ★ 逻辑是指条件和结果之间的关系,即因
果关系。因果关系是二值逻辑。
★ 电路的输入信号作为条件,输出信号作 为结果,输入输出代表一定逻辑关系。
★ 逻辑代数是描述/分析/设计逻辑电路的 数学工具。逻辑代数也叫布尔代数。
★ 运用逻辑运算可以设计最简逻辑电路。
2.1 逻辑代数及基本运算
★ 逻辑代数:是由逻辑变量集、常量 “0”、“1”及“与”、“或”、“非” 等 运算符号构成的代数系统。
★ 逻辑变量集是指逻辑代数中所有可能的 变量集合,可用任何字母表示,但变量的 取值只能是1或0。
★ 简单逻辑代数可描述任何复杂逻辑网络。
1、基本逻辑单元
三种基本的逻辑运算与逻辑单元是: 逻辑“与”运算和“与门”电路 逻辑“或”运算和“或门”电路 逻辑“非”运算和“非门”电路
2)逻辑“或”运算和“或门”电 路
逻辑“或”又称为逻辑加运算。
运算符号:“+”、“v”、 “OR”等。
逻辑表达式: L=A+B=A∨B= 1 (A、B中任一为1)
或门电路符号:
0 (A、B均为0)
A
B
L
逻辑真值表:
A B L=A+B 00 0 01 1 10 1 11 1
3)逻辑“非”运算和“非门”电 路
011
A
101
B
L
110
4)同或门
逻辑表达式:L=A⊙B=A⊕B=AB+–A–B
真值表:
AB 00 01 10 11
电路符号:
L
1
A
0
B
L
0
1
3、基本运算规律和公式
基本运算规律: 加:A+0=A,A+1=1,A+A=A,A+A=1 乘:A ·0=0,A ·1=A,A ·A=A,A ·A=0 非:A+—A=1,A ·—A=0,A=A
逻辑“或”又称为逻辑反运算.
运算符号:“ — ”(上加横线)
逻辑表达式为 非门电路符号:
—
L= A =
1 (A=0) 0 (A=1)
A
L
逻辑真值表:
AL 01 10
2、常用的组合逻辑单元
基本逻辑运算可以构成复杂逻辑关系;
基本逻辑电路也可以形成组合逻辑电路。
常见组合逻辑及其电路如下:
