线性代数 第一章复习题
线性代数复习题及答案

《 线性代数复习提纲及复习题 》理解或掌握如下内容:第一章 n 阶行列式 .行列式的定义,排列的逆系数,行列式性质,代数余子式, 行列式的计算,三角化法及降阶法,克莱姆法则。
第二章 矩阵及其运算矩阵的线性运算,初等变换与初等矩阵的定义,方阵的逆矩阵定义及性质 方阵的逆矩阵存在的充要条件,用初等变换求逆矩阵,矩阵方程的解法,矩阵的秩的定义及求法;齐次线性方程组只有零解、有非零解的充要条件,;非齐次线性方程组有解的充要条件,解的判定。
第三章 线性方程组n维向量的线性运算,向量组线性相关性的定义及证明,向量空间,向量组的极大线性无关组、秩;齐次线性方程组的基础解系,解的结构,方程组求解;非齐次线性方程组解的结构,用初等变换解方程组,增广矩阵含有字母元素的方程组的求解。
复习题:一、填空(1)五阶行列式的项5441352213a a a a a 前的符号为 负 ;(2)设)3,3,2(2),3,3,1(-=+-=-βαβα,则α= (1,0,0) ;(3)设向量组γβα,,线性无关,则向量组γβαβα2,,+-线性 无关 ;(4)设*A 为四阶方阵A 的伴随矩阵,且*A =8,则12)(2-A = 4 ;(5)线性方程组054321=++++x x x x x 的解空间的维数是 4 ; (6)设⎪⎪⎪⎭⎫ ⎝⎛=k k A 4702031,且0=T A 则k = 0或6 ;(7)n 元齐次线性方程组0=Ax 的系数矩阵A 的秩r(A)秩是r,则其解空间的维数是 n-r ;(8)的解的情况是:方程组b Ax b A R A R 2),,()3(== 有解 ;(9)方阵A 的行向量组线性无关是A 可逆的 充要 条件;(10)设n 阶矩阵A 非奇异,n 阶矩阵B 满秩,则矩阵B A *的标准形是n E 。
()()11000010000101111211112111121111125100001000010111152111121111211111521111211112111121211112111121111221.1413121114131211441413121144===+++=-+-=====-+-A A A A M M M M D D M M M M a M D D ij ij 解的值。
《线性代数复习资料》第一章习题答案与提

详细描述:本题主要考察学生对线性方程组解法的理解 ,通过给定的线性方程组,要求学生判断其解的情况, 并求解当有解时的解向量。
习题二解析
在此添加您的文本17字
总结词:向量空间
在此添加您的文本16字
详细描述:本题主要考察学生对向量空间的定义和性质的 理解,要求学生判断给定的集合是否构成向量空间,并说 明理由。
线性变换与矩阵表示
线性变换是线性代数中的重要概念,理解如何用 矩阵表示线性变换以及其性质是解决相关问题的 关键。
向量空间的维数与基底
向量空间的维数与基底的概念较为抽象,理解其 定义和性质有助于更好地解决相关问题。
04
典型例题解析
例题一解析
总结词
矩阵的乘法
详细描述
本题考查了矩阵乘法的规则和计算方法。首先,我们需要明确矩阵乘法的定义,即第一个矩阵的列数必须等于第 二个矩阵的行数。然后,我们按照矩阵乘法的步骤,逐一计算结果矩阵的元素。在计算过程中,需要注意矩阵元 素的位置和计算方法。
导致在解题时无法正确应用它们。
THANK YOU
感谢聆听
例题二解析
总结词
行列式的计算
详细描述
本题考查了行列式的计算方法和性质。首先,我们需要明确行列式的定义,即由n阶方阵的元素按照 一定排列顺序构成的二阶方阵。然后,我们根据行列式的性质,逐步展开并化简计算结果。在计算过 程中,需要注意行列式的展开顺序和符号的变化。
例题三解析
总结词
向量的线性组合
详细描述
习题三解析
总结词:行列式计算 总结词:矩阵的秩 总结词:特征值与特征向量
详细描述:本题主要考察学生对行列式的计算能力,通 过给定的矩阵,要求学生计算其行列式的值。
《线性代数》课程复习大纲与练习题

《线性代数》课程复习大纲与练习题第一章 线性方程组1.线性方程组的概念(1)线性方程组的一般形式:⎪⎪⎩⎪⎪⎨⎧=+⋅⋅⋅++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=+⋅⋅⋅++=+⋅⋅⋅++sn sn s s n n n n b x a x a x a b x a x a x a b x a x a x a 22112222212*********(2)用消元法判断线性方程组是否有解,并求出解 2.初等变换对线性方程组进行求解 (1)初等变换的定义(2)用初等变换将线性方程组化为同解的阶梯形方程组,从而判断是否有解3.用矩阵的秩判断线性方程组是否有解记⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=sn s s n n a a a a a a a a a A 212222111211称为线性方程组的系数矩阵;⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=ssns s nn b a a a b aa ab a a a A 21222221111211称为线性方程组的增广矩阵 (1)线性方程组有解⇔秩(A )=秩(A )当线性方程组有解时:秩(A )=未知量个数n 时, 线性方程组有唯一解;秩(A )<未知量个数n 时,线性方程组有无穷多解。
(2)线性方程组无解⇔秩(A )<秩(A )4.齐次线性方程组:常数项全为0的线性方程组⎪⎪⎩⎪⎪⎨⎧=+⋅⋅⋅++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=+⋅⋅⋅++=+⋅⋅⋅++0)1(00221122221211212111n sn s s nn n n x a x a x a x a x a x a x a x a x a (1)解的情况:r(A)=n ,(或系数行列式0≠D )只有零解;r(A)<n ,(或系数行列式D =0)有无穷多组非零解。
(2)解的结构:r n r n c c c X --+++=ααα 2211。
(3)求解的方法和步骤:①将增广矩阵通过行初等变换化为最简阶梯阵; ②写出对应同解方程组;③移项,利用自由未知数表示所有未知数; ④表示出基础解系; ⑤写出通解。
线性代数第1章复习题解答

《线性代数》第一章复习题解答求1-6题中行列式的值:1.75423)1(125410022321412022311110214012002231111021412112405322222344142-=-⨯==--=--=-=++--展开按展开按r c c c r r r r D . 2.2233441122334411223344114433221140000000000000000000004242a b b a a b b a a b b a a b b a b a a b a b b a a b a b b a b a D c c r r ⋅==-==↔↔))((32324141b b a a b b a a --=. (先按第一行、第四行、第一列、第四列展开也都可以)3.yxy x y xy y xx y x y x x xyy x x y x y x D n c n 00000000)1(0000000000000000000000011+-+==展开按n n ny x 1)1(+-+=4.1111100000000001111100000000022122111+--=---=+n x x x x x x x x x x x D n n n n n 各列加到第一列n n nn x x x n x x x x x x n21332211)1()1)(1(0000000)1)(1(-+=---+=++各列加到第一列.5. )0(,10010001000100011112112101≠=-+n nn n a a a a a a a a D. 也是一种爪形行列式。
000000000001111111121210111 11211111nn nc a c c a c c a c n a a a a a a a a D n n n n nn ----+---=-+++n nn n a a a a a a a 212102)1()111()1(----=+. 6. )!2(220300001000012203000012222200001222221222223222222222221223212--=---=---=-=---n n n n n nn D c r r r r r r nn展开按. 7. 已知行列式32510711020214214=D ,求44434141A A A A +++.解:612211014617110202110014111171102021421433134244434241---=---==+++--展开按c r r r r A A A A 3682141)1(018211414136313-=--=-=++展开按r c c .8. 求函数xx x x xx f 111123111212)(-=的表达式中4x 的系数及3x 的系数.解:(1)由定义知,当且仅当取自行列式不同行、不同列的元素均含有x 时,函数表达式中4x 才会出现。
《线性代数》课后习题集与答案第一章B组题

《线性代数》课后习题集与答案第一章B组题基础课程教学资料第1章矩阵习题一(B)1、证明:矩阵A 与所有n 阶对角矩阵可交换的充分必要条件是A 为n 阶对角矩阵. 证明:先证明必要性。
若矩阵A 为n 阶对角矩阵. 即令n 阶对角矩阵为:A =??n a a a 00000021,任何对角矩阵B 设为n b b b0000021,则AB=??n n b a b a b a000002211,而BA =??n n a b a b a b000002211,所以矩阵A 与所有n 阶对角矩阵可交换。
再证充分性,设 A =??nn n n n n b b b b b b b b b 212222111211,与B 可交换,则由AB=BA ,得:nn n n n n n n n b a b a b a b a b a b a b a b a b a 221122222111122111=nn n n n n n n n b a b a b a b a b a b a b a b a b a 212222221211121111,比较对应元素,得0)(=-ij j i b a a ,)(j i ≠。
又j i a a ≠,)(j i ≠,所以0=ij b ,)(j i ≠,即A 为对角矩阵。
2、证明:对任意n m ?矩阵A ,T AA 和A A T均为对称矩阵. 证明:(TAA )T =(A T )T A T =AA T,所以,TAA 为对称矩阵。
(A A T)T =A T (A T )T =A T A ,所以,A A T 为对称矩阵。
3、证明:如果A 是实数域上的一个对称矩阵,且满足O A =2 ,则A =O . 证明:设A =??nn n n n n a a a a a a a a a 212222111211,其中,ij a 均为实数,而且ji ij a a =。
由于O A =2,故A 2=AA T =nn n n n n a a a a a a a a a 212222111211nn nnn n a a a a a a a a a 212221212111=0。
线性代数综合复习资料

《线性代数》综合练习资料第一章 n 阶行列式一、判断题1.如果n (n>1)阶行列式的值等于零,则行列式中必有两行成比例。
( × ) 2.如果n (n>1)阶行列式的值等于零,则行列式中必有一行全为零。
( × ) 3.交换一个行列式的两行(或两列),则行列式值改变符号 ( √ ). 4. 已知n 阶矩阵A 各列元素之和为0,则A =0 ( √ ) 5.ij ijA a D ,33⨯=为ij a 的代数余子式,则0231322122111=++A a A a A a . ( √ )6、齐次线性方程组有非零解,则系数行列式的值一定为零。
( √ )7、1122121233443434a b a b a a b b a b a b a a b b ++=+++ ( × )二.填空题:1.多项式=)(x P 333322221111x c b a x c b a xcb a (其中a,b,c 是互不相同的数)的根是 ,,x a x b x c === .2.. 三阶行列式 D =333222111435214352143521a a k a a a k a a a k a +++++++++ = 0 。
3、(),____1________.nn ij ij D a a D a a ===-=-若则4.设A 为m 阶方阵,B 为n 阶方阵,且|A |=3,|B|=2,C=00A B⎛⎫⎪⎝⎭,则|C |=______()16nm-⋅_____. 5、设四阶行列式3214214314324321,ij A 是其()j i ,元的代数余子式,则_______3331=+A A ,_______3432=+A A .根据定义求即可 6 .已知4阶行列式D 的第一行元素分别是-1,1,0,2;第四行元素对应的余子式依次为5,x ,7,4,则x = 3-7、已知n 阶行列式100110111 =D ,则D 的所有元素的代数余子式之和等于 n .三.选择题1、设)(则B a a a a a a a a a a a a D a a a a a a a a a D =---===333231312322212113121111333231232221131211324324324,1 (A)0 ; (B)―12 ; (C )12 ; (D )12.已知四阶行列式D 中第三列元素依次为-1,2,0,1,它们的余子式依次分别为5,3,-7,4, 则D= ( A )(A ) -15 (B ) -5 (C ) 5 (D ) 1 3、已知四阶行列式A 的值为2,将A 的第三行元素乘以―1加到第四行的对应元素上去,则现行列式的值( A )(A ) 2 ; (B ) 0 ; (C ) ―1 ; (D ) ―24、n 阶行列式D 不为零的充分必要条件是( D )(A )D 中至少有n n -2个元素不为零 (B )D 中所以元素都不为零(C )D 的任意两列元素之间不成比例 (D )以D 为系数行列式的非齐次线性方程组有唯一解5.如果行列式02002000110011=kk k ,则( A )。
线性代数第一章测试题

线性代数第一章测试题1. 向量空间的定义:- 简述向量空间的定义,并给出一个例子。
2. 向量的线性组合:- 解释什么是向量的线性组合,并给出一个具体的例子。
3. 基和维数:- 描述什么是基(Basis)和维数(Dimension),并解释它们之间的关系。
4. 线性相关与线性无关:- 给出线性相关和线性无关的定义,并用一组向量来说明它们。
5. 向量空间的子空间:- 解释什么是向量空间的子空间,并给出一个例子。
6. 线性变换:- 定义线性变换,并给出一个线性变换的例子。
7. 矩阵的秩:- 描述矩阵的秩是什么,并解释如何计算一个矩阵的秩。
8. 行列式:- 解释行列式的概念,并给出计算2x2和3x3矩阵行列式的方法。
9. 逆矩阵:- 定义什么是逆矩阵,并说明一个矩阵何时有逆矩阵。
10. 特征值和特征向量:- 描述特征值和特征向量的概念,并给出一个计算矩阵特征值和特征向量的例子。
11. 线性方程组的解:- 解释线性方程组的解集,并讨论其解的性质。
12. 矩阵的运算:- 给出矩阵加法、乘法和转置的定义,并给出相应的例子。
13. 正交性和正交基:- 解释正交性和正交基的概念,并给出一个正交基的例子。
14. 投影矩阵:- 定义投影矩阵,并说明如何使用它来投影向量。
15. 线性变换的几何解释:- 描述线性变换在几何上的解释,并给出一个具体的例子。
16. 矩阵的分解:- 简述矩阵分解的概念,并给出LU分解和QR分解的例子。
17. 范数:- 解释向量范数的概念,并给出1-范数、2-范数和无穷范数的定义。
18. 线性映射的矩阵表示:- 描述如何将一个线性映射表示为矩阵。
19. 线性代数在实际问题中的应用:- 给出一个实际问题,并展示如何使用线性代数的概念来解决它。
20. 附加题:- 给出一个矩阵,并要求学生找到它的逆矩阵,如果存在的话。
如果不存在,解释为什么。
【线代期末复习题】大学线代 考研线代第一章行列式复习题答案

4. 当( )时,齐次线性方程组⎪⎩⎪⎨⎧=λ++=+λ+=++λ000321321321x x x x x x x x x ,有非零解(A) 1或2 (B) -1或-2 (C) 1或-2 (D) -1或25. 下列行列式计算正确的是:(A )A 、0141030430-=-- B 、161111111111111111=------------ C 、0011111111011110=------ D 、121150202473004--=-6. 若11121321222331323312a a a a a a a a a =,则111112132121222331313233424242a a a a a a a a a a a a --=-(D ) A 、0 B 、4 C 、1 D 、-27. 设2312781239325232D -=-,则=+++42322212A A A A (C )。
A 、1B 、-1C 、0D 、28. 设2100000121000000000001210000012ΛΛΛM M M M ΛΛ=n D ,则=n D ( B ) A 、1 B 、1+n C 、1-n D 、-1 9. 设(.....)τ 表示排列的逆序数, 则(431625)τ=( B ) (A )1 (B) 7 (C)3 (D) 2三、计算题:1..求阶n 行列式D=000x x x x x x K K L L L L K0(1)(1)(1)000x x n x n x n x x xx x D xx x xx---==K L L L L L L L L L L L L L= 111100(1)(1)(1)0n n x n xn x x---=---L LL L L L L2. 计算行列式 1111111111111111x x D y y+-=+-.原式22101000101000111100111100y x yy yx x y yyx x x=-=--=3.. 问当k 取何值时,Ax b =无解、有唯一解或有无穷多解?当有无穷多解时写出Ax b =的全部解12312312321,2,455 1.x kx x kx x x x x x +-=⎧⎪-+=⎨⎪+-=-⎩解1 作方程组的增广矩阵M (A b ),并对它施以初等变换: ()()32213135521121121111221032103455165506540021r r r r r r r k k k A A b k k k k k k k -+-----⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪==-−−−→+-−−−→+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-----+⎝⎭⎝⎭⎝⎭再 于是, (4分) 当45k =-时,原方程组无解;当41,5k k ≠≠-时,原方程组有唯一解;当1k =时,原方程组有无穷多组解,其全部解为1231,1,x x k x k ==-+=(其中k 为任意常数),(或()()()123011110TTTx x x k =+-(k 为任意常数). (9分) 解2()()()()()232121111101115415445455405k k k c c D k k k k k k k ---+=-=--=----=-+---,当41,5k k ≠≠-时,方程组有唯一解.当1k =时,原方程组为1231231232124551x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=-⎩;()()12213124211111121112111221110333455145510999r r r r r r A A b ↔-----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪==-−−−→-−−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭2123239111210010111011100000000r r r r r +--⎛⎫⎛⎫ ⎪ ⎪−−−−→--−−−→-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭再,同解方程组为12311x x k x k =⎧⎪=-+⎨⎪=⎩,即()()()123011110T T Tx x x k =+-(k 为任意常数).当45k =-时,原方程组为12312312342154254551x x x x x x x x x ⎧--=⎪⎪⎪--+=⎨⎪+-=-⎪⎪⎩,即12312312310455455104551x x x x x x x x x --=⎧⎪+-=-⎨⎪+-=-⎩,这时第二个第三个方程左边相同,而右边不等,故方程组无解.4. 计算行列式 abbb a bb b aD n ΛΛΛΛΛΛΛ=..解 abb a b b b n a a b bb a b b b aD n ΛΛΛΛΛΛΛΛΛΛΛΛΛΛ111])1([-+==1)]()1([0001])1([---+---+=n b a b n a b a b a b b b n a ΛΛΛΛΛΛΛ5. 计算行列式 65429720199321原式65431132110012---r r 1812151224156-=++---= 6. 计算行列式11115312259141252718--解:(允许多种方法解答)该行列式为范德蒙行列式原式=11112312(35)(15)(25)(13)(23)(21)491482718-=+++----672=7.. 81278419421321111----解:(允许多种方法解答)该行列式为范德蒙行列式原式=11112313(32)(12)(32)(13)(33)(31)2404919827127-=----++-=-8.计算四阶行列式 3111131111311113的值。
《线性代数复习资料》第一章习题答案与提示
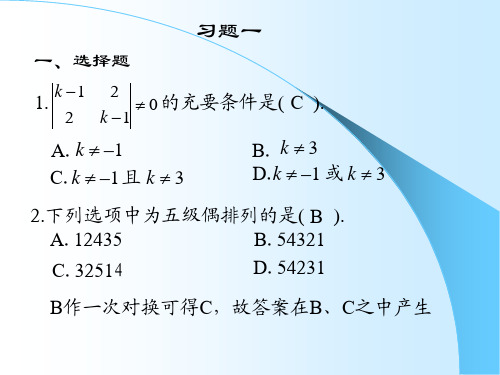
c2 2b2 a2
3a2
c3
a1
2b3 a3 18 ,则 a2
3a3
a3
b1 c1
b2 c2 的
b3 c3
A.3
B.-3 C. 6
D.-6
11.若
2x ky kx 2y
c1 c2
(c1 c2 0)
有唯一解,则k满足( D
).
A.k=0
B.k=-2或k=2
C.k≠-2或k≠2 D.k≠-2且k≠2
( A ).
A.10d B.15d C.-10d D.-15d
D1 第一列乘3加到第二列,乘4加到第三列
a1 2a2 5a3
a1 a2 a3
D1 b1 2b2 5b3 1 (2) 5 b1 b2 b3 10d
c1 2c2 5c3
c1 c2 c3
c1
10. 若 2b1 a1
3a1
值为 ( A ).
1234
8.若 5
0
6 0
7 x
8 3
0,则x=
12 5
.
0045
1234 5 6 7 8 1 2x 3
0 0 x 3 5 64 5 0045
三、计算题
2 3 11 5
4 1 1 2
1.计算行列式 D1
1 2
1 1
5 3
2 4
和 D2
3 2
1 3
2 5 .
41
11 3 4
1 2 11
10
A. 零元素最多为 n 1 个,即必有一行元全为零。
C. 列等和行列式,把各行加到第一行,则第一 行全为零。
D.反例
0 1
1 1
0
0001
大学线性代数期末考试练习题复习资料附答案

第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ). (A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x x x x f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ).(A)1- (B)2- (C)3- (D)011. 若22351011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解. ( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=0100111010100111.6.行列式=-000100002000010n n .7.行列式=--0001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cca b b a b c a c b a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D00103012112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.yxyx x y x y y x y x +++;2.解方程001111101110=x x xx ; 3. na a a a111111111111210(n j a j ,,1,0,1 =≠);4.21000120000021000121000125.aa a aa a a a aD ---------=1101100011000110001.四、证明题1.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a x b a -=++++++. 2.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a dcbad c b a +++------=.3.设c b a ,,两两不等,证明0111333=c b a c b a 的充要条件是0=++c b a .参考答案一.单项选择题A D A C C D A B C D B B 二.填空题1.n ;2.”“-; 3.43312214a a a a ; 4.0; 5.0; 6.!)1(1n n --; 7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-; 13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk kn ; 17.3,2-≠k ;18.7=k 三.计算题1.)(233y x +-; 2. 1,0,2-=x ; 3. )111()1(00∑∏==-+-nk knk k a a ; 4 1+n ; 5. )1)(1(42a a a ++-. 四. 证明题 (略)第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
线性代数第一章习题及解答

n(n−1) 2
D. a11 . . . a1n ··· ··· ··· D an1 . . . ann
因为 D = D , 而 D =
T
对 DT 作上述行交换得, 于是
D2 = (−1)
n(n−1) 2
D = (−1)
T
n(n−1) 2
5
对 D2 依次进行相邻列交换, 然后转置得
D2 = (−1)
4
a+b 1 Dk = 0 ··· 0 0
ab a+b 1 ··· 0 0 1
0 ab a+b ··· 0 0 a+b 0 ··· 0 0 a+b 1 0 ··· 0 0
··· ··· ··· ··· ··· ··· ab a+b 1 ··· 0 0 ab a+b 1 ··· 0 0
0 0 0 ··· a+b 1 0 ab a+b ··· 0 0 0 ab a+b ··· 0 0
··· ··· ··· ···
(a − n)n (a − n)n−1 . . . a−n
1 1 ··· 1 解:将 Dn 一次进相邻行交换, 然后进行相邻列交换得 1 1 ··· 1 a−n a−n+1 ··· a 2 2 (a − n + 1) · · · a2 (xj = a − j, j = 0, 1, . . . , n) Dn = ( a − n ) . . . . . . . . ··· . (a − n)n (a − n + 1)n ∏ = (xj − xi ) 0≤i<j ≤n ∏ = (i − j )
a a . . . x ··· a 0 . . . x−a (rj − r1 , j = 1, 2, . . . , n)
线性代数习题集-第一章

第一章:行列式I.单项选择题 1.排列1,3,,(2n 1),2,4,,(2n)-的逆序数为( )(1) n 1- (2) (n 1)n - (3) (n 1)n + (4) (n 1)/2n - 2.排列1,3,,(21),(2),(22),,2n n n --的逆序数为( )(1) n (2) (n 1)n - (3) (n 1)n + (4) (n 1)/2n - 3.四阶行列式中含有因子1123a a 的项是( )(1) 11233442a a a a (2) 11233344a a a a (3)11233342a a a a (4) 11233442a a a a -4.行列式abac aebdcd de bfcfef---的值是( ) (1) 2abcdef (2) 4abcdef (3) 6abcdef (4) 8abcdef 5. 设A 为n 阶方阵,λ为数,则A λ等于( ) (1) A λ (2) A λ (3) n A λ (4) 2A λ6.设ab cD de f g hi=,则元素h 的代数余子式为( ) (1)a c gi(2) a cdf -(3) a c g i - (4)a c df7.设行列式000000a bcD d e f g h i j=,则D 的值等于( ) (1) abdg - (2) abdg (3) abdg ceh fi j -+- (4) abdg ceh fi j ++- 8.设A 为n 阶矩阵,则( )(1) A A -= (2) A A -=- (3) (1)n A A -=- (4) 1A A --=9.设A 为n 阶矩阵,且A 的行列式0A a =≠,而A *是A 的伴随矩阵,则A *等于()(1) a (2) 1/a (3) n a (4) 1n a -10.若12312,,,,αααββ都是四维列向量,且1231m αααβ=,1223n ααβα=四阶行列式,则32112()αααββ+四阶行列式等于( ) (1) n m - (2) m n - (3) m n + (4) ()m n -+11.设44⨯ 矩阵[]234,,,A αγγγ= ,[]234,,,B βγγγ=,其中234,,,,αβγγγ均为4维列向量,且已知行列式1,1A B ==,则行列式A B +等于( ) (1)5 (2)10 (3)30 (4)4012.设设A 为m 阶方阵,设B 为n 阶方阵,且,A a B b ==,00AC B =,则C 等于( )(1) ab (2) ab - (3) (1)nm - (4) (1)nm ab -13.设行列式D aba b b a b a a b ab+=++,则D 的值为( )(1) 332()a b -+ (2) 332()a b + (3) 332()a b - (4) 33()a b -+ 14.元素是0和1的三阶行列式D 之值只能是( ) (1) 3 (2) 3- (3) 4 (4) 0,1,2±± II.填空题1.n 阶行列式的完全展开式,应由________项组成,每项位于行列式中________的n 个元素的乘机,而且项1212n j j nj a a a 的符号为_____.2. n 阶行列式1111nn nna a A a a =,则按第i 行的展开式为__________;按第j 行展开式为__________.3.当A 可逆是1A -=____________.4.设A 是一个n 阶方阵,k 是一个有理数,则kA =________,5.在行列式2121113211x x x x j j x-的展开式中,3x 的系数为________,4x 的系数为_________.6.三角行列式110nn nna a a =_________ 7.行列式2111131111411115A ==__________ 8.行列式11101210011000000111002A --==--__________ III.判断题1.交换行列式中任意两行的位置,行列式的值不变。
线性代数精简版

专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日
专业班级学号末两位姓名成绩批改日期月日。
线性代数(含全部课后题详细答案)1第一章一元多项式习题及解答.docx

A 组1.判别Q (厉)二{0 +勿亦|0,处0}是否为数域?解是.2.设/(x) = x3 4-x2 4-x+l, g(兀)=兀2+3兀+ 2,求 /(兀)+ g(x),/(x)-g(x), f(x)g(x). 解/(x) + g (x) = x3 4- 2x2 + 4x + 3 ,/(兀)-g(x)"-2x-l,f(x)g(x) = x5 +4x4 +6兀'+6兀$ +5x + 2 .3.设/(%) = (5x-4),993(4x2 -2x-l),994 (8x3 -1 lx+2)'995,求 /(%)的展开式中各项系数的和.解由于/(兀)的各项系数的和等于/⑴,所以/(I) = (5-4严3(4-2- 1尸94(8-11 + 2)1995 =-1.4.求g(兀)除以/(兀)的商q(x)与余式心).(1)f (x) —— 3%2— x — 1, g(兀)=3F - 2兀+1 ;(2)/(x) = x4 -2x4-5, g(x) = x2 -x + 2 .解(1)用多项式除法得到x 73x~ — 2x +13_93X + 3—x —x-i3 37 ° 14 7-- 无_+ —x --3 9 926 2-- X ---9 9所以'恥)十岭心)W(2)用多项式除法得到x4— 2x + 5兀4 —”丫" + 2 兀2— 2x~ — 2 兀+5 jy?—兀~ + 2 兀-x2-4x4-5-兀? + X - 2—5x + 7所以,q(x) = x2 +x-l, r(x) = -5x + 7 .5.设是两个不相等的常数,证明多项式/(兀)除以(x-a)(x-b)所得余式为af(b)_bg)a-b a-h证明依题意可设/(x) = (x - a)(x - b)q(x) + cx+d,则”(a) = ca + d,[f(b) = cb + d.解得F=(/a) --,\d = (af(b)-bf(a))/(a-b).故所得余式为a-b a-b6.问m,p,q适合什么条件时,/(兀)能被g(x)整除?(1) /(x) = x3 + px + q , g(x) = x2 + nvc-1;(2) f(x) = x4 + px2 +q , g(兀)=x2 + mx+l.解(1)由整除的定义知,要求余式r(x) = 0 .所以先做多项式除法,3x2 + mx -1x-in“+ “X + q3 2x + mx^ - x-mx1 +(〃 + l)x + g2 2一 mx_ — m^x + m°(# +1 + 加〜)兀 + (g —m)要求厂(x) = (/? + l +加2)兀+ (§ —加)=0 ,所以(“ + 1 +加2) = 0, q-m = 0.即p = -l-m2, q - m时, 可以整除.(2)方法同上.先做多项式除法,所得余式为厂(兀)=加(2 — ”一nr )兀+ (1 + @ —卩一加〜),所以 m (2-p-/772) = 0, 1 + ^ - p - m 2= 0 ,即 m = 0, p = q + \ 或“二 2— 加[q = l 时,可以整除.7. 求/(兀)与gCr )的最大公因式:(1) f (x) — x 4 + — 3%2 — 4x — 1, g (x)=兀彳 + — x — 1 ; (2) f(x) = x 4— 4x 3+ 1, g(x) = x 3— 3x 2+1 ;(3) /(x) = x 4 -10x 2 +1, g(x) = x 4 -4A /2X 3 +6X 2 +4A /2X +1 .解(1)用辗转相除法得到用等式写出來,就是所以(/(x),g(x)) = x + l ・(2)同样地,<8 4 / 3 3= -X + — — -X-—(3 344-2x 2-3x-l1 1 --- X 4——2 -- 4 X 3+ X 2- X - 1 x 4 + x 3- 3x 2- 4x- 11 2 3 , -2x 2 — 3兀—12 21 2 3 1 -- X ----- X ---—2兀~ — 2兀2 4 433-- X ----X -144一丄 184—X H - 3 3 0心宀丄兀2 24 3 2牙+牙-X - Xf(x) = xg(x)^(-2x 2-3x-l),g(x) =所以(/⑴,g (兀)) = 1.⑶ 同样用辗转相除法,可得(/(x),g(x)) = F —2血兀一1.8.求 w(x),仄兀)使 w(x) f\x) + v(x)g(ji) = (/(x), g(%)):(1) f (x) = %4 4- 2x^ — %2 — 4x — 2, (x) = %4 + x — x~ — 2x — 2 : (2) /(x) = 4x 4-2x 3-16x 2+5x4-9, g(x) = 2兀3-x 2-5x+4:(3) /(x) = x A-x 3-4x 2 +4x + l, g (兀)=x 2 -x-l.解(1)利用辗转相除法,可以得到/(x) = g (A :) + (x 3-2x)'g (兀)=(x+l)(x 3 - 2x) + (x 2 -2),x — 2兀=x(^x~ — 2).因而,(/(x),g(x)) = x 2-2,并且(/(兀),g (兀))=/ 一 2 = g (兀)_ (兀+1)(疋 _ 2兀) =g (兀)一(X +1) (f(x) -g (兀))=(一兀 一 1)/(兀)+ (兀+2)g(x),所以 u(x) = -x-\, v(x) = x + 21 10 -- X H --- 3 9x 3 - 3x 2x-13 1 2 2X H —X X 3 3 10 2 2~~'- ---- X H 兀+ 13 -- 3 10 ° 10 20 X --- 兀 3 9 916~~1T —X ------ 9 927 441 --------- X ---------------16 256-3x 2+—x1649一一539 兀+ --- 27 256(2)利用辗转相除法,可以得到/(x) = 2xg(x)-(6x 2 +3兀-9),(\ 1Ag(x) = —(6x_ + 3兀一9) ——% + — — (% — 1), —(6x - + 3x — 9) = —(x —1)(6% + 9).因而,(/⑴,g(Q) = x-1,并且(1 1 …厶— —X + _ f (x) + _兀_—x~\ I 3 3丿 (3 3丿] 1 2 7 2fi/f 以 W (X )= X H —, V (X )= — --- X — \ •3 3 3 3(3) 利用辗转相除法,可以得到fM = X —3)g(x) + (x — 2),g(x) = (x+l)(x-2) + l ・因而( f(x), g(x)) = 1 ,并且(/(兀),g(x)) = 1 = g(x) - (x+1)(兀一 2)=g (兀)-(兀+1)(/(兀)-(x 2 一3)gCr))—(—兀―1) f (x) + (兀'+ 兀2 — 3兀—2)g(x),所以u (兀)= -x-l, v(x) = x 3 +x 2 -3x-2.9.设/(x) = %3+ (14-t)x 2+ 2x + 2w, g(x)二F+zx + u 的最大公因式是一个二次多项式,求/,凤的值.解利用辗转相除法,可以得到/(%) = g(x) + (l + /)兀2 +(2-/)兀 + « ,(/(x), g(x)) = x-l = -(6x 2+ 3x-9)+ | _g(x)I d J J(I ] \= (/(x)-2xg(x)) --x+- -g(x)\ 3丿 <2 o 2 d ,、 U 3 广—---- 兀+ (1 + r t-2(l +r)2(尸 + r—w)(i+r) + (t— 2)~u[(l + t)2 — (r —2)]由题意,/(x)与g(Q的最大公因式是一个二次多项式,所以(广 + / —w)(l + /) + (f— 2)~(T H?皿(l + r)2-(r-2)] A ;=0,(l + O2解得u = o^t = -4.10.设(x —I)[(A/+ B F+I),求A和B.由题意要求知解用(兀一1)2 去除f\x) = Ar4 + Bx2 +1 ,得余式”(x) = (4A + 2B)兀+1 -3人一B,斤(兀)=0,即4A + 2B = 0,1-3A-B = O,解得A = l,B = -2.11.证明:如果(/(x),g(x)) = l, (/(x),/z(x)) = l,那么(/(x), g(x)/z(x)) = l. 证明由条件可知,存在络(兀)和片⑴ 使得旳(兀)/(兀)+岭⑴g(x) = l,存在如(兀)和卩2(兀)使得u2(x)f(x) + v2(x)h(x) = 1.用/?(兀)乘以第一式得坷(x)f(x)h(x) + V, (x)g(x)h(x) = h(x),代入第二式得u2(x)f(x) + v2 (x) [u t (x)f(x)h(x) 4-Vj (x)g(x)/z(x)] = 1, 即[w2(兀)+ u\ (x)v2(x)h(x)]f(x) + [v, (x)v2(x)]g(x)h(x) = 1,所以(/(x),g(x)/z(x)) = l.12.证明:如果/(x)与g(x)不全为零,且/心)/(兀)+ 咻)g(兀)=(/(%), g(Q),证明由于w(x)/(x) + v(x)g(x) = (/(x),g(x)), /(X )与 g(x)不全为零,所以(/(x),g(x))HO.两 边同时除以(/(Hg(Q)HO,有所以(弘(兀),咻)) = 1 .13.证明:如果〃(兀)|/(兀),〃(兀)|g(x),且〃(兀)为/(兀)与g(x)的一个组合,那么〃(兀)是/G)与 g(x)的一个最大公因式.证明由题意知d(x)是/(X )与g(x)的公因式.再由条件设d(x) = w(x)/(x) + v(x)^(x) •又设h(x) 为/(x)与g(x)的任一公因式,即/z(x)|/(x), h(x)\g(x),则由上式有h(x)\d(x).故而”(兀)是/(兀)与 g(x)的一个最大公因式.14.证明:(.fO)/2(X ), gO)/2(X )) = (.f(X ), g(x))〃(x),其中力(兀)的首项系数为 1.证明显然(/(x), g(x))/?(x)是f{x)h{x)与g(x)h(x)的一个公因式.下面來证明它是最大公因式. 设 /心),v(x)满足 w(x)/(x) + v(x)g(x) = (/(x), g(X>),贝iJu(x)f(x)h(x) + v(x)g(x)h(x) = (/(x),g(x))/z(x).由上题结果知,(/(兀),g(X ))/7(X )是/(X )/?(X )与g(JC”7(X )的一个最大公因式,又首项系数为1,所以(/(x)A(x), ^(%)/?(%)) = (/(x), ^(x))/i(x)・/⑴ g (兀)、(/(兀),g (兀))’(f(x),g(x))丿证明设〃(兀)=(/(兀),g(x)),则存在多项式M (x), v(x),使d(x) = u(x)f(x) + v(x)g(x)・因为/(X )与g (尢)不全为零,所以d(x)HO.上式两边同时除以〃(兀),有故 /(兀) _____________ g (x)l (/(x),g(x))‘(/(x),g(x))‘u(x) /(X ) (/(%), g(x)) + v(x) g(x) (y (x ),^(x ))15.设多项式/(x)与gS)不全为零,证明1 = u(x)/(兀)(/(兀),g(x))+咻)g(x) (/(兀),g(x))=1成立.16. 分别在复数域、实数域和有理数域上分解兀4+ 1为不可约因式之积.在有理数域上兀°+1是不可约多项式.否则,若+ +1可约,有以下两种可能.(1) 兀4+1有一次因式,从而它有有理根,但/(±1)工0,所以卍+1无有理根.(2) x 4+ 1 无一次因式,设x 4+1 = (x 2+处 +方)(F +cx + d),其中 a,b y c,cl 为整数.于是a + c = O, b+ 〃 + ac = O, cut + be = 0 , bd = \,又分两种情况:① b = d = \,又 a = —c,从而由 b + 〃 + ac = O,得 a 2=2,矛盾; ② b = d = — \,则 a 2= —2 ,矛盾.综合以上情况,即证.17. 求下列多项式的有理根: (1) /(x) = x 3-6x 2+15兀一 14 ;(2) ^(X ) = 4X 4-7X 2-5X -1;(3) /z(x) = x 5+ %4— 6x^ — 14x~ — 1 lx — 3 ・解(1)由于/(x)是首项系数为1的整系数多项式,所以有理根必为整数根,且为-14的因数.-14的 因数有:±1, ±2, ±7, ±14,计算得到:/(D = -4, /(-1) = -36, /(2) = 0, /(-2) = -72,/(7) = 140, /(-7) = -756, /(14) = 1764, /(一 14) = —4144,故x = 2是/(兀)的有理根.再由多项式除法可知,x = 2是于(兀)的单根.⑵ 类似(1)的讨论可知,g(x)的可能的有理根为:故x = --是巩兀)的有理根.再由多项式除法可知,兀二-丄是/(劝的2重根.2 2⑶ 类似地,加兀)的可能的有理根为:±1,±3,计算得到解在实数域上的分解式为X4+ 1 = (X 2 + 1)2-2X 2 =(X 2+V2X + 1)(X 2-V2X +1).在复数域上的分解式为x + ----------1 2 2%4+ 1 = f亠迈亠近、X ---------- 12 2/±1, ±1 ±?计算得到g(l) = -9,g(-1) = 1, g(]、r 、171=-5, g —=0, g — 一 —‘ g —〔2< 264 ,4丿11A(l) = -28, /?(-l) = 0,(3) = 0,加一3) = -96.故x = -l, x = 3是//(兀)的有理根.再由多项式除法可知,x = -\是/z(x)的4重根,兀=3是//(兀)的单根.18.若实系数方程x34- px + q = 0有一根a + bi (a,b为实数,/?工0),则方程x3 + px-q = 0有实根2—证明设原方程有三个根不失一般性,令=a + bi,从而有a2 =a-bi,由根与系数的关系可知0 = $ + 冬 + 他=(° + 勿)+ (a - bi) + ,所以冬二-2d,即(-2a)‘ + /?(-2a) + g = 0,故(2a)' + p(2a)-q = 0.这说明x3 + /zr-g = 0有实根2a .19.证明:如果(%-i)|/(r),那么证明因为u-i)|/(z),所以/(r)= /(i)= 0.因此,令y(x)=(x-i)g(x),则有E =(*-i)g(;),即(伙-1)|/(疋).20.下列多项式在有理数域上是否可约?(1)土 (%) = F+1;(2)/;(X)= X4-8?+12X2+2;(3)人(x) = x" +『+1 ;(4)厶(无)=* + "; + 1,门为奇素数;(5)厶(兀)=兀°+4尬+ 1, A为整数.解(1) ./;(兀)的可能的有理根为:±1,而/(±1) = 2,所以它在有理数域上不可约.(2)由Eisenstein判别法,取素数p = 2,则2不能整除1,而2|(-8), 2|12, 2|2,但是2?不能整除2,所以该多项式在有理数域上不可约.(3)令x=y + l,代入厶(x) = P+x'+l有^(y) = ^(y + l) = / + 6/+15/+21/+18y24-9y4-3.取素数0 = 3,由Eisenstein判别法知,g(y)在有理数域上不可约,所以/(兀)在有理数域上不可约.(4)令兀= y_l,代入f4(x) = x p 4-px + 1,得g(y)=厶(y j) = -+ cy~2——C;-2y2 + (Cf* + p)y-p,取素数p,由Eisenstein判别法知,g(y)在有理数域上不可约,所以£(兀)在有理数域上不可约.(5)令x=y + l,代入农(兀)=兀4+4Ax+l,得g(.y)=厶(y +1) = y" + 4y‘ + 6y2 + (4k + 4)y + 4R + 2 ,収素数p = 2,由Eisenstein判别法知,g(y)在有理数域上不可约,所以点(兀)在有理数域上不可约.1•设/(X),g(X),加兀)是实数域上的多项式,(1)若/2U) = xg2(x) + x/z2(x),则/(x) = g(x) = h{x) = 0 .(2)在复数域上,上述命题是否成立?证明(1)当g(兀)=/2(兀)=0时,有严⑴=0,所以/(%) = 0 ,命题成立.如果g(x), /z(x)不全为零,不妨设g(x)H0・当h(x) = 0时,a(xg2(x) + x/i2U)) = l + 2a^(x)为奇数;当加兀)工0时,因为g(x),瓜兀)都是实系数多项式,所以Xg2(x)与兀胪(兀)都是首项系数为正实数的奇次多项式,于是也有d(xg2(x) + x/『(x))为奇数.而这时均有/2(x)^0 ,且df\x) = 2df(x)为偶数,矛盾.因此有g(兀)=力(兀) = 0,从而有f(x) = 0 .(2)在复数域上,上述命题不成立.例如,设f(x) = 0 , g(x) = x\ h(x) = ix,1,其中斤为自然数, 有/2 (x) = xg2 (x)xh2 (x),但g(x) / 0 ,力(兀)工0.2.设/(x), g(x)9 h(x)e P[x],满足(x2 4-l)h(x)4-(x-l)/(x) + (x+2)g(x) = 0,(x2 + l)/?(x) + (x+ l)/(x) + (x - 2)^(%) = 0.证明(X2+1)|(/U), g(X))・证明两式相加得到2(x2 + l)h(x) + 2x(/(x) + g(兀))=0.由(x2+l,兀)=1可知(x2 + l)|(/(x) + g(x)).两式相减得到-2f(x) + 4g(x) = 0, f(x) = 2g(x).故(x2 + l)|/(x), (x2+l)|g(x), BP(X2+1)|(/(X),g(x)).3・设gi(x)g2(x)\f{(x)f2(x),证明(1)若/(x)|g](x),/(X)H0,则g2(x)\f2(x);(2)若g2(x)|/;(x)/;(x),是否有g2(x)\f2(x)?解(1)因为gi(兀)g2(兀)庞(兀)£(兀),/O)|gi(X),故存在多项式h(x), h}(x)使得fl(x)f 2(x) = g](x)g 2(x)h(x\ g](兀)=Z (x)h }(x).于是/;(兀)£(兀)=/(兀)人(兀)g2(x)力(兀)•由于 土(兀)工0,故有 f 2(x) = h l (x)g 2(x)h(x),即g 2(x)\f 2(x).(2)否•例如取 g {(x) = x-2 , ^2(X ) = X 2-1 , (x) = (x-l)(x-2), (x) = (x + l)(x4-2).虽 然 gSx)g 2(x)\f^x)f 2(x)且 g 2(x)\f {(x)f 2(x),但 g 2(x)不能整除 f 2(x).4.当R 为何值时,/(x) = X 2 +伙+ 6)x + 4k + 2和g(x) = F+(£ + 2)x + 2R 的最大公因式是一次 的?并求出此吋的最大公因式.解 显然 g(x) = (x + £)(x+2).当(/(x),g(Q) = x + 2时'/(一2) = 4 — 2伙+ 6) + 4£ + 2 = 0‘ 则k = 3.当(于(兀),g(Q )=兀 + £ 时’/(一灯=k 2 - k(k + 6) + 4Z: + 2 = 0 ‘ 则 k = l.这时(/(x), g(x))=兀+1. 5.证明:对于任意正整数斤,都有(/(x),g(Q)"=(/"(x),g"(x))・证明 由题意可知/(%)与&(兀)不全为零.令(/(x), g(x)) = d(x),Z 、” g(x) 、d(x)丿/心)/"(兀)+ 咚)g"(兀)=d\x).又由 d(x)\f(x), d(x)|g(x),有 d n (x) f l \x), d"(x) g"(x),因此 d"(x)是厂(x)与 g"(x)的首项系数为1的最大公因式,从而有(广(x),g"(x))= 〃"(兀)=(/(x),g(x))" •6.设 / (x) = af(x) + bg(x), g[ (x) = c/(x) + dg(x),且 ad - be H 0 ,证明(/(x),g(x)) = (/](x), g](X ))・证明设(/(x), g(x)) = d(x),则 d(x)\f(x\d(x)\g(x).由于 “所以对任意正整如,有爲J 寫〕"卜 于是有u{x) +咻) 则〃(兀)工0,从而fi (兀)=妙(x) + bg(x) , g] (x) = (x) + dg (x),故d (x)| (x), d (x)|g t (x).又设h(x)\ (x), /z(x)|(x),由上式及ad-bc^O ,可得从而/?(x)|/(x), h(x)\g(x),于是h(x)\d(x),即〃(兀)也是/;(兀)和g|(x)的最大公因式,即(/(x), g(x)) = (/;(x),&(兀))・7.设 /(x) = t/(x)/(x), g(Q 二 dCr)g](x),且/O)与 gd)不全为零,证明〃(兀)是/O)与 gCO的一个最大公因式的充分必要条件是(/(劝,g|(x)) = 1.证明必要性.若〃(x)是/(兀)与g (兀)的一个最大公因式,则存在多项式w(x),v(x)使W (x)/(x) +v(x)g(x) = d(x),于是u(x)d(x)f t (x) + v(x)d(x)g l (x) = d(x).由/(力与g (兀)不全为零知如工0,因此有u(x)f l (x) + v(x)g l (x) = l f 即(土(兀),g©))i •充分性.若(f l (x),g l (x)) = l ,则存在多项式u(x),v(x),使 u(x)f l (x)+ v(x)g l (x) = l. 两边同吋乘〃(兀)有u(x)f(x) + v(x)g(x) = d(x)・由d(x)是/(x)与g(x)的一个公因式知,d(x)是f(x)与g(x)的一个最大公因式.8.设于(兀)和g(x)是两个多项式,证明(f(x), g(x)) = l 当且仅当(f(x)-l-g(x), f(x)g(x)) = l. 证明 必要性.设(f(x)9g(x)) = l,若f(x) + g(x)与/⑴g(x)不互素,则有不可约公因式p(x), 使p(x)lf(x)g(x)f所以 p(x)| /(X )或 0(x)|g(x).不妨设 p(x)\ /(x),由 P (x)|(/(x) + g (兀))可知 p(x)|g(x),因此 P (兀)是 /(兀)和g“)的公因式,与/(%), g (x)互素矛盾,故 蚀+g (兀)与蚀g (兀)互素.充分性.设(/(兀)+ gO) J(x)g (兀)) = 1,则存在w(x), v(x)使(/(兀)+ g (兀))心)+ /(x)g(x)v(x) = 1 , f(x)u(x) + g (兀)(臥兀)+d ad-be zw- h ad 一gi (兀), g(x) -c ad -be a ad -be g](x),/(x)v(x)) = 1, 上式说明(/(兀),g(兀)) = 1.9.如果(x2 +x + l)|/j(x3) + x/^(x3),那么(x-l)|/;(x), 0 — 1)|/;(兀)・T;®所以,^3=£23 = 1.证明X2+X + l的两个根为£\= 士护和£2=因为U2+x+l)|(/;(^3) + x/;(^3)),所以(兀一£|)(x - £2)|/;(X')+/(F),故有y 窗)+ £/(郃)=0,[爪哥)+ £2£(哥)=0,即解得/(l) = /;(l) = o,从而(兀—1)|久(兀),(x-1)|/;(%).10.若f(x)\f(x H),则/(x)的根只能是零或单位根.证明因为f(x)\f(x n),故存在多项式g(x),使/(x n) = /(x)^(x).设。
线性代数第一章§1.4-1.6,习题

互换 i, j (i < j)两行得到
a11 a j1 D1 ai1 an1
a1 p a jp aip anp
a1n a jn ain ann
b11 bi1 b j1 bn1
b1 p bip b jp bnp
r4 – 3r1
1 1 2 3 0 0 1 0 0 2 0 4 0 2 1 5
r2 r3
1 0
1 2
2 0
3 4
0 0 1 0 0 2 1 5
1 0 0 0 1 2 0 0 2 0 1 1 3 4 0 1
r4 + r2
r 4 + r3
1 1 2 3 0 2 0 4 2 0 0 1 0 0 0 0 1
n
更一般的有
1 0 Dn 1 0 0 an
(形如
1 0 0 0
1 0
1 a1 0 0 0
a0 1 1 1 1
(a1a2 an 0)
a2 0 0
an 1
,称为箭形(或爪形)行列式)
另外还有
§1.6 行列式按行(列)展开
一、余子式与代数余子式
定义:
0 b11 b1n bn1 bnn ,
a11 a1k b11 b1n D1 , D2 , a k 1 a kk bn1 bnn 证明: D = D1D2.
证明: 对D1作行运算 ri + t rj , 把D1化为下三角形 行列式: p 0
11
D1 p11 pkk ; pk 1 pkk
则D = D1D2.
线性代数第一章作业及其答案
第一章行列式一、单项选择题1.行列式D 非零的充分条件是()(A)D 的所有元素非零(B)D 至少有n 个元素非零(C)D 的任何两行元素不成比例(D)以D 为系数矩阵的非齐次线性方程组有唯一解2.二阶行列式1221--k k ≠0的充分必要条件是()A.k≠-1B.k≠3C.k≠-1且k≠3D.k≠-1或≠33.已知2阶行列式2211b a b a =m ,2211c b c b =n ,则222111c a b c a b ++=()A.m -nB.n -mC.m +nD.–(m +n )4.设行列式==1111034222,1111304zy x zyx则行列式()A.32B.1C.2D.385.下列行列式等于零的是()A .100123123- B.031010300-C.100310-D.261422613-6.行列式111101111011110------第二行第一列元素的代数余子式21A =()A.-2B.-1C.1D.27.如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解,则k=()A.-2B.-1C.1D.28.(考研题)行列式0000000ab a bc dc d=()A.()2ad bc - B.()2ad bc -- C.2222a db c- D.2222b c a d-二、填空题1.四阶行列式中带负号且含有因子12a 和21a 的项为。
2.行列式1112344916中位于(3,2)元素的代数余子式A 32=。
3.设1578111120963437D --=--,则1424445A A A ++=。
4.已知行列式212300111a=-,则数a =。
5.若a ,b 是实数,则当a =且b =时,有000101ab ba-=--。
6.设13124321322)(+--+-+=x x x x f ,则2x 的系数为。
7.五阶行列式000130003201830207530026=。
(精选)线性代数行列式第一章练习题答案

《线性代数》(工)单元练习题一、填空题1、设矩阵A 为4阶方阵,且|A|=5,则|A*|=__125____,|2A|=__80___,|1-A |= 1/52、若方程组⎪⎩⎪⎨⎧=+=+=+a bz cy b az cx ay bx 0 有唯一解,则abc ≠ 03、把行列式的某一列的元素乘以同一数后加到另一列的对应元素上,行列式 0 .4、当a 为 1 or 2 时,方程组⎪⎩⎪⎨⎧=++=++=++040203221321321x a x x ax x x x x x 有非零解.5、设=-+----=31211142,410132213A A A D 则 .0二、单项选择题1.设)(则=---===333231312322212113121111333231232221131211324324324,1a a a a a a a a a a a a D a a a a a a a a a D B (A)0 ; (B)―12 ; (C )12 ; (D )12.设齐次线性方程组⎪⎩⎪⎨⎧=+-=++=+02020z y kx z ky x z kx有非零解,则k = ( A )(A )2 (B )0 (C )-1 (D )-23.设A=792513802-,则代数余子式 =12A ( B )(A) 31- (B) 31 (C) 0 (D) 11-4.已知四阶行列式D 中第三列元素依次为-1,2,0,1,它们的余子式依次分别为5,3,-7,4,则D= ( A ) (A ) -15 (B ) 15 (C ) 0 (D ) 1 三、计算行列式1、111a b c b c a c a b +++ ( 0 ) 2、. 1212301112042411D --=----(-10)3、1111111111111111x x y y+-+- (x 2y 2) 4、 3321322132113211111b a a a a b a a a a b a a a a +++(b 1b 2b 3)5、3222232222322223ΛM M M M M ΛΛΛ=n D (2n+1)三、已知n 阶行列式12312001030100n nD n=LLLM M M O M L,求第一行各元素的代数余子式之和. 解:A 11+A 12+…+A 1n 11111200111(1)!103023100n nn==----⋅LLL LM M M O M L(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
《线性代数》第一章行列式精选习题及解答

a1 ...
∏ a2
...
... ...
an ...
=
(a j − ai ) .
1≤i< j≤n
a1n−1
a
n−1 2
... ann−1
1.2.6 计算行列式的常用方法
1.利用对角线法则计算行列式,它只适用于 2、3 阶行列式;
2.利用 n 阶行列式定义计算行列式;
3.利用行列式的性质化三角形法计算行列式;
(C) 10 (D) 9
解 在排列 14536287 中,1 排在首位,逆序数为 0;4、5、6、8 各数的前面没有比它们
自身大的数,故这四个数的逆序数为 0;3 的前面比它大的数有 2 个(4、5),故逆序数为 2;
2 的前面比它大的数有 4 个(4、5、3、6),故逆序数为 4;7 的前面比它大的数有 1 个(8),
MM MM
M
11 1 1L2
1 −1 −1 −1 L −1
n +1 0 0 0 L 0
11 0 0L0
求和,故共有 n!项. 1.2.2 行列式的性质
1.行列式和它的转置行列式相等; 2.行列式的两行(列)互换,行列式改变符号; 3.行列式中某行(列)的公因子可提到行列式的的外面,或若以一个数乘行列式等于 用该数乘此行列式的任意一行(列);
4.行列式中若有两行(列)成比例,则该行列式为零; 5.若行列式的某一行(列)的元素都是两数之和,则此行列式等于两个行列式之和, 即
即 ( A31 + A32 + A33 ) + 2( A34 + A35 ) =0. 同理 2( A31 + A32 + A33 ) + ( A34 + A35 ) =0
