线性代数-第一章作业题
线性代数章节练习题

b b2 ac
c
a
c2 a2
ab abc
b b2 abc
c c2 abc
abc
111
(a b c) a2 b2 c2 (a b c) a b c
111
a2 b2 c2
(a b c)(b a)(c a)(c b)
246 427 327 1000 427 327 1000 100 327 (2) 1014 543 443 2000 543 443 2000 100 443
D 2 0
2 7
2 0
2 0
5 3 2 2
求第四行各元素的余子式之和的值。
8 计算 n 阶行列式
x y 00 0 0 x y0 0 Dn 0 0 0x y y 0 00 x
3 1 1 9 计算行列式 D 1 5 1 。
1 1 3
3 2 2 10 计算三阶行列式 D k 1 k 。
(C) C PT AP
(D) C PAPT
13 计算
0 1 0 2007 1 2 3 0 1 0 2006 1 0 0 4 5 61 0 0 0 0 1 7 8 9 0 0 1
14 设 A 为 n 阶可逆阵,交换 A 的第 i 行与第 j 行后得到 B。 (1)证明 B 可逆;(2)求 AB-1
(C)当 n m 时,必有 AB 0
(D)当 n m 时,必有 AB 0 18 证明 R( A B) R( A) R(B)
4 1 41 则
R(BA 2A)
19 A 为 m p 矩阵,B 为 p n 矩阵,若 AB=0 证明: R( A) R(B) P
20 设 A 为 n 阶矩阵,且 A2=A,若 R( A) . 证明 R( A E) n r ,其中 E 为 n 阶单位阵
线性代数同步练习册第一章(15题,18页)

第一章 行列式1、利用对角线法则计算行列式.(1)abn b a m -.(2) 40230120.(3)38114112---. (4) 321a a a aaa .(5)yxyx x y x y y x y x+++.2、利用行列式的性质计算行列式.(1)004003002001000.(2)10315398122299331201221---.(3) 1132211313213211------.(4)3214214314324321.(5) 2100032000002100032100032.(6)vu d c y x b a 00000000.(7)yy x x -+-+1111111111111111.(8)33221111110011001b b b b b b ------.3、计算n 阶行列式(1)....0010...3010...021...321nn .(2)xa a a a x aaa a x a a a a x ............................(3) xa x a x a x a a D nn n 0...01...00..................00...000...100 (011321)---=-.4、证明:(1) 设c b a ,,为互异实数, 证明行列式:ba a c cbc b a cb aD +++=222为零的充要条件是0=++c b a .(2) 0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a .(3)bz ay by ax bx az by ax bx az bzay bxaz bz ay by ax +++++++++yxzx z yz y x b a )(33+=.5、设行列式 aa a a a a a a a D 20...0012...0000......... (000)...120000...012000 (00122)222=证明 n n a n D )1(+=.6、设5021011321011111---=D ,求14131211432A A A A +++,其中j i A 为行列式中元素j i a 的代数余子式.7、求行列式 2235007022220403--=D 的第四行各元素的余子式之和.8、如果齐次方程组⎪⎩⎪⎨⎧===+++++000433322111kx kx kx x x x x 有非零解, k 应取什么值?9、λ为何值时,齐次线性方程组⎪⎩⎪⎨⎧===+---++0002333222111x x x x x x x x x λλ只有零解.10、问μλ,取何值时,齐次线性方程组⎪⎩⎪⎨⎧===++++++002333222111x x x x x x x x x μμλ有非零解.11、解方程02002003211121=xx x .12、利用范德蒙行列式计算行列式 (1)27181914131211111--.(2) 2222................3 (33)2 (22)1 (11)n n nD n n n =.13、用克莱姆法则解下列线性方程组 (1)⎩⎨⎧=+=+273152y x y x .(2) ⎪⎩⎪⎨⎧=+-=+--=-+44522272532z y x z y x z y x .14、求三次多项式)(x f ,使得16)3(,3)2(,410(,0)1(====-f f f f .15、已知m 阶行列式,a A =n 阶行列式,b B =求*B AO D =的值.第一章 行列式 自测题一、选择题: 1、行列式01221≠--k k 的充分必要条件是( ).(A)1-≠k (B )3≠k(C)1-≠k 且3≠k (D) 1-≠k 或3≠k2、行列式01110212=-kk的充要条件是( ).(A)2-=k (B )3=k(C)2-=k 且3=k (D) 21-=k 或3=k 3、设四阶行列式0=A ,则A 中( ).(A) 必有一行元素全为零; (B) 必有两行元素对应成比例;(C) 必有一行元素可以表示为其余各行对应元素的线性关系; (D) 对角线上元素全为零.4、行列式8040703362205010的值为 ( ). (A) 72-; (B) 24-; (C)36-; (D)12-.二、填空题 1、设行列式12211=b a b a ,22211=c a c a ,则=++222111c b a c b a .2、设三阶行列式22=-A ,则=A .3、若三阶行列式6222321332211321=---c c c a b a b a b a a a , 则行列式 =321321321c c c b b b a a a . 4、设100100200001000-=aa ,则=a . 5、若行列式1333231232221121211==a a a a a a a a a D , 则行列式=---333231312322212112121111324324324a a a a a a a a a a a a .6、设3214214314324321=A , 则=+++24232221432A A A A .三、计算四阶行列式(1)dcd c b a b a 00000000.(2)1111111111111111--+---+---x x x x四、计算n 阶行列式1...12...1..................3 (11)2 (211)1...3211 (4321)x xxx x x n x x n x n n---.五、设347534453542333322212223212)(---------------=x x x x x x x x x x x x x x x x x f ,求方程0)(=x f 根的个数?六、求方程08814412211111)(32=--=x xxx f 的根.七、如果齐次线性方程组⎪⎩⎪⎨⎧===+-+++-0002333222111x x x x kx x kx x x 有非零解, k 应取什么值?八、判定方程组;.0)2(03)3(5;02)2(32132213212⎪⎩⎪⎨⎧=++=-++-=-+-x a x x x a x x x x a 是否只有零解.九、证明等式 ∑∏=≤≤≤-==414144434241242322214321)(1111i i i j j i x x x x x x x x x x x x x x x A .十、用克莱姆法则解方程组 ⎪⎩⎪⎨⎧=++=++=++1132132523z y x z y x z y x .。
线性代数第一章习题参考答案

解:4234231142342311)1342(4432231144322311)1324()1()1(a a a a a a a a a a a a a a a a =--=-ττ4.计算abcdef abcdef abcdef abcdef efcf bfde cd bdae ac ab r r r r c c c r f r d r a c ec c c b 420020111111111111111111111)1(12133213213211,1,11,1,1-=--=--=---=-----++5.求解下列方程10132301311113230121111112121)1(12322+-++-++=+-++-+=+-+-+++x x x x x x x x x x x x c c r r 1132104201)3(113210111)3(21+-+--++=+-+-++=-x x x x x x x x x r r 3,3,30)3)(3(11421)3(3212-==-==-+=+---++=x x x x x x x x x 得二列展开cx b x a x b c a c a b x c x b x a c b a x c b a x c b a x ====------=32133332222,,0))()()()()((1111)2(得四阶范得蒙行列式6.证明322)(11122)1(b a b b a a b ab a -=+右左证明三行展开先后=-=-=-----=----=+=+--323322222)(11)()()()1(100211122)1(:2132b a b a b a ba ba b a b b a a b b a b a b b ab ab a b b a ab ab ac c c c1432222222222222222222222222(1)(2)(3)(1)2369(1)(2)(3)(1)2369(3))(1)(2)(3)(1)2369(1)(2)(3)(1)2369c c c ca a a a a a a ab b b b b b b b cc c c cc c cd d d d d d d d --++++++++++++==++++++++++++二三列成比例))()()()()()((1111)4(44442222d c b a d c d b c b d a c a b a d c b a dcbad c b a D +++------==44444333332222211111)(x d c b a xdcbax d c b a x d c b a x f 五阶范得蒙行列式解考虑函数=(5)))()()()()()(())()()()()()(()()())()()()()()()()()((454545453453d c d b c b d a c a b a d c b a A M D d c d b c b d a c a b a d c b a A ,A x x f ,Mx x f D a b b c a b c d b d a d d x c x b x a x ------+++-==------+++-=----------=于是的系数是中而对应的余子式中是(5)n n a a a a a xx x x 12101000000000100001----解:nn n n n n n n n n nn x a x a a x a x a a a a a a a xx x x D +++=-++--+--=---=+++-++++-10)1()1(1211110121)1()1()1()1()1(1000000000100001按最后一行展开7、设n 阶行列式)det(ij a D =把D 的上下翻转、或逆时针旋转090、或依副对角线翻转、依次得111131111211111,,a a a a D a a a a D a a a a D n n nn n nn n nnnn=== 证明D D D D D n n =-==-32)1(21,)1(证明:将D 上下翻转,相当于将对D 的行进行)1(21-n n 相邻对换得1D ,故D D n nn 2)1(1)1(--=将D 逆时针旋转090相当于将T D 上下翻转,故D n n D n n D T 2)1(2)1(2-=-=D 依副对角线翻转相当于将D 逆时针旋转090变为2D , 然后再2D 左右翻转变为3D ,故D D D D n n n n n n =--=-=---2)1(2)1(22)1(3)1()1()1(8、计算下列行列式(k D 为k 阶行列式)(1)aa D n 11=,其中对角线上元素都是a ,未写出的元素都是0;解:)1()1(0100)1(1122211111-=-+=-+==--++-+a a a a a aa a a D n n n n n n n n n n 列展开按行展开按(2)x a a a x a a a x D n=解:xaa x a a a n x x a aa x a a a x D nc c c n111])1([21-+==+++12)]()1([0001])1([1--≥--+=---+=n r r k a x a n x ax a x a a a n x k(3)111111)()1()1()()1()1(11111n a n a a a n a n a a a n a n a a a D n n n n n nnm n -+---+---+--=----+解:11111(1)(1)22111111(1)(1)()(1)(1)()111111111111()()()((1)(1)()(1)(1)()n nnn n n n n n n n n n n j i n n n n mnnna a a n a n a a a n a n D a a a n a n a a a n a n j i a a a n a n a a a n a n ----++++≥>≥------+---+-=--+---+-=-=--=--+---+-∏上下翻11)n j i i j +≥>≥-∏(4)n n nnn d c d c b a b a D11112=(未写出的均为0)解:)1(2)1(211112)(02232--↔↔-===n n n n n n n nnn r r c c nnnnn D c b d a D d c b a d c d c b a b a D mn得递推公式)1(22)(--=n n n n n n D c b d a D ,而11112c b d a D -=递归得∏=-=ni i i i i n c b d a D 12)((5)det(),||n ij ij D a a i j ==-解111,2,,1120121111110121111210311111230123010001200(1)(1)211201231i i j r r n i n c c n n n n D n n n n n n n n n n n n +-=-+-------==-------------==---------解:11211*222,3,,1111111(6)1111111111101111000111100:01111i n nr r n i n nna a D a a a a a D D a a -=+++=++-+-===+-解111211121,2,,12111(1)1110001(1)0000i inc c na n i ni ina a a a a a a a a a ++==++++==+∑9.设3351110232152113-----=D ,D 的),(j i 元的代数余子式为ij A ,求44333231223A A A A +-+解:24335122313215211322344333231=-----=+-+A A A A。
线性代数作业习题

第一章:行列式1、计算下列行列式1 2 2 … 2 22 2 2 … 2 22 23 … 2 2:::::2 2 2 … n-1 22 2 2 … 2 n解:首先利用每一行元素分别减去第二行元素得到:-1 0 0 02 2 2 00 0 1 00 0 0 2 00 0 0.......n-2可利用代数余子式求出:(-1)*2*(n-2)!2、计算下列行列式:|x y x+y||y x+y y||x+y y xl解:|x y x+y||y x+y y||x+y y x|=x|x+y y|+y(-1)| y y|+(x+y)| y x+y|| y x| |x+y x| |x+y y |=x(x²+xy-y²)-y(xy-xy-y²)+(x+y)(y²-x²-2xy-y²)=x(x²+xy-y²)-y(-y²)+(x+y)(-x²-2xy)=x³+x²y-xy²+y³-x³-x²y-2x²y-2xy²=y³-2x²y-3xy²=y(y²-2x²-3xy)3、计算下列行列式:1 2 -5 1-3 1 0 -62 0 -1 24 1 -7 6解:根据行(列)与行(列)之间互换,行列式值改变符号。
所以第一列与第二列互换,得出2 1 -5 11 -3 0 -60 2 -1 21 4 -7 6根据行列式倍加不变原理。
第四列乘以-2加上第一列,第四列乘以-1加上第二列,结果如下。
0 -7 9 -110 -7 7 -120 2 -1 21 4 -7 6根据行列式倍加不变原理。
第四列乘以-2加上第一列,第四列乘以-1加上第二列0 -7 9 -110 -7 7 -12- 0 2 -1 21 4 -7 6根据计算,得出= (-14)+49-62=-274、求二阶行列式1-x^2 2x----- -----1+X^2 1+X^2解:原式=([1-x²]²+4x²)/(1+x²)²=(1+x²)²/(1+x²)²=15、设A B为n阶方阵,满足ATA=AAT=E,BTB=BBT=E及|A|+|B|=0,求|A+B|解:原式=([1-x²]²+4x²)/(1+x²)²=(1+x²)²/(1+x²)²=1由已知, |A|^2=|B|^2 = 1所以|A|, |B| 等于1 或-1因为|A|+|B|=0所以|A||B|= -1所以有|A+B|= - |A||A+B||B|= - |A^T||A+B||B^T|= - |A^T AB^T+A^T BB^T|= - |B^T+A^T|= - |(A+B)^T|= - |A+B|.所以|A+B| = 0.第二章:矩阵1、已知矩阵A=[1 1 1][2 -1 0][1 0 1]B=[3 1 1][2 1 2][1 2 3 ] 求:AB解:AB=[1×3+1×2+1×1 1×1+1×1+1×2 1×1+1×2+1×32×3-1×2+0×1 2×1-1×1+0×2 2×1-1×2+0×31×3+0×2+1×1 1×1+0×2+1×2 1×1+0×2+1×3]=[6 4 6][ 4 3 4]2、设A=[2 2 3][1 -1 0][3 1 2] A*为A的伴随矩阵,求A(-1)A*解:AA*=|A|EA* = |A|A^-1所以A^-1A* = |A| (A^-1)^2|A|=4AA*=|A|EA* = |A|A^-1所以A^-1A* = |A| (A^-1)^2|A|=4A^-1=-1/2 -1/4 3/4-1/2 -5/4 3/41 1 -1(A^-1)^2=9/8 19/16 -21/1613/8 39/16 -33/16-2 -5/2 5/2所以A^-1A* = |A| (A^-1)^2 =9/2 19/4 -21/413/2 39/4 -33/4-8 -10 103、判断关于逆矩阵(A+B)的逆等于不等于A的逆加B的逆解:一般不等于,反例:令A=B=E则(A+B)=2E,(A+B)逆=E/2而A逆+B逆=E+E=2E所以不等4、求矩阵的秩[1 3 2 a][2 -4 -1 b]其中a,b,c为任意实数解:r(A)=3因为[1 3 2][2-4-1][3-2 0]的行列式不为0,说明原矩阵有一个3阶子式不为0,秩至少是3;又因为原矩阵是3*4的矩阵,它的秩最多为3,所以答案就是35、一个方程组x+y+z=22x+y+3z=03y+4z=1求方程的解解:设A=[111213034]B=[21]A的逆阵为C=(1/7)*[5,1,-28,-4,1-6,3,1]x=C.B=1/7[817-11]第三章:向量空间1、已知α1=(1,1,2,-1)α2=(-2,1,0,0,)α3=(-1,2,0,1)又β满足3(α1-β)+2(α3+β)=5(α2+β)求β解:由题设,有3α1-3β+2α3+2β=5α2+5β3α1+2α3-5α2=6β(3,3,0,-3)+(-2,4,0,2)-(-10,5,0,0)=6β6β=(11,2,0,-1)β=(11/6,1/3,0,-1/6)2、设数域F上向量空间V的向量组{α1 , α2 , α3}线性无关,向量β1可由α1 , α2 , α3线性表示,而β2不能由α1 , α2 , α3线性表示。
线性代数作业及参考答案

第一章 矩阵作业答案班级: 姓名: 学号 : 得分:一、选择题 (每小题5分,共20分)1. 设A 为任意n 阶矩阵,下列4项中( B )是反对称矩阵。
(A )T A A + (B )T A A - (C )T AA (D )A A T2.设n 阶矩阵A ,B 是可交换的,即BA AB =,则不正确的结论是( D )。
(A )当A ,B 是对称矩阵时,AB 是对称矩阵 (B )2222)(B AB A B A ++=+ (C )22))((B A B A B A -=-+(D )当A ,B 是反对称矩阵时,AB 是反对称矩阵3.设n 阶矩阵A ,B 和C 满足E ABAC =,则( A)。
(A )E C A B A T T T T = (B )E C A B A =2222 (C )E C BA =2 (D )E B CA =24. 设÷øöçèæ=21,0,0,21a ,a a T E A -=,a a T E B 2+=,则AB =( B )(A) a a TE + (B) E (C) E - (D) 0二、计算与证明题 (每小题20分,共80分)1.已知úûùêëé--=1121A ,试求与A 可交换的所有二阶矩阵X得分得分2. 已知úúúûùêêêëé=010101001A , (1)证明:E A A A n nn -+=³-223时,(2)求100A.3. 已知矩阵,,试作初等变换把A 化成B ,并用初等矩阵表示从A 到B 的变换.BQ AQ Q Q B a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a A c c c c =úúúûùêêêëé=úúúûùêêêëé==úúúûùêêêëé+++¾¾®¾úúúûùêêêëé+++¾¾®¾úúúûùêêêëé=«+21213133323321232223111312133333323123232221131312113332312322211312110010101001100100013123所以,设解:4.已知矩阵,试作初等行变换,把分块矩阵化成,其中E 是单位矩阵,B 是当左块A 化成E 时,右块E 所变成的矩阵;并计算矩阵的乘积AB 与BA .úúúûùêêêëé----¾¾¾®¾úúúûùêêêëé+-+-101110012430001321100431010212001321312112r r r r )()(解:úúúûùêêêëé----¾¾¾®¾úúúûùêêêëé---¾¾®¾úúúûùêêêëé----¾¾®¾+-+-+--+«3151004160101120013151001011100013210124301011100013211213233321223113r r r r rr r r r r r )()()()(úúúûùêêêëé==úúúûùêêêëé----=100010001315416112BA AB B 则第二章 行列式与矩阵求逆作业答案班级: 姓名: 学号 : 得分:一.计算下列行列式:(每题10分,共30分)1. 已知4阶行列式44332211400000a b a b b a b a D =, 求4D 的值. 解:得分2. 计算n 阶行列式111111111111nn n n D n ----=3. 计算5阶行列式242322214321500032100111011110x x x x x x x x D =二.计算题:(每题15分,共60分)1. 已知3阶行列式2101123z y x D =,且,1,0322213331311-=++=+-M M M M M M2132131=+-M M M其中的值的余之式,求中元素是33D a D M ij ij .得分2. 求4阶行列式22350070222204034--=D 中第4行各元素余之式之和.3. 设úúúúûùêêêêëé=5400320000430021A , 则求1-A .4. 若úúúúûùêêêêëé=121106223211043a A 可逆,则求a 的值.三.(10分)问m l 、取何值时,齐次方程组ïîïíì=+m +=+m +=++l 0200321321321x x x x x x x x x有非零解?零解。
线性代数第一章测试题

线性代数第一章测试题1. 向量空间的定义:- 简述向量空间的定义,并给出一个例子。
2. 向量的线性组合:- 解释什么是向量的线性组合,并给出一个具体的例子。
3. 基和维数:- 描述什么是基(Basis)和维数(Dimension),并解释它们之间的关系。
4. 线性相关与线性无关:- 给出线性相关和线性无关的定义,并用一组向量来说明它们。
5. 向量空间的子空间:- 解释什么是向量空间的子空间,并给出一个例子。
6. 线性变换:- 定义线性变换,并给出一个线性变换的例子。
7. 矩阵的秩:- 描述矩阵的秩是什么,并解释如何计算一个矩阵的秩。
8. 行列式:- 解释行列式的概念,并给出计算2x2和3x3矩阵行列式的方法。
9. 逆矩阵:- 定义什么是逆矩阵,并说明一个矩阵何时有逆矩阵。
10. 特征值和特征向量:- 描述特征值和特征向量的概念,并给出一个计算矩阵特征值和特征向量的例子。
11. 线性方程组的解:- 解释线性方程组的解集,并讨论其解的性质。
12. 矩阵的运算:- 给出矩阵加法、乘法和转置的定义,并给出相应的例子。
13. 正交性和正交基:- 解释正交性和正交基的概念,并给出一个正交基的例子。
14. 投影矩阵:- 定义投影矩阵,并说明如何使用它来投影向量。
15. 线性变换的几何解释:- 描述线性变换在几何上的解释,并给出一个具体的例子。
16. 矩阵的分解:- 简述矩阵分解的概念,并给出LU分解和QR分解的例子。
17. 范数:- 解释向量范数的概念,并给出1-范数、2-范数和无穷范数的定义。
18. 线性映射的矩阵表示:- 描述如何将一个线性映射表示为矩阵。
19. 线性代数在实际问题中的应用:- 给出一个实际问题,并展示如何使用线性代数的概念来解决它。
20. 附加题:- 给出一个矩阵,并要求学生找到它的逆矩阵,如果存在的话。
如果不存在,解释为什么。
线性代数第一章行列式练习题

班级__________ 姓名__________ 学号_______第一章第一次练习题一)填空题1)计算(1465372)τ=________;[135(21)246(2)]n n τ-L L =________;2)写出四阶行列式中含有因子1123a a 的项及符号__________;3)在四阶行列式中,21143243a a a a 的符号为__________;4)设12134453k l a a a a a 在五阶行列式中带有负号,则k =________;l =________.二)解答题5)计算三阶行列式 222111a bc a b c .6)用定义证明1(1)212100000(1)0000n nn nnλλλλλλ--=-LLLLL.7)设n阶行列式中有多于2n n 个元素为零,证明这个行列式为零.班级__________ 姓名__________ 学号_______第一章第二次练习题一)填空题1)把行列式111222a b c a b c ++定出两个行列式之和______________________; 2)把行列式132412340000a a a a x yb b z w b b 写成两个行列式之积_________________________________; 3)提取行列式第二行公因子后111213212223313233333a a a a a a a a a =__________________________; 4)行列式223456789ab c d a ab ac ad=_________________________________.二)解答题5)化简行列式1111 2222 3333 x y x a z x y x a z x y x a z+++6)计算行列式5222 2522 2252 22257)计算行列式3112 5134 2011 1533------班级__________ 姓名__________ 学号_______第一章第三次练习题一)填空题1)将行列式123123123x x xy y yz z z按第三列展开为__________________________________;2)已知四阶行列式D中第三行元素依次为2,5,3,4;它们的余子式分别为3,1,2,4;则D=__________;3)计算1111234549162582764125=__________;4)设3961246812035436D=,则41424423A A A++=__________.二)解答题5)计算行列式100 110 011 001abcd---.6)当λ为何值时,线性方程组12312330(3)22040x x x x x x x λλ++=⎧⎪--+=⎨⎪=⎩有非零解?7)设曲线230123y a a x a x a x =+++通过四个点(1,3),(2,4),(3,4) ,(4,3)-;求系数0123,,,a a a a .班级__________ 姓名__________ 学号_______第一章复习题。
线代第一章测试题及答案

线代第一章测试题及答案一、选择题(每题5分,共20分)1. 以下哪个选项不是线性代数的研究对象?A. 向量空间B. 线性方程组C. 矩阵D. 微分方程答案:D2. 矩阵的秩是指:A. 矩阵的行数B. 矩阵的列数C. 矩阵中非零行(或列)的最大数目D. 矩阵的元素个数答案:C3. 以下哪个矩阵是可逆的?A. 零矩阵B. 单位矩阵C. 奇异矩阵D. 任意矩阵答案:B4. 向量空间的基是指:A. 空间中的任意一组向量B. 空间中的一组线性无关的向量C. 空间中的一组线性相关的向量D. 空间中的一组正交向量答案:B二、填空题(每题5分,共20分)1. 矩阵的元素个数称为矩阵的______。
答案:阶数2. 如果一个矩阵的行向量组线性无关,则该矩阵是______矩阵。
答案:满秩3. 向量空间中,一组向量如果满足线性组合的系数全为零,则称这组向量是______的。
答案:线性无关4. 一个n阶方阵的行列式等于______。
答案:0三、简答题(每题10分,共20分)1. 请简述什么是线性方程组的解。
答案:线性方程组的解是指满足方程组中所有方程的未知数的取值。
2. 请解释什么是矩阵的转置。
答案:矩阵的转置是指将矩阵的行向量变成列向量,列向量变成行向量,即交换矩阵的行和列。
四、计算题(每题15分,共40分)1. 计算矩阵A的行列式,其中A = \[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\]。
答案:\[ \text{det}(A) = (1)(4) - (2)(3) = 4 - 6 = -2 \]2. 已知矩阵B = \[\begin{bmatrix} 2 & 1 \\ 4 & 2\end{bmatrix}\],求B的逆矩阵。
答案:\[ B^{-1} = \frac{1}{(2)(2) - (1)(4)} \begin{bmatrix} 2 & -1 \\ -4 & 2 \end{bmatrix} = \begin{bmatrix} 1 & -0.5 \\-2 & 1 \end{bmatrix} \]。
线性代数作业本 第一章课件

。
二、选择题 1、五阶行列式的展开式共有 ( )项。
(A) 5 (C)
2
; ;
(B) (D)
5! 15
; 。
10
2、设,
3a1 D1 0 3a 2 3a n 0
a1 D2 0 a2
0
an
其中 a1 , a2 an 0, 则( 1 ; D (B) ( A) 3D1 D2
a32 a43 a14 a51 a66 a25 各应带什么符号?
八、根据行列式定义,计算
2x x 1 2 1 x 1 1 4 3 中 x 与x 的系数 f(x)= 3 2 x 1 1 1 1 x
九、(选作题)求排列
n (n 1) 3 21 3 7 1 D 5 9 2 4 6 1
2 4 7 2
1 5 1 1 三、设 D 1 1 2 2
1 3 2 3
3 4 3 4
,计算
A41 A42 A43 A44 ,其中
A4 j 是元素a4 j ( j 1,2,3,4) 的代数余子式。
四、计算n阶行列式:
五、设
3 1 1 2 5 1 3 4 D , 求A31 3 A32 2 A33 2 A34 2 0 1 1 1 5 3 3
六、计算
an D2 n cn a1 c1 b1 d1 dn , 其中未写出的元素都是 0 bn
1 2 3 4 5 5 5 5 3 3 七、选作题:设 D 3 2 5 4 2 2 2 2 1 1 4 5 6 2 3
线性代数作业本
第1次作业
一、填空题 1、排列25431的逆序数为 (奇偶)排列; 2、排列217986354的逆序数为 (奇偶)排列 3、行列式 3 5 = ; 2 4 4、设 a , b 为实数,则当
《线性代数》第1章习题详解

一、习题1参考答案1. 求下列排列的逆序数,并说明它们的奇偶性.(1)41253; (2)3712456; (3)57681234; (4)796815432 解(1)()4125330014τ=+++= 偶排列(2)()37124562500007τ=+++++= 奇排列(3)()576812344544000017τ=+++++++= 奇排列 (4)()7968154326755032129τ=+++++++= 奇排列 2. 确定i 和j 的值,使得9级排列.(1)1274569i j 成偶排列; (2)3972154i j 成奇排列. 解 (1) 8,3i j == (2) 8,6i j == 3.计算下列行列式.(1) 412-3- (2) 2211a a a a ++-1 (3) cos sin sin cos x xx x -(5)2322a a bab (6) 1log log 3b aab (7) 000xy x z y z--- 解(1)131523125=⨯-⨯=- (2)4(3)2(1)4212=-⨯--⨯=--3- (3)()22322211(1)11a a a a a a a a a a =-++-=--++-1 (4)22cos sin cos sin 1sin cos x x x x x x -=+= (5)233232220a a a b a b bab =-=(6)1log 3log log 2log 3b b aa ab a b=-=(7) 0000000xyxz xyz xyz y z -=+----=--4. 当x 取何值时3140010xx x≠ ? 解 因为314010xx x2242(2)x x x x =-=-所以当0x ≠且2x ≠时,恒有3140010xx x ≠5. 下列各项,哪些是五阶行列式ij a 中的一项;若是,确定该项的符号.1225324154(1);a a a a a 3112435224(2);a a a a a 4221351254(3)a a a a a解 (1)不是 (2)不是 (3)不是6. 已知行列式11121314212223243132333441424344a a a a a a a a a a a a a a a a ,写出同时含21a 和21a 的那些项,并确定它们的正负号.解 12213443a a a a (2143)2τ= 符号为正; 14213243a a a a (2134)1τ= 符号为负. 7. 用行列式定义计算下列行列式.(1) 11121314152122232425313241425152000000a a a a a a a a a a a a a a a a (2)020200002200(3) 01000200001000n n-解 (1)行列式的一般项为12345()1122334455(1)j j j j j j j j j j a a a a a τ-若345,,j j j 中有两个取1,2列,则必有一个取自3,4,5列中之一的零元素,故该行列式的值为零,即原式0=(2)行列式中只有一项(3241)13223441(1)16a a a a τ-=不为零,所以原式16= (3)行列式的展开项中只有(2,3,4)11223341,1(1)(1)!n n n n n a a a a a n τ---=- 一项不为零,所以原式1(1)!n n -=-8. 用行列式性质计算下列行列式.(1) 111314895(2)1234234134124123(3)41241202105200117⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(4)2141312112325062⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦(5)ab ac aebd cd debf cf ef---(6)a b aa a bb a aa b a解 (1) 111314895321331r rr r--111021013--232r r-111005013--23r r↔111013005---5=(2)12342341341241232341c c c c+++10234103411041210123123413411014121123=121314r rr rr r-+-+-+123401131002220111------34222r rr r-+123401131000440004---160=(3)4124120210520011712r r↔12024124105200117-2131410r rr r--120207240152200117-----24r r↔120201170152200724----3242157r rr r++1202011700178500945342r r-12020117001500945=--(4) 2141312112325062-13r r↔1232312121415062--213141325r rr rr r---12320775032301098----------232r r -12320131032301098-3242310r r r r --123201310076002118----0=(5) abac ae bdcd de bfcfef---每列都提取公因式bc eadf bc e b c e ---每列都提取公因式111111111adfbce --- 1213r r r r ++11102020abcdef -23r r ↔11120002abcdef --4abcdef = (6)0000a b a a a b b a a a b a 4321r r r r +++2222000a b a b a b a ba a bb a a a b a ++++()11110200aa b a b b a a a ba =+121314ar r br r ar r -+-+-+()1111002000a b aa b a b b a b b a a --+----- 3232r r r r +-()11110020000a b aa b b b b b --+---=()2111100201100101a b a b a b --+--- 3424r r r ar ++()211110002200110101b a b a b -+---24c c ↔()211110101200110002b a b b a-+---()()2422224b a b b a b a b =+-=-9. 证明下列等式.(1) 111222222222111333333333a b c bc a c ab a bc a b c b c a c a b a b c =-+(2)11122122111211121112111221222122212221220000a a a a a a b b c c b b a a b b c c b b = (3) ax byay bzaz bxay bzaz bx ax by az bxax by ay bz +++++++++=33()xy z a b y z x zxy+(4) 222244441111a b c da b c d a b c d ()()()()()a b a c a d b c b d =-----()()c d a b c d ⋅-+++ 证明 (1)左式123123123321213132a b c b c a c a b a b c a b c a b c =++--- 133321233212332()()()a b c b c b a c a c c a b a b =---+-=222222111333333b c a c a b a b c b c a c a b -+=右式(2)1112212211121112212221220000a a a a c c b b c c b b 按第一行展开222111121112121111122221222121220000a a a c b b a c b b c b b c b b - 111211121122122121222122b b b b a a a a b b b b =-1112111221222122a ab b a a b b =(3) ax byay bzaz bxay bzaz bx ax by az bxax by ay bz +++++++++ 按第一列分开x ay bzaz bxa y az bx ax by z ax by ay bz ++++++ y ay bzaz bxb z az bx ax by x ax by ay bz +++++++2(0)xay bz z ay az bx x z ax by y +++++分别再分(0)yz az bxb z x ax by x y ay bz++++33x y z y z x a y z x b z x y zxy x yz +分别再分332(1)x y z x y za yz x b yz x z xy zxy=+-=右边 (4) 222244441111a b c d a b c d a b c d 213141c c c c c c --- 222222244444441000a b a c a d aa b a c a d a a b a c a d a --------- 按第一列展开222222222222222()()()b ac ad ab ac ad a b b a c c a d d a --------- 每列都提取公因式222111()()()()()()b ac ad a b a c a d a b b a c c a d d a ---++++++ 1213c c c c -+-+()()()b ac ad a ---222221()()()()()b ac bd bb b ac c a b b ad d a b b a +--++-++-+ 按第一列展开()()()()()b ac ad a c b d b -----222211()()()()c bc b a c bd bd b a d b ++++++++()()()()()a b a c a d b c b d =-----()()c d a b c d -+++10.设行列式30453221--,求含有元素2的代数余子式的和. 解 含有元素2的代数余子式是12222313A A A A +++()()()()345453343050111121212222--=-+-+-+---11161026=---=- 11. 设行列式3040222207005322=--D ,求第四行各元素余子式之和的值是多少? 解 解法一:第四行各元素余子式之和的值为41424344M M M M +++040340300304222222222222700000070070=+++---780314(7)(1)(2)28=-⨯++⨯+-⨯-⨯-=-解法二:第四行各元素余子式之和的值为4142434441424344M M M M A A A A +++=-+-+3040222207001111=---按第3行展开32340(7)(1)222111+----232r r +340704111--按第2行展开34282811-=---12.已知 1012110311101254-=-D ,试求: (1) 12223242A A A A -+- (2) 41424344A A A A +++ 解 (1)方法一:虽然可以先计算处每个代数余子式,然后再求和,但是这很烦琐.利用引理知道,第一列每个元素乘以第二列的代数余子式的和等于零。
线性代数习题集(带答案)

第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a cb a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a d b a dc ad c b dcbad c b a d c b a++++++++33332222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠); 6. bn b b ----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a x a a a a x a a a a x n nn321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a aa a a a aD ---------=1101100011000110001.四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b a d c b a +++------=.4.∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明0111333=c b a c ba 的充要条件是0=++cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ------+++-; 2. )(233y x +-; 3. 1,0,2-=x ; 4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略)第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
线性代数第一章作业

第一章作业一、填空1、设一个n m ⨯型线性方程组的系数矩阵为A ,增广矩阵为B ,若n m <,则该方程组或 解,或有 解;若n B R A R ==)()(,则该方程组必有 解;2.设n m ⨯线性方程组的系数矩阵为A ,增广矩阵为B . 如果该方程组无解,那么 )(A R _____)(B R ;3.设一个n m ⨯齐次线性方程组的系数矩阵为A ,那么该方程组有无穷多个解的充分必要条件是_______________;仅有零解的充分必要条件是 ;4.已知方程⎪⎩⎪⎨⎧=-+=+++=++423)2(3212321321321x ax x x a x x x x x 无解,则=a .5.设一个m n ⨯线性方程组的系数矩阵为A ,它等价于000rm nE ⨯⎛⎫ ⎪⎝⎭;其增广矩阵为B ,它等价于(1)000km n E ⨯+⎛⎫ ⎪⎝⎭. 那么方程组有解的充分必要条件可以用r 和k 描述成 ;6.两个矩阵等价当且仅当它们的 数相等, 数相等,而且 数相等;7.方阵⎪⎪⎭⎫ ⎝⎛-2311的标准形是 .二、利用增广矩阵化简下列线性方程组,并讨论其解的情况:1. 8311102322421321321⎪⎩⎪⎨⎧=+=+-=-+x x x x x x x x ;2. 69413283542432 ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++z y x z y x z y x z y x ;3.⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534432312 ωωωz y x z y x z y x三、计算下列矩阵的秩:1. 174034301320⎪⎪⎪⎭⎫ ⎝⎛----=A ;2.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------=12433023221453334311B ; 四、利用判定定理一判断下列方程组是否有解。
1.⎪⎩⎪⎨⎧=+++=+++=+++1035125422536372432143214321x x x x x x x x x x x x ;2.⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x .五、λ取何值时,非齐次线性方程组⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x1.有唯一解;2.无解;3.有无穷多个解. 六、设⎪⎩⎪⎨⎧--=-+--=--+=-+1)5(4224)5(2122321321321λλλx x x x x x x x x ,问λ为何值时,此方程组有唯一解,无解或有无穷解.七、求下列矩阵的标准形:1.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--121144013111;2.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---21022400130110221011。
线性代数习题集-第一章

第一章:行列式I.单项选择题 1.排列1,3,,(2n 1),2,4,,(2n)-的逆序数为( )(1) n 1- (2) (n 1)n - (3) (n 1)n + (4) (n 1)/2n - 2.排列1,3,,(21),(2),(22),,2n n n --的逆序数为( )(1) n (2) (n 1)n - (3) (n 1)n + (4) (n 1)/2n - 3.四阶行列式中含有因子1123a a 的项是( )(1) 11233442a a a a (2) 11233344a a a a (3)11233342a a a a (4) 11233442a a a a -4.行列式abac aebdcd de bfcfef---的值是( ) (1) 2abcdef (2) 4abcdef (3) 6abcdef (4) 8abcdef 5. 设A 为n 阶方阵,λ为数,则A λ等于( ) (1) A λ (2) A λ (3) n A λ (4) 2A λ6.设ab cD de f g hi=,则元素h 的代数余子式为( ) (1)a c gi(2) a cdf -(3) a c g i - (4)a c df7.设行列式000000a bcD d e f g h i j=,则D 的值等于( ) (1) abdg - (2) abdg (3) abdg ceh fi j -+- (4) abdg ceh fi j ++- 8.设A 为n 阶矩阵,则( )(1) A A -= (2) A A -=- (3) (1)n A A -=- (4) 1A A --=9.设A 为n 阶矩阵,且A 的行列式0A a =≠,而A *是A 的伴随矩阵,则A *等于()(1) a (2) 1/a (3) n a (4) 1n a -10.若12312,,,,αααββ都是四维列向量,且1231m αααβ=,1223n ααβα=四阶行列式,则32112()αααββ+四阶行列式等于( ) (1) n m - (2) m n - (3) m n + (4) ()m n -+11.设44⨯ 矩阵[]234,,,A αγγγ= ,[]234,,,B βγγγ=,其中234,,,,αβγγγ均为4维列向量,且已知行列式1,1A B ==,则行列式A B +等于( ) (1)5 (2)10 (3)30 (4)4012.设设A 为m 阶方阵,设B 为n 阶方阵,且,A a B b ==,00AC B =,则C 等于( )(1) ab (2) ab - (3) (1)nm - (4) (1)nm ab -13.设行列式D aba b b a b a a b ab+=++,则D 的值为( )(1) 332()a b -+ (2) 332()a b + (3) 332()a b - (4) 33()a b -+ 14.元素是0和1的三阶行列式D 之值只能是( ) (1) 3 (2) 3- (3) 4 (4) 0,1,2±± II.填空题1.n 阶行列式的完全展开式,应由________项组成,每项位于行列式中________的n 个元素的乘机,而且项1212n j j nj a a a 的符号为_____.2. n 阶行列式1111nn nna a A a a =,则按第i 行的展开式为__________;按第j 行展开式为__________.3.当A 可逆是1A -=____________.4.设A 是一个n 阶方阵,k 是一个有理数,则kA =________,5.在行列式2121113211x x x x j j x-的展开式中,3x 的系数为________,4x 的系数为_________.6.三角行列式110nn nna a a =_________ 7.行列式2111131111411115A ==__________ 8.行列式11101210011000000111002A --==--__________ III.判断题1.交换行列式中任意两行的位置,行列式的值不变。
线性代数1-5章习题1

线性代数习题集第一章行列式一、判断题1.行列式如果有两列元素对应成比例,则行列式等于零. ( )2. 213210 124121 012342=-.( )3. 13434121.42042=-( )4.123213123213123213.a a ab b bb b b a a ac c c c c c=( )5.123123123123123123.a a a a a ab b b b b bc c c c c c---------=---( )6. n阶行列式n D中元素ij a的代数余子式ij A为1n-阶行列式. ( )7. 312143 245328 836256=.( )8.111213212223313233a a aa a aa a a122r r+111213211122122313313233222+++a a aa a a a a aa a a( )9.如果齐次线性方程组有非零解,则它的系数行列式必等于零. ( )10. 如果方程个数与未知数个数相等,且系数行列式不为零,则方程组一定有解. ( )二、选择题1.若12532453r sa a a a a是5阶行列式中带正号的一项,则,r s的值为().A.1,1r s ==B.1,4r s ==C.4,1r s ==D.4,4r s ==2.下列排列是偶排列的是( )A. 4312B. 51432C. 45312D. 6543213.若行列式210120312x --=-, 则x =( ).A.–2B. 2C. -1D. 14.行列式0000000000a bc d e f的值等于( ). A. abcdef B. abdf - C. abdf D. cdf5.设abc ≠0,则三阶行列式00000d c b a的值是( ).A .aB .-bC .0D .abc 6.设行列式2211b a b a =1,2211c a c a =2,则222111c b a c b a ++=( ).A .-3B .-1C .1D .37.设非齐次线性方程组123123123238223105ax x x ax x x x x bx ++=⎧⎪++=⎨⎪++=⎩有唯一解,则,a b 必须满足( )..0,0A a b ≠≠ 2.,03B a b ≠≠ 23.,32C a b ≠≠ 3.0,2D a b ≠≠ 8. 215152521112223030223-=---是按( )展开的.A .第2列B .第2行C .第1列D .第1行9.设111211212ni i inn n nna a a D a a a a a a =则下式中( )是正确的. 1122.0i i i i in in A a A a A a A +++= 1122.0i j i j ni nj B a A a A a A +++=1122.i i i i in ni C a A a A a A D +++= 1122.i j i j ni nj D D a A a A a A =+++10. 349571214的23a 的代数余子式23A 的值为( ).A. 3B. -3C. 5D. -5 三、填空题1. 排列36715284的逆序数是________.2. 四阶行列式中的一项14322341a a a a 应取的符号是_______. 3.若,0211=k 则k=___________. 4.行列式1694432111中32a 元素的代数余子式A 32=____________.5.598413111=__________. 6.行列式0001001010000100=______.7.行列式0004003002001000=__________. 8.非零元素只有1n -行的n 阶行列式的值等于__________.9. 1231231238,a a a b b b c c c =则123123123222c c c b b b a a a ---=__________. 10.n 阶行列式nD 中元素ij a 的代数余子式ij A 与余子式ij M 之间的关系是ij A =__________,n D 按第j 列展开的公式是n D =__________.四、计算题1.写出五阶行列式中含1325a a 并带有正号的所有项.2.计算四阶行列式1002210002100021的值.3.求4阶行列式1111112113114111的值.4.计算行列式D =1111123414916182764的值.5. 计算行列式122224242λλλ--+---+6.计算n 阶行列式011110111101111.7. 计算n 阶行列式 00 n a D a⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅, 其中对角线上元素都是a , 未写出的元素都是0;8. 计算n 阶行列式 n x a a a xaD a ax⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅五、证明题1.33()ax byay bz az bx x y z ay bzaz bx ax by a b yz x az bx ax byay bzzxy++++++=++++2.2222222222222222(1)(2)(3)(1)(2)(3)0(1)(2)(3)(1)(2)(3)a a a a b b b b cc c cd d d d ++++++=++++++六.用克拉默法则解方程1. 12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩; 2.121232343454556156056056051x x x x x x x x x x x x x +=⎧⎪++=⎪⎪++=⎨⎪++=⎪⎪+=⎩.七. 问λ取何值时, 齐次线性方程组123123123(1)2402(3)0(1)0x x x x x x x x x λλλ--+=⎧⎪+-+=⎨⎪++-=⎩有非零解?第二章 矩 阵一、判断题1.若A 是23⨯矩阵,B 是32⨯矩阵,则AB 是22⨯矩阵. ( )2.若,AB O =且,A O ≠则.=B O ( )3. 12103425X ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭的解110122534X -⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭. ( ) 4.若A 是n 阶对称矩阵,则2A 也是n 阶对称矩阵. ( ) 5. n 阶矩阵A 为零矩阵的充分必要条件是0.A = ( )6. 若,A B 为同阶可逆矩阵,则11()kA kA --=. ( )7. 42042069126232110110⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭. ( )8. n 阶矩阵A 为逆矩阵的充分必要条件是0.A ≠ ( )9.设,A B 为同阶方阵,则 A B A B +=+. ( )10.设 ,A B 为n 阶可逆矩阵,则 111A O A O O B OB ---⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭.( ) 二、选择题1. 若,A B 为n 阶矩阵,则下式中( )是正确的.22.()()A A B A B A B -+=- .(),=.-=≠B A B C O A O B C 且,必有222.(+)+2+B A B A AB B = .D AB A B =2.若,s n n l A B ⨯⨯,则下列运算有意义的是( )..T T A B A .B BA .+C A B .+T D A B3.若,m n s t A B ⨯⨯,做乘积AB 则必须满足( )..=A m t .=B m s .=C n s .=D n t4.矩阵1111A --⎛⎫=⎪⎝⎭的伴随矩阵*=A ( )A .⎪⎪⎭⎫ ⎝⎛--1111B .⎪⎪⎭⎫ ⎝⎛--1111C .⎪⎪⎭⎫ ⎝⎛--1111D .⎪⎪⎭⎫ ⎝⎛--11115.设2阶矩阵a b A c d ⎛⎫= ⎪⎝⎭,则*=A ( ) A .⎪⎪⎭⎫ ⎝⎛--a c b d B .⎪⎪⎭⎫ ⎝⎛--a b c d C .⎪⎪⎭⎫ ⎝⎛--a cb dD .⎪⎪⎭⎫⎝⎛--a b c d 6. 矩阵⎪⎪⎭⎫⎝⎛-0133的逆矩阵是( )A .⎪⎪⎭⎫ ⎝⎛-3310B .⎪⎪⎭⎫ ⎝⎛-3130C .⎪⎪⎭⎫⎝⎛-13110 D .⎪⎪⎪⎭⎫ ⎝⎛-01311 7. 设2阶方阵A 可逆,且A -1=⎪⎭⎫ ⎝⎛--2173,则A=( ).A .⎪⎭⎫ ⎝⎛--3172 B .⎪⎭⎫ ⎝⎛3172 C .⎪⎭⎫ ⎝⎛--3172 D .⎪⎭⎫ ⎝⎛21738. n 阶矩阵A 行列式为,A 则kA 的行列式为( ).A. kA B. n k A C. k A D. -k A9. 设,A B 为n 阶矩阵满足=,AB A 且A 可逆,则有( )..==A A B E .=B A E .=B B E .,D A B 互为逆矩阵10.设A 是任意阶矩阵,则( )是对称阵..(+)T T A A A .+T B A A .T C AA .T T D A AA三、填空题1.设矩阵120210001A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,100021013B ⎛⎫⎪= ⎪ ⎪⎝⎭,则2+=A B _____________2.设A=⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤411023,B=,010201⎢⎣⎡⎥⎦⎤则AB =___________. 3.设矩阵A=⎪⎪⎭⎫ ⎝⎛21,B=⎪⎪⎭⎫ ⎝⎛31,则A TB =____________. 4.⎪⎪⎪⎭⎫⎝⎛321(1,2,3)=__________. 5.n1111⎪⎪⎭⎫ ⎝⎛=__________. 6.⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-0410******** =______________________. 7.设2阶矩阵A =⎪⎪⎭⎫⎝⎛3202,则A *A =_____________.8.设矩阵A=⎪⎭⎫⎝⎛4321,则行列式|A 2|=__________. 9.设A=⎪⎪⎭⎫ ⎝⎛d c b a ,且det(A)=ad-bc≠0,则A -1=__________ .10. 设 ,A B 为n 阶可逆矩阵,则 1O A B O -⎛⎫= ⎪⎝⎭_______________.四、计算题1.已知110123011,124,111021A B ⎡⎤⎡⎤⎢⎥⎢⎥=----⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求()TA B +.2.计算下列乘积1).431712325701⎛⎫⎛⎫ ⎪⎪- ⎪⎪ ⎪⎪⎝⎭⎝⎭;2).3(123)21⎛⎫⎪⎪ ⎪⎝⎭;3).)21(312-⎪⎪⎭⎫⎝⎛;4).13121400121134131402⎛⎫⎪-⎛⎫ ⎪⎪ ⎪--⎝⎭⎪-⎝⎭;5).111213112312222321323333()a a a xx x x a a a xa a a x⎛⎫⎛⎫⎪⎪⎪⎪⎪⎪⎝⎭⎝⎭.3.求矩阵方程.1)25461321X-⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭;2)211113210432111X-⎛⎫-⎛⎫⎪=⎪⎪⎝⎭⎪-⎝⎭;3)142031121101X⎛⎫⎛⎫⎛⎫=⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭;4)010100143100001201001010120X-⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭.4.设矩阵21=53A⎛⎫⎪⎝⎭,13=20B⎛⎫⎪⎝⎭,求矩阵方程=XA B的解X.5.设321=111101A ⎡⎤⎢⎥⎢⎥⎢⎥⎦⎣,求-1A .6.设101=210,325A ⎛⎫ ⎪⎪ ⎪--⎝⎭求-1A7.设101=210325A ⎛⎫ ⎪ ⎪ ⎪--⎝⎭,求-1A .8.设⎪⎪⎪⎪⎪⎭⎫⎝⎛=2500380000120025A ,⎪⎪⎪⎪⎪⎭⎫⎝⎛=2600140000540023B . 求:AB BA 和9. 设A 为3阶矩阵, , 求-1(2)-5A A *.10.设(1,2,1),28,A diag A BA BA E *=-=- 求.B11.设34432022O A O ⎛⎫⎪- ⎪= ⎪ ⎪⎝⎭, 求8A |及4A .五、证明题1. 设,A B 为n 阶矩阵,且A 为对称矩阵,证明TB AB 也是对称矩阵.2.设,A B 为n 阶对称矩阵,证明AB 是对称矩阵的充分必要条件是AB BA =.3.设为n 阶矩阵A 满足235,A A E O --=试证A E +可逆,且()14A E A E -+=-.4. 设A 为n 阶矩阵,且2,A A =且A E ≠,证明A 是不可逆矩阵.第三章 矩阵的初等变换与线性方程组一、选择题1.设n 元齐次线性方程组0AX =的系数矩阵的秩为r ,则0AX =有非零解的充分必要条件是( )(A) r n = (B) r n <(C) r n ≥ (D) r n >2.设A 是m n ⨯矩阵,则线性方程组AX b =有无穷解的充要条件是( )(A) ()r A m < (B) ()r A n < (C) ()()r Ab r A m =< (D) ()()r Ab r A n =<3.设A 是m n ⨯矩阵,非齐次线性方程组AX b =的导出组为0AX =,若m n <,则( )(A) AX b =必有无穷多解 (B) AX b =必有唯一解 (C) 0AX =必有非零解 (D) 0AX =必有唯一解4.已知12,ββ是非齐次线性方程组AX b =的两个不同的解,12,αα是导出组0AX =的基础解系,12,k k 为任意常数,则AX b =的通解是( ) (A) 1211212()2k k ββααα-+++(B) 1211212()2k k ββααα++-+(C) 1211212()2k k ββαββ-+++ (D) 1211212()2k k ββαββ++-+5.设A 为m n ⨯矩阵,则下列结论正确的是( )(A) 若0AX =仅有零解 ,则AX b =有唯一解 (B) 若0AX =有非零解 ,则AX b =有无穷多解 (C) 若AX b =有无穷多解 ,则0AX =仅有零解(D) 若AX b =有无穷多解 ,则0AX =有非零解6.线性方程组123123123123047101x x x x x x x x x ++=⎧⎪++=⎨⎪++=⎩ ( )(A) 无解 (B) 有唯一解 (C) 有无穷多解 (D) 其导出组只有零解 二、判断题1.若,αβ是线性方程组Ax b =的两个解向量, 则αβ-是方程组0Ax =的解。
线性代数第一章作业及其答案
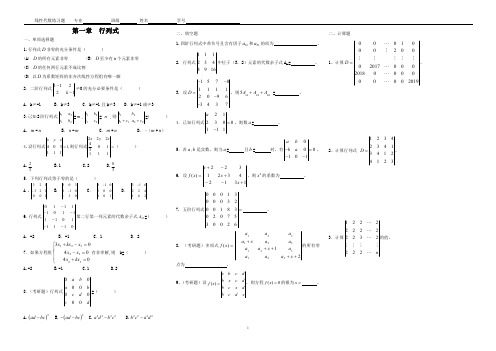
第一章行列式一、单项选择题1.行列式D 非零的充分条件是()(A)D 的所有元素非零(B)D 至少有n 个元素非零(C)D 的任何两行元素不成比例(D)以D 为系数矩阵的非齐次线性方程组有唯一解2.二阶行列式1221--k k ≠0的充分必要条件是()A.k≠-1B.k≠3C.k≠-1且k≠3D.k≠-1或≠33.已知2阶行列式2211b a b a =m ,2211c b c b =n ,则222111c a b c a b ++=()A.m -nB.n -mC.m +nD.–(m +n )4.设行列式==1111034222,1111304zy x zyx则行列式()A.32B.1C.2D.385.下列行列式等于零的是()A .100123123- B.031010300-C.100310-D.261422613-6.行列式111101111011110------第二行第一列元素的代数余子式21A =()A.-2B.-1C.1D.27.如果方程组⎪⎩⎪⎨⎧=+=-=-+0404033232321kx x x x x kx x 有非零解,则k=()A.-2B.-1C.1D.28.(考研题)行列式0000000ab a bc dc d=()A.()2ad bc - B.()2ad bc -- C.2222a db c- D.2222b c a d-二、填空题1.四阶行列式中带负号且含有因子12a 和21a 的项为。
2.行列式1112344916中位于(3,2)元素的代数余子式A 32=。
3.设1578111120963437D --=--,则1424445A A A ++=。
4.已知行列式212300111a=-,则数a =。
5.若a ,b 是实数,则当a =且b =时,有000101ab ba-=--。
6.设13124321322)(+--+-+=x x x x f ,则2x 的系数为。
7.五阶行列式000130003201830207530026=。
线性代数第一章习题答案

线性代数第一章习题答案习题1:向量空间的定义向量空间是一个集合V,配合两个运算:向量加法和标量乘法,满足以下公理:1. 向量加法的封闭性:对于任意的u, v ∈ V,有u + v ∈ V。
2. 向量加法的结合律:对于任意的u, v, w ∈ V,有(u + v) + w = u + (v + w)。
3. 向量加法的交换律:对于任意的u, v ∈ V,有u + v = v + u。
4. 存在零向量:存在一个向量0 ∈ V,使得对于任意的v ∈ V,有v + 0 = v。
5. 每个向量都有一个加法逆元:对于任意的v ∈ V,存在一个向量w ∈ V,使得v + w = 0。
6. 标量乘法的封闭性:对于任意的实数k和向量v ∈ V,有k * v∈ V。
7. 标量乘法的结合律:对于任意的实数k, l和向量v ∈ V,有(k * l) * v = k * (l * v)。
8. 标量乘法与向量加法的分配律:对于任意的实数k和向量u, v ∈ V,有k * (u + v) = k * u + k * v。
9. 单位标量乘法:对于任意的向量v ∈ V,有1 * v = v。
习题2:线性组合与线性无关线性组合是指由向量空间中的向量,通过加法和标量乘法组合而成的向量。
如果一组向量\{v_1, v_2, ..., v_n\}的任何非平凡线性组合(即不是所有标量系数都是零的组合)都不能得到零向量,那么这组向量就是线性无关的。
习题3:基与维数基是向量空间中的一组线性无关的向量,任何该空间中的向量都可以唯一地表示为这组向量的线性组合。
向量空间的维数是其基中向量的数量。
习题4:线性映射的定义与性质线性映射是一个函数T: V → W,它将向量空间V中的向量映射到向量空间W中的向量,并且满足以下性质:1. 对于任意的u, v ∈ V,有T(u + v) = T(u) + T(v)。
2. 对于任意的实数k和向量v ∈ V,有T(k * v) = k * T(v)。
(精选)线性代数行列式第一章练习题答案

《线性代数》(工)单元练习题一、填空题1、设矩阵A 为4阶方阵,且|A|=5,则|A*|=__125____,|2A|=__80___,|1-A |= 1/52、若方程组⎪⎩⎪⎨⎧=+=+=+a bz cy b az cx ay bx 0 有唯一解,则abc ≠ 03、把行列式的某一列的元素乘以同一数后加到另一列的对应元素上,行列式 0 .4、当a 为 1 or 2 时,方程组⎪⎩⎪⎨⎧=++=++=++040203221321321x a x x ax x x x x x 有非零解.5、设=-+----=31211142,410132213A A A D 则 .0二、单项选择题1.设)(则=---===333231312322212113121111333231232221131211324324324,1a a a a a a a a a a a a D a a a a a a a a a D B (A)0 ; (B)―12 ; (C )12 ; (D )12.设齐次线性方程组⎪⎩⎪⎨⎧=+-=++=+02020z y kx z ky x z kx有非零解,则k = ( A )(A )2 (B )0 (C )-1 (D )-23.设A=792513802-,则代数余子式 =12A ( B )(A) 31- (B) 31 (C) 0 (D) 11-4.已知四阶行列式D 中第三列元素依次为-1,2,0,1,它们的余子式依次分别为5,3,-7,4,则D= ( A ) (A ) -15 (B ) 15 (C ) 0 (D ) 1 三、计算行列式1、111a b c b c a c a b +++ ( 0 ) 2、. 1212301112042411D --=----(-10)3、1111111111111111x x y y+-+- (x 2y 2) 4、 3321322132113211111b a a a a b a a a a b a a a a +++(b 1b 2b 3)5、3222232222322223ΛM M M M M ΛΛΛ=n D (2n+1)三、已知n 阶行列式12312001030100n nD n=LLLM M M O M L,求第一行各元素的代数余子式之和. 解:A 11+A 12+…+A 1n 11111200111(1)!103023100n nn==----⋅LLL LM M M O M L(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
线性代数第一章典型习题

0
0 0 x an
(x ai )( x aj )
i 1 j 1
i n
j n
3. 行列式按某一行(列)展开(降阶法): 例 3:计算 n 阶行列式
2 2 3 D
1 2 2 2 2 2
2 2 2
2 2 2
2 2 2 n 1 2 2 2 2 2 n
2 2 1 1 3
3 2 2 1 1
4 1 4 2 5
5 1 5 27 2 0
求 A41+ A42+ A43 ;
A44+ A45
解:由条件得 A 41 + A42 + A43 +2( A44 + A45 ) 27
2( A 41 + A42 + A43 ) + A44 + A45 0 解得 A41+ A42+ A43= -9 , A44+ A45=18
以下用归纳法:
,结论成立; 当 n=1 时, D1 假设对 k<n 的自然数成立,则
Dn ( ) Dn Dn 1 2
n n n 1 n 1 n 1 n 1 ( )
x a1 D a1 a1
x a i x a i D x a i
i 1 i 1 i n i 1 i n i n
a1 a2 x a2 a2 x a2
a3
an an an x
解:将各列加到第一列得
a1 x a2 a2 a3 a2 a2 x x an an an
7.加边法(升阶法): 例 7:证明
1 a1 1 Dn 1 1
线代第1章练习附答案

1 d
的值。
d2 d4
111 1 1
abcd x 【分析】 利用范作范德蒙行列式 D1 a 2 b2 c 2 d 2 x 2 ,则行
a3 b3 c3 d 3 x3 a4 b4 c4 d 4 x4
列式 D 就是行列式 D1 元素 x3 的余子式 M 45 ,即 D M 45
又 D1 (x a)(x b)(x c)(x d)(d a)(d b)(d c)(c a)(c b)(b a)
2341 2 3 4 1 2341
D
10
3412 3 4 1 2 3412
4123 4 1 2 3 4123
1 1 1 1 11 1 1
0 1 2 1 0 1 2 1
10
10
160
0 1 2 1 0 0 4 0
0 3 2 1 0 0 0 4
1 222
2 2 22
3.计算 2 2 3 2 的值。
3
111
111
A. 2
B.1
3
5.下列行列式等于零的是(
3 21
A . 3 2 1
003
B. 0 1 0
0 01
130
C.2
D. 8
3
D)
0 1 0
C. 3 0 0
001
3 1 6
D. 2 2 4
162
0 1 1 1
6.行列式 1 0 1 1
1 0
1 1
第二行第一列元素的代数余子式
A21=(
B)
1 1 1 0
2013 0 0
。
00 0 00 0 0 0 2015
【分析】方法一:此行列式刚好只有 n 个非零元素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 行列式
§1.1
一.填空:
(1)、 04
010
11>-a
a
a
,则a 。
(2)、x
x x x x x f 1111323111212)(--=,则3x 和4
x 的系数分别是 、 。
二.利用n 阶行列式定义,求解下列各题的练习:
1、n 阶行列式ij a A =中每个元素ij a 都乘以j
i b -(0≠b )得行列式B ,证明:B A =。
2、n 阶行列式中有n n -2
个以上元素为零,证明该行列式为零。
3、用行列式定义计算下列行列式: (1) 0
0001002001000
n
n - (2) 0
100002000010
n
n - (3) 选择l k ,,使l k a a a a a 54234213成为5阶行列式ij a 中带有负号的项。
一.用行列式性质证明: (1) 3
332221113
3
3332222
21111
1c b a c b a c b a c c b kb a c c b kb a c c b kb a =++++++ (2) x z y
y x z z y x z
y y
x x
z x z z y y
x y x x z z y 2=+++++++++ (3) 已知204,527及255都能被17整除,求证行列式5
527254
02也能被17整除。
二.计算下列行列式(k D 为k 阶行列式):
(1)
216472954
17321
52----- (2) 0
111101********* (3) x a a a
x a a
a x D n
= (4) n
D n
22
223
2
2222
22221=
(5) n
n x a a
a
a
a x a a a a a x a a a a a x a D ++++=
32
1
)0(21≠n x x x 其中
一.求行列式1
22305
4
03--中元素2和-2的代数余子式。
二.已知四阶行列式D 中第三列元素依次为1,0,2,1-,它们的余子式依次分别为4,73,5-,求D =?
三.已知4
52101113
011
2101--=
A ,求42322212A A A A -+-的值。
四.利用降阶的方法计算下列各行列式(k D 为k 阶行列式):
(1)
216472954
17321
52----- (2) 0410013025210215-- (3) 1
111111*********--+---+---x x x x (4) 0
0000
00
00000
000
β
βαββαβ
α
=
n D (5) d
c
d
c d c b
a b
a b
a
D n
=
2
四.求解方程3
2
1279318
4
211111)(x x x x f --=
(提示:应用范徳蒙行列式或行列式性质) 五.求证:12
10
1200000
21000121000
1
2
+=------=
n D n
一.用克拉默法则解下列线性方程组: (1) ⎪⎩
⎪
⎨⎧=+-=+--=-+44522272532z y x z y x z y x (2)
⎪⎩
⎪
⎨⎧=+=-+-=+-003202az cx bc bz cy ab ay
bx (其中0≠abc )
(3) ⎪⎪⎩⎪⎪⎨⎧
=++=++=++=++43213
21421431432x x x x x x x x x x x x
二.求解下列有关齐次线性方程组的各题:
(1) 求b a ,,使齐次线性方程组⎪⎩
⎪
⎨⎧=++=++=++0200
z by x z by x z y ax 有非零解。
(2) 问λ取何值时,齐次方程组⎪⎩⎪
⎨⎧=-++=+-+=+--0
)1(0)3(2042)1(321
321321x x x x x x x x x λλλ只有零解?。
