第四章 正弦振荡器
合集下载
LC正弦波振荡器
波振荡器。
第４章 正弦波振荡器
正弦波振荡器输出信号的频率范围是很宽的，基本上可 以分成两大类。一类是由电阻、电容元件组成的RC振荡器， 它适用于产生低频正弦波振荡信号，其振荡频率范围为几赫 兹到几十千赫兹。另一类是由集中参数LC元件组成的高频振 荡器，它的振荡频率在几十千赫兹到几十兆赫兹。如果频率 更高，进入米波、分米波范围，则由分布参数系统组成超高
(4-3)
第４章 正弦波振荡器 式(4-3)可以分为两部分， 即
AuFu=1 j=jA+j F=2n (n=0,1,2,……) (4-4) (4-5)
式(4-4)为自激振荡的振幅平衡条件， 式(4-5)为自激振荡的相 位平衡条件。 一个电路要产生自激振荡必须满足上述两个条 件。
第４章 正弦波振荡器
第４章 正弦波振荡器
4.1 概
4.1.1 振荡器的概念和用途
所谓振荡器是一种不需要外加激励信号，而能将直流电
源的能量转变为交流能量的电子设备。它与放大器最根本的 区别在于它的工作不需要外加信号的推动。
第４章 正弦波振荡器
振荡器电路是一种用途非常广泛的基本电子线路。例如，
在无线电通信、广播、电视发射系统中，高频振荡器是个核
环过程，进入到晶体管的饱和区和截止区，放大器的增益下
降，AuFu也就减小，使振荡从AuFu>1过渡到AuFu=1，振荡稳
定下来，最后达到平衡状态。
第４章 正弦波振荡器
由增幅振荡到稳幅振荡的建立过程，说明前者由起振条 件来保证，即AuFu>1，后者由晶体管特性的非线性来实现自 动限幅，而LC回路起选频作用，使振荡回路输出单一频率的 正弦信号。
式(4-2)
u A
(4-2)
u 都为 F
第４章 正弦波振荡器
正弦波振荡器输出信号的频率范围是很宽的，基本上可 以分成两大类。一类是由电阻、电容元件组成的RC振荡器， 它适用于产生低频正弦波振荡信号，其振荡频率范围为几赫 兹到几十千赫兹。另一类是由集中参数LC元件组成的高频振 荡器，它的振荡频率在几十千赫兹到几十兆赫兹。如果频率 更高，进入米波、分米波范围，则由分布参数系统组成超高
(4-3)
第４章 正弦波振荡器 式(4-3)可以分为两部分， 即
AuFu=1 j=jA+j F=2n (n=0,1,2,……) (4-4) (4-5)
式(4-4)为自激振荡的振幅平衡条件， 式(4-5)为自激振荡的相 位平衡条件。 一个电路要产生自激振荡必须满足上述两个条 件。
第４章 正弦波振荡器
第４章 正弦波振荡器
4.1 概
4.1.1 振荡器的概念和用途
所谓振荡器是一种不需要外加激励信号，而能将直流电
源的能量转变为交流能量的电子设备。它与放大器最根本的 区别在于它的工作不需要外加信号的推动。
第４章 正弦波振荡器
振荡器电路是一种用途非常广泛的基本电子线路。例如，
在无线电通信、广播、电视发射系统中，高频振荡器是个核
环过程，进入到晶体管的饱和区和截止区，放大器的增益下
降，AuFu也就减小，使振荡从AuFu>1过渡到AuFu=1，振荡稳
定下来，最后达到平衡状态。
第４章 正弦波振荡器
由增幅振荡到稳幅振荡的建立过程，说明前者由起振条 件来保证，即AuFu>1，后者由晶体管特性的非线性来实现自 动限幅，而LC回路起选频作用，使振荡回路输出单一频率的 正弦信号。
式(4-2)
u A
(4-2)
u 都为 F
高频电子线路-第4章--习题答案
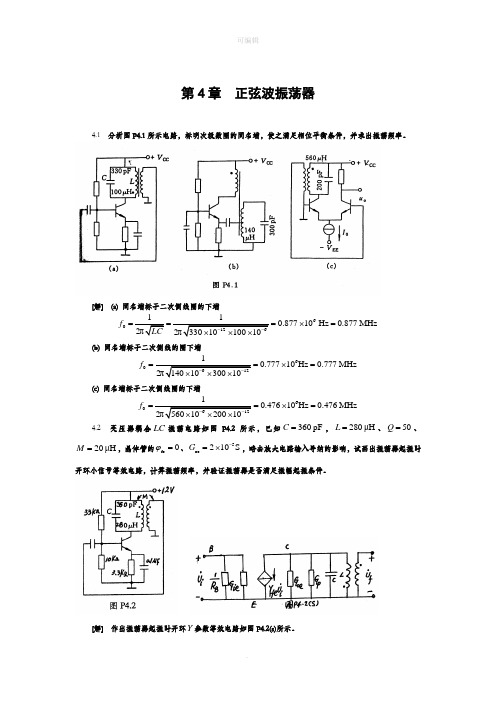
第4章 正弦波振荡器4.1 分析图P4.1所示电路，标明次级数圈的同名端，使之满足相位平衡条件，并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端601260.87710Hz 0.877MHz 2π2π3301010010f LC--===⨯=⨯⨯⨯(b) 同名端标于二次侧线的圈下端606120.77710Hz 0.777MHz 2π1401030010f --==⨯=⨯⨯⨯(c) 同名端标于二次侧线圈的下端606120.47610Hz 0.476MHz 2π5601020010f --==⨯=⨯⨯⨯4.2 变压器耦合LC 振荡电路如图P4.2所示，已知360pF C =，280μH L =、50Q =、20μH M =，晶体管的fe 0ϕ=、5oe 210S G -=⨯，略去放大电路输入导纳的影响，试画出振荡器起振时开环小信号等效电路，计算振荡频率，并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环Y 参数等效电路如图P4.2(s)所示。
略去晶体管的寄生电容，振荡频率等于0612Hz =0.5MHz 2π2π2801036010f LC--==⨯⨯⨯略去放大电路输入导纳的影响，谐振回路的等效电导为5661121042.7μS 502π0.51028010e oe oe o G G G G S S Q Lρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流EQ I 为12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以，三极管的正向传输导纳等于/0.6/260.023S fe m EQ T Y g I U mA mV ≈===因此，放大器的谐振电压增益为o muo eiU g A G U -==而反馈系数为f oU j M M F j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280meg M T A F G L -====⨯ 由于T >1，故该振荡电路满足振幅起振条件。
正弦波振荡器
要维持一定振幅的振荡，反馈系数F应设计得大 一些。一般取 1/ 2 ~ 1/8，这样就可以使得在 AoF 1 时 的情况下起振。
由上分析知，反馈型正弦波振荡器的起振条件是：
AoF 1
即
AAo
F1 F
2n
(n 1, 1, )
分别称为振幅起振条件和相位起振条件。
应用：无线电通讯、广播电视，工业上的高频感 应炉、超声波发生器、正弦波信号发生器、半导体 接近开关等。
正弦波振荡电路的组成
(1) 放大电路: 放大信号
(2) 反馈网络: 必须是正反馈，反馈信号即是 放大电路的输入信号
(3) 选频网络: 保证输出为单一频率的正弦波 即使电路只在某一特定频率下满足 自激振荡条件
17.3.2 正弦波振荡电路
正弦波振荡电路用来产生一定频率和幅值的正弦 交流信号。它的频率范围很广，可以从一赫以下到 几百兆以上；输出功率可以从几毫瓦到几十千瓦； 输出的交流电能是从电源的直流电能转换而来的。 常用的正弦波振荡器
LC振荡电路:输出功率大、频率高。 RC振荡电路:输出功率小、频率低。 石英晶体振荡电路：频率稳定度高。
在平衡条件下，反馈到放大管的输入信号正好等于放 大管维持及所需要的输入电压，从而保持反馈环路各点电 压的平衡，使振荡器得以维持。
4.1.2平衡条件
振荡器的平衡条件即为
T ( j) K( j)F( j) 1 也可以表示为 T ( j) KF 1
(4 ─ 9a)
T K F 2n
2) 相位平衡的稳定条件
相位稳定条件指相位平衡条件遭到破坏时，线路本 身能重新建立起相位平衡点的条件；若能建立则仍能保 持其稳定的振荡。
强调指出：相位稳定条件和频率稳定条件实质上是 一回事。因为振荡的角频率就是相位的变化率 d 。
4章正弦波振荡器
第 4 章 正弦波振荡器
u 反馈振荡器的工作原理 u LC正弦波振荡器 u 振荡器的频率和振幅稳定度 u 石英晶体振荡器
高频电子线路
西南科技大学网络教育学院
振荡器作用：产生一定频率和幅度的信号
按振荡波形分 按振荡原理分
正弦波振荡器
非正弦波振荡器 利用负阻器件的负阻
负振荡器
效应产生振荡
利用正反馈原理构成 反馈振荡器
U IQ
Q’点是不稳定平衡点。若要使该振荡器进入稳定的平衡点，在起
振时给晶体管加一电冲激，并使冲激电压大于UIB，这样自由振荡 就可以产生，这种起振时需要外加冲激的振荡称为“硬激励”。
与此相对，那些冲激能自由产生振荡的现象称为“软激励”。
高频电子线路
西南科技大学网络教育学院
2）相位稳定条件
相位稳定条件是指：当处于平衡状态的系统受到某一 外来因素的干扰，相位平衡状态被破坏，总相角φ大于或 小于2nπ时，环路自动恢复平衡状态φ＝2nπ的条件。
v 若有正反馈环路的话，其不断补偿消耗掉的能量，则能 维持正弦振荡。
高频电子线路
西南科技大学网络教育学院
一、 反馈振荡器的组成
放大器
Ui
Au
无外加输入信号
Uo
正弦波振荡器由放大器、
反馈网络
Uf
Fu
反馈网络组成
T&
=
U& f U& i
= A& F&
高频电子线路
西南科技大学网络教育学院
二、 反馈振荡器的工作原理
φ（ω）曲线在平衡 点附近应为负斜率， 如图所示。
j (w )
¶j (w )
<0
¶w w =w0
ω ω0
u 反馈振荡器的工作原理 u LC正弦波振荡器 u 振荡器的频率和振幅稳定度 u 石英晶体振荡器
高频电子线路
西南科技大学网络教育学院
振荡器作用：产生一定频率和幅度的信号
按振荡波形分 按振荡原理分
正弦波振荡器
非正弦波振荡器 利用负阻器件的负阻
负振荡器
效应产生振荡
利用正反馈原理构成 反馈振荡器
U IQ
Q’点是不稳定平衡点。若要使该振荡器进入稳定的平衡点，在起
振时给晶体管加一电冲激，并使冲激电压大于UIB，这样自由振荡 就可以产生，这种起振时需要外加冲激的振荡称为“硬激励”。
与此相对，那些冲激能自由产生振荡的现象称为“软激励”。
高频电子线路
西南科技大学网络教育学院
2）相位稳定条件
相位稳定条件是指：当处于平衡状态的系统受到某一 外来因素的干扰，相位平衡状态被破坏，总相角φ大于或 小于2nπ时，环路自动恢复平衡状态φ＝2nπ的条件。
v 若有正反馈环路的话，其不断补偿消耗掉的能量，则能 维持正弦振荡。
高频电子线路
西南科技大学网络教育学院
一、 反馈振荡器的组成
放大器
Ui
Au
无外加输入信号
Uo
正弦波振荡器由放大器、
反馈网络
Uf
Fu
反馈网络组成
T&
=
U& f U& i
= A& F&
高频电子线路
西南科技大学网络教育学院
二、 反馈振荡器的工作原理
φ（ω）曲线在平衡 点附近应为负斜率， 如图所示。
j (w )
¶j (w )
<0
¶w w =w0
ω ω0
电工学-第四章 正弦波振荡电路
R
1 jL jC j(L 1
C
)
( R L)
.
I
L/C
R j(L 1 )
C
+ L
•
U
C
_
R
2020/4/18
24
LC并联谐振回路的选频特性
•
Z
U
•
I
L/C
R j(L
1)
C
.
I
+ L
•
U
C
_
R
•
当LC并联回路发生谐振时，端电压 U 与总电
流
•
I
同相，即阻抗Z表现为纯电阻性。
谐振频率
o
Uf
•
F
Uo
•
•
由以上知，放大电路产生自激振荡的条件是 U f U i
••
•
则
AuF
Uo
•
U
•
f
U
•
f
1
Ui Uo Ui
2020/4/18
7
自激振荡
总结出自激振荡的条件：
（1）相位平衡条件
反馈电压
•
U
f
与输入电压
•
U
i
同相位，形成正反馈
（2）幅值平衡条件
反馈电压与输入电压大小相等： U f U i
C2
uf
首先判断相位平衡条件，见瞬时极性
2020/4/18
35
RB1
RC
+
RB2
uf
+
ube
RE
UCC
+
C1
L
+
C2
CE
《正弦波振荡器》word版
第4章 正弦波振荡器振荡电路是一种能量转换装置，它无需外加信号，就能自动地将直流电能转换成具有一定频率、一定幅度和一定波形的交流信号。
振荡器按输出信号波形的不同，可分为正弦波振荡器和非正弦波振荡器两类。
本章将讨论正弦波振荡器，先介绍自激振荡的概念、产生自激振荡的条件及用相位平衡条件判别电路能否起振，然后介绍正弦波振荡电路的基本工作原理及RC 振荡器、LC 振荡器和石英晶体振荡器的结构特点及应用。
4.1 自激振荡4.1.1自激振荡如果在输入端不外接信号，只是将输出信号的一部分正反馈到输入端以代替输入信号，输出端仍有一定频率和幅度的信号输出，这种现象称为自激振荡。
自激振荡不仅在振荡电路中产生，在放大电路中也可能产生，例如现实生活中在使用扩音机时，如果话筒和音箱的位置安排不合适时，此时虽然没有输入信号，音箱中仍可能会出现啸叫声，这其实也是一种自激振荡，这时的自激振荡是有害的，应尽量消除。
而在振荡电路中，则正是利用自激振荡来工作。
4.1.2振荡条件1.自激振荡的条件产生自激振荡的条件常用图4-1所示框图来分析。
N 是放大电路，放大系数为A ，F 是反馈电路，反馈系数为。
当开关S 接在2位置时，放大电路的输入端与正弦波信号相接，输出电压：＝A。
通过反馈电路得到反馈电压：＝。
4-1 产生自激振荡的条件 若适当调整放大电路和反馈电路的参数，使＝，即两者大小相等，相位相同。
再将开关S 接到1位置，反馈电压即可代替原来的输入信号，仍维持输出电压不变，这样，整个电路就成为一个自激振荡电路。
由此可知：因 ＝ （4-1）故 ＝AU o （4-2） 即 A＝1 （4-3）式（4-3）即为自激振荡的条件。
因为A ＝A (4-4）＝F （4-5）式（4-5）即可用向量的模和幅角来表示。
A ＝AF＋由此可得到自激振荡的两个条件：(1) 幅值平衡条件AF＝1 (4-6)(2) 相位平衡条件＋＝2nπ(4-7)2.起振过程实际的振荡电路并不需要外接信号源，而是靠电路本身“自激”起振。
第 4 章 正弦波振荡器
高频电子线路
首页
上页
下页
退出
2．电感三点式
1）容易起振，输出电压幅度较大。
2）C采用可变电容后很容易实现振荡频率在较宽频 段内的调节，且调节频率时基本上不影响反馈系数。
3）由于反馈电压取自电感L2两端，它对高次谐波阻 抗大，故LC回路对高次谐波反馈强，因而输出电压 中谐波成分多，输出波形差。 4）由于L1、L2的分布电容及管子的输入输出电容分 别与L1、L2的两端并联，使振荡频率较高时反馈系 数减小，不满足起振条件，所以振荡频率不宜很高， 一般最高只有几十兆赫兹。
高频电子线路
首页
上页
下页
退出
图4-2 满足起振条件和平衡条件的环路增益特性
高频电子线路
首页
上页
下页
退出
振荡的建立和平衡过程输出电压波形如图4-3所示。
图4-3 振荡幅度的建立和平衡过程
高频电子线路
首页
上页
下页
退出
4.2 LC正弦波振荡器
据振荡器选频网络的不同分，振荡器可 分为：LC振荡器，石英晶体振荡器和
2 LC L L1 L2 2 M f0 1
（4-8）
式中，M为电感L1、L2间的互感。
高频电子线路
首页
上页
下页
退出
4.2.3 电容三点式振荡器
电容三点式振荡器又称考毕兹（Colpitts）
振荡器，其原理电路如图4-6所示。
图中，L、C1和C2为并联谐振回路，作为
集电极交流负载；RB1、RB2和RE为分压
高频电子线路
首页
上页
下页
退出
4.2.6 振荡器的频率稳定和振幅稳定
第4章 正弦波振荡器
L1 M L1 L2 2M
gm
gL Kf
=(g
oe
+g
L
)
1 Kf
+gie K f
0
1 LC
L=L1 L2 2M
1
1
0
LC
gie
( g oe
g
L
)(L1L2
M
)
29
电容三端式
比较
电感三端式
电容有滤波作用,波形好
改变抽头位置即可改变反 馈系数,较方便
可由极间电容取代C1,C2 最高工作频率相对较高
仍由 C1,C2决定,反馈与调谐分开
由于振荡频率1 不受结电容影响,所以稳定度提
高!
32
问题:1.调谐范围窄,主要适合于窄带工作.
fmax 1.1 1.2 f min
1
2.
P1
C1
1
C , C1
调谐对P1有影响.( P1
UC UT
)
C
3.
RL
P12 R0
( C C1
)2
R0 ,
C1 RL K0
U cA
Uc3
放大特性为非线性, Uc2
U c1
反馈特性为线性.
Yfe.RL 放大倍数
1 F
A 平衡点
0 Ub1 Ub2
Ub3
U bA
Ub
(大信号 ,因而放大倍数下降)
Ub Yfe.RL
Ub
UbA时,Yfe.RL
1 , 满足起振条件 F
8
过程: 电子骚动-->放大选频-->增幅等幅(A点,平衡点)
1.增加电容C3(克拉泼):串联改进
Ec R
第四章正弦波振荡器
EC Lc Rb1
Rb2
Re Ce
Cb
C1 C2 L
+
+
uce
ube - -
C2
C1
L
第19页/共80页
分析起振条件时可以利用高频小信号放大器的 分析法. 如右图为小信号微变等效电路,如果忽
略 yre
且由于 Cie C2 ,Coe C1 , y fe gm
C2
C1
L
(即忽略ic 与 ube 的相移)而回路线圈的损
u be
ub e
goe gL
gm ube 1
jC1 jL
1
1
1
gie jC2 jL 1 gie jC2
gie jC2
1
ub e
gm
gie jC2
ub e
goe gL
1
jC1
jL
1
1
jL
1
gie jC2
令上式虚部为零,可得:
gie jC2
(C1 C2 ) Lgie ( goe gL ) 3 LC1C2 0
电容反馈振荡器 电感反馈振荡器
第17页/共80页
例4-1 在例图4-7所示振荡器等效电路中，设有下列四种情况
（1）L1C1＞L2C2＞L3C3 （2）L1C1＜L2C2＜L3C3
电容反馈 电感反馈
（3）L1C1=L2C2＞L3C3
电容反馈
（4）L1C1＜L2C2=L3C3 …………
不振荡
解：只要满足三点式组成法则，该振荡器就能正常工作。
由（3-7）式可知： K( j)= Yf( j) ZL 引入一与F( j)反号的反馈系数F’(j)
U s (s) Ui (s)
正弦波振荡器
或者写成：
A F 1
A0F 1
A F 2n
课后思考题：在LC振荡器中，谐振回路是否等效成一个 电阻？振荡频率是否严格等于谐振回路的谐振频率？
三. 稳定条件
振荡器在工作过程中, 不可避免地要受到各种外界因素变化
的定影因响素,将如引电起源放电大压器波和动回、路温的度参变数化发、生变噪化声,干结扰果等使A。F这些变不化稳,
Uf
是反馈电压、 Ui 是输入电压、
A
是开环电压增益，
F 是反馈系数,
反馈型振荡器 正常工作的 三个条件：
一：起振条件
在接通电源瞬间, 电路中存在各种电扰动, 这些扰动均具
有很宽的频谱。 如果选频网络是由ＬＣ并联谐振回路组成,
则其中只有角频率为 谐振角频率ω0的分量才能通 过反馈产生
较大的 反馈电压 U f 。 如果在谐振频率处, U f 与原输入电
U f
j(
X
jX be be X
bc
)
U
c
X be X ce
U c
由电于路必中须U i满与足U正 c反反馈相：，所所以以UUi与f
U f
与
同相，而在共射 U c 反相
即：
X be 0 X ce
V
X1
X2
C2
C1
X3 L
(a)
V
L2
L1
X1
X2
X3 C
(b)
(a) 电容反馈振荡器; (b) 电感反馈振荡器
A 0
U c UC UCQ
Z
0
0
1)振幅平衡的稳定条件
2)相位平衡的稳定条件
第三节 反馈型LC振荡器
一 ，互感耦合振荡电路 二，电容反馈振荡电路 三，电感反馈振荡电路 电感三点式和电容三点式振荡电路的比较
第4章《高频电子线路》_(曾兴雯)_版高等教育出版社课后答案
4
第4章 正弦波振荡器
第一节
反馈振荡器的原理
一、反馈振荡器的原理分析
组成： （1）放大器
放大器通常是以某种选频网络(如振荡回路)作负载， 是调谐放大器。
（2）反馈网络 一般是由无源器件组成的线性网络。 正反馈： U’i(s)与Ui(s)相位相同。
5
第4章 正弦波振荡器
一、反馈振荡器的原理分析
Ui (s) Us (s) Ui(s)
若 Uo Uc
jL Uc ZL R L e 放大器的负载阻抗 所以 Ic T(j) Yf (j)ZLF(j) Yf ( j)ZL F( j) 1
9
U Uc Uo Ic c 又 K( j) Yf (j)ZL I Ui Ub c Ub 因为 jf Ic Yf ( j) Yf e 晶体管的正向转移导纳 Ub
振幅条件的图解表示
U0 U02 U01 Ub1 Ub2 Ub3 Ub
振荡开始时应为增幅振荡！
12
第4章 正弦波振荡器
四、稳定条件 1、振幅稳定条件
T U i
K U i
0
Ui UiA
0
U i U iA
U’i UiA U’’i
因此，振荡器由增幅振荡过渡到稳幅振荡，是由放
大器的非线性完成的。由于放大器的非线性，振幅稳定 条件很容易满足。
②相位平衡条件，即正反馈条件
U b jX 2 I
U c jX 1 I
X1、X2为同性质电抗元件
判断三端式振荡器能否振荡的原则：
“射同余异”
或 “源同余异”
18
第4章 正弦波振荡器
一、振荡器的组成原则
第4章 正弦波振荡器
第一节
反馈振荡器的原理
一、反馈振荡器的原理分析
组成： （1）放大器
放大器通常是以某种选频网络(如振荡回路)作负载， 是调谐放大器。
（2）反馈网络 一般是由无源器件组成的线性网络。 正反馈： U’i(s)与Ui(s)相位相同。
5
第4章 正弦波振荡器
一、反馈振荡器的原理分析
Ui (s) Us (s) Ui(s)
若 Uo Uc
jL Uc ZL R L e 放大器的负载阻抗 所以 Ic T(j) Yf (j)ZLF(j) Yf ( j)ZL F( j) 1
9
U Uc Uo Ic c 又 K( j) Yf (j)ZL I Ui Ub c Ub 因为 jf Ic Yf ( j) Yf e 晶体管的正向转移导纳 Ub
振幅条件的图解表示
U0 U02 U01 Ub1 Ub2 Ub3 Ub
振荡开始时应为增幅振荡！
12
第4章 正弦波振荡器
四、稳定条件 1、振幅稳定条件
T U i
K U i
0
Ui UiA
0
U i U iA
U’i UiA U’’i
因此，振荡器由增幅振荡过渡到稳幅振荡，是由放
大器的非线性完成的。由于放大器的非线性，振幅稳定 条件很容易满足。
②相位平衡条件，即正反馈条件
U b jX 2 I
U c jX 1 I
X1、X2为同性质电抗元件
判断三端式振荡器能否振荡的原则：
“射同余异”
或 “源同余异”
18
第4章 正弦波振荡器
一、振荡器的组成原则
正弦波振荡器
由
(4 ─ 1)
U o (s) A( s ) U i (s) U i( s ) F ( s) U o ( s) U i ( s ) U e ( s ) U i ( s )
(4 ─ 2)
(4 ─ 3) (4 ─ 4) (4 ─ 5) (4 ─ 6)
得 其中
A( s) A( s) Au ( s) 1 A( s) F ( s) 1 T ( s) U i( s ) T ( s) A( s) F ( s) U i (s)
率的特点。因而
振幅稳定条件为
T U i
U i U iA
0
(4 ─ 17) 0
vI
当反馈网络为线性网络， 即反馈系数大小F不随输入信号改 变，要使振幅稳定，故振幅稳定条件又可写为
A (4 ─ 18) a U i U iA 0 U i 在稳定平衡点上，放大器的增益应随输入电压的增大而减小。 要使放大器增益A随Ui 变化，放大器一定要工作在非线性状 态。所以说振幅稳定是由放大器的非线性工作保证的，振荡 器必然是非线性电子线路。称这种振幅稳定方式叫内稳幅方 式。 F p 0 (4 ─ 18) b U i 当A=常数时，振幅稳定条件为
f
F′
)
L
1
0
(4 ─ 20)
－
图4-3 振荡器稳定工作时回路的相频特性
注意： ①相频曲线负斜率越大，f02偏离f01越小，频率稳定度越高。提高 回路Q值可加大负斜率，石英晶体Q值极高，故频率稳定性好； ②使固有φLC→0，即原f01接近f0
4.2
LC 振 荡 器
采用LC振荡回路作为选频网络的反馈振荡器统称为LC振荡器。 根据反馈网络的类型，可以有互感（变压器）耦合型LC振荡器 和三点式LC振荡器等两种实现结构。 互感耦合型LC振荡器： 4种互感耦合的LC振荡器电路 如图。具有LC选频网络，其互感 同名端方向满足正反馈要求。 这4种振荡器的实际电路如图。 必须有合适的偏置电压和交流信 号通路才能正常工作。
(4 ─ 1)
U o (s) A( s ) U i (s) U i( s ) F ( s) U o ( s) U i ( s ) U e ( s ) U i ( s )
(4 ─ 2)
(4 ─ 3) (4 ─ 4) (4 ─ 5) (4 ─ 6)
得 其中
A( s) A( s) Au ( s) 1 A( s) F ( s) 1 T ( s) U i( s ) T ( s) A( s) F ( s) U i (s)
率的特点。因而
振幅稳定条件为
T U i
U i U iA
0
(4 ─ 17) 0
vI
当反馈网络为线性网络， 即反馈系数大小F不随输入信号改 变，要使振幅稳定，故振幅稳定条件又可写为
A (4 ─ 18) a U i U iA 0 U i 在稳定平衡点上，放大器的增益应随输入电压的增大而减小。 要使放大器增益A随Ui 变化，放大器一定要工作在非线性状 态。所以说振幅稳定是由放大器的非线性工作保证的，振荡 器必然是非线性电子线路。称这种振幅稳定方式叫内稳幅方 式。 F p 0 (4 ─ 18) b U i 当A=常数时，振幅稳定条件为
f
F′
)
L
1
0
(4 ─ 20)
－
图4-3 振荡器稳定工作时回路的相频特性
注意： ①相频曲线负斜率越大，f02偏离f01越小，频率稳定度越高。提高 回路Q值可加大负斜率，石英晶体Q值极高，故频率稳定性好； ②使固有φLC→0，即原f01接近f0
4.2
LC 振 荡 器
采用LC振荡回路作为选频网络的反馈振荡器统称为LC振荡器。 根据反馈网络的类型，可以有互感（变压器）耦合型LC振荡器 和三点式LC振荡器等两种实现结构。 互感耦合型LC振荡器： 4种互感耦合的LC振荡器电路 如图。具有LC选频网络，其互感 同名端方向满足正反馈要求。 这4种振荡器的实际电路如图。 必须有合适的偏置电压和交流信 号通路才能正常工作。
正弦振荡器
Af
A 1 AB
为什么？
•若AB=1，1-AB=0，Af;
•即使Us=0，无外加信号，也有Uo，环路内部达到能量平衡， 此时反馈放大器成为振荡器。
•因此正反馈是振荡的必要条件。
1 AB 0 --------巴克豪森条件。
•下面以互感耦合LC振荡器为例来具体讨论：
•如果不看反馈电路，它就 是典型的调谐放大器; •输入信号Ui经过放大在LC 两端输出Uo。 •当谐振时Uo与Ui反相，经 过互感耦合在次级得到反馈
第二节 三点式LC振荡器
前述的LC互感耦合振荡器特点:
•优点：电路简单，易起振等； •缺点：频稳度较低（和晶体管参数有关），振荡频率不高。
•为解决上述问题： •目前分立电路中采用较多的是三点式LC振荡器。 •本节就典型的三点式振荡器进行分析和讨论。
一、三点式电路的组成法则
所谓三点式振荡器：指LC回路的三个端点分别接在晶体
GP’
C1
L
GP
C2
r
f 1
1
1.74MHz
2 LC 2 50 106 167 1012
•如果用精确公式求解振荡频率，结果非常接近。
（2）求起振所需的最小跨导：
•先求并联在C1两端的等效损耗电导：
Gp
1 Q
C 1 L 80
167 1012 50 106
0.0228ms
p C2 1000 0.83 C1 C2 200 1000
稳定条件：振幅条件
A
＜０
U i A 1 B
相位条件
d d
0
•起振 、平衡 、 稳定三个条件缺一不可。
（三）振荡器的频率稳定度：
•频率稳定度是衡量振荡器的重要指标； •根据测试时间的长短分为：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电容三点式 电感三点式 波形 频率 较好 较高 较差 较低 较差 较易
频率稳定度 较好 起振、调节 较难
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
五、LC三点式振荡器相位平衡条件的判断准则 三点式振荡器相位平衡条件的判断准则 1、Xce与Xbe的电抗性质相同； 的电抗性质相同； 2、Xcb与Xce、Xbe的电抗性质相反； 的电抗性质相反； 3、对于振荡频率，满足Xce+Xbe+Xcb=0。 、对于振荡频率，满足 。
首页
上页
下页 退出
高频电子线路
c
b
e
′ C2 = C2 + Cie
' g 0 = p12 g 0
' C1' + C2 p1 = ' C2
C = C1 + Coe
' 1
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
& 电压增益 A0
' g Σ = g oe + g L + g 0 + p 2 gie
∆f = f − f c
f − fc ∆f = fc fc
绝对频率准确度
相对频率准确度
3、频率稳定度的定义: 、频率稳定度的定义
在一定时间间隔内，振荡器相对频率偏差的最大值，用 。
∆f max fc
表示
时间间隔
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
4、三种常用的频率稳定度 、
长期频率稳定度：一般指一天以上甚至数月的时间间隔内的相对频率 长期频率稳定度 变化的最大值。这种变化通常是由振荡器中元器件老 化而引起 的。 短期频率稳定度：一般指一天以内，以小时、分或秒计算的时间间隔内 短期频率稳定度 的频率相对变化。产生这种频率不稳的因素有温度、 电源电压等。 瞬时频率稳定度：一般指秒或毫秒时间间隔内的频率相对变化。 瞬时频率稳定度 引起这类频率不稳定的主要因素是振荡器内部噪 声。
1 f0 ≈ 2π L1C
4、互感耦合振荡电路的特点 、
优点： 优点 互感耦合振荡电路在调整反ቤተ መጻሕፍቲ ባይዱ（改变M）时
，基本不影响振荡频率 缺点： 缺点：工作频率不易过高，应用于中短波段
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
二、电容反馈振荡电路
1、电路形式 、
c
e
晶体管的三个极 （c.e.b）分别连 接于回路电容的 三端，称为电容 三点式振荡器， 也称为考比 兹 考比 振荡器。 振荡器。
∂A ∂U c
<0
U C =U CQ
平衡的稳定条件
∂ϕ Z ∂ω
<0
ω =ωC
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
反馈型LC LC振荡器 第三节 反馈型LC振荡器
反馈型LC振荡器是由调谐放大器和正反馈网络构成.
按反馈耦合元件可以分为： 按反馈耦合元件可以分为：
互感耦合振荡器 电容反馈式振荡器
<0
U C =U CQ
物理意义:A随放大器 物理意义 输出电压的变化为负 斜率
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
消除这种情况的方法: 消除这种情况的方法 ①调节静态工作点 ②选择适当的反馈系数
B点也满足振幅平衡的条件A=1/F，而此点的 ∂U Q点 点
∂A ∂U c <0
U C =U CQ
这是用来判断三点式振荡器 有没有可能振荡的基本原则
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
例题: 例题 图示为三回路振荡器的等效电路，设有以下四种情况：
(1) L1C1 > L2C2 > L3C3
(2) L1C1 < L2C2 < L3C3
(3) L1C1 = L2C2 > L3C3
(4) L1C1 < L2C2 = L3C3
下页 退出
高频电子线路
三、主要技术指标 1、振荡频率； 、振荡频率； 2、频率稳定度； 、频率稳定度； 3、振荡幅度； 、振荡幅度； 4、振荡波形； 、振荡波形；
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
反馈型LC LC振荡原理 第二节 反馈型LC振荡原理
一、组成
反馈型LC振荡器是由调谐放大器和正反馈网络构成.
∂A
C U C =U CB
> 0 ，不能满足稳定条件。
为稳定平衡点. 为稳定平衡点
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路 2、相位平衡的稳定条件 、 相位平衡条件ϕY + ϕ Z + ϕ F = 0 ，可得
ϕ Z = −(ϕY + ϕ F ) = −ϕYF
相位平衡的稳定条件:
∂ϕ Z ∂ω
< 0
ϕ 由于电路中有源器件、寄生参量及阻隔元件的确影响， Y + ϕ F ≠ 0 ，为了使电路工作在相位平衡状态， Z ≠ 0 ，因此振荡器的频率 ϕ 并不等于回路的谐振频率。回路处于微小失谐状态。为简化问题 ，通常都近似地认为振荡频率就等于回路的谐振频率
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
四、振荡平衡状态的稳定条件
一、振荡电路的功能
在没有外加输入信号的条件下，电路自动将直流电源提供的能量转换 为具有一定频率,一定波形,一定振幅的交变振荡信号输出。
二、振荡电路的分类
反馈型 正弦波振荡器
RC振荡器 LC振荡器 晶体振荡器 负阻型(100MHz以上)
振荡器
非正弦波振荡器
按波形分
按原理分
按元件分
哈尔滨工程大学
首页
上页
高频电子线路 Pspice仿真振荡器输出波形 仿真振荡器输出波形
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
三、振荡的平衡与平衡条件
1、振荡的平衡条件 、 AF=1 物理意义:等幅振荡 物理意义:正反馈
ϕ A + ϕ F = 2nπ (n=0，1，2，…)
平衡过程：刚起振时A0F>1，增幅振荡，随着反馈回来的输入振幅的不断增大 平衡过程 ，谐振放大器进入非线性状态。 非线性状态电压增益A随着振幅增大而降低, 直到AF=1时,达到平衡 时 达到平衡. 达到平衡
首页
上页
下页
退出
高频电子线路
第四章 正弦波振荡器
主要内容 第一节 第二节 第三节 第四节 第五节 第六节 概述 反馈型LC振荡原理 反馈型 振荡原理 反馈型LC振荡器 反馈型 振荡器 振荡器的频率稳定原理 高稳定度的LC振荡器 高稳定度的 振荡器 晶体振荡器
首页
上页
下页 退出
高频电子线路
第一节 概述
4、振荡频率的估算 、
ω0 =
1 LCΣ
' C1'C2 其中： CΣ = ' ' C2 + C2
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
三、电感反馈振荡电路
1、电路形式 、
它是利用并联谐振回路中的 电感分压实现正反馈的。 电感分压实现正反馈的。由 于晶体管的三个极分别连接 于回路电感的三端， 于回路电感的三端，称为电 感三点式振荡器， 感三点式振荡器，也称为哈 特莱（ 特莱（Hartley）振荡器。 ）振荡器。
稳定平衡:是指因某一外因的变化，振荡的原平衡条件遭到破坏，振荡器能在新 稳定平衡 的条件下建立新的平衡，当外因去掉后，电路能自动返回原平衡状态。平衡的 稳定条件也包含振幅稳定条件 相位稳定条件。 振幅稳定条件和相位稳定条件 振幅稳定条件 相位稳定条件
1、振幅平衡的稳定条件 、 振幅平衡的稳定条件:
∂A ∂U c
试分析上述四种情况是否可能振荡?振荡频率f0与回路谐振频率有何关系?
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
第四节 振荡器的频率稳定原理
一、频率稳定度的定义
频率稳定度在数量上通常用频率偏差来表示。 频率偏差是指振荡器的实际工作频率和标称频率之间的偏差。它 频率偏差 可分为绝对偏差和相对偏差。 设f为实际振荡频率，fc为指定标称频率，则 1、绝对频率偏差： 、 2、相对频率偏差 、
ω =ω C
物理意义:平衡点并联谐振 物理意义 回路的相频特性为负斜率.
并联回路的相频特性
哈尔滨工程大学
首页
上页
下页 退出
高频电子线路
总结:
起振条件
A0 F > 1
ϕ A + ϕ F = 2nπ (n = 0,1,2L)
平衡条件
AF = 1 ϕ A + ϕ F = 2nπ (n = 0,1,2L)
y fe Uc Ao = = Ui gΣ
.
其中: 其中
' p = C1' / C2
电路的反馈系数F（忽略各个g的影响） 电路的反馈系数
C1' F= = ' U c C2 Uf
y fe C1' b、起振条件 A0 F = 、 . ' >1 g Σ C2
得
' C2 1 1 ' ' y fe > ' gΣ = ( goe + g L + g0 + p 2 gie ) = ( goe + g L + g0 ) + Fgie C1 F F
哈尔滨工程大学
首页
上页