数学模型 汽车厂生产计划
汽车厂生产计划

6
对于( 式的处理有下面3种方法: 对于(*)式的处理有下面3种方法: 式分解为8种情况, (a)将(*)式分解为8种情况,对每一种情况求 比较目标函数值。 解,比较目标函数值。 引入0 变量, 只取0 两个值, (b)引入0-1变量,设 y1 只取0,1两个值,则
x1 = 0或 ≥ 80 等价于 x1 ≤ My1 , x1 ≥ 80 y1 , y1 ∈ {0,1}
直接求解得设每月生产小、 用 lingo直接求解得设每月生产小 、 中 、 大型汽车 直接求解得设每月生产小 的数量分别为64, 的数量分别为 , 168, 0 , 工厂的最大利润为 , 632.
4
进一步讨论:对于问题中提出的“ (3)进一步讨论:对于问题中提出的“如果生产 某一类型的汽车, 则至少生产80 80辆 的限制, 某一类型的汽车 , 则至少生产 80 辆 ” 的限制 , 上 面得到的最优解不满足这个条件, 面得到的最优解不满足这个条件 , 我们需要将决 策变量的约束条件改为: : 策变量的约束条件改为x1 , x2 , x3 = 0或 ≥ 80 相应的模型化为: 相应的模型化为:
1
小型
钢材(吨) 劳动时间(小时) 利润(万元)
中型 3 250 3
大型 现有量 5 4 600
1.5 280 2
400 60000
汽车厂的生产数据
2
模型建立与求解 设每月生产小、 建立与求解: ( 2 ) 模型 建立与求解 : 设每月生产小 、 中 、 大型 工厂的利润为z 汽车的数量分别为 x1 , x2 , x3 , 工厂的利润为 z , 在 题目所给参数均不随生产数量变化的假设下, 可 题目所给参数均不随生产数量变化的假设下 , 得整数规划模型如下: 得整数规划模型如下:
汽车制造企业的生产计划模式与模型研究

汽车制造企业的生产计划模式与模型研究随着改革开放的不断深入和经济的持续增长,中国的汽车市场需求不断扩大,汽车制造企业的生产能力大幅提升,企业要提高自身的竞争力必须提高客户服务水平和不断缩短接收订单至交货的前置时间。
同时在汽车产能不断攀高的同时,年同比增长率出现一定的波动,因此如果只是根据历史的销量数据对未来的计划进行预测并进行生产的准备和安排,后续的市场波动将对零部件的需求计划及其生产排程带来一定的冲击,如何在这种市场大的变化中通过零部件需求计划和生产的柔性安排来保证生产的及时完成将是汽车制造企业面临和需要解决的问题。
大部分汽车制造企业普遍采用企业资源计划(ERP)系统,但由于ERP的计划管理模型仍然是制造资源计划(MRPII),其编制计划的方法仍然采用物料需求计划(MRP)和主生产计划(MPS)计算物料的需求、发布补充定单等,虽然ERP系统在做生产计划时考虑了能力资源的约束,但仍旧是一种串行过程的校验处理。
高级计划与排程(APS)是基于约束的有限能力计划排程,它是一种在资源约束前提下的优化技术,既可用于单个企业内部的短期计划与排程,又可用于在已知条件下的长期预测和在企业间进行计划。
APS系统和ERP系统可以通过分离集成和公用集成的方式进行系统集成。
汽车制造企业在基于APS的计划框架中,其企业的计划可分为战略层计划、战术层计划和经营层计划。
其中战略层计划决定企业的发展方向;战术层计划决定如何实现企业战略;经营层计划体现战术的具体计划。
这三个计划层次组成了企业的计划层面,通过计划的执行层面来实现企业的计划层面的战略和战术规划。
由于MRP系统所使用的物料清单(BOM)是一个静态的物料结构,没有生产过程的细节信息,因此在APS系统中需要建立一个可配置BOM,将生产过程中所涉及到的不同的工序、工序所需时间、工序所需物料、所需资源和不同工序之间的逻辑关系等生产信息都放在一个随时间而动态变化的系统内,建立起一个动态的生产过程和生产方式的结构。
汽车厂生产计划数学建模

汽车厂生产计划数学建模汽车厂生产计划数学建模是指利用数学方法和技术对汽车生产计划进行优化和调整的过程。
该过程包括生产计划的制定、排产和调度等环节,通过对各项因素的定量分析和综合考虑,以最小化成本、最大化效益为目标,实现汽车生产计划的合理化和优化。
本文将从数学建模的基本概念开始,一步一步详细解析汽车厂生产计划数学建模的过程。
数学建模是将现实问题抽象为数学模型,并通过数学方法进行求解和分析的过程。
对于汽车厂生产计划的数学建模,首先需要明确问题的目标与约束条件。
目标是指生产计划优化的目标,通常是最小化成本或最大化效益。
约束条件是指限制生产计划的条件,如生产线能力、原材料供应、工人数量等。
在汽车厂生产计划中,目标通常是最小化生产成本,约束条件包括生产线的最大产能、原材料的供应量和质量、以及工人的数量和技能水平等。
在确定问题目标和约束条件后,下一步是建立数学模型。
汽车厂的生产计划可以看作是一个生产排队系统,即一系列任务需要在不同的机器上进行加工,并按照一定的顺序进行安排和分配。
该问题可以采用离散事件模拟(DES)方法进行建模。
在离散事件模拟中,时间被分割为一系列离散的时间点,每个时间点发生一个事件。
在汽车厂生产计划中,每个事件可以表示一个任务的进入或完成。
对于每个任务,需要确定其进入时间、加工时间和完成时间等参数。
同时还需要考虑任务之间的先后顺序和约束条件,如任务之间的依赖关系和限制条件。
建立数学模型后,可以采用启发式算法或优化算法对生产计划进行求解。
启发式算法是一种以经验和启发式规则为基础的算法,通过不断调整和优化当前解来逼近最优解。
优化算法则是通过数学方法,寻找最优解的算法。
常用的优化算法包括线性规划、整数规划、遗传算法和模拟退火算法等。
对于汽车厂生产计划问题,可以采用启发式算法和优化算法相结合的方式进行求解。
首先,可以采用启发式算法确定初始的生产计划。
启发式算法通常通过一系列规则和策略来进行计算,并根据问题的性质和实际情况进行调整和改进。
数学建模-工厂生产安排问题
问题一的程序:
min=500*x1+800*x2+200*x3+400*x4+500*x5+800*x6+200*x7+600*x8+1000*x9;
x1<=275;
x2<=100;
x5<=200;
x6<=50;
x8<=100;
x9<=50;
x1+x2-x3-x4=150;
x5+x6+x3-x7=250;
起点
止点
单位货物的运输单价/元
一号
市场
500
三号
200
五号
300
二号
市场
800
四号
200
六号
200
三号
市场
500
五号
100
四号
市场
800
六号
0
五号
市场
600
六号
市场
1000
求满足运输条件的最低运输成本。
200元 500元
300元 600元
问题二、三、四的求解:
问题二是设计一个线性规划模型,用来安排后3个月常态下的生产和超时加班的生产。
问题求解
问题一的求解
要求把这个问题设计成一个运输问题,则根据题中条件可设计为:
现有6个仓库(起始节点),它们的存货量分别为275,100,200,50,100,50个单位,其中一、二号仓库需向市场(终止节点)运送150个单位的货物,三、四号仓库需向市场运送250个单位的货物,五、六号仓库需向市场运送300个单位的货物,每个仓库的单位运输成本如下表:
对于问题二,我们要求考虑每个月的实际生产能力和每生产单位产品所需要的成本价的变化,在满足订货需求的条件下合理的安排生产,使总成本最小。所以设出每月生产的产品的量,其中:
数学建模优化建模实例【精选】

x1=80,x2= 150,x3=0,最优值z=610 8
• 若生产某类汽车,则至少生产80辆,求生产计划。
方法2:引入0-1变量,化为整数规划
x1=0 或 80 x2=0 或 80 x3=0 或 80
x1 My1, x1 80 y1, y1 {0,1} M为大的正数,
x2 My2, x2 80 y2, y2 {0,1} 可取1000
4
25
20
合计
100
135
成本(千元/千箱)
5.0 5.1 5.4 5.5
• 剩余产品需要支付贮存费,每周0.2千元/千箱;
应如何安排计划,在满足每周市场需求的条件下,使 四周的总费用最小 ?
11
问题分析
周次 1 2 3 4
合计
需求 15 25 35 25 100
能力 30 40 45 20 135
现有量 600 60000
• 制订月生产计划,使工厂的利润最大。
• 由于各种条件限制,如果生产某一类型汽车,则至少 要生产80辆,那么最优的生产计划应作如何改变。
6
汽车厂生产计划
模型建立
设每月生产小、中、大型 汽车的数量分别为x1, x2, x3
小型 钢材 1.5 时间 280 利润 2
中型 3
250 3
成本 5.0 5.1 5.4 5.5
• 除第4周外每周的生产 能力超过每周的需求; • 生产成本逐周上升; •前几周应多生产一些。
模 • 饮料厂在第1周开始时没有库存;
型 • 从费用最小考虑, 第4周末不能有库存;
假 设
• 周末有库存时需支出一周的存贮费;
3500
2850
如何装运, 使本次飞行 获利最大?
(四)-可化为线性规划的问题

max R 2x1 3x2 4x3
s.t .218.50xx11
3x2 5x3 600, 250x2 400x3
60000,
方法三 从数学上讲,
要 么xi 0要 么xi 80等 价 于: 对 非 负 变 量xi 满 足 xi ( xi 80) 0.
x11 0.5( x11 x21 ); x12 0.6( x12 x22 ).
购买原油A的成本为
10x,
c(
x)
5000
8( x
500),
5000 4000 6( x 1000),
0 x 500 500 x 1000 1000 x 1500
0 x 500 500 x 1000 1000 x 1500
取分点b1=0,b2=500,b3=1000, b4= 12000 1500.取分点的比例z1,z2,z3,z4. 当x 9000 落在区间[b1,b2]时,取x=b1z1+b2z2, 5000 z1+z2=1;当x落在区间[b2,b3]时,取 x=b2z2+b3z3, z2+z3=1;当x落在区间 [b3,b4]时,取x=b3z3+b4z4, z3+z4 =1; 由于c(x)是x的线性函数,自然也是 zi的线性函数.
x, x11, x12 , x21, x22 0.
其中
10x,
c(
x)
1000
8
x,
3000 6x,
0 x 500 500 x 1000 1000 x 1500
模型求解
数学建模实验答案__数学规划模型二.

实验05 数学规划模型㈡(2学时)(第4章数学规划模型)1.(求解)汽车厂生产计划(LP,整数规划IP)p101~102(1) (LP)在模型窗口中输入以下线性规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3≥ 0并求解模型。
★(1) 给出输入模型和求解结果(见[101]):(2) (IP)在模型窗口中输入以下整数规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3均为非负整数并求解模型。
LINGO函数@gin见提示。
★(2) 给出输入模型和求解结果(见[102]模型、结果):2.(求解)原油采购与加工(非线性规划NLP ,LP 且IP )p104~107模型:已知 ⎪⎩⎪⎨⎧≤≤+≤≤+≤≤=)15001000(63000)1000500(81000)5000(10)(x x x x x xx c注:当500 ≤ x ≤ 1000时,c (x ) = 10 × 500 + 8( x – 500 ) = (10 – 8 ) × 500 + 8x112112221112212211112112122211122122max 4.8() 5.6()()500100015000.50.6,,,,0z x x x x c x x x x x x x x x x x x x x x x x x =+++-+≤++≤≤≥+≥+≥2.1解法1(NLP )p104~106将模型变换为以下的非线性规划模型:1121122212311122122111121121222123122312311122122max4.8()5.6()(1086)50010000.50.6(500)0(500)00,,500,,,,0z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++-+++≤++≤≥+≥+=++-=-=≤≤≥LINGO 软件设置:局部最优解,全局最优解,见提示。
关于汽车总装线配置问题的数学模型

第36卷第3期邢台职业技术学院学报Vol.36No.32019年6月Journal of Xingtai Polytechnic College Jun.2019收稿日期:2019—03—05作者简介:于倩(1989—),女,河北邢台人,邢台职业技术学院,助教。
92关于汽车总装线配置问题的数学模型于倩,郝全枝,宋景红,张洁(邢台职业技术学院,河北邢台054035)摘要:研究了2018年“高教社杯”全国大学生数学建模竞赛D 题,该题是在满足品牌、配置、动力、驱动、颜色的装配要求下,完成车辆在总装线上的装配排序且具有较低的生产成本。
利用启发式算法,针对附件中的数据,根据五种装配要求的高低,对其进行组合优化,分层交叉分析设计了汽车总装线排序问题的可行算法。
根据设计的排序算法,给出了一天的装配生产顺序,进而验证了设计的合理性。
关键词:装配排序;启发式算法;组合优化中图分类号:O223;TP18文献标识码:A文章编号:1008—6129(2019)03—0092—06一、问题背景某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色等5种属性确定。
品牌分为A1和A2两种,配置分为B1、B2、B3、B4、B5和B6六种,动力分为汽油和柴油两种,驱动分为两驱和四驱两种,颜色分为黑、白、蓝、黄、红、银、棕、灰、金九种。
公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小时)各230辆。
每天生产各种型号车辆的具体数量根据市场需求和销售情况确定。
由于工艺流程的制约和质量控制的需要以及降低成本的考虑,对经过生产线的车辆型号有多种装配要求。
由于该公司的生产线24小时不间断作业,各项要求对相邻班次(包括当日晚班与次日白班)的车辆同样适用。
公司的装配流程如图1所示。
待装配车辆按一定顺序排成一列,首先匀速通过总装线依次进行总装作业,随后按序分为C1、C2线进行喷涂作业。
图1装配流程图该企业给出了未来一周的生产计划,根据生产线上的装配要求,本文针对17日~20日的生产计划进行分析,设计算法,使其能给出符合要求且具有较低生产成本的装配顺序。
汽车制造企业的生产计划模式与模型研究

汽车制造企业的生产计划模式与模型研究汽车制造企业的生产计划模式与模型研究摘要:随着汽车产业的快速发展,汽车制造企业面临着逐渐增长的市场需求和激烈的竞争压力。
为了提高生产效率、降低成本并满足市场需求,汽车制造企业需要优化其生产计划模式与模型。
本文主要研究汽车制造企业的生产计划模式与模型,并探讨了其中的关键因素和方法。
一、引言随着全球汽车市场的不断扩大和技术的进步,汽车制造企业面临着诸多挑战和机遇。
有效的生产计划模式与模型对于提高企业的竞争力和持续发展至关重要。
因此,研究汽车制造企业的生产计划模式与模型具有重要的理论和实践意义。
二、汽车制造企业的生产计划模式1. 全面规划模式全面规划模式是指企业根据市场需求、产品特性、生产能力等因素进行全面规划,制定长期、中期和短期的生产计划。
这种模式能够确保企业在生产过程中有足够的时间来准备和调整,能够更好地适应市场需求的变化。
2. Just-in-Time模式Just-in-Time模式是指企业在生产过程中,根据需求量和交付时间,准确计算所需零部件和材料的供应时间,并在需要时进行生产和交付。
这种模式能够有效减少库存和成本,提高生产效率和响应速度。
3. 按订单生产模式按订单生产模式是指企业根据订单的具体要求,进行生产和交付。
这种模式能够更好地满足个性化需求,减少存货和浪费,提高客户满意度。
三、汽车制造企业的生产计划模型1. 生产规划与控制系统(PPCS)PPCS是一种综合管理系统,用于规划、控制和监测汽车制造企业的生产过程。
它通过收集、分析和处理大量数据,提供决策支持和资源配置,实现生产计划与实际生产的协调。
2. 供应链管理模型供应链管理模型是一种综合管理模型,用于协调汽车制造企业和其供应商之间的生产计划和物流流程。
它能够高效地管理零部件和材料的供应,减少库存和物流成本,提高供应链的效率和稳定性。
3. 任务分配模型任务分配模型是一种协作模型,用于分配和调度汽车制造企业内部的生产任务。
汽车部件企业的生产配置最优规划数学模型设计

41.91% higher than that of the nonlinear modeling method,and 9.31% higher than that of the dynamic modeling method;the
time consumption of the improved modeling method is about 172.2 s shorter than that of the nonlinear modeling method,and
basis of the batch analysis for production configurations of auto parts enterprises,the production configurations of auto parts en⁃
terprises are distributed,and planned by using the BP neural network method. The optimal planning mathematical model for pro⁃
modeling method
0
引
汽车制造业的需求,不断推出高性能、高灵敏度的汽车
言
部 件 ,同 时 汽 车 部 件 企 业 的 产 品 研 发 能 力 也 在 不 断 提
近 年 来 ,国 内 汽 车 制 造 业 随 着 市 场 开 放 程 度 的 提
高,汽车部件企业得到了快速发展。随着各种高新技术
the BP neural network method is proposed for production configurations of auto parts enterprises. An optimal planning mathemati⁃
数学建模——工厂计划模型

数学建模——工厂生产计划模型学院:数学与统计学院专业:信息与计算科学教师:郑**姓名:杨**学号:***********摘要本文以工厂所获得的总收益为研究对象,采用了线性规划的分析方法,通过求解不同产品的生产计划以及按计划生产所获得的利润,解决了工厂为达到最大总收益的产品生产计划问题。
在问题一的求解过程中,以每月每种产品的销售量和生产量为自变量,以工厂所获得的收益为目标函数,结合各种约束条件,建立了一个动态规划方程组,将各月份各种产品生产的最佳配置转化为动态规划方程组的求解问题,得到了最大收益为6.9256万元。
问题二在问题一的基础上考虑了市场价格的变化及引入新机床两个因素,为使模型简化,首先考虑市场价格的变化对计划和收益的影响。
然后假定市场价格不变,利用Lingo 软件,模拟出引入新机床对计划和收益的影响。
它是问题一的拓展,通过更改约束方程,利用模型一的计算程序,从而得到拓展模型的最优解。
关键字:总收益销售量生产量动态规划一、问题重述某厂拥有4台磨床、2台立式钻床、3台卧式钻床、一台镗床和一台刨床,用以生产7种产品,记作P1至P7。
工厂收益规定为产品售价减去原材料费用之剩余。
每种产品单件的收益及所需各机床的加工工时(以小时计)列于下表:产品P1 P2 P3 P4 P5 P6 P7收益10 6 8 4 11 9 3磨0.5 0.70 0 0 0.3 0.2 0.5垂直钻孔0.1 0.2 0 0.3 0 0.6 0水平钻孔0.2 0 0.8 0 0 0 0.6镗孔0.05 0.03 0 0.07 0.1 0 0.08刨0 0 0.01 0 0.05 0 0.05本月(一月)和随后的5个月中,下列机床停工维修:一月磨床一台二月卧式钻床2台三月镗床一台四月立式钻床一台五月磨床一台,立式钻床一台,上台下六月刨床一台,卧式钻床一台各种产品各月份的市场容量如下表:产品P1 P2 P3 P4 P5 P6 P7一月500 1000 300 300 800 200 100二月600 500 200 0 400 300 150三月300 600 0 0 500 400 100四月200 300 400 500 200 0 100五月0 100 500 100 1000 300 0有存货50件。
数学建模-工厂最优生产计划模型

数学建模与数学实验课程设计报告学院数理学院专业数学与应用数学班级学号学生姓名指导教师2015年6月工厂最优生产计划模型【摘要】本文针对工厂利用两种原料生产三种商品制定最优生产计划的问题,建立优化问题的线性规划模型。
在求解中得到了在不同生产计划下收益最优化的各产品的产量安排策略、最大收益,以及最优化生产计划的灵敏度分析。
对于问题一,通过合理的假设,首先根据题中所给的条件找出工厂收益的决定条件,利用线性规划列出目标函数MAX。
由题目中所得,工厂原料及价格的约束条件下运用lingo软件算出最优生产条件下最大收益为1920元,其次是不同产品的产量。
对于问题二,灵敏度分析是研究当目标函数的费用系数和约束右端项在什么范围变化时,最优基保持不变。
对产品结构优化制定及调整提供了有效的帮助。
根据问题一所给的数据,运用lingo软件做灵敏度分析。
关键词:最优化线性规划灵敏度分析 LINGO一、问题重述某工厂利用两种原料甲、乙生产A1、A2、A3三种产品。
如果每月可供应的原料数量(单位:t),每万件产品所需各种原料的数量及每万件产品的价格如下表所示:(1)试制定每月和最优生产计划,使得总收益最大;(2)对求得的最优生产计划进行灵敏度分析。
二、模型假设(1)在产品加工时不考虑排队等待加工的问题。
(2)假设工厂的原材料足够多,不会出现原材料断货的情况。
(3)忽略生产设备对产品加工的影响。
(4)假设工厂的原材料得到充分利用,无原材料浪费的现象。
三、符号说明Xij(i=1,2,;j=1,2,3;)表示两种原料分别生产出产品的数量(万件);Max为最大总收益;A1,A2,A3为三种产品。
四、模型分析问题一分析:对于问题一的目标是制定每月和最优生产计划,求其最大生产效益。
由题中所给的条件找出工厂收益的决定条件,利用线性规划列出目标函数MAX。
由题目中所得,工厂原料工厂原料及价格的约束,列出约束条件。
问题二分析:研究当目标函数的费用系数和约束右端项在什么范围变化时,最优基保持不变。
汽车的生产与销售问题 数模

108汽车公司的最佳生产方案摘要本文针对汽车的生产策略中最佳生产方案的确定做了深入的研究,根据生产方案的不同对最终利润的影响分析可知该问题是基于整数规划的寻找最优值问题。
对此,本文建立了规划模型进行讨论求解。
对于问题A(1),根据文中所给的数据及车间生产零件的规律,我们可以知道,车间的生产能力是一定的。
所以,我们采取将能力归一化的方法,对车间的能力进行约束。
例如就发动机装配车间而言,生产1台A101型货车需要消耗1 3300的车间生产能力,生产1台A102型货车需要消耗11667的车间生产能力。
冲压车间的情况也类似。
最后得到的最优方案为每月生产A101型货车2048台,生产A102型货车632台,此时获利450600元/月。
对于问题A(2),根据上半年度的收入报表可知在当前生产方案下获得的毛收益g211166.7元/月。
若要通过“外包加工”增加发动机的装配能力,则“外包加工”后的毛收益必须比当前方案所得的毛收益高,这样“外包加工”才有意义。
根据生产部门经理的意见,A102型货车的生产方案已定,各车间剩余的生产能力只分配给A101型货车。
“外包加工”费用在537908.3元/月以下可以接受。
这只是总费用,若要求得到外包单价,需要进一步的规划。
对于问题B,公司考虑通过加工,增加发动机装配车间的生产能力,使其他车间能充分发挥它们的生产能力。
在发动机装配车间的生产能力提高的同时该车间的直接劳动费用提高,在加班情况下的最佳生产方案是A101型货车生产1428辆,A102型货车生产1500辆,此时的利润为495460元。
比不考虑加班的最佳生产方案获得的利润高,所以可以考虑用加班的方法提高发动机装配车间的生产能力,进而提高收益。
关键词:整数规划;生产能力归一;最佳生产方案一、问题的重述南洋汽车公司生产2种型号货车:A101型和A102型,为完成这两种车型生产,公司设有4各车间,其分别为冲压车间、发动机装配车间、A101型装配车间、A102型装配车间,而各车间的生产能力有一定限制的。
汽车公司的最优生产模型

汽车公司的最优生产模型1陈才兴23任冠峰黄晓瑜(韶关学院,广东韶关512005)1. 韶关学院02级应用数学本科班2. 韶关学院03级信息技术(1)班3. 韶关学院02级应用数学本科班摘要本模型讨论的是汽车公司最优的生产安排问题.通过分析各种数据,了解各种费用的换算关系,利用标准成本给出了毛利润函数,同时又引进了货车之间的兑换比例,建立了汽车公司的最优生产模型.同时还考虑了”外包加工”和加班对生产模型的影响.对于模型的求解,本文主要是应用数学软件MATLAB.对于利用现有资源,公司的生产方案是A101型和A102型的产量分别是2056和622,此时每月的最大毛利润是449500;对于采用”外包加工”,公司要从其他公司最多以226元/台的价格购买A101型发动机1129台;对于加班,公司的最大毛利润是216210,低于利用现有资源,因此加班是不值得采用的.关键词:标准成本;兑换比例;毛利润1. 问题的提出一汽车公司为了使公司目前的情况得到最大的改观,要求在现有资源的条件下,应采取怎样的生产方案安排生产最为合理.如果可以通过”外包加工”增加发动机的装配能力,什么范围内的”外包加工”费用可以接受.如果考虑用加班的方法来提高发动机装配车间的生产能力,在知道发动机装配能力的增加值,提高的直接劳动力费用,和加班的固定管理费用的条件下,讨论加班的方法是否值得采用.2. 基本假设1. 公司各个车间的月生产能力固定不变2. 货车在各个车间装配的时间忽略不计3. 货车的销售时间忽略不计,即货车生产出后立刻销售出4. 两种类型货车的直接材料费用固定不变5. 两种类型货车的直接劳动力费用固定不变3.符号约定:sij表示第j 个车间单生产第i 型的月生产能力 )4,3,2,1(=j:j λ表示在第j 个车间同时生产两种车型,型型与102101A A 的兑换比例)4,3,2,1(=j:kij表示在第j 个车间同时生产两种车型,第i 型的生产系数 )4,3,2,12,1(==j i:p i表示第i 型车的售价:q i表示每辆第i 型车的标准成本:a i表示每辆第i 型车的直接材料费用:bij表示每辆第i 型车在第j 个车间所需的直接劳动费用:mij表示每辆第i 型车在第j 个车间所需的管理费用:w j表示第j 个车间每月不变的管理费用:cij表示每辆第i 型车在第j 个车间所需的基本管理费用:n i表示每月第i 型车的产量:G 表示每月的毛收益:x i 表示外包加工的辆数 :y i表示外包加工的价钱:L 表示毛利润所必须达到的指标 :D 表示外包加工总费用4. 问题的分析4.1 货车生产的流程图:4.2 相关概念的理解标准成本:是指每个月分摊给每辆车的成本费用.是根据货车的产量的变化而变化的,与产量成反比.产量增加,标准成本就会减少;产量减少,标准成本就会增加.每月总的管理费用:可分为每月不变管理费用和每月可变管理费用,而每月可变管理费用又与货车的产量成正比例关系.兑换比例:由于车间生产A101型和A102型所需的人力、科技、复杂程度和生产时间的不同,同时生产A101型和A102型时,产量就会存在一定的比例关系4.3 每月不变管理费用的分摊规则由于A101型和A102型之间存在一个兑换比例,那么每月每辆A101型和A102型的不变管理费用也就不同,应该根据这个兑换比例进行分摊5.模型的建立5.1 模型一的建立目标函数:()i i i i n q p G ⨯-=∑=21m a x其中∑==++=4141j ij j ij i i m b a qij i iijjij ij k n kw c m ⨯⨯+=∑=21约束条件:()1 各个车间产量的约束: {}4,3,2,1m a x 21=≤⨯∑=j s n kij i i ij()2整数约束:0≥i n 2,1=i Z ∈i n 2,1=i5.2 模型二的建立 目标函数: ()ii iiy x ∑=⨯21m a x约束条件:()1 毛利润的约束: ()L n q p G ii ii≥⨯-=∑=21其中()()i ii j i i ij ij j ii i i j ij i i i i j ij i i n y x n k k w n x n c c n x n b b a q ⨯+⎪⎪⎪⎪⎭⎫ ⎝⎛⨯⨯+-⨯++-⨯++=∑∑∑∑====412124,3,124,3,1 ()2 各个车间产量的约束:(){}2212max i i iii s x n k =-∑={}4,3,1m a x 21=≤⨯∑=j s n kij i i ij()3 产量与外包加工量的关系:2,1=≤i n x ii()4 整数约束:2,1000=≥≥≥i ,y ,x n i i i2,1,,=Z∈i y x n i i i6. 模型的求解6.1 兑换比例λ与生产系数k通过对题目中的各种表格中的数据进行对比和计算,我们可以得出各个车间的兑换比例:⎪⎪⎪⎪⎪⎭⎫⎝⎛=1:00:12:11:4.1λ 而为了模型表达的方便,我们令生产系数ij k 表示兑换比例j λ的比例前项与比例后项,即:⎪⎪⎪⎪⎪⎭⎫⎝⎛=10012114.1k6.2 模型一的求解6.2.1 根据问题一的数据利用数学软件MATLAB ,得出模型一的最优解为 ⎪⎪⎭⎫⎝⎛=6222056n 449500=G此时在这种生产水平下的标准成本:6.2.2 根据问题三的数据对模型一进行求解,得出的最优解为⎪⎪⎭⎫⎝⎛=15001429n2162=G 所以,加班的方法不值得采用.6.3 模型二的求解由于公司是为了得到更多的毛利润才采用外包加工,也就是说模型二的毛利润应该比模型一的要大,所以我们取500000=L 利用MATLAB 得出模型二的最优解 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=02260112915001429y x n254790=D7.模型的评价与改进本模型充分考虑了汽车公司的经济利益,使汽车公司所获得的毛利润最大,同时又使公司的现有资源得到了较充分的利用.为了具有较强的现实意义,模型还分析了利用”外包加工”和加班提高装配能力、增加收益的可行性.此外,还给出了每辆货车的标准成本(以及分摊给每辆车的各种费用),使得汽车公司的盈亏和收益一目了然.当然,模型也存在一些不足,为了使模型简化,有些费用都固定不变,而在实际中是变化的.另外,由于本模型是一个整数规划问题,在用MATLAB 求解时,求出的值有些是小数,我们就运用了定界搜索的方法,尽量避免有小数出现,因此得到的值有一定的误差.8.参考文献[1] 王沫然电子工科学计算与],[0.6,M matlab业出版社,2001年 [2] 李强8,maple 基础应用教程],[M 中国水利水电出版社,2004年。
数学模型 汽车厂生产计划
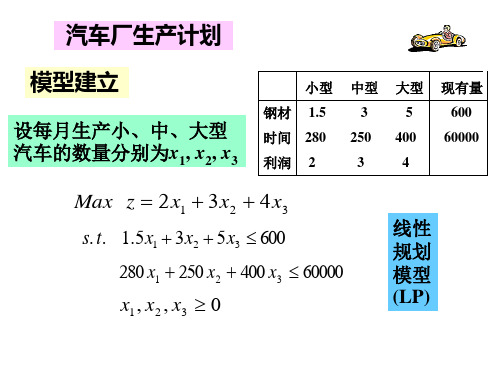
例2 原油采购与加工
库存500吨 原油 吨 原油A 库存 库存1000吨 原油 吨 原油B 库存 汽油甲 售价 售价4800元/吨 元吨 (A≥50%) ≥ 汽油乙 售价 售价5600元/吨 元吨 (A≥60%) ≥
市场上可买到不超过1500吨的原油 : 吨的原油A: 市场上可买到不超过 吨的原油 • 购买量不超过 购买量不超过500吨时的单价为 吨时的单价为10000元/吨; 吨时的单价为 元 • 购买量超过 购买量超过500吨但不超过 吨但不超过1000吨时,超过 吨时, 吨但不超过 吨时 超过500吨的 吨的 部分8000元/吨; 部分 元 • 购买量超过 购买量超过1000吨时,超过 吨时, 吨的部分6000元/吨。 吨时 超过1000吨的部分 吨的部分 元 应如何安排原油的采购和加工 ?
x1 ≥ 80, x2 ≥ 80, x3 = 0
x1 ≥ 80, x2 = 0, x3 ≥ 80
x1 ≥ 80, x2 ≥ 80, x3 ≥ 80
x1 , x 2 , x 3 = 0
× ×
x1=80,x2= 150,x3=0,最优值 , , ,最优值z=610
• 若生产某类汽车,则至少生产80辆,求生产计划。 若生产某类汽车,则至少生产80辆 求生产计划。 80 方法2:引入 变量 变量, 方法 :引入0-1变量,化为整数规划 x1=0 或 ≥80 x2=0 或 ≥80 x3=0 或 ≥80
IP 的最优解 1=64,x2=168,x3=0,最优值 的最优解x , , ,最优值z=632
汽车厂生产计划
• 若生产某类汽车,则至少生产80辆,求生产计划。 若生产某类汽车,则至少生产80辆 求生产计划。 80
s. t. 1.5x1 + 3x2 + 5x3 ≤ 600
汽车生产计划(lingo)

汽车公司的生产计划与决策摘要当今社会发展迅速,社会的需求也在增加,特别是代步的轿车的需求更是供不应求。
针对问题一:为计算每一种车型的生产成本和预计销售利润,建立成本函数:0i j k C c e d w =+++ 和预计销售利润函数:().*R P C Q =-,根据函数,利用Matlab 程序将算出结果。
针对问题二:首先针对如何计算最大利润的问题建立模型一:最大预计销售利润模型181max R=i i i x r =∑,利用lingo 软件求解出结果为只生产NH16和HA16两种车型;然后运用winQSB 的LP ILP -对模型一进行检验,得出结果为只生产NA18和NH16两种车型,为了计算出题中车型在哪一生产线生产接着建立模型二:0-1规划模型,以求得每条生产线具体生产哪种车型,最后为了计算出该问题的多种最优解我们再次运用Lingo 进行编程计算出生产了NA18、NH16和HA16三种车型并计算出了三种车型分别在哪一生产线上生产。
针对问题三:首先根据dynasearch 算法,建立模型三:最优解模型,得出最优解为只生产HA20;然后为计算出生产HA20具体的量,根据Lingo 中的01-整数规划思想,建立模型四:最优解模型,得出生产HA20300辆且最大利润为930万元。
针对问题四:首先根据销售量的概率分布,利用matlab 编程计算出每种车型预期需求的期望,建立模型五:最大期望获利模型,然后利用Lingo 软件算出最优解为只生产HA20型号车且最大利润为905.2万元。
由于概率是一个预测值,通过matlab 随机产生概率值进行运算得出:最优解在18EH 的销售量小等于293时最优解发生改变,因此此生产方案不具有稳定性。
针对问题五:运用与问题四相同的方法计算得出生产16NH 和16HA 两种车型,同样由于概率是一个预测值,通过matlab 随机产生概率进行运算得出最优解和最优值的大小相同,因此此生产方案具有稳定性。
数学建模——工厂计划模型

数学建模——工厂生产计划模型学院:数学与统计学院专业:信息与计算科学教师:郑**姓名:杨**学号:***********摘要本文以工厂所获得的总收益为研究对象,采用了线性规划的分析方法,通过求解不同产品的生产计划以及按计划生产所获得的利润,解决了工厂为达到最大总收益的产品生产计划问题。
在问题一的求解过程中,以每月每种产品的销售量和生产量为自变量,以工厂所获得的收益为目标函数,结合各种约束条件,建立了一个动态规划方程组,将各月份各种产品生产的最佳配置转化为动态规划方程组的求解问题,得到了最大收益为6.9256万元。
问题二在问题一的基础上考虑了市场价格的变化及引入新机床两个因素,为使模型简化,首先考虑市场价格的变化对计划和收益的影响。
然后假定市场价格不变,利用Lingo 软件,模拟出引入新机床对计划和收益的影响。
它是问题一的拓展,通过更改约束方程,利用模型一的计算程序,从而得到拓展模型的最优解。
关键字:总收益销售量生产量动态规划一、问题重述某厂拥有4台磨床、2台立式钻床、3台卧式钻床、一台镗床和一台刨床,用以生产7种产品,记作P1至P7。
工厂收益规定为产品售价减去原材料费用之剩余。
每种产品单件的收益及所需各机床的加工工时(以小时计)列于下表:产品P1 P2 P3 P4 P5 P6 P7收益10 6 8 4 11 9 3磨0.5 0.70 0 0 0.3 0.2 0.5垂直钻孔0.1 0.2 0 0.3 0 0.6 0水平钻孔0.2 0 0.8 0 0 0 0.6镗孔0.05 0.03 0 0.07 0.1 0 0.08刨0 0 0.01 0 0.05 0 0.05本月(一月)和随后的5个月中,下列机床停工维修:一月磨床一台二月卧式钻床2台三月镗床一台四月立式钻床一台五月磨床一台,立式钻床一台,上台下六月刨床一台,卧式钻床一台各种产品各月份的市场容量如下表:产品P1 P2 P3 P4 P5 P6 P7一月500 1000 300 300 800 200 100二月600 500 200 0 400 300 150三月300 600 0 0 500 400 100四月200 300 400 500 200 0 100五月0 100 500 100 1000 300 0有存货50件。
制定汽车生产计划的优化模型

生产控制目标也发生了很大的变化。为满足市场需 一段时间内, 记作t=T时刻, 提交的汽车产品数量为
求, 降低生产成本, 加快企业内部的流通, 产品按时 Q。任一时刻t已经生产的汽车数量记作N( t) ( 假设N
交货, 已经成为各大汽车公司生存和发展所追求的 目标。而在传统的汽车生产管理体制下, 产品交货期 准时率差, 生产不均衡, 制品积压数量较大, 使得制 造周期进一步延长, 交货期也一再拖延, 致使生产计 划失控, 企业生产进入恶性循环。因此, 在汽车生产 管理中, 怎样客观地分析市场需求和生产状况, 制定 可行的最优生产计划, 以期提高汽车产品交货期的 准时率和生产中所需的费用, 这是一个很重要的问 题。
[ J] .同济大学学报, 2000, 28( 3) : 337- 341. [ 4] 孙 凌 玉.有 关 汽 车 内 部 声 场 分 析 的 几 点 讨 论 [ J] .汽 车 工
程, 2003, 25( 1) : 74- 77. [ 5] James D Knittel,Lawrence J Oswald. An experimental tech-
定提供了科学思路, 其思想对解决其它实际规划问题也具有较强的参考价值。
关键词: 生产计划; 最优化; 模型; 汽车
中图分类号: F402.1
文献标识码: A
文章编号: 1005- 2550( 2005) 06- 0046- 03
在市场经济竞争日益激烈的今天, 汽车企业的 生产线开始运作生产的时刻, 为满足市场需求应在
Application of acoustic- str uctur al coupled modal analysis method in bus inter ior noise contr ol
数学建模-最优生产计划安排

最优生产计划安排关键词:最优解有效解弱有效解线性加权摘要:企业内部的生产计划有各种不同情况,从空间层次来看,在工厂级要根据外部需求和内部设备,人力,原料,等条件,以最大利润为目标制定生产计划,在车间级则要根据产品的生产计划,工艺流程,资源约束及费用参数等,以最小成本为目标制定生产批量计划。
从空间层次来看,若在短时间内认为外部需求和内部资源等随时间变化,可以制定但阶段的生产计划,否则就要制定多阶段深产计划。
本模型则仅考虑设备,工艺流程以及费用参数的情况下,通过线性规划来为企业求解最有生产方案。
I问题的提出:某厂生产三种产品I∏I I I每种产品要经过A、B两道工序加工。
设该厂有两种规格的设备能完成A工序,他们以A1、A2表示;有三种规格的设备能完成B工序,它们以B1、B2、B3表示,产品I可以在A、B任何一种规格设备上加工;产品∏可在任何一种规格的A设备上加工,但完成B工序时只能在B1设备上加工;产品I I I只能在A2与B2设备上加工。
已知各种机床设备的单件工时,原材料费,产品销售价格,各种设备有效台时以及满负荷操作时机床的设备费用,如下表所示,要求安排最优的生产计划,使厂方利润最大。
II问题分析:这个问题的目标是获利最大,有两个方面的因素,一是产品销售收入能否最大,二是设备费用能否最小。
我们要做的决策是生产计划,决策受到的限制有:原材料费,产品价格,各种设备有效台时以及满负荷操作时机床的设备费用。
显然这是一个多目标线性规划问题。
III问题假设1不允许出现半成品,即每件产品都必须经过两道工序。
2不考虑加工过程中的损失。
符号设定:设Z为净利润,Z1为产品销售纯收入,Z2为设备费用,iλ为权植,(i=1,2)且121=+λλ设经过工序A1、A2、B1、B2、B3加工的产品I 的数量依次为Xi1(i=1--5); 设经过工序A1、A2、B1、B2、B3加工的产品∏的数量依次为Xi2(i=1--5); 设经过工序A1、A2、B1、B2、B3加工的产品I I I 的数量依次为Xi3(i=1--5)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
约束 条件
原油供应
x11 + x12 ≤ 500 + x
购买x↓ 购买 ↓ 库存500吨 A 库存 吨
x21 + x 22 ≤ 1000
x ≤ 1500
x21
x11 x12
库存1000吨 B x22 吨 库存
约束 条件
汽油含原油A 汽油含原油 的比例限制
A B
x11 ≥ 0.5 ⇔ x11 ≥ x21 x11 + x21
利润: 购买原油A的支出 问题 • 利润:销售汽油的收入 - 购买原油 的支出 分析 • 难点:原油 的购价与购买量的关系较复杂 难点:原油A的购价与购买量的关系较复杂 原油A的购买量 原油A, 生产汽油甲 乙的数量 的购买量, 生产汽油 决策 原油 的购买量,原油 B生产汽油甲,乙的数量 x11 变量 4.8千元 吨 千元/吨 购买x→ 购买 → A
汽车厂生产计划 模型建立
钢材 小型 1.5 中型 3 250 3 大型 5 400 4 现有量 600 60000
设每月生产小、 设每月生产小、中、大型 汽车的数量分别为x 汽车的数量分别为 1, x2, x3
时间 280 利润 2
Max z = 2 x1 + 3x 2 + 4 x3
s. t. 1.5x1 + 3x2 + 5x3 ≤ 600
模型求解
方法1 方法
x1 , x2 , x3 ~以价格 以价格10, 8, 6(千元/吨)采购 的吨数 千元/ 采购A的吨数 以价格 千元 x= x1+x2+x3, c(x) = 10x1+8x2+6x3 目标 Max z = 4.8( x11 + x21) + 5.6( x12 + x22 ) − (10x1 + 8x2 + 6x3 ) 函数 • 500吨≤ x≤ 1000吨,超过 吨的8千 吨 ≤ 吨 超过500吨的 千元/吨 吨的 增加约束 只有当以10千元 吨的价格购买x 千元/吨的价格购买 只有当以 千元 吨的价格购买 1=500(吨),才能以 ( 8千元 吨的价格购买 2 千元/吨的价格购买 千元 吨的价格购买x
非线性规划( 非线性规划(Non- Linear Programming,简记 ,简记NLP) ) NLP 虽 然 可 用 现 成 的 数 学 软 件 求 解 ( 如 LINGO, , MATLAB),但是其结果常依赖于初值的选择。 ) 但是其结果常依赖于初值的选择。 实践表明, 本例仅当初值非常接近上面方法算出 实践表明 , 的最优解时,才能得到正确的结果。 的最优解时,才能得到正确的结果。
用库存的500吨原油 、500吨原油 吨原油A、 吨原油 吨原油B 用库存的 吨原油 生产汽油甲,不购买新的原油A, 生产汽油甲,不购买新的原油 , 利润为4,800千元。 利润为 千 LINGO得到的是局部最优解,还 得到的是局部最优解, 得到的是局部最优解 能得到更好的解吗? 能得到更好的解吗?
方法1: 方法 :LINGO求解 求解
Objective value: 4800.000 Variable Value Reduced Cost X11 500.0000 0.0000000E+00 X21 500.0000 0.0000000E+00 X12 0.0000000E+00 0.0000000E+00 X22 0.0000000E+00 0.0000000E+00 X1 0.1021405E-13 10.00000 X2 0.0000000E+00 8.000000 X3 0.0000000E+00 6.000000 X 0.0000000E+00 0.0000000E+00
IP 的最优解 1=64,x2=168,x3=0,最优值 的最优解x , , ,最优值z=632
汽车厂生产计划
• 若生产某类汽车,则至少生产80辆,求生产计划。 若生产某类汽车,则至少生产80辆 求生产计划。 80
s. t. 1.5x1 + 3x2 + 5x3 ≤ 600
Max z = 2 x1 + 3 x 2 + 4 x3
x21 x12
甲(A≥50%) ≥
千元 吨
B x 22
千元/吨 千元 乙(A≥60%) 5.6千元 吨 ≥ c(x) ~ 购买原油 的支出 购买原油A的支出
目标 函数
利润(千元 利润 千元) 千元
Max z = 4.8( x11 + x21 ) + 5.6( x12 + x22 ) − c( x)
c(x)如何表述? 如何表述? 如何表述
模型求解
整数规划( 整数规划(Integer Programming,简记 ) ,简记IP) IP可用 可用LINDO直接求解 可用 直接求解
max 2x1+3x2+4x3 st 1.5x1+3x2+5x3<600 280x1+250x2+400x3<60000 end gin 3 “gin 3”表示“前3个变量为 表示“ 表示 个变量为 整数” 等价于: 整数”,等价于: gin x1 gin x2 gin x3
LINDO 中 对 01变量的限定: 变量的限定: 变量的限定 int y1 int y2 int y3
x1 ≤ My1 , x1 ≥ 80 y1 , y1 ∈{0,1} M为大的正数, 为大的正数, 为大的正数 可取1000 x2 ≤ My2 , x2 ≥ 80 y2 , y2 ∈{0,1} 可取
280x1 + 250x2 + 400x3 ≤ 60000
x1 , x 2 , x3 ≥ 0
线性 规划 模型 (LP)
模型 求解
结果为小数, 结果为小数, 怎么办? 怎么办?
OBJECTIVE FUNCTION VALUE 1) 632.2581 VARIABLE VALUE REDUCED COST X1 64.516129 0.000000 X2 167.741928 0.000000 X3 0.000000 0.946237 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 0.731183 3) 0.000000 0.003226
x1 = 0, x 2 = 0, x3 ≥ 80
x1 = 0, x 2 ≥ 80, x 3 = 0
280x1 + 250x2 + 400x3 ≤ 60000 x1 = 0, x2 ≥ 80, x3 ≥ 80 × x1,x2,, x3=0 或 ≥80 x1 ≥ 80, x 2 = 0, x3 = 0
方法1:分解为 个 子模型 方法 :分解为8个LP子模型 其中3个子模型应去掉, 其中 个子模型应去掉,然后 去掉 逐一求解,比较目标函数值, 逐一求解,比较目标函数值, 再加上整数约束,得最优解: 再加上整数约束,得最优解:
x1 ≥ 80, x2 ≥ 80, x3 = 0
x1 ≥ 80, x2 = 0, x3 ≥ 80
x1 ≥ 80, x2 ≥ 80, x3 ≥ 80
x1 , x 2 , x 3 = 0
× ×
x1=80,x2= 150,x3=0,最优值 , , ,最优值z=610
• 若生产某类汽车,则至少生产80辆,求生产计划。 若生产某类汽车,则至少生产80辆 求生产计划。 80 方法2:引入 变量 变量, 方法 :引入0-1变量,化为整数规划 x1=0 或 ≥80 x2=0 或 ≥80 x3=0 或 ≥80
例2 原油采购与加工
库存500吨 原油 吨 原油A 库存 库存1000吨 原油 吨 原油B 库存 汽油甲 售价 售价4800元/吨 元吨 (A≥50%) ≥ 汽油乙 售价 售价5600元/吨 元吨 (A≥60%) ≥
市场上可买到不超过1500吨的原油 : 吨的原油A: 市场上可买到不超过 吨的原油 • 购买量不超过 购买量不超过500吨时的单价为 吨时的单价为10000元/吨; 吨时的单价为 元 • 购买量超过 购买量超过500吨但不超过 吨但不超过1000吨时,超过 吨时, 吨但不超过 吨时 超过500吨的 吨的 部分8000元/吨; 部分 元 • 购买量超过 购买量超过1000吨时,超过 吨时, 吨的部分6000元/吨。 吨时 超过1000吨的部分 吨的部分 元 应如何安排原油的采购和加工 ?
x12 ≥ 0.6 ⇔ 2x12 ≥ 3x22 x12 + x22
x21 x22
x11 x12
甲(A≥50%) ≥ 乙(A≥60%) ≥
目标函数中c(x)不是线性函数,是非线性规划; 不是线性函数,是非线性规划; 目标函数中 不是线性函数 对于用分段函数定义的c(x),一般的非线性规划软 , 对于用分段函数定义的 件也难以输入和求解; 件也难以输入和求解; 想办法将模型化简,用现成的软件求解。 想办法将模型化简,用现成的软件求解。
1)舍去小数:取x1=64,x2=167,算出目标函数值 )舍去小数: , ,算出目标函数值z=629,与 , LP最优值 最优值632.2581相差不大。 相差不大。 最优值 相差不大 2)试探:如取 1=65,x2=167;x1=64,x2=168等,计算函数 )试探:如取x , ; , 等 值z,通过比较可能得到更优的解。 ,通过比较可能得到更优的解。 • 但必须检验它们是否满足约束条件。为什么? 但必须检验它们是否满足约束条件。为什么? 3) 模型中增加条件:x1, x2, x3 均为整数,重新求解。 均为整数,重新求解。 ) 模型中增加条件:
( x 2 − 500) x3 = 0
( x1 − 500) x 2 = 0
0 ≤ x1 , x2 , x3 ≤ 500
非线性规划模型,可以用 非线性规划模型,可以用LINGO求解 求解
