2019高考数学第一轮复习函数与方程.ppt
高考数学(文)一轮复习课件:1-9函数与方程(人教A版)

高考考点预览
■ ·考点梳理· ■ 1. 函数的零点 (1)函数零点的定义 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数 y=f(x)的零点. (2)几个等价关系 方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交 点⇔函数y=f(x)有零点.
思考:上述等价关系在研究函数零点、方程的根及 图象交点问题时有什么作用?
思考:若函数y=f(x)在区间(a,b)内有零点,则y= f(x)在区间[a,b]上的图象是否一定是连续不断的一条曲 线,且有f(a)·f(b)<0呢?
提示:不一定.由图(1)、(2)可知.
3.二分法 (1)二分法的定义 对于在区间[a,b]上连续不断且ff((aa))··ff((bb)<0 的函数y= f(x),通过不断地把函数f(x)的零点所在的区间一分为二 , 使区间的两端点逐步逼近零点,进而得到零点的近似值 的方法叫做二分法. (2)用二分法求函数零点近似解的步骤 第一步:确定区间[a,b],验证f(a)·f(b)<0 ,给定精 确度ε;
观察图象可以发现它们有4个交点,即函数y=f(x)- log3|x|有4个零点.
3. [2012·徐州模拟]根据下面表格中的数据,可以判
定方程ex-x-2=0的一个根所在的区间为________.
x
-1 0 1 2
3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4
5
答案:(1,2)
3. 二分法是求方程的根的近似值的一种计算方法.其 实质是通过不断地“取中点”来逐步缩小零点所在的范 围,当达到一定的精确度要求时,所得区间的任一点就是 这个函数零点的近似值.
4. 要熟练掌握二分法的解题步骤,尤其是初始区间的 选取和最后精确度的判断.
高考数学一轮复习第二章函数概念及基本初等函数Ⅰ第8节函数与方程课件新人教A版

D.[1,2)
解析 依题意直线y=a与y=f(x)的图象有两个交点. 作出y=a,y=f(x)的图象,如图所示. 又当 x≤1 时,f(x)=12|x|∈(0,1]; 当x>1时,f(x)=-x2+4x-2=-(x-2)2+2, ∴当x=2时,f(x)有最大值f(2)=2. 结合图象,当 a∈0,12∪[1,2)时,两图象有 2 个交点. 此时,方程a=f(x)有两个不同实根. 答案 B
【训练3】 (1)(角度1)(202X·全国Ⅲ卷)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零
点,则a=( )
A.-12
1 B.3
1
C.2
D.1
(2)(角度2)若函数y=x+log2(a-2x)+2在R上有零点,则实数a的最小值为________.
解析 (1)f(x)=(x-1)2-1+a(ex-1+e1-x),则f(2-x)=(2-x-1)2-1+a[e2-x-1+ e1-(2-x)]=(1-x)2-1+a(ex-1+e1-x)=f(x),即f(x)的图象关于直线x=1对称. 若 f(x)有唯一的零点,则只有 f(1)=0,∴a=12. 或:作出y=a(ex-1+e-x+1)与y=-x2+2x的图象.
x0 所在的区间是________.
解析 (1)由函数 f(x)=x-1 a为奇函数,可得 a=0, 则 g(x)=ln x-2f(x)=ln x-2x. 又 g(2)=ln 2-1<0,g(3)=ln 3-23>0,
所以g(2)·g(3)<0. 故函数g(x)的零点所在区间为(2,3).
(2)设 f(x)=x3-12x-2,则 x0 是函数 f(x)的零点,在同一坐 标系下画出函数 y=x3 与 y=12x-2的图象如图所示. 因为 f(1)=1-12-1=-1<0,f(2)=8-120=7>0, 所以f(1)·f(2)<0,所以x0∈(1,2). 答案 (1)C (2)(1,2)
北师版高考总复习一轮数学精品课件 第3章函数与基本初等函数 第9节函数与方程

变式探究2
(变条件)本例(2)中,其他条件不变,条件“函数g(x)=f(x)-m有零点”改为“函数
2
g(x)=f(x)-m有2个不同的零点”,则实数m的取值范围是 [ 2 ,1) .
重复第(2)~(4)步.
常用结论
1.奇偶函数的非零零点成对出现,且互为相反数.
2.周期函数若存在零点,则必有无穷多个零点.
自主诊断
题组一基础自测
1.思考辨析(判断下列结论是否正确,正确的画“ ”,错误的画“×”).
(1)函数f(x)=x2-1的两个零点是(-1,0)和(1,0).( × )
(2)如果函数f(x)在区间(a,b)上单调且存在零点,则f(a)·f(b)<0.(
A=
1
;f( )=
12
解析 由题意知
3cos
- 2
π
π
f(3)=Asin3 −
π
x=2sin(x- ),故
3
x 的一个零点为3 ,则
.
π
3cos3
=
3
3
A- 2 =0,所以
2
π
π
π
π
f( )=2sin( − )=2sin(- )=12
12
3
4
2.
A=1.从而 f(x)=sin x-
2 研考点 精准突破
(3)偶函数若有零点必有偶数个.( × )
(4)只要函数有零点,就可以用二分法求出其近似值.( × )
)
2.已知函数f(x)的图象是连续不断的,且有如下对应值表:
高考数学一轮复习9 第9讲 函数与方程
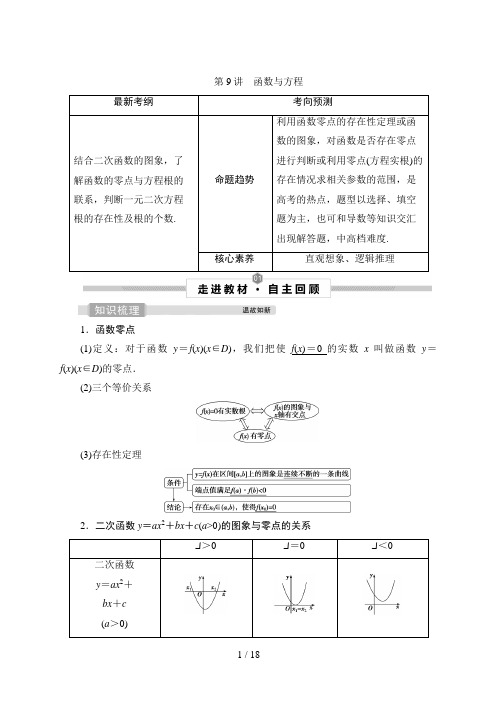
第9讲函数与方程最新考纲考向预测结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.命题趋势利用函数零点的存在性定理或函数的图象,对函数是否存在零点进行判断或利用零点(方程实根)的存在情况求相关参数的范围,是高考的热点,题型以选择、填空题为主,也可和导数等知识交汇出现解答题,中高档难度.核心素养直观想象、逻辑推理1.函数零点(1)定义:对于函数y=f(x)(x∈D),我们把使f(x)=0的实数x叫做函数y=f(x)(x∈D)的零点.(2)三个等价关系(3)存在性定理2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象与x轴(x1,0),(x2,0)(x1,0)无交点的交点零点x1,x2x1无常用结论有关函数零点的三个结论(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.(3)连续不断的函数图象通过零点时,函数值可能变号,也可能不变号.常见误区1.函数f(x)的零点是一个实数,是方程f(x)=0的根,也是函数y=f(x)的图象与x 轴交点的横坐标.2.函数零点存在性定理是零点存在的一个充分条件,而不是必要条件;判断零点个数还要根据函数的单调性、对称性或结合函数图象等综合考虑.1.判断正误(正确的打“√”,错误的打“×”)(1)函数y=f(x)在区间(a,b)内有零点(函数图象连续不断),则f(a)·f(b)<0.()(2)只要函数有零点,我们就可以用二分法求出零点的近似值.()(3)二次函数y=ax2+bx+c(a≠0)在b2-4ac<0时没有零点.()(4)若函数f(x)在(a,b)上连续单调且f(a)·f(b)<0,则函数f(x)在[a,b]上有且只有一个零点.()答案:(1)×(2)×(3)√(4)√2.(易错题)(多选)下列说法中正确的是()A.函数f(x)=x+1的零点为(-1,0)B.函数f(x)=x+1的零点为-1C.函数f(x)的零点,即函数f(x)的图象与x轴的交点D.函数f(x)的零点,即函数f(x)的图象与x轴的交点的横坐标解析:选BD.根据函数零点的定义,可知f(x)=x+1的零点为-1.函数y =f (x )的零点,即函数y =f (x )的图象与x 轴的交点的横坐标,因此B ,D 正确,A ,C 错误.3.函数f (x )=ln x -2x 的零点所在的大致范围是( ) A .(1,2)B .(2,3)C .⎝⎛⎭⎪⎫1e ,1和(3,4)D .(4,+∞)解析:选B.易知f (x )为增函数,由f (2)=ln 2-1<0,f (3)=ln 3-23>0,得f (2)·f (3)<0.故选B.4.已知函数y =f (x )的图象是连续不断的曲线,且有如下的对应值表:则函数y =f 解析:依题意,f (2)>0,f (3)<0,f (4)>0,f (5)<0,根据零点存在性定理可知,f (x )在区间(2,3),(3,4),(4,5)上均至少含有一个零点,故函数y =f (x )在区间[1,6]上的零点至少有3个.答案:35.已知函数f (x )=2ax -a +3,若∃x 0∈(-1,1),使得f (x 0)=0,则实数a 的取值范围是________.解析:依题意可得f (-1)·f (1)<0,即(-2a -a +3)(2a -a +3)<0,解得a <-3或a >1.答案:(-∞,-3)∪(1,+∞)函数零点所在区间的判断(一题多解)函数f(x)=log3x+x-2的零点所在的区间为() A.(0,1)B.(1,2)C.(2,3) D.(3,4)【解析】方法一(定理法):函数f(x)=log3x+x-2的定义域为(0,+∞),并且f(x)在(0,+∞)上单调递增,图象是一条连续曲线.由题意知f(1)=-1<0,f(2)=log32>0,f(3)=2>0,根据零点存在性定理可知,函数f(x)=log3x+x-2有唯一零点,且零点在区间(1,2)内.方法二(图象法):函数f(x)的零点所在的区间转化为函数g(x)=log3x,h(x)=-x+2图象交点的横坐标所在的范围.作出两个函数的图象如图所示,可知f(x)的零点所在的区间为(1,2).故选B.【答案】 B判断函数零点所在区间的方法方法解读适合题型定理法利用函数零点的存在性定理进行判断能够容易判断区间端点值所对应函数值的正负图象法画出函数图象,通过观察图象与x轴在给定区间上是否有交点来判断容易画出函数的图象1.已知实数a >1,0<b <1,则函数f (x )=a x +x -b 的零点所在的区间是( ) A .(-2,-1) B .(-1,0) C .(0,1)D .(1,2)解析:选 B.因为a >1,0<b <1,f (x )=a x +x -b ,所以f (-1)=1a -1-b <0,f (0)=1-b >0,由零点存在性定理可知f (x )在区间(-1,0)上存在零点.2.设函数f (x )=13x -ln x ,则函数y =f (x )( )A .在区间⎝ ⎛⎭⎪⎫1e ,1,(1,e)内均有零点 B .在区间⎝ ⎛⎭⎪⎫1e ,1,(1,e)内均无零点C .在区间⎝⎛⎭⎪⎫1e ,1内有零点,在区间(1,e)内无零点 D .在区间⎝ ⎛⎭⎪⎫1e ,1内无零点,在区间(1,e)内有零点 解析:选D.令f (x )=0得13x =ln x . 作出函数y =13x 和y =ln x 的图象,如图,显然y =f (x )在区间⎝⎛⎭⎪⎫1e ,1内无零点,在区间(1,e)内有零点.函数零点个数的判断(一题多解)函数f (x )=⎩⎨⎧x2+x -2,x≤0,-1+ln x ,x>0的零点个数为( )A .3B .2C .1D .0【解析】 方法一(方程法):由f (x )=0,得⎩⎪⎨⎪⎧x≤0,x2+x -2=0或⎩⎪⎨⎪⎧x>0,-1+ln x =0, 解得x =-2或x =e. 因此函数f (x )共有2个零点.方法二(图形法):函数f (x )的图象如图所示,由图象知函数f (x )共有2个零点. 【答案】 B判断函数零点个数的3种方法(1)方程法:令f (x )=0,如果能求出解,则有几个解就有几个零点.(2)定理法:利用定理不仅要求函数在区间[a ,b ]上是连续不断的曲线,且f (a )·f (b )<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点.(3)图形法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的横坐标有几个不同的值,就有几个不同的零点.1.已知函数f (x )=⎩⎪⎨⎪⎧x2-2x ,x≤0,1+1x ,x>0,则函数y =f (x )+3x 的零点个数是( )A .0B .1C .2D .3解析:选C.令f (x )+3x =0,则⎩⎪⎨⎪⎧x≤0,x2-2x +3x =0或⎩⎨⎧x>0,1+1x +3x =0,解得x =0或x =-1,所以函数y =f (x )+3x 的零点个数是2.2.函数f (x )=3x +x 3-2在区间(0,1)内的零点个数是( ) A .0 B .1 C .2D .3解析:选 B.由题意知f (x )单调递增,且f (0)=1+0-2=-1<0,f (1)=3+1-2=2>0,即f (0)·f (1)<0且函数f (x )在(0,1)内连续不断,所以f (x )在区间(0,1)内有一个零点.3.函数f (x )=|x -2|-ln x 在定义域内的零点个数为( ) A .0 B .1 C .2D .3解析:选 C.由题意可知f (x )的定义域为(0,+∞).在同一平面直角坐标系中画出函数y =|x -2|(x >0),y =ln x (x >0)的图象.如图所示.由图可知函数f (x )在定义域内的零点个数为2.故选C.函数零点的应用(1)函数f (x )=x 2-ax +1在区间⎝⎛⎭⎪⎫12,3上有零点,则实数a 的取值范围是( )A .(2,+∞)B .[2,+∞)C .⎣⎢⎡⎭⎪⎫2,52D .⎣⎢⎡⎭⎪⎫2,103(2)已知函数f (x )=⎩⎨⎧ex , x≤0,ln x , x>0,g (x )=f (x )+x +a .若g (x )存在2个零点,则a 的取值范围是________.【解析】 (1)由题意知方程ax =x 2+1在⎝ ⎛⎭⎪⎫12,3上有解,即a =x +1x 在⎝ ⎛⎭⎪⎫12,3上有解,设t =x +1x ,x ∈⎝ ⎛⎭⎪⎫12,3,则t 的取值范围是⎣⎢⎡⎭⎪⎫2,103.所以实数a 的取值范围是⎣⎢⎡⎭⎪⎫2,103.(2)函数g (x )=f (x )+x +a 存在2个零点,即关于x 的方程f (x )=-x -a 有2个不同的实根,即函数f (x )的图象与直线y =-x -a 有2个交点,作出直线y =-x -a 与函数f (x )的图象,如图所示,由图可知,-a ≤1,解得a ≥-1.【答案】 (1)D (2)[-1,+∞)根据函数零点的情况求参数有三种常用方法(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数形结合求解.1.函数f (x )=2x -2x -a 的一个零点在区间(1,2)内,则实数a 的取值范围是( ) A .(1,3) B .(1,2) C .(0,3) D .(0,2)解析:选C.由题意,知函数f (x )在(1,2)上单调递增,又函数一个零点在区间(1,2)内,所以⎩⎪⎨⎪⎧f (1)<0,f (2)>0,即⎩⎪⎨⎪⎧-a<0,4-1-a>0,解得0<a <3,故选C.2.若函数f (x )=|2x -4|-a 存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( )A .(0,4)B .(0,+∞)C .(3,4)D .(3,+∞)解析:选C.令g (x )=|2x -4|,其图象如图所示,若f (x )=|2x -4|-a 存在两个零点,且一个为正数,另一个为负数,则a ∈(3,4).思想方法系列6 破解嵌套函数的零点问题函数的零点是高考命题的热点,主要涉及判断函数零点的个数或范围,常考查三次函数与复合函数相关零点,与函数的性质和相关问题交汇.对于嵌套函数的零点,通常先“换元解套”,将复合函数拆解为两个相对简单的函数,借助函数的图象、性质求解.类型一 嵌套函数零点个数的判断(2021·沈阳市教学质量监测(一))已知函数f (x )是定义在(-∞,0)∪(0,+∞)上的偶函数,且当x ∈(0,+∞)时,f (x )=⎩⎨⎧(x -1)2,0<x≤2f (x -2)+1,x>2,则函数g (x )=f 2(x )-f (x )的零点个数为( )A .4B .5C .6D .7【解析】 因为当x ∈(0,2]时,f (x )=(x -1)2,当x >2时,f (x )=f (x -2)+1,所以将f (x )在区间(0,2]上的图象向右平移2个单位长度,同时再向上平移1个单位长度,得到函数f (x )在(2,4]上的图象.同理可得到f (x )在(4,6],(6,8],…上的图象.再由f (x )的图象关于y 轴对称得到f (x )在(-∞,0)上的图象,从而得到f (x )在其定义域内的图象,如图所示:令g (x )=0,得f (x )=0或f (x )=1,由图可知直线y =0与y =1和函数y =f (x )的图象共有6个交点,所以函数g (x )共有6个零点.故选C.【答案】 C破解此类问题的主要步骤(1)换元解套,转化为t =g (x )与y =f (t )的零点.(2)依次解方程,令f (t )=0,求t ,代入t =g (x )求出x 的值或判断图象交点个数. 类型二 求嵌套函数零点中的参数函数f (x )=⎩⎨⎧ln (-x -1),x<-1,2x +1,x≥-1,若函数g (x )=f (f (x ))-a 有三个不同的零点,则实数a 的取值范围是________.【解析】 设t =f (x ),令g (x )=f (f (x ))-a =0,则a =f (t ).在同一平面直角坐标系内作y =a ,y =f (t )的图象(如图).当a ≥-1时,y =a 与y =f (t )的图象有两个交点.设交点的横坐标为t 1,t 2(不妨设t 2>t 1),则t 1<-1,t 2≥-1.当t 1<-1时,t 1=f (x )有一解;当t 2≥-1时,t 2=f (x )有两解.综上,当a ≥-1时,函数g (x )=f (f (x ))-a 有三个不同的零点.【答案】 [-1,+∞)(1)求解本题抓住分段函数的图象性质,由y =a 与y =f (t )的图象,确定t 1,t 2的取值范围,进而由t =f (x )的图象确定零点的个数.(2)含参数的嵌套函数方程,还应注意让参数的取值“动起来”,抓临界位置,动静结合.设定义域为R 的函数f (x )=⎩⎨⎧|lg|x -2||,x≠2,0,x =2.若b <0,则关于x 的方程[f (x )]2+bf (x )=0的不同实数根共有( )A .4个B .5个C .7个D .8个解析:选C.由[f (x )]2+bf (x )=0,得f (x )=0或f (x )=-b .所以方程[f (x )]2+bf (x )=0的根的个数即为函数y =f (x )与函数y =0,y =-b (b <0)的图象的交点个数.作出函数f (x )的图象如图所示,结合图象可知,f (x )=0有3个实数根,f (x )=-b (b <0)有4个实数根,所以[f (x )]2+bf (x )=0共有7个不同的实数根.故选C.[A 级 基础练]1.(2021·河南商丘九校联考)函数f (x )=(x 2-1)·x2-4的零点个数是( ) A .1 B .2 C .3D .4解析:选B.要使函数有意义,则x 2-4≥0,解得x ≥2或x ≤-2.由f (x )=0得x 2-4=0或x 2-1=0(不成立舍去),即x =2或x =-2.所以函数的零点个数为2.故选B.2.(2021·重庆模拟)函数f (x )=⎝ ⎛⎭⎪⎫12x -15x 的零点位于区间( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)解析:选B.函数f (x )在R 上为减函数,其图象为一条不间断的曲线. 因为f (1)=12-15=310>0,f (2)=14-25=-320<0,所以f (1)·f (2)<0,所以由零点存在性定理可知,函数f (x )的零点位于区间(1,2).故选B.3.(2021·南充市第一次适应性考试)函数f (x )=⎩⎨⎧1-x2,|x|≤1,|x|,|x|>1,若方程f (x )=a 有且只有一个实数根,则实数a 满足( )A .a =1B .a >1C .0≤a <1D .a <0解析:选A.方程f (x )=a 有且只有一个实数根,即直线y =a 与f (x )的图象有且只有一个交点,作出函数f (x )的图象如图所示,当a =1时,直线y =a 与函数f (x )的图象有且只有一个交点,故选A.4.(多选)给出以下四个方程,其中有唯一解的是( ) A .ln x =1-x B .e x =1x C .2-x 2=lg |x |D .cos x =|x |+1解析:选ABD.对于A ,设f (x )=ln x +x -1,易知y =f (x )为增函数,又f (1)=0,故ln x =1-x 有唯一解,符合题意;对于B ,设g (x )=e x -1x ,易知y =g (x )为增函数,又g ⎝ ⎛⎭⎪⎫12=e -2<0,g (1)=e -1>0,由函数零点存在定理可得e x =1x 有唯一解,符合题意;对于C ,设h (x )=x 2+lg x -2,易知y =h (x )为增函数,由h (1)=1-2<0,h (2)=2+lg 2>0,由函数零点存在定理可得h (x )=x 2+lg x -2有唯一零点,又h (x )=2-x 2-lg|x |为偶函数,则2-x 2=lg|x |有两个解,不符合题意;对于D ,因为cos x ∈[-1,1],|x |+1≥1,当且仅当x =0时,cos x =x +1,即cos x =|x |+1有唯一解,符合题意.5.已知函数f (x )=⎩⎪⎨⎪⎧1,x≤0,1x ,x>0,则使方程x +f (x )=m 有解的实数m 的取值范围是( )A .(1,2)B .(-∞,-2]C .(-∞,1)∪(2,+∞)D .(-∞,1]∪[2,+∞)解析:选D.当x ≤0时,x +f (x )=m ,即x +1=m ,解得m ≤1;当x >0时,x +f (x )=m ,即x +1x =m ,解得m ≥2,即实数m 的取值范围是(-∞,1]∪[2,+∞).故选D.6.已知函数f (x )=23x +1+a 的零点为1,则实数a 的值为________.解析:由已知得f (1)=0,即231+1+a =0,解得a =-12.答案:-127.函数f (x )=⎩⎨⎧ln x -x2+2x ,x>0,4x +1,x≤0的零点个数是________.解析:当x >0时,作出函数y =ln x 和y =x 2-2x 的图象,由图知,当x >0时,f (x )有2个零点;当x ≤0时,由f (x )=0,得x =-14. 综上,f (x )有3个零点. 答案:38.若函数f (x )=⎩⎨⎧2x -a ,x≤0,ln x ,x>0有两个不同的零点,则实数a 的取值范围是________.解析:当x >0时,由f (x )=ln x =0,得x =1.因为函数f (x )有两个不同的零点,则当x ≤0时,函数f (x )=2x -a 有一个零点.令f (x )=0,得a =2x .因为0<2x ≤20=1,所以0<a ≤1,所以实数a 的取值范围是(0,1].答案:(0,1]9.设函数f (x )=⎪⎪⎪⎪⎪⎪1-1x (x >0).(1)作出函数f (x )的图象;(2)若方程f (x )=m 有两个不相等的正根,求m 的取值范围. 解:(1)如图所示.(2)由函数f (x )的图象可知,当0<m <1时,方程f (x )=m 有两个不相等的正根. 10.设函数f (x )=ax 2+bx +b -1(a ≠0). (1)当a =1,b =-2时,求函数f (x )的零点;(2)若对任意b ∈R ,函数f (x )恒有两个不同的零点,求实数a 的取值范围. 解:(1)当a =1,b =-2时,f (x )=x 2-2x -3,令f (x )=0,得x =3或x =-1. 所以函数f (x )的零点为3或-1.(2)依题意,f (x )=ax 2+bx +b -1=0有两个不同的实根,所以b 2-4a (b -1)>0恒成立,即对于任意b ∈R ,b 2-4ab +4a >0恒成立,所以有(-4a )2-4×(4a )<0⇒a 2-a <0,解得0<a <1,因此实数a 的取值范围是(0,1).[B 级 综合练]11.已知奇函数f (x )是R 上的单调函数,若函数y =f (2x 2+1)+f (λ-x )只有一个零点,则实数λ的值是( )A .14B .18C .-78D .-38解析:选C.因为函数y =f (2x 2+1)+f (λ-x )只有一个零点,所以方程f (2x 2+1)+f (λ-x )=0只有一个实数根,又函数f (x )是定义在R 上的奇函数,所以f (2x 2+1)+f (λ-x )=0⇔f (2x 2+1)=f (x -λ)⇔2x 2+1=x -λ,所以方程2x 2-x +1+λ=0只有一个实数根,所以Δ=(-1)2-4×2×(1+λ)=0,解得λ=-78.故选C 项.12.(多选)已知函数f (x )=⎩⎨⎧-x2-2x ,x≤0,|log2x|,x>0,若x 1<x 2<x 3<x 4,且f (x 1)=f (x 2)=f (x 3)=f (x 4),则下列结论正确的是( )A .x 1+x 2=-1B .x 3x 4=1C .1<x 4<2D .0<x 1x 2x 3x 4<1解析:选BCD.由函数f (x )=⎩⎪⎨⎪⎧-x2-2x ,x≤0,|log2x|,x>0,作出其函数图象:由图可知,x 1+x 2=-2,-2<x 1<-1; 当y =1时,|log 2x |=1,有x =12,2,所以12<x 3<1<x 4<2;由f (x 3)=f (x 4),有|log 2x 3|=|log 2x 4|, 即log 2x 3+log 2x 4=0, 所以x 3x 4=1,则x 1x 2x 3x 4=x 1x 2=x 1(-2-x 1)=-(x 1+1)2+1∈(0,1).故选BCD. 13.已知函数f (x )=ax 2+bx +c (a ≠0),满足f (0)=2,f (x +1)-f (x )=2x -1. (1)求函数f (x )的解析式;(2)若函数g (x )=f (x )-mx 的两个零点分别在区间(-1,2)和(2,4)内,求m 的取值范围.解:(1)由f (0)=2得c =2,又f (x +1)-f (x )=2x -1,得2ax +a +b =2x -1,故⎩⎪⎨⎪⎧2a =2,a +b =-1,解得a =1,b =-2,所以f (x )=x 2-2x +2. (2)g (x )=x 2-(2+m )x +2,若g (x )的两个零点分别在区间(-1,2)和(2,4)内,则满足⎩⎪⎨⎪⎧g (-1)>0,g (2)<0,g (4)>0⇒⎩⎪⎨⎪⎧5+m>0,2-2m<0,10-4m>0,解得1<m <52.所以m 的取值范围为⎝ ⎛⎭⎪⎫1,52. 14.已知函数f (x )=-x 2-2x ,g (x )=⎩⎪⎨⎪⎧x +14x ,x>0,x +1,x≤0.(1)求g [f (1)]的值;(2)若方程g [f (x )]-a =0有4个实数根,求实数a 的取值范围. 解:(1)利用解析式直接求解得g [f (1)]=g (-3)=-3+1=-2.(2)令f (x )=t ,则原方程化为g (t )=a ,易知方程f (x )=t 在t ∈(-∞,1)上有2个不同的解,则原方程有4个解等价于函数y =g (t )(t <1)与y =a 的图象有2个不同的交点,作出函数y =g (t )(t <1)的图象,如图,由图象可知,当1≤a <54时,函数y =g (t )(t <1)与y =a有2个不同的交点,即所求a 的取值范围是⎣⎢⎡⎭⎪⎫1,54.[C 级 创新练]15.已知a ,b ∈R ,定义运算“⊗”:a ⊗b =⎩⎨⎧a ,a -b≤1,b ,a -b>1.设函数f (x )=2x +1⊗(2-4x ),x ∈R .若函数y =f (x )-c 的图象与x 轴恰有两个公共点,则实数c 的取值范围是( )A .(0,1)B .(0,2)∪(2,3)C .(0,2)D .(0,3-1)∪(3-1,2)解析:选A.若2x +1-(2-4x )≤1,则(2x )2+2×2x -3≤0,即2x ≤1,解得x ≤0;若2x +1-(2-4x )>1,则(2x )2+2×2x -3>0,解得2x >1或2x <-3(舍去),即x >0.所以f (x )=⎩⎪⎨⎪⎧2x +1,x≤0,2-4x ,x>0.作出函数f (x )的图象和y =c 的图象如图所示.因为y =f (x )-c 有两个零点,所以f (x )=c 有两个解,所以0<c <1.故选A.16.定义:设不等式F (x )<0的解集为M ,若M 中只有唯一整数,则称M 是最优解.若关于x 的不等式|x 2-2x -3|-mx +2<0有最优解,则实数m 的取值范围是( )A.⎝ ⎛⎦⎥⎤23,74B.⎣⎢⎡⎭⎪⎫-72,-2 C.⎣⎢⎡⎦⎥⎤-72,-2∪⎣⎢⎡⎦⎥⎤23,74 D.⎣⎢⎡⎭⎪⎫-72,-2∪⎝⎛⎦⎥⎤23,74 解析:选D.|x 2-2x -3|-mx +2<0可转化为|x 2-2x -3|<mx -2,在同一平面直角坐标系中分别作出函数f (x )=|x 2-2x -3|,g (x )=mx -2的图象,如图所示.易知m =0时不满足题意.当m >0时,要存在唯一的整数x 0,满足f (x 0)<g (x 0), 则⎩⎪⎨⎪⎧f (2)≥g (2),f (3)<g (3),f (4)≥g (4),即⎩⎪⎨⎪⎧3≥2m -2,0<3m -2,5≥4m -2,解得23<m ≤74. 当m <0时,要存在唯一的整数x 0,满足f (x 0)<g (x 0), 则⎩⎪⎨⎪⎧f (0)≥g (0),f (-1)<g (-1),f (-2)≥g (-2),即⎩⎪⎨⎪⎧3≥-2,0<-m -2,5≥-2m -2,解得-72≤m <-2. 综上,实数m 的取值范围是⎣⎢⎡⎭⎪⎫-72,-2∪⎝⎛⎦⎥⎤23,74.故选D.。
高考一轮复习第2章函数导数及其应用第9讲函数与方程

第九讲函数与方程知识梳理·双基自测ZHI SHI SHU LI SHUANG JI ZI CE知识梳理知识点一函数的零点1.函数零点的定义对于函数y=f(x)(x∈D),把使f(x)=0成立的实数x叫做函数y=f(x)(x∈D)的零点.注:函数的零点不是点.是函数f(x)与x轴交点的横坐标,而不是y=f(x)与x轴的交点.2.几个等价关系方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.3.函数零点的判定(零点存在性定理)如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)f(b)<0,那么函数y =f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.知识点二二分法1.对于在区间[a,b]上连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:(1)确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;(2)求区间(a,b)的中点c;(3)计算f(c);①若f(c)=0,则c就是函数的零点;②若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));③若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b)).(4)判断是否达到精确度ε,即:若|a-b|<ε,则得到零点近似值a(或b);否则重复(2)(3)(4).重要结论1.有关函数零点的结论(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.(3)连续不断的函数图象通过零点时,函数值可能变号,也可能不变号.(4)由函数y=f(x)在闭区间[a,b]上有零点不一定能推出f(a)·f(b)<0,如图所示.所以f(a)·f(b)<0是y=f(x)在闭区间[a,b]上有零点的充分不必要条件.事实上,只有当函数图象通过零点(不是偶个零点)时,函数值才变号,即相邻两个零点之间的函数值同号.(5)若函数f(x)在[a,b]上单调,且f(x)的图象是连续不断的一条曲线,则f(a)·f(b)<0⇒函数f(x)在[a,b]上只有一个零点.2.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ>0 Δ=0 Δ<0 二次函数y=ax2+bx+c(a>0)的图象与x轴的交点(x1,0),(x2,0) (x1,0) 无交点零点个数两个零点一个零点无零点双基自测题组一走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)函数的零点就是函数的图象与x轴的交点.( ×)(2)二次函数y=ax2+bx+c(a≠0)在当b2-4ac<0时没有零点.( √)(3)函数y=f(x)在区间(a,b)内有零点(函数图象连续不断),则f(a)·f(b)<0.(×)(4)若f(x)在区间[a,b]上连续不断,且f(a)·f(b)>0,则f(x)在(a,b)内没有零点.( ×)(5)函数y=2x与y=x2只有两个交点.( ×)[解析](1)函数的零点是函数图象与x轴交点的横坐标.(2)当b2-4ac<0时,抛物线与x轴无交点,故没有零点.(3)函数图象若没有穿过x轴,则f(a)·f(b)>0.(4)若在区间[a,b]内有多个零点,f(a)·f(b)>0也可以.(5)y=x2与y=2x在y轴左侧一个交点,y轴右侧两个交点,如在x=2和x=4处都有交点.题组二走进教材2.(必修1P92AT2改编)已知函数f(x)的图象是连续不断的,且有如下对应值表:x 1 2 3 4 5f(x) -4 -2 1 4 7在下列区间中,函数f(x)A.(1,2) B.(2,3)C.(3,4) D.(4,5)[解析]由所给的函数值的表格可以看出,x=2与x=3这两个数字对应的函数值的符号不同,即f(2)·f(3)<0,所以函数在(2,3)内有零点,故选B.3.(必修1P92AT1改编)下列函数图象与x轴均有公共点,其中能用二分法求零点的是( C )[解析]A,B图中零点两侧不异号,D图不连续.故选C.4.(必修1P92AT4改编)为了求函数f(x)=2x+3x-7的一个零点,某同学利用计算器得到自变量x和函数f(x)的部分对应值(精确度0.1)如下表所示:x 1.25 1.312 5 1.375 1.437 5 1.5 1.562 5f(x) -0.871 6 -0.578 8 -0.281 3 0.210 1 0.328 43 0.641 15则方程2x+3x=7的近似解(精确到0.1)可取为( C )A.1.32 B.1.39C.1.4 D.1.3[解析]通过上述表格得知函数唯一的零点x0在区间(1.375,1.437 5)内,故选C.题组三走向高考5.(2015·安徽,5分)下列函数中,既是偶函数又存在零点的是( A )A.y=cos x B.y=sin xC.y=ln x D.y=x2+1[解析]y=cos x是偶函数且有无数多个零点,y=sin x为奇函数,y=ln x既不是奇函数也不是偶函数,y=x2+1是偶函数但没有零点,故选A.6.(2019·全国卷Ⅲ,5分)函数f(x)=2sin x-sin 2x在[0,2π]的零点个数为( B )A.2 B.3C.4 D.5[解析]f(x)=2sin x-2sin xcos x=2sin x(1-cos x),令f(x)=0,则sin x=0或cos x=1,所以x=kπ(k∈Z),又x∈[0,2π],所以x=0或x=π或x=2π.故选B.考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU考点一,函数的零点考向1 确定函数零点所在区间——自主练透例1 (1)若函数f(x)的图象是连续不断的,且f(0)>0,f(1)·f(2)·f(4)<0,则下列命题正确的是( D )A.函数f(x)在区间(0,1)内有零点B.函数f(x)在区间(1,2)内有零点C.函数f(x)在区间(0,2)内有零点D.函数f(x)在区间(0,4)内有零点(2)(2021·开封模拟)函数f(x)=x+ln x-3的零点所在的区间为( C )A.(0,1) B.(1,2)C.(2,3) D.(3,4)(3)(多选题)若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)·(x-c)+(x-c)(x-a)的零点位于区间可能为( BC )A.(-∞,a) B.(a,b)C.(b,c) D.(c,+∞)[解析](1)因为f(1)·f(2)·f(4)<0,所以f(1)、f(2)、f(4)中至少有一个小于0.若f(1)<0,则在(0,1)内有零点,在(0,4)内必有零点;若f(2)<0,则在(0,2)内有零点,在(0,4)内必有零点;若f(4)<0,则在(0,4)内有零点.故选D.(2)解法一:利用零点存在性定理因为函数f(x)是增函数,且f(2)=ln 2-1<0,f(3)=ln 3>0,所以由零点存在性定理得函数f(x)的零点位于区间(2,3)内,故选C.解法二:数形结合函数f(x)=x+ln x-3的零点所在区间转化为g(x)=ln x,h(x)=-x+3的图象的交点横坐标所在范围.如图所示,可知f(x)的零点在(2,3)内.(3)易知f(a)=(a-b)(a-c),f(b)=(b-c)·(b-a),f(c)=(c-a)(c-b).又a<b<c,则f(a)>0,f(b)<0,f(c)>0,又该函数是二次函数,且图象开口向上,可知两个零点分别位于区间(a,b)和(b,c)内,故选B、C.名师点拨MING SHI DIAN BO确定函数零点所在区间的方法(1)解方程法:当对应方程f(x)=0易解时,可先解方程,然后再看求得的根是否落在给定区间上.(2)利用函数零点的存在性定理:首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.(3)数形结合法:通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断. 考向2 函数零点个数的确定——师生共研例2 (1)函数f(x)=⎩⎪⎨⎪⎧x 2+x -2,x≤0,-1+ln x ,x>0的零点个数为( B )A .3B .2C .7D .0(2)已知f(x)=⎩⎪⎨⎪⎧|lg x|,x>0,2|x|,x≤0,则函数y =2f 2(x)-3f(x)+1的零点个数为5.[解析] (1)解法一:(直接法)由f(x)=0得⎩⎪⎨⎪⎧x ≤0,x 2+x -2=0或⎩⎪⎨⎪⎧x>0,-1+ln x =0,解得x =-2或x =e. 因此函数f(x)共有2个零点.解法二:(图象法)函数f(x)的图象如图所示,由图象知函数f(x)共有2个零点. (2)令2f 2(x)-3f(x)+1=0,解得f(x)=1或f(x)=12,作出f(x)的简图:由图象可得当f(x)=1或f(x)=12时,分别有3个和2个交点,则关于x 的函数y =2f 2(x)-3f(x)+1的零点的个数为5.名师点拨 MING SHI DIAN BO函数零点个数的判定有下列几种方法(1)直接求零点:令f(x)=0,如果能求出解,那么有几个解就有几个零点.(2)零点存在性定理:利用该定理不仅要求函数在[a ,b]上是连续的曲线,且f(a)·f(b)<0,还必须结合函数的图象和性质(如单调性)才能确定函数有多少个零点.(3)数形结合法:利用函数y =f(x)的图象与x 轴的交点的个数,从而判定零点的个数,或转化为两个函数图象交点个数问题.画两个函数图象,看其交点的个数有几个,其中交点的横坐标有几个不同的值,就有几个不同的零点.〔变式训练1〕(1)已知函数f(x)=⎩⎪⎨⎪⎧x 2-2x ,x≤0,1+1x ,x>0,则函数y =f(x)+3x 的零点个数是( C )A .0B .1C .2D .3(2)设函数f(x)是定义在R 上的奇函数,当x>0时,f(x)=e x+x -3,则f(x)的零点个数为( C ) A .1 B .2 C .3D .4(3)(2020·河南名校联考)函数f(x)=⎩⎪⎨⎪⎧|log 2x|,x>0,2x ,x≤0,则函数g(x)=3[f(x)]2-8f(x)+4的零点个数是( A )A .5B .4C .3D .6[解析] (1)由已知得y =f(x)+3x =⎩⎪⎨⎪⎧x 2+x ,x≤0,1+1x+3x ,x>0.令x 2+x =0,解得x =0或x =-1.令1+1x +3x =0(x>0)可得3x 2+x +1=0.因为Δ=1-12<0,所以方程3x 2+x +1=0无实根.所以y =f(x)+3x 的零点个数是2.(2)f(x)=e x+x -3在(0,+∞)上为增函数,f ⎝ ⎛⎭⎪⎫12=e 12-52<0,f(1)=e -2>0,∴f(x)在(0,+∞)上只有一个零点,由奇函数性质得f(x)在(-∞,0)上也有一个零点,又f(0)=0,所以f(x)有三个零点,故选C .(3)本题考查函数的零点与方程根的个数的关系.函数g(x)=3[f(x)]2-8f(x)+4=[3f(x)-2][f(x)-2]的零点,即方程f(x)=23和f(x)=2的根.函数f(x)=⎩⎪⎨⎪⎧|log 2x|,x>0,2x ,x≤0的图象如图所示,由图可得方程f(x)=23和f(x)=2共有5个根,即函数g(x)=3[f(x)]2-8f(x)+4有5个零点. 考向3 函数零点的应用——多维探究 角度1 与零点有关的比较大小例3 已知函数f(x)=2x+x ,g(x)=x -log 12x ,h(x)=log 2x -x 的零点分别为x 1,x 2,x 3,则x 1,x 2,x 3的大小关系为( D )A .x 1>x 2>x 3B .x 2>x 1>x 3C .x 1>x 3>x 2D .x 3>x 2>x 1[解析] 由f(x)=2x+x =0,g(x)=x -log 12x =0,h(x)=log 2x -x =0,得2x=-x ,x =log 12x ,log 2x=x ,在平面直角坐标系中分别作出y =2x与y =-x 的图象;y =x 与y =log 12x 的图象;y =log 2x 与y =x 的图象,由图可知:-1<x 1<0,0<x 2<1,x 3>1.所以x 3>x 2>x 1.角度2 已知函数的零点或方程的根求参数例4 (2018·全国Ⅰ)已知函数f(x)=⎩⎪⎨⎪⎧e x,x≤0,ln x ,x>0,g(x)=f(x)+x +a.若g(x)存在2个零点,则a 的取值范围是( C ) A .[-1,0) B .[0,+∞) C .[-1,+∞) D .[1,+∞)[解析]令h(x)=-x -a ,则g(x)=f(x)-h(x).在同一坐标系中画出y =f(x),y =h(x)图象的示意图,如图所示.若g(x)存在2个零点,则y =f(x)的图象与y =h(x)的图象有2个交点.由图知-a≤1,∴a≥-1.名师点拨 MING SHI DIAN BO 1.比较零点大小常用方法:(1)确定零点取值范围,进而比较大小; (2)数形结合法.2.已知函数有零点(方程有根)求参数值常用的方法和思路:(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后观察求解. 〔变式训练2〕(1)(角度1)(2021·安徽蚌埠月考)已知函数f(x)=3x+x ,g(x)=log 3x +x ,h(x)=x 3+x 的零点依次为a ,b ,c ,则a ,b ,c 的大小关系为( B )A .a<b<cB .a<c<bC .a>b>cD .c>a>b(2)(角度2)(2021·杭州学军中学月考)已知函数f(x)=⎩⎪⎨⎪⎧2x-a ,x≤0,2x -1,x>0(a∈R),若函数f(x)在R 上有两个零点,则a 的取值范围是( D )A .(-∞,-1)B .(-∞,-1]C .[-1,0)D .(0,1][分析] (1)解法一:依据零点存在定理,确定a ,b ,c 所在区间,进而比较大小;解法二:分别作出y =3x、y =log 3x 、y =x 3与y =-x 的图象,比较其交点横坐标的大小即可.[解析](1)解法一:∵f(-1)=3-1-1=-23,f(0)=1,∴a∈⎝ ⎛⎭⎪⎫-23,0,又g ⎝ ⎛⎭⎪⎫13=log 313+13=-23,g(1)=1,∴b∈⎝ ⎛⎭⎪⎫13,1,显然c =0,∴a<c<b,故选B .解法二:数形结合法,在同一坐标系中分别作出y =3x、y =log 3x 、y =-x 的图象,结合图象及c =0可知a<c<b ,故选B .解法三:由概念知b>0,a<0,c<0,∴b 最大,选B .(2)∵当x>0时,f(x)=2x -1, 由f(x)=0得x =12,∴要使f(x)在R 上有两个零点, 则必须2x-a =0在(-∞,0]上有解. 又当x ∈(-∞,0]时,2x∈(0,1]. 故所求a 的取值范围是(0,1].考点二 二分法及其应用——自主练透例5 (1)用二分法研究函数f(x)=x 3+3x -1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x 0∈(0,0.5),第二次应计算f(0.25).(2)在用二分法求方程x 3-2x -1=0的一个近似解时,现在已经将根锁定在区间(1,2)内,则下一步可判定该根所在的区间为⎝ ⎛⎭⎪⎫32,2. (3)在用二分法求方程x 2=2的正实数根的近似解(精确度0.001)时,若我们选取初始区间是[1.4,1.5],则要达到精确度要求至少需要计算的次数是7.[解析] (1)因为f(0)<0,f(0.5)>0,由二分法原理得一个零点x 0∈(0,0.5);第二次应计算f ⎝ ⎛⎭⎪⎫0+0.52=f(0.25).(2)区间(1,2)的中点x 0=32,令f(x)=x 3-2x -1,f ⎝ ⎛⎭⎪⎫32=278-4<0,f(2)=8-4-1>0,则根所在区间为⎝ ⎛⎭⎪⎫32,2. (3)设至少需要计算n 次,由题意知1.5-1.42n<0.001,即2n >100.由26=64,27=128,知n =7. 名师点拨 MING SHI DIAN BO1.用二分法求函数零点的方法:定区间,找中点,中值计算两边看,同号去,异号算,零点落在异号间.周而复始怎么办?精确度上来判断.2.利用二分法求近似解需注意的问题(1)在第一步中:①区间长度尽量小;②f(a),f(b)的值比较容易计算且f(a)·f(b)<0; (2)根据函数的零点与相应方程根的关系,求函数的零点与相应方程的根是等价的.(3)虽然二分法未单独考过,但有可能像算法中的“更相减损术”一样,嵌入到程序框图中去考查.名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG函数零点的综合问题例6 (2021·山西五校联考)已知函数f(x)=⎩⎪⎨⎪⎧-2x ,x≤0-x 2+x ,x>0,若函数g(x)=f(x)-a 恰有三个互不相同的零点x 1,x 2,x 3,则x 1x 2x 3的取值范围是( A )A .⎝ ⎛⎭⎪⎫-132,0B .⎝ ⎛⎭⎪⎫-116,0 C .⎝ ⎛⎭⎪⎫0,132 D .⎝ ⎛⎭⎪⎫0,116 [解析] 解法一:显然x≤0时,-2x =a ,有一根不妨记为x 1,则x 1=-a 2(a≥0),当x>0时-x 2+x=a 即x 2-x +a =0有两个不等正根,不妨记为x 2,x 3,则Δ=1-4a>0,即a<14,从而-a 2∈⎝ ⎛⎭⎪⎫-116,0且x 2x 3=a.∴x 1x 2x 3=-a 22∈⎝ ⎛⎭⎪⎫-132,0,故选A .解法二:作出y =f(x)及y =a 的图象,显然0<a<14,不妨设x 1<x 2<x 3显然x 1<0,x 2>0,x 3>0,∴x 1x 2x 3<0排除C 、D ,又当x 2趋近x 3时,x 2x 3趋近14,x 1趋近-18,故x 1x 2x 3趋近-132.故选A .名师点拨 MING SHI DIAN BO以函数图象、图象的变换方法及函数的零点等相关知识为基础,通过作图、想象,发现该问题的相关数学知识及其联系,快速解决该问题.〔变式训练3〕(2021·东北三省四市模拟)已知函数f(x)=⎩⎪⎨⎪⎧x 2+2x +1,x≤0,|lg x|,x>0.若f(x)=a(a∈R)有四个不等实根,则所有实根之积的取值范围是( B )A .(-∞,1)B .[0,1)C .(0,1)D .(1,+∞)[解析] 本题考查已知方程根的个数求根的乘积的取值范围. 设四个根依次为x 1,x 2,x 3,x 4(x 1<x 2<x 3<x 4), 则-2≤x 1<-1,-1<x 2≤0,x 1+x 2=-2, 由|lg x 3|=|lg x 4|,得-lg x3=lg x4,则lg x3+lg x4=lg(x3x4)=0,∴x3x4=1,∴x1x2x3x4=x1x2=(-2-x2)x2=-(x2+1)2+1∈[0,1).故选B.。
第07讲函数与方程(课件)-2024年高考数学一轮复习(新教材新高考)

【答案】 −∞, −1
2
当 < 0时,令′ = 0,解得 = 0或 = − ,
【解析】因为 = 3 + 3 2 − 4,所以′ = 3 2 + 6 = 3 + 2
当 = 0时,有 = 3 2 − 4 = 0,解得 = ± 2 3,
公共点.
N
Q
Z
R
N
(3)函数零点存在定理
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有
f(a)f(b)<0
(a,b) 内至少有一个零点,即存
__________,那么,函数y=f(x)在区间
在c∈(a,b),使得 f(c)=0 ,这个c也就是方程f(x)=0的解.
2.二分法
2
−∞, −
=
2
2
2
−∞, −
2
当 ∈ 0, − ,′ > 0, 在区间 0, − 上单调递增;
当 > 0时,由′ = 0,解得 = 0或 = − ,
2
且有 0 = −4, −
> 0,
, 存在一个正数零点,所以不符合题意;
2 3
,0
3
2
2 3
3
2024
高考一轮复习
第07讲 函数与方程
导师:稻壳儿
目录
C
O
N
T
E
01
考情分析
N
T
S
02
03
04
网络构建
知识梳理
题型归纳
真题感悟
01
考情分析
考点要求
考题统计
考情分析
《课堂新坐标》高考数学一轮总复习课件:第二章 第八节 函数与方程(共33张PPT)

2+4 确度 ε=0.01,取区间(2,4)的中点 x1= 2 =3,计算
得 f(2)·f(x1)<0,则此时零点 x0 所在的区间为( )
A.(2,4)
B.(3,4)
探究·提知能
C.(2,3)
D.(2.5,3)
课后作
【解析】 由零点存在性定理知x0∈(2,3),故选C.
【答案】 C
菜单
新课标 ·文科数学(广东专用)
菜单
新课标 ·文科数学(广东专用)
Δ=b2-4ac
落实·固基础
Δ>0
二次函数 y=ax2+bx+c
(a>0)的图象
Δ=0
Δ<0
高考体验·明
探究·提知能与x轴的交点 零点个数
_(_x_1,___0_),___(x_2_,__0__) __(_x_1,___0_)_
2
1
无交点 课后作 0
菜单
新课标 ·文科数学(广东专用)
菜单
新课标 ·文科数学(广东专用)
落实·固基础
1.解答本题一要从图表中寻找数量信息,二要注 高考体验·明 意“精确度”的含义,切不可与“精确到”混淆.
2.(1)用二分法求函数零点的近似解必须满足①y
=f(x)的图象在[a,b]内连续不间断,②f(a)·f(b)<0.(2)
在第一步中,尽量使区间长度缩短,以减少计算量及计
落实·固基础
新课标 ·文科数学(广东专用)
第八节 函数与方程
高考体验·明
探究·提知能 菜单
课后作
新课标 ·文科数学(广东专用)
落实·固基础 1.函数零点
高考体验·明
(1)定义:对于函数y=f(x)(x∈D),把使____f_(x_)_=_0___成
高考数学一轮总复习课件:函数y=Asin(ωx+φ)

sin
π
x+
4
图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到y=
sin12x+π4 的图象;再将图象上各点的纵坐标都伸长到原来的2倍(横坐标
不变),得到y=2sin12x+π4 的图象,即y=2cos-12x+π4 的图象.
【答案】 见解析
(2)如何由y=13sin2x+π3 的图象得y=sinx的图象.
例1
用五点法作出y=2sin
2x+π3
在[-
π 3
,
2π 3
]内的图
象.
【解析】 2·-π3 +π3 =-π3 ,2·2π 3 +π3 =5π 3 ,
令2x+π3 =0,解得x=-π6 .
ππ
π
2x+ 3 = 2 ,解得x=12.
π
π
2x+ 3 =π,解得x= 3 .
2x+π3 =3π 2 ,解得x=71π2 .
(2)变换作图.
相位
周期
振幅
①y=sinx―变―换→y=sin(x+φ)―变―换→y=sin(ωx+φ)―变―换→y=
Asin(ωx+φ)
周期
相位
振幅
②y=sinx―变―换→y=sinωx―变―换→y=sin(ωx+φ)―变―换→
y=Asin(ωx+φ)
【说明】 前一种方法第一步相位变换是_向_左__(φ_>_0_)_或_向__右_(_φ_<_0_)
π
π
则ω= 3 -2kπ(k∈Z),结合0<ω<2,得ω= 3 ,
所以f(x)=sinπ3 x+π6 =cosπ2 -π3 x-π6
=cosπ3 (x-1),
所以只需将函数g(x)=cos
π 3
