DSP答案第七章第五章
DSP简答题答案.WOC

复习大纲第一章绪论教学内容:DSP芯片的特点;DSP芯片的发展;DSP芯片的应用。
基本要求:掌握:DSP芯片的特点;了解:DSP芯片的发展;DSP芯片的应用。
第二章TMS320C54X的硬件结构教学内容:总线结构;中央处理器;中央存储器;复位电路。
基本要求:掌握:各类存储器的特点;理解:中央处理器中各部件的主要功能;了解:了解各总线的用途和复位电路。
第三章TMS320C54X的指令系统教学内容:寻址方式;指令系统;流水线。
基本要求:掌握:各寻址方式的特点;理解:指令系统中各指令的意义;不同指令的流水线特点。
第四章TMS320C54X应用系统开发过程教学内容:汇编,链接,COFF文件格式。
基本要求:掌握:常用汇编伪指令的使用、汇编器的使用;链接伪指令的使用、链接器的使用;理解:COFF文件格式。
第五章汇编语言程序设计教学内容:程序的控制与转移;堆栈的使用;加减法和乘法运算;重复操作;数据块传送;双操作数乘法;长字运算和并行运算;小数运算;除法运算;浮点运算。
第一章DSP技术概述1. DSP应用系统模型包括哪些主要部分?答:典型的DSP系统为:2. DSP系统有何特点?答:(1)精度高(2)可靠性强(3)集成度高(4)接口方便(5)灵活性好(6)保密性好(7)时分复用3. 试列举DSP芯片的特点。
答:(1)哈佛结构(2)多总线结构和多处理单元(3)流水线技术(4)特殊的DSP指令(5)指令周期短(6)运算精度高(7)硬件配置强(8)耗电省第二章DSP芯片结构介绍1. TMS320C54x芯片存储器采用什么结构?有何特点?答:1)采用改善的哈佛结构和存储器分区特点:改善的哈佛结构特点是:将程序和数据存储在不同的存储空间(即程序存储器和数据存储器是两个相互独立的存储器)存储器分区特点是:存储器分为3个可单独选择的空间后,在任何一个存储空间,RAM、ROM、EPROM、EEPROM或存储器影响外围设备,都可以驻留在片内或片外2. TMS320C54x芯片的总线有哪些?它们各自的作用和区别是什么?答:在TMS320C54x内部有P、C、D、E四种16位总线:(1)程序总线(PB)C54x用1条程序总线传送取自程序存储器的指令代码和立即操作数。
DSP原理及应用-(修订版)--课后习题答案

第一章:1、数字信号处理的实现方法一般有哪几种?答:数字信号处理的实现是用硬件软件或软硬结合的方法来实现各种算法。
(1) 在通用的计算机上用软件实现;(2) 在通用计算机系统中加上专用的加速处理机实现;(3) 用通用的单片机实现,这种方法可用于一些不太复杂的数字信号处理,如数字控制;(4)用通用的可编程 DSP 芯片实现。
与单片机相比,DSP 芯片具有更加适合于数字信号处理的软件和硬件资源,可用于复杂的数字信号处理算法;(5) 用专用的 DSP 芯片实现。
在一些特殊的场合,要求的信号处理速度极高,用通用 DSP 芯片很难实现( 6)用基于通用 dsp 核的asic 芯片实现。
2、简单的叙述一下 dsp 芯片的发展概况?答:第一阶段, DSP 的雏形阶段( 1980 年前后)。
代表产品: S2811。
主要用途:军事或航空航天部门。
第二阶段, DSP 的成熟阶段( 1990 年前后)。
代表产品: TI 公司的 TMS320C20主要用途:通信、计算机领域。
第三阶段, DSP 的完善阶段( 2000 年以后)。
代表产品:TI 公司的 TMS320C54 主要用途:各个行业领域。
3、可编程 dsp 芯片有哪些特点?答: 1、采用哈佛结构( 1)冯。
诺依曼结构,( 2)哈佛结构( 3)改进型哈佛结构2、采用多总线结构 3.采用流水线技术4、配有专用的硬件乘法-累加器5、具有特殊的 dsp 指令6、快速的指令周期7、硬件配置强8、支持多处理器结构9、省电管理和低功耗4、什么是哈佛结构和冯。
诺依曼结构?它们有什么区别?答:哈佛结构:该结构采用双存储空间,程序存储器和数据存储器分开,有各自独立的程序总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,使取指令操作、指令执行操作、数据吞吐并行完成,大大地提高了数据处理能力和指令的执行速度,非常适合于实时的数字信号处理。
冯。
诺依曼结构:该结构采用单存储空间,即程序指令和数据共用一个存储空间,使用单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行。
DSP(知识点+思考题)

DSP复习要点第一章绪论1、数的定标:Qn表示。
例如:16进制数2000H=8192,用Q0表示16进制数2000H=0.25,用Q15表示2、‟C54x小数的表示方法:采用2的补码小数;.word 32768 *707/10003、定点算术运算:乘法:解决冗余符号位的办法是在程序中设定状态寄存器STl中的FRCT位为1,让相乘的结果自动左移1位。
第二章CPU结构和存储器设置一、思考题:1、C54x DSP的总线结构有哪些特点?答:TMS320C54x的结构是围绕8组16bit总线建立的。
(1)、一组程序总线(PB):传送从程序存储器的指令代码和立即数。
(2)、三组数据总线(CB,DB和EB):连接各种元器件,(3)、四组地址总线(PAB,CAB,DAB和EAB)传送执行指令所需要的地址。
2、C54x DSP的CPU包括哪些单元?答:'C54X 芯片的CPU包括:(1)、40bit的算术逻辑单元(2)、累加器A和B(3)、桶形移位寄存器(4)、乘法器/加法器单元(5)、比较选择和存储单元(6)、指数编码器(7)、CPU状态和控制寄存器(8)、寻址单元。
1)、累加器A和B分为三部分:保护位、高位字、地位字。
保护位保存多余高位,防止溢出。
2)、桶形移位寄存器:将输入数据进行0~31bits的左移(正值)和0~15bits的右移(负值)3)、乘法器/加法器单元:能够在一个周期内完成一次17*17bit的乘法和一次40位的加法4)、比较选择和存储单元:用维比特算法设计的进行加法/比较/选择运算。
5)、CPU状态和控制寄存器:状态寄存器ST0和ST1,由置位指令SSBX和复位指令RSBX控制、处理器模式状态寄存器PMST2-3、简述’C54x DSP的ST1,ST0,PMST的主要功能。
答:’C54x DSP的ST1,ST0,PMST的主要功能是用于设置和查看CPU的工作状态。
•ST0主要反映处理器的寻址要求和计算机的运行状态。
DSP应用技术教程部分习题答案

《TMS320C54x DSP应用技术教程》部分习题答案注意:未提供的参考答案习题(因考试为开卷形式,部分在课堂讲过,部分需要自行思考归纳总结或编程),请参考PPT和书上示例,自行解答。
第1章绪论1.简述Digital Signal Processing 和Digital Signal Processor 之间的区别与联系。
答:前者指数字信号处理的理论和方法,后者则指用于数字信号处理的可编程微处理器,简称数字信号处理器。
数字信号处理器不仅具有可编程性,而且其数字运算的速度远远超过通用微处理器,是一种适合于数字信号处理的高性能微处理器。
数字信号处理器已成为数字信号处理技术和实际应用之间的桥梁,并进一步促进了数字信号处理技术的发展,也极大地拓展了数字信号处理技术的应用领域。
2.什么是DSP技术?答:DSP技术是指使用通用DSP处理器或基于DSP核的专用器件,来实现数字信号处理的方法和技术,完成有关的任务。
5.数字信号处理的实现方法有哪些?答:参见P3-4 1.1.3节。
6.DSP的结构特点有哪些?答:哈佛结构和改进的哈佛结构、多总线结构、流水线技术、多处理单元、特殊的DSP指令、指令周期短、运算精度高、硬件配置强。
7.什么是哈佛结构和冯洛伊曼结构?它们有什么区别?答:参见P5-6 1.2.2节。
8.什么是哈佛结构和冯.诺依曼结构?它们有什么区别?答:DSP处理器将程序代码和数据的存储空间分开,各空间有自己独立的地址总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,这就是哈佛结构。
以奔腾为代表的通用微处理器,其程序代码和数据共用一个公共的存储空间和单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行的,这样的结构称为冯·诺伊曼结构。
采用哈佛结构,可同时取指令和取操作数,并行地进行指令和数据的处理,从而可以大大地提高运算的速度,非常适合于实时的数字信号处理。
而冯·诺伊曼结构当进行高速运算时,取指令和取操作数是分时操作的,这样很容易造成数据传输通道的瓶颈现象,其工作速度较慢。
DSP应用技术教程 部分习题答案

《TMS320C54x DSP应用技术教程》部分习题答案注意:未提供的参考答案习题(因考试为开卷形式,部分在课堂讲过,部分需要自行思考归纳总结或编程),请参考PPT和书上示例,自行解答。
第1章绪论1.简述Digital Signal Processing 和Digital Signal Processor 之间的区别与联系。
答:前者指数字信号处理的理论和方法,后者则指用于数字信号处理的可编程微处理器,简称数字信号处理器。
数字信号处理器不仅具有可编程性,而且其数字运算的速度远远超过通用微处理器,是一种适合于数字信号处理的高性能微处理器。
数字信号处理器已成为数字信号处理技术和实际应用之间的桥梁,并进一步促进了数字信号处理技术的发展,也极大地拓展了数字信号处理技术的应用领域。
2.什么是DSP技术?答:DSP技术是指使用通用DSP处理器或基于DSP核的专用器件,来实现数字信号处理的方法和技术,完成有关的任务。
5.数字信号处理的实现方法有哪些?答:参见P3-4 1.1.3节。
6.DSP的结构特点有哪些?答:哈佛结构和改进的哈佛结构、多总线结构、流水线技术、多处理单元、特殊的DSP指令、指令周期短、运算精度高、硬件配置强。
7.什么是哈佛结构和冯洛伊曼结构?它们有什么区别?答:参见P5-6 1.2.2节。
8.什么是哈佛结构和冯.诺依曼结构?它们有什么区别?答:DSP处理器将程序代码和数据的存储空间分开,各空间有自己独立的地址总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,这就是哈佛结构。
以奔腾为代表的通用微处理器,其程序代码和数据共用一个公共的存储空间和单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行的,这样的结构称为冯·诺伊曼结构。
采用哈佛结构,可同时取指令和取操作数,并行地进行指令和数据的处理,从而可以大大地提高运算的速度,非常适合于实时的数字信号处理。
而冯·诺伊曼结构当进行高速运算时,取指令和取操作数是分时操作的,这样很容易造成数据传输通道的瓶颈现象,其工作速度较慢。
DSP在无线通信系统中的应用

1.3 应用领域
数字峰窝通信系统、个人通信系统、 个人数据处理、数字无绳电话通信、无 线数据通信、无线局域网络、无线识别 器、计算机电话、语音打包传输、便携 Internet音响、Mode、2G/3G手机、 数字照相机、IP电话等等
1.4 为什么用DSP 为什么用DSP
考虑一个数字信号处理的实例,比如有限 冲击响应滤波器(FIR)。用数学语言来说, FIR滤波器是做一系列的点积。取一个输入量 和一个序数向量,在系数和输入样本的滑动窗 口间作乘法,然后将所有的乘积加起来,形成 一个输出样本。 类似的运算在数字信号处理过程中大量地 重复发生,使得为此设计的器件必须提供专门 的支持,促成了了DSP器件与通用处理器(GPP) 的分流:
软件无线电包括的核心技术主要有:
带通采样(欠采样) 数字上下变频 调制解调 多速率信号处理 高效数字滤波等
3.2 软件无线电结构 射频全宽开低通采样软件无 线电结构 射频直接带通采样软件无线 电结构 宽带中频带通采样软件无线 电结构
3.2.1 Nyquist 采样定理
设有一个频率带限信号x(t),其频带限制 在(0,fh)内,如果以不小于fs=2fh的采 样速率对x(t)进行等间隔采样,得到时间 离散的采样信号x(n)=x(nTs)(其中Ts=1/fs 称为采样间隔),原信号x(t)将被所得到 的采样值x(n)完全确定。
7.5 ’C54X的结构特点5 ’C54X的结构特点 的结构特点5
连接内部振荡器或外部时钟源的锁相环( 连接内部振荡器或外部时钟源的锁相环(PLL) ) 发生器 支持8-或 支持 或16-bit传送的全双工串口 传送的全双工串口 时分多路( 时分多路(TDM)串口 ) 缓冲串口( 缓冲串口(BSP) ) McBSPs串口 串口 8/16-bit并行主机接口(HPI) 并行主机接口( 并行主机接口 ) 一个16-bit定时器 一个 定时器
DSP原理及应用(修订版)邹彦课后习题答案

DSP原理及应用(修订版)邹彦课后习题答案第一章:1、数字信号处理的实现方法一般有哪几种?答:数字信号处理的实现是用硬件软件或软硬结合的方法来实现各种算法。
(1) 在通用的计算机上用软件实现;(2) 在通用计算机系统中加上专用的加速处理机实现;(3) 用通用的单片机实现,这种方法可用于一些不太复杂的数字信号处理,如数字控制;(4)用通用的可编程DSP 芯片实现。
与单片机相比,DSP 芯片具有更加适合于数字信号处理的软件和硬件资源,可用于复杂的数字信号处理算法;(5) 用专用的DSP 芯片实现。
在一些特殊的场合,要求的信号处理速度极高,用通用DSP 芯片很难实现(6)用基于通用dsp 核的asic 芯片实现。
2、简单的叙述一下dsp 芯片的发展概况?答:第一阶段,DSP 的雏形阶段(1980 年前后)。
代表产品:S2811。
主要用途:军事或航空航天部门。
第二阶段,DSP 的成熟阶段(1990 年前后)。
代表产品:TI 公司的TMS320C20主要用途:通信、计算机领域。
第三阶段,DSP 的完善阶段(2000 年以后)。
代表产品:TI 公司的TMS320C54 主要用途:各个行业领域。
3、可编程dsp 芯片有哪些特点?答:1、采用哈佛结构(1)冯。
诺依曼结构,(2)哈佛结构(3)改进型哈佛结构2、采用多总线结构3.采用流水线技术4、配有专用的硬件乘法-累加器5、具有特殊的dsp 指令6、快速的指令周期7、硬件配置强8、支持多处理器结构9、省电管理和低功耗4、什么是哈佛结构和冯。
诺依曼结构?它们有什么区别?答:哈佛结构:该结构采用双存储空间,程序存储器和数据存储器分开,有各自独立的程序总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,使取指令操作、指令执行操作、数据吞吐并行完成,大大地提高了数据处理能力和指令的执行速度,非常适合于实时的数字信号处理。
冯。
诺依曼结构:该结构采用单存储空间,即程序指令和数据共用一个存储空间,使用单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行。
DSP第五章课后答案
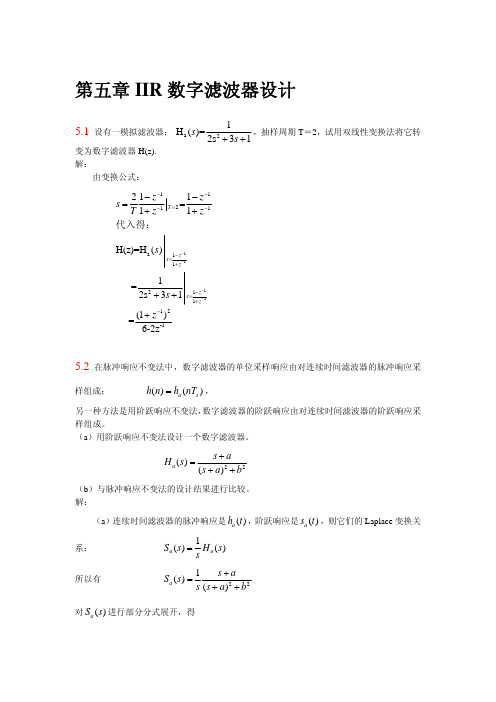
(b)用脉冲响应不变法, 所以
H ( z)
1 e ( a jb )Ts z 1 1 e ( a jb )Ts z 1 1 cos(bTs )e aTs z 1 1 2 cos(bTs )e aTs z 1 e 2 aTs z 2
1 2
butterworth 低通滤波器阶次 N:
lg 100.301 1 / 101.5 1 1.941 N 2 lg 2 / 4.828
所以选 N=2 滤波器的截止频率 c
2.000
10
0.301
1
1/ 4
2
再查表可求得模拟滤波器的系统函数为
所以有
对 S a ( s ) 进行部分分式展开,得
Sa ( s)
由
1 a a jb a jb 2 2 2 2 2 s a b 2(a b )( s a jb) 2(a b 2 )( s a jb)
1 1 得 Ts 1 1 e z s 1 a a jb 1 a jb 1 S ( z) ( a jb )Ts 1 ( a jb )Ts 1 1 2 2 2 2 2 2 1 z a b 2(a b ) 1 e z 2(a b ) 1 e z
Ap
H z
i 1
N
1 e siT z 1
5.6
试用双线性变换法(T=1)设计一低通数字滤波器,并满足技术指标如下:
(1)通带和阻带都是频率的单调下降函数,而且没有起伏 (2)频率在 0.5 处的衰减为-3.01db (3)频率在 0.75 处的衰减至少为 15db。 解: 根据题意,显然要先设计一个原型 butterworth 低通滤波器。 (1) 利用 T=1 对技术要求频率先进行反畸变: 因为 wp 0.5 , ws 0.75 所以 p
数字信号处理训练题

第一章习题一. 判断题1. 周期分别为N1,N2的两离散序列,在进行周期卷积后,其结果也是周期序列。
对2. FFT可用来计算IIR滤波器,以减少运算量。
错3. 相同的Z变换表达式一定对应相同的时间序列。
正确答案是: 错4. 频率采样法设计FIR滤波器,增加过渡带采样点可增加过渡带衰减。
正确答案是: 对二、选择题1. 采样率过低时,______。
A 量化误差增加 b. 必须增加信号频率c. 产生混叠2. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。
a. 频率响应b. 幅度c. 相位3. 滤波器的单位脉冲响应的DTFT给出了滤波器的_____。
a. 频率响应b. 幅度c. 相位4. ____序列的收敛域在Z平面上是一环状的。
a. 右边序列b. 双边序列c. 有限长序列5. 稳定系统的收敛域应当_______。
a. 包含单位圆b. 不包含单位圆c. 可以包含单位圆6. A/D 是_____的缩写a. asynchronous digitalb. analog to digitac. analog to discrete7. 连续信号的理想采样值是_____。
a. 连续的b. 离散的c. 时间上连续的8. 一个离散系统,a. 若因果必稳定b. 若稳定必因果c. 稳定与因果无关9. 下列哪一个不是信号的实例a. 语音b. 音乐c. 调制解调器10. 若输出不超前于输入,该系统称为______。
a. 线性b. 非线性c. 因果11. 抗混叠滤波器的目的是a. 去掉模拟信号混叠b. 等效一个高通滤波器c. 将高于采样率一半的频率分量去掉12. 抽样可以表述为______。
a. 将数字信号转化为模拟信号b. 将模拟信号转化为数字信号c. 获得模拟信号的幅度值13. 下面哪个表达式是将x(n)左移三位得到_______a. 3x(n)b. x(3n)c. x(n+3)14. 下面哪个表达式是将x(n)右移三位得到_______a. 3x(n)b. x(3+n)c. x(n-3)15. 关于线性系统的描述正确的是_____a. 遵从叠加原理b. 非时变c. 因果16. D/A变换的第一步是a. 零阶保持 b . 低通抗混叠滤波 c. 将数字代码转换为相应的模拟电平级三、计算题1. 和表示一个序列及其傅氏变换,并且为实因果序列,利用求下列各序列的傅氏变换:解:注意:当t为偶数时[ .] =2x(2n),当t为奇数时[ .] =0分析:以频率为400Hz的正弦信号为例,分别以2000Hz和1000Hz进行采样,序列长分别为2048点和1024点,对应的频谱如图1、图2所示。
数字信号处理智慧树知到答案章节测试2023年山东科技大学

绪论单元测试1.数字系统具有很多优点,比如精度高、抗干扰能力强、分辨率高、功能强等A:错B:对答案:B2.离散时域信号英文简称DTSA:错B:对答案:B3.DSP其中的P可代表processor,也可代表processingA:错B:对答案:B4.人口普查信号是:A:CTSB:DSC:DTSD:AS答案:C5.系统按照输入信号的类型可分为:A:CTSB:DTSC:ASD:DS答案:ABCD第一章测试1.离散时间信号可以用序列来表示。
A:对B:错答案:A2.N点的矩形序列可用单位阶跃信号u(n)表示为RN(n)=u(n)-u(n-N)。
A:错B:对答案:B3.线性时不变系统可用它的单位冲激响应来表征。
A:对B:错答案:A4.如果满足抽样定理,则抽样后不会产生频谱混叠,可以重建原信号。
A:对B:错答案:A5.只知道输入的情况下,是不能根据差分方程求解系统输出的。
A:错B:对答案:B6.线性卷积运算反映了LTI系统的输入输出关系,可用于求解LTI系统的输出。
A:对B:错答案:A7.从定义上看,线性卷积运算可分解为换元、反转、移位、乘加四个步骤。
A:错B:对答案:B8.某线性时不变系统当输入x[n]=δ[n]时输出y[n]=δ[n-2],当输入信号为为u[n]时,输出信号为:A:δ[n]B:u[n-2]C:δ[n-2]D:u[n]δ[n-2]答案:B9.要从抽样信号不失真恢复原连续信号,应满足下列条件的哪几条:Ⅰ.原信号为带限;Ⅱ.抽样频率大于两倍信号谱的最高频率;Ⅲ.抽样信号通过理想低通滤波器。
A:Ⅰ、ⅡB:Ⅰ、ⅢC:Ⅱ、ⅢD:Ⅰ、Ⅱ、Ⅲ答案:D10.单位阶跃序列u(n)的能量为:A:0B:1C:∞D:N答案:C第二章测试1.10点的矩形序列,其DTFT为X(e jw),则X(e j0)为:A:1B:2C:5D:10答案:D2.序列的频谱函数X(e^jw)是w的离散函数,且以2π为周期。
A:对B:错答案:B3.下面哪个序列的傅里叶变换周期是2Π:A:单位采样序列B:矩形序列C:收敛的指数序列D:单位阶跃序列答案:ABCD4.序列的频谱可分为实部谱和虚部谱。
(南京邮电大学)DSP习题答案汇总~~

(南京邮电⼤学)DSP习题答案汇总~~第⼀章习题1.1 在⼀间暗室⾥通过⼀个闪光频率为8Hz 的闪光灯观察⼀个以6Hz 为频率旋转的转轮。
求转轮表现出的转速并判断观察者对转轮旋转⽅向的判断正误。
若闪光灯频率变为12Hz ,16Hz 或24Hz ,重复上述问题。
本题涉及了转轮的问题,⽤到了公式)mod(s a f f f =,当a f 和f 符号相同时,观察者能观察到正确的转动⽅向;当a f 和f 符号相反时,观察者观察到的是错误的转动⽅向;否则,观察者不能辨别转轮的⽅向。
参考课本28页例题1.4.10。
1.2 对模拟信号x(t)=10sin(2πt)+10sin(8πt)+5sin(12πt) (其中t 以秒为单位)进⾏采样,采样频率s f =5Hz ,求x(t)的重建信号)(t x a 的表达式;证明两个信号具有相同的采样值,即)()(nT x nT x a =。
若采样率s f =10Hz ,重复上述问题。
本题通过证明说明了当a f1.3 以3Hz 的频率对信号x(t)=cos(5πt)+4sin(2πt)sin(3πt)进⾏抽样(其中t 以毫秒为单位)。
求(1)x(t)的重建信号)(t x a ;(2)写出重建信号是)(t x a ,但⼜不同于x(t)的另外两个信号x 1(t)和x 2(t)。
⽤到了公式)mod(s a f f f =,参见课本19页例1.4.7。
1.9 Consider the following sound wave, where t is in millisecond: x(t )=sin(10πt )+sin(20πt )+sin(60πt )+sin(90πt )This signal is prefiltered by an analog antialiasing prefilter H (f ) and then sampled at audio rate of 40kHz.The resulting samples are immediately reconstructed using an ideal reconstructor. Determine the output ya(t ) of the reconstructor in the following cases and compare it with the audible part of x(t ):a. When there is no prefilter ,that is, H(f )≡1.b. When H(f ) is an ideal prefilter with cutoff of 20kHz.c. When H(f ) is a practical prefilter that has a flat passband up to 20kHz and attenuates at arate of 48db?ocate beyond 20kHz.(You may ignore the effects of the phase response of the filter.)1.11 Give Eq.(1.5.4), prove the inverse DTFT property (1.5.5),that is,)(f X ∧=∞-∞=∑n x(nT)ejfTnπ-2 => x(nT)=-221fs fs sf )(f X ∧ejfTnπ2df1.12 Consider a pure sinusoid of frequency f 0 , x (t )=cos(2πf 0t ). Show that the spectrum of the sampled sinusoid x (n T) is : )(f X ∧=)]()([2100s s m mf f f mf f f T ++δ+--δ∑∞-∞=第⼆章习题2.1考虑⼀个3⽐特长的双极性⼆进制补码的逐次逼近A/D 转换器,其中满量程幅度为R =16V 。
DSP应用技术教程 部分习题答案(DOC)

《TMS320C54x DSP应用技术教程》部分习题答案注意:未提供的参考答案习题(因考试为开卷形式,部分在课堂讲过,部分需要自行思考归纳总结或编程),请参考PPT和书上示例,自行解答。
第1章绪论1.简述Digital Signal Processing 和Digital Signal Processor 之间的区别与联系。
答:前者指数字信号处理的理论和方法,后者则指用于数字信号处理的可编程微处理器,简称数字信号处理器。
数字信号处理器不仅具有可编程性,而且其数字运算的速度远远超过通用微处理器,是一种适合于数字信号处理的高性能微处理器。
数字信号处理器已成为数字信号处理技术和实际应用之间的桥梁,并进一步促进了数字信号处理技术的发展,也极大地拓展了数字信号处理技术的应用领域。
2.什么是DSP技术?答:DSP技术是指使用通用DSP处理器或基于DSP核的专用器件,来实现数字信号处理的方法和技术,完成有关的任务。
5.数字信号处理的实现方法有哪些?答:参见P3-4 1.1.3节。
6.DSP的结构特点有哪些?答:哈佛结构和改进的哈佛结构、多总线结构、流水线技术、多处理单元、特殊的DSP指令、指令周期短、运算精度高、硬件配置强。
7.什么是哈佛结构和冯洛伊曼结构?它们有什么区别?答:参见P5-6 1.2.2节。
8.什么是哈佛结构和冯.诺依曼结构?它们有什么区别?答:DSP处理器将程序代码和数据的存储空间分开,各空间有自己独立的地址总线和数据总线,可独立编址和独立访问,可对程序和数据进行独立传输,这就是哈佛结构。
以奔腾为代表的通用微处理器,其程序代码和数据共用一个公共的存储空间和单一的地址和数据总线,取指令和取操作数都是通过一条总线分时进行的,这样的结构称为冯·诺伊曼结构。
采用哈佛结构,可同时取指令和取操作数,并行地进行指令和数据的处理,从而可以大大地提高运算的速度,非常适合于实时的数字信号处理。
而冯·诺伊曼结构当进行高速运算时,取指令和取操作数是分时操作的,这样很容易造成数据传输通道的瓶颈现象,其工作速度较慢。
DSP课后习题答案

K_FIR_BFFR .set 80 K_FIR_INDEX .set 1 K_FRAME_SIZE .set 256 stack_len .set 100 stack .usect "STACK",stack_len FIR_DP .usect "fir_vars",0 d_filin .usect "fir_vars",1 d_filout .usect "fir_vars",1 fir_coff_table .usect "fir_coff",K_FIR_BFFR d_data_buffer .usect "fir_bfr",K_FIR_BFFR ; buffer size for the filter FIR_Dinbuf .usect "fir_dinbuf",K_FRAME_SIZE FIR_Doutbuf .usect "fir_doutbuf",K_FRAME_SIZE .asg AR0, FIR_INDEX_P .asg AR4,FIR_DATA_P .asg AR5,FIR_COFF_P .asg AR6,INBUF_P .asg AR7,OUTBUF_P .copy "FIRInput.inc" .copy "FIRCoef.inc" .text _c_int00: ssbx INTM ; INTM=1,禁止所有可屏蔽中断 ssbx FRCT ;-------------------------------------------------------------------stm #0, CLKMD ; 切换 CPU 内部 PLL 到分频模式 Clk_Status: ldm CLKMD, A and #01b, A bc Clk_Status, ANEQ ;检查是否已经切换到分频模式? stm #0x07ff,CLKMD ;设置 DSP 时钟 16.384MHZ ;-------------------------------------------------------------------nop stm #0x3FF2,PMST stm stm stm stm #0x7FFF,SWWSR #0xF800,BSCR #0x0000, IMR ; 禁止所有可屏蔽中断 #0xFFFF, IFR ; 清VDM 86H, AR4 运行以上程序后,(80H)、 (84H) 、*AR3 和 AR4 的值分别等于多少? 解:(80H)=50H,(84H)=50H,*AR3=50H,AR4=50H 2、已知,(80H)=20H、 (81H)=30H。 LD #0,DP LD 80H,16,B ADD 81H,B 运行以上程序,B 等于多少? 答: (B)=00 0000 0000H 3、阅读以下程序,分别写出运行结果。 .bss x,4 .data table:.word 4,8,16,32 …… STM #x,AR1 RPT #2 MVPD table,*AR1+ 解:数据表 table 中的常量 4 传送到以变量 x 的地址为地址的存储单元中;数据表 table 中 的常量 8 传送到以变量 x+1 的地址为地址的存储单元中;数据表 table 中的常量 16 传送到 以变量 x+2 的地址为地址的存储单元中; .bss x,4 .data table: .word 4,8,16,32 …… STM #x,AR1 RPT #2 MVPD table,*+AR2 解:数据表 table 中的常量 4 传送到以变量 x+1 的地址为地址的存储单元中;数据表 table 中的常量 8 传送到以变量 x+2 的地址为地址的存储单元中;数据表 table 中的常量 16 传送 到以变量 x+3 的地址为地址的存储单元中; 第四章 汇编语言程序的开发工具及 CCS 集成开发环境 1、软件开发环境有哪几种?在非集成开发环境中,软件开发常采用哪些部分? 答:可以在两种开发环境中进行 C54X 的开发:非集成的开发环境和集成的开发环境。在非 集成开发环境中,软件开发常采用:编辑、汇编、链接、调试等部分。 2、链接器对段是如何处理的? 答: 链接器将一个或多个 COFF 目标文件中的各种段作为链接器的输入段, 经过链接后在一 个可执行的 COFF 输出模块中建立各个输出段, 通过情况下是将不同目标文件中的同名段进 行合并,并为各个输出段分配进具体的存储器中。 3、链接器能完成什么工作?链接器命令文件中,MEMORY 命令和 SECTIONS 命令的任务是 什么? 答:链接器将各个目标文件合并起来,并完成如下工作: (1)将各个段配置到目标系统的存储器。
DSP习题及答案

第一章作业1、C54x有哪些寻址方式?都是如何寻址的?2、块循环共使用了哪些寄存器,可以嵌套使用吗?重复次数如何确定?3、中断向量地址是如何确定的?4、现在要开放外中断2,应该如何编程?5、晶振为10M,实现5mS定时,应该如何编程?第五章作业1:作整数乘法Z= (其中XI= 1,2,3,4,5,6,7,8,9,10, YI=11,12,13,14,15,16,17,18,19,20 )2:分别用块循环操作法和banz 循环方法对的100个变量分别初始化为1,2,3,…,100.bss x,100 ;3:初始化变量X=5555 5555H,Y=AAAA AAAAH,并将X 与Y 的乘积结果保存在变量Z 中4:作小数乘法Z= 其中a i 和x i 分别为常量-0.4,-0.3,-0.2,-0.1,0.1,0.2,0.3,0,4,并将乘积结果保存在变量Z 中。
5:C 程序调用汇编子程序,应如何编写,举例说明(参考实验3)i i i y x *9∑=i i i x a *30∑=1、C54x有哪些寻址方式?都是如何寻址的?答:有即立即寻址、绝对寻址、累加器寻址、直接寻址间接寻址、存储器映像寄存器寻址和堆栈寻址7种寻址方式。
如何寻址略:2、块循环共使用了哪些寄存器,可以嵌套使用吗?重复次数如何确定?答:在块循环中使用了BRC,RSA REA三个寄存器,因为在DSP内部只有这样一组用于块循环操作的寄存器因此不能嵌套使用。
重复次数等于加载BRC的数值加一。
3、中断向量地址是如何确定的?答:中断向量地址由中断向量指针IPTR和所使用的中断向量号共同来确定。
用公式表示就是:中断向量地址=IPTR* 27+中断序号*44、现在要开放外中断2,应该如何编程?经查IMR和IFR寄存器,外部中断2的允许(标志)位都是第2位,即位码为04H。
对编成的叙述略。
SSBX INTM;关闭可屏蔽中断总开关STM 04H,IFR;清除历史中断标志STM 04H,IMR;设置中断屏蔽寄存器允许响应中断RSBX INTM;开放中断屏蔽总开关5、晶振为10M,实现5mS定时,应该如何编程?定时器初始化程序如下:Prd=10000,tddr=10计算略STM # 0000H,SWWSRSSBX INTM; 停止所有可屏蔽中断STM #17ffH,CLKMD;PLL*2 方式CLKOUT=20MHzSTM #0010H,TCR; 停止定时器STM #9999,PRD; 设置时间常数STM #270fH,PRDSTM #0C29H,TCR;启动定时器,设置TDDR =9STM #08H,IMR ;开放屏蔽寄存器的允许位STM #08H,IFR ;清除历史中断标志第五章习题答案1:作整数乘法Z= 要求在运算之前初始化X I = 1,2,3,4,5,6,7,8,9,10, Y I =11,12,13,14,15,16,17,18,19,20.mmregs.bss X,10.bss Y,10.bss Z,1.text_c_int00: stm #X,AR1;ld #1,ASTM #19,AR2LOOP:STL A,*AR1+ADD #1,ABANZ LOOP,*AR2-STM #X,*AR2i i i y x *90∑=STM #Y,AR3RPTZ A,#9MAC *AR2+,*AR3+,ASTM #Z,AR0STL A,*AR0.end2:分别用块循环操作法和banz 循环方法对的100个变量分别初始化为1,2,3,…,100 .bss x,100.bss x,100 ; .text.text_c_int00:STM #x,AR0_c_int00: STM #x,AR0 LD #0,ASTM #99,AR2 STM 99,BRCLD #1,A RPTB NEXT-1LOOP:STL A,*AR0+ADD #1,AADD #1,A STL A,*AR0+BANZ LOOP,*AR2-NEXT: nop3:初始化变量X=5555 5555H,Y=AAAA AAAAH,并将X与Y的乘积结果保存在变量Z中.mmregs.data.bss z,4x.long 55555555hY .long 0aaaaaaaahstm #x+1,ar2;取x低字stm #y+1,ar3;取x低字ld *ar2,Tmpyu *ar3-,Astl a,@z+1ld a,-16,amacsu *ar2-,*ar3+,a stl a,@z+2;macsu *ar3-,*ar2,a sth a,@z+3;stl a,@z .endld a,-16,amac *ar2,*ar3,a4:作小数乘法Z= 其中a i 和x i 分别为常量-0.4,-0.3,-0.2,-0.1,0.1,0.2,0.3,0,4,并将乘积结果保存在变量Z 中。
DSP原理与应用课后答案邹彦主编

DSP原理与应用课后答案邹彦主编第五章 TMS320C54x的汇编语言程序设计1、伪指令和注释有什么差别?它们在程序中的作用一样吗? 答:伪指令用于为程序提供数据并指示汇编程序如何汇编程序,是汇编语言程序的一个重要内容。
汇编伪指令主要完成以下工作:(1)将代码和数据汇编进指定的段(2)为未初始化的变量在存储器中保留空间(3)控制清单文件是否产生(4)初始化存储器(5)汇编条件代码块(6)定义全局变量(7)为汇编器指定可以获得宏的库(8)考察符号调试信号注释是程序的任选项。
注释可以由ASCII码和空格组成。
注释在汇编源清单中要显示,但不能影响汇编。
注释在程序中的作用是说明程序语句的含义,以便对软件进行维护。
5、在堆栈操作中,PC当前地址为4020H,SP当前地址为3H,运行PSHM AR7后,PC和SP的值分别是多少?解:SP=2H;PC=4021H6、试编写0.25×(-0.1)的程序代码。
参考程序如下: .title \_c_int00: ssbx FRCT .mmregs stm#x,ar1 .global _c_int00 rpt #0x1 .bss x,1 mvpd #Coef,*ar1+ .bss y,1 stm #x,ar2 .bss z,1 stm #y,ar3 .data mpy *ar2,*ar3,A Coef: .word25*32768/100 sth A,*ar1 .word -1*32768/10 Wait: b Wait .text .end 7、将定点数0.00125用浮点数表示。
解:A=28H;T=19H8、试写出以下两条指令的运行结果:①EXP AA=FFFD876624 T=0000则以上指令执行后,B、T的值各是多少?解:A=0xFFFD876624;T=5 ②NORM BB=420D0D0D0D, T=FFF9则以上指令执行后,B、T的值各是多少?解:B=0x841A1A1A, T=FFF9第七章 TMS320C54x片内外设、接口及应用2、已知TMS320C54X的CLKOUT频率为4MHz,那么,①在SAM工作方式下,主机的时钟频率是多少?解:在SAM工作方式下,主机频率可达3.2MHz或2.4MHz。
DSP答案第七章第五章

这里
H ( z) =
∑ bk z −k
1 − ∑ ak z
k =0 k =0 N −k
M
=
∏ (1 − β ∏ (1 − α
k =1 k =1 N
M
k
z −1 )
,如果系统是稳定因果系统,极点一定在
k
z )
−1
单位圆内,因此 α k < 1 。 (b) 现在 y[ n] 输入另一个系统 H ′( z ) , 输出是 w[ n] , 由于 m x = 0 , 得出 m y = 0 , mw = 0 求白化滤波器,即求一个系统函数,使输入为 y[ n] 时,输出为白噪 w[ n] 。
第五章 线性时不变系统的变换分析
5.4 设一个线性时不变系统的输入 x[ n] 和输出 y[ n] 满足以下二阶差分方程:
y[n − 1] −
10 y[n] + y[n + 1] = x[n] 3
(a) 画出在 z 平面的零极点分布图。 (b) 求系统的冲激响应。 解:对系统差分方程进行 z 变换,可得:
(a)求系统函数 H ( z ) = Y ( z ) / X ( z ) ,画出 H ( z ) 的零极点分布图,并标出收敛域。 (b)求系统的冲激响应 h[ n] 。 (c)如果该系统是一个不稳定系统,找一个稳定(可以非因果)的冲激响应,使该结 果也满足上述差分方程。 解: (a)对系统差分方程进行 z 变换,可得:
ROCh ∩ ROC x 的部分由 X ( z ) 和 H ( z ) 的零极点相抵消引起。故而可得: ROC y :
1 < z < 2。 2
(c)只有一种可能: h[ n] = δ [ n] − δ [ n − 2]
【免费下载】DSP课后习题答案

答:常见的运算速度指标有如下几种: (1) 指令周期:执行一条指令所需的最短时间,数值等于主频的倒数;指令周期通
常以 ns(纳秒)为单位。例如,运行在 200MHz 的 TMS320VC5510 的指令周 期为 5ns。 (2) MIPS:每秒百万条指令数。 (3) MOPS:每秒百万次操作数。 (4) MFLOPS:每秒百万次浮点操作数。 (5) BOPS:每秒十亿次操作数。 (6) MAC 时间:一次乘法累加操作花费的时间。大部分 DSP 芯片可在一个指令周 期内完成 MAC 操作; (7) FFT 执行时间:完成 N 点 FFT 所需的时间。FFT 运算是数字信号处理中的典 型算法而且应用很广,因此该指标常用于衡量 DSP 芯片的运算能力。
答:两个。第一阶段是取流水线,即从内存中取出 32 位的指令包,放入指令缓冲队 (IBQ)中,然后为流水线的第二阶段提供 48 位的指令包。第二阶段是指执行流水线,这 部分的功能是对指令进行解码,完成数据的存取和计算。
5.TMS320C55x DSP 有哪些片上外设?
2
答:两个 20 位的定时器。一个看门狗定时器。6 通道直接存储器存取控制器(DMA)。 外部存储器接口(EMIF)。三个串口支持最多三个多通道缓冲串口(McBSP)或最多两个 多媒体/安全数字卡接口。增强型主机接口(EHPI)是一个 16 位的并行接口。可编程锁相 环(DPLL)时钟发生器。USB 全速(12Mbps)从端口。ITMS320C55x DSP 有哪些特征和优点?(表 2-2) 答:一个 32 位 x 16 位指令缓冲队列:缓冲变长指令并完成有效的块重复操作; 两个 17 位 x17 位的乘法累加器:在一个单周期执行双乘法累加操作; 一个 40 位算术逻辑单元(ALU):实现高精度算术和逻辑操作; 一个 40 位桶形移位寄存器:能够将一个 40 位的计算结果最高向左移 31 位或向右 移 32 位; 一个 16 位算术逻辑单元(ALU):对主 ALU 并行完成简单的算术操作; 4 个 40 位的累加器:保留计算结果,减少对存储单元的访问; 12 条独立总线,其中包括 3 条读数据总线、2 条写数据总线、5 条数据地址总线、 1 条读程序总线、1 条程序地址总线:为各种计算单元并行地提供将要处理的指令 和操作数——利用 C55x 的并行机制的优点; 用户可配置 IDLE 域:改进了低功耗电源管理的灵活性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
′ 是任意的,因此 H w ( z ) 不是唯一的。 (c)在保持 r ≤ 0 的情况下,选取 α k
5.24 设一 LTI 系统,其系统函数为
H ( z) =
(1 − 1.5 z −1 − z −2 )(1 + 0.9 z −1 ) (1 − z −1 )(1 + 0.7 jz −1 )(1 − 0.7 jz −1 )
这里
H ( z) =
∑ bk z −k
1 − ∑ ak z
k =0 k =0 N −k
M
=
∏ (1 − β ∏ (1 − α
k =1 k =1 N
M
k
z −1 )
,如果系统是稳定因果系统,极点一定在
k
z )
−1
单位圆内,因此 α k < 1 。 (b) 现在 y[ n] 输入另一个系统 H ′( z ) , 输出是 w[ n] , 由于 m x = 0 , 得出 m y = 0 , mw = 0 求白化滤波器,即求一个系统函数,使输入为 y[ n] 时,输出为白噪 w[ n] 。
解:对输入输出分别进行 z 变换得:
1 −1 + −1 1 1 − z −1 1 − 2 z 2 1 1 Y (z ) = 6 ⋅ − 6⋅ 1 3 1 − z −1 1 − z −1 2 4 X (z ) =
(a) H ( z ) =
1 < z <2 2 z > 3 4
Y (z ) 1 − 2 z −1 = 2⋅ 3 X (z ) 1 − z −1 4 1 的零极点对消。 2
−1
设
1+ i 5 6 −1 = re jω0 ,其中 r = , ω 0 = tan ( 5 ) 。 2 2 1 − i 5 re jω0 5
即有: h[ n] =
{
(
)
n
+ i 5 re − jω0
(
) }⋅ u[n]
n
=
1 2 5 n 2 5r n sin nω 0 ⋅ u[n] = r sin (nω 0 ) ⋅ u[n] 5 5 6 。此时: 2
k
z −1 )∏ (1 − α k z ) z )∏ (1 − β k z )
−1
k =1 k =1 M
k
如果 H w ( z ) 也是一个因果稳定系统,则 H w ( z ) 的极点一定在单位圆内,上式中的 极点在 β k 和
1
βk
处,现在设
β k ≠ 1 ,那么我们从 β k 和
1
βk
中一定可以找到 M 个
(
)
ROC x :
(b)由 H ( z ) =
1 < z < 2。 2 ROCh : z ≠ 0 。
Y ( z) −2 可得: H ( z ) = 1 − z , X ( z)
又由 Y ( z ) = X ( z ) ⋅ H ( z ) 可知 ROC y 应该包括 ROCh ∩ ROC x ,且 ROC y 中不属于
k =1 k =1
N
M
b0 = 1
(a)自相关函数 φ yy [ n] 的 z 变换 Φ yy ( z ) 是什么?有时候要用一个线性滤波器来处理
y[n] 以使 y[n] 的频谱“白化” ,也就是说要找到一个系统,在输入为 y[ n] 时,其输
出的功率谱是平坦的。假设已知自相关函数 φ yy [ n] 和它的 z 变换 Φ yy ( z ) ,但是不知 道系数 ak 和 bk 。 (b)讨论求该白化滤波器系统函数 H w ( z ) 的步骤。 (c)该白化滤波器是唯一的么? 解: (a)LTI 系统满足以下的差分方程:
所以差分方程为 y[n] −
[(
)]
3 y[n − 1] = 2 x[n] − 4 x[n − 1] 4 3 因为 H ( z ) 的收敛域位于唯一极点 z = 的外面且包含单位圆,所以系统既稳定又因果。 4
5.8 设某一线性时不变系统满足以下条件: (i)系统因果; (ii)当输入
11 4 n x[n] = − u[n] − (2 ) u[−n − 1] 3 2 3
(a)写出满足系统输入输出关系的差分方程。 (b)作零极点图,并指出该系统函数的收敛域。 (c)画出
H ( e jω )
。
(d)关于该系统,下列说法是对是错? (i)系统是稳定的;
(ii)对于大的 n 值,冲激响应趋于某一常数; (iii)频率响应幅度在近似 ω = ±π / 4 处有一峰值; (iv)该系统有稳定且因果的逆系统。
(a)求系统函数 H ( z ) = Y ( z ) / X ( z ) ,画出 H ( z ) 的零极点分布图,并标出收敛域。 (b)求系统的冲激响应 h[ n] 。 (c)如果该系统是一个不稳定系统,找一个稳定(可以非因果)的冲激响应,使该结 果也满足上述差分方程。 解: (a)对系统差分方程进行 z 变换,可得:
时,输出的 z 变换为
n
Y ( z) = (1 −
(a)求 x[ n] 的 z 变换。 (b) Y ( z ) 可能的收敛域是什么?
1− z2 1 −1 z )(1 − 2 z −1 ) 2
(c)系统的冲激响应有几种可能的选择? 解: (a) X ( z ) = −
1 1 4 1 1 , ⋅ +− ⋅ = −1 3 1 − 1 z −1 3 1 − 2z 1 −1 −1 1 − z ⋅ 1 − 2 z 2 2
ROCh ∩ ROC x 的部分由 X ( z ) 和 H ( z ) 的零极点相抵消引起。故而可得: ROC y :
1 < z < 2。 2
(c)只有一种可能: h[ n] = δ [ n] − δ [ n − 2]
5.12 设一稳定的线性时不变系统可由以下差分方程描述:
y[n] = y[n − 1] + y[n − 2] + x[n − 1] 。
′ ( k = 1,L, M ) 值,他们的绝对值小于 1。这些值称为 β k ,另外 M 个值就是
因此
1 。 β k′
σ H w ( z) = w σx
∏ (1 − α ′ z
k
N
−1
) )
∏ (1 − β ′ z
k k =1
k =1 M
(− z )r ⋅ A
−1
′ ,是从 α k 和 分子的零点是 α k
y[n] = ∑ ak y[n − k ] + ∑ bk x[n − k ]
k =1 k =1
N
M
而 x[n] 为零均值的白噪声,设 φ xx [n] = σ x δ [ n] ,由书中的式子有:
2 2 Φ yy ( z ) = Φ xx [ z ] ⋅ H ( z ) ⋅ H ( z −1 ) = σ x ⋅ H ( z ) ⋅ H ( z −1 )
(b)将系统函数整理成零极点式: H ( z ) = 得 到零极点分布如图解 5.24-1。
(1 − 2 z −1 )(1 + 0.5 z −1 )(1 + 0.9 z −1 ) ,很容易 (1 − z −1 )(1 + j 0.7 z −1 )(1 − j 0.7 z −1 )
ℑm
1
ℜe
图解 5.24-1 其中系统收敛域可有系统为收敛得到: z > 1 。 (c)根据零极点分布分析可得,系统频率响应幅度,如图解 5.24-2。
− 1 5 5 = ⋅ + 5 1 + i 5 −1 1 − i 5 −1 1− z 1− z 2 2
ROC : z >
6 1± i 5 ,即: z > 。 2 2
ℑm
系统的零极点分布如图解 5.12。
ROC
1
6 2
ℜe
图解 5.12
n n 1− i 5 1+ i 5 1 + i 5 ⋅ (b) h[ n] = Z {H ( z )} = ⋅ − i 5 ⋅ ⋅ u[n] 5 2 2
∴ h[n] =
16 10 3 δ [n] − ⋅ u[n] 3 3 4
n
Y ( z ) 2 1 − 2 z −1 = (c)Q X ( z ) 1 − 3 z −1 4
(
)
3 ∴ Y ( z )1 − z −1 = X ( z ) 2 1 − 2 z −1 4
解: (a) H ( z ) =
1 − 0.6 z −1 − 2.35 z −2 − 0.9 z −3 ,即系统差分方程为: 1 − z −1 + 0.49 z −2 − 0.49 z −3
y[n] − y[n − 1] + 0.49 y[n − 2] − 0.49 y[n − 3] = x[n] − 0.6 x[n − 1] − 2.35 x[n − 2] − 0.9 x[n − 3]
3 < z <2 4
其中 z =
零点 z=2,
Im
0
× 3 4
2 。 Re
极点 z=
3 4
3 < z <2 4
5 8 −1 3 − 2 zБайду номын сангаас− 3 16 10 1 (b) H ( z ) = 2 = − ⋅ 3 −1 3 3 3 1 − z −1 1− z 4 4
z −1Y ( z ) −
故而: H ( z ) =
10 Y ( z ) + zY ( z ) = X ( z ) 。 3
Y ( z) = X ( z) 1 1 = z −1 10 10 z −1 − + z 1 − z −1 + z − 2 3 3
