第8章 时间序列分析
统计学 第8章 时间序列分析

8章-时间序列分析练习题参考答案

第八章 时间数列分析一、单项选择题1.时间序列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的,后者是根据变量值大小排列的D 前者是根据变量值大小排列的,后者是根据时间顺序排列的 C2.时间序列中,数值大小与时间长短有直接关系的是( )A 平均数时间序列B 时期序列C 时点序列D 相对数时间序列 B3.发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 C4.计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平 B5.某车间月初工人人数资料如下:则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人 C6.某地区某年9月末的人口数为150万人,10月末的人口数为150.2万人,该地区10月的人口平均数为( )A 150万人B 150.2万人C 150.1万人D 无法确定 C7.由一个9项的时间序列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 A8.采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 A9.某企业的科技投入,2010年比2005年增长了58.6%,则该企业2006—2010年间科技投入的平均发展速度为( ) A5%6.58 B 5%6.158 C6%6.58 D 6%6.158B10.根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数,采用的公式是( ) A 简单平均法 B 几何平均法 C 加权序时平均法 D 首末折半法 D11.在测定长期趋势的方法中,可以形成数学模型的是( )A 时距扩大法B 移动平均法C 最小平方法D 季节指数法12.动态数列中,每个指标数值相加有意义的是()。
A.时期数列B.时点数列C.相对数数列D.平均数数列A13.按几何平均法计算的平均发展速度侧重于考察现象的()A.期末发展水平B.期初发展水平C.中间各项发展水平D.整个时期各发展水平的总和A14.累计增长量与其相应的各逐期增长量的关系表现为()A.累计增长量等于相应各逐期增长量之和B.累计增长量等于相应各逐期增长量之差C.累计增长量等于相应各逐期增长量之积D.累计增长量等于相应各逐期增长量之商A15.已知某地区2010年的粮食产量比2000年增长了1倍,比2005年增长了0.5倍,那么2005年粮食产量比2000年增长了()。
第八章时间序列分析

第⼋章时间序列分析第⼋章时间序列分析与预测【课时】6学时【本章内容】§ 时间序列的描述性分析时间序列的含义、时间序列的图形描述、时间序列的速度分析§ 时间序列及其构成分析时间序列的构成因素、时间序列构成因素的组合模型§ 时间序列趋势变动分析移动平均法、指数平滑法、模型法§ 时间序列季节变动分析[原始资料平均法、趋势-循环剔除法、季节变动的调整§ 时间序列循环变动分析循环变动及其测定⽬的、测定⽅法本章⼩结【教学⽬标与要求】1.掌握时间序列的四种速度分析2.掌握时间序列的四种构成因素3.掌握时间序列构成因素的两种常⽤模型4.掌握测定长期趋势的移动平均法5.了解测定长期趋势的指数平滑法6.;7.掌握测定长期趋势的线性趋势模型法8.了解测定长期趋势的⾮线性趋势模型法9.掌握分析季节变动的原始资料平均法10.掌握分析季节变动的循环剔出法11.掌握测定循环变动的直接法和剩余法【教学重点与难点】1.对统计数据进⾏趋势变动分析,利⽤移动平均法、指数平滑法、线性模型法求得数据的长期趋势;2.对统计数据进⾏季节变动分析,利⽤原始资料平均法、趋势-循环剔除法求得数据的季节变动;3.对统计数据进⾏循环变动分析,利⽤直接法、剩余法求得循环变动。
【导⼊】;很多社会经济现象总是随着时间的推移不断发展变化,为了探索现象随时间⽽发展变化的规律,不仅要从静态上分析现象的特征、内部结构以及相互关联的数量关系,⽽且应着眼于现象随时间演变的过程,从动态上去研究其发展变动的过程和规律。
这时需要⼀些专门研究按照时间顺序观测的序列数据的统计分析⽅法,这就是统计学中的时间序列分析。
通过介绍⼀些时间序列分析的例⼦,让同学们了解时间序列的应⽤,并激发学⽣学习本章知识的兴趣。
1.为了表现中国经济的发展状况,把中国经济发展的数据按年度顺序排列起来,据此来研究。
2.公司对未来的销售量作出预测。
这种预测对公司的⽣产进度安排、原材料采购、存货策略、资⾦计划等都⾄关重要。
时间序列分析

时期序列
计算公式:
n
YY1Y2Yn
Yi i1
n
n
【例8.1】 根据表8.1中的国内生产总值序 列,计算各年度的平均国内生产总值
n
Yi
Yi1
4288.585 476.95( 43 亿元)
n
9
绝对数序列的序时平均数
(计算方法)
时点序列— 间隔不相等
Y1 Y2
Y3 Y4
T1
T2
T3
Yn-1
发展速度与增长速度的计算(实例)
【例8.5】 根据表8-3中第三产业国内生产总值序列, 计算各年的环比发展速度和增长速度,及以1994年 为基期的定基发展速度和增长速度
表8- 4 第三产业国内生产总值速度计算表
年份
1994 1995 1996 1997 1998
国内生产总值(亿元)
发展速度 (%)
第8章 时间序列分析
第一节 时间序列的对比分析 第二节 时间序列及其构成因素 第三节 长期趋势分析 第四节 季节变动分析 第五节 循环波动分析
第一节 时间序列的对比分析
一. 时间序列及其分类 二. 时间序列的水平分析 三. 时间序列的速度分析
时间序列及其分类
1. 同一现象在不同时间上的相继观察值排 列而成的数列
803 896 1070 1331 1781 2311 2726 2944 3094
时间序列的分类
时间序列
绝对数序列 相对数序列 平均数序列
时期序列 时点序列
时间序列的分类
1. 绝对数时间序列 一系列绝对数按时间顺序排列而成 时间序列中最基本的表现形式 反映现象在不同时间上所达到的绝对水平 分为时期序列和时点序列
第8章 时间序列趋势分析

我国年末人口数(万人) 我国人口自然增长率(‰)
某厂职工年平均工资(元/人)
12000
13000
15000……
.
时间序列的构成要素
现象在各时间上的指标数值 时间序列分析的目的
描述现象在过去时间的状态。 分析现象发展变化的规律性。 根据现象的过去行为预测其未来行为。 将相互联系的时间序列进行对比,研究有关现象之 间的联系程度。
4.
不规则变动 (Irregular Variations )
包括随机变动和突然变动。 随机变动—现象受到各种偶然因素影响而呈现出方 向不定、时起时伏、时大时小的变动。 突然变动—战争、自然灾害或其它社会因素等意外 事件引起的变动。影响作用无法相互抵消,影响幅 度很大。 一般只讨论有随机波动而不含突然异常变动的情况。 随机变动与时间无关,是一种无规律的变动,难以 测定,一般作为误差项处理。
8.2.2 长期趋势的测定
长期趋势分析主要是指长期趋势的测定,采用一定的方法
对时间序列进行修匀,使修匀后的数列排除季节变动、循环
.
变动和无规则变动因素的影响,显示出现象变动的基本趋势, 作为预测的依据。
测定长期趋 势的方法
移动平均法 趋势方程拟和法(数学模型法)
.
研究长期趋势的目的和意义
1. 认识和掌握现象随时间演变的趋势和规律,为 制定相关政策和进行管理提供依据;
表8- 2 1981-1998年我国汽车产量数据
年 份
1981 1982 1983 1984 1985 1986 1987 1988 1989
产量(万辆)
17.56 19.63 23.98 31.64 43.72 36.98 47.18 64.47 58.35
第八章时间序列分析

第八章时间序列分析一、填空题:1. 由于决定时间数列变化的因数是多方面的,因此通常把时间数列上各期发展水平按其影响因素的不同分解成几个不同的组成部分,即长期趋势、、循环波动和不规则变动。
2.时间序列按照数列中排列指标的性质不同,可分为、和。
3. “增长1%绝对值”指标其实质是水平的1%。
4. 是把原动态数列的时距扩大,再采用逐项移动的方法计算扩大了时距的序时平均数。
5.就是研究某种现象在一个相当长的时期内持续向上或向下发展变动的趋势。
6. 就是指某些社会现象由于受生产条件或自然条件因素的影响,在一年内随着季节的更换而呈现出比较有规律的变动。
二、单项选择题:1. 时间序列在一年内重复出现的周期性波动称为()A、趋势B、季节性C、周期性D、随机性2. 增长一个百分点而增加的绝对数量称为()A、环比增长率B、平均增长率C、年度化增长率D、增长1%绝对值3. 某银行投资额2004年比2003年增长了10%,2005年比2003年增长了15%,2005年比2004年增长了()A、15%÷10%B、115%÷110%C、(110%×115%)+1D、(115%÷110%)-14.某种股票的价格周二上涨了10%,周三上涨了5%,两天累计张幅达()A、15%B、15.5%C、4.8%D、5%5.如果某月份的商品销售额为84万元,该月的季节指数为1.2,在消除季节因素后该月的销售额为()A、60万元B、70万元C、90.8万元D、100.8万元6. 时间数列的构成要素是()。
A、变量和次数B、时间和指标数值C、时间和次数D、主词和宾词7. 定基增长速度与环比增长速度的关系为()。
A、定基增长速度等于相应的环比增长速度各个的算术和B、定基增长速度等于相应的环比增长速度各个的连乘积C、定基增长速度等于相应的环比增长速度加1后的连乘积再减1D、定基增长速度等于相应的环比增长速度各个的连乘积加18. 以1950年a0为最初水平,1997年a n为最末水平,计算钢产量的年平均发展速度时,须开()。
第八章 季节性时间序列分析方法

81❝§8.1 季节性时间序列的重要特征82❝§8.2 季节性时间序列模型❝§8.3 季节性检验❝§8.4 季节性时间序列模型的建立所谓是指具有某种周期性变化季节性时间序列,是指具有某种周期性变化规律的随机序列,并且这种周期性的变化规律往往是由于季节变化引起由于季节变化引起。
如果一个随机序列经过个时间间隔后观测数据呈现相似性比如同处于波峰或波谷则我们称该序S 呈现相似性,比如同处于波峰或波谷,则我们称该序列具有以为周期的周期特征,并称其为季节性时S 间序列,为季节长度。
S季节性时间序列存在着规则的周期如果我们把季节性时间序列存在着规则的周期,如果我们把原序列按周期重新排列,即可得到一个所谓的二维表。
对于季节性时间序列按周期进行重新排列是极其有益的不仅有助于考察同周期点的变化情况加有益的,不仅有助于考察同一周期点的变化情况、加深对序列周期性的理解,而且对于形成建模思想和理解季节模型的结构也都是很有帮助的。
影响一个季节性时间序列的因素除了季节因素外❝影响一个季节性时间序列的因素除了季节因素外,往往还存在趋势变动和随机变动等。
t t t tX S T I =++❝研究季节性时间序列的目的,就是分解影响经济指标变动的季节因素、趋势因素和随机因素,从而了解它们对经济的影响。
❝1. 简单季节模型❝2. 乘积季节模型季节性时间序列表现出也就是说时间 同期相关性,也就是说时间相隔为的两个时间点上的随机变量有较强的相关性。
比如对于月度数据S 12比如,对于月度数据则与相关性较强。
我们可以利用这种同期相关性在与之12,S =t X 12t X -t X 12t X -间进行拟合。
简单季节模型通过简单的趋势差分季节差分之通过简单的趋势差分、季节差分之后序列即可转化为平稳,它的模型结构通常表示如下:()(1)(),(*)S S D St tB B X B aΦ-=ΘSAR算子其中为白噪声序列,{}ta2()1,S S S pSB B B BΦ=-Φ-Φ--Φ12212()1.pS S S qSqB B B BΘ=-Θ-Θ--ΘSMA算子称(*)为简单季节模型,或季节性自回归求和移动SARIMA p D q平均模型,简记为模型。
统计学第八章 时间序列分析

季节指数
乘法模型中的季节成分通过季节指数来反映。 季节指数(季节比率):反映季节变动的相
对数。 1、月(或季)的指数之和等于1200%(或
400%) 。 2、季节指数离100%越远,季节变动程度
越大,数据越远离其趋势值。
用移动平均趋势剔除法计算季节指数
1、计算移动平均值(TC),移动期数为4或 12,注意需要进行移正操作。
移动平均的结果 4000 3500 3000 2500 2000 1500 1000 500 0
Example 2
移动平均法可以作为测定长期趋势的一种 较为简单的方法,在股市技术分析中有广 泛的应用。比如对某只股票的日收盘价格 序列分别求一次5日、10日、一个月的移动 平均就可以得到其5日、10日、一个月的移 动平均股价序列,进而得到5日线、10日线、 月线,用以反映股价变动的长期趋势。
1987 1800 1992 1980 1997 2880
1988 1620 1993 2520 1998 3060
1989 1440 1994 2559 1999 2700
4000
3500
销售收入
3000
2500
2000
1500
1000
500
0
年份
2000 2001 2002 2003 2004
销售 收入 3240 3420 3240 3060 3600
部分数据
销售 收入
t
1985 1080
1
1986 1260
2
1987 1800
3
1988 1620
4
1989 1440
5
……
…
2003 3060
19
第八章时间序列分析精品PPT课件

时间序列
随机过程的一次实现称为时间序列,可用{xt}或 xt表示。随机过程与时间序列的关系图示如下:
样本空间
4
比如某河流一年的水位值, {x1, x2, …, xT-1, xT,}, 可以看做一个随机过程,每一年的水位记录则是一 个时间序列,如{x11, x21, …, xT-11, xT1}。
13
时域分析方法的发展过程
❖ 基础阶段 ❖ 核心阶段 .U.Yule
❖1927年,AR模型
❖ G.T.Walker
❖1931年,MA模型,ARMA模型
15
核心阶段
❖G.E.P.Box和 G.M.Jenkins
❖1970年,出版《Time Series Analysis Forecasting and Control》
❖ 由于SAS系统具有全球一流的数据仓库功能, 因此在进行海量数据的时间序列分析时它具有 其它统计软件无可比拟的优势
18
三、平稳性(Stationarity)
1.严平稳
如果一个时间序列xt的联合概率分布不随时 间而变,即对于任何n和k,x1,x2,…,xn的联合 概率分布与x1+k,x2+k,…xn+k 的联合分布相同,则
而在每年中同一时刻(如t=2时)的水位记录是不 同的,{ x21, x22, …, x2n,} 构成了x2取值的样本空间。
5
时间序列 xt通常包含四个成分: 趋势因素(trend),季节因素(seasonality), 循环因素(cycle)和不规则因素(irregular)。 时间序列的分解通常有加法分解法则和乘法分解 法则,有兴趣的读者可以参阅其他文献。
❖ 特点
❖ 理论基础扎实,操作步骤规范,分析结果易于 解释,是时间序列分析的主流方法
第8章时间序列趋势分析

第8章时间序列趋势分析时间序列趋势分析是一种用于分析时间序列数据中趋势变化的方法。
它可以帮助我们理解时间序列数据中的长期趋势,并预测未来的发展趋势。
本章将介绍时间序列趋势分析的基本概念和常用方法。
1.时间序列的趋势:时间序列是按照时间先后顺序排列的一系列数据观测值的集合。
时间序列的趋势是指其长期平均水平的变化趋势,包括上升、下降或平稳变化。
趋势可以是线性的,也可以是非线性的。
2.趋势分析的目的:趋势分析的目的是识别和描述时间序列数据中的趋势变化,以便预测未来的发展趋势。
趋势分析可以帮助我们了解时间序列数据的长期变化趋势,从而做出有效的决策。
3.常用的趋势分析方法:(1)平均移动方法:平均移动方法是一种简单的趋势分析方法,它利用移动平均值来平滑原始数据,从而识别出数据的长期趋势。
平均移动方法有简单移动平均法、加权移动平均法和指数移动平均法等。
(2)线性趋势分析:线性趋势分析是一种通过拟合线性模型来描述时间序列数据的趋势变化的方法。
它可以用来估计趋势的斜率和截距,从而判断趋势的上升或下降趋势。
(3)非线性趋势分析:非线性趋势分析是一种通过拟合非线性模型来描述时间序列数据的趋势变化的方法。
它可以用来捕捉数据中的曲线、周期性和季节性等非线性特征。
(4)季节性调整:季节性调整是一种用来消除时间序列数据季节性变化影响的方法。
它可以使得数据更加稳定,更容易分析长期趋势。
4.趋势分析的应用领域:时间序列趋势分析在许多领域都有广泛的应用,包括经济学、金融学、市场研究、气象学、环境科学、交通规划等。
它可以用来预测市场走势、分析经济周期、预测天气变化等。
5.趋势分析的局限性:趋势分析的结果受到许多因素的影响,如数据质量、样本大小和选择的分析方法等。
此外,趋势分析只能应用于具有明显趋势的时间序列数据,对于无趋势或具有周期性的数据效果不佳。
总结起来,时间序列趋势分析是一种用于分析时间序列数据中趋势变化的方法。
它可以帮助我们理解时间序列数据的长期趋势,并预测未来的发展趋势。
第八章 时间序列

环比 定基 环比 定基
120.2 120.2 20.2 20.2
113.8 136.8 13.8 36.8
117.7 161.0 17.7 61.0
108.6 174.8 8.6 74.8
33
三、平均发展速度和平均增长速度
1. 观察期内各环比发展速度 的平均数 2. 说明现象在整个观察期内平均发展变化的 程度
动态速度指标
10
第二节
时间序列的水平分析
一、发展水平
• 是时间序列中每一项具体的指标数值。说明
现象在某一时间上所达到的水平。可是绝对数、 相对数、平均数。
• 假如时间序列为: a 0
a1
a 2 an 1 an
• a 0 叫最初水平, an 叫最末水平。 • 还有中间各项水平、基期水平和报告期水平
ai a0 ai Gi 1 a0 a0
(i 1,2,, n)
32
发展速度与增长速度的计算
第三产业国内生产总值速度计算表
年 份
国内生产总值(亿元)
2004
14930.0 — — — —
2005
17947.2
2006
20427.5
2007
24033.3
2008
26104. 3
发展速度 (%) 增长速度 (%)
18
日期 人数
•
12.31 1000
1.31 1050
3.31 1070
6.30 1100
• 求前半年的平均人数 。 1月份平均人数= (1000 1050) 2、3月份平均人数= (1050 1070)
2
2
1025
1060
4、5、6月份平均人数= (1070 1100)
统计学_第八章__时间序列分析
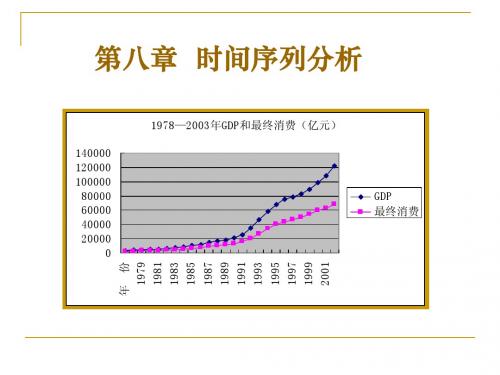
1978—2003年GDP和最终消费(亿元) 140000 120000 100000 80000 60000 40000 20000 0
年 份 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
GDP 最终消费
4、二者关系 (1)各逐期增长量之和等于相应的累计增长量
an a0 (a1 a0 ) (a2 a1 ) (a3 a2 ) (an an1 )
(2)相邻两期的逐期增长量之和等于相应的 累计增长量;相邻两期的累计增长量之差等于 相应的逐期增长量
(二)平均增长量 1、概念 一段时期内平均每期增加或者减少的绝 对数量。或者说是逐期增长量的序时平均数。 2、计算公式
a0 a1 a 2 a n 或 a n 1
af a f
B、如果是间断时点数列,计算方法为: 『两个假设条件: 一是假设上期期末水平等于本期期初水平; 二是假设现象在间隔期内数量变化是均匀的。』 Ⅰ、间隔期相等的时点数列,采用“首尾(首末)折半 法”计算。 先计算各间隔期的平均数;然后再将这些平均数进行 简单算术平均。例如:
第一节
时间序列分析概述
一、时间序列的概念和作用
(一)、概念: 1、时间序列:将不同时间的某一统计指标数据按照 时间的先后顺序排列起来而形成的统计序列,也称时间 数列或动态数列。 2、基本构成要素(从形式上看): 一是时间顺序(现象所属的时间)。可以是年份、季 度、月份或其他任何时间,称时间要素(常用t表示); 二是不同时间的统计数据(现象在不同时间上的观察 值)。可以是绝对数、相对数、平均数,称数据要素 (常用小写的英文字母a、b、c表示)。
时间序列分析 第8章 时间序列的深度学习预测

• 感知机则是由两层神经元组成,输入层(input layer)接收外界信号后传递给输出层(output layer)。
2022年9月4日
4
神经元
2022年9月4日
9
2022年9月4日
10
2022年9月4日
11
卷积神经网络预测
2022年9月4日
12
卷积神经网络
• 卷积神经网络(convolutional neural network,简称 CNN或ConvNet)采用卷积(convolution)运算,来 改善神经网络中待估参数多、数据之间空间信息丢失 等问题。
• 循环神经网络中的三个基本的循环网络:简单循 环单元网络、长短期记忆网络和门控循环单元网 络。
2022年9月4日
18
简单循环单元网络
输出层
ht
ht
隐藏层
延迟器
Xt
输入层
ht-1
图:简单循环单元
2022年9月4日
19
长短期记忆网络
2022年9月4日
20
长短期记忆网络
2022年9月4日
21
长短期记忆网络
• 卷积神经网络具有两个特有的网络层级:卷积层和汇 聚层。
-1 2 1 1 1
-1 -1 -1 -1 -1 00000 11111
1 1 2 -1 1 -2 1
卷积结果 信号序列
图:一维时间序列的卷积
11111
×-1 ×0 ×0
-1 0 -3 0 1
×0 ×0 ×0
统计学第8章 时间序列分析

a n 1
a0
(二)增长速度(增减速度)
增长速度=
增减量 基期水平
报告期水平 基期水平 基期水平
报告期水平 基期水平 1
发展速度1
环比增长速度= an an1 an 1
an1
an1
=环比发展速度 - 100%
定基增长速度= an a0 an 1
a0
a0
=定基发展速度 - 100%
例题:
时间序列的构成要素与模型
(构成要素与测定方法)
时间序列的构成要素
长期趋势
季节变动
循环波动 不规则波动
线性趋势 非线性趋势
按月(季)平均法
移动平均法
二次曲线 指数曲线
趋势剔出法
半数平均法
修正指数曲线
最小平方法
Gompertz曲线 Logistic曲线
剩余法
线性趋势
一、移动平均法
(Moving Average Method)
移动平均法(趋势图)
200
汽 150
车
产 100
量
(万辆)50
产量 五项移动平均趋势值 五项移动中位数
0
1981
1985
1989
1993
1997
(年份)
图11-1 汽车产量移动平均趋势图
移动平均法特点
1、对原数列有修匀作用,移动项数越大,修匀 作用越强。
2、移动平均时,项数为奇数时,只需一次移动 平均,其平均值作为移动平均项中间一期; 当为偶数时,需再进行一次相邻两平均值的 移动平均。
年份
销售额 逐 期 增 减 量 环比发展速度 定基增长速
(万元) (万元)
(%)
度(%)
第八章 时间序列分析

y ab
t
某企业某种产品销售量及有关数据(二次曲线)
时间(季) 1997.1 1997.2 1997.3 1997.4 1998.1 1998.2 1998.3 1998.4 1999.1 1999.2 1999.3 合计 销售量 1000 1200 1440 1721 2040 2402 2803 3243 3725 4246 4808 28028 逐期增长 —— 200 240 281 320 361 401 440 482 521 562 二级增长 —— —— 40 41 39 41 40 39 42 39 41
长期趋势的测定方法
时间序列的长期趋势可分为线性趋势和非线性趋 势。 线性趋势:当时间序列的长期趋势近似的呈现为 直线发展,每期的增减数量大致相同。 测定方法:
时距扩大法 移动平均法 趋势方程拟合法。
移动平均法
基本思想:扩大原时间序列的时间间隔, 并按一定的间隔长度逐期移动,分别计 算出一系列移动平均数,由这些移动平 均数形成的新的时间序列对原序列的波 动起到一定的修匀作用,削弱了原序列 中短期偶然因素的影响,从而呈现出现 象在较长时期的发展趋势。 计算方法:见下页
合计 274978.1 162562.6
——
——
——
编制原则
保持数列中各项指标数值的可比性。
时间长短和时点间隔应该前后一致。 总体范围统一。 经济内容统一。 计算方法和计量单位统一。
时间序列的速度分析
发展速度 增长速度 平均发展速度和平均增长速度 速度的分析与应用
发展速度
用于描述现象在观察期内相对的发展变化 速度。 报告期发展水平与基期发展水平之比。 由于采用的基期不同,发展速度分为:
第八章时间序列分析

4 261.30411.949% 149.030
平均增长率 G R 1 1.9 1 % 9 4 1 1 .9 4 % 9
【例】某企业近四年产品销售量分别增长了9% 、8%、7%、6%,计算四年来的平均增长率。
几何法基本原理
1. 从最初水平出发,每期按平均发展速度发展, 经过n期后将达到最末期水平
2. 按平均发展速度推算的最后一期的数值与最 后一期的实际观察值一致
3. 只与序列的最初观察值和最末观察值有关 4. 如果关心现象在最后一期应达到的水平,采
用水平法计算平均发展速度比较合适
累计法计算平均发展速度
ai ai1 ai a0 a0 ai1
增长速度
(要点)
1. 增长量与基期水平之比 2. 又称增长率 3. 说明现象的相对增长程度 4. 有环比增长速度与定基增长速度之分 5. 计算公式为
增长速 基 增 度 期 长水 量 报平告 基期 期 基 水 水 期 平 平 水平 发展速 1 度
计法)计算
水平法计算平均发展速度
(要点)
又称几何平均法,它是根据各期的环比发
展速度采用几何平均法计算出来的。计算公
式为:
x n a1 a2 an n
ai
a0 a1
an1
ai1
n an n R a0
(i 1,2,,n)
平均发展速度与平均增长速度
(算例)
【例】 根据前表中的有关数据,计算1994~2019年 间我国第三产业国内生产总值的年平均发展速度和 年平均增长率例子 平均发展速度
114333 115823 117171 118517 119850 121121 122389 123626 124810
