近四年(2005-2008)上海高考立体几何试题

合集下载

上海市历年高三数学高考试题汇编：向量与解析几何沪教版新课标

上海市03-08年高考数学试题汇编向量与解析几何1、教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是 .（04上海理）2、在△ABC 中，若90C ∠=，4AC BC ==，则BA BC ⋅= . （05上海春）3、双曲线116922=-y x 的焦距是 . （05上海春）4、已知1:210l x my ++=与2:31l y x =-，若两直线平行，则m 的值为 _____（07上海理）5、过抛物线x y 42=的焦点F 作垂直于x 轴的直线，交抛物线于A 、B 两点，则以F 为圆心、AB 为直径的圆方程是________________.（04上海春季）6、已知P 是双曲线22219x y a -=右支上的一点，双曲线的一条渐近线方程为30x y -=. 设12F F 、分别为双曲线的左、右焦点. 若23PF =，则1PF = . 7、已知两条直线l 1：ax+3y －3=0, l 2：4x+6y －1=0,若l 1∥l 2,则a= .8、直角坐标平面xoy 中，若定点)2,1(A 与动点),(y x P 满足4=∙OA OP ，则点P 的轨迹方程是__________。

（05上海理）9、若双曲线的渐近线方程为x y 3±=，它的一个焦点是()0,10，则双曲线的方程是__________。

（05上海理） 10、将参数方程⎩⎨⎧=+=θθsin 2cos 21y x （θ为参数）化为普通方程，所得方程是__________。

（05上海理）11、设抛物线的顶点坐标为(2，0)，准线方程为x ＝－1，则它的焦点坐标为 .（04上海理）12、在平面直角坐标系xOy 中，若抛物线x y 42=上的点P 到该抛物线的焦点的距离为6，则点P 的横坐标=x .（07上海春）13、在平面直角坐标系xOy 中，若曲线24y x -=与直线m x =有且只有一个公共点，则实数=m .（07上海春）14、已知直线l 过点)1,2(P ，且与x 轴、y 轴的正半轴分别交于B A 、两点，O 为坐标原点，则三角形OAB 面积的最小值为 . (06上海春)15、若向量b a 、的夹角为150，4,3==b a ，则=+b a 2 . (06上海春)16、若向量a b 、满足1,2,a b ==且a 与b 的夹角为3π，则a b +＝ .（08上海理）17、已知圆2x －4x －4＋2y ＝0的圆心是点P ，则点P 到直线x －y －1＝0的距离是．（06上海理） 18、在极坐标系中，定点A ),2,1(π点B 在直线0sin cos =+θρθρ上运动，当线段AB 最短时，点B 的极坐标是 . (03上海理)19、给出问题：F 1、F 2是双曲线201622y x -=1的焦点，点P 在双曲线上.若点P 到焦点F 1的距离等于9，求点P 到焦点F 2的距离.某学生的解答如下：双曲线的实轴长为8，由 ||PF 1|－|PF 2||=8，即|9－|PF 2||=8，得|PF 2|=1或17.该学生的解答是否正确？若正确，请将他的解题依据填在下面空格内，若不正确，将正确的结果填在下面空格内. (03上海理)20、设M(p ,0)是一定点，0∠p ∠1，点A(a ,b )是椭圆1422=+y x 上距离M 最近的点，则a =f (p )= . (03上海春季)21、已知点A (1，－2)，若向量与＝{2，3} ＝213，则点B 的坐标为 .（04上海理） 22、在极坐标系中，点M (4，3π)到直线l ：ρ(2cos θ＋sin θ)＝4的距离d ＝ .（04上海理）23、圆心在直线2x －y －7＝0上的圆C 与y 轴交于两点A (0， -4)，B (0， -2)，则圆C 的方程为 .（04上海理）24、若平移椭圆369)3(422=++y x ，使平移后的椭圆中心在第一象限，且它与x 轴、y 轴分别只有一个交点，则平移后的椭圆方程是________________（04上海春季）25、已知双曲线中心在原点,一个顶点的坐标是(3,0),且焦距与虚轴长之比为5：4,则双曲线的标准方程是 . （06上海文）26、已知双曲线22145x y -=，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为_____（07上海理）27、已知椭圆中心在原点，一个焦点为F （－23，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是．（06上海理）28、若曲线2y ＝|x |＋1与直线y ＝kx ＋b 没有公共点，则k 、b 分别应满足的条件是．（06上海理）29、在极坐标系中，O 是极点，设点A （4，3π），B （5，－65π），则△OAB 的面积是．（06上海理）30、已知实数x 、y 满足 x+y －3≥0, 则y －2x 的最大值是 .x+2y －5≤0x ≥0y ≥0（06上海文）31、已知圆)0()5(:222>=++r r y x C 和直线053:=++y x l . 若圆C 与直线l 没有公共点，则r 的取值范围是 . (06上海春) 32、如图,平面中两条直线l 1和l 2相交于点O.对于平面上任意一点M,若p 、q 分别是M 到直线l 1和l 2的距离,则称有序非负实数对(p,q)是点M 的“距离坐标”.根据上述定义, “距离坐标”是(1,2)的点的个数是 .（06上海文）33、已知圆的方程()2211x y +-=，P 为圆上任意一点（不包括原点）。

2005全国高考(II)卷立体几何第(2)题另外五种解法

2005全国高考(II)卷立体几何第(2)题另外五种解法2005全国高考(II)卷20题如图四棱锥P-ABCD 中,底面ABCD 为矩形, PD ⊥底面ABCD,AD=PD,E 、F 分别为CD 、PB 的中点. (I)求EF ⊥平面PAB ；(II)设AB=2BC ，求AC 与平面AEF 所成的角的大小。

针对第(II)题写出另外五种解法。

解法一延长BC 、AE 交与G , ∵底面ABCD 为矩形, E 为CD 的中点..∴C 为BG 的中点. 设BC=a, ∴AB=AP=2a ,又 F 为PB 的中点∴BF ⊥FA 由EF ⊥平面PAB ∴EF ⊥PB ；EF ∩FA=F ∴BF ⊥平面EFA ∵ BF=a 即B 到平面AEF 距离为a ∴C 到平面AEF 距离为21a 设AC 与平面AEF 所成的角为θ ∵AC=a 3∴sin θ=AC a21=63所以AC 与平面AEF 所成的角为arcsin 63解法二：(利用体积法求C 到平面AEF 距离, 再求AC 与平面AEF 所成的角的大小)设BC=a 由已知算得AEC S ∆=21CE ⨯AD=222a F 为PB 的中点，F 到平面CEA 距离为21 a ∵EF ⊥平面PAB ∴EF ⊥FA ∵FA=a EA=a 26∴EF=a 22算得AFE S ∆=21EF ⨯FA=242a设C 到平面AEF 距离为h,则CEA F EAF C V V --=∴31AFE S ∆⨯h=31AEC S ∆⨯21a ∴h=21a 设AC 与平面AEF 所成的角为θ ∵AC=a 3 ∴sin θ=AC a21=63所以AC 与平面AEF 所成的角为arcsin 63PADCBEFGP A DC BEF解法三：连PG ，取GP 的中点M,连CM 交GF 与N ∴CN ∥BF 且CN=21BF ∵BF ⊥底面EFA ∴CN ⊥底面EFA, ∴∠CAN 为AC 与平面AEF 所成的角BF=a ∴CN=21a 设AC 与平面AEF 所成的角为θ ∵AC=a 3∴sin θ=AC a21=63所以AC 与平面AEF 所成的角为arcsin 63解法四：连BD 交AC 与O,AE 交DB 与H 可得21=HB HD ∴HD=31DB, OH=21DB -31DB =61DB ∵BH=21DB +61DB=32DB ∴41=BH OH ∵BF ⊥底面EFA BF=a ∴O 到平面AEF 距离为41a 设AC 与平面AEF 所成的角为θ ∵OA=23a ∴sin θ=AO a41=63所以AC 与平面AEF 所成的角为arcsin63解法五：设BC=1如图建立空间直角坐标系 D(0,0,0) P(0,0,1) A(1,0,0) B(1,2,0) C(0,2F(21,22,21)∴A F =(21,-22,-21)E A =(-1,22设平面AEF 的法向量为n=(x,y,z) A F •n=0 ∴x=-zE A •n=02x=y 令x=2 n=(2,2, -2)设AC 与平面AEF 所成的角为θ∴sin θ=nC A n C A ∙=63 所以AC 与平面AEF 所成的角为arcsin 63PA DCBE F OH DNMPADC BEF G。

2005年高考数学立体几何参考答案

参考答案 1．解法一：（Ⅰ）⊥BF 平面ACE. .AE BF ⊥∴∵二面角D —AB —E 为直二面角，且AB CB ⊥， ⊥∴CB 平面ABE..AE CB ⊥∴ .B C EAE 平面⊥∴ （Ⅱ）连结BD 交AC 于C ，连结FG ，∵正方形ABCD 边长为2，∴BG ⊥AC ，BG=2，⊥BF 平面ACE ，由三垂线定理的逆定理得FG ⊥AC.BGF ∠∴是二面角B —AC —E 的平面角.由（Ⅰ）AE ⊥平面BCE ，又EB AE = ，∴在等腰直角三角形AEB 中，BE=2. 又直角,6,22=+=∆BE BC EC BCE 中332622=⨯=⋅=ECBE BC BF ，.362332sin ,===∠∆∴BG BF BGF BFG 中直角∴二面角B —AC —E 等于.36arcsin（Ⅲ）过点E 作AB EO ⊥交AB 于点O.OE=1.∵二面角D —AB —E 为直二面角，∴EO ⊥平面ABCD. 设D 到平面ACE 的距离为h ，,ACD E ACED V V --= .3131EO S h S ACD ACB ⋅=⋅∴∆∆⊥AE 平面BCE ，.EC AE ⊥∴ .332622112221221=⨯⨯⨯⨯=⋅⋅⋅=∴EC AE EODC AD h ∴点D 到平面ACE 的距离为.332 解法二：（Ⅰ）同解法一.（Ⅱ）以线段AB 的中点为原点O ，OE 所在直线为x 轴，AB 所在直线为y 轴，过O 点平行于AD 的直线为z 轴，建立空间直角坐标系O —xyz ，如图.⊥AE 面BCE ，BE ⊂面BCE ， BE AE ⊥∴，在AB O AB AEB Rt 为中,2,=∆的中点，).2,1,0(),0,0,1(),0,1,0(.1C E A OE -∴=∴).2,2,0(),0,1,1(== 设平面AEC 的一个法向量为),,(z y x =，则⎩⎨⎧=+=+⎪⎩⎪⎨⎧=⋅=⋅.022,0,0,0x y y x 即解得⎩⎨⎧=-=,,x z x y令,1=x 得)1,1,1(-=是平面AEC 的一个法向量.又平面BAC 的一个法向量为)0,0,1(=，.3331||||),cos(==⋅=∴n m ∴二面角B —AC —E 的大小为.33arccos（III ）∵AD//z 轴，AD=2，∴)2,0,0(=， ∴点D 到平面ACE 的距离.33232||,cos |||==>=<⋅=n d 2．解法（一）（1）证明：∵AE ⊥平面AA 1DD 1，A 1D ⊥AD 1，∴A 1D ⊥D 1E（2）设点E 到面ACD 1的距离为h ，在△ACD 1中，AC=CD 1=5，AD 1=2，故.2121,232152211=⋅⋅==-⋅⋅=∆∆BC AE S S ACE C AD 而 .31,23121,3131111=∴⨯=⨯∴⋅=⋅=∴∆∆-h h h S DD S V C AD AEC AEC D（3）过D 作DH ⊥CE 于H ，连D 1H 、DE ，则D 1H ⊥CE ，∴∠DHD 1为二面角D 1—EC —D 的平面角. 设AE=x ，则BE=2－x,,,1,.1,4,211x EH DHE Rt x DE ADE Rt DH DHD DH D Rt =∆∴+=∆=∴=∠∆中在中在中在 π.4,32.32543.54,3122π的大小为二面角时中在中在D EC D AE x x x x x x CE CBE Rt CH DHC Rt ---=∴-=⇒+-=+∴+-=∆=∆解法（二）：以D 为坐标原点，直线DA ，DC ，DD 1分别为x,y,z 轴，建立空间直角坐标系，设AE=x ，则A 1（1，0，1），D 1（0，0，1），E （1，x ，0），A （1，0，0）C （0，2，0）（1）.,0)1,,1(),1,0,1(,1111D DA x D ⊥=-=所以因为（2）因为E 为AB 的中点，则E （1，1，0），从而)0,2,1(),1,1,1(1-=-=D ，)1,0,1(1-=AD ，设平面ACD 1的法向量为),,(c b a n =，则⎪⎩⎪⎨⎧=⋅=⋅,0,01AD 也即⎩⎨⎧=+-=+-002c a b a ，得⎩⎨⎧==c a b a 2，从而)2,1,2(=n ，所以点E 到平面AD 1C 的距离为.313212||1=-+==n h （3）设平面D 1EC 的法向量),,(c b a =，∴),1,0,0(),1,2,0(),0,2,1(11=-=-=DD D x 由⎩⎨⎧=-+=-⇒⎪⎩⎪⎨⎧=⋅=⋅.0)2(02,0,01x b a c b D 令b=1, ∴c=2,a =2－x ，∴).2,1,2(x n -=依题意.225)2(222||||4cos211=+-⇒=⋅=x DD n π∴321+=x （不合，舍去），322-=x .∴AE=32-时，二面角D 1—EC —D 的大小为4π. 3．解：在长方体1111ABCD A BC D -中，以AB 所在的直线为x 轴，以AD 所在的直线为y 轴，1AA 所在的直线为z 轴建立如图示空间直角坐标系由已知12,1,AB AA ==可得(0,0,0),(2,0,0A B ，(1,0,1)F 又AD ⊥平面11AAB B ，从而BD 与平面11AAB B 所成的角为30DBA ∠=︒，又2AB =，AE BD ⊥，1,3AE AD ==从而易得13,,0,0,,0223E D ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭（I）因为()1,1,0,12AE BF ⎛⎫==- ⎪ ⎪⎝⎭所以()cos ,AE BFAE BF AE BF ⋅=14-=-，易知异面直线AE BF 、所成的角为arccos4。

上海市近四年(2005-)高考数学试题分类汇编——解析几何

上海市近四年（2005-2008）高考数学试题分类汇编——解析几何一．填空题:只要求直接填写结果，每题填对得4分，否则一律得零分. 1 ( 2005春季7 ) 双曲线116922=-y x 的焦距是 .65 2 (2005年3) 直角坐标平面xoy 中，若定点)2,1(A 与动点),(y x P 满足4=∙OA OP ，则点P 的轨迹方程是__________。

解答：设点P 的坐标是(x,y)，则由4=∙知04242=-+⇒=+y x y x3 (2005年5) 若双曲线的渐近线方程为x y 3±=，它的一个焦点是()0,10，则双曲线的方程是__________。

解答：由双曲线的渐近线方程为x y 3±=，知3=ab，它的一个焦点是()0,10，知1022=+b a ，因此3,1==b a 双曲线的方程是1922=-y x 4 (2005年6) 将参数方程⎩⎨⎧=+=θθsin 2cos 21y x （θ为参数）化为普通方程，所得方程是__________。

解答：4)1(22=+-y x5 (2006春季5) 已知圆)0()5(:222>=++r r y x C 和直线053:=++y x l . 若圆C 与直线l 没有公共点，则r 的取值范围是 . )10,0(6 (2006春季11) 已知直线l 过点)1,2(P ，且与x 轴、y 轴的正半轴分别交于B A 、两点，O 为坐标原点，则三角形OAB 面积的最小值为 . 4.7 (2006年2) 已知圆2x －4x －4＋2y ＝0的圆心是点P ，则点P 到直线x －y －1＝0的距离是；解：由已知得圆心为：(2,0)P ，由点到直线距离公式得：d ； 8 (2006年7) 已知椭圆中心在原点，一个焦点为F （－23，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是；解：已知222222242,161164(b a b c y x a a b c F =⎧⎪==⎧⎪⎪⇒=⇒+=⎨⎨-=⎪⎪⎩-⎪⎩为所求； 9 (2006年8)在极坐标系中，O 是极点，设点A （4，3π），B （5，－65π），则△OAB 的面积是；解：如图△OAB 中，554,5,2(())366OA OB AOB ππππ==∠=---=1545sin 526AOB S π∆⇒== (平方单位)；10 (2006年11) 若曲线2y ＝|x |＋1与直线y ＝kx ＋b 没有公共点，则k 、b 分别应满足的条件是．解：作出函数21,0||11,0x x y x x x +≥⎧=+=⎨-+<⎩的图象，如右图所示：所以，0,(1,1)k b =∈-；11 (2007春季6) 在平面直角坐标系xOy 中，若抛物线x y 42=上的点P 到该抛物线的焦点的距离为6，则点P 的横坐标=x . 5.12 (2007春季7) 在平面直角坐标系xOy 中，若曲线24y x -=与直线m x =有且只有一个公共点，则实数=m . 2. 13 (2007年2) 若直线1210l x my ++=：　与直线231l y x =-：平行，则=m ． 32-14 (2007年8) 以双曲线15422=-y x 的中心为焦点，且以该双曲线的左焦点为顶点的抛物线方程是．)3(122+=x y15 (2007年11) 已知P 为圆1)1(22=-+y x 上任意一点（原点O 除外），直线OP 的倾斜角为θ弧度，记||OP d =．在右侧的坐标系中，画出以()d θ，为坐标的点的轨迹的大致图形为16 (2008春季7) 已知P 是双曲线22219x y a -=右支上的一点，双曲线的一条渐近线方程为30x y -=. 设12F F 、分别为双曲线的左、右焦点. 若23PF =，则1PF = 5.17 (2008春季12) 已知(1,2),(3,4)A B ，直线1l ：20,:0x l y ==和3:l x +3y 10-=.设i P 是i l (1,2,3)i =上与A 、B 两点距离平方和最小的点，则△123PP P 的面积是32二．选择题:每题都给出四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，选对得 4分，否则一律得零分.18 (2005年15) 过抛物线x y 42=的焦点作一条直线与抛物线相交于A 、B 两点，它们的横坐标之和等于5，则这样的直线（ B ）A ．有且仅有一条B ．有且仅有两条C ．有无穷多条D ．不存在解答：x y 42=的焦点是(1，0)，设直线方程为0)1(≠-=k x k y (1)将(1)代入抛物线方程可得0)42(2222=++-k x k x k ，x 显然有两个实根，且都大于0，它们的横坐标之和是33243542222±=⇒=⇒=+k k k k ，选B 19 (2006春季13) 抛物线x y 42=的焦点坐标为 ( B )（A ）)1,0(. （B ）)0,1(. （C ）)2,0(. （D ）)0,2(.20 (2006春季15) 若R ∈k ，则“3>k ”是“方程13322=+--k y k x 表示双曲线”的 ( A ) （A ）充分不必要条件. （B ）必要不充分条件.（C ）充要条件. （D ）既不充分也不必要条件.21 (2008春季14) 已知椭圆221102x y m m +=--，长轴在y 轴上. 若焦距为4，则m 等于（ D ）（A ）4. （B ）5. （C ）7. （D ）8. 三．解答题:解答下列各题必须写出必要的步骤.22 ( 2005春季22) (本题满分18分)本题共有3个小题，第1小题满分5分，第2小题满分8分. 第3小题满分5分.（1）求右焦点坐标是)0,2(，且经过点)2,2(--的椭圆的标准方程；（2）已知椭圆C 的方程是12222=+by a x )0(>>b a . 设斜率为k 的直线l ，交椭圆C 于A B 、两点，AB 的中点为M . 证明：当直线l 平行移动时，动点M 在一条过原点的定直线上；（3）利用（2）所揭示的椭圆几何性质，用作图方法找出下面给定椭圆的中心，简要写出作图步骤，并在图中标出椭圆的中心.[解]（1）设椭圆的标准方程为12222=+by a x ，0>>b a ，∴ 422+=b a ，即椭圆的方程为142222=++b y b x ， ∵ 点（2,2--）在椭圆上，∴124422=++bb ，解得 42=b 或22-=b （舍），由此得82=a ，即椭圆的标准方程为14822=+y x . …… 5分 [证明]（2）设直线l 的方程为m kx y +=， …… 6分与椭圆C 的交点A (11,y x )、B (22,y x )，则有⎪⎩⎪⎨⎧=++=12222b y a x m kx y ，解得 02)(222222222=-+++b a m a kmx a x k a b ，∵ 0>∆，∴ 2222k a b m +<，即 222222k a b m k a b +<<+-.则 222221212222212,2k a b mb m kx m kx y y k a b kma x x +=+++=++-=+，∴ AB 中点M 的坐标为⎪⎪⎭⎫⎝⎛++-22222222,k a b m b k a b km a . …… 11分∴ 线段AB 的中点M 在过原点的直线 022=+y k a x b 上. …… 13分[解]（3）如图，作两条平行直线分别交椭圆于A 、B 和D C 、，并分别取AB 、CD 的中点N M 、，连接直线MN ；又作两条平行直线（与前两条直线不平行）分别交椭圆于1A 、1B 和11D C 、，并分别取11B A 、11D C 的中点11N M 、，连接直线11N M ，那么直线MN 和11N M 的交点O 即为椭圆中心. …… 18分23 (2005年19)（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分．如图，点A 、B 分别是椭圆2213620x y +=长轴的左、右端点，点F 是椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，PA PF ⊥．（1）求点P 的坐标；（2）设M 是椭圆长轴AB 上的一点，M 到直线AP 的距离等于MB ，求椭圆上的点到点M 的距离d 的最小值．[解]（1）由已知可得点A （－6，0），F （4，0）设点P 的坐标是},4{},,6{),,(y x FP y x AP y x -=+=则，由已知得.623,018920)4)(6(120362222-===-+⎪⎩⎪⎨⎧=+-+=+x x x x y x x y x 或则由于).325,23(,325,23,0的坐标是点于是只能P y x y ∴==> （2）直线AP 的方程是.063=+-y x 设点M 的坐标是（m ，0），则M 到直线AP 的距离是2|6|+m ，于是,2,66|,6|2|6|=≤≤--=+m m m m 解得又椭圆上的点),(y x 到点M 的距离d有,15)29(94952044)2(222222+-=-++-=+-=x x x x y x d 由于.15,29,66取得最小值时当d x x =∴≤≤- 24 (2006春季20) (本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图：航天器运行（按顺时针方向）的轨迹方程为12510022=+y x ，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y 轴为对称轴、⎪⎭⎫ ⎝⎛764,0M 为顶点的抛物线的实线部分，降落点为)0,8(D .观测点)0,6()0,4(B A 、同时跟踪航天器.（1）求航天器变轨后的运行轨迹所在的曲线方程；（2）试问：当航天器在x 轴上方时，观测点B A 、测得离航天器的距离分别为多少时，应向航天器发出变轨指令？ [解]（1）设曲线方程为7642+=ax y ，由题意可知，764640+⋅=a . 71-=∴a .……4分 ∴ 曲线方程为764712+-=x y . ……6分（2）设变轨点为),(y x C ，根据题意可知⎪⎪⎩⎪⎪⎨⎧+-==+)2(,76471)1(,125100222x y y x得 036742=--y y ， 4=y 或49-=y （不合题意，舍去）.4=∴y . ……9分得 6=x 或6-=x （不合题意，舍去）. ∴C 点的坐标为)4,6(， ……11分 4||,52||==BC AC .答：当观测点B A 、测得BC AC 、距离分别为452、时，应向航天器发出变轨指令. ……14分25 (2006年20)（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）在平面直角坐标系x O y 中，直线l 与抛物线2y ＝2x 相交于A 、B 两点．（1）求证：“如果直线l 过点T （3，0），那么→--OA →--⋅OB ＝3”是真命题；（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由． [解]（1）设过点T(3,0)的直线l 交抛物线y 2=2x 于点A(x 1,y 1)、B(x 2,y 2).当直线l 的钭率不存在时,直线l 的方程为x=3,此时,直线l 与抛物线相交于点A(3,6)、B(3,－6). ∴OB OA ⋅=3；当直线l 的钭率存在时,设直线l 的方程为(3)y k x =-，其中0k ≠，由22(3)y xy k x =⎧⎨=-⎩得 2122606ky y k y y --=⇒=- 又 ∵ 22112211,22x y x y ==，∴2121212121()34OA OB x x y y y y y y =+=+=，综上所述，命题“如果直线l 过点T(3,0)，那么⋅=3”是真命题；(2)逆命题是：设直线l 交抛物线y 2=2x 于A 、B 两点,如果⋅=3,那么该直线过点T(3,0).该命题是假命题. 例如：取抛物线上的点A(2,2)，B(21,1)，此时OA OB =3, 直线AB 的方程为：2(1)3y x =+，而T(3,0)不在直线AB 上；说明：由抛物线y 2=2x 上的点A (x 1,y 1)、B (x 2,y 2) 满足OB OA ⋅=3，可得y 1y 2=－6，或y 1y 2=2，如果y 1y 2=－6，可证得直线AB 过点(3,0)；如果y 1y 2=2，可证得直线AB 过点(－1,0),而不过点(3,0).26 (2007春季17. (14分) 求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题.例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”.求出体积316后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为316，求侧棱长”；也可以是“若正四棱锥的体积为316，求所有侧面面积之和的最小值”.试给出问题“在平面直角坐标系xOy 中，求点)1,2(P 到直线043=+y x 的距离.”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题.评分说明：(ⅰ) 在本题的解答过程中，如果考生所给问题的意义不大，那么在评分标准的第二阶段所列6分中，应只给2分，但第三阶段所列4分由考生对自己所给问题的解答正确与否而定. (ⅱ) 当考生所给出的“逆向”问题与所列解答不同，可参照所列评分标准的精神进行评分. [解] 点)1,2(到直线043=+y x 的距离为243|1423|22=+⋅+⋅. …… 4分“逆向”问题可以是：(1) 求到直线043=+y x 的距离为2的点的轨迹方程. …… 10分 [解] 设所求轨迹上任意一点为),(y x P ，则25|43|=+y x ，所求轨迹为01043=-+y x 或01043=++y x . …… 14分 (2) 若点)1,2(P 到直线0:=+by ax l 的距离为2，求直线l 的方程. …… 10分 [解]2|2|22=++b a b a ，化简得0342=-b ab ，0=b 或b a 34=，xyxy 所以，直线l 的方程为0=x 或043=+y x . …… 14分意义不大的“逆向”问题可能是：(3) 点)1,2(P 是不是到直线043=+y x 的距离为2的一个点？ …… 6分 [解] 因为243|1423|22=+⋅+⋅，所以点)1,2(P 是到直线043=+y x 的距离为2的一个点. ……10分 (4) 点)1,1(Q 是不是到直线043=+y x 的距离为2的一个点？ …… 6分 [解] 因为25743|1413|22≠=+⋅+⋅，所以点)1,1(Q 不是到直线043=+y x 的距离为2的一个点. ……10分 (5) 点)1,2(P 是不是到直线0125=+y x 的距离为2的一个点？ …… 6分 [解] 因为21322125|11225|22≠=+⋅+⋅，所以点)1,2(P 不是到直线0125=+y x 的距离为2的一个点. ……10分 27 (2007春季18)(14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分. 如图，在直角坐标系xOy 中，设椭圆)0(1:2222>>=+b a by a x C 的左右两个焦点分别为21F F 、. 过右焦点2F 且与x 轴垂直的直线l 与椭圆C 相交，其中一个交点为()1,2M.(1) 求椭圆C 的方程；(2) 设椭圆C 的一个顶点为),0(b B -，直线2BF 交椭圆C 于另一点N ，求△BN F 1的面积.[解] (1) [解法一] x l ⊥ 轴，2F ∴的坐标为()0,2.…… 2分由题意可知 ⎪⎩⎪⎨⎧=-=+,2,1122222b a ba 得 ⎩⎨⎧==.2,422b a ∴ 所求椭圆方程为12422=+y x . …… 6分 [解法二]由椭圆定义可知a MF MF 221=+. 由题意12=MF ，121-=∴a MF . …… 2分又由Rt △21F MF 可知 ()122)12(22+=-a ，0>a ，2=∴a ，又222=-b a ，得22=b . ∴ 椭圆C 的方程为12422=+y x . …… 6分 (2)直线2BF 的方程为2-=x y . …… 8分由 ⎪⎩⎪⎨⎧=+-=,124,222y x x y 得点N 的纵坐标为32. …… 10分又2221=F F ，3822322211=⨯⎪⎪⎭⎫ ⎝⎛+⨯=∴∆BN F S . …… 14分 28 (2007年21)（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．我们把由半椭圆12222=+b y a x (0)x ≥与半椭圆12222=+cx b y (0)x ≤合成的曲线称作“果圆”，其中222c b a +=，0>a ，0>>c b ．如图，点0F ，1F ，2F 是相应椭圆的焦点，1A ，2A 和1B ，2B 分别是“果圆”与x ，y轴的交点．（1）若012F F F △是边长为1的等边三角形，求 “果圆”的方程；（2）当21A A >21B B 时，求ab的取值范围；（3）连接“果圆”上任意两点的线段称为“果圆” 的弦．试研究：是否存在实数k ，使斜率为k 的“果圆”平行弦的中点轨迹总是落在某个椭圆上？若存在，求出所有可能的k 值；若不存在，说明理由．解：（1）(()012(0)00F c F F ，，，，，021211F F b F F ∴====，，于是22223744c a b c ==+=，，所求“果圆”方程为 2241(0)7x y x +=≥，2241(0)3y x x +=≤．（2）由题意，得 b c a 2>+，即a b b a ->-222．2222)2(a c b b =+> ，222)2(a b b a ->-∴，得54<a b ．又21,222222>∴-=>a b b a c b ． 45b a ⎫∴∈⎪⎪⎝⎭，．（3）设“果圆”C 的方程为22221(0)x y x a b +=≥，22221(0)y x x b c +=≤．记平行弦的斜率为k ．当0=k 时，直线()y t b t b =-≤≤与半椭圆22221(0)x y x a b +=≥的交点是P t ⎛⎫ ⎪ ⎪⎝⎭，与半椭圆22221(0)y x x b c +=≤的交点是Q t ⎛⎫- ⎪ ⎪⎝⎭． ∴ P Q ，的中点M ()x y ，满足 221,2a ct x b y t ⎧-⎪=-⎨⎪=⎩，得122222=+⎪⎭⎫⎝⎛-b y c a x ． b a 2<，∴ 22220222a c a c b a c b b ----+⎛⎫-=≠ ⎪⎝⎭．综上所述，当0=k 时，“果圆”平行弦的中点轨迹总是落在某个椭圆上．当0>k 时，以k 为斜率过1B 的直线l 与半椭圆22221(0)x y x a b +=≥的交点是22232222222ka b k a b b k a b k a b ⎛⎫- ⎪++⎝⎭，．由此，在直线l 右侧，以k 为斜率的平行弦的中点轨迹在直线x kab y 22-=上，即不在某一椭圆上．当0<k 时，可类似讨论得到平行弦中点轨迹不都在某一椭圆上．29 (2008春季18. (本题满分12分) 在平面直角坐标系xOy 中，A B 、分别为直线2x y +=与x y 、轴的交点，C 为AB 的中点. 若抛物线22(0)y px p =>过点C ，求焦点F 到直线AB 的距离.[解] 由已知可得 (2,0),(0,2),(1,1)A B C ， …… 3分解得抛物线方程为 2y x =. …… 6分于是焦点 1,04F ⎛⎫⎪⎝⎭. …… 9分∴ 点F 到直线AB 的距离为=. …… 12分30 (2008春季22)(本题满分18分)本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.已知z 是实系数方程220x bx c ++=的虚根，记它在直角坐标平面上的对应点为(Re ,Im )z P z z .（1）若(,)b c 在直线20x y +=上，求证：z P 在圆1C ：22(1)1x y -+=上；（2）给定圆C ：222()x m y r -+=（R m r ∈、，0r >），则存在唯一的线段s 满足：①若z P 在圆C 上，则(,)b c 在线段s 上；② 若(,)b c 是线段s 上一点（非端点），则z P 在圆C 上. 写出线段s 的表达式，并说明理由；（3）由（2）知线段s 与圆C 之间确定了一种对应关系，通过这种对应关系的研究，填写表一（表中1s 是（1）中圆1C 的对应线段）.[证明]（1）由题意可得 20b c +=，解方程2220x b x b +-=，得z b =-， …… 2分∴点(),z P b -或(),z P b -，将点z P 代入圆1C 的方程，等号成立， ∴ z P 在圆1C ：22(1)1x y -+=上. …… 4分（2）[解法一] 当0∆<，即2b c <时，解得z b =-，∴点(),z P b -或(),z P b -，由题意可得222()b m c b r --+-=，整理后得 222c mb r m =-+-， …… 6分()240b c ∆=-<，222()b m c b r ++-=， (,)b m r m r ∴∈---+.∴ 线段s 为： 222c mb r m =-+-，[,]b m r m r ∈---+.若(,)b c 是线段s 上一点（非端点），则实系数方程为222220,(,)x bx mb r m b m r m r +-+-=∈---+.此时0∆<，且点(),z P b -、(),z P b -在圆C上.…… 10分[解法二] 设i =+z x y 是原方程的虚根，则2(i)2(i)0++++=x y b x y c ，解得22,2,x b y x bx c =-⎧⎨=++⎩①②由题意可得，222()x m y r -+=. ③解①、②、③ 得 222c mb r m =-+-. …… 6分以下同解法一. [解]（3）表一。

历年上海高考试题(立体几何)

历年上海高考试题(立体几何)(01春)若有平面α与β，且l P P l ∉α∈β⊥α=βα,,, ，则下列命题中的假命题为（）（A ）过点P 且垂直于α的直线平行于β．（B ）过点P 且垂直于l 的平面垂直于β．（C ）过点P 且垂直于β的直线在α内．（D ）过点P 且垂直于l 的直线在α内．（01）已知a 、b 为两条不同的直线，α、β为两个不同的平面，且a ⊥α，b ⊥β，则下列命题中的假命题是（）DA. 若a ∥b ，则α∥βB.若α⊥β，则a ⊥bC.若a 、b 相交，则α、β相交D.若α、β相交，则a 、b 相交(02春)下图表示一个正方体表面的一种展开图，图中四条线段AB 、CD 、EF 和GH 在原正方体中相互异面的有对。

3(02)若正四棱锥的底面边长为cm 32,体积为34cm ，则它的侧面与底面所成的二面角的大小是 30(03春)关于直线l b a ,,以及平面N M ,，下列命题中正确的是( ).(A) 若M b M a //,//,则b a // (B) 若a b M a ⊥,//,则M b ⊥(C) 若M b M a ⊂⊂,,且b l a l ⊥⊥,,则M l ⊥ (D) 若N a M a //,⊥,则N M ⊥ D(03) 在正四棱锥P —ABCD 中，若侧面与底面所成二面角的大小为60°，则异面直线PA1C CB1B1A与BC 所成角的大小等于 .（结果用反三角函数值表示）arctg2 (03)在下列条件中，可判断平面α与β平行的是（）A ．α、β都垂直于平面r .B ．α内存在不共线的三点到β的距离相等.C ．l ，m 是α内两条直线，且l ∥β，m ∥β.D ．l ，m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β. D (04春)如图,在底面边长为2的正三棱锥V-ABC 中,E 是BC 的中点,若△V AE 的面积是41,则侧棱V A 与底面所成角的大小为 (结果用反三角函数表示) arctg 41(04) 在下列关于直线l 、m 与平面α、β的命题中,真命题是( ) (A)若l ⊂β且α⊥β,则l ⊥α. (B) 若l ⊥β且α∥β,则l ⊥α. (C) 若l ⊥β且α⊥β,则l ∥α. (D) 若α∩β=m 且l ∥m,则l ∥α. B(05春)已知直线n m l 、、及平面α，下列命题中的假命题是（A ）若//l m ，//m n ，则//l n . （B ）若l α⊥，//n α，则l n ⊥.（C ）若l m ⊥，//m n ，则l n ⊥. （D ）若//l α，//n α，则//l n .D(05)有两个相同的直三棱柱,高为a2,底面三角形的三边长分别为3a 、4a 、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a 的取值范围是．0<a<315(06春)正四棱锥底面边长为4，侧棱长为3，则其体积为 .316 (06文)若空间中有两条直线，则“这两条直线为异面直线”是“这两条直线没有公共点”的（）（A ）充分非必要条件（B ）必要非充分条件（C ）充分必要条件（D ）既非充分又非必要条件 A(06理)若空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 [答]（）A （A ）充分非必要条件；（B ）必要非充分条件；（C ）充要条件；（D ）非充分非必要条件． (07文) 如图，在直三棱柱111C B A ABC -中，90=∠ACB ， 21=AA ，1==BC AC ，则异面直线B A 1与AC 所成角的大小是（结果用反三角函数值表示）．66arccos(07理)在平面上，两条直线的位置关系有相交、平行、重合三种．已知αβ，是两个相交平面，空间两条直线12l l ，在α上的射影是直线12s s ，，12l l ，在β上的射影是直线12t t ，．用1s 与2s ，1t 与2t 的位置关系，写出一个总能确定1l 与2l 是异面直线的充分条件：．21//s s ，并且1t 与2t 相交（//1t 2t ，并且1s 与2s 相交）(01春) 用一块钢锭浇铸一个厚度均匀，且全面积为2平方米的正四棱锥形有盖容器（如图），设容器的高为h 米，盖子边长为a 米．（1）求a 关于h 的函数解析式；（2）设容器的容积为V 立方米，则当h 为何值时，V 最大？求出V 的最大值．（求解本题时，不计容器的厚度）解（1）设'h 为正四棱锥的斜高由已知⎪⎪⎩⎪⎪⎨⎧=+=⋅+,'h a 41h ,2a 'h 214a 2222解得)0(112>+=h h a（2）)0()1(33122>+==h h hha V 易得)h1h (31V +=因为2121=⋅≥+h h h h ，所以61≤V 等式当且仅当hh 1=，即1=h 时取得。

历年高考立体几何真题+答案

历年高考真题1、2003（理科）（本题满分12分）已知平行六面体ABCD —A 1B 1C 1D 1中，A 1A ⊥平面ABCD ，AB=4，AD=2.若B 1D ⊥BC ，直线B 1D 与平面ABCD 所成的角等于30°，求平行六面体ABCD —A 1B 1C 1D 1的体积.．[解]连结BD ，因为B 1B ⊥平面ABCD ，B 1D ⊥BC ，所以BC ⊥BD.在△BCD 中，BC=2，CD=4，所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°，所以 ∠B 1DB=30°，于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 2.2005（理科）(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.已知正三棱锥ABC P -的体积为372，侧面与底面所成的二面角的大小为 60. （1）证明：BC PA ⊥；（2）求底面中心O 到侧面的距离.[证明]（1）取BC 边的中点D ，连接AD 、PD ，则BC AD ⊥，BC PD ⊥，故⊥BC 平面APD . BCPA ⊥[解]（2）如图，由（1）可知平面⊥PBC 平面APD ，则PDA ∠面所成二面角的平面角.过点O 作E PD OE ,⊥为垂足，则OE 就是点O 到侧面的距离. 设OE 为h ，由题意可知点O 在AD 上，∴ 60=∠PDO ，h OP 2=.h BC h OD 4,32=∴=,∴ 2234)4(43h h S ABC ==∆， ∵ 3233823431372h h h =⋅⋅=，∴ 3=h . 即底面中心O 到侧面的距离为3.3、2006（理科）（本题满分 14分）本题共有 2个小题，第 1小题满分 5分，第 2小题满分满分 9分。

在三棱柱 ABC —A1B1C1 中，∠ABC=90°，AB=BC=1。

历届数学高考中的试题空间向量与立体几何

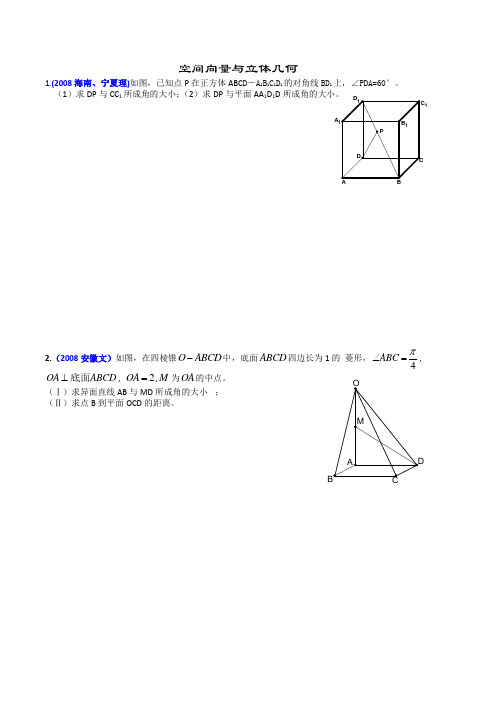
空间向量与立体几何1.(2008海南、宁夏理)如图，已知点P 在正方体ABC D －A 1B 1C 1D 1的对角线BD 1上，∠PDA=60°。

（1）求DP 与CC 1所成角的大小；（2）求DP 与平面AA 1D 1D2.（2008安徽文）如图，在四棱锥O ABCD -中，底面ABCD 四边长为1的菱形，4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点。

（Ⅰ）求异面直线AB 与MD 所成角的大小；（Ⅱ）求点B 到平面OCD 的距离。

1A3.（2005湖南文、理）如图1，已知ABCD 是上、下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴OO 1折成直二面角，如图2。

（Ⅰ）证明：AC ⊥BO 1；（Ⅱ）求二面角O －AC －O 1的大小。

4.（2007安徽文、理)如图,在六面体1111D C B A ABCD -中,四边形ABCD 是边长为2的正方形,四边形1111D C B A 是边长为1的正方形,⊥1DD 平面1111D C B A ,⊥1DD 平面ABCD ，DD 1=2。

(Ⅰ)求证:11C A 与AC 共面，11D B 与BD 共面. (Ⅱ)求证:平面;1111BDD B ACC A 平面⊥ (Ⅲ)求二面角C BB A --1的大小.A BC D O O 1 A B O C O 1 D5.(2007海南、宁夏理)如图，在三棱锥S ABC -中，侧面SAB 与侧面SAC 均为等边三角形，90BAC ∠=°，O 为BC 中点．（Ⅰ）证明：SO ⊥平面ABC ；（Ⅱ）求二面角A SC B --的余弦值．6.(2007四川理）如图，PCBM 是直角梯形，∠PCB ＝90°，PM ∥BC ，PM ＝1，BC ＝2，又AC ＝1，∠ACB ＝120°，AB ⊥PC ，直线AM 与直线PC 所成的角为60°. （Ⅰ）求证：平面PAC ⊥平面ABC ; （Ⅱ）求二面角B AC M --的大小; （Ⅲ）求三棱锥MAC P -的体积.OS B AC7.(2006全国Ⅰ卷文、理)如图，1l 、2l 是互相垂直的异面直线,MN 是它们的公垂线段.点A 、B 在1l 上，C 在2l 上，AM MB MN ==。

近五年上海高考分类汇编——立体几何(供参考)(新)

1近五年上海高考汇编——立体几何一、填空题1.（2009年高考5）如图，若正四棱柱1111-ABCD A B C D 的底面边长为2，高为4，则异面直线1BD 与AD 所成角的大小是_____ ___.（结果用反三角函数值表示）答案：arctan 52.（2009年高考理科8）已知三个球的半径1R ，2R ，3R 满足32132R R R =+，则它们的表面积1S ，2S ，3S 满足的等量关系是_____ ___. 答案：12323S S S +=3.（2009年高考文科6）若球12,O O 的面积之比124S S =，则它们的半径之比12RR =___ ____. 答案：24.（2009年高考文科8）若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是____ ____. 答案：83π5.（2010年高考理科12）如图所示，在边长为4的正方形纸片ABCD 中，AC 与BD 相交于点O ，剪去AOB ，将剩余部分沿,OC OD 折叠，使,OA OB 重合，则以(),A B ,,C D O 为顶点的四面体的体积是_____ ___.答案：826.（2010年高考文科6）已知四棱锥P ABCD -的底面是边长为6的正方体，侧棱PA ⊥底面ABCD ，且8PA =，则该四棱锥的体积是_____ ___.2答案：967.（2011年高考理科7）若圆锥的侧面积为2π，底面面积为π，则该圆锥的体积为_____ __. 答案：33π 8.（2011年高考文科7）若一个圆锥的主视图是边长为3，3，2的三角形，则该圆锥的侧面积为_____ ____. 答案：3π9.（2012年高考理科6）有一列正方体，棱长组成以1为首项、12为公比的等比数列，体积分别记为12,,...,,...n V V V ，则12lim(...)n n V V V →∞+++=_____ ____.答案：8710.（2012年高考理科8）若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为_____ ____. 答案：33π 11.（2012年高考理科14）如图，AD 与BC 是四面体ABCD 中互相垂直的棱，2BC =，若2AD c =，且2AB BD AC CD a +=+=，其中,a c 为常数，则四面体ABCD 的体积的最大值是_____ ____.答案：22213c a c -- 12.（2012年高考文科5）一个高为2的圆柱，底面周长为2π，该圆柱的表面积为_____ ____. 答案：6π13.（2013年高考理科13）在xOy 平面上，将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y =和1y =-围成的封闭图形记为D ，如图中阴影部分．记D 绕y 轴旋转一周而成的几何体为Ω．过(0,)(||1)y y ≤作Ω的水平截面，所得截面面积为2418y ππ-+．试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为_____ ____.3答案：2216ππ+14.（2013年高考文科10）已知圆柱Ω的母线长为l ，底面半径为r ，O 是上底面圆心，A 、B 是下底面圆周上两个不同的点，BC 是母线，如图．若直线OA 与BC 所成角的大小为6π，则l r =_____ ____.3二、选择题1.（2009年高考文科16）如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的主视图是（）Oxyz443(D)(C)(B)(A)54433444答案：B三、解答题1.（2009年高考理科19）如图，在直三棱柱ABC A B C '''-中，2AA BC AB '===,AB BC ⊥,求二面角B A C C '''--的大小4答案：如图，建立空间直角坐标系则 A ()2,0,0，C ()0,2,0，A 1()2,0,2，B 1()0,0,2，C 1()0,2,2，设AC 的中点为M ，BM ⊥AC ，BM ⊥CC 1，∴ BM ⊥平面AC 1C ，即BM =()1,1,0是平面AC 1C 的一个法向量。

2005高考立体几何解答题

2005年——立体几何解答题已知四棱锥P-ABCD 的底面为直角梯形，AB ∥DC ，⊥=∠PA DAB ,90 底面ABCD ，且PA=AD=DC=21AB=1，M 是PB 的中点。

（Ⅰ）证明：面PAD ⊥面PCD ；（Ⅱ）求AC 与PB 所成的角；（Ⅲ）求面AMC 与面BMC 所成二面角的大小。

2．如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PD ⊥底面ABCD,AD=PD,E 、F 分别为CD 、PB 的中点. (Ⅰ)求证:EF ⊥平面PAB(Ⅱ)设BC AB 2=,求AC 与平面AEF 所成的角的大小.3．[2005全国卷Ⅲ（四川、陕西、云南等地区用）理第18题，文第19题，满分12分]如图，在四棱锥V-ABCD 中，底面ABCD 是正方形，侧面V AD 是正三角形, 平面V AD ⊥底面ABCD ．（Ⅰ）证明AB ⊥平面V AD ；（Ⅱ）求面V AD 与面VDB 所成的二面角的大小． 4．如图，直二面角D-AB-E 中，四边形ABCD 是边长为2的正方形，AE ＝EB ，F 为CE 上的点，且BF ⊥平面ACE ．（Ⅰ）求证：AE ⊥平面BCE ；（Ⅱ）求二面角B-AC-E 的大小；（Ⅲ）求点D 到平面ACE 的距离。

5．如图1，已知ABCD 是上．下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴OO 1折成直二面角，如图2.（Ⅰ）证明：AC ⊥BO 1；（Ⅱ）求二面角O －AC －O 1的大小.6．如图，在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝kP A ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ．(Ⅰ)求证OD ∥平面PAB ； (文Ⅱ)当k ＝21时，求直线OD 与平面PBC 所成角的大小；(理Ⅱ)当k ＝21时，求直线P A 与平面PBC 所成角的大小；(理Ⅲ) 当k 取何值时，O 在平面PBC 内的射影恰好为△PBC 的重心？7．如图, 在直四棱柱ABCD －A 1B 1C 1D 1中，AB ＝AD ＝2，DCEF D C BAA BCDOP＝23，AA 1＝3，AD ⊥DC ，AC ⊥BD , 垂足为E ，（I ）求证：BD ⊥A 1C ；（II ）求二面角A 1－BD －C 1的大小；（III ）求异面直线 AD 与 BC 1所成角的大小．8．如图, 在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AA 1＝4，点D 是AB 的中点，（I ）求证：AC ⊥BC 1；（II ）求证：AC 1//平面CDB 1；（III ）求异面直线 AC 1与 B 1C 所成角的余弦值． 9．如图， PA=BC=6，AB=8，PB=AC=10，342=PB ，F 是线段PB 上一点，173415=CF ，点E 在线段AB 上，且EF ⊥PB（I ）求证：PB ⊥平面CEF（II ）求二面角B —CE —F 的大小10．如图，在五棱锥S —ABCDE 中，SA ⊥底面ABCDE ，SA=AB=AE=2，3==DE BC ，︒=∠=∠=∠120CDE BCD BAE 。

上海历年高考数学解析几何真题

Ⅰ 点到直线的距离公式（11春17）直线)21(:+=x k y l 与圆1:22=+y x C 的位置关系是的位置关系是的位置关系是 ( ) ( ) （（A ）相交或相切）相交或相切. . . （（B ）相交或相离）相交或相离. . （（C ）相切）相切. . . （（D ）相交）相交. .（10理5文7）圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = 。

（06理2）已知圆2x －4x －4＋2y ＝0的圆心是点P ，则点P 到直线x －y －1＝0的距离是．．Ⅰ 圆的方程（04理8）圆心在直线2x 2x－－y －7=0上的圆C 与y 轴交于两点A(0, -4),B(0, -2),-2),则圆则圆C 的方程为方程为 . .（04文8）圆心在直线x =2上的圆C 与y 轴交于两点A(0, A(0, －－4),B(0, 4),B(0, －－2),2),则圆则圆C 的方程为 .Ⅰ 圆锥曲线的基本概念：标准方程、焦点、渐近线、准线、定义（12文16）对于常数m 、n ，“0mn >”是“方程221mx ny +=的曲线是椭圆”的（的曲线是椭圆”的（） A 、充分不必要条件、充分不必要条件 B 、必要不充分条件、必要不充分条件 C 、充分必要条件、充分必要条件 D 、既不充分也不必要条件、既不充分也不必要条件（11理3）设m 为常数，若点(0,5)F 是双曲线2219y x m -=的一个焦点，则m = 。

（11春9）若椭圆C 的焦点和顶点分别是双曲线14522=-y x 的顶点和焦点，的顶点和焦点，则椭圆则椭圆C 的方程是程是_______________________________________。

（10理3文8）动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等，则P 的轨迹方程为 ______。

（08文6）若直线01=+-y ax 经过抛物线x y 42=的焦点，则实数=a .（08文12）设P 是椭圆1162522=+y x 上的点上的点. . . 若若1F 、2F 是椭圆的两个焦点，则21PF PF +等于等于 ( ) ( )(A) 4. (B) 5. (C) 8. (D) 10.（07理8）已知双曲线22145x y -=，则以双曲线中心为焦点，以双曲线左焦点为顶点的抛物线方程为_____（07文5）以双曲线15422=-y x 的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是程是．．（06理7）已知椭圆中心在原点，一个焦点为F （－（－223，0），且长轴长是短轴长的2倍，则该椭圆的标准方程是则该椭圆的标准方程是．．（06文7）已知双曲线中心在原点，一个顶点的坐标为(3,0),且焦距与虚轴长之比为5:4，则双曲线的标准方程是则双曲线的标准方程是____________________. ____________________.（05文7）若椭圆长轴长与短轴长之比为2，它的一个焦点是()0,152，则椭圆的标准方程是__________.（05理5）若双曲线的渐近线方程为x y 3±=，它的一个焦点是()0,10，则双曲线的方程是____________________。

2008年高考数学试题分类汇编立体几何

2008年高考数学试题分类汇编立体几何2008年高考数学试题分类汇编立体几何一．选择题：1．（上海卷13）给定空间中的直线l 及平面α，条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的（ C ）条件A ．充要B ．充分非必要C ．必要非充分D ．既非充分又非必要 2.（全国一11）已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ C ）A ．13B 2C 3D ．233.（全国二10）已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（ C ）A ．13B ．23C ．33D ．234.（全国二12）已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ C ） A ．1B ．2C ．3D ．25.（北京卷8）如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上．过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设BP x =，MN y =，则函数()y f x =的图象大致是（ B ）7.（四川卷８）设,M N 是球心O 的半径OP 上的两点，且NP MN OM ==，分别过,,N M O 作垂线于OP 的面截球得三个圆，则这三个圆的面积之比为：( D )A BC D M N P A 1 B 1C 1D 1y x A ． O y x B ． O y x C ． O yx D ． O（Ａ）3,5,6 （Ｂ）3,6,8 （Ｃ）5,7,9 （Ｄ）5,8,98.（四川卷９）设直线l ⊂平面α，过平面α外一点A 与,l α都成030角的直线有且只有：( B )（Ａ）１条（Ｂ）２条（Ｃ）３条（Ｄ）４条9.（天津卷5）设b a ,是两条直线，βα,是两个平面，则b a ⊥的一个充分条件是C（A ）βαβα⊥⊥,//,b a （B ）βαβα//,,⊥⊥b a （C ）βαβα//,,⊥⊂b a （D ）βαβα⊥⊂,//,b a10.（安徽卷4）．已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是（D ）A ．,,m n m n αα若则‖‖‖B ．,,αγβγαβ⊥⊥若则‖C ．,,m m αβαβ若则‖‖‖D ．,,m n m n αα⊥⊥若则‖11.（山东卷6）右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是D (A)9π （B ）10π (C)11π (D)12π 12.（江西卷10）连结球面上两点的线段称为球的弦。

上海近5年高考数学真题分析仅供参考

6 12+12+14+14+16+18=86 150
6 12+12+14+14+16+18=86 150
2007 11 11*4=44 4
4*4=16
6 12+14+14+14+18+18=90 150
2008 11 11*4=44 4
4*4=16
6 12+13+15+16+16+18=90 150
（05年上海高考）椭圆问题
立体几何
题型年份 2004 2005 2006 2007 2008 合计
填空题题号分值
11
4
10
4
10
4
12
选择题题号分值
13
4
4
解答题
题号分值
21
16
17
12
19
14
16
12
16
12
66
合计
16 16 18 16 16 82
（08年上海高考）正方体线面角（07年上海高考）直三棱柱求线面角（06年上海高考）四棱锥：体积和异面直线的夹角（05年上海高考）直四棱柱：异面直线的夹角
选择题
题号分值
13
4
14
4
8
解答题
题号分值
22
9
22
9
21
16
20
18
21
18
70
合计
21 13 16 18 22 90
复数
题型年份 2004 2005 2006 2007 2008 合计

(完整版)历年上海高考题(立体几何)

17．（2017-21-17）如图，直三棱柱ABC-A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5．（1）求三棱柱ABC-A 1B 1C 1的体积；（2）设M 是BC 中点，求直线A 1M 与平面ABC 所成角的大小．17.【解析】（1）∵直三棱柱ABC-A 1B 1C 1的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱AA 1的长为5．∴三棱柱ABC ﹣A 1B 1C 1的体积V=S △ABC ·AA 1=12AB ·AC ·AA 1=12×4×2×5=20.（2）连接AM.∵直三棱柱ABC-A 1B 1C 1， ∴AA 1⊥底面ABC.∴∠AMA 1是直线A 1M 与平面ABC 所成角. ∵△ABC 是直角三角形，两直角边AB 和AC 的长分别为4和2，点M 是BC 的中点，∴AM=12BC=12×42+22= 5.由AA 1⊥底面ABC ，可得AA 1⊥AM,∴tan ∠A 1MA=AA 1AM =55= 5.∴直线A 1M 与平面ABC 所成角的大小为arctan 5．19．（2016•23-19）将边长为1的正方形AA 1O 1O （及其内部）绕OO 1旋转一周形成圆柱，如图，AC 长为π，A 1B 1长为，其中B 1与C 在平面AA 1O 1O 的同侧．（1）求三棱锥C ﹣O 1A 1B 1的体积；（2）求异面直线B 1C 与AA 1所成的角的大小．【考点】异面直线及其所成的角．【专题】计算题；转化思想；综合法；空间位置关系与距离．【分析】（1）连结O1B1，推导出△O1A1B1为正三角形，从而=，由此能求出三棱锥C﹣O1A1B1的体积．（2）设点B1在下底面圆周的射影为B，连结BB1，则BB1∥AA1，∠BB1C为直线B1C与AA1所成角（或补角），由此能求出直线B1C与AA1所成角大小．【解答】解：（1）连结O1B1，则∠O1A1B1=∠A1O1B1=，∴△O1A1B1为正三角形，∴=，==．（2）设点B1在下底面圆周的射影为B，连结BB1，则BB1∥AA1，∴∠BB1C为直线B1C与AA1所成角（或补角），BB1=AA1=1，连结BC、BO、OC，∠AOB=∠A1O1B1=，，∴∠BOC=，∴△BOC为正三角形，∴BC=BO=1，∴tan∠BB1C=45°，∴直线B1C与AA1所成角大小为45°．【点评】本题考查三棱锥的体积的求法，考查两直线所成角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．19、（2015.上海）如图。

2005全国高考试题分类解析立体几何

2005全国高考立体几何题一网打尽河北、河南、山西、安徽(全国卷I)（2）一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为（C ）（A ）π28（B ）π8（C ）π24（D ）π4（4）如图，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且BCF ADE ∆∆、均为正三角形，EF ∥AB ，EF=2，则该多面体的体积为（C ）（A ）32（B ）33 （C ）34 （D ）23 （16）在正方形''''D C B A ABCD -中，过对角线'BD 的一个平面交'AA 于E ，交'CC 于F ，则① 四边形E BFD '一定是平行四边形 ② 四边形E BFD '有可能是正方形③ 四边形E BFD '在底面ABCD 内的投影一定是正方形 ④ 四边形E BFD '有可能垂直于平面D BB '以上结论正确的为 ①③④ 。

（写出所有正确结论的编号）（18）（本大题满分12分）已知四棱锥P-ABCD 的底面为直角梯形，AB ∥DC ，⊥=∠PA DAB ,90底面ABCD ，且PA=AD=DC=21AB=1，M 是PB 的中点。

（Ⅰ）证明：面PAD ⊥面PCD ；（Ⅱ）求AC 与PB 所成的角；（Ⅲ）求面AMC 与面BMC 所成二面角的大小。

18．本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分. 方案一：（Ⅰ）证明：∵PA ⊥面ABCD ，CD ⊥AD ， ∴由三垂线定理得：CD ⊥PD.因而，CD 与面PAD 内两条相交直线AD ，PD 都垂直， ∴CD ⊥面PAD.又CD ⊂面PCD ，∴面PAD ⊥面PCD.（Ⅱ）解：过点B 作BE//CA ，且BE=CA ，则∠PBE 是AC 与PB 所成的角.连结AE ，可知AC=CB=BE=AE=2，又AB=2，所以四边形ACBE 为正方形. 由PA ⊥面ABCD 得∠PEB=90°在Rt △PEB 中BE=2，PB=5， .510cos ==∠∴PB BE PBE .510arccos所成的角为与PB AC ∴ （Ⅲ）解：作AN ⊥CM ，垂足为N ，连结BN. 在Rt △PAB 中，AM=MB ，又AC=CB ， ∴△AMC ≌△BMC,∴BN ⊥CM ，故∠ANB 为所求二面角的平面角. ∵CB ⊥AC ，由三垂线定理，得CB ⊥PC ，在Rt △PCB 中，CM=MB ，所以CM=AM. 在等腰三角形AMC 中，AN ·MC=AC AC CM ⋅-22)2(， 5625223=⨯=∴AN . ∴AB=2，322cos 222-=⨯⨯-+=∠∴BN AN AB BN AN ANB 故所求的二面角为).32arccos(-方法二：因为PA ⊥PD ，PA ⊥AB ，AD ⊥AB ，以A 为坐标原点AD 长为单位长度，如图建立空间直角坐标系，则各点坐标为A （0，0，0）B （0，2，0），C （1，1，0），D （1，0，0），P （0，0，1），M （0，1，)21. （Ⅰ）证明：因.,0),0,1,0(),1,0,0(DC AP ⊥=⋅==所以故由题设知AD ⊥DC ，且AP 与AD 是平面PAD 内的两条相交直线，由此得DC ⊥面PAD. 又DC 在面PCD 上，故面PAD ⊥面PCD. （Ⅱ）解：因),1,2,0(),0,1,1(-==.510||||,cos ,2,5||,2||=⋅>=<=⋅==PB AC PB AC 所以故（Ⅲ）解：在MC 上取一点N （x ，y ，z ），则存在,R ∈λ使,λ=..21,1,1),21,0,1(),,1,1(λλ==-=∴-=---=z y x z y x要使.54,0210,==-=⋅⊥λ解得即只需z x MC AN MC AN),52,1,51(),52,1,51(,.0),52,1,51(,54=⋅-===⋅=MC BN BN AN N 有此时能使点坐标为时可知当λANB MC BN MC AN ∠⊥⊥=⋅=⋅所以得由.,0,0为所求二面角的平面角. ).32arccos(.32||||),cos(.54,530||,530||--=⋅=∴-=⋅==故所求的二面角为BN AN文科数学（全国卷Ⅰ）（11）点O 是三角形ABC 所在平面内的一点，满足⋅=⋅=⋅，则点O 是ABC ∆的（A ）三个内角的角平分线的交点（B ）三条边的垂直平分线的交点（C ）三条中线的交点（D ）三条高的交点 2005高考全国卷Ⅱ数学（理）试题（吉林、黑龙江、广西等地区用）(2) 正方体ABCD —A 1 B 1 C 1 D 1中，P 、Q 、R 、分别是AB 、AD 、B 1 C 1的中点。