图形折叠问题

合集下载

图形的折叠问题的习题带答案

折叠问题中的角度运算1、三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为_____度。

分析：利用三角形的内角和和四边形的内角和即可求得．解：∠A+∠B+∠C=180°，∠C=180°-∠A-∠B=180°-55°-75°=50°①，∠C+∠CED+∠CDE=180°，∠CED+∠CDE=180°-∠C=180°-50°=130°②，∠B+∠A+∠CED+∠CDE+∠1+∠2=360°③，把①②分别代入③得75°+55°+130°+∠1+∠2=360°，得∠1+∠2=100°2、如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处。

若∠A=22°，则∠BDC等于______。

分析：△ABC中，∠ACB=90°，∠A=22°，∴∠B=90°－∠A=68°。

由折叠的性质可得：∠CED=∠B=68°，∠BDC=∠EDC，∴∠ADE=∠CED﹣∠A=46°。

3、如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于______。

分析：根据折叠前后角相等可知．解：∵∠1=50°，∴∠AEF=180°-∠BFE=180°-(180°-50°)÷2=115°．点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．4、如图，把一张长方形纸条ABCD沿EF折叠，若∠1=56°，则∠EGF应为______.分析：本题根据平行线的性质和翻折的性质，求解即可．解答：解：因为折叠，且∠1=56°，所以∠C′FB=180°-2×56°=68°，∵D′E//C′F，∴∠EGF=∠C′FB=68°．5、如图，D、E分别为△ABC的边AB、AC上的点，DE∥BC，将△ABC沿线段DE折叠，使点A落在BC上的点F处，若∠B=55°，则∠BDF的度数为______。

初中折叠问题题型

初中数学中常见的折叠问题题型有以下几种：
折纸问题：给定一张矩形纸，将其沿着某些折痕折叠，问最后得到的图形是什么。

这类问题涉及到几何图形的变形和对称性质，需要掌握基本的折叠技巧和对称关系。

线段折叠问题：给定一条线段，将其沿着某些点折叠成一些角度，然后问折叠后的图形是什么。

这类问题涉及到三角函数和几何图形的变形，需要掌握基本的三角函数知识和折叠技巧。

立体图形折叠问题：给定一个立体图形的展开图，将其折叠成一个实体立体图形，然后问最终得到的图形是什么。

这类问题涉及到几何图形的空间变形和对称性质，需要掌握立体几何的基本概念和折叠技巧。

以上是初中数学中常见的折叠问题题型，需要注意的是，这些问题不仅考察计算能力，还要求学生具备一定的几何直观和空间想象能力。

中考数学专题训练：图形的折叠问题(附参考答案)

中考数学专题训练：图形的折叠问题（附参考答案）1．如图，在平面直角坐标系中，矩形ABCD的边AD＝5，OA∶OD＝1∶4，将矩形ABCD沿直线OE折叠到如图所示的位置，线段OD1恰好经过点B，点C落在y轴的点C1处，则点E的坐标是( )A．(1，2) B．(－1，2)C．(√5－1，2) D．(1－√5，2)2．如图，将矩形纸条ABCD折叠，折痕为EF，折叠后点C，D分别落在点C′，D′处，D′E与BF交于点G.已知∠BGD′＝30°，则∠α的度数是( )A．30°B．45°C．74°D．75°3．如图，在矩形ABCD中，AB＝2，BC＝2√5，E是BC的中点，将△ABE沿直线AE翻折，点B落在点F处，连接CF，则cos ∠ECF的值为( )A．23B．√104C．√53D．2√554．把一张矩形纸片ABCD按如图所示方法进行两次折叠，得到等腰直角三角形BEF.若BC＝1，则AB的长度为( )A．√2B．√2+12C．√5+12D．435．如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D，E分别在AB，AC 上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上．若FD平分∠EFB，则AD的长为( )A．259B．258C．157D．2076．如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为__________．7．如图，在Rt△ABC纸片中，∠ACB＝90°，CD是边AB上的中线，将△ACD沿CD折叠，当点A落在点A′处时，恰好CA′⊥AB.若BC＝2，则CA′＝_______．8．如图，点E在矩形ABCD的边CD上，将△ADE沿AE折叠，点D恰好落在边BC 上的点F处．若BC＝10，sin ∠AFB＝45，则DE＝_____．9．如图，在扇形AOB中，点C，D在AB⏜上，将CD⏜沿弦CD折叠后恰好与OA，OB 相切于点E，F.已知∠AOB＝120°，OA＝6，则EF⏜的度数为________；折痕CD 的长为_______．10．如图，在矩形ABCD中，AB＝5，AD＝4，M是边AB上一动点(不含端点)，将△ADM沿直线DM对折，得到△NDM.当射线CN交线段AB于点P时，连接DP，则△CDP的面积为______；DP的最大值为_______．11．如图，在矩形ABCD中，AB＝2，AD＝√7，动点P在矩形的边上沿B→C→D →A运动．当点P不与点A，B重合时，将△ABP沿AP对折，得到△AB′P，连接CB′，则在点P的运动过程中，线段CB′的最小值为_________．12．如图，DE平分等边三角形ABC的面积，折叠△BDE得到△FDE，AC分别与DF，EF相交于G，H两点．若DG＝m，EH＝n，用含m，n的式子表示GH的长是______．13．如图，在Rt△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E，将△DEC沿DE折叠得到△DEF，DF交AC于点G.若AGGE ＝73，则tan A＝______．14．如图，在等边三角形ABC中，过点C作射线CD⊥BC，点M，N分别在边AB，BC上，将△ABC沿MN折叠，使点B落在射线CD上的点B′处，连接AB′，已知AB＝2.给出下列四个结论：①CN＋NB′为定值；②当BN＝2NC时，四边形BMB′N为菱形；③当点N与C重合时，∠AB′M＝18°；④当AB′最短时，MN＝7√21.20其中正确的结论是__________．(填序号)15．将一个矩形纸片OABC放置在平面直角坐标系中，点O(0，0)，点A(3，0)，点C(0，6)，点P在边OC上(点P不与点O，C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q，且∠OPQ＝30°，点O的对应点O′落在第一象限．设OQ＝t.(1)如图1，当t＝1时，求∠O′QA的大小和点O′的坐标；(2)如图2，若折叠后重合部分为四边形，O′Q，O′P分别与边AB相交于点E，F，试用含有t的式子表示O′E的长，并直接写出t的取值范围；(3)若折叠后重合部分的面积为3√3，则t的值可以是__________________________________________．(请直接写出两个不同．．．．的值即可)16．如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4.将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有________．(填序号)①BD＝8；②点E到AC的距离为3；③EM＝103；④EM∥AC.17．综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动，有一位同学操作过程如下：操作一：对折正方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；操作二：在AD上选一点P，沿BP折叠，使点A落在正方形内部点M处，把纸片展平，连接PM，BM，延长PM交CD于点Q，连接BQ.(1)如图1，当点M在EF上时，∠EMB＝________；(填度数)(2)改变点P在AD上的位置(点P不与点A，D重合)如图2，判断∠MBQ与∠CBQ 的数量关系，并说明理由．参考答案1.D 2．D 3．C 4．A 5．D6. 3√2－3 7．2√3 8．5 9．60°4√6 10．10 2√511．－2 12．√m2+n2 13．3√7714．①②④15．(1)∠O′QA＝60°点O′的坐标为(32，√32)(2)O′E＝3t－6，其中t的取值范围是2<t<3 (3)3或103(答案不唯一，满足3≤t<2√3即可) 16．①④17．(1)30°(2)∠MBQ＝∠CBQ，理由略。

三年级折叠问题巧妙解题技巧

三年级折叠问题巧妙解题技巧
在三年级数学中，折叠问题是一个常见的题型。

这类问题通常涉及到图形折叠后的形状和大小变化。

为了更好地解决这类问题，我们需要掌握一些解题技巧。

解题技巧：
1. 理解折叠原理：折叠图形时，相对的两边会重合，而相对的两角会重合。

因此，在折叠前后的图形中，线段长度和角度大小是不变的。

2. 画图分析：通过画图可以帮助我们更好地理解题目的要求和图形的变化。

在画图时，要特别注意折叠后的图形与原图的关系，以及线段和角度的变化。

3. 利用已知条件：题目中通常会给出一些已知条件，如线段的长度、角度的大小等。

这些条件可以帮助我们确定折叠后的图形形状和大小。

4. 逻辑推理：在解决折叠问题时，逻辑推理是非常重要的。

我们需要根据已知条件和图形变化规律，逐步推导出未知的答案。

5. 反复练习：通过反复练习，我们可以加深对折叠问题的理解，提高解题速度和准确性。

示例题目：
1. 把一张长方形纸对折，每份是它的(1/2)，这张纸被折成多少份？
答案：2份
2. 把一张正方形纸对折两次，每份是它的多少？
答案：(1/4)
通过掌握这些解题技巧，我们可以更好地解决三年级数学中的折叠问题。

(完整版)几何图形折叠问题

几何图形折叠问题【疑难点拨】1.折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2.折叠(翻折)意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图)，从而构造相似三角形，利用相似三角形求边或者角的度数．4.凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1..（2018•四川凉州•3分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（）AD=BC′B．∠EBD=∠EDB C．△ABE∽△CBD D．sin∠ABE=A．2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交于点D，点F是上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A．36π-108 B．108-32π C．2πD．π3. （2017浙江衢州）如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD 于点F，则DF的长等于（）A．B．C．D．4.（2018·山东青岛·3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=，则BC的长是（）A．B．32C．3 D．335.（2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4且∠AFG=60°，GE=2BG，则折痕EF的长为（）A．1 B．C．2 D．二、填空题：6.（2018·辽宁省盘锦市）如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC.AB 上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为．7.（2018·山东威海·8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C 与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=+1，则BC的长．8.（2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB= ．三、解答与计算题：9.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．10.（2018•山东枣庄•10分）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2，求BE的长．【能力篇】一、选择题：11.（2018·辽宁省阜新市）如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A1处，BC=8，那么线段AE的长度为( )．A．4 B．5 C．6 D．712.（2018·四川省攀枝花·3分）如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（）A．1 B．2 C．3 D．413.（2018·湖北省武汉·3分）如图，在⊙O中，点C在优弧上，将弧沿BC折叠后刚好经过AB的中点D．若⊙O的半径为，AB=4，则BC的长是（）A． B．C．D．二、填空题：14. (2018·辽宁省葫芦岛市) 如图，在矩形ABCD中，点E是CD的中点，将△BCE沿BE折叠后得到△BEF、且点F在矩形ABCD的内部，将BF延长交AD于点G．若=，则= ．15.（2018·四川宜宾·3分）如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE 折叠，使点B落在矩形内点F处，下列结论正确的是（写出所有正确结论的序号）①当E为线段AB中点时，AF∥CE；②当E为线段AB中点时，AF=95；③当A、F、C三点共线时，AE=；④当A、F、C三点共线时，△CEF≌△AEF．三、解答与计算题：16.（2018·湖北省宜昌·11分）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B 的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；（2）如图2，①求证：BP=BF；②当AD=25，且AE＜DE时，求cos∠PCB的值；③当BP=9时，求BE•EF的值．17.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．18.（2018•江苏盐城•10分）如图，在以线段为直径的上取一点，连接、.将沿翻折后得到.（1）试说明点在上；（2）在线段的延长线上取一点，使.求证：为的切线；（3）在（2）的条件下，分别延长线段、相交于点，若，，求线段的长.【探究篇】19.（2018年江苏省泰州市•12分）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）（1）根据以上操作和发现，求的值；（2）将该矩形纸片展开．①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P，再将该矩形纸片展开．求证：∠HPC=90°；②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P在折痕上，请简要说明折叠方法．（不需说明理由）20.（2018年江苏省宿迁）如图，在边长为1的正方形ABCD中，动点E、F分别在边AB、CD上，将正方形ABCD 沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A、D重合），点C落在点N处，MN与CD交于点P，设BE=x，（1）当AM= 时，求x的值；（2）随着点M在边AD上位置的变化，△PDM的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；（3）设四边形BEFC的面积为S，求S与x之间的函数表达式，并求出S的最小值.几何图形折叠问题【疑难点拨】1.折叠(翻折)问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用．解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系．2.折叠(翻折)意味着轴对称，会生成相等的线段和角，这样便于将条件集中．如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解．3.矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度．矩形中的两次或多次折叠通常出现“一线三直角”的模型(如图)，从而构造相似三角形，利用相似三角形求边或者角的度数．4.凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量．1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等．【基础篇】一、选择题：1..（2018•四川凉州•3分）如图将矩形ABCD沿对角线BD折叠，使C落在C′处，BC′交AD于点E，则下到结论不一定成立的是（）A．AD=BC′B．∠EBD=∠EDB C．△ABE∽△CBD D．sin∠ABE=【分析】主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案．【解答】解：A、BC=BC′，AD=BC，∴AD=BC′，所以正确．B、∠CBD=∠EDB，∠CBD=∠EBD，∴∠EBD=∠EDB正确．D、∵sin∠ABE=，∴∠EBD=∠EDB∴BE=DE∴sin∠ABE=．故选：C．【点评】本题主要用排除法，证明A，B，D都正确，所以不正确的就是C，排除法也是数学中一种常用的解题方法．2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB．已知OA=6，取OA的中点C，过点C作CD⊥OA交于点D，点F是上一点．若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD，DF，FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（）．A．36π-108 B．108-32π C．2πD．π【考点】MO：扇形面积的计算；P9：剪纸问题．【分析】先求出∠ODC=∠BOD=30°，作DE⊥OB可得DE=OD=3，先根据S弓形BD=S扇形BOD﹣S△BOD求得弓形的面积，再利用折叠的性质求得所有阴影部分面积．【解答】解：如图，∵CD⊥OA，∴∠DCO=∠AOB=90°，∵OA=OD=OB=6，OC=OA=OD，∴∠ODC=∠BOD=30°，作DE⊥OB于点E，则DE=OD=3，∴S弓形BD=S扇形BOD﹣S△BOD=﹣×6×3=3π﹣9，则剪下的纸片面积之和为12×（3π﹣9）=36π﹣108，故答案为：36π﹣108．故选A3. （2017浙江衢州）如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD 于点F，则DF的长等于（）A．B．C．D．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】根据折叠的性质得到AE=AB，∠E=∠B=90°，易证Rt△AEF≌Rt△CDF，即可得到结论EF=DF；易得FC=FA，设FA=x，则FC=x，FD=6﹣x，在Rt△CDF中利用勾股定理得到关于x的方程x2=42+（6﹣x）2，解方程求出x．【解答】解：∵矩形ABCD沿对角线AC对折，使△ABC落在△ACE的位置，∴AE=AB，∠E=∠B=90°，又∵四边形ABCD为矩形，∴AB=CD，∴AE=DC，而∠AFE=∠DFC，∵在△AEF与△CDF中，，∴△AEF≌△CDF（AAS），∴EF=DF；∵四边形ABCD为矩形，∴AD=BC=6，CD=AB=4，∵Rt△AEF≌Rt△CDF，∴FC=FA，设FA=x，则FC=x，FD=6﹣x，在Rt△CDF中，CF2=CD2+DF2，即x2=42+（6﹣x）2，解得x=，则FD=6﹣x=．故选：B．4.（2018·山东青岛·3分）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕现交于点F．已知EF=，则BC的长是（）A．B．32C．3 D．33【分析】由折叠的性质可知∠B=∠EAF=45°，所以可求出∠AFB=90°，再直角三角形的性质可知EF=AB，所以AB=AC的长可求，再利用勾股定理即可求出BC的长．【解答】解：∵沿过点E的直线折叠，使点B与点A重合，∴∠B=∠EAF=45°，∴∠AFB=90°，∵点E为AB中点，∴EF=12AB，EF=32，∴AB=AC=3，∵∠BAC=90°，∴BC=2，故选：B．【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出∠AFB=90°是解题的关键．5.（2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4且∠AFG=60°，GE=2BG，则折痕EF的长为（）A．1 B．C．2 D．【考点】PB：翻折变换（折叠问题）；LB：矩形的性质．【分析】由折叠的性质可知，DF=GF、HE=CE、GH=DC、∠DFE=∠GFE，结合∠AFG=60°即可得出∠GFE=60°，进而可得出△GEF为等边三角形，在Rt△GHE中，通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC= EC，再由GE=2BG结合矩形面积为4，即可求出EC的长度，根据EF=GE=2EC即可求出结论．【解答】解：由折叠的性质可知，DF=GF，HE=CE，GH=DC，∠DFE=∠GFE．∵∠GFE+∠DFE=180°﹣∠AFG=120°，∴∠GFE=60°．∵AF∥GE，∠AFG=60°，∴∠FGE=∠AFG=60°，∴△GEF为等边三角形，∴EF=GE．∵∠FGE=60°，∠FGE+∠HGE=90°，∴∠HGE=30°．在Rt△GHE中，∠HGE=30°，∴GE=2HE=CE，∴GH==HE=CE．∵GE=2BG，∴BC=BG+GE+EC=4EC．∵矩形ABCD的面积为4，∴4EC•EC=4，∴EC=1，EF=GE=2．故选C．二、填空题：6.（2018·辽宁省盘锦市）如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，点M、N分别在线段AC.AB 上，将△ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△DCM为直角三角形时，折痕MN的长为．【解答】解：分两种情况：①如图，当∠CDM=90°时，△CDM是直角三角形，∵在Rt△ABC中，∠B=90°，∠A=60°，AC=2+4，∴∠C=30°，AB=AC=，由折叠可得：∠MDN=∠A=60°，∴∠BDN=30°，∴BN=DN=AN，∴BN=AB=，∴AN=2BN=．∵∠DNB=60°，∴∠ANM=∠DNM=60°，∴∠AMN=60°，∴AN=MN=；②如图，当∠CMD=90°时，△CDM是直角三角形，由题可得：∠CDM=60°，∠A=∠MDN=60°，∴∠BDN=60°，∠BND=30°，∴BD=DN=AN，BN=BD\1AB=，∴AN=2，BN=，过N作NH⊥AM于H，则∠ANH=30°，∴AH=AN=1，HN=，由折叠可得：∠AMN=∠DMN=45°，∴△MNH是等腰直角三角形，∴HM=HN=，∴MN=．故答案为：或．7.（2018·山东威海·8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C 与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=+1，求BC的长．【分析】由题意知∠3=180°﹣2∠1=45°、∠4=180°﹣2∠2=30°、BE=KE、KF=FC，作KM⊥BC，设KM=x，知EM=x、MF=x，根据EF的长求得x=1，再进一步求解可得．【解答】解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K作KM⊥BC于点M，设KM=x，则EM=x、MF=x，∴x+x=+1，解得：x=1，∴EK=、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3++，∴BC的长为3++．【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．8.（2018·湖南省常德·3分）如图，将矩形ABCD沿EF折叠，使点B落在AD边上的点G处，点C落在点H处，已知∠DGH=30°，连接BG，则∠AGB= 75°．【分析】由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，从而可证明∠EBG=∠EGB．，然后再根据∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH，由平行线的性质可知∠AGB=∠GBC，从而易证∠AGB=∠BGH，据此可得答案．【解答】解：由折叠的性质可知：GE=BE，∠EGH=∠ABC=90°，∴∠EBG=∠EGB．∴∠EGH﹣∠EGB=∠EBC﹣∠EBG，即：∠GBC=∠BGH．又∵AD∥BC，∴∠AGB=∠GBC．∴∠AGB=∠BGH．∵∠DGH=30°，∴∠AGH=150°，∴∠AGB=∠AGH=75°，故答案为：75°．【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．三、解答与计算题：9.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE ≌△CED（SSS）；（2）根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出EF=DF，由此即可证出△DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ADE和△CED中，，∴△ADE≌△CED（SSS）．（2）由（1）得△ADE≌△CED，∴∠DEA=∠EDC，即∠DEF=∠EDF，∴EF=DF，∴△DEF是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出AD=CE、AE=CD；（2）利用全等三角形的性质找出∠DEF=∠EDF．10.（2018•山东枣庄•10分）如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．（1）求证：四边形EFDG是菱形；（2）探究线段EG、GF、AF之间的数量关系，并说明理由；（3）若AG=6，EG=2，求BE的长．【分析】（1）先依据翻折的性质和平行线的性质证明∠DGF=∠DFG，从而得到GD=DF，接下来依据翻折的性质可证明DG=GE=DF=EF；（2）连接DE，交AF于点O．由菱形的性质可知GF⊥DE，OG=OF=GF，接下来，证明△DOF∽△ADF，由相似三角形的性质可证明DF2=FO•AF，于是可得到GE、AF、FG的数量关系；（3）过点G作GH⊥DC，垂足为H．利用（2）的结论可求得FG=4，然后再△ADF中依据勾股定理可求得AD的长，然后再证明△FGH∽△FAD，利用相似三角形的性质可求得GH的长，最后依据BE=AD﹣GH求解即可．【解答】解：（1）证明：∵GE∥DF，∴∠EGF=∠DFG．∵由翻折的性质可知：GD=GE，DF=EF，∠DGF=∠EGF，∴∠DGF=∠DFG．∴GD=DF．∴DG=GE=DF=EF．∴四边形EFDG为菱形．（2）EG2=GF•AF．理由：如图1所示：连接DE，交AF于点O．∵四边形EFDG为菱形，∴GF⊥DE，OG=OF=GF．∵∠DOF=∠ADF=90°，∠OFD=∠DFA，∴△DOF∽△ADF．∴，即DF2=FO•AF．∵FO=GF，DF=EG，∴EG2=GF•AF．（3）如图2所示：过点G作GH⊥DC，垂足为H．∵EG2=GF•AF，AG=6，EG=2，∴20=FG（FG+6），整理得：FG2+6FG﹣40=0．解得：FG=4，FG=﹣10（舍去）．∵DF=GE=2，AF=10，∴AD==4．∵GH⊥DC，AD⊥DC，∴GH∥AD．∴△FGH∽△FAD．∴，即=．∴GH=．∴BE=AD﹣GH=4﹣=．【点评】本题主要考查的是四边形与三角形的综合应用，解答本题主要应用了矩形的性质、菱形的判定和性质、相似三角形的性质和判定、勾股定理的应用，利用相似三角形的性质得到DF2=FO•AF是解题答问题（2）的关键，依据相似三角形的性质求得GH的长是解答问题（3）的关键．【能力篇】一、选择题：11.（2018·辽宁省阜新市）如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A1处，BC=8，那么线段AE的长度为( )．A．4 B．5 C．6 D．7【解答】解：由折叠的性质可得AE=A1E．∵△ABC为等腰直角三角形，BC=8，∴AB=8．∵A1为BC的中点，∴A1B=4，设AE=A1E=x，则BE=8﹣x．在Rt△A1BE中，由勾股定理可得42+（8﹣x）2=x2，解得x=5．故答案为：5．故选B12.（2018·四川省攀枝花·3分）如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（）A．1 B．2 C．3 D．4解：①如图，EC，BP交于点G；∵点P是点B关于直线EC的对称点，∴EC垂直平分BP，∴EP=EB，∴∠EBP=∠EPB．∵点E为AB中点，∴AE=EB，∴AE=EP，∴∠PAB=∠PBA．∵∠PAB+∠PBA+∠APB=180°，即∠PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，∴∠PAB+∠PBA=90°，∴AP⊥BP，∴AF∥EC；∵AE∥CF，∴四边形AECF是平行四边形，故①正确；②∵∠APB=90°，∴∠APQ+∠BPC=90°，由折叠得：BC=PC，∴∠BPC=∠PBC．∵四边形ABCD是正方形，∴∠ABC=∠ABP+∠PBC=90°，∴∠ABP=∠APQ，故②正确；③∵AF∥EC，∴∠FPC=∠PCE=∠BCE．∵∠PFC是钝角，当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，如右图，△PCF不一定是等腰三角形，故③不正确；④∵AF=EC，AD=BC=PC，∠ADF=∠EPC=90°，∴Rt△EPC≌△FDA（HL）．∵∠ADF=∠APB=90°，∠FAD=∠ABP，当BP=AD或△BPC是等边三角形时，△APB≌△FDA，∴△APB≌△EPC，故④不正确；其中正确结论有①②，2个．故选B．13. （2018·湖北省武汉·3分）如图，在⊙O 中，点C 在优弧上，将弧沿BC 折叠后刚好经过AB 的中点D ．若⊙O 的半径为，AB=4，则BC 的长是（）A ．B ．C ．D ．【分析】连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图，利用垂径定理得到OD ⊥AB ，则AD=BD=AB=2，于是根据勾股定理可计算出OD=1，再利用折叠的性质可判断弧AC 和弧CD 所在的圆为等圆，则根据圆周角定理得到=，所以AC=DC ，利用等腰三角形的性质得AE=DE=1，接着证明四边形ODEF 为正方形得到OF=EF=1，然后计算出CF 后得到CE=BE=3，于是得到BC=3 2．【解答】解：连接OD 、AC 、DC 、OB 、OC ，作CE ⊥AB 于E ，OF ⊥CE 于F ，如图， ∵D 为AB 的中点， ∴OD ⊥AB ， ∴AD=BD=AB=2，在Rt △OBD 中，OD=22(5)2 =1， ∵将弧沿BC 折叠后刚好经过AB 的中点D ．∴弧AC 和弧CD 所在的圆为等圆， ∴=，∴AC=DC ， ∴AE=DE=1，易得四边形ODEF 为正方形， ∴OF=EF=1，在Rt △OCF 中，CF=22(5)1 ， ∴CE=CF+EF=2+1=3，而BE=BD+DE=2+1=3， ∴BC=3．故选：B ．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理和垂径定理．二、填空题：14. (2018·辽宁省葫芦岛市) 如图，在矩形ABCD 中，点E 是CD 的中点，将△BCE 沿BE 折叠后得到△BEF 、且点F 在矩形ABCD 的内部，将BF 延长交AD 于点G ．若=，则= ．【解答】解：连接GE ．∵点E 是CD 的中点，∴EC=DE ．∵将△BCE 沿BE 折叠后得到△BEF 、且点F 在矩形ABCD 的内部，∴EF=DE ，∠BFE=90°．在Rt △EDG 和Rt △EFG 中，∴Rt △EDG ≌Rt △EFG （HL ），∴FG=DG ．∵=，∴设DG=FG=a，则AG=7a，故AD=BC=8a，则BG=BF+FG=9a，∴AB==4a，故==．故答案为：．15.（2018·四川宜宾·3分）如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE 折叠，使点B落在矩形内点F处，下列结论正确的是①②③（写出所有正确结论的序号）①当E为线段AB中点时，AF∥CE；②当E为线段AB中点时，AF=95；③当A、F、C三点共线时，AE=；④当A、F、C三点共线时，△CEF≌△AEF．【考点】PB：翻折变换（折叠问题）；KB：全等三角形的判定；LB：矩形的性质．【分析】分两种情形分别求解即可解决问题；【解答】解：如图1中，当AE=EB时，∵AE=EB=EF，∴∠EAF=∠EFA，∵∠CEF=∠CEB，∠BEF=∠EAF+∠EFA，∴∠BEC=∠EAF，∴AF∥EC，故①正确，作EM⊥AF，则AM=FM，在Rt△ECB中，EC==，，∵∠AME=∠B=90°，∠EAM=∠CEB，∴△CEB∽△EAM，∴=，∴=，∴AM=，∴AF=2AM=95，故②正确，如图2中，当A、F、C共线时，设AE=x．则EB=EF=3﹣x，AF=13﹣2，在Rt△AEF中，∵AE2=AF2+EF2，∴x2=（﹣2）2+（3﹣x）2，∴x=，，∴AE=，故③正确，如果，△CEF≌△AEF，则∠EAF=∠ECF=∠ECB=30°，显然不符合题意，故④错误，故答案为①②③．【点评】本题考查翻折变换、全等三角形的性质、勾股定理、矩形的性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考填空题中的压轴题．三、解答与计算题：16.（2018·湖北省宜昌·11分）在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B 的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F．（1）如图1，若点E是AD的中点，求证：△AEB≌△DEC；（2）如图2，①求证：BP=BF；②当AD=25，且AE＜DE时，求cos∠PCB的值；③当BP=9时，求BE•EF的值．【分析】（1）先判断出∠A=∠D=90°，AB=DC再判断出AE=DE，即可得出结论；（2）①利用折叠的性质，得出∠PGC=∠PBC=90°，∠BPC=∠GPC，进而判断出∠GPF=∠PFB即可得出结论；②判断出△ABE∽△DEC，得出比例式建立方程求解即可得出AE=9，DE=16，再判断出△ECF∽△GCP，进而求出PC，即可得出结论；③判断出△GEF∽△EAB，即可得出结论．【解答】解：（1）在矩形ABCD中，∠A=∠D=90°，AB=DC，∵E是AD中点，∴AE=DE，在△ABE和△DCE中，，∴△ABE≌△DCE（SAS）；（2）①在矩形ABCD，∠ABC=90°，∵△BPC沿PC折叠得到△GPC，∴∠PGC=∠PBC=90°，∠BPC=∠GPC，∵BE⊥CG，∴BE∥PG，∴∠GPF=∠PFB，∴∠BPF=∠BFP，∴BP=BF；②当AD=25时，∵∠BEC=90°，∴∠AEB+∠CED=90°，∵∠AEB+∠ABE=90°，∴∠CED=∠ABE，∵∠A=∠D=90°，∴△ABE∽△DEC，∴，设AE=x，∴DE=25﹣x，∴，∴x=9或x=16，∵AE＜DE，∴AE=9，DE=16，∴CE=20，BE=15，由折叠得，BP=PG，∴BP=BF=PG，∵BE∥PG，∴△ECF∽△GCP，∴，设BP=BF=PG=y，∴，∴y=，∴BP=，在Rt△PBC中，PC=，cos∠PCB==；③如图，连接FG，∵∠GEF=∠BAE=90°，∵BF∥PG，BF=PG，∴▱BPGF是菱形，∴BP∥GF，∴∠GFE=∠ABE，∴△GEF∽△EAB，∴，∴BE•EF=AB•GF=12×9=108．【点评】此题是四边形综合题，主要考查了矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，折叠的性质，利用方程的思想解决问题是解本题的关键．17.（2018·广东·7分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△ADE≌△CED；（2）求证：△DEF是等腰三角形．【分析】（1）根据矩形的性质可得出AD=BC、AB=CD，结合折叠的性质可得出AD=CE、AE=CD，进而即可证出△ADE ≌△CED（SSS）；（2）根据全等三角形的性质可得出∠DEF=∠EDF，利用等边对等角可得出EF=DF，由此即可证出△DEF是等腰三角形．【解答】证明：（1）∵四边形ABCD是矩形，∴AD=BC，AB=CD．由折叠的性质可得：BC=CE，AB=AE，∴AD=CE，AE=CD．在△ADE和△CED中，，∴△ADE≌△CED（SSS）．（2）由（1）得△ADE≌△CED，∴∠DEA=∠EDC，即∠DEF=∠EDF，∴EF=DF，∴△DEF是等腰三角形．【点评】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质，解题的关键是：（1）根据矩形的性质结合折叠的性质找出AD=CE、AE=CD；（2）利用全等三角形的性质找出∠DEF=∠EDF．18.（2018•江苏盐城•10分）如图，在以线段为直径的上取一点，连接、.将沿翻折后得到.（1）试说明点在上；（2）在线段的延长线上取一点，使.求证：为的切线；（3）在（2）的条件下，分别延长线段、相交于点，若，，求线段的长. 【答案】（1）解：连接OC，OD，由翻折可得OD=OC，∵OC是⊙O的半径，∴点D在⊙O上。

2024年中考数学考点必备方法必备09几何综合题的三类折叠问题(解析版)

方法必备09几何综合题的三类折叠问题题型一：翻折与几何基本图形题型二：翻折与隐形圆题型三：翻折与二次函数题型一：翻折与几何基本图形1．（2024·山东泰安·一模）如图，把平行四边形纸片ABCD 沿BD 折叠，点C 落在点C 处，BC 与AD 相交于点E ．求证：EB ED 【答案】见详解【分析】本题主要考查利用平行四边形的性质和折叠得性质证明ABE C DE ≌ ，即可证明结论成立．【详解】证明：∵四边形ABCD 为平行四边形，∴A C ，AB CD ，∵沿BD 折叠，点C 落在点C 处，∴C C A ，C D CD AB ，在ABE 和C DE 中AEB C ED A C AB C D∴ ABE C DE AAS ≌，∴EB ED ．2．（2023·江苏泰州·二模）如图1，将 Rt 90ABC A 纸片按照下列图示方式折叠：①将ABD △沿BD 折叠，使得点A 落在BC 边上的点M 处，折痕为BD ；②将BEF △沿EF 折叠，使得点B 与点D 重合，折痕为EF ；③将DEF 沿DF 折叠，点E 落在点'E 处，展开后如图2，BD 、PF 、DF 、DP 为图1折叠过程中产生的折痕．(1)求证：DP BC ∥；(2)若'DE 落在DM 的右侧，求C 的范围；(3)是否存在C 使得DE 与MDC 的角平分线重合，如存在，请求C 的大小；若不存在，请说明理由．【答案】(1)见解析；(2)030C ；(3)不存在，理由见解析．【分析】本题考查了直角三角形的性质，折叠的性质，菱形的判定与性质，角平分线的性质，熟练掌握折叠的性质是解题的关键．（1）由第二次翻折可得EF 垂直平分BD ，由第一次翻折可得EF EP ，证出四边形PBFD 是菱形，则可得出结论；（2）设ABD ，求出BDF ，902ADP FDM C ，当DE 落在DM 的右侧时，902 ，求出30a ，则可得出答案；（3）设ABD ，902ADP FDM C ，2MDC ，得出902 ，求出45 ，0C ，则可得出结论．【详解】（1）证明：由第二次翻折可得EF 垂直平分BD ，由第一次翻折可得EF EP ，PF 与BD 垂直且互相平分，四边形PBFD 是菱形，DP BC ∥；（2）解：设ABD ，∵四边形PBFD 是菱形，PB DF ∥，BDF ，902ADP FDM C ，当'DE 落在DM 的右侧时，902 ，30a ，90230 ，030C ；（3）解：不存在．若存在C 使得DE 与MDC 的角平分线重合，设ABD ，902ADP FDM C ，2MDC ，902 ，45 ，0C ，不存在C 使得DE 与MDC 的角平分线重合．3．（2023·吉林松原·三模）如图①，在Rt ABC △中，90ACB ，60A ，CD 是斜边AB 上的中线，点E 为射线CA 上一点，将ADE V 沿DE 折叠，点A 的对应点为点F ．(1)若AB a =，直接写出CD 的长（用含a 的代数式表示）；(2)若点E 与点C 重合，连接BF ，如图②，判断四边形DBFC 的形状，并说明理由；(3)若DF AB ，直接写出CDE 的度数．【点睛】本题主要考查了折叠问题，菱形的判定，直角三角形的性质，等边三角形的判定与性质，灵活运用相关知识是解答本题的关键．4．（2023·广东茂名·二模）如图，正方形ABCD中，E是边BC的中点，将ABE沿AE折叠，得到AFE，延长EF 交边CD于点P．(1)求证：DP FP；AB ，求CP的长．(2)若6连接AP，∵四边形ABCD是正方形，∴AD AB，B D5．（2023·广西贵港·二模）综合与实践【问题情境】数学活动课上，老师准备了若干张正方形纸片ABCD ，组织同学们进行折纸探究活动．【初步尝试】把正方形对折，折痕为EF ，然后展开，沿过点A 与点E 所在的直线折叠，点B 落在点B 处，连接 B C ，如图1，请直接写出AEB 与ECB 的数量关系．【能力提升】把正方形对折，折痕为EF ，然后展开，沿过点A 与BE 上的点G 所在的直线折叠，使点B 落在EF 上的点P 处，连接PD ，如图2，猜想APD 的度数，并说明理由．【拓展延伸】在图2的条件下，作点A 关于直线CP 的对称点A ，连接PA ，BA ，AC ，如图3，求PA B 的度数．【答案】初步尝试：AEB ECB ；能力提升：猜想：60APD ，理由见解析；拓展延伸：15PA B【分析】初步尝试：连接BB ，由折叠的性质可知，BE CE ，BE BE ，AEB AEB ，BB AE ，根据等边对等角的性质和三角形内角和定理，得出90BB C ，推出AE CB ∥，即可得出答案；能力提升：根据正方形的性质和折叠的性质，易证 SAS AFP DFP ≌，从而证明APD △是等边三角形，即可得到答案；拓展延伸：连接A C 、AA ，由（2）得APD △是等边三角形，进而得出30PDC ，再结合等边对等角的性质和三角形内角和定理，求得15PAC ，30ACP ，由对称性质得：AC A C ，30ACP A CP ，证明 SSS AA B CA B ≌，得到30CA B ，再由15CA P CAP ，即可求出PA B 的度数．【详解】解：初步尝试：AEB ECB ，理由如下：如图，连接BB ，由折叠的性质可知，BE CE ，BE BE ，AEB AEB ，BB AE ，∴BE CE BE ，∴EBB EB B ，ECB EB C ，∵ 2180EBB EB B EB C ECB EB B EB C ，∴90BB C ，即BB CB ，∴AE CB ∥，∴AEB ECB ，∴AEB ECB ；解：能力提升：猜想：60APD ，理由如下：理由：∵四边形ABCD 是正方形，∴AB AD ，90ADC ，由折叠性质可得：AF DF ，EF AD ，AB AP ，在AFP 和DFP △中，90AF DF AFP DFP FP FP，∴ SAS AFP DFP ≌，∴AP PD ，∴AP AD PD ，由（2）得APD △是等边三角形，∴PAD PDA APD ∵90ADC ，∴30PDC ，又∵PD AD DC ，∴12DPC DCP ∴PAC PAD DAC 由对称性质得：AC 6．（2023·吉林长春·模拟预测）如图1，平面上，四边形ABCD 中，4AB ，6CD ，BC 3DA ，90A ，点M 在AD 边上，且1DM ．点P 沿折线AB BC 以1个单位速度向终点C 运动，点A 是点A 关于直线MP 的对称点，连接A P ，设点P 在该折线上运动的时间为 0t t ．(1)直接写出线段BP的长；(2)如图2，连接BD．的度数，并直接写出当A 、M、A共线时t的值；①求CBD②若点P到BD的距离为1，求tan A MP 的值；t 时，请直接写出点A 到直线AD的距离（用含t的式子表示）．(3)当04∵PM 平分A MA ，90PMA ，∴PM AB ∥，DNM DBA △∽△，DN DM MN ，3sin 5AD DBA BD，153sin 5PQ BP DBA ，90PQB CBD DAB ∵，90QPB PBQ DBA ，PQB BAD △∽△，,PQ QB PB 即,PQ QB PB 由A PE MA F ∽，7．（2023·河南周口·模拟预测）综合与实践课上，老师让同学们以“正方形的折叠”为主题开展实践活动．(1)操作判断操作一：如图（1），正方形纸片ABCD，点E是BC边上（点E不与点B，C重合）任意一点，沿AE折叠ABE到△，如图（2）所示；AFE操作二：将图（2）沿过点F的直线折叠，使点E的对称点G落在AE上，得到折痕MN，点C的对称点记为H，如图（3）所示；操作三：将纸片展平，连接BM，如图（4）所示．根据以上操作，回答下列问题：①B，M，N三点（填“在”或“不在”)一条直线上；②AE和BN的位置关系是，数量关系是；③如图（5），连接AN，改变点E在BC上的位置，（填“存在”或“不存在”)点E，使AN平分DAE．(2)迁移探究苏钰同学将正方形纸片换成矩形纸片ABCD，4BC ，按照（1）中的方式操作，得到图（6）或图（7）．请AB ，6完成下列探究：①当点N在CD上时，如图（6），BE和CN有何数量关系？并说明理由；8．（2023·山东枣庄·中考真题）问题情境：如图1，在ABC 中，1730AB AC BC ，，AD 是BC 边上的中线．如图2，将ABC 的两个顶点B ，C 分别沿,EF GH 折叠后均与点D 重合，折痕分别交,,AB AC BC 于点E ，G ，F ，H ．猜想证明：(1)如图2，试判断四边形AEDG 的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN 折叠，使得顶点B 与点H 重合，折痕分别交,AB BC 于点M ，N ，BM 的对应线段交DG 于点K ，求四边形MKGA 的面积．∵1122CHG S CH HG ∴154302CG HE，9．（2023·内蒙古通辽·中考真题）综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动，有一位同学操作过程如下：操作一：对折正方形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，把纸片展平；操作二：在AD 上选一点P ，沿BP 折叠，使点A 落在正方形内部点M 处，把纸片展平，连接PM 、BM ，延长PM 交CD 于点Q ，连接BQ ．(1)如图1，当点M 在EF 上时，EMB ___________度；(2)改变点P 在AD 上的位置（点P 不与点A ，D 重合）如图2，判断MBQ 与CBQ 的数量关系，并说明理由．10．（2023·辽宁大连·中考真题）综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质．已知,90AB AC A ，点E 为AC 上一动点，将ABE 以BE 为对称轴翻折．同学们经过思考后进行如下探究：独立思考：小明：“当点D 落在BC 上时，2EDC ACB ．”小红：“若点E 为AC 中点，给出AC 与DC 的长，就可求出BE 的长．”实践探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰ABC 中，,90,AB AC A BDE △由ABE 翻折得到．（1）如图1，当点D 落在BC 上时，求证：2EDC ACB ；（2）如图2，若点E 为AC 中点，43AC CD ,，求BE 的长．问题解决：小明经过探究发现：若将问题1中的等腰三角形换成90A 的等腰三角形，可以将问题进一步拓展．问题2：如图3，在等腰ABC 中，90,4,2A AB AC BD D ABD ．若1CD ，则求BC 的长．∵AB BD，∴AM MD，ABM ，∵2BDC ABD，∴BDC DBM∥，∴BM CD，∴CD AD又CG BM，∴四边形CGMD是矩形，则CD GM，在Rt ACD△中，1CD ，11．（2023·江苏无锡·中考真题）如图，四边形ABCD 是边长为4的菱形，60A ，点Q 为CD 的中点，P 为线段AB 上的动点，现将四边形PBCQ 沿PQ 翻折得到四边形PB C Q ．(1)当45QPB 时，求四边形BB C C 的面积；(2)当点P 在线段AB 上移动时，设BP x ，四边形BB C C 的面积为S ，求S 关于x 的函数表达式．12．（2023·重庆·中考真题）在Rt ABC 中，90ACB ，=60B ，点D 为线段AB 上一动点，连接CD ．(1)如图1，若9AC，BD ，求线段AD 的长．(2)如图2，以CD 为边在CD 上方作等边CDE ，点F 是DE 的中点，连接BF 并延长，交CD 的延长线于点G ．若G BCE ，求证：GF BF BE ．(3)在CD 取得最小值的条件下，以CD 为边在CD 右侧作等边CDE ．点M 为CD 所在直线上一点，将BEM 沿BM 所在直线翻折至ABC 所在平面内得到BNM ．连接AN ，点P 为AN 的中点，连接CP ，当CP 取最大值时，连接BP ，将BCP 沿BC 所在直线翻折至ABC 所在平面内得到BCQ ，请直接写出此时NQCP的值．∵F 是DE 的中点则DF FE ，FH FG ， ∴ SAS GFD HFE ≌，∴H G ，∴EH GC ∥，在CD 取得最小值的条件下，即CD 设4AB a ，则2BC a ，23AC a∵S 是AB 的中点，60ABC∴SC SB BC ，∴BCS △是等边三角形，则60PCB ，∴30PCA ACB BCP ，∵2BC a ，4AB a ，∴PU AR ∥，P 是AN 的中点，∴1NU NP UR PA即PU 是ANR 的中位线，同理可得PT 是ANR ∴54NU UR PT a，12PU AR AT ∵BCS △是等边三角形，将BCP 沿BC 所在直线翻折至∴2120QCP BCP【点睛】本题考查了解直角三角形，全等三角形的性质与判定，等腰三角形的性质，三角形中位线的性质，折叠的性质，圆外一点到圆上距离的最值问题，垂线段最短，矩形的性质，等边三角形的性质与判定，熟练掌握以上知识是解题的关键．题型二：翻折与隐形圆一、单选题1．（湖北鄂州·中考真题）如图，菱形ABCD 的边AB =8，∠B =60°，P 是AB 上一点，BP =3，Q 是CD 边上一动点，将梯形APQD 沿直线PQ 折叠，A 的对应点A ′．当CA ′的长度最小时，CQ 的长为（）A．5B．7C．8D．13 22．如图，菱形ABCD边长为4，∠A＝60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C的最小值是（）A ．B C ．2D ．3【点睛】本题考查翻折变换、菱形的性质、勾股定理、两点之间线段最短等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，突破点是正确寻找点3．（22-23九年级上·浙江金华·期末）如图，正方形ABCD 的边长为4，点E 是正方形ABCD 内的动点，点P 是BC 边上的动点，且EAB EBC ．连结AE ，BE ，PD ，PE ，则PD PE 的最小值为（）A．2 B．2C．2D．2作正方形ABCD关于直线BC对称的正方形则点D的对应点是F，连接FO交BC于P，交半圆O于根据对称性有：PD PF，则有：PE PD PE PF，二、填空题4．（2022·广东汕头·一模）如图，在△ABC中，∠C＝90°，AC＝8，AB＝10，D是AC上一点，且CD＝3，E是BC 边上一点，将△DCE沿DE折叠，使点C落在点F处，连接BF，则BF的最小值为．【点睛】本题考查了折叠的性质、圆的性质、勾股定理解直角三角形的知识，该题涉及的最值问题属于中考常考题5．△ABC 中，AB ＝AC ＝5，BC ＝6，D 是BC 的中点，E 为AB 上一动点，点B 关于DE 的对称点B 在△ABC 内（不含△ABC 的边上），则BE 长的范围为．②如图所示，当点B 恰好落在由题意，BD DB DC ，∴DBB DB B ，DB ∴DBB DCB DB22综上，BE长的范围为9 5故答案为：95 52BE．【点睛】本题考查等腰三角形的性质和判定，以及勾股定理解直角三角形等，能够根据题意准确分析出动点的运动6．如图，在矩形ABCD中，AB=4，AD=6，E是AB边的中点，F是线段BC上的动点，将ΔEBF沿EF所在直线折叠得到ΔEB'F，连接B'D，则B'D的最小值是．故答案为210 2．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、B 'D 的值最小是解决问题的关键．7．（22-23九年级下·江苏宿迁·阶段练习）如图，矩形ABCD ，4AB ，8BC ，E 为AB 中点，F 为直线BC 上动点，B 、G 关于EF 对称，连接AG ，点P 为平面上的动点，满足12APB AGB ，则DP 的最小值．【答案】21022【分析】由题意可知，90AGB 上，（要使DP 最小，则点P 要靠近蒂点∴90AGB ，∵12APB AGB ，即1452APB AGB ，8．如图，在矩形ABCD中，AB＝6，AD＝8，点E，F分别是边CD，BC上的动点，且∠AFE＝90°（1）证明：△ABF∽△FCE；（2）当DE取何值时，∠AED最大．9．（2022·天津河东·二模）已知，平面直角坐标系中有一个边长为6的正方形OABC，M为线段OC上的动点，将AOM沿直线AM对折，使O点落在O 处．(1)如图①，当30OAM 时，求点O 的坐标；(2)如图②，连接 CO ，当CO AM ∥时．①求点M 的坐标；②连接OB ，求AO M △与AOB 重叠部分的面积；(3)当点M 在线段OC （不包括端点）上运动时，请直接写出线段O C 的取值范围．由①得：tan AO AMO OM 设,CE x 则3,ME x O ¢=-()()222332,x x \=-+解得：6,5x =（不符合题意的根舍去）当,Q O ¢重合时， CO 取得最小值，此时226662,6,AC AQ AO =+===626,CO ¢\=-所以 CO 的取值范围为：626CO ¢-£【点睛】本题考查的是正方形的性质，等边三角形的判定与性质，轴对称的性质，一次函数的几何应用，圆的基本性质，锐角三角函数的应用，熟练的利用一次函数的性质解决几何图形面积问题，利用圆的基本性质求解线段长度的最小值是解本题的关键．10．（2022·重庆·三模）在ABC 中，90ACB ，CA ＝2CB ．将线段CA 绕点C 旋转得到线段CD ．(1)如图1，当点D 落在AB 的延长线上时，过点D 作DE AD 交AC 的延长线于点E ，若BC ＝2，求DE 的长；(2)如图2，当点D 落在CB 的延长线上时，连接AD ，过点C 作CF ⊥AB 于点F ，延长CF 交AD 于点E ，连接BE ，求证：AB CE BE ；(3)如图3，在（2）的条件下，将ACF △沿AC 翻折得到ACF △，M 为直线AD 上一个动点．连接BM ，将BDM 沿BM 翻折得到BMD △．当D F 最小时，直接写出F D FF 的值．由题意得，D ¢在以B 为圆心，BC 长为半径的圆上运动，当设1CB ，∵2CA CB ，∴2CA ．∵90ACB ，1CB ，2CA ，∴225AB CA CB ，sin CAB ∵CF ⊥AB ，90ACB ，题型三：翻折与二次函数1．（21-22九年级下·湖南株洲·开学考试）如图，在平面直角坐标系中，抛物线22y ax ax c 经过 2,0A ， 0,4C 两点．(1)求抛物线的解析式；(2)点P 是第一象限抛物线上一动点，连接CP ，CP 的延长线与x 轴交于点Q ，过点P 作PE y 轴于点E ，以PE 为轴，翻折直线CP ，与抛物线相交于另一点R ．设P 点横坐标为t ，R 点横坐标为s ，求出s 与t 的函数关系式；（不要求写出自变量t 的取值范围）；(3)在（2）的条件下，连接RC ，点G 在RP 上，且RG RC ，连接CG ，若45OCG ，求点Q 坐标．根据题意得：212EF CE t ∴2142OF OE EF t t ∵点R 的横坐标为s ，∴点R 的坐标为21,42s s s∵45OCG ，PE CE ，∴45EIC ．∵45EIC GCP CPE ∴4545RCH GPE ．∴RCH GPE ．2．（2023·天津河西·三模）如图，在平面直角坐标系中，抛物线214y x bx c 与x 轴交于 30A ,， 4,0B 两点，在y 轴正半轴上有一点C ，OC OB ．点D ，E 分别是线段AC ，AB 上的动点，且均不与端点重合．(1)求此抛物线的解析式；(2)如图①，连接BD ，将BCD △沿x 轴翻折得到BFG ，当点G 在抛物线上时，求点G 的坐标；(3)如图②，连接CE ，当CD AE 时，求BD CE 的最小值．∵BCD △与BFG 关于x 轴对称，∴DG AB ，DM GM ，∵3OA ，4OB OC ，∴4tan 3OC CAO OA ，设 0OM a a ，则3AM a ，DM GM AM 4连接EQ 、CQ ，∵AE CD ，∴AEQ CDB ≌，∴EQ BD ，当C ，E ，Q 三点共线时，过点C 作CH AQ ，垂足为H ∵OC OB ^，4OC OB ，∴45CBA ，42BC ．∵180CAH CAB EAQ 2523．（2023·广西贵港·三模）抛物线222y x x c 与x 轴交于A 、B 两点，且点A 在点B 的左侧，与y 轴交于点C ，点 32D ，为抛物线上一点，且直线CD x ∥轴，点M 是抛物线上的一动点．(1)求抛物线的解析式与A、B两点的坐标．，，，为顶点的四边形是平行四边形，求此时点M的坐标．(2)若点E的纵坐标为0，且以A E D M沿CM翻折，点N的对应点为N ，则是否存在点M，使点N (3)过点M作直线CD的垂线，垂足为N，若将CMN则恰好落在x轴上？若存在，求出此时点M的坐标；若不存在，说明段理由．当AD 为边时，11AE M D Y ，此时1M 和点C 重合，23AM E D Y 时，点2M 的纵坐标和点D 的纵坐标互为相反数，即21322,22x x 341,2x 32341341,2,,2,22M M 由折叠知，CNM CN M ∵90NCN ，∴四边形CNMN 是矩形，∵CN CN 时，∴矩形CNMN 是正方形，∴CM 平分NCN ，。

初中数学中的折叠问题

初中数学中的折叠问题一、矩形中的折叠折叠后BG 和BH 在再过点A ′折叠使边与对角线BD 重形中根据勾股定合，然后再沿着则∠DFB 等于的位置，已知重合部分是以折痕为底边的等腰三角形理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD 的边长为8，将其沿EF 折叠，则图中①②③④四个三角形的周长之和为折叠前后对应边相等9．如图，将边长为4的正方形ABCD 沿着折痕EF 折叠，使点B落在边AD 的中点G 处，求四边形BCFE 的面积注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等 10．如图，将一个边长为1的正方形纸片ABCD 折叠，使点B 落在边AD 上不与A 、D 重合．MN 为折痕，折叠后B ’C ’与DN 交于P ．(1)连接BB ’，那么BB ’与MN 的长度相等吗？为什么？(2)设BM =y ，AB ’=x ，求y 与x 的函数关系式；(3)猜想当B 点落在什么位置上时，折叠起来的梯形MNC ’B ’面积最小？并验证你的猜想．二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）C题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm的长方形纸条成如图所示的形状，那么折痕PQ的长是注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ 14．如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（）本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b∠GFC=140°，图c中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm的长方形纸片ABCD，沿对称轴EF折叠成如图的形状，若折叠后，AB与CD间的距离为60cm，则原纸片的宽AB是（）16．一根30cm、宽3cm的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P的长度相等，则最初折叠时，求MA的长三、三角形中的折叠实践与运用：(1)将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图③）；再沿过点E的直线折叠，使点D落在BE上的点D’处，折痕为EG（如图④）；再展平纸片（如图⑤）．求图⑤中∠α的大小．由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

折叠几何综合专题---16道题目(含答案)

折叠几何综合专题---16道题目(含答案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN01如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E 处，过点E作EG∥CD交AF于点G，连接DG.(1)求证：四边形EFDG是菱形；(2)探究线段EG，GF，AF之间的数量关系，并说明理由；(3)若AG＝6，EG＝25，求BE的长．(1)证明：由折叠性质可得，EF ＝FD ，∠AEF ＝∠ADF ＝90°，∠EFA ＝∠DFA ，EG ＝GD ，∵EG ∥DC ，∴∠DFA ＝∠EGF ， ∴∠EFA ＝∠EGF ，∴EF ＝EG ＝FD ＝GD ，∴四边形EFDG 是菱形；(2)解：EG 2＝12GF ·AF .理由如下：如解图，连接ED ，交AF 于点H ，∵四边形EFDG 是菱形，∴DE ⊥AF ，FH ＝GH ＝12GF ，EH ＝DH ＝12DE ， ∵∠FEH ＝90°－∠EFA ＝∠FAE ，∠FHE ＝∠AEF ＝90°， ∴Rt △FEH ∽Rt △FAE ，∴EFAF ＝FHEF ，即EF 2＝FH ·AF ，又∵FH ＝12GF ，EG ＝EF ，∴EG 2＝12GF ·AF ；(3)解：∵AG ＝6，EG ＝25，EG 2＝12AF ·GF ，∴(25)2＝12(6＋GF )·GF ，解得GF ＝4或GF ＝－10(舍)，∴GF ＝4，∴AF ＝10.∵DF ＝EG ＝25，∴AD ＝BC ＝AF 2－DF 2＝45，DE ＝2EH ＝2EG 2－（12GF ）2＝8，∵∠CDE ＋∠DFA ＝90°，∠DAF ＋∠DFA ＝90°，∴∠CDE ＝∠DAF ，∵∠DCE ＝∠ADF ＝90°，∴Rt △DCE ∽Rt △ADF ，∴EC DF ＝DE AF ，即EC 25＝810，∴EC ＝855，∴BE ＝BC －EC ＝1255.02如图，将矩形ABCD 沿对角线BD 对折，点C 落在E 处，BE 与AD 相交于点F ，若DE ＝4，BD ＝8.(1)求证：AF ＝EF ；(2)求证：BF 平分∠ABD .证明：(1)在矩形ABCD 中，AB ＝CD ，∠A ＝∠C ＝90°， ∵△BED 是△BCD 对折得到的，∴ED ＝CD ，∠E ＝∠C ，∴ED ＝AB ，∠E ＝∠A ，(2分)又∵∠AFB ＝∠EFD ，∴△ABF ≌△EDF (AAS)，∴AF ＝EF ；(4分)(2)在Rt △BCD 中，∵DC ＝DE ＝4，BD ＝8，∴sin ∠CBD ＝DC BD ＝12， ∴∠CBD ＝30°，(5分)∴∠EBD ＝∠CBD ＝30°，∴∠ABF＝90°－30°×2＝30°，(7分)∴∠ABF＝∠EBD，∴BF平分∠ABD.(8分)03把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F 重合（E、F两点均在BD上），折痕分别为BH、DG。

强化训练图形的折叠问题

(建议用时45分钟)基础巩固1．(2022·烟台模拟)如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝6，将△ADE沿DE翻折，使点A与点B重合，则CE的长为()A．198B．2C．254D．74D解析：设CE＝x，则AE＝8－x＝EB．在Rt△BCE中，BE2＝CE2＋BC2，即(8－x)2＝x2＋62，解得x＝74．故选D．2．(2022·泰山区模拟)如图，将矩形ABCD折叠，使点C和点A重合，折痕为EF，EF与AC交于点O．若AE＝5，BF＝3，则AO的长为()A． 5 B．35 2C．25D．45 C解析：∵矩形ABCD，∴AD∥BC，AD＝BC，AB＝CD．∴∠EFC＝∠AEF．由折叠得∠EFC ＝∠AFE ， ∴∠AFE ＝∠AEF ．∴AE ＝AF ＝5．由折叠得FC ＝AF ，OA ＝OC ， ∴BC ＝3＋5＝8．在Rt △ABF 中，AB ＝52－32＝4，在Rt △ABC 中，AC ＝42＋82＝45，∴OA ＝OC ＝25．故选C ．3．(2022·舟山)如图，在扇形AOB 中，点C ，D 在AB 上，将CD 沿弦CD 折叠后恰好与OA ，OB 相切于点E ，F ．已知∠AOB ＝120°，OA ＝6，则EF 的度数为________；折痕CD 的长为________．60° 46 解析：作O 关于CD 的对称点M ，连接MD 、ME 、MF 、MO ，MO 交CD 于N ，则ON ＝MN ．∵将CD ︵沿弦CD 折叠，∴点D 、E 、F 、C 都在以M 为圆心，半径为6的圆上．∵将CD ︵沿弦CD 折叠后恰好与OA ，OB 相切于点E ，F ，∴ME ⊥OA ，MF ⊥OB ． ∴∠MEO ＝∠MFO ＝90°．∵∠AOB ＝120°，∴四边形MEOF 中，∠EMF ＝360°－∠AOB －∠MEO －∠MFO ＝60°．即EF ︵的度数为60°．∵∠MEO ＝∠MFO ＝90°，ME ＝MF ，MO ＝MO ， ∴△MEO ≌△MFO (HL)．∴∠EMO ＝∠FMO ＝12∠FME ＝30°． ∴OM ＝ME cos ∠EMO ＝6cos 30°＝43．∴MN ＝23． ∵MO ⊥DC ， ∴DN ＝DM 2－MN 2＝62－(23)2＝26＝12CD ．∴CD ＝46．故答案为60°，46．4．(2022·东平月考)如图，在矩形纸片ABCD 中，AB ＝6，BC ＝9，M 是BC 上的点，且CM ＝3，将矩形纸片ABCD 沿过点M 的直线折叠，使点D 落在AB 上的点P 处，点C 落在点C ′处，折痕为MN ，则线段AN 的长是________．4 解析：连接PM ，如图．∵AB ＝6，BC ＝9，CM ＝3， ∴BM ＝BC －CM ＝9－3＝6．由折叠性质得，CD ＝PC ′＝6，∠C ＝∠PC ′M ＝∠PBM ＝90°，C ′M ＝CM ＝3，在Rt △PBM 和Rt △MC ′P 中， ⎩⎪⎨⎪⎧PM ＝MP BM ＝CP， ∴Rt △PBM ≌Rt △MC ′P (HL)． ∴PB ＝C ′M ＝3．∴P A ＝AB －PB ＝6－3＝3．设AN ＝x ，则ND ＝9－x ＝PN ．在Rt △APN 中，AN 2＋AP 2＝PN 2，即x 2＋32＝(9－x )2，解得x ＝4． ∴AN 的长是4．故答案为4．5．(2021·抚顺)如图，将矩形纸片ABCD 折叠，使点A 与点C 重合，折痕EF 与AC 相交于点O ，连接BO ．若AB ＝4，CF ＝5，则OB 的长为________．25 解析：连接AF ，过O 作OH ⊥BC 于H ，如图：∵将矩形纸片ABCD 折叠，使点A 与点C 重合，折痕EF 与AC 相交于点O ， ∴AF ＝CF ＝5，OA ＝OC ．在Rt △ABF 中，BF ＝AF 2－AB 2＝52－42＝3，∴BC ＝BF ＋CF ＝8．∵OA＝OC，OH⊥BC，AB⊥BC，∴O为AC中点，OH∥AB．∴OH是△ABC的中位线．∴BH＝CH＝12BC＝4，OH＝12AB＝2．在Rt△BOH中，OB＝BH2＋OH2＝42＋22＝25．故答案为25．6．(2021·巴中)如图，矩形AOBC的顶点A，B在坐标轴上，点C的坐标是(－10,8)，点D在AC上，将△BCD沿BD翻折，点C恰好落在OA边上点E处，则tan∠DBE等于()A．34B．35C．33D．12D解析：∵四边形AOBC为矩形，且点C(－10,8)，∴AC＝OB＝8，AO＝BC＝10，∠C＝∠A＝∠EOB＝90°．∵△BCD沿BD翻折，点C恰好落在OA边上点E处，∴CD＝DE，BC＝BE＝10．在Rt△OBE中，OE＝BE2－OB2＝102－82＝6．设AD＝m，则CD＝DE＝8－m．∵∠ADE＋∠AED＝∠AED＋∠OEB＝90°，∴∠ADE＝∠OEB．∵∠A＝∠AOB，∴△ADE∽△OEB．∴DADE＝OEBE．即m8－m＝610．解得m＝3．∴DE＝8－3＝5．在Rt△BDE中，DE＝5，BE＝10，∴tan∠DBE＝510＝12．另一种思路：OE＝6，则AE＝4．在Rt△ADE中，(8－m)2＋42＝m2，解得m＝5．∴DE＝5．在Rt△BDE中，BE＝10，∴tan∠DBE＝510＝12．故选D．能力提升7．(2022·宁阳检测)如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D，E分别在AB，AC上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上，若FD平分∠EFB，则AD的长为()A．259B．258C．157D．207D解析：作DH⊥BC于H．在Rt△ABC中，∠ACB＝90°，由勾股定理得AB＝32＋42＝5．∵将△ADE沿DE翻折得△DEF，∴AD＝DF，∠A＝∠DFE．∵FD平分∠EFB，∴∠DFE＝∠DFH．∴∠DFH＝∠A．设DH＝3x．在Rt△DHF中，sin∠DFH＝sin A＝35，∴DF＝5x．∴BD＝5－5x．∵△BDH∽△BAC，∴BDAB＝DHAC．∴5－5x5＝3x4．∴x＝47．∴AD＝5x＝207．故选D．8．(2021·泰安)如图，将矩形纸片ABCD折叠(AD＞AB)，使AB落在AD上，AE为折痕，然后将矩形纸片展开铺在一个平面上，E点不动，将BE边折起，使点B落在AE上的点G处，连接DE．若DE＝EF，CE＝2，则AD的长为______．4＋22解析：由翻折的性质可知，EB＝EB′，∠B ＝∠AB ′E ＝∠EB ′D ＝90°．在Rt △EBF 和Rt △EB ′D 中，⎩⎪⎨⎪⎧EF ＝ED EB ＝EB ′，∴Rt △EBF ≌Rt △EB ′D (HL)． ∴BF ＝B ′D ．∵四边形ABCD 是矩形， ∴∠C ＝∠CDB ′＝∠EB ′D ＝90°． ∴四边形ECDB ′是矩形． ∴DB ′＝EC ＝2． ∴BF ＝EC ＝2．由翻折的性质可知，BF ＝FG ＝2，∠F AG ＝45°，∠AGF ＝∠B ＝90°，∴AG ＝FG ＝2．∴AF ＝22．∴AB ＝AB ′＝2＋22． ∴AD ＝AB ′＋DB ′＝4＋22．故答案为4＋22．9．(2022·岱岳区模拟)如图，边长为1的正方形ABCD 中，点E 为AD 的中点，连接BE ，将△ABE 沿BE 折叠得到△FBE ，BF 交AC 于点G ，求CG 的长．答案：327解析：延长BF 交CD 于H ，连接EH ． ∵四边形ABCD 是正方形，∴AB ∥CD ，∠D ＝∠DAB ＝90°，AD ＝CD ＝AB ＝1． ∴AC ＝AD 2＋CD 2＝12＋12＝2．由翻折的性质可知，AE ＝EF ，∠EAB ＝∠EFB ＝90°，∠AEB ＝∠FEB ． ∵点E 是AD 的中点，∴AE ＝DE ＝EF ．在Rt △EHD 和Rt △EHF 中，⎩⎪⎨⎪⎧EH ＝EH ED ＝EF ，∴Rt △EHD ≌Rt △EHF (HL)． ∴∠DEH ＝∠FEH ． ∵∠DEF ＋∠AEF ＝180°， ∴2∠DEH ＋2∠AEB ＝180°． ∴∠DEH ＋∠AEB ＝90°． ∵∠AEB ＋∠ABE ＝90°， ∴∠DEH ＝∠ABE ． ∴△EDH ∽△BAE ． ∴ED AB ＝DH EA ＝12． ∴DH ＝14，CH ＝34． ∵CH ∥AB ， ∴CG GA ＝CH AB ＝34． ∴CG ＝37AC ＝327．10．(2022·天津)将一个矩形纸片OABC放置在平面直角坐标系中，点O(0,0)，点A(3,0)，点C(0,6)，点P在边OC上(点P不与点O，C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q，且∠OPQ＝30°，点O的对应点O′落在第一象限．设OQ＝t．(1)如图1，当t＝1时，求∠O′QA的大小和点O′的坐标；(2)如图2，若折叠后重合部分为四边形，O′Q，O′P分别与边AB相交于点E，F，试用含有t的式子表示O′E的长，并直接写出t的取值范围；(3)若折叠后重合部分的面积为33，则t的值可以是__________．(请直接写出两个不同．．．．的值即可)答案：(1)∠O′QA＝60°点O′的坐标为(32，32)(2)O′E＝3t－6，其中t的取值范围是2<t<3(3)3或103(答案不唯一，满足3≤t<23即可)解析：(1)在Rt△POQ中，∠OQP＝90°－∠OPQ＝60°．根据折叠，知△PO′Q≌△POQ，∴O′Q＝OQ，∠O′QP＝∠OQP＝60°．∵∠O′QA＝180°－∠O′QP－∠OQP，∴∠O′QA＝60°．如图，过点O′作O′H⊥OA，垂足为H，则∠O′HQ＝90°．∴在Rt△O′HQ中，得∠QO′H＝90°－∠O′QA＝30°．由t＝1得OQ＝1，则O′Q＝1．在Rt△O′HQ中，QH＝12O′Q＝12，O′H＝O′Q2－QH2＝32．∴OH＝OQ＋QH＝3 2．∴点O′的坐标为(32，32)．(2)∵点A(3,0)，∴OA＝3．又∵OQ＝t，∴QA＝OA－OQ＝3－t．由(1)知O′Q＝t，∠O′QA＝60°．∵四边形OABC是矩形，∴∠OAB＝90°．在Rt△EAQ中，∠QEA＝90°－∠EQA＝30°．∴QA＝12QE．∴QE＝2QA＝2(3－t)＝6－2t．∵O′E＝O′Q－QE，∴O′E＝3t－6．如图，当点O′落在AB上时，OQ＝O′Q＝t，∠AQO′＝60°，则∠AO′Q＝30°．∴AQ＝12O′Q＝12t．∴t＋12t＝3．解得t＝2．∴t的取值范围是2<t<3．(3)当点Q与点A重合时，AO′＝3，∠DAO′＝30°．∴AD＝AO′cos 30°＝23．则S△ADP＝12×23×3＝33．∴t＝3时，重合部分的面积是33．从t＝3之后重合部分的面积始终是33．当P与C重合时，OP＝6，∠OPQ＝30°，此时t＝OP·tan 30°＝23．∵P不能与C重合，∴t<23．∴3≤t<23都符合题意．拓展训练11．(2022·青岛)如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC 的平分线交AD于点E，且DE＝4．将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有：________．(填写序号)①BD＝8；②点E到AC的距离为3；③EM ＝103；④EM∥AC．①④解析：∵AB＝AC，BC＝16，AD⊥BC，∴BD＝DC＝12BC＝8．故①正确．如图，过点E作EF⊥AB于F，EH⊥AC于H．∵AD⊥BC，AB＝AC，∴AD平分∠BAC．∴EH＝EF．∵BE是∠ABD的角平分线，ED⊥BC，EF⊥AB，∴EF＝ED．∴EH＝ED＝4．故②不正确．∵将∠C沿GM折叠使点C与点E恰好重合，∴EM＝MC，DM＋MC＝DM＋EM＝CD＝8．设DM＝x，则EM＝8－x．在Rt△EDM中，EM2＝DM2＋DE2，DE＝4，∴(8－x)2＝42＋x2．解得x＝3．∴EM＝MC＝5．故③不正确．设AE＝a，则AD＝AE＋ED＝4＋a，BD＝8，AB2＝(4＋a)2＋82．∵S△ABES△BDE＝12AB·EF12BD·ED＝12AE·BD12ED·BD，∴AEED＝ABBD．∴a4＝AB8．∴AB＝2a．∴(4＋a)2＋82＝(2a)2．解得a＝203或a＝－4(舍去)．∴tan C＝ADDC＝203＋48＝43．∵tan∠EMD＝EDDM＝43，∴∠C＝∠EMD．∴EM∥AC．故④正确．故答案为①④．12．(2022·肥城检测)如图，已知AD∥BC，AB⊥BC，AB＝3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC于M，N两点，当B′为线段MN的三等分点时，BE 的长为()A．32B．322C．32或322D．322或355D解析：①当MB′＝13MN时，如图．Rt△AMB′中，AB′＝AB＝3，MB′＝13AB＝1，∴AM＝AB′2－MB′2＝22．∵AD∥BC，AB⊥BC，MN⊥AD，∴四边形ABNM是矩形．∴BN＝AM＝22，MN＝AB＝3．设BE＝x，则B′E＝x，EN＝22－x．Rt△B′EN中，B′N＝MN－MB′＝2，EN2＋B′N2＝B′E2，∴(22－x)2＋22＝x2．解得x＝32 2．∴BE的长为32 2．②当NB′＝13MN时，如图：∵NB′＝13MN＝1，∴MB′＝2．∴AM＝5．设BE＝y，同①可得y＝355．∴BE的长为355．综上所述，BE的长为322或355．故选D．。

折叠问题的处理技巧八道例题

折叠问题解答技巧八道例题例1. 如图，矩形ABCD 中，AB ＝2，BC ＝23，以AC 为轴翻折半平面，使二平面角B —AC —D 为120°，求：(1)翻折后，D 到平面ABC 的距离；(2)BD 和AC 所成的角.解析：研究翻折问题，通常要画出翻折前的平面图形和翻折后的空间图形，对应点的字母要相同.解分别过B 、D 作AC 的垂线，垂足是E 、F ，过F 作FB ′∥BE ，过B 作BB ′∥AC ，交点B ′，则四边形EFB ′B 是矩形.∵AC ⊥DF ，AC ⊥B ′F ，∴AC ⊥平面B ′FD ，即∠DF ′B 就是二面角B —AC —D 的平面角，亦即∠DFB ′＝120°.过D 作DO ⊥B ′F ，垂足为O.∵DO ⊂平面DFB ′，AC ⊥平面DFB ′.∴DO ⊥AF ，DO ⊥平面ABC. 在Rt ΔADC 中，CD ＝2，AD ＝23，∴DF ＝3，OD ＝DF ·sin60°＝23.(2)在ΔDFB ′中，DB ′＝︒⋅'⋅⋅-'+120cos 22F B DF F B DF ＝3.又由(1)可知，AC ∥BB ′，AC ⊥平面DFB ′⊥平面DFB ′.∴BB ′⊥平面DFB ′，∴ΔDB B ′是直角三角形，又BB ′＝EF ＝2.∴tan ∠DBB ′＝23.∵AC ∥BB ′,∴AC 与BD 所成的角就是∠DBB ′，即为arctan 23.例2. 正三棱柱ABC —A 1B 1C 1中，各棱长均为2，M 为AA 1中点，N 为BC 的中点，则在棱柱的表面上从点M 到点N 的最短距离是多少?并求之.解析： (1)从侧面到N ，如图1，沿棱柱的侧棱AA 1剪开，并展开，则MN ＝22ANAM+＝22)12(1++＝10(2)从底面到N 点，沿棱柱的AC 、BC 剪开、展开，如图2. 则MN ＝︒⋅-+120cos 222AN AM ANAM＝21312)3(122⨯⨯⨯++＝34+∵34+＜10∴min MN ＝34+.如图，ABCDEF 为正六边形，将此正六边形沿对角线AD 折叠.(1)求证：AD ⊥EC ，且与二面角F —AD —C 的大小无关； (2)FC 与FE 所成的角为30°时，求二面角F —AD —C 的余弦值. 解析：(1)正六边形ABCDEF ，在折叠前有AD ⊥EC ，设AD 与EC 交于M ，折叠后即有AD ⊥ME ，AD ⊥MC.则AD ⊥平面EMC ，无论∠EMC 的大小如何，总有AD ⊥EC.(2)利用余弦定理，有cos ∠EMC ＝97例3（2005·湖南）如图７－１，已知A B C D 是上、下底边长分别为2和6，高为3的等腰梯形，将它沿对称轴1OO 折成直二面角．（Ⅰ）证明：1ACBO ⊥；（Ⅱ）求二面角1O AC O --的大小．ABOCO 1D解法1（I ）证明：由题设知1O A O O ⊥，1OB OO ⊥．所以A O B ∠是所折成的直二面角的平面角，即O A O B⊥．故可以O 为原点，1,,O A O B O O 所在直线分别为x 轴、y轴、z 轴建立空间直角坐标系，如图７－２，则相关各点的坐标是(3,0,0)A，(0,3,0)B，C ，1(0,O ．从而(3,3)AC =-，1(0,BO =-，130AC BO ⋅=-+=．所以1AC BO ⊥．解法２（I ）证明：由题设知1O A O O ⊥，1OB OO ⊥，所以A O B ∠是所折成的直二面角的平面角，即O A O B ⊥．从而A O ⊥平面1O B C O ，O C 是A C在面1O B C O 内的射影．因为11tan O B O O B OO ∠==，111tan 3O C O O C O O ∠==，所以13O O B π∠=，16O O Cπ∠=，从而1OC BO ⊥，由三垂线定理得1ACBO ⊥．（II ）解由（I ）1OCBO ⊥，1AC BO ⊥，知1BO ⊥平面O A C ．设1O C O B E = ，过点E作EFAC⊥于F ，连结1O F （如图７－３），则E F是1O F 在平面A O C 内的射影，由三垂线定理得1O F AC⊥．所以1O FE ∠是二面角1O AC O --的平面角．由题设知113,1OA OO O C ===，所以ABC DFE GA'1O A==，AC ==，从而1332111=⋅=ACCO A O F O ，又11sin62O E O O π==，所以111sin 4O E O FE O F∠==，即二面角1O ACO --的大小是arcsin 4．一、折叠与展开中的垂直问题例4.如图在ΔABC 中， AD ⊥BC ， ED=2AE ，过E 作FG ∥BC ，且将ΔAFG 沿FG 折起，使∠A 'ED=60°，求证:A 'E ⊥平面A 'BC解： ∵FG ∥BC ，AD ⊥BC ∴A 'E ⊥FG ∴A 'E ⊥BC 设A 'E=a ，则ED=2a 由余弦定理得：A 'D 2=A 'E 2+ED 2-2•A 'E •EDcos60°=3a 2 ∴ED 2=A 'D 2+A 'E 2 ∴A 'D ⊥A 'E ∴A 'E ⊥平面A 'BC例5如图：D 、E 是是等腰直角三角形ABC 中斜边BC 的两个三等分点，沿AD 和AE 将△ABD 和△ACE 折起，使AB 和AC 重合，求证：平面ABD ⊥平面ABE.ＥＤＢＡＥＤＣＢＡ解析：过D作DF⊥AB交AB于F，连结EF，计算DF、EF的长，又DE为已知，三边长满足勾股定理，∴∠DFE＝090；三、折叠与展开中的距离与体积问题例6.如图，矩形ABCD中，AB＝2，BC＝23，以AC为轴翻折半平面，使二平面角B—AC—D为120°，求：翻折后，D到平面ABC的距离；解析：研究翻折问题，通常要画出翻折前的平面图形和翻折后的空间图形，对应点的字母要相同.解：分别过B、D作AC的垂线，垂足是E、F，过F作FB′∥BE，过B作BB′∥AC，交点B′，则四边形EFB′B是矩形.∵AC⊥DF，AC⊥B′F，∴AC⊥平面B′FD，即∠DF′B就是二面角B—AC—D的平面角，∠DFB′＝120°.过D作DO⊥B′F，垂足为O.∵DO 平面DFB′，AC⊥平面DFB′.∴DO⊥AF，DO⊥平面ABC.3. 在RtΔADC中，CD＝2，AD＝23，∴DF＝3，OD＝DF·sin60°＝2例7. 正三棱柱ABC —A 1B 1C 1中，各棱长均为2，M 为AA 1中点， N 为BC 的中点，在棱柱表面上从点M 到点N 的最短距离是多少?解析： (1)从侧面到N ，如图1，沿棱柱的侧棱AA 1剪开，并展开，则MN ＝22ANAM+＝22)12(1++＝10(2)从底面到N 点，沿棱柱的AC 、BC 剪开、展开，如图2.则MN ＝︒⋅-+120cos 222AN AM ANAM＝21312)3(122⨯⨯⨯++＝34+∵34+＜10∴min MN ＝34+.二、折叠与展开中的空间角问题例8. 矩形ABCD ，AB=3，BC=4，沿对角线BD 把△ABD 折起，使点A 在平面BCD 上的射影A′落在BC 上，求二面角A —BD-—C 的余弦值。

图形的折叠问题课件

动态折叠问题
要点一
总结词
动态折叠问题涉及到如何将一个动态变化的二维图形准确无误地折叠成一个动态变化的三维结构，是图形折叠问题中的一大挑战。
要点二
详细描述
动态折叠问题需要考虑图形的动态属性和变化规律，以及如何通过一系列的动态折叠步骤实现动态的三维结构。解决这类问题需要深入理解图形的动态属性和折叠过程中的力学原理。
06 图形折叠问题的挑战和未来发展
复杂图形的折叠问题
总结词
复杂图形的折叠问题涉及到如何将复杂的二维图形准确无误地折叠成三维结构，是图形折叠问题中的一大挑战。
详细描述
复杂图形的折叠问题需要考虑图形的形状、大小、对称性、弯曲角度等因素，以及如何通过折叠实现预定的三维结构。解决这类问题需要深入理解图形的几何属性和折叠过程中的力学原理。
未来发展
随着计算机科学和数学理论的不断进步，复杂图形的折叠问题有望得到更深入的研究和解决。未来的研究可能会集中在开发更有效的算法和优化技术，以解决更复杂的图形折叠问题。
多面体的折叠问题
01
总结词
多面体的折叠问题涉及到如何将一个二维的多面体图形折叠成一个三维的多面体结构，是图形折叠问题中的另一大挑战。
解析法定义
解析法是一种通过数学公式和逻辑推理来解决问题的策略。在解决图形折叠问题时，解析法通常用于建立数学模型，以描述图形的折叠过程和结果。
解析法的应用
解析法可以用于解决各种复杂的图形折叠问题，例如平面图形的折叠、三维模型的折纸等。通过建立数学方程，解析法可以预测折叠后的形状和位置，以及解决折叠过程中的动态变化问题。
总结词
三角形是具有三条边的多边形，其折叠问题主要涉及到三角形的边与角的关系以及空间想象。

几何图形的折叠问题

纸艺制作
产品设计
通过折叠纸张或其他材料，制作各种纸艺作品，如纸飞机、千纸鹤等。
在产品设计中，折叠结构可以用于节省空间、便于携带和运输，如折叠家具、折叠雨伞等。
建筑模型
数学教育
通过折叠纸张或其他材料，制作建筑模型，展示建筑的三维形态。
折叠问题在数学教育中用于培养学生的空间想象能力和几何思维能力，帮助学生理解平面与立体几何之间的关系。
应用拓展
探索几何图形折叠问题在建筑、航空航天、生物医学等领域的应用，以推动相关领域的技术进步和创新。
感谢您的观看
THANKS
1 2
正方体折叠成三棱锥
将一个正方体的一个面朝下，然后将其顶点与正方体的中心相连，可以得到一个三棱锥。
长方体折叠成三棱柱
将一个长方体的一个面朝下，然后将其顶点与长方体的中心相连，可以得到一个三棱柱。
3
球体折叠成椭球体
将一个球体的赤道线何图形折叠实例
01
02
需要开发更有效的算法和软件工具，以模拟和优化几何图形
的折叠过程。
未来发展方向
新材料与技术应用
探索新型材料和加工技术，以提高几何图形折叠的效率和精度。
智能化与自动化
利用人工智能和机器学习技术，实现几何图形折叠过程的智能化和自动化。
多学科交叉研究
加强数学、物理学、工程学等多个学科在几何图形折叠问题上的交叉研究，以推动理论和实践的深入发展。
02
几何图形的折叠问题解析
平面几何图形的折叠
定义
平面几何图形的折叠问题是指将一个平面图形沿着一条或几条折痕进行折叠，使其从一个平面状
态变为立体状态的过程。
常见类型
如正方形、三角形、圆形等平面图形的折叠问题，以及由这些基本图形组合形成的复杂图形的折叠问题。

图形的折叠问题小学数学巩固提高

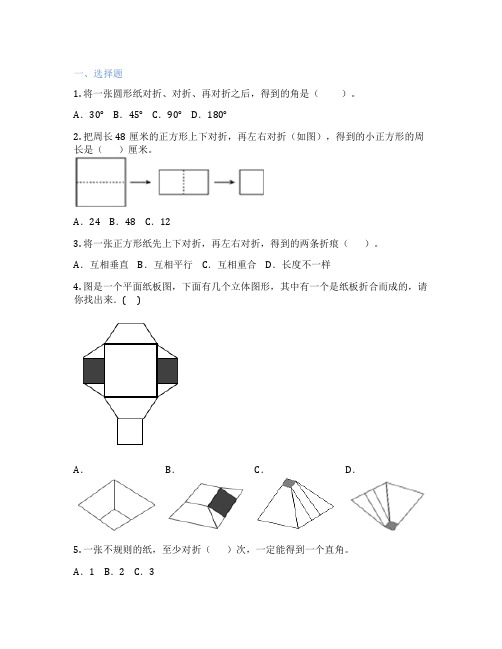
一、选择题1. 将一张圆形纸对折、对折、再对折之后，得到的角是（）。

A．30°B．45°C．90°D．180°2. 把周长48厘米的正方形上下对折，再左右对折（如图），得到的小正方形的周长是（）厘米。

A．24 B．48 C．123. 将一张正方形纸先上下对折，再左右对折，得到的两条折痕（）。

A．互相垂直B．互相平行C．互相重合D．长度不一样4. 图是一个平面纸板图，下面有几个立体图形，其中有一个是纸板折合而成的，请你找出来．( )A．B．C．D．5. 一张不规则的纸，至少对折（）次，一定能得到一个直角。

A．1 B．2 C．3二、填空题6. 把一张长方形纸连续对折3次后展开，每份是这张长方形纸的。

7. 把一张长方形纸连续对折3次，按下面的方式剪一剪，能剪出( )只完整的蝴蝶。

8. 如图，把一张长40厘米，宽32厘米的长方形纸对折成了两个小长方形，每个小长方形的周长是( )厘米。

9. 一张正方形纸片，对折再对折后，正方形可能被分成4个________形，也可能被分成4个________形。

10. 一张正方形的纸对折一次后，周长是6厘米，这个正方形的实际周长是____．三、解答题11. 以“感恩”为主题的班会上，乐乐给王老师做了一张可对折的感恩卡，对折后的贺卡刚好是一个正方形，这个正方形的周长是28厘米，这张贺卡打开后的周长是多少厘米？12. 如图，把一张长方形的一个角折过来，已知∠1＝70°，求∠2。

13. 把一张长方形纸折成下图的形状，求阴影部分的面积。

14. 把一张纸沿虚线对折后剪去两个小三角形，展开后得到第二行的哪个图形？把它圈起来。

七年级折叠问题解题技巧

七年级折叠问题解题技巧一、折叠问题中的基本性质与关系1. 折叠性质在折叠过程中，折叠前后的图形全等。

这意味着对应边相等，对应角相等。

例如，将一个三角形沿着某条直线折叠，折叠后的三角形与原三角形的对应边长度不变，对应角的大小也不变。

折痕是对应点连线的垂直平分线。

比如将矩形ABCD沿着EF折叠，使得点A与点C重合，那么EF就是AC的垂直平分线。

2. 常见的几何图形中的折叠三角形折叠例1：在△ABC中，∠C = 90°，将△ABC沿着直线DE折叠，使点A与点B 重合，若AC = 6，BC = 8，求折痕DE的长。

解析：因为点A与点B重合，所以DE是AB的垂直平分线。

先根据勾股定理求出AB=公式。

设AB中点为F，则AF=公式。

由于△ADE和△BDE全等，所以AD = BD。

设BD = x，则AD = x，CD = 8 x。

在Rt△ACD中，根据勾股定理公式，即公式，解得公式。

再根据相似三角形，△ADE∽△ABC，公式，即公式，解得DE=公式。

矩形折叠例2：矩形ABCD中，AB = 3，BC = 4，将矩形沿对角线AC折叠，求重叠部分（△AEC）的面积。

解析：因为矩形沿对角线AC折叠，所以△ADC≌△AEC。

设AE = x，则BE = 4 x。

在Rt△ABE中，根据勾股定理公式，即公式，解得公式。

所以公式。

二、解题步骤与技巧1. 步骤第一步：根据折叠性质确定相等的边和角。

这是解决折叠问题的基础，只有明确了这些关系，才能进一步进行计算。

第二步：设未知数。

通常根据所求的量或者与所求量相关的线段设未知数，然后利用勾股定理、相似三角形等知识建立方程。

第三步：求解方程。

通过解方程得到未知数的值，从而求出最终答案。

2. 技巧利用勾股定理在直角三角形中，折叠后常常会形成新的直角三角形，此时可以利用勾股定理建立方程求解。

如上述矩形折叠的例子中，在Rt△ABE中利用勾股定理求出AE的长度。

利用相似三角形当折叠后的图形与原图形存在相似关系时，利用相似三角形的对应边成比例来求解。

四年级上册折叠问题易错点

四年级上册折叠问题易错点
四年级上册的折叠问题是数学课程中的一个重要内容，也是学
生容易出现错误的地方。

首先，折叠问题主要涉及到图形的对称性
和折叠后的变化，学生在解题时需要注意以下几个易错点：
1. 对称性理解不清，学生可能会混淆图形的对称轴，导致在折
叠时出现错误。

他们需要理解对称轴的概念，并能够准确地找到图
形的对称轴。

2. 折叠方向混淆，在折叠问题中，学生有时会弄混折叠的方向，导致最终的图形与预期不符。

他们需要明确理解折叠的方向，并在
解题时仔细思考折叠后的图形变化。

3. 折叠线的位置选择错误，有些学生在选择折叠线的位置时容
易出错，他们需要理解折叠线的作用，并能够准确地选择合适的折
叠线。

4. 折叠后图形的位置关系，学生在折叠后图形的位置关系上也
容易出现错误，他们需要注意折叠后各部分的位置关系，确保折叠
后的图形符合要求。

针对以上易错点，老师可以通过讲解、示范和练习来帮助学生加深理解和掌握。

同时，鼓励学生多进行实际折叠操作，加强对折叠问题的理解和应用能力。

希望这些建议能够帮助学生更好地掌握四年级上册的折叠问题。

图形折叠问题

图形折叠问题图形的折叠实际就是反射变换或者说是对称变换，或者说是翻折。

这类问题大都联系实际，内容丰富,解法灵活,具有开放性，有利于考查解题者的动手能力,空间观念和几何变换的思想.例1. 折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠AD边与对角线BD 重合，得折痕DG.若AB=2，BC=1，求AG。

解：作GE⊥BD，垂足为E。

设AG=x，则，易知,则GE=x,根据勾股定理可知，所以在中，由勾股定理得，解得例2. 如图2,矩形纸片ABCD的长AD=9cm，宽AB=3cm，将其折叠,使点D与点B 重合，那么折叠后DE的长和折痕EF的长分别是多少？解法一：设，则,在中，由勾股定理得，解得,即。

连结BD，设BD与EF交于点O，易得,由题意可知EF是BD的中垂线，所以,EF⊥BD，在中，由勾股定理得，所以。

解法二：求DE同上法,再作EG⊥BC，垂足为点G。

易知,，所以，所以。

例3. 四边形ABCD是一块矩形纸片，E是AB上一点，且BE:EA=5：3,EC=，将△BCE沿折痕EC翻折，若点B恰好落在AD边上的点F上,求AB、BC的长。

解：连结EF、FC、BF。

设BF交EC于M.因为B、F关于EC对称，所以BF⊥EC，BE=EF,。

设BE=5x,则.因为，所以因为,所以，所以，所以BC=30.所以，即，所以，所以。

例4。

如图4，一张宽为3，长为4的矩形纸片ABCD，先沿对角线BD对折,点C落在点的位置，交AD于G，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M，则ME的长为多少？解法一：延长BA、交于F，由轴对称性质知.所以又因为，所以，所以.再根据EN是折痕可知：EN垂直平分AD，所以EN//AB。

又因为M是AD中点，所以E是DF中点，所以EM是△DFA的中位线.令EM=x，则FA=2x，FD=FB=2x+3，所以。

解得，即.解法二：连结GN，易证△BGD是等腰三角形.因为A点、D点关于EN对称，所以N是BD的中点,所以GN⊥BD，所以Rt△GND∽Rt△BAD,所以。

知识卡片-翻折变换(折叠问题)

翻折变换（折叠问题）能量储备● 翻折变换（折叠问题）实质上就是轴对称变换．● 折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．● 在解决实际问题时，对于折叠较为复杂的问题可以实际操作图形的折叠，这样便于找到图形间的关系．通关宝典★ 基础方法点方法点1.利用轴对称性质，解决折纸问题例1：将长方形纸片ABCD(如图①所示)按如下步骤操作：(1)以过点A 的直线为折痕折叠纸片，使点B 恰好落在AD 边上，折痕与BC 边交于点E(如图②所示)；(2)以过点E 的直线为折痕折叠纸片，使点A 落在EC 边上，折痕EF 交AD 边于点F(如图③所示)；(3)将纸片展平，那么∠AFE 的度数为( )A .60°B ．67.5°C ．72°D ．75°分析：根据轴对称的性质，可知第一次折叠后∠EAD ＝45°，∠AEC ＝135°；第二次折叠后，∠AEF ＝67.5°，∠FAE ＝45°，所以∠AFE ＝67.5°.解：B方法点2.折叠与剪纸的综合应用例1：请分析如图所示的图形，该怎样剪？设法使所剪的次数尽可能少．解：图(1)可以先折叠1次，剪出它的一半即可得到整个图形；图(2)可以折叠2次，剪出它的14即可得到整个图形．方法点3.解决矩形折叠问题的方法(1)利用折叠的性质：折叠前后的图形能够完全重合，折叠前后的图形对应边相等，对应角相等．(2)此类问题往往通过图形间的折叠找出折叠部分与原图形之间线段或角的联系，从而得到折叠部分与原图形或其他图形之间的关系．(3)尽量将数量关系利用勾股定理列方程．例1：如图所示，将矩形ABCD 沿对角线BD 折叠，点C 的对应点为点C′，BC′与AD 交于点E.若AD ＝8 cm ，AB ＝4 cm ，求△BDE 的面积．解：设DE ＝x cm ，则AE ＝(8－x)cm .由折叠的性质知△BCD 与△BC′D 全等，则∠1＝∠2.在矩形ABCD 中，∵ AD ∥BC ，∴ ∠1＝∠3，∴ ∠2＝∠3，∴ BE ＝DE ＝x.在Rt △ABE 中，由勾股定理，得BE 2＝AB 2＋AE 2，即x 2＝42＋(8－x)2，解得x ＝5.∴ △BDE 的面积为12DE·AB ＝12×5×4＝10(cm 2)． ★★ 易混易误点1.误认为折叠几次就有几条对称轴把一个图形沿一条直线折叠后，如果直线两旁的部分能够相互重合，这条直线才是这个轴对称图形的对称轴，并非是把这个图形折叠的次数当成对称轴的条数．例1：将一张正方形的纸沿对角线对折一次后得到等腰三角形，沿等腰三角形底边上的高对折一次，又得到等腰三角形，再沿着底边上的高对折一次，共对折了三次后，在中间剪去一个小圆，则展开后得到的图形至少有几条对称轴？解：4条．蓄势待发考前攻略折纸由于取材方便，又能有效地考查实践操作、归纳探索、逻辑推理、空间想象等各种能力，因而备受中考命题者的青睐，题型主要以选择题为主.完胜关卡。

图形折叠问题

图形的折叠问题的习题带答案

初中折叠问题题型

中考数学专题训练：图形的折叠问题(附参考答案)

三年级折叠问题巧妙解题技巧

(完整版)几何图形折叠问题

2024年中考数学考点必备方法必备09几何综合题的三类折叠问题(解析版)

初中数学中的折叠问题

折叠几何综合专题---16道题目(含答案)

强化训练 图形的折叠问题

折叠问题的处理技巧八道例题

图形的折叠问题课件

几何图形的折叠问题

图形的折叠问题 小学数学 巩固提高

七年级折叠问题解题技巧

四年级上册折叠问题易错点

图形折叠问题

知识卡片-翻折变换(折叠问题)

强化训练图形的折叠问题

图形的折叠问题小学数学巩固提高