初一几何练习题及答案33294

合集下载

初一几何练习题及答案

初一几何三角形一.选择题 (本大题共 24 分)1.以下列各组数为三角形的三条边，其中能构成直角三角形的是（）（A）17，15，8 （B）1/3，1/4，1/5 （C) 4，5，6 (D) 3，7，112.如果三角形的一个角的度数等于另两个角的度数之和，那么这个三角形一定是（）(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形3.下列给出的各组线段中，能构成三角形的是（）(A)5，12，13 (B)5，12，7 (C)8，18，7 (D)3，4，84.如图已知：Rt△ABC中，∠C=90°，AD平分∠BAC，AE=AC，连接DE，则下列结论中，不正确的是（）(A) DC=DE (B) ∠ADC=∠ADE (C) ∠DEB=90°(D) ∠BDE=∠DAE5.一个三角形的三边长分别是15，20和25，则它的最大边上的高为（）（A）12 （B）10 （C) 8 (D) 56.下列说法不正确的是（）（A）全等三角形的对应角相等（B）全等三角形的对应角的平分线相等（C）角平分线相等的三角形一定全等（D）角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8，第三边长是整数的三角形一共有（）(A)3个(B)4个(C)5个(D)无数个8.下列图形中，不是轴对称图形的是（）（A）线段MN （B）等边三角形（C) 直角三角形(D) 钝角∠AOB9.如图已知：△ABC中，AB=AC，BE=CF，AD⊥BC于D，此图中全等的三角形共有（）(A)2对(B)3对(C)4对(D)5对10.直角三角形两锐角的平分线相交所夹的钝角为（）(A)125°(B)135°(C)145°(D)150°11.直角三角形两锐角的平分线相交所夹的钝角为（）(A)125°(B)135°(C)145°(D)150°12.如图已知：∠A=∠D，∠C=∠F，如果△ABC≌△DEF，那么还应给出的条件是（）(A) AC=DE (B) AB=DF (C) BF=CE (D) ∠ABC=∠DEF二.填空题 (本大题共 40 分)1.在Rt△ABC中，∠C=90°，如果AB=13，BC=12，那么AC= ；如果AB=10，AC：BC=3：4，那么BC=2.如果三角形的两边长分别为5和9，那么第三边x的取值范围是。

初一下数学几何试题及答案

七年级下学期数学几何阶段测试题一、选择题：（每题3分，共30分）1．下面有4个汽车标志图案，其中是轴对称图形的是（）A．②③④B．①③④C．①②④D．①②③2．小华在电话中问小明：“已知一个三角形三边长分别是4，9，12，如何求这个三角形的面积？”小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（）A. B. C.D.3．小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是（）A．B．C．D．4、在△ABC所在的平面内存在一点P，它到A、B、C三点的距离都相等，那么点P一定是（）A．△ABC三边中垂线的交点B．△ABC三边上高线的交点7题图 C ．△ABC 三内角平分线的交点 D ．△ABC 三条中线的中点5．△ABC 中，AC=5，中线AD=7，则AB 边的取值范围是（）A ．1＜AB ＜29 B ．9＜AB ＜19C ．5＜AB ＜19D ．4＜AB ＜246．已知：如图，下列三角形中，AB=AC ，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（）A ．①③④B ．①②③④C ．①②④D ．①③7．如图，在一个规格为6×12（即6×12个小正方形）的球台上，有两个小球A ，B ．若击打小球A ，经过球台边的反弹后，恰好击中小球B ，那么小球A 击出时，应瞄准球台边上的点（）A ．P 1B ．P 2C ．P 3D ．P 48．如图，在Rt △ABC 中，∠ACB=90°，∠BAC=30°，∠ACB 的平分线与∠ABC 的外角平分线交于E 点，连接AE ，则∠CEA 是（）A ．15°B ．20°C ．30°D．35°8题图9．如图，已知∠AOB=40°，点P关于OA、OB的对称点分别为C、D，CD交OA、OB于M、N两点，则∠MPN的度数是（）A．70°B．80°C．90°D．100°10．如图，C为线段AE上一动点（不与A、E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ、OC，以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOE=120°；⑥OC平分∠AOE。

七年级几何试卷【含答案】

七年级几何试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 在一个直角三角形中，如果一条直角边的长度是3厘米，斜边的长度是5厘米，那么另一条直角边的长度是：A. 4厘米B. 6厘米C. 8厘米D. 10厘米2. 下列哪个图形是平行四边形？A. 所有边都相等的四边形B. 对边平行且相等的四边形C. 有一个角是直角的四边形D. 所有角都相等的四边形3. 下列哪个多边形是正六边形？A. 所有边都相等，所有角都相等的多边形B. 有六个边的多边形C. 所有角都相等的多边形D. 所有边都相等的多边形4. 在一个等腰三角形中，如果底边的长度是8厘米，腰的长度是5厘米，那么这个三角形的周长是：A. 16厘米B. 18厘米C. 20厘米D. 22厘米5. 下列哪个图形是梯形？A. 有一个角是直角的四边形B. 对边平行且相等的四边形C. 有两条对边平行的四边形D. 所有边都相等的四边形二、判断题（每题1分，共5分）1. 等边三角形的三条边都相等，三个角也都相等。

（）2. 平行四边形的对边平行且相等。

（）3. 矩形是一种特殊的平行四边形，它有一个角是直角。

（）4. 在一个等腰三角形中，底边的中点到顶点的线段是高，也是中线，也是角平分线。

（）5. 任意多边形的外角和都是360度。

（）三、填空题（每题1分，共5分）1. 在一个直角三角形中，如果一条直角边的长度是3厘米，斜边的长度是5厘米，那么另一条直角边的长度是____厘米。

2. 下列哪个图形是平行四边形？____3. 下列哪个多边形是正六边形？____4. 在一个等腰三角形中，如果底边的长度是8厘米，腰的长度是5厘米，那么这个三角形的周长是____厘米。

5. 下列哪个图形是梯形？____四、简答题（每题2分，共10分）1. 请简述平行四边形的性质。

2. 请简述矩形的性质。

3. 请简述等腰三角形的性质。

4. 请简述梯形的性质。

5. 请简述多边形的外角和定理。

七年级数学几何图形练习题及答案

七年级数学几何图形练习题及答案[答案表]以下是七年级数学几何图形练习题的答案。

1. 判断下列说法是否正确，并用对或错来回答：a) 正方形有四个直角。

答案：对。

b) 所有矩形都是正方形。

答案：错。

c) 所有正方形都是矩形。

答案：对。

d) 所有正方形都是长方形。

答案：对。

2. 根据图形的描述，选择正确的图形并填写在括号内：a) 一个有两条等长直角边的三角形是( )。

①直角三角形②等腰三角形③锐角三角形④钝角三角形答案：②等腰三角形b) 一条边为直径的圆叫作( )。

①半圆②椭圆③圆锥④圆答案：④圆c) 具有四条边且都相等的四边形是( )。

①正方形②长方形③梯形④平行四边形答案：①正方形3. 请计算下列图形的周长：a) 边长为4 cm的正方形的周长是多少？答案：正方形的四边相等，所以周长=4cm+4cm+4cm+4cm=16cm。

b) 边长分别为5 cm和8 cm的长方形的周长是多少？答案：长方形的周长=5cm+8cm+5cm+8cm=26cm。

c) 一张和纸短边长7 cm，长边长10 cm的长方形纸片，它的周长是多少？答案：周长=7cm+10cm+7cm+10cm=34cm。

4. 请计算下列图形的面积：a) 边长为6 cm的正方形的面积是多少？答案：正方形的面积=边长 ×边长 = 6cm × 6cm = 36cm²。

b) 边长分别为3 cm和7 cm的长方形的面积是多少？答案：长方形的面积=长 ×宽 = 3cm × 7cm = 21cm²。

c) 一张长边长为12 cm，短边长为5 cm的长方形纸片，它的面积是多少？答案：面积=长 ×宽 = 12cm × 5cm = 60cm²。

5. 请判断图形是否相似，并用是或否来回答：a) 下图中的两个三角形是否相似？答案：是。

（图形描述省略）b) 下图中的两个四边形是否相似？答案：否。

完整版)初一几何练习题及答案

完整版)初一几何练习题及答案初一几何：三角形一、选择题（本大题共24分）1.以下列各组数为三角形的三条边，其中能构成直角三角形的是（）A。

17，15，8B。

1/3，1/4，1/5C。

4，5，6D。

3，7，112.如果三角形的一个角的度数等于另两个角的度数之和，那么这个三角形一定是（）A。

锐角三角形B。

直角三角形C。

钝角三角形D。

等腰三角形3.下列给出的各组线段中，能构成三角形的是（）A。

5，12，13B。

5，12，7C。

8，18，7D。

3，4，84.如图已知：Rt△ABC中，∠C=90°，AD平分∠BAC，AE=AC，连接DE，则下列结论中，不正确的是（）A。

DC=DEB。

∠___∠ADEC。

∠DEB=90°D。

∠___∠DAE5.一个三角形的三边长分别是15，20和25，则它的最大边上的高为（）A。

12B。

10C。

8D。

56.下列说法不正确的是（）A。

全等三角形的对应角相等B。

全等三角形的对应角的平分线相等C。

角平分线相等的三角形一定全等D。

角平分线是到角的两边距离相等的所有点的集合7.两条边长分别为2和8，第三边长是整数的三角形一共有（）A。

3个B。

4个C。

5个D。

无数个8.下列图形中，不是轴对称图形的是（）A。

线段MNB。

等边三角形C。

直角三角形D。

钝角∠AOB9.如图已知：△ABC中，AB=AC，BE=CF，AD⊥BC于D，此图中全等的三角形共有（）A。

2对B。

3对C。

4对D。

5对10.直角三角形两锐角的平分线相交所夹的钝角为（）A。

125°B。

135°C。

145°D。

150°11.直角三角形两锐角的平分线相交所夹的钝角为（）A。

125°B。

135°C。

145°D。

150°12.___已知：∠A=∠D，∠C=∠F，如果△ABC≌△DEF，那么还应给出的条件是（）A。

AC=DEB。

AB=DFC。

初一几何图形初步试题及答案

初一几何图形初步试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是几何图形？A. 圆B. 三角形C. 正方形D. 直线答案：D2. 一个正方形的边长为4厘米，它的周长是多少厘米？A. 8厘米B. 12厘米C. 16厘米D. 20厘米答案：C3. 一个圆的半径是5厘米，它的直径是多少厘米？A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案：A4. 下列哪个图形是轴对称图形？A. 正方形B. 圆形C. 长方形D. 所有选项答案：D5. 如果一个三角形的三个内角之和为180度，它是什么类型的三角形？A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等边三角形答案：B二、填空题（每题2分，共10分）6. 平行四边形的对边________。

答案：平行且相等7. 一个圆的周长公式是________。

答案：C = 2πr8. 如果一个多边形的内角和是900度，那么它是________边形。

答案：六9. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的斜边长度是________厘米。

答案：510. 一个正六边形的内角是________度。

答案：120三、简答题（每题5分，共15分）11. 描述什么是几何图形的对称性？答案：几何图形的对称性是指图形在某个点、直线或平面上翻转或反射后，能够与原图形完全重合的性质。

12. 解释什么是相似图形？答案：相似图形是指两个图形在形状上完全相同，但大小可以不同，且它们的对应角相等，对应边成比例。

13. 什么是圆周角定理？答案：圆周角定理是指一个圆周角的度数是它所截取的弧所对圆心角的一半。

四、计算题（每题10分，共20分）14. 已知一个三角形的三个顶点坐标分别为A(1,2)，B(4,6)，C(7,4)，请计算这个三角形的面积。

答案：首先计算AB和AC的长度，然后使用海伦公式计算三角形的面积。

15. 一个圆的半径为7厘米，求这个圆的面积。

答案：使用圆的面积公式A = πr²，代入半径r=7厘米，计算得到面积。

七年级数学几何练习题及答案

七年级数学几何练习题及答案练题一：直线的性质1. 试述直线的定义和特点。

答案：直线是由一连串无限延伸的点组成，它没有弯曲和拐角。

直线上的任意两点可以用唯一一条直线连接。

2. 画出以下直线的标志并写出它们的名称：水平线、垂直线、倾斜线、平行线、相交线。

答案：- 水平线：⎕，两端点的纵坐标相同。

- 垂直线：⎈，两端点的横坐标相同。

- 倾斜线：/，连接两个不同的点。

- 平行线：//，在同一平面内永不相交的两条直线。

- 相交线：+，两条直线在同一点相交。

练题二：三角形的性质1. 试述三角形的定义和特点。

答案：三角形是由三条线段组成的图形。

它的特点是三条边相连的三个点不在一条直线上。

2. 根据三角形的边长关系，判断以下三角形的类型：等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形。

答案：- 等边三角形：三条边的长度都相等。

- 等腰三角形：两条边的长度相等。

- 直角三角形：有一个角度为90度。

- 锐角三角形：三个角都小于90度。

- 钝角三角形：有一个角度大于90度。

练题三：四边形的性质1. 试述四边形的定义和特点。

答案：四边形是由四条线段组成的图形。

它的特点是四条边相连的四个点不在一条直线上。

2. 根据四边形的边长关系，判断以下四边形的类型：平行四边形、矩形、正方形、菱形、梯形。

答案：- 平行四边形：有两对平行的边。

- 矩形：有四个直角。

- 正方形：既是矩形又是菱形，四个边的长度相等且都是直角。

- 菱形：四个边的长度相等。

- 梯形：有一对平行的边。

练题四：圆的性质1. 试述圆的定义和特点。

答案：圆是平面上所有到中心点距离相等的点的集合。

圆由一个中心点和半径组成。

2. 根据圆的性质，判断以下说法的正误：半径相等的圆周长相等、直径相等的圆周长相等。

答案：半径相等的圆周长相等是正确的，直径相等的圆周长相等也是正确的。

以上是七年级数学几何练习题及答案的简要概述，希望对你的学习有所帮助。

七年级上册《数学》几何图形专项练习题((含答案)

七年级上册《数学》几何图形专项练习题第1课时几何图形一、能力提升1.下列所列举的物体中,与圆锥的形状类似的是()A.足球B.字典C.易拉罐D.标枪的尖头2.下列图形属于柱体的是()3.下列第一行所示的四个图形,每个图形均是由四种简单的图形a,b,c,d(圆、直线、三角形、长方形)中的两种组成.例如由a,b组成的图形记作a☉b,那么由此可知,下面第二行的图中可以记作a☉d的是()4.如图,下面各几何体中,是三棱柱的是.(只填序号)5.下列说法:①圆锥和圆柱的底面都是圆;②棱锥底面边数与侧棱数相等;③棱柱的上、下底面是形状、大小相同的多边形;④四棱柱是长方体.其中正确的是.(填序号)6.有一个几何体,形状如图所示,这个几何体的面数为.7.如图,下列各图形主要由哪些简单的几何图形组成?二、创新应用8.请利用图中的几何体拼出蘑菇、台灯等图案,并和同伴一起交流,尽量拼出最多的图案.答案一、能力提升1.D.2.C.3.A.根据题意,知a代表长方形,d代表直线,因此记作a☉d的图形是长方形和直线的组合,故选A.4.④.5.①②③.6.6.7.解:(1)由圆组成;(2)由长方形和正方形组成;(3)由菱形(或四边形)组成;(4)由圆和圆弧组成(或由一个圆和两个小半圆组成).二、创新应用8.分析:本题是开放性试题,只要所给答案合理即可.解:答案不唯一,如图.第2课时几何图形的三种形状图与展开图一、能力提升1.如图,小李书桌上放了一本书,从上往下看得到的平面图形是()2.如图,一个带有方形空洞、圆形空洞的儿童玩具.如果用下列几何体作为塞子,那么既可以堵住方形空洞又可以堵住圆形空洞的几何体是()3.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看到的图形如图所示,则这张桌子上碟子的总数为()A.11B.12C.13D.144.有3块正方体积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同.现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是()A.白B.红C.黄D.黑5.图①是一个小正方体的侧面展开图,小正方体从图②所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是.图①图②6.根据下列多面体的平面展开图,填写多面体的名称:(1),(2),(3).7.如图,将下列图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去.(填序号)8.如图,画出所给几何体的从正面看、从左面看和从上面看得到的图形.9.如图①,在正方体中,点P,Q,S分别是所在边的中点,将此正方体展开,请在展开图②中标出点P,Q,S的位置.二、创新应用10.火箭的示意图如图所示(火箭圆柱底面的周长不等于圆柱的高),请你画出火箭的平面展开图.11.如图,在一个长方体的展开图上,每一面上都标注了字母(标字母的面是外表面),根据要求回答问题:(1)如果D面在多面体的左面,那么F面在哪里?(2)B面和哪个面是相对的面?(3)如果C面在前面,从上面看是D面,那么左面是哪个面?(4)如果B面在后面,从左面看是D面,那么前面是哪个面?(5)如果A面在右面,从下面看是F面,那么B面在哪里?答案一、能力提升1.A.2.B.从正面与上面分别看圆柱体所得的平面图形分别是长方形和圆,它既可以堵住方形空洞又可以堵住圆形空洞.3.B.因为右上角的碟子有5个,左下角的碟子有3个,左上角的碟子有4个,所以碟子的总数为3+4+5=12.4.C.根据第一个图和第二个图可知,与绿色相邻的四个面的颜色分别为白、黑、蓝、红,从第三个图可知第六个面为黄色,即为绿色一面的对面.5.国.翻到题图②第1格时朝下的为“了”字,第2格为“害”字,第3格为“厉”字,其对面为“国”字,即为这时小正方体朝上一面的字.6.(1)长方体.(2)三棱柱.(3)三棱锥.7.1或2或6.8.解:9.解:如图所示.二、创新应用10.解:11.解:(1)右面.(2)E面.(3)B面.(4)E面.(5)后面.4.1.2点、线、面、体一、能力提升1.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是()2.下列几何体有6个面的有()①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.A.1个B.2个C.3个D.4个3.如果一个直棱柱有12个顶点,那么它的面的个数是()A.10B.9C.8D.74.下列说法正确的有()①四面体的各个面都是三角形;②棱柱的顶点数一定是偶数,棱的条数一定是3的倍数;③圆柱是由两个面围成的;④长方体的面不可能是正方形.A.1个B.2个C.3个D.4个5.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是()6.薄薄的硬币在桌面上转动时,看上去像球,这说明了.7.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:(1)一只小蚂蚁爬行留下的路线可解释为.(2)电动车车辐条运动形成的图形可解释为.8.如图,正方形ABCD的边长为3cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是cm2.9.观察右图,填空:(1)这个图形的名称是;(2)这个几何体有个面,有个底面,有个侧面,底面是形,侧面是形.(3)侧面的个数与底面多边形的边数有什么关系?10.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.11.如图①,把一张长为6厘米、宽为10厘米的长方形纸板分成两个相同的直角三角形.(1)甲三角形(如图②)绕轴旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?(2)乙三角形(如图③)绕轴旋转一周,可以形成一个怎样的几何体?它的体积是多少立方厘米?二、创新应用12.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:顶点数多面体面数(F) 棱数(E)(V)四面体 4 4长方体8 6 12正八面体8 12正十二面20 12 30体你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是.(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是.(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表三角形的个数为x,八边形的个数为y,求x+y的值.答案一、能力提升1.D.2.C.3.C.直棱柱有12个顶点,一定是六棱柱,因此它的面的个数是8.4.B.5.D.由题中图形可以看出,左边的长方形的竖直的两条边与已知的直线平行,因而这两条边旋转形成两个柱形表面,旋转一周后可能形成的立体图形是一个管状的物体.6.面动成体.从运动的观点可知,薄薄的硬币在桌面上转动时,看上去像球,这种现象说明面转动成体.7.(1)点动成线.(2)线动成面.8.18.将正方形旋转一周所形成的图形是圆柱,从正面看圆柱是一个长方形,长方形的一边长为3cm,另一边长为6cm.因此面积为18cm2. 9.解:(1)六棱柱.(2)8;2;6;六边;长方.(3)侧面的个数与底面多边形的边数相等.10.解:从第一行的平面图形绕某一边旋转或沿某一方向平移可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.(1)→(三)→(D);(2)→(二)→(C);(3)→(四)→(B);(4)→(一)→(A).11.解:(1)甲三角形绕它的一条直角边所在直线旋转一周,形成一个底面半径是6厘米,高是10厘米的圆锥,它的体积是×π×62×10=120π(立方厘米).(2)乙三角形(如题图③)绕轴旋转一周,形成一个圆柱,且中间挖去了一个和圆柱同底等高的圆锥,它的体积是π×62×10-π×62×10=240π(立方厘米).二、创新应用12.解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为V+F-E=2.(2)由题意,得F-8+F-30=2,解得F=20.(3)因为有24个顶点,每个顶点处都有3条棱,两点确定一条直线,所以共有24×3÷2=36条棱.由(1)得24+F-36=2,解得F=14,所以x+y=14.。

初一上几何试题大全及答案

初一上几何试题大全及答案一、选择题1. 一个点可以确定几条直线？A. 0条B. 1条C. 无数条D. 不确定答案：C2. 线段AB和线段CD是平行的，那么线段AB和线段CD的长度关系是？A. 相等B. 不相等C. 可能相等D. 无法确定答案：C3. 在平面内，不共线的三点可以确定几个平面？A. 1个B. 2个C. 3个D. 无数个答案：A4. 一个角的度数是30°，那么它的补角是？A. 30°B. 60°C. 90°D. 120°答案：B5. 直角三角形的两条直角边分别为3和4，那么它的斜边长是？A. 5B. 6C. 7D. 8答案：A二、填空题6. 如果一个三角形的内角和为180°，那么一个四边形的内角和为______。

答案：360°7. 一个圆的半径为5厘米，那么它的直径是______厘米。

答案：10厘米8. 如果两条直线相交，那么它们所形成的角中，最大的角是______。

答案：平角9. 一个正方体的棱长为2厘米，那么它的表面积是______平方厘米。

答案：24平方厘米10. 如果一个角是直角的一半，那么这个角是______。

答案：45°三、解答题11. 如图所示，点A、B、C在同一条直线上，点D不在直线AB上。

如果AB=5厘米，BC=3厘米，求线段AD的长度。

答案：由于点D不在直线AB上，根据题意，我们无法直接得出AD 的长度。

需要更多信息，例如点D的位置或与AB、BC的关系。

12. 一个正五边形的内角和是多少度？答案：正五边形的每个内角都是108°，因为正五边形的内角和=(n-2)×180°，其中n是边的数量。

对于五边形，n=5，所以内角和=(5-2)×180°=540°。

四、证明题13. 证明：如果两条直线平行，那么它们与第三条直线所形成的同位角相等。

几何试题题目及答案初中

几何试题题目及答案初中
一、选择题
1. 下列哪个选项不是几何图形？
A. 圆形
B. 三角形
C. 正方形
D. 音乐符号
答案：D
2. 一个正方形的对角线长度是其边长的：
A. 1倍
B. 2倍
C. √2倍
D. √3倍
答案：C
3. 在一个等腰三角形中，如果底边长为6厘米，腰长为5厘米，那么这个三角形的高是多少厘米？
A. 4厘米
B. 5厘米
C. 6厘米
D. 7厘米
答案：A
二、填空题
1. 一个圆的周长是其直径的______倍。

答案：π
2. 如果一个矩形的长是10厘米，宽是5厘米，那么它的面积是
______平方厘米。

答案：50
3. 一个等边三角形的每个内角是______度。

答案：60
三、解答题
1. 已知一个直角三角形的两条直角边长分别为3厘米和4厘米，求斜边的长度。

答案：斜边的长度是5厘米。

2. 一个矩形的长是宽的两倍，如果宽是4厘米，求矩形的周长。

答案：矩形的周长是24厘米。

3. 一个圆的半径是7厘米，求圆的面积。

答案：圆的面积是153.94平方厘米。

初一下数学几何试题及答案

初一下数学几何试题及答案初一下数学几何试题及答案一、选择题1、下列图形中，是轴对称图形的是（） A. 直角三角形 B. 等边三角形 C. 平行四边形 D. 梯形2、下列说法正确的是（） A. 平移不改变图形的形状和大小，只改变图形的位置 B. 经过直线外一点，有且只有一条直线与这条直线平行 C. 两条对角线相等的四边形是矩形 D. 任意一组数据通过计算它的平均数和中位数，得到的结果相同3、如图，下列条件中，不能判定直线l1∥l2的是（） A. ∠3=∠2B. ∠1=∠3C. ∠4+∠5=180°D. ∠2=∠4二、填空题 4. 在平静的湖面上，有一枝荷花，高出水面1米，一阵风吹来，荷花被吹到一边，花朵齐及水面。

已知荷花移动的水平距离为2米，这里水深________米。

5. 为了防盗，在门上装一个“猫眼”，使屋内的人能看清屋外的人（是一个缩小的像），而屋外的人却看不清屋内的人，则“猫眼”应该是________镜，该装置位于门的________侧。

三、解答题 6. 已知直线AB上有一点O，射线OC平分∠AOB的补角，且∠AOE=∠COE，∠EOF=90°，试说明A、E、F在同一直线上。

解：∵射线OC平分∠AOB的补角∴∠AOC=∠BOC ∵∠AOE=∠COE ∴∠AOE-∠AOC=∠COE-∠BOC 即∠EOF=∠FOC=90°∴ EF\AB ∵点O 是直线AB上的一点∴ A、E、F在同一直线上 7. 将直角三角形ABC （其中∠ABC=90°）沿BC方向平移得到三角形DEF，已知BC的长度为6，三角形ABC的面积为8，求阴影部分的面积。

解：∵将直角三角形ABC沿BC方向平移得到三角形DEF，BC的长度为6 ∴ BD=EC=6 ∵直角三角形ABC的面积为8 ∴ AB×BC=16 ∴ AB=4 ∴四边形AECF的面积为：6×4=24 ∴阴影部分的面积为：24﹣8=16。

初一几何体试题及答案

初一几何体试题及答案一、选择题（每题2分，共10分）1. 下列几何体中，属于多面体的是：A. 球体B. 圆柱C. 圆锥D. 立方体答案：D2. 如果一个几何体有8个顶点和12条棱，那么它可能是：A. 立方体B. 正四面体C. 正八面体D. 正十二面体答案：A3. 正方体的每个面都是：A. 圆形B. 椭圆形C. 长方形D. 正方形答案：D4. 一个长方体的长、宽、高分别是a、b、c，那么它的体积是：A. abcB. a+b+cC. ab+bc+caD. a^2+b^2+c^2答案：A5. 一个正四面体的每个面都是：A. 等边三角形B. 等腰三角形C. 直角三角形D. 等腰直角三角形答案：A二、填空题（每题2分，共10分）6. 一个长方体的长为5厘米，宽为3厘米，高为2厘米，它的表面积是______平方厘米。

答案：627. 一个正方体的棱长为4厘米，它的体积是______立方厘米。

答案：648. 如果一个几何体的底面是一个正方形，且边长为x厘米，高为y厘米，那么它的体积是______立方厘米。

答案：xy^29. 一个圆锥的底面半径为r厘米，高为h厘米，它的体积是______立方厘米。

答案：πrh^2/310. 一个圆柱的底面半径为r厘米，高为h厘米，它的体积是______立方厘米。

答案：πr^2h三、简答题（每题5分，共10分）11. 描述一个正方体的特征。

答案：正方体是一个有6个面，每个面都是正方形的立体图形。

它的12条棱的长度相等，每个顶点连接3条棱。

12. 解释为什么球体不属于多面体。

答案：球体是一个连续的曲面，没有平面的面和棱，因此它不属于多面体。

多面体是由多个平面多边形面、直线棱和顶点组成的立体图形。

结束语：通过本试题的练习，同学们应该对初一几何体的基本概念和计算方法有了更深入的理解。

希望同学们能够继续努力，掌握更多的几何知识，为今后的学习打下坚实的基础。

初一几何体试题及答案

初一几何体试题及答案一、选择题（每题2分，共10分）1. 下列几何体中，属于柱体的是（）A. 圆锥B. 圆柱C. 球体D. 棱柱2. 一个长方体的长、宽、高分别为3cm、4cm、5cm，那么它的体积是（）A. 60cm³B. 30cm³C. 40cm³D. 50cm³3. 一个正方体的棱长是2cm，那么它的表面积是（）A. 12cm²B. 24cm²C. 36cm²D. 48cm²4. 一个圆柱的底面半径是4cm，高是10cm，它的体积是（）A. 502.4cm³B. 503.4cm³C. 504.4cm³D. 505.4cm³5. 一个球的体积是（）A. 4/3πr³B. 2/3πr³C. πr³D. 3/4πr³二、填空题（每题3分，共15分）6. 一个长方体的长、宽、高分别是a、b、c，那么它的体积是______。

7. 一个正方体的棱长是x，那么它的表面积是______。

8. 一个圆柱的底面半径是r，高是h，那么它的体积是______。

9. 一个球的体积公式是______。

10. 如果一个圆锥的底面半径是3cm，高是4cm，那么它的体积是______。

三、解答题（每题5分，共20分）11. 一个长方体的长、宽、高分别是5cm、3cm、2cm，求它的体积。

12. 一个正方体的棱长是4cm，求它的表面积。

13. 一个圆柱的底面直径是6cm，高是8cm，求它的体积。

14. 一个球的直径是7cm，求它的体积。

答案：一、选择题1. B2. A3. B4. A5. A二、填空题6. abc7. 6x²8. πr²h9. 4/3πr³10. 37.68cm³三、解答题11. 体积= 5cm × 3cm × 2cm = 30cm³12. 表面积= 6 × (4cm × 4cm) = 96cm²13. 体积= π × (3cm)² × 8cm = 72πcm³14. 体积= 4/3π × (3.5cm)³ = 133.07cm³。

初中初一几何试题及答案

初中初一几何试题及答案一、选择题（每题3分，共15分）1. 下列哪个选项是平行四边形的性质？A. 对角线互相垂直B. 对边相等C. 对角线相等D. 对角线互相平分答案：B2. 直角三角形中，如果一个锐角为30°，另一个锐角的度数是多少？A. 30°B. 60°C. 90°D. 120°答案：B3. 一个等腰三角形的底边长为6cm，腰长为8cm，那么底边上的高是多少？A. 4cmB. 6cmC. 8cmD. 10cm答案：A4. 一个圆的半径为3cm，那么它的周长是多少？A. 6π cmB. 9π cmC. 12π cmD. 15π cm答案：C5. 下列哪个图形是轴对称图形？A. 平行四边形B. 等边三角形C. 矩形D. 任意四边形答案：B二、填空题（每题2分，共10分）1. 一个矩形的长为10cm，宽为5cm，那么它的面积是________cm²。

答案：502. 一个等腰直角三角形的斜边长为5cm，那么它的直角边长是________cm。

答案：5√2/23. 一个圆的直径为8cm，那么它的半径是________cm。

答案：44. 一个三角形的内角和为________°。

答案：1805. 一个扇形的圆心角为60°，半径为4cm，那么它的面积是________cm²。

答案：4π/3三、解答题（每题5分，共10分）1. 已知一个三角形的三边长分别为3cm、4cm和5cm，求证这个三角形是直角三角形。

答案：根据勾股定理，3² + 4² = 5²，即9 + 16 = 25，因此这个三角形是直角三角形。

2. 已知一个圆的周长为25.12cm，求这个圆的半径。

答案：根据圆的周长公式C = 2πr，可得半径r = C / (2π) = 25.12 / (2 × 3.14) = 4cm。

初一几何题练习题含答案

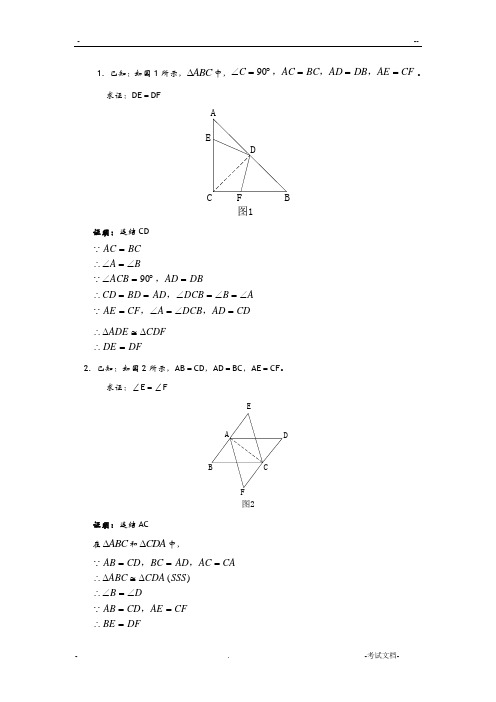
1. 已知：如图1求证：DE ＝证明：连结CDAC BC A BACB CD BD AD DCB B A AE CF A DCB AD CD=∴∠=∠∠=︒∴==∠=∠=∠=∠=∠=90，，，∴≅∴=∆∆ADE CDFDE DFAB CD BC AD AC CA ABC CDA SSS B D AB CD AE CFBE DF===∴≅∴∠=∠==∴=，，，∆∆()在∆BCE 和∆DAF 中，BE DF B D BC DA BCE DAF SAS E F=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∆∆()∴=∠∠ABH NBH 又BH ⊥AH∴==︒∠∠AHB NHB 90 BH ＝BH∴≅∴==∆∆ABH NBH ASA BA BN AH HN()，同理，CA ＝CM ，AK ＝KM ∴KH 是∆AMN 的中位线 ∴KH MN // 即KH//BC4. 已知：如图4所示，AB ＝AC ，∠，，A AE BF BD DC =︒==90。

求证：FD ⊥EDBAC BD DCBD ADB DAB DAE=︒=∴=∴==∠，∠∠∠90在∆ADE 和∆BDF 中，AE BF B DAE AD BD ADE BDF FD ED===∴≅∴∠=∠∴∠+∠=︒∴⊥，∠∠，∆∆3132905. 已知：如图6所示在∆ABC 中，∠=︒B 60，∠BAC 、∠BCA 的角平分线AD 、CE 相交于O 。

又∠=︒B 60∴∠+∠=︒∴∠=︒∴∠+∠=︒∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC()即AC AE CD =+6. 已知：如图7所示，正方形ABCD 中，F 在DC 上，E 在BC 上，∠=︒EAF 45。

求证：EF ＝BE ＋DF证明：延长CB 至G 在正方形ABCD∴≅∴=∠=∠∆∆ABG ADF AG AF ，13又∠=︒EAF 45∴∠+∠=︒∴∠+∠=︒23452145即∠GAE ＝∠FAE ∴=∴=+GE EFEF BE DF如图8所示，已知∆ABC 为等边三角形，延长BC 到D ，延长BA 到E ，并且使AE ＝BD ，连结CE 、DE 。