基础光学课后重点习题答案
物理光学基础教程答案刘娟

物理光学基础教程答案刘娟1、5.用素描炭笔在纸上连续、均匀的画一笔,放在低倍显微镜下观察,笔迹变得浓淡而间断,此现象说明()[单选题] *A.物质是由微粒组成的,各个微粒紧靠在一起,形成物质的连续体B.物质是由微粒组成的,微粒之间有空隙(正确答案)C.固体由微粒组成,液体连成一片,固体微粒可以挤进液体中D.固体和液体均连成一片,气体是由微粒组成的2、举重运动员把杠铃举在空中停三秒,此时运动员对杠铃的举力做功[判断题] *对错(正确答案)答案解析:有力无距离,不做功3、2.高空雨滴下落的运动是自由落体运动.[判断题] *对错(正确答案)4、1.两个孩子共提一桶水时,要想省力,两个人拉力间的夹角应大些.() [判断题] *对错(正确答案)5、下列物体中,质量约为2×105mg的是()[单选题] *A. 一颗图钉B. 一本初二物理课本(正确答案)C. 一张课桌D. 一支黑水笔6、30.如图,我国首款国际水准的大型客机C919在上海浦东机场首飞成功,标志着我国航空事业有了重大突破。
它的机身和机翼均采用了极轻的碳纤维材料。
这种材料的优点是()[单选题] *A.密度大B.密度小(正确答案)C.熔点低D.硬度小7、人耳听不到次声波,是因为响度太小[判断题] *对错(正确答案)答案解析:次声波和超声波的频率超过了人耳的听觉范围8、84.如图所示是甲和乙两种液体物质的质量和体积的关系图像,下列说法正确的是()[单选题] *A.甲物质的密度比乙小B.体积为60cm3的乙物质的质量为48g(正确答案)C.质量为25g的甲物质的体积为30cm3D.甲和乙两种液体等体积混合后的密度小于1g/cm39、40.小明家的厨房里有一个恰好能装下1kg水的玻璃瓶子,现有汽油、酒精和硫酸三种液体,它能够装下1kg的哪种液体()(已知ρ汽油<ρ酒精<ρ水<ρ硫酸)[单选题] *A.汽油B.酒精C.硫酸(正确答案)D.都能装下10、汽油的热值比柴油的热值大,完全燃烧时汽油比柴油产生的热量多[判断题] *对错(正确答案)答案解析:质量相同的前提下11、10.同学们进入图书馆都会自觉地轻声细语,从物理的角度分析,这样做的目的是()[单选题] *A.减小声音的响度(正确答案)B.降低声音的音调C.改变声音的音色D.减小声带振动的频率12、6.物块静止放在桌面上,物块所受重力和物块对桌面的压力是一对作用力和反作用力.[判断题] *对错(正确答案)13、44.下列现象不可能出现的是()[单选题] *A.衣柜里的樟脑丸放置很长时间后会变小B.潮湿的夏天,从冰箱里取出的啤酒瓶上会出现小水珠C.有风的天气,游泳后从水中出来会感觉冷D.冬天,戴眼镜的人从室内走到室外,眼镜上会出现小水珠(正确答案)14、38.在日常生活中,常见的几种物态变化现象中,属于液化的是()[单选题] * A.太阳光下晒的衣服变干B.房间窗户玻璃的内表面出现冰花C.湖面结了一层厚厚的冰D.在炎热的夏天,从冷饮柜中取出啤酒瓶,啤酒瓶变得模糊(正确答案)15、1.与头发摩擦过的塑料尺能吸引碎纸屑。
工程光学基础 习题参考答案

1.β = 0, l' = 0, l = −50 2.β = −0.1, l' = −550, l = −55 3.β = −0.2, l' = −60, l = −300 4.β = −1, l'= −100, l = −100 5.β = 1, l' = 0, l = 0 6.β = 5, l' = −200, l = −40 7.β = 10, l' = −450, l = 45 8.β = ∞, l' = +∞, l = −50
n
1.5 10 15
Q L = −∞,∴U = 0
∴U'= I − I'
L'
=
r
1
+
sin I' sin U '
=
100
1
+
1 / 15 sin(1.9166)
=
299.332
则 实 际 光 线 的 像 方 截 距 为 299.332 , 与 高 斯 像 面 的 距 离 为 :
根据公式 n' − n = n'−n (1-20)有: n' − 1 = n'−1 ,可以看出此种情况不存在。
l' l r
r −∞ r
计算第②种情况:易知入射光线经第一面折射后过光轴与反射面的交点。
其余参考题 14。
21、一物体位于半径为 r 的凹面镜前什么位置时,可分别得到:放大 4 倍的实 像,放大 4 倍的虚像、缩小 4 倍的实像和缩小 4 倍的虚像? 解: (1)放大 4 倍的实像
(2)放大四倍虚像 (3)缩小四倍实像 (4)缩小四倍虚像
工程光学习题答案(附试题样本)

测控09级复习资料工程光学基础教程(课后重点习题答案)测控09级二○一一年六月二日第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
《光学教程》课后习题解答

《光学教程》(XX)习题解答第一章光的干涉1、波长为的绿光投射在间距为的双缝上,在距离处的光屏上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长为的XX投射到此双缝上, 两个亮纹之间的距离为多少?算出这两种光第2级亮纹位置的距离。
解:l8^ 500 10 — 0.409cmd 0.022改用700 10^ = 0.573cm0.022两种光第二级亮纹位置的距离为::y =2 :y2 -2 y =0.328cm2、在杨氏实验装置中,光源波长为,两狭缝间距为,光屏离狭缝的距离为,试求:⑴光屏上第1亮条纹和中央亮纹之间的距离;⑵若P点离中央亮纹为问两束光在P点的相位差是多少?⑶求P点的光强度和中央点的强度之比。
解:⑴⑵由光程差公式、.二 a - R 二 d si n r - d —r o⑶中央点强度:P 点光强为:3、把折射率为的玻璃片插入杨氏实验的一束光路中, 光屏上原来第5级亮条纹所在的位置变为中央亮条纹,试求插入的玻璃片的厚度。
已 知光波长为解:,设玻璃片的厚度为由玻璃片引起的附加光程差为:n -1 d =55 丸5_7_6Ad6 10=6 10 m =6 10 cm(n —1 ) 0.527.y4、波长为的单色平行光射在间距为的双缝上。
通过其中一个缝的能 量为另一个的倍,在离狭缝的光屏上形成干涉图样,求干涉条纹间距和 条纹的可见度。
解:由干涉条纹可见度定义:由题意,设,即代入上式得5、波长为的光源与菲涅耳双镜的相交棱之间距离为, 棱到光屏间的 距离为,若所得干涉条纹中相邻亮条纹的间隔为,求双镜平面之间的夹 角。
解:XX 耳双镜干涉条纹间距公式r L _ 20 180 2r y 2 200. 1L y =r L2r si n0. 0035180…smo.0035—60「26、在题1.6图所示的xx 镜实验中,光源S 到观察屏的距离为,到 xx 镜面的垂直距离为。
xx 镜长,置于光源和屏之间的中央。
大学物理通用教程 习题解答 光学

大学物理通用教程习题解答光学1. 引言光学是物理学中非常重要的一个分支,主要研究光的传播、反射、折射、干涉、衍射等现象。
在大学物理课程中,光学是必修的内容之一。
本文将为大家提供一些习题解答,旨在帮助学习光学的同学更好地理解光学原理和应用。
2. 光的特性Q1: 什么是光的双折射现象?光的双折射现象是指光线在某些材料中传播时会发生折射率的变化,使光线被分裂成两个方向传播的分量。
这种现象通常发生在具有非中心对称晶格结构的材料中,如石英等。
Q2: 请解释光的偏振现象。
光的偏振现象是指光波中的电场矢量在特定方向上振动的现象。
光波中的电场矢量可以沿任意方向振动,如果只能在一个方向上振动,则称为线偏振光;如果在所有方向上振动,则称为非偏振光。
3. 光的传播和反射Q1: 什么是光的全反射现象?光的全反射是指光从光密介质射向光疏介质的界面时,当入射角大于临界角时,光完全被反射回光密介质,不再从界面透射到光疏介质中去。
Q2: 请解释折射定律。
折射定律描述了光从一种介质传播到另一种介质时光线的弯曲现象。
按照折射定律,入射光线、折射光线和法线所在的平面相互垂直,并且入射光线的折射角和折射光线的入射角之间满足一个简单的数学关系。
4. 光的折射和透镜Q1: 什么是凸透镜和凹透镜?凸透镜是指中央较厚、边缘较薄的透镜,可以使平行光线聚焦到一个点上;凹透镜则相反,中央较薄、边缘较厚,会使平行光线发散。
Q2: 请解释透镜的焦距。
透镜的焦距是指平行光线通过透镜后会聚或发散的距离。
对于凸透镜,焦点在透镜的正面,焦距为正值;对于凹透镜,焦点在透镜的反面,焦距为负值。
5. 干涉和衍射Q1: 什么是干涉现象?干涉现象是指当两束或多束光线相遇时,由于光波的叠加和相长干涉,产生了明暗相间的干涉条纹。
干涉班纹的形态和颜色取决于光的频率、波长、入射光线的角度等因素。
Q2: 请解释衍射现象。
衍射现象是指当光通过绕过或通过一个障碍物时,会出现光的弯曲或扩散的现象。
工程光学基础 习题参考答案-第二章_02

注意: 注意: − l + l ' ≠ 7200mm ,因为对于一般理想光学系统两主面不重合。 4、已知一透镜把物体放大 − 3× 投影在屏幕上, 投影在屏幕上,当透镜向物体移近 18mm 时,物体 将被放大 − 4 × ,试求透镜的焦距, 试求透镜的焦距,并用图解法校核之。 并用图解法校核之。 解:
tan U 1 ' = h1 100 = = 1 = tan U 2 f1 ' 100 h2 90 = 1+ = 2.8 = tan U 3 f2 50 h3 62 = 2 .8 + = 1.56 f3 − 50
h2 = h1 − d1 tan U 1 ' = 100 − 10 = 90 tan U 2 ' = tan U 2 +
3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
工程光学基础教程课后重点习题答案

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学基础 习题参考答案-第二章_02

3、设一系统位于空气中, 设一系统位于空气中,垂轴放大 率 β = −10 × , 由物面到像面的距离 (共轭距) 共轭距)为 7200mm,物镜两焦点 间距离为 1140mm。求该物镜焦距, 求该物镜焦距, 并绘出基点位置图。 并绘出基点位置图。 解: 由公式 β = − x' f = − (2-4) , f' x
f 2 ' = −240mm
8、一短焦距物镜 一短焦距物镜, 焦距物镜,已知其焦距为 35mm,筒长 L=65mm,工作距离 l k ' = 50mm ,按 最简单结构的薄透镜系统考虑, 最简单结构的薄透镜系统考虑,求系统结构。 求系统结构。 解: (仿照 (仿照 P32 P32 例 2) 利用正切计算法,设 h1 = 100mm ,有公式:
1 1 1 d (2-33) = + − f ' f1 ' f 2 ' f1 ' f 2 '
f1 ' f 2 ' nr1 r2 f ' = − f = − ∆ = ( n − 1)[n( r − r ) + ( n − 1)d ] 2 1 1 Φ = f ' − dr2 l ' = H n( r2 − r1 ) + ( n − 1)d − dr1 l = H n( r2 − r1 ) + ( n − 1)d
xx' = ff ' = − f ' 2 ∴ x' = − f2 x
代入数据得:
x = −∞, x' = 0.5625mm x = −10m, x' = 0.703mm x = −6m, x' = 0.9375mm x = −4m, x' = 1.406mm x = −2m, x' = 2.813mm
光学教程答案word版精品文档9页

第三章 几何光学1.证明反射定律符合费马原理证明:设界面两边分布着两种均匀介质,折射率为1n 和2n (如图所示)。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
(1)反正法:如果反射点为'C ,位于ox 轴与A 和B 点所著称的平面之外,那么在ox 轴线上找到它的垂足点"C 点,.由于'''''',AC AC BC BC >>,故光线'AC B 所对应的光程总是大于光线''AC B 所对应的光程而非极小值,这就违背了费马原理。
故入射面和反射面在同一平面内。
(2)在图中建立坐xoy 标系,则指定点A,B 的坐标分别为11(,)x y 和22(,)x y ,反射点C 的坐标为(,0)x 所以ACB 光线所对应的光程为:根据费马原理,它应取极小值,所以有 即: 12i i =2.根据费马原理可以导出在近轴光线条件下,从物点发出并会聚到像点的所有光线的光程都相等。
证:如图所示,有位于主光轴上的一个物点S 发出的光束经薄透镜折射后成一个明亮的实象点'S 。
设光线SC 为电光源S 发出的任意一条光线,其中球面AC 是由点光源S 所发出光波的一个波面,而球面DB 是会聚于象点'S 的球面波的一个波面,所以有关系式SC SA =,''S D S B =.因为光程根据费马原理,它们都应该取极值或恒定值,这些连续分布的实际光线,在近轴条件下其光程都取极大值或极小值是不可能的,唯一的可能性是取恒定值,即它们的光程相等。
3.睛E 和物体PQ 之间有一块折射率为1.5的玻璃平板,平板的厚度d 为30cm 。
求物体PQ 的像''P Q 与物体PQ 之间的距离2d 为多少?解:根据例题3.1的结果 4.玻璃棱镜的折射棱角A 为060,对某一波长的光其折射率n为1.6。
光学课后练习题参考答案(2022年)

光学课后练习题参考答案(2022年)一、单项选择和填空题1.C2.B3.C4.B5.C6.C7.D8.A9.D10.B11.B12.A13.B14.C15.B16.B17.B18 .D19.D20.A21.A22.D23.A24.D25.C26.C27.C28.D29.D30.D31.C32.D33.A34.C35.A36.B38.D39.B40.B41.B42.B43.__ -0.2米______,____眼前0.2米_______。
44.两透明介质面上的反射损失__,__介质吸收的损失__反射面的光能损失__45.它能将自然光分解成两个分得较开光矢量相互⊥的线偏振光46.___50勒克斯;_________25.6勒克斯__________。
47.左,宽(宽或窄)。
48.n11n22.49.Sma某Ct愈好分波前法和分振幅法50.50051.1.26某10-3cm52.短波53.1.72某106m/m/.54.0.515cm55.12.5cm56.640057.1558.0.515cm59.6.7km60.4.8某10-7m61.4.332cm12.2.693eV62.振幅和位相63.__2________.__1/4____64.65.粒子数反转二、简答题1.答:求出每一个给定光阑或透镜边缘由其前面那部分光具组所成的象,找出所有这些象和第一个透镜对指定参考点所张的角,在这些张角中,找出最小的那一个,和这最小张角对应的光阑就是有效光阑。
2.答:双折射,全反射。
3.答:提示:把一个/4片和一个偏振片前后放置在光路中,迎着光的传播方向旋转偏振片,在旋转一周的过程中,若光强无变化则是自然光;若光强有变化且出现两次消光,则该束光便是圆偏振光。
4.答:提示:既能记录光波振幅的信息,又能记录光波相位信息的摄影称为全息照相。
其主要特点有:①它是一个十分逼真的立体像。
它和观察到的实物完全一样,具有相同的视觉效应。
光学课后习题解答

第一章 光的干涉1、波长为nm 500的绿光投射在间距d 为cm 022.0的双缝上,在距离cm 180处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为nm 700的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离.解:由条纹间距公式λd r y y y j j 01=-=∆+ 得cm 328.0818.0146.1cm146.1573.02cm818.0409.02cm573.010700022.0180cm 409.010500022.018021222202221022172027101=-=-=∆=⨯===⨯===⨯⨯==∆=⨯⨯==∆--y y y drj y d rj y d r y d r y j λλλλ2.在杨氏实验装置中,光源波长为nm 640,两狭缝间距为mm 4.0,光屏离狭缝的距离为cm 50.试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若p 点离中央亮条纹为mm 1.0,问两束光在p 点的相位差是多少?(3)求p 点的光强度和中央点的强度之比.解:(1)由公式λd r y 0=∆得λd r y 0=∆ =cm 100.8104.64.05025--⨯=⨯⨯(2)由课本第20页图1-2的几何关系可知52100.01sin tan 0.040.810cm 50y r r d d dr θθ--≈≈===⨯521522()0.8106.4104r r πππϕλ--∆=-=⨯⨯=⨯(3) 由公式2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆= 得8536.042224cos 18cos 0cos 421cos 2cos42cos 422202212212020=+=+==︒⋅=∆∆==πππϕϕA A A A I I pp3.把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m .解:未加玻璃片时,1S 、2S 到P 点的光程差,由公式2rϕπλ∆∆=可知为 Δr =215252r r λπλπ-=⨯⨯=现在1S 发出的光束途中插入玻璃片时,P 点的光程差为()210022r r h nh λλϕππ'--+=∆=⨯=⎡⎤⎣⎦所以玻璃片的厚度为421510610cm 10.5r r h n λλ--====⨯-4. 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解:6050050010 1.250.2r y d λ-∆==⨯⨯=mm122I I = 22122A A =12A A =7. 试求能产生红光(λ=700nm)的二级反射干涉条纹的肥皂膜厚度.已知肥皂膜折射率为1.33,且平行光与发向成30°角入射. 解:根据题意222(210)2700710nm30d n j d λ-=+∴===8. 透镜表面通常镀一层如MgF 2(n=1.38)一类的透明物质薄膜,目的是利用干涉来降低玻璃表面的反射.为了使透镜在可见光谱的中心波长(550nm )处产生极小的反射,则镀层必须有多厚? 解:可以认为光是沿垂直方向入射的。
光学(吴强版)课后部分习题答案

λ0 λ = ( 2 k + 1) 0 2 2
k = 0,1, 2,3, L
利用上述关系,将分别取 k=1、2、3、4,可以算出在 400~ 700nm 范围内,干涉 增强的光为 :
k =3 k =4
干涉相消的光为:
λ0 = 594(nm) λ0 = 424.3(nm)
k =3
λ0 = 495(nm)
2-23 为了测量一精密螺距,可用此螺栓来移动迈克耳孙干涉仪中的一面反射镜。已知螺栓 旋转一周后视场中移过 2023 条干涉条纹,求螺栓的螺距,所用光波的波长为 546nm.。 解:设螺距为 ∆h ,螺栓旋转一周后产生的额外光程差值
∆l = 2∆h = ∆k λ
所以: ∆h =
∆k λ 2023× 5460× 10-10 = =0. 552 × 10−3 ( m ) 2 2
r=
所以,第 5 和第 15 级暗环的直径分别为
kRλ n
D5 =
0.7 1.33 1.7 1.33
= 0.607(mm)
D15 = λ2 r2 = = 2e= ∆λ R
= 1.474(mm)
2-18
l0 = ∆lmax
λ2 R r= = ∆λ
2-20
(4000 ×10 )
2 × 10
−10 2 −10
D λ 1.0 × 6328 × 10−10 ⋅ = = 4.75 × 10−4 (m) −3 d n 1.0 ×10 ×1.33
2-2 在杨氏干涉装置中, 双缝至屏幕的垂直距离为 2.00m. 测得第 10 级干涉亮纹 至中央亮纹之间的距离为 3.44cm,双缝间距为 0.342mm , 试求光源的单色光波 长. 解:在杨氏干涉装置中,两束相干光的光程差为 : x δ = d sin θ = d D 根据出现亮条纹的条件 δ = ± kλ0 ,对第 10 级亮条纹, k 取 10,于是有:
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
光学原理课后答案

光学原理课后答案1. (a) 光的折射是指光线从一种介质进入另一种介质时发生的方向改变。
根据斯涅尔定律,入射角i和折射角r之间的正弦比始终等于两种介质的折射率之比,即sin(i)/sin(r) = n1/n2,其中n1和n2分别为两种介质的折射率。
(b) 光的衍射是指光线通过一个开口或遇到一条障碍物后的传播现象。
根据惠更斯-菲涅耳原理,每个波前上的每一点都可以看作是一个次波源,这些次波源发出的次波在波前后方形成新的波前,并经过相干叠加构成衍射图样。
2. (a) 鱼眼镜是一种球面透镜,其弧面既可凸出也可凹入。
凸透镜可以使进入镜筒的光线向中心汇聚,形成一个放大而上下颠倒的实像。
凹透镜则使光线分散,看起来像是在反向朝出镜筒。
鱼眼镜透镜的特殊形状使其具有更广阔的视野,因为光线的大部分都被聚焦到观察者的眼睛中。
(b) 望远镜是利用透镜或反射镜来聚焦远处的光线,使观察者可以看到较远处的物体。
望远镜一般由目镜和物镜两个部分组成。
物镜负责收集远处物体的光线,并形成物体的实像,目镜则进一步放大该实像,使观察者能够清晰地看到物体的细节。
3. (a) 全息术是一种利用激光光源和全息记录介质记录和再现光场分布的技术。
在全息术中,一束光通过被记录的物体,然后分为两部分,一部分成为直射光,另一部分被物体反射或散射后形成的波前称为散射光。
通过将这两束光分别照射到全息记录介质上,可以记录下物体的波前分布,再通过合适的照明方式,可以使物体的完整三维形象出现在观察者的眼前。
(b) 全息图像具有真实感和三维感,观察者可以从不同角度观察物体,并且能够看到物体的背面。
这是因为全息图像是通过记录物体的波前信息来生成的,而传统的图像只是记录了物体的透射光强度。
然而,全息图像的记录和再现需要用到激光光源和全息记录介质,硬件设备要求较高。
4. (a) 一束射向凸透镜的平行光线将会在透镜的焦点处集中,并形成一个焦点。
这个焦点就是透镜的主焦点,通常记为F。
光学教程第1章参考答案

光学教程第1章_参考答案光学教程第1章参考答案光学是研究光的传播、反射、折射、干涉和衍射等现象的科学。
光学是一门非常重要的学科,广泛应用于各个领域,包括物理学、化学、生物学、医学、通信等等。
本章主要介绍了光的基本性质和光的传播规律。
1. 光的基本性质光是一种电磁波,具有波粒二象性。
光波的波长和频率决定了光的颜色和能量。
光的传播速度是光在真空中的速度,约为每秒3×10^8米。
2. 光的传播规律光的传播遵循直线传播原则。
当光传播到介质边界时,会发生反射和折射现象。
反射是光从界面上反射回去,折射是光从一种介质传播到另一种介质中。
根据菲涅尔定律,入射角、反射角和折射角之间满足一定的关系。
3. 光的反射和折射光的反射是光从界面上反射回去的现象。
根据角度关系,入射角等于反射角。
光的折射是光从一种介质传播到另一种介质中的现象。
根据斯涅尔定律,入射角、折射角和两种介质的折射率之间满足一定的关系。
4. 光的干涉和衍射光的干涉是指两束或多束光波相遇时产生的干涉现象。
干涉可分为构造性干涉和破坏性干涉。
光的衍射是指光通过一个小孔或绕过一个障碍物后产生的衍射现象。
衍射使得光的传播方向发生偏转。
5. 光的偏振光的偏振是指光波中的电矢量在某一平面上振动的现象。
光的偏振可以通过偏振片来实现。
偏振片可以选择只允许某一方向的偏振光通过。
6. 光的吸收和散射光的吸收是指光能量被介质吸收并转化为其他形式的能量的现象。
光的散射是指光在介质中传播时与介质中的微粒发生相互作用,并改变光的传播方向的现象。
总结:光学是研究光的传播、反射、折射、干涉和衍射等现象的科学。
光的传播遵循直线传播原则,当光传播到介质边界时会发生反射和折射现象。
光的干涉是指光波相遇时产生的干涉现象,光的衍射是指光通过小孔或绕过障碍物后产生的衍射现象。
光的偏振是指光波中的电矢量在某一平面上振动的现象,可以通过偏振片来实现。
光的吸收是光能量被介质吸收并转化为其他形式的能量,光的散射是光在介质中传播时与介质中的微粒发生相互作用并改变光的传播方向的现象。
光学蔡履中版课后答案山东大学版

光学第一章课后习题解答1-1解:由折射定律sin i=n*sin i` 正弦定理 R/sin(90+i`)=d/sin bcos i`=dRcos b 折射定理 nsin b`=sin b 所以 sin b=n sin b`=n R d cos i`=n R d (1-sin 2 i`)1/2=n Rd[1-(n 1)2sin 2 i]1/2=Rd (n 2-sin 2i)1/2所以 b=arcsin Rd(n 2-sin 2i)1/21-2 解:证明:①由折射定律sin i 1=nsin i 1` n shin i 2=sin i 2` i 1`=i 2 所以 sin i 1=sin i 2` i 1=i 2`②OP=h/cos i 1` ∠POQ=i 1-i 1`PQ=OP sin ∠POQ=OPsin(i 1+i 1`)= OPsin(i 1+i 1`)*h/ cos i 1` ③当 i 1 很小时 sin i 1= i 1 sin i 1`=i 1` cos i 1`=1 由折射定律(小角度时) n i 1=i 1` 所以 i 1`=n i 1/n`由上面 PQ=sin(i 1+i 1`)*h/cos i 1`=(i 1-i 1`)*h=(i 1- n i 1/n`)*h =(n`-n)*i 1*h/n` 1-3 解:全反射时 n sin i=1所以 sin i=1/n=2/3 sin i=R/(R+d)光线①②都要发生全反射 但光线②的入射角要小于光线①的入射角所以取光线②研究 可得上式R/(R+d)= 2/3 3R=2R+2d R/d=2 当R/d>=2 时全部通过 1-6 解:①n=sin[(δmin +a)/2]/sin(a/2)=sin 56°36`/sin 30°=0.835/0.5=1.67 ②棱镜折射率 n=sin(50°+35°)/sin(50°/2)=0.675/0.5=1.598 取得最小偏向角时i'1= α/2=250 由折射定律 n sin i 1=n`sin i 1` 所以 1.33 sin i 1=1.598 sin (50°/2) 所以 sin i 1=0.507777 i 1=30.5189°δmin =2i 1-a=2*30.52°-50°=11.032°=11°2' 1-8 解:从左看时 光线自右向左传播0=-''sns n (平面折射) 因 s=+20 s'=+12.5 n'=1 61.=''=s n s n从右看时 光线自左向右传播rnn s n s n -'=-'' s=-20 r=-12 n=1.6 n'=1 代入数 s'=-33.3cm1-10 解:单球面成象rnn s n s n -'=-'' n=1 n'=1.5 s=-5 r=2 代入数 s'=3041-=''=sn s n β 第二球面 n=1.5 n`=1.33 s=(30-2) r=-2 代入数成像公式 s'=9.638702.=''=sn s n β 所以β=β1*β2=-1.546 象为倒立的放大的实象,象高为1.5461-12 解: 球面镜反射rs s 211=+' y=2 r=-16 s=-10 代入得 s'=-40焦距 f '=r/2=-8 β=-s`/ s=-4 所以 y`=y β=-8cm 1-18 解:由焦距公式代入数 f '=120由成像公式s=-40 所以代入数 s'=-60 β1=s`/ s=3/2球面反射 1/s'+1/s=2/r 因 s=-60 r=-15 代入数 s`=-60/7β2=s`/ s=-1/7再成象 1/s`-1/s=1/f ` s=-60/7 f `=120 (光线自右向左传播) 所以 s`=-8 β3=s`/ s=14/15 所以β1β2β3=-1/5 象为缩小的倒立的实象1-19 解:空气中当在cs 2中使用时: 两焦距之比:⎪⎪⎭⎫ ⎝⎛-'+-'='21r n n r n n n f L L 1='=n n 5.1=L n 201-=r 152-=r f s s '=-'111)11)(1(11112121r r n r n r n f f L L L --=⎪⎪⎭⎫ ⎝⎛-+-=-='⎪⎪⎭⎫ ⎝⎛-'+-'='21r n n r n n n f L L 64.82-=''空气f f cs该式说明:①对于同一个透镜,放在不同介质中使用,焦距是不同的,对于该题在二硫化碳中使用时焦距比空气中使用时要大。
光学教程第四版课后习题答案

参 考 答 案光学教程( 姚启钧 原著)目录第一章第二章第三章第四章第五章第六章第七章光的干涉 (3)光的衍射 (15)几何光学的基本原理 (27)光学仪器的基本原理 (49)光的偏振 (59)光的吸收、散射和色散 (70)光的量子性 (73)第一章 光的干涉波长为 500nm 的绿光投射在间距 d 为 0.022cm 的双缝上,在距离180cm 处的光屏 1. 上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为700nm 的红光投射到此双缝上, 两个亮条纹之间的距离又为多少?算出这两种光第2 级亮纹位置的距离. - y = r 0λ ∆y = y j +1 jd 解:由条纹间距公式得 ∆y = r 0 λ = 180 ⨯ 500 ⨯10 -7 = 0.409cm 1 1d 0.022 180 ∆y = r 0 λ = ⨯ 700 ⨯10 -7 = 0.573cm 2 2 d 0.022 r 0y 21 = j 2 λ1 = 2 ⨯ 0.409 = 0.818cmd r 0y 22 = j 2 2 = 2 ⨯ 0.573 = 1.146cmd∆y j 2 = y 22 - y 21 = 1.146 - 0.818 = 0.328cm2.在杨氏实验装置中,光源波长为640nm ,两狭缝间距为 0.4mm ,光屏离狭缝的距离为 50cm .试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若 p 点离中央亮条纹为 0.1mm ,问两束光在 p 点的相位差是多少?(3)求 p 点的光强度和中央点的强度之比.∆y = r 0 λd 解 :( 1)由公式∆y =r 0 λ 50⨯ 6.4 ⨯ 10 -5 = 8.0 ⨯ 10 -2 cm d = 0.4得(2)由课本第 20 页图 1-2 的几何关系可知r - r ≈ d sin θ ≈ d t an θ = d y = 0.04 0.01 = 0.8 ⨯10-5cm 2 1r 050∆ϕ =2π (- r ) = 2π ⨯ 0.8 ⨯10-5 = π 2 1 6.4 ⨯10-5λ 4 I = A 2 + A 2 + 2AA cos ∆ϕ = 4A 2 cos2∆ϕ(3) 1 2 1 2 1 2 由公式得4A 2 cos 2 ∆ϕ cos 2 1 ⋅ π 2 I p = A p = 2 = 2 4 1 = cos 2 π 4A 2 cos 2 ∆ ϕ 2 2I 0 A cos 0︒ 8 00 121 + cos π =2 + 2 = 4 = 0.8536 2 43 . 把折射率为 1.5 的玻璃片插入杨氏实验的一束光路中,光屏上原来第 5 级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为 6×10-7m .∆ϕ = ∆r解:未加玻璃片时, S 1 、 S 2 到 P 点的光程差,由公式2π λ 可知为 λ r 2 - r 1 = 2π⨯ 5 ⨯ 2π = 5λΔr = 现在S 1 发出的光束途中插入玻璃片时, P 点的光程差为λ λ r 2 - ⎡⎣(r 1- h ) + nh ⎤⎦ = ∆ϕ ' = ⨯ 0 = 0 2π 2π所以玻璃片的厚度为h = r 2 - r 1 5λ= 10λ = 6 ⨯10-4 cm n - 1 0.54. 波长为 500nm 的单色平行光射在间距为 0.2mm 的双狭缝上.通过其中一个缝的能量 为另一个的 2 倍,在离狭缝 50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.∆y = r 0 λ = 500 ⨯ 500 ⨯10-6 = 1.25d 0.2 mm 解:A 1I 1 = 2I 2 2 2A 1 = 2 A 2 A 22(A1 / A2 )== 0.9427 ≈0.94∴V =1+(A/ A )21+21 25. 波长为700nm 的光源与菲涅耳双镜的相交棱之间距离为20cm,棱到光屏间的距离L 为180cm,若所得干涉条纹中相邻亮条纹的间隔为1mm,求双镜平面之间的夹角θ。
《光学》讲义笔记习题答案
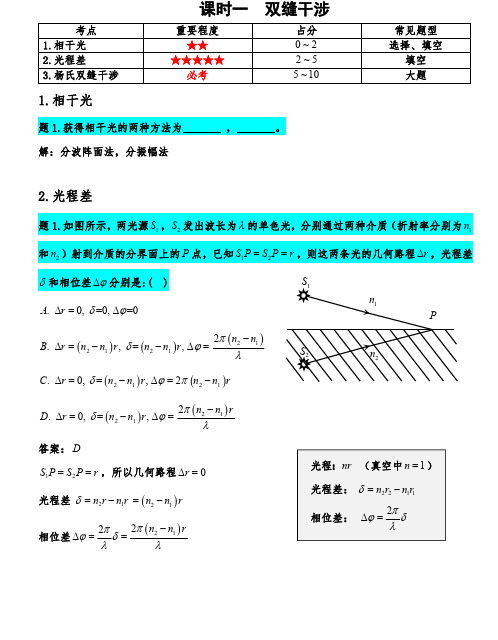
题 1.如图所示,折射率为 n2 ,厚度为 e 的透明介质薄膜的上方和下方的透明介质的折射率分
别为 n1 和 n3 ,已知 n1 n2 n3 ,若用真空中波长为 的单色平行光垂直入射到该薄膜上,则
从上、下表面反射的光束(用①,②示意)的光程差是( )。
①②
A. 2n2e
B.
2n2e
2n2
C. 2n2e
题 4.在图示的双缝干涉实验中,若用半圆筒形的薄玻璃片(折射率 n1 1.4 )覆盖缝 S1 ,用同
样厚度的玻璃片(折射率 n2 1.7 )覆盖缝 S2 ,将使屏上原来未放玻璃时的中央明纹所在处 O 变为第五级明纹,设单色光波长 480nm ,求玻璃片的厚度 d 。
解:未覆盖
r2 r1 0
d
S1
n1
r1
覆盖后
r2 d n2d r1 d n1d 5
整理得
r2 r1 n2 n1 d 5
O
联立可得 d 5 5 480 109 8 106m S2 n2
r2
n2 n1 1.7 1.4
题 5.如图所示,把折射率 n 1.5 的玻璃插入杨氏双缝干涉实验的一束光路中,光屏原来是 5 级亮纹所在的位置变为中央亮纹,已知光波长 6.0107 m ,求插入玻璃片的厚度。
到双缝的距离 D 2m ,求:
(1)两相邻明纹的间距;
(2)中央明纹上方第 5 级明纹的位置,以及下方第 3 级暗纹的位置。
解:(1)
x
D d
2 480 109 2 104
4.810 3m
(2)上方明纹:
x5
k
D d
5
4.8 10 3
2.4102m
下方暗纹: x3
