spss均值检验

合集下载

均值检验、方差分析 SPSS

一、实验目的及要求：1、目的用SPSS软件实现均值检验和方差分析。

2、内容及要求用SPSS对所要求数据进行相应的数据处理和分析：均值检验、方差分析。

二、仪器用具：三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到SPSS中，并且把学校变量改为数值型变量，用1、2分别代替“A”和“B”。

四、实验结果与数据处理：首先用SPSS软件对单变量进行正态性检验，结果如下：因为样本数n=60<2000，所以此处选用Shapiro-Wilk统计量。

由Sig.值我们可以认为五科的录取分数均遵从正态分布。

用SPSS的GLM模块进行多元正态分布有关均值与方差的检验，结果如下：第一张主体间因子表展示了样本数据分别来自两个学校的个数。

第二张多变量检验表给出了几个统计量，由Sig.值可以看出，无论从哪个统计量来看，两个学校的录取分数都是有显著差别的。

由于模型通过了显著性检验，意味着两所学校的录取分数线是不同的。

主体间因子N学校 A 30B 30由上面主体间效应的检验表可知五科分数的Sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。

协方差矩阵等同性的 Box 检验aBox 的 M 14.729F .891df1 15df2 13544.526Sig. .575检验零假设，即观测到的因变量的协方差矩阵在所有组中均相等。

a. 设计 : 截距 + 学校该表为协方差阵相等的检验表，检验统计量为Box’s M，由Sig.值可以认为两个学校(总体)的协方差阵是相等的。

由误差方差等同性的Levene检验表，可以得知，在显著性水平为0.05水平下，五科分数的误差平方在两个学校间是没有显著差别。

下页成对比较表给出了不同学校五科录取分数的比较与检验及检验的可信性统计量。

综上：通过对两个学校的本科录取分数线的具体的比较分析，所得的数据表明，两个学校的本科录取分数线存在着明显的差异，并且在语文、数学、英语、物理和化学这五门课程的录取分数上均有显著的差异。

第6章 SPSS参数检验——均值比较

总体2
抽取简单随机样均值之差的检验 (s12、 s22 已知)
• 1.假定条件
两个样本是独立的随机样本两个总体都是正态分布若不是正态分布, 可以用正态分布来近似(n130和
n230) 2.检验统计量为
Z ( X1 - X 2 ) - (m1 - m2 ) ~ N (0,1)
6.2 MEANS 过程
• 功能：分组计算、比较指定变量的描述统计量。包括均值、标准差、总和、观测数、方差等等，还可以给出方差分析表和线性检验结果。
• Analyze-> Compare Means->Means
n Dependent List：用于选入需要分析的变量，如果选入两个以上变量，系统会在同一张输出表中依次给出分析结果。
)
1. 检验具有不等方差的两个总体的均值
2. 假定条件
两个样本是独立的随机样本
两个总体都是正态分布
两个总体方差未知且不相等 s12 s22
3. 检验统计量
( S12 S22 )2
t

(
X1
-
X2) S12 n1
- (m1 S22
n2
-
m2
)
~
t(
(
S12 n1
)2
/(
n1
n1 -1)
s
2 1

s
2 2
n1 n2
两个总体均值之差的检验 (s12、 s22 未知，大样本)
• 检验统计量为
Z (X1 - X 2 ) - (m1 - m2 ) ~ N (0,1)
s12 s22 n1 n2
两个总体均值之差的检验 (s12、 s22 未知但相等,小样本)

SPSS统计分析平均数差异检验

SPSS统计分析平均数差异检验统计分析是研究中常常使用的一种方法，它通过对数据进行整理、描述和分析，从而得出结论。

而SPSS（Statistical Package for the Social Sciences）则是一款广泛应用于统计学领域的软件，它提供了丰富的统计分析工具和功能，方便研究者进行数据处理和统计分析。

其中一个常用的统计分析方法是平均数差异检验。

平均数差异检验可以用来比较两组或多组样本之间的平均数是否存在显著差异。

这个方法在实际研究中非常重要，因为它可以帮助我们确定不同群体或条件下的差异是否真实存在，从而为决策提供依据。

SPSS作为一款专业的统计软件，提供了多种平均数差异检验方法，能够帮助研究者快速准确地完成数据分析。

下面将介绍SPSS中两种常用的平均数差异检验方法：独立样本t检验和配对样本t检验。

1. 独立样本t检验独立样本t检验用于比较两个独立样本之间的平均数差异是否显著。

它适用于两个样本之间没有联系的情况，比如男性和女性之间的差异、两个地区之间的差异等。

在SPSS中进行独立样本t检验，依次选择"Analyze"、"Compare Means"、"Independent Samples T Test"，然后将要比较的两个变量分别添加到"Test Variable(s)"和"Grouping Variable"中，最后点击"OK"即可得出结果。

2. 配对样本t检验配对样本t检验用于比较同一组样本在不同条件下的平均数差异是否显著。

它适用于实验前后的比较或者相同个体在两个不同时间点的比较等情况。

在SPSS中进行配对样本t检验，依次选择"Analyze"、"Compare Means"、"Paired-samples T Test"，然后将要比较的变量添加到"Paired Variables"中，最后点击"OK"即可得出结果。

SPSS-5-均值比较(t检验)

Test for linearity 检验线性相关性，实际上就是上面的单因素方差分析。
一、平均数分析（Compare Means Means）
2、例题分析
打开“2000级课堂调查数据.sav”,按性别分组比较政治成绩的平均值、标准差和方差。操作：点击Analyze Compare Means Means，在【Dependent List框】中选入“政治成绩”变量；在【Independent List框】中选入分类变量 “性别”；点击【Options钮】弹出Options对话框，选择需要计算的描述统计量。结果分析：统计结果见下表。这里输出的是政治成绩的均数，样本量大小、标准差和方差。由于我们选择了分组变量“性别”，因此四项指标均给出分组及合计值，可见以这种方式列出统计量可以非常直观的进行各组间的比较。
第五讲均值比较（Compare Means）
P131页
均值比较的假设检验，并非考察的是两样本的均值是否相等，而是考察两样本所来自的总体的均值是否相等。由于所要考察的两总体的方差是未知的，因而两样本的均差假设检验采用t检验。
t检验是用小样本检验总体参数，特点是在总体方差未知的情况下，可以检验样本平均数的显著性。
Group Statistics 性别（ t1）男女 N 8 11 Mean 63.125 64.909 Std. Deviation 2.4749 7.0492 Std. Error Mean .8750 2.1254
政治成绩（ t7，分）
三、两独立样本的均值检验
2、例题分析
结果分析：下表为两独立样本t检验表，下面从左到右依次为Levene's方差齐性检验的F值和F检验的P值(Sig.) 、t值(t)、自由度(df)、P值(Sig.2-tailed)、两均数的差值(Mean Difference)、差值的标准误(Std. Error Difference)、差值的95%置信区间。（1）先进行方差齐性检验：F=7.834，P=0.012。由于 P<α ，要拒绝原假设（原假设为两组数据的方差相等或齐性），因此男、女生政治成绩这两组数据的方差是不相等的。（2）由方差齐性检验的结果来选择t检验的统计量。由于方差不等，因此选择“Equal Variance not assumed”这一行的t检验值来判断：t=－0.776，P=0.451。因为相伴概率 P>α ，要接受原假设（原假设为两独立样本所来自总体的均值相等），因此可以认为教科院2000级男生和女生的政治平均成绩没有明显差异。

第5章 SPSS 20.0均值检验

对总体特征的推断一般采用参数估计（点估计和区间估计）和假设检验两类方法实现。SPSS兼顾了这两类方式，由于其核心原理基本类似，这里仅以对假设检验的基本思想做重点讨论。假设检验的基本思想是首先对总体参数提出假设，然后利用样本告之的信息去验证提出的假设是否成立。如果样本数据不能充分证明和支持假设，则在一定的概率条件下，应拒绝该假设；相反，如果样本数据不能够充分证明或者支持假设是不成立的，则不能推翻假设。上述假设检验推断过程所依据的基本信息是小概率原理，即发生概率很小的随机事件，在某一次特定的实验中是几乎不可能发生的。

表5-1 单个样本统计量
N 钢管内径 10
均值 100.1040
标准差 .47596
均值的标准误 .15051
表5-1给出了单一样本均值检验的描述性统计量、标准差和均值标准误差。钢管内径均值为100.1040，接近总体100

表5-2是单一样本均值检验的结果列表，给出了t统计量、自由度、双尾概率以及显著性水平及置信区间。双尾概率P=0.507>显著性水平0.05，接受原假设，说明钢管内径与平均值100无显著差异。
表5-6 独立样本检验方差方程的 Levene 检验均值方程的 t 检验差分的 95% 置 Sig.( F 电池使用假设方差时间相等假设方差不相等 5.456 20.17 2 .000 .100 Sig. .755 t 5.484 df 21 双侧) .000 均值差值 1.133 33 1.133 33 .20771 标准误差值 .20665 信区间下限 .7035 9 .7003 0 上限 1.563 08 1.566 36

0
其中

二用SPSS软件进行均值检验和求均值的置信区间

二、用SPSS软件进行均值检验和求均值的置信区间（一）求单个样本均值的置信区间及均值检验例1某区初三英语统一测验平均分为65分，现从某中学随机抽取20份试卷。

其分数为：72，76，68，78，62，59，64，85，70，75，61，74，87，83，54，76，56，66，68，62。

（1）问该校初三英语平均分数与全区是否基本一致（α=0.05）。

（2）求该校初三英语测验平均分数的95%的置信区间。

（1）建立数据文件定义变量方法：用鼠标单击Varible View按键，弹出一图，在此图的Name 栏中给出所需的变量名，如X，回车便定义了一个数值型变量。

如果需要对变量的类型、变量的宽度、小数位数、变量标签、变量值标签、丢失值处理方式、数据列的宽度、数据对齐方式等进行修改，则用鼠标击相应栏便可以进行修改。

若要定义多个变量，则在后面各行中做类似于上面的操作。

然后用击Data View 按键，将其相应数据输入为图1的形式，并保存。

（2）选择统计方法按顺序[Analyze][Compare mean][One-Sample T Test]单击各项,最后弹出如图2所示的对话框，将左边源变量分数送入Test Variable右方框中，在底部Test小框中输入检验值，本例要输入65。

系统默认水平为α=0.05,[若不是0.05，则点击右下角的options进行修改，修改完后点击continue，返回主对话框，]点击OK键，输出表2和表3。

（3）结果说明表2的第2栏是样本个数，第3栏是样本均值，第4栏是样本标准差，第5栏是样本均值标准误差。

表3中，Test Value = 65表示是检验假设H0：μ=65,t=2.266,自由度df=19，显著性概率P= Sig.=0.035.由于Sig.<0.05，所以拒绝假设H0，即认为某中学学生的平均分数不是65，平均差是4.8。

平均差的95%的置信区间为（0.37，9.23）。

spss 均值的比较与检验

输出结果：
结果分析：
1、两种样本的均数分别为3318.75, 2506.25, 样本个数均为8。
2、相关系数r=0.584, p=0.129>0.05 ，认为两配对变量无相关关系。
3、t=4.207，自由度df=7, p=0.004<0.05, 故可认为两组样本的均值差异显著。
4、配对数差的均数为812.50, 标准差为546.25 ，标准误为193.13， 95％的可信区间为355.82～1269.18。结论：两配对变量无相关关系，且两组样本的均值差异显著。
结论：
处理前后两组样本方差相等，均值有明显差异。
例5-5-3 以银行男女职工的现工资为例，数据e5-5-4.sav, 检验男女职工现工资是否有显著性差异。执行结果如下：
结果分析：
1、各组观测数目，男258人，女216人。
2、男性平均工资：41441.8, 女性工资为： 26031.9. 3、方差齐次性检验结果（levene检验)，F值为119.669, 显著性概率为P=0.000<0.05.因此，两组方差差异显著。在下面的t 检验结果中应该选择Equal variances not assumed (假设方差不相等）一行的数据作为本例t检验的结果数据。
z ~ t (n 1) sz / n
在显著水平α下，双侧检验的H0拒绝区域为： | t | t (n 1)
2
二、配对样本T检验功能与应用
配对样本T检验是进行配对样本均数的比较。执行该过程， SPSS显示：
每个变量的均数、标准差、标准误和样本含量；
每对变量的相关系数；
每对变量的均数的差值、差值的标准误和可信区间；检验每对变量均数的差值是否来自总体均数为0 的t检验结果。三、应用举例例5-5-4 ：(e5-5-5.sav)

SPSS软件中几种常用的统计方法

独立样本的均值检验配对样本的均值检验
单因素的方差分析
.
单一样本均值的检验
-检验样本所在总体的均值与给定的已知值之间是否存在显著性差异
.
18
单一样本均值的检验
对单一变量的均值加以检验
如检验今年新生的身高、体重等是否和往年有显著差异；推断某地区今年的人均收入与往年的人均收入是否有显著差异等等。
OR值即是相对危险度的精确估计值。
.
优势比（odds ratio，OR）
吸烟与食管癌关系的病例对照调查结果
吸烟的优势 309/5171.49非吸烟的优势 126/3690.52
208/517
243/369OR1.49 Fra bibliotek.87 0.52
.
OR值的意义：
OR值等于1，表示该因素对疾病的发生不起作用；
如，一组病人治疗前和治疗后身体的指标；一个年级学生的期中成绩和期末成绩等等。
.
单因素方差分析
one-way ANVOA
-推断完全随机设计的多个样本所代表的各总体均数是否相等
.
31
完全随机设计（completely random design）不考虑个体差异的影响，仅涉及一个处理因素，但可以有两个或多个水平，所以亦称单因素实验设计。在实验研究中按随机化原则将受试对象随机分配到一个处理因素的多个水平中去，然后观察各组的试验效应；在观察研究（调查）中按某个研究因素的不同水平分组，比较该因素的效应。
SPSS软件中几种常用的统计方法
.
目录
1、卡方检验中的OR值 2、均值检验
.
.
卡方检验
χ2检验是以χ2分布为基础的一种假设检验方法，主要用于分类变量，根据样本数据推断总体的分布与期望分布是否有显著差异，或推断两个分类变量是否相关或相互独立。

SPSS统计分析第四章均值比较与T检验

N 258 216
Mean $41441.8 $26031.9
Std. Dev iation $19,499.214 $7,558.021
Std. Error Mean $1213.97
$514.258
左第一栏为分析变量标签和分类变量标签 N观测量数目 Mean均值 Std. Deviation标准差 Std. Error Mean标准误
三、配对样本T检验
配对样本T检验（Paired Sample T test）用于检验两个相关的样本是否来自具有相同均值的总体。这种相关的或配对的样本常常来自这样的实验结果，在实验中被观测对象在实验前后均被观测。两个变量可以是before after，配对分析的测度也不是必须来自同一个观测对象。一对可以两者组合而成。
练习题
已知某水样中含CaCO3的真值为20.7mg/L，现用某方法重复测定该水样11次CaCO3的含量（mg/L）为：20.99，20.41，20.10， 20.00，20.91，22.60，20.99，20.41， 20.00，23.00，22.00。问该方法测得的均值是否偏高？
2、Independent Sample T test（独立样本T检验）
例题一
现有银行雇员工资为例，检验男女雇员现工资是否有显著差异。一个是要比较salary变量的均值，另一个是gender变量作为分水平变量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
如果你试图比较的变量明显不是正态分布的，则应该考虑使用一种非参数检验过程（Nonparametric test）。如果想比较的变量是分类变量，应该使用Crosstabs 功能。

spss均值检验（均数分析单样本t检验独立样本t检验）

在统计学中，我们往往从样本的特性推知随机变量总体的特性。

但由于总体中个体之间存在差异，样本的统计量和总体的参数之间往往会有误差。

因此，均值不相等的样本未必来自不同分布的总体，而均值相等的样本未必来自有相同分布的总体。

也就是说，如何从样本均值的差异推知总体的差异，这就是均值比较的内容。

SPSS提供了均值比较过程，在主菜单栏单击“Analyze”菜单下的“Compare Means”项，该项下有5个过程，如图4-1。

平均数比较Means过程用于统计分组变量的的基本统计量。

这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。

Means过程还可以列出方差表和线性检验结果。

[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化，统计暴雨前和暴雨后的统计量，其数据如下：暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。

1）准备分析数据在数据编辑窗口输入分析的数据，如图4-2所示。

或者打开需要分析的数据文件“DATA4-1.SAV”。

图4-2 数据窗口2）启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。

出现对话框如图4-3。

图4-3 Means设置窗口3）设置分析变量从左边的变量列表中选中“百株卵量”变量后，点击变量选择右拉按钮，该变量就进入到因子变量列表“Dependent List:”框里，用户可以从左边变量列表里选择一个或多个变量进行统计。

从左边的变量列表中选中“调查时候”变量，点击“Independent List”框左边的右拉按钮，该变量就进入分组变量“IndependentList”框里，用户可以从左边变量列表里选择一个或多个分组变量。

均值检验、方差分析SPSS

均值检验、方差分析SPSS以下是为大家整理的均值检验、方差分析spss的相关范文，本文关键词为均值,检验,方差,分析,spss,实验,目的,要求,spss，您可以从右上方搜索框检索更多相关文章，如果您觉得有用，请继续关注我们并推荐给您的好友，您可以在综合文库中查看更多范文。

一、实验目的及要求：1、目的用spss软件实现均值检验和方差分析。

2、内容及要求用spss对所要求数据进行相应的数据处理和分析：均值检验、方差分析。

二、仪器用具：仪器名称计算机spss软件规格/型号数量11备注有网络环境三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到spss中，并且把学校变量改为数值型变量，用1、2分别代替“A”和“b”。

四、实验结果与数据处理：首先用spss软件对单变量进行正态性检验，结果如下：正态性检验Kolmogorov-smirnova统计量语文数学英语物理化学.084.102.071.087.073df6060606060sig..200*.192.200.200*.200**sha piro-wilk统计量.986.972.982.990.984df6060606060sig..698.185.512.894.627a.Lilliefo rs显著水平修正*.这是真实显著水平的下限。

因为样本数n=60用spss的gLm模块进行多元正态分布有关均值与方差的检验，结果如下：1第一张主体间因子表展示了样本数据分别来自两个学校的个数。

第二张多变量检验表给出了几个统计量，由sig.值可以看出，无论从哪个统计量来看，两个学校的录取分数都是有显著差别的。

由于模型通过了显著性检验，意味着两所学校的录取分数线是不同的。

主体间因子学校Abn3030多变量检验b效应截距pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根学校pillai的跟踪wilks的Lambdahotelling的跟踪Roy的最大根 a.精确统计量 b.设计:截距+学校值.999.0011554.6561554.656.851.1495.7105.710F16790.281a16790.28 1a16790.281a16790.281a61.672a61.672a61.672a61.672a假设df5.0005.0005.0005.0005.0005.0005.0005.000误差df54.00054.00054.00054.00054.00054.00054.00054.000sig..000.000.00 0.000.000.000.000.000主体间效应的检验源校正模型因变量语文数学英语物理化学截距语文数学英语物理化学学校语文数学英语物理III 型平方和1050.017a1470.150b1135.350c1859.267d1560.600e372408.817376833. 750388010.417389781.600383360.2671050.0171470.1501135.3501859. 267df11111111111111均方1050.0171470.1501135.3501859.2671560.600372408.817376833.75038 8010.417389781.600383360.2671050.0171470.1501135.3501859.267F4 8.25186.03439.83183.39241.65217113.20XX2052.62613612.47917482. 60010231.72248.25186.03439.83183.392sig..000.000.000.000.000.000.000.000.000.000.000.000.000.0002化学误差语文数学英语物理化学总计语文数学英语物理化学校正的总计语文数学英语物理化学a.R方=.454（调整R方=.445）b.R方=.597（调整R方=.590）c.R方=.407（调整R方=.397）d.R方=.590（调整R方=.583） e.R方=.418（调整R方=.408）1560.6001262.167991.1001653.2331293.1332173.133374721.00037929 5.000390799.000392934.000387094.0002312.1832461.2502788.583315 2.4003733.73315858585858606060606059595959591560.60021.76117. 08828.50422.29537.46841.652.000由上面主体间效应的检验表可知五科分数的sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。

spss t检验均数标准差

spss t检验均数标准差SPSS t检验均数标准差。

SPSS（Statistical Product and Service Solutions）是一种统计分析软件，广泛应用于各个领域的数据分析和研究中。

在SPSS中，t检验是一种常用的假设检验方法，用于比较两组样本均数是否存在显著差异。

本文将介绍如何在SPSS中进行t 检验，并解释如何计算均数和标准差。

首先，我们需要明确t检验的基本概念。

t检验用于比较两组样本均数的差异是否显著。

在进行t检验之前，我们需要先对两组数据进行描述性统计分析，计算它们的均数和标准差。

均数是样本数据的平均值，用来衡量一组数据的集中趋势；标准差是样本数据的离散程度的度量，用来衡量数据的分散程度。

在SPSS中进行t检验，首先需要导入数据。

在“数据编辑器”中输入或导入两组数据，然后点击“分析”菜单中的“比较均数”选项。

在弹出的对话框中，选择“独立样本t检验”，将两组数据分别输入到“变量1”和“变量2”中，然后点击“确定”按钮进行分析。

SPSS将自动生成t检验的结果报告，其中包括了两组数据的均数、标准差、t 值、自由度和显著性水平等统计指标。

我们可以根据这些指标来判断两组数据的均数是否存在显著差异。

如果t值的绝对值较大，且显著性水平小于0.05，我们就可以拒绝原假设，认为两组数据的均数存在显著差异；反之，则接受原假设，认为两组数据的均数没有显著差异。

除了SPSS自动生成的结果报告，我们也可以手动计算两组数据的均数和标准差，然后利用t检验的公式来进行计算。

假设两组数据分别为X和Y，它们的均数分别为μ1和μ2，标准差分别为σ1和σ2，样本量分别为n1和n2，t值的计算公式为：t = (μ1 μ2) / √(σ1²/n1 + σ2²/n2)。

在计算t值之后，我们可以利用t分布表或SPSS软件来查找对应的显著性水平，从而判断两组数据的均数是否存在显著差异。

总之，t检验是一种常用的假设检验方法，用于比较两组样本均数的差异是否显著。

SPSS学习系列21. 均值的T检验

21. 均值的T检验T检验，是一种针对连续变量的参数假设检验，用来检验“单样本均值与已知均值（单样本T检验）、两独立样本均值（独立样本T 检验）、配对设计资料的均值（配对样本T检验）”是否存在差异，这种差异是否能推论至总体。

例如，检查学生成绩平均分是否等于某分值；比较两个班学生的平均分是否存在差异；正常饲料组和维E缺乏组大白鼠肝中维生素A 含量的均值是否存在差异。

T检验适用于样本含量较小（比如n<60，大样本数据可以用U 检验），适用条件：①数据服从正态分布；②满足方差齐性；注：若数据不满足①，②，可以尝试对数据做变量变换：对数变换、平方根变换、倒数变换、平方根反正弦变换等。

有数据文件：由第19,20篇的“正态性检验”和“方差齐性检验”知，“数学成绩”满足正态性和方差齐性。

一、单样本T检验要求数据满足正态性、方差齐性。

问题1：检验“数学成绩”的平均值是否等于75分。

【分析】——【比较均值】——【单样本T检验】，打开“单样本T检验”窗口，将变量“数学成绩”选入【检验变量】框，【检验值】框输入“75”，【选项】按钮设置置信限，保持默认即可。

点【确定】得到结果说明：单样本T检验的原假设H0: 均值μ = μ0；备择假设H1: 均值μ≠μ0本例中，t值=0.395, P值=0.694>0.05, 故接受原假设，即“数学成绩的平均分=75”有统计学意义；“平均分=75”的95%置信限为[75-3.19, 75+4.75]二、独立样本T检验要求数据满足：独立性、正态性、方差齐性。

问题2：检验1班和2班的数学成绩是否存在差异。

1.【分析】——【比较均值】——【独立样本T检验】，打开“独立样本T检验”窗口，将变量“数学成绩”选入【检验变量】框，将分组变量“班级”选入【分组变量】框，2.点【定义组】打开“定义组”子窗口，【使用指定值】下面的组1框中填入“1”，组2框中填入“2”，点【继续】回到原窗口，点【确定】得到结果说明：（1）甲班的数学平均分=72.29，乙班的数学平均分=79；（2）方差齐性检验的P值=0.884>0.05, 接受原假设H0，即方差齐；（3）独立样本T检验的原假设H0: 均值μ1=μ2；备择假设H1: 均值μ1≠μ2.T检验结果有两种：假设方差相等、不相等。

SPSS实验三均值检验试验

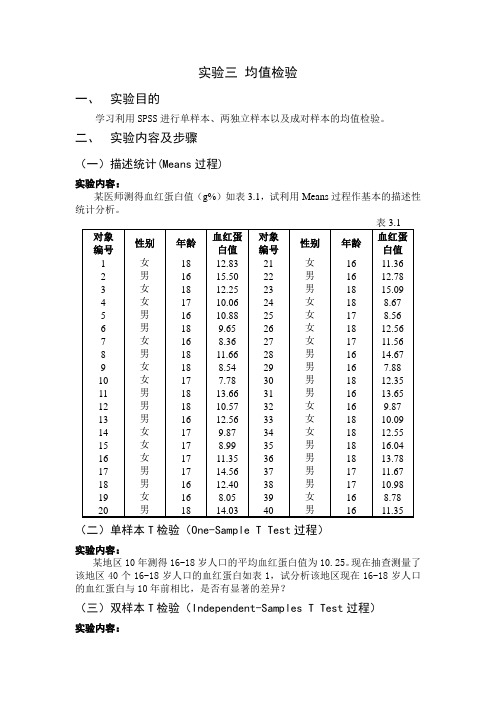
实验三均值检验
一、实验目的
学习利用SPSS进行单样本、两独立样本以及成对样本的均值检验。

二、实验内容及步骤
（一）描述统计(Means过程)
实验内容：
某医师测得血红蛋白值（g%）如表3.1，试利用Means过程作基本的描述性统计分析。

（二）单样本T检验（One-Sample T Test过程）
实验内容：
某地区10年测得16-18岁人口的平均血红蛋白值为10.25。

现在抽查测量了该地区40个16-18岁人口的血红蛋白如表1，试分析该地区现在16-18岁人口的血红蛋白与10年前相比，是否有显著的差异？
（三）双样本T检验（Independent-Samples T Test过程）
实验内容：
分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇
（四）成对样本T检验（Paired-Samples T Test过程）
实验内容：
某单位研究饲料中缺乏维生素E与肝中维生素A含量的关系，将大白鼠按性别、体重等配为8对，每对中两只大白鼠分别喂给正常饲料和维生素E缺乏饲料，一段时期后将之宰杀，测定其肝中维生素A含量（μmol/L）如下，问饲料中缺乏维生素E对鼠肝中维生素A含量有无影响？。

SPSS实验报告——均值比较

实验报告一、实验目的1、掌握均值比较，用于计算指定变量的综合描述统计量2、掌握独立样本T检验（Independent Samples Test），用于检验两组来自独立总体的样本，企图理综题的均值或中心位置是否一样二、实验步骤第1步数据导入；打开“EG5-2城市和农村学生心理素质测试得分.sav”第2步确定要进行T检验的变量；选择Analyze→ Compare Means →Independent-Samples ，选择“p”变量作为检验变量，移入“Test Variable(s)”框中。

第4步确定分组变量；选择变量“group”作为分组变量，将其移入下图中的“Grouping variable”文本框中，并定义分组的变量值：Group1—1，Group2—2。

三、结果及分析两独立样本T检验的基本描述统计量分析：1、根据结果，方差齐性检验的p值为0.791，大于0.05，故应接受原假设。

2、因为方差相等，两独立样本T检验的结果应该看两独立样本T检验结果报中的Equal variances assumed”一行，第5列为相应的双尾检测概率（Sig.（2-tailed））为0.07，在显著性水平为0.05的情况下，T统计量的概率p值大于0.05，故接受原假设假设,即认为两样本的均值是相等的，在本题中，不能认为两组的成绩有显著性差异。

实验报告一、实验目的1、掌握均值比较，用于计算指定变量的综合描述统计量2、掌握配对样本T检验（Paired Samples Test），用于检验两个相关的样本是否来自具有相同均值的总体。

二、实验步骤第1步数据组织；打开“EG5-1学生培训前后心理测试得分.sav”第2步确定配对分析的变量选择Analyze→ Compare Means →Paired-Samples T Test，将变量“before”和“after”添加到“Paired Variables”框中，作为一对分析的配对变量三、结果及分析分析：表“paired samples test”显示，学生培训前后的平均成绩相差 -0.158，平均成绩差值的标准差为1.5048，差值标准差的标准误为0.4344.在置信水平为95%时平均值差值的置信区间为-1.114~0.798。

spss均值和标准差

spss均值和标准差SPSS均值和标准差。

在统计学中，均值和标准差是描述数据分布和集中趋势的重要指标。

SPSS作为一款强大的统计分析软件，可以帮助研究者快速计算和分析数据的均值和标准差。

本文将介绍如何在SPSS中进行均值和标准差的计算，并对其结果进行解释和应用。

1. 数据导入。

在进行均值和标准差的计算之前，首先需要将数据导入SPSS软件中。

可以通过“文件”-“导入数据”命令，选择相应的数据文件进行导入。

在导入数据时，需要注意数据的格式和变量的命名，确保数据的准确性和完整性。

2. 计算均值。

在SPSS中，计算变量的均值非常简单。

选择“分析”-“描述统计”-“均值”命令，在弹出的对话框中选择需要计算均值的变量，然后点击“确定”按钮即可得到相应变量的均值。

此外，还可以通过计算新变量的方式，利用公式计算多个变量的均值。

均值的计算结果可以帮助研究者了解数据的集中趋势，即数据整体的平均水平。

通过对均值的比较，可以发现不同变量之间的差异，进而进行更深入的数据分析和解释。

3. 计算标准差。

标准差是衡量数据离散程度的重要指标，可以通过SPSS快速计算得出。

选择“分析”-“描述统计”-“频率”命令，在弹出的对话框中选择需要计算标准差的变量，然后点击“统计量”按钮，在弹出的对话框中勾选“标准差”选项，最后点击“确定”按钮即可得到相应变量的标准差。

标准差的计算结果可以帮助研究者了解数据的离散程度，即数据的分散情况。

通过对标准差的比较，可以发现数据的波动程度，进而进行数据的波动程度，进而进行更深入的数据分析和解释。

4. 结果解释和应用。

得到均值和标准差的计算结果之后，需要对其进行解释和应用。

首先，可以通过直方图、箱线图等可视化手段展示数据的分布情况，进一步分析数据的特点和规律。

其次，可以利用均值和标准差进行假设检验和方差分析，探究不同变量之间的关系和差异。

最后，可以将均值和标准差作为数据描述的重要依据，用于撰写研究报告和论文。

spss教程第二章--均值比较检验与方差分析

第二章均值比较检验与方差分析在经济社会问题的研究过程中，常常需要比较现象之间的某些指标有无显著差异，特别当考察的样本容量n比较大时，由随机变量的中心极限定理知，样本均值近似地服从正态分布。

所以，均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。

◆本章主要内容：1、单个总体均值的 t 检验（One-Sample T Test）；2、两个独立总体样本均值的 t 检验（Independent-Sample T Test）；3、两个有联系总体均值均值的 t 检验（Paired-Sample T Test）；4、单因素方差分析（One-Way ANOVA）；5、双因素方差分析（General Linear Model Univariate）。

◆假设条件：研究的数据服从正态分布或近似地服从正态分布。

在Analyze菜单中，均值比较检验可以从菜单Compare Means，和General Linear Model得出。

如图2.1所示。

图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验（One-Sample T Test）分析单个总体的 t 检验分析也称为单一样本的 t 检验分析，也就是检验单个变量的均值是否与假定的均数之间存在差异。

如将单个变量的样本均值与假定的常数相比较，通过检验得出预先的假设是否正确的结论。

例1：根据2002年我国不同行业的工资水平（数据库SY-2），检验国有企业的职工平均年工资收入是否等于10000元，假设数据近似地服从正态分布。

首先建立假设：H0：国有企业工资为10000元；H1：国有企业职工工资不等于10000元打开数据库SY-2，检验过程的操作按照下列步骤：1、单击Analyze →Compare Means →One-Sample T Test，打开One-Sample T Test 主对话框，如图2.2所示。

图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量（国有单位）进入检验框中。

第5章spss总体均值的显著性检验

27
方差不齐时
两两比较方法选择：当各组方差齐性时，常用方法: S-N-K(Student-Newman-Keuls)：亦称SNK-q检验，是运用最广泛的一种两两比较方法,该方法控制第一类错误，只能为0.05
TUKEY：它控制的是所有比较中最大的一类错误不超过规定的错误,适合于各组人数相等，只能为0.05. Scheffe：适合于各组人数不等时。 LSD(Least-significant difference)：最小显著差t检验, 可指定0-1之间任何显著性水平，默认值为0.05；检验最为敏感。
检验线性相关性。检验的假设：因变量的均值是第一层自变量值的线性函数。给出相关系数及平方。【注意】只有第一层自变量有三个以上水平时才会出现分析结果。
4
结果形式：
5
5.1 One-Samples t Test(单样本t检验)
t检验的前提条件是样本总体服从正态分布，单样本t 检验用于检验总体均数与某常数是否有显著差异。原假设H0:总体均值与某常数相等。
21
6.1 One -Way ANOVA：单因素方差分析是研究在某种因素影响过程中，因变量在各个因素水平下样本总体均值的显著性检验。方差分析前提条件：独立性、正态性及方差齐性。方差分析采用F检验：先将总变异平方和SST分解为组间离差平方和SSA(控制因素引起)及组内离差平方和SSE(随机因素引起)，即 SST=SSA+SSE 然后构造F统计量为
33
13
分析结果:
两均值差的标准误
14
5.3 Paired-Samples T Test 通过两配对样本，进行两总体均数的比较检验。检验的前提条件：（1）两样本必须配对，而不独立，即数目相同且两样本值顺序不能更改；（2）两样本的总体必须服从正态分布。

在SPSS中利用均数和标准差做两独立样本t检验

在SPSS中利用均数和标准差做两独立样本t检验一、引言在统计学中，两个独立样本t检验被广泛应用于比较两个独立样本的均值是否存在显著差异。

它可以用于各个领域，比如医学、心理学、社会科学等等。

本文将介绍如何使用SPSS软件进行两独立样本t检验，以及如何使用均数和标准差来解读结果。

二、数据准备首先，我们需要准备好两组独立的样本数据。

例如，我们对男性和女性的身高进行比较。

我们需要收集到足够的样本数据，分别记录男性身高和女性身高。

这里我们假设每组数据的样本量相等，并且服从正态分布。

数据准备完毕后，我们可以开始进行两独立样本t检验。

三、SPSS分析步骤1. 打开SPSS软件，新建数据文件，并将收集到的数据录入到不同的变量列中。

确保每列代表一个变量，每行代表一个样本。

2. 点击“分析”选项卡，选择“比较手段”下的“独立样本t检验”。

3. 在弹出的对话框中，将两组独立样本的变量分别拖拽到左右两栏中。

点击“确定”。

4. SPSS会进行假设检验，计算两组样本的均值和标准差，并给出两组样本均值是否有显著差异的判断结果。

同时，SPSS 还会给出相关的统计指标和可视化图表帮助解读结果。

四、结果解释1. 假设检验结果SPSS会给出一个包括假设检验结果的统计表，其中包括两组样本的均值、标准差、t值、自由度、显著性水平等信息。

通过观察显著性水平是否小于设定的显著性水平（通常为0.05），我们可以判断两组样本的均值是否存在显著差异。

如果显著性水平小于设定的显著性水平，我们可以得出结论：两组样本的均值存在显著差异，即可以认为两组样本在某个变量上有不同的表现。

反之，如果显著性水平大于设定的显著性水平，我们则无法准确地判断两组样本的均值是否存在显著差异。

2. 相关统计指标除了假设检验结果，SPSS还会给出两组样本的均值和标准差，以及t值和自由度。

均值表示两组样本的平均水平，标准差代表样本值的差异程度。

t值则表示两组样本均值之差的标准误差，自由度代表样本数据参与构建t统计量的程度。