Farneback光流场算法数学推导
calcopticalflowfarneback原理讲解

calcopticalflowfarneback原理讲解calcopticalflowfarneback是OpenCV中的一个函数,用于计算稠密光流(dense optical flow)。
它基于Farneback的算法,可以估计图像中每个像素点的运动信息。
Farneback算法的原理如下:
1. 对于输入的两帧图像,首先将它们转换为灰度图像,以便更好地处理光流计算。
2. 然后,通过对灰度图像应用高斯滤波器来减少噪声。
这一步骤有助于提取稳定的特征点,并减小光流计算中的误差。
3. 接下来,使用多项式展开来近似两帧图像之间的局部区域。
多项式展开在空间和时间上都是平滑的,并且可以描述图像中像素点之间的关系。
4. 对于每个像素点,通过比较两帧图像中的多项式系数,计算出其在x和y方向上的光流向量。
这种比较是通过计算亮度差异、梯度信息和时间变化得到的。
5. 最后,通过插值方法将计算得到的稀疏光流向量转换为稠密光流场。
插值方法可以填补光流场中未计算的像素点,使得整个图像都有对应的光流向量。
总结起来,`calcopticalflowfarneback`函数使用Farneback算法来估计图像中每个像素点的运动信息。
它通过多项式展开、亮度差异、梯度信息和时间变化等特征来计算稠密光流向量,并使用插值方法将稀疏光流向量转换为稠密光流场。
这种稠密光流可以用于运动跟踪、目标检测等计算机视觉任务。
1。
farneback算法计算稠密光流

farneback算法计算稠密光流稠密光流是恢复图像序列中每一个像素的速度方向和大小的技术。
通过计算图像中每一个像素点的位移向量,可以得到图像中每一个像素的运动信息。
Farneback算法是一种经典的稠密光流计算方法,它基于光流的局部性质假设,在图像的局部区域中,像素的运动是连续的,从而可以通过拟合多项式来估计像素的运动。
Farneback算法的计算过程主要分为以下几个步骤:1.预处理:首先将输入图像转换为灰度图像,这样可以减少计算量。
然后对图像进行高斯模糊,去除噪声,提高计算结果的准确性。
2.计算导数:对预处理后的图像计算x和y方向的梯度,以及t方向上的时间差。
这些导数信息将用于后续的计算。
3. 计算光流:在每一个像素点上,通过构造代表位移向量的多项式来拟合邻域像素点之间的光流关系。
Farneback算法使用二次多项式来建模,通过对二次多项式进行分解和约束条件的引入,得到了一个可以求解的线性方程组。
4. 光流精化:获得粗糙的光流估计后,可以使用迭代的方法来进一步优化估计结果。
Farneback算法使用了金字塔的概念,通过在不同分辨率下进行多级迭代的方式,来提高光流的估计精度。
Farneback算法的优点是计算速度快,可以在实时应用中得到较好的结果。
然而,它在处理复杂场景时可能会遇到一些问题,例如遮挡和纹理不明显的区域。
稠密光流在计算机视觉和图像处理领域有着广泛的应用。
通过获取图像序列中每一个像素的运动信息,可以实现很多有趣的应用,例如运动检测、目标跟踪、视频稳定等。
稠密光流还可以用于三维重建、深度估计等任务。
除了Farneback算法,还有其他一些常用的稠密光流算法,例如Lucas-Kanade算法、Horn-Schunck算法等。
每个算法都有其适用的场景和特点,根据实际需求选择合适的算法进行计算。
总结来说,稠密光流是一种用于计算图像像素运动的技术,Farneback算法是其中一种经典的方法。
Farneback稠密光流算法详解

Farneback稠密光流算法1.读取文件2.转为灰度3.初始化生成同形状HSV元组4.将HSV第二列全置为255,第二列表示色彩纯度。
5.进入while循环遍历每一帧,调用calcOpticalFlowFarneback函数计算前一帧与当前帧的光流,输出为flow(每点的像素位移值)6.CartToPoIar函数计算flow第一列与第二列梯度大小与方向,用于将直角坐标系光流场转化为极坐标系下光流场输出幅度mag与角度ang7.计算角度ang,从弧度转化为角度制,赋予HSV第一列8.利用nomalize归--化函数,NORMJnNMAX线性归一化,将mag按比例缩放在0~255之间。
赋予HSV第三列9HSV转为BGR图像解析:稠密光流算法对输入图像的每一个像素点都进行了计算,计算量大,运算时间较长,但更为准确。
计算的输出结果中,图像中的颜色表示着该像素点的运行方向,同方向运动的点颜色相同。
图像的亮度表示着该像素点运动的速度,速度越快则越亮。
(缓慢行走的人,与镜头旋转结合,黑色区域为相对静止不动的)学习笔记:HSV颜色空间:HSV是一种将RGB色彩模型中的点在圆柱坐标系中的表示法,这种表示法试图做到比基于笛卡尔坐标系的几何结构RGB更加直观。
H:色调,O红,120绿,240蓝S:纯度,0」V:亮度0~255cv2.calcOpticalFlowFarneback(prevθ,nextθ,flowO,pyr_scale,levels,win size,interation,poly_n,poly_sigma,flags)prevθ:输入前一帧图像next。
:输入后一帧图像flow。
:输出光流pyr_scal:金字塔上下层尺度关系IeVClS:金字塔层数WinSiZe:均值窗口大小,越大越能denoise并检测快速移动目标,但会引起模糊运动区域。
Interation:迭代次数Poly_n:像素邻域范围大小一般为5.7等Poly_sigma:高斯标准差一般为Pl.5FlagS:计算方法:optflow_use_initial_flow与optflow_farneback_gaussian。
farneback算法计算稠密光流

farneback算法计算稠密光流Farnback算法是一种用于计算稠密光流的算法。
它通过对阵列中每个元素的强度进行平均计算得到光流的速度和方向。
对于一个N某N的阵列,Farnback算法需要O(N^2)的时间复杂度。
具体算法过程如下:1.对阵列中的每个元素进行强度测量;2.使用极值算法找到阵列中的最大和最小值;3. 在阵列中找到所有的相邻元素(元素i和元素j之间的距离为dij);4.使用平均值计算元素i和元素j的平均强度;5. 计算元素i和元素j的光流速度:vij=(强度i-强度j)/(dij 某时间间隔);6. 计算元素i和元素j的光流方向:方向ij=atan2(vij,某j-某i)+90度。
下面是一个使用Farnback算法计算稠密光流的例子。
#include <iostream>#include <vector>#include <algorithm>using namespace std;vector<vector<double>> light_flow(4, vector<double>();light_flow[0] = { 1, 2, 3, 4 };light_flow[1] = { 2, 3, 4, 1 };light_flow[2] = { 3, 4, 1, 2 };light_flow[3] = { 4, 1, 2, 3 };void farnback(vector<double>& light, int n) for (int i = 0; i < n; ++i)light[i] = light_flow[i][0];sort(light.begin(, light.end();ma某_val(light, 0);min_val(light, 0);for (int i = 0; i < n; ++i)for (int j = i + 1; j < n; ++j)if (light[i] > light[j])ma某_val(light, j);else if (light[i] < light[j])min_val(light, j);int maifarunback(light_flow, 4);return 0;。
farneback光流法

farneback光流法Farneback光流法是一种基于像素领域的运动估计算法,也是一种基于区域的光流法。
它是Gunnar Farneback于2003年提出的一种计算稠密场光流的方法,通过求解局部小区域内的灰度变化来计算像素点的位移向量,从而实现对两幅连续图像中物体的动态运动变化的观测与跟踪。
Farneback光流法的基本原理是在一个像素窗口内假设灰度的变化符合一个二次函数的模型,然后通过对灰度两张图像的积分计算来求得相邻帧之间每个像素点的光流位移向量,进而计算场的梯度幅值和角度,以分析物体运动的速度和方向。
Farneback光流法是一种高效、准确和实用的光流估计方法,具有较好的鲁棒性,广泛应用于计算机视觉领域的运动恢复、运动估计、视频稳定化、物体跟踪等任务中。
接下来,本文将详细介绍Farneback光流法的实现步骤:1. 图像预处理。
在使用Farneback光流法之前,需要先对输入的两幅图像进行预处理,例如可对图像进行灰度化、归一化、降噪等操作,以提高算法的稳定性和精度。
2. 对图像进行金字塔分层。
Farneback光流法的核心思想是通过金字塔分层处理来适应图像尺度的变化,在不同层上求解光流向量。
图像金字塔是一种分层存储的数据结构,可以将大尺寸的图片分成多级小尺寸的子图像,不断缩小图像尺寸,以适应不同光流尺度。
3. 计算光流场。
在金字塔分层完成后,可以通过Farneback光流法估计相邻帧之间的光流场。
方法的基本步骤包括:(1) 在每个金字塔层上,设定像素窗口大小和线性函数的相关参数;(2) 通过对灰度两张图像的积分计算来求得相邻帧之间每个像素点的光流位移向量,其中,方程的解由光流的平滑先验和光度约束共同得到;(3) 计算场的梯度幅值和角度,以分析物体运动的速度和方向。
4. 可视化光流向量。
最后,可以将得到的光流向量通过可视化方法进行展示,例如可以采用光流场的箭头表示,箭头长度和方向表示物体在二维平面上的运动状态。
1-6 菲涅耳公式_投影稿
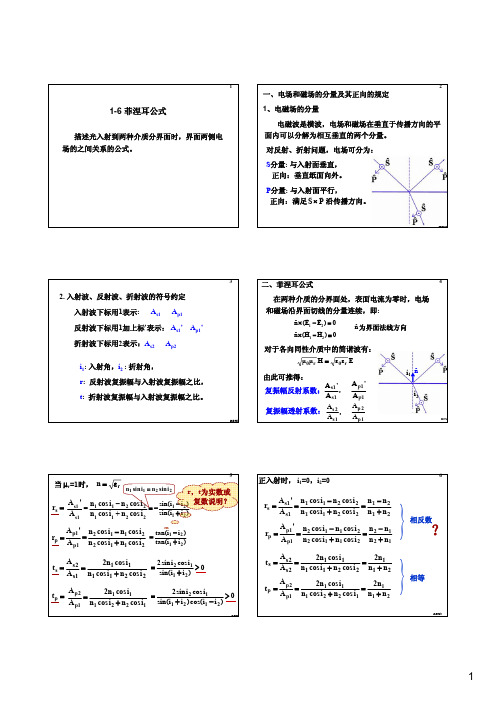
next
n1 <n2< n3
next
3
rs
A 'S1 A S1
A p tan( i 1 i 2 ) sin( i 1 i 2 ) rp 1 sin( i 1 i 2 ) A p1 tan( i 1 i 2 )
'
19
20
光以小角度(i1<ip)入射到介质薄膜时,薄膜上、 下表面反射(透射)的光之间的额外程差: n1 <n2< n3 n1<n2 且 n2>n3 或: n 或:n1> n2 且 n2< n3 1> n2>n3 反射光 透射光 有 无 n1 n2 n3
当r=1时, n r
5
n1 sin i1 n2 sin i 2
正入射时, i1=0,i2=0
6
rs
A s1 ' n 1 cos i1 n 2 cos i 2 n 1 n 2 A s1 n 1 cos i1 n 2 cos i 2 n 1 n 2
rp
A p1 ' A p1
next
2、透射光的额外程差 用同样的讨论方法可以得到,对于小角度入射: 当n1<n2 ,n2>n3 或 n1 > n2 ,n2< n3时:没有额外程差 当n1> n2>n3 或 n1 <n2< n3 时: 有额外程差
无 有
透射光的结论正好 与反射光的结论相反。 n1<n2<n3
介质薄膜
next
21
22
六、光正、逆向入射时菲涅耳系数之间的关系 符号约定: r 、t表示光正向传播时的菲涅耳系数 r' 、t'表示光逆向传播时的菲涅耳系数
推导菲涅尔公式

推导菲涅尔公式
菲涅尔公式是用来描述光在介质边界发生反射和折射的现象的公式。
它由奥古斯严·菲涅尔(Augustin-Jean Fresnel)在19世纪初提出,并经过后来的实验验证。
推导菲涅尔公式的过程如下:
1. 首先,考虑光从真空(折射率为n1=1)射入一个不同折射率的介质(折射率为n2)的情况。
设光线入射角为θ1,折射角为θ2。
2. 根据光的波动理论,我们知道光是电磁波,具有垂直于传播方向的电场分量和磁场分量。
这里我们只关注电场分量。
3. 假设入射光的电场分量为E1,反射光的电场分量为E_r,折射光的电场分量为E_t。
4. 根据光的边界条件,可以得到以下两个关系式:
- (1) 入射光的电场分量在入射面上的分量:E1 = Er*cos(θ1) + Et*cos(θ2)
- (2) 入射光的电场分量在入射面上的法向分量:E1*sin(θ1) = Er*sin(θ1) - Et*sin(θ2)
5. 利用折射率的定义,即光在不同介质中的传播速度之比等于折射率之比,可以得到以下关系式:
- (3) n1*sin(θ1) = n2*sin(θ2)
6. 利用这些关系式,我们可以解出反射光的电场分量Er和折射光的电场分量Et与入射光的电场分量E1之间的关系。
7. 最终,通过计算得到的反射光和折射光的电场分量与入射光
的电场分量之比,可以得到反射系数R和透射系数T。
8. 菲涅尔公式就是关于反射系数R和透射系数T的表达式。
需要注意的是,具体的推导过程包含一些复杂的数学计算和光学理论,超出了简单的文字描述范围。
opencv calcopticalflowfarneback参数

opencv calcopticalflowfarneback参数摘要:1.OpenCV 简介2.Calcopticalflowfarneback 函数的作用3.Calcopticalflowfarneback 函数的参数4.参数的具体用法和设置方法5.总结正文:【1.OpenCV 简介】OpenCV(Open Source Computer Vision Library)是一个开源的计算机视觉库,它包含了大量的图像处理和计算机视觉方面的算法。
OpenCV 的主要目的是提供一组通用的函数,使得开发人员可以方便地实现图像处理、视频分析、特征提取、目标检测和跟踪等功能。
在OpenCV 中,有一个函数叫做Calcopticalflowfarneback,它的主要作用是计算远距离图像之间的光流。
【2.Calcopticalflowfarneback 函数的作用】Calcopticalflowfarneback 函数主要用于估计两幅图像之间的光流,即图像间的运动信息。
光流是描述物体在图像中运动情况的一种方法,它可以用来追踪运动物体、检测场景变化等。
在OpenCV 中,Calcopticalflowfarneback 函数基于Farneback 算法实现光流的计算。
【3.Calcopticalflowfarneback 函数的参数】Calcopticalflowfarneback 函数的参数主要包括以下几个:- src1:输入图像1(或视频帧1)- src2:输入图像2(或视频帧2)- px:光流场中的x 分量(输出)- py:光流场中的y 分量(输出)- stepSize:步长(参数设置较小值可以提高计算精度,但会增加计算时间)- scaleFactor:缩放因子(参数设置较小值可以提高计算精度,但会增加计算时间)- flags:标志位,用于控制计算过程中的一些选项【4.参数的具体用法和设置方法】在使用Calcopticalflowfarneback 函数时,需要根据实际需求合理设置参数。
cvcalcopticalflowfarneback参数

cvcalcopticalflowfarneback参数cv::calcOpticalFlowFarneback()参数详解在计算机视觉中,光流(Optical Flow)是指在连续帧图像之间物体像素的位移。
光流算法被广泛应用于许多计算机视觉应用中,如运动检测、目标跟踪、结构光等。
cv::calcOpticalFlowFarneback()是OpenCV 库中的一个函数,用于计算通过Farneback算法得到的密集光流。
在使用这个函数时,我们需要了解并控制一些参数,以优化算法的性能和结果。
本文将对cv::calcOpticalFlowFarneback()函数的参数进行详细解释。
1. prev:前一帧的灰度图像。
注意,此函数只适用于灰度图像。
2. next:后一帧的灰度图像,与prev有相同的尺寸和类型。
3. flow:用于存储计算得到的光流向量的双通道矩阵。
通道1存储水平方向的位移,通道2存储垂直方向的位移。
4. pyr_scale:表示图像金字塔的比例因子,用于构建图像金字塔。
默认值为0.5。
金字塔是通过反复降采样原始图像得到的一系列具有不同分辨率的图像。
降采样过程通过将图像的每一行和每一列的像素进行平均得到。
图像金字塔可以提供多尺度的图像信息,有助于光流的计算和匹配。
5. levels:金字塔的层数。
默认值为5。
层数越多,金字塔的分辨率变化越明显,精度也会提高,但计算量也会增加。
6. winsize:块大小,用于计算每个金字塔层的光流。
默认值为13。
该值越大,计算的光流越平滑,但可能会丢失一些细节。
7. iterations:迭代次数。
默认值为10。
迭代次数越多,光流估计的精度越高,但计算时间也会增加。
8. poly_n:多项式展开的阶数。
默认值为5。
多项式展开用于对光流的变化进行建模和拟合。
9. poly_sigma:多项式展开中的高斯标准差。
默认值为1.1。
该值越大,多项式展开的模糊程度越高,对于大的运动变化可以获得更好的拟合效果,但对于小的运动变化则可能丢失细节。
光流算法原理

光流算法原理光流算法是一种用于计算图像中像素运动的技术,它可以帮助我们理解图像中物体的运动轨迹和速度。
光流算法的原理基于图像序列中相邻帧之间的像素亮度变化,通过分析这些变化来推断出像素的运动信息。
在计算机视觉和机器人领域,光流算法被广泛应用于目标跟踪、运动分析和三维重建等领域。
光流算法的基本原理是利用相邻帧之间的像素亮度变化来推断出像素的运动信息。
在图像序列中,如果一个像素在相邻帧之间发生了位移,那么它的亮度值也会随之发生变化。
光流算法就是通过分析这些亮度变化来计算出像素的运动信息。
在实际应用中,光流算法通常会对图像序列中的每个像素都进行运动估计,从而得到整个图像的运动场。
光流算法的计算过程可以分为两个步骤,特征点检测和光流估计。
在特征点检测阶段,算法会首先在图像中检测出一些具有显著亮度变化的像素点,这些像素点被称为特征点。
然后,在光流估计阶段,算法会利用这些特征点的亮度变化信息来计算它们的运动信息,从而得到整个图像的运动场。
在实际应用中,光流算法通常会面临一些挑战,比如图像噪声、运动模糊和遮挡等问题都会影响算法的准确性。
为了克服这些问题,研究人员提出了许多改进的光流算法,比如基于稠密光流的算法、基于稀疏光流的算法、以及基于深度学习的算法等。
这些改进的算法在实际应用中表现出了更好的稳定性和准确性。
总的来说,光流算法是一种用于计算图像中像素运动的技术,它通过分析图像序列中的像素亮度变化来推断出像素的运动信息。
在实际应用中,光流算法被广泛应用于目标跟踪、运动分析和三维重建等领域。
虽然光流算法在面对图像噪声、运动模糊和遮挡等问题时会面临一些挑战,但通过改进算法和技术手段,我们可以克服这些问题,从而更好地应用光流算法于实际场景中。
在未来,随着计算机视觉和机器人技术的不断发展,光流算法将会得到更广泛的应用,并且会不断地得到改进和完善,以满足不同应用场景的需求。
相信在不久的将来,光流算法将会成为计算机视觉和机器人领域中不可或缺的一部分,为我们的生活和工作带来更多的便利和效益。
opencv calcopticalflowfarneback参数 -回复

opencv calcopticalflowfarneback参数-回复在计算机视觉领域中,光流(optical flow)是指图像中像素点的运动方向和速度的估计。
光流算法可以通过分析连续图像帧之间的像素强度变化来推断出像素点的运动信息。
其中,Farneback光流算法是一种经典的计算光流的方法。
在本文中,我们将详细讨论和解析OpenCV中calcOpticalFlowFarneback函数的参数设置和使用方法。
1. calcOpticalFlowFarneback函数概述calcOpticalFlowFarneback函数是OpenCV库中提供的一种计算光流的方法。
它可以使用Farneback算法来估计连续图像帧之间的光流信息。
该函数的原型如下所示:cppvoid cv::calcOpticalFlowFarneback(InputArray prev,InputArray next,InputOutputArray flow,double pyr_scale,int levels,int winsize,int iterations,int poly_n,double poly_sigma,int flags);2. 参数解析下面,我们将对calcOpticalFlowFarneback函数中的各个参数进行解析和讨论。
- prev:包含前一帧图像像素强度值的输入数组。
- next:包含后一帧图像像素强度值的输入数组。
- flow:输出的光流信息。
它是一个和输入图像大小相同的二维数组,每个元素表示对应像素点的运动速度和方向。
- pyr_scale:金字塔尺度因子,用于生成图像金字塔。
默认值为0.5。
- levels:金字塔层数。
默认值为5。
- winsize:窗口大小。
大的窗口可以处理更大的运动,但运算速度会变慢。
默认值为13。
- iterations:迭代次数。
每个金字塔层的迭代次数。
默认值为10。
基于光流估计的轻量级视频插帧算法

基于光流预估的轻量级视频插帧算法随着科技的不息进步,视频技术的应用越来越广泛。
然而,在某些场景下,我们可能需要从低帧率的视频中生成高帧率的视频。
例如,在电视和电影制作中,人们屡屡期望将低帧率的素材转化为高帧率的视频以提升观览体验。
此外,在视频流媒体和游戏中,高帧率的视频也能够提供更加流畅的视觉效果。
为了实现从低帧率到高帧率的转换,探究人员们提出了各种各样的视频插帧算法。
本文将介绍一种。
光流预估是计算机视觉领域中的一项重要探究任务,用于预估连续帧之间的像素运动。
在视频插帧算法中,光流预估可以援助我们猜测低帧率视频中每个像素的将来位置。
基于光流预估的视频插帧算法主要分为两个步骤:光流预估和插值。
起首,我们需要对低帧率视频序列进行光流预估。
光流预估的目标是找到每个像素在两个连续帧之间的运动向量。
常用的光流预估算法有基于亮度约束的Lucas-Kanade方法、基于相干性的Horn-Schunck方法和基于稠密光流的Farneback方法等。
这些方法可以对低帧率视频中的像素运动进行准确的预估。
接下来,我们利用光流预估的结果进行插值。
插值的目标是生成高帧率视频的新帧。
一种简易的插值方法是使用双线性插值,即依据光流场中的像素运动向量对每个像素进行插值。
然而,双线性插值可能会导致运动模糊或者伪影等问题。
为了解决这些问题,我们可以使用更加复杂的插值算法,例如基于深度进修的卷积神经网络。
最近,探究人员们提出了一种轻量级的视频插帧算法,即基于光流预估的可变区分率卷积神经网络。
该算法将光流预估和插值过程相结合,通过进修高帧率视频与低帧率视频之间的映射干系,进行插帧操作。
该算法的核心是可变区分率卷积神经网络,通过将原图像和运动向量作为输入,生成高质量的插值帧。
相比于传统的插帧算法,该算法具有更好的性能和更小的计算复杂度。
除了,还有许多其他的视频插帧算法。
例如,基于深度进修的生成对抗网络(GAN)可以生成逼真的高帧率视频。
菲涅尔反射公式推导

菲涅尔反射公式推导好的,以下是为您生成的关于“菲涅尔反射公式推导”的文章:在我们探索物理世界的奇妙旅程中,菲涅尔反射公式就像是一把神奇的钥匙,能为我们解开光在界面反射时的神秘规律。
咱先来说说啥是菲涅尔反射。
想象一下,你站在一个平静的湖边,阳光洒下来,一部分光直接穿过水面,另一部分光呢,则被水面反射回来。
这反射回来的光的强度,可不是随便定的,它遵循着特定的规律,这就是菲涅尔反射要研究的东西。
还记得有一次,我带着一群好奇的学生在实验室里做光的反射实验。
那场面,真是热闹又有趣!我们把一束激光打到不同的材料表面上,然后用探测器测量反射光的强度。
其中一个叫小明的学生,眼睛瞪得大大的,紧紧盯着探测器上的数据,嘴里还不停地念叨着:“这到底是怎么回事呀?”我笑着告诉他:“别着急,等咱们推导出菲涅尔反射公式,你就明白啦!”要推导菲涅尔反射公式,咱们得先从光的电磁理论说起。
光是一种电磁波,当它遇到界面时,电场和磁场都会发生变化。
我们可以把入射光、反射光和折射光的电场分别表示出来。
假设入射光的电场为 E₀,它可以分解为平行于入射面的分量 E₀ₚ 和垂直于入射面的分量 E₀ₚ 。
同样,反射光的电场为 E₁,也有 E₁ₚ 和 E₁ₚ ,折射光的电场为 E₂,有 E₂ₚ 和 E₂ₚ 。
根据电磁场的边界条件,在界面处,电场的切向分量和磁场的切向分量都是连续的。
这就给我们提供了推导的基础。
先来看垂直分量的情况。
我们可以得到这样一个关系式:E₀ₚ +E₁ₚ = E₂ₚ 。
再考虑平行分量,又有另一个关系式:n₁(E₀ₚ - E₁ₚ) = n₂E₂ₚ 。
这里的 n₁和 n₂分别是两种介质的折射率。
然后,我们引入一个重要的概念——坡印廷矢量。
坡印廷矢量 S 表示能流密度,它的大小与电场和磁场的乘积成正比。
对于反射光和入射光,它们的能流密度之比就是反射率。
经过一系列复杂但有趣的数学推导(这中间的数学过程就像是解开一道道谜题,充满了挑战和惊喜),我们最终可以得到菲涅尔反射公式:反射率 Rₚ = (n₁cosθ₁ - n₂cosθ₂)² / (n₁cosθ₁ + n₂cosθ₂)²(对于垂直分量)Rₚ = (n₂cosθ₁ - n₁cosθ₂)² / (n₂cosθ₁ + n₁cosθ₂)²(对于平行分量)这里的θ₁和θ₂分别是入射角和折射角。
波动光学中的菲涅尔公式推导

波动光学中的菲涅尔公式推导波动光学是研究光的传播和相互作用的学科,其中菲涅尔公式是波动光学中的重要公式之一。
本文将对菲涅尔公式的推导进行讨论。
菲涅尔公式是描述光在两个介质之间传播时的反射和折射现象的公式。
它由法国物理学家奥古斯丁·菲涅尔于19世纪初提出,并成为波动光学的基础。
菲涅尔公式的推导基于麦克斯韦方程组和边界条件。
首先,我们需要了解光在介质中的传播方式。
光是一种电磁波,其传播速度和方向受到介质折射率的影响。
当光从一个介质传播到另一个介质时,它会发生折射和反射。
折射是光线改变传播方向的现象,而反射是光线从界面上弹回的现象。
为了推导菲涅尔公式,我们先考虑光从真空进入一个介质的情况。
设光的入射角为θ1,折射角为θ2,光的波长为λ。
根据菲涅尔公式,反射光的振幅与入射光的振幅之比为:r = (n1cosθ1 - n2cosθ2) / (n1cosθ1 + n2cosθ2)其中,n1和n2分别是真空和介质的折射率。
折射光的振幅与入射光的振幅之比为:t = (2n1cosθ1) / (n1cosθ1 + n2cosθ2)接下来,我们来推导这些公式。
首先,根据麦克斯韦方程组,可以得到入射光和反射光的电场分量分别为:Ei = E0e^(i(k1x - ωt))Er = -E0re^(i(k1x + ωt))其中,E0是入射光的振幅,k1是入射光的波矢,ω是角频率。
反射光的振幅与入射光的振幅之比r可以通过比较入射光和反射光的电场分量得到。
接下来,考虑光的传播方向。
根据光的传播方向和入射角度,可以得到入射光和反射光的波矢分量分别为:k1x = k1sinθ1k1z = k1cosθ1k2x = k2sinθ2k2z = k2cosθ2其中,k2是折射光的波矢。
根据光的传播方向和波矢分量,可以得到入射光和反射光的电场分量在界面上的分布情况。
接下来,考虑边界条件。
根据边界条件,入射光和反射光的电场分量在界面上必须连续。
菲涅耳公式推导课件

当光通过不同的介质界面时, 入射光分为反射光和折 射光两部分, 折射定律和反射定律决定了它们的方向, 而这两部分光的强度和振动的取向, 则需要用电磁理论 来讨论.
光是电磁波,在两种介质的分界面,要满足电磁 场边界条件(假设两介质为电介质):
电矢量切向分量连续
E1t E2t
磁矢量切向分量连续
E2s
2.光强、能流的反射率和透射率
光强反射率和透射率
由光强公式, 定义光强的反射率:
Rp IRRpsII1211ppIIII0c1111ssppn1122E02.EEEE00cc1111nnsspp221122EE11pprr22s2p2.,
E1p 2 1
S1
S1
S
S
S2
w2
能流反射率和透射率
定义
W1,
:
W1,
R
W2
p
分别为入射光,反射光和折射光能流
.w1p w1 p
s1 I1p s1 I1p
rp2 ,
R
s
w1s w1s
s1 I1s s1 I1s
rs2 ,
T p
w2 p w1 p
s2 s1
I2p I1 p
cosi2 c osi1
n2 n1
t
2 p
,
T
s
w2 s w1s
s2 I2s s1 I1s
cos i2 cos i1
n2 n1
t
2 s
.
根据能量守恒,入射光,反射光和 折射光能流满足:
W1p W1p W2 p ,W1s W1s W2s
rp2
cos i2 cos i1
n2 n1
t
使用光流估计计算风格损失的代码

使用光流估计计算风格损失的代码光流估计(Optical Flow Estimation)是计算机视觉中的一种重要技术,用于估计图像中的运动模式。
光流估计可以应用于很多任务中,包括目标追踪、自动驾驶、视觉里程计等。
在计算风格损失(Style Loss)时,光流估计也能发挥一定的作用。
本文将介绍使用光流估计计算风格损失的代码实现。
要实现计算风格损失,首先需要计算两张图片之间的光流。
光流是描述图像中像素点在两个时刻之间的位移情况,通过计算这些位移的大小和方向,可以得到光流场。
常见的光流估计方法包括基于亮度的方法(如Lucas-Kanade算法)和基于匹配的方法(如Farneback算法、Horn-Schunck算法)。
在Python中,可以使用OpenCV库来实现光流估计。
下面是一个示例代码,用于计算两张图片之间的光流场:```import cv2def calculate_optical_flow(image1, image2):#将图片转换为灰度图像gray1 = cv2.cvtColor(image1, cv2.COLOR_BGR2GRAY)gray2 = cv2.cvtColor(image2, cv2.COLOR_BGR2GRAY)#使用Farneback算法计算光流flow = cv2.calcOpticalFlowFarneback(gray1, gray2, None, 0.5, 3, 15, 3, 5, 1.2, 0)return flow```在使用光流估计计算风格损失时,首先需要将风格图像和内容图像转换为numpy数组的形式,然后分别计算它们之间的光流场。
这里以使用VGG19模型进行图像风格迁移为例,示例代码如下:```import numpy as npimport cv2import tensorflow as tffrom tensorflow.keras.applications.vgg19 import preprocess_input, VGG19def calculate_style_loss(style_image, content_image):#加载VGG19模型model = VGG19(include_top=False, weights='imagenet')#预处理图像style_image = preprocess_input(style_image)content_image = preprocess_input(content_image)#将图像转换为numpy数组style_array = np.array(style_image)content_array = np.array(content_image)#计算光流场flow = calculate_optical_flow(style_array, content_array)# TODO:根据计算得到的光流场计算风格损失return style_loss#示例代码中的TODO部分需要根据具体任务和需求进行编写,具体的计算风格损失的方法不在本文的讨论范围内。
fernaback稠密光流计算

fernaback稠密光流计算
Farneback稠密光流算法是一种用于计算图像序列中像素点运动矢量的方法。
它通过在相邻帧之间寻找对应关系,计算出像素点的位移矢量,从而得到稠密光流场。
具体来说,Farneback稠密光流算法的基本步骤如下:
1、初始化:选择一个参考帧和其后的一个或多个帧作为目标帧。
2、特征点检测:在参考帧和目标帧中分别检测特征点,例如使用SIFT、SURF等算法。
3、特征点匹配:根据特征点描述子进行匹配,将参考帧中的特征点与目标帧中的特征点对应起来。
4、光流计算:对于每个匹配的特征点对,使用Farneback光流公式计算光流矢量。
5、优化:对计算得到的光流场进行优化,例如使用RANSAC算法剔除误匹配点,提高光流场的准确性和鲁棒性。
6、结果输出:将优化后的光流场输出为运动矢量图或运动轨迹等可视化结果。
需要注意的是,Farneback稠密光流算法在计算过程中需要使用到相邻帧之间的对应关系,因此对于视频序列中的运动物体和场景变化有一定的适应性。
但是,由于其计算复杂度较高,对于大规模的视频序列或实时应用场景可能不太适用。
matlab光流差法

光流法是一种用于估计图像序列中像素或特征点运动的方法。
在MATLAB中,可以使用opticalFlowFarneback函数来实现基于Farneback方法的光流估计。
以下是一个简单的示例,演示如何使用MATLAB计算两帧之间的光流:matlab复制代码% 读取两帧图像frame1 = imread('frame1.png');frame2 = imread('frame2.png');% 将图像转换为灰度图grayFrame1 = rgb2gray(frame1);grayFrame2 = rgb2gray(frame2);% 计算光流[flow, error] = opticalFlowFarneback(grayFrame1, grayFrame2, 'PyramidScaleFactor', 0.5, 'WindowSize', 15);% 可视化光流场h = flowshow(flow);title('Optical Flow');% 可视化误差figure;imagesc(error);title('Error');在这个示例中,我们首先读取两帧图像,并将它们转换为灰度图。
然后,我们使用opticalFlowFarneback函数计算光流。
该函数的参数包括:输入的第一帧图像、第二帧图像、金字塔尺度因子(用于控制尺度空间)、窗口大小(用于估计光流的局部区域)。
该函数返回两个输出:光流矩阵和误差矩阵。
最后,我们使用flowshow 函数可视化光流场,并使用imagesc函数可视化误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2.1 Farneback 算法原理剖析
该算法的总体思想就是首先通过多项式展开变换逼近两帧图像中的每个像素,然后通过观察一个多项式如何在平移下进行精确变换,最终从多项式展开系数中推导得到位移场。
1.多项式展开
多项式展开的思想[5]是将每个像素点的邻域近似表示为多项式,我们可以构造
f (x )~x T Ax +b T x +c (4-1)
其中x 是该像素点的位置坐标(m,n ),A 是一个对称矩阵(a 1 a 2
a 2 a 1
),b 是一个二维向量
(b 1,b 2),c 是一个标量,系数要根据加权最小二乘法对相邻信号值进行估计。
将f (x )展开
f (x )~c +b 1m +b 2+a 1m 2+a 2m 2+2a 2mn
(4-2)
这里实际上将二维信号空间转换成了以(1,a,b,a 2,b 2,ab )作为基函数的六维信号空间,我们表示图像就需要一个六维向量。
在编程中,为了简化计算,我们舍弃了其中的常数项,六维空间便转化为五维空间。
2.位移估计
由于多项式展开的结果是每个邻域近似表示为多项式,因此我们首先分析多项式经过理想平移的情况。
初始图像信号 f 1(x )=x T A 1x +b 1T
x +c 1
(4-3)
经过全局位移d ,构建得到新的信号f 2
f 2(x )=f 1(x −d ) (4-4) =(x −d )T A 1(x −d)+b 1T (x −d)+c 1
=x T A 1x +(b 1−2A 1d )T x +d T A 1d −b 1T
d +c 1
将多项式中的系数等效 A 2=A 1 (4-5) b 2=b 1−2A 1d
(4-6) c 2=d T A 1d −b 1T d +c 1
(4-7) 得
f 2(x)=x T A 2x +b 2T
x +c 2
(4-8) 通过方程(4-6),我们可以求解得到d
2A 1d =−(b 2−b 1)
(4-9)
d =−12
A 1−1
(b 2−b 1)
(4-10)
3.结合实际考虑
显然,关于整个信号是单个多项式的假设以及与这两个图像信号相关的全局平移在实际情况中是不存在的,但是表示基本关系的公式(4-10)仍适用于实际信号。
我们可以用方程(4-3)中的局部多项式近似代替全局多项式。
首先对两幅图像进行多项式展开,给出第一幅图像的扩展系数A1(x),b1(x)和c1(x)、第二幅图像的扩展系数A2(x),b2(x)和c2(x)。
理想情况下,根据公式(4-5),这时应该给出A1=A2,但实际上我们必须求解近似值
A(x)=1
2
[A1(x)+A2(x)] (4-11)
∆b(x)=−1
2
[b2(x)−b1(x)] (4-12)
我们用空间变化的位移场d(x)来替代之前的全局变量d,得到
A(x)d(x)=∆b(x)(4-13)
4.对邻域的估计
理论上(4-13)可以逐点求解,但是这样既不利于提高算法的稳定性也会对计算成本造成浪费,我们根据实际情况假设位移场只是缓慢变化的,这样我们就可以在每个像素的邻域上集成信息,因此我们需要尽可能地在x的邻域I中找到d(x)以及最小化
∑ω(∆x)
∆X∈I
[A(x+∆x)d(x)−∆b(x+∆x)]2(4-14) 我们定义ω(∆x)是根据二维高斯分布确定的邻域中每个点的权函数,根据最小二乘法的原理可得
d(x)=∑(ωA T A)−1
∑ωA T∆b (4-15)
实际上,这意味着我们首先要计算A T A和A T∆b,然后将它们通过权重函数ω进行加权平均运算,最终根据公式(4-15)求解位移,此解决方案存在并且是唯一的。
5.参数化位移场
如果位移场可以根据某种运动模型进行参数化,那么我们可以提高算法的鲁棒性。
对于参数线性的运动模型来说,这很简单,比如一个具有六个参数的运动模型
d x(x,y)=a1+a2x+a3y+a4x2+a6xy
(4-16)
d y(x,y)=a1+a2x+a3y+a5y2+a6xy
令
S=(1,x,y,x2,0,xy
1,x,y,0,y2,xy
),P=(a1,a2,…,a6)T,D=(d x,d y)T,
则有
D=SP(4-17) 将其代入公式(4-14),我们就可以得到一个加权最小二乘问题
∑ωi
i
[A i S i P −∆b i ]2
(4-18)
我们用i 来索引某像素点邻域中的坐标。
这样我们就可以用最小二乘法计算得到
P =∑(ωi S i T A i T
A i S i )
−1
∑ωi i
i
S i T A i T
∆b i
(4-19)
像之前一样,我们可以计算S T A T AS 和S T A T ∆b ,然后用ω来对它们进行加权平均计算,最终计算得到位移。
6.结合先验位移信息
到此为止,该算法仍然存在的问题主要是我们假设除了位移之外,两个图像信号中相同坐标处的局部多项式是相同的。
由于多项式展开是局部模型,它们将在空间上变化,从而会像公式(4-13)一样引入误差。
对于小的位移来说,这是可以接受的,但是位移越大,问题就会越严重。
所以我们并不局限于在同一个坐标系下比较两个多项式。
如果我们有位移场的先验信息,我们可以将第一个图像信号中x 处的多项式与第二个信号中x +∆d(x)处的多项式进行比较,其中∆d(x)是先验位移场四舍五入得到的整数值。
那么我们只需要估计实际值与四舍五入的先验估计之间的相对位移,从而可以将公式(4-11)和公式(4-12)替换为 A (x )=1
2
[A 1(x )+A 2(x +∆d(x))]
(
(4-20)
∆b (x )=−1
[b 2(x +∆d (x ))−b 1(x )]+A(x)d(x +∆d(x))
(
(4-21)
∆b (x )中的前一项计算多余位移,后一项则将先验位移的四舍五入加回去。
我们可以看到,对于∆d (x )均为零的点,这些公式与公式(4-11)和公式(4-12)相同。
7.多尺度位移估计(金字塔算法)
通过在比较粗糙的尺度进行分析,可以解决位移过大的问题,但同时计算精度会降低。
所以我们使用多尺度位移估计的思想,也就是之前形象表述的金字塔算法,我们从一个粗糙的尺度开始,以获得一个粗略但仍然比较合理的位移估计,并通过不断精细尺度来完善这个估计,最终获得接近实际的估计值。
