一二三元相图
第五章 三元相图

D a2 a1
C
课堂练习
• 绘出C / B =1/3的合金
C 1 25% B 3 75%
B
90 10 20 30 40
80
70
60 • 绘出A / C = B% 50 1/4的合金 40 30 20 10 A 90 80 70 60 50 40 ← A%
50
C%
B
10 20 30 40
80
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
课堂练习
• 确定合金I、II、 III、IV的成分
II点: A%=20% B%=50% C%=30% 70 60 B% 50 40 30 20 10 A 90 80 70 60 90
B
10 20 30 40 II
课堂练习
90 • 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
课堂练习
90 • 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B
10 20 30 40
50
C%
60
70 80
90 50 40 ← A% 30 20 10 C
2. 浓度三角形中具有特定意义的直线
90 80 70
B 10 20 30 40 50
三元系统相图

三元系统相图
一、三元系统相图概述
三元凝聚系统相律: F=C-P+1=4-P
1、三元系统组成表示方法
——浓度(组成)三角形 应用: 1)已知点 的位置, 确定其组成; 2)已知组成,确定 点的位置;
双线法:
2、浓度三角形规则
(1)等含量规则 等含量规则:平行于浓度 三角形一边的直线上的各点, 其第三组分的含量不变,即: MN线上C%相等。
在在mn外mpn二三元系统相图基本类型一具有一个低共熔点的简单三元系统相图二生成一个一致熔融二元化合物的三元系统相图三具有一个一致熔融三元化合物的三元系统相图四生成一个不一致熔融二元化合物的三元系统相图五具有一个不一致熔融三元化合物的三元系统相图六生成一个固相分解的二元化合物的三元系统相图七具有多晶转变的三元系统相图八形成一个二元连续固溶体的三元系统相图九具有液相分层的三元系统相图一具有一个低共熔点的简单三元系统相图1立体相图2平面投影图投影图上温度表示法
T转 > Te3 、 T转 < Te2——多晶转变点P
T转 < Te2 、Te3——多晶转变点P1、P2
(八)形成一个二元连续固溶体的三元系统相图
(九)具有液相分层的三元系统相图
总结:
分析实际三元系统(复杂三元系统)相图的步骤
一、判断化合物的性质;
二、划分副三角形; 三、判断界线上温度变化——连(结)线规则; 四、判断界线性质——切线规则; 五、确定三元无变量点的性质——重心原理;
(三) 具有一个一致熔融三元化合物的三元系统相图
(四) 生成一个不一致熔融二元化合物的三元系统相图 1、相图组成
(1)不一致熔融化合物S不在自己的相区内; (2)化合物S性质的改变,导致CS连线、无变 量点P、界线的性质改变。 (a)CS连线 (b)无变量点:P点
第八章三元相图

第八章三元相图第八章三元相图三元合金系(ternery system)中含有三个组元,因此三元相图是表示在恒压下以温度变量为纵轴,两个成分变量为横轴的三维空间图形。
由一系列空间区面及平面将三元图相分隔成许多相区。
第一节三元相图的基础知识三元相图的基本特点:(1) 完整的三元相图是三维的立体模型;(2) 三元系中可以发生四相平衡转变。
四相平衡区是恒温水平面;(3) 三元相图中有单相区、两相区、三相区和四相区。
除四相平衡区外,一、二、三相平衡区均占有一定空间,是变温转变。
一、三元相图成分表示方法三元相图成分通常用浓度(或成分)三角形(concentration/composition triangle)表示。
常用的成分三角形有等边成分三角形、等腰成分三角形或直角成分三角形。
(一) 等边成分三角形-图形1. 等边成分三角形图形在等边成分三角形中,三角形的三个顶点分别代表三个组元A、B、C,三角形的三个边的长度定为0~100%,分别表示三个二元系(A—B系、B—C系、C—A系)的成分坐标,则三角形内任一点都代表三元系的某一成分。
其成分确定方法如下:由浓度三角形所给定点S,分别向A、B、C顶点所对应的边BC、CA、AB 作平行线(sa、sb、sc),相交于三边的c、a、b点,则A、B、C组元的浓度为:WA = sc = Ca WB = sa= AbWC = sb= Bc注:sa+ sb+ sc = 1 Ca + Ab+ Bc= 12. 等边成分三角形中特殊线(1) 平行等边成分三角形某一边的直线。
凡成分点位于该线上的各三元相,它们所含与此线对应顶角代表的组元的质量分数(浓度)均相等。
(2) 通过等边成分三角形某一顶点的直线位于该线上的所有三元系,所含另外两顶点所代表的的组元质量分数(浓度)比值为恒定值。
(二) 成分的其它表示法1.等腰成分三角形当三元系中某一组元B含量较少,而另外两组元(A、C)含量较多,合金点成分点必然落在先靠近成分三角形的某一边(如AC)附近的狭长地带内。
第八章 三元相图

e3 e1
LA+ C
e2
LA+ B
E
L B +C
面
图中a,b,c分别是组元A,B,C的熔点。在共 晶合金中,一个组元的熔点会由于其他组 元的加入而降低,因此在三元相图中形成 了三个向下汇聚的液相面。其中, ae1Ee3a是组元 A的初始结晶面; be1Ee2b是组元 B的初始结晶面; ce2Ee3c是组元C的初始结晶面
四、三元相图中的杠杆定律及重心定律
3.重心定律
当一个相完全分解成三个新相,或是一个相在分 解成两个新相的过程时,研究它们之间的成分和 相对量的关系,则须用重心定律。 根据相律,三元系处于三相平衡时,自由度为1。 在给定温度下这三个平衡相的成分应为确定值。 合金成分点应位于三个平衡相的成分点所连成的 三角形内。
第八章 三元相图
三元合金系(ternery system)中含有三个组元,因此 三元相图是表示在恒压下以温度变量为纵轴,两个成分变量 为横轴的三维空间图形。由一系列空间区面及平面将三元图 相分隔成许多相区。
8.1 三元相图的基础知识
三元相图的基本特点: (1) 完整的三元相图是三维的立体模型; (2) 三元系中可以发生四相平衡转变。四相 平衡区是恒温水平面; (3) 三元相图中有单相区、两相区、三相区 和四相区。除四相平衡区外,一、二、三相平 衡区均占有一定空间,是变温转变。
二、三元相图的空间模型
三、三元相图的截面图 投影图
•
三元相图各类图形有等温(水平)截面图、垂直 (变温)截面图、投影图。
1. 等温水平截面图
第5章-三元相图PPT课件

2、结晶过程分析 O 自液态缓冷至于液互
相相交时,开始从液相中结晶出 α 固溶体,此时液相的成分l1即为合金成分, 而固相的成分为固相面某一点 s。
α 相越来 越多,固相的成分由s1点沿固相面移至s2 点,液相成分自l1点移至 l2点,由直线法则可知,合金的成分点必落 在l2和s2的连线上。
Ca=WA=30% Ac=WC=60% Ab=WB=10%。
中都有应用,但应用最为广泛的还是等边 三角形。
•10
2、等边成分三角形中特定意义的线 (1) 平行 于三角形某一边的直线 凡成分位于该线上的所有合金,它们 所含的由这条边对应顶点所代表的组元的 含量为一定值。如图5-103中ef直线上代表 B组元的含量均为Ae。
•15
•16
•17
由直线法则可得到以下规律: a、 当温度一定时,若已知两平衡相的 成分,则合金的成分必位于两平衡相成分 的连线上; b、 当温度一定时,若已知一相的成分 及合金的成分,则另一平衡相的成分必位 于两已知成分点的连线的延长线上; c、 当温度变化时,两平衡相的成分变 化时,其连线一定绕合金的成分点而转动。
•1
三元相图与二元相图比较,组元数增加 了1个,即成分变量是两个,故表示成分的坐 标轴应为2个,需要用一个平面表示,再加上 垂直于该平面的温度轴,这样三元相图就 演变成一个在三维空间的立体图形,分隔 相区的是一系列空间曲面,而不是二元相 图的平面曲线。
•2
1、三元相图的成分表示方法 (1) 等边成分三角形 这样的三角形称为浓度三角形或成分三角 形(Composition Triangle)。常用的成分三 角形是等边三角形和直角三角形。
•38
•11
•12
(2)通过三角形顶点的任一直线 凡成分位于该直线上的所有合金
第八章-三元相图

1. 三元匀晶相图
B
C
A
33
液相面
固相面
B
C
A
34
液相面
—— 由液相线演化而来
L
固相面
—— 由固相线演化而来
单相区:
B
L、
C
双相区: L+
A
35
结晶过程
L B
L→
t1
t2
C
A
36
1. 水平截面图
B
C
L+
L
A
37
等温截面图 为便于研究,通常采用三元合金相图的等温截面图
10
10 20 30 40 C% 50 60
70
III
80
90
A 90 80 70 60 50 40 30 20 10 C
← A%
11
B
90 10
IV 点:
A%=40% B%=0% C%=60%
80 70 60 B% 50 40 30 20
20 30 40 C% 50 60
70 80
10
90
IV
A 90 80 70 60 50 40 30 20 10 C
WP Af W Ae W Ag (W W ) Af W Ae W Ag WP Af ' W Ae W Ag (W W )Af W Ae W Ag
W W
( (
Af Af
Ae) W ( Ae) W
← A%
9
B
II点:
A%=20% B%=50% C%=30%
90
80 70 60 B% 50 40 30 20
三元相图

2.几个特殊点的冷却过程分析: 在这类三元相图上,M1.M2.M3是几个有代表性的特殊点,其 冷却过程分析清楚了,该类相图所有点的冷却过程也就 清楚了。 A . M1点的冷却过程 首先,我们必须明确以下两点: (1)M1在△ADC中,凝固结束后,所得固相为A,D,C; (2)M1点位于CD线左侧,当二元包晶反应完成以后,液相不 足,而固相A过剩;凝固结束在P点,或者在P点发生三 元包晶反应。(与二元系比较) 冷却过程如下: (1)连接AM1,当组成为M1的冷相冷却到液相面上时(对二元 系为液相线),体系中析出固相A,随着体系中固相A上 不断析出,液相组分变化沿 方向,直至液相组分变化 到三元包晶线IP上的a点; (2)在a点发生包晶反应:La + A = AmBn(D); (3)随着包晶反应的进行,固相A不断减少,化合物D不断增 加;固相组成的变化方向由A→a’,A,D比例由杠杆原理确 定;液相组成的变化方向由a →P。
4.2.1.2等含量规则
等含量规则:与某一边平行的直线上,任一 点对应顶点组元的量都相等。
B
a P b
A
c
d
C
4.2.1.3定比例规则
从一顶点画一条斜线到对边,则该条斜线上的任何 点,由其它二顶点所代表的二组分成分之比是不 % B NC 变的。如图4-13中,x1 、x2 、x3 三点,%C BN 常数。
此时,液相成分在P点不变; 固相A,D,C的组成有a’变化到b’。 (4)在P点发生的三元包晶反应最终以固相A的消失而结束,此时 液相组分由P点向E点移动,与此同时发生二元共晶反应, LP→E=D+C; 固相组分(仅有固相D和C)由b’和c’方向移动; (5)液相组分变化到E点,发生三元共晶反应LE=SC+SD+SB,随着 反应进行,液相组分不变,液相的量不断减少,直至完全消失; 固相在c’点,由于固相B的生成,其组成由c’向M2移动; 当液相在E点消失时,固相组成到达M2,M2是由固相D,C,B组成的 共晶体,其总量与冷却前的液相量根据浓度三角形△DCB确定。 C . M3点冷却过程 首先,如图1-4-25所示,我们必须明确一下三点,并注意与M2的 区别: (1)M3位于△DCB内,凝固结束时,所得固相为B,C,D这点与M2 相同; (2)M3位于DC线右下侧,首先发生二元包晶反应,是液相与先 结晶出的固相A反应,生成D,当液相组分没有变化到P点时, 由于固相A的提前消失,二元包晶反应结束,不会发生三元包晶 反应;
第五章 三元相图
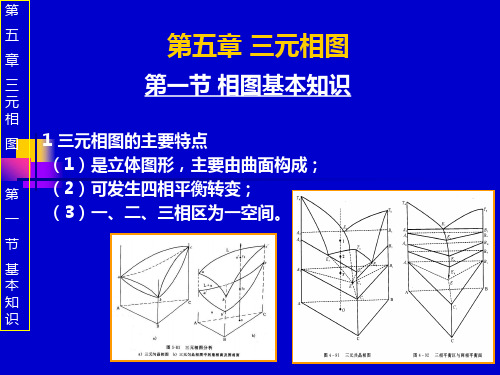
三 一 组元在固态互不相溶的共晶相图
元 相
(1)相图分析
图
点:熔点;二相共晶点;三相共晶点。
两相共晶线
第
液相面交线
三
线:EnE 两相共晶面交线
液相单变量线
节
液相区与两相共晶面交线 共
晶
相
图
11
第 五
第三节 三元共晶相图
章 一 组元在固态互不相溶的共晶相图
三
(1)相图分析
元
液相面
相
固相面
图
面: 两相共晶面 三相共晶面
三 (1)相图分析
元
点:熔点;二元共晶点;三元共晶点。
相
两相共晶线 液相面交线
图
线:EnE 两相共晶面交线
液相单变量线
液相区与两相共晶面交线
第
固相单变量线
三
液相面
固相面(组成)
节 面: 二相共晶面
共
三相共晶面
晶
溶解度曲面:6个
相
两相区:6个
图
区: 单相区:4个
三相区:4个
四相区:1个
16
第 五
第三节 三元共晶相图
三 5 共线法则与杠杆定律
元 两条推论
相
(1)给定合金在一定温度下处于两相平衡时,若其中一个
图 相的成分给定,另一个相的成分点必然位于已知成分点连线
的延长线上。
第
(2)若两个平衡相的成分点已知,合金的成分点必然位于
一 两个已知成分点的连线上。
节
基 本 知 识
5
第 五
第一节 相图基本知识
章 6 重心法则
7
第 五
第二节 三元匀晶相图
章 3 等温截面(水平截面)
相图的类型名词解释

相图的类型名词解释相图是指用来描述物质在不同温度、压力、组分等条件下的相态行为的图表或图像。
通过相图,可以直观地了解物质在各种环境条件下的相变规律、相互作用和共存情况。
在材料科学、地球科学、化学工程等领域,相图是非常重要的工具,有助于实现材料设计、地质勘探和化工过程的优化等。
相图主要有以下几个常见的类型:1. 二元相图二元相图是描述两个组分物质在不同温度和组分条件下的相态行为。
常见的二元相图有二元平衡相图和二元不平衡相图。
二元平衡相图反映了物质在平衡状态下的相变和相互作用规律,如共晶现象、共熔现象等。
二元不平衡相图则对应于非平衡条件下的相变行为,如快速淬火等。
2. 三元相图三元相图描述了三个组分物质在不同温度和组分条件下的相态行为。
三元相图常用于合金材料的研究和制备。
通过分析三元相图,可以了解合金中各种相的形成、变化和相互作用规律,从而指导材料设计和工艺控制。
三元相图通常比二元相图更加复杂,因为存在更多的组分之间的相互作用。
3. 非平衡相图非平衡相图描述了物质在非平衡条件下的相变行为。
这些条件可能包括快速冷却、快速加热、强烈的外界场等。
非平衡相图可以帮助我们了解物质在非平衡状态下的相变机制和相互作用规律,这对于材料加工、矿物学研究和能源领域的应用具有重要意义。
4. 反常相图反常相图是指在某些特殊条件下,物质的相态行为不符合通常的相图规律。
在反常相图中,可能存在异常的相变行为,如某一相的化学组成、稳定性等随温度的变化呈非线性关系。
反常相图常见于某些特殊组分比例的合金材料或某些非均匀性体系。
总结起来,相图通过图表或图像形式展示了物质在不同条件下的相变行为和相互作用规律。
不同类型的相图适用于不同领域的研究和应用。
正确理解和分析相图可以帮助我们深入了解物质的相态行为,为材料设计、工艺优化和科学研究提供依据。
在未来的研究和应用中,相图将继续扮演重要角色,推动科学技术的发展。
第七章 三元相图
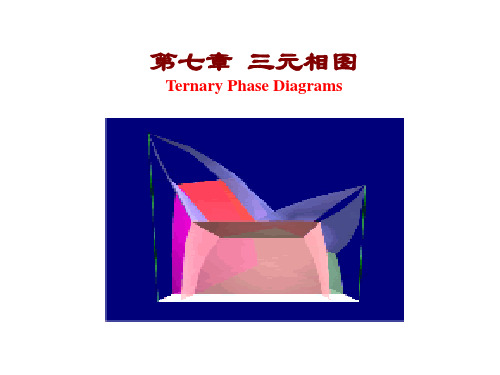
共轭连线
共轭曲线
s2 s1
三相平衡情况:
三相平衡时,3个自由能-成分曲面只有唯一的公切面;3个公切点投影 到成分三角形上构成的成分点,即3个平衡相在该温度下的成分点
三元相图中的三相平衡
可以分为两类:
共晶型转变:降温时,从一相转化为两相的转变,即 I II + III
共晶转变: L +
量线,代表了三相平衡时,一相(此处为L相)的成分随温度的变化
(四) 相及相区
相:L、A、B、C 相区: 单相区(4个):1个液相区、3个 固相单相区(垂直线) 两相区(3个):3个包含液相的 两相区(L+A、 L+B、 L+C) 三相区(4个):1个由固相组成 的三相区A+B+C(正三棱柱体)、 3个包含液相的三相区(L+A+B、 L+A+C、L+B+C) 四相区(1个):L+A+B + C
等边三角形中特殊线
B B
wC wC
e
wB
p o
f
o p C
A g
wA wA
A
— 组元B的含量 wB 都相同
C
ef 线上各点代表的三元成分
Bg 线上各点代表的三元成分
— 组元A和C的含量之比 wA/wC都相同
3点
三元相图的成分
— 等腰成分三角形 由于某一组元含量很少,可取等边成分三角形中等腰梯形部分 等边成分三角形中靠近底部的有用部分
B o
a
a2
wa(B) wo(B)
b
b1 o1
wb(A)
C
o2
b2
wo(A)
a1
wa(A)
wb(B)
证明:
A
A组元含量 wo(A) = wb(A)· 固 + wa(A) · 1- w固) w (
相平衡-三元相图

在C’CAA’平面内
38
M (熔体) M’(熔体) P=1, L F=3 M[C,(C)] P=2, P=2 L C F=2 D[C, C+(A)] C (A)] P=3, L A+C F=1 F 1 E(到达)[F, A+C+(B)] P=4, , L A+B+C F=0 E(结束)[M, A+B+C]
40
杠杆规则计算液相量和固相量
液相到达 点时 液相到达D点时:
固相量 MD 液相量 CM
固相量 MD 固液总量(原始配料量) CD CM 液相量 固液总量(原始配料量) CD
41
液相刚刚到达E点时: 点时
固相量 液相量 = ME FM
固相量 固液总量
=
ME EF
E点析晶结束时,固相点与系统组成点重合
液相线:cd, df, bb’ 二相区:L+Pb L+Cd L+Sn 三相区:L Pb Cd 三相区:L+Pb+Cd f=0, 所以组成一定
Te1 , Te 2 , TE 200 o C Tm, Pb , Tm,Cd , Tm, Sn , Te 2
31
二相区(3) 三相区(3) 一相区( 相区(L)
28
Pb-Sn-Cd相图
29
等温截面
1. 液相线aa’,bb’; 2 二相区L+Pb,L+Cd, 2. f=3-=1,如果液相Sn含 量为m%,作ml//AC, 可得液相组成l; 3 结线 Al、Ak 3.
TE , Te, Tm, Sn 280 C Tm , Pb , Tm,Cd
o
30
定比例规则
高温熔体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投影图
投影原理 1空间点投影成为平面点
2空间曲线投影成为平面曲线
3空间曲面投影成为平面区域
4空间与平面间的点(或线),成分上一一对应
用投影图分析组织变化
冷却过程组织变化 1液相析出纯固相;液相点变化至二元共晶线
2二元共晶线上的(剩余)液相,分解为:
2结果:导致分析简化
两相平衡的公切线与共轭线
三相平衡的公切面及其投影
固相完全不互溶的三元共晶相图
相图特点
单相区与两相区 纯A, 纯B, 纯C, 液相; L+A, L+B, L+C 三相区
L+A+B,L+A+C,L+B+C
A+B+C
三元共晶反应
反应式
LE→A+B+C
自由能切面图
水平截面图
水平截面图中的重心法则
共晶相图
特点 共晶反应;液相公切点位于两个固溶体之间 183 C
LE M N
三相平衡温度下的相对量 1理论上三个相的相对量不可计算; 2取略高或略低于水平线的温度,以便避开上 述理论问题。
重新学习相图目的之一:分析组织
组织的定义-不可定义性与认知方法
由单相或多相组成的,具有特定空间分布状态 与性质,能够相互区分的物质集团。 组织组成百分比的概念 以组织为考察对象,从而计算出不同组织所占 百分比。它是与相组成百分比对应的新概念。 组织与相的差别 着眼点不同,组织以特定的空间分布为准
一元相图
-前几章几何结构,相图:能量结构
一元相图
背景与问题 相图:实验PK计算→算出:1亚稳相;2难测系统 思路与方法
GL(T,p)=Gg(T,p)→气-液平衡线; GL(T,p)=Gg(T,p)=Gs(T,p)→三相平衡点 结果 相图:被线(点)分割的p-T平面,表示相的稳定性 提示 1哪些相被考虑由经验决定;2数学分析之美
同学讲解内容
固-液平衡线是如何得来的?
气-液平衡线是如何得来的? ★液相区中的固-气亚稳线是如何得来的? 相对于实验相图,计算相图的优势?
二元相图
背景与问题
四元函数G=G(T,p,nA,nB) → 一元函数G=G(x) 思路与方法(或新事实) 1略去p,且将T参数化(平衡要求等温-不是重点)
2凝聚态的经验事实
二元共晶(固相)+沿二元共晶线的(剩余)液相
3最后剩下的、成分为E的液相发生如下反应
LE→A+B+C
4通常情况下的室温组织:
A+(A+C)+(A+B+C)
分析:投影图PK立体图
固相有限互溶的三元共晶相图
固相有限互溶的三元共晶相图
相区 单相区:固溶体α, 固溶体β, 固溶体γ, 液相区 两相区:L+α, L+β, L+γ ; α+β,β+γ,γ+α 三相区:L+α+β, L+β+γ, L+γ+α; α+β+γ
上凸的成分区间随温度降低而变宽
上凸的高度随温度降低而变大
变化规律的解释 内能项与温度无关;熵项作用随温度降低而减弱
G 1 x GA xGB x 1 x Z kBT 1 x ln 1 x x ln x
背景与问题
没有适用于任何二元系的G=G(x)表达式 思路与方法 1由简到繁,在理想溶液模型上前进一步
G1 nA GA nBGB Gm nA GA nBGB U m T S m nA GA nBGB U m k BT nA ln xA nB ln xB
ZrO2-CaO相图
1单相区
2两相区 3重要三相反应
三元相图
成分表示法 原则:靠谁近,谁的百分比大 浓度三角形中特殊线的意义 角分线:两个组分浓度比例不变
平行线:某一组分浓度不变
三元相图的基本分析思路
从几何、公式等方面,与二元相图对比
自由能-成分曲面
自由能函数形式 等温下,G=G(xA,xB)。几何上是空间曲面。 自由能-成分曲面 1形状:正三角形弹力棉被重球压成凹面(Ω≤0) 2公切线特点:无穷多个共轭线,线上两相平衡。 3公切面含义:三个公切点内,三相机械混合最 稳定。温度一定时,公切面是唯一的。 自由能点 1来源:固态间的不相溶
G 1 x GA xGB x 1 x Z kBT 1 x ln 1 x x ln x
G=G(x)的几何形状类型
函数G=G(x)的几何分析
目的
1形象化; 2单相自身稳定性与曲线形状有关
稳定性的准则
物质守恒,温度不变时,可以任意假定系统所处 的状态,其中自由能最低者最稳定。 结论 下凹曲线稳定;上凸曲线在两个拐点内不稳定 复习 固溶体因原子半径差导致应变能; 纯溶剂没有
Pb-10%Sn合金的组织演变
Pb-50%Sn亚共晶合金的组织演变
偏晶相图及其G-x曲线
偏晶相图特点
偏晶反应
L36 Cu L87
液相分层
955 C
L1+L2(含Cu多的L1浮在上;含Pb多的L2沉在下)
固相完全不互溶 意味着Ω>>0
铁碳相图
1单相区 2两相区 3重要三相反应 ★4亚稳相概念 ★5组织变化及相对量 例:含碳2.4%(重量)合金的组织变化与相对量 解 组织:Ld+Fe3CII+P(图4-26) 相对量:Ld%=(2.4-2.1)/(4.3-2.1)=14% Fe3CII%=86%×22.6%=19% P%=1-(14%+19%)=67%
三元共晶反应
LE→α+β+γ
说明
上式是液相自由能-成分曲面与三个固溶体自由能成分曲面公切的结果。
两相区与三相区立体形状(部分)
水平截面图
投影图
投影图
共晶反应、包共晶反应和包晶反应
共晶反应:“三进无出” 包共晶反应:“两进一出”
包晶反应:“一进两出”
等温,成分不变下:广度量是总摩尔数的线性函数
即G=nG(x)
规则溶液模型
1 A,B原子结构相同,配位数均为Z;
2 A,B原子半径相同(没有应变能)
3 结合能遵循最近邻假设,结合能不随温度、成 分变化。 其背景
在理想液态混合物模型基础上,进一步考虑内能 因素,且是以最简单的方式考虑
规则溶液模型下的G=G(x)
2规则溶液模型对ΔUm的处理思路: 只考虑结合键种类变化对内能的影响。
结果
nA ZxA eAA nB ZxBeBB nA ZeAA nB ZeBB U m nB ZxA eAB 2 2 2 nA nB Z nA nB
G1 G1 nA , nB nA nB nA nB nAGA nBGB Z kBT nA ln nB ln nA nB nA nB nA nB
匀晶相图
匀晶相图总结
背景与问题 液相与连续固溶体先决存在。
问题:如何通过GL-x与Gs-x得到匀晶相图 思路与方法 1纯组分: GL(纯A)=Gs(纯A)→TA
GL(纯B)=Gs(纯B)→TB
2合金:两相G-x曲线直最低;
提示 不同温度下各个相的G-x曲线包含相平衡的所有信息
G-x曲线上公切线的相关知识 1做切线可得溶液(或固溶体)的μA、μB 2两点公切意味着两相平衡
3公切线上的点是机械混合物的总摩尔自由能
4三点公切意味着三相平衡
共晶相图
亚稳线的由来与应用-下面的图不好
共晶相图中固溶体G-x曲线总结
存在上凸现象 单相固溶体分裂为两个相; 三相平衡因此存在 上凸现象变化规律
