11专题十一 数阵图
66666小学奥数专题之数阵图练习题例

小学奥数专题之——————数阵图数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
数阵的特点是:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
\1.10.5.2辐射型数阵例1 将1~5五个数字,分别填入下图的五个○中,使横、竖线上的三个数字和都是10。
解:已给出的五个数字和是:1+2+3+4+5=15题中要求横、竖每条线上数字和都是10,两条线合起来便是20了。
20-15=5,怎样才能增加5呢?因为中心的一个数是个重复使用数。
只有5连加两次才能使五个数字的和增加5,关键找到了,中心数必须填5。
确定中心数后,按余下的1、2、3、4,分别填在横、竖线的两端,使每条线上数的和是10便可。
例2将1~7七个数字,分别填入图中的各个○内,使每条线上的三个数和相等。
:解:图中共有3条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,则a被重复使用了2次。
即,1+2+3+4+5+6+7+2a=28+2a,28+2a应能被3整除。
(28+2a)÷3=28÷3+2a÷3其中28÷3=9…余1,所以2a÷3应余2。
由此,便可推得a只能是1、4、7三数。
当a=1时,28+2a=30 30÷3=10,其他两数的和是10-1=9,只要把余下的2、3、4、5、6、7,按和为9分成三组填入两端即可。
六年级下册数学试题-小升初:第十一讲 数字谜与数阵图(解析版)全国通用

第十一讲数字谜与数阵图1.回顾常用的数字谜的解题技巧。
2.精讲经典数字谜、及数阵数表。
【解题技巧】(一)解题的突破口多在于竖式或横式中的特殊之处,例如首位、个位以及位数的差异。
(二)要根据不同的情况逐步缩小范围,并进行恰当的估算。
(三)当题目中涉及多个字母或汉字时,要注意利用不同符号代表不同数字这一条件来排除若干可能性。
(四)注意结合进位及退位来考虑。
(五)有时可运用到数论中的分解质因数等方法。
【例1】★★★(小学数学ABC)从12,13,14,16,18中选出四个填入下式的中,使得等式成立.那么A有种可能的值.÷ = ÷ =A【解】考虑五个分数的分母2,3,4,6,8.因为2×6=3×4,所以11112634⨯=⨯,由此得到1 2÷14=13÷16=2;12÷13=14÷16=32;1 6÷14=13÷12=23;16÷13=14÷12=12.同理,由3×8=4×6得到1 3÷14=16÷18=43;13÷16=14÷18=2;1 8÷14=16÷13=12;18÷16=14÷13=34.所以,A有6种可能值,分别是2,12,32,23,43,34.有人把数字谜问题叫做思维锻炼的体操,这一部分问题可以很好的培养学生的观察力、判断及推理能力。
数字谜是一类非常有趣的数学问题,在小学数学竞赛中经常出现.解这类问题必须认真审题,根据题目的特点,找出突破口,从而逐步简化题目直至问题完全解决.教学目标专题回顾【例2】★★★请在下式中填入+和×,使等式成立(不要求每两个数之间都填入符号,但不能填+和×以外的符号):1 2 3 4 5 6 7 8 9 9=1998 。
【解】:1234+5+678+9×9=1998【例3】★★★(小学数学奥林匹克决赛民族卷第4题) 在下面三个算式中,三个方框内都填同一个数.口一0.07=1950 口×0.75=9280.375÷口=56如果在这三个算式中,恰好有两个算式是正确的,那么方框中所填的数是_______.【解】:如果三个算式都是正确的,那么三个方框依次应其中9209出现两次,所以方框中填的数是20【例4】★★★(101中学选拔试题)()()()11112=++(括号内必须填不同的自然数)【解】: 11111123637421111112444520=+=++=+=++或等等 答案并不唯一.【例5】★★★★(清华附中入学真题) 在47152口中的“口”内,可以填写的整数只有_________. ①10、11、12、13; ②9、10、11、12、13; ③8、9、10、11、12、13; ④无数个.199359007075=0375********+=÷÷=9、,、,、28【解】: 由71714214=,得口口又47749101112135985=,而,所以口,,,,,应选○2.数字谜【例1】★★★(北京市“迎春杯”决赛第一题第7题)下面乘法的算式1 A B C D E × 3 A B C D E 1则ABCDE 是____________. 【解】:从乘法算式最后一位看起,由于积E ×3的禾位数字是l ,我们可以断定E=7.于是,再根据积D × 3的末位数字是7—2=5,可以断定D=5;同样,根据积C ×3的末位数字是5一l=4,可以断定C=8;根据积B ×3的末位数字是8—2=6,可以断定B=2;根据积A ×3的末位数字是6,从而断定A=4. 答:ABCDE 是42857.【例2】★★★(南京市“兴趣杯”少年数学邀请赛预赛C 卷笫3题)在算式131abcde abcde ⨯=中,不同的字母代表不同的数字,相同的字母代表相同的数字,那么_______abcde =. 【解】:令,abcde x =则(100000+z)×3=x ×10+1,即 7x =299999, 解得 x =42857.【例4】★★(《小数报》数学竞赛初赛填空题第5题)在右边的算式中,相同的符号代表相同的数字,不同的符号代表不同的数字,根据这个算式,可以推算出: △□□〇 +〇□□△ □□☆☆口+○+△+☆=_________. 【解】: 比较竖式中个位与千位的加法,推知口比☆大1.由十位于百位数的加法可知 口+口=10+☆专题精讲并且口=☆+1将后一式代入上一式得口+口=10+口一1,从而口=9,☆=8.再由个位加法,推知○+△=8.从而口+○+△+☆=9+8+8=25【例5】★★★(小学“希望杯”全国数学邀请赛)右边是一个六位乘以一个一位数的算式,不同的汉字表示不同的数,相同的汉字表示相同的数,其中的六位数是______ 。
66666小学奥数专题之数阵图练习题例

小学奥数专题之——————数阵图数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
数阵的特点是:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
1.10.5.2辐射型数阵例1 将1~5五个数字,分别填入下图的五个○中,使横、竖线上的三个数字和都是10。
解:已给出的五个数字和是:1+2+3+4+5=15题中要求横、竖每条线上数字和都是10,两条线合起来便是20了。
20-15=5,怎样才能增加5呢?因为中心的一个数是个重复使用数。
只有5连加两次才能使五个数字的和增加5,关键找到了,中心数必须填5。
确定中心数后,按余下的1、2、3、4,分别填在横、竖线的两端,使每条线上数的和是10便可。
例2将1~7七个数字,分别填入图中的各个○内,使每条线上的三个数和相等。
解:图中共有3条线,若每条线数字和相等,三条线的数字总和必为3的倍数。
设中心数为a,则a被重复使用了2次。
即,1+2+3+4+5+6+7+2a=28+2a,28+2a应能被3整除。
(28+2a)÷3=28÷3+2a÷3其中28÷3=9…余1,所以2a÷3应余2。
由此,便可推得a只能是1、4、7三数。
当a=1时,28+2a=30 30÷3=10,其他两数的和是10-1=9,只要把余下的2、3、4、5、6、7,按和为9分成三组填入两端即可。
小学奥数数阵图

第十七周数阵图把一些数字按照一定的要求,排列成各种各样的图形,叫做数阵图。
数阵是由幻方演化出来的另一种数字图。
幻方一般均为正方形。
图中纵、横、对角线数字和相等。
数阵则不仅有正方形、长方形,还有三角形、圆、多边形、星形、花瓣形、十字形,甚至多种图形的组合。
变幻多姿,奇趣迷人。
一般按数字的组合形式,将其分为三类,即辐射型数阵、封闭型数阵、复合型数阵。
【解题技巧】数阵的分类:封闭型:封闭型数阵图的解题突破口,是确定各边顶点所应填的数。
为确定这些数,采用的方法是建立有关的等式,通过以最小值到最大值的讨论,来确定每条边上的几个数之和,再将和数进行拆分以找到顶点应填入的数,其余的数再利用和与顶点的数就容易被填出。
(1—6)辐射型:辐射型数阵图,解法的关键是确定中心数。
具体方法是:通过所给条件建立有关等式,通过整除性的讨论,确定出中心数的取值,然后求出各边上数的和,最后将和自然数分拆成中心数的若干个自然数之和,确定边上其他的数。
复合型:复合型数阵图,解题的关键是要以中心数和顶点数为突破口。
数阵的特点:每一条直线段或由若干线段组成的封闭线上的数字和相等。
它的表达形式多为给出一定数量的数字,要求填入指定的图中,使其具备数阵的特点。
解数阵问题的一般思路是:1.求出条件中若干已知数字的和。
2.根据“和相等”,列出关系式,找出关键数——重复使用的数。
3.确定重复用数后,对照“和相等”的条件,用尝试的方法,求出其他各数。
有时,因数字存在不同的组合方法,答案往往不是唯一的。
【铜牌例题】将2、3、4、5、6、7、8、9、10填入下图中的9个方格中,使每行、每列及对角线之和相等,小明已经填了5个数,请将其余4个数填入。
【答案】【解析】先根据最左边一列求出幻和,然后根据这个和和给出的数字逐步推算。
3+8+7=18;第二行中间的数是:18-8-4=6;第三行中间的数是:18-7-9=2;第一行第一个数是:18-4-9=5;第一行中间的数是:18-3-5=10;【举一反三1】(第十届走美杯初赛)小华需要构造一个3×3的乘积魔方,使得每行、每列、每条对角线上三个正整数的乘积都相等;现在他已经填入了2,3,6三个数,那当小华的乘积魔方构造完毕后,x等于______。
全国通用六年级下册数学试题-小升初:第十一讲 数字谜与数阵图(解析版)

【例 10】★★★如图为一个三阶幻方,其中两个数已填好,求标有*的空格中所填的数。
*
19
95
【解】如图,设第一行第三个数为 x,则通过比较过中心方格的一行及一条对角线知第二行 第一个数为 x+76,再比较第一行与第一列得标有*的方格内数为:95+(x+76)-x=171.
x
x+76
19
95
【点评】本题本来是填幻方的题目中较难的一道,题目中已知每个条件这么少,还能得到 这样的结论,可见幻方是多么的有趣。这里有一种重要的思想,就是在相交于一格的两条 线(行与列,行或列与对角线),则必有除相交格的剩余格之和相等。
÷ = ÷ =2;
2 43 6
1 11 13
÷= ÷= ;
2 34 62
1 11 12 1 11 11
÷=÷=; ÷=÷=.
6 43 23 6 34 22
同理,由 3×8=4×6 得到
1 11 14 1 11 1
÷ = ÷ = ; ÷ = ÷ =2;
3 46 83 3 64 8
1 11 11 1 11 13
4
在
7
1
中的“口”内,可以填写的整数只有_________.
5口 2
①10、11、12、13; ②9、10、11、12、13;
③8、9、10、11、12、13; ④无数个.
【解】: 由 7 1 7 ,得口 14 口 2 14
又 4 7 ,而,7 所4以口,,,,9 1,0应11选12 1有人把数字谜问题叫做思维锻炼的体操,这一部分问题可以很好的培养学生的观察力、 判断及推理能力。数字谜是一类非常有趣的数学问题,在小学数学竞赛中经常出现.解这类 问题必须认真审题,根据题目的特点,找出突破口,从而逐步简化题目直至问题完全解决.
11 数阵图之谜

【课前挑战】
巧填五连环
小朋友们你知道奥运五环象征什么吗?今天,我们来做一个“填数五连环”的游戏,图上的五个圆环组成了9个区域,9个区域分别要填上从19的任意数字,要求数字不能重复使用。
其中3
这个区域分别要填从到的任意数字,要求数字不能重复使用其中个
把4、5、6、7、8这5个数分别填入图中的圆圈内,使两条直线上的
三个数之和都等于18。
把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的都等
和都等于15。
把1~9这九个数字填入下列圆圈内,使每条线上的三个圆圈内的数都等
之和都等于15。
把1~7这七个数分别填入图中的各○内,使每条直线上三个○里数的相等共有多少种法
的和相等。
一共有多少种方法?把1、2、3、4、5、7这6个数分别填入图中的圆圈内,使每个大圆上个数的和都等
的4个数的和都等于13。
把1,2,3,4,5,6这6个数分别填入下图的6个圆圈中,使得三角每数都等
形每条边上的3个数的和都等于10。
把10,20,30,40,50,60,70这7个数填在圆圈里,使每条直线上每的数的都
和每个圆周上的三个数的和都是120。
数阵图讲解
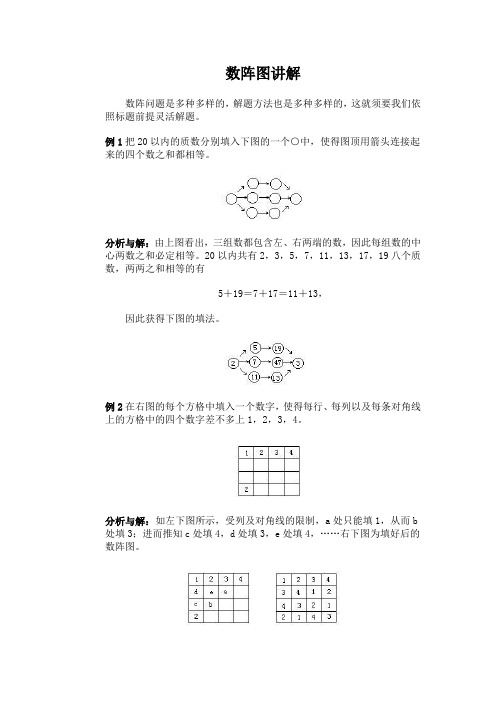
数阵图讲解数阵问题是多种多样的,解题方法也是多种多样的,这就须要我们依照标题前提灵活解题。
例1把20以内的质数分别填入下图的一个○中,使得图顶用箭头连接起来的四个数之和都相等。
分析与解:由上图看出,三组数都包含左、右两端的数,因此每组数的中心两数之和必定相等。
20以内共有2,3,5,7,11,13,17,19八个质数,两两之和相等的有5+19=7+17=11+13,因此获得下图的填法。
例2在右图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数字差不多上1,2,3,4。
分析与解:如左下图所示,受列及对角线的限制,a处只能填1,从而b 处填3;进而推知c处填4,d处填3,e处填4,……右下图为填好后的数阵图。
例3将1~8填入左下图的○内,要求按照天然数次序相邻的两个数不克不及填入有直线连接的相邻的两个○内。
分析与解:因为中心的两个○各自只与一个○不相邻,而2~7中的任何一个数都与两个数相邻,因此这两个○内只能填1和8。
2只能填在与1不相邻的○内,7只能填在与8不相邻的○内。
其余数的填法见右上图。
例4在右图的六个○内各填入一个质数(可取雷同的质数),使它们的和等于20,同时每个三角形(共5个)顶点上的数字之和都相等。
分析与解:因为大年夜三角形的三个顶点与中心倒三角形的三个顶点正好是图中的六个○,又因为每个三角形顶点上的数字之和相等,因此每个三角形顶点上的数字之和为20÷2=10。
10分为三个质数之和只能是2+3+5,由此获得右图的填法。
例5在右图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,同时k不克不及被未标出的数整除。
分析与解:设未被标出的数为a,则被标出的八个数之和为1+2+…+9-a =45-a。
因为每个顶点都属于三个面,因此六个面的所有顶点数字之和为6k=3×(45-a),2k=45-a。
2k是偶数,45-a也应是偶数,因此a必为奇数。
四年级下册数学试题-奥数专题讲练:第十一讲 数阵图与数字谜 竞赛篇(解析版)全国通用

第十一讲数阵图与数字谜编写说明在四年级秋季第九、十讲和春季第三讲我们对数阵图进行了讲解,在寒假第6、7讲对数字谜进行了讲解. 本讲我们将针对这两部分知识进一步巩固和提高. 此部分内容我们在一步步分析时比较占用时间,所以本讲的例题量设置较少!同时教师也可用来缓解前几讲习题的压力!你还记得吗【复习1】请你把1~7这七个自然数,分别填在右图的圆圈内,使每条直线上的三个数的和都相等.应怎样填?分析:关键在于确定中心数a和每条直线上几个圆圈内数的和k. 为了叙述方便,先在各圆圈内填上字母,如右下图.设每条直线上的数字和为k.根据题意可得:2a+28=3k 由于28与2a的和为3的倍数,a又为1~7中的数字,经过尝试可知:a为1、4或7.若a=1,则k=10,直线上另外两个数的和为9. 得到一个解为:a=1,b=2,c=3,d=4,e=7,f=6,g=5.若a=4,则k=12,直线上另外两个数的和为8. 得到第二个解为:a=4,b=1,c=2,d=3,e=7,f=6,g=5.若a=7,则k=14,直线上另外两个数的和为7. 得到第三个解为:a=7,b=1, c=2,d=3,e=6,f=5,g=4.【复习2】将1~7这七个数分别填入右图的○里,使得每条直线上三个数之和与每个圆圈上的三个数之和都相等.分析:所有的数都是重叠数,中心数重叠两次,其它数重叠一次. 所以三条边及两个圆周上的所有数之和为:(1+2+…+7)×2+中心数=56+中心数.因为每条边及每个圆周上的三数之和都相等,所以这个和应该是5的倍数,再由中心数在1至7之间,所以中心数是4. 每条边及每个圆周上的三数之和等于(56+4)÷5=12.中心数是4,每边其余两数之和是12-4=8,两数之和是8的有1,7;2,6;3,5. 于是得到右下图的填法.【复习3】在右图所示的竖式中,相同的汉字表示相同的数字,不同的汉字表示不同的数字。
如果:巧+解+数+字+谜=30,那么“数字谜”所代表的三位数是多少?分析:还是先看个位,5个“谜”相加的结果个位还是等于“谜”,“谜”必定是5(0显然可以排除); 接着看十位,四个“字”相加再加上进位2,结果尾数还是“字”,那说明“字”只能是6; 再看百位,三个“数”相加再加上进位2,结果尾数还是“数”,“数”可能是4或9; 再看千位,(1)如果“数”为4,两个“解”相加再加上进位1,结果尾数还是“解”,那说明“解”只能是9;5+6+4+9=24,30-24=6,“巧”等于6与“字”等于6重复,不能;(2)如果“数”为9,两个“解”相加再加上进位2,结果尾数还是“解”,那说明“解”只能是8;5+6+9+8=28,30-28=2,可以. 所以“数字谜”代表的三位数是965.数 阵 图数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵. 幻方是特殊的数阵图,一般地,将九个不同的数填在3×3(即三行三列)的方格中,使每行、每列、及二条对角线上的三数之和均相等,这样的3×3的数阵阵列称为三阶幻方. n 阶幻方的定义与三阶幻方相仿!【例1】 (1)将九个数填入下图(1)的九个空格中,使得任一行、任一列以及两条对角线上的三个数之和都等于定数k,则中心方格中的数必为3k.请你说明理由!(2)将九个数填入下图(2)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a be +=.请你说明理由!(3)将九个数填入下图(3)的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有:2a bc +=.请你说明理由!分析:(1)因为每行的三数之和都等于k,共有三行,所以九个数之和等于3k.如右下图所示,经过中心方格的有四条虚线,每条虚线上的三个数之和都等于k,四条虚线上的所有数之和等于4k,其中只有中心方格中的数是“重叠数”,九个数各被计算一次后,它又被重复计算了三次.所以有:九数之和+中心方格中的数×3=4k, 3k+中心方格中的数×3=4k,中心方格中的数=3k (2)和=3e ,a+e+b=和=3e,所以a+b=2e,即得:2a be +=.(3)设中心数为d. 每行、每列、每条对角线上的三个数之和都等于3d. 由此可得右图,那么有:c +(2d-b )= a +(2d-c ),由此可得:2a bc +=. 值得注意的是,这个结论对于a 和b 并没有什么限制,可以是自然数,也可以是分数、小数;可以相同,也可以不同.【巩固】在下图的每个空格中填入个自然数,使得每一行、每一列及每条对角线上的三个数之和都相等.分析:右下角的数为(8+10)÷2=9,中心数为(5+9)÷2=7,且每行、每列、每条对角线上的三数之和都等于7×3=21.由此可得右下图 的填法.【巩固】(必讲题目)在右图的每个空格中,填入不大于12且互不相同的八个自然数,使得每行、每列、每条对角线上的三个数之和都等于21 .分析:中央一数必定是21÷3=7.从而一条对角线为8,7,6.另两个角上的数,和为14=2+12=3+11=4+10=5+9,不难验证只有3、11与4、10两种符合要求.于是填法有:【例2】 将1,3,5,7,9,11,13,15,17填入3×3的方格内,使其构成一个幻方.分析:(法1):易得中心数为9,然后将剩余那么其余8个数分为4组,每组两个数的和是18,把它们分别填入图中关于中心格对称的格子内,实验可得结果,如右图. 答案不唯一,仅供参考.(法2):其实会学习的小朋友就知道理利用已经学习过的一些典型题目结果加以变形得到新题答案.事实上我们可以把结果中的幻方看作是1~9填图的幻方相应位置数字乘2减1得来的.推广开来可以知道等差数列填图的三阶幻方几乎都具有相似的形式.我们可以把它推广到等差数的幻方 ,等差数列可与序号1~9一一对应,把等差数填在相应的序号中.【前铺】将自然数1至9,分别填在右图的方格中,使得每行、每列以及两条对角线上的三个数之和都相等.分析:(法1):三行的总和=1+2+3+4+…+9=45,所以每行三个数的和是45÷3=15,所以E代表15÷3=5,由于在同一条直线的三个数之和是15,因此若某格中的数是奇数,那么与这个数在同一条直线上的另两个数的奇偶性相同.因此,四个角上的数A、C、G、I必为偶数.(否则,若A为奇数,则I为奇数.此时若B 为奇数,则其余所有格亦为奇数;若B为偶数,则其余所有格亦为偶数.无论哪种情形,都与1至9中有5个奇数,4个偶数这一事实矛盾.)因此,B、D、F、H为奇数.我们不妨认为A=2(否则,可把3×3方格绕中心块旋转即能做到这一点).此时I=8.此时有两种选择:C=4或G=4.因而,G=6或C=6.其他格的数随之而定.如果把经过中心块旋转而能完全重合的两种填数法视作一种的话,一共只有两种不同的填数法:A=2,C=4或A=Z,G=4(2,4被确定位置后,其他数的位置随之而定).(法2):从法1知道中心数为5,那么其余8个数分为4组,每组两个数的和是10,把它们分别填入图中关于中心格对称的格子内,实验可得结果.这种试填的方法更易让学生接受.【拓展】如图(1)的3×3的阵列中填入了l~9的自然数,构成大家熟知的3阶幻方.现在另有一个3×3的阵列,如图(2),请选择9个不同自然数填人9个方格中,使得其中最大者为20,最小者大于5,且要求横加、竖加、对角线方式相加的3个数之和都相等.分析:①观察原表中的各数是从1~9不同的九个自然数,其中最大的数是9,最小的数是1,且横加、竖加、对角线方式相加结果相等.②根据题意,要求新制的幻方最大数为20,而9+11=20,因此,如果原表中的各数都增加11,就能符合新表中的条件了.【例3】在1~13这十三个自然数中选十二个填在图中的空格内,使每横行四数之和相等,每数列三数之和相等.分析:由和的整除性质,首先确定使用哪十二个数填图.由于每横行四数之和相等.每竖行三数之和相等知十二个数之和既是3的倍数也是4的倍数,因此是12的倍数,由此可知不用填图的数字是7,所选十二个数和为:[(1+13)×1 3÷2]-7=84,每横行四个数和为:84÷3=28,每竖行三个数和为:84÷4=21.由于竖行和为21,因此可知1,2,3,4在不同竖行,而5只能跟3或4在同一竖行,由此可确定竖行分组有如下两种情况:(1,8,12),(2,9,10),(3,5,13),(4,6,11)或(1,9,11),(2,6,13),(3,8,10),(4,5,12).再根据横行和为28,易得如下结果:【拓展】右图是一个四阶幻方,请将其补全:分析:根据各行,各列,各对角线和相等为34,可得图(1),此时我们可以设未知数,如图(2),将一些数表示出来,进而根据和为34求得x代表9,随后得到答案,如图(3).【拓展】在图中所示方格表的每个方格内填入—个恰当的字母;可使每行、每列及两条对角线上4个方格中字母都是A、B、C、D,那么标有“*”的方格内应填的字母是什么?分析:考虑含A和*的对角线上的元素.第二行第二个元素与C同行,因此不是C,第三行第三个元素与C同列,因此也不是C,所以*代表的元素必为C.【巩固】在右图的每个方格中填入一个数字,使得每行、每列以及每条对角线上的方格中的四个数字都是1,2,3,4.分析:如下图所示,受列及对角线的限制,a处只能填1,从而b处填3;进而推知c处填4,d处填3,e处填4,……右下图为填好后的数阵图.【例4】在右图所示立方体的八个顶点上标出1~9中的八个,使得每个面上四个顶点所标数字之和都等于k,并且k不能被未标出的数整除.分析:标出的八个数是每面四个数和的2倍,是偶数,1~9和为45 ,因此未标出的数是一个奇数,在1,3,5,7,9中选一个数,并使余下八个数之和的一半不能被这个数整除,依此可知未标出的数是7.下面用余下的8个数填图,每面四个数和为:(45-7)÷2=19.如果已知某一面上四个数和为19.那么与其平行的面上四数和也必为19.因此我们只考虑有公共顶点的三个面即可.下面我们考虑以9为公共顶点的三个面.由于8,9不公面,因此8在顶点9的对顶点上,有公共点9的三个面上,每面其余三个数和为10,且每两个面有一个公共顶点.由此试验易得三个面上的数分别为:(6,3,1),(5,4,1),(3,2,5),填图如右下图.【例5】右图中大三角形被分成九个小三角形,大三角形的每条边都与其中五个小三角形有公共点,试将1~9九个自然数分别填入这九个小三角形内,使得每条边上的五个小三角形内的数字之和都相等.问这个和最小值是多少?最大值是多少?分析:1~9和为45.设3个只属于一条边的数的和为k,则每条边上五个数和为:(45×2-k)÷3=30-13 k.K最小时,取k=1+2+3=6,一边上的和为:30-13×6=28;K最大时,取k=7+8+9=24,一边上的和为:30-13×24=22,因此这个和最大为28,最小为22.【巩固】将自然数1~11填入右图的11个○中,使得每条直线(共10条)上的三个数字之和都相等.分析:左下角的数属于5条直线共有,对角线上中间的数属于4条直线共有,其余数只属于2条或3条直线,所以左下角的数和对角线上中间的数处于特殊地位,应当首先确定这两个数以及每条直线上三数之和.设每条直线上三数之和为k.由图(1)中5条实线上所有数字之和,可列方程:5k=(1+2+…+11)+4a ,即6645ak+=;因为k是整数,所以a只能取1,6或11;再由图(2)中四条实线上所有数字之和,可列方程:4k=(1+2=…+11)+a , 即664a k+ =.得到a只能取2,6或10. 综合以上讨论知a=6,k=18.在图(3)中的5条实线中,只有b属于3条实线共有. 注意到这5条实线上的数字没有6,在剩下的十个数字中,三个数的和等于18的共有以下八组:3+4+11;1+8+9;1+7+10;3+5+10;2+7+9;2+5+11;3+7+8;4+5+9,其中同时出现在三个算式中的数只有3和9,所以b只可能是3或9,此时c等于9或3. 由同时含有3的三个算式知,若b=3,c=9,则d,e只能取4,11或5,10或7, 8,由于每条直线上的三个数之和为18,且c=9,故d,e不能等于10或11,所以d,e只能取7,8. 由此可得左下图中的答案.同理,若b=9,c=3,则可得右下图的另一答案.【巩固】右图是大家都熟悉的奥林匹克的五环标志. 请将1~9分别填入五个圆相互分割的九个部分,并且使每个圆环内的数字之和都相等.分析:设每个圆内的数字之和为k,则五个圆内的数字之和是5k,它等于1~9的和45,再加上两两重叠处的四个数之和. 而两两重叠处的四个数之和最小是1+2+3+4=10,最大是6+7+8+9=30,所以,5k≤45+30=75且5k≥45+10=55,即11≤k≤15 .当k=11,13,14时可得四种填法(见右下图),k=12,15时无解.【例6】自然数1~12中已有一些填人图中的圆圈中,试填入其余各数,使得每条直线上的四数之和相等.分析:十二个数中每个数都出现在两条直线上,每条直线上四个数之和为:[(1+12)×12÷2]×2÷6=26.考虑以a、b、c标出顶点的大三角形的三条边,如图(1):则:10264261226a bb cc a++=⎧⎪++=⎨⎪++=⎩,可得a=4,b=12,c=10同理可得另一个大三角形三个顶点的数.结果如图(2):【例7】自然数1~12中有一些已填入图中圆圈内,请将其余的分别填入空圆圈内,使得圆中的四个三角形周边上的数字之和相等.分析:如下图(1),我们设六条边和分别为S1~S6,则根据题目有S 1 +S 2 +S 3 = S 1 +S 5 +S 6 =S 2 +S 4 +S 6 = S 3+S 4+S 5 , 于是我们有:56233526S S S S S S S S +=+⎧⎨+=+⎩,进而可得:2536S S S S =⎧⎨=⎩因此图中六边和满足:142536,,S S S S S S ===,由14S S =及已知1和3的位置知1S 和4S ,两边圆圈中的数差2,同理,另两组对应相等边中的空圆圈中的数差为4和4.也就是说我们要把2,4,6,8,10,12分成三组差分别为2,4,4的数,这里的分法不唯一,给出答案如图(2)仅供参考.142536,,S S S S S S ===数 字 谜【例8】 在下面的算式中,汉字“第、十、一、届、华、杯、赛”代表1,2,3,4,5,6,7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于多少?分析:根据加法规则,“第”=1.“届”+“赛”=6或“届”+“赛”=16.若“届”+“赛”=6,只能是“届”、“赛”分别等于2或4,此时“一”+“杯”=10 只能是“一”、“杯”分别为3或7.此时“十”+“华”=9,“十”、“华’’分别只能取 (1,8),(2,7),(3,6),(4,5).但l,2,3,4均已被取用,不能再取.所以,“届”+ “赛”=6填不出来,只能是“届”+“赛”=16.这时“届”、“赛”只能分别取9和7.这 时只能是“一”+“杯”+1=10,且“十”+“华”+1=10,也就是“一”+“杯”=9, 同时“十”+“华”=9.所以它们可以分别在(3,6),(4,5)两组中取值.因此“第、十、一、届、华、杯、赛”所代表的7个数字的和等于1+9+9+16=35.【例9】 右面算式寓意第8届华杯赛于新世纪的第1年举办.新、世、纪、华、杯、赛代表1,2,3,4,5,6,7,8,9中的六个数字(不同的文字代表不同的数字),请把这个算式恢复出来.分析:原式变形为=华杯赛新世纪8.华杯赛最大可能是987.易知新=1. 由12×8=96,13×8=104,可知世=2.若纪≥5,新世纪×8≤987<1000,所以纪等于4或3;若纪=4,124×8=992,出现华=杯=9,世=赛=2,与题设条件不符; 若纪=3,123×8=984,合乎题意. 所以,题设等式恢复出来是81984123=.【例10】 将0~9中的8个不同的数字分别用a 、b 、c 、d 、e 、f 、g 、h 替换.在替换规则下:g×g =db ,g ×c=bd ,g ×f=ef ,ag b eh +=,如上面4个式子中,“+”、“×”、“=与平常算术中相应的符号意义相同,而且也是十进位制.在这种替换规则下,ca e ⨯的数值等于 .分析:由g×g =db 知,g≥4. 若g=4,d=1,与g ×c=bd 是偶数矛盾; 若g=5,则d=2,b=5,与g ≠b 矛盾; 若g=6,则d=3,b=6,与g ≠b 矛盾;若g=7,则d=4,b=9,由g×c =bd =94,得到c =4÷7=3137也不合题意; 若g=8,则d=6,b=4,由g×c =bd 46,得到c=46÷8=354,仍不合题意; 若g=9,则d=8,b=1,由g×c =bd =18,得到c=18÷9=2,再由g ×f=ef ,f=5,e=4,再由ag b eh +=,得a=e-1=3.所以23492ca e ⨯=⨯=.【例11】 下面算式中不同的汉字代表不同的数字,相同的汉字代表相同的数字。
三年级数学思维训练:第11讲有趣的数阵图

三年级数学思维训练:第11讲有趣的数阵图第 1 讲找规律填图第 1 讲找规律填图能力检测第 2 讲加减法巧算第 2 讲加减法巧算能力检测第 2 讲加减法巧算能力检测第 3 讲高斯求和第 3 讲高斯求和能力检测第 4 讲找规律填数第 4 讲找规律填数能力检测第 5 讲简单推理第 5 讲简单推理能力检测第 6 讲植树中的学问第 6 讲植树中的学问能力检测第 7 讲学会倒着想第 8 讲简单周期第 8 讲简单周期能力检测第 9 讲填运算符号第 9 讲填运算符号能力检测第 10 讲神奇的一笔画第 10 讲神奇的一笔画能力检测第 11 讲有趣的数阵图传说大禹治水的时候,一只灵龟从水中翩然浮出。
令人称奇的是,这只乌龟的背上竟刻有一幅图(如图①所示)。
如果将图上的点转化成数字,一个点记为一个“1”,那么图①就转变成了数字图(图②)。
研究这幅数字图你会发现:每一行、每一列,甚至每一条对角线上的三个数的和都相等。
像上面的图②这样,把一些数按照定要求排列成各种图形,使图形中的每一条直线段或若干条线段的数字和相等,这样呈现的图形,就叫作数阵图。
数阵图可以是正方形,还可以是长方形、三角形、圆、多边形、星形、花瓣形、十字形……但不管是哪一种形状的数阵图,填写时都应注意两点:1.抓住数阵中的“特殊数”,比如两线交点上的数、长方形和正方形的顶点上的数……这些数与其他数相比,往往重复计算了多次,因而不妨作为解决数阵问题的一个突破口。
2.确定突破口后,对照“和相等”的条件,用尝试的方法求解其他数。
但有时因为数字存在不同的组合方法,因此答案往往不是唯一的。
【例1】将1、2、3、4、5这五个数分别填入右图中,组成一个“十字数阵图”,使图中横行三个数的和与竖列三个数的和相等。
分析图中最中间的那个数最特殊,因为横行三个数相加和竖行三个数相加都算了它,即它被算了2次。
因此不妨把它当作解决问题的突破口。
假设它填1,剩下的四个数刚好可以分成2 + 5 = 3 + 4,因而得到本题的一个解;假设它填2,由于剩下的四个数不能分组成两组,使两组的和相等。
学会《数阵图》,一年级数学就容易拿到100分,赶紧试试看!

学会《数阵图》,一年级数学就容易拿到100分,赶紧试试
看!
数阵图,是小学一年级的一个稍有难度的题型。
很多同学一开始不是很习惯做这类题,但是,也有不少同学玩这个题型很带劲!
今天,翼翔老师给大家带来几个练习,让你发掘其中的秘密,各种嗨起来!
有什么问题,请留言,私信!
当然,您的点赞是对我莫大的鼓励与支持!文末有更多教育链接,可以查看!
特别提醒:
一开始,最好是自行练习,不要提示,试着把数字填进去,给一个试探的过程。
答案其实不重要,重要的是过程。
我们在做这些题目的时候,需要有一个不断评估判断,做决定的过程。
这个思维的过程其实很宝贵,有时候如果某些同学遇到困难,需要给一些提示,需要给一些鼓励,那么剩下的工作都是可以自行完成的。
第一类题:比较简单,已知两个数,求剩下的一个数,不需要试,直接就可以写出答案。
第二类题:需要找到突破口,即,找到已经有2个数字的某一行,某一列,或者是斜行。
第三类题:开放型,没有特定答案
剩下的,就给大家自行练习吧!。
数阵图---精品模板

解: . a . 1
65 243
b. 1
56
3 42
c.
2
64
1 53
d. 2
46
e。 3
54
f。 3
45
3 51
1 62
2 61
练习一
1、把 1~8 个数分别填入○中,使每条边上三个数的和相等。
第1页共6页
2、把 1~7 填入下图中,使每条线段上三个○内的数的和相等。
3、把 1~11 填入图中,使每条线上三个数的和相等。
5+19=7+17=11+13 解: 于是得到下图的填法。
第2页共6页
练Байду номын сангаас二
1、将 1~8 个数分别填入图中,使每个圆圈上五个数和分别为 20,21,22。 2、把 1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等。
3、把 1~12 这十二个数,填入下图中的 12 个○内,使每条线段上四个数的和相等,两个同 心圆上的数的和也相等。
10
6
4、把 1~8,填入图中,使每条线及正方形四个顶点上的数的和相等。
5、把 1~16 这 16 个数,填入图中的 16 个○内,使五个正方形的四个顶点上○内数的和 相等.
6、将 1-12 这十二个数分别填入图中的十二个小圆圈里,使每条直线上的四个小圆圈中的 数字之和 26。
第5页共6页
7、将 1~10 这十个数分别填入下图中的十个○内,使每条线段上四个○内数的和相等,每 个三角形三个顶点上○内数的和也相等。
解:
练习三
1、把 1~8 这 8 个数填入下图,使每边上的加、减、乘、除成立.
-=
÷
+
= =
×= 2、把 0~9 填入 10 个小三角形中,使每 4 个小三角形组成的大三角形的和相等。
数阵问题整理版

数阵问题整理版-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN数阵趣味导读:有些数按照一定的要求排列成各种各样的图形,就叫做数阵图,数阵填数的游戏是非常有趣的,有时也有一定的难度。
不过它能促使我们积极地思考问题,分析问题,拓展我们的能力。
有的同学说:这样的数阵图填写时只能采取试的方法,没有其他捷径好走。
其实这话不对。
填写数阵图时,我们应抓住数阵中的关键位置(例如两种线的交点,长方形和正方形的顶点),再根据题目的要求,进行必要的计算,先填写这些关键位置的数,再填写出其他位置的数。
一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为“数阵图”,数阵图的种类繁多,绚丽多彩,这里只向大家介绍三种数阵图,即封闭型数阵图、辐射型数阵图和复合型数阵图。
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字:要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力,思维的灵活性和严密性。
【解法总结】:做数阵题目,我们的一般步骤是:①.先观察在图中有哪些格子重复了,重复了几次。
②.根据题中给出的数字以及图形来发现重复的这几个数有什么特点。
③.看看在给出的数中有哪些数符合我们特点,再通过试算,确定每个格子中的数。
【例题1】将1,2,3,4,5这五个数分别填入下图的各正方形中,组成一个“十字数阵图”使图中横行三个数的和与竖行三个数据的和相等。
解析:根据图形的特点,中间那个数是横行与竖行共用的,要使横行与竖行三个数的和相等,可以先确定中间的数,再让左右两数的和与上、下两数的和相等。
①中间填1,则剩下2,3,4,5,而2+5=4+3,共有8种填法。
②中间填2,则剩下1,3,4,5而这四个数无法组成□+□=□+□的形式所以中间不可填?③中间填3,则剩下1,2,4,5,而1+5=2+4,共有8种填法:④中间填4,则剩下1,2,3,5而这四个数无法组成□+□=□+□的形式所以中间可能填4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题十一数阵图
第一讲三阶幻方
【母题详解】把1~9这九个数字填写在右图正方形的九个方格中,使得每一横行、每一竖列和每条对角线上的三个数之和都相等。
分析:我们首先要弄清每行、每列以及每条对角线上三个数字之和是几。
我们可以这样去想:因为1~9这九个数的和是45,正好是三个横行数字之和,所以每一横行的数字之和等于45÷3=15。
也就是说,每一横行、每一竖列以及每条对角线上三个数字之和都等于15。
在1~9这九个数字中,三个不同的数相加等于15的有:
9+5+1,9+4+2,8+6+1,8+5+2,
8+4+3,7+6+2,7+5+3,6+5+4。
因此每行、每列以及每条对角线上的三个数字可以是其中任一个算式中的三个数字。
因为中心方格中的数既在一个横行中,又在一个竖列中,还在两对角线上,所以它应同时出现在上述的四个算式中,只有5符合条件,因此应将5填在中心方格中。
同理,四个角上的数既在一个横行中,又在一个竖列中,还在一条对角线上,所以它应同时出现在上述的三个算式中,符合条件的有2,4,6,8,因此应将2,4,6,8填在四个角的方格中,同时应保证对角线两数的和相等。
解:经试验,有下面八种不同填法:
图11-1-1
上面的八个图,都可以通过一个图的旋转和翻转得到。
例如,第一行的后三个图,依次由第一个图顺时针旋转90°,180°,270°得到。
又如,第二行的各图,都是由它上面的图沿竖轴翻转得到。
所以,这八个图本质上是相同的,可以看作是一种填法。
金钥匙:
一般地,将九个不同的数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,那么这样的图称为三阶幻方,相等的和我们称为幻和。
通过观察可以发现,在三阶幻方中,幻和正好是中间数的3倍。
【举一反三】
变式一:用11,13,15,17,19,21,23,25,27编制成一个三阶幻方。
【解】给出的九个数形成一个等差数列, 1~9也是一个等差数列。
对照1~9排成的三阶幻方,不难发现:中间方格里的数字应填等差数列的第五个数,即应填19;填在四个角上方格中的数是位于偶数项的数,即13,17,21,25,而且对角两数的和相等,即13+25=17+21;余下各数就不难填写了(见图11-1-2)。
图11-1-2
变式二:在下面的阵列中,第一行第三列的位置上填5,第二行第一列的位置上填6,如图11-1-3,请你在其它方格中填上适当的数,使方阵横、纵、斜三个方向的三个数之和为36。
图11-1-3
【解】为了叙述方便,我们将其余空格的数字用字母表示,如图11-1-4。
图11-1-4
36÷3=12,所以C=12
从第二行可求出D=36-12-6=18
从对角线中可求出E=36-12-5=19
从第一列可求出A=36-6-19=11
从第一行可求出B=36-5-11=20
从第二列可求出F=36-20-12=4
从第三列可求出G=36-5-18=13
得到三阶幻方如下:
图11-1-5
变式三:将九个连续自然数填入3行3列的九个空格中,使每一横行,每一竖行及每一条对角线上三个数的和都等于45。
因为幻和为45,所以中心数为45÷3=15,因为是9个连续的自然数,则这9数是11、12、13、14、15、16、17、18、19。
这些数正好比1-9这9个数分别大10,因此我们可以借助1-9的填数方法排出三阶幻方。
图11-1-7
【高分密码】
解决三阶幻方时,中心数起着至关重要的作用。
利用幻和=中心数×3这个关系式,在已知幻和的情况下,可先求出中心数,在已知中心数的情况下,可求出幻和,以便其它数的求出。
第二讲复杂的数阵问题
【母题详解】把20以内的质数分别填入图11-2-1的○中,使得图中用箭头连接起来的四个数之和都相等。
分析:由图11-2-2看出,三组数都包括左、右两端的数,所以每组数的中间两数之和必然相等。
20以内共有2,3,5,7,11,13,17,19八个质数,两两之和相等的有5+19=7+17=11+13,因此2和3只能填在两端,其他的填写时注意对应就可以了。
解:
图11-2-2
金钥匙:
解决复杂的数阵问题时,要分析数阵的特点,抓住题目中填写的要求,找出突破口,然后再解决问题。
【举一反三】
变式一:在图11-2-3的六个○内各填入一个质数(可取相同的质数),使它们的和等于20,而且每个三角形(共5个)顶点上的数字之和都相等。
图11-2-3
【解】因为大三角形的三个顶点与中间倒三角形的三个顶点正好是图中的六个○,又因为每个三角形顶点上的数字之和相等,所以每个三角形顶点上的数字之和为20÷2=10。
10分为三个质数之和只能是2+3+5,由此得到图11-2-4的填法。
图11-2-4
变式二:将3-10这八个自然数分别填入图11-2-5中正方体的八个顶点上
的○中,使正方体每个面四个顶点上○中的数的和相等。
图11-2-5
【解】从图11-2-5上可以看出,这8个数正好分布在上、下两个面的顶点上,因为每个面上四个顶点上的数字之和相等,所以每个面上4个数的和是(3+10)×8÷2÷4=26。
由于每个面上四个顶点上的数字之和等于26,所以与10在一个面上的另外三个顶点数之和应等于16。
在3-9中,三个数之和等于10的有三组:16=3+4+9
=4+5+7
=3+5+8,
将这三组数填入10所在的三个面上,而6没有出现,所以6应该填在与10没有共同面的顶点上。
经过尝试可得到图11-2-6的填法。
图11-2-6
变式三:从1~13这13个数中挑出12个数,填入图1中的方格中,使每一横行,四数之和相等,每一竖列三个数之和相等。
如图11-2-7:
图11-2-7
【解】因为要使方格中4个竖行和3个横行的数的和都相等,所以这些数的和应该既是4的倍数,又是3的倍数,也就是4×3=12的倍数。
在1~13这13个数中,因为1+2+3+……+13=91,91÷12=7……7,所以1~13中去掉7,剩下12个数的和是91-7=84,因此要求横行和为84÷3=28,竖列和为84÷4=21,先将除7外的12个数分为4组,每组中3个数之和为21,然后再调整,使每横行四个数的和为28,这样可得出解,如图11-2-8:
1 11 913104
2312
685
13
3
5
1410
12112
869
图11-2-8
【高分密码】
解决复杂的数阵问题时,我们一般根据数阵的特点去分析,比如找出重叠数或根据观察的解度把所给的数据分成若干组,然后再进行尝试与调整,最终找出正确的填写方法。
