《c语言数据结构》2第二章 线性表
数据结构课后习题答案第二章 线性表

第二章线性表2.1描述以下三个概念的区别:头指针,头结点,首元结点(第一个元素结点)。
并说明头指针和头结点的作用。
答:头指针是一个指针变量,里面存放的是链表中首结点的地址,并以此来标识一个链表。
如链表H,链表L等,表示链表中第一个结点的地址存放在H、L中。
头结点是附加在第一个元素结点之前的一个结点,头指针指向头结点。
当该链表表示一个非空的线性表时,头结点的指针域指向第一个元素结点,为空表时,该指针域为空。
开始结点指第一个元素结点。
头指针的作用是用来惟一标识一个单链表。
头结点的作用有两个:一是使得对空表和非空表的处理得以统一。
二是使得在链表的第一个位置上的操作和在其他位置上的操作一致,无需特殊处理。
2.2填空题1、在顺序表中插入或删除一个元素,需要平均移动(表中一半)元素,具体移动的元素个数与(表长和该元素在表中的位置)有关。
2、顺序表中逻辑上相邻的元素的物理位置(必定)相邻。
单链表中逻辑上相邻的元素的物理位置(不一定)相邻。
3、在单链表中,除了首元结点外,任一结点的存储位置由(其直接前驱结点的链域的值)指示。
4、在单链表中设置头结点的作用是(插入和删除元素不必进行特殊处理)。
2.3何时选用顺序表、何时选用链表作为线性表的存储结构为宜?答:在实际应用中,应根据具体问题的要求和性质来选择顺序表或链表作为线性表的存储结构,通常有以下几方面的考虑:1.基于空间的考虑。
当要求存储的线性表长度变化不大,易于事先确定其大小时,为了节约存储空间,宜采用顺序表;反之,当线性表长度变化大,难以估计其存储规模时,采用动态链表作为存储结构为好。
2.基于时间的考虑。
若线性表的操作主要是进行查找,很少做插入和删除操作时,采用顺序表做存储结构为宜;反之,若需要对线性表进行频繁地插入或删除等的操作时,宜采用链表做存储结构。
并且,若链表的插入和删除主要发生在表的首尾两端,则采用尾指针表示的单循环链表为宜。
2.10 Status DeleteK(SqList &a,int i,int k)//删除线性表a中第i个元素起的k个元素{if(i<1||k<0||i+k-1>a.length) return INFEASIBLE;for(count=1;i+count-1<=a.length-k;count++) //注意循环结束的条件a.elem[i+count-1]=a.elem[i+count+k-1];a.length-=k;return OK;}//DeleteK2.11设顺序表中的数据元素递增有序,试写一算法,将X插入到顺序表的适当位置上,以保持该表的有序性。
数据结构(C)第2章线性表

第1章介绍了几种基本逻辑结构:线性结构、 树形结构和图结构。线性结构是最简单、最基本 的数据结构,本章讨论线性表的基本概念、存储 结构以及相关运算。 主要内容:
• 线性表的基本概念 • 线性表的顺序存储结构及实现 • 线性表的链表存储结构及实现 • 线性表的应用
2021/6/12
1
2.1 线性表的基本概念
2021/6/12
5
2.2.1 线性表的顺序存储结构
顺序存储结构是最简单常用 的方法。顺序存储结构也称为 向量存储。向量是内存中一批 地址连续的存储单元。
线性表的顺序存储结构, 要求逻辑上相邻的数据元素在 物理位置上也一定是相邻的, 如图所示。
2021/6/12
6
特点:逻辑上相邻—物理地址相邻; 可以随机存取数据;
typedef int ElemType ;
class SqList1
{ private:
ElemType elem[MAXSIZE]; //一维数组
int length ;
//线性表长度
public:
………;//其他成员函数;
};
2021/6/12
9
在面向对象的程序设计中,通常将数据元素 的存储结构和对数据的操作封装在一个类之中。
2021/6/12ห้องสมุดไป่ตู้
3
2.1.2 线性表的抽象数据类型
ADT Linear_list {
数据对象:D={ai | ai∈ ElemSet , i=1,2,…,n, n≥0 ;} 数据关系:R={<ai-1 ,ai > | ai-1 ,ai∈D, i=2,3, …,n } 基本操作:初始化空线性表;
求线性表表长;
《数据结构C语言版》----第02章

同理可证:顺序表删除一元素的时间效率为: 同理可证:顺序表删除一元素的时间效率为: T(n)=(n-1)/2 ≈O(n) O(n) (
插入效 E = ∑ is 率: i=0
n
1 n n pi ( n − i ) = ∑ (n − i) = 2 n + 1 i=0
n −1 删除效 1 n −1 n −1 Edl = ∑ qi (n − i ) = ∑ (n − i ) = 率: n i =0 2 i =0
2.2 线性表的顺序表示和实现
顺序存储结构的线性表称作顺序表 1.顺序表的存储结构 顺序表的存储结构
实现顺序存储结构的方法是使用数组。数组把线性表 实现顺序存储结构的方法是使用数组。 使用数组 的数据元素存储在一块连续地址空间的内存单元中, 连续地址空间的内存单元中 的数据元素存储在一块连续地址空间的内存单元中,这样 线性表中逻辑上相邻的数据元素在物理存储地址上也相邻。 线性表中逻辑上相邻的数据元素在物理存储地址上也相邻。 数据元素间的逻辑上的前驱、 数据元素间的逻辑上的前驱、后继逻辑关系就表现在数据 元素的存储单元的物理前后位置上。 元素的存储单元的物理前后位置上。 顺序表的存储结构如图所示
2.线性表抽象数据类型 2.线性表抽象数据类型
数据集合:{ 的数据类型为DataType 数据集合 { a0, a1, … , an-1 }, ai的数据类型为 (1) ListInitiate(L) 初始化线性表 (2) ListLength(L) 求当前数据元素个数 操作集合: 操作集合 (3) ListInsert(L,i,x) 插入数据元素 (4) ListDelete(L,i,x) 删除数据元素 (5) ListGet(L,i,x) 取数据元素
printf("参数 不合法 \n"); 参数i不合法 参数 不合法! return 0;
数据结构(C语言版)第2章 线性表

案例2.3 :图书信息管理系统
图书顺序表
图书链表
总结
01
线性表中数据元素的类型可以为简单类型,也 可以为复杂类型。 许多实际应用问题所涉的基本操作有很大相似
02
性,不应为每个具体应用单独编写一个程序。
从具体应用中抽象出共性的逻辑结构和基本操 作(抽象数据类型),然后实现其存储结构和 基本操作。
03
04级计算机1班 04级计算机2班 04级计算机3班 04级计算机4班
:
:
:
:
:
数据元素都是记录;
元素间关系是线性
同一线性表中的元素必定具有相同特性
目 录 导 航
Contents
2.1 2.2 2.3 2.4 2.5
线性表的定义和特点 案例引入 线性的类型定义 线性表的顺序表示和实现 线性表的链式表示和实现
线性表
目标
target
01 02 03 04
OPTION
了解线性结构的特点
OPTION
掌握顺序表的定义、查找、插入和删除
掌握链表的定义、创建、查找、插入和删除 能够从时间和空间复杂度的角度比较两种存储结构的不同 特点及其适用场合
OPTION
OPTION
目 录 导 航
Contents
2.1 2.2 2.3 2.4 2.5
4
查找
3
目 录 导 航
Contents
2.1 2.2 2.3 2.4 2.5
线性表的定义和特点 案例引入 线性的类型定义 线性表的顺序表示和实现 线性表的链式表示和实现
2.6
2.7 2.8
顺序表和链表的比较
线性表的应用 案例分析与实现
线性表的顺序表示和实现
数据结构(C语言描述)——线性表

prior
data
next
非空双向循环链表: L a
b p
A c
B
p->prior->next= p= p->next->proir;
删除
a
p->prior->next=p->next;
b c
P 算法描述
p->next->prior=p->prior;
void del_dulist(Dulinklist p) {p->prior->next=p->next; p->next->prior=p->prior; free(p); }
∴ T (n ) = O (n )
p
否则,为n
插入:在线性表两个数据元素a和b间插入x,已知p指向a a b x
p->next=s; s
算法描述 算法评价
s->next=p->next;
T (n ) = O (1 )
删除:单链表中删除b,设p指向a p a b c
p->next=p->next->next;
Eis =
∑
n +1 i =1
Pi ( n − i + 1 )
∴ T (n ) = O (n )
1 若认为 Pi = n +1 1 n +1 n 则 Eis = ∑ ( n − i + 1) = 2 n + 1 i =1
删除
定义:线性表的删除是指将第i(1≤i ≤ n)个元素删除, 使长度为n的线性表
§2.3 线性表的链式存储结构
特点:
用一组任意的存储单元存储线性表的数据元素 利用指针实现了用不相邻的存储单元存放逻辑上相邻 的元素 每个数据元素a ,除存储本身信息外,还需存储其直 a 接后继的信息 结点 结点
算法与数据结构——C语言描述-第2章 线性表

09001001 张丰 男 09001002 刘小红 女 09001003 李静 女 09001004 王建平 男 …………………
• • • • • •
表中所含元素的个数称为表的长度。 长度为零的表称为空表。 k0称为第一个元素, kn-1称为最后一个元素, ki(0≤i≤n-2)是ki+1的前驱, ki+1是ki的后继。
2.3 链接表示
这种存储结构不要求逻辑关系上相邻 的两个元素在物理位置上也相邻存储,而 是通过增加指针来指示元素之间的逻辑关 系和后继元素的位置。
3.2.1 单链表表示
每个元素除了需要存储自身的信息外, 还要存储一个指示其后继的信息(即后 继元素存储位置),这两部分信息组成 了一个数据元素的存储结构,称为一个 结点(注意:每个结点所占用的存储单 元应该是连续的).
如果palist是一个指向SeqList类型的指针变量,则:
palist->MAXNUM:顺序表中最大元素的个数;
palist->n:顺序表中实际元素的个数;
palist->element[0] ,…,palist->element[palist->n - 1]: 顺序表中的各个元素。
2.2.2 运算的实现
2.2.3 分析与评价
• 在有n个元素的线性表里,在下标为i(第i+1 个)的元素之前插入一个元素需要移动n - i 个元素;删除下标为i(第i+1个)的元素需 要移动n - i - 1个元素。如果在下标为i的位置 上插入和删除元素的概率分别是Pi和Pi′,则 插入时的平均移动数是: • 删除的平均移动数是:
线性表的逻辑结构:L=<K,R> 其中K={ k0,k1,…,kn-1}, R={<ki, ki+1>|0≤i≤n-2 }, i称为元素ki的索引或下标。 表中的元素又称表目。
数据结构(C语言版)-第2章线性表
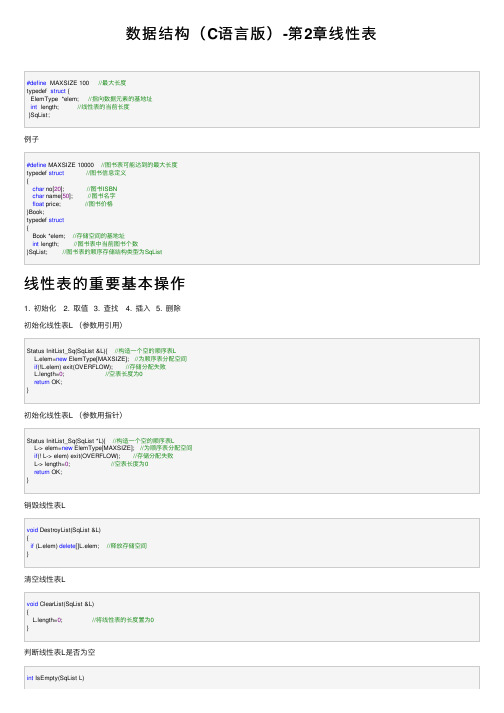
数据结构(C语⾔版)-第2章线性表#define MAXSIZE 100 //最⼤长度typedef struct {ElemType *elem; //指向数据元素的基地址int length; //线性表的当前长度}SqList;例⼦#define MAXSIZE 10000 //图书表可能达到的最⼤长度typedef struct//图书信息定义{char no[20]; //图书ISBNchar name[50]; //图书名字float price; //图书价格}Book;typedef struct{Book *elem; //存储空间的基地址int length; //图书表中当前图书个数}SqList; //图书表的顺序存储结构类型为SqList线性表的重要基本操作1. 初始化2. 取值3. 查找4. 插⼊5. 删除初始化线性表L (参数⽤引⽤)Status InitList_Sq(SqList &L){ //构造⼀个空的顺序表LL.elem=new ElemType[MAXSIZE]; //为顺序表分配空间if(!L.elem) exit(OVERFLOW); //存储分配失败L.length=0; //空表长度为0return OK;}初始化线性表L (参数⽤指针)Status InitList_Sq(SqList *L){ //构造⼀个空的顺序表LL-> elem=new ElemType[MAXSIZE]; //为顺序表分配空间if(! L-> elem) exit(OVERFLOW); //存储分配失败L-> length=0; //空表长度为0return OK;}销毁线性表Lvoid DestroyList(SqList &L){if (L.elem) delete[]L.elem; //释放存储空间}清空线性表Lvoid ClearList(SqList &L){L.length=0; //将线性表的长度置为0}判断线性表L是否为空int IsEmpty(SqList L){if (L.length==0) return1;else return0;}获取线性表L中的某个(第i 个)数据元素的内容int GetElem(SqList L,int i,ElemType &e){if (i<1||i>L.length) return ERROR;//判断i值是否合理,若不合理,返回ERRORe=L.elem[i-1]; //第i-1的单元存储着第i个数据return OK;}在线性表L中查找值为e的数据元素int LocateELem(SqList L,ElemType e){for (i=0;i< L.length;i++)if (L.elem[i]==e) return i+1; //返回是第⼏个元素return0;}在线性表L中第i个数据元素之前插⼊数据元素eStatus ListInsert_Sq(SqList &L,int i ,ElemType e){if(i<1 || i>L.length+1) return ERROR; //i值不合法if(L.length==MAXSIZE) return ERROR; //当前存储空间已满for(j=L.length-1;j>=i-1;j--)L.elem[j+1]=L.elem[j]; //插⼊位置及之后的元素后移L.elem[i-1]=e; //将新元素e放⼊第i个位置++L.length; //表长增1return OK;}//见下图(1)判断插⼊位置i 是否合法。
数据结构第02章线性表C

104
108
112
116
119
若此分量定义为指针型,属于动态链表; 若此分量定义为整型(放下标),则属于静态链表。
静态单链表的类型定义如下:
#define MAXSIZE 1000 //预分配最大的元素个数(连续空间 typedef struct { ElemType data ; //数据域 int cur ; //指示域 }component , SLinkList[MAXSIZE] ; //这是一维结构型数组
(2)
(3)
微软亚洲研究院 招聘的笔试题 例3:试用C或类C语言编写一个高效算法,将一循 环单链表就地逆置。 操作前:(a1, a2, … ai-1,ai, ai+1 ,…, an)
操作后:( an, … ai+1 ,ai, ai-1 ,…, a2, a1 )
操作后:( an, … ai+1 ,ai, ai-1 ,…, a2, a1 )
4. 如何编程实现两个一元多项式相加?
1. 一元多项式的数学通式?
A( x ) am1 x
em1
a m 2 x
em 2
...a0 x
e0
机内存储方式? 一般用顺序存储——只存系数项(但零系数项也不能遗漏)
… + a5 aP a a2 3x1000 x1)= 1+ x2000am-1 0 2000( m-2
双向链表的删除操作:
设p指向第 i 个元素,删除第 i 个 元素 p ai-1 ai ai+1 注意:要修改 双向指针!
指针域的变化:
后继方向:ai-1的后继由 ai ( 指针p)变为 ai+1(指针 p ->next ); p ->prior->next = p->next ;
数据结构(C语言)_2

第二章线性表本章的重点:掌握顺序表和单链表上实现的各种基本算法及相关的时间性能分析;难点:使用本章所学的基本知识设计有效算法解决与线性表相关的应用问题。
要求达到“识记”的内容:线性表的逻辑结构特征,线性表上定义的基本运算,并利用基本运算构造出较复杂的运算。
要求达到“综合应用”的内容:顺序表的含义及特点,顺序表上的插入、删除操作,解决简单应用问题。
链表如何表示线性表中元素之间的逻辑关系;单链表、双链表、循环链表链接方式上的区别;单链表上实现的建表、查找、插入和删除等基本算法及其时间复杂度。
循环链表上尾指针取代头指针的作用,以及单循环链表上的算法与单链表上相应算法的异同点。
双链表的定义和相关算法。
利用链表设计算法解决简单应用问题。
要求达到“领会”的内容:顺序表和链表的比较,以及如何选择其一作为其存储结构才能取得较优的时空性能。
线性结构的特点:在数据元素的非空有限集中,⑴存在唯一的一个被称做“第一个”的数据元素;⑵存在唯一的一个被称做“最后一个”的数据元素;⑶除第一个之外,集合中的每个数据元素均只有一个前驱;⑷除最后一个之外,集合中每个数据元素均只有一个后继。
2.1线性表的逻辑结构一、线性表的定义线性表是最常用且最简单的一种数据结构。
一个线性表是n个数据元素的有限序列。
数据元素可以是一个数、一个符号、也可以是一幅图、一页书或更复杂的信息。
线性表例:1、2、3、数据元素也可由若干个数据项组成(如上例3)。
这时常把数据元素称为记录。
含有大量记录的线性表又称文件。
线性表中的数据元素类型多种多样,但同一线性表中的元素必定具有相同特性,即属同一数据对象,相邻数据元素之间存在着序偶关系。
ai是ai+1的直接前驱元素,ai+1是ai的直接后继元素。
线性表中元素的个数n定义为线性表的长度,为0时称为空表。
在非空表中的每个数据元素都有一个确定的位置。
ai是第i个元素,把i 称为数据元素ai在线性中的位序。
二、线性表的类型定义⒈抽象数据类型线性表的定义如下:ADT List{数据对象: D={ai| ai(-ElemSet,i=1,2,...,n,n>=0}数据关系: R1={<ai-1,ai>| ai-1,ai(- D,i=2,...,n}基本操作:InitList(&L)DestroyList(&L)ClearList(&L)ListEmpty(L)ListLength(L)GetElem(L,i,&e)LocateElem(L,e,compare())PriorElem(L,cur_e,&pre_e)NextElem(L,cur_e,&next_e)ListInsert(&L,i,e)ListDelete(&L,i,&e)ListTraverse(L,visit())}ADT List2、部分操作的类C实现:InitList(&L){ L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));if(!L.elem)exit(OVERFLOW);L.length=0;L.listsize=LIST_INIT_SIZE;return OK;}//InitListGetElem(L,i,&e){ *e=L.lem[i]}//GetElemListInsert(List &L,int i,ElemType e){ if(i<1||i>L.length+1) return ERROR;q=&(L.elem[i-1]);for(p=&(L.elem[L.length-1]);p>=q;--p) *(p+1)=*p;*q=e;++L.length;return OK;}//ListInsertvoid union(List &La,List &Lb)//利用两个线性表LA和LB分别表示两个集合A和B,现要求一个新的集合A=A∪B。
数据结构2第二章:线性表

单链表的删除图例
单链表的删除算法
Status ListDelete(LinkList L,int i,ElemType &e) //算法2.10 { //在带头结点的单链表L中,删除第I个元素,并由e返回其值。 p=L;j=0; while(p->next&&j<i-1) // 寻找第i个结点,并令p指向其前趋 { p=p->next; ++ j; } if(!p->next||j>i-1) return ERROR; // 删除位置不合理 q=p->next; // 删除并释放结点 p->next=q->next; e=q->data; free(q); return OK; }
顺序表的运算
• 插入运算 • 删除运算 • 总结
–由此可见,在顺序表中插入或删除一个数 据元素时,平均约移动表中的一半数据元 素。所以当n很大时,算法的效率是很低的。 若表长为n,则上述算法的时间复杂度为 O(n)。
顺序表的插入图例
顺序表的插入运算
Status ListInsert(SqList &L,int i,ElemType e) // 算法2.4
ai
逆置单链表
逆置单链表的算法如下:
void nz(NODE *h) {// 逆置头指针为h的带表头结点的单链表 NODE *s,*p; p=h->link;// p先指向原表中第一个结点 h->link=NULL;// 逆表的初态为空表 while (p!=NULL) {s=p; // s指向当前逆转的结点 p=p->link; s->link=h->link; h->link=s; // 把s结点插入逆表 } }
数据结构讲义第2章-线性表

t个单元
a1 a2 ai-1 ai ai+1 an
2.2 线性表的顺序存储和实现
线性表的顺序存储结构——顺序表 一 线性表的顺序存储结构 顺序表
顺序表的定义: 一维数组+表长
例1: 写出线性表(6,17,28,50,92,188)的顺序 存储结构表示。 # define ListSize 100 typedef int ElemType; ElemType List[ListSize]; int length;
思考:采用其它的定义如何初始化空表?
2.2 线性表的顺序存储和实现
三 顺序表应用举例
1. 设有两个按元素值递增有序排列的顺序表A和B,请编写算法将A 和B归并成一个按元素值递增有序排列的线性表C。 void merge(SeqList A,SeqList B,SeqList &C) {i=0;j=0;k=0; while ( i<A.length && j<B.length ) if (A.data[i]<B.data[j]) C.data[k++]=A.data[i++]; else C.data[k++]=B.data[j++]; while (i<A.length ) C.data[k++]= A.data[i++]; while (j<B.length ) C.data[k++]=B.data[j++]; C.length=k; }
调用示例: main() {SeqList L; ElemType e; ... delete_ListSq(L,2,e); ... }
数据结构第2章 线性表

};
当初始化此类型的一个线性表时,要使list指针指向大小为MaxSize的动 态数组空间。
2.2.2 顺序存储下的线性表的操作实现
1. 初始化线性表L,即进行动态存储空间分配并置L为一个空表 void InitList(struct List *L,int ms) { /*检查ms是否有效,若无效则退出运行*/ if(ms<=0) {printf("ms值非法!\n"); exit(1);} /*置线性表空间大小为ms*/ L->MaxSize=ms; /*动态存储空间分配,若分配失败则退出运行*/ L->list=malloc(ms*sizeof(ElemType)); if(!L->list) { printf("动态存储分配失败!\n"); exit(1); /*执行此函数则中止程序运行,此函数在stdlib.h中有定义*/ } /*初始置线性表为空*/ L->size=0; }
5. 向有序线性表L中插入元素x,使得插入后仍然有序 有序线性表是指按元素值从小到大顺序排列的线性表,如(23,36,45,49,56,73,80) 就是一个有序线性表。向有序线性表中插入一个新元素后要保证仍然是有序的,需要进 行的插入过程为: (1) 检查表空间是否用完,若是则分配更大的存储空间; (2) 采用顺序查找的方法查找出x的插入位置; (3) 从表尾到插入位置止,把所有位置上的元素均后移一个位置; (4) 把新元素写入到空出的位置上; (5) 线性表的长度增1。 算法描述为: void InsertOrderList(struct List *L, ElemType x) { int i,j; /*若数组空间用完则重新分配更大的存储空间*/ if(L->size==L->MaxSize) againMalloc(L); /*顺序查找出x的插入位置*/ for(i=0; i<L->size; i++) if(x<L->list[i]) break; /*从表尾到下标i元素依次后移一个位置,把i位置空出*/
数据结构第二章线性表

线性表的顺序存储结构可用数组来实现。 数组元素的类型就是线性表中数据元素 的类型,数组的大小,最好大于线性表 的长度。因此,顺序存储结构是把线性 表中每个元素a1, a2, a3, …, an依次存放到数 组下标为0, 1, 2,…, n1的位置上。
假设用数组data[MAXSIZE]存储线性 表 A =(a1, a2, a3, …, an) 其顺序存储结构如图2.1所示。
➢2.2.1 线性表的顺序存储结构 ➢2.2.2 顺序表的基本运算 ➢2.2.3 插入和删除运算的时间分析 ➢2.2.4 顺序表的优点和缺点
2.2.1 线性表的顺序存储结构
线性表的顺序存储方法是:将线性表的所有元素 按其逻辑顺序依次存放在内存中一组连续的存储 单元中,也就是将线性表的所有元素连续地存放 到计算机中相邻的内存单元中,以保证线性表元 素逻辑上的有序性。 顺序表的特点是:其逻辑关系相邻的两个结点在 物理位置上也相邻,结点的逻辑次序和物理次序 一致。
图2.1 顺序存储结构示意图
由于线性表中所有结点的数据类型是相同 的,因此每个结点占用的存储空间也是
相同的。假设每个结点占用d个存储单元,
若 线 性 表 中 第 一 个 结 点 a1 的 存 储 地 址 为 LOC(a1) , 那 么 结 点 ai 的 存 储 地 址 LOC(ai) 可以通过下面的公式计算得到:
【例2.3】学生成绩统计表也是一个线性表, 见表2.1。在线性表中每个学生的成绩是
一个数据元素,它由学号、姓名、数学、 外语、物理、总分这6个数据项组成。该 线性表的长度为5。
学号 1 2 3 4 5
姓名 李华 王放 张利 田勇 成惠
表 2.1 某班学生成绩统计表
精品课件-数据结构实用教程(C语言版)-第二章 线性表

线性结构的基本特征:
1.集合中必存在唯一的一个“第一元素”; 2.集合中必存在唯一的一个 “最后元素” 3.除最后元素之外,均有 唯一的后继; 4.除第一元素之外,均有 唯一的前驱。
例如:alphabet=(a,b,c,…,z) 和 prime=(2,3,5,7,11,…,97)alphabet是字母表,其结点是一个英 文字母,prime是100以内的素数表,结点是整型数。且只有一个 域的线性表,
void * malloc(unsigned int size); 在内存的动态存储区中分配一个长度size的连续空间.此函数
的返回值是一个指向分配域起始地址的指针(类型为void). 2. calloc函数
void * calloc(unsigned n,unsigned size); 其作用是在内存的动态分配区中分配n个长度为size的连续空
(n
n 1 i1
i
1)
n 2
在线性表中任何一个位置上删除一个元素所移动元素的平均次
数为:
Edl
1
n
(n
n i1
i)
n 1 2
利用上述定义的线性表类型 可以实现其它更复杂的操作
例 2-1 例 2-2
例 2-1
假设:有两个集合 A 和 B 分别用两个线性表 LA 和 LB 表示,即:线性表中的数据元素即为集合中的成员。
(a1, …, ai-1, ai, …, an) 改变为 (a1, …, ai-1, e, ai, …, an)
<ai-1, ai>
<ai-1, e>, <e, ai>
a1 a2
《数据结构用C语言描述》第二章

25 34 57 16
63
i
插入x 50
01 23 4 5
48 09 67
25 34 570 50 16 48
09 63 顺序表插入时,平均数据移动次数 AMN在各表项 插入概率相等时平均时间复杂度: T(n)=O(n)
· 删除
25 34 571650 16 48 09 63 删除 x
01 23 4 5 6 7
sequenlist *L, int i )
■{
■ if ( i >= 0 && i < (*L).last) return
(*L).data[i];
■ else
■ printf ( “参数i 不合理! \n” );
· 插入
01 23 4 5 6 7
25 34 57 16
63
i
插入x 50
01 23 4 5
return 0;
//插入不成功
else {
for ( j =( * L ) . l a s t ; j >=i-1; j - - )
(*L).data[j] =(* )L.data[j -1];
(*L).data[i] =x; (*L).last++; }
return 1; //插入成
}
01 23 4 5 6 7
链表(linked List)
链表是线性表的链接存储表示 · 单链表 · 静态链表 · 循环链表 · 双向链表
单链表(Singly linked List)
定义: 用一组地址任意的存储单元存 放线性表中的数据元素。(ZHOU ZHAO
SUN G
存储地址 1 7 13 19
数据结构c语言PPT 2

5. 线性表的特点
同一性:线性表由同类数据元素组成,每一个ai 必
须属于同一数据对象。
有穷性:线性表由有限个数据元素组成, 表长度就
是表中数据元素的个数。
有序性:线性表中相邻数据元素之间存在着序偶关
系<ai, ai+1>。
线性表的抽象数据类型定义:
ADT List { 数据对象:D={ ai | ai ElemSet, i=1,2,…n, n0 } 数据关系: R={<ai-1,ai> | ai-1,ai D, i=1,2,…n} 基本运算: InitList(&L); DestroyList(&L); Length(L); GetElem(L,i,&e); LocateElem(L,e,compare()); InsertElem(&L,i,e); DeleteElem(&L,i,&e); …… } ADT List
补充内容:
int *s;
s = new int;
或 s = (int *)malloc(sizeof(int)); *s = 5; free(s); int *s, *p;
void main() { int *s, *p;
s = new int; *s = 5; delete s; p = new int[10]; p[0] = 0; p[1] = 1; *(p+8) = 8; *(p+9) = 9; delete [] p }
Loc(ai) = Loc(a1) + (i - 1) * d
其中Loc(a1)称为基地址
(1≤i≤n)
3. 顺序表的描述(顺序表存储的C语言实现):
数据结构(C语言版)第2章线性表

2.二维数组
若定义数组A[n][m],表示此数组有n行m列,如下图2-3所示。
0
1 2 i n-1 0 a00 a10 a20 ai 0 1 a01 a11 a21 ai1 2 … a02 … a12 a22 ai2 j … m-1 a0j … a0 m-1
… a1j … a1 m-1 … … a2j … a2 m-1 ai j … ai m-1 an-1,j … an-1,m-1
9. NextElem(L,cur_e,&next_e)求后继 若cur_e是L的 数据元素,且不是最后一个,则用next_e返回它的后继,否 则操作失败, next_e无定义。 10. ListInsert(&L,i,e) 插入 在L中第i个位置之前插入 新的数据元素e,L的长度加1 。1=<i <=Listlength(L)+1 11. ListDelete(&L,i,&e) 删除 删除L的第i个数据元素, 并用e返回其值,L的长度减1 。1=<i <=Listlength(L)+1 12. ListTraverse(L,visit()) 遍历 对给定的线性表L, 依次输出L的每一个数据元素。遍历时不许重复 13. Copy(L,C) 复制 将给定的线性表L复制到线性表 C中。 14. Merge(A,B,C) 合并 将给定的线性表A和B合并为 线性表C。 }ADT List
逻辑地址 数据元素 存储地址 名称
0 1
a0 a1
Loc(A[0]) Loc(A[0]) +d
A[0] A[1]
n -1
空闲空间
…
i
…
…
ai
a n-1
数据结构2线性表

Templete <class type> listNode<type> * list<type>::find(int i){ If( i<-1) return NULL; If(i==-1) return first; listNode<type> *p=first->link; int j=0; while(p!=NULL && j<i) { p=p–>link; j++; } return p; }
第二章 数组
2.1 线性表
2.2
顺序表 2.3 单链表 2.4线性链表的其他变形 2.5单链表的应用:多项式及其运 算
2.1线性表
线性表(Linear List) :由n(n≧0)个数据元素(结 点)a1,a2, …an组成的有限序列。其中数据元 素的个数n定义为表的长度。当n=0时称为空 表,常常将非空的线性表(n>0)记作: (a1, a2,…an) ( )
线性表的链式表示和实现
顺序存储 线性表存储结构 非顺序存储 链表
顺序表的优点:取数方便快速。 缺点:删除、插入平均要移o(n)个元素。 适应性 不强。
链表:是指用一组任意的存储单元来存 放线性表的结点,这组存储单元可以是 零散分布在内存中的任意位置上的。 任意的存储单元如何存放线性表 例:(a1,a2,a3,a4) 链表中的结点结构: data link
12 15 33 45 67 89 57 78
0 1 2 3 4 5 6 7
程序实现
Templet <class type> int Seqlist<type> ::Find(type &x ) const{ Int i=0; while(i<=last && data[i]!=x) i++; If (i>last) return -1; //没找到 Else return i; //找到 }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
存储地址 Loc(a0) Loc(a0)+1*t ...... Loc(a0)+i*t ...... Loc(a0)+(n-1)*t
在表中的位置(下标)
a0 a1
......
0 1 ...... i ...... n-1
......
ai
An-1
其中,L为每个数据元素所占据的存储单元数目。 相邻两个数据元素的存储位置计算公式 LOC(ai+1)=LOC(ai)+t 线性表中任意一个数据元素的存储位置的计算公式为: LOC(ai)=LOC(a0)+i*t
第五遍比较1次后为 15 22 33 43 45 67
就地逆置顺序表
Last=8 下标 i mid=last/2 8-4
0
1
2
3
4
8-3 8-2 8-1 8-0
data[4]与data[8-4]要白交换一次
Last=9 下标 i
mid=last/2
0
1
2
3
4
9-4 9-3 9-2 9-1 9-0 data[4]与data[5]要交换
2.1.2 线性表的基本操作
1. 线性表初始化:Init_List(L) 2. 求线性表的长度:Length_List(L) 3. 取表元:Get_List(L,i) 4. 按值查找:Locate_List(L,x) 5. 插入操作:Insert_List(L,i,x) 6. 删除操作:Delete_List(L,i)
for(i=0;i<=mid;i++) data[i] data[last-i] //
交换
合并两个升序的顺序表(ppt37)
2.3 线性表的链式存储结
特点: 用一组任意的存储单元存储线性表的数据元素 利用指针实现了用不相邻的存储单元存放逻辑上相邻 的元素 每个数据元素ai,除存储本身信息外,还需存储其直接 后继的信息 结点 结点 数据域 指针域 数据域:元素本身信息 指针域:指示直接后继的存储位置
2.2
线性表的顺序存储结构
2.2.1 线性表的顺序存储结构 线性表的顺序存储结构是指用一组连续的
存储单元依次存储线性表中的每个数据元素。如 下图所示:
顺序存储
一维数组的存储
数组的特点: 类型相同、 固定长度、 顺序连续存放、 数组名就是首地址。 数组的定义及初始化 short A[5]={1,3,5,7,9};
选择排序法(从小到大) 思路:用第一个与后面的比较,后面的小,则交换位 置 未排序时 45 33 22 67 43 15 第一遍比较5次后为 15 45 33 67 43 22 第二遍比较4次后为 15 22 45 67 43 33
第三遍比较3次后为 15 22 33 67 45 43
第四遍比较2次后为 15 22 33 43 67 45
数组的遍历
int ary[last+1],*sp; //整型数组及指针变量 for(i=0;i<=last;i++) //下标从0到最大下标 {„} for(sp=ary;sp<=ary+last;sp++)//指针从数组名到数组名+last {„} 链表的遍历 一 通常用 While语句,从头结点开始,直到最后一个结点(指针域为 空)。 curr=head->next; //head是头指针,curr指向第一结点 while(p!=NULL) //结点的指针不为空就一直作 { „ curr=curr->next; //求下一结点的指针 „ }
顺序存储
二维数组的存储方式
设二维数组a[5][3]如下: 56 68 76 78 76 85 90 59 65 48 90 98 a[3][2] 95 89 78 在内存中是以“行优先”一维存储 56 68 76 78 76 85 90 59 65 48 90 98 95 89 78 下标 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 根据二维数组中某元素的下标,可以求出一维中的下标 一维下标=行号×列宽+列号=3×3+2=11
ruler
h8
bag
∧
结点:内存的某区域,包括数据域和指针域。 1.每个结点都有其自身的指针。 2.将某结点的指针赋予另一结点的指针域,就 建立了结点之间的联系,由此生成链表。 3.在形成的链表中,必有一个结点的指针作为 整个链表的指针,通常是头结点的指针。 4.顺序存储和鏈式存储的区别:数组的大小是 固定的,元素是顺序连续存储的,通过下标 可以很方便的访问数组元素;链表的大小是 动态的,元素的存储是不连续的,访问结点 必须通过指针。在顺序存储中,各种操作是 对下标操作;在链式存储中的各种操作都是 对指针域操作。分析问题的方法与顺序存储 也是不一样的。
h1 ∧ h1
循环内: 生成链表结点 1)申请新结点 2)将数据赋予新结点的数据域 3)将指针赋予老结点的指针域 4)新结点作老结点
退出循环: 1)最后一个结点的指针 域赋为NULL 2)返回头指针
h2
h2
h3
h4
book
h5
desk
h6
h3
pen
h7
h4
room
h8
h5
table
h6
rubble
h7
空单链表
∧
数据域
指针域
链式存储:带头结点在后插入(统一插入方式:都是对当前 结点与前驱结点指针域进行操作) 循环前:
循环内: 生成空链表 生成链表结点 1)申请结点 1)申请新结点 保存结点指针 2)对新结点的数据域赋值 2)对指针域赋 3)将前驱结点的指针域赋予新结点的指针 NULL 域 3)头结点作前驱 4)将新结点的指针赋予前驱结点的指针域 结点 5)新结点作下一次的老结点 pre head
stu[2]
stu[3]
数据结构中常把数组和最大下标定义成结构体 #define max 40 //表最大长度 typedef struct //定义结构体标识符 { int data[max]; //数组 int last; //最大下标 }SeqList; //结构体标识符
对于此种数据类型,常用操作举例如下:
①
② ③ ④ ⑤ ⑥
43
64 78 83
43
64 78 83
43
64
78
83
83
移位前,最 大下标:7
移位后
插入后,最 大下标+1
删除后,最 大下标 -1
void Insert_List(SeqList *L)//插入(用指针作形参) { int i,j,x; //循环变量,插入位置,插入数 printf("输入插入位置和插入的数据:",0,L->last+1); fflush(stdin); scanf("%d%d",&i,&x); //从最大下标到插入位置依次把每个元素后移一位, for(j=L->last;j>=i;j--) L->data[j+1]=L->data[j]; //移位 L->data[i]=x; //插入 L->last++; //最大下标加 1 }
void Out_List(SeqList L) //输出(结构体变量作形参) { int i; for(i=0;i<=st;i++) printf("%4d",L.data[i]); printf("\n"); }
对于其它数据类型,如结构体数组等也有类似操作。详见程序 2-0插入删除
起泡排序法(设为从小到大) 思路:两辆比较,后面的小,则交换位置 未排序时 45 33 22 67 43 15 第一遍比较5次后为 33 22 45 43 15 67 第二遍比较4次后为 22 33 43 15 45 67 第三遍比较3次后为 22 33 15 43 45 67 第四遍比较2次后为 22 15 33 43 45 67 第五遍比较1次后为 15 22 33 43 45 67 改进的起泡排序法 当未发生交换位置则表示已排好序,可结束排序。
void Ini_List(SeqList *L) //初始化(键入表数据。) { //要返回参数,故要用指针作形参 int i,len; printf("请输入长度[%d,%d]:",1,max); fflush(stdin); //多次键入必须先更新标准输入文件流 scanf("%d",&len); L->last=len-1; i=0; //输入表数据 printf("请输入数值(整型量):"); for(i=0;i<=L->last;i++) scanf("%d",&L->data[i]); }
序列。通常表示成下列形式:
L=( a0, a1,...,ai-1,ai,ai+1,...,an)
其中:L为线性表名称,习惯用大写书写; ai为组成该线性表的数据元素,习惯用小写书写; 当0<i≤n时,ai是ai-1的直接后继是ai+1的直接前驱, a0无直接前驱, an无直接后继
举例 La=(34,89,765,12,90,-34,22) 数据元素类型为int。 Ls=(“Hello”,"World”, “China”, “Welcome”) 数据元素类型为string Lb=(book1,book2,...,book100) 数据元素类型为下列所示的结构类型: struct bookinfo { int No; //图书编号 char *name; //图书名称 char *auther; //作者名称 ...; }
