北京市西城区2018—2019学年度第一学期期末试卷

合集下载

北京市西城区2018-2019学年度第一学期期末试卷参考答案及评分标准

北京市西城区2018-2019学年度第一学期期末试卷八年级语文参考答案及评分标准2019．1一．基础·运用（共10分）1．（1）C（2）A （3）B2．答案示例一：请问王老师，您希望学生如何去读书呢？答案示例二：王老师您好，请问您是如何指导学生读书的？）评分标准：语言得体1分，内容1分。

3．“基因编辑婴儿”诞生引发巨大争议。

评分标准：共10分，每小题2分。

二．古诗文阅读（共22分）（一）古诗文默写（共6分）4．烈士暮年5．贫贱不能移6．谁家新燕啄春泥7．惊起一滩鸥鹭8．此中有真意欲辨已忘言评分标准：共6分，每空1分。

（二）古诗阅读（共5分）9．D评分标准：共2分。

10．雄浑、奇美、壮丽晴川历历汉阳树芳草萋萋鹦鹉洲评分标准：共3分，每空1分。

（三）文言文阅读（共10分）11．（1）衡．于虑衡，同“横”，梗塞、不顺。

（2）而后喻．喻，了解，明白。

评分标准：共2分。

每个1分。

12．D评分标准：共2分。

13．示例：了解到这一切之后，就会明白常处忧愁祸患之中可以使人生存，常处安逸快乐之中可以使人死亡。

评分标准：共2分。

14．出身都很贫贱（平凡）或都经过了艰苦磨练；都增长了才干或都成就了不平凡的事业（都成了圣君贤臣、都被明主发现并委以重任）评分标准：共2分，每点1分，答出2点意思对即可。

15．饿其体肤（空乏其身）困于心，衡于虑，而后作评分标准：共2分，每空1分。

附：乙文译文：淮阴侯韩信是江苏淮阴人，还是普通百姓时，经常在别人那里混吃混喝，……有许多人都很讨厌他。

（一天）韩信在城下钓鱼，有几位老太太在河边漂洗丝绵。

有位（在水边漂洗丝绵的）老太太看到他饿了，就拿饭来给他吃，连续漂洗了几十天，天天如此。

韩信非常高兴，对那位老太太说：“我一定会重重地报答您老人家。

”附：丙文译文：西伯姬昌被拘禁而扩写《周易》；孔子受困窘而作《春秋》；屈原被放逐，才写了《离骚》；左丘明失去视力，才有《国语》；孙膑被剜去膝盖骨，《兵法》才撰写出来；吕不韦被贬谪蜀地，后世才流传着《吕氏春秋》；韩非被囚禁在秦国，写出《说难》、《孤愤》；《诗经》三百篇，大都是一些圣贤们抒发愤慨而写作的。

2018-2019北京西城区七年级初一数学第一学期期末考试试题含答案

如图ꎬ数轴上ＡꎬＢ两点对应的有理数分别为ｘＡ＝－５和ｘＢ＝６ꎬ动点Ｐ从点Ａ出发ꎬ以
(１) 当ｔ＝２时ꎬ点Ｐ对应的有理数ｘＰ＝
(２) 当０ < ｔ ɤ １１时ꎬ若原点Ｏ恰好是线段ＰＱ的中点ꎬ求ｔ的值ꎻ 写出此整点对应的数.
ꎬＰＱ＝
ꎻ
(３) 我们把数轴上的整数对应的点称为整点 . 当Ｐ ꎬＱ两点第一次在整点处重合时ꎬ直接
解:(１) 当ｔ＝２时ꎬ ｘＰ＝ (２)
ꎬＰＱ＝
.
(３) 当Ｐ ꎬＱ两点第一次在整点处重合时ꎬ此整点对应的数为
.
七年级期末㊀数学试卷㊀第８页( 共８页)
北京市西城区２０１８
２０１９学年度第一学期期末试卷
七年级数学参考答案及评分标准
一㊁选择题( 本题共２４分ꎬ第１ ~ ４题每小题３分ꎬ第５ ~ １０题每小题２分) 题号答案Ｂ１Ｄ２Ａ３Ｂ４Ａ５Ａ６Ｃ７Ｃ８９
证明:ȵ øＯ＋ øＯＣＡ＝９０ʎ ꎬøＯ＋ øＯＢＣ＝９０ʎ ꎬ ʑ øＯＣＡ＝ ø ( 理由: . ) . ) )
请将下面的证明过程补充完整:
ȵ ＣＡ平分 øＯＣＤꎬ ʑ øＡＣＤ＝ ( 理由:
ʑ øＡＣＤ＝ øＯＢＣ. ( 理由:
２５. 任务画图( 本题４分)
任务:在网格中画出一个顶点为Ｏ且等于１８０ʎ －２α 的角. ∙∙ 要求:画图并标记符合要求的角ꎬ写出简要的画图步骤. ( 说明:可以借助网格㊁量角器)
１６. 一个由９个大小相同的正方体组成的立体图形如图所示ꎬ 从左面观察这个立体图形ꎬ 将得到的平面图形的示意图画在如下的画图区中. ∙∙∙

北京市西城区2018-2019学年度第一学期期末试卷

北京市西城区2018-2019学年度第一学期期末试卷(北区)八年级语文 2018．1 试卷满分100分考试时间：120分钟一、选择题。

下列各题四个选项中只有一个是符合题意的，请将答案写在下面的表格中。

（共10分，每小题21A．箱箧．（jiā）夹．带（jiá）仄．歪（zè）克．扣（kē）B．憋．住（biē）瞥．见（piē）脊．椎（jí）屹．立（yì）C．举箸．（zhù）踌躇．（chú）寒噤．（jìn）殷．红（yīn）D．估量．（liáng）模．样（mú）适应．（yìng）煞．风景（shā）2．下列词语中有错别字的一项是（）A．荒谬杀戮缭绕穷愁潦倒B．阻遏扼制流萤草长莺飞C．吆喝呵斥销魂消声匿迹D．和蔼凑合致密因地制宜3．下列加点的词语在句中的意思解释有误的一项是（） A．在渡江战役中，中国人民解放军英勇善战，锐不可．．．当．。

锐不可当：锋利无比，不可抵挡。

B．阿长夜间的伸开手脚，占领全床，那当然是情有可．．．原．的了。

情有可原：按照情理，对出现的某种情况有可以原谅的地方。

C．赵州桥的设计完全合乎科学原理，施工技术更是巧．妙绝伦．．．。

巧妙绝伦：灵巧高明，精美神奇。

D．每年损失高达两千多亿美元，面对这样的天文数字，人们岂能无动于衷．．．．。

无动于衷：内心毫无触动，一点也不动心。

4．下列病句修改不正确．．．的一项是（）A．首都市民的文明素质与礼仪规范在稳步提高。

修改：在“规范”后加上“水平”B．广大师生都争先恐后地踊跃给贫困儿童捐书捐款。

修改：把“给贫困儿童”移至“捐款”后C．对于新闻的语言，首先要准确，这是新闻语言的一个显著特征。

修改：去掉“对于”D．为了防止疫情不再反弹，市领导要求各单位进一步加强管理，制订措施。

修改：把“不再”改为“再度”5．下列文学常识内容完全正确的一项是（）A．这学期语文书中提到的外国作家西蒙诺夫、奥斯特洛夫斯基、雨果、阿西莫夫分别是苏联人、苏联人、法国人和美国人。

2019北京西城区高一化学第一学期期末试卷带答案Word版

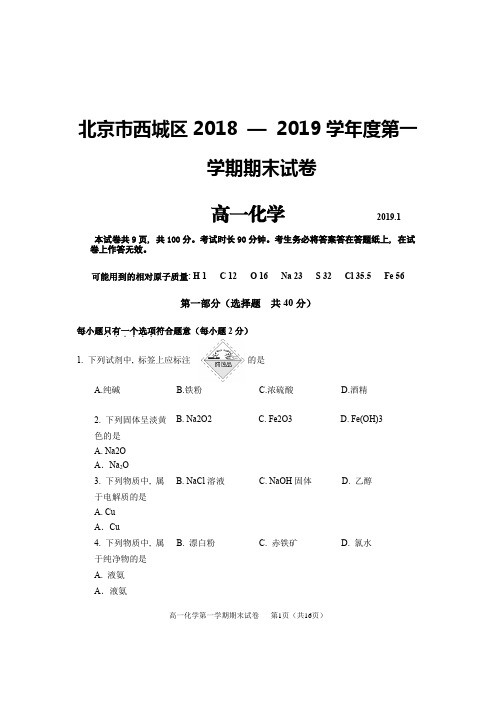
北京市西城区2018 —2019学年度第一学期期末试卷高一化学2019.1本试卷共9页, 共100分。

考试时长90分钟。

考生务必将答案答在答题纸上, 在试卷上作答无效。

可能用到的相对原子质量: H 1 C 12 O 16 Na 23 S 32 Cl 35.5 Fe 56第一部分（选择题共40分）每小题只有一个选项．．．．．．符合题意（每小题2分）1. 下列试剂中, 标签上应标注的是A.纯碱B.铁粉C.浓硫酸D.酒精B. Na2O2C. Fe2O3D. Fe(OH)32. 下列固体呈淡黄色的是A. Na2OA．Na2OB. NaCl溶液C. NaOH固体D. 乙醇3. 下列物质中, 属于电解质的是A. CuA．CuB. 漂白粉C. 赤铁矿D. 氯水4. 下列物质中, 属于纯净物的是A. 液氨A．液氨高一化学第一学期期末试卷第1页（共16页）B. CO2C. NO2D. NO5. 下列气体过量排放不会导致酸雨的是A. SO2A．SO26. 胶体与其它分散系的本质区别是B. 胶体微粒能通过滤纸A. 能产生丁达尔效应A．能产生丁达尔效应C. 分散质微粒直径在1~100 nm之间D. 胶体在一定条件下能稳定存在7. 合金是一类用途B. 青铜C. 生铁D. 水银广泛的金属材料。

下列物质不属于合金的是A. 不锈钢A．不锈钢B. 浓盐酸C. 硫酸铜溶液D. 稀硫酸8. 下列溶液中, 常温下可以用铁制容器装运的是A. 浓硝酸A．浓硝酸B. 金属钠C. 氯化铁D. 稀硝酸9. 下列物质中, 常用作还原剂的是A. 氯气A．氯气10. 下列四种基本反应类型与氧化还原反应的关系图中, 正确的是A. B., 不正确的是高一化学第一学期期末试卷第2页（共16页）A. 新制氯水需要避光保存B. Na可保存在煤油中C. NaOH固体需要密封保存D. 保存FeCl3溶液时需加入少量Fe粉12．下列各组离子中, 能在水溶液中大量共存的是A. Na＋、Ag＋、Cl－、CO3B. Na＋、Mg2＋、Cl－、SO4C. Fe3＋、K＋、SO4.OH－D. Fe2＋、H＋、SO4.NO13．配制100 mL 1 mol/L的NaCl溶液时, 下列做法不正确的是A. 选择容积100 mL的容量瓶B. 在容量瓶中溶解NaCl固体C. 转移NaCl溶液时用玻璃棒引流D. 定容时向容量瓶中滴加蒸馏水至液面与刻度线相切14. 下列实验能达到目的的是A. 加热除去Na2CO3固体中的NaHCO3B. 用NaOH溶液除去CO2中的SO2气体C. 用氯水除去Fe2(SO4)3溶液中的少量FeSO4D. 用BaCl2溶液除去NaCl溶液中的K2SO415. 下列有关实验现象与物质性质对应关系的说法中, 错误的是A. Na2CO3溶液遇酚酞变红, 说明Na2CO3溶液呈碱性B. Cl2使湿润的有色布条褪色, 说明Cl2具有漂白性C. NO遇空气变为红棕色, 说明NO具有还原性D．新制的Fe(OH)2遇氧气变为红褐色, 说明Fe(OH)2具有还原性16. 下列离子方程式书写正确的是A. Fe＋2H+ === Fe3+＋H2↑B. Fe2O3＋6H+ === 2Fe3+＋3H2OC. Na＋2H2O === Na +＋OH－＋H2↑D. Cl2＋H2O === 2H +＋Cl－＋ClO－17. 下列说法正确的是A. NaCl的摩尔质量是58.5 gB. 标准状况下, 22.4 L水中约含6.02×1023个H2O分子C. 常温常压下, 22 g CO2中所含氧原子数约为6.02×1023D. 将40 g NaOH固体溶于1 L H2O中, 得到1 mol/L的NaOH溶液18．下图是进行气体性质实验的常用装置, 下列对有关实验现象的描述中, 不正确的是高一化学第一学期期末试卷第3页（共16页）A. 若水槽中盛有水, 试管中盛满SO2, 可看到试管中液面上升B. 若水槽中盛有水, 试管中盛满NO2, 可看到试管中液面上升并充满试管C. 若水槽中盛有水（滴有酚酞）, 试管中是NH3, 可看到试管内液面上升并呈红色D．若水槽中盛有NaOH溶液, 试管中是Cl2, 可看到试管内液面上升, 黄绿色褪去高一化学第一学期期末试卷第4页（共16页）20. 将SO2通入BaCl2溶液至饱和的过程中, 始终未观察到溶液中出现浑浊, 若再通入另一种气体A, 则产生白色沉淀。

北京市西城区2018 — 2019学年度第一学期期末试卷数学试题

北京市西城区2018 — 2019学年度第一学期期末试卷高三数学（理科）第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合{|2,}A x x k k ==∈Z ，2{|5}B x x =≤，那么A B =（A ）{0,2,4} （B ）{2,0,2}- （C ）{0,2}（D ）{2,2}-2．在等比数列{}n a 中，若32a =，58a =，则7a = （A ）10（B ）16（C ）24（D ）323．一个四棱锥的三视图如图所示，那么这个四棱锥最长棱的棱长为（A（B（C）（D4．在极坐标系中，点(2,)2P π到直线cos 1ρθ=-的距离等于（A ）1 （B ）2 （C ）3 （D5. 在平面直角坐标系xOy 中，点(1,1)A ，点B 在圆224x y +=上，则||OA OB -的最大值为（A ）3 （B）1（C）2+（D ）4侧(左)视图正(主)视图俯视图国际象棋棋盘6. 设,0M N >，01a <<，则“log log a b M N >”是“1M N <+”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件7. 已知函数()sin πf x x =，2()2g x x x =-+，则（A ）曲线()()y f x g x =+不是轴对称图形（B ）曲线()()y f x g x =-是中心对称图形（C ）函数()()y f x g x =是周期函数（D ）函数()()f x y g x =最大值为478. 一个国际象棋棋盘（由88⨯个方格组成），其中有一个小方格因破损而被剪去（破损位置不确定）. “L ”形骨牌由三个相邻的小方格组成，如图所示. 现要将这个破损的棋盘剪成数个“L ”形骨牌，则（A ）至多能剪成19块“L ”形骨牌（B ）至多能剪成20块“L ”形骨牌（C ）一定能剪成21块“L ”形骨牌（D ）前三个答案都不对第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分． 9．复数z 满足方程1i i z -⋅=，则z =____．10．已知角α的终边经过点(3,4)-，则tan α=____；cos(π)α+=____．11．执行如图所示的程序框图，若输入的1m=，则输出数据的总个数为____．12．设x，y满足约束条件230,3,20,x yx yx y-+--+⎧⎪⎨⎪⎩≥≤0≥则的取值范围是____．13. 能说明“若定义在R上的函数满足(0)(2)0f f>，则在区间(0,2)上不存在零点”为假命题的一个函数是____．14．设双曲线的左焦点为F，右顶点为. 若在双曲线C 上，有且只有2个不同的点P使得=PF PAλ⋅成立，则实数λ的取值范围是____．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13分）在ABC∆中，3a=，b=2B A=．（Ⅰ）求cos A 的值；（Ⅱ）试比较B ∠与C ∠的大小．16．（本小题满分14分）如图，在三棱柱111ABC A B C -中，侧面11B BCC 为正方形，M ，N 分别是11A B ，AC 的中点，AB ⊥平面BCM ．（Ⅰ）求证：平面11B BCC ⊥平面11A ABB ；（Ⅱ）求证：1//A N 平面BCM ；（Ⅲ）若11A ABB 是边长为2的菱形，求直线1A N与平面1MCC 所成角的正弦值．B 1AMBA 1CC 1N17．（本小题满分13分）为保障食品安全，某地食品监管部门对辖区内甲、乙两家食品企业进行检查，分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本，并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下：根据质量指标值的分组，统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表（图表如下,其中0a ）.0.080甲企业乙企业（Ⅰ）现从甲企业生产的产品中任取一件，试估计该件产品为次品的概率；（Ⅱ）为守法经营、提高利润，乙企业将所有次品销毁．．．．．．．，并将一、二、三等品的售价分别定为120元、90元、60元.一名顾客随机购买了乙企业销售的2件该食品，记其支付费用为X元，用频率估计概率，求X的分布列和数学期望；（Ⅲ）根据图表数据，请自定标准，对甲、乙两企业食品质量的优劣情况进行比较.已知函数()ln f x x x a =-+，其中a ∈R ．（Ⅰ）如果曲线()y f x =与x 轴相切，求a 的值；（Ⅱ）如果函数2()()=f xg x x 在区间(1,e)上不是单调函数，求a 的取值范围．19．（本小题满分14分）已知椭圆222 1(2x y C a a +=>：的离心率为2，左、右顶点分别为,A B ，点M 是椭圆C 上异于,A B 的一点，直线AM 与y 轴交于点P . （Ⅰ）若点P 在椭圆C 的内部，求直线A M 的斜率的取值范围；（Ⅱ）设椭圆C 的右焦点为F ，点Q 在y 轴上，且//AQ BM ，求证：PFQ∠为定值.设正整数数列12 ,,,(3)N A a a a N >：满足i j a a <，其中1i j N<≤≤. 如果存在{2,3,,}k N ∈，使得数列A 中任意k 项的算术平均值均为整数，则称为“k 阶平衡数列”.（Ⅰ）判断数列2, 4, 6, 8, 10和数列1, 5, 9, 13, 17是否为“4阶平衡数列”？（Ⅱ）若N 为偶数，证明：数列 1,2,3,,A N ：不是“k阶平衡数列”，其中{2,3,,}k N ∈.（Ⅲ）如果2019N a ≤，且对于任意{2,3,,}k N ∈，数列均为“k阶平衡数列”，求数列A 中所有元素之和的最大值.AA。

北京市西城区2018-2019学年度高三第一学期期末考试

北京市西城区2018-2019学年度高三第一学期期末考试语文试题（2019.1）一、本大题共7小题，共22分。

阅读下面的材料，完成1-7题。

材料一超级计算机（以下简称“超算”），是具有超强计算能力的计算机，能够执行个人电脑无法处理的大资料量与高速运算，是计算机中功能最强、运算速度最快、存储容量最大的一类。

从技术角度简要而言，家用电脑一般只有一颗CPU，每颗CPU内通常只有2-8个物理核心。

而一般的超算有成千上万颗CPU，每颗CPU通常有几十个物理核心，这么大数量的CPU是为了通过并行计算，完成繁重的计算任务的。

一些复杂的问题，如果用单个CPU核心计算，可能要花上几个月甚至是几年的时间才能得到结果。

毫无疑问，这么长的计算时间是难以接受的，所以人类需要用多个CPU核心并行计算以提高效率，集成大量CPU于一身的超级计算机就应需而生了。

超算多用于国家高科技领域和尖端技术研究，被誉为计算机中的“珠穆朗玛峰”。

超算的研制水平，长久以来一直被当作一个国家综合国力及创新能力的象征，制造强大的超算，已被视为衡量一国科研实力的重要指标。

尤其是在大数据和移动互联网发展迅猛的当今时代，现代传播体系发生了本质性的改变，而超算则是未来超级传播的引擎动力。

超算能够深度推进时下风头正劲的人工智能改革。

例如，智能交通传播方面，预计无人驾驶汽车将于2020年在中美等大国被广泛使用。

2017年10月，美国的英伟达公司推出了专门针对level5无人驾驶的超算Pegasus，Pegasus每秒可完成320万亿次浮点计算。

这台超算虽然只有车牌大小，但其AI性能可以抵得上一百台数据服务器，英伟达公司由此成为首个提供完整level4/level5自动驾驶堆栈的厂商。

超算还能够支撑物联网传播的实现。

物联网的核心，一是传感器，二是物联网连接的网络技术，三是应用。

传感器能够源源不断地向互联网虚拟的大脑中枢传送世界各个方面的神经信号和感觉信息，并将其普遍连接，形成一张物联网，而要将这样巨大的物联网与互联网整合起来，必须通过超算强大的数据处理能力才能实现。

2018-2019北京市西城区初三(上)期末化学试题及答案

2018-2019北京市西城区初三(上)期末化学试题及答案北京市西城区2018-201年度第一学期期末试卷九年级化学可能用到的相对原子质量：H 1，C 12，O 16，Mg 24，Al 27，S 32，K 39，Mn 55，Cu 64，Zn 65第一部分选择题（共20分）1.下列变化中，属于化学变化的是A。

粮食酿酒B。

冰雪融化C。

酒精挥发D。

矿石粉碎2.下列属于纯净物的是A。

糖水B。

大理石C。

加碘食盐D。

五氧化二磷3.青少年正处于成长期，需要摄入足量钙，这里的“钙”是指A。

元素B。

原子C。

分子D。

单质4.碳元素与氧元素的本质区别是A。

电子数不同B。

质子数不同C。

中子数不同D。

最外层电子数不同5.铝能制成铝箔是因为铝具有良好的A。

延展性B。

导电性C。

导热性D。

抗腐蚀性6.下列安全标志中，表示“禁止烟火”的是ABCD7.下列有关物质性质的描述中，属于化学性质的是A。

干冰易升华B。

酒精能燃烧C。

二氧化碳比空气密度大D。

二氧化硫有刺激性气味8.下列符号中，表示2个氢原子的是A。

H2B。

2H2C。

2HD。

2H+9.下列实验操作中，正确的是A。

熄灭酒精灯B。

倾倒液体C。

称量固体D。

检查气密性10.6000 L氧气在加压的情况下，可装入容积为40 L的钢瓶中，由此说明A。

分子在不断地运动B。

分子体积很小C。

分子由原子构成D。

分子间有间隔11.某同学制作的试剂标签如下，其中化学式书写不正确的是硝酸铜 Cu(NO3)2氯化镁硫酸钾氧化铁 FeO MgCl2 K2SO4 DAB12.下列事故的处理方法中，不正确的是A。

正在使用的电器着火，立即用水浇灭B。

燃着的酒精灯不慎碰倒，立即用湿布盖灭C。

炒菜时油锅中的油着火，立即放入较多的蔬菜D。

厨房中天然气泄漏，立即关闭阀门并开窗通风13.碳-14常用于测量古生物的生活年代。

碳-14原子的核电荷数为6，中子数为8.下列关于碳-14原子的说法中，正确的是A。

最外层电子数为6B。

北京市西城区2018-2019学年七年级上学期期末考试语文试题及答案

北京市西城区2018-2019学年七年级上学期期末考试语文试题及答案北京市西城区2018-201年度第一学期期末质量检测七年级语文试卷满分:100分考试时间:120分钟一、语文基础.下面各题均有四个选项,其中只有一个符合题意,请将答案写在下面的表格中.（共14分.每小题2分）题号答案、下列词语中加点字注音全都正确的一项是A、滑稽（jì）嬉戏（xī）花团锦簇（cù）．．．B、栖息（qī）吆喝（yāo）昂首挺立（áng）．．．C、沐浴（mù）澄澈（chéng）津津有味（jīng）．．．D、寻觅（mì）霹雳（lì）混为一谈（hǔn）．．．2、下列句中没有错别字的一项是A、后来发生了分岐：母亲要走大路,大路平顺；我儿子要走小路,小路成心思.B、我没想到她已病成那样.看着三轮车远去,也绝没有想到那竟是永远的决别.C、复原的恐龙、猛犸仿佛在引颈长吼,重现的远古林木多么葱茏、幽雅.D、XXX觉得在这六合之间,应该添一点什么工具进去,让它生长篷勃起来才好.3、顺次填入上面语段横线中的词语,最得当的一项为哪一项天上的云,真是,变革无常.有的像羽毛,有的像鱼鳞,有的像羊群……它们有时把天空得很美丽,有时又把天空得很阴森.刚才还是白云朵朵,阳光灿烂；一霎间却又是乌云密布,大雨倾盆.A、多姿多彩点缀覆盖B、姿态万千点染覆盖C、多姿多彩点染笼罩D、姿态万千点缀笼罩4、下列句子中加点成语使用有误的一项是A、会场里鸦雀无声,大家都被他那精彩的讲话吸引住了.．．．．B、马戏团里小丑的滑稽幽默,植物的顽皮可爱,引得观众忍俊不由.．．．．C、同学们觉得他提出的办法很有创意,都随声拥护表示同意.．．．．D、只有独具慧眼的匠师才能把看似普通的紫砂变成美妙的艺术品。

．．．．5、和例句运用的修辞方法相同的一项是例句：早高峰时,地铁里挤得连根针也插不下.A、山那边的山啊,XXX着脸,给我的幻想打了一个零分!B、他每一天每一点钟都要换一套衣服.人们提到他,总是说：“皇上在更衣室里.”C、在一个孩子的眼睛里,他的教师是多么慈祥,多么公正,多么巨大的人啊！D、母亲啊!你是荷叶,我是XXX,心中的雨点来了,除了你,谁是我在无遮拦天空下的荫蔽?6.结合语境,将下列句子填入横线处,顺序最恰当的一项是XXX2014年将在改善市民居住条件、发展公共交通、优化生态环境等方面加大工作力度.如.①从而不断进步市民的糊口质量②实现地铁7号线等建成通车③筹集保障性住房7万套④建成市级生态绿道200公里A、③④②①B、①④②③C、①②④③D、③②④①7、下列对文学常识的表述有误的一项是A、《论语》是儒家的典范著作之一,由XXX及其弟子、再传弟子编写的,以语录体和对话体为主,记录了XXX及其弟子的言论.B、《礼记》是儒家经典著作之一,是秦汉以前各种礼仪论著的选集,相传为西汉戴圣编撰.C、《荷叶母亲》的作者XXX,原名XXX,现代作家,代表作有《繁星》《春水》《寄小读者》等.D、现存的《伊索寓言》是古希腊、古罗马时代流传下来的故事,经后人汇集,统归在伊索名下.二、语文积累（共11分）8、默写（8分）（1）,以XXX.（XXX《观沧海》）（2）商女不知亡国恨。

北京市西城区2018-2019学年高一上学期期末考试数学试卷 Word版含解析

北京市西城区2018 — 2019学年度第一学期期末试卷高一数学试卷满分：150分考试时间：120分钟A卷 [三角函数与平面向量] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1.的值是A. B. C. D.【答案】D【解析】【分析】由题意结合诱导公式求解三角函数值即可.【详解】由题意可得：.本题选择D选项.【点睛】本题主要考查三角函数的诱导公式，特殊角的三角函数值等知识，属于基础题目.2.函数的最小正周期为A. B. C. D.【答案】C【解析】【分析】由题意结合最小正周期公式求解函数的最小正周期即可.【详解】由最小正周期公式可得函数的最小正周期为.本题选择C选项.【点睛】本题主要考查三角函数的周期公式，属于基础题.3.如果向量，，那么（）A. B. C. D.【答案】B【解析】【分析】首先求得的坐标表示，然后求解其模长即可.【详解】由题意可得，则.本题选择B选项.【点睛】本题主要考查平面向量的坐标运算，向量的模的求解等知识，意在考查学生的转化能力和计算求解能力.4.（）A. B. C. 1 D.【答案】C【解析】【分析】由题意结合诱导公式化简三角函数式即可.【详解】由题意结合诱导公式可得：.本题选择C选项.【点睛】本题主要考查诱导公式的应用，，三角函数式的化简等知识，意在考查学生的转化能力和计算求解能力.5.已知函数和在区间I上都是减函数，那么区间I可以是A. B. C. D.【答案】B【解析】【分析】逐一考查函数在所给区间的单调性确定满足题意的区间即可.【详解】逐一考查所给的区间：A.，函数在区间上单调递增，函数在区间上单调递减，不合题意；B.，函数在区间上单调递减，函数在区间上单调递减，符合题意；C.，函数在区间上单调递减，函数在区间上单调递增，不合题意；D.，函数在区间上单调递增，函数在区间上单调递增，不合题意；本题选择B选项.【点睛】本题主要考查三角函数的单调性及其应用等知识，意在考查学生的转化能力和计算求解能力.6.如图，在中，D是BC上一点，则（）A. B. C. D.【答案】D【解析】【分析】由题意结合向量的运算整理计算即可求得最终结果.【详解】由题意可得：.本题选择D选项.【点睛】本题主要考查平面向量的加法公式、减法公式等知识，意在考查学生的转化能力和计算求解能力.7.已知为单位向量，且，那么向量的夹角是（）A. B. C. D.【答案】D【解析】【分析】由题意结合向量的夹角公式求解向量的夹角即可.【详解】设向量的夹角是，由题意可得：，则，即向量的夹角是.本题选择D选项.【点睛】本题主要考查平面向量夹角的计算，特殊角的三角函数值等知识，意在考查学生的转化能力和计算求解能力.8.设，则使成立的的取值范围是A. B. C. D.【答案】B【解析】【分析】由题意结合三角函数的图像确定不等式的解集即可.【详解】绘制函数在区间上的图像如图所示，且易知，观察可得，使成立的的取值范围是.本题选择B选项.【点睛】本题主要考查三角不等式的解法，三角函数图像的应用等知识，意在考查学生的转化能力和计算求解能力.9.已知函数，，其图象如图所示为得到函数的图象，只需先将函数图象上各点的横坐标缩短到原来的倍纵坐标不变，再A. 向右平移个单位B. 向右平移个单位C. 向左平移个单位D. 向左平移个单位【答案】A【解析】【分析】首先确定函数的解析式，然后确定函数的变换即可.【详解】由图1可知，函数的周期为，则，当时，，则，令可得，则，同理可得.将函数图象上各点的横坐标缩短到原来的倍纵坐标不变，据此可得函数的解析式为：，而，则图象上各点的横坐标缩短到原来的倍纵坐标不变，再将函数图像向右平移个单位即可得到函数的图象.【点睛】已知f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的部分图象求其解析式时，A比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：(1)由ω＝即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0，则令ωx0＋φ＝0(或ωx0＋φ＝π)，即可求出φ.(2)代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求.10.在中，，，是BC边上的动点，则的取值范围是A. B. C. D.【答案】A【解析】【分析】由题意结合平面向量的加减法和向量的数量积运算法则确定的取值范围即可.【详解】设，则：，，由于，故：，由于，故，结合一次函数的性质可知.本题选择A选项.【点睛】求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.11.若，且为第三象限的角，则______．【答案】【解析】【分析】由题意结合同角三角函数基本关系求解的值即可.【详解】由题意结合同角三角函数基本关系可得：，则.【点睛】本题主要考查同角三角函数基本关系及其应用，意在考查学生的转化能力和计算求解能力.12.已知向量与向量共线的一个非零向量的坐标可以是______．【答案】【解析】【分析】由题意结合向量共线的充分必要条件确定一个非零向量的坐标即可.【详解】由向量共线的充分必要条件可知满足题意的向量为：，取可得：与向量共线的一个非零向量的坐标可以是.【点睛】本题主要考查向量共线的定义及其应用，属于基础题.13.如果，那么x的最小值是______．【答案】【解析】【分析】由题意求解三角方程确定x的最小值即可.【详解】解三角方程可得：，则，由于，故取可得的最小值为.【点睛】本题主要考查三角方程的解法，正切函数的性质等知识，意在考查学生的转化能力和计算求解能力.14.如图，已知正方形．若，其中，，则______．【答案】【解析】【分析】由题意首先确定的值，然后求解其比值即可.【详解】由题意可得：，则，即.【点睛】(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．(2)用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．15.在直角坐标系中，已知点，，，是坐标平面内的一点．① 若四边形是平行四边形，则点的坐标为______；② 若，则点的坐标为______．【答案】(1). (2).【解析】【分析】由题意结合平面向量的坐标运算求解点的坐标即可.【详解】①.设点的坐标为，四边形是平行四边形，则：，，据此可得：，点的坐标为.②.由题意可得：，，故，设，由题意可得：，据此可得：，解得：，点的坐标为.【点睛】本题主要考查平面向量的坐标运算，向量在几何中的应用等知识，意在考查学生的转化能力和计算求解能力.16.设函数若的图象关于直线对称，则的取值集合是___．【答案】【解析】【分析】由题意结合三角函数的性质确定的取值集合即可.【详解】由题意可知，函数的对称轴方程为：，即，结合题意有：，整理可得的取值集合是.【点睛】本题主要考查三角函数的性质及其应用，三角函数的对称轴等知识，意在考查学生的转化能力和计算求解能力.三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤.17.，且．Ⅰ求的值；Ⅱ求的值．【答案】(Ⅰ)；(Ⅱ).【解析】【分析】(Ⅰ)首先求得的值，然后利用两角和差正切公式求解三角函数式的值即可；(Ⅱ)由题意结合降幂公式和两角和的正切公式求解三角函数式的值即可.【详解】（Ⅰ）因为，，所以．所以．（Ⅱ）因为，，所以．所以．【点睛】本题主要考查同角三角函数基本关系的应用，三角函数公式的应用等知识，意在考查学生的转化能力和计算求解能力.18.函数的部分图象如图所示，其中，，．Ⅰ求的解析式；Ⅱ求在区间上的最大值和最小值；Ⅲ写出的单调递增区间．【答案】（Ⅰ）；（Ⅱ）最大值；最小值．（Ⅲ）（）．【解析】【分析】(Ⅰ)结合函数图像分别确定的值即可确定函数的解析式；(Ⅱ)由函数的解析式结合正弦函数的性质确定函数的最值即可；(Ⅲ)结合函数的解析式写成函数的单调增区间即可.【详解】（Ⅰ）由图象可知．因为的最小正周期为，所以．令，解得，适合．所以．（Ⅱ）因为，所以．所以，当，即时，取得最大值；当，即时，取得最小值．（Ⅲ）的单调递增区间满足：，求解不等式组可得其在区间为：（）．【点睛】本题主要考查三角函数解析式的求解，函数最值的求解，函数单调区间的求解等知识，意在考查学生的转化能力和计算求解能力.19.在直角坐标系xOy中，已知点，，，其中．Ⅰ求的最大值；Ⅱ是否存在，使得为钝角三角形？若存在，求出的取值范围；若不存在，说明理由．【答案】（Ⅰ）．（Ⅱ）答案见解析.【解析】【分析】(Ⅰ)首先求得向量的坐标表示，然后求解其数量积，结合三角函数的性质确定其最大值即可；(Ⅱ)首先确定最大的角，然后结合(Ⅰ)中的结论求解三角不等式确定的取值范围即可.【详解】（Ⅰ），．所以．因为，所以．所以当，即时，取得最大值．（Ⅱ）因为，，．又，所以，，所以，．所以若△为钝角三角形，则角是钝角，从而．由（Ⅰ）得，解得．所以，即．反之，当时，，又三点不共线，所以△为钝角三角形．综上，当且仅当时，△为钝角三角形．【点睛】本题主要考查平面向量数量积的坐标运算，向量在几何中的应用等知识，意在考查学生的转化能力和计算求解能力.B卷 [学期综合]本卷满分：50分四、填空题：本大题共5小题，每小题4分，共20分．把答案填在题中横线上．20.若集合，，则____．【答案】【解析】【分析】结合题意由并集的定义求解即可.【详解】由题意结合并集的定义可得：.【点睛】本题主要考查并集的定义，属于基础题.21.函数的定义域是____．【答案】，或【解析】【分析】由题意结合函数的解析式求解函数的定义域即可.【详解】函数有意义，则：，求解不等式组可得函数的定义域为，或.【点睛】求函数的定义域，其实质就是以函数解析式有意义为准则，列出不等式或不等式组，然后求出它们的解集即可．22.已知三个实数，，将a，b，c按从小到大排列为___．【答案】【解析】【分析】由题意结合函数的单调性和所给的数与1的大小关系比较其大小即可.【详解】由题意可得：，，则a，b，c按从小到大排列为.【点睛】对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．当底数与指数都不相同时，选取适当的“媒介”数（通常以“0”或“1”为媒介），分别与要比较的数比较，从而可间接地比较出要比较的数的大小．23.里氏震级M的计算公式为：，其中是标准地震的振幅，A是测震仪记录的地震曲线的最大振幅在一次地震中，测震仪记录的地震曲线的最大振幅是500，则此次地震的里氏震级为__级；8级地震的最大振幅是5级地震最大振幅的___倍【答案】(1). (2).【解析】【分析】由题意结合定义的知识和对数的运算法则整理计算即可求得最终结果.【详解】由题意可得，地震曲线的最大振幅是500时，地震的里氏震级为级，设8级地震的最大振幅为，则：，解得：，据此可知：8级地震的最大振幅是5级地震最大振幅的倍.【点睛】本题主要考查新定义的应用，对数的运算法则及其应用等知识，意在考查学生的转化能力和计算求解能力.24.已知函数若，则的值域是____；若的值域是，则实数的取值范围是____．【答案】(1). (2).【解析】若，由二次函数的性质，可得，的值域为，若值域为，时，且时，，要使的值域为，则，得，实数的取值范围是，故答案为.五、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤.25.已知函数．Ⅰ证明：是奇函数；Ⅱ判断函数在区间上的单调性，并用函数单调性的定义加以证明．【答案】(Ⅰ)证明见解析；(Ⅱ)答案见解析.【解析】【分析】(Ⅰ)首先确定函数的定义域，然后考查与的关系即可证得函数为奇函数；(Ⅱ)由题意结合函数的单调性的定义确定并证明函数的单调性即可.【详解】（Ⅰ）函数的定义域为.对于任意，因为，所以是奇函数．（Ⅱ）函数在区间上是减函数．证明：在上任取，，且，则．由，得，，，，所以，即.所以函数在区间上是减函数.【点睛】本题主要考查奇函数的判定，函数的单调性的判定等知识，意在考查学生的转化能力和计算求解能力.26.已知函数定义在区间上，其中．Ⅰ若，求的最小值；Ⅱ求的最大值．【答案】(Ⅰ)-2；(Ⅱ)当时，的最大值为；当时，的最大值为．【解析】【分析】(Ⅰ)由题意结合函数的解析式确定函数的单调性，然后确定函数的最值即可；(Ⅱ)由题意分类讨论，，和三中情况确定函数的最大值即可.【详解】（Ⅰ）当时，．所以在区间上单调递增，在上单调递减．因为，，所以的最小值为．（Ⅱ）①当时，．所以在区间上单调递增，所以的最大值为．当时，函数图像的对称轴方程是.②当，即时，的最大值为.③当时，在区间上单调递增，所以的最大值为．综上，当时，的最大值为；当时，的最大值为．【点睛】二次函数、二次方程与二次不等式统称“三个二次”，它们常结合在一起，有关二次函数的问题，数形结合，密切联系图象是探求解题思路的有效方法．一般从：①开口方向；②对称轴位置；③判别式；④端点函数值符号四个方面分析．27.已知函数的定义域为若对于任意，，且，都有，则称函数为“凸函数”．Ⅰ判断函数与是否为“凸函数”，并说明理由；Ⅱ若函数b为常数是“凸函数”，求a的取值范围；Ⅲ写出一个定义在上的“凸函数”，满足只需写出结论【答案】(Ⅰ)答案见解析；(Ⅱ)；(Ⅲ)【解析】【分析】(Ⅰ)由题意结合“凸函数”的定义判断所给的函数是否是“凸函数”即可；(Ⅱ)由题意得到关于a的不等式，讨论确定实数a的取值范围即可；(Ⅲ)按照“凸函数”的定义给出一个满足题意的函数即可.【详解】（Ⅰ）对于函数，其定义域为．取，有，，所以，所以不是“凸函数”．对于函数，其定义域为．对于任意，且，由，所以．因为，，所以，所以是“凸函数”．（Ⅱ）函数的定义域为．对于任意，且，．依题意，有．因为，所以．（Ⅲ）．【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.。

北京市西城区2018-2019学年度第一学期期末试卷高三数学(理科)(解析版)

基础题．
2. 在等比数列
A. 10
中，若
，
B. 16
，则
C. 24
【答案】 D
【解析】解：等比数列
中，若
，
，则
故选： D．根据等比数列的性质即可求出．本题考查了等比数列的性质，考查了运算和求解能力，属于基础题
D. 32
，
3. 一个四棱锥的三视图如图所示，那么这个四棱锥最长棱的棱长为
A.
B.
C.
北京市西城区 2018-2019 学年度第一学期期末试卷
高三数学（理科）
一、选择题（本大题共 8 小题，共 40.0 分）
1. 已知集合
，
，那么
A. 2，
B. 0，
C.
D.
【答案】 B
【解析】解：集合
，
，
故选： B．
0，．
先求出集合 A，B，由此能求出
．
本题考查交集的求法，考查交集定义、不等式性质等基础知识，考查运算求解能力，是
，则输出数据的总个数为 ______．
【答案】 6 【解析】解：模拟程序的运行，可得
满足条件
，执行循环体，
，输出 n 的值为 3，
满足条件
，执行循环体，
，输出 n 的值为 7，
满足条件
，执行循环体，
，输出 n 的值为 15，
满足条件
，执行循环体，
，输出 n 的值为 31，
满足条件
，执行循环体，
，输出 n 的值为 63，
D. 前三个答案都不对
【答案】 C
【解析】解：由下图的一个图形能剪成 2 块“ L”形骨牌，
在个国际象棋棋盘由
个方格组成，其中有一个小方格因破损而被剪去破损位置

2018-2019学年北京市西城区八年级上学期期末数学试卷(含答案)

北京市西城区2018— 2019学年度第一学期期末试卷八年级数学 2019.1试卷满分：100分，考试时间：100分钟一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．图书馆的标志是浓缩了图书馆文化的符号，下列图书馆标志中，不是．．轴对称的是（A ）（B ）（C ）（D ）2．500米口径球面射电望远镜，简称FAST ，是世界上最大的单口径球面射电望远镜，被誉为“中国天眼”． 2018年4月18日， FAST 望远镜首次发现的毫秒脉冲星得到国际认证，新发现的脉冲星自转周期为0.00519秒，是至今发现的射电流量最弱的高能毫秒脉冲星之一．将0.00519用科学记数法表示应为（A ）0.519×10-2（B ）5.19×10-3（C ）51.9×10-4（D ）519×10-63．在△ABC 中，AB =3，AC =5，第三边BC 的取值范围是（A ）10＜BC ＜13 （B ） 4＜BC ＜12 （C ）3＜BC ＜8 （D ） 2＜BC ＜84．如图，∠1+∠2+∠3+∠4+∠5等于（A ）360° （B ）540° （C ）720° （D ）900°5．对于一次函数y ＝（k -3）x ＋2，y 随x 的增大而增大，k 的取值范围是（A ）k ＜0 （B ） k ＞0 （C ）k ＜3 （D ） k ＞36．下列各式中，正确的是（）．（A ）2242ab b a c c = （B ） 1a b bab b ++= （C ）23193x x x -=-+ （D ）22x y x y-++=-7．如图，已知△ABC ，下面甲、乙、丙、丁四个三角形中，与△ABC 全等的是图1（A ）甲（B ）乙（C ）丙（D ）丁8．小东一家自驾车去某地旅行，手机导航系统推荐了两条线路，线路一全程75km ，线路二全程90 km ，汽车在线路二上行驶的平均时速是线路一上车速的1.8倍，线路二的用时预计比线路一用时少半小时，如果设汽车在线路一上行驶的平均速度为x km/h ，则下面所列方程正确的是（A ）759011.82x x =+ （B ） 759011.82x x =- （C ）759011.82x x =+ （D ）759011.82x x =-9．如图，△ABC 是等边三角形，AD 是BC 边上的高，E 是AC 的中点，P 是AD 上的一个动点，当PC 与PE 的和最小时，∠CPE 的度数是（A ）30° （B ）45°（C ）60°（D ）90°10. 如图，线段AB =6cm ，动点P 以2cm/s 的速度从A ---B---A 在线段AB 上运动，到达点A 后，停止运动；动点Q 以1cm/s 的速度从B---A 在线段AB 上运动，到达点A 后，停止运动．若动点P ，Q 同时出发，设点Q 的运动时间是t （单位：s ）时，两个动点之间的距离为s （单位：cm ），则能表示s 与t 的函数关系的是（A ）（B ）（C ）（D ）63263ots46363o t s636o t s64263ot s58°72°B cC ba 50°Ac a 50°乙甲50°58°bca58°丙ba 50°甲PEDCB A二、填空题（本题共18分，第11～16题，每小题2分，第17题3分，第18题3分）11．若分式11x x -+的值为0，则x 的值为．12．在平面直角坐标系xOy 中，点（1，-2）关于x 轴对称的点的坐标为．13．计算20 + 2-2 = ．14．如图，在△ABC 中，AB 的垂直平分线MN 交AC 于点D ，连接BD ．若AC =7，BC =5，则△BDC 的周长是．15．如图，边长为a cm 的正方形，将它的边长增加b cm ，根据图形写一个等式．16．如图，在△ABC 中，CD 是它的角平分线，DE ⊥AC 于点E ．若BC =6 cm ，DE =2 cm ，则△BCD 的面积为 cm 2．第16题图第17题图17．如图，在平面直角坐标系xOy 中，点A 的坐标为（4，－3），且OA =5，在x 轴上确定一点P ，使△AOP 为等腰三角形．（1）写出一个符合题意的点P 的坐标；（2）请在图中画出所有．．符合条件的△AOP ． 18．（1）如图1，∠MAB =30°，AB =2cm ．点C 在射线AM 上，利用图1，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题．你画图时，选取的BC 的长约为 cm （精确到0.1cm ）．（2）∠MAB 为锐．角．，AB =a ，点C 在射线AM 上，点B 到射线AM 的距离为d ， BC =x ，若△ABC 的形状、大小是唯一确定的，则x 的取值范围是．E C D B A三、解答题（本题共30分，每小题6分）19．（1）分解因式()()x x a y a x -+- （2）分解因式321025x y x y xy -+ （1）解：（2）解：20．计算2212441x x x x x x x --++÷++解：21．解方程6133x x x +=-+ 解：22．如图，点A,B,C, D在一条直线上，且AB=CD，若∠1=∠2，EC=FB．求证：∠E=∠F.证明：23．在平面直角坐标系xOy中，直线l1: y=3x与直线l2: y=kx+b交于点A(a，3) ，点B(2，4)在直线l2上．（1）求a的值；（2）求直线l2的解析式；（3）直接写出关于x的不等式3x＜kx+b的解集．解：（1）（2）（3）关于x的不等式3x＜kx+b的解集为_________________．四、解答题（本题共12分，第24题7分，第25题5分）24．在平面直角坐标系xOy中，正方形ABCD的两个顶点的坐标分别为A(-2，0) ，D(-2，4) ，顶点B在x轴的正半轴上．（1）写出点B，C的坐标；（2）直线y=5x+5与x轴交于点E，与y轴交于点F．求△EFC的面积．25．阅读下列材料下面是小明同学“作一个角等于60°的直角三角形”的尺规作图过程．请你参考小明同学解决问题的方式，利用图3再设计一种“作一个角等于60°的直角三角形”的尺规作图过程（保留作图痕迹），并写出作法，证明，及推理依据．作法：图3证明：五、解答题（本题8分）26．在△ABC 中，AB ＝AC ，在△ABC 的外部作等边三角形△ACD ，E 为AC 的中点，连接DE 并延长交BC 于点F ，连接BD ．（1）如图1，若∠BAC =100°，求∠BDF 的度数；（2）如图2，∠ACB 的平分线交AB 于点M ，交EF 于点N ，连接BN ．①补全图2；②若BN =DN ，求证：MB =MN ．图1 图2（1）解：（2）① 补全图形； ② 证明：BDACEFBDACEF北京市西城区2018— 2019学年度第一学期期末试卷八年级数学参考答案及评分标准 2019.1一、选择题（本题30分，每小题3分）题号 1 2 3 4 5 6 7 8 9 10 答案 A BD B DCCA CD 二、填空题（本题共18分，第11～16题每小题2分，第17，18题每小题3分）题号 11 12 1314 1516 答案 1（1， 2）11412a 2 + 2ab + b 2 = ( a + b ) 26题号1718答案（1）答案不唯一，如：（-5，0）；（2）如图，(1) 答案不唯一，如： BC =1.2cm ；(2) x =d 或x ≥a ．三、解答题（本题共30分，每小题6分）19．（1）解： ()()x x a y a x -+- =()()x x a y x a ---=()()x a x y -- ............................................................................................................ 3分（2）解：321025x y x y xy -+ =2(1025)xy x x -+=2(5)xy x - ................................................................................................................... 3分20．解：2212441x x x x x x x --++÷++=212(1)(1)(2)x x x x x x -++⋅+- M BA=11(2) x x x+-=21 (2)(2) xx x x x-+--=1(2)xx x--............................................................................................................................ 6分21．解：方程两边乘(x - 3)(x + 3)，得x(x+3)+ 6 (x-3)= x2-9．解得x =1 ．检验：当x =1时，(x - 3)(x + 3)≠0．所以，原分式方程的解为x =1 ． ..................................................................................... 6分22．证明：∵∠1+∠3＝180°，∠2+∠4＝180°．又∵∠1=∠2，∴∠3=∠4，∵AB = CD，∴AB + BC = CD + BC即AC = DB． ...................................... 3分在△ACE和△DBF中，∵,43,, AC DB EC FB=⎧⎪∠=∠⎨⎪=⎩∴△ACE≌△DBF．....................................................................................................... 5分∴∠E=∠F．.................................................................................................................... 6分23．解：（1）直线l1: y=3x与直线l2: y=kx+b交于点A(a，3) ，所以3a =3．解得a =1．（2）由（1）点A(1，3) ，直线l2: y=kx+b过点A(1，3) ，点B(2，4) ，所以3,2 4.k bk b+=⎧⎨+=⎩．解方程组得1,2. kb=⎧⎨=⎩直线l2的解析式为y=x+2．.............. 4分4321ECFDHBA（3）x＜1．............................................................................................................................................... 6分四、解答题（本题共12分，第24题8，第25题6分）24．解：（1）点B的坐标为(2，0) ，点C的坐标(2，4)；................................................. 2分直线EC的解析式为4433y x=+，（2）直线y=5x+5与x轴交于点E (-1，0) ，与y轴交于点F(0，5) ． ....................... 4分直线EC的解析式为4433y x=+，EC与y轴交于点H（0，43），所以FH=113．所以S△EFC=1()2E CEH x x⋅+=112． ......................................................................... 8分25．（本题5分）本题答案不唯一，如：作法：如图3,（1）延长BA至B’，使得AB’=AB；（2）分别以点B ，点B’ 为圆心，BB’长为半径画弧，两弧交于点C；（3）连接AC，BC．△ABC就是所求的直角三角形．.............................. 1分证明:连接B’C．由作图可知，BC= BB’ = B’C，AB’=AB，∴△ABC是等边三角形(等边三角形定义)．∴∠B=60° (等边三角形每个内角都等于60°)．∴AC⊥BB’于点E (等边三角形一边上的中线与这边上的高相互重合)．∴△ABC就是所求作的直角三角形．........................................................................ 6分四、解答题（本题共8分）26．（1）解：在等边三角形△ACD中，∠CAD =∠ADC =60°，AD＝AC．∵E为AC的中点，∴∠ADE=12∠ADC＝30°．................................................................................. 2分∵AB＝AC，∴ AD ＝AB ．∵ ∠BAD =∠BAC +∠CAD ＝160°．∴ ∠ADB =∠ABD ＝10°．∴ ∠BDF =∠ADF -∠ADB ＝20°． ................................................................. 4分（2）①补全图形，如图所示． ......................................................................................................... 5分②证明：连接AN ．∵ CM 平分∠ACB ，∴ 设 ∠ACM =∠BCM =α．∵ AB ＝AC ，∴ ∠ABC =∠ACB =2α．在等边三角形△ACD 中，∵ E 为AC 的中点，∴DN ⊥AC ．∴ NA =NC ．∴ ∠NAC =∠NCA =α．∴ ∠DAN =60°+ α．在△ABN 和△ADN 中，∵ ,,,AB AD BN DN AN AN =⎧⎪=⎨⎪=⎩∴ △ABN ≌△ADN ．∴ ∠ABN =∠ADN ＝30°，∠BAN =∠DAN ＝60°+ α．∴ ∠BAC ＝60°+ 2α．在△ABC 中，∠BAC +∠ACB +∠ABC ＝180°，∴ 60°+ 2α+ 2α+2α=180°．∴α=20°．∴ ∠NBC =∠ABC -∠ABN = 10°．∴ ∠MNB =∠NBC + ∠NCB =30°．∴ ∠MNB =∠MBN ．∴ MB =MN ． ................................................................................................................... 8分 N B D A CE F M。

西城区2018-2019学年度第一学期期末九年级数学试题参考答案

北京市西城区2019— 2019学年度第一学期期末试卷九年级数学参考答案及评分标准2019.1一、选择题（本题共30分，每小题3分）三、解答题（本题共72分，第17﹣26题，每小题5分，第27题7分，第28题7分，第29题8分）17．解：原式=24(2-………………………………………………………3分=162-=112．…………………………………………………………………………5分18．解：∵AD⊥BC于点D，∴∠ADB=∠ADC=90°．∵在Rt△ABD中，AB=12，∠BAD=30°，∴BD=12AB=6，…………………………………1分AD=AB·cos∠BAD =12·cos30°=……………………………………2分∵BC=15，∴CD= BC－BD=15－6=9．………………………………………………………3分∴在Rt△ADC中，tan C=ADCD……………………………………………………4分………………………………………5分19．解：（1）令0=y，则2230x x-++=．解得11-=x，32=x．………………………………………………………1分∵点A在点B的左侧，∴A （1-，0），B （3，0）． …………………………………………………2分对称轴为直线1=x ． …………………………………………………………3分（2）∵当1x =时，4=y ，∴顶点C 的坐标为（1，4）． …………………………………………………4分∵点C ，D 关于x 轴对称，∴点D 的坐标为（1，4-）．∵AB =4，∴=ACB DCB ACBD S S S ∆∆+四边形1442162=⨯⨯⨯=． ………………………………5分20．（1）证明：∵AD ∥BC ，∴∠ADB=∠DBC ． ……………………1分 ∵∠A =∠BDC ，∴△ABD ∽△DCB ． ……………………3分（2）解：∵△ABD ∽△DCB ，∴AB ADDC DB=． …………………………………………………………4分 ∵AB =12，AD =8，CD =15， ∴12815DB=． ∴DB =10． ………………………………………………………………5分21．解：根据题意，得 (213)(82)6x x --=． …………………………………………2分整理得 211180x x -+=．解得 12x =，29x =． …………………………………………………………3分 ∵9x =不符合题意，舍去，∴2x =． ……………………………………………………………………………4分答：人行通道的宽度是2米． ……………………………………………………5分 22．解：（1）∵抛物线1C ：2124y x x k =-+与x 轴有且只有一个公共点，∴方程2240x x k -+=有两个相等的实数根．∴2(4)420k ∆=--⨯=． ……………………………………………………1分解得 2k =． …………………………………………………………………2分（2）∵抛物线1C ：21242y x x =-+22(1)x =-，顶点坐标为（1，0），抛物线2C ：222(1)8y x =+-的顶点坐标为（-1，-8）， ………………3分∴将抛物线1C 向左平移2个单位长度，再向下平移8个单位长度就可以得到抛物线2C ． …………………………………………………………………4分（3）31m -<<． ……………………………………………………………………5分 23．解：（1）∵OC ⊥AB 于点D ，∴AD =DB ， ……………………………………1分∠ADO =90°．∵AB =∴AD =∵∠AOD =2∠E ，∠E =30°，∴∠AOD =60°． ………………………………………………………………2分∵在Rt △AOD 中， ∴OA =︒=∠60sin 32sin AOD AD =4． ………………………………………………3分（2）∠BAF =75°或15°． ……………………………………………………………5分24．解：（1）∵在Rt △ADB 中，∠ADB =90°，∠B =45°，∴∠BAD =90°—∠B =45°． ∴∠BAD =∠B ．∴AD =DB ． ……………………………1分设AD =x ，∵在Rt △ADC 中，tan ∠ACD =ADDC，∠ACD =58°， ∴DC =tan58x． ………………………………………………………………3分∵DB = DC + CB =AD ，CB =90，∴tan58x+90=x ． ……………………………………………………………4分将tan58°≈1.60代入方程，解得x ≈240． …………………………………………………………………5分答：最高塔的高度AD 约为240米． 25．（1）证明：连接OC ，如图1．∵ PC 是⊙O 的切线，C 为切点，∴OC ⊥PC ． ……………………………1分 ∴∠PCO =∠1+∠2=90°． ∵PD ⊥AB 于点D ， ∴∠EDA =90°．图1∴∠A +∠3=90°． ∵OA =OC ， ∴∠A =∠1． ∴∠2=∠3． ∵∠3=∠4， ∴∠2=∠4．即∠PCE =∠PEC ． …………………………………………………………2分（2）解：作PF ⊥EC 于点F ，如图2．∵AB 是⊙O 的直径， ∴∠ACB =90°．∵在Rt △ABC 中，AB =10，3sin 5A =， ∴BC =AB ·sin A =6．∴AC =22BC AB -=8．3分 ∵在Rt △AED 中，ED =32， ∴AE =sin ED A =52． ∴EC=AC －AE =112． ∵∠2=∠4， ∴PE=PC ．∵PF ⊥EC 于点F ， ∴FC=12……………………………………………………………4分 ∠PFC =90°． ∴∠2+∠5=90°．∵∠A +∠2=∠1+∠2=90°． ∴∠A =∠5． ∴sin ∠5 =35． ∴在Rt △PFC 中，PC =sin 5FC ∠=1255． ……………………………………5分26．解：（2）抛物线如图所示； ……………………1分（3）x =4-，1-或1； ……………………3分（4）41x -<<-或1x >． ……………………5分27．解：（1）∵二次函数212y x bx c =-++，当0x =和5x =时所对应的函数值相等，∴二次函数212y x bx c =-++的图象的对称轴是直线52x =．∵二次函数212y x bx c =-++的图象经过点A （1，0），∴10,25.2b c b ⎧=-++⎪⎪⎨⎪=⎪⎩……………………………………………………………1分解得 2,5.2c b =-⎧⎪⎨=⎪⎩∴二次函数的表达式为215222y x x =-+-． ………………………………2分（2）过点B 作BD ⊥x 轴于点D ，如图1．∵一次函数3y x =-+与二次函数212y x bx c =-++的图象分别交于B ，C 两点，∴2153222x x x -+=-+-．解得 12x =，25x =． ………………3分 ∴交点坐标为（2，1），（5，2-）． ∵点B 在第一象限，∴点B 的坐标为（2，1）． ∴点D 的坐标为（2，0）．在Rt △ABD 中，AD =1，BD =1，∴AB=2． …………………………………………………4分（3）结论：四边形ABCN 的形状是矩形． ………………………………………5分证明：设一次函数3y x =-+的图象与x 轴交于点E ，连接MB ，MN ，如图2．∵点B 绕点M 旋转180°得到点N ，∴M 是线段BN 的中点．∴MB = MN ．∵M 是线段AC 的中点， ∴MA = MC ．∴四边形ABCN 是平行四边形． ∵一次函数3y x =-+的图象与x 当0y =时，3x =． ∴点E 的坐标为（3，0）． ∴DE =1= DB ．∴在Rt △BDE 中，∠DBE =∠DEB =45°．同理∠DAB =∠DBA =45°． ∴∠ABE =∠DBA +∠DBE =90°．∴四边形ABCN 是矩形． ……………………………………………7分28．解：（1 …………………………2分（2）①补全图形如图所示； ………………3 ②结论：（1）中NM 与AB 证明：∵∠ACB =90°，AC =BC ， ∴∠CAB =∠B =45°． ∴∠CAN +∠NAM =45°．∵AD 绕点A 逆时针旋转90°得到线段AE ， ∴AD =AE ，∠DAE =90°． ∵N 为ED 的中点，∴∠DAN =12∠DAE =45°， AN ⊥DE ．∴∠CAN +∠DAC =45°， ∠AND =90°．∴∠NAM =∠DAC ． 4分在Rt △AND 中，ANAD =cos ∠DAN ．在Rt △ACB 中，ACAB =cos ∠CAB． ∵M 为AB 的中点，∴AB =2AM ．∴2AC AC AB AM ==．∴AM AC ． ∴AN AD =AMAC． ∴△ANM ∽△ADC ． ∴∠AMN =∠ACD ．∵点D 在线段BC 的延长线上， ∴∠ACD =180°－∠ACB =90°． ∴∠AMN =90°．∴NM ⊥AB ． ………………………………………………………5分（3）当BD 的长为 6 时， ……………………………7分 29．解：（1）所得图形，如图1所示． ……………………1分（2）①45°； ………………………………………3分②(2，12)或(12-，2)； ……………5分（3）①如图2，直线OQ 与⊙M 相切于点Q ，点Q 在第一象限，连接MQ ，过点Q 作QH ⊥x 轴于点H ． ∵直线OQ 与⊙M 相切于点Q ， ∴MQ ⊥OQ ． ∴∠MQO =90°． ∵MO =2，MQ =1，∴在Rt △MQO 中，sin ∠MOQ=21=MO MQ ．∴∠MOQ =30°．∴OQ =OM ﹒cos ∠MOQ =3． ∵QH ⊥x 轴， ∴∠QHO =90°．∵∠QOH =90°-∠MOQ =60°，∴在Rt △QOH 中，QH = OQ ﹒sin ∠QOH =23． …………………………6分 ②如图3，当反射光线PN 与坐标轴平行时，连接MP 并延长交x 轴于点D ，过点P 作PE ⊥OD 于点E ，过点O 作OF ⊥PD 于点F ．∵直线l 是⊙M 的切线， ∴MD ⊥l ．∴∠1+∠OPD =∠2+∠NPD =90°．图2∵∠1=∠2，∴∠OPD =∠NPD ． ∵PN ∥x 轴，∴∠NPD =∠PDO ． ∴∠OPD =∠PDO ． ∴OP =OD ． ∵OF ⊥PD ， ∴∠MFO =90°，PF =FD ．∵cos OMF ∠=MF MOMO MD=，设PF =FD =x ，而MO =2，MP =1， ∴12212x x+=+．解得x =∵0x >，∴x =． ∵PE ⊥OD ， ∴∠PED =90°=∠MOD ． ∴PE ∥MO ．∴∠EPD =∠OMF ．∴cos ∠EPD = cos ∠OMF ． ∴MOMF PD PE =． ∴PD MO MFPE ⋅==122x x +⋅ (1)x x =+=158-． …………………………………………………………7分．可知，当反射点P 从②中的位置开始，在⊙M 上沿逆时针方向运动，到与①中的点Q 重合之前，都满足反射光线与坐标轴无公共点，所以反射点P32P y <． ………………………………8分。

北京西城区2018-2019年高一数学上学期期末考试试题

北京市西城区2018 —2019学年度第一学期期末试卷高一数学2019.1试卷满分：150分考试时间：120分钟A卷[三角函数与平面向量] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.（A）向右平移6个单位（B）向右平移3个单位（C）向左平移π6个单位（D）向左平移π3个单位二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.11．若1cos 2θ=-，且θ为第三象限的角，则tan θ=______．12．已知向量(1,2)=a ．与向量a 共线的一个非零向量的坐标可以是______．13．如果πtan()0(0)3x x +=>，那么x 的最小值是______．14．如图，已知正方形ABCD ．若AD AB AC λμ−−→−−→−−→=+，其中λ，μ∈R ，则λμ=______． 15．在直角坐标系xOy 中，已知点(3,3)A ，(5,1)B ，(2,1)P ，M ① 若四边形APBM 是平行四边形，则点M 的坐标为______； ② 若2PA PB PM −−→−−→−−→+=，则点M 的坐标为______．16．设函数π()sin()3f x x ω=+．若()f x 的图象关于直线6x π=对称，则ω的取值集合是_____.三、解答题：本大题共3小题，共36分.解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知(0,)2απ∈，且3sin 5α=．（Ⅰ）求πsin()4α-的值；（Ⅱ）求2πcos tan()24αα++的值．18．（本小题满分12分）函数()sin()f x A x ωϕ=+的部分图象如图所示，其中0,0,||πA ωϕ>><．（Ⅰ）求()f x 的解析式；（Ⅱ）求()f x 在区间[,]2ππ上的最大值和最小值；（Ⅲ）写出()f x 的单调递增区间． 19．（本小题满分12分）在直角坐标系xOy 中，已知点(1,0)A -，B ，(cos ,sin )C θθ，其中[0,]2θπ∈．（Ⅰ）求AC BC ⋅的最大值；（Ⅱ）是否存在[0,]2θπ∈，使得△ABC 为钝角三角形？若存在，求出θ的取值范围；若不存在，说明理由．B 卷 [学期综合]本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分．把答案填在题中横线上． 1．若集合{|03}A x x =<<，{|12}B x x =-<<，则A B =_____． 2．函数21()log f x x=的定义域为_____. 3．已知三个实数123a =，b 3log 2c =．将,,a b c 按从小到大排列为_____． 4．里氏震级M 的计算公式为：0lg lg M A A =-，其中00.005A =是标准地震的振幅，A 是测震仪记录的地震曲线的最大振幅．在一次地震中，测震仪记录的地震曲线的最大振幅是500，则此次地震的里氏震级为_____级；8级地震的最大振幅是5级地震最大振幅的_____倍．5．已知函数21,2,(),3.x x x c f x x c x -⎧+-⎪=⎨<⎪⎩≤≤≤若0c =，则()f x 的值域是____；若()f x 的值域是1[,2]4-，则实数c 的取值范围是_____．二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6．（本小题满分10分）已知函数2()1xf x x =-．（Ⅰ）证明：()f x 是奇函数；（Ⅱ）判断函数()f x 在区间(1,1)-上的单调性，并用函数单调性的定义加以证明．7．（本小题满分10分）已知函数2()f x ax x =+定义在区间[0,2]上，其中[2,0]a ∈-．（Ⅰ）若1a =-，求()f x 的最小值；（Ⅱ）求()f x 的最大值．8．（本小题满分10分）已知函数()f x 的定义域为D ．若对于任意12,x x D ∈，且12x x ≠，都有1212()()2()2x x f x f x f ++<，则称函数()f x 为“凸函数”．（Ⅰ）判断函数1()2f x x =与2()f x = （Ⅱ）若函数()2x f x a b =⋅+（,a b 为常数）是“凸函数”，求a 的取值范围；（Ⅲ）写出一个定义在1(,)2+∞上的“凸函数”()f x ，满足0()f x x <<．（只需写出结论）。

北京市西城区2018-2019学年度第一学期英语期末试卷

北京市西城区2018-2019学年度第一学期期末试卷高三英语2019. I本试卷共10页，共120分。

考试时长100分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

第一部分：知识运用（共两节，45分）第一节阅读下列短文，根据短文内容填空。

（共10小题；每小题1.5分，共15分）在未给提示词的空白处仅填写1个适当的单词，在给出提示词的空白处用括号内所给词的正确形式填空。

AFor most of her life , Anna Mary Roberts worked very hard making a living on a farm. She began to paint1 her seventies. She displayed her artworks in her town at age eighty. The paintings 2 (notice) by an art collector, 3 recognized Anna's remarkable talent. He bought all the paintings on display. Later, three of her paintings were exhibited in a well-known art museum in New York City. Soon, people around the world 4 (hear) of Anna and her delightful artworks. People loved looking at the old-fashioned scenes that Anna had created.BLegos are popular with kids. But 5 (make) them can hurt the environment. Why? Legos are made of plastic. The plastic is made from oil. That is a nonrenewable resource. Recently, Lego 6 (introduce) earth-friendly pieces. They are made of plastic taken from sugarcane. That is a renewable material. The green pieces are part of a bigger plan for Lego. The company plans to use renewable materials in all its 7 (toy) by 2030. The actions the company takes today can have an influence on the planet of tomorrow.CMany organizations try to inspire people 8 (do) kind acts, wherever and whenever they can. The idea behind this is that it doesn't take any major plan to be kind, just a little bit of effort. Perhaps the strongest supporter of this idea is the Random Acts of Kindness Foundation. It operates under the beliefs that kindness can be taught and that it is 9 ( easy) spread. Its activities range from suggesting kind acts to allowing its website-users to officially register 10 (they) as activists of kindness.第二节完形填空（共20小题；毎小题1.5分，共30分）阅读下面短文，掌握其大意，从每题所给的A.B.C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

西城区2018-2019学年七年级第一学期数学期末考试及参考答案

ꎬｍｎ＝ .
.
１４. 写出一个次数为４的单项式ꎬ要求其中所含字母只有ｘꎬｙ:
七年级期末㊀数学试卷㊀第㊀２页( 共８页)
１５. 如图ꎬ在以下建筑物的图片上做标记得到三个角 αꎬβꎬγꎬ 将这三个角按从大到小的顺序 ∙∙∙∙ ꎬ ꎬ . 排列:
１６. 一个由９个大小相同的正方体组成的立体图形如图所示ꎬ 从左面观察这个立体图形ꎬ 将得到的平面图形的示意图画在如下的画图区中. ∙∙∙
二㊁填空题( 本题共２０分ꎬ其中第１１㊁１３㊁１４㊁１６㊁１７题每小题２分ꎬ第１２㊁１５题每小题３分ꎬ第１１. －６的相反数等于１８题４分) .
２
１２. 如果ｍ＋３＋ ( ｎ－２) ＝０ꎬ那么ｍ＝１３. ４５ʎ２５ᶄ 的余角等于 ʎ
ᶄ.
ꎬｎ＝
１７. 线段ＡＢ＝６ꎬ在直线ＡＢ上截取线段ＢＣ＝３ＡＢ ꎬＤ为线段ＡＢ的中点ꎬＥ为线段ＢＣ的中点ꎬ 那么线段ＤＥ的长为 . １８. 我国现行的二代身份证号码是１８位数字ꎬ由前１７位数字本体码和最后１位校验码组成. 校 ∙∙∙∙∙ ∙∙∙ 验码通过前１７位数字根据一定规则计算得出ꎬ如果校验码不符合这个规则ꎬ那么该号码肯定是假号码. 现将前１７位数字本体码记为Ａ１Ａ２Ａ３ ��Ａ１６Ａ１７ ꎬ其中Ａｉ( ｉ＝１ꎬ��ꎬ１７) 表示第ｉ ∙∙∙∙∙ 位置上的身份证号码数字值ꎬ按下表中的规定分别给出每个位置上的一个对应的值Ｗｉ . ∙∙ ｉ１２３４５６７８９１０１１１２１３１４１５１６１７Ｗｉ７９１０５８４２１６３７９１０５８４２Ａｉ４４０５２４１９８００１０１００１

北京市西城区2018-2019学年高一上学期期末考试数学试题(解析版)

北京市西城区2018-2019学年高一上学期期末考试数学试题（解析版）一、选择题（本大题共10小题，共40.0分） 1. sin(−π3)的值是( )A. 12B. −12C. √32D. −√32【答案】D【解析】解：sin(−π3)=−sin π3=−√32，故选：D ．由条件利用诱导公式进行化简求值，可得结论．本题主要考查利用诱导公式进行化简求值，属于基础题．2. 函数f(x)=sin(x2+π3)的最小正周期为( )A. πB. 2πC. 4πD. 6π【答案】C【解析】解：函数f(x)=sin(x 2+π3)的最小正周期为：T =2π12=4π．故选：C ．直接利用三角函数的周期求解即可．本题考查三角函数的简单性质的应用，周期的求法，考查计算能力．3. 如果向量a ⃗ =(0,1)，b ⃗ =(−2,1)，那么|a ⃗ +2b⃗ |=( ) A. 6B. 5C. 4D. 3【答案】B【解析】解：由向量a ⃗ =(0,1)，b ⃗ =(−2,1)，所以a ⃗ +2b ⃗ =(−4,3)，由向量的模的运算有：|a ⃗ +2b ⃗ |=√(−4)2+33=5，故选：B ．本由向量加法的坐标运算有：a ⃗ +2b ⃗ =(−4,3)，由向量的模的运算有|a ⃗ +2b ⃗ |=√(−4)2+33=5，得解．本题考查了向量加法的坐标运算及向量的模的运算，属简单题． 4.sin(π2−α)cos(−α)=( )A. tanαB. −tanαC. 1D. −1【答案】C 【解析】解：sin(π2−α)cos(−α)=cosαcosα=1．故选：C ．利用诱导公式化简即可计算得解．本题主要考查了诱导公式在三角函数化简求值中的应用，属于基础题．5. 已知函数y =sinx 和y =cosx 在区间I 上都是减函数，那么区间I 可以是( )A. (0,π2)B. (π2,π) C. (π,3π2) D. (3π2,2π)【答案】B【解析】解：A ：y =sinx 在(0,π2)上是增函数； C ：y =cosx 在(π,3π2)上是增函数；D ：y =cosx 在(3π2,2π)上是增函数．故选：B ．依次分析四个选项可得结果．本题考查了正、余弦函数的单调区间，熟练掌握函数图象是关键，属基础题．6. 如图，在△ABC 中，D 是BC 上一点，则AB⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ −AD ⃗⃗⃗⃗⃗⃗ =( ) A. BD⃗⃗⃗⃗⃗⃗ B. DB ⃗⃗⃗⃗⃗⃗ C. CD ⃗⃗⃗⃗⃗ D. DC ⃗⃗⃗⃗⃗【答案】D【解析】解：AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ −AD ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AD ⃗⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ．故选：D ．根据向量加法和减法的几何意义即可得出答案．考查向量加法和减法的几何意义．7. 已知a ⃗ ，b ⃗ 为单位向量，且a ⃗ ⋅b ⃗ =−√22，那么向量a ⃗ ，b ⃗ 的夹角是( )A. π4B. π2C. 2π3D. 3π4【答案】D【解析】解：∵a ⃗ ,b ⃗ 为单位向量，且a ⃗ ⋅b ⃗ =−√22； ∴a ⃗ ⋅b ⃗ =|a ⃗ ||b ⃗ |cos <a ⃗ ,b ⃗ >=cos <a ⃗ ,b ⃗ >=−√22；又0≤<a ⃗ ,b ⃗ >≤π；∴<a ⃗ ,b ⃗ >=3π4．故选：D ．根据条件即可求出cos <a ⃗ ,b ⃗ >=−√22，根据向量夹角的范围即可求出向量a ⃗ ,b ⃗ 的夹角．考查单位向量的概念，向量数量积的计算公式，以及向量夹角的范围．8. 设α∈[0,2π)，则使sinα>12成立的α的取值范围是( )A. (π3,2π3)B. (π6,5π6)C. (π3,4π3)D. (7π6,11π6)【答案】B【解析】解：∵α∈[0,2π)，sinα>12， ∴π6<α<5π6．∴设α∈[0,2π)，则使sinα>12成立的α的取值范围是(π6,5π6).故选：B ．利用正弦函数的图象和性质直接求解．本题考查满足正弦值的角的取值范围的求法，考查正弦函数的图象和性质等基础知识，考查运算求解能力，是基础题．9. 已知函数f(x)=A 1sin(ω1x +φ1)，g(x)=A 2sin(ω2x +φ2)，其图象如图所示.为得到函数g(x)的图象，只需先将函数f(x)图象上各点的横坐标缩短到原来的12倍(纵坐标不变)，再( )A. 向右平移π6个单位 B. 向右平移π3个单位 C. 向左平移π6个单位D. 向左平移π3个单位【答案】A【解析】解：函数f(x)=A 1sin(ω1x +φ1)，g(x)=A 2sin(ω2x +φ2)，其图象如图所示，可见f(x)的周期为2π，g(x)的周期为π，且f(x)图象上的点(0,0)，在g(x)的图象上对应(π6,0)，为得到函数g(x)的图象，只需先将函数f(x)图象上各点的横坐标缩短到原来的12倍(纵坐标不变)，在向右平移π6个单位，故选：A ．利用函数y =Asin(ωx +φ)的图象变换规律，得出结论．本题主要考查函数y =Asin(ωx +φ)的图象变换规律，属于基础题．10. 在△ABC 中，A =π2，AB =2，AC =1.D 是BC 边上的动点，则AD ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 的取值范围是( )A. [−4,1]B. [1,4]C. [−1,4]D. [−4,−1]【答案】A【解析】解：建立平面直角坐标系，如图所示；则A(0,0)，B(2,0)，C(0,1)，设D(x,y)，则x2+y =1，x ∈[0,2]； ∴AD⃗⃗⃗⃗⃗⃗ =(x,y)， BC ⃗⃗⃗⃗⃗ =(−2,1)，∴AD ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =−2x +y =−2x +(1−12x)=−52x +1∈[−4,1]，则AD ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 的取值范围是[−4,1]．故选：A ．建立平面直角坐标系，利用坐标表示向量AD ⃗⃗⃗⃗⃗⃗ 、BC ⃗⃗⃗⃗⃗ ，求出AD ⃗⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 的取值范围即可．本题考查了平面向量数量积的计算问题，是基础题．二、填空题（本大题共11小题，共44.0分）11. 若cosθ=−12，且θ为第三象限的角，则tanθ=______．【答案】√3【解析】解：∵cosθ=−12，且θ为第三象限的角， ∴sinθ=−√1−sin 2θ=−√32， ∴tanθ=sinθcosθ=−√32−12=√3．故答案为：√3．由已知利用同角三角函数基本关系式先求sinθ，进而可求tanθ的值．本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．12. 已知向量a ⃗ =(1,2).与向量a ⃗ 共线的一个非零向量的坐标可以是______．【答案】(2,4)【解析】解：2a⃗ =(2,4)与a ⃗ 共线；即与向量a⃗ 共线的一个非零向量的坐标可以是(2,4)．故答案为：(2,4)．可求出2a ⃗ =(2,4)，而2a ⃗ 与a ⃗ 共线，即得出与向量a ⃗ 共线的一个非零向量的坐标可以是(2,4)．考查共线向量基本定理，向量坐标的数乘运算．13. 如果tan(x +π3) =0 (x >0)，那么x 的最小值是______．【答案】2π3【解析】解：tan(x +π3) =0 (x >0)，可得x +π3=kπ，即x =kπ−π3，k ∈N ∗，可得x 的最小值为π−π3=2π3，故答案为：2π3，由正切韩寒说的图象和性质可得x +π3=kπ，k 为正整数，即可得到所求最小值．本题考查三角方程的解法，注意运用正切函数的图象和性质，考查运算能力，属于基础题．14. 如图，已知正方形ABCD.若AD ⃗⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC⃗⃗⃗⃗⃗ ，其中λ，μ∈R ，则λμ=______．【答案】−1【解析】解：∵AC ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ ， ∴AD⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ ， ∴λ=−1，μ=1， ∴λμ=−1，故答案为：−1．利用向量加减法容易把AD ⃗⃗⃗⃗⃗⃗ 表示成AB ⃗⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗⃗ ，从而得λ，μ，得解．此题考查了向量加减法，属容易题．15. 在直角坐标系xOy 中，已知点A(3,3)，B(5,1)，P(2,1)，M 是坐标平面内的一点．①若四边形APBM 是平行四边形，则点M 的坐标为______； ②若PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ =2PM ⃗⃗⃗⃗⃗⃗ ，则点M 的坐标为______．【答案】(6,3) (4,2)【解析】解：①设M(x,y)，则：AP ⃗⃗⃗⃗⃗ =(−1,−2),MB ⃗⃗⃗⃗⃗⃗ =(5−x,1−y)； ∵四边形APBM 是平行四边形； ∴AP ⃗⃗⃗⃗⃗ =MB ⃗⃗⃗⃗⃗⃗ ；∴(−1,−2)=(5−x,1−y)； ∴{1−y =−25−x=−1；解得{y =3x=6；∴点M 的坐标为(6,3)；②PA ⃗⃗⃗⃗⃗ =(1,2),PB ⃗⃗⃗⃗⃗ =(3,0),PM ⃗⃗⃗⃗⃗⃗ =(x −2,y −1)； ∵PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ =2PM ⃗⃗⃗⃗⃗⃗ ；∴(1,2)+(3,0)=2(x −2,y −1)； ∴(4,2)=(2(x −2),2(y −1))； ∴{2(y −1)=22(x−2)=4；解得{y =2x=4；∴点M 的坐标为(4,2)．故答案为：(6,3)，(4,2)．①可设M(x,y)，得出AP ⃗⃗⃗⃗⃗ =(−1,−2),MB ⃗⃗⃗⃗⃗⃗ =(5−x,1−y)，根据四边形APBM 为平行四边形即可得出AP ⃗⃗⃗⃗⃗ =MB ⃗⃗⃗⃗⃗⃗ ，从而得出(−1,−2)=(5−x,1−y)，从而得到{1−y =−25−x=−1，解出x ，y 即可；②可求出PA ⃗⃗⃗⃗⃗ =(1,2),PB ⃗⃗⃗⃗⃗ =(3,0),PM ⃗⃗⃗⃗⃗⃗ =(x −2,y −1)，根据PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ =2PM ⃗⃗⃗⃗⃗⃗ 即可得出(4,2)=(2(x −2),2(y −1))，从而得出{2(y −1)=22(x−2)=4，解出x ，y 即可．考查相等向量的概念，根据点的坐标可求向量的坐标，向量坐标的加法和数乘运算．16.设函数f(x)=sin(ωx+π3).若f(x)的图象关于直线x=π6对称，则ω的取值集合是______．【答案】{ω|ω=6k+1,k∈Z}【解析】解：由题意ωπ6+π3=kπ+π2，k∈Z，得ω=6k+1，k∈Z，故答案为：{ω|ω=6k+1,k∈Z}．利用正弦函数图象的对称轴为x=kπ+π2，列出关于ω的方程，得解．此题考查了正弦函数的对称性，难度不大．17.若集合A={x|0<x<3}，B={x|−1<x<2}，则A∪B=______．【答案】{x|−1<x<3}【解析】解：∵集合A={x|0<x<3}，B={x|−1<x<2}，∴A∪B={x|−1<x<3}．故答案为：{x|−1<x<3}．利用并集定义直接求解．本题考查并集的求法，考查并集定义、不等式性质等基础知识，考查运算求解能力，是基础题．18.函数f(x)=1log2x的定义域是______．【答案】{x|0<x<1或x>1}【解析】解：由函数的解析式可得log2x≠0，即{x≠1x>0，解得函数的定义域为{x|0<x<1或x>1}，故答案为{x|0<x<1或x>1}．由函数的解析式可得log2x≠0，即{x≠1x>0，由此求得函数的定义域．本题主要考查函数的定义域的求法，对数函数的单调性和特殊点，对数函数的定义域，属于基础题．19.已知三个实数a=312，b=√2，c=log32.将a，b，c按从小到大排列为______．【答案】c<b<a【解析】解：312=√3>√2>1，log32<log33=1；∴c<b<a．故答案为：c<b<a．容易得出312>√2>1，log32<1，从而a，b，c从小到大排列为c<b<a．考查对数函数和y =√x 的单调性，以及增函数的定义．20. 里氏震级M 的计算公式为：M =lgA −lgA 0，其中A 0=0.005是标准地震的振幅，A 是测震仪记录的地震曲线的最大振幅.在一次地震中，测震仪记录的地震曲线的最大振幅是500，则此次地震的里氏震级为______级；8级地震的最大振幅是5级地震最大振幅的______倍. 【答案】5 1000【解析】解：根据题意，假设在一次地震中，测震仪记录的最大振幅是500，此时标准地震的振幅为0.005，则M =lgA −lgA 0=lg500−lg0.005=lg105=5．设8级地震的最大的振幅是x ，5级地震最大振幅是y ， 8=lgx +5，5=lgy +5，解得x =103，y =1， ∴x y=1000．故答案为：5；1000．根据题意中的假设，可得M =lgA −lgA 0=lg500−lg0.005=lg105=5；设8级地震的最大的振幅是x ，5级地震最大振幅是y ，8=lgx +5，5=lgy +5，由此知8级地震的最大的振幅是5级地震最大振幅的1000倍．本题考查对数的运算法则，解题时要注意公式的灵活运用，是基础题．21. 已知函数f(x)={x −1, c <x ≤3.x 2+x, −2≤x≤c若c =0，则f(x)的值域是______；若f(x)的值域是[−14,2]，则实数c 的取值范围是______．______．【答案】[−14,+∞) [12,1] [12,1]【解析】解：c =0时，f(x)=x 2+x =(x +12)2−14， f(x)在[−2,−12)递减，在(−12,0]递增，可得f(−2)取得最大值，且为2，最小值为−14；当0<x ≤3时，f(x)=1x 递减，可得f(3)=13，则f(x)∈[13,+∞)，综上可得f(x)的值域为[−14,+∞)；∵函数y =x 2+x 在区间[−2,−12)上是减函数，在区间(−12,1]上是增函数，∴当x ∈[−2,0)时，函数f(x)最小值为f(−12)=−14，最大值是f(−2)=2；由题意可得c>0，∵当c<x≤3时，f(x)=1x 是减函数且值域为[13,1c)，当f(x)的值域是[−14,2]，可得12≤c≤1．故答案为：[−14,+∞)；[12,1]．若c=0，分别求得f(x)在[−2,0]的最值，以及在(0,3]的范围，求并集即可得到所求值域；讨论f(x)在[−2,1]的值域，以及在(c,3]的值域，注意c>0，运用单调性，即可得到所求c的范围．本题给出特殊分段函数，求函数的值域，并在已知值域的情况下求参数的取值范围，着重考查了函数的值域和二次函数的单调性和最值等知识，属于中档题．三、解答题（本大题共6小题，共66.0分）22.已知α∈(0,π2)，且sinα=35．(Ⅰ)求sin(α−π4)的值；(Ⅱ)求cos2α2+tan(π4+α)的值．【答案】解(Ⅰ)：因为α∈(0,π2)，sinα=35，所以cosα=√1−sin2α=45．所以sin(α−π4)=√22(sinα−cosα)=−√210．(Ⅱ)：因为sinα=35，cosα=45，所以tanα=sinαcosα=34．所以cos2α2+tan(π4+α)=1+cosα2+1+tanα1−tanα=7910．【解析】(Ⅰ)根据同角的三角函数的关系，以及两角差的正弦公式即可求出，(Ⅱ)根据二倍角公式和两角和的正切公式即可求出．本题考查同角的三角形函数的关系，以及两角差的正想说和二倍角公式，属于中档题23.函数f(x)=Asin(ωx+φ)的部分图象如图所示，其中A>0，ω>0，|φ|<π．(Ⅰ)求f(x)的解析式；(Ⅱ)求f(x)在区间[π2,π]上的最大值和最小值；(Ⅲ)写出f(x)的单调递增区间．【答案】(Ⅰ)解：由函数f(x)=Asin(ωx +φ)的部分图象可知 A =3，因为 f(x)的最小正周期为T =7π6−π6=π，所以 ω=2πT=2．令 2×π6+φ=π2，解得 φ=π6，适合|φ|<π．所以 f(x)=3sin(2x +π6)．(Ⅱ)解：因为x ∈[π2,π]，所以2x +π6∈[7π6, 13π6]．所以，当2x +π6=13π6，即x =π时，f(x)取得最大值32，当2x +π6=3π2，即x =2π3时，f(x)取得最小值−3．(Ⅲ)解：结合f(x)的图象可得它的单调递增区间为[ kπ−π3, kπ+ π6 ](k ∈Z)．【解析】(Ⅰ)由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，可得f(x)的解析式．(Ⅱ)利用正弦函数的定义域和值域，求得f(x)在区间[π2,π]上的最大值和最小值． (Ⅲ)由f(x)的图象，可得它的单调递增区间．本题主要考查由函数y =Asin(ωx +φ)的部分图象求解析式，由函数的图象的顶点坐标求出A ，由周期求出ω，由五点法作图求出φ的值，正弦函数的定义域和值域，正弦函数的增区间，属于中档题．24. 在直角坐标系xOy 中，已知点A(−1,0)，B(0,√3)，C(cosθ,sinθ)，其中θ∈[ 0, π 2]． (Ⅰ)求AC ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 的最大值；(Ⅱ)是否存在θ∈[ 0, π 2]，使得△ABC 为钝角三角形？若存在，求出θ的取值范围；若不存在，说明理由．【答案】解：(Ⅰ)由题意，AC⃗⃗⃗⃗⃗ =(cosθ+1,sinθ)， BC ⃗⃗⃗⃗⃗ =(cosθ,sinθ−√3)； ……………………(2分)所以 AC ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =(cosθ+1)⋅cosθ+sinθ⋅(sinθ−√3)……………………(3分)=cosθ−√3sinθ+1=2cos(θ+π3)+1； ……………………(4分)因为 θ∈[ 0, π2]，所以 θ+π3∈[π3, 5π6]； ……………………(5分)所以当θ+π3=π3，即θ=0时，AC ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 取得最大值2； ……………………(6分) (Ⅱ)因为|AB|=2，|AC| =√(1+cosθ)2+sin 2θ=√2+2cosθ，|BC| =√cos 2θ+(sinθ−√3)2=√4−2√3sinθ；又 θ∈[ 0, π2]，所以 sinθ∈[0,1]，cosθ∈[0,1]，所以|AC|≤2，|BC|≤2；所以若△ABC 为钝角三角形，则角C 是钝角，从而CA⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ <0；………………(8分) 由(Ⅰ)得2cos(θ+π3)+1<0，解得cos(θ+π3)<−12； ……………………(9分)所以 θ+π3∈(2π3, 5π6]，即θ∈(π3, π2]； ……………………(11分) 反之，当θ∈(π3, π2]时，CA ⃗⃗⃗⃗⃗ ⋅CB⃗⃗⃗⃗⃗ <0，又 A ，B ，C 三点不共线，所以△ABC 为钝角三角形；综上，当且仅当θ∈(π3, π2]时，△ABC 为钝角三角形.……………………(12分)【解析】(Ⅰ)由平面向量数量积的坐标运算，利用三角恒等变换求得AC ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ 的最大值2； (Ⅱ)由两点间的距离公式求得|AC|、|BC|，并判断△ABC 为钝角三角形时角C 是钝角，利用CA ⃗⃗⃗⃗⃗ ⋅CB⃗⃗⃗⃗⃗ <0，结合题意求得θ的取值范围．本题考查了平面向量的数量积与解三角形的应用问题，是中档题．25. 已知函数f(x)=xx 2−1．(Ⅰ)证明：f(x)是奇函数；(Ⅱ)判断函数f(x)在区间(−1,1)上的单调性，并用函数单调性的定义加以证明．【答案】解：(Ⅰ)：函数f(x)的定义域为D ={x|x ≠±1}.……………………(1分) 对于任意x ∈D ，因为 f(−x)=−x(−x)2−1=−f(x)，……………………(3分) 所以 f(x)是奇函数. ……………………(4分)(Ⅱ)解：函数f(x)=xx 2−1在区间(−1,1)上是减函数.……………………(5分) 证明：在(−1,1)上任取x 1，x 2，且 x 1<x 2，……………………(6分)则 f(x 1)−f(x 2)=x 1x 12−1−x2x 22−1=(1+x 1x 2)(x 2−x 1)(x 12−1)(x 22−1). ……………………(8分)由−1<x 1<x 2<1，得 1+x 1x 2>0，x 2−x 1>0，x 12−1<0，x 22−1<0，所以 f(x 1)−f(x 2)>0，即 f(x 1)>f(x 2).所以函数f(x)=xx 2−1在区间(−1,1)上是减函数.……………………(10分)【解析】(Ⅰ)先求定义域，再用奇函数的定义f(−x)=−f(x)证明f(x)为奇函数； (Ⅱ)按照①取值，②作差，③变形，④判号，⑤下结论，这5个步骤证明．本题考查了奇偶性与单调性的综合，属中档题．26. 已知函数f(x)=ax 2+x 定义在区间[0,2]上，其中a ∈[−2,0]．(Ⅰ)若a =−1，求f(x)的最小值； (Ⅱ)求f(x)的最大值．【答案】解：(Ⅰ)根据题意，当a =−1时，f(x)=−x 2+x =−(x −12)2+14；所以 f(x)在区间(0,12)上单调递增，在(12,2)上f(x)单调递减．因为 f(0)=0，f(2)=−2，所以 f(x)的最小值为−2． (Ⅱ)①当a =0时，f(x)=x ．所以 f(x)在区间[0,2]上单调递增，所以 f(x)的最大值为f(2)=2．当−2≤a <0时，函数f(x)=ax 2+x 图象的对称轴方程是x =−12a ． ②当0<−12a ≤2，即−2≤a ≤−14时，f(x)的最大值为f(−12a )=−14a ． ③当−14<a <0时，f(x)在区间[0,2]上单调递增，所以 f(x)的最大值为f(2)=4a +2．综上，当−2≤a ≤−14时，f(x)的最大值为f(−12a )=−14a ；当−14<a ≤0时，f(x)的最大值为4a +2．【解析】(Ⅰ)根据题意，将a =−1代入函数的解析式，结合二次函数的性质分析可得 f(x)在区间(0,12)上单调递增，在(12,2)上f(x)单调递减，分析可得答案；(Ⅱ)根据题意，按a 的取值范围分情况讨论，求出函数的最大值，综合即可得答案．本题考查二次函数的性质以及函数的最值，注意结合函数的单调性进行讨论．27. 已知函数f(x)的定义域为D.若对于任意x 1，x 2∈D ，且x 1≠x 2，都有f(x 1)+f(x 2)<2f(x 1+x 22)，则称函数f(x)为“凸函数”．(Ⅰ)判断函数f 1(x)=2x 与f 2(x)=√x 是否为“凸函数”，并说明理由； (Ⅱ)若函数f(x)=a ⋅2x +b(a,b 为常数)是“凸函数”，求a 的取值范围； (Ⅲ)写出一个定义在(12,+∞)上的“凸函数”f(x)，满足0<f(x)<x.(只需写出结论)【答案】(本小题满分10分)(Ⅰ)解：对于函数f 1(x)=2x ，其定义域为R ．取x 1=0，x 2=1，有f(x 1)+f(x 2)=f(0)+f(1)=2，2f(x 1+x 22)=2f(12)=2，所以 f(x 1)+f(x 2)=2f(x 1+x 22)，所以 f 1(x)=2x 不是“凸函数”.…………(2分)对于函数f 2(x)=√x ，其定义域为[0,+∞)．对于任意x1，x2∈[0,+∞)，且x1≠x2，由[f(x1)+f(x2)]2−[2f(x1+x22)]2=(√x1+√x2)2−(2√x1+x22)2=−(√x1−√x2)2<0，所以[f(x1)+f(x2)]2<[2f(x1+x22)]2．因为f(x1)+f(x2)>0，2f(x1+x22)>0，所以f(x1)+f(x2)<2f(x1+x22)，所以f2(x)=√x是“凸函数”.……………(4分) (Ⅱ)解：函数f(x)=a⋅2x+b的定义域为R．对于任意x1，x2∈R，且x1≠x2，f(x1)+f(x2)−2f(x1+x22)=(a⋅2x1+b)+(a⋅2x2+b)−2(a⋅2x1+x22+b)……………………(5分)=a(2x1+2x2−2×2x1+x22)=a(2x12−2x22)2.……………………(7分)依题意，有a(2x12−2x22)2<0．因为(2x12−2x22)2>0，所以a<0.……………………(8分)(Ⅲ)f(x)=√x−12 (x>12).(注：答案不唯一)……………………(10分)【解析】(Ⅰ)取x1=0，x2=1，有f(x1)+f(x2)=f(0)+f(1)=2，2f(x1+x22)=2f(12)=2，验证，然后利用单调性证明即可．(Ⅱ)函数f(x)=a⋅2x+b的定义域为R.对于任意x1，x2∈R，且x1≠x2，f(x1)+f(x2)−2f(x1+x22)转化证明即可．(Ⅲ)f(x)=√x−12 (x>12)．本题考查函数与方程的应用，考查转化思想以及计算能力．。

02--2018-2019学年北京市西城区八年级上学期期末数学试题(答案)

北京市西城区2018— 2019学年度第一学期期末试卷八年级数学参考答案及评分标准 2019.1一、选择题（本题30分，每小题3分）二、填空题（本题共18分，第11～16题每小题2分，第17，18题每小题3分）三、解答题（本题共30分，每小题6分）19．（1）解： ()()x x a y a x -+- =()()x x a y x a ---=()()x a x y -- ·················································································· 3分（2）解：321025x y x y xy -+ =2(1025)xy x x -+=2(5)xy x - ······················································································· 3分20．解：2212441x x x x x x x --++÷++=212(1)(1)(2)x x x x x x -++⋅+- =11(2)x x x +-=21(2)(2)x x x x x -+-- =1(2)x x x --······························································································ 6分21．解：方程两边乘 (x - 3)(x + 3)，得 x (x +3) + 6 (x -3)= x 2 -9．解得 x = 1 ．检验：当x = 1时，(x - 3)(x + 3)≠0．所以，原分式方程的解为x =1 ． ································································ 6分22．证明：∵ ∠1+∠3＝180°，∠2+∠4＝180°．又 ∵ ∠1=∠2， ∴ ∠3=∠4， ∵ AB = CD ，∴ AB + BC = CD + BC即AC = DB ． ···························· 3分在△ACE 和△DBF 中， ∵ ,43,,A C D BE CF B =⎧⎪∠=∠⎨⎪=⎩∴ △ACE ≌△DBF ． ············································································· 5分 ∴ ∠E =∠F ． ······················································································· 6分23．解：（1）直线l 1: y =3x 与直线l 2: y =kx +b 交于点A (a ，3) ，所以 3a =3．解得 a =1．（2）由（1）点A (1，3) ，直线l 2: y =kx +b 过点A (1，3) ，点B (2，4) ，所以 3,2 4.k b k b +=⎧⎨+=⎩．解方程组得 1,2.k b =⎧⎨=⎩直线l 2的解析式为 y =x +2． ·········· 4分（3）x ＜1．············································································································ 6分4321EC FDHB A四、解答题（本题共12分，第24题8，第25题6分）24．解：（1）点B的坐标为(2，0) ，点C的坐标(2，4)；····································· 2分直线EC的解析式为4433y x=+，（2）直线y=5x+5与x轴交于点E (-1，0) ，与y轴交于点F(0，5) ． ················· 4分直线EC的解析式为4433y x=+，EC与y轴交于点H（0，43），所以FH=113．所以S△EFC=1()2E CEH x x⋅+=112． ······················································· 8分25．（本题5分）本题答案不唯一，如：作法：如图3,（1）延长BA至B’，使得AB’=AB；（2）分别以点B ，点B’ 为圆心，BB’长为半径画弧，两弧交于点C；（3）连接AC，BC．△ABC就是所求的直角三角形． ······················ 1分证明:连接B’C．由作图可知，BC= BB’ = B’C，AB’=AB，∴△ABC是等边三角形(等边三角形定义)．∴∠B=60° (等边三角形每个内角都等于60°)．∴AC⊥BB’于点E (等边三角形一边上的中线与这边上的高相互重合)．∴△ABC就是所求作的直角三角形． ······················································ 6分四、解答题（本题共8分）26．（1）解：在等边三角形△ACD中，∠CAD =∠ADC =60°，AD＝AC．∵E为AC的中点，∴∠ADE=12∠ADC＝30°．····························································· 2分∵AB＝AC，∴AD＝AB．∵∠BAD=∠BAC+∠CAD＝160°．∴ ∠ADB =∠ABD ＝10°．∴ ∠BDF =∠ADF -∠ADB ＝20°． ················································· 4分（2）①补全图形，如图所示． ··············································································· 5分②证明：连接AN ．∵ CM 平分∠ACB ，∴ 设 ∠ACM =∠BCM =α． ∵ AB ＝AC ，∴ ∠ABC =∠ACB =2α．在等边三角形△ACD 中， ∵ E 为AC 的中点， ∴DN ⊥AC ． ∴ NA =NC ．∴ ∠NAC =∠NCA =α． ∴ ∠DAN =60°+ α．在△ABN 和△ADN 中， ∵ ,,,A B A DB N D NA N A N =⎧⎪=⎨⎪=⎩∴ △ABN ≌△ADN ．∴ ∠ABN =∠ADN ＝30°，∠BAN =∠DAN ＝60°+ α． ∴ ∠BAC ＝60°+ 2α．在△ABC 中，∠BAC +∠ACB +∠ABC ＝180°， ∴ 60°+ 2α+ 2α+2α=180°． ∴α=20°．∴ ∠NBC =∠ABC -∠ABN = 10°． ∴ ∠MNB =∠NBC + ∠NCB =30°． ∴ ∠MNB =∠MBN ．∴ MB =MN ． ······················································································· 8分N BDA CEFM。

北京市西城区2018-2019学年高一上期末数学试卷含答案解析

【分析】利用二倍角公式求出2sin15°cos15°，sin215°﹣cos215°，1﹣2sin215°的值，利用同角三角函数的基本关系式求出sin215°+cos215°的值，即可得到选项．
故选A
5．在△ABC中，D是BC边上一点，则等于（）
A． B． C． D．
【考点】向量的减法及其几何意义．
【分析】根据题意，由两个向量的减法的几何意义可得 = ．
【解答】解：在△ABC中，D是BC边上一点，则由两个向量的减法的几何意义可得 = ，
故选C．
6．若tanα=3，tanβ=2，则tan（α﹣β）=（）
7．函数y=sinx图象的一个对称中心的坐标是（）
A．（0，0）B． C． D．
8．下列各式中，值为的是（）
A．2sin15°cos15°B．sin215°﹣cos215°
C．1﹣2sin215°D．sin215°+cos215°
9．已知正方形ABCD的边长为1，设，，，则| |等于（）
【考点】三角函数的周期性及其求法．
【分析】分别找出四个选项函数的λ值，代入周期公式T= 中求出各自的周期，即可得到最小正周期为π的函数．
【解答】解：A、y=cos4x的周期T= = ，本选项错误；
B、y=sin2x的周期T= =π，本选项正确；
C、y=sin 的周期为T= =4π，本选项错误；
D、y=cos 的周期为T= =8π，本选项错误，
2019-2019学年北京市西城区普通中学高一（上）期末数学试卷
一、选择题：本大题共10小题，每小题4分，共40分.
1．sin（﹣60°）的值等于（）
A． B． C． D．
2．下列函数中，最小正周期为π的是（）