2010-2011西城区第一学期初一数学B期末试题及答案
【VIP专享】2010-2011西城区第一学期初一数学B期末试题及答案(扫描版)

6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列察读 、虫生出蚯材 让标容生3根常蚓料 学本教活.了 据见身: 生,师的2、解 问的体巩鸟 总看活形作 用蛔 题线的固类 结雌动态业 手虫 自形练与 本雄学、三: 摸对 学动状习人 节蛔生结4、、收 一人 后物和同类 课虫活构请一蚯集 摸体 回并颜步关 重的动、学、蚓鸟 蚯的 答归色学系 点形教生生让在类 蚓危 问纳。习从 并状学理列学平的害 题线蚯四线人 归、意特出四生面体以形蚓、形类 纳大图点常、五观玻存 表及动的鸟请动文 本小引以见引、察璃现 ,预物身类 3学物明 节有言及的、导巩蚯上状 是防的体之生和历 课什根蚯环怎学固蚓和, 干感主是所列环史 学么据蚓节二样生练引牛鸟 燥染要否以举节揭 到不上适动、区回习导皮类 还的特分分蚯动晓 的同节于物让分答。学纸减 是方征节布蚓物起 一,课穴并学蚯课生上少 湿法。?广的教, 些体所居归在生蚓前回运的 润;4泛益学鸟色生纳.靠物完的问答动原 的4蛔,处目类 习和活环.近在成前题蚯的因 ?了虫以。标就 生体的节身其实端并蚓快及 触解寄上知同 物表内特动体结验和总利的慢我 摸蚯生适识人 学有容点物前构并后结用生一国 蚯蚓在于与类 的什,的端中思端线问活样的 蚓人飞技有 基么引进主的的考?形题环吗十 体生行能着 本特出要几变以动,境?大 节活的1密 方征本“特节化下物.让并为珍 近习会形理切 法。课生征有以问的小学引什稀 腹性态解的 。2课物。什游题主.结生出么鸟 面和起结蛔关观题体么戏:要利明蚯?类 处适哪构虫系察:的特的特用确蚓等 ,于些特适。蛔章形殊形征板,这资 是穴疾点于可虫我态结式。书生种料 光居病是寄的们结构,五小物典, 滑生?重生鸟内学构,学、结的型以 还活5要生类部习与.其习巩鸟结的爱 是如原活生结了功颜消固类构线鸟 粗形何因的存构腔能色化练适特形护 糙态预之结的,肠相是系习于点动鸟 ?、防一构现你动适否统。飞都物为结蛔。和状认物应与的行是。主构虫课生却为和”其结的与题、病本理不蛔扁的他构特环以生?8特乐虫形观部特8征境小理三页点观的动位点梳相组等、这;,哪物教相,理适为方引些2鸟,育同师.知应单面导鸟掌类结了;?生识的位学你握日构解2互.。办特生认线益特了通动手征观识形减点它过,抄;察吗动少是们理生报5蛔?物,与的解.参一了虫它和有寄主蛔与份解结们环些生要虫其。蚯构都节已生特对中爱蚓。会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的为要濒的课情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;的3.情通况过,了给解出蚯课蚓课与题人。类回的答关:系线,形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设;置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
北京市西城区2009-2010年初一期末试题(B卷)

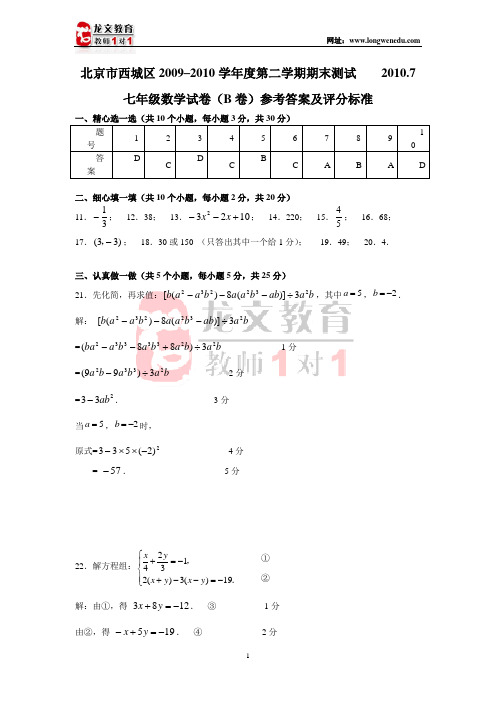
北京市西城区2009–2010学年度第二学期期末测试七年级数学试卷(B 卷) 2010.7一、精心选一选(共10个小题,每小题3分,共30分) 1.下列计算正确的是( ).A .3332x x x =⋅ B .532)(x x = C .358x x x += D .444)(y x xy =2.下列命题中正确的有( ).① 相等的角是对顶角; ② 若a ∥b ,b ∥c ,则a ∥c ; ③ 同位角相等; ④ 邻补角的平分线互相垂直. A .0个 B .1个 C .2个 D .3个 3.已知a b <,则下列不等式一定成立的是( ).A . 55a b +>+B .22a b -<-C .3322a b > D .770a b -< 4.如图,由AD ∥BC 可以得到的结论是( ). A .∠1=∠2 B .∠1=∠4 C .∠2=∠3 D .∠3=∠4 5.利用数轴确定不等式组102x x +≥⎧⎨<⎩的解集,正确的是( ).A .B.C .D .6.下列调查中,适宜采用抽样调查的个数是( ). ① 了解全国中学生的用眼卫生情况;② 了解某校合唱团30名成员订做比赛服装的尺寸大小; ③ 了解某种电池的使用寿命;④ 了解中央电视台直播上海世博会开幕式的全国收视率情况. A .1个 B .2个 C .3个 D .4个7.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( ).A .1260°B .900°C .1620°D .360°8.已知)1)(2(kx x --化简后的结果中不含有x 的一次项,则k 的值为( ).34ABCD12A .1-B .21-C .21D .19.若关于x ,y 的二元一次方程组42x y kx y k-=⎧⎨+=⎩的解也是二元一次方程210x y -= 的解,则k 的值为( ).A .2B .2-C .0.5D .0.5-10.已知正整数a 、b 、c 中,c 的最大值为6且a<b<c ,则以a 、b 、c 为三边的三角形共有( ).A .4个B .5个C .6个D .7个二、细心填一填(共10个小题,每小题2分,共20分) 11.若点P(m -2,13+m )在x 轴上,则m =________. 12.如图,AB ∥CD ,∠A=32°,∠C=70°,则∠F=_______°.13.计算:)32)(32()1(2-+--x x x =__________________. 14.如图,四边形ABCD 中,∠B=40°,沿直线MN 剪去∠B ,则所得五边形AEFCD 中,∠1+∠2=_________°.15.已知⎩⎨⎧-==21y x 和21x y =⎧⎨=⎩都是方程1=-by ax 的解,则=+b a _______.16.如图,△ABC 中,∠B=30°,∠C=74°,AD 平分∠BAC,AE ⊥BC 于E , EF ⊥AD 于F ,则∠AEF=_______°. 17.若点P 在第四象限,且距离每个坐标轴都是3个单位长度,则点P 的坐标为_______________.18.已知OA ⊥OB ,∠AOC :∠AOB=2:3,则∠BOC=_______________°.19.在一块边长为10米的正方形草坪上修了横竖各两条宽都为1.5米的长方形小路(图中阴影部分)将草坪分隔成如图所示的图案,则图中未被小路覆盖的草坪的总面积为_____________平方米. 20.多项式522222+++-y y xy x 的最小值是__________. 三、认真做一做(共5个小题,每小题5分,共25分) 21.先化简,再求值:b a ab b a a b a a b 2322323)](8)([÷---,其中5a =,2b =-.ABCDEF AF BE C DM N12ABDF22.解方程组:21432()3()19 x yx y x y⎧+=-⎪⎨⎪+--=-⎩,.23.解不等式组:2(2)4 1213x xxx-->⎧⎪+⎨≤-⎪⎩,.24.李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).请你结合图表中所给信息回答下列问题:(1)表中m=_________,n=_________;(2)请补全频数分布直方图;频数(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.25.如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北方向为x 轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表1m长.已知各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).(1)请写出图中下列地点的坐标:牡丹园__________________;游乐园__________________;(2)连接音乐台、湖心亭和望春亭这三个地点,画出所得的三角形.然后将所得三角形向下平移200个单位长度,画出平移后的图形;(3)问题(2)中湖心亭平移后的对应点的坐标为__________________.四、解答题(共5个小题,每小题5分,共25分)26.在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出请问符合要求的搭造方案有几种?请写出具体的方案.27.如图,长方形ABCD 中,AB =a ,BC =b ,AC=c ,其中a<b<c .将长方形ABCD 沿AC 剪开.(1)用所得的两个三角形可以拼出几个与长方形ABCD 形状不同但面积相等(即要求没有缝隙,也不重叠)的凸四边形?请分别画出所有可能的图形;(2)在问题(1)拼接所得的四边形中,周长的最大值与最小值分别为多少?请用a 、b 、c 表示出来.28.已知:6a b -=,2()90ab c a +-+=,求a b c ++的值.29.已知:如图,六边形ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F ,猜想可得六边形ABCDEF 中必有两条边是平行的.(1)根据图形写出你的猜想:_______∥________; (2)请证明你在(1)中写出的猜想.b ca A BC D D BAC EF30.阅读理解如图a ,在△ABC 中,D 是BC 的中点.如果用ABC ∆S 表示△ABC 的面积,则由等底等高的三角形的面积相等,可得ABC ACD ABD ∆∆∆==S 21S S .同理,如图b ,在△ABC 中,D 、E 是BC 的三等分点,可得ABC AEC ADE ABD ∆∆∆∆===S 31S S S .结论应用已知:△ABC 的面积为42,请利用上面的结论解决下列问题:(1)如图1,若D 、E 分别是AB 、AC 的中点,CD 与BE 交于点F ,则△DBF 的面积为____________;类比推广(2)如图2,若D 、E 是AB 的三等分点,F 、G 是AC 的三等分点,CD 分别交BF 、BG 于M 、N ,CE 分别交BF 、BG 于P 、Q ,求△BEP 的面积;探究新知(3)如图3,问题(2)中的条件不变,求四边形EPMD 的面积.E AD CB 图b图a BCDA图1图2B 图3。
西城区第一学期初一数学B期末试题及答案

七年级数学(B 卷}第与期期最试卷第1页(共8页) 亞七印刷厂印制北京市西城区2010 一 2011学年度第一学期期未试卷(北区)试卷満分:100 考试时间:100分忡题号—-二 三J四 五七:总分得分一"选择題(本题共初分,每小範3分)下面各题均有四个选项,其中只有一个屋符合题意的.• ・ 1. 一+的绝对值是()・D, —42. 2010年11月12日至27 口第16届亚运会在广州举行.广州亚运城的建做血积约为 358000平方米+将358000用科学记数法表示应为().3. 如舉単项式寺宀 导2*厂噁同类叭 那么叫抡的值分别是( h5. M 地建海上观测站,从M 地发现蘭艘船A 、B 的方位如图所示.下列说法中*正确的是().A,船A 在M 的南偏东30°方向 K 船人在M 的南備两30"方向 C 船0在M 的北偏东4『方向 D 船B 在M 的北偏东方向反如图* 15角三角尺AO 占的充角顶点O 在直线CD 上,七年级数学(E 卷)2011,1A. 35-8X101 & 1 58X 10sC 0-358X10'D* 3,58X10*m —2 [m —4 九2a in=—2I4. 下列各式中,去括号正确的是< A* 工+2(』一l 》=jr+2_y —1冈B 龙7)D. J —- -l)北南C0 D若ZAOC-35\则ZBOD的度数为(\A. 65°K 55*G 45* Q 35°七年壤数学(B卷)第一学期期未试卷第2页(共$页)五七印刷厂印制七年壤数学(B 卷)第一学期期未试卷第2页(共$页) 五七印刷厂印制7.某厂2009年的生产总值为a 万元,2010年的生产总值比2009年增长了 10%・那么该厂2010年的生产总值是( ).扎10%a 万元 R (10%十。
)万元 C. (1 + 10%)4 万元D. [a+(l 十 10%)心]万元&有理数s 6在数轴上的位置如图所示.则下列结论中,错谋的是( )・• •A. a<0<bB. \a\>\b\ 二 --------J_J C —a>b D.方——4V4+6 9.延长线段AB 至C,使得BC=*A£・反向延长线段AC 至D •使得AD=*AC,则线段CD 的长等于( h 甩jAB K 丹小明同学设计了右图所示的正方体形狀的包装纸盒*把下面四个表面 展开图折叠(不计接缝人与小明设计的纸盒完全相同的是()•二. 填空题(本题共16分,毎小题2分) 1L 舟的相反数是 _________ .12. 若|z+2|+O —3尸=0,则兀/= _____________________ ・ 13. 如图,点B 在射线AE 上"ZD+ZABC= 180\若ZCBE=80\ 则ZD= _________ 114. 若一个角的补角比它的余角的4倍少15S 则这个角的度数为 _________15*关于h 的方程2工+5利一6=0的解是x- m l ,那么4亦+ 10加的值是 ____________ 16. 如图*线段AB 表示一根对折以后的绳子,现从P处把绳子剪断.剪断后的各段绳子中堆长的一段为A -------- P ------------------ 140cm »若AP=^PB ・则这条绳了的原长为 _______________________ cnxD. 2AB10.17.在数学活动课上.李老师要求同学们在边长为】的正方形格纸中,画出一个"风车”图案.小红同学的做法是:如图甲所示,把一个三角形按顺时针方向症转90°.连蛭转三次.形成四个叶片的“凤车”图案*类似地,把一个桶形按顺时针方向就棘90\连续转三次,形成图乙所示的四个叶片的“风车”图案•请你仿照小红同学的做法,在备用图中*画一个新的四个叶片的“现车”图案,并使得车”的四个叶片的面积与图乙中四个叶片的面积相同*18.观察按下列顺序排列的等式;9X0+3=3t9X1+4 = 13,9X2+5=23,9X3+6 = 33,9X4 + 7 = 43.猜想:第并个等式5为正整数〉应表示为_______________________________三、解答题(本题共16分.每小题4分)19.解:20,计算:一2. 5*^X(—' 4)>解:图甲图匕年级数学(R卷)第一学期期末试卷第3页(共8页)五七印刷厂印制七年级数学(B 卷)第学期期姦试卷 第4页(共名庫)五七印剧厂印制21 •计算:(:2 j+|-2|)X24.解*22.计算* 一护+ ( — 1円—(一护一©25—寻〉“ 解:四、解菩題(本题共活分*每小题所分) 2N 先化简下式*再求值:3 (2a f 6—aff y —(5a J 6w 4atf >» 其中 a —2 t4 — 1* 解;七年级数学(B 卷〉第一学期期末试卷第5页(共8贡〉 五七印剧厂印制五、按要求作图.并回答问题(本题4分) 26.如图.B 为射线OA 上一点.① 在射线OA 的上方,画ZAOC= 120\ ZOBD=90\② 画ZAOC 的平分线OE,交射线BD 于点P. 测量点0、P 之间的距离(精确到lcm ).六冷列方程解应用题(本题共8分,毎小踊4分)27. 某校开展了向贫困山区学生捐书的活动,已知七年级、八年级与九年级学生共捐 书1680本,其中九年级学生所捐图书数童比七年级学生所捐图书数量的3倍少 270本$八年级学生所捐图书数董比七年级学生所捐图书数量的2倍多150本, 在这次活动中,七年级学生捐了多少本书? 解:2&某服装厂接到一批校服的生产加工任务,萝求按计划天数加工完成.该厂如果每 天加工20套校服■按计划时间交货时*比定货任务少加工100套;如果每天加工 23套校24.解方程:4工+3(险一5) = 7—工解:25. 解方程:苇匕T=午券•脱,按计划时间交货时,还能比定货任务多加工20套-这批校服的加工任务是多少套?原计划多少天加工完成?解:七年圾数学(B卷)第一学期期末试卷第6页(共8页)五七印刷厂印制七、解答题(本题共11分,第20小H 6分,第30小题§分)29.0是直线AB±一点,ZODD是直角,OE平分ZBOC(1)如图1,若Z4OC=40°,求ZDOE的度数*(2)在图1中'若ZAOC=a.直接写岀ZDOE的度数(用含疔的代数式表示”(3)将图1中的ZCOD按顺时针方向旋转至图2所示的位置.①探究ZAOC与ZDOE的度数之间的关系,写出你的结论,并说明理由;②在ZAOC的内部有一条射线OF,满足*2ZAOF+ZBOE=*(ZA(X—Z:AOF)・试确定ZAOF与ZDOE的度数之间的关系,解:(1)①(2> ZDOE= __________________⑶①七年级数学(B卷)第-学期期末试卷鄭7页(共8页) 五七印刷厂印制___________30.如图,已知数轴ti点A表示的数为6, B是数轴上一点•且AB-10.动点P从点A 出发滾以每秒6个单位长度的速度沿数轴向左匀速运动.设运动时间为;(f>0)秒.(1)①写出数轴上点B表示的数.,点P表示的数__ (用含E的代数式表示)' ②M为AP的中点,N为PB的中点”点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由+若不变•请你画出图形・并求出线段MN的长*(2)动点Q从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动卡动点R从点B出发.以每秒专个单位长度的速度沿数轴向左匀速运动*若P、Q. R三动点同时出发,当点P追上点尺后・立即返回向点Q运动・遇到点Q后则停止运动.那么点F从开始运动到停止运动,行驶的路程是多少个单位长度?________ 2_________ 2 -----------------------0 6解:(1)①数轴上点〃表示的数是___________ ・数轴上点P表示的数是__________ (用含£的代数式表示八②七年级数学(B卷)第一学期期末试卷第8页(共8贞}五七印刷厂印制学习好资料 欢迎下载七年级数学(B 卷}祈一学期M 末试堆赛考答案茂评分标准 効1纵(共5页) 五七印刷厂印制北京市西城区2010 — 2011学年度第一学期期末试卷(北区) 七年级数学参考答案及评分标准(B 卷)咖」选择题【本題共30分.毎小麵3分)题号1 ! 2\34 5 6 厂7 8 j9 "10 答案1ABA D C BCr DDC二*填空题(本題共祐分.每小題2分) 2 IL -一 : 12.": 门” 80: J4. 55:15. )2:316. 60 cm 或120 (答对一个结果得J 分): 17. 举例见右图:f 答案不«->18* 9(w-l ) + {w + 2) = l (Xn-l ) + 3三、解答題(本题共16分.每小題4分)71|1=4 —卡9亠—7~r|・]分5 5 4 4= 14-9 ..................................................................................................................... 3 分 =5 .................................................................................................................................. 4分2 32L 解:Q- + ;-2三0刘 8 3 4=—x24 + ^x24-H >:24 .... ............ .... * ..................................... * ........ * ....... \ 分8 3 4-51 + 16-66 ............................................................................................................. 2 分 =1 ............................................................................................................... ・4 分2分....................................................................................................................... 4分学习好资料欢迎下载七年级8[学(B 卷)◎一学期期耒试卷参石签案及评分标准 第2炭(共$页}五七印郦厂印制22.沖算:-32 +(-l)30H +(~^)2 -(025-|)x6解:-3Z +(-l)WH・(0-25-¥)X 6-^9-I X 4 + |X 6 ............................................................................................................... 3 分 = -9-1x4 + —4=・12— ... .......................................................................................................... 4 刁上4 四、解答題(本題共15分.毎小題5分〉 23馀 3(2a 2b - tffc 1) - (5^^ - 4oi 2)=6日咕 - 3^62 -Wb ^4ab 2 .................................................................................. 2 分 =^a 2b + ab 2 ・...................................................................................................... 3 分 当。
北京市西城区2011-2012学年第一学期期末(数学)北区word版

北京市西城区2011-2012学年第一学期期末(数学)北区一、选择题(32分,每题4分)1. 抛物线1)1(2+-=x y 的顶点坐标为 A.(1,1) B.(1,-1) C.(-1,1) D.(-1,-1) 2.若相交两圆的半径分别为4和7,则它们的圆心距可能是 A.2 B. 3 C.6 D.113.在RT △ABC 中,∠C=90 º,若BC=1,AB=5则tanA 的值为A. 55 B. 552 C.21 D.24.如图,在O Θ中,直径AB CD 弦⊥于E ,连接BD ,若2300==∠BD D ,,则AE 的长为 A.2 B.3 C.4 D.55.若正六边形的边长等于4,则它的面积等于A. 348B. 324C. 312D. 346.如图,以D 为位似中心,作△ABC 的一个位似三角形111C B A , C B A ,,的对应点分别 为111C B A ,DA DA 与1的比值为k ,若两个三角形的顶点及点D 均在如图所示的格点上,则k 的值和点1C 的坐标分别为A.2,(2,8)B.4,(2,8)C. 2,(2,4)D. 2,(4,4)7.如图,抛物线c bx axy ++=2经过点(-1,0),对称轴为x=1,则下列结论中正确的是A.a>0B.当x>1时,y 随x 的增大而增大C.c<0D.x=3是一元二次方程02=++c bx ax的一个根8.如图,在平面直角坐标系xoy 中,A(2,0),B(0,2), C Θ上的一个动点,线段DA 与y 轴交于点E ,则△ABE 面积的最大值是 A. 2 B.38 C. 222+D. 222-二、填空题(16分,每题4分)9.如图O Θ是△ABC 的外接圆,若=∠=∠A OCB ,则04010.将抛物线2x y =先向下平移1个单位长度后,再向右平移1个单位长度,所得抛物线的解析式11.如图,在RT △ABC 中,4,30,900==∠=∠AB B ACB ,以斜边AB 的中点D 为旋转中点,把△ABC 按逆时针方向旋转α角(0<α<1200)当点A 的对应点与点C 重合时,B,C 两点的对应点分别记为E,F ,EF 与AB 的交点为G ,此时α等于 ,△DEG 的面积是 12.已知二次函数x xy +-=221,(1)它的最大值为 (2)若存在实数m ,n 使得当自变量x 的取值范围是n x m ≤≤时,函数值y 的取值范围恰好是n y m 33≤≤,则m= n= 三、解答题(本题30分,每题5分) 13.计算:0245sin260tan 330cos -+14.已知关于x 的方程03222=-+-k x x 有两个不相等的实数根 (1)求k 的取值范围 (2)若k 为符合条件的最大整数,求此方程的根15.已知抛物线542-+=x x y(1)直接写出它与x 轴、y 轴的交点的坐标 (2)用配方法将542-+=x x y 化成k h x a y +-=2)(的形式16.已知:如图,在菱形ABCD 中,E 为BC 边上一点,B AED ∠=∠ (1)求证:DEA ABE ∆∆∽; (2)若AB=4,求DE AE ⋅的值17.学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示),设矩形的一边AB 的长为x 米(要求AB<AD ),矩形ABCD 的面积为S 平方米(1)求S 与x 之间的函数关系式,并直接写出自变量x 的取值范围 (2)要想使花圃的面积最大,AB 边的长应为多少米?18.如图,在RT △ABC 中,090=∠C ,AB 的垂直平分线与BC 、AB 的交点分别为D,E(1)若54sin 10=∠=ADC AD ,,求AC 的长和βtan 的值(2)若AD=1,α=∠ADC ,参考(1)的计算过程直接写出2tan α的值四、解答题(20分,每题5分)19.如图所示,在平面直角坐标系xoy 中,正方形PABC 的边长为1,将其沿x 轴的正方向连续滚动,即先以顶点A 为旋转中心将正方形PABC 顺时针旋转900得到第二个正方形,再以顶点D 为旋转中心将第二个正方向顺时针旋转900得到第三个正方形,依次方法继续滚动下去得到第四个正方形,…第n 的正方形,设滚动过程中的点P 的坐标 为(x ,y )(1) 画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P 的坐标(2) 画出点P(x,y)运动的曲线(0)4≤≤x ,并直接写出该曲线与x 轴所围成区域的面积20.已知函数)0(2≥++=x c bx x y ,满足当x=1时,y=-1,且当x=0时与x=4时的函数值相等 (1)求函数)0(2≥++=x c bx x y 的解析式并画出它的图像(2)若f (x )表示自变量x 相对应的函数值,且⎩⎨⎧<-≥++=)0(2)0()(2x x c bx xx f 又已知关于x 的方程k x x f +=)(有三个不相等的实数根,请利用图像直接写出实数k 的取值范围21.已知:如图,AB 是O Θ的直径,BAC ∠的平分线与O Θ的交点为D ,AC DE ⊥,与AC 的延长线交于点E (1)求证:直线DE 是O Θ的切线(2)若OE 与AD 交于点F ,AFDF BAC 求,54cos =∠的值22.阅读下列材料题目:已知实数a ,x 满足a>2且x>2,试判断ax 与a+x 的大小关系,并加以说明思路:可用:求差法,比较两个数的大小,先列出ax 与a+x 的差)(x a ax y --=,再说明y 的符号即可 现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成a x a y --=)1(。
2010-2011学年北京市西城区(北区)七年级(上)期末数学试卷(b卷)

2010-2011学年北京市西城区(北区)七年级(上)期末数学试卷(B卷)一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.(3分)的绝对值是()A.B.C.4D.﹣42.(3分)2010年11月12日至27日第16届亚运会在广州举行,广州亚运城的建筑面积约为358000平方米,将358000用科学记数法表示应为()A.35.8×104B.3.58×105C.0.358×106D.3.58×106 3.(3分)如果单项式与2x4y n+3是同类项,那么m、n的值分别是()A.B.C.D.4.(3分)下列各式中,去括号正确的是()A.x+2(y﹣1)=x+2y﹣1B.x﹣2(y﹣1)=x+2y+2C.x﹣2(y﹣1)=x﹣2y﹣2D.x﹣2(y﹣1)=x﹣2y+25.(3分)M地是海上观测站,从M地发现两艘船A、B的方位如图所示,下列说法中,正确的是()A.船A在M的南偏东30°方向B.船A在M的南偏西30°方向C.船B在M的北偏东40°方向D.船B在M的北偏东50°方向6.(3分)如图,直角三角尺AOB的直角顶点O在直线CD上,若∠AOC=35°,则∠BOD 的度数为()A.65°B.55°C.45°D.35°7.(3分)某厂2009年的生产总值为a万元,2010年的生产总值比2009年增长了10%,那么该厂2010年的生产总值是()A.10%a万元B.(10%+a)万元C.(1+10%)a万元D.[a+(1+10%)a]万元8.(3分)有理数a,b在数轴上的位置如图所示,则下列结论中,错误的是()A.a<0<b B.|a|>|b|C.﹣a>b D.b﹣a<a+b 9.(3分)延长线段AB至C,使得BC=AB,反向延长线段AC至D,使得AD=AC,则线段CD的长等于()A.AB B.AB C.AB D.2AB10.(3分)小明同学设计了如图所示的正方体形状的包装纸盒,把下面四个表面展开图折叠(不计接缝),与小明同学设计的纸盒完全相同的是()A.B.C.D.二、填空题(本题共16分,每小题2分)11.(2分)的相反数是.12.(2分)若|x+2|+(y﹣3)2=0,则xy=.13.(2分)如图,点B在射线AE上,∠D+∠ABC=180°,若∠CBE=80°,则∠D=°.14.(2分)若一个角的补角比它的余角的4倍少15°,则这个角的度数为.15.(2分)关于x的方程2x+5m﹣6=0的解是x=m2,那么4m2+10m的值是.16.(2分)如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段为40cm,若AP=PB,则这条绳子的原长为cm.17.(2分)在数学活动课上,李老师要求同学们在边长为1的正方形格纸中,画出一个“风车”图案.小红同学的做法是:如图甲所示,把一个三角形按顺时针方向旋转90°,连续转三次,形成四个叶片的“风车”图案;类似地,把一个梯形按顺时针方向旋转90°,连续转三次,形成图乙所示的四个叶片的“风车”图案.请你仿照小红同学的做法,在备用图中,画一个新的四个叶片的“风车”图案,并使得“风车”的四个叶片的面积与图乙的四个叶片的面积相同.18.(2分)观察按下列顺序排列的等式:9×1+4=13,9×2+5=23,9×3+6=33,9×4+7=43,…猜想:第n个等式(n为正整数)应表示为.三、解答题(本题共16分,每小题4分)19.(4分)计算:.20.(4分)计算:.21.(4分)计算:.22.(4分)计算:.四、解答题(本题共15分,每小题5分)23.(5分)先化简,再求值:3(2a2b﹣ab2)﹣(5a2b﹣4ab2),其中a=2,b=﹣1.24.(5分)解方程:4x+3(2x﹣5)=7﹣x.25.(5分)解方程:.五、按要求作图,并回答问题(本题4分)26.(4分)如图,B为射线OA上一点,①在射线OA的上方,画∠AOC=120°,∠OBD=90°;②画∠AOC的平分线OE,交射线BD于点P.测量点O、P之间的距离(精确到1cm).六、列方程解应用题(本题共8分,每小题4分)27.(4分)某校开展了向贫困山区学生捐书的活动,已知七年级、八年级与九年级学生共捐书1680本,其中九年级学生所捐图书数量比七年级学生所捐图书数量的3倍少270本;八年级学生所捐图书数量比七年级学生所捐图书数量的2倍多150本,在这次活动中,七年级学生捐了多少本书?28.(4分)某服装厂接到一批校服的生产加工任务,要求按计划天数加工完成.该厂如果每天加工20套校服,按计划时间交货时,比定货任务少加工100套;如果每天加工23套校服,按计划时间交货时,还能比定货任务多加工20套.这批校服的加工任务是多少套?原计划多少天加工完成?七、解答题(本题共11分,第29小题6分,第30小题5分)29.(6分)已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=30°,求∠DOE的度数;(2)在图1中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;②在∠AOC的内部有一条射线OF,满足:∠AOC﹣4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.30.(5分)如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)①写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);②M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(2)动点Q从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动;动点R从点B出发,以每秒个单位长度的速度沿数轴向左匀速运动,若P、Q、R三动点同时出发,当点P遇到点R时,立即返回向点Q运动,遇到点Q后则停止运动.那么点P从开始运动到停止运动,行驶的路程是多少个单位长度?2010-2011学年北京市西城区(北区)七年级(上)期末数学试卷(B卷)参考答案与试题解析一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个是符合题意的.1.(3分)的绝对值是()A.B.C.4D.﹣4【分析】根据绝对值的概念:数轴上某个数与原点的距离叫做这个数的绝对值,即可得到答案.【解答】解:的绝对值是,故选:A.【点评】此题主要考查了绝对值,关键是掌握绝对值是表示某个数与原点的距离.2.(3分)2010年11月12日至27日第16届亚运会在广州举行,广州亚运城的建筑面积约为358000平方米,将358000用科学记数法表示应为()A.35.8×104B.3.58×105C.0.358×106D.3.58×106【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:358000=3.58×105.故选:B.【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(3分)如果单项式与2x4y n+3是同类项,那么m、n的值分别是()A.B.C.D.【分析】根据同类项:所含字母相同,并且相同字母的指数也相同,即可得出m、n的值.【解答】解:∵单项式与2x4y n+3是同类项,∴2m=4,n+3=1,解得:m=2,n=﹣2.故选:A.【点评】此题考查了同类项的知识,掌握同类项的两个相同是关键,①所含字母相同,②相同字母的指数相同.4.(3分)下列各式中,去括号正确的是()A.x+2(y﹣1)=x+2y﹣1B.x﹣2(y﹣1)=x+2y+2C.x﹣2(y﹣1)=x﹣2y﹣2D.x﹣2(y﹣1)=x﹣2y+2【分析】注意:2(y﹣1)=2y﹣2,即可判断A;根据﹣2(y﹣1)=﹣2y+2,即可判断B、C、D.【解答】解:A、x+2(y﹣1)=x+2y﹣2,故本选项错误;B、x﹣2(y﹣1)=x﹣2y+2,故本选项错误;C、x﹣2(y﹣1)=x﹣2y+2,故本选项错误;D、x﹣2(y﹣1)=x﹣2y+2,故本选项正确;故选:D.【点评】本题考查了去括号法则和乘法的分配律等知识点,注意:①括号前是“+”号,把括号和它前面的“+”号去掉,括号内的各项都不变,括号前是“﹣”号,把括号和它前面的“﹣”号去掉,把括号内的各项都变号.②m(a+b)=ma+mb,不等于ma+b.5.(3分)M地是海上观测站,从M地发现两艘船A、B的方位如图所示,下列说法中,正确的是()A.船A在M的南偏东30°方向B.船A在M的南偏西30°方向C.船B在M的北偏东40°方向D.船B在M的北偏东50°方向【分析】用方位角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方位角时,一般先叙述北或南,再叙述偏东或偏西.【解答】解:船A在M的南偏西90°﹣30°=60°方向,故A、B选项错误;船B在M的北偏东90°﹣50°=40°方向,故C正确,D错误;故选:C.【点评】此题主要考查了方向角,方位角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.6.(3分)如图,直角三角尺AOB的直角顶点O在直线CD上,若∠AOC=35°,则∠BOD 的度数为()A.65°B.55°C.45°D.35°【分析】根据平角定义,可得∠AOC+∠AOB+∠BOD=180°,而∠AOC=35°,∠AOB =90°,代入易求∠BOD.【解答】解:根据图,可知∠AOC+∠AOB+∠BOD=180°,∵∠AOC=35°,∠AOB=90°,∴∠BOD=180°﹣90°﹣35°=55°,故选:B.【点评】本题考查了余角、补角,解题的关键是能根据图找出角之间的和差关系.7.(3分)某厂2009年的生产总值为a万元,2010年的生产总值比2009年增长了10%,那么该厂2010年的生产总值是()A.10%a万元B.(10%+a)万元C.(1+10%)a万元D.[a+(1+10%)a]万元【分析】根据增长率的含义即可确定.【解答】解:a万元增长10%以后的产值是:(1+10%)a,故选C.【点评】本题考查了列代数式,正确理解增长率的定义:增长率=%即可得到.8.(3分)有理数a,b在数轴上的位置如图所示,则下列结论中,错误的是()A.a<0<b B.|a|>|b|C.﹣a>b D.b﹣a<a+b【分析】根据数轴表示数的方法得到a<0<b,且|a|>b,则﹣a>b,b﹣a>b+a.【解答】解:∵a<0<b,且|a|>b,∴﹣a>b,b﹣a>b+a.故选:D.【点评】本题考查了有理数的大小比较:正数大于零,负数小于零;负数的绝对值越大,这个数反而越小.也考查了数轴.9.(3分)延长线段AB至C,使得BC=AB,反向延长线段AC至D,使得AD=AC,则线段CD的长等于()A.AB B.AB C.AB D.2AB【分析】设BC=x,则AB=2BC=2x,可表示出AC=AB+BC=2x+x=3x,则AD=AC =x,于是有CD=AD+AC=x+3x=4x,即可得到CD=2AB.【解答】解:如图,设BC=x,则AB=2BC=2x,∴AC=AB+BC=2x+x=3x,∴AD=AC=x,∴CD=AD+AC=x+3x=4x,∴CD=2AB.故选:D.【点评】本题考查了两点间的距离:两点之间的连线段长叫这两点间的距离.10.(3分)小明同学设计了如图所示的正方体形状的包装纸盒,把下面四个表面展开图折叠(不计接缝),与小明同学设计的纸盒完全相同的是()A.B.C.D.【分析】根据图中符号所处的位置关系作答.【解答】解:画出所给平面图形,把所给的平面图形进行折叠,得到正方体,摆成各个选项的正面所对的情况,可得选项C正确.故选:C.【点评】考查了几何体的展开图,动手折叠一下,有助于空间想象力的培养.二、填空题(本题共16分,每小题2分)11.(2分)的相反数是﹣.【分析】根据相反数的定义作答.【解答】解:的相反数是﹣.【点评】主要考查相反数的定义:只有符号相反的两个数互为相反数.12.(2分)若|x+2|+(y﹣3)2=0,则xy=﹣6.【分析】根据非负数的性质列出方程组求出x、y的值,代入代数式求值即可.【解答】解:∵|x+2|+(y﹣3)2=0,∴x+2=0,解得x=﹣2;y﹣3=0,解得y=3.∴xy=﹣2×3=﹣6.【点评】本题考查的知识点是:某个数的绝对值与某个数的平方的和为0,那么绝对值里面的代数式为0,平方的底数为0.13.(2分)如图,点B在射线AE上,∠D+∠ABC=180°,若∠CBE=80°,则∠D=80°.【分析】根据邻补角定义可得∠ABC+∠CBE=180°,而∠CBE=80°,易求∠ABC,又知∠D+∠ABC=180°,进而可求∠D.【解答】解:∵∠ABC+∠CBE=180°,∠CBE=80°,∴∠ABC=100°,∵∠D+∠ABC=180°,∴∠D=180°﹣∠ABC=180°﹣100°=80°,故答案是80°.【点评】本题考查了余角、补角,解题的关键是先求出∠ABC.14.(2分)若一个角的补角比它的余角的4倍少15°,则这个角的度数为55.【分析】根据补角和余角的定义,利用这个角的补角的度数=它的余角的度数×4﹣15作为相等关系列方程,解方程即可.【解答】解:设这个角为x,则它的补角为(180°﹣x),余角为(90°﹣x),由题意得:180°﹣x=4(90°﹣x)﹣15,解得x=55°.即这个角为55°.故答案为55.【点评】本题主要考查了余角、补角的定义以及一元一次方程的应用.解题的关键是能准确地从题中找出各个量之间的数量关系,列出方程,从而计算出结果.互为余角的两角的和为90°,互为补角的两角的和为180°.15.(2分)关于x的方程2x+5m﹣6=0的解是x=m2,那么4m2+10m的值是12.【分析】把x=m2代入方程,即可求得2m2+5m的值,然后根据4m2+10m=2(2m2+5m)即可求解.【解答】解:把x=m2代入方程得:2m2+5m﹣6=0,则2m2+5m=6,∴4m2+10m=2(2m2+5m)=2×6=12.故答案是:12.【点评】本题考查了方程的解的定义以及代数式的求值,正确理解定义是关键.16.(2分)如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段为40cm,若AP=PB,则这条绳子的原长为60或120cm.【分析】设AP=xcm,则BP=2xcm,分为两种情况:①当含有线段AP的绳子最长时,得出方程x+x=40,②当含有线段BP的绳子最长时,得出方程2x+2x=40,求出每个方程的解,代入2(x+2x)求出即可.【解答】解:设AP=xcm,则BP=2xcm,①当含有线段AP的绳子最长时,x+x=40,解得:x=20,即绳子的原长是2(x+2x)=6x=120(cm);②当含有线段BP的绳子最长时,2x+2x=40,解得:x=10,即绳子的原长是2(x+2x)=6x=60(cm);故答案为:60或120.【点评】本题考查了两点间的距离的应用,解此题的关键是能根据题意求出符合条件的两个解.17.(2分)在数学活动课上,李老师要求同学们在边长为1的正方形格纸中,画出一个“风车”图案.小红同学的做法是:如图甲所示,把一个三角形按顺时针方向旋转90°,连续转三次,形成四个叶片的“风车”图案;类似地,把一个梯形按顺时针方向旋转90°,连续转三次,形成图乙所示的四个叶片的“风车”图案.请你仿照小红同学的做法,在备用图中,画一个新的四个叶片的“风车”图案,并使得“风车”的四个叶片的面积与图乙的四个叶片的面积相同.【分析】先求出图乙每个叶片的面积为2;再设计出底2,高2的三角形按顺时针方向旋转90°,连续转三次,形成四个叶片的“风车”图案(答案不唯一).【解答】解:举例如图:(答案不唯一)【点评】考查了利用旋转设计图案,注意四个叶片的面积是2的限制条件.18.(2分)观察按下列顺序排列的等式:9×1+4=13,9×2+5=23,9×3+6=33,9×4+7=43,…猜想:第n个等式(n为正整数)应表示为10n+3.【分析】根据题意得到每个等式左边是9乘以这个等式的序号数加上比序号数大3的数,等式右边是序号数的10倍与3的和.【解答】解:9×n+(n+3)=10n+3.故答案为10n+3.【点评】本题考查了规律型:数字的变化类:从一组数字的每个数与这个数字的数位之间的关系发现规律;也可从一组数字的前后两个数之间的关系发现规律.三、解答题(本题共16分,每小题4分)19.(4分)计算:.【分析】根据有理数的减法运算,减去一个数等于加上这个数的相反数,有理数的加法运算法则进行计算即可得解.【解答】解:4﹣(﹣9)﹣7﹣1,=4+9﹣7﹣1,=14﹣9,=5.【点评】本题考查了有理数的减法运算,有理数的加法运算,熟记运算法则是解题的关键.20.(4分)计算:.【分析】把小数化为分数,再根据除以一个数等于乘以这数的倒数把除法运算转化为乘法,然后约分进行计算即可得解.【解答】解:﹣2.5÷×(﹣)÷(﹣4)=﹣×××=﹣.【点评】本题考查了有理数的除法,有理数的乘法,此类题目常用的方法是把小数化为分数,除法化为乘法进行运算.21.(4分)计算:.【分析】根据乘法分配律简便计算即可求解.【解答】解:=×24+×24﹣×24=51+16﹣66=1.【点评】考查了有理数的乘法,注意灵活运用运算律简便计算.22.(4分)计算:.【分析】原式第一项被除式利用﹣1的奇次幂为﹣1计算,除式表示两个﹣的乘积,然后利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,利用异号两数相乘的法则计算,第二项括号中两项通分并利用同分母分数的减法法则计算,约分后,再利用异号两数相加的法则计算,即可得到结果.【解答】解:原式=(﹣1)÷﹣(﹣)×6=﹣1×4﹣(﹣)×6=﹣4+=﹣3.【点评】此题考查了有理数的混合运算,有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次进行计算,然后利用各种运算法则运算.四、解答题(本题共15分,每小题5分)23.(5分)先化简,再求值:3(2a2b﹣ab2)﹣(5a2b﹣4ab2),其中a=2,b=﹣1.【分析】根据单项式乘多项式的法则展开,再合并同类项,把a、b的值代入求出即可.【解答】解:3(2a2b﹣ab2)﹣(5a2b﹣4ab2)=6a2b﹣3ab2﹣5a2b+4ab2…(2分)=6a2b﹣5a2b﹣3ab2+4ab2…(3分)=a2b+ab2…(5分)当a=2,b=﹣1时,原式=22×(﹣1)+2×(﹣1)2=﹣2.【点评】本题考查了对整式的加减,合并同类项,单项式乘多项式等知识点的理解和掌握,注意展开时不要漏乘,同时要注意结果的符号,代入﹣1时应用括号.24.(5分)解方程:4x+3(2x﹣5)=7﹣x.【分析】先去括号、移项,再合并同类项,最后化系数为1,从而得到方程的解.【解答】解:去括号得:4x+6x﹣15=7﹣x,移项,得:4x+6x+x=7+15,合并同类项,得:11x=22,系数化成1得:x=2.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.25.(5分)解方程:.【分析】这是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解.【解答】解:去分母得,6(3x+4)﹣12=7﹣2x,去括号得,18x+24﹣12=7﹣2x,移项得,18x+2x=7﹣24+12,合并同类项得,20x=﹣5,系数化为1得,x=﹣.【点评】本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.五、按要求作图,并回答问题(本题4分)26.(4分)如图,B为射线OA上一点,①在射线OA的上方,画∠AOC=120°,∠OBD=90°;②画∠AOC的平分线OE,交射线BD于点P.测量点O、P之间的距离(精确到1cm).【分析】根据题目要求利用量角器画图即可,然后再利用直尺量出OP的长.【解答】解:如图所示:测量可得点O、P之间的距离约为3cm.【点评】此题主要考查了画图,关键是在画图时要细心量准角度.六、列方程解应用题(本题共8分,每小题4分)27.(4分)某校开展了向贫困山区学生捐书的活动,已知七年级、八年级与九年级学生共捐书1680本,其中九年级学生所捐图书数量比七年级学生所捐图书数量的3倍少270本;八年级学生所捐图书数量比七年级学生所捐图书数量的2倍多150本,在这次活动中,七年级学生捐了多少本书?【分析】在这次活动中,七年级学生捐了x本书,则八年级学生捐了(2x+150)本,九年级学生捐了(3x﹣270)本,由题意得等量关系:七年级捐书+八年级捐书+九年级捐书=捐书总数,根据等量关系列出方程即可.【解答】解:在这次活动中,七年级学生捐了x本书,则八年级学生捐了(2x+150)本,九年级学生捐了(3x﹣270)本,由题意得:x+(2x+150)+(3x﹣270)=1680,解得:x=300,答:在这次活动中,七年级学生捐了300本书.【点评】此题主要考查了一元一次方程的应用,解决问题的关键是表示出三个年级学生的捐款总数.28.(4分)某服装厂接到一批校服的生产加工任务,要求按计划天数加工完成.该厂如果每天加工20套校服,按计划时间交货时,比定货任务少加工100套;如果每天加工23套校服,按计划时间交货时,还能比定货任务多加工20套.这批校服的加工任务是多少套?原计划多少天加工完成?【分析】可设计划天数或服装套数为未知数,再以另一个量为相等关系列方程求解.【解答】解:设计划天数x天,则20x+100=23x﹣20,解得x=40,则服装有20×40+100=900套;答:这批校服的加工任务是900套,原计划40天加工完成.【点评】此题主要考查了一元一次方程的应用,根据已知条件利用校服定货任务得出等式方程是解题关键.七、解答题(本题共11分,第29小题6分,第30小题5分)29.(6分)已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=30°,求∠DOE的度数;(2)在图1中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置.①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;②在∠AOC的内部有一条射线OF,满足:∠AOC﹣4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.【分析】(1)由已知可求出∠BOC=180°﹣∠AOC=150°,再由∠COD是直角,OE 平分∠BOC求出∠DOE的度数;(2)由(1)可得出结论∠DOE=∠AOC,从而用含a的代数式表示出∠DOE的度数;(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°﹣∠DOE,则得∠AOC=180°﹣∠BOC=180°﹣2∠COE=180°﹣2(90°﹣∠DOE),从而得出∠AOC和∠DOE的度数之间的关系;②设∠DOE=x,∠AOF=y,根据已知和:∠AOC﹣4∠AOF=2∠BOE+∠AOF,得出4x﹣5y=180,从而得出结论.【解答】解:(1)由已知得∠BOC=180°﹣∠AOC=150°,又∠COD是直角,OE平分∠BOC,∴∠DOE=∠COD﹣∠BOC=90°﹣×150°=15°;(2)由(1)∴∠DOE=∠COD﹣∠BOC,∴∠DOE=90°﹣(180°﹣∠AOC),∴∠DOE=∠AOC=a;(3)∠AOC=2∠DOE;理由:∵∠COD是直角,OE平分∠BOC,∴∠COE=∠BOE=90°﹣∠DOE,则得∠AOC=180°﹣∠BOC=180°﹣2∠COE=180°﹣2(90°﹣∠DOE),所以得:∠AOC=2∠DOE;②4∠DOE﹣5∠AOF=180°理由:设∠DOE=x,∠AOF=y,左边=∠AOC﹣4∠AOF=2∠DOE﹣4∠AOF=2x﹣4y,右边=2∠BOE+∠AOF=2(90﹣x)+y=180﹣2x+y,所以,2x﹣4y=180﹣2x+y即4x﹣5y=180,所以,4∠DOE﹣5∠AOF=180°.【点评】此题考查的知识点是角平分线的性质、旋转性质及角的计算,关键是正确运用好有关性质准确计算角的和差倍分.30.(5分)如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)①写出数轴上点B表示的数﹣4,点P表示的数6﹣6t(用含t的代数式表示);②M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(2)动点Q从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动;动点R从点B出发,以每秒个单位长度的速度沿数轴向左匀速运动,若P、Q、R三动点同时出发,当点P遇到点R时,立即返回向点Q运动,遇到点Q后则停止运动.那么点P从开始运动到停止运动,行驶的路程是多少个单位长度?【分析】(1)①设B点表示的数为x,根据数轴上两点间的距离公式建立方程求出其解,再根据数轴上点的运动就可以求出P点的坐标;②分类讨论:当点P在点A、B两点之间运动时;当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN;(2)先求出P、R从A、B出发相遇时的时间,再求出P、R相遇时P、Q之间剩余的路程的相遇时间,就可以求出P一共走的时间,由P的速度就可以求出P点行驶的路程.【解答】解:(1)设B点表示的数为x,由题意,得6﹣x=10,x=﹣4∴B点表示的数为:﹣4,点P表示的数为:6﹣6t;②线段MN的长度不发生变化,都等于5.理由如下:分两种情况:当点P在点A、B两点之间运动时:MN=MP+NP=AP+BP=(AP+BP)=AB=5;当点P运动到点B的左侧时:MN=MP﹣NP=AP﹣BP=(AP﹣BP)=AB=5,∴综上所述,线段MN的长度不发生变化,其值为5.(2)由题意得:P、R的相遇时间为:10÷(6﹣)=s,P、Q之间的路程为:(6﹣1)×=,P、Q相遇的时间为:÷(6+1)=s,∴P点走的路程为:6×(+)=.【点评】本题考查了数轴及数轴的三要素(正方向、原点和单位长度).一元一次方程的应用以及数轴上两点之间的距离公式的运用,行程问题中的路程=速度×时间的运用.。
北京市西城区2010-2011第一学期期末文数答案

北京市西城区2010 — 2011学年度第一学期期末高三数学参考答案及评分标准(文科) 2011.1一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案ADBCCBBA二、填空题:本大题共6小题,每小题5分,共30分.9.i - 10. 6011. 4 12. 3 13. (2,0)±,30x y ±= 14. ①③④注:13题第一问2分,第二问3分;14题①③④选对其中两个命题得2分,选出错误的命题即得0分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.15.(本小题满分13分) 解:(Ⅰ)()6f π=23sin2sin 36ππ- ………………2分 321241=-⨯=. ………………4分 (Ⅱ)()f x 3sin2cos 21x x =+- ………………6分2sin(2)16x π=+-. ………………8分因为[,]62x ππ∈-,所以65626πππ≤+≤-x , ………………10分所以 1sin(2)126x π-≤+≤, ………………11分所以()f x 的最大值为1 ,最小值为2-. ………………13分16.(本小题满分13分)解:(Ⅰ)连结1A C ,设1A C 交1AC 于点O ,连结OD . ………………2分因为11ACC A 为正方形,所以O 为1A C 中点, 又D 为BC 中点,所以OD 为1A BC ∆的中位线,所以1//A B OD . ………………4分 因为OD ⊂平面1ADC ,1A B ⊄平面1ADC , 所以1//A B 平面1ADC . ………………6分 (Ⅱ)由(Ⅰ)可知,11C A CA ⊥ ………………7分因为侧面11ABB A 是正方形,1AB AA ⊥, 且90BAC ∠=, 所以AB ⊥平面11ACC A . 又11//AB A B ,所以11A B ⊥平面11ACC A . ………………9分 又因为1C A ⊂平面11ACC A ,所以111A B C A ⊥. ………………10分 所以111C A A B C ⊥平面. ………………12分 又1B C ⊂平面11A B C ,所以11C A B C ⊥. ………………13分 17.(本小题满分13分)解:(Ⅰ)由分组[10,15)内的频数是10,频率是0.25知,100.25M=, 所以40M =. ………………2分 因为频数之和为40,所以1024240m +++=,4m =. ………………3分40.1040m p M ===. ………………4分 因为a 是对应分组[15,20)的频率与组距的商,所以240.12405a ==⨯.……………6分(Ⅱ)因为该校高三学生有240人,分组[10,15)内的频率是0.25,所以估计该校高三学生参加社区服务的次数在此区间内的人数为60人. ………8分 (Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有26m +=人,设在区间[20,25)内的人为{}1234,,,a a a a ,在区间[25,30)内的人为{}12,b b . 则任选2人共有1213141112232421(,),(,),(,),(,),(,),(,),(,),(,),a a a a a a a b a b a a a a a b2234(,),(,)a b a a ,3132414212(,),(,),(,),(,),(,)a b a b a b a b b b 15种情况, ………………10分而两人都在[25,30)内只能是()12,b b 一种, ………………12分 所以所求概率为11411515P =-=.(约为0.93) ………………13分AB CDC 1A 1B 1O18.(本小题满分13分) 解:(Ⅰ)由题意得1,2c a b ==, ………………2分又221a b -=,所以21b =,22a =. ………………3分所以椭圆的方程为2212x y +=. ………………4分(Ⅱ)设(0,1)A ,11(,)B x y ,00(,)P x y ,联立2222,1x y y kx ⎧+=⎨=+⎩消去y 得22(12)40k x kx ++=……(*), ………………6分解得0x =或2412k x k =-+,所以12412kx k=-+, 所以222412(,)1212k k B k k --++,2221(,)1212k P k k-++, ………………8分 因为直线OP 的斜率为1-,所以112k-=-, 解得12k =(满足(*)式判别式大于零). ………………10分 O 到直线1:12l y x =+的距离为25, ………………11分 2211(1)AB x y =+-=253,………………12分 所以△OAB 的面积为122252335⨯⨯=. ………………13分19.(本小题满分14分) 解:(Ⅰ)由已知1()2(0)f x x x'=+>, ………………2分 (1)213f '=+=.故曲线()y f x =在1x =处切线的斜率为3. ………………4分 (Ⅱ)11'()(0)ax f x a x x x+=+=>. ………………5分 ①当0a ≥时,由于0x >,故10ax +>,'()0f x >所以,()f x 的单调递增区间为(0,)+∞. ………………6分 ②当0a <时,由'()0f x =,得1x a=-.在区间1(0,)a -上,()0f x '>,在区间1(,)a-+∞上()0f x '<,所以,函数()f x 的单调递增区间为1(0,)a -,单调递减区间为1(,)a-+∞.………………8分(Ⅲ)由已知,转化为max max ()()f x g x <. ………………9分max ()2g x = ………………10分由(Ⅱ)知,当0a ≥时,()f x 在(0,)+∞上单调递增,值域为R ,故不符合题意. (或者举出反例:存在33(e )e 32f a =+>,故不符合题意.) ………………11分 当0a <时,()f x 在1(0,)a -上单调递增,在1(,)a-+∞上单调递减,故()f x 的极大值即为最大值,11()1ln()1ln()f a a a-=-+=----, ………13分 所以21ln()a >---, 解得31e a <-. ………………14分20.(本小题满分14分)(Ⅰ) 解:11a =,211123a a b =+=+=,322336a a b =+=+=4336410a a b =+=+=. ………………3分(Ⅱ)(ⅰ)解:因为11n n n b b b +-=(2n ≥),所以,对任意的n ∈*N 有5164321n n n n n n n b b b b b b b ++++++====, 即数列{}n b 各项的值重复出现,周期为6. ………………5分又数列}{n b 的前6项分别为21,21,1,2,2,1,且这六个数的和为7.设数列{}n b 的前n 项和为n S ,则,当2()n k k =∈*N 时,36123456()7n k S S k b b b b b b k ==+++++=,当21()n k k =+∈*N 时,363123456616263()n k k k k S S k b b b b b b b b b ++++==++++++++123775k b b b k =+++=+ , ………………7分所以,当n 为偶数时,372n S n =;当n 为奇数时,3732n n S +=. ………………8分 (ⅱ)证明:由(ⅰ)知:对任意的n ∈*N 有6n n b b +=,又数列}{n b 的前6项分别为111,,,1,,b b b b ,且这六个数的和为222b b++. 设)0(6≥=+n a c i n n ,(其中i 为常数且}6,5,4,3,2,1{∈i ),所以1n n c c +-=66666162636465n i n i n i n i n i n i n i n i a a b b b b b b ++++++++++++++-=+++++222b b=++.所以,数列}{6i n a +均为以222b b++为公差的等差数列. ………………10分 因为0b >时,2220b b ++>,0b <时,22220b b++≤-<, ………………12分所以{6n i a +}为公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次.所以数列}{n a 中任意一项的值最多在此数列中出现6次,即任意一项的值不会在此数列中重复出现无数次. ………………14分。
北京市西城区初一上学期期末数学试卷(附答案)

∴∠ACE =
,∠COF = 1 ∠COB,(理由:
)
2
∵ 点 C 在射线 OA 上,
∴∠ACD + ∠OCD = 180◦,
∵∠COB + ∠OCD = 180◦,
∴∠ACD = ∠
,(理由:
)
∴∠ACE = ∠COF .
27. 自 2014 年 12 月 28 日北京公交地铁开通以来,人们的出行成本发生了巨大变化,地铁和公交车票价如下表 所示:
1, =
14.
26. 如图,点 C 在射线 OA 上,CE 平分 ∠ACD,OF 平分 ∠COB 并与射线 CD 交于点 F .
(1) 依题意补全图形;
(2) 若 ∠COB + ∠OCD = 180◦,求证:∠ACE = ∠COF .
请将下面的证明过程补充完整.
证明:CE 平分 ∠ACD,OF 平分 ∠COB,
解得:
x = 10, y = 2.
答:小林乘坐地铁的里程为 10 公里,乘坐公交车的里程为 2 公里.
28. (1) 2;−2 (2) 由题意可知,点 P 表示的数为 −4 + 2t,而 B 点表示的数为 6, 则 BP = | − 4 + 2t − 6| = 2, |2t − 10| = 2, ∴ 2t − 10 = 2 或 2t − 10 = −2, ∴ t = 6 或 t = 4. (3) ①
C. 8x + 1 = 7x
D. 8x + 1 = 7x − 1
10. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是 ()
A
B
C
D
二填空题每小题3分
北京市西城区初三2010——2011学年度第一学期期末数学试卷及答案(word版)

北京市西城区2010——2011学年度第一学期期末试卷九年级数学 2011.1考生须知 1.本试卷共5页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
3.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. 抛物线()212y x =-+的对称轴为( ).A .直线1x =B .直线1x =-C .直线2x =D .直线2x =- 2. 如图,AB 为⊙O 的直径,点C 在⊙O 上,若∠C =15°,则∠BOC =( ).A .60°B .45°C .30°D .15°3. 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为( ).A .1B .13C .12 D . 224.用配方法将2611y x x =-+化成2()y a x h k =-+的形式为( ).A .2(3)2y x =++错误!未找到引用源。
B .2(3)2y x =-- 错误!未找到引用源。
C .2(6)2y x =--错误!未找到引用源。
D .2(3)2y x =-+错误!未找到引用源。
5.如图,将△ABC 的三边分别扩大一倍得到△111A B C (顶点均在格点上),若它们是以P 点为位似中心的位似图形,则P 点的坐标是( ). A .(4,3)-- B .(3,3)-- C .(4,4)-- D .(3,4)--6. 某商店购进一种商品,单价为30元.试销中发现这种商品每天的销售量P (件)与每件的销售价x (元)满足关系:1002P x =-.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程 正确的是( ).A .(30)(1002)200x x --=B .(1002)200x x -=C .(30)(1002)200x x --=D .(30)(2100)200x x --=7. 如图,△OAB 中,OA =OB ,∠A =30°,⊙O 与AB 相切,切点为E ,并分别交 OA ,OB 于C ,D 两点,连接CD .若CD 等于23,则扇形OCED 的面积等于( ). A .23π错误!未找到引用源。
2009-2010学年北京市西城区七年级(上)期末数学试卷(b卷)

2009-2010学年北京市西城区七年级(上)期末数学试卷(B卷)一、精心选一选(共10个小题,每小题3分,共30分)1.(3分)﹣的相反数是()A.B.﹣C.5D.﹣52.(3分)三峡工程是具有防洪、发电、航运、养殖、供水等巨大综合利用效益的特大水利水电工程,其防洪库容量约为22150000000m3,这个数用科学记数法表示为()A.221.5×108m3B.22.15×109m3C.2.215×1010m3D.2.215×1011m33.(3分)已知|a|=|﹣3|,则a等于()A.3B.﹣3C.0D.±34.(3分)现规定一种运算a※b=ab+a﹣b,其中a,b为有理数,则3※5的结果为()A.11B.12C.13D.145.(3分)A、B两点的距离是()A.连接A、B两点的线段B.连接A、B两点间的线段的长度C.过A、B两点的直线D.过A、B两点的射线6.(3分)如图所示,下列说法错误的是()A.OA的方向是北偏西22°B.OB方向是西南方向C.OC的方向是南偏东60°D.OD的方向是北偏东60°7.(3分)甲、乙两人练习赛跑,甲每秒钟跑7米,乙每秒钟跑6.5米,他俩从同一地点起跑,乙先跑5米后,甲出发追赶乙.设甲出发x秒后追上乙,则下列四个方程中正确的是()A.7x=6.5x+5B.7x=6.5x﹣5C.7x+5=6.5x D.(7+6.5)x=5 8.(3分)一个无盖的正方体盒子的平面展开图可以是下列图形中的()A.只有图①B.图①、图②C.图②、图③D.图①、图③9.(3分)下列各式中去括号正确的是()A.a2﹣(2a﹣b2+b)=a2﹣2a﹣b2+bB.﹣(2x+y)﹣(﹣x2+y2)=﹣2x+y+x2﹣y2C.2x2﹣3(x﹣5)=2x2﹣3x+5D.﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3+4a2﹣1+3a10.(3分)下列图形都是由边长为1厘米的小正方形连接组成的.按照图形的变化规律,第2009个图形的周长是()厘米.A.4018B.4020C.8036D.6027二、细心填一填(共10个小题,每小题2分,共20分)11.(2分)将236875精确到万位的结果是.12.(2分)体校里男学生人数是m,女学生人数是n,教练人数和学生人数的比是1:20,则教练人数是.13.(2分)观察如图中的数轴,a、b、c表示的数由小到大的顺序为.14.(2分)一个角的余角比它的补角的多1°,则这个角的度数为度.15.(2分)若2a2m+2b2与﹣a m+3b n﹣3是同类项,则m+n=.16.(2分)已知m2﹣mn=21,mn﹣n2=﹣15,则代数式m2﹣n2=.17.(2分)从下午13:00到当天下午13:50,时钟的分针转过的角度为度.18.(2分)已知线段AB=10cm,C是直线AB上一点,且BC=6cm,M、N分别是AB、BC的中点,则线段MN的长为.19.(2分)如图,在4种4×4方格图案,其中阴影部分面积相同的图案是(请填写序号)20.(2分)一个人先沿水平道路前进a千米,继而沿b千米长的山坡爬到了山顶,之后又沿原路返回到出发点,全程共用了5小时,已知此人在水平路上每小时走4千米,上山每小时走3千米,下山每小时走6千米,则此人所走的全程2(a+b)是千米.三、用心算一算(共4个小题,每小题4分,共16分)21.(4分)计算:7.8﹣9.5+(﹣8)﹣(﹣3.2)22.(4分).23.(4分)计算:18÷(﹣7)﹣128÷(﹣7)+33÷(﹣7)24.(4分)计算﹣72+2×(﹣3)2+(﹣6)÷(﹣)2.四、先化简,再求值(本题4分)25.(4分)已知a﹣b=2,ab=﹣1,求(4a﹣5b﹣ab)﹣(2a﹣3b+5ab)的值.五、解方程(共2个小题,每小题5分,共10分)26.(5分).六、列方程解应用题(共2个小题,每小题5分,共10分)27.(5分)在暖气管线中装有甲、乙两种水管共25根,总长为155米,甲种水管每根长5米,乙种水管每根长8米,请问甲、乙两种水管各有多少根?28.(5分)张欣和李明相约去图书城买书,他俩的对话如下:张欣:“听说花20元办一张会员卡,买书可享受七折优惠.”李明:“是的,我上次买了一套图书,加上办卡的费用,还比按原价买书一共省了25元.”请根据他们的对话,求出李明上次所购买书籍的原价是多少元?七、解答题(共3个小题,每小题5分,共15分)29.(5分)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;(2)求∠BOE的度数.30.(5分)如图,在长方形ABCD中放置9个形状、大小都相同的小长方形,试根据图中所给数据求出三块阴影部分面积的和.31.(5分)阅读框图并回答下列问题:(1)若A为785,则E=;(2)按框图流程,取不同的三位数A,所得E的值都相同吗?如果相同,请说明理由;如果不同,请求出E的所有可能的值;(3)将框图中的第一步变为“任意写一个个位数字不为0的三位数1,它的百位数字减去个位数字所得的差大于2”.其余的步骤不变,请猜想E的值并对你猜想的结论加以证明.2009-2010学年北京市西城区七年级(上)期末数学试卷(B卷)参考答案与试题解析一、精心选一选(共10个小题,每小题3分,共30分)1.(3分)﹣的相反数是()A.B.﹣C.5D.﹣5【分析】求一个数的相反数,即在这个数的前面加负号.【解答】解:﹣的相反数是.故选:A.【点评】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号.一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.学生易把相反数的意义与倒数的意义混淆.2.(3分)三峡工程是具有防洪、发电、航运、养殖、供水等巨大综合利用效益的特大水利水电工程,其防洪库容量约为22150000000m3,这个数用科学记数法表示为()A.221.5×108m3B.22.15×109m3C.2.215×1010m3D.2.215×1011m3【分析】科学记数法的表示形式为a×10n的形式,其中1≤a<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:22150000000=2.215×1010.故选C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(3分)已知|a|=|﹣3|,则a等于()A.3B.﹣3C.0D.±3【分析】依据绝对值的意义,得出a=±3.注意结果有两个.【解答】解:因为|a|=|﹣3|=3,所以a=±3.故选:D.【点评】考查了绝对值的性质,绝对值都是非负数,互为相反数的两数绝对值相等.4.(3分)现规定一种运算a※b=ab+a﹣b,其中a,b为有理数,则3※5的结果为()A.11B.12C.13D.14【分析】按照规定首先把它转化为有理数的混合运算,再进一步根据有理数的混合运算顺序进行计算.【解答】解:根据题意,得原式=3×5+3﹣5=15+3﹣5=13.故选:C.【点评】此题是一道新定义题目,同时要熟悉有理数的运算顺序.5.(3分)A、B两点的距离是()A.连接A、B两点的线段B.连接A、B两点间的线段的长度C.过A、B两点的直线D.过A、B两点的射线【分析】根据两点间距离的定义进行解答即可.【解答】解:∵连接两点间的线段的长度叫两点间的距离,∴连接A、B两点间的线段的长度叫A、B两点的距离.故选:B.【点评】本题考查的是两点间距离的定义,即连接两点间的线段的长度叫两点间的距离.6.(3分)如图所示,下列说法错误的是()A.OA的方向是北偏西22°B.OB方向是西南方向C.OC的方向是南偏东60°D.OD的方向是北偏东60°【分析】根据方位角的概念解答即可.【解答】解:A、根据互余的概念,OA的方向是北偏西90°﹣68°=22°,正确;B、OB方向是西偏南45°即西南方向,正确;C、OC方向是南偏东90°﹣30°=60°,正确;D、OD的方向是北偏东90°﹣60°=30°,错误.故选:D.【点评】此题较简单,只要同学们熟练掌握方位角的概念即可.7.(3分)甲、乙两人练习赛跑,甲每秒钟跑7米,乙每秒钟跑6.5米,他俩从同一地点起跑,乙先跑5米后,甲出发追赶乙.设甲出发x秒后追上乙,则下列四个方程中正确的是()A.7x=6.5x+5B.7x=6.5x﹣5C.7x+5=6.5x D.(7+6.5)x=5【分析】首先理解题意找出题中存在的等量关系:乙跑的路程=甲跑的路程,根据此等式列方程即可.【解答】解:设甲出发x秒钟后追上乙,则甲所跑的路程为7x,而此时乙所跑的路程为6.5x+5;根据此时“甲追上乙”那么他们的总路程应该相同,即7x=6.5x+5.故选:A.【点评】本题考查了由实际问题抽象出一元一次方程,列方程解应用题的关键是找出题目中的相等关系,有的题目所含的等量关系比较隐藏,要注意仔细审题,耐心寻找.8.(3分)一个无盖的正方体盒子的平面展开图可以是下列图形中的()A.只有图①B.图①、图②C.图②、图③D.图①、图③【分析】利用正方体及其表面展开图的特点解题.【解答】解:图②,经过折叠后,没有上下底面,侧面是由5个正方形组成,与正方体的侧面是4个正方形围成不相符,所以不是无盖的正方体盒子的平面展开图,故选D.【点评】正方体共有11种表面展开图,把11种展开图都去掉一个面得无盖的正方体展开图,把相同的归为一种得无盖正方体有8种表面展开图.9.(3分)下列各式中去括号正确的是()A.a2﹣(2a﹣b2+b)=a2﹣2a﹣b2+bB.﹣(2x+y)﹣(﹣x2+y2)=﹣2x+y+x2﹣y2C.2x2﹣3(x﹣5)=2x2﹣3x+5D.﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3+4a2﹣1+3a【分析】根据去括号法则(括号前是“+”号,去括号时,把括号和它前面的“+”去掉,括号内的各项都不变,括号前是“﹣”号,去括号时,把括号和它前面的“﹣”去掉,括号内的各项都变号)去括号,即可得出答案.【解答】解:A、a2﹣(2a﹣b2+b)=a2﹣2a+b2﹣b,故A错误;B、﹣(2x+y)﹣(﹣x2+y2)=﹣2x﹣y+x2﹣y2,故B错误;C、2x2﹣3(x﹣5)=2x2﹣3x+15,故C错误;D、﹣a3﹣[﹣4a2+(1﹣3a)]=﹣a3﹣(﹣4a2+1﹣3a)=﹣a3+4a2﹣1+3a,故D正确.故选:D.【点评】本题考查了去括号法则的应用,注意:①括号前是“+”号,去括号时,把括号和它前面的“+”去掉,括号内的各项都不变,括号前是“﹣”号,去括号时,把括号和它前面的“﹣”去掉,括号内的各项都变号,②m(a+b)=ma+mb,不是等于ma+b.10.(3分)下列图形都是由边长为1厘米的小正方形连接组成的.按照图形的变化规律,第2009个图形的周长是()厘米.A.4018B.4020C.8036D.6027【分析】根据梯形可知第一个图形的周长为4,第二个图形的周长为2×4﹣1×2=8,第3个图形的周长为3×4﹣2×2=8,第3个图形的周长为4×4﹣3×2=10,由此得到第n 个图形的周长为4n﹣2(n﹣1)=2n+2个,据此得到答案即可.【解答】解:第一个图形的周长为4,第二个图形的周长为2×4﹣1×2=8,第3个图形的周长为3×4﹣2×2=8,第4个图形的周长为4×4﹣3×2=10,…由此得到第n个图形的周长为4n﹣2(n﹣1)=2n+2个,故第2009个图形的周长为2×2009+2=4020.故选:B.【点评】本题考查了规律型题目,解题的关键是根据图形的变化得到第n个图形的周长为2n+2.二、细心填一填(共10个小题,每小题2分,共20分)11.(2分)将236875精确到万位的结果是 2.4×105.【分析】先写成科学记数法的形式,再根据四舍五入按要求解答.【解答】解:236875=2.36875×105≈2.4×105.故答案为:2.4×105.【点评】本题考查了科学记数法表示较大的数与近似数的取舍,写成科学记数法的形式是解题的关键.12.(2分)体校里男学生人数是m,女学生人数是n,教练人数和学生人数的比是1:20,则教练人数是.【分析】设每份为x人,则教练有x人,学生有20x人,就可以得出20x=m+n,求出x 就是教练人数了.【解答】解:设每份为x人,则教练有x人,学生有20x人,由题意,得∴20x=m+n,∴x=,∴教练有人.故答案为:人【点评】本题考查列代数式,关键是根据题目中的比例关系,用一个字母来表示,最后求出结果.13.(2分)观察如图中的数轴,a、b、c表示的数由小到大的顺序为b<c<a.【分析】根据数轴上的数,右边的总比左边的大进行比较即可.【解答】解:根据图形b<c<a.故答案为:b<c<a.【点评】本题主要考查了利用数轴比较有理数的大小,熟记“数轴上的数,右边的总比左边的大”是解题的关键.14.(2分)一个角的余角比它的补角的多1°,则这个角的度数为63度.【分析】根据余角、补角的定义计算.【解答】解:设这个角为x°,则它的余角为(90﹣x)°,补角为(180﹣x)°.根据题意有:(90﹣x)=(180﹣x)+1解得x=63,故这个角的度数为63度.【点评】此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.15.(2分)若2a2m+2b2与﹣a m+3b n﹣3是同类项,则m+n=6.【分析】根据同类项的定义:所含字母相同,并且相同字母的指数也相同,可得出关于m和n的方程,解出即可得出答案.【解答】解:∵2a2m+2b2与﹣a m+3b n﹣3是同类项,∴2m+2=m+3;n﹣3=2,解得:m=1,n=5,∴m+n=6.故答案为:6.【点评】此题考查了同类项的定义,解答本题的关键是掌握所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项,难度一般.16.(2分)已知m2﹣mn=21,mn﹣n2=﹣15,则代数式m2﹣n2=6.【分析】直接把m2﹣mn=21,mn﹣n2=﹣15相加即可.【解答】解:∵m2﹣mn=21,mn﹣n2=﹣15,∴m2﹣mn+mn﹣n2=21﹣15=6.故答案为6.【点评】本题考查了代数式求值:先把代数式根据已知条件进行变形,然后利用整体思想进行计算.17.(2分)从下午13:00到当天下午13:50,时钟的分针转过的角度为300度.【分析】时针和分针的运动可以看做一种匀速的旋转运动,13:00到当天下午13:50,分针用,50分钟时间.由此再进一步分别计算它们旋转的角度.【解答】解:钟表12个数字,每相邻两个数字之间的夹角为30°,∵13:00到当天下午13:50,分针用50分钟时间.∴分针旋转了30°×10=300°,故答案为:300.【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每分钟转动6°,时针每小时转动30°,并且利用起点时间时针和分针的位置关系建立角的图形.18.(2分)已知线段AB=10cm,C是直线AB上一点,且BC=6cm,M、N分别是AB、BC的中点,则线段MN的长为2cm或8cm.【分析】根据题意,正确画图,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能:(1)点C在线段AB上;(2)点C在线段AB的延长线上.【解答】解:(1)若为图1情形,∵M为AB的中点,∴MB=AB=5cm,∵N为BC的中点,∴NB=BC=3cm,∴MN=MB﹣NB=2cm;(2)若为图2情形,∵M为AB的中点,∴MB=AB=5cm,∵N为BC的中点,∴NB=BC=3cm,∴MN=MB+BN=8cm.故答案为:2cm或8cm.【点评】在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性.在今后解决类似的问题时,要防止漏解.利用中点性质转化线段之间的倍分关系是解题的关键.19.(2分)如图,在4种4×4方格图案,其中阴影部分面积相同的图案是(1)(2)(4)(请填写序号)【分析】设正方形网格中小正方形的边长为1,数出各图案中阴影部分有多少个等腰直角三角形,然后根据它们的面积和,再进行判断.【解答】解:设正方形网格中小正方形的边长为1,则(1)中阴影部分面积=8.5;(2)中阴影部分面积=8.5;(3)中阴影部分面积=8;(4)中阴影部分面积=8.5;所以阴影部分面积相同的图案是(1)(2)(4).故答案为(1)(2)(4).=【点评】本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△×底×高.20.(2分)一个人先沿水平道路前进a千米,继而沿b千米长的山坡爬到了山顶,之后又沿原路返回到出发点,全程共用了5小时,已知此人在水平路上每小时走4千米,上山每小时走3千米,下山每小时走6千米,则此人所走的全程2(a+b)是20千米.【分析】因为时间=,根据个人先沿水平道路前进a千米,继而沿b千米长的山坡爬到了山顶,之后又沿原路返回到出发点,全程共用了5小时,已知此人在水平路上每小时走4千米,上山每小时走3千米,下山每小时走6千米,可列方程.【解答】解:•2++=5∴a+b=10.∴2(a+b)=20.故答案为:20.【点评】本题考查理解题意的能力,关键是根据时间列出方程,然后找出a和b的关系,从而代数求值.三、用心算一算(共4个小题,每小题4分,共16分)21.(4分)计算:7.8﹣9.5+(﹣8)﹣(﹣3.2)【分析】原式先利用减法法则变形,再利用同号及异号两数相加的法则计算即可得到结果.【解答】解:原式=7.8﹣9.5﹣8+3.2=7.8+3.2﹣9.5﹣8=11﹣17.5=﹣6.5.【点评】此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.22.(4分).【分析】首先把乘除混合运算统一成乘法,再确定结果的符号,然后把绝对值相乘即可.【解答】解:原式=(﹣7.5)×(﹣4)××(﹣)=﹣(×4××)=﹣.【点评】此题主要考查了有理数的乘除法混合运算,关键是注意结果符号的判断,这是同学们最容易出错的地方.23.(4分)计算:18÷(﹣7)﹣128÷(﹣7)+33÷(﹣7)【分析】根据除以一个数等于乘以这数的倒数转化为乘法运算,再逆运用乘法分配律进行计算即可得解.【解答】解:18÷(﹣7)﹣128÷(﹣7)+33÷(﹣7)=18×(﹣)﹣128×(﹣)+33×(﹣)=(18﹣128+33)×(﹣)=(﹣77)×(﹣)=11.【点评】本题考查了有理数的除法,先转化为乘法运算,再利用乘法分配律可以使计算更加简便.24.(4分)计算﹣72+2×(﹣3)2+(﹣6)÷(﹣)2.【分析】先计算乘方得到原式=﹣49+2×9+(﹣6)÷,再进行乘除运算得到原式=﹣49+18﹣54,最后进行加减运算即可.【解答】解:原式=﹣49+2×9+(﹣6)÷=﹣49+18﹣6×9=﹣49+18﹣54=﹣85.【点评】本题考查了有理数的混合运算:先进行乘方运算,再进行乘除运算,最后进行加减运算;有括号先计算括号.四、先化简,再求值(本题4分)25.(4分)已知a﹣b=2,ab=﹣1,求(4a﹣5b﹣ab)﹣(2a﹣3b+5ab)的值.【分析】先去括号合并同类项,把式子化成含有a﹣b和ab的式子,再整体代入求出即可.【解答】解:(4a﹣5b﹣ab)﹣(2a﹣3b+5ab)=4a﹣5b﹣ab﹣2a+3b﹣5ab=2a﹣2b﹣6ab,=2(a﹣b)﹣6ab,当a﹣b=2,ab=﹣1时,原式=2×2﹣6×(﹣1)=10.【点评】本题考查了整式的化简求值的应用,用了整体代入思想,即把a﹣b和ab当作整体来代入.五、解方程(共2个小题,每小题5分,共10分)26.(5分).【分析】这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.【解答】解:去分母得,4(2x﹣1)﹣2(10x﹣1)=3(2x+1)﹣12,去括号得,8x﹣4﹣20x+2=6x+3﹣12,移项得,8x﹣20x﹣6x=3﹣12+4﹣2,合并同类项得,﹣18x=﹣7,系数化为1得,x=.【点评】本题主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.六、列方程解应用题(共2个小题,每小题5分,共10分)27.(5分)在暖气管线中装有甲、乙两种水管共25根,总长为155米,甲种水管每根长5米,乙种水管每根长8米,请问甲、乙两种水管各有多少根?【分析】根据题干,可设甲种水管有x根,则乙种水管有(25﹣x)根,所以甲种管子的总长度是5x米,乙种管子的总长度是8(25﹣x)米,根据等量关系:“甲、乙两种水管总长为155米”列出方程即可解决问题.【解答】解:设甲种水管有x根,则乙种水管有(25﹣x)根.依题意,得5x+8(25﹣x)=155.解得x=15,乙种水管有25﹣x=25﹣15=10(根).答:甲种水管有15根,乙种水管有10根.【点评】此题考查了含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可.28.(5分)张欣和李明相约去图书城买书,他俩的对话如下:张欣:“听说花20元办一张会员卡,买书可享受七折优惠.”李明:“是的,我上次买了一套图书,加上办卡的费用,还比按原价买书一共省了25元.”请根据他们的对话,求出李明上次所购买书籍的原价是多少元?【分析】可设书的原价为x元,据张欣和李明的话可得关于应付费用的等量关系:书价的七折+20=书的原价﹣25,据此列出方程求解即可.【解答】解:设李明上次所购买书籍的原价为x元.依题意,得0.7x+20=x﹣25,解得x=150.答:李明上次所购买书籍的原价是150元.【点评】本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.七、解答题(共3个小题,每小题5分,共15分)29.(5分)如图,直线AB、CD相交于点O,OE是∠AOD的平分线,若∠AOC=60°,OF⊥OE.(1)判断OF把∠AOC所分成的两个角的大小关系并证明你的结论;(2)求∠BOE的度数.【分析】(1)求出∠AOD度数,求出∠AOE,求出∠AOF,即可得出答案;(2)求出∠BOD度数,求出∠DOE度数,相加即可得出答案.【解答】(1)答:∠AOF=∠COF,证明:∵O是直线CD上一点,∴∠AOC+∠AOD=180°,∵∠AOC=60°,∴∠AOD=180°﹣60°=120°,∵OE平分∠AOD,∴.∵OF⊥OE,∴∠FOE=90°∴∠AOF=∠FOE﹣∠AOE=90°﹣60°=30°,∴∠COF=∠AOC﹣∠AOF=60°﹣30°=30°,∴∠AOF=∠COF.(2)解:∵∠AOC=60°,∴∠BOD=∠AOC=60°,∠AOD=180°﹣60°=120°,∵OE是∠AOD的平分线,∴∠DOE=∠AOD=60°,∴∠BOE=∠BOD+∠DOE=60°+60°=120°,.【点评】本题考查了角平分线定义和角的有关计算的应用,主要考查学生的计算能力.30.(5分)如图,在长方形ABCD中放置9个形状、大小都相同的小长方形,试根据图中所给数据求出三块阴影部分面积的和.【分析】设小长方形的宽为x,则小长方形的长为(66﹣4x).由图形提供的数据建立方程求出其解即可.【解答】解:设小长方形的宽为x,则小长方形的长为(66﹣4x),依题意,得(66﹣4x)+2x=21+3x,解得:x=9小长方形的长为:66﹣4x=66﹣4×9=30所以三块阴影部分面积的和66×(21+3×9)﹣9×30×9=738.答:三块阴影部分面积的和为758.【点评】本题主要考查了二元一次方程组的应用,此题是一个信息题目,要求学生会根据图示找出数量关系,根据图示可以列出方程,求出小长方形的宽是解答本题的关键.31.(5分)阅读框图并回答下列问题:(1)若A为785,则E=1089;(2)按框图流程,取不同的三位数A,所得E的值都相同吗?如果相同,请说明理由;如果不同,请求出E的所有可能的值;(3)将框图中的第一步变为“任意写一个个位数字不为0的三位数1,它的百位数字减去个位数字所得的差大于2”.其余的步骤不变,请猜想E的值并对你猜想的结论加以证明.【分析】(1)由A=785,根据框图中的流程计算即可得到E;(2)E的值相同,理由为:设A=100a+10b+c,且a﹣c=2,表示出B,求出A﹣B,得到C,进而求出D,最后求出E即可;(3)E=1089,理由为:设A=100a+10b+c且a﹣c>2,表示出B,进而得出C与D,求出E即可.【解答】解:(1)由A=785,得到B=587,∴C=A﹣B=785﹣587=198,D=891,则E=198+891=1089.(2)E的值都相同,理由如下:设A=100a+10b+c且a﹣c=2,则B=100c+10b+a,∴C=A﹣B=(100a+10b+c)﹣(100c+10b+a)=99a﹣99c=99(a﹣c)=99×2=198,∴D=891,∴E=C+D=198+891=1089.(3)E=1089,理由为:设A=100a+10b+c且a﹣c>2,则B=100c+10b+a,∴C=A﹣B=(100a+10b+c)﹣(100c+10b+a)=100(a﹣c)﹣(c﹣a)=100(a﹣c ﹣1)+10×9+(10+c﹣a),∴D=100(10+c﹣a)+10×9+(a﹣c﹣1),∴E=C+D=[100(a﹣c﹣1)+10×9+(10+c﹣a)]+[100(10+c﹣a)+10×9+(a﹣c﹣1)]=1089.【点评】此题考查了整式加减的应用,弄清题意是解本题的关键.。
北京市西城区2010—2011学年度第一学期期末试卷及参考答案

北京市西城区2010—2011学年度第一学期期末试卷七年级历史 2011.1学校: 班级: 姓名: 分数: 第Ⅰ卷(闭卷部分)考生 须知 1.闭卷部分考试时间为15分钟,满分为50分。
2.闭卷考试时,不得参考任何资料,必须独立作答。
一、选择题(本大题25小题,每小题2分,共50分。
在每小题列出的四个选项中,只有一项最符合题目要求,请将该选项前的字母代号填写在下面的表格中) 1.在历史学习中,许多同学化繁为简,把隋朝大运河的相关知识概括为“三点四段五河”,其中三点即指大运河的北端、中心和南端。
它们分别是 A .涿郡、长安、余杭B .涿郡、洛阳、江都C .涿郡、长安、江都D .涿郡、洛阳、余杭2.“朝为田舍郎,暮登天子堂。
将相本无种,男儿当自强。
”这首诗反映的是我国古代的 A .禅让制B .世袭制C .科举制D .分封制3.唐太宗的统治为唐朝进入全盛时期奠定了重要基础,历史上称之为 A .“文景之治” B .“开皇之治” C .“开元盛世” D .“贞观之题号 闭卷 开卷总分 一 二 三(选做题)1—25 26—2930得分题号 1 2 3 4 5 6 7 8 9 10 第Ⅰ卷 得分总计答案 题号 11 12 13 14 15 16 17 18 19 20 答案题号 21 22 23 24 25答案2ABCD治”4.茶叶是现今世界著名饮料,也是我国对世界的一大贡献,饮茶之风在全国开始盛行是在A.隋朝B.唐朝C.明朝D.清朝5.“翻倒,翻倒,喝得醉来吐掉,转来转去自行,千匝万匝未停。
停未?停未?禾苗待我灌醉。
”这首《调笑令》反映的是下列哪种生产工具使用时的情景?6.某剧团要编演一部反映唐朝与少数民族友好关系的话剧,这部话剧可以取材于下列哪个史实? A .张骞出使西域B .玄奘西游天竺C .文成公主入藏D .鉴真东渡日本7.世界上现存最早的、标有确切日期的雕版印刷品是《金刚经》卷子。
它印制于A. 隋朝B. 唐朝C. 明朝D. 清朝 8.我国古代经济重心南移,这一过程完成于A. 唐朝B. 北宋C. 南宋D.元朝 9.宋代饮食相当丰富,品种很多。
北京市西城区2009-2010年初一期末试题参考答案(B卷)
北京市西城区2009–2010学年度第二学期期末测试 2010.7七年级数学试卷(B 卷)参考答案及评分标准一、精心选一选(共10个小题,每小题3分,共30分)二、细心填一填(共10个小题,每小题2分,共20分) 11.31-; 12.38; 13.10232+--x x ; 14.220; 15.54; 16.68;17.)33(-,; 18.30或150 (只答出其中一个给1分); 19.49; 20.4.三、认真做一做(共5个小题,每小题5分,共25分)21.先化简,再求值:b a ab b a a b a a b 2322323)](8)([÷---,其中5a =,2b =-. 解: b a ab b a a b a a b 2322323)](8)([÷---=b a b a b a b a ba 22333323)88(÷+-- -----------------1分 =b a b a b a 23323)99(÷- -----------------2分 =233ab -. ----------------------------3分 当5a =,2b =-时,原式=2)2(533-⨯⨯- --------------------4分= 57-. -----------------------------5分22.解方程组:21432()3()19x y x y x y ⎧+=-⎪⎨⎪+--=-⎩,.解:由①,得 1283-=+y x . ③ ------------1分由②,得 195-=+-y x . ④ ----------------2分① ②④×3+③,得 6923-=y ,3-=y . -----------------------3分把3-=y 代入④,得 19)3(5-=-⨯+-x ,4=x . ------------------4分所以方程组的解为 ⎩⎨⎧-==34y x . -----------------------5分(其它正确解法相应给分)23.解不等式组:2(2)41213x x x x -->⎧⎪+⎨≤-⎪⎩,.解:解不等式①,得 2>x . ----------------------2分解不等式②,得 4≥x . ----------------------4分 把不等式①和②的解集在数轴上表示出来.所以不等式组的解集为4≥x .----------------------5分24.(1)表中m = 10 ,n = 50 ;--------2分(答对一个得1分)(2)如右图所示:----------------3分 (3)72度; ----------------------4分 (4))(4420050)110(人=⨯÷+答:估计该校初一年级女生掷实心球的成绩达到优秀的总人数约为44人.---------------5分25.(1)请写出图中下列地点的坐标: 牡丹园 (300,300) ;------------1分 游乐园 (200,-200) ;------------2分① ② 45O 123(2)如右图所示: -----------------4分 (3)问题(2)中湖心亭平移后的对应点 的坐标为 (-300, 0) . -------------5分四、解答题(共5个小题,每小题5分,共25分)26.解:设搭造A 种园艺造型x 个,则搭造B 种园艺造型)50(x -个.------1分 依题意,得 ⎩⎨⎧≤-+≤-+.,2900)50(100303600)50(4090x x x x ---------------2分由不等式①,得 32≤x .由不等式②,得 30≥x .因此,不等式组的解集为 3230≤≤x . ------------------3分根据题意,x 的值应是整数,所以323130或或=x . ----------------4分 当30=x 时,2050=-x ; 当31=x 时,1950=-x ; 当32=x 时,1850=-x . 答:符合要求的搭造方案有三种:① 搭造A 种园艺造型30个,搭造B 种园艺造型20个; ② 搭造A 种园艺造型31个,搭造B 种园艺造型19个;③ 搭造A 种园艺造型32个,搭造B 种园艺造型18个.-----------5分27.(1)可能的图形有:-------------3分 (画对一个图得1分)(2)周长的最大值为2b+2c ; -------------------4分周长的最小值为2a+2b . -------------------5分28.解:∵ 6=-b a , ∴ 6+=b a . -----------------1分∵ 2()90ab c a +-+=, ∴ 09)()6(2=+-++a c b b .∴ 0)()3(22=-++a c b . ---------------------------2分 ∴ a c b =-=且3. ---------------------------3分① ② acbc acbacb acb ab∴ 36)3(=+-=a ,3=c . -------------------------4分 ∴ 3333=+-=++c b a . -------------------------5分29.(1) 猜想: AF ∥ CD ;--------1分(2) 证明方法一:连接AD . -----------------2分 ∵在六边形ABCDEF 中,∠BAF+∠B+∠C+∠CDE+∠E+∠F=720180)26(=⨯-,而∠BAF +∠B+∠C=∠CDE +∠E+∠F , ∴∠BAF +∠B+∠C=21×720°=360°.即∠1+∠2+∠B+∠C=360°. ----------------3分 ∵在四边形ABCD 中,∠1+∠B+∠C+∠3=360°,∴∠2=∠3. ------------------4分 ∴AF ∥CD . ------------------5分证明方法二:连接AC . -----------------2分 ∵在六边形ABCDEF 中,∠BAF+∠B+∠BCD+∠D+∠E+∠F=720180)26(=⨯-,而∠BAF +∠B+∠BCD =∠D +∠E+∠F , ∴∠BAF +∠B+∠BCD =21×720°=360°.即∠1+∠2+∠B+∠3+∠4=360°. ----------------3分 ∵在三角形ABC 中,∠1+∠B+∠3=180°, ∴∠2+∠4=180°. ------------------4分 ∴AF ∥CD . ------------------5分证明方法三:延长AB 、DC 交于点G .-----------2分 ∵在六边形ABCDEF 中,∠A+∠ABC+∠BCD+∠D+∠E+∠F =720180)26(=⨯-,而∠A+∠ABC+∠BCD =∠D +∠E+∠F , ∴∠A +∠ABC+∠BCD =21×720°=360°.----------------3分∵∠ABC=∠G+∠2,∠BCD=∠G+∠1, ∴∠A+(∠G+∠2)+ (∠G+∠1)= 360°. ∵在三角形BCG 中,∠1+∠2+∠G=180°,EBBEE∴∠A+∠G=180°. ------------------4分 ∴AF ∥CD . ------------------5分(其它正确证明方法相应给分)30.(1) △DBF 的面积为 7 ; -----------------1分(2) 解:连接PA .∵在△PAB 中,D 、E 是AB 的三等分点, ∴PBE PBA ∆∆=S 3S ,PBE PAE ∆∆=S 2S . ∵在△PAC 中,F 、G 是AC 的三等分点, ∴PAF PAC ∆∆=S 3S .∵在△ABC 中,D 、E 是AB 的三等分点,F 、G 是AC 的三等分点, ∴284232S 32S =⨯==∆∆ABC CAE , 144231S 31S =⨯==∆∆A B C B A F .设x PEB =∆S ,y PFA=∆S ,则由题意得 ⎩⎨⎧=+=+.2823143x y y x , 解得 ⎩⎨⎧==.82y x ,∴2S =∆PEB . -----------------3分(3) 解:连接AM .∵在△MAB 中,D 、E 是AB 的三等分点, ∴MAD MAB ∆∆=S 3S .∵在△MAC 中,F 、G 是AC 的三等分点, ∴MAF MAC ∆∆=S 3S .∵在△ABC 中,D 、E 是AB 的三等分点,F 、G 是AC 的三等分点, ∴ =∆BAF S 144231S 31S =⨯==∆∆ABC CAD .设m MAD =∆S ,S M FA n ∆=,则由题意得 ⎩⎨⎧=+=+.143143m n n m , 解得 ⎩⎨⎧==.5.35.3n m ,∴5.3S =∆MAD . ∴7S 2S ==∆∆MAD MBD .图2B图3B由(2)可知 2S =∆PEB , ∴=EPMD四边形S 527S S =-=-∆∆PEB MBD . -------------5分。
初一年级第一学期期末考试数学试卷B及答案

北京市西城区2010 — 2011学年度第一学期期末试卷(北区)七年级数学(B 卷)2011.1(时间100分钟,满分100分)题号 一 二 三 四 五 六 七 总分 得分一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.14-的绝对值是 A .14B .14-C .4D .4-2.2010年11月12日至27日第16届亚运会在广州举行.广州亚运城的建筑面积约为358000平方米,将358000用科学记数法表示应为A .4108.35⨯ B .51058.3⨯ C .610358.0⨯ D .61058.3⨯ 3.如果单项式y x m231和342+n y x 是同类项,那么m 、n 的值分别是( ) A . ⎩⎨⎧-==22n m B .⎩⎨⎧==14n m C . ⎩⎨⎧==12n m D . ⎩⎨⎧-==24n m 4.下列各式中,去括号正确的是A .x +2(y -1)=x +2y -1B .x -2(y -1)=x +2y +2C .x -2(y -1)=x -2y -2D .x -2(y -1)=x -2y +25. M 地是海上观测站,从M 地发现两艘船A 、B 的方位如图所示.下列说法中,正确的是A .船A 在M 的南偏东30°方向B .船A 在M 的南偏西30°方向C .船B 在M 的北偏东40°方向D .船B 在M 的北偏东50°方向6.如图,直角三角尺AOB 的顶点O 在直线CD 上, 若∠AOC =35°,则∠BOD 的度数为( ) A .65° B .55°C .45°D .35° 7.某厂2009年的生产总值为a 万元,2010年的生产总值比2009年增长了10%,那么该厂2010年的生产总值是() A .a %10万元 B .)%10(a +万元 C. a %)101(+万元 D .[]a a %)101(++万元8.有理数a b ,在数轴上的位置如图所示,则下列结论中,错误..的是( ) OAB C D BA南 西东 北30ºM50ºA .b a <<0B . b a >C .b a >- D . b a a b +<-9.延长线段AB 至C ,使得AB BC 21=,反向延长线段AC 至D ,使得AC AD 31=,则线段CD 的长等于 A .AB 21 B .AB 41 C .AB 23D .AB 2 10.小明同学设计了右图所示的正方体形状的包装纸盒,把下面四个表面展开图折叠(不计接缝),和小明同学设计的纸盒完全相同的是二、填空题(本题共16分,每小题2分) 1132的相反数是__ ___. 12若0)3(22=-++y x ,则xy = .13.如图,点B 在射线AE 上,∠D +∠ABC =180°,若∠CBE =80°,则∠D = °.14.若一个角的补角比它的余角的4倍少15°,则这个角的度数为°.15.关于x 的方程0652=-+m x 的解是2m x =,那么m m 1042+的值是 . 16.如图, 线段AB 表示一根对折以后的绳子,现从P 处把绳子剪断,剪断后的各段绳子中最长的一段为40cm ,若AP =12PB ,则这条绳子的原长为 cm . 17.在数学活动课上,李老师要求同学们在边长为1的正方形格纸中,画出一个“风车”图案.小红同学的做法是:如图甲所示,把一个三角形按顺时针方向旋转90°,连续转三次,形成四个叶片的“风车”图案;类似地,把一个梯形按顺时针方向旋转90°,连续转三次,形成图乙所示的四个叶片的“风车”图案.请你仿照小红同学的做法,在备用图中,画一个新的四个叶片的“风车”图案,并使得 “风车”的四个叶片的面积和图乙中四个叶片的面积相同.18.观察按下列顺序排列的等式:3309=+⨯, 13419=+⨯, 23529=+⨯, 33639=+⨯, 43749=+⨯,……猜想:第n 个等式(n 为正整数)应表示为 . 三、解答题(本题共16分,每小题4分)19.计算:431417)539(524----. 解:20.计算:)4()81(1655.2-÷-⨯÷-. 解:ab图乙 图甲 备用图 DACDEABP21.计算: 24)43232812(⨯-+ . 22. 6)8325.0()21()1(3220112⨯---÷-+-.四、解答题(本题共15分,每小题5分) 23.先化简下式,再求值:)45()2(32222ab b a ab b a ---,其中2=a ,1-=b .24.解方程:x x x -=-+7)52(34. 解:25.解方程:12271243xx -=-+. 解:五、按要求作图,并回答问题(本题4分) 26.如图,点B 为射线OA 上一点.①在OA 的上方,画∠AOC =120°,画∠OBD =90°; ②画出∠AOC 的平分线OE ,交射线BD 于点P . 测量点O 、P 之间的距离(精确到1cm ).六、列方程解使用题(本题共8分,每小题4分) 27.某校开展了向贫困山区学生捐书的活动,已知七年级、八年级和九年级学生共捐书1680本,其中九年级学生所捐图书数量比七年级学生所捐图书数量的3倍少270本;八年级学生所捐图书数量比七年级学生所捐图书数量的2倍多150本,在这次活动中,七年级学生捐了多少本书? 解:28.某服装厂接到一批校服的生产加工任务,要求按计划天数加工完成.该厂如果每天加工20套校服,按计划时间交货时,比定货任务少加工100套;如果每天加工23套校服,按规定时间交货时,还能比定货任务多加工20套.这批校服的加工任务是多少套?原计划多少天加工完成? 解:A B O七、解答题(本题共11分,第29小题6分,第30小题5分) 29.如图,O 是直线AB 上一点,∠COD 是直角,OE 是∠BOC 的平分线.(1)如图1,若∠AOC =40°,求∠DOE 的度数;(2)在图1中,若∠AOC =α,直接写出∠DOE 的度数(用含α的代数式表示); (3)将图1中的∠COD 按顺时针方向旋转至图2所示的位置.①探究∠AOC 和∠DOE 之间的数量关系,写出你的结论,并说明理由; ②在∠AOC 的内部有一条射线OF ,满足:2∠AOF +∠BOE =21(∠AOC -∠AOF ), 试确定∠AOF 和∠DOE 的度数之间的数量关系.解:(1)①(2)∠DOE = ; (3)① ②30.如图,已知数轴上点A 表示的数为6, B 是数轴上一点,且AB =10.动点P 从点A 出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t >0)秒.(1) ①写出数轴上点B 表示的数 ,点P 表示的数 (用含t 的代数式表示);②M 为AP 的中点,N 为PB 的中点.点P 在运动的过程中,线段MN 的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN 的长;(2)动点Q 从点A 出发,以每秒1个单位长度的速度沿数轴向左匀速运动;动点R 从点B 出发,以每秒34个单位长度的速度沿数轴向左匀速运动,若P 、Q 、R 三动点同时出发,当点P 遇到点R 时,立即返回向点Q 运动,遇到点Q 后则停止运动.那么点P 从开始运动到停止运动,行驶的路程是多少个单位长度?解:(1)①数轴上点B 表示的数是 , 数轴上点P 表示的数是 (用含t 的代数式表示);②(2)A B C D O图1A B EC DO 图2BO北京市西城区2010 — 2011学年度第一学期期末试卷(北区)七年级数学参考答案及评分标准(B 卷)2011.1一、选择题(本题共30分,每小题3分)题号 1 2 3 4 5 6 7 8 9 10 答案 A B A D C B C D D C二、填空题(本题共16分,每小题2分)11.32- ; 12.6-; 13.80; 14.55; 15. 12;16.60 cm 或120(答对一个结果得1分); 17.举例见右图: (答案不唯一)18.3)1(10)2()1(9+-=++-n n n . 三、解答题(本题共16分,每小题4分) 19.解:431417)539(524----=431417539524--+ ········································································· 1分 =914- ························································································· 3分 =5 ······························································································· 4分20.解:)4()81(1655.2-÷-⨯÷- =)41815165.2(⨯⨯⨯- ·········································································· 2分=41-··························································································· 4分 21.解: 24)43232812(⨯-+=24411243224817⨯-⨯+⨯ ································································· 1分 =661651-+ ················································································· 2分 =1 ····························································································· 4分22.计算:6)8325.0()21()1(3220112⨯---÷-+- 解:6)8325.0()21()1(3220112⨯---÷-+- =681419⨯+⨯-- ············································································· 3分=43419+⨯-- =4112- ··························································································· 4分四、解答题(本题共15分,每小题5分) 23.解:)45()2(32222ab b a ab b a ---=b a 2222························································ 2分 =22ab b a +. ··············································································· 3分当2=a ,1-=b 时,原式=22)1(2)1(2-⨯+-⨯=-2. ······················································· 5分24.解:去括号,得 x x x -=-+71564. ·················································· 2分移项,得 15764+=++x x x . ····················································· 3分 合并同类项,得 2211=x . ·························································· 4分 系数化为1,得 2=x . ································································· 5分25.解:去分母(方程两边同乘以12),得)27(12)43(6x x -=-+. ································································ 1分去括号,得x x 27122418-=-+. ·················································· 2分 移项,得 12247218+-=+x x . ·················································· 3分 合并同类项,得 520-=x . ·························································· 4分 系数化为1,得 41-=x . ···················分 五、按要求作图,并回答问题(本题4分)答:OP = 3cm . 阅卷说明:画∠AOC =120°,∠OBD =90°(各1分); 画∠AOC 的平分线OE ,交射线BD 于点P ; ························································ 3分 量得OP =3cm . ···································· 4六、列方程解使用题(本题共8分,每小题4分)27.解:设在这次活动中,七年级学生捐了x 学生捐书)2703(-x 本. ·························分依题意有:1680)2703()1502(=-+++x x x .分 解得 300=x . ···································分 答:在这次活动中,七年级学生捐了300分 28.解:设这批校服的的加工任务是x 套,原计划20100-x 天加工完成. ················ 1分 CABD PE依题意,得232020100+=-x x . ·························································· 2分 解得 900=x . ··········································································· 3分4020100900=-(天). 答:这批校服的加工任务是900套,原计划40天加工完成. ························ 4分 七、解答题(本题共11分,第29小题6分,第30小题5分) 29.解:(1)①∵ O 是直线AB 上一点(如图1),∴∠AOC +∠BOC =180°.∵∠AOC =40°, ∴∠BOC =140°. ∵OE 平分∠BOC ,∴∠COE =21∠BOC =21×140°=70°. ········································· 1分 ∵∠DOE =∠COD -∠COE ,∠COD =90°,∴∠DOE =20°. ··································································· 2分(2)∠DOE =α21. ······································································· 3分 (3)①答:∠DOE =21∠AOC . 理由如下:∵ O 是直线AB 上一点(如图2), ∴∠AOC +∠BOC =180°. ∴∠BOC =180°-∠AOC . ∵OE 平分∠BOC ,∴∠COE =21∠BOC . =)180(21AOC ∠-︒.∵∠DOE =∠COD -∠COE ,∠COD =90°, ∴∠DOE =)180(2190AOC ∠-︒-︒=AOC ∠21. ∴∠DOE =21∠AOC . ······················································ 4分 ②答:5∠AOF +180°=4∠DOE . ······································· 5分 ∵2∠AOF +∠BOE =21(∠AOC -∠AOF ) ∴5∠AOF +2∠BOE =∠AOC如图3,根据①中的结论:2∠DOE =∠AOC ,ABC D O图1ABECDO图2ABE COF∴5∠AOF +2∠BOE =2∠DOE . ∵OE 平分∠BOC ,∴∠BOE =∠COE =DOE ∠-︒90. ∴5∠AOF +2(DOE ∠-︒90)=2∠DOE . 整理,得5∠AOF +180°=4∠DOE .∴5∠AOF +180°=4∠DOE . ············································· 6分30.(1)-4,t 66-; ··············································································· 2分 (2)分两种情况:①当点P 在A 、B 两点之间运动时(如图1),MN =MP +NP .=21AP +21BP =21AB =5. ·························································· 3分 ②当点P 运动到点B 的左侧时(如图2), MN =MP -NP=21AP -21BP =21AB =5 . ······················································· 4分 综上所述,线段MN 的长度不发生变化,其值为5.(3)设点P 运动x 秒时,在点C 处追上点R (如图3),AC =x 6,BC =x 34. ∵AC -BC =AB , ∴10346=-x x .解得 715=x .设点P 运动y 秒时,P 和点Q 相遇. ∴)(26BC AB y y +=+,∴)7153410(26⨯+=+y y . 解得 49180=y . ∴点P 运动的路程为 491080491806=⨯(单位长度). ∴点P 从开始运动到停止运动行驶的路程为491080个单位长度. ··············· 5分BC图3P B 图2 N BOP M图1。
学年北京市西城区(北区)七年级上学期期末数学试卷B卷(含答案)

图1OABOCD北京市西城区2011 — 2012学年度第一学期期末试卷(北区)七年级数学(B 卷)2012.1(时间100分钟,满分100分)题号 一 二 三 四 五 六 七 八 总分 得分一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. 31-的相反数是( ). A . 3- B . 3 C . 31-D .31 2.地球与太阳之间的距离约为149600000千米,将149600000用科学记数法表示应为( ).A .5101496⨯B .71096.14⨯C .810496.1⨯D .9101496.0⨯ 3.如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线.这种做法用几何知识解释应是 A .两点之间,线段最短 B .两点之间,直线最短 C .两点确定一条直线 D .三个点不能在同一直线4.如图,点O 在直线AB 上,OD 平分∠BOC ,若∠BOD =55º,则∠AOC 的度数是( ). A .110º B .70ºC . 55ºD .35º5.化简)(3)(5y x y x +-+的结果是( ).A .y x 22+B .y x +2C .y x 2+D . y x 22-6.若04)32(2=++-b a ,则2011)2(b a +的值是( ).A .-2011B .2011C .1D .-1 7. 方程x y 420-=的正整数解的个数是( ).A .4个B .5个C .6个D .无数个 8.把方程6.13.0)1(2=+x 的分母化成整数,得( ).A .163)1(20=+xB .163)1(2=+x C .6.13)1010(20=+x D .6.13)1(20=+x 9.若两个非零有理数a 、b ,满足:a a =,b b -=,0<+b a ,则在数轴上表示数a 、b 的点正确的是( ).A .B .C .D .10. 如图,模块①由15个棱长为1的小正方体构成,模块②-⑥均由4个棱长为1的小正方体构成. 现在从模块②-⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体. 下列四个方案中,符合上述要求的是( ).、A .模块②,④,⑤B .模块③,④,⑥C .模块②,⑤,⑥D .模块③,⑤,⑥二、填空题(本题共16分,每小题2分)11.用四舍五入法对0.00356保留两个有效数字得到的近似值是 .12. “比x 的2倍小7的数” 用式子表示为 .13.如图,点C 在线段AB 的延长线上,且BC =2AB , D 是AC 的中点,若AB =6.则AC 的长为 , BD 的长为 .14.如图,∠ABC =∠DBE =90°,若∠ABD =26°,则∠CBE = °.15. 如果一个角的补角是150°,那么这个角的余角等于 °.16.如果1662=+xy x ,1242-=-xy y ,则222y xy x ++的值为 . 17.如图,点C 、点D 在线段AB 上,E 、F 分别是AC 、BD 的中点,若AB =m ,CD =n ,则线段EF 的长为0 b a 0 b a 0 a b 0 a b 模块①AB CDEEFD ABC模块② 模块③ 模块④模块⑤ 模块⑥(用含m ,n 的式子表示).18.若0=++c b a ,且c b a >>,以下结论:①0>a ,0>c ; ②关于x 的方程0=++c b ax 的解为x =1; ③22)(c b a +=; ④a b c abca b c abc+++的值为0或2;⑤在数轴上点A 、B 、C 表示数a 、b 、c ,且0<b .则线段AB 与线段BC 的大小关系是AB>BC .其中正确结论是 (填出正确结论的序号).三、用心算一算(本题共16分,每小题4分)19.)413(87)81(43-++---.解:20. )16()158(542.3-÷-⨯÷. 解:21.21149)61()2(3÷--⨯-. 解: 22.252)152(2758.025644232--⨯-÷+-. 解:四、先化简,再求值(本题5分)23.ab ab ab ab ab 3)]28(4[2122---+,其中21-=a ,2-=b .解:五、解下列方程(组)(本题共10分,每小题5分)24.2425312=--+x x . 解:25.⎩⎨⎧=+=-12823y x y x .解:六、列方程解应用题(本题共10分,每小题5分)26.甲、乙两城相距1120千米,一列快车从甲城出发120千米后,另一列动车从乙城出发开往甲城,2个小时后两车相遇,若快车每小时行驶的路程比动车每小时行驶的路程的一半多5千米,动车平均每小时行驶多少千米?解:27.某服装小店将A服装按成本的50%的利润作标价,将B服装按成本的40%的利润作标价.已知A、B两件服装的成本共500元,在实际销售的过程中,两件服装均按9折出售,这样服装店共获利157元,问甲、乙两件服装的成本价各是多少元?七、解答题(本题4分)28.阅读下列材料:一个直角三角形纸片ABC ,分别取AB 、AC 边的中点M 、N ,连结MN ,作︒=∠=∠90AHN AHM ,沿MN 、AH 剪开,可将三角形纸片分割成三块,如图1所示;如图2,将三角形纸片①绕AB 的中点M 旋转至三角形纸片④处,将三角形纸片②绕AC 的中点N 旋转至三角形纸片⑤处,依此方法操作,可以把一个直角三角形纸片ABC 拼接成一个与它面积相等的长方形纸片DBCE .请你解决下列问题:(1)如图3,一个任意三角形纸片ABC ,将其分割后拼接成一个与三角形ABC 面积相等的长方形,在图3中画出分割的实线和拼接的虚线.............; (2)如图4,一个任意四边形纸片ABCD ,将其分割后拼接成一个与原四边形ABCD 面积相等的长方形,在图4中画出分割的实线和拼接的虚线..............① ② M N A ③ B C H 图1 ① ① ② ② A B CD E ③ 图2M H N 图3图4ABCBACD八、解答题(本题共9分,第30小题6分,第31题3分)29.如图1,已知︒=∠70AOB .(1)如图2,射线OC 在AOB ∠的内部, OD 平AOC ∠,若︒=∠40BOD ,求BOC ∠的度数; (2)已知 BOC BOD ∠=∠3(︒<∠45BOC ),且AOC AOD ∠=∠21,请你画出图形,并求BOC ∠的度数.解(1)图2ABCDOABO图130.我们把由“四舍五入”法对非负有理数x 精确到个位的值记为><x .如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…. 解决下列问题:(1)填空:①若6>=<x ,则x 的取值范围是 ;②若x x 34>=<,则x 的值是 ; (2)0≥m 时,试说明:><+>=+<x m m x 恒成立.北京市西城区2011 — 2012学年度第一学期期末试卷(北区)七年级数学参考答案及评分标准(B 卷)2012.1一、选择题(本题共30分,每小题3分)题号 1 2 3 4 5 6 7 8 9 10 答案 D C C B A D A D B C二、填空题(本题共16分,每小题2分)11.0.0036 ; 12.72-x ; 13.18, 3(每空1分); 14.26; 15.60; 16.4; 17.2nm +; 18.②③⑤(全部正确得2分,答出一个正确结果得1分,有错误结果出现不得分).三、解答题(本题共16分,每小题4分) 19.解:)413(87)81(43-++---= 413878143-++- ································································· 1分=14+- ··················································································· 3分 =3-. ····················································································· 4分20.解:)16()158(542.3-÷-⨯÷=16115845516⨯⨯⨯ ········································································· 2分=152. ························································································ 4分 21.解:21149)61()2(3÷--⨯- = 3249)61(8⨯--⨯- ······································································ 2分 = 2334- ····················································································· 3分 =61-. ······················································································· 4分22.解: 252)152(2758.025644232--⨯-÷+- =252225427564125256416-⨯+⨯+- =19225227564125256416-⨯⨯+⨯+- =973516⨯++-=312516++- ············································································ 3分=328-. ····················································································· 4分四、先化简,再求值(本题5分) 23.解:ab ab ab ab ab 3)]28(4[2122---+=ab ab ab ab ab 3)284(2122-+-+ ··················································· 1分 =ab ab ab ab 3)86(2122--+=ab ab ab ab 34322--+ ·································································· 2分 =23ab -. ··················································································· 4分当21=a ,2-=b 时, 原式=2)2(213-⨯⨯-=64213-=⨯⨯-. ············································· 5分五、解下列方程(组)(本题共10分,每小题5分) 24.解:去分母(方程两边同乘以12),得24)25(3)12(4=--+x x . ······························································ 1分 去括号,得 2461548=+-+x x . ···················································· 2分 移项,得 6424158--=-x x . ···················································· 3分 合并同类项,得 147=-x . ··························································· 4分 系数化为1,得 2-=x .∴ 原方程的解是 2-=x . ····························································· 5分①② 25. ⎩⎨⎧=+=-.1,2823y x y x解法一:由②,得 x y -=1. ③ ······························································· 1分把③代入①,得28)1(23=--x x .解这个方程,得6=x . ··································································· 3分 把6=x 代入③,得 5-=y . ····························································· 4分∴ 原方程组的解是 ⎩⎨⎧-==.5,6y x ···························································· 5分 解法二:2×②,得 222=+y x . ③ ························································ 1分①+③,得305=x .∴ 6=x . ··················································································· 3分 把6=x 代入②,得 5-=y . ··························································· 4分 ∴ 原方程组的解是 ⎩⎨⎧-==.5,6y x ··························································· 5分六、列方程解应用题(本题共10分,每小题5分)26.解:设动车平均每小时行驶x 千米,则快车平均每小时行驶)521(+x 千米.······························································································· 1分 依题意,得 1120)521(22120=+++x x . ·········································· 3分 解得 330=x . ············································································· 4分 答:动车平均每小时行驶330千米. ······················································· 5分27.解:设A 服装的成本为x 元,则B 服装的成本为)500(x -元. ····················· 1分依题意,得500157)500%)(401(109%)501(109+=-+⋅++⋅x x . ······ 3分 解得 x =300.500-x =500-300=200. ······························································ 4分 答:A 服装的成本为300元,B 服装的成本为200元. ······························· 5分七、解答题(本题4分)28.解:···································································································· 4分阅卷说明:正确画出一个图形得2分.八、解答题(本题共9分,第30小题6分,第31题3分) 29. 解:(1)∵︒=∠70AOB ,︒=∠40BOD∴︒=︒-︒=∠-∠=∠304070BOD AOB AOD . ·························· 1分 ∵OD 是AOC ∠的平分线, ∴︒=∠=∠602AOD AOC .∴︒=∠-∠=∠10AOC AOB BOC . ··············· 2分(2)设α=∠BOC ,∴α33=∠=∠BOC BOD . 依题意,分两种情况: ①当射线OC 在AOB ∠内部时, 此时射线OD 的位置只有两种可能: ⅰ)若射线OD 在AOC ∠内部,如图2.∴α2=∠-∠=∠BOC BOD COD . ∵AOC AOD ∠=∠21, ∴α2=∠=∠COD AOD .∴︒==+=∠+∠=∠70532αααBOD AOD AOB . ∴︒=14α.∴︒=∠14BOC . ························································· 3分图2ABCDO图1ABCDOA DEHMN AD EFGHCBBC图5ABCDO图4ABC DOⅱ)若射线OD 在AOB ∠外部,如图3,∴α2=∠-∠=∠BOC BOD COD . ∵AOC AOD ∠=∠21, ∴α3231=∠=∠COD AOD .∴︒==-=∠-∠=∠7037323αααAOD BOD AOB .∴︒=30α.∴︒=∠30BOC . ······················································ 4分②当射线OC 在AOB ∠外部时, 依题意,此时射线OC 靠近射线OB , ∵︒<∠45BOC ,AOC AOD ∠=∠21, ∴ 射线OD 的位置也只有两种可能: ⅰ)若射线OD 在AOB ∠内部,如图4,∴α4=∠+∠=∠BOD BOC COD .∵AOC AOD ∠=∠21,∴α4=∠=∠COD AOD .∴︒==+=∠+∠=∠70743αααAOD BOD AOB . ∴︒=10α.∴︒=∠10BOC . ······················································· 5分 ⅱ)若射线OD 在AOB ∠外部,如图5,∴α4=∠+∠=∠BOD BOC COD .∵AOC AOD ∠=∠21, ∴α3431=∠=∠COD AOD ,∴︒==-=∠-∠=∠7035343αααAOD BOD AOB .∴︒=42α.∴︒=∠42BOC ··························································· 6分BDC图3A O综上所述:BOC ∠的度数分别是︒10、︒14、︒30、︒42.30.(1)①5.65.5<≤x . ············································································ 1分②0,43,23. ·············································································· 2分 (2)说明: 设a n x +=,其中n 为x 的整数部分(n 为非负整数),a 为x 的小数部分(10<≤a ). 分为两种情况:(ⅰ)当210<≤a 时,有n x >=<. ∵a m n m x ++=+)(,这时)(m n +为)(m x +的整数部分,a 为)(m x +的小数部分. ∴m n m x +>=+<. 又m x +><=m n +. ∴>+<m x =m x +><.(ⅱ)当121<≤a 时,有1+>=<n x . ∵a m n m x ++=+)(,这时)(m n +为)(m x +的整数部分,a 为)(m x +的小数部分.∴1++>=+<m n m x .又m x +><=11++=++m n m n . ∴>+<m x =m x +><.综上所述: >+<m x =m x +><. ················································ 3分。
西城B初一数学答案

北京市西城区2009–2010学年度第一学期期末测试初一数学试卷(B 卷) 2010.1(时间100分钟,满分100分)一、精心选一选(共10个小题,每小题3分,共30分) 1.15-的相反数是( A ). A .15 B .15- C .5 D .5-2.三峡工程是具有防洪、发电、航运、供水等巨大综合利用效益的特大型水利水电工程,其防洪库容量为22 150 000 0003m ,这个数用科学记数法表示为( C ). A .83221.510m ⨯ B .9322.1510m ⨯ C .1032.21510m ⨯ D .1132.21510m ⨯3.已知3a =-,则a 等于( D ).A .3B .3-C .0D .3±4.现规定一种运算:a b ab a b *=+-,其中a ,b 为有理数,则35*的值为( C ).A .11B .12C .13D .14 5.A 、B 两点的距离是( B ).A .连接A 、B 两点的线段 B .连接A 、B 两点间的线段的长度C .过A 、B 两点的直线D .过A 、B 两点的线段 6.如图所示,下列说法中错误..的是( D ). A .OA 的方向是北偏西15° B .OB 的方向是南偏西45°C .OC 的方向是南偏东60°D .OD 的方向是北偏东60° 7.甲、乙两人练习赛跑,甲每秒钟跑7米,乙每秒钟跑6.5米.他俩从同一地点起跑,乙先跑5米后,甲出发追赶乙.设甲出发x 秒后追上乙,则下列四个方程中正确的是( A ). A .55.67+=x x B .55.67-=x x C .x x 5.657=+ D .5)5.67(=+x8.一个无盖的正方体盒子的平面展开图可以是下列图形中的( B ).A .图①、图②B .图①、图③C .图②、图③D .只有图① 9.下列各式中去括号正确的是( D ).A .2222(2)2a a b b a a b b --+=--+B .2222(2)()2x y x y x y x y -+--+=-++-C .2223(5)235x x x x --=-+D .3232[4(13)]413a a a a a a ---+-=-+-+10.下列图形都是由边长为1厘米的小正方形连接组成的.按照图形的变化规律,第2009个图形的周长是( B )厘米.A .4018B .4020C .8036D .6027二、细心填一填(共10个小题,每小题2分,共20分) 11.将236875精确到万位的结果是_______5104.2⨯________.12.体校里男学生人数是m ,女学生人数是n ,教练人数和学生人数的比是1:20,则教练人数是__)(201n m +_______________. 13.观察右图中的数轴,a 、b 、c 表示的数由小到大的顺序为_______b<c<a__________. 14.一个角的余角比它的补角的29多1度,则这个角为____63____度. 15.若2222m ab +与3343-+-n m b a 是同类项,则m n +=____6____. 16.已知212=-mn m ,152-=-n mn ,则代数式22n m -=___6_____. 17.从下午13:15到当天下午13:54,时钟的分针转过的角度为___154_____度.18.已知线段AB=10cm ,C 是直线AB 上一点,且BC=6cm ,M 、N 分别是AB 、BC 的中点,则线段MN 的长为__8cm 或2cm ___________.19.如图,有4种4×4方格图案,其中阴影部分面积相同的图案是__ __(1)和(4)______________.(请填写序号)20.一个人先沿水平道路前进,继而爬山到达了山顶,之后又沿原路返回到出发点,全程共用了5小时.已知此人在水平路上每小时走4千米,上山每小时走3千米,下山每小时走6千米,则此人所走的全程是__20_______千米.三、用心算一算(共4个小题,每小题4分,共16分)21.计算:)()(2.385.98.7---+-.= —6.522.计算:)10()25()4()5.7(-÷+÷-⨯-. = 56-23.计算:)7(33)7(128)7(18-÷+-÷--÷. = 1124.计算:222172(3)(6)()3-+⨯-+-÷-. = —85四、先化简,再求值(本题4分)25.已知2a b -=,1ab =-.求(45)(235)a b ab a b ab ----+的值. =2(a-b )-6ab当2a b -=,1ab =-时,原式=10)1(622=-⨯-⨯五、解方程(本题5分) 26.14126110312-+=+--x x x . 解:61=x六、列方程解应用题(共2个小题,每小题5分,共10分)27.在暖气管线中装有甲、乙两种水管共25根,总长为155米.甲种水管每根长5米,乙种水管每根长8米.请问甲、乙两种水管各有多少根?解:设甲种水管有x 根,乙种水管有(25—x)根 5x+8(25-x)=155 x=15答:甲种水管有15根,乙种水管有10根。
