六年级高斯学校竞赛构造论证二含答案
六年级高斯学校竞赛应用题综合二含答案

第17讲应用题综合二内容概述各种具有较强综合性的复杂应用题.包含多种可能情况,需要进行分类讨论的问题;需要进行合理守排对策,以达到最佳效果的问题.典型问题兴趣篇1.有一批砖,每块砖的长和宽都是自然数,且长比宽长12厘米.如图17-1,若把这批砖横着铺,则可铺897厘米长;如图17-2,若竖横相间铺,则可铺657厘米长,请问:如图17-3这样铺,可铺多少厘米长?2.一种商品的定价为整数元,100元最多能买3件,甲、乙两人各带了若干张百元钞票,甲带的钱最多能买7件这种商品,乙带的钱最多能买14件,两人的钱凑在一起就能多买1件,求这件商品的定价.3.小明要写152页字,小强要写150页字.从暑假第一天起,小明一天写3页,天天写;小强第一天写4页,但是隔一天写一次,请问:第多少天写完字后,小强没写的页数是小明没写的页数的2倍?4.现有甲、乙、丙三种食盐水各200克,浓度依次为42%、36%、30%,现在要配制浓度是34%的食盐水420克,至少要取甲种食盐水多少克?5.要生产某种产品100吨,需用A种原料200吨,或B种原料200.5吨,或C种原料195.5吨,或D种原料192吨,或E种原料180吨.现知用A种原料及另外一种(指B、C、D、E 中的一种)原料共19吨生产此种产品10吨.试分析所用另外一种原料是哪一种,这两种原料各用了多少吨?6.某城出租车的计价方式为:起步价是3千米8元,之后每增加2千米(不足2千米按2千米计算)增加3元.现从甲地到乙地乘出租车共支出车费44元;如果从甲地到乙地先步行900米,然后再乘出租车只要41元,那么从甲、乙两地的中点乘出租车到乙地需支付多少钱?7.现有21块巧克力,A、B、C、D、E五个人轮流把这些巧克力吃光了,但不知道他们吃的先后顺序.A说:“我吃了剩下巧克力数量的三分之二.”B说:“我吃了剩下巧克力数量的一半,”说:“我吃了剩下巧克力数量的一半.”D说:“我吃光了剩下的巧克力,”E说:“我们每人吃的数量互不相同.”已知每人吃的数量都是正整数,请问:E吃了多少块巧克力?8.已知A、B、C、D、E、F六人分别看了5、5、6、8、8、10场演出.每场演出票价不变,成人票的票价是儿童票的2倍,且均为整数元.已知这六人买演出票共支出了1026元,求成人票单价.9.甲、乙两厂生产同一规格的上衣和裤子,甲厂每月用16天生产上衣,14天生产裤子,共生产448套衣服(每套上衣、裤子各一件);乙厂每月用12天生产上衣,18天生产裤子,共生产720套衣服.现两厂合并后,100天最多可以生产多少套衣服?10.如图17-4,圆形湖泊周长1200米,除了A点和B之外,每隔100米就有一只蜜蜂,一共十只蜜蜂.它们按照顺时针的方向飞行,各个蜜蜂的速度均标在了图上,单位是“米/秒”,小偷从A点出发沿湖顺时针逃到位于B点的家中,只要被沿途的蜜蜂碰到,小偷就会被蜇一下.请问:小偷最少会被几只蜜蜂蜇到?拓展篇1.有8个盒子,各盒内分别装有奶糖9、17、24、28、30、31、33、44块.甲先取走了一盒,其余各盒被乙、丙、丁三人所取走.已知乙、丙取到的糖的块数相同且为丁的2倍.问:甲取走的一盒中有多少块奶糖?2.商店进了一批同样规格的袜子甩卖,为了避免找零,按40%的利润先定价,实际上收取高于“定价×双数”的最小整数元.结果买2双袜子需要5元,3双袜子需要8元,5双袜子需要12元,已知每双袜子的成本和利润都是整数分,求每双袜子的成本.3.甲站有车26辆,乙站有30辆.从上午8点开始,每隔5分钟由甲站向乙站开出一辆车,每隔7.5分钟由乙站向甲站开出一辆车,都经过1小时到达对方车站,问:最早在什么时刻,乙站车辆数是甲站的3倍?总共持续多长时间?4.有4种颜色的卡片每种各3张,每张卡片上写有一个正整数,相同颜色的卡片上写有相同的数,不同颜色的卡片上写有不同的数.把这些卡片发给6个人,每人得到2张不同色的卡片,将上面的数相加,得到了6个和:88、121、129、143、154、187.但是,其中有一个人算错了.请从小到大依次写出四种颜色卡片上所写的数,请写出所有可能.5.生产某种产品100吨,需用A 原料250吨,或B 原料300吨,或C 原料225吨,或D 原料240吨,或E 原料200吨.现知用了A 原料和另外两种原料共15吨生产该产品7吨,每种原料都用了至少1吨,且某种原料占了原料总量的一半,那么另两种原料是什么?分别用了多少吨?6.北京九章书店对顾客实行一项优惠措施:每次买书200元至499.99元者(包含200元)优惠5%.每次买书500元以上者(包含500元)优惠10%.某顾客到书店买了三次书,如果第一次与第二次合并一起买,比分开买便宜13.5元;如果三次合并一起买比三次分开买便宜39.4元.已经知道第一次的书价是第三次书价的85.问:这位顾客第二次买了多少钱的书?7.甲、乙两人同时从A 地出发,以相同的速度向B 地前进,甲每行5分钟休息2分钟,乙每行210米休息3分钟,甲出发后50分钟到达B 地,乙到达B 地比甲迟了10分钟.已知两人最后一次的休息地点相距70米,求两人的速度.8.货运公司要用若干辆最大载重2.1吨的汽车一次性搬运总重18.6吨的货物.为方便搬运,公司把这18.6吨货物包装成若干箱,每箱重量相同.由于包装规格所限,每箱的重量不能超过320千克,且包装好后,货物只能整箱搬运,不得拆箱.请问:要保证一定能一次搬运所有货物,至少需要多少辆汽车?此时每箱货物重量为多少千克?9.某车间有30名工人,计划要加工A 、B 两种零件,这些工人按技术水平分成甲、乙、丙三类人员,其中甲类人员有6人,乙类有16人,丙类有8人.各类人员每人每天加工两种零件的个数如表17-1所示.如果要求加工A 、B 两种零件各3000个,那么最少要用几天?10.有三个一样大的桶,一个装有浓度为60%的酒精100升,一个装有水100升,还有一个桶是空的.现在要配置浓度为36%的酒精,只有5升和3升的空桶各一个可以作为量具,并且桶上无其他刻度.如果倒溶液的时候最多只允许往每个量具里倒4次,那么最多能配置出浓度为36%的酒精多少升?11.一条环形道路,周长为2千米.甲、乙、丙三人从同一地点同时出发,每人环行2周.现有自行车两辆,乙和丙骑自行车出发,甲步行出发,中途乙和丙下车步行,把自行车留给其他人骑.已知甲步行的速度都是每小时5千米,乙和丙步行的速度都是每小时4千米,三人骑车的速度都是每小时20千米.请你设计一种走法,使三个人两辆车同时到达终点,环行2周最少要用多少分钟?12.幼儿园分大、中、小三个班,小班人数最少,大班比小班多61人,中班共27人.把25筐苹果分给他们,每筐苹果在50至60之间不等.已知苹果总数的个位数字是7,若每人分得19个,则苹果不够;若大班比中班每人多1个,中班比小班每人多一个,则苹果刚好分完.那么按第二种分法,大班每人分得几个苹果?小班有多少人?超越篇1.如图17-5所示,在直角三角形ABC 中,AC 长3厘米,CB 长4厘米,AB 长5厘米.有一只小虫从C 点出发,沿CB 以l 厘米/秒的速度向B 爬行;同时,另一只小虫从B 点出发,沿BA 以1厘米/秒的速度向A 爬行,请问经过多少秒后,两只小虫所在的位置D 、E 与B 组成的三角形DBE 是等腰三角形?(请写出所有答案)2.七个人围坐在圆桌周围,在每个人面前都有一个牛奶杯.第一个人把自己的牛奶都平均分到其余的杯子中去,接着第二个人照样做一遍,然后第三个人到第七个人也同样做一遍.最后发现每个杯子中的牛奶都和最开始时一样多.如果所有杯子的牛奶共有7升,那么第一个人到第七个人的杯子里开始时分别有牛奶多少升?3.甲、乙两人切蛋糕,两人轮流切,每人切走了五块.已知:①甲切了5次蛋糕,每次切走的蛋糕恰是切蛋糕时蛋糕大小的61、62、63、64和65各1次,但不全对应切蛋糕顺序;②乙切了5次蛋糕,每次切走的蛋糕恰是切蛋糕时蛋糕大小的51、52、53、54和55各1次,也是不全对应切蛋糕顺序;③切的最大的两块都是原来蛋糕的91,另外还有一块大小是原来蛋糕的2251.求切的第八块蛋糕与原来蛋糕的大小之比.4.师徒两人共同组装50台机器,每台机器组装必须经过A 、B 两道工序.对于每台机器,师傅操作A 工序需要15分钟,操作B 工序需要5分钟;徒弟操作A 工序需要45分钟,操作启工序需要20分钟,每台机器每道工序只能由一人完成,不同工序可以由不同人分别完成,但必须A 先B 后.试问:如果两人合作至少要花多少分钟才能完成工作?5.甲、乙两人在如图17-6的跑道上练习跑步,两人从A 点同时出发,甲在A 、E 之间做折返跑(转身时间不计),乙则沿着正方形跑道ABCD 顺时针跑步,已知AB=BE=100米,且两人跑步的速度都在每秒3米到每秒8米之间.如果两人出发2分钟后第一次相遇,之后隔了15秒后两人第二次相遇,那么两人第二次相遇处距离A 多远?6.某电器商场开展促销活动,每次消费超过1500元不足3000元者(含1500元)优惠5%,超过3000元者(含3000元)优惠10%.甲、乙、丙三个人各买了一件电器,如果甲、乙一起结算,比分开结算便宜130元;如果甲、丙一起结算,比分开结算便宜260元;如果三人一起结算,比三人分开结算便宜405元.请问:三人购买的电器价格分别是多少?7.某商场进行酬宾,规定现金消费每满50元返回10元礼券,多出不足50元部分不计(比如消费99元只能返回1张10元礼券),用礼券产生的消费不参与返券.妈妈看中了3件商品,分别是100多元、200多元、300多元,且都是10的倍数,更巧的是,有两件商品的价格之和正好是整百.为了充分利用返券,妈妈打算先买其中的两件,然后兑换成返券,这样买第三件商品的时候,就可以用上返券了,当然,如果返券不够买第三件,自己还得再掏一些钱,她合计了一下,这样安排的话,共有三种可能的消费结果:第一种恰好花640元,礼券也用完了;另外两种情况都要花670元,但最后又返回40元礼券.问:三种商品的价格分别是多少元?8.学校运来125个桃和若干个梨,分别平分给每位老师,最后剩下一些梨和桃不够分,这时又运来了26个水果(桃梨若干),和之前剩下的水果凑在一起,再平分给老师,每个老师多分得3个水果(每位老师的桃数相同,梨数相同).最后又运来40个水果(桃梨若干),但是发现所剩的桃和梨竞不够每位老师同时多拿一个,那么第一次分后剩下了多少个梨?第 17 讲 应用题综合二兴趣篇1、有一批砖,每块砖的长和宽都是自然数,且长比宽长 12 厘米。
2013-2014学年六年级高思杯-思维部分 解析模板

6年级 试卷解析 高思学校2013-2014 学年 六年级 高思杯 综合解答及评析思维部分一、判断题1、 答案:×. 知识点:质数与合数. 详解:举出反例即可,如 4 和 9 的和就不是合数. 2、 答案:√. 知识点:立体几何. 3、 答案:√. 知识点:分数定义. 4、 答案:×. 知识点:质数与合数. 详解:1 既不是质数也不是合数. 5、 答案:×. 知识点:浓度问题. 详解:喝去的是溶液整体的一半,酒精和酒都变为原来的一半,所以浓度不变.2013 年秋季二、单项选择题6、 答案:B. 知识点:计数问题. 详解:A-B、A-C-B、A-C-D-B、A-D-B、A-D-C-B. 7、 答案:A. 知识点:概率问题.1 详解:符合要求的点数搭配有(2,6)(6,2)(3,4)(4,3)共四种,其概率为 4÷36= . 、 、 、 98、 答案:B 知识点:经济问题 详解:2500÷6000×100%≈42%.高思杯六年级试卷解析 2013 年秋季 9、 答案:B. 知识点:不定方程. 详解:将两人的牌数设为 5x+3、7y-2,根据总牌数为 54 列出不定方程求解即可. 10、 答案:D 知识点:立体几何.6年级 高思学校三、填空题 I11、 答案:12 知识点:约数倍数 详解:两个数的最大公约数与最小公倍数的乘积等于两数的乘积. 12、 答案:123456789 知识点:定义新运算 详解:按规律列竖式即可. 13、 答案:56 知识点:对应计数 详解:插板法,八个空插三个板,即为八选三的组合数. 14、 答案:13.42 知识点:平面几何 详解:阴影=半径是 2 的一个四分之三圆+一个边长为 2 的正方形. 15、 答案:8 . 15知识点:分数计算 详解:按四则运算顺序依次乘除即可. 16、 答案:48 知识点:往返接送 详解:画往返接送的典型分段行程图即可.四、填空题 II17、 答案:40 知识点:平面几何 详解:高 10 只能是边长为 8 的边上的高,否则会画出一个直角边为 10、斜边为 8 的直角三角 形,显然不成立. 18、 答案:66年级 知识点:不定方程试卷解析 高思学校2013 年秋季详解: 设下午卖出 x 只鸡, 且单价为 a 元. 可列出不定方程: ( 24 − x ) + ax = , 36 + ax = , 7 132 即 7x 那么 x 为 36 的约数且 x 大于 12,所以 x 为 18,因此上午卖出了 24 − 18 = 6 只鸡. 19、 答案:80 知识点:工程问题 详解: (比例法)甲、乙的工效比为 2:3,所以当甲完成时两队完成的工作量之比为 2:3.而一 开始甲、 乙的工作任务之比为 1:3, 可化为 2:6. 所以乙还剩下的 30 米对应的份数为 6 − 3 = 份, 3 即 1 份对应 10 米,因此这条路的总长度为 ( 2 + 6 ) × 10 = 米. 80 20、 答案:2022 知识点:质数合数 详解:从 8 开始往后的偶数可以拆成两个偶合数的和;从 13 开始的奇数可以拆成 9+2n 的形式 (n 大于等于 2) ,而 1、2、3、4、5、6、7、9、11 要划去,所以剩下的数列为 8、10、12、13、 14、15……,第 2013 项即为 2022. 21、 答案:3 知识点:流水行船问题 详解:老师逆流而上时,人与木筏的运动属于相遇运动,路程和等于速度和(速度和即为人在 静水中的速度)乘以 10 分钟;老师顺流而下时,人与木筏的运动属于追及运动,之前的路程和 变为了现在路程差,而现在的速度差也为人在静水中的速度,因此要 10 分钟即可追上木筏,所 以前后木筏共漂了 20 分钟,则水流的速度为 1000 ÷ 20 =米/分钟=3 千米/时. 50 22、 答案:560 知识点:排列组合 详解: 8 选 3 的情况数×5 选 2 的情况数×3 选 3 的情况数.五、填空题 III23、 答案:11 知识点:平面几何 详解:由等高三角形可知,三角形 BFD 与三角形 CFD 面积相等,同理可知三角形 BED 与三角 形 AED 面积相等,所以四边形 ABFD 的面积为 5 + 5 + 12 = .由等高三角形可知三角形 BEF 22 的面积为三角形 ABF 的一半,且三角形 ABF 与三角形 BFD 的面积相等都为 12,因此三角形高思杯六年级试卷解析 2013 年秋季 BEF 的面积为 6,所以三角形 EFD 的面积为 22 − 6 − 5 = . 11 24、 答案:282 知识点:复杂应用题6年级 高思学校详解:一开始三人的金币数之比为 3:2:1,总数为 6 份,所以总数为 6 的倍数.设重新分配后各 占 x、y、z 个,由题意列方程组,整理后即可的 x:y:z=33:13:1,即把总数又可分成 47 小份,所 以总数为 47 的倍数.因此总数为 6 和 47 的公倍数,且为 200 多,所以总数为 282. 25、 答案:116 知识点:计数问题 详解:显然 C 中只能填 11,而和为 36 的四个数要满足题目条件,只能有以下两种情况: (11、 10、9、6)(11、10、8、7) 、 .两种情况下各自按大小顺序分类排列可得共有 64+52=116 种情 况.六、操作题26、 答案:1 1 2 3 21 4 4 3 53 3 5 1 45 1 5 1 52 5 3 2 43 2 2 4 4知识点:数阵问题 详解:将 55,22,33 做突破口.七、解答题27、 答案: (1)3; (2)6; (3)108. 知识点:间隔发车问题 详解:每 4 秒钟发出一发炮弹,炮弹的间距为 36 米. (1)炮弹和僵尸做相遇运动,相遇时间为36 ÷ ( 9 + 3) = (2)炮弹和僵尸做追及运动,追及时间为 36 ÷ ( 9 − 3) = (3)考虑极端 3 秒; 6 秒;情况, 从僵尸进入射程开始到僵尸碰到豌豆, 豌豆刚好发出 10 发炮弹, 其所用时间为 9 × 4 = 36 秒,即僵尸走了 36 秒,因此此时射程为 36 × 3 = 米,所以射程应该大于 108 米. 108高思学校2013 年秋季6年级 试卷解析 。
第二届高思杯 六年级综合素质测评_数学试卷解析

二、填空题
6. 【答案】144.
【简答】 8,12,18 72 , 8,12,18 2 ,乘积是 72 2 144 . 【评析】主要考察多个数的最大公约数与最小公倍数的计算.
简答天天欢欢乐乐三人总分是97分所以欢欢乐乐凯凯欣欣的总分是291279111评析这是一个与平均数有关的应用题处理时注意理清平均数与总数之间的联系可能有些同学对于四年级时候学的平均数问题已经有些忘了希望大家在以后的学习过程中一定要注意对之前所学知识的复习
第二届高思杯 六年级综合素质测评
思维部分 第一试
9. 【答案】10.
【简答】由平行的性质及等高三角形的性质,有
CD : DB AE : BE 6 : 9 2 : 3 ,所以 S ABD : S ACD BD : CD 3 : 2 ,
A E
6
D C
9
B
S ACD 6 9
2 10 . 3
【评析】综合考察平行线的性质及三角形中的比例关系,需要同学对两方面都有一定的认识.
5. 【答案】B.
【简答】取 1 元 4 张,5 元 1 张,10 元 1 张,20 元 2 张,50 元 1 张即可表示出 1 到 100 元的所 有整数元钱数. 【评析】这是一个构造的问题,只要思考清楚,不难构造出 9 张纸币的情形,但要证明 9 张纸
币就是最少的就不是那么容易了,同学们可以自己尝试着论证一下!
9. 【答案】22.28.
高斯小学奥数六年级上册含答案第24讲 构造论证

第二十四讲构造论证二例1. (1)把1、2、3、…、8、9按合适的顺序填在图中第二行的空格中,使得每两个上、下对齐的数之和都是平方数.(2)能否将1、2、3、…、10、11按合适的顺序填在图中第二行的空格中,使得每两个上、下对齐的数之和都是平方数?若不能请说明理由. 「分析」(1)首先判断由1到9可以凑成的平方数的范围,然后逐一计算一下哪些数一起可以凑成平方数,从情况唯一或较少的数字填起;(2)分析方法同上一问,注意是否一定能填出.练习1、把1、2、…、13、14按合适的顺序填在图中第二行的空格中,使得每列的两个数之和都是平方数.例2. (1)能否将1至15排成一行,使得任意相邻两数之和都为平方数?(2)能否将1至15排成一行,使得任意相邻两数之和都为质数?「分析」(1)对于1~15的每一数来说,能都凑成平方数的情况并不多,我们就可以从这里入手分析,同学们尝试一下看能不能得到一种合适的方案.(2)注意到除了2以外,质数只能是奇数,那我们是不是能从奇偶性的分析入手呢?练习2、能否将1至41排成一行,使得任意相邻两数之和都为质数?例3.有3堆石子,每次可以从这三堆中同时拿走相同数目的石子(每次这个数目可以改变),也可以由一堆中取一半石子放入另外任一堆石子中.请问:(1)如果开始时,3堆石子的数目分别是34、55、82,按上述操作,能否把3堆石子都拿光?(2)如果开始时,3堆石子的数目分别是80、60、50,按上述操作,能否把3堆石子都拿光?如果可以,请设计一种取石子的方案;如果不可以,请说明理由.「分析」每次从这三堆中同时拿走相同数目的石子意味着每次拿走的石子数是3的倍数,所以,我们可以从石子总数这个角度分析这道题目.练习3、有4堆石子,每次可以从这四堆中同时拿走1个石子;也可以从任一堆中取出3个石子,另三堆各放1个.如果开始时,4堆石子的数目分别是14、25、32、44,能否把4堆石子都拿光?例4.黑板上写着3个数8,18,28,老师现在请一些同学上黑板对这3个数进行操作.进行一次操作是指:一些数减1,其它数加2;或者都减1;或者都加2.那么能否经过若干次操作后得到6,7,8?能否经过若干次操作后得到8,8,8?「分析」这道题可以从三个数中任意两数除以3的余数角度去分析.练习4、黑板上写着3个数9、18、27,老师现在请一些同学上黑板对这3个数进行操作.进行一次操作是指:把3个数进行如下变化,一些数减1、其它数加2;或者都减1;或者都加2.请问:能否经过若干次操作后得到11,12,13?能否经过若干次操作后得到8,8,8?例5.图中是把一张6×6的方格纸去掉两个角所得的图形.Array(1)请把所有的格子涂上红、蓝两色之一,使得每个1×2小长方形(不论横竖)的2个方格中都恰有1个红格和1个蓝格;(2)能否用1×2的小长方形恰好拼满这张表格?「分析」本题可以采用“染色法”进行分析.例6.(1)能否用16个如图所示的“T 型”拼成一个的棋盘? (2)能否用8个“T 型”和8个“L 型”拼成一个的棋盘?「分析」碰到这样的问题,我们首先要考虑的是能不能填出,而不是一上来就去试,这时就需要我们进行染色分析了,同学们可以先尝试一下黑白相间染色,论述一下是否成立?如果成立,那就需要找到一种合适的拼法.88⨯ 88⨯阿兹台克文明根据传说,阿兹台克人的祖先是从北方一个叫阿兹特兰的地方来的,他们根据太阳神威齐洛波契特里的指示往南来到阿纳瓦克谷的特斯科科湖;当他们来到湖中央的岛屿时,他们看到一只叼着蛇的老鹰停歇在仙人掌上,这个意像告诉他们应该在这里建造城市.1325年阿兹台克人在这个地方建立了特诺奇提特兰,一座巨大的人工岛,现在墨西哥城的中心.阿兹台克人原属纳瓦语系发展水平较低的一个部落,后来因吸收、融合这个地区其他印第安优秀文化传统而迅速崛起.公元11~12世纪间,从北部迁入墨西哥中央谷地,1325年在特斯科科湖西部岛上建造特诺奇蒂特兰城.1426年,阿兹台克同特斯科科、特拉科潘结成了“阿兹台克联盟”,由阿兹台克国王伊兹科亚特尔任首领,势力日盛,在谷地建立了霸主地位.继承人蒙特祖马一世及其后的国王不断对外用兵,开疆拓土,至16世纪初,其疆域东西两面已抵墨西哥湾和太平洋沿岸,北与契契梅克为邻,南至今日之危地马拉,人口约300万,发展到极盛时期.1519年,西班牙殖民者埃尔南·科尔特斯利用印第安人内部矛盾,进攻阿兹台克国,蒙特苏马二世在入侵者面前动摇不定,最后成为西班牙殖民者的傀儡.1520年6月向人民劝降时被群众击伤而死.科尔特斯在所谓“悲惨之夜”侥幸逃命后,又于1521年卷土重来,阿兹台克人在新国王夸乌特莫克率领下,与围城的西班牙殖民者展开殊死搏斗,最后由于粮食和水源断绝,加之天花肆虐而失败.1521年8月,西班牙人占领特诺奇蒂特兰,在城中大肆屠杀,并将该城彻底毁坏,后在其废墟上建立墨西哥城.阿兹台克文明在发展过程中,吸收了托尔特克文化和玛雅文明的许多成就,但自己也有独创.其文字仍属图画文字,但已含有象形文字成分.天文历法方面,使用太阳历与圣年历,已知一年为365天,每逢闰年补加一天.医学方面,知道利用各种草药治病,并已使用土法麻醉.阿兹台克人的陶器和绘画均极精致,建筑和艺术也达到相当高的水平.首都特诺奇蒂特兰的公共建筑物多以白石砌成,十分宏丽壮观.一般房屋的周围,在固定在水面的木排上种植花草,形成水上田园.城中心的主庙基部长100米、宽90米,四周有雉堞围墙环绕,塔顶建有供奉主神威济洛波特利和雨神特拉洛克的神殿,其祭坛周围有蛇头石雕,坛下发现的重达10吨的大石上,刻有被肢解的月亮女神图案,1790年在墨西哥城中心广场发现的“第五太阳石”直径近4米,重约120吨,刻有阿兹台克宗教传说中创世以来四个时代的图像,代表了阿兹台克人石雕艺术的高度水平.阿兹台克人是优秀的建筑师.首府特诺奇蒂特兰是一座岛城,有3条宽达10米的石堤与湖外陆地相通,石堤每隔一定距离就留一横渠,渠上架设吊桥,可随时收放,以防外敌入侵.城内建有宫殿、神庙、官邸、学校,建筑宏伟,最大一座金字塔台庙其规模甚至可与古埃及的媲美.为了满足城市稠密人口对粮食的需要,在湖泊中建造了独特的“水上园地”,以扩大种植面积.岛城四面环水,市内河道纵横,景色富丽,殖民者为之倾倒,惊呼为“世界花园”.阿兹台克人主要生产工具仍为石器,多由黑曜岩制成,但已会制造铜、金物品.作业1.桌上放有5枚硬币,正面朝上,第一次翻动1枚,第二次翻动其中的2枚,第三次翻动其中的3枚,第四次翻动其中的4枚,第五次翻动其中的5枚.能否恰当地选择每次翻动的硬币,使得最后桌上所有的硬币都正面朝下?2.把1、2、3、…、13按合适的顺序填在图中第二行的空格中,使得每列两个数字之和都是平方数.3.《三国英雄传》共有10篇故事,这些故事占的篇幅从2页到11页各不相同.如果从书的第1页开始印第一个故事,每一个故事总是从新的一页开始印,那么故事从奇数页起头的最多有多少篇,最少有多少篇?4.能否将1至12排成一行,使得任意相邻两数之和都为质数?5.能否将1~13排成一行,使得任意相邻两数之和都为平方数?如果可以的话请给出一种排列方式,如果不能请说明理由.第二十四讲 构造论证二例7. 答案:(1)如下图,(2)不能详解:(1)略;(2)配成的平方数只有4、9、16三种可能,11只能和5配对,而4也只能和5配对,所以没有满足要求的填法.例8. 答案:(1)9、7、2、14、11、5、4、12、13、3、6、10、15、1、8;(2)1、2、3、14、5、12、7、10、9、8、11、6、13、4、15 详解:(2)奇数与奇数不能相邻,所以需要有7个偶数把它们分开. 例9.答案:(1)能,(2)不能 详解:(1)可以按如下操作:(34,55,82)→(0,21,48)→(24,21,24)→(4,1,4)→(2,3,4)→(0,1,2)→(1,1,1)→(0,0,0);(2)本题中三堆石子数目和要是3的倍数,190不是3的倍数,所以,不能. 例10. 答案:(1)能;(2)不能 详解:(1)可以按如下操作:(8,18,28)→(0,10,20)→(6,7,17)→(8,9,16)→(7,8,15)→(6,7,14)→(6,7,8);(2)所有操作不能改变三个数的两两之差被3除的余数大小.例11. 答案:(1)如图,白框涂红、黑框涂蓝;(2)不能 详解:(2)1×2的小长方形每次恰覆盖1个红格和1个蓝格,而由(1)可知红格与蓝格的数目不相等.例12. 答案:能,能 详解:方法同上.练习:练习1、答案:如下图练习2、答案:能简答:如下:1、40、3、38、5、…、37、4、39、2、41.练习3、答案:不能简答:总数不是4的倍数.练习4、答案:不能;能简答:(1)所有操作不能改变三个数的两两之差被3除的余数大小(2)可以实现,方法不唯一.作业1.答案:能简答:第一次翻动第一枚,第二次翻动第一、二枚,第三次翻动第三、四、五枚,第四次翻动第二、三、四、五枚,第五次全部翻动.2.答案:如下表3.答案:8;3简答:2~11页,只考虑页数总和的奇偶不考虑数值,最多可以是偶、偶、偶、偶、偶、奇、奇、奇、奇、奇,其中以奇数页开始的是8篇,改变顺序即可得出最少为3篇.4.答案:能简答:如下:11、12、1、2、3、4、7、6、5、8、9、10.5.答案:不能简答:9只能和7相邻,10只能和6相邻,11只能和5相邻,所以这3个数必须放在两端,显然无法满足.。
历届高思杯 六年级综合素质测评改编题答案与解析

历届高思杯六年级综合素质测评改编题答案与解析一、选择填空(10×1)1. He studies ______ every dayA. enough hardB. hard enoughC. enough hardlyD.hardly enough1.B.enough “足够的,足够地”,作形容词时,修饰名词时需放在名词前,作副词时,修饰形容词或副词时需放形容词或副词后。
2. ______ clever the boy is!A. HowB.WhatC.What aD. How a2.A.what与how引导的感叹句的区别;What+形容词+(a,an)名词(其中主谓部分常省略)。
What+形容词+ 名词复数(其中主谓部分常省略)。
例如:What a nice girl (she is)!How+ 形容词/副词+ 主语+谓语例如:How nice the girl is! nice(形容词)How hard she studies! hard(副词)3.There is ______ on the table.A. lot of breadB. many breadsC. lots of breadD. many bread3.C. bread 为不可数名词,lots of/ a lot of既可修饰可数也可修饰不可数名词, many与 a few 只能修饰可数名词。
4. –You have dropped _____ “f” in the word “office”.–Oh, ____ letter “f ” should be doubled like this “office”.A. a, aB. an, aC. a, theD. an, the4.D.“f”发音以元音开头故用“an”;26个字母中有8个辅音字母是以元音发音开头。
f h l m n r s x.5. ______ nice girl! We all like herA. HowB.WhatC.What aD. How a5.C. 参考第二题讲解6.My sister is the only one of these students who ______ able to sing this new song.A. hasB. areC. isD. have6.C. 什么叫定语从句?用来说明主句中某一名词或代词(有时也可说明整个主句或主句中一部分)而起定语作用的句子叫作定语从句。
高斯小学奥数六年级下册含答案第02讲_余数问题综合提高

第二讲 余数问题综合提高本讲知识点汇总:一. 求余数1. 直接做除法.2. 特征求余(注意和整除特征对比);3. 替换求余4. 周期求余5. 分解求余二. 物不知数问题(求被除数)1. 也称“韩信点兵”,关于它的解法,后人总结出“中国剩余定理”(也称“孙子定理”).物不知数问题的基本解法是:逐步增加条件,逐步找寻2. 分解求余三. 同余1. 概念如果a 和b 除以c 的余数相同,则称a 、b 对c 同余,例如:10和28对9同余.2. 如果a 、b 对c 同余,则是c 的倍数.例1. (1)4188141616⨯⨯除以7、8、9、11的余数分别是多少?(2)892除以7的余数是多少?(3)89143的个位数字是多少?除以7的余数是多少?除以11和13的余数呢?「分析」(1)替换求余法;(2)周期求余法解这道题目;(3)同上.a b -练习1、的个位数字是多少?除以7的余数是多少?例2. 44443444421Λ200320032003032003200320个除以9的余数是多少?除以11的余数是多少?除以99的余数是多少?「分析」截段求和法.练习2、201320132003200320032003n L 14444244443除以9的余数是多少?除以11的余数是多少?除以99的余数是多少?例3. 有一种三位数,它除以9所得的余数等于它的各位数字的平方和,这样的三位数可能是多少?请写出所有可能答案.「分析」尝试枚举出一个符合题意数来,总结一下这样的数有什么特点.练习3、一个布袋中装有5000多个小球,如果10个一包,最后还剩9个;如果9个一包,最后还剩8个;…;如果5个一包,最后还剩4个.那么如果13个一包,最后还剩多少个?例4.(1)一个三位数除以9余2,除以12余2,那么这个三位数最小是多少? (2)一个数除以4余3,除以6余5,除以7余6,那么这个数最小是多少?(3)一个三位数除以3余2,除以5余3,除以7余4,那么这个三位数最小是多少? 「分析」(1)余数相同;(2)余数和除数的差相同;(3)逐步满足条件法.20132013练习4、(1)一个三位数除以6余2,除以8余2,那么这个三位数最小是多少?(2)一个数除以3余2,除以5余4,除以7余6,那么这个数最小是多少?(3)一个数除以6余2,除以11余1,那么这个数最小是多少?例5.三个连续自然数依次是13、11、7的倍数,那么这三个连续自然数之和最小为多少?「分析」能否将这道题目中三个连续的被除数,转化为同一个数,而这个数又有什么样的特点呢?例6.有一个整数,用它分别去除157、234和324,得到的三个余数之和是100,这个整数是多少?「分析」如果把余数都去掉后,剩余的数有什么特点?作业1. 的个位数字是多少?除以7的余数是多少?2. (1)一个三位数除以4余2,除以6余2,那么这个三位数最小是多少?(2)一个三位数除以3余1,除以4余2,除以6余4,那么这个三位数最小是多少?(3)一个数除以9余2,除以12余5,那么这个数最小是多少?3. 一个盒子中装有棒棒糖100多个,如果每次取5个最后剩4个,如果每次取4个最后剩3个,如果每次取3个最后剩2个.那么如果每次取12个,最后剩多少个?4. 一个两位数去除531,得到的余数是69,这个两位数是多少?5. 有一个自然数,用它分别去除61、90、130都有余数,3个余数的和是26,这3个余数中最大的一个是多少?36629第二讲 余数问题综合提高例7. 答案:(1)4、0、8、0;(2)4;(3)3;5;0;0.解答:(1)按替换求余计算即可;(2)按周期求余:2、22、32、42……、除以的余数依次是2、4、1、2、4……、每三个数一个周期,所以,892除以7的余数是4;(3)按周期求余即可,143=11×13,143是11和13的倍数.例8. 答案:7;1;34.解答:除以9的余数,按“特性求余”数字和为()2003200310015+++⨯=,而100157++++=,所以,200320032003200320032003n L 14444244443除以9的余数是7;除以11的余数,也可用“特性求余”法;除以99的余数,两位截段求和判断即可.例9.答案:100、101、110、111. 解答:一个数除以9的余数就是等于这个数的数字和除以9的余数,又要等于它的各位数字的平方和,所以只有上述的4种答案.例10. 答案:110;83;158.解答:(1)余数相同,9和12的最小公倍数时36,所以,除以9余2,除以12余2,的数最小是36238+=,又由于要符合三位数这个条件,所以,38362110+⨯=;(2)“差同”差为1,[]4,6,784=,84183-=;(3)逐步满足条件.例11. 答案:627.解答:一个数满足:是13的倍数,且加1后是11的倍数,那么这个数最小是65,下一个是65143208+=,而209、210分别是11、7的倍数,所以和最小是208209210627++=.例12. 答案:41.解答:157、234和324的和是715,减去100的差是615,615是这个整数的倍数,而615的约数有1、3、5、15、41、123、205、615,验算只有41满足余数和是100.练习:练习1、答案:3;1.简答:20132013的个位数字只与个位数字有关相当于20133的个位数字,3n 的个位数字依次3、9、7、1、……,每四个数一周期,20134÷余1,所以,20132013的个位数字是3;20137÷余1,1的2013次方除以7的余数也是1.练习2、答案:3;0;66.简答:同例题2.练习3、答案: 8.简答:布袋中的小球数除以10余9,除以9余8,除以8余7……,除以5余4,[][]5,6,7,8,9,105,7,8,957892520==⨯⨯⨯=,所以,布袋中球数是2520125205039-+=,503913÷余8.练习4、答案:(1)122;(2)104;(3)56.简答:同例题4.作业1.答案:1;1.简答:29n的个位数字依次是9、1、9……,所以,366÷余1,29的个位数字是1;297所以,36629除以7余1.2.答案:110;106;29.简答:(1)[]+⨯=;(2)按“差同”计算;(3)按“差同”=,141281104,612计算.3.答案:11.简答:除以5余4,除以4余3,除以3余2的数最小是59,满足上述条件的100以上的数是59加上若干个60,如119、179等,这些数除以12余11.4.答案:77.简答:53169462-=,462的约数中比69大的两位数只有77.5.答案:11.简答:61、90和130的和减去26得到255,255的约数中验证得满足条件的只有17,所以这个自然数是17,所以余数中最大的是130除以17的余数11.。
2012-2013学年六年级高思杯-思维部分+解析

本题评析:对于这种复杂分数的计算,通常采用“相互抵消”的方法.或是前后加减 相消,Байду номын сангаас是上下乘除相消.并且要注意找规律,尤其要注意最后剩下的是哪些项.
18、 答案:40
知识点:比例与方程解行程问题 详解:此题既可以用比例,也可以用方程.如果熟悉方程的话,思路可能更直接些. 解:设大货车的速度为 x 千米/时,小轿车原来的速度为 y 千米/时,依题意可得:
5、 答案: (×)
知识点:几何——图形的剪拼. 详解:完全相同的两个梯形一定能拼成平行四边形。但面积相等的两个梯形,不一定能拼成平 行四边形。例如下图中的两个上底、下底、高都相等的梯形:
高思杯六年级试卷解析
2012 年秋季
6年 级
本题评析:我们可以进一步追问,反过来:拼成平行四边形的两个梯形,一定要求面 积相等吗?
三、填空题 I
11、 答案:1
知识点:计算——分数四则运算
本题评析:本题主要考察同学们计算的基本功.
12、 答案:6
知识点:倒推法 详解:遇到第二家酒店加倍后是 8 两,故遇到第二家酒店之前酒壶里有 4 两酒.所以最初酒壶 里有 6 两酒.
本题评析:求得答案后,可再顺着题意验证一下.
13、 答案:628
高思学校
本题评析:此题涉及到“特性求余法”以及“分解求余法” ,还需要找规律,有一定 难度.
本大题总体评价:本大题有一定难度,由于同学们对各个知识点掌握情况不同,对每道题的难度感 受也会不同.如果遇到不会做的题目,也要平心静气,认真踏实的做好后面的题目,良好的心理素质会 决定你的能力水平能否充分发挥.
6年 级
试卷解析
2012-2013 学年 六年级 高思杯 综合解答及评析
第01讲构造论证二-高思数学_6年级下第一讲构造论证二

在现实生活中,我们经常需要自己设计一些方案来解决问题,设计方案的过程就是构造.但仅仅构造出一种方案是不行的,我们还要对方案的可行性进行分析,严格的讨论方案的正确与否,有的时候还需考虑方案是否最优,这个过程就是论证.构造与论证经常是合在一起的,没有构造出方案,也就无从论证,但仅仅构造出方案也是不行的,我们还需要证明方案是正确的.很多时候,构造论证问题都和最值问题结合在一起,这时我们就需要找到最优解.分析 要破坏一个三角形,只需去掉三角形的一条边就可以了,但要求我们去掉的线段最少,那么我们就应该更多地去掉多个三角形的公共边,那么去掉多少个边才行呢?练习1. 如图33×的表格中,最少去掉多少条线段,才能使图中没有正方形?很多问题中,不仅需要构造出方案,还需要讨论方案是否正确,有的时候还需要论证方案是否存在.下面我们来看这样的一道问题.分析 (1)对于1~15的数来说,能凑成平方数的情况并不多.我们可以从这里入手分析.同学们尝试一下看能不能得到一种合适的方案.线段.请问:这5(2)注意到除了2以外,质数只能是奇数,那我们是不是能从奇偶性的分析入手呢?练习2.能否将1至12重新排列,使得任意相邻两数的和都是质数?如果能请写出一组,如果不能请说明理由.构造论证的问题中,经常会用到很多其他的知识,例如数论的分析、抽屉原理、奇偶性分析等.分析 我们从第一页开始考虑.如果第二篇故事是奇数页开头的,那么第一篇故事一定是偶数页的,如果第三篇故事是奇数页开头的,那么前两篇的和一定是偶数页的,而故事最多有几篇是奇数页开头的,就需要考虑前面几篇的和,最多有多少个是偶数.练习3. 一个数列有7项,每相邻两项作差,发现所得的6个差里面有3个是1,3个是2.问:这个数列中最多有几个奇数,最少有几个奇数?构造与论证中有一类操作问题,需要我们对已有的对象进行操作和变化,以期得到需要的结果,在解决这类问题的时候,一定要考虑问题是否可行,不要上来就开始操作.而在分析问题的可行性时,不变量经常是解决问题的关键.页各不相同.如果从书的第一页开始印,那么故事从奇数页起头的最多有几篇?最少有几篇?分析 首先,同学们可以尝试着变化一下,看看能不能得到想要的结果,但在变化的过程中,能发现三个数有什么是没有变化的吗?怎么能说明是否能得到8、8、8呢?练习4. 黑板上写着9、18、27这三个数,老师现在请一些同学上黑板对这两个数进行操作,进行一次操作是指把两个数都进行如下变化:或者减2,或者加1.请问:能否经过若干次操作后得到11、12、13?能否经过若干次操作后得到8、8、8?下面我们来看一下构造与论证中常用的方法——染色法.我们举个例子来说明:在一个55×的方格表(图1)中放入25枚棋子,每格1枚;接着将所有棋子都移动到相邻方格中,且仍然每格1枚,能否办到?答案是不能.如果用一般的方法来说明将会变得非常复杂,但如果我们将方格阵按照如图2的方式染色,那么将所有棋子都放入到相邻的位置中,一定是黑格的棋子进白格,白格的棋子进黑格,但是共有13个黑格,只有12个白格,黑格的棋子不可能全部转移,所以我们的要求是达不到的.通过例子,同学们对于染色法有了初步的了解.但在实际的问题中,我们要根据题目的要求采用不同的染色方式,同学们一定要在做题的过程中积累不同的染色方法,这样才能做到有备无患.黑板对这三个数进行操作,进行一次操作是指把三个数都进行如下变化:者减若干次操作后得到 21分析 碰到这样的问题,我们首先要考虑的是能不能填出,而不是一上来就去试,这时就需要我们进行染色分析了.同学们可以先尝试一下黑白相间染色,论述一下是否成立?如果成立,那就需要找到一种合适的拼法.练习5. (1)能否用12个如图1所示的“T 型”拼成一个68×的长方形?(2)能否用12个如图2所示的“L 型”拼成一个68×的长方形?(3)能否用8个如图1所示的“T 型”和4个如图2所示的“L 型”拼成一个68×的长方形?棋盘?拼成一个图212本讲知识点汇总一、构造合理的方案.二、奇偶性的分析方法.三、操作中的不变性.四、经典的染色问题.作业1.如图,平面上有9个点,他们之间连着16条线段,从而围出了8个三角形.请问:至少要去掉多少条线段,才能使得其中没有以这9个点为顶点的三角形?2.能否将1~15排成一行,使得任意相邻两数之差都为质数?3.(1)能否将1 ~ 7这7个数放在一条直线上,使得任意三个相邻数的和都不大于12?(2)能否将1 ~ 7这7个数放在一个圆圈上,使得任意三个相邻数的和都不大于12?4.黑板上写着两个数9、99,现在老师请一些同学上黑板对这两个数进行操作是指把两个数都进行如下变化:或者减1,或者加3.请问:能否经过若干次操作后得到11、22?能否经过若干次操作后得到1、11?能否经过若干次操作后得到2、22?5.(1)能否用若干个图2的“L型”不重叠地拼出图1?(2)能否用若干个图3的“L型”不重叠地拼出图1?第1题1 2 3第5题。
六年级高斯学校竞赛计算综合二含答案
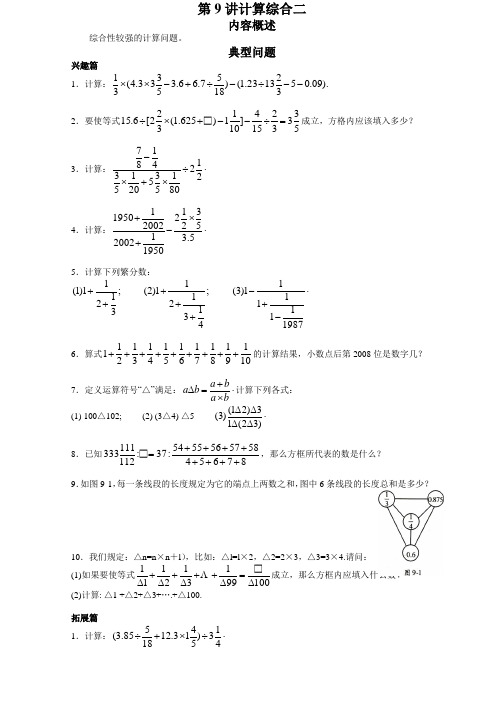
第9讲计算综合二内容概述综合性较强的计算问题。
典型问题兴趣篇1.计算:).09.05321323.1()1857.66.35333.4(31--÷-÷+-⨯⨯2.要使等式53332154]1011) □625.1(322[6.15=÷--+⨯÷成立,方格内应该填入多少?3.计算:⋅÷⨯+⨯-212805520541874.计算:⋅⨯-++5.353212195020022002119505.计算下列繁分数:;31211)1(++;431211)2(+++⋅-+-198711111)3(6.算式10191817161514131211+++++++++的计算结果,小数点后第2008位是数字几?7.定义运算符号“△”满足:⋅⨯+=∆ba ba b a 计算下列各式: (1) 100△102; (2) (3△4) △5⋅∆∆∆∆)32(13)21()3(8.已知876545857565554:37 □:112111333++++++++=,那么方框所代表的数是什么?9.如图9-1,每一条线段的长度规定为它的端点上两数之和,图中6条线段的长度总和是多少?10.我们规定:△n=n ×n +l ),比如:△l=l ×2,△2=2×3,△3=3×4.请问: (1)如果要使等式100□991312111∆=∆++∆+∆+∆ 成立,那么方框内应填入什么数? (2)计算: △1 +△2+△3+….+△100.拓展篇1.计算:⋅÷⨯+÷413)5413.1218585.3(2.计算:⋅÷÷-+⨯8721654333113612141873.计算:).19956.15.019954.01993(22.550276951922.510939519+⨯⨯÷+--+4.我们规定:符号“O ”表示选择两数中较大数的运算,例如:3.5 O 2.9= 2.9 O3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9 =2.9△3.5=2.9.请计算:⋅∆+⨯∆)25.2104235()3.0 ○31()4.0 ○384155()3323625.0(5.计算:⋅+⨯+++-++⨯++)975753357579()531135975753357579135531()531135975753357579()975753357579135531(6.算式2004)1311211111019181716151413121(⨯+++++++++++计算结果的小数点后第2004位数字是多少?7.古埃及人计算圆形面积的方法是:将直径减去直径的91,然后再平方.由此看来,古埃及人认为圆周率л等于多少?(结果精确到小数点后两位数字)8.(1)将下面这个繁分数化为最简真分数: (2)若下面的等式成立,工应该等于多少?;21314151+++⋅=+++1184112111x 9.已知符号“*”表示一种运算,它的含义是:))(1(11*A b a ab b a +++=,已知413*2=,那么:(1)A 等于多少? (2)计算⋅++++)100*99()6*5()4*3()2*1(10.已知19991100211001110001,200019991651431211++++=⨯++⨯+⨯+⨯=B A 比较A 和B 的大小,并计算出它们的差.11.根据图9-2中5个图形的变化规律,求第99个图形中所有圆圈(实心圆圈与空心圆圈)的个数.12.定义:)11()311()211()111(1nn na +⨯⨯+⨯+⨯+=(1)求出20010021,,,a a a a 的大小; (2)计算:⋅+++++10043211004321a a a a a超越篇1.⋅-++⨯----⨯2141121117331311227331393766)43322(17412.真分数27a化为小数后,如果小数点后连续2004个数字之和是8684,那么a 可能等于多少?3.定义运算“Ω”满足:304.)]1([2,1=Ω+-Ω⨯=Ω=Ωm a n a n a a a 已知②①。
第二届高思杯 六年级综合素质测评_语文试卷解析

2
三、文学常识(15 分)
10. 《凡卡》是俄国著名短篇小说家________的代表作。与其齐名的两位短篇小说巨匠是美国的欧·亨利 和法国的__________,后者主要代表作有《______》、《我的叔叔于勒》等。(6 分)
【答案】契诃夫,莫泊桑,《羊脂球》等任选一个。 【解析】本题略有难度,《凡卡》为小学课本中课文,拓展与作者契诃夫齐名的短篇小说三圣手。部 分同学将《凡卡》作者答成里面的人物茹科夫。
15. 用简洁的语言分别概括直接描写季羡林和冰心两位老人的事。(4 分) 【答案】季先生为年轻学子看行李;病魔缠身的冰心老人仍关心年老病人。 【解析】这道小题主要考察对相应段落有效信息的概括能力。主要有效信息分别在第四段和第六、七 段。季羡林和冰心两位老人的事例都比较清晰,主要是把他们所作所为用简洁的语言概括出来。
2... 下列各句中,没有错别字的一项是(4 分) A.季羡林先生对许多重大问题,他都提出过意见,只不过他很少采取怒目而视的方式,而是锦里藏针。 B.我坐在沙滩上,跳望浩渺的大海,观看着吵闹的海鸥,打量那些在海滩上寻找贝壳的孩童。 C.初春,周围的一切在闪烁、在融化,大地蒸腾起热气„„融雪炫目的反光使我不由自主地眯起眼睛。 D.世人仅以沧海一粟之身,却能领略茫茫宇宙与纷繁人世的壮丽之美,这是何等的竟界! 【答案】C 【解析】A 选项中“锦”应为“棉”。B 选项中“跳”应为“眺”。D 选项中“竟”应为“境”。
4. 下列依次在①②③处填入的词语和句子,语意和衔接都最恰当的一项是(4 分)
白莲水库是群山中的一座大型水库,最大的一条干渠通向山脚下, ① 着那里的苍生万物。
白莲水库的水是绿蓝绿蓝的, ② ,触须沿途四散, ③ 着白莲浦方圆几十里的农田。
A. ①滋养 ②流到渠里就一路变成白色的游龙 ③浸润
高斯小学奥数六年级上册含答案第01讲比赛中的推理

第一讲比赛中的推理快*布,这定我找体仟 老算抄来的比我们 高出臥进了不少球叽 駅近矗思、IT 罗.工林三所守校之间锻 行了一轮足竦骼环翌- 刚比完・小豪盛皓大 案带回* .战fti rK4rSf BL・■社KVteI■yA**kHf7n#>n这一讲我们学习的主要内容是与比赛有关的逻辑推理问题. 这些问题有各种不同的形式:有分析对阵情况的,有计算各队积分的,有利用积分排名的,甚至还有讨论进球数、失球数的•不同类型的问题我们应该用不同的方法来处理.在逻辑推理中,特别有用的方法是画示意图或表格,这种方法相信大家并不陌生,用它来分析比赛问题,能够让我们对比赛的情况更为直观明了.例题1」 ..................... …一…. ...... . .... . ........ ..编号为1、2、3、4、5、6的同学进行围棋比赛,每2个人都要赛1盘.现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号一样,那么编号为6的同学赛了几盘?「分析」为了让问题更加直观,我们可以画出一个示意图,用6个点来表示这6个同学•如果两个同学之间比赛过,则把对应的两个点用实线连起来,如果没比赛过,则用虚线连起来.A、B、C、D、E五所小学,每所小学派出1支足球队,共5支足球队进行友谊比赛•不同学校间只比赛1场,比赛进行了若干天后,A校的队长发现另外4支球队赛过的场数依次为4、3、2、1.问:这时候A校的足球队已赛过的场数?例题2———— ... —I,每天同A、B、C、D、E、F六个国家的足球队进行单循环比赛(即每队都与其他队赛一场)时在3个场地各进行一场比赛,已知第一天B对D,第二天C对E,第三天D对F,第四天B对C•那么第五天与A队比赛的是那个队?A B C D E F1D B2E C3F D4C B5「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第二列从上到下依次表示A在5天中分别遇到的对手,第三列表示B在5天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什么特点?练习五个国家足球队A、B、C、D、E进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是A与D , C轮空;第二天A与B比赛,E轮空;第三天A与E比赛;第四天A与C比赛;B与C的比赛在B与D的比赛之前进行.那么C与E在哪一天比赛?例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?时在3个场地各进行一场比赛,已知第一天B 对D ,第二天C 对E ,第三天D 对F ,第四天「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?时在3个场地各进行一场比赛,已知第一天B 对D ,第二天C 对E ,第三天D 对F ,第四天「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?时在3个场地各进行一场比赛,已知第一天B 对D ,第二天C 对E ,第三天D 对F ,第四天「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?时在3个场地各进行一场比赛,已知第一天B 对D ,第二天C 对E ,第三天D 对F ,第四天「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 4 5B C DEC BDE B CF例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同 时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?B 对C •那么第五天与A 队比赛的是那个队?A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同 时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?B 对C •那么第五天与A 队比赛的是那个队?A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同 时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?B 对C •那么第五天与A 队比赛的是那个队?A1 2 3 45 B C DEC BD E B CF「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第 二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一 天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天 C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 45 B C DEC BD EBC F 「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示 B 在 5 天中遇到的对手,依 此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与例题 2A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天 C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?B 对C •那么第五天与A 队比赛的是那个队?A 1 2 3 4 5BC DE C BD EBCF「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示 B 在 5 天中遇到的对手,依此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与例题 2C 比赛;B 与C 的比赛在B 与D 的比赛之前进行.那么 C 与E 在哪一天比赛?A 、B 、C 、D 、E 、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场) ,每天同 时在3个场地各进行一场比赛,已知第一天 B 对D ,第二天C 对E ,第三天D 对F ,第四天 「分析」题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示•如图,第二列从上到下依次表示 A 在 5 天中分别遇到的对手,第三列表示 B 在 5 天中遇到的对手,依 此类推•观察表格,这个表格的每行有几个字母?每列有几个字母?每行、每列的字母有什 么特点?练习 2五个国家足球队 A 、B 、C 、D 、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是 A 与D , C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天 A 与 B 对C •那么第五天与A 队比赛的是那个队? A1234 5 B C D E C BD E B C F。
六年级数学竞赛上册奥数高思第7讲逻辑推理二(彩色)(20200403195539)

六年级上册第7讲7逻辑推理二48身体健康逻辑推理二课本这一讲我们学习的主要内容是与比赛有关的逻辑推理问题.这些问题有各种不同的形式:有分析对阵情况的,有计算各队积分的,有利用积分排名的,甚至还有讨论进球数、失球数的.不同类型的问题我们应该用不同的方法来处理.在逻辑推理中,特别有用的方法是画示意图或表格,这种方法相信大家并不陌生,用它来分析比赛问题,能够让我们对比赛的情况更为直观明了.例题1编号为1、2、3、4、5、6的六名同学进行围棋比赛,每2个人都要赛1盘.现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号一样,那么编号为6的同学赛了几盘?分析为了让问题更加直观,我们可以画出一个示意图,用6个点来表示这6个同学.如果两个同学之间比赛过,则把对应的两个点用实线连起来,如果没比赛过,则用虚线连起来.练习1.A、B、C 三所小学,每所小学派出2支足球队,共6支足球队进行友谊比赛.同一所学校的两队之间不比赛,不同学校的每2个队间只比赛1场,比赛进行了若干天后,A 校的甲队队长发现另外5支球队赛过的场数各不相同.问:这时候 A 校甲队与 A 校乙队哪个队已赛过的场数多?例题2A、B、C、D、E、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同时在3个场地各进行一场比赛,已知第一天B 对D,第二天 C 对E,第三天 D 对F,第四天 B 对C.那么第五天与A 队比赛的是哪个队?分析题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示.如图,第二列从上到下依次表示 A 在5天中分别遇到的对手,第三列表示B 在5天中遇到的对手,依此类推.观察表格,这个表格的每行有几个字母?49身体健康六年级上册第7讲每列有几个字母?每行、每列的字母有什么特点?A B C D E F1 D B2 E C3 F D4 C B5练习2.五个国家足球队A、B、C、D、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是 A 与D,C 轮空;第二天 A 与B 比赛,E 轮空;第三天 A 与E 比赛;第四天A 与C 比赛;B 与C 的比赛在与D 的比赛之前进行.那么 C 与E 在哪一天比赛?前两个例题,我们讨论的是比赛场数与对阵情况,接下来要讨论的问题是比赛中的积分情况.例题3甲、乙、丙、丁四个同学进行象棋比赛,每两人都比赛一场,比赛规定:胜者得2分,平局各得1分,输者得0分.请问:(1)一共有多少场比赛?(2)四个人最后得分的总和是多少?(3)如果最后结果甲得第一,乙、丙并列第二,丁最后一名,那么乙得了多少分?分析(1)每两人之间都比赛一场,总比赛场数就是从四个人中挑出两人的方法数;(2)比赛的胜负情况有很多种可能,那么总分也有很多种可能吗?大家考虑一下每场比赛双方的得分之和就知道了;(3)乙、丙最后的分数一样,由于总分是固定的,这个相同的分数既不能太大,也不能太小,那么会是多少呢?50身体健康逻辑推理二课本练习3.有A、B、C、D 四支足球队进行单循环比赛,每两队都比赛一场.比赛规定:胜一场得2分,平局各得1分,负一场得0分.全部比赛结束后,A、B 两队的总分并列第一名,C 队第二名,D 队第三名, C 队最多得多少分?淘汰赛与循环赛淘汰赛:赛程相对较短,可以容纳较多的队参加.淘汰赛中,每进行一轮比赛都要淘汰一些队,在比赛中失败的队要退出比赛,再无参与比赛的机会,胜利者之间将继续进行比赛,并由获得最后胜利的队伍赢得冠军.在淘汰赛中,每个队只能与部分队进行比赛.由于各队所遇到对手的强弱不同,加之淘汰赛一场定胜负的方法使比赛产生的名次有一定的偶然性.循环赛:循环赛赛程较长,比赛中每一队轮流与其他队比赛一场(单循环)或两场(双循环),累计成绩最好的队为冠军.循环赛中每个队的对手强弱相同,因此对各参赛队最为公平,比赛名次能够较好的反映每个队的实际水平.两种赛制各有优劣,分别适用于不同情况.以足球为例,目前世界各国的足球联赛大部分采用双循环赛制,各洲杯赛一般都采用淘汰赛.而世界杯赛则采用两种赛制混合的方式,充分的扬长避短,即首先分若干小组进行循环赛,小组前几名出线后再通过淘汰赛角逐最终的冠军.例题44支足球队进行单循环比赛,即每两队之间都比赛一场. 每场比赛胜者得3分,负者得0分,平局各得1分. 比赛结束后,各队的总得分恰好是4个连续的自然数. 问:输给第一名的队的总分是多少?分析4支球队之间一共比赛了多少场?所有比赛的总分最多是多少,最少是多少?你能由此推断出各队的得分吗?练习4.甲、乙、丙、丁4个队举行足球单循环赛.规定:每场比赛胜者得3分,负者得0分,51身体健康六年级上册第7讲平局各得1分.已知:(1)比赛结束后4个队的得分都是奇数;(2)甲队总分超过其他各队,名列第一;(3)乙队恰有两场平局,并且其中一场是与丙队平局.那么丁队得了多少分?四国足球邀请赛荷兰阿姆斯特丹每年都要举办一场四国足球邀请赛,它的得分规则与我们平时所知不尽相同——胜、平、负仍分别得3、1、0分,但为了鼓励进攻,突出荷兰攻势足球的特点,同时也为了使比赛更富有激情,大赛规定每一个进球也能得1分.这样做确实提高了比赛的观赏性,因此不少人建议国际足联把现在的积分规则也改为阿姆斯特丹杯的积分规则,但每次都没有成功.这是为什么呢?提高比赛的观赏度难道不好吗?其实四国赛规则并不是无懈可击的,在这种情况下,很容易出现两队事先商量好放弃防守、一味进攻的情况.如果打出100:100的比分,那么两个队一场比赛就能得101分.进球数越是可观,由胜负决出的那三分就越可以忽略不计,甚至可能会出现三战全败的队获得总冠军的情况.(请你想一想,这种结果会在什么情况下出现?)设想一下,如果四国赛不是一场普通的邀请赛,而是一场举足轻重的大赛,那估计比赛早就会变成一个灌球大赛了!在本讲的最后,我们以两道综合较强的逻辑推理问题作结尾,一道注重极端分析,一道注重整体分析,这两种方法前的学习中已经有所涉及,这里再回顾一下,希望同学们能够重视,因为它们在各类组合问题(即逻辑推理、构造论证、最值问题等)中都是极其常用并且行之有效的方法.例题5有九个外表完全相同的小球,重量分别是1克,2克,…,9克.为了加以区分,它们都被贴上了数字标签.可是有一天,这些标签不知被哪个调皮鬼重新乱贴了一通.我们用天平做了两次称量,得到如下结果:(1)①②>③④⑤⑥⑦;(2)③⑧= ⑦.请问:⑨号小球的重量是多少?分析在条件(1)中,左边两个球竟比右边五个球还重!这两个球肯定比较重,会是怎样的两个球呢?再结合条件(2),你能知道⑨号小球有多重吗?52身体健康逻辑推理二课本练习5.有九个外表完全相同的小球,重量分别是1克,2克,…,9克.为了加以区分,它们都被贴上了数字标签.可是有一天,这些标签不知被哪个调皮鬼重新乱贴了一通.我们用天平做了三次称量,得到如下结果:(1)①>②③④;(2)⑤>⑥⑦;(3)⑧>⑨.请问:⑨号小球的重量是多少?例题6A、B、C、D、E 五位同学分别从不同的途径打听到五年级那位获得数学竞赛第一名的同学的情况:A 打听到的:姓李,是女同学,13岁,东城区;B 打听到的:姓张,是男同学,11岁,海淀区;C 打听到的:姓陈,是女同学,13岁,东城区;D 打听到的:姓黄,是男同学,1岁,西城区;E 打听到的:姓张,是男同学2岁,东城区.实际上该同学的情况在上面都出现过,而且这五位同学的消息都仅有一项正确,那么第一名的同学应该是哪个区的,今年多少岁呢?分析每个同学打听到的消息都只有一项正确,可谓相当的少!5×4=20个判断,一共才5个正确的,其中关于姓氏、性别、年龄、地区的判断各有几项是正确的呢?练习6.某商品的编号是一个三位数.现有5个三位数:874、765、123、364、925,其中每一个数与商品编号恰好有一个数字完全对得上(即位置和大小都一样,例如912与925只有百位的9对得上).那么这个三位数是多少?53身体健康六年级上册第7讲思考题A、B、C、D 四个足球队进行循环比赛,赛了若干场后,A、B、C 三队的比赛情况如下:场数胜平负进球失球A 321020B 211043C 200236D问:D 赛了几场? D 所参与的各场比赛的比分分别是什么?本讲知识点汇总一、画图、列表分析方法在逻辑推理问题中的应用.二、与比赛积分有关的推理问两种常见的计分法:1. 2分制计分法:“每场比赛胜者得2分,负者得0分,平局各得1分”.这种情况下,每场比赛无论结果如何,双方总分都是2分,因此所有参赛选手的总分就等于“比赛场数×2”.2. 3分制计分法:“每场比赛胜者得3分,负者得0分,平局各得1分”.这种情况下,总分就是“胜负场数×3+ 平局场数×2”,或者写成“比赛场数×3-平局场数”.三、极端思想与整体思想在逻辑推理问题中的应用.作业1. A、B、C、D 四支球队进行足球比赛,每两队都要比赛一场.已知A、B、C 三队的成绩分别是: A 队二胜一负, B 队二胜一平, C 队一胜二负.那么 D 队的成绩是什么?54身体健康逻辑推理二课本2.6名同学进行象棋比赛,每两人都比赛一场,比赛规定胜者得2分,平局各得1分,输者得0分.请问:(1)一共有多少场比赛?(2)6个人最后得分的总和是多少?(3)得分最高的三名同学的分数之和最多是多少?3.六个人参加乒乓球比赛,每两人之间都要比赛一场,胜者得2分,负者得0分,没有平局.比赛结束时发现,有两人并列第二名,两人并列第五名.那么第一名和第四名各得了多少分?4.足球甲 A 联赛共有12个足球俱乐部参加,实行主客场双循环赛制,即任何两队分别在主场和客场各比赛一场,胜一得3分,平一场各得1分,负一场得0分,在联赛结束后按积分的高低排出名次.,在积分榜上第一名与第二名的积分差距最多可达多少分?5.有六个外表完全相同的小球,重量分别是1克,2克,……,6克.为了加以区分,它们都被贴上了数字标签.可是有一天,不知被哪个调皮鬼重新乱贴了一通.我们用天平做了两次称量,得到如下结果:(1)①②>③④⑤⑥;(2)③④⑤= ②.请问:①号小球的重量是多少克?55身体健康。
高斯小学奥数六年级下册含答案第05讲抽屉原理

第五讲抽屉原理二本讲学问点汇总:一、最不利原则:为了保.证.能完成一件事情,需要考虑在最倒霉〔最不利〕的状况下,如何能到达目标.二、抽屉原理:形式1:把n +1个苹果放到n 个抽屉中,确定有2 个苹果放在一个抽屉里;形式2:把m⨯n +1 个苹果放到n 个抽屉中,确定有m +1个苹果放在一个抽屉里.例1.中国奥运代表团的173 名运发动到超市买饮料,超市有可乐、雪碧、芬达、橙汁、味全和矿泉水 6 种饮料,每人各买两种不同的饮料,那么至少多少人买的饮料完全一样?「分析」此题的“抽屉”是饮料的选法,“苹果”是173名运发动.练习1、中国奥运代表团的83 名运发动到超市买饮料.超市有可乐、雪碧、芬达和橙汁,每人各买两种不同的饮料,那么至少多少人买的饮料完全一样?例2.国庆嘉年华共有5 项游艺活动,每个学生至多参与2 项,至少参与1 项.那么至少有多少个学生,才能保证至少有4 个人参与的活动完全一样?「分析」此题的“抽屉”是参与活动的方法.练习2、高思运动会共有4 个工程,每个学生至多参与3 项,至少参与1 项.那么至少有多少个学生,才能保证至少有5 个人参与的活动完全一样?例3.从1 到50 这50 个自然数中,至少选出多少个数,才能保证其中确定有两个数的和是50「分析」思考一下:哪两个数的和是50?练习3、从1 到35 这35 个自然数中,至少选出多少个数才能保证其中确定有两个数的和为34?例4.从1 到100 这100 个自然数中,至少选出多少个数才能保证其中确定有两个数的和是7 的倍数?假设要保证是6 的倍数呢?「分析」两个数的和是7 的倍数,这两个数除以7 的余数要符合什么条件哪?练习4、从1 至99 这99 个自然数中任意取出一些数,要保证其中确定有两个数的和是5 的倍数,至少要取多少个?例5.至少取出多少个正整数,才能保证其中确定有两个整数的和或差是100 的倍数?「分析」从余数角度思考一下:什么样的两个数的和或差是100?例6.在边长为 2 的正六边形中,放入50 个点,任意三点不共线,请证明:确定能从中选出三个点,以它们为顶点的三角形面积不大于1.「分析」通过把正六边形均分,来构造“抽屉”.四大制造之印刷术印刷术是中国古代的四大制造之一,是中国古代汉族劳动人民经过长期实践和争论才制造的.活字印刷的方法是先制成单字的阳文反文字模,然后依据稿件把单字排列在字盘内涂墨印刷.自从汉朝制造纸以后,书写材料比起过去用的甲骨、简牍、金石和缣帛要轻松、经济多了,但是抄写书籍还是格外费工的,远远不能适应社会的需要.至迟到东汉末年的熹平年间〔公元172~178年〕,消灭了摹印和拓印石碑的方法.大约在公元600年前后的隋朝,人们从刻印章中得到启发,在人类历史上最早制造了雕版印刷术.雕版印刷是在确定厚度的平滑的木板上,粘贴上抄写工整的书稿,薄而近乎透亮的稿纸正面和木板相贴,字就成了反体,笔划清楚可辨.雕刻工人用刻刀把版面没有字迹的局部削去,就成了字体凸出的阳文,和字体凹入的碑石阴文截然不同.印刷的时候,在凸起的字体上涂上墨汁,然后把纸覆在它的上面,轻轻拂拭纸背,字迹就留在纸上了.到了宋朝,雕版印刷事业进展到全盛时期.雕版印刷对文化的传播起了重大作用,但是也存在明显缺点:第一,刻版费时费工费料;其次,大批书版存放不便;第三,有错字不简洁更正.北宋平民制造家毕昇总结了历代雕版印刷的丰富的实践阅历,经过反复试验,在宋仁宗庆历年间〔公元1041~1048〕制成了胶泥活字,实行排版印刷,完成了印刷史上一项重大的革命.毕昇的方法是这样的:用胶泥做成一个个规格全都的毛坯,在一端刻上反体单字,字划突起的高度象铜钱边缘的厚度一样,用火烧硬,成为单个的胶泥活字.为了适应排版的需要,一般常用字都备有几个甚至几十个,以备同一版内重复的时候使用.遇到不常用的冷僻字,假设事前没有预备,可以随制随用.为便于拣字,把胶泥活字按韵分类放在木格子里,贴上纸条标明.排字的时候,用一块带框的铁板作底托,上面敷一层用松脂、蜡和纸灰混合制成的药剂,然后把需要的胶泥活字拣出来一个个排进框内.排满一框就成为一版,再用火烘烤,等药剂略微熔化,用一块平板把字面压平,药剂冷却凝固后,就成为版型.印刷的时候,只要在版型上刷上墨,覆上纸,加确定的压力就行了.为了可以连续印刷,就用两块铁板,一版加刷,另一版排字,两版交替使用.印完以后,用火把药剂烤化,用手轻轻一抖,活字就可以从铁板上脱落下来,再按韵放回原来木格里,以备下次再用.毕昇还试验过木活字印刷,由于木料纹理疏密不匀,刻制困难,木活字沾水后变形,以及和药剂粘在一起不简洁分开等缘由,所以毕昇没有承受.毕昇的胶泥活字版印书方法,假设只印二三本,不算省事,假设印成百上千份,工作效率就极其可观了,不仅能够节约大量的人力物力,而且可以大大提高印刷的速度和质量,比雕版印刷要优越得多.现代的凸版铅印,虽然在设备和技术条件上是宋朝毕昇的活字印刷术所无法比较的,但是根本原理和方法是完全一样的.活字印刷术的制造,为人类文化做出了重大奉献.这中间,中国的平民制造家毕昇的功绩是不行磨灭的.可是关于毕昇的生平事迹,我们却一无所知,幸亏毕昇制造活字印刷术的事迹,比较完整地记录在北宋著名科学家沈括的名著《梦溪笔谈》里.但是除开西夏文字的几本推想为活字印刷的佛经外,中原地区无觉察活字印刷的中文印刷品!作业1.〔1〕一个班有37 个人,那么至少有多少人是同一星座的?〔2〕一副扑克牌,共54 张,那么至少从中摸出多少张牌,才能保证至少有6 张牌的花色一样?2.动物王国进展运动会,共有101 位运发动,有短跑、跳高、跳远、10 米跳台、3 米跳板五个工程,每位运发动最多项选择三个工程,最少选一个工程.那么至少有多少位运发动所选的工程都一样?3. 1 至70 这70 个自然数中,最多可以取出多少个数,使得其中每两个数的差都不等于6?4. 1 至40 这40 个自然数中,最多可以取出多少个数,使得其中每两个数的和都不是4 的倍数?5.在半径为1 的圆内,画13 个点,其中任意3 点不共线.请证明:确定存在3 个点,以它们为顶点的三角形面积小于.6第五讲抽屉原理二例7.答案:12.解答:共有C2 =15 种不同的选择方式,而173 ÷15 =11L 8 ,所以至少有12 个人买的饮料完全一样.6例8.答案:46.解答:共有C2 +C1 =15 种参与方法,所以至少15⨯3 +1 =46 人.5 5例9.答案:27.解答:可构造出26个组数:〔1,49〕、〔2,48〕、…、〔24,26〕、〔25〕、〔50〕.所以至少要取27个数才能保证取到一组和为50 的数.例10.答案:46,37.解答:由题意可知,假设取出的数没有两个数的和是7 的倍数,则:除以7 余1 的数与除以7 余6 的数不能共存,除以7 余2 的数与除以7 余5 的数不能共存,除以7 余3 的数与除以7 余4 的数不能共存.而除以7 余0 的数只能取1 个,且100 =14⨯7L 2 ,所以最不利的状况是取尽余1、余2、余3 和一个余0 的数,共45 个数,所以至少选出46 个数才可满足要求.同理至少选出37 个数才能保证是6 的倍数.〔留意此时除以6余3和余0的数都只能选1个〕例11.答案:52.解答:可构造出51个组数:〔1,8〕、〔2,9〕…〔7,14〕;〔15,22〕、〔16,23〕…〔21,28〕;……〔85,92〕、〔86,93〕…〔91,98〕;〔99〕、〔100〕.每组数中的两数的差为7.只取出每个数组中较小的数明显不能满足要求,所以至少要取出52 个数,这时由抽屉原理知必定能取到某一个数组的两个数.例12.解答:先将正六边形分割成6 个边长为2 的正三角形,再将每个三角形等分成4 个边长为1 的正三角形,这样就把正六边形分割成24 个边长为1 的正三角形,则由抽屉原理知,必有3 点在一个等边三角形中,以它们为顶点的三角形面积明显不大于1.〔边长是1的等边三角形面积小于1〕练习1、答案:14.简答:共有C 2=6 种不同的选择方式,而83 =6 ⨯13 +5 ,所以至少有14个人买的饮料完全一样.4练习2、答案:57.简答:共有C3+C 2+C1=14 种参与方法,所以至少14 ⨯4 +1 =57 人.4 4 4练习3、答案:20.简答:可构造出19个组数:〔1,33〕、〔2,32〕、…、〔16,18〕、〔17〕、〔34〕、〔35〕.所以至少要取20 个数才能保证取到一组和为34 的数.练习4、答案:42.简答:1~99 这99 个数中除以5 余1 的有20 个,余2 的有20 个,余3 的有20 个,余4 的有20 个,余0 的有19 个,选出余 1 和余 2 的数,再选一个余0 的数,再任选一个数确定符合题意,20 +20 +1+1 =42 个.作业6. 答案:〔1〕4 个;〔2〕23 张.简答:〔1〕抽屉原理;〔2〕最不利原则.7. 答案:5 位.简答:首先运发动的工程有C1 +C 2+C3 = 25 种可能,依据抽屉原理,至少有5 位运发动的工程一样.5 5 58. 答案:36 个.简答:每12 个数中最多取出6 个.9. 答案:12 个.简答:将1~40 依据除以4 的余数分为四组:A 组:{1,5,…,37};B 组:{2,6,…,38};C 组:{3,7,…,39};D 组:{4,8,…,40}.首先,B、D 组最多取一个.取了A 组就不能取C 组.所以最多能取12 个.10. 证明:将半径为1 的圆六等分,分为六个扇形,每个扇形的面积是π6.依据抽屉原理,至少有三个点在同一局部中,这三个点组成的三角形不会大于所在的扇形,即π.6。
六年级数学竞赛上册奥数高思第7讲逻辑推理二(彩色)

六年级数学竞赛上册奥数高思第7讲逻辑推理二(彩色)上册第7讲逻辑推理二48逻辑推理二这一讲我们学习的主要内容是与比赛有关的逻辑推理问题.这些问题有各种不同的形式:有分析对阵情况的,有计算各队积分的,有利用积分排名的,甚至还有讨论进球数、失球数的.不同类型的问题我们应该用不同的方法来处理.在逻辑推理中,特别有用的方法是画示意图或表格,这种方法相信大家并不陌生,用它来分析比赛问题,能够让我们对比赛的情况更为直观明了.编号为1、2、3、4、5、6的六名同学进行围棋比赛,每2个人都要赛1盘.现在编号为1、2、3、4、5的同学已经赛过的盘数和他们的编号一样,那么编号为6的同学赛了几盘?分析为了让问题更加直观,我们可以画出一个示意图,用6个点来表示这6个同学.如果两个同学之间比赛过,则把对应的两个点用实线连起来,如果没比赛过,则用虚线连起来.1.A、B、C 三所小学,每所小学派出2支足球队,共6支足球队进行友谊比赛.同一所学校的两队之间不比赛,不同学校的每2个队间只比赛1场,比赛进行了若干天后,A 校的甲队队长发现另外5支球队赛过的场数各不相同.问:这时候A 校甲队与A 校乙队哪个队已赛过的场数多?A、B、C、D、E、F 六个国家的足球队进行单循环比赛(即每队都与其他队赛一场),每天同时在3个场地各进行一场比赛,已知第一天B 对D,第二天C 对E,第三天D 对F,第四天B 对C.那么第五天与A 队比赛的是哪个队?分析题目的条件比较多,如何才能看清楚呢?我们可以用下面的表格来表示.如图,第二列从上到下依次表示A 在5天中分别遇到的对手,第三列表示B 在5天中遇到的对手,依此类推.观察表格,这个表格的每行有几个字母?49上册第7讲每列有几个字母?每行、每列的字母有什么特点?A B C D E F1 D B2 E C3 F D4 C B52.五个国家足球队A、B、C、D、E 进行单循环比赛,每天进行两场比赛,一队轮空.已知第一天比赛的是A 与D,C 轮空;第二天A 与B 比赛,E 轮空;第三天A 与E 比赛;第四天A 与C 比赛;B 与C 的比赛在与D 的比赛之前进行.那么C 与E 在哪一天比赛?前两个例题,我们讨论的是比赛场数与对阵情况,接下来要讨论的问题是比赛中的积分情况.甲、乙、丙、丁四个同学进行象棋比赛,每两人都比赛一场,比赛规定:胜者得2分,平局各得1分,输者得0分.请问:(1)一共有多少场比赛?(2)四个人最后得分的总和是多少?(3)如果最后结果甲得第一,乙、丙并列第二,丁最后一名,那么乙得了多少分?分析(1)每两人之间都比赛一场,总比赛场数就是从四个人中挑出两人的方法数;(2)比赛的胜负情况有很多种可能,那么总分也有很多种可能吗?大家考虑一下每场比赛双方的得分之和就知道了;(3)乙、丙最后的分数一样,由于总分是固定的,这个相同的分数既不能太大,也不能太小,那么会是多少呢?50逻辑推理二3.有A、B、C、D 四支足球队进行单循环比赛,每两队都比赛一场.比赛规定:胜一场得2分,平局各得1分,负一场得0分.全部比赛结束后,A、B 两队的总分并列第一名,C 队第二名,D 队第三名,C 队最多得多少分?淘汰赛与循环赛淘汰赛:赛程相对较短,可以容纳较多的队参加.淘汰赛中,每进行一轮比赛都要淘汰一些队,在比赛中失败的队要退出比赛,再无参与比赛的机会,胜利者之间将继续进行比赛,并由获得最后胜利的队伍赢得冠军.在淘汰赛中,每个队只能与部分队进行比赛.由于各队所遇到对手的强弱不同,加之淘汰赛一场定胜负的方法使比赛产生的名次有一定的偶然性.循环赛:循环赛赛程较长,比赛中每一队轮流与其他队比赛一场(单循环)或两场(双循环),累计成绩最好的队为冠军.循环赛中每个队的对手强弱相同,因此对各参赛队最为公平,比赛名次能够较好的反映每个队的实际水平.两种赛制各有优劣,分别适用于不同情况.以足球为例,目前世界各国的足球联赛大部分采用双循环赛制,各洲杯赛一般都采用淘汰赛.而世界杯赛则采用两种赛制混合的方式,充分的扬长避短,即首先分若干小组进行循环赛,小组前几名出线后再通过淘汰赛角逐最终的冠军.4支足球队进行单循环比赛,即每两队之间都比赛一场. 每场比赛胜者得3分,负者得0分,平局各得1分. 比赛结束后,各队的总得分恰好是4个连续的自然数. 问:输给第一名的队的总分是多少?分析4支球队之间一共比赛了多少场?所有比赛的总分最多是多少,最少是多少?你能由此推断出各队的得分吗?4.甲、乙、丙、丁4个队举行足球单循环赛.规定:每场比赛胜者得3分,负者得0分,51上册第7讲平局各得1分.已知:(1)比赛结束后4个队的得分都是奇数;(2)甲队总分超过其他各队,名列第一;(3)乙队恰有两场平局,并且其中一场是与丙队平局.那么丁队得了多少分?四国足球邀请赛荷兰阿姆斯特丹每年都要举办一场四国足球邀请赛,它的得分规则与我们平时所知不尽相同——胜、平、负仍分别得3、1、0分,但为了鼓励进攻,突出荷兰攻势足球的特点,同时也为了使比赛更富有激情,大赛规定每一个进球也能得1分.这样做确实提高了比赛的观赏性,因此不少人建议国际足联把现在的积分规则也改为阿姆斯特丹杯的积分规则,但每次都没有成功.这是为什么呢?提高比赛的观赏度难道不好吗?其实四国赛规则并不是无懈可击的,在这种情况下,很容易出现两队事先商量好放弃防守、一味进攻的情况.如果打出100:100的比分,那么两个队一场比赛就能得101分.进球数越是可观,由胜负决出的那三分就越可以忽略不计,甚至可能会出现三战全败的队获得总冠军的情况.(请你想一想,这种结果会在什么情况下出现?)设想一下,如果四国赛不是一场普通的邀请赛,而是一场举足轻重的大赛,那估计比赛早就会变成一个灌球大赛了!在本讲的最后,我们以两道综合较强的逻辑推理问题作结尾,一道注重极端分析,一道注重整体分析,这两种方法前的学习中已经有所涉及,这里再回顾一下,希望同学们能够重视,因为它们在各类组合问题(即逻辑推理、构造论证、最值问题等)中都是极其常用并且行之有效的方法.有九个外表完全相同的小球,重量分别是1克,2克,…,9克.为了加以区分,它们都被贴上了数字标签.可是有一天,这些标签不知被哪个调皮鬼重新乱贴了一通.我们用天平做了两次称量,得到如下结果:(1)①②>③④⑤⑥⑦;(2)③⑧= ⑦.请问:⑨号小球的重量是多少?分析在条件(1)中,左边两个球竟比右边五个球还重!这两个球肯定比较重,会是怎样的两个球呢?再结合条件(2),你能知道⑨号小球有多重吗?52逻辑推理二5.有九个外表完全相同的小球,重量分别是1克,2克,…,9克.为了加以区分,它们都被贴上了数字标签.可是有一天,这些标签不知被哪个调皮鬼重新乱贴了一通.我们用天平做了三次称量,得到如下结果:(1)①>②③④;(2)⑤>⑥⑦;(3)⑧>⑨.请问:⑨号小球的重量是多少?A、B、C、D、E 五位同学分别从不同的途径打听到五年级那位获得数学竞赛第一名的同学的情况:A 打听到的:姓李,是女同学,13岁,东城区;B 打听到的:姓张,是男同学,11岁,海淀区;C 打听到的:姓陈,是女同学,13岁,东城区;D 打听到的:姓黄,是男同学,1岁,西城区;E 打听到的:姓张,是男同学2岁,东城区.实际上该同学的情况在上面都出现过,而且这五位同学的消息都仅有一项正确,那么第一名的同学应该是哪个区的,今年多少岁呢?分析每个同学打听到的消息都只有一项正确,可谓相当的少!5×4=20个判断,一共才5个正确的,其中关于姓氏、性别、年龄、地区的判断各有几项是正确的呢?6.某商品的编号是一个三位数.现有5个三位数:874、765、123、364、925,其中每一个数与商品编号恰好有一个数字完全对得上(即位置和大小都一样,例如912与925只有百位的9对得上).那么这个三位数是多少?53上册第7讲思考题A、B、C、D 四个足球队进行循环比赛,赛了若干场后,A、B、C 三队的比赛情况如下:场数胜平负进球失球A 321020B 211043C 200236D问:D 赛了几场?D 所参与的各场比赛的比分分别是什么?一、画图、列表分析方法在逻辑推理问题中的应用.二、与比赛积分有关的推理问两种常见的计分法:1. 2分制计分法:“每场比赛胜者得2分,负者得0分,平局各得1分”.这种情况下,每场比赛无论结果如何,双方总分都是2分,因此所有参赛选手的总分就等于“比赛场数×2”.2. 3分制计分法:“每场比赛胜者得3分,负者得0分,平局各得1分”.这种情况下,总分就是“胜负场数×3+ 平局场数×2”,或者写成“比赛场数×3?平局场数”.三、极端思想与整体思想在逻辑推理问题中的应用.1. A、B、C、D 四支球队进行足球比赛,每两队都要比赛一场.已知A、B、C 三队的成绩分别是:A 队二胜一负,B 队二胜一平,C 队一胜二负.那么D 队的成绩是什么?54逻辑推理二2.6名同学进行象棋比赛,每两人都比赛一场,比赛规定胜者得2分,平局各得1分,输者得0分.请问:(1)一共有多少场比赛?(2)6个人最后得分的总和是多少?(3)得分最高的三名同学的分数之和最多是多少?3.六个人参加乒乓球比赛,每两人之间都要比赛一场,胜者得2分,负者得0分,没有平局.比赛结束时发现,有两人并列第二名,两人并列第五名.那么第一名和第四名各得了多少分?4.足球甲A 联赛共有12个足球俱乐部参加,实行主客场双循环赛制,即任何两队分别在主场和客场各比赛一场,胜一得3分,平一场各得1分,负一场得0分,在联赛结束后按积分的高低排出名次.,在积分榜上第一名与第二名的积分差距最多可达多少分?5.有六个外表完全相同的小球,重量分别是1克,2克,……,6克.为了加以区分,它们都被贴上了数字标签.可是有一天,不知被哪个调皮鬼重新乱贴了一通.我们用天平做了两次称量,得到如下结果:(1)①②>③④⑤⑥;(2)③④⑤= ②.请问:①号小球的重量是多少克?55。
6年级奥数构造与论证问题(下)例题解析

【内容概述】组合证明题,在论证中,有时需进行分类讨论,有时则要着眼于极端情形,或从整体把握.若干点及连接它们的一些线段组成图,与此相关的题目称为图论问题,这里宜从特殊的点或线着手进行分析.各种以染色为内容,或通过染色求解的组合问题,基本的染色方式有相间染色与条形染色.【例题】1.某学校的学生中,没有一个学生读过学校图书馆的所有图书,又知道图书馆内任何两本书都至少被一个同学都读过.问:能否找到两个学生甲、乙和三本书A,B,C,使得甲读过A,B,没读过C,乙读过B,C,没读过A?说明判断过程.[分析与解]首先从读书数最多的学生中找一人甲.由题设,甲至少有一本书C未读过.设B是甲读过的书中一本,由题意知,可找到学生乙,乙读过B、C.由于甲是读书数最多的学生之一,乙读书数不能超过甲的读书数,而乙读过C书.甲未读过C书,所以甲一定读过一本书A,乙没读过A书,否则乙就比甲至少多读过一本书,这样一来,甲读过A、B,未读过C;乙读过B、C 未读过A.因此可以找到满足要求的两个学生.2.甲、乙、丙三个班人数相同,在班级之间举行象棋比赛.各班同学都按l,2,3,4,…依次编号.当两个班比赛时,具有相同编号的同学在同一台对垒.在甲、乙两班比赛时,有15台是男、女生对垒;在乙、丙班比赛时,有9台是男、女生对垒.试说明在甲、丙班比赛时,男、女生对垒的台数不会超过24.并指出在什么情况下,正好是24?[分析与解]不妨设甲、乙比赛时,1~15号是男女对垒,乙、丙对赛时,在1~15号中有a台男女对垒,15号之后有(9-a)台男女对垒(0≤a≤9)甲、丙比赛时,前15号,男女对垒的台数时15-a(如果1号乙与1号丙是男女对垒,那么1号甲与1号丙就不是男女对垒),15号之后,有(9-a)台男女对垒.所以甲、丙比赛是,男女对垒的台数为(15-a)+(9-a)=24-2a≤24.仅在a=0,即必须乙、丙比赛时男、女对垒的号码,与甲、乙比赛时男、女对垒的号码完全不同,甲、丙比赛时,男、女对垒的台数才等于24.3.将5×9的长方形分成10个边长为整数的长方形.证明:无论怎样分法,分得的长方形中必有两个是完全相同的.[分析与解]10个边长为整数的长方形,其面积显然也均是正整数.划分出的长方形按面积从小到大为:1×1,1×2,1×3,1×4,2×2,1×5,1×6,2×3,1×7,1×8,2×4,1×9,3×3,2×5,2×6,3×4,2×7,3×5,2×8,4×4,2×9,3×6,……从这些长方形中选出10个不同的长方形,其面积和最小为:1×1+1×2+1×3+1×4+2×2+1×5+1×6+2×3+1×7+1×8=46,而原长方形的面积为5×9=45<46,所以分出的长方形必定有某两个是完全一样的.在8×8的棋盘上至少要取出多少个边长为整数的正方形,才能保证使取出的正方形中有两类图形的个数不小于2?4.将15×15的正方形方格表的每个格涂上红色、蓝色或绿色.证明:至少可以找到两行,这两行中某一种颜色的格数相同.[分析与解]如果找不到两行的某种颜色数一样,那么就是说所有颜色的列与列之间的数目不同.那么红色最少也会占:0+1+2+…+14=105个格子.同样蓝色和绿色也是,这样就必须有至少:3×(0+1+2+…+14)=315个格子.但是,现在只有15×15=225个格子,所以和条件违背,假设不成立,结论得证.能否在8×8的棋盘上每个空格内分别填入一个数字,1,2或3,使每行每列及两条对角线上的各个数字之和互不相同?请说明理由;5.有9位数学家,每人至多能讲3种语言,每3个人中至少有2个人有共通的语言.求证:在这些数学家中至少有3人能用同一种语言交谈.[分析与解]假设任意三位科学家都没有共同会的语言,这表明每种语言至多有两人会说.记这九位科学家为A、B、C、D、E、F、G、H、I.由于一位科学家最多会三种语言,而每种语言至多有两人会说,所以一位科学家至多能和另外三人通话,即至少与五人语言不通.不妨设A不能与B,C,D,E,F 通话.同理,B也至多能和三人通话,因此在C,D,E,F中至少有一人与B语言不通,设为C.则A、B、C三人中任意两人都没有共同语言,与题意矛盾.这表明假设不成立.6.4个人聚会,每人各带了2件礼品,分赠给其余3个人中的2人.试证明:至少有2对人,每对人是互赠过礼品的.[分析与解]将这四个人用4个点表示,如果两个人之间送过礼,就在两点之间连一条线.由于每人送出2件礼物,图中共有(4×2=)8条线,由于每人礼品都分增给2个人,所以每两点之间至多有(1+1=)2条线.四点间,每两点连一条线,一共6条线,现在有8条线,说明必有两点之间连了2条线,还有另外两点(有一点可以与前面的点相同)之间也连了2条线.即为所证结论.有5个人站成一周,每人手里有一只玩具手枪和3发子弹,每个人都可以向圆周上的其他三人各开一枪,试证明:至少有5对人是相互开过枪的。
高斯小学奥数六年级上册含答案第24讲 构造论证

第二十四讲构造论证二例1. (1)把1、2、3、…、8、9按合适的顺序填在图中第二行的空格中,使得每两个上、下对齐的数之和都是平方数.(2)能否将1、2、3、…、10、11按合适的顺序填在图中第二行的空格中,使得每两个上、下对齐的数之和都是平方数?若不能请说明理由. 「分析」(1)首先判断由1到9可以凑成的平方数的范围,然后逐一计算一下哪些数一起可以凑成平方数,从情况唯一或较少的数字填起;(2)分析方法同上一问,注意是否一定能填出.练习1、把1、2、…、13、14按合适的顺序填在图中第二行的空格中,使得每列的两个数之和都是平方数.例2. (1)能否将1至15排成一行,使得任意相邻两数之和都为平方数?(2)能否将1至15排成一行,使得任意相邻两数之和都为质数?「分析」(1)对于1~15的每一数来说,能都凑成平方数的情况并不多,我们就可以从这里入手分析,同学们尝试一下看能不能得到一种合适的方案.(2)注意到除了2以外,质数只能是奇数,那我们是不是能从奇偶性的分析入手呢?练习2、能否将1至41排成一行,使得任意相邻两数之和都为质数?例3.有3堆石子,每次可以从这三堆中同时拿走相同数目的石子(每次这个数目可以改变),也可以由一堆中取一半石子放入另外任一堆石子中.请问:(1)如果开始时,3堆石子的数目分别是34、55、82,按上述操作,能否把3堆石子都拿光?(2)如果开始时,3堆石子的数目分别是80、60、50,按上述操作,能否把3堆石子都拿光?如果可以,请设计一种取石子的方案;如果不可以,请说明理由.「分析」每次从这三堆中同时拿走相同数目的石子意味着每次拿走的石子数是3的倍数,所以,我们可以从石子总数这个角度分析这道题目.练习3、有4堆石子,每次可以从这四堆中同时拿走1个石子;也可以从任一堆中取出3个石子,另三堆各放1个.如果开始时,4堆石子的数目分别是14、25、32、44,能否把4堆石子都拿光?例4.黑板上写着3个数8,18,28,老师现在请一些同学上黑板对这3个数进行操作.进行一次操作是指:一些数减1,其它数加2;或者都减1;或者都加2.那么能否经过若干次操作后得到6,7,8?能否经过若干次操作后得到8,8,8?「分析」这道题可以从三个数中任意两数除以3的余数角度去分析.练习4、黑板上写着3个数9、18、27,老师现在请一些同学上黑板对这3个数进行操作.进行一次操作是指:把3个数进行如下变化,一些数减1、其它数加2;或者都减1;或者都加2.请问:能否经过若干次操作后得到11,12,13?能否经过若干次操作后得到8,8,8?例5.图中是把一张6×6的方格纸去掉两个角所得的图形.Array(1)请把所有的格子涂上红、蓝两色之一,使得每个1×2小长方形(不论横竖)的2个方格中都恰有1个红格和1个蓝格;(2)能否用1×2的小长方形恰好拼满这张表格?「分析」本题可以采用“染色法”进行分析.例6.(1)能否用16个如图所示的“T 型”拼成一个的棋盘? (2)能否用8个“T 型”和8个“L 型”拼成一个的棋盘?「分析」碰到这样的问题,我们首先要考虑的是能不能填出,而不是一上来就去试,这时就需要我们进行染色分析了,同学们可以先尝试一下黑白相间染色,论述一下是否成立?如果成立,那就需要找到一种合适的拼法.88⨯ 88⨯阿兹台克文明根据传说,阿兹台克人的祖先是从北方一个叫阿兹特兰的地方来的,他们根据太阳神威齐洛波契特里的指示往南来到阿纳瓦克谷的特斯科科湖;当他们来到湖中央的岛屿时,他们看到一只叼着蛇的老鹰停歇在仙人掌上,这个意像告诉他们应该在这里建造城市.1325年阿兹台克人在这个地方建立了特诺奇提特兰,一座巨大的人工岛,现在墨西哥城的中心.阿兹台克人原属纳瓦语系发展水平较低的一个部落,后来因吸收、融合这个地区其他印第安优秀文化传统而迅速崛起.公元11~12世纪间,从北部迁入墨西哥中央谷地,1325年在特斯科科湖西部岛上建造特诺奇蒂特兰城.1426年,阿兹台克同特斯科科、特拉科潘结成了“阿兹台克联盟”,由阿兹台克国王伊兹科亚特尔任首领,势力日盛,在谷地建立了霸主地位.继承人蒙特祖马一世及其后的国王不断对外用兵,开疆拓土,至16世纪初,其疆域东西两面已抵墨西哥湾和太平洋沿岸,北与契契梅克为邻,南至今日之危地马拉,人口约300万,发展到极盛时期.1519年,西班牙殖民者埃尔南·科尔特斯利用印第安人内部矛盾,进攻阿兹台克国,蒙特苏马二世在入侵者面前动摇不定,最后成为西班牙殖民者的傀儡.1520年6月向人民劝降时被群众击伤而死.科尔特斯在所谓“悲惨之夜”侥幸逃命后,又于1521年卷土重来,阿兹台克人在新国王夸乌特莫克率领下,与围城的西班牙殖民者展开殊死搏斗,最后由于粮食和水源断绝,加之天花肆虐而失败.1521年8月,西班牙人占领特诺奇蒂特兰,在城中大肆屠杀,并将该城彻底毁坏,后在其废墟上建立墨西哥城.阿兹台克文明在发展过程中,吸收了托尔特克文化和玛雅文明的许多成就,但自己也有独创.其文字仍属图画文字,但已含有象形文字成分.天文历法方面,使用太阳历与圣年历,已知一年为365天,每逢闰年补加一天.医学方面,知道利用各种草药治病,并已使用土法麻醉.阿兹台克人的陶器和绘画均极精致,建筑和艺术也达到相当高的水平.首都特诺奇蒂特兰的公共建筑物多以白石砌成,十分宏丽壮观.一般房屋的周围,在固定在水面的木排上种植花草,形成水上田园.城中心的主庙基部长100米、宽90米,四周有雉堞围墙环绕,塔顶建有供奉主神威济洛波特利和雨神特拉洛克的神殿,其祭坛周围有蛇头石雕,坛下发现的重达10吨的大石上,刻有被肢解的月亮女神图案,1790年在墨西哥城中心广场发现的“第五太阳石”直径近4米,重约120吨,刻有阿兹台克宗教传说中创世以来四个时代的图像,代表了阿兹台克人石雕艺术的高度水平.阿兹台克人是优秀的建筑师.首府特诺奇蒂特兰是一座岛城,有3条宽达10米的石堤与湖外陆地相通,石堤每隔一定距离就留一横渠,渠上架设吊桥,可随时收放,以防外敌入侵.城内建有宫殿、神庙、官邸、学校,建筑宏伟,最大一座金字塔台庙其规模甚至可与古埃及的媲美.为了满足城市稠密人口对粮食的需要,在湖泊中建造了独特的“水上园地”,以扩大种植面积.岛城四面环水,市内河道纵横,景色富丽,殖民者为之倾倒,惊呼为“世界花园”.阿兹台克人主要生产工具仍为石器,多由黑曜岩制成,但已会制造铜、金物品.作业1.桌上放有5枚硬币,正面朝上,第一次翻动1枚,第二次翻动其中的2枚,第三次翻动其中的3枚,第四次翻动其中的4枚,第五次翻动其中的5枚.能否恰当地选择每次翻动的硬币,使得最后桌上所有的硬币都正面朝下?2.把1、2、3、…、13按合适的顺序填在图中第二行的空格中,使得每列两个数字之和都是平方数.3.《三国英雄传》共有10篇故事,这些故事占的篇幅从2页到11页各不相同.如果从书的第1页开始印第一个故事,每一个故事总是从新的一页开始印,那么故事从奇数页起头的最多有多少篇,最少有多少篇?4.能否将1至12排成一行,使得任意相邻两数之和都为质数?5.能否将1~13排成一行,使得任意相邻两数之和都为平方数?如果可以的话请给出一种排列方式,如果不能请说明理由.第二十四讲 构造论证二例7. 答案:(1)如下图,(2)不能详解:(1)略;(2)配成的平方数只有4、9、16三种可能,11只能和5配对,而4也只能和5配对,所以没有满足要求的填法.例8. 答案:(1)9、7、2、14、11、5、4、12、13、3、6、10、15、1、8;(2)1、2、3、14、5、12、7、10、9、8、11、6、13、4、15 详解:(2)奇数与奇数不能相邻,所以需要有7个偶数把它们分开. 例9.答案:(1)能,(2)不能 详解:(1)可以按如下操作:(34,55,82)→(0,21,48)→(24,21,24)→(4,1,4)→(2,3,4)→(0,1,2)→(1,1,1)→(0,0,0);(2)本题中三堆石子数目和要是3的倍数,190不是3的倍数,所以,不能. 例10. 答案:(1)能;(2)不能 详解:(1)可以按如下操作:(8,18,28)→(0,10,20)→(6,7,17)→(8,9,16)→(7,8,15)→(6,7,14)→(6,7,8);(2)所有操作不能改变三个数的两两之差被3除的余数大小.例11. 答案:(1)如图,白框涂红、黑框涂蓝;(2)不能 详解:(2)1×2的小长方形每次恰覆盖1个红格和1个蓝格,而由(1)可知红格与蓝格的数目不相等.例12. 答案:能,能 详解:方法同上.练习:练习1、答案:如下图练习2、答案:能简答:如下:1、40、3、38、5、…、37、4、39、2、41.练习3、答案:不能简答:总数不是4的倍数.练习4、答案:不能;能简答:(1)所有操作不能改变三个数的两两之差被3除的余数大小(2)可以实现,方法不唯一.作业1.答案:能简答:第一次翻动第一枚,第二次翻动第一、二枚,第三次翻动第三、四、五枚,第四次翻动第二、三、四、五枚,第五次全部翻动.2.答案:如下表3.答案:8;3简答:2~11页,只考虑页数总和的奇偶不考虑数值,最多可以是偶、偶、偶、偶、偶、奇、奇、奇、奇、奇,其中以奇数页开始的是8篇,改变顺序即可得出最少为3篇.4.答案:能简答:如下:11、12、1、2、3、4、7、6、5、8、9、10.5.答案:不能简答:9只能和7相邻,10只能和6相邻,11只能和5相邻,所以这3个数必须放在两端,显然无法满足.。
小学六年级奥数系列讲座构造与论证含复习资料解析

构造与论证1内容概述各种探讨给定要求能否实现,设计最佳安排和选择方案的组合问题.这里的最佳通常指某个量达到最大或最小.解题时,既要构造出取得最值的具体实例,又要对此方案的最优性进行论证.论证中的常用手段包括抽屉原则、整除性分析和不等式估计.典型问题2.有3堆小石子,每次允许进行如下操作:从每堆中取走同样数目的小石子,或是将其中的某一石子数是偶数的堆中的一半石子移入另外的一堆.开始时,第一堆有1989块石子,第二堆有989块石子,第三堆有89块石子.问能否做到:(1)某2堆石子全部取光(2)3堆中的所有石子都被取走【分析与解】 (1)可以,如(1989,989,89) →(1900,900,0)→(950,900,950)→(50,0,50)→(25,25,50)→(O,0,25).(2)因为操作就两种,每堆取走同样数目的小石子,将有偶数堆石子堆中一半移至另一堆,所以每次操作石子总数要么减少3的倍数,要么不变.现在共有1989+989+89=3067,不是3的倍数,所以不能将3堆中所有石子都取走.4.在某市举行的一次乒乓球邀请赛上,有3名专业选手与3名业余选手参加.比赛采用单循环方式进行,就是说每两名选手都要比赛一场.为公平起见,用以下方法记分:开赛前每位选手各有10分作为底分,每赛一场,胜者加分,负者扣分,每胜专业选手一场加2分,每胜业余选手一场加1分;专业选手每负一场扣2分,业余选手每负一场扣1分.问:一位业余选手最少要胜几场,才能确保他的得分比某位专业选手高【分析与解】当一位业余选手胜2场时,如果只胜了另两位业余选手,则他得10+2-3=9(分).此时,如果专业选手间的比赛均为一胜一负,而专业选手与业余选手比赛全胜,则每位专业选手的得分都是10+2-2+3=13(分).所以,一位业余选手胜2场,不能确保他的得分比某位专业选手高.当一位业余选手胜3场时,得分最少时是胜两位业余选手,胜一位专业选手,得10+2+2-2=12(分).此时,三位专业选手最多共得30+0+4=34(分),其中专业选手之间的三场比赛共得0分,专业选手与业余选手的比赛最多共得4分.由三个人得34分,34÷3=1113,推知,必有人得分不超过11分.也就是说,一位业余选手胜3场,能确保他的得分比某位专业选手高.6.如图35-1,将1,2,3,4,5,6,7,8,9,10这10个数分别填入图中的10个圆圈内,使任意连续相邻的5个圆圈内的各数之和均不大于某个整数M.求M的最小值并完成你的填图.【分析与解】要使M最小,就要尽量平均的填写,因为如果有的连续5个圆圈内的数特别小,有的特别大,则M就只能大于等于特别大的数,不能达到尽量小的目的.因为每个圆圈内的数都用了5次,所以10次的和为5×(1+2+3+…+10)=275.每次和都小于等于朋,所以IOM大于等于275,整数M大于28.下面来验证M=28时是否成立,注意到圆圈内全部数的总和是55,所以一定是一边五个的和是28,一边是27.因为数字都不一样,所以和28一定是相间排列,和27也是相问排列,也就是说数组每隔4个差值为l,这样从1填起,容易排出适当的填图.8.1998名运动员的号码依次为1至1998的自然数.现在要从中选出若干名运动员参加仪仗队,使得剩下的运动员中没有一个人的号码等于另外两人的号码的乘积.则,选为仪仗队的运动员最少有多少人【分析与解】我们很自然的想到把用得比较多的乘数去掉,因为它们参与的乘式比较多,把它们去掉有助于使剩下的构不成乘式,比较小的数一定是用得最多的,因为它们的倍数最多,所以考虑先把它们去掉,但关键是除到何处考虑到44的平方为1936,所以去到44就够了,因为如果剩下的构成了乘式,则乘式中最小的数一定小于等于44,所以可以保证剩下的构不成乘式.因为对结果没有影响,所以可以将1保留,于是去掉2,3,4,…,44这43个数.但是,是不是去掉43个数为最小的方法呢构造2×97,3×96,4×95,…,44×45,发现这43组数全不相同而且结果都比1998小,所以要去掉这些乘式就至少要去掉43个数,所以43位最小值,即为所求.10.在10×19方格表的每个方格内,写上0或1,然后算出每行及每列的各数之和.问最多能得到多少个不同的和数【分析与解】首先每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个.下面我们说明如果0出现,则必然有另外一个数字不能出现.如果0出现在行的和中,说明有1行全是0,意味着列的和中至多出现0到9,加上行的和至多出现10个数字,所以少了一种可能.如果0出现在列的和中,说明在行的和中19不可能出现,所以0出现就意味着另一个数字不能出现,所以至多是19,下面给出一种排出方法.12.在1000×1000的方格表中任意选取n个方格染为红色,都存在3个红色方格,它们的中心构成一个直角三角形的顶点.求n的最小值.【分析与解】首先确定1998不行.反例如下:其次1999可能是可以的,因为首先从行看,1999个红点分布在1000行中,一定有一些行含有2个或者以上的红点,因为含有0或1个红点的行最多999个,所以其他行含有红点一定大于等于1999-999=1000,如果是大于1000,则根据抽屉原理,一定有两个这样红点在一列,则就会出现红色三角形;如果是等于1000而没有这样的2个红点在一列,说明有999行只含有1个红点,而剩下的一行全是红点,那也一定已经出现直角三角形了,所以n的最小值为1999.14.在图35-2中有16个黑点,它们排成了一个4×4的方阵.用线段连接其中4点,就可以画出各种不同的正方形.现在要去掉某些点,使得其中任意4点都不能连成正方形,则最少要去掉多少个点【分析与解】至少要除去6个点,如下所示为几种方法:构造与论证2内容概述组合证明题,在论证中,有时需进行分类讨论,有时则要着眼于极端情形,或从整体把握.若干点及连接它们的一些线段组成图,与此相关的题目称为图论问题,这里宜从特殊的点或线着手进行分析.各种以染色为内容,或通过染色求解的组合问题,基本的染色方式有相间染色与条形染色.典型问题2.甲、乙、丙三个班人数相同,在班级之间举行象棋比赛.各班同学都按l,2,3,4,…依次编号.当两个班比赛时,具有相同编号的同学在同一台对垒.在甲、乙两班比赛时,有15台是男、女生对垒;在乙、丙班比赛时,有9台是男、女生对垒.试说明在甲、丙班比赛时,男、女生对垒的台数不会超过24.并指出在什么情况下,正好是24 ?【分析与解】不妨设甲、乙比赛时,1~15号是男女对垒,乙、丙比赛时.在1~15号中有a台男女对垒,15号之后有9-a台男女对垒(0≤a≤9)甲、丙比赛时,前15号,男女对垒的台数是15-a(如果1号乙与1号丙是男女对垒,则1号甲与1号丙就不是男女对垒),15号之后,有9-a台男女对垒.所以甲、丙比赛时,男女对垒的台数为15-a+9-a=24-2a≤24.仅在a=0,即必须乙、丙比赛时男、女对垒的号码,与甲、乙比赛时男、女对垒的号码完全不同,甲、丙比赛时,男、女对垒的台数才等于24.4.将15×15的正方形方格表的每个格涂上红色、蓝色或绿色.证明:至少可以找到两行,这两行中某一种颜色的格数相同.【分析与解】如果找不到两行的某种颜色数一样,则就是说所有颜色的列与列之问的数目不同.则红色最少也会占:0+1+2+…+14=105个格子.同样蓝色和绿色也是,这样就必须有至少:3×(0+l+2+…+14)=315个格子.但是,现在只有15×15=225个格子,所以和条件违背,假设不成立,结论得证.6. 4个人聚会,每人各带2件礼品,分赠给其余3个人中的2人.试证明:至少有2对人,每对人是互赠过礼品的.【分析与解】将这四个人用4个点表示,如果两个人之间送过礼,就在两点之间连一条线. 由于每人送出2件礼物,图中共有4×2=8条线,由于每人礼品都分赠给2个人,所以每两点之间至多有1+1=2条线.四点间,每两点连一条线,一共6条线,现在有8条线,说明必有两点之间连了2条线,还有另外两点(有一点可以与前面的点相同)之间也连了2条线.即为所证结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第21讲构造论证二内容概述各种需要构造具体实例或给出严格论证的组合问题.论证中的常用手段包括抽屉原则、整除性分析、染色分析和不等式估计等.典型问题兴趣篇1.如图21-1所示,在6×6的警戒方格内,每个哨所可以监视横、竖、斜方向的全部单位方格.现在已经建了两个哨所.请你挑选一个方格,再建立一个哨所,使得所有的方格都被监视到。
2.(1)把1,2,3,…,8,9按合适的顺序填在图21-2第二行的空格中,使得每一列上、下两数之和都是平方数.(2)能否将1,2,3,…,10,1 1按合适的顺序填在图21-3第二行的空格中,使得每一列上、下两数之和都是平方数?3.今有长度为1,2,3,…,198,199的金属杆各一根.请问:能否用上全部的金属杆,不弯曲其中的任何一根,把它们焊接成:(1)一个正方体框架;(2)一个长方体框架?4.老师对六位同学的三门功课语文、数学、体育进行了一次测验,六位同学的体育得分是1分或者2分,数学得分是1分、2分或者3分,语文得分是1分、2分、3分或者4分.如果一位同学的三门功课成绩都不低于另一个同学的三门功课成绩,就说这个同学比另一个同学优秀.测验完成后老师发现这六位同学谁也不比别人优秀,请问:这六位同学三科得分分别为多少?5.把图21-4中的圆圈任意涂上红色或蓝色.问:能否使得每一条直线上的红圈个数都是奇数? 6.(1)能否在4×4的方格表的各个小方格内分别填人数1,2,…,15,16,使得从每行中都可以选择若干个数,这些数的和等于该行中其余各数之和?(2)能否在5×5方格表的各个小方格内分别填人数1,2,…,24,25,使得从每行中都可以选择若干个数,这些数的和等于该行中其余各数之和?7.图21-5是把一张6×6的方格纸去掉两个角所得的图形.(1)请把所有的格子涂上红、蓝两色之一,使得每个1×2小长方形(不论横竖)的2个方格中都恰有1个红格和1个蓝格;(2)能否用1×2的小长方形恰好拼满这张表格?8.全班25名同学分五排,每排五人坐在教室里,每个座位的前、后、左、右位子称为它的邻座.在儿童节每一位同学都买了一份礼物送给他的一个邻座,能否可以让大家适当地送出礼物,使得每一位同学都刚好收到一份礼物呢?9.将一个4×4的方格表分为如图21-6的5块区域,在其中填人16个互不相同的正整数,使得每一块区域中所填数的和都相等.这16个数的总和最小是多少?10.能否将1,2,3,…,9,10排成一行,使得任意相邻三个数之和都不大于167能否使得任意相邻三个数之和都不大于15 7拓展篇1.有7个不为0的自然数,它们的和正好等于它们的积.请写出一组满足要求的数.2.如图21-7,平面上有5个点,它们之间可以连10条线段,请问:至少要去掉多少条线段,才能使得其中没有以这5个点为顶点的三角形?3.如图21-8,一个幸运转盘分成内圆和外环两部分,并且被五条半径平均分割开.其中内圆是固定的,外环可以转动,但转动后必须使得分割线重新组成半径.请把0至9这10个数字分别填入图中的10个区域,使得不管外环怎么转动,总有大圆的一个扇形的两部分所填数字的和为9.4.平面上6条直线,它们的交点称为“结点”,每条直线上“结点”的个数称为这条直线的“标志数”,图21-9中的3条直线的“标志数”都等于2,只有一种取值;图21-10中的3条直线的“标志数”却有两种取值.现在请你用直尺画出6条直线,使得它们中间任何3条直线都不共点,且相应的6个“标志数”至少取3个不同的数值.5.(1)能否将1至8这8个数放在一条直线上,使得任意三个相邻数的和都不小于13?(2)能否将l至8这8个数放在一个圆圈上,使得任意三个相邻数的和都不小于13?6.一本故事书有10篇故事,这些故事占的篇幅从1页到10页各不相同,如果从书的第1页开始印第一个故事,每一个故事总是从新的一页开始印,那么故事从奇数页起头的最多有几篇?最少有几篇?7.在4×4的方格表中至少应该去掉多少个格子,才能使得剩下的图形中不存在如图21-11所示的“L型”?8.黑板上写着3个数8、18、28,老师现在请一些同学上黑板对这3个数进行操作.进行一次操作是指:把3个数进行如下变化,或者减1,或者加2.请问:能否经过若干次操作后得到6、7、87能否经过若干次操作后得到8、8、879.有3堆石子,每次可以从这三堆中同时拿走相同数目的石子(各次这个数目可以改变),也可以由一堆中取一半石子放人另外任一堆石子中.请问:(1)如果开始时,3堆石子的数目分别是34、55、82,按上述操作,能否把3堆石子都拿光?(2)如果开始时,3堆石子的数目分别是80、60、50,按上述操作,能否把3堆石子都拿光?如果可以,请设计一种取石子的方案;如果不可以,请说明理由.10.(1)能否将l至15排成一行,使得任意相邻两数之和都为平方数?(2)能否将1至15排成一行,使得任意相邻两数之和都为质数?11.(1)能否用16个如图21-12所示的“T型”拼成一个8×8的棋盘?(2)能否用8个如图21-12所示的“T型”和8个如图21-13所示的“L型”拼成一个8×8的棋盘?(3)能否用1个如图21-12所示的“T型”和15个如图21-13所示的“L型”拼成一个8×8的棋盘?12.(1)能否用9个如图21-14所示的1×4的长方形拼成一个6×6的棋盘?(2)能否用9个如图21-15所示的“L型”拼成一个6×6的棋盘?超越篇1.能否可以用77个3×3×1的长方体小木块装满一个7×9×11的长方体匣子(匣内不留任何空隙)?若能,请给出具体装法;若不能,请说明理由.2.黑板上写着两个数1和2,按下列规则增写新数,若黑板有两个数a和b,则增写a×b + a + b 这个数,比如:可增写5(因为1×2 + 1 + 2 = 5);可增写11(因为1×5 + l + 5 = 11).一直写下去,请问:能否得到下面两个数?若能,请你写出得出的过程;若不能,请说明理由.(1) 143;(2) 144.3.将平面上每一点都染成红、黄两种颜色之一.证明:无论怎样染色,都一定存在长为1的线段,它的两个端点是同样颜色的.4.在6×6的方格表中至少需要放多少个棋子,才能保证每行、每列以及每一条与对角线平行的直线上都有棋子?(角上单独一个格子也可以组成一条与对角线平行的直线,图21-16中阴影部分的三个格子组成的直线也是与对角线平行的直线.)5.(1)能否从图21-17中的A格出发,每次走到相邻的小格子,最后走到B格,并且每个格子都刚好到一次?(2)中国象棋的马是走“日”字型路线.如图21-18,如果马在A点,那么它能跳到B、C、D、E 四点之一.如果马开始在A点,它能否跳3步后回到A点;能否跳9步后回到A点?6.如图21-19,用若干个1×6和1×7的小长方形既不重叠,也不留孔隙地拼成一个11×12的大长方形,最少要用小长方形共多少个?7.六位音乐家在一个音乐节上相聚,在安排的每场音乐会上,有某些音乐家演奏,而另外几位音乐家就作为观众欣赏演出.要使每位音乐家都能够作为观众观看其他任何一位音乐家的表演,这样的音乐会至少要安排几场?为什么?8.把11×11的方格纸分成若干张3×3、2×2或1×1的小纸片,最少能分成多少张?第21 讲构造论证二兴趣篇1、如图所示,在 6⨯ 6 的警戒方格内,每个哨所可以监视横、竖、斜方向的全部单位方格。
现在已经建了两个哨所。
请你挑选一个方格,再建立一个哨所,使得所有的方格都被监 视到。
【分析】第二行第三列2、(1)把 1,2,3,…,8,9 按合适的顺序填在图 1 第二行的空格中,使得每一列上、下两数 之和都是平方数。
(2)能否将 1,2,3,…,10,11 按合适的顺序填在图 2 第二行的空格中,使得每一列上、 下两数之和都是平方数?【分析】(1)考虑到 9 只能和 7 配,先填入 9 和 7;剩下的 6 只能和 3 配,4 只能和 5 配, 依次填好;所以从左至右填入的数依次是 8,2,6,5,4,3,9,1,7; (2)考虑 11 只能和 5 配,那么没有数和 4 配,不能3、今有长度为 1,2,3,…,198,199 的金属杆各一根。
请问:能否用上全部的金属杆,不弯 曲其中的任何一根,把它们焊接成:(1)一个正方体框架;(2)一个长方体框架? 【分析】(1)总长(1 + 199) ⨯199 ÷ 2 = 19900 ,不是 12 的倍数,不能; (2)能,此时长方体框架的长、宽、高之和为199 ⨯ 25 ,可以分别为 4577、199、1994、老师对六位同学的三门功课语文、数学、体育进行了一次测验,六位同学的体育得分是 1 分或者 2 分,数学得分是 1 分、2 分或者 3 分,语文得分是 1 分、2 分、3 分或者 4 分。
如果一位同学的三门功课成绩都不低于另一个同学的三门功课成绩,就说这个同学比另 一个同学优秀。
测验完成后老师发现这六位同学谁也不比别人优秀,请问:这六位同学 三科得分分别为多少? 【分析】这 6 位同学在三门课上的得分分别是(1 分,1 分,4 分),(1 分,2 分,3 分),(1 分,3 分,2 分),(2 分,1 分,3 分),(2 分,2 分,2 分),(2 分,3 分,1 分)5、把图中的圆圈任意涂上红色或蓝色。
问:能否使得每一条直线上的红圈个数都是奇数?【分析】如果每边红色圈数目都是奇数,那么5条边总红色圈个数就是奇数;而实际上每个红圈被计算了2次,总红色圈数目是2的倍数,是偶数,矛盾,所以不能(1)能否在4⨯4 的方格表的各个小方格内分别填入数1,2,…,15,16,使得从每行中都可6、以选择若干个数,这些数的和等于该行中其余各数之和?(2)能否在5 ⨯5方格表的各个小方格内分别填入数1,2,…,24,25,使得从每行中都可以选择若干个数,这些数的和等于该行中其余各数之和?每行数字和都是偶数,那么总数字和是偶数,而1~16 的数字和是奇数,矛盾,所以不能7、如图是把一张6⨯6 的方格纸去掉两个角所得的图形。
(1)请把所有的格子涂上红、蓝两色之一,使得每个1⨯2 小长方形(不论横竖)的2个方格中都恰有1个红格和1个蓝格;(2)能否用1⨯2 的小长方形恰好拼满这张表格?(1),其中空白的格子涂上蓝色,R涂红色;(2)不能,因为每次1⨯2 的小长方形恰好覆盖了1红1蓝,如果可以的话,覆盖的红与蓝的数目应该一样,但图中红蓝数目是不一样的,所以不能。
