2012版步步高高考数学考前三个月抢分训练16：算法初步、复数

合集下载

2012高考数学新题分类汇编算法初步与复数(高考真题+模拟新题)

2012高考数学新题分类汇编算法初步与复数（高考真题+模拟新题）课标文数12.L1[2011·某某卷] 如图1－3所示，程序框图(算法流程图)的输出结果是________．图1－3课标文数12.L1[2011·某某卷] 【答案】 15 【解析】第一次进入循环体有T ＝0＋0，第二次有：T ＝0＋1，第三次有T ＝0＋1＋2，…第k ＋1次有T ＝0＋1＋2＋…＋k ＝k k ＋12，若T ＝105，解得k ＝14，继续执行循环，这时k ＝15，T >105，所以输出的k 的值是15.课标理数11.L1[2011·某某卷] 如图1－3所示，程序框图(算法流程图)的输出结果是________．图1－3课标理数11.L1[2011·某某卷] 15 【解析】第一次进入循环体有T ＝0＋0，第二次有：T ＝0＋1，第三次有T ＝0＋1＋2，…，第k ＋1次有T ＝0＋1＋2＋…＋k ＝k k ＋12，若T ＝105，解得k ＝14，继续执行循环，这时k ＝15，T >105，所以输出的k 的值是15.课标理数4.L1[2011·卷] D 【解析】第(i ＝0)一步，i ＝0＋1＝1，s ＝2－12＋1＝13；第(i ＝1)二步，i ＝1＋1＝2，s ＝13－113＋1＝－12；第(i ＝2)三步，i ＝2＋1＝3，s ＝－12－1－12＋1＝－3；第(i ＝3)四步，i ＝3＋1＝4，s ＝－3－1－3＋1＝2；第(i ＝4)五步，i ＝4<4不成立，输出s ＝2，故选D.课标文数6.L1[2011·卷] 执行如图1－2所示的程序框图，若输入A 的值为2，则输出的P 值为( )图1－2A ．2B ．3C ．4D ．5课标文数6.L1[2011·卷] C 【解析】第一步，P ＝1＋1＝2，S ＝1＋12＝32；第二步，P ＝2＋1＝3，S ＝32＋13＝116；第三步，P ＝3＋1＝4，S ＝116＋14＝2512>2，输出P ＝4，故选C.课标理数1.A1，L4[2011·某某卷] i 是虚数单位，若集合S ＝{－1,0,1}，则( )A ．i ∈SB ．i 2∈SC ．i 3∈S D.2i∈S课标理数1.A1、L4[2011·某某卷] B 【解析】由i 2＝－1，而－1∈S ，故选B.课标文数5.L1[2011·某某卷] 阅读图1－1所示的程序框图，运行相应的程序，输出的结果是( )图1－1A ．3B ．11C ．38D ．123课标文数5.L1[2011·某某卷] B 【解析】该程序框图是当型的循环结构，由程序框图可知，第一次循环，a ＝12＋2＝3；第二次循环，a ＝32＋2＝11；当a ＝11时，a <10不成立，输出a ＝11，故选B.课标理数13.L1[2011·某某卷] 若执行如图1－3所示的框图，输入x 1＝1，x 2＝2，x 3＝3，x ＝2，则输出的数等于________．图1－3课标理数13.L1[2011·某某卷] 23【解析】由累加的赋值符号S ＝S ＋(x i －x )2得到S ＝(1－2)2＋(2－2)2＋(3－2)2＝2，而最后输出的结果为S ＝1i S ＝13×2＝23.课标文数11.L1[2011·某某卷] 若执行如图1－2所示的框图，输入x 1＝1，x 2＝2，x 3＝4，x 4＝8，则输出的数等于________．图1－2课标文数11.L1[2011·某某卷] 154【解析】由累加的赋值符号x ＝x ＋x i 得到x ＝x 1＋x 2＋x 3＋x 4＝1＋2＋4＋8＝15，而最后输出的结果为x ＝14x ＝14×15＝154.课标理数13.L1[2011·某某卷] 图1－6是某算法的程序框图，则程序运行后输出的结果是________．图1－6课标理数13.L1[2011·某某卷] 【答案】 10【解析】第一次，s ＝0＋(－1)1＋1＝0，n ＝2，第二次，s ＝0＋(－1)2＋2＝3，n ＝3，第三次，s ＝3＋(－1)3＋3＝5，n ＝4，第四次，s ＝5＋(－1)4＋4＝10>9，终止循环，输出结果10.课标文数13.L1[2011·某某卷] 图1－6是某算法的程序框图，则程序运行后输出的结果是________．图1－6课标文数13.L1[2011·某某卷] 27 【解析】第一次：s ＝(0＋1)×1＝1，n ＝1＋1＝2，第二次：s ＝(1＋2)×2＝6，n ＝3，第三次：s ＝(6＋3)×3＝27，n ＝4，而n ＝4>3，退出循环，输出s ＝27.故填27.课标理数3.L1[2011·课标全国卷] 执行如图1－1所示的程序框图，如果输入的N 是6，那么输出的p 是( )图1－1A．120 B．720C．1440 D．5040课标理数3.L1[2011·课标全国卷] B【解析】k＝1时，p＝1；k＝2时，p＝1×2＝2；k＝3时，p＝2×3＝6；k＝4时，p＝6×4＝24；k＝5时，p＝24×5＝120；k＝6时，p＝120×6＝720.课标文数9.L1[2011·某某卷] 执行下面的程序框图，如果输入的n是4，则输出的p 是( )图1－5A．8 B．5 C．3 D．2课标文数9.L1[2011·某某卷] C 【解析】由于n＝4，所以当k＝1时，p＝1，s＝1，t＝1；当k＝2时，p＝2，s＝1，t＝2；当k＝3时，p＝3，s＝2，t＝3，此时k＝4，输出p，此时p＝3，故选C.课标文数5.L1[2011·课标全国卷] 执行下面的程序框图，如果输入的N是6，那么输出的p是( )图1－1A．120 B．720C．1440 D．5040课标文数5.L1[2011·课标全国卷] B 【解析】k＝1时，p＝1；k＝2时，p＝1×2＝2；k＝3时，p＝2×3＝6；k＝4时，p＝6×4＝24；k＝5时，p＝24×5＝120；k＝6时，p＝120×6＝720.课标理数13.L1[2011·某某卷] 执行图1－3所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．图1－3课标理数13.L1[2011·某某卷] 68 【解析】把l＝2，m＝3，n＝5代入y＝70l＋21m ＋15n得y＝278，此时y＝278>105，第一次循环y＝278－105＝173，此时y＝173>105，再循环，y＝173－105＝68，输出68，结束循环．课标文数14.L1[2011·某某卷] 执行图1－4所示的程序框图，输入l＝2，m＝3，n＝5，则输出的y的值是________．图1－4课标文数14.L1[2011·某某卷] 68 【解析】把l＝2，m＝3，n＝5代入y＝70l＋21m ＋15n得y＝278，此时y＝278>105，第一次循环y＝278－105＝173，此时y＝173>105，再循环，y＝173－105＝68，输出68，结束循环．课标理数8.L1[2011·某某卷] 图1－3中，x1，x2，x3为某次考试三个评阅人对同一道题的独立评分，p为该题的最终得分．当x1＝6，x2＝9，p＝8.5时，x3等于( )图1－3A ．11B ．10C ．8D ．7课标理数8.L1[2011·某某卷] C 【解析】由题目中所给的数据p ＝8.5，x 1＝6，x 2＝9，则若满足条件|x 3－x 1|s ＜|x 3－x 2|时，不成立，故应不满足条件|x 3－x 1|＜|x 3－x 2|，此时满足x 2＋x 32＝8.5，则x 3＝8，并且代入也符合题意，故选C.课标文数7.L1[2011·某某卷] 如下框图，当x 1＝6，x 2＝9，p ＝8.5时，x 3等于( )图1－4A ．7B ．8C ．10D ．11课标文数7.L1[2011·某某卷] B 【解析】因为x 1＝6，x 2＝9，p ＝8.5，p ＝x 1＋x 22或p ＝x 2＋x 32，当x 1＝6，x 2＝9，p ＝x 1＋x 22＝7.5，不合题意，故p ＝x 2＋x 32＝8.5，x 2＝9，得x 3＝8，故答案为B.课标数学4.L1[2011·某某卷] 根据如图所示的伪代码，当输入a ，b 分别为2,3时，最后输出的m 的值为________．Read a ，b If a >b Then m ←a Else m ←b End If Print m课标数学4.L1[2011·某某卷] 3 【解析】因为a ＝2<b ＝3，所以m ＝3.课标理数3.L1[2011·某某卷] 阅读程序框图1－1，运行相应的程序，则输出i的值为( )图1－1A．3 B．4 C．5 D．6课标理数3.L1[2011·某某卷] B 【解析】i＝1时，a＝1×1＋1＝2；i＝2时，a＝2×2＋1＝5；i＝3时，a＝3×5＋1＝16；i＝4时，a＝4×16＋1＝65>50，∴输出i＝4，故选B.图1－2课标文数3.L1[2011·某某卷] 阅读图1－2所示的程序框图，运行相应的程序，若输入x的值为－4，则输出y的值为( )A．0.5 B．1C．2 D．4课标文数3.L1[2011·某某卷] C 【解析】当x＝－4时，x＝|x－3|＝7；当x＝7时，x＝|x－3|＝4；当x＝4时，x＝|x－3|＝1<3，∴y＝2.课标理数12.L1[2011·某某卷] 若某程序框图如图1－4所示，则该程序运行后输出的k的值是________．图1－4课标理数12.L1[2011·某某卷] 5【解析】k＝3时，a＝43＝64，b＝34＝84，a<b；k＝4时，a＝44＝256，b＝44＝256，a＝b；k＝5时，a＝45＝256×4，b＝54＝625，a>b.图1－5课标文数14.L1[2011·某某卷] 某程序框图如图1－5所示，则该程序运行后输出的k 的值是________．课标文数14.L1[2011·某某卷] 5 【解析】k＝3时，a＝43＝64，b＝34＝84，a<b；k＝4时，a＝44＝256，b＝44＝256，a＝b；k＝5时，a＝45＝256×4，b＝54＝625，a>b.课标理数11.L2[2011·某某卷] 运行如图1－4所示的程序，输出的结果是________．a＝1b＝2a＝a＋bPRINT aEND图1－4课标理数11.L2[2011·某某卷] 【答案】 3【解析】由已知，输入a＝1，b＝2，把a＋b的值赋给a，输出a＝3.课标理数16.L3[2011·某某卷] 对于n ∈N *，将n 表示为n ＝a 0×2k ＋a 1×2k －1＋a 2×2k －2＋…＋a k －1×21＋a k ×20，当i ＝0时，a i ＝1，当1≤i ≤k 时，a i 为0或1.记I (n )为上述表示中a i 为0的个数(例如：1＝1×20,4＝1×22＋0×21＋0×20，故I (1)＝0，I (4)＝2)，则(1)I (12)＝________； (2)∑127n ＝12I(n)＝________.课标理数16.L3[2011·某某卷] (1)2 (2)1093【解析】 (1)本题实考二进制与十进制间的互化：因为I (12)＝1×23＋1×22＋0×21＋0×20，根据题目给出的定义可得到： I (12)＝2；(2)∑n ＝11272I (n )＝2I (1)＋2I (2)＋2I (3)＋…＋2I (127)利用二进制与十进制间的互化，列举得： I (1)＝1(2)共一个，则S 1＝2I (1)＝20＝1； I (2)＝10(2)，I (3)＝11(2)共2个，则S 2＝2I (2)＋2I (3)＝21＋20＝3；I (4)＝100(2)，I (5)＝101(2)，I (6)＝110(2)，I (7)＝111(2)共4个，则S 3＝2I (4)＋…＋2I (7)＝9；I (8)＝1000(2)，I (9)＝1001(2)，…，I (15)＝1111(2) 共8个，则S 4＝2I (8)＋…＋2I (15)＝27； ……I (64)＝100000(2)，…，I (127)＝1111111(2)共64个，则S 7＝2I (64)＋…＋2I (127)＝729；故∑n ＝11272I (n )＝2I (1)＋2I (2)＋2I (3)＋…＋2I (127)＝S 1＋S 2＋S 3＋S 4＋S 5＋S 6＋S 7＝1＋3＋9＋27＋81＋243＋729＝1093.课标文数1.L4[2011·某某卷] 设i 是虚数单位，复数1＋a i2－i为纯虚数，则实数a 为( )A ．2B ．－2C ．－12 D.12课标文数 1.L4[2011·某某卷] A 【解析】法一：1＋a i 2－i ＝1＋a i ·2＋i2－i 2＋i＝2－a ＋2a ＋1i5为纯虚数，所以⎩⎪⎨⎪⎧2－a ＝0，2a ＋1≠0，解得a ＝2.法二：1＋a i 2－i ＝i a －i 2－i为纯虚数，所以a ＝2.答案为A.课标理数1.L4[2011·某某卷] 设i 是虚数单位，复数1＋a i2－i为纯虚数，则实数a 为( )A ．2B ．－2C ．－12 D.12课标理数 1.L4[2011·某某卷] A 【解析】法一：1＋a i 2－i ＝1＋a i ·2＋i2－i 2＋i＝2－a ＋2a ＋1i5为纯虚数，所以⎩⎪⎨⎪⎧2－a ＝0，2a ＋1≠0，解得a ＝2.法二：1＋a i 2－i ＝i ()a －i 2－i为纯虚数，所以a ＝2.答案为A.课标理数2.L4[2011·卷] 复数i －21＋2i＝( )A ．iB ．－iC ．－45－35iD ．－45＋35i课标理数2.L4[2011·卷] A 【解析】 i －21＋2i ＝i －21－2i 1＋2i1－2i ＝5i5＝i ，故选A.课标文数2.L4[2011·卷] 复数i －21＋2i＝( )A ．iB ．－iC ．－45－35iD ．－45＋35i课标文数2.L4[2011·卷] A 【解析】 i －21＋2i ＝i －21－2i 1＋2i1－2i ＝5i5＝i ，故选A.大纲理数1.L4[2011·全国卷] 复数z ＝1＋i ，z 为z 的共轭复数，则z z －z －1＝( )A ．－2iB ．－iC ．iD ．2i大纲理数1.L4[2011·全国卷] B 【解析】 ∵z ＝1－i ，∴z z －z －1＝(1＋i)(1－i)－(1＋i)－1＝－i ，故选B.课标文数2.L4[2011·某某卷] i 是虚数单位，1＋i 3等于( ) A ．i B ．－i C ．1＋i D ．1－i课标文数2.L4[2011·某某卷] D 【解析】由1＋i 3＝1＋i 2·i＝1－i ，故选D.课标理数1.L4[2011·某某卷] 设复数z 满足(1＋i)z ＝2，其中i 为虚数单位，则z ＝( )A ．1＋iB ．1－iC ．2＋2iD ．2－2i课标理数1.L4[2011·某某卷] B 【解析】 z ＝21＋i ＝21－i 1＋i 1－i ＝21－i2＝1－i ，故选B.课标文数1.L4[2011·某某卷] 设复数z 满足i z ＝1，其中i 为虚数单位，则z ＝( ) A ．－i B ．i C ．－1 D ．1课标文数1.L4[2011·某某卷] A 【解析】由i z ＝1得z ＝1i ＝ii2＝－i ，所以选A.课标理数1.L4[2011·某某卷] i 为虚数单位，则⎝ ⎛⎭⎪⎫1＋i 1－i 2011＝( )A ．－iB ．－1C ．iD ．1课标理数1.L4[2011·某某卷] A 【解析】因为1＋i 1－i ＝()1＋i 2()1－i ()1＋i ＝i ，所以⎝ ⎛⎭⎪⎫1＋i 1－i 2011＝i 502×4＋3＝i 3＝－i.课标理数1.L4[2011·某某卷] 若a ，b ∈R ，i 为虚数单位，且(a ＋i)i ＝b ＋i ，则( ) A ．a ＝1，b ＝1 B ．a ＝－1，b ＝1 C ．a ＝－1，b ＝－1 D ．a ＝1，b ＝－1 课标理数1.L4[2011·某某卷] D 【解析】由(a ＋i)i ＝b ＋i 得－1＋a i ＝b ＋i ，根据复数相等的充要条件，得a ＝1，b ＝－1，故选D.课标文数2.L4[2011·某某卷] 若a ，b ∈R ，i 为虚数单位，且(a ＋i)i ＝b ＋i ，则( ) A ．a ＝1，b ＝1 B ．a ＝－1，b ＝1 C ．a ＝1，b ＝－1 D ．a ＝－1，b ＝－1 课标文数2.L4[2011·某某卷] C 【解析】由(a ＋i)i ＝b ＋i 得－1＋a i ＝b ＋i ，根据复数的相等，a ＝1，b ＝－1，故选C.课标理数1.L4[2011·某某卷] 若z ＝1＋2ii，则复数z ＝( )A ．－2－iB ．－2＋iC ．2－iD ．2＋i课标理数1.L4[2011·某某卷] D 【解析】 z ＝1＋2i i ＝i 1＋2ii 2＝－(i －2)＝2－i ，故z ＝2＋i.故选D.课标文数1.L4[2011·某某卷] 若(x －i)i ＝y ＋2i ，x ，y ∈R ，则复数x ＋y i ＝( ) A ．－2＋i B ．2＋iC ．1－2iD ．1＋2i课标文数1.L4[2011·某某卷] B 【解析】由题设得x i ＋1＝y ＋2i ，∴x ＝2，y ＝1，即x ＋y i ＝2＋i.故选B.课标理数1.L4[2011·课标全国卷] 复数2＋i1－2i的共轭复数是( )A ．－35i B.35iC ．－iD ．i课标理数1.L4[2011·课标全国卷] C 【解析】 2＋i 1－2i ＝2＋i 1＋2i 1－2i 1＋2i ＝5i5＝i ，所以其共轭复数为－i.故选C.图1－1课标文数2.L4[2011·某某卷] i 为虚数单位，1i ＋1i 3＋1i 5＋1i7＝( )A ．0B ．2iC ．－2iD ．4i课标文数2.L4[2011·某某卷] A 【解析】 1i ＋1i 3＋1i 5＋1i 7＝－i ＋i －i ＋i ＝0，故选A.课标文数2.L4[2011·课标全国卷] 复数5i1－2i＝( )A ．2－iB ．1－2iC ．－2＋iD ．－1＋2i课标文数2.L4[2011·课标全国卷] C 【解析】 5i 1－2i ＝5i 1＋2i 1－2i 1＋2i ＝5i －105＝－2＋i.课标理数2.L4[2011·某某卷] 复数z ＝2－i2＋i(i 为虚数单位)在复平面内对应的点所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限课标理数2.L4[2011·某某卷] D 【解析】 z ＝2－i 2＋i ＝2－i 22＋i 2－i ＝3－4i 4＋1＝35－45i ，又点⎝ ⎛⎭⎪⎫35，－45在第四象限，所以该复数在复平面内对应的点也在第四象限．课标文数2.L4[2011·某某卷] 复数z ＝2－i2＋i(i 为虚数单位)在复平面内对应的点所在象限为( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限课标文数2.L4[2011·某某卷] D 【解析】 z ＝2－i 2＋i ＝2－i 22＋i 2－i ＝3－4i 4＋1＝35－45i ，又点⎝ ⎛⎭⎪⎫35，－45在第四象限，所以该复数在复平面内对应的点也在第四象限．课标文数8.A1，L4[2011·某某卷] 设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪⎪⎪⎪⎪⎪x i ＜1，i 为虚数单位，x ∈R ，则M ∩N 为( )A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1]课标文数8.A1，L4[2011·某某卷] C 【解析】对M ，由基本不等式得y ＝|cos 2x －sin 2x |＝|cos2x |，故0≤y ≤1.对N ，⎪⎪⎪⎪⎪⎪x i <1，即|－x i|<1，所以－1<x <1，故M ∩N ＝[0,1)，故答案为C.课标数学1.A1[2011·某某卷] 已知集合A ＝{－1,1,2,4}，B ＝{－1,0,2}, 则A ∩B ＝________.课标数学1.A1[2011·某某卷] {－1,2} 【解析】因为集合A ，B 的公共元素为－1,2，故A ∩B ＝{－1,2}．课标数学3.L4[2011·某某卷] 设复数z 满足i(z ＋1)＝－3＋2i(i 为虚数单位)，则z 的实部是________．课标数学3.L4[2011·某某卷] 1 【解析】因为z ＋1＝－3＋2i i ＝－3i ＋2i2i2＝2＋3i ，所以z ＝1＋3i ，故实部为1.大纲理数2.L4[2011·某某卷] 复数－i ＋1i＝( )A ．－2i B.12i C ．0 D ．2i大纲理数2.L4[2011·某某卷] A 【解析】－i ＋1i＝－i －i ＝－2i ，所以选A.课标理数1.L4[2011·某某卷] i 是虚数单位，复数1－3i1－i＝( )A ．2＋iB ．2－iC ．－1＋2iD ．－1－2i课标理数1.L4[2011·某某卷] B 【解析】 1－3i 1－i ＝1－3i 1＋i 1－i 1＋i ＝4－2i2＝2－i.课标文数1.L4[2011·某某卷] i 是虚数单位，复数1－3i1－i＝( )A ．2－iB ．2＋iC ．－1－2iD ．－1＋2i课标文数1.L4[2011·某某卷] A 【解析】 1－3i 1－i ＝1－3i 1＋i 1－i 1＋i ＝4－2i2＝2－i.课标理数2.L4[2011·某某卷] 把复数z 的共轭复数记作z ，i 为虚数单位．若z ＝1＋i ，则(1＋z )·z ＝( )A ．3－iB ．3＋iC ．1＋3iD ．3课标理数2.L4[2011·某某卷] A 【解析】 ∵z ＝1＋i ，∴z ＝1－i ，∴(1＋z )·z ＝(2＋i)(1－i)＝3－i.课标文数2.L4[2011·某某卷] 若复数z ＝1＋i ，i 为虚数单位，则(1＋z )·z ＝( ) A ．1＋3i B ．3＋3i C ．3－i D ．3课标文数2.L4[2011·某某卷] A 【解析】 ∵z ＝1＋i ，∴(1＋z )·z ＝(2＋i)(1＋i)＝1＋3i.大纲理数1.L4[2011·某某卷] 复数i 2＋i 3＋i41－i＝( )A ．－12－12iB ．－12＋12iC.12－12iD.12＋12i 大纲理数 1.L4[2011·某某卷] C 【解析】 i 2＋i 3＋i 41－i ＝－1－i ＋11－i ＝－i1－i＝－i 1＋i 1－i 1＋i ＝－i －12＝12－12i.故选C.[2011·某某期末] 若框图(如图K48－2)所给的程序运行结果为S ＝20，那么判断框中应填入的关于k 的条件是( )[2011·某某期末] 已知(x ＋i)(1－i)＝y ，则实数x ，y 分别为( ) A ．x ＝－1，y ＝1 B ．x ＝－1，y ＝2 C ．x ＝1，y ＝1 D ．x ＝1，y ＝2[2011·高考样卷] 若a －ii＝b ＋2i ，其中a ，b ∈R ，i 是虚数单位，则a －b 的值为( )A ．－1B ．－3C ．3D ．1。

2012版步步高高考数学考前三个月专题复习课件7(2)：概率与统计、算法初步、复数

3．(2011·课标全国改编有 3 个兴趣小组，甲、乙两位同学各自．课标全国改编)有个兴趣小组，课标全国改编参加其中一个小组，每位同学参加各个小组的可能性相同，参加其中一个小组，每位同学参加各个小组的可能性相同， 1 3 ．则这两位同学参加同一个兴趣小组的概率为________．则这两位同学参加同一个兴趣小组的概率为

0.05 0.20 0.28 0.30 0.15 0.02
(2)因为 0.30＋0.15＋0.02＝0.47，所以数据落在因为＋＋＝，所以数据落在[1.15，1.30)中的，中的概率约为 0.47. 120×100 × (3) ＝2 000，所以水库中鱼的总条数约为 2 000. ， 6
(1)在下面表格中填写相应的频率；在下面表格中填写相应的频率；在下面表格中填写相应的频率分组

频率

1.00，1.05 ， 1.05，1.10 ， 1.10，1.15 ， 1.15，1.20 ， 1.20，1.25 ， 1.25，1.30 ，

， (2)估计数据落在 1.15，1.30中的概率为多少；中的概率为多少；估计数据落在 (3)将上面捕捞的 100 条鱼分别作一记号后再放回水库．几天后将上面捕捞的条鱼分别作一记号后再放回水库．条鱼，再从水库的多处不同位置捕捞出 120 条鱼，其中带有记号的鱼请根据这一情况来估计该水库中鱼的总条数．有 6 条．请根据这一情况来估计该水库中鱼的总条数．
解析
这是一道几何概型的概率问题，点 Q 取自△ABE 1 S△ABE 2·|AB|·|AD| 1 内部的概率为＝＝ . |AB|·|AD| 2 S矩形ABCD

2012版步步高高考数学考前三个月专题复习课件4(1)：数列、推理与证明

二、等比数列的有关问题例 2 (2011· 安徽)在数 1 和正实数 a 之间插入 n 个正实数，使得这 n＋2 个数构成等比数列，将这 n＋2 个数的乘积记作 bn，且 an＝logabn. (1)求数列{an}和{bn}的通项公式； (2)求数列{bn}的前 n 项和 Sn.
解 (1)设 t1，t2，„，tn＋2 构成等比数列， ① ② 其中 t1＝1，tn＋2＝a，则 bn＝t1· · tn＋1· ＋2， t2 „· tn bn＝tn＋2· ＋1· t2· . tn „· t1 ①×②并利用 ti· ＋3－i＝t1tn＋2＝a(1≤i≤n＋2)，得 tn b2＝(t1tn＋2)· 2tn＋2)· (tn＋1t2)· n＋2t1)＝an＋2，又 bn>0， (t „· (t n 1 1 (n＋2) 2 ∴bn＝a ，an＝ (n＋2)． 2
归纳拓展
数列项的变化呈规律性，这是等差、等比数列的特
征，在高考中，这种变化的规律性经常用数表或图形给出，也可以是给出信息根据新信息解题，对考查学生的创新能力提出了较高的要求．解这类问题要先读懂题意，从题目中获取有用信息，然后根据相关知识作进一步的演算和推理，综合运用新的信息和数学知识分析，解决新情境问题．
1 bn 1 a (2) 1 a 2 (常数 );{bn }为等比数列 . ( n 2) bn 2 a 当a 1时, S n n;
1 ( n 3) 2
当a 1时, S n
a (1 a ) 1 a
1 2
3 2
n 2
.
n 3 n S n a 2 (1 a 2 ) 1 1 a 2
1(n＝1)， a2＝3S1＝3a1＝3，∴an＝－ 3×4n 2(n≥2).

2012版步步高高考数学考前三个月专题复习课件8(1)系列4选讲

2．(2011·江苏)如图，圆 O1 与圆 O2 内切于点 A，其半径分别为 r1 与 r2(r1>r2)．圆 O1 的弦 AB 交圆 O2 于点 C(O1 不在 AB 上)．求证：AB∶AC 为定值．
证明如图，连接 AO1 并延长，分别交两圆于点 E 和点 D.连接 BD，CE.
因为圆 O1 与圆 O2 内切于点 A，所以点 O2 在 AD 上，故 AD， AE 分别为圆 O1，圆 O2 的直径．从而∠ABD＝∠ACE＝π2. 所以 BD∥CE，于是AACB＝AADE＝22rr12＝rr12. 所以 AB∶AC 为定值．
6．圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的一半．
7．圆心角定理圆心角的度数等于它所对弧的度数．
8．圆内接四边形的性质定理 (1)圆的内接四边形的对角互补． (2)圆内接四边形的外角等于它的内角的对角．
9．圆内接四边形判定定理如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．
4．相似三角形的性质 (1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比； (2)相似三角形周长的比等于相似比； (3)相似三角形面积的比等于相似比的平方．
5．直角三角形的射影定理直角三角形中，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项；斜边上的高是两条直角边在斜边上的射影的比例中项．
考点整合
1．平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．
2．平行截割定理 (平行线分线段成比例定理)三条平行线截两条直线，所得的对应线段成比例．
3．相似三角形的判定定理判定定理 1：对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．判定定理 2：如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．判定定理 3：对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似．

2012年高考真题汇编——理科数学：16：复数.pdf

感受器和感觉器官(一) 1.眼球的基本结构和功能：探究主题一眼是感受外界光线的视觉器官视神经感光睫状体瞳孔瞳孔白色支持、保护脉络膜血管黑色素营养 2.视觉的形成：进入眼球的光线经过_______等的折射作用，在_______上形成物像。

视网膜上大量的_________受到刺激后形成_________，神经冲动沿着_______传递到_________，形成视觉。

晶状体视网膜感光细胞神经冲动视神经大脑皮层 3.近视与远视：近视远视形成原因眼球前后径_____或晶状体的_____过大，物像落在_______的前方眼球的前后径 _____，物像落在_______的后方矫正配戴_______ 配戴_______ 过长曲度视网膜过短视网膜凹透镜凸透镜【特别提醒】预防近视的方法：三要四不看一要：读写姿势要正确，眼与书的距离要在33厘米左右。

二要：看书、看电视或使用电脑1小时后要休息一下，远眺几分钟。

三要：要定期检查视力，认真做眼保健操。

一不看：不在直射的强光下看书。

二不看：不在光线暗的地方看书。

三不看：不躺卧看书。

四不看：不走路看书。

1.眼球和照相机在哪些结构上比较相似？提示：眼球结构与照相机结构的对应关系眼球晶状体瞳孔视网膜脉络膜照相机镜头光圈胶卷暗室的壁2.在眼球的结构中，对物体反射进眼球中的光线起折射作用的结构有哪些？最主要的结构是什么？提示：晶状体和玻璃体。

晶状体。

探究主题二耳是接收声音刺激的听觉器官 1.耳的基本结构和功能：收集耳廓外耳道传送鼓膜听小骨鼓室半规管头部位置变动前庭耳蜗听觉感受器咽鼓管咽 2.听觉的形成：当声波引起的振动传到内耳时，耳蜗_____ _______受振动刺激而产生_________，神经冲动沿着位听神经传到大脑皮层的_____中枢，形成听觉。

【步步高】2012高考数学考前三个月抢分训练16 算法初步、复数

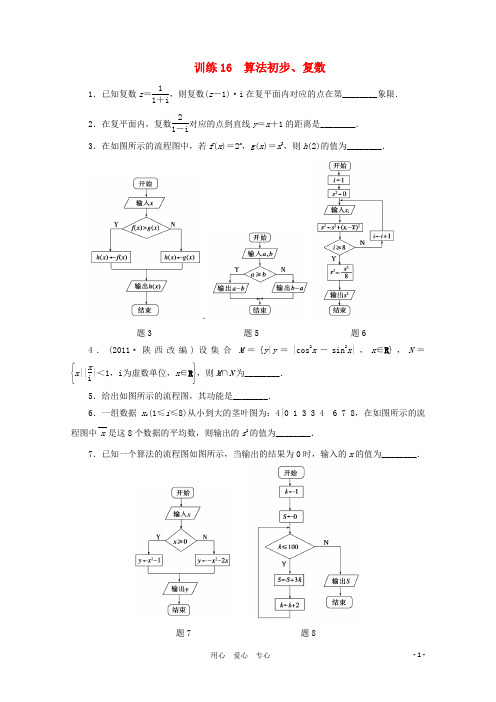
训练16 算法初步、复数1．已知复数z ＝11＋i ，则复数(z －1)·i 在复平面内对应的点在第________象限．2．在复平面内，复数21－i 对应的点到直线y ＝x ＋1的距离是________．3．在如图所示的流程图中，若f (x )＝2x，g (x )＝x 3，则h (2)的值为________．．题3 题5 题64．(2011·陕西改编)设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫x ||xi |＜1，i 为虚数单位，x ∈R ，则M ∩N 为________．5．给出如图所示的流程图，其功能是________．6．一组数据x i (1≤i ≤8)从小到大的茎叶图为：4|0 1 3 3 4 6 7 8，在如图所示的流程图中x 是这8个数据的平均数，则输出的s 2的值为________．7．已知一个算法的流程图如图所示，当输出的结果为0时，输入的x 的值为________．题7 题88．执行如图所示的流程图，则输出的S ＝________.9.若复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，则复数(z 1－z 2)i 的实部为________．10．已知集合A ＝⎩⎨⎧⎭⎬⎫12i，i 2，|5i 2|，＋2i，－i 22，则集合A ∩R ＋的子集个数为________．11．(2010·北京)在复平面内，复数2i1－i 对应的点的坐标为______．12．阅读如图所示的流程图，运行相应的程序，输出的结果是________．题12 题13 题1413．某地区为了解70岁～80岁的老人的日平均睡眠时间(单位：h)，随机选择了50位老人进行调查，下表是这50位老人睡眠时间的频率分布表：14．若如图所示的算法流程图中输出y 的值为0，则输入x 的值可能是________(写出所有可能的值)．答案1．四 2.223．8 4.[)0，1 5．求|a－b|的值 6．7 7．－2或18．7 500 9．－20 10．8 11．(－1,1) 12．8 13．6.42 14．0，－3,1。

2012版步步高高考数学考前三个月专题复习课件6(2汇总

§ 2椭圆.双曲线、抛物线真题热身1. （2011-安徽改编）双曲线2X2-/=8的实轴长是_12解析•/ 2x2 - y2 = 8,・••才 $:.a = 2, 2a = 4.・•・/ +，= 9.由①②得«2= 5, Z?2 = 4.2 2・・・双曲线的标准方程为1.2. (2011-广东改编)设，+(y —3尸=1外切，与直线y=0相切，则C 的 E I 心轨迹为抛物线・解析设圆C 的半各为厂，则圆心C 到直线y = O 的距离为厂.由两圆外切可得，圆心C 到点(0,3)的距离为厂+1,也就是说，圆心C 到点(0,3)的距离比到直线y = ()的距离大 1,故点C 到点(0,3)的距离和它到直线- 1的距离相等, 符合抛物线的特征，故点C 的轨迹为抛物线.3. (2011-山东改编线均和圆X 2 v 2£、2下1(4>0, 〃>0)的两条渐近,且双曲线的右焦点为圆C 的圆心，则该双曲线的方程为5一 4 = 192解析・・•双曲线1的渐近线方程为厂 b ±-X,a 圆C 的标准方程为(x - 3)2+ y 2= 4,・・・圆心为C(3,0).又渐近线方程与圆C 相切, 即直线bx - ay =()与圆C 相切,又：•缶-話=1的右焦点尸2(#2 +①b\ 0)为圆心 C(3,0),4. （2011-iI宁）已知点（2,3）在双曲线C：》一器=1（4>0, 〃>0）上，C的焦距为4,则它的离心率为___________ •4 9解析由题意知7 一戸=1'疋=/ + /?2= 4得a = 1,/? =羽,C.e = 2.锥曲线的又 F X F 2 = 2^/3, 由余弦定理可知COS ZF I PF 2 = -壬.范围丄皿QO几何性质(0,0)顶 "7±a,0)(0, ±b)(±a,0) 对称性关于X 轴，丿轴和原点对称关于x 轴对称焦点 (±c,0)§ o )轴长轴长2a 9 短轴长2b实轴长2a f 虚轴长”离心率C e=~FA /1-? (0<e<l)c e=~=A /1+?(e>l)e=l准线x=~2渐近线by =±a x锥曲鋸亘义及几何性质 °例1 (1)已知P 为椭圆亍+b=l 和双曲线X 2-^=1的一个交点尺、F2为椭圆的两个焦点，那么ZF.PF2的余弦值为 _____ ・ (2)已知直线y=k(x+2)(k>0)与抛物线G ?=8r 相交于A 、〃两点，F 为C 的焦点.若FA = 2FB 9则比= ______________ ・(1) 由椭圆和双曲线的方程可知，Fp 尸2为它们的公共 PF { + PF? = 4PF\_ PF? = 2所以解析不妨设\PFi = 3回2 = 1又F X F2 = 2^/3, 由余弦定理可知COS ZF I PF2 = -壬.（2）方+ 2)(* > 0)恒过定点 P( - 2,0). 如图，过A 、B 分别作AM 丄Z 于点M, BN 丄I 于点N ・由皿=2FB 9则AM = 2BN,点B 为AP 的中点. 连结OB,则OB = R F ,・・・OB = BF,点B 的横坐标为1, 故点B 的坐标为(1,2^2). . 2岛0 _2\耳・・ 1_(_2)一 3 ••匹 BB‘ 1 9AC~AA f"2J即B 是AC 的中点. .2x 〃 ■必 _ 2,* * [2yn = y AJ42= 8X4，yin =张〃，联立可得4(4,4迈)，〃(1,2迈). . 4迈一 2^2 2^2• ^AB = 川―- =2一•答案⑴一扌（2）2屮方法二如F, AA f-AF,归纳拓展1 •圆锥曲线的定义是根本，它是标准方程和几何性质的“源”，“回归定义”是一种重要的解题策略.对于圆锥曲线的定义不仅要熟记，还要深入理解细节部分：比如椭圆的定义中要■求PF. + PF2 > F X F2,双曲线的定义中要求IPFj - PF2\ < FX F2，抛物线上的点到焦点的距离与到准线的距离相等的转化.2.注意数形结合，提倡画出合理草图.变式训练1卫欖交点，F1、尸2分别是它们的左、右焦点，设椭圆离心率为"双曲线离心率为巾，若两•航=0,则A+A = ______________ ・(2)如图，过抛物线j2=2px(p>0)的焦点的直线Z依次交抛物线及其准线与点A、B、C,若BC=2BF,且AF=3,则抛物线的方程是_____________________ ・=i ・(2)作丄垂足分别娇则由抛物线定义得， Ag = AF-3, BF = BM.— 2BF,所以 BC = 2BM.解析(1兄轴长为0,双曲线实半轴长为",由题意，得PFi + PFi = 2a,①由BM//二、圆锥曲线的方程及应用= l(a>b>0)的离心率e=例2 (2010-天津)已知椭圆弓,连结椭圆的四个顶点得到的菱形的面积为4・(1)求椭圆的方程；(2)设直线/与椭圆相交于不同的两点A, B,已知点A的坐标为(一0,0),点0(0,为)在线段的垂直平分线上，且QA QIi =4,求旳的值.=i ・由方程组消今三严―F(1 + 4k 2)x 2 + 16k 2x + (16k 2- 4) = 0.16, - 4 由根与系数的关系，得-加L〒W ，所以从而J, =1^4p*设线段4B 的中点为M, 则M 的坐标为(一岸気，以下分两种情况讨论：①当Ar = 0时，点B 的坐标是(2,0),线段AB 的垂直平分线为y 轴，于是鬲=(-2, -jo),筋=(2, -jo). 由芮L •函=4,得为=±2\「2・②当直平分线的方程为 2k y T^P =-*"1 + 40・令x = 0,解得旳=-务.由QA = (~2f -jo), QB = (xi ，yi -j 0)，一 2(2 一蛇) 6k z 4k ~ +1+ 4*^1 + 4*2 + 4(16^4 +丄5宀卫+ 4J12)2QA-QB = ~ 2xi-jo(yi- jo)整理得7k27・综上，jo = ±2-\/2或为=归纳拓展1 •求圆锥曲线的标准方程的基本步骤： ⑴定型（确定圆锥曲线类型）.（2）定位（判断它的中心在原点，焦点在哪条坐标轴上）. （3）定量（建立关于基本量的方程或方程组，解得基本量a, b 的值）.2.椭圆、双曲线.抛物线是常见的曲线，利用它们的方程及几何性质，可以解决一些简单的实际问题；利用方程可以研究它们与直线的交点、相交弦等有关问题.的点M 与椭圆右焦点F 、的连线MF X 与 x 轴垂直，且OM （O 是坐标原点）与椭圆长轴和短轴端点的连线AB 平行. （1）求椭圆的离心率；⑵巧是椭圆的左焦点，C 是椭圆上的任一点，证明：ZF X CF 2^⑶过F I 且与4〃垂直的直线交椭圆于P 、Q,若△PAO 的面积是2叭5,求此时椭圆的方程.=1±变式训练y B M:.—=~=^b = c=>a = y<2c ac a v⑵证明由椭圆定义得：FiC +尺< =加,COSZF1CF2 =4a 1 2-4c 2- 2F& F2C即 j = - \[2(x - c).代入椭圆方程消去工得：^(c~^y)2+^= 1, 整理得：5y 2- 2yj2cy - 2<?2 = 0,. 2\l2c 2c 2・・ Jl +J2= 5 ' ^1J2= 一亏一・ m 警沪誓：礬S&F Q |-2<-lyi -j 2l == 2叭/§, c 2= 25,因此a 2= 50,沪= 25,所以椭圆方程为备+幺".2F I CF 2C一 FiC + F 2C 2F]C ・F2CW(」2 )=2b 22c 2•••COSZF1CF2 工 72■- 1 =茲2 -1 = 0, ・・・ZF1CF2W 务则M(c,-2F X CF 2C 2b 2F I CF 2C 2 0),b "a (1)解设你，k OM = k设冼=(七兀3 =加1 +例 3 (2011 •江西)P(x 0, ,o)(xoH±a)是双曲线 E ：》一点2= 1(°>0, 〃>0)上一点，M, N 分别是双曲线E 的左，右顶点，直线 PM, PV 的斜率之积为占⑴求双曲线的离心率；(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A, B 两点，O 为坐标原点，C 为双曲线上一点，且满足荒=2芮 +OB 9求久的值.解（1）由点竺由题意有—.Jo Jo5’⑵联立设 A （x 5c +（加1 + X 2）2丹卅-50 + （xl - 5yl ） + 2>.（X J X 2 - 5丿也）=5b 2.又A(x n J O ，B(X 29力)在双曲线上，所以 xj - 5yi = 5b 2, xj - 5yl= 5b 2.由①式又有- 5JIJ 2 =小*2 - 5(*1 - c)(x 2 - c)=一 4XJ X 2 + 5c(*i + x 2) 一 5c 2= 10b 2, ②式可化为A 2 + 4x = 0,解得久=0或2二-4.归纳拓展本题考查了双曲线方程和它的几何性质，同时还考查了直线与双曲线的位置关系，圆锥曲线与直线的综合类题目中数形结合法是解题首选，根与系数的关系是解题利器，方程思想是解题的切入点.变式训练3 (20U ・江西)已知过抛物线y 2=2px(p>0)的焦点，斜率为2边的直线交抛物线于A (X|, yi)9 B(X 2,歹2)仗心2)两点，且AB=9. (1)求该抛物线的方程，(2)0为坐标原点，C 为抛物线上一点，若OC=OA+；VB,求 2的值.又C 为双b\有⑴直线^牡鱼科2 ,2（x-伶），与y2 = 2px联立,从而有4x2 - 5px + p2 = 0, 所以Xi+X2*由抛物线定义得AB +x2 + p - 9,所以p = 4,从而抛物线方程是y2 = Sx・(2)由” _ 4 知4x2— 5px + _ o 可化为x2— 5x + 4 — 0,从而Xi = 1, x2 = 4, Ji = - 2^/2, y2 = 4^/2, 从而4(1, -2迈)，3(4,4迈)・设OC = (x3, J3)= (b - 2迈)+ 2(4,4迈)= (4z+l, 4血-2^2), 又J3 = 8x3,所以[2^(22-1)]2 = 8(42+1),即(22-1)2 = 42+1,解得；＞0或・一、填空题1. AB是某平面上一定线段，点P是该半面内的一动点,满足质I一I两1 = 2, I芮一苛1 = 2诟，则点P的轨迹是双曲线的一支.解析由I芮-丙1 = 2击得I芮l = 2\S. 又I芮I - I萌=2 <2审，由双曲线定义可得轨迹为双曲线的一支线y 2=2px （p>0）^J 焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为（一2, -1）,则双曲线的焦距为 _______ ・解析双曲线左顶点为人（-Q,0）, 渐近线为y = 土务，抛物线y 2= 2px （p>0）焦点为F 時、0）, 准线为直线%= - 2- 由题意知-纟=-2,•*.p = 4,由题意知 2 + a = 4, /.a = l.-1）的渐近线为歹=尹, - 1 pX (- 2),/.c 2 = a 2 + Z>2 = 5, ・・・c = \M,・・.2c = 2迟答案2^52. (2011 天津雷毬fjg^=lS>0, b>0）的左顶点与抛物・•・双曲线渐近线y = 中与准线x = -纟交于（- 2,2,焦点与椭圆£+£ =1的焦点相同，那么双曲线的焦点坐标为_1±红QL；渐近线方程为心/±)=°.解析・••双曲线的焦点与椭圆的焦点相同，・= 4.Ve = - =2,・\a = 2,・\b2 = 12,・\b = 2^/3.a v・・•焦点在x轴上，・・・焦点坐标为(±4,0),渐近线方程为y= 土务，即y = ±^/3x, 化为一般式为帝兀土y = 0.4. (2010-陕西)已知抛物线y2=2px(p>0)的准线与圆x2+y2—6x 一7=0相切，则D的值为 2 .解析抛物线y2 = 2px(p>0)准线为x=圆x2 + y2 - 6x - 7 = 0 即(x - 3)2 + y2 = 16,则圆心为(3,0),半径为4;又因为抛物线b = 2px(p>0)的准线与圆x2 + y2 - 6x - 7 = 0 相切，所以3+号=4,解得p = 2.=0的距离的最小值为&）・解析设P （x （）,为），则点P 到直线x + 2y + 8 = 0的距离 ,+ 2y （）+ 81 d =―疋—■ 又点P 在抛物线y =上，所以y （）= 2x ＜）,所以 d=+x （）+ 81,所以当Xo = 一+时，46.设抛物线_/=2p.心＞0）的焦点为F,点4（0,2）.若线段皿的中点B 在抛物线上,则B 到该抛物线准线的距离为卫_・解析抛物线的焦点F 的坐标为（£ 0）,线段朋的中点B 的坐标为（? 1）,代入抛物线方程得1 =2pX^,解得p = d 故点B 的坐标为序，1,故点B 到该抛物线准线的距5.已知抛八、、127审则点P 到127审80 -〃min离为普+警普.7.已知点F为抛物线y =—8x的焦点，O为原点,点尸是抛物线准线上一动点，点4在抛物线上，且AF=4,则必+ PO的毘小値为2屈.解析抛物线的准线方程为x = 2,因为AF = 4,由抛物线定义可得，点A的横坐标为-2,取点A( - 2,4)・因为原点O关于准线的对称点为3(4,0),贝y M + PO = M + PBMAB = 2(13.8.已知A(—刃0),3是・・・B4 + PF=2,即P 到两定点A 、F 距离之和为定值2且大于两定点A 、F 之间的距离1, 故3-4 - 2 b 1一29右焦点为(2迈，0).斜率为1的直线/与椭圆G 交于A 、B 两点，以4〃为底边作等腰三角形，顶点为尸(一3,2)・ (1)求椭(2)求的面积. ft? (1)由已知得c = 2翻,'=半，解得■。

2012版步步高高考数学考前三个月专题复习课件7(4)：概率与统计、算法初步、复数

解析
①中实数与虚数不能比较大小；
②两个复数互为共轭复数时其和为实数，但两个复数的和为实数时这两个复数不一定是共轭复数； ③x＋yi＝1＋i 的充要条件为 x＝y＝1 是错误的，因为没有标明 x，y 是否是实数； ④当 a＝0 时，没有纯虚数和它对应．
(2)若若
3 5 θ∈ π， π，则复数(cos ∈ ，则复数 4 4
答案 22
归纳拓展 1.解答此类问题，首先要读懂流程图，要熟练
掌握流程图的三个基本结构． 2．解答循环结构的流程图，最好的方法是逐步执行每一步，保证完整性，防止执行程序不彻底，造成错误．
执行下边的流程图，变式训练 3 执行下边的流程图，若 P＝0.8，则输出的 n＝＝，＝ ________.
3．(2011·天津阅读右边的流程图，运行相应．天津)阅读天津阅读右边的流程图，的程序，的值为－，的程序，若输入 x 的值为－ 4，则输出 y
2 的值为________．．的值为
解析当 x＝－4 时，|x|＝4>3，
x 赋值为 x＝|－4－3|＝7>3， ∴x 赋值为 x＝|7－3|＝4>3， x 再赋值为 x＝|4－3|＝1<3，则 y＝21＝2，输出 2.
1＋i ＋ 2 011 －i 2．(2011·湖北改编为虚数单位，则．湖北改编)i 为虚数单位，＝ ______. 湖北改编－ 1－i
1＋i (1＋i)2 解析 ∵ ＝＝i， 1－i (1－i)(1＋i) 1＋i × ＋ 2 011 ∴ ＝i2 011＝i4 502 3＝i3＝－i. 1－i
归纳拓展复数的乘除运算是复数运算的难点，在乘法运算中要注意 i 的幂的性质，区分(a＋bi)2＝a2＋2abi－b2 与(a＋b)2＝ a2＋2ab＋b2；在除法运算中，关键是“分母实数化”(分子、分母同乘以分母的共轭复数)，此时要注意区分(a＋bi)·(a－bi) ＝a2＋b2 与(a＋b)(a－b)＝a2－b2，防止实数中的相关公式与复数运算混淆，造成计算失误．

【步步高】2012高考数学考前三个月抢分训练4 不等式

训练4 不等式1．“a >0且b >0”是“a ＋b2≥ab ”成立的________条件．2．(2010·江西改编)对于实数a ，b ，c ，“a ＞b ”是“ac 2＞bc 2”的________条件． 3．若实数x ，y 满足1x 2＋1y2＝1，则x 2＋2y 2的最小值为________．4．不等式x 2－4>3|x |的解集是________．5．(2011·天津)已知集合A ＝{x ∈R ||x ＋3|＋|x －4|≤9}，B ＝{x ∈R |x ＝4t ＋1t－6，t ∈(0，＋∞)}，则集合A ∩B ＝________.6．已知p ：关于x 的不等式|x －2|＋|x ＋2|>m 的解集为R ；q ：关于x 的不等式x 2＋mx ＋4>0的解集为R .则p 成立是q 成立的________条件．7．设a ＞b ＞0，则a 2＋1ab ＋1a a －b的最小值是________．8．(2011·大纲全国)若变量x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≤6，x －3y ≤－2，x ≥1，则z ＝2x ＋3y 的最小值为________．9．已知关于x 的不等式组⎩⎪⎨⎪⎧x 2－x －2>0，2x 2＋k ＋x ＋5k <0的解集是M ，若M ∩Z ＝∅，则常数k的取值范围是________．10．若关于x 的不等式(a ＋b )x ＋2a －3b <0的解集是⎩⎨⎧⎭⎬⎫x |x <－13，则(a －3b )x ＋b －2a >0的解集是________．11．(2010·江苏)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≥0，1，x <0，则满足不等式f (1－x 2)>f (2x )的x的取值范围是________．12．若不等式|3x －b |<4的解集中的整数有且仅有1,2,3，则b 的取值范围为________． 13．若关于x 的不等式(2x －1)2<ax 2的解集中整数恰好有3个，则实数a 的取值范围是__________．14．(2011·四川改编)某运输公司有12名驾驶员和19名工人，有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车．某天需送往A 地至少72吨的货物，派用的每辆车需满载且只运送一次，派用的每辆甲型卡车需配2名工人，运送一次可得利润450元；派用的每辆乙型卡车需配1名工人，运送一次可得利润350元．该公司合理计划当天派用两类卡车的车辆数，可得最大利润为________．答案1．充分不必要 2．必要不充分 3．3＋2 2 4．(－∞，－4)∪(4，＋∞) 5．{x |－2≤x ≤5} 6．必要不充分 7．4 8．5 9．2≤k ≤310．{x |x <－3} 11．(－1，2－1) 12．5<b <7 13.⎝ ⎛⎦⎥⎤259，4916 14．4 900元。

2012版步步高高考数学考前三个月专题复习课件10(汇总

二.函数与导数高频考点整合函数单调性：若0（X ）MO, /（ r ）为增函数；若（x ）WO /（；）为减函数〔（1）求导数.＜（；£）（2）求方程f 3=0的根（3）检查/（ Q 在方程根左右的值的符号，女口果左正右负，那么「（」：）取得极大值；如果左负右正，那么f （.Q 取得极小值函数在闭区间上的最值：将在区间内取得的极值与边界值比较，得到最值映射T 函数图象常见函数的图象函数图象的变换概念函数的定义导数的概念: 导数的几何意义基本导数公式导数的运算两个函数和、差、积、商的导数复合函数的导数导数的应基础回扣训练1.已知函数/(x)=^=+(x-l)°的定义域为M,g(x)=ln (2 —x)的定义域为N,则出门"={刘一2<丫<2 IlxHl} .解析由函数—c== +(X - 1)°有意义可知，2 +x>0 \]2+ x且X - 1H0, M=[x\x> -2,且力工1}；同理N= {xlv<2}. :.MQN= {x\-2<x<2且xHl}.2.曲线y = e条在点(4, e?)处的切线与坐标轴所围三角形的面积为e? .解析・・・f (心昇"，・・・曲线在点(4, e?)处的切线的斜率为£=f (4)=芬,切线方程为y- e2 =^e2(x- 4),即^e2x-y-e2 = 0,切线与兀轴和y轴的交点坐标分别为A(2,0)、3(0, -e2),则切线与坐标轴围成的三角形043 的面积为^X2Xe2 = e2.3.定义在R上的函数/（x）既是奇函数，又是周期函数，T 是它的一个正周期.若将方程/（兀）=0在闭区间［一八T］上的根的个数记为小则〃至少为5 •解析由于/U）是R上的奇函数，则夬0） = 0.又yu）是以丁为周期的周期函数，则=/（o）=x-n = o.头為=4. ____________________________________________ 幕函数当。

2012版步步高高考数学考前三个月专题复习课件10(2)：教材回扣

3．定义在 R 上的函数 f(x)既是奇函数，又是周期函数，T ．既是奇函数，既是奇函数又是周期函数，是它的一个正周期．是它的一个正周期．若将方程 f(x)＝0 在闭区间－T，T] ＝在闭区间[－，至少为________．上的根的个数记为 n，则 n 至少为， 5 ．
解析由于 f(x)是 R 上的奇函数，则 f(0)＝0.又 f(x)是以 T T 为周期的周期函数，则 f(T)＝f(0)＝f(－T)＝0.又 f( )＝ 2 T T T T f( －T)＝f(－ )，所以 f( )＝f(－ )＝0，故 n 至少为 5. 2 2 2 2
解析
对于① 对于①，当 x1＜x2 时，f(x1)－f(x2)＞0，即 f(x1)＞f(x2)；－＞，＞；
当 x1＞ x2 时，f(x1)－f(x2)＜0，即 f(x1)＜f(x2)，所以 f(x)为减函－＜，＜，为减函正确；对于② ＝－f(2＋－＝－＝－f(x)＝数，故①正确；对于②， f(x－2)＝－＋ x－2)＝－＝ f(x －＝－正确；对于③ ＝＋ 2)，所以 f(x)＝f(x＋4)，故②正确；对于③， y＝2x 时，两，＝＋，图象重合；对于④， x＜0 时， f′(x)＞0，g′(x)＜0，f′(x) 图象重合；对于④ ＜ ′ ＞， ′ ＜，′ 正确．＞ g′(x)，故④正确． ′ ，
8．给出下列命题：．给出下列命题：都有(x ①如果函数 f(x)对任意的 x1， x2∈ R，且 x1≠ x2，都有 1 对任意的，－ x2)[f(x1)－f(x2)]＜0，则函数 f(x)在 R 上是减函数．－＜，在上是减函数．＝－f(2＋， ②如果函数 f(x)对任意的 x∈R，都满足 f(x)＝－＋ x)，对任意的 ∈ ，＝－是周期函数；那么函数 f(x)是周期函数；是周期函数 ③函数 y＝f(x)与函数 y＝f(x＋1)－2 的图象一定不能重合；＝与函数＝＋－的图象一定不能重合；＝－f(x)，－＝ ④对于任意实数 x，有 f(－x)＝－，g(－x)＝g(x)，且 x ，－＝－， f′ ＞， g′ ＞，＜ f′ ＞ ′ ．＞ 0 时，′ (x)＞0， ′ (x)＞0， x＜0 时， ′(x)＞g′(x)．则其中正确的命题是________．请将所有正确命题的序号都． (请将所有正确命题的序号都其中正确的命题是填上) 填上

2012版步步高高考数学考前三个月专题复习课件2(5汇总

§ 5导数及其应用（一）真题热身2. （2011-福建改编）若4>0,方>0,且函数f（x）=4x y—ax2—2bx +2在x=l处有极值，则ab的最大值为9 •解析f（兀）=12x2 - 2ax - 2b,•・了仗）在x = 1处有极值，:.f（1）= 12 - 2a-2b = 0, ・・・a + b = 6.又a>0, b>0,・\a + b^2\fab,・*.2\[ab^6^:.cibW当且仅当a = b = 3时等号成立，:.ab的最大值为9.解析由题4. (2011-湖南改空三岂題数 f(x)=x 2, ^(x)=lnx 的图象分别交于点M,N,则当MN 达到最小时/的值为 _.当Ovrv*时，y' <0,可知y 在此区间内单调递减；当/>¥时，W >0,可知y 在此区庾内单调递增.故当/ =申时，IMM 有最小值.考点整合1.导数的几何意义(1) 函数7=/(x)在X=x o 处的导数/'(如)就是曲线y=/(x)在点(心，/(兀0))处的切线的斜率，即k=f (x 0).(2) 曲线y=/(x)在点(心，/(•“))处的切线方程为 y —f(x^=f (x 0)(x —x 0).(3) 导数的物理意义：s' (t)=v(t)9 v r所示，2.基本初等函⑵导数(T)[u(x)±v(x)]f =u f (x)±v f (x).② [“(兀)巩x)]‘ =u f(x)v(x)^u(x)v fU).③ 譌,=3册口卄。

)(3) 复合函数求导复合函数y=/@(x))的导数和y =/(")，U =g(x)的导数之间的关系为y/ =f (”)g‘ (x). 3. 函数的性质与导数(1) 在区间(4, b)内,如果f (x)>0,那么函数/(X )在区间S ，方)上单调递增；在区间S ，方)内，如果f (x)<0,那么函数/(x)在区间(a, “)上单调递减.原函数导函数fM=cf 3)=0 /(x)=x w(neN*)f (x)=nx w -1 f(x)=sinx f f(x)=cosx f(x)=cosx f (x)=—sinx f(x)=a x(a>0 且 aHl)f (x)=a x\na f(x)=e xf 3)=e" f(x)=logaX(a>0 且 aHl)f (力=盒 f(x)=lnxf (x )=£法则(2)求可导函数极值的步骤①求f (x)；②求f (x)=0的根；③判定根两侧导数的符号；④下结论.⑶求函数/(X)在区间［4,列上的最大值与最小值的步骤①求f (x)；②求f (兀)=0的根(注意取舍)；③求出各极值及区间端点处的函数值；④比较其大小，得结论(最大的就是最大值，最小的就是最小值).例 1 设函数f(x)=ax+^~^ (a f曲线y=f(x)在点(2, /⑵)处的切线方程为y=3・⑴求冷)的解析式；(2)证明：函数y=f(x)^J图象是一个中心对称图形，并求其对称中心；(3)证明：曲线y=/(x)上任一点的切线与直线兀=1和直线y=x所围三角形的面积为定值，并求出此定值.2a + c _ 3,⑴解f (力=°-(」疣于是* 2 + b^■(2VI7 =(X - x 0). 切线与直线工1的交点为1，；k 工0 一丄丿 I2x o -21-2.所以函数g+ ；也是奇函数，其图象是以原点为中心的中心对称图形.F5fix) = x - 11.可知，函数g(x)的图象按向量4 = (1,1)平移，即得到函数/仗)的图象，故函数/(工)的图象是以点(1,1)为中心的中心对称图形.( 1 、(3)证明在曲线上任取一点兀0，Xo + ；二］,I x«丄丿由/'(X 。

2012版步步高高考数学考前三个月专题复习课件11(2)：应试指导

一、及早准备好“最后复习时间”所需的书面资料及早准备好“最后复习时间” 考试期间，每一门课都有一小段复习时间，称之曰“最后考试期间，每一门课都有一小段复习时间，称之曰“ 复习时间” 例如 6 月 7 日上午开始高考，日上午开始高考，第二天上午考理综，复习时间”．第二天上午考理综，第一天下午考完数学到次日早晨，考生自然要花一定的时间复第一天下午考完数学到次日早晨，习理、生三门课，习理、化、生三门课，平均每科有 1～2 个小时，这就是理综～个小时，三科的“最后复习时间 ” 三科的 “最后复习时间”． “最后复习时间”的使用方法不同，效果相差很大．如果最后复习时间”的使用方法不同，效果相差很大．事先没有安排，面对一大堆课本、资料、考卷，事先没有安排，面对一大堆课本、资料、考卷，你实在不清楚该看什么好．翻翻这、看看那，时间很快就过去了．看得挺多，该看什么好．翻翻这、看看那，时间很快就过去了．看得挺多，所得甚少，只落得心里乱糟糟的．浪费了这段宝贵时间，所得甚少，只落得心里乱糟糟的．浪费了这段宝贵时间，这会带来心理上的不安和烦躁．带来心理上的不安和烦躁．正确的做法是，在高考前的一个多月里，慢慢积累在“最正确的做法是，在高考前的一个多月里，慢慢积累在“ 后复习时间”里要看的资料，它应当包括：后复习时间”里要看的资料，它应当包括：
要做好克服困难夺取胜利的准备，要做好克服困难夺取胜利的准备，宁可把困难想得多一些，考题意外的难，怎么样？考题意外的容易，怎么样？考场考题意外的难，怎么样？考题意外的容易，怎么样？上遇到干扰怎么办？考试过程中天气很热怎么办？上遇到干扰怎么办？考试过程中天气很热怎么办？身体不舒服怎么办？把最好、最坏的可能都想到，考场上才不会出现影服怎么办？把最好、最坏的可能都想到，响情绪的“意外” 就有可能全心全意地做题了．响情绪的“意外”，就有可能全心全意地做题了．四、考试期间要及时调节心理 1．适当降低求胜动机，以一个平常心去考试，不可有不．适当降低求胜动机，以一个平常心去考试，切实际的期望值．要顺其自然，只求发挥出自己的实际水平．切实际的期望值．要顺其自然，只求发挥出自己的实际水平． 2．考试期间要注意避免与人发生纠纷．遇到一些不愉快．考试期间要注意避免与人发生纠纷．的事，例如与家长意见相左、与同学出现矛盾、的事，例如与家长意见相左、与同学出现矛盾、与某人发生利益冲突，这都会影响考试情绪．在考试期间要特别注意不要使益冲突，这都会影响考试情绪．矛盾激化，低调处理，大事化小，小事化无，矛盾激化，低调处理，大事化小，小事化无，以免影响考场情绪．情绪．

2012版步步高高考数学考前三个月专题复习课件10(7)教材回扣

易错点 4 忽视圆锥曲线定义中的条件致误利用椭圆、双曲线的定义解题时，要注意两种曲线的定义形式及其限制条件．如在双曲线的定义中，有两点是缺一不可的：其一，|PF1－PF2|＝2a；其二，2a＜2c.如果满足第二个条件，动点到两定点的距离之差为常数，而不是差的绝对值为常数，那么其轨迹只能是双曲线的一支．
易错点 5 忽视特殊性、误判直线与圆锥曲线位置关系过定点的直线与双曲线的位置关系问题，基本的解决思路有两个，一个是利用一元二次方程的判别式来确定，但一定要注意，利用判别式的前提是二次项系数不为零，当二次项系数为零时，直线平行于双曲线的渐近线，也就是直线与双曲线只有一个交点时，直线不一定与双曲线相切，但相切只有一个交点；二是利用数形结合的思想，画出图形，根据图形判断直线和双曲线各种位置关系所满足的条件．在直线与圆锥曲线的位置关系中，抛物线和双曲线都有特殊情况，在解题时要注意，不要忘了其特殊性．
名师警示
易错点 1 直线的倾斜角与斜率关系不清致误由直线的斜率求其倾斜角的范围问题，一般是：先求出直线的斜率 k 的取值范围，再利用三角函数的单调性，借助函数的图象，数形结合，确定倾斜角的范围．在这里要特别注意：正切函数在[0，π)上并不是单调的函数，这一点是最容易被忽略的．反过来，已知直线的倾斜角的范围求其斜率范围的问题，也同样要注意这一点．还要特别关注一点：当直线的倾斜角为π2时，直线斜率是不存在的．
＝4,故直线 AB 的方程是 y－1＝4(x－2)，即 4x－y－7＝0.
9．已知圆 C1：x2＋y2＋2x＋ay－3＝0 和圆 C2：x2＋y2－4x－
2y－9＝0 的公共弦长为 2 6，则实数 a 的值为__4_或__－__2_70__．
解析两圆的方程作差即可得公共弦所在直线的方程为 6x ＋(a＋2)y＋6＝0，而圆 C2 的方程又可化为(x－2)2＋(y－1)2 ＝14，圆心(2,1)到直线 6x＋(a＋2)y＋6＝0 的距离为 d＝ |123＋6＋a＋(a2＋＋26)2|＝ 14－6，故 a＝4 或 a＝－270.

2012版步步高高考数学考前三个月抢分训练11立体几何

训练11 立体几何1．(2011·浙江改编)若直线l 不平行于平面α，且l ⊄α，则下列结论判断正确的为________．(填序号)①α内的所有直线与l 异面；②α内不存在与l 平行的直线；③α内存在唯一的直线与l 平行；④α内的直线与l 都相交．2．以下命题中，正确的命题为________．(填序号)①已知A 、B 、C 、D 是空间任意四点，则AB →＋BC →＋CD →＋DA →＝0；②若{a ，b ，c }为空间一个基底，则{a ＋b ，b ＋c ，c ＋a }构成空间的另一个基底；③对空间任意一点O 和不共线三点A 、B 、C ，若OP →＝xOA →＋yOB →＋zOC →(其中x ，y ，z ∈R )，则P 、A 、B 、C 四点共面．3．过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线，其中与平面ABB 1A 1平行的直线共有________条．4．如图，AB 为圆O 的直径，点C 在圆周上(异于点A ，B )，直线P A 垂直于圆O 所在的平面，点M 为线段PB 的中点．有以下四个命题：①P A ∥平面MOB ；②MO ∥平面P AC ；③OC ⊥平面P AC ；④平面P AC ⊥平面PBC .其中正确的命题是________(填上所有正确命题的序号)．5．平面α外有两条直线m 和n ，如果m 和n 在平面α内的射影分别是m ′和n ′，给出下列四个命题：①m ′⊥n ′⇒m ⊥n ；②m ⊥n ⇒m ′⊥n ′；③m ′与n ′相交⇒m 与n 相交或重合；④m ′与n ′平行⇒m 与n 平行或重合．其中不正确的命题个数为________．6．过正方形ABCD 的顶点A ，引P A ⊥平面ABCD .若P A ＝BA ，则平面ABP 和平面CDP 所成的二面角的大小为________．7.如图，在直三棱柱ABC－A1B1C1中，∠ACB＝90°，AA1＝2，AC＝BC＝1，则异面直线A1B与AC所成角的余弦值是________．8．在正三棱锥S—ABC中，M、N分别是棱BC、SC的中点，且MN⊥AN，若侧棱SA＝23，则正三棱锥S—ABC外接球的表面积是________．9．如图是一个由三根细铁杆组成的支架，三根细铁杆的两夹角都是60°，一个半径为1的球放在该支架上，则球心到P的距离为________．10．设α，β是空间两个不同的平面，m，n是平面α及平面β外的两条不同直线．从“①m⊥n；②α⊥β；③n⊥β；④m⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：________(填序号)．11．(2011·福建)如图，正方体ABCD—A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度为________．12.如图，在正三棱柱ABC－A1B1C1中，D为棱AA1的中点，若截面△BC1D是面积为6的直角三角形，则此三棱柱的体积为______．13．已知四棱锥P—ABCD的底面ABCD是矩形，P A⊥底面ABCD，点E、F分别是棱PC、PD的中点，则①棱AB与PD所在直线垂直；②平面PBC 与平面ABCD 垂直；③△PCD 的面积大于△P AB 的面积；④直线AE 与直线BF 是异面直线．以上结论正确的是________．(写出所有正确结论的序号)14.三棱锥S －ABC 中，∠SBA ＝∠SCA ＝90°，△ABC 是斜边AB ＝a 的等腰直角三角形，则以下结论中：①异面直线SB 与AC 所成的角为90°；②直线SB ⊥平面ABC ；③平面SBC ⊥平面SAC ；④点C 到平面SAB 的距离是12a . 其中正确结论的序号是________．答案1．② 2．①② 3．6 4．②④ 5．4 6．45° 7.668．36π 9. 3 10．①③④⇒②(或②③④⇒①) 11. 2 12．8 3 13．①③14．①②③④高`考。

2019步步高高考数学考前三个月抢分练习16：算法初步、复数

2019步步高高考数学考前三个月抢分练习16：算法初步、复数注意事项：认真阅读理解，结合历年的真题，总结经验，查找不足！重在审题，多思考，多理解！无论是单选、多选还是论述题，最重要的就是看清题意。

在论述题中，问题大多具有委婉性，尤其是历年真题部分，在给考生较大发挥空间的同时也大大增加了考试难度。

考生要认真阅读题目中提供的有限材料，明确考察要点，最大限度的挖掘材料中的有效信息，建议考生答题时用笔将重点勾画出来，方便反复细读。

只有经过仔细推敲，揣摩命题老师的意图，积极联想知识点，分析答题角度，才能够将考点锁定，明确题意。

1、复数z ＝11＋i ，那么复数(z －1)·i 在复平面内对应的点在第________象限、2、在复平面内，复数21－i 对应的点到直线y ＝x ＋1的距离是________、3、在如下图的流程图中，假设f (x )＝2x ，g (x )＝x 3，那么h (2)的值为________、、题3题5题64、(2017·陕西改编)设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫x ||x i |＜1，i 为虚数单位，x ∈R ，那么M ∩N 为________、5、给出如下图的流程图，其功能是________、6、一组数据x i (1≤i ≤8)从小到大的茎叶图为：4|01334678，在如下图的流程图中x 是这8个数据的平均数，那么输出的s 2的值为________、7、一个算法的流程图如下图，当输出的结果为0时，输入的x 的值为________、题7题88、执行如下图的流程图，那么输出的S ＝________.9.假设复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，那么复数(z 1－z 2)i 的实部为________、10、集合A ＝⎩⎨⎧⎭⎬⎫12i ，i 2，|5i 2|，1＋i 2i ，－i 22，那么集合A ∩R ＋的子集个数为________、11、(2017·北京)在复平面内，复数2i1－i 对应的点的坐标为______、12、阅读如下图的流程图，运行相应的程序，输出的结果是________、题12题13题1413、某地区为了解70岁～80岁的老人的日平均睡眠时间(单位：h)，随机选择了50位在上述统计数据的分析中一部分计算见算法流程图，那么输出的S的值为________、14、假设如下图的算法流程图中输出y的值为0，那么输入x的值可能是________(写出所有可能的值)、答案1、四2.223、84.[)0，15、求|a－b|的值6、77、－2或18、75009、－2010、811、(－1,1)12、813、6.4214、0，－3,1。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

训练16 算法初步、复数
1．已知复数z ＝
1
1＋i
，则复数(z －1)·i 在复平面内对应的点在第________象限． 2．在复平面内，复数2
1－i 对应的点到直线y ＝x ＋1的距离是________．
3．在如图所示的流程图中，若f (x )＝2x ，g (x )＝x 3，则h (2)的值为________．
．
题3 题5 题6
4．(2011·陕西改编)设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝
⎩⎨⎧⎭
⎬⎫
x ||x i |＜1，i 为虚数单位，x ∈R ，则M ∩N 为________． 5．给出如图所示的流程图，其功能是________．
6．一组数据x i (1≤i ≤8)从小到大的茎叶图为：4|0 1 3 3 4 6 7 8，在如图所示的流程图中x 是这8个数据的平均数，则输出的s 2的值为________．
7．已知一个算法的流程图如图所示，当输出的结果为0时，输入的x 的值为________．
题7 题8
8．执行如图所示的流程图，则输出的S ＝________.
9.若复数z 1＝4＋29i ，z 2＝6＋9i ，其中i 是虚数单位，则复数(z 1－z 2)i 的实部为________．
10．已知集合A ＝⎩⎨⎧⎭⎬⎫12i
，i 2，|5i 2|，(1＋i )2
i ，－i 22，则集合A ∩R ＋的子集个数为________．
11．(2010·北京)在复平面内，复数2i
1－i 对应的点的坐标为______．
12．阅读如图所示的流程图，运行相应的程序，输出的结果是________．
题12 题13 题14
13．某地区为了解70岁～80岁的老人的日平均睡眠时间(单位：h)，随机选择了50位老人进行调查，下表是这50位老人睡眠时间的频率分布表：
14．若如图所示的算法流程图中输出y 的值为0，则输入x 的值可能是________(写出所有可能的值)．
答案
1．四 2.
2
2
3．8 4.[)0，1 5．求|a －b |的值 6．7 7．－2或1
8．7 500 9．－20 10．8 11．(－1,1) 12．8 13．6.42 14．0，－3,1。