自适应控制讲义—--教材讲义
第11讲 自适应控制概论

这三方面的功能是自适应控制系统所必须具有的功能.
1 自适应控制的定义(3/4)
由此可见,自适应控制系统必须具有三个特征或功能: 过程信息的在线积累
在线积累过程信息的目的,是为了降低对被控系统的 的结构和参数值的原有的不确定性.
为此,可用系统辨识的方法在线辨识被控系统的结构 和参数,直接积累过程信息;也可通过量测能反映过程 状态的某些辅助变量,间接积累过程信息. 可调控制器
Quotation: “We learnt from bitter experience”.
1 自适应控制的定义(2/4)
从自适应控制能修正自己的特性主动适应被控系统和其 所处的环境的变化这一角度来说,Gibson的定义较好的刻 划了自适应控制的特征.
下面通过Gibson的定义来研究自适应控制研究的内容和 范围.
第十讲 自适应控制概论(8/10)
60年代中期--Parks的基于Lyapunov稳定性理论的模型 参考自适应控制设计 60年代末期--Landau等人的基于Popov超稳定性理论 的模型参考自适应控制设计
李雅普诺夫
朗道
第十讲 自适应控制概论(8/10)
自校正控制方法 50年代末期--Kalmann提出的边辨识边控制的思想
第十讲 自适应控制概论(10/10)
出于实际控制系统设计和应用的需要,以及微处理器等计算工 具或器件的迅猛发展,都为自适应控制应用的发展创造了条件, 这又反过来促进了自适应控制理论的发展. 经过30多年的发展,自适应控制已成为现代控制理论的一 个相当重要的分支,并且是发展最为迅速的分支之一. 下面,将分别介绍: 自适应控制的定义 自适应控制系统的形式. 自适应控制研究中的理论问题 自适应控制的应用情况
第5章自适应控制

5.1不断地检测系统参数( 系统工作过程中,系统本身能不断地检测系统参数(模型 参数) 根据参数的变化,改变控制参数或改变控制作用, 参数),根据参数的变化,改变控制参数或改变控制作用, 使系统运行于最优或接近于最优工作状态。 使系统运行于最优或接近于最优工作状态。 自适应控制的核心: ⊙自适应控制的核心:通过系统输出或状态输出检测系统参 调整控制参数。 数,调整控制参数。 自适应控制是一种复杂的反馈控制, ⊙自适应控制是一种复杂的反馈控制,即使对于线性定常对 其自适应控制是非线性时变反馈。 象,其自适应控制是非线性时变反馈。自适应控制系统系 统设计与分析,要比一般的反馈控制复杂得多。 统设计与分析,要比一般的反馈控制复杂得多。采用非线 性系统分析方法。 性系统分析方法。
5.4 自适应控制的发展
50年代 MIT的Whitaker等提出了飞机自动驾驶仪的模型 年代: ☞ 50年代:MIT的Whitaker等提出了飞机自动驾驶仪的模型 参考自适应控制,称为MIT方案。MIT方案中 MIT方案 方案中, 参考自适应控制,称为MIT方案。MIT方案中,采用局部参 数最优化理论求得自适应控制律, 数最优化理论求得自适应控制律,但系统的稳定性无法保 Kalman提出自校正思想 提出自校正思想, 证。Kalman提出自校正思想,即用最小二乘估计对象的参 在此基础上计算最优控制,系统称为自最优控制系统。 数,在此基础上计算最优控制,系统称为自最优控制系统。 60年代 建立了Lyapunov稳定性理论体系, 年代: Lyapunov稳定性理论体系 ☞ 60年代:建立了Lyapunov稳定性理论体系,为自适应控 制系统稳定性分析提供了有效的工具。Popov提出了超稳 制系统稳定性分析提供了有效的工具。Popov提出了超稳 定性理论。Butchart和Shachcloth、Parks、 定性理论。Butchart和Shachcloth、Parks、Phillipson 等提出了用Lyapunov Lyapunov稳定性理论设计模型参考自适应控制 等提出了用Lyapunov稳定性理论设计模型参考自适应控制 系统的方法,从而保证了系统的稳定性。 系统的方法,从而保证了系统的稳定性。 ☞ 70年代:Monopoli仅用对象输入输出测量值设计模型参 70年代:Monopoli仅用对象输入输出测量值设计模型参 年代 考自适应控制系统。 考自适应控制系统。证明了模型参考自适应控制系统的全 局稳定性( 局稳定性(即模型参考自适应控制系统的内部信号有界且 输出误差收敛于0)。Astrom Wittenmark进一步发展和 Astrom和 输出误差收敛于0)。Astrom和Wittenmark进一步发展和 完善了自校正控制,讨论了自校正控制的收敛性。 完善了自校正控制,讨论了自校正控制的收敛性。 Wellstead提出了零极点配置自校正调节器设计方法 提出了零极点配置自校正调节器设计方法。 Wellstead提出了零极点配置自校正调节器设计方法。
自适应控制 课件

自适应控制与应用自适应控制与应用第一章自适应控制基本概念第二章模型参考自适应系统设计初步第三章用李亚普诺夫稳定性理论设计MRAC第四章用波波夫超稳定性理论设计MRAC第五章自校正技术及自校正控制器调节器的设计第六章极点配置的自校正技术第一章自适应控制的基本概念1-1 自适应控制的产生1-2自适应控制的定义1-3 自适应控制的基本原理1-4 自适应控制系统的主要类型1-5自适应控制的应用1-1 自适应控制的产生传统的控制系统设计方法,通常是首先建立被控对象的数学模型,然后根据所建数学模型的特性设计控制器(控制律),实施控制。
为了要成功的设计一个控制系统,无论是常规的反馈控制系统还是最优控制系统,都必须要设计者事先知道被控对象的所有特征,及其结构和参数。
1-1 自适应控制的产生设计都要求事先掌握被控对象或被控过程的数学模型。
然而有些数学模型是很难事先确知的,或者由于种种原因,一些系统的数学模型会在运行过程中发生较大范围的变化,这就是说,设计者对系统的特性并不是完全掌控的,或者说系统的特性是不肯定的。
在这些情况下,常规控制就往往达不到预定的控制要求。
引起被控对象特性发生变化的主要原因有:(1)由于系统所处环境的变化而引起的被控对象的参数值的变化。
1-1 自适应控制的产生许多控制对象的数学模型随着时间或工作环境的改变而发生变化,而变化规律往往事先不知道。
例如:引起被控对象特性发生变化的主要原因有:(1)由于系统所处环境的变化而引起的被控对象的参数值的变化。
1-1 自适应控制的产生许多控制对象的数学模型随着时间或工作环境的改变而发生变化,而变化规律往往事先不知道。
(2)系统本身由于工作情况的变化而引起自身参数值的改变.1-1 自适应控制的产生当被控对象的数学模型参数在小范围内变化时,可用一般的反馈控制、最优控制或补偿控制等方法使得系统对外部的扰动或内部参数的小范围变动不很敏感,以达到预期性能。
而当被控对象的数学模型参数在大范围内变化时,上述方法就不能圆满解决问题了,为了使控制对象的参数在大范围变化时,系统仍能自动的工作于最优或次优状态,因而提出了自适应控制的问题。
自适应控制讲稿_03

自适应控制_3系统工程研究所冯祖仁2007.9第三章自校正控制(一)—3.1•自校正调节器(Self-tuning regulator)一词来源于早期的文献。
使用自适应控制器的一个重要原因是对象或环境的参数不断变化。
分析这样的系统非常困难。
•于是假设对象的参数定常但未知。
•“自校正”一词表示了控制器的参数收敛于“理想”控制器参数这样一种性质,该“理想”控制器是假设对象已知时设计的。
第三章自校正控制(一)—3.1•示意框图中的内容可有多种方式实现。
可以选择许多可能的模型和控制器结构。
参数估计可以在线连续地进行,也可以离线“批处理”。
在通常采用的数字控制器中,控制和参数估计的采样速率可以不同。
甚至可以采用混合方式:连续控制+离散参数估计。
参数估计和控制器设计都可以采用各种不同的方式。
还可以采用非线性模型和非线性控制方式。
•在自校正控制中,估计的参数被当作真实参数使用,这样做的依据是:确定性等价原理(Certainty equivalence principle)第三章自校正控制(一)—3.1•这样看来,示意框图表示了内涵非常丰富的结构。
对于自校正调节器,模型结构和参数表示是非常重要的。
一个直接的做法是估计传递函数的参数,这是间接自适应算法。
不直接修改控制器参数,而是根据估计的过程参数间接地计算控制器参数。
第三章自校正控制(一)—3.1•另一种经常性的做法是改变模型的表示形式,使得可以直接估计控制器的参数,这是直接自适应算法。
•间接自适应算法——显式自适应法(因为要识别过程参数,即基于辨识的自适应控制方法)•直接自适应算法——隐式自适应法(因为不要识别过程参数,即无辨识的自适应控制方法)第三章自校正控制(一)• 3.2 极点配置设计(Pole Placement Design )这是一种简单的控制设计方法,基本思想是设计一个控制器,使闭环系统的极点为给定极点。
这样,反馈系统的响应就是所需要的。
•过程模型(Process Model )设过程可以表示为如下SISO 系统:y 是输出,u 是输入,v 是扰动。
《自适应控制》课件

参考文献
文献1 文献2 ……
通过对被控对象进行实验测 定,确定其动态特性参数。
状态观测理论
通过滤波、估计等方法,对 被控对象未知状态进行实时 观测。
模型参考自适应控 制理论
基于模型参考原理的自适应 控制理论,如MRAC算法、 Model-free算法等。
基于模型参考自适应控制算法
1
基于最小二乘法的MRAC算法
通过建立被控对象和控制器的最优权重匹配模型进行控制。
自适应控制的基本概念
系统模型的表示
通过构建合适的系统模型来描 述被控对象的动态特性。
控制器的表示
通过合理设计控制器结构和参 数,实现对被控对象的自适应 控制。
自适应控制算法的分类
基于系统模型或反馈信号进行 参数计算的算法,如MRAC算 法、Model-free算法等。
自适应控制的基础理论
参数辨识理论
自适应控制在飞行器控 制中的应用
通过改进控制方法,提高飞行 器的控制精度和稳定性,并提 高飞机的效率。
总结
1 自适应控制的优势和限制
2 优点, 但也存在精度不高、计算量大等限制。
随着计算机技术的不断进步,自适应控制 将在更广泛的工业应用中得到应用。
2
基于模型预测控制的MRAC算法
通过预测被控对象的状态和输出,实现控制器参数的逐步修正。
自适应控制在实际应用中的应用实例
自适应控制在电机控制 中的应用
通过改进控制方法,提高电机 效率和精度,并提高电机的动 态响应性。
自适应控制在化工过程 中的应用
通过精细含水率控制、温度控 制等,实现精细控制和生产效 率的提高。
《自适应控制》PPT课件
了解自适应控制的定义、基本概念,了解自适应控制在实际应用中的应用实 例,以及自适应控制的优势和限制。
自适应控制

目录第一章自适应控制概述 (1)第一节自适应控制的产生背景及分类 (1)一.自适应控制产生的背景 (1)二.自适应控制的原理及分类 (2)第二章模型参考自适应控制(MODEL REFERENCE ADAPTIVE CONTROL)简称MRAC3第一节MRA C的基本概念 (3)第二节最优化的设计方法 (4)一、利用梯度法的局部参数最优化的设计方法 (4)第三节基于李雅普诺夫第二方法稳定性理论的MRA C设计方法 (7)一.关于李雅普诺夫( Liaupunov) 稳定性的第二方法 (7)第四节基于超稳定理论的MRA C设计方法 (13)一、关于超稳定性理论的基本概念 (13)二、用超稳定理论设计MRAC系统 (15)第三章自校正控制 (18)第一节自校正控制的原理及组成 (18)第二节最小方差控制律 (21)第一章自适应控制概述任何一个动态系统,通常都具有程度不同的不确定性。
这种不确定性因素的产生主要由于:(1)系统的输入包含有随机扰动,如飞行器飞行过程中的阵风;(2) 系统的测量传感器具有测量噪声;以上两者又称为不确定性的(或随机的)环境因素。
(3) 系统数学模型的参数甚至结构具有不确定性。
如导弹控制系统中气动力参数随导弹飞行高度、速度、导弹质量及重心的变化而变化。
在只存在不确定环境因素,但系统模型具有确定性的情况下,这是随机控制需要解决的问题;而自适应控制是解决具有数学模型不确定性为特征的最优控制问题。
这时如果系统基本工作于确定环境下,则称为确定性自适应控制;如果系统工作于随机环境下,则称为随机自适应控制。
自适应控制的提法可归纳为:在系统数学模型不确定的条件下(工作环境可以是基本确定的或是随机的),要求设计控制规律,使给定的性能指标尽可能达到及保持最优。
为了完成以上任务,自适应控制必须首先要在工作过程中不断地在线辨识系统模型(结构及参数)或性能,作为形成及修正最优控制的依据,这就是所谓的自适应能力,它是自适应控制主要特点。
自适应控制课件

x x 1得大.若到于在控零质制的量律数m,u已由知m这(的个m情控况2制下~x器,可结以2 ~x合得) 二到其阶按中系指~x统数传x收(t递敛) 函的数误m (、t差)表跟系示踪统跟误:踪差x 误一2差般,表~x 达是式一2我~x个们严可0格以
2.现在假设质量m这个参数是未知的。我们可以用如下的控制规律:
是关于时间t的m x 1维向量函数,v(t)是可以测量的m x 1维向量。如果向量(t) 服从如下
规律:
(t) sgn(k )ev(t)
(2)
其中γ是正常数,那么e(t)和φ(t)全局有界。而且,如果v(t)有界,那么
当 t 时,e(t) 0
简单地说,上述lemma告诉我们,如果输入信号以(2)的形式依赖于输出信号,那么整 个系统是全局稳定的(所有的状态都有界)
mˆ
0 t
, w x
w2dr
0
实际上,未知参数m是慢变的,在每一个新时刻,上述估计必须重新计算。根据 优化理论,我们可以用一种迭代公式代替重复使用上式。我们可以定义:
1 P(t) t
w2dr
0
函数P(t)称为估计增益。他的更新可以直接由下式获得:
d [P1] w2 dt
t
J e2(r)dr e(t) mˆ (t)x(t) u(t)
0
估算最小预测误差的方法:
dJ 0 ,这里 为被估计的参数
d
e.g.8.2
预测误差的实质就是参数的估计值 mˆ 与已知输入u的匹配误差。总误差最小化可
以潜在的平均掉测量噪声的影响。从而得到估计方程:
t
wudr
e.g.8.1
考虑一个质量弹簧阻尼系统,其外部作用力f(t)被视为输入u,其性态可以描述为:
第二章 自适应控制

(PN 1 x(n N 1)xT (n N 1))1
为避免矩阵求逆,并使 N 1 与 N 具
有一个简单的关系,利用矩阵求逆定理
PN1 PN KN1xT (n N 1)PN
(8)
K N 1
1
xT
PN x(n N (n N 1)PN
1) x(n
N
1)
将(8)式带入(7)式,整理得到最小二乘的递推公式
可写成矩阵方程
y(n 1)
YN
y(n
2)
y(n
N
)
e(n 1)
N
e(n
2)
e(n N )
xT (n 1) y(n) y(1) u(n 1) u(1)
XN
xT
n
2
y(n 1)
y(2)
u(n 2)
u(2)
xT n N y(n N ) y(N ) u(n N ) u(N )
所以新的参数估计
N 1
是用新的观测值与基于老
模型预测得到的量xT (n N
数
N
加以修正得到。
K N 1
1为)修N 正之系偏数差.,对老参
因此,若知道前一时刻的
道
N 1
了,
N
PN
,我们就可以知
确定
o
Po
的初值的方法
(1)若已知参数的大致范围,可在此范围内确定初 值
(2)若完全不知道,参数范围可简单取
n 方程的阶数;e(k) 为不可测量的随机干扰
问题: 假设方程阶数n已知,如何由输入输出的 观测数
据 y(k) , u(k) 来估计模型的参数 a1,a2 an,b0,b1, bn
2模型参数的最小二乘估计方法
自适应控制课件

控制器 参数计算
过程模型 在线辨识
w(k )
可调控制器 u(k)
被控过程
y(k)
-
自校正控制系统结构图
2.2 模型参考自适应控制
生物能够通过自觉调整自身参数改变自己的习性,以适应新的环境特性
自适应控制器:通过及时修正自己的特性以适应对象和扰动的动态特性变化, 使整个控制系统始终获得满意的性能。
自适应控制的特点:
研究具有不确定性的对象或难以确知的对象 能消除系统结构扰动引起的系统误差 对数学模型的依赖很小,仅需要较少的验前知识 自适应控制是较为复杂的反馈控制
标量输入信号
Dm ( p) ym Nm ( p)r
标量输出信号
微分算子
n
Dm ( p) ami pi i0
m
Nm ( p) bmi pi i0
(2.7)
(2.8) (2.9)
参考模型的输入输出方程的常系数
在参数自适应方案中,可调系统的输入输出方程
信号综合自适应方案的系统模型
x(k 1) Ax(k) Bu(k) ua (e,k) x(0) x0 , ua (0) ua0
(2.4) (2.5) (2.6)
2.2.1.1 并联模型参考自适应系统的数学模型 二、用输入-输出方程描述的模型参考自适应系统
参考模型 对于连续系统一般采用微分算子的形式表示
(2.3)
根据广义误差信号,按照一定的自适应规律产生的
对于离散模型参考自适应控制系统
参考模型
8自适应控制(共32张)

23
第23页,共32页。
1 问题(wèntí)描述
n阶SISO非线性系统:
其中,
自适应控制设计目标:使系统的输出渐近地跟踪一个期望的输出 yd (t)
•
xm 4xm 4r 取自适应增益\gamma为2 ,两个控制器参数的初制均为0。系统和参考模型的初 是条件都取为0
18
第18页,共32页。
跟踪误差 (wùchā)收敛,
参数误差 (wùchā)不收敛
(只有当参考信号r(t)满足一定的条件时,估计参数才会收敛到 理想19 控制器参数?)
第19页,共32页。
最简单的方法: 此方法的缺点:噪声大;加速度有可能为0
较好的方法:最小二乘法,选择估计规律使总的预测误差
其中,e为
从而得到估计值
••
其中 w x
最小
这样,如果未知参数是慢变的,在每一个新的时刻,上述估计必须重新计算。
12
第12页,共32页。
8.1.2 如何设计(shèjì)自适应控制器
自适应控制设计包括以下3个步骤:
定义组合跟踪误差的量度s为
定义信号量v为
得闭环误差方程
校正参数
^
m的方法之一是下面的
参数更新规律:
• ^
m vs,其中正常数称为自适应增益
8
第8页,共32页。
使用Lyapunov理论分析这个自适应(shìyìng)系统的稳定性和收敛性。
取Lyapunov函数为
得
•
根据参数更新规律
^
自适应控制(研究生经典教材)

自适应控制Adaptive control1.关于控制2.关于自适应控制3.模型参考自适应控制4.自校正控制5.自适应替代方案6.预测控制参考文献主要章节内容说明:第一部分:第一章自适应律的设计§1.参数最优化方法§2.基于Lyapunov稳定性理论的方法§3.超稳定性理论在自适应控制中的应用第二章误差模型§1.Narendra误差模型§2.增广矩阵§3.线性误差模型第三章MRAC的设计和实现第四章小结第二部分:第一章模型辨识及控制器设计§1.系统模型:CARMA模型§2.参数估计:LS法§3.控制器的设计方法:利用传递函数模型§4.自校正第二章最小方差自校正控制§1.最小方差自校正调节器§2.广义最小方差自校正控制第三章极点配置自校正控制§1.间接自校正§2.直接自校正1.About control engineering education1)control curriculum basic concept(1)dynamic system●The processes and plants that are controlled have responses that evolvein time with memory of past responses●The most common mathematical tool used to describe dynamic system isthe ordinary differential equation (ODE).●First approximate the equation as linear and time-invariant. Thenextensions can be made from this foundation that are nonlinear 、time-varying、sampled-data、distributed parameter and so on.●Method of building model (or equation )a)Idea of writing equations of motion based on the physics andchemistry of the situation.b)That of system identification based on experimental data.●Part of understanding the dynamical system requires understanding theperformance limitations and expectation of the system.2.stabilityWith stability, the system can at least be used●Classical control design method, are based on a stability test.Root locus 根轨迹Bode‟s frequency response 波特图Nyquist stability criterion 奈奎斯特判据●Optimal control, especially linear-quadratic Gaussian (LQG) control (线性二次型高斯问题) was always haunted by the fact that method did notinclude a guarantee of margin of stability.The theory and techniques of robust (鲁棒)design have been developedas alternative to LQG●In the realm of nonlinear control, including adaptive control, it iscommon practice to base the design on Lyapunov function in order to beable to guarantee stability of final result.3.feedbackMany open-loop devices such as programmable logic controllers (PLC) are in use, their design and use are not part of control engineering.●The introduction of feedback brings costs as well as benefits. Among thecosts are need for both actuators and sensors, especially sensors.●Actuator defines the control authority and set the limits of speed indynamic response.●Sensor via their inevitable noise, limit the ultimate(最终) accuracy ofcontrol within these limits, feedback affords the benefit of improveddynamic response and stability margins, improved disturbancerejection(拒绝) ,and improved robustness to parameter variability.●The trade off between costs and benefits of feedback is at the center ofcontrol design.4.Dynamic compensation●In beginning there was PID compensation, today remaining a widely usedelement of control, especially in the process control.●Other compensation approaches : lead-and-log networks (超前-滞后)observer-based compensators include : pole placement, LQG designs.●Of increasing interest are designs capable of including trade-off amongstability, dynamic response and parameter robustness.Include: Q parameterization, adaptive schemes.Such as self-tuning regulators, neural-network-based-controllers.二、historical perspectives (透视)●Most of early control manifestations appear as simple on-off (bang-bang)controllers with empirical (实验;经验性的) setting much dependent uponexperience.●The following advances such as Routhis and Hurwitz stability analysis(1877).Lyapunov‟s state model and nonlinear stability criteria(判据) (1890) .Sperry‟s early work on gyroscope and autopilots (1910), and Sikorsky‟swork on ship steering (1923)Take differential equation, Heaviside operators and Laplace transform astheir tools.●电机工程(electrical engineering)The largely changed in the late 1920s and 1930s with Black‟s developmentof the feedback electronic amplifier, Bush‟s differential analyzer, Nyquist‟sstability criterion and Bode‟s frequency response methods.The electrical engineering problems faced usually had vary complex albeitmostly linear model and had arbitrary (独立的;随机的) and wide-ringingdynamics.●过程控制(process control in chemical engineering)Most of the progress controlled were complex and highly nonlinear, butusually had relatively docile (易于处理的) dynamics.One major outcome of this type of work was Ziegler-Nichols‟PIDthres-term controller. This control approach is still in use today, worldwidewith relatively minor modifications and upgrades (including sampled dataPID controllers with feed forward control, anti-integrator-windupcontrollers :抗积分饱和,and fuzzy logic implementations).●机械工程(mechanical engineering)The application of controls in mechanical engineering dealt mostly in thebeginning with mechanism controls, such as servomechanisms, governorsand robots.Some typical control application areas now include manufacturing processcontrols, vehicle dynamic and safety control, biomedical devices and geneticprocess research.Some early methodological outcomes were the olden burger-Kahenbugerdescribing function method of equivalent linearization, and minimum-time,bang-bang control.●航空工程(aeronautical engineering )The problems were generally a hybrid (混合) of well-modeled mechanicsplus marginally understood fluid dynamics. The models were often weaklynonlinear, and the dynamics were sometimes unstable.Major contributions to framework of controls as discipline were Evan‟s rootlocus (1948) and gain-scheduling.●Additional major contributions to growth of the discipline of control over thelast 30-40 years have tended to be independent of traditional disciplines.Examples include:Pontryagin‟s maximum principle (1956) 庞特里金Bellman‟s dynamic programming (1957)贝尔曼Kalman‟s optimal estimation (1960)And the recent advances in robust control.三、Abstract thoughts on curriculum●The possibilities for topic to teach are sufficiently great. If one tries topresent proofs of all theoretical results. One is in danger of giving thestudents many mathematical details with little physical intuition orappreciation for the purposes for which the system is designed.●Control is based on two distinct streams of thought. One stream is physicaland discipline-based. Because one must always be controlling some thing.The other stream is mathematics-based, because the basis concepts ofstability and feedback are fundamentally abstract concepts best expressedmathematically. This duality(两重性) has raised, over the years, regularcomplaints about the …gap‟ between theory and practice.●The control curriculum typically begins with one or two courses designed topresent an overview of control based on linear, constant, ODE models,s-plane and Nyquist‟s stability ideas, SISO feedback and PID, lead-lay andpole-placement compensation.These introductory courses can then be followed by courses in linear systemtheory, digital of control, optimal control, advanced theory of feedback, andsystem identification.四、Main control courses●Introduction to controlLumped system theoryNonlinear controlOptimal controlAdaptive controlRobot controlDigital controlModeling and simulationAdvanced theoryStochastic processesLarge scale multivariable systemManufacturing systemFuzzy logic Neural Networks外文期刊:《Automatic》IFAC 国际自动控制联合会Computer and control abstractsIEEE translations on Automatic controlAutomation●Specialized \ experimental courses✓Intelligent controlApplication of Artificial IntelligenceSimulation and optimization of lager scale systems robust control ✓System identification✓Microcomputer-based control systemDiscrete-event systemsParallel and Distributed computationNumerical optimization methodsNumerical system theory●Top key works from 1963-1995 in IIACAdaptive control 305Optimal control 277Identification 255Parameter estimation 244Stability 217Linear system 184Non-linear systems 168Robust control 158Discrete-time systems 143Multivariable systems 140Robustness 140Multivariable systems control systems 110Optimization 110Computer control 104Large-scale systems 103Kalman filter 102Modeling 107为什么自适应 《Astrom 》chapter 1✓ 反馈可以消除扰动。
自适应控制讲稿_05

第五章 模型参考自适应系统—5.2
• 根据这个近似, MIT规则可以写为:
⎛ ⎞ am dθ1 b 1 = −γ ′e ⎜ uc ⎟ = −γ ′b u c e = −γ uc e p + am dt p + am ⎝ p + a + bθ 2 ⎠ ⎛ ⎞ am dθ 2 1 b = −γ ′e ⎜ − y ⎟ = γ ′b ye = γ ye, dt p + am p + am ⎝ p + a + bθ 2 ⎠
• 误差和参数的收敛性(Error and Parameter Convergence) • 构造模型参考自适应系统的目的是为了使跟踪误差 e=y-ym 趋于零。但这并不意味着控制器的参数一定收敛到正确值。 • 例5.3 Lack of parameter convergence • 考虑例5.1的前馈自适应问题。设 G(s)=1,过程的输入输出 关系成为 y=ku ,控制律为 u=θuc ,期望的响应为 ym=k0uc 。跟踪误差:
J (θ ) = 1 2 e 2
为使 J 减小,合理的想法是:总是沿着 J 的负梯度方向改变 θ: ∂J ∂e dθ
dt = −γ ∂θ = −γ e ∂θ
这就是著名的 MIT 规则。
第五章 模型参考自适应系统—5.2
• 偏导 ∂e / ∂θ (有时称为系统的敏感度导数)表示了误差是如 何受可调参数影响的。如果假设相比系统变量的变化,参数 变化的速率很慢,则可以认为 θ 是常数。 • 还可以选择其他形式的损失函数,如:
自 适 应 控 制_5
系统工程研究所 冯祖仁 2007.9
第五章 模型参考自适应系统
Model Reference Adaptive Systems
自适应控制讲稿_7自适应逆控制
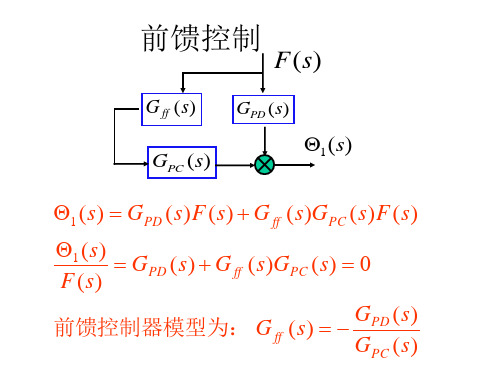
第八章 自适应逆控制——8.2
• 抖动信号迭加方法A(直接迭加)
抖动 δk
uk
Σ
对象输入 uk 对象 P(z)
yk
对象扰动 nk Σ 误差k
对象输出 zk
期望响应 Σ 信号
uk
自适应模型 ˆ Pk ( z )
ˆ yk
ˆ k P ( z )( uk k ) nk Pk ( z )( uk k ) ˆ ( P ( z ) Pk ( z ))( uk k ) nk
d (k ) x(k ) 其中,P 是输入信号和期望响应 d ( k ) x ( k 1) 之间的互相关向量: P E d ( k ) xk E d ( k ) x ( k L )
R 是输入信号的相关矩阵(对称正定)
x(k ) x(k ) x ( k ) x ( k 1) T R E xk xk E
T 2 ( k ) d 2 ( k ) 2 d ( k ) h T xk h T x k x k h 均方误差: 2 2
T T MSE E (k ) E d (k ) 2 E d (k ) xk h hT E xk xk h
E d 2 (k ) 2 PT h hT Rh
前馈控制
G ff (s)
F (s )
1 ( s)
GPD (s)
GPC (s)
1 ( s ) G PD ( s ) F ( s ) G ff ( s )G PC ( s ) F ( s ) 1 ( s ) G PD ( s ) G ff ( s )G PC ( s ) 0 F (s) G PD ( s ) 前馈控制器模型为: G ff ( s ) G PC ( s )
自适应控制课件——多模型自适应控制

0.0096 6.8978 B1 0.2652 0.0131 0.0556
,
0.0193 0.3138 0.1649 18.7269 1.4760
A2 B2 r r
三、多模型自适应飞行控制律重构
假设操纵面故障只影响系统的控制矩阵B,而正常模态和故障模态下的
A, d都相同。事实上,操纵面故障主要影响操纵效率. 当飞机发生故障时采用相应的重构控制律, 是一种典型的多模态切换控制。 采用多模型自适应控制可以自动监测 飞机状态的变化,并选择相应的控制律 飞行高度为3000米、速度0.5马赫 双引擎喷气式飞机线性化模型
1 q M Iy
令 f ( X ) q f q ( X ) 得到扩展线性化方程:
f ( X ) A f q ( X ) f ( X ) f ( X ) U q B f q ( X ) f q ( X ) q U
三、多模型自适应飞行控制律重构
对线性化系统采用线性反馈
u u K ( x x ) G(w w)
通过选择合适的K使系统具有与平衡点无关的常值稳定闭环极点, 通过选择合适的G可以使系统跟踪期望指令w
三、多模型自适应飞行控制律重构
纵向运动的控制
纵向短周期运动的状态变量 简化的速度方程: V
X [ q]T
u u1
重构控制器1
。 。 。
固定模型N
。 。 。
yN
eN
固定模型1
y1 y
e1
飞机
自适应控制讲义(模型参考部分)2013-v1
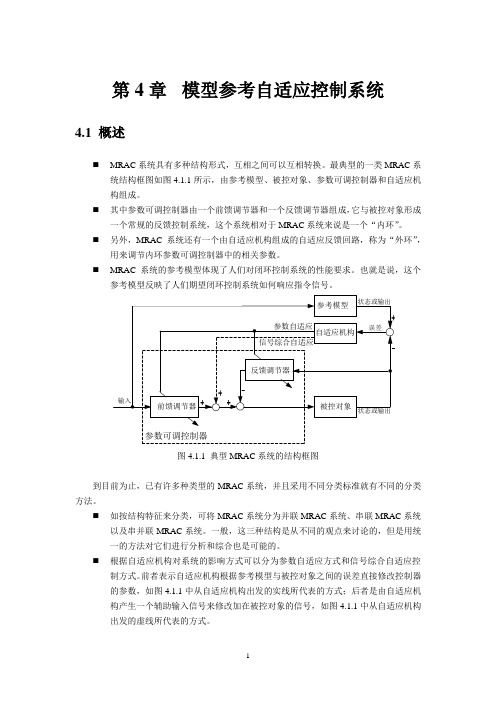
第4章模型参考自适应控制系统4.1 概述⏹MRAC系统具有多种结构形式,互相之间可以互相转换。
最典型的一类MRAC系统结构框图如图4.1.1所示,由参考模型、被控对象、参数可调控制器和自适应机构组成。
⏹其中参数可调控制器由一个前馈调节器和一个反馈调节器组成,它与被控对象形成一个常规的反馈控制系统,这个系统相对于MRAC系统来说是一个“内环”。
⏹另外,MRAC系统还有一个由自适应机构组成的自适应反馈回路,称为“外环”,用来调节内环参数可调控制器中的相关参数。
⏹MRAC系统的参考模型体现了人们对闭环控制系统的性能要求。
也就是说,这个参考模型反映了人们期望闭环控制系统如何响应指令信号。
图4.1.1 典型MRAC系统的结构框图到目前为止,已有许多种类型的MRAC系统,并且采用不同分类标准就有不同的分类方法。
⏹如按结构特征来分类,可将MRAC系统分为并联MRAC系统、串联MRAC系统以及串并联MRAC系统。
一般,这三种结构是从不同的观点来讨论的,但是用统一的方法对它们进行分析和综合也是可能的。
⏹根据自适应机构对系统的影响方式可以分为参数自适应方式和信号综合自适应控制方式。
前者表示自适应机构根据参考模型与被控对象之间的误差直接修改控制器的参数,如图4.1.1中从自适应机构出发的实线所代表的方式;后者是由自适应机构产生一个辅助输入信号来修改加在被控对象的信号,如图4.1.1中从自适应机构出发的虚线所代表的方式。
根据MRAC系统的设计方法可以分为如下三类:基于局部参数最优化的方法、基于Lyapunov稳定性理论的方法以及基于Popov超稳定性理论的方法。
⏹基于局部参数最优化的方法是最早采用的MRAC系统设计方法,通常称为MIT律。
⏹基于Lyapunov稳定性理论的方法是Butcharty及Parks于六十年代中期相继提出的,这种方法与局部参数最优化方法相比,不仅可保证系统的稳定性,还具有自适应速度快的优点。
⏹由法国学者Landau于1969年提出的基于Popov超稳定性理论的方法,主要是以Popov超稳定性理论为基础,由于不需要选择Lyapunov函数,并且能给出一族自适应规律,从而该方法有利于设计者结合实际系统灵活地选择合适的自适应规律。
自适应控制讲稿_06

自适应控制_6系统工程研究所冯祖仁2007.10第六章MRAC 鲁棒性分析• 6.1 MRAC 的鲁棒性问题•鲁棒性(Robustness,强健性)对一个控制问题进行求解首先需要对被控对象、环境预设一些理想条件。
然后根据控制指标要求和设计约束,设计出控制策略。
成功设计出的控制策略在对象和环境满足理想条件的情况下,自然可以使控制系统的行为达到控制指标。
•鲁棒性检验检验在一些理想条件不能满足时,按理想条件设计的控制策略是否还能使控制系统的行为达到控制指标。
•鲁棒设计放松一些理想条件,根据控制指标要求和设计约束,设计出控制策略。
第六章MRAC 鲁棒性分析—6.1•MRAC 的鲁棒性问题•理想条件:–对象线性时不变–没有扰动,没有未建模动态(对象阶已知,模型与对象同阶)–逆稳定(对象为最小相位系统)–相对阶差已知–增益符号已知–满足“完全可匹配条件”(对于状态可测的MRAC)•控制指标要求:全局渐近稳定性•然而,一个实际对象很难满足这些条件。
那么,检验在一些理想条件不能满足的情况下MRAC 的性能,以及设计非理想条件下的MRAC(即鲁棒性检验和鲁棒设计),就是模型参考自适应控制的鲁棒性问题。
第六章MRAC 鲁棒性分析—6.22)线性回路的不稳定性•这种不稳定性表现为:当控制器增益漂移到或固定在某个足够高的值时,即使中断自适应作用,系统仍然不稳定。
•这种不稳定由增益过高造成,可以用经典的线性反馈理论解释。
例:具有小寄生时间常数μ的实际对象的自适应调节器问题:调节器为可知,k B 单调增!闭环方程为:)(2)()()()()()(t u t z t zt u t z t y a t yp p p +−=−+= μ2)()()(pB B p B y k t y t k t u γ=−= )()()(2)()()())(()(t z t y t k t zt z t y t k a t yp B p B p p −=++= μ第六章MRAC 鲁棒性分析—6.23)快速自适应与稳定鲁棒性•所谓快速和慢速自适应是指参数自适应律的增益(Γ或γ)过大或过小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 概述1.1 自适应控制的研究对象自适应控制是研究具有“不确定性”的控制系统的特性分析和综合(控制器设计)。
1. 系统不确定性产生的原因 1)内部不确定性(1)被控对象的结构(阶次)和参数由于建模误差引起的不确定性。
(2)被控对象的结构(阶次)和参数或者动态特性是时变的或随工作作条件改变而变化。
2)外部不确定性被控对象的运行环境(外部干扰)是随机信号而且它们的统计特性不确切知道或者是时变的。
2. 系统“不确定性”的数学描述 1)状态方程设一个线性离散时间系统,其状态方程如下:(1)(,)()(,)()()x k A k x k B k u k k θθε+=++ (1.1-1)()(,)()()y k C k x k v k θ=+式中:()()r r ()m 1 m x k y k u k ⨯⨯⨯——状态向量 n 1——输出向量 1 (由传感器数量决定)——控制向量 (由执行机构决定){()}}{()}k u k ε——单位动态噪声称为随机序列,其统计特性未知——测量噪声(,)A k θ,(,)B k θ,(,)C k θ 分别为系统矩阵,输入矩阵,输出矩阵,其维数为,n n m n ⨯⨯⨯n ,v 。
k ——离散时间,k ~k T 。
其中T 为采样周期。
θ——S 维未知参数向量,可能A ,B ,C 中未知参数不同,为了简单起见,都设为S 维。
2)系统框图根据(1.1-1)式可以画出被控对象的结构框图。
1Z -(,)C k θ(,)B k θ(,)A k θ()u k ()k ε()x k ()y k ()v k (1)x k +图 1.1-1 被控对象的结构框图图中1z -是时间延迟因子,1()(1)x k z x k -=+,噪声{()k ε}和{v (k )}作用于对象的不同部位,对于线性系统,可以等效于作用在输出端的一个噪声。
其统计特性例如期望值、相关函数等由于不确定性而未知,或随时间变化。
1.2 自适应控制系统的结构分类1 克服被控对象不确定性的方法通常采用两种方法:①在线辨识参数;②设定参考模型。
1)在线辨识对象的参数,一般采用递推算法,不辨识对象的阶次(结构),修改控制器得参数,称为自矫正方法。
2)设定参考模型,它代表给定的性能指标,将实测的性能指标和给定的性能指标进行比较,得到广义误差,由他来修改控制器规律,称为参考模型方法。
2 按结构分类由上述克服不确定性的方法将自适应控制系统分为两大类:1)自校正调节(控制)系统(Self-Tuning Regulator-Controller ) 通常自适应系统的结构框图如图1.2-1所示。
由图看以看出:② 常规控制系统比较增加了参数辨识和控制器设计两个部分,称为自适应环节。
②它的结构呈现双环系统,内环为常规反馈系统构成参数可调整系统;外环为自适应环节,它调整控制器参数,以达到性能最优或次优。
控制器被控对象内环外环()y k ()u k ()v k ()e k -+()r y k 调节器参数计算参数辨识自适应环节()y k ()u k ()y k ˆ()xk ˆ()k θ图1.2-1 自校正控制系统框图上图为显式结构,当参数辨识环节直接辨识控制器参数时,两个方框合二为一,形成隐式结构。
③参数自适应环节估计器输入控制信号()u k 和对象输出()y k ,计算出对象的状态估计值ˆ()x k 和参数的估计值ˆ()k θ(θ个参数未知或时变)。
由估计值ˆ()x k 和ˆ()k θ来修改控制规律。
2)模型参考自适应控制系统)(MRAC )(Model Reference Adaptive Control System — MRACS)这类自适应控制系统结构框图如图1.2-2所示。
由图可以看出:① 它有一个参考模型(Reference Model )。
它是要求(期望)性能指标的代表,其输入为()r y k 输出()m y k 是期望输出的表示,也可以是某种性能指标。
控制器被控对象参考模型自适应机构内环外环()y k ()u k ()v k ()e k ()y k ()m y k -+()r y k图1.2-2 模型参考自适应控制系统结构框图② 它也可以看成是双环系统,内环是通常的反馈,外环调节控制器参数和结构,为自适应闭环。
它的输入为广义误差()e t ,可能是输出的偏差,也可能是某种性能指标的误差,称为广义误差。
③ 由广义误差和参考输入来按照某种规律来修改控制器的参数,称为自适应结构。
只要()()m y k y k =系统就达到了优化状态。
1.3 自适应控制的理论问题自适应控制系统是具有非线性、时变参数和随机干扰等特性,内部机理相当复杂的系统。
理论分析和研究落后于应用。
目前各种各样的结构和算法也逐步得到广泛的应用,但它的理论课题还未彻底解决。
主要集中在三性的研究。
①稳定性 Stability ②收敛性 Convergence ③ 鲁棒性 Robustness 。
1 稳定性:指系统的状态、输出和参数的有界性。
目前的稳定性理论,李雅普诺夫稳定性理论、波波夫稳定性理论(超稳定性理论)还不能完全处理已有的自适应控制系统稳定性分析。
2 收敛性指一个自适应算法在指定的初始条件下,能渐进达到预期的目标,而且在此渐进的过程中保持系统的所有变量有界。
3 鲁棒性在存在扰动和未建模部分条件下,系统保持其稳定性和优良性能指标的能力。
其它理论问题有:①自适应速度分析和计算理论;②自适应控制系统的优化和简化设计; ③非线性对象的自适应控制系统理论。
第二章 自校正控制系统(STC 系统)2.1 被控对象的数学描述(数学模型)(Mathematical Description for Controlled Plant ) 1 被控对象的输入输出关系(P8)被控对象为单输入、单输出线性系统,用下列线性差分方程描述。
将微分方程化为差分方程可参看《过程辨识》,p75~p78,方崇智,清华大学出版社。
111011()(1)()()(1)()n n y k a y k y k n b u k d bu k d u k d n '''''+-+-=-+--+--+a +b (2.1-1)式中: u(k),y(k) ——对象输入和输出; n 1 ——被控对象的阶次;k —— 采样时刻,k ~ k T 0(T 0——采样周期);d —— 系统总延迟时间,d ~ d T 0,d = L +1,L 为对象纯延迟时间,d ≥1,“1”是对象有惯性环节,离散化结果一定出现一个周期的延迟。
为了书写和运算的方便,引入时间平移因子1z -,1(1)()y k z y k --=,则(2.1-1)式可写成:1111()()()()d A z y k z B z u k ---= (2.1-2)式中:11111111111111010()11()n n in i i n n i ni i A z a z za z B zb b z b z b z ----=----='''=+++=+''''=++=∑∑a也可写成: 1111()()()()dB z y k zu k A z ---= (2.1-3)说明: ① 用1z -表示时间平移一个采样周期后,(2.1-1)式差分方程可以简化为以1z -为变量的代数多项式的代数方程;② 对于1z -多项式A 1 (1z -)和B 1(1z -)可以进行四则运算,解差分方程可以变为解代数方程。
③ 对象的脉冲传递函数为:11111()()()dB z H z zA z ----= 它和(2.1-3)式()()y k u k 的形式相同,但两者的含义是有差别的。
1()H z -中的Z 是Z 平面(Z 变换)上的一点,而(2.1-3)式中为时域变量。
2被控对象运行环境的描述(噪声数学模型)工业实际中被控对象运行时可能受到各种干扰,作用于对象的不同点,由于对象是线性系统,利用叠加原理,将作用于系统的全部干扰用一个作用于系统输出的等价噪声v (k )来等效。
通常{v (k )}是一个具有有理谱密度的平稳随机信号,它代表很大一类干扰噪声信号。
1)平稳随机序列(过程) Stationary Random Sequence 其统计特性具有时间平移不变特性的随机信号。
统计特性是分布函数和数字特征。
数字特征有两个:①数学期望;②相关函数(协方差函数)。
(1)数学期望(均值):描述变化的平稳性。
Expectation 。
{()}()v v E v k m k m ==或为0;E{}()v xf x dx +∞-∞⋅=⎰(概率空间的总体平均值)(2)相关函数:描述变化的相关性(前后相关程度)。
Relative Function 。
{()()}(,)()v v E v k v k R k R λλλ+== {()()}R R λλ=- 121212(,)(,,,)v R k x x f x x R dx dx λλ+∞+∞-∞-∞=⎰⎰若随机过程的数学期望为常数,相关函数与k 无关,称为平稳随机过程。
2)谱密度 (Spectrum )自相关函数的傅里叶(Fourier )变换称为平稳随机过程的功率频谱或谱密度。
()()j kv v k eR k ωω∞-=-∞Φ=⋅∑ (2.1-4)1()()2j k v v R k e d πωπωωπ--=Φ⎰ (2.1-5)当k =0,2(0){()}v R v k =,设()v k 为电压(或电流),则2()v k 为功率(即干扰强度)。
由(2.1-5)式得到:()(0)2v v R d ππωωπ-Φ=⎰平均功率(0)v R 是各种频率噪声的功率总和,()vd ππωω-Φ⎰的平均值(即除以2π),因此()v ωΦ表示频率为ω的干扰噪声信号的功率(强度)。
也就是说源噪声可以看成各种频率噪声的混合。
不同噪声其包含的各种频率信号的大小不同。
例如:有的噪声以高频为主,可以用电容来消除。
3)白噪声(White Noise )若一随机信号的期望值为0,相关函数为脉冲函数20{()()}{E k εσελελ≠⋅+= k=0 k 0 ,则称它为白噪声。
其谱密度为:2()()j k k R k e ωεεεωσ∞-=-∞Φ==∑(常数)。
表明它的各个分量的强度都是一样的,相当于白光的光谱在各个频率上有相同的强度。
不具有上述条件的噪声称为有色噪声。
4)随机扰动模型 (Stochastic disturbance model )由谱表示定理可知:对于所有具有有理谱密度的平稳随机过程,都可以用白噪声激励一个稳定的线性的动态系统来产生(或表示)。
